A Fully Coupled Hydro-Mechanical Approach for Multi-Fracture Propagation Simulations
Abstract
1. Introduction
2. Unified Extended Finite Element Method
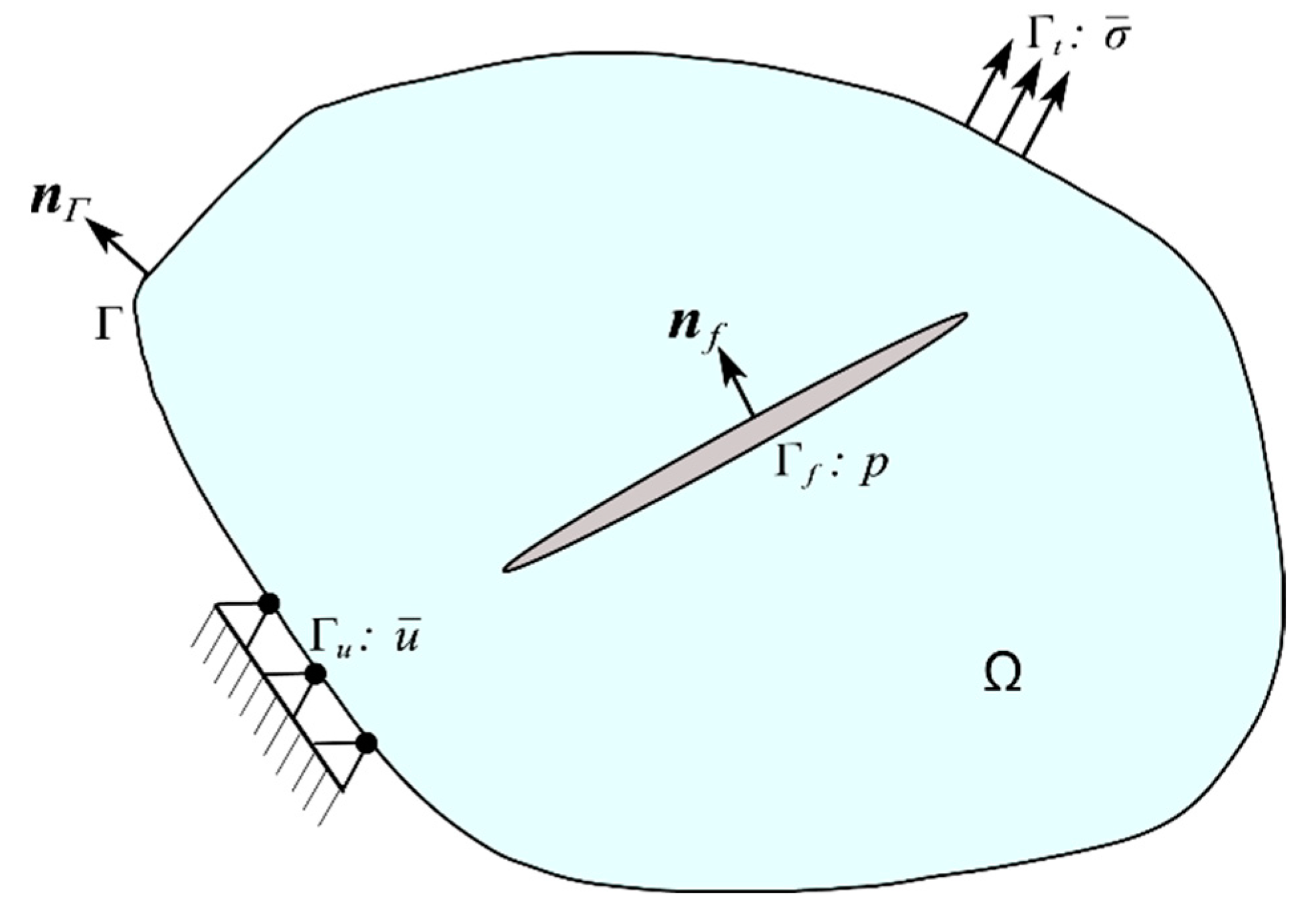
2.1. Fracture Description
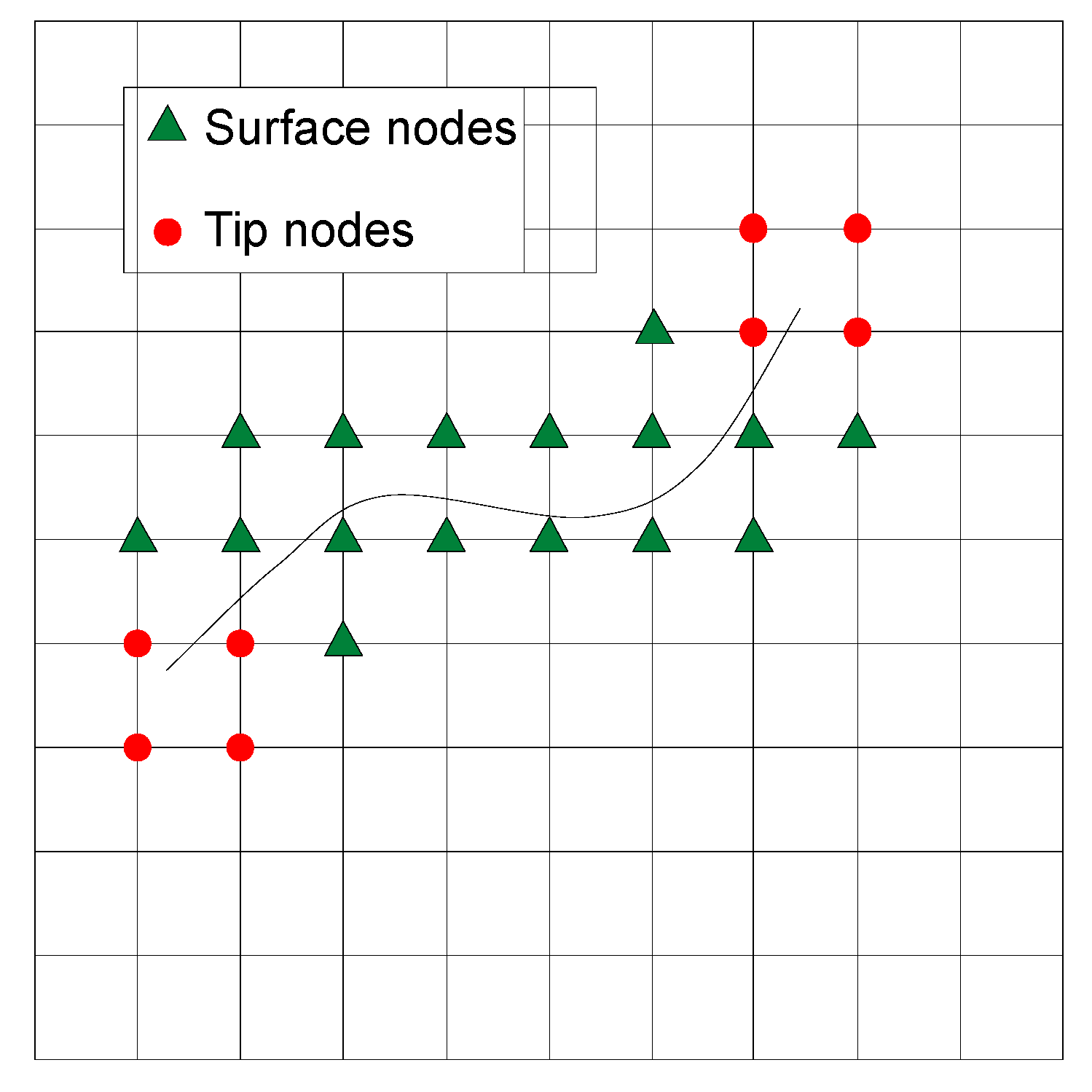
2.2. Solid Displacement Field Approximation and Enrichment Functions
2.3. Fluid Pressure Field Approximation and Enrichment Functions
2.4. XFEM Discretization
3. Fracture Propagation and Solution Strategy
3.1. Fracture Propagation Criterion
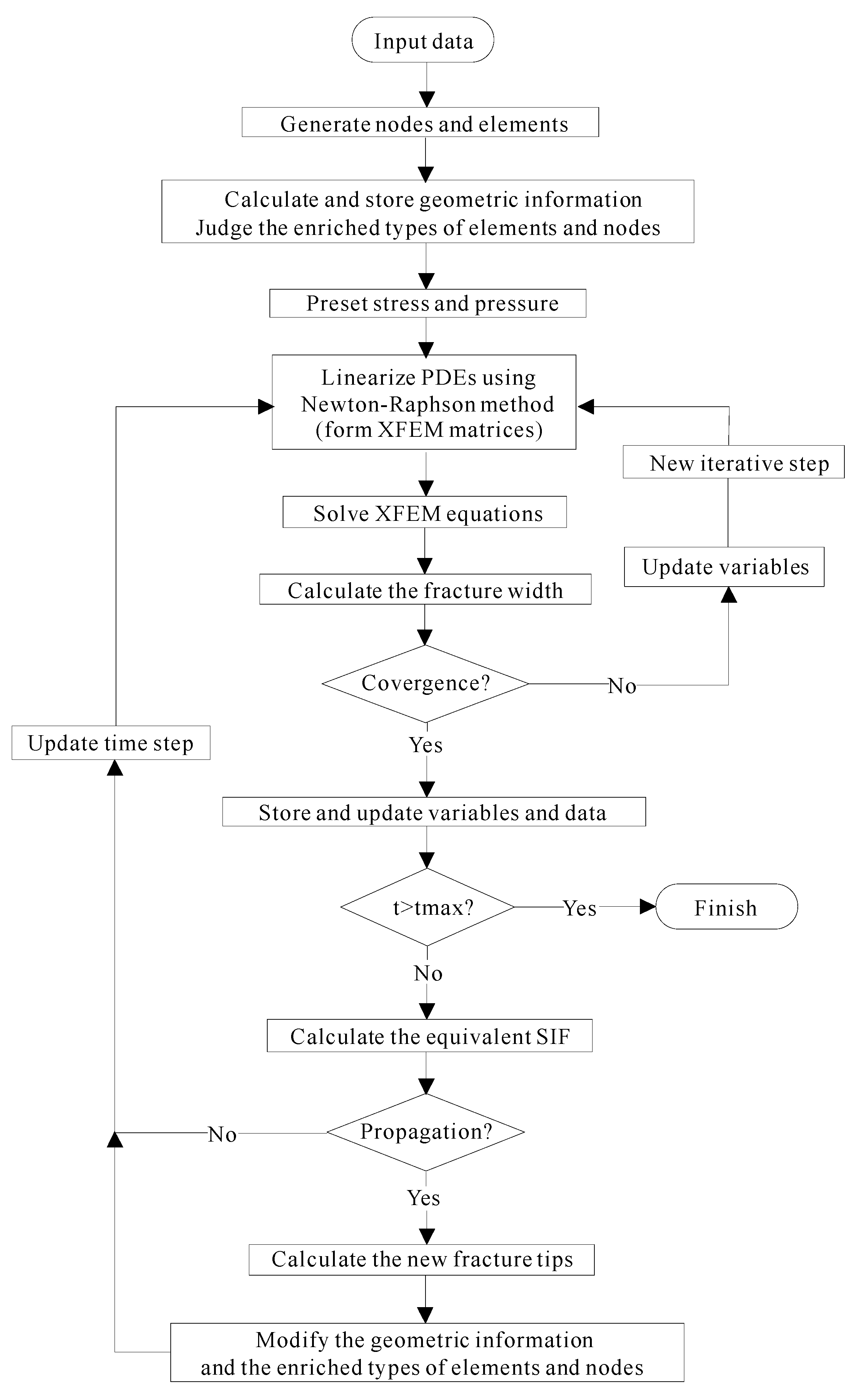
3.2. HMFM Fracturing Simulation Process
4. Results and Discussions
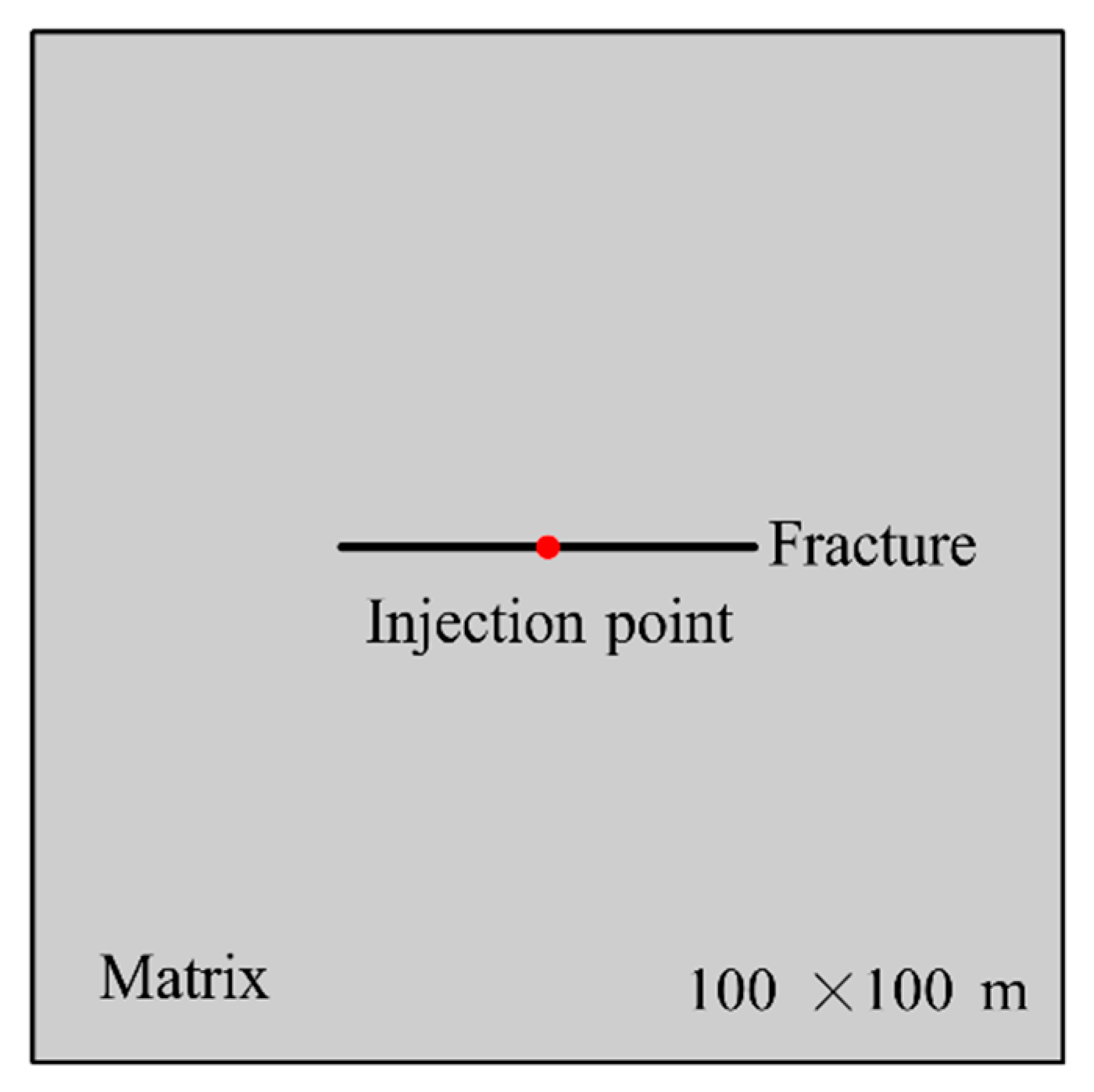
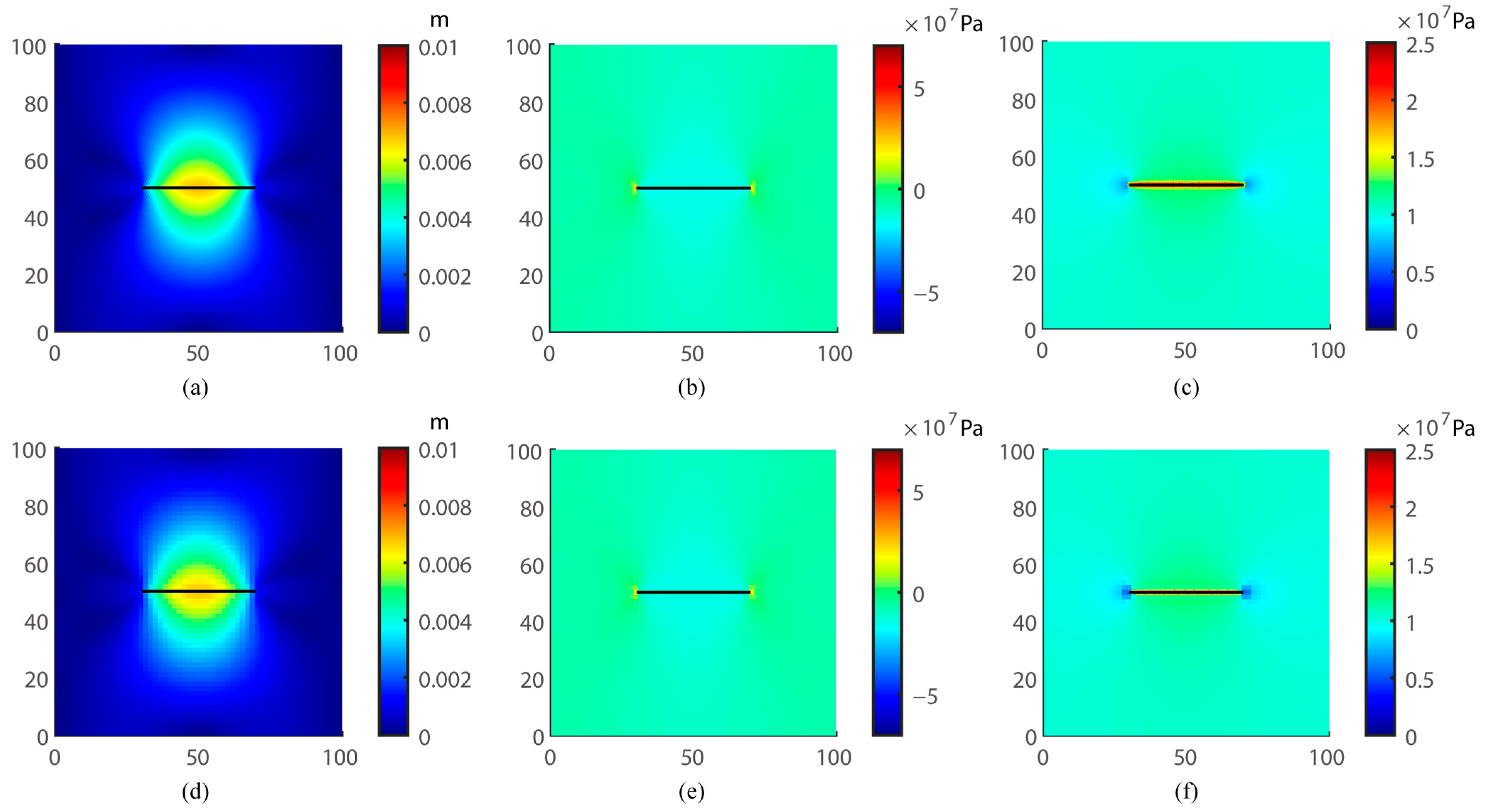
4.1. Validation 1: Comparison between UXFEM and KGD Model
4.2. Validation 2: Comparison of KI and KII in Numerical Simulation and Analytical Solution
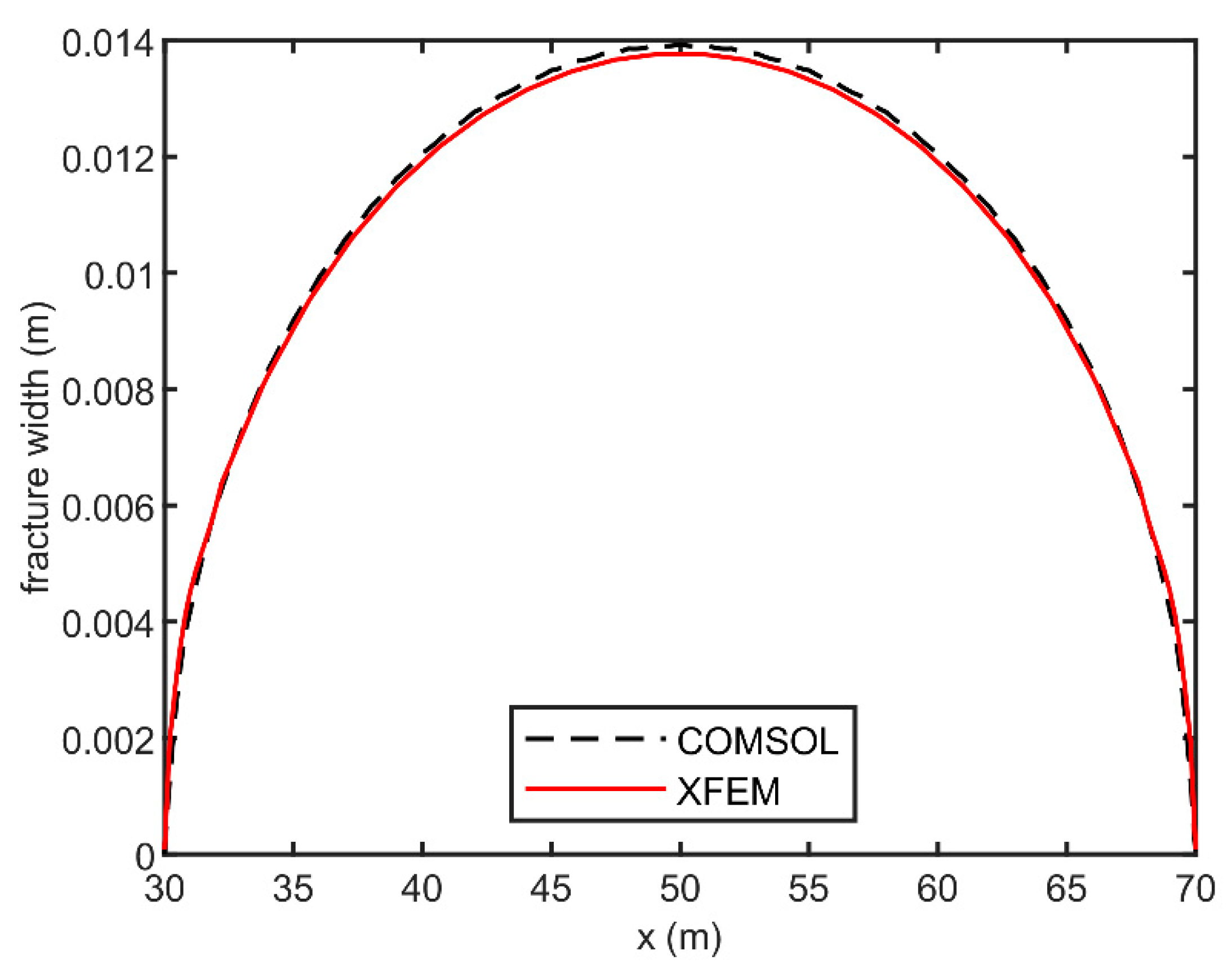
4.3. Validation 3: Comparison between UXFEM and COMSOL Multiphysics® 5.6
4.4. Case Study1: Propagation of Three Parallel Fractures
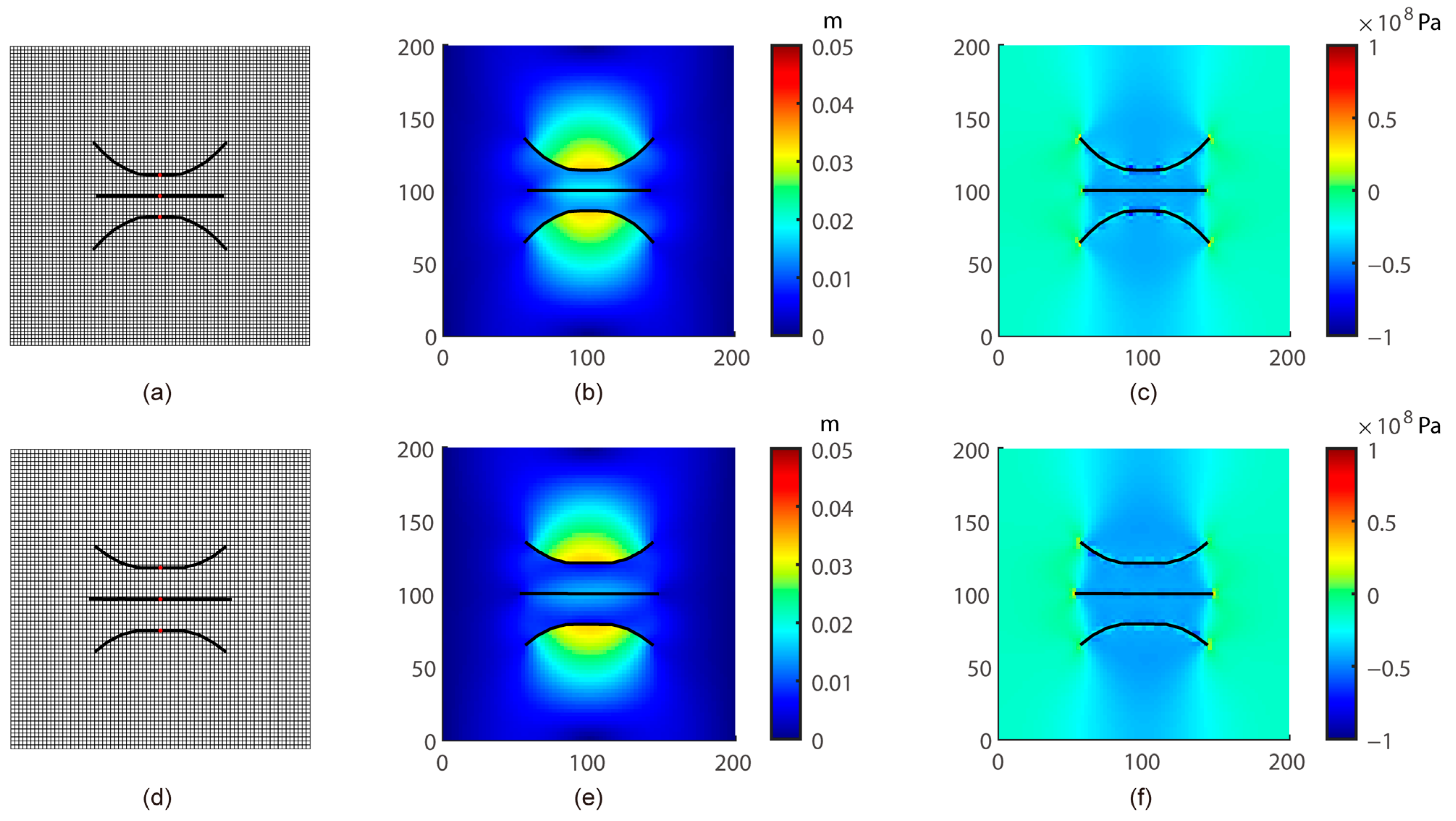
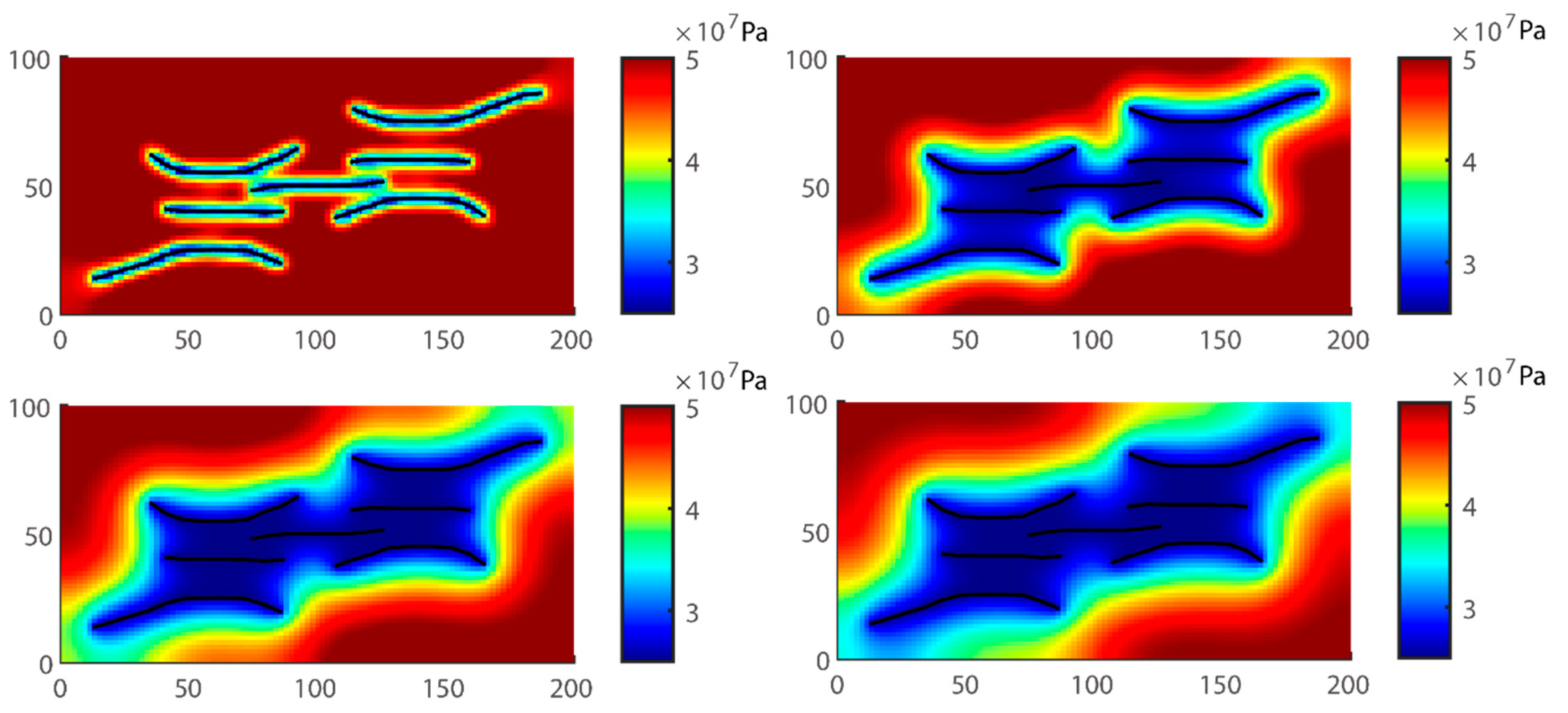
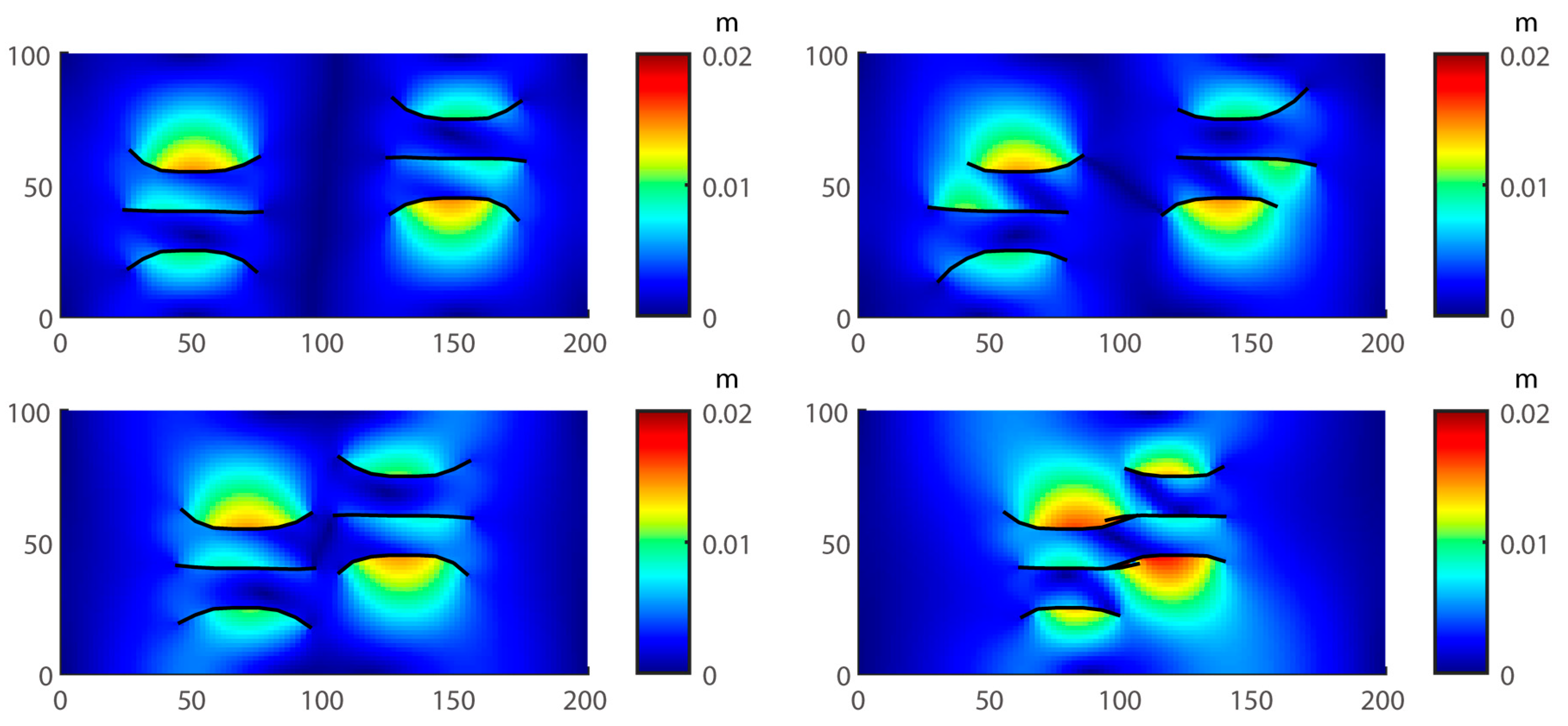
4.5. Case Study2: Propagation in Multiple En Échelon Fractures
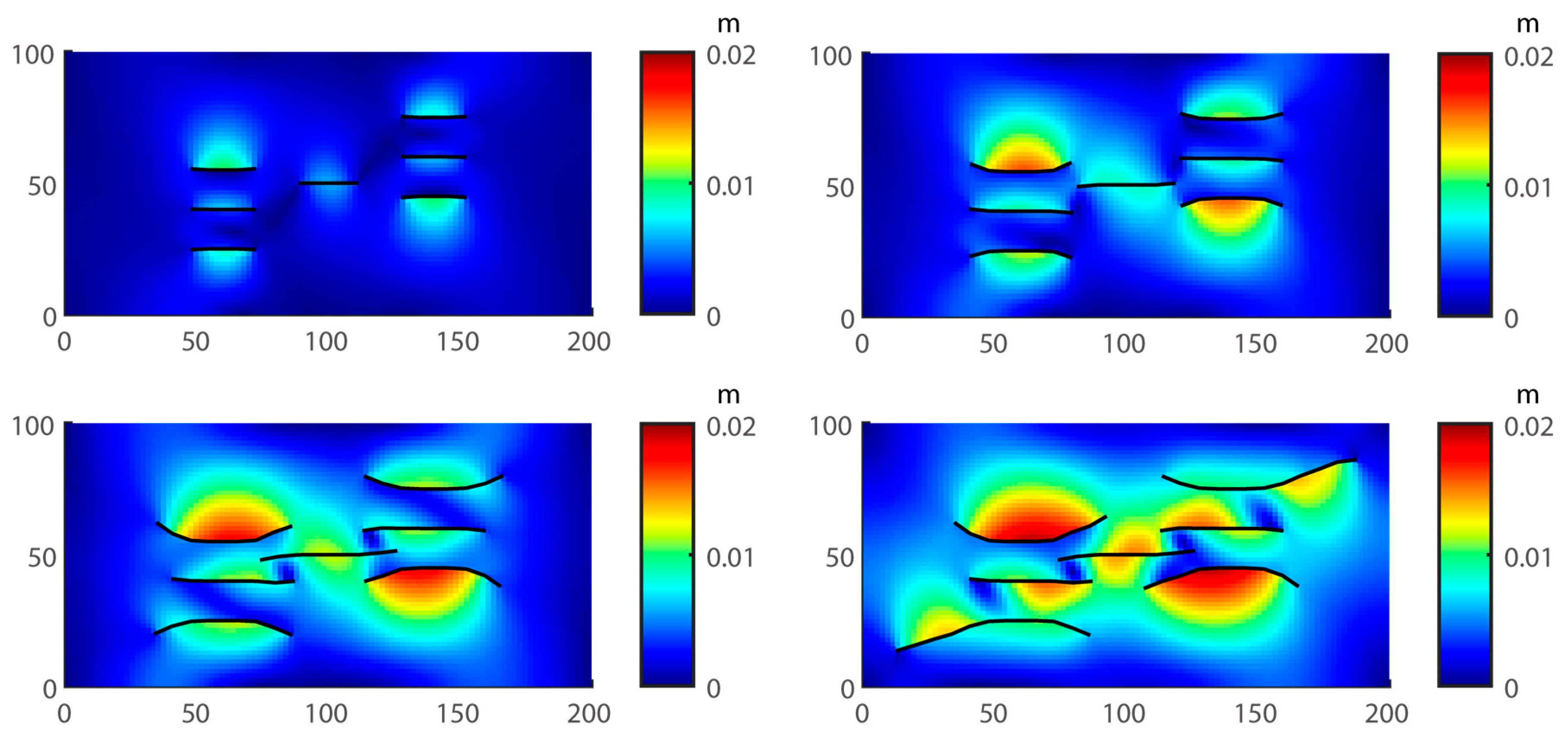
4.6. Case Study3: Multi-Well and Multi-Cluster Simultaneous Fracturing and Production
- (1)
- The fractures will undergo obvious diversion. For well #1, Frac. 1–3 have different degrees of deflection. The deflection of the two Frac. 1 and 3 are more prominent. In the early stage, the middle fracture Frac. 2 does not deflect obviously due to the interference of superimposed stress. In the later stage of fracturing, Frac. 2 and 4 attract each other, showing En échelon fracture morphology [69].
- (2)
- There are noticeable differences in fracture length and width. The length of Frac. 2 and 6 of the two horizontal wells is shorter, followed by Frac. 3 and 5, and the longest is Frac. 1 and 7. Frac. 4 cannot propagate far enough and even the front edge of the fracture tends to close. Although Frac. 1 and 7 have propagated long enough, one side of the fracture tends to close under the effect of stress shadow. These phenomena are very likely to lead to the reduction of fracturing efficiency and cost waste.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Liu, W.; Yao, J.; Chen, Z.; Liu, Y. Effect of quadratic pressure gradient term on a one-dimensional moving boundary problem based on modified Darcy’s law. Acta Mech. Sin. 2016, 32, 38–53. [Google Scholar] [CrossRef]
- Bunger, A.P.; Kear, J.; Jeffrey, R.G.; Prioul, R.; Chuprakov, D. Laboratory investigation of hydraulic fracture growth through weak discontinuities with active ultrasound monitoring. In Proceedings of the 13th ISRM International Congress of Rock Mechanics, Montreal, QC, Canada, 10–13 May 2015. [Google Scholar]
- Guo, J.; Luo, B.; Lu, C.; Lai, J.; Ren, J. Numerical investigation of hydraulic fracture propagation in a layered reservoir using the cohesive zone method. Eng. Fract. Mech. 2017, 186, 195–207. [Google Scholar] [CrossRef]
- Yang, D.; Zhou, Y.; Xia, X.; Gu, S.; Xiong, Q.; Chen, W. Extended finite element modeling nonlinear hydro-mechanical process in saturated porous media containing crossing fractures. Comput. Geotech. 2019, 111, 209–221. [Google Scholar] [CrossRef]
- Olson, J.E.; Wu, K. Sequential versus simultaneous multi-zone fracturing in horizontal wells: Insights from a non-planar, multi-frac numerical model. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 6–8 February 2012; OnePetro: Richardson, TX, USA, 2012. [Google Scholar]
- Zoback, M.D.; Rummel, F.; Jung, R.; Raleigh, C.B. Laboratory hydraulic fracturing experiments in intact and pre-fractured rock. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1977, 14, 49–58. [Google Scholar] [CrossRef]
- Bunger, A.P.; Gordeliy, E.; Detournay, E. Comparison between laboratory experiments and coupled simulations of saucer-shaped hydraulic fractures in homogeneous brittle-elastic solids. J. Mech. Phys. Solids 2013, 61, 1636–1654. [Google Scholar] [CrossRef]
- Guo, T.; Zhang, S.; Qu, Z.; Zhou, T.; Xiao, Y.; Gao, J. Experimental study of hydraulic fracturing for shale by stimulated reservoir volume. Fuel 2014, 128, 373–380. [Google Scholar] [CrossRef]
- Hou, B.; Chang, Z.; Fu, W.; Muhadasi, Y.; Chen, M. Fracture initiation and propagation in a deep shale gas reservoir subject to an alternating-fluid-injection hydraulic-fracturing treatment. SPE J. 2019, 24, 1839–1855. [Google Scholar] [CrossRef]
- Yang, H.; Guo, Y.; Wang, L.; Bi, Z.; Guo, W.; Zhao, G.; Yang, C. Study on the Stimulation Effectiveness Evaluation of Large-Scale Hydraulic Fracturing Simulation Experiment based on Optical Scanning Technology. SPE J. 2022, 27, 2941–2959. [Google Scholar] [CrossRef]
- Advani, S.H.; Lee, J.K. Finite element model simulations associated with hydraulic fracturing. SPE J. 1982, 22, 209–218. [Google Scholar]
- Devloo, P.R.; Fernandes, P.D.; Gomes, S.M.; Bravo, C.M.A.A.; Damas, R.G. A finite element model for three dimensional hydraulic fracturing. Math. Comput. Simul. 2006, 73, 142–155. [Google Scholar] [CrossRef]
- Wangen, M. Finite element modeling of hydraulic fracturing in 3D. Comput. Geosci. 2013, 17, 647–659. [Google Scholar] [CrossRef]
- Bao, J.Q.; Fathi, E.; Ameri, S. A coupled finite element method for the numerical simulation of hydraulic fracturing with a condensation technique. Eng. Fract. Mech. 2014, 131, 269–281. [Google Scholar] [CrossRef]
- Chen, Z.; Jeffrey, R.G.; Zhang, X.; Kear, J. Finite-element simulation of a hydraulic fracture interacting with a natural fracture. SPE J. 2017, 22, 219–234. [Google Scholar] [CrossRef]
- Pakzad, R.; Wang, S.; Sloan, S.W. 3D finite element modelling of fracturing in heterogeneous rock: From pure solid to coupled fluid/solid analysis. In Proceedings of the ISRM European Rock Mechanics Symposium-EUROCK, St. Petersburg, Russia, 22–26 May 2018; Society of Petroleum Engineers: Richardson, TX, USA, 2018. [Google Scholar]
- Pezzulli, E.; Nejati, M.; Salimzadeh, S.; Matthai, S.K.; Driesner, T. Finite element simulations of hydraulic fracturing: A comparison of algorithms for extracting the propagation velocity of the fracture. Eng. Fract. Mech. 2022, 274, 108783. [Google Scholar] [CrossRef]
- Ji, L.; Settari, A.; Sullivan, R.B. A novel hydraulic fracturing model fully coupled with geomechanics and reservoir simulation. SPE J. 2009, 14, 423–430. [Google Scholar] [CrossRef]
- Kim, J.; Moridis, G.J. Numerical analysis of fracture propagation during hydraulic fracturing operations in shale gas systems. Int. J. Rock Mech. Min. 2015, 76, 127–137. [Google Scholar] [CrossRef]
- Duarte, C.A.; Reno, L.G.; Simone, A. A high-order generalized FEM for through-the-thickness branched cracks. Int. J. Numer. Methods Eng. 2007, 72, 325–351. [Google Scholar] [CrossRef]
- Gupta, V.; Kim, D.J.; Duarte, C.A. Analysis and improvements of global–local enrichments for the generalized finite element method. Comput. Methods Appl. Mech. Eng. 2012, 245, 47–62. [Google Scholar] [CrossRef]
- Belytschko, T.; Black, T. Elastic crack growth in finite elements with minimal remeshing. Int. J. Numer. Meth. Eng. 1999, 45, 601–620. [Google Scholar] [CrossRef]
- Belytschko, T.; Moës, N.; Usui, S.; Parimi, C. Arbitrary discontinuities in finite elements. Int. J. Numer. Meth. Eng. 2001, 50, 993–1013. [Google Scholar] [CrossRef]
- Moës, N.; Dolbow, J.; Belytschko, T. A finite element method for crack growth without remeshing. Int. J. Numer. Meth. Eng. 1999, 46, 131–150. [Google Scholar] [CrossRef]
- Mohammadnejad, T.; Andrade, J.E. Numerical modeling of hydraulic fracture propagation, closure and reopening using XFEM with application to in-situ stress estimation. Int. J. Numer. Anal. Met. 2016, 40, 2033–2060. [Google Scholar] [CrossRef]
- Xia, Y.; Jin, Y.; Chen, M.; Chen, K.P. An enriched approach for modeling multi-scale discrete-fracture/matrix interaction for unconventional-reservoir simulations. SPE J. 2019, 24, 349–374. [Google Scholar] [CrossRef]
- Zheng, H.; Pu, C.; Xu, E.; Sun, C. Numerical investigation on the effect of well interference on hydraulic fracture propagation in shale formation. Eng. Fract. Mech. 2020, 228, 106932. [Google Scholar] [CrossRef]
- Olson, J.E. Predicting Fracture Swarms—The Influence of Subcritical Crack Growth and the Crack-Tip Process Zone on Joint Spacing in Rock; Geological Society, Special Publications: London, UK, 2004; Volume 231, pp. 73–88. [Google Scholar]
- Weng, X.; Kresse, O.; Cohen, C.; Kresse, O.; Cohen, C.-E.; Wu, R.; Gu, H. Modeling of hydraulic-fracture-network propagation in a naturally fractured formation. SPE Prod. Oper. 2011, 26, 368–380. [Google Scholar]
- Castonguay, S.T.; Mear, M.E.; Dean, R.H.; Schmidt, J.H. Predictions of the growth of multiple interacting hydraulic fractures in three dimensions. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 30 September–2 October 2013; Society of Petroleum Engineers: Richardson, TX, USA, 2013. [Google Scholar]
- Hou, B.; Chen, M.; Cheng, W.; Diao, C. Investigation of hydraulic fracture networks in shale gas reservoirs with random fractures. Arab. J. Sci. Eng. 2016, 41, 2681–2691. [Google Scholar] [CrossRef]
- Tang, H.; Winterfeld, P.H.; Wu, Y.S.; Huang, Z.Q.; Di, Y.; Pan, Z.; Zhang, J. Integrated simulation of multi-stage hydraulic fracturing in unconventional reservoirs. J. Nat. Gas. Sci. Eng. 2016, 36, 875–892. [Google Scholar] [CrossRef]
- Kumar, D.; Ghassemi, A. Three-dimensional poroelastic modeling of multiple hydraulic fracture propagation from horizontal wells. Int. J. Rock Mech. Min. 2018, 105, 192–209. [Google Scholar] [CrossRef]
- Shen, B.; Shi, J. A numerical scheme of coupling of fluid flow with three-dimensional fracture propagation. Eng. Anal. Bound. Elem. 2019, 106, 243–251. [Google Scholar] [CrossRef]
- Salimzadeh, S.; Paluszny, A.; Zimmerman, R.W. Three-dimensional poroelastic effects during hydraulic fracturing in permeable rocks. Int. J. Solids Struct. 2017, 108, 153–163. [Google Scholar] [CrossRef]
- Li, S.; Firoozabadi, A.; Zhang, D. Hydromechanical modeling of non-planar three-dimensional fracture propagation using an iteratively coupled approach. J. Geophys. Res. Solid Earth. 2020, 125, e2020JB020115. [Google Scholar] [CrossRef]
- Cundall, P.A. A computer model for simulating progressive, large-scale movement in blocky rock system. In Proceedings of the International Symposium on Rock Mechanics, Nancy, France, 4–6 October 1971. [Google Scholar]
- Li, S.; Feng, X.T.; Zhang, D.; Tang, H. Coupled thermo-hydro-mechanical analysis of stimulation and production for fractured geothermal reservoirs. Appl. Energy 2019, 247, 40–59. [Google Scholar] [CrossRef]
- Li, S.; Zhang, D.; Li, X. A new approach to the modeling of hydraulic-fracturing treatments in naturally fractured reservoirs. SPE J. 2017, 22, 1064–1081. [Google Scholar] [CrossRef]
- Li, S.; Li, X.; Zhang, D. A fully coupled thermo-hydro-mechanical, three-dimensional model for hydraulic stimulation treatments. J. Nat. Gas. Sci. Eng. 2016, 34, 64–84. [Google Scholar] [CrossRef]
- Settgast, R.R.; Fu, P.; Walsh, S.D.; White, J.A.; Annavarapu, C.; Ryerson, F.J. A fully coupled method for massively parallel simulation of hydraulically driven fractures in 3-dimensions. Int. J. Numer. Anal. Met. 2017, 41, 627–653. [Google Scholar] [CrossRef]
- Guo, X.; Wu, K.; An, C.; Tang, J.; Killough, J. Numerical Investigation of Effects of Subsequent Parent-Well Injection on Interwell Fracturing Interference Using Reservoir-Geomechanics-Fracturing Modeling. SPE J. 2019, 24, 1884–1902. [Google Scholar] [CrossRef]
- Zeng, Q.; Liu, W.; Yao, J. Hydro-mechanical modeling of hydraulic fracture propagation based on embedded discrete fracture model and extended finite element method. J. Petrol. Sci. Eng. 2018, 167, 64–77. [Google Scholar] [CrossRef]
- Wang, C.; Huang, Z.; Wu, Y.S. Coupled numerical approach combining X-FEM and the embedded discrete fracture method for the fluid-driven fracture propagation process in porous media. Int. J. Rock. Mech. Min. 2020, 130, 104315. [Google Scholar] [CrossRef]
- Ren, G.; Younis, R.M. An integrated numerical model for coupled poro-hydro-mechanics and fracture propagation using embedded meshes. Comput. Methods Appl. Mech. Eng. 2021, 376, 113606. [Google Scholar] [CrossRef]
- Liu, W.; Yao, J.; Zeng, Q. A numerical hybrid model for non-planar hydraulic fracture propagation in ductile formations. J. Petrol. Sci. Eng. 2021, 196, 107796. [Google Scholar] [CrossRef]
- Zhang, J.; Yu, H.; Xu, W.; Lv, C.; Micheal, M.; Shi, F.; Wu, H. A hybrid numerical approach for hydraulic fracturing in a naturally fractured formation combining the XFEM and phase-field model. Eng. Fract. Mech. 2022, 271, 108621. [Google Scholar] [CrossRef]
- Ouchi, H.; Katiyar, A.; Foster, J.T.; Sharma, M.M. A peridynamics model for the propagation of hydraulic fractures in heterogeneous, naturally fractured reservoirs. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 3–5 February 2015; OnePetro: Richardson, TX, USA, 2015. [Google Scholar]
- Rabczuk, T.; Ren, H. A peridynamics formulation for quasi-static fracture and contact in rock. Eng. Geol. 2017, 225, 42–48. [Google Scholar] [CrossRef]
- Qin, M.; Yang, D.; Chen, W.; Xia, X. Hydraulic fracturing network modeling based on peridynamics. Eng. Fract. Mech. 2021, 247, 107676. [Google Scholar] [CrossRef]
- Diehl, P.; Lipton, R.; Wick, T.; Tyagi, M. A comparative review of peridynamics and phase-field models for engineering fracture mechanics. Comput. Mech. 2022, 69, 1259–1293. [Google Scholar] [CrossRef]
- Moinfar, A.; Sepehrnoori, K.; Johns, R.T.; Varavei, A. Coupled geomechanics and flow simulation for an embedded discrete fracture model. In Proceedings of the SPE Reservoir Simulation Symposium, The Woodlands, TX, USA, 18–20 February 2013; Society of Petroleum Engineers: Richardson, TX, USA, 2013. [Google Scholar]
- Zidane, A.; Firoozabadi, A. An efficient numerical model for multicomponent compressible flow in fractured porous media. Adv. Water Resour. 2014, 74, 127–147. [Google Scholar] [CrossRef]
- Garipov, T.T.; Karimi-Fard, M.; Tchelepi, H.A. Discrete fracture model for coupled flow and geomechanics. Comput. Geosci. 2016, 20, 149–160. [Google Scholar] [CrossRef]
- McClure, M.W.; Babazadeh, M.; Shiozawa, S.; Huang, J. Fully Coupled Hydromechanical Simulation of Hydraulic Fracturing in 3D Discrete-Fracture Networks. SPE J. 2016, 21, 1302–1320. [Google Scholar] [CrossRef]
- Wei, S.; Kao, J.; Jin, Y.; Shi, C.; Xia, Y.; Liu, S. A discontinuous discrete fracture model for coupled flow and geomechanics based on FEM. J. Petrol. Sci. Eng. 2021, 204, 108677. [Google Scholar] [CrossRef]
- Dolbow, J.E. An Extended Finite Element Method with Discontinuous Enrichment for Applied Mechanics. Ph.D. Dissertation, Northwestern University, Evanston, IL, USA, December 1999. [Google Scholar]
- Gordeliy, E.; Peirce, A. Enrichment strategies and convergence properties of the XFEM for hydraulic fracture problems. Comput. Methods Appl. Mech. Eng. 2015, 283, 474–502. [Google Scholar] [CrossRef]
- Moës, N.; Cloirec, M.; Cartraud, P.; Remacle, J.F. A computational approach to handle complex microstructure geometries. Comput. Methods Appl. Mech. Eng. 2003, 192, 3163–3177. [Google Scholar] [CrossRef]
- Chen, K.P.; Jin, Y.; Chen, M. Pressure-gradient singularity and production enhancement for hydraulically fractured wells. Geophys. J. Int. 2013, 195, 923–931. [Google Scholar] [CrossRef]
- Xia, Y.; Jin, Y.; Huang, Z.; Lu, Y.; Wang, H. An Extended Finite Element Method for Hydro-Mechanically Coupled Analysis of Mud Loss in Naturally Fractured Formations. In Proceedings of the 53rd US Rock Mechanics/Geomechanics Symposium, New York, NY, USA, 23–26 June 2019; Society of Petroleum Engineers: Richardson, TX, USA, 2019. [Google Scholar]
- Xia, Y.; Jin, Y.; Oswald, J.; Chen, M.; Chen, K. Extended finite element modeling of production from a reservoir embedded with an arbitrary fracture network. Int. J. Numer. Methods Fluids 2018, 86, 329–345. [Google Scholar] [CrossRef]
- Liu, P.; Liu, F.; She, C.; Zhao, L.; Luo, Z.; Guan, W.; Li, N. Multi-phase fracturing fluid leakoff model for fractured reservoir using extended finite element method. J. Nat. Gas. Sci. Eng. 2016, 28, 548–557. [Google Scholar] [CrossRef]
- Coussy, O. Poromechanics; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Schöllmann, M.; Richard, H.A.; Kullmer, G.; Fulland, M. A new criterion for the prediction of crack development in multiaxially loaded structures. Int. J. Fract. 2002, 117, 129–141. [Google Scholar] [CrossRef]
- Olson, J.E.; Taleghani, A.D. Modeling simultaneous growth of multiple hydraulic fractures and their interaction with natural fractures. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 19–21 January 2009; Society of Petroleum Engineers: Richardson, TX, USA, 2009. [Google Scholar]
- Detournay, E. Propagation regimes of fluid-driven fractures in impermeable rocks. Int. J. Geomech. 2004, 4, 35–45. [Google Scholar] [CrossRef]
- Rice, J.R. Mathematical analysis in the mechanics of fracture. Fract. Adv. Treatise 1968, 2, 191–311. [Google Scholar]
- Liu, X.; Rasouli, V.; Guo, T.; Qu, Z.; Sun, Y.; Damjanac, B. Numerical simulation of stress shadow in multiple cluster hydraulic fracturing in horizontal wells based on lattice modelling. Eng. Fract. Mech. 2020, 238, 107278. [Google Scholar] [CrossRef]
- Schultz, R. Discontinuity Patterns and Their Interpretation. In Geologic Fracture Mechanics; Cambridge University Press: Cambridge, UK, 2019; pp. 170–208. [Google Scholar]
- Miller, C.; Waters, G.; Rylander, E. Evaluation of production log data from horizontal wells drilled in organic shales. In Proceedings of the North American Unconventional Gas Conference and Exhibition, The Woodlands, TX, USA, 14–16 June 2011; Society of Petroleum Engineers: Richardson, TX, USA, 2011. [Google Scholar]
- Lecampion, B.; Desroches, J. Simultaneous initiation and growth of multiple radial hydraulic fractures from a horizontal wellbore. J. Mech. Phys. Solids 2015, 82, 235–258. [Google Scholar] [CrossRef]
- Lu, Y.; Wei, S.; Xia, Y.; Jin, Y. Modeling of geomechanics and fluid flow in fractured shale reservoirs with deformable multi-continuum matrix. J. Petrol. Sci. Eng. 2021, 196, 107576. [Google Scholar] [CrossRef]
- Hughes, T.J.R. The Finite Element Method: Linear Static and Dynamic Finite Element Analysis; Prentice-Hall: Englewood Cliffs, NJ, USA, 1987. [Google Scholar]
- Witherspoon, P.A.; Wang, J.S.; Iwai, K.; Gale, J.E. Validity of cubic law for fluid flow in a deformable rock fracture. Water Resour. Res. 1980, 16, 1016–1024. [Google Scholar] [CrossRef]






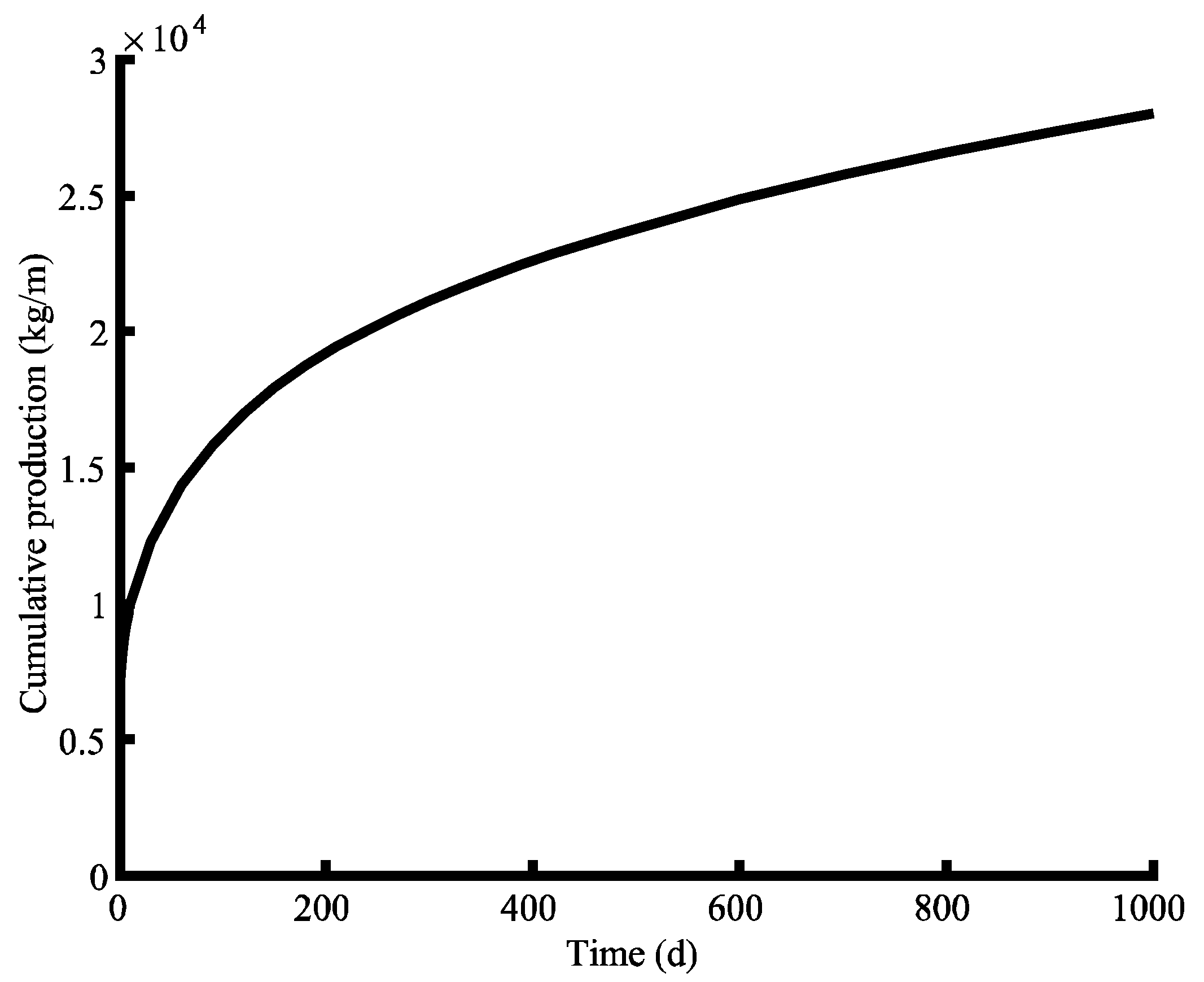


| Parameters | Value | Unit |
|---|---|---|
| Young modulus | 60 | GPa |
| Poisson ratio | 0.25 | / |
| Fracture toughness | 1.2 | MPa·m0.5 |
| Fluid viscosity | 50 | mPa·s |
| Injection rate | 0.01 | m2/s |
| Convergence tolerance | 0.01 | / |
| Parameters | Value | Unit |
|---|---|---|
| Young’s modulus | 60 | GPa |
| Poisson’s ratio | 0.25 | / |
| Maximum horizontal in-situ stress | 60 | MPa |
| Minimum horizontal in-situ stress | 55 | MPa |
| Hydrostatic pressure applied to the fracture surface | 65 | MPa |
| Half-length of the fracture | 5 | m |
| Parameters | Value | Unit |
|---|---|---|
| Initial reservoir pressure | 10 | MPa |
| Pressure at injection point | 25 | MPa |
| Maximum horizontal in-situ stress | 20 | MPa |
| Minimum horizontal in-situ stress | 15 | MPa |
| Young’s modulus | 40 | GPa |
| Poisson’s ratio | 0.2 | / |
| Matrix permeability | 1 × 10−18 | m2 |
| Initial matrix porosity | 0.15 | / |
| Bulk modulus of the solid | 50 | GPa |
| Bulk modulus of the fluid | 2.5 | GPa |
| Fluid density | 1000 | kg/m3 |
| Fluid viscosity | 10 | mPa·s |
| Biot coefficient | 0.85 | / |
| Parameters | Value | Unit |
|---|---|---|
| Initial reservoir pressure | 50 | MPa |
| Maximum horizontal in situ stress | 60 | MPa |
| Minimum horizontal in situ stress | 55 | MPa |
| Matrix permeability | 1 × 10−17 | m2 |
| Initial matrix porosity | 0.1 | / |
| Initial fracture length | 10 | m |
| Injection rate at injection points | 0.01 | m2/s |
| Bulk modulus of the fluid | 2.5 | GPa |
| Fluid density | 1000 | kg/m3 |
| Fluid viscosity | 50 | mPa·s |
| Fracture toughness | 5 | MPa·m0.5 |
| Biot coefficient | 0.85 | / |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, Y.; Wang, D.; Jin, Y.; Xia, Y. A Fully Coupled Hydro-Mechanical Approach for Multi-Fracture Propagation Simulations. Energies 2023, 16, 1601. https://doi.org/10.3390/en16041601
Deng Y, Wang D, Jin Y, Xia Y. A Fully Coupled Hydro-Mechanical Approach for Multi-Fracture Propagation Simulations. Energies. 2023; 16(4):1601. https://doi.org/10.3390/en16041601
Chicago/Turabian StyleDeng, Yinghao, Di Wang, Yan Jin, and Yang Xia. 2023. "A Fully Coupled Hydro-Mechanical Approach for Multi-Fracture Propagation Simulations" Energies 16, no. 4: 1601. https://doi.org/10.3390/en16041601
APA StyleDeng, Y., Wang, D., Jin, Y., & Xia, Y. (2023). A Fully Coupled Hydro-Mechanical Approach for Multi-Fracture Propagation Simulations. Energies, 16(4), 1601. https://doi.org/10.3390/en16041601







