Classification of Wear State for a Positive Displacement Pump Using Deep Machine Learning †
Abstract
1. Introduction
- ✓
- Diagnostic systems for hydraulics (components) based on the developed model of the diagnosed system
- ✓
- Diagnostic systems for hydraulic systems (components) based on signal analysis
- ✓
- Diagnostic systems for hydraulics (components) using the so-called intelligent fault identification
- -
- The application of the minimum redundancy maximum relevance (MRMR) algorithm in ranking the features determined from the measured signals;
- -
- Designing a neural classifier of the pump wear state based on the ranked features of the measured signals;
- -
- Preparing and carrying out a test experiment to naturally obtain the wear and tear of the pump components based on the lengthy operation of the pump at a lower oil grade;
- -
- The use of signals measured across the entire operating range of the pump (i.e., when in stationary and non-stationary operating conditions) to assess the wear state of the tested pump.
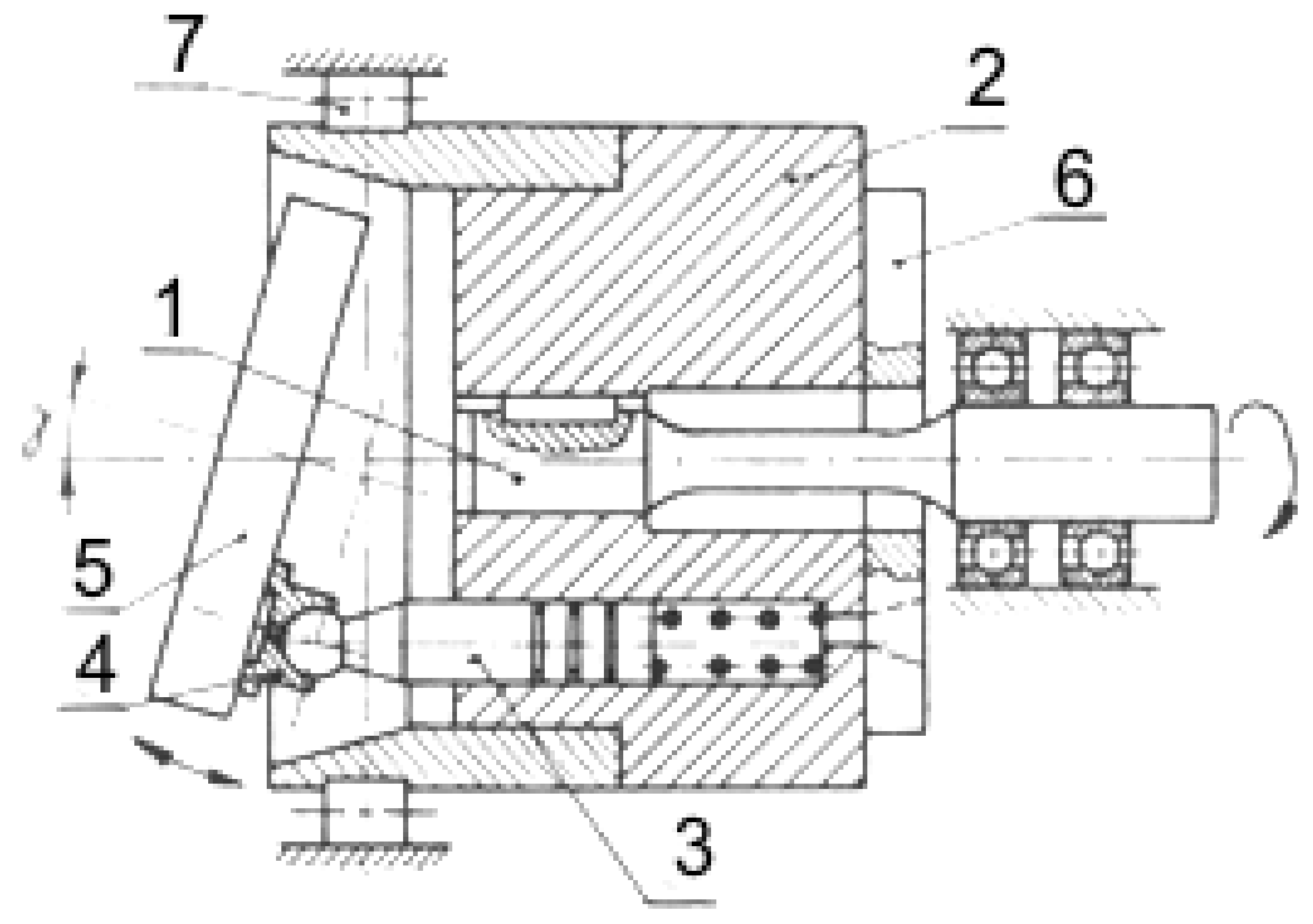
2. Object of the Study
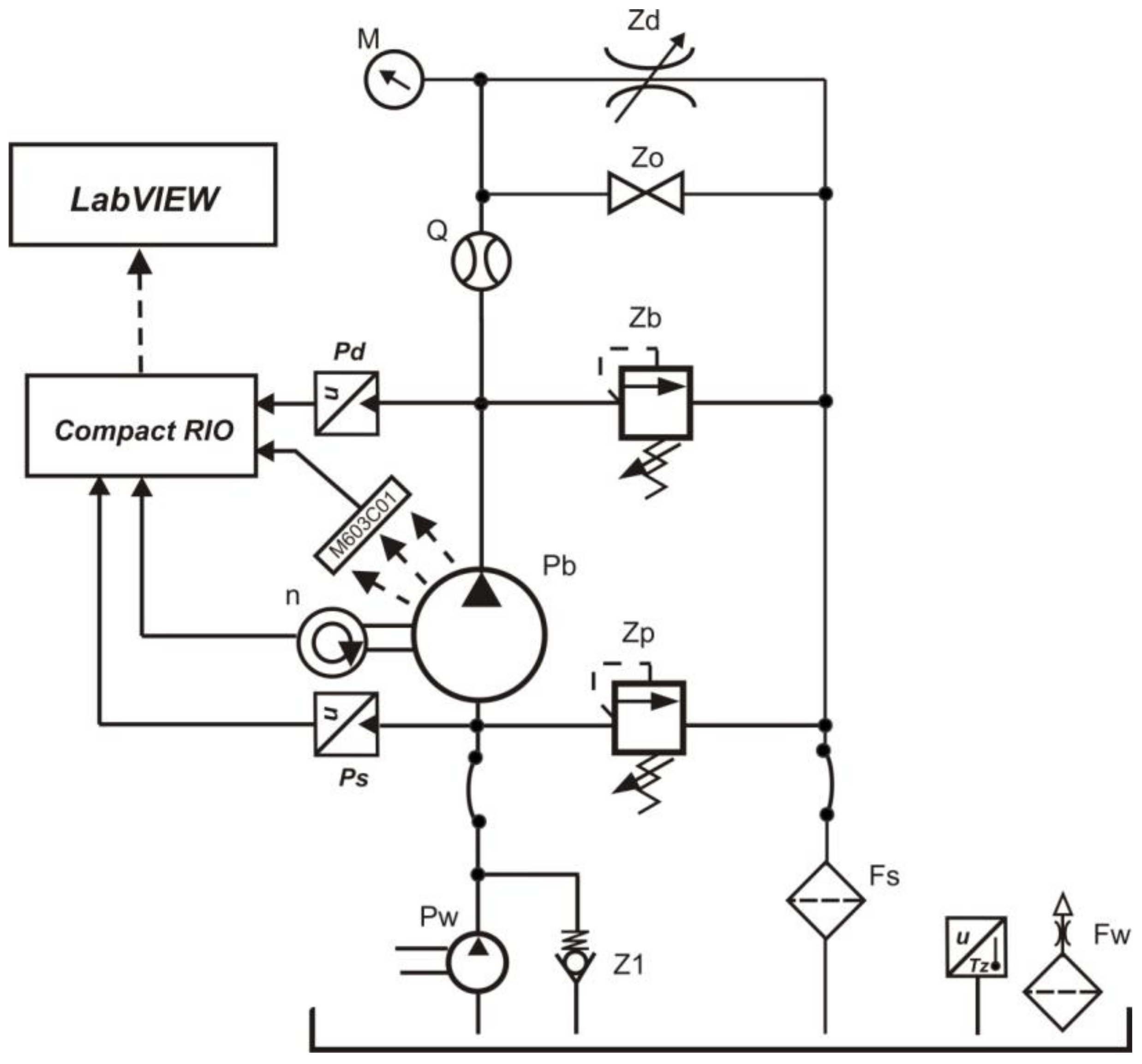
3. Course of the Study
- A static pressure transducer;
- A dynamic pressure transducer;
- A pump body vibration acceleration transducer.
- The selection and calculation of appropriate signal features;
- The ranking of the calculated features with regard to the information they contained;
- Designing the structure of a neural network in a classifier system;
- Evaluating the effectiveness of the designed network in the classification of the wear state of the studied pump.
Selection of Classification System Features
4. Significance Ranking of Signal Features
Application of the Minimum Redundancy Maximum Relevance (MRMR) Algorithm in Ranking Calculated Features of Measured Signals
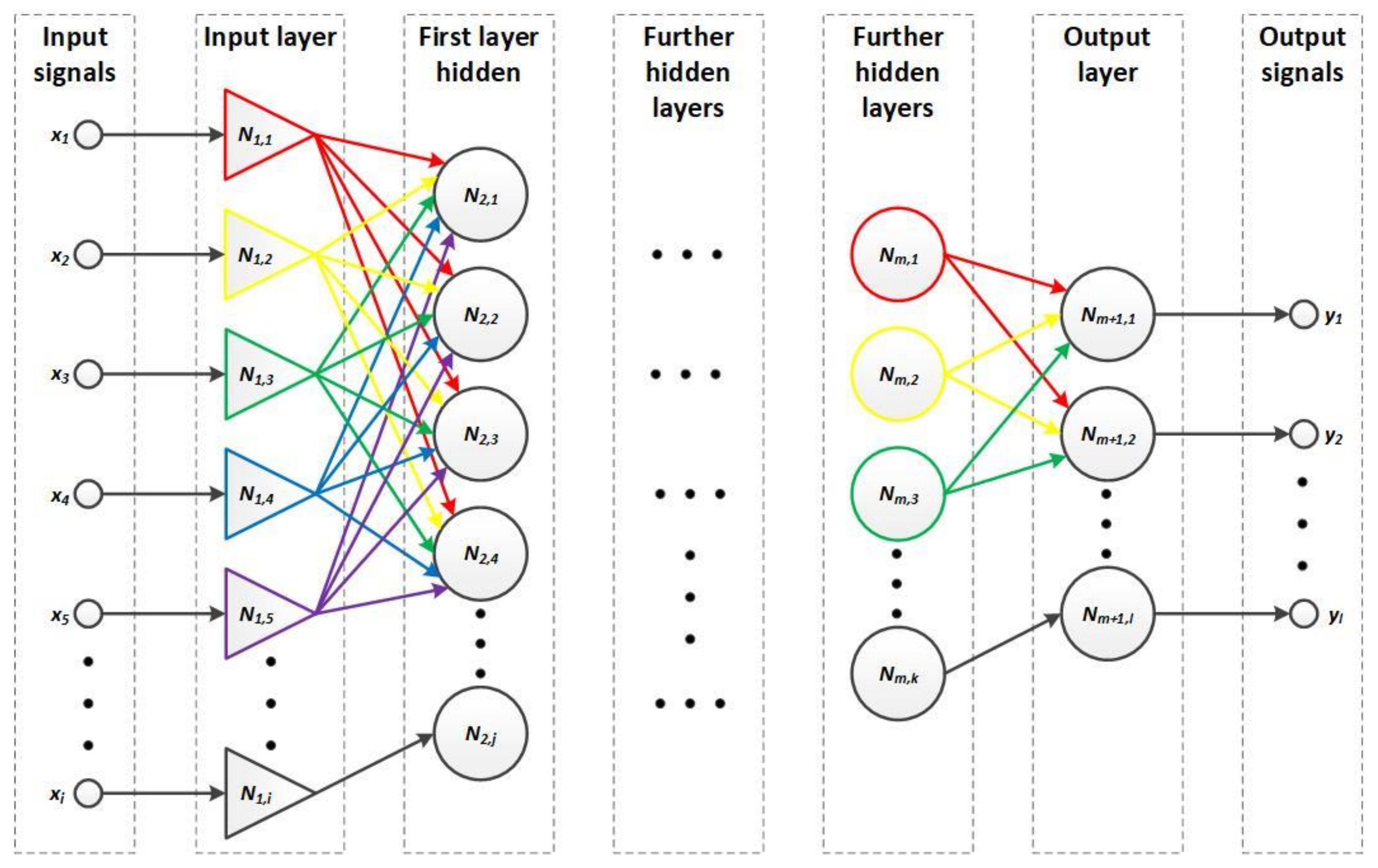
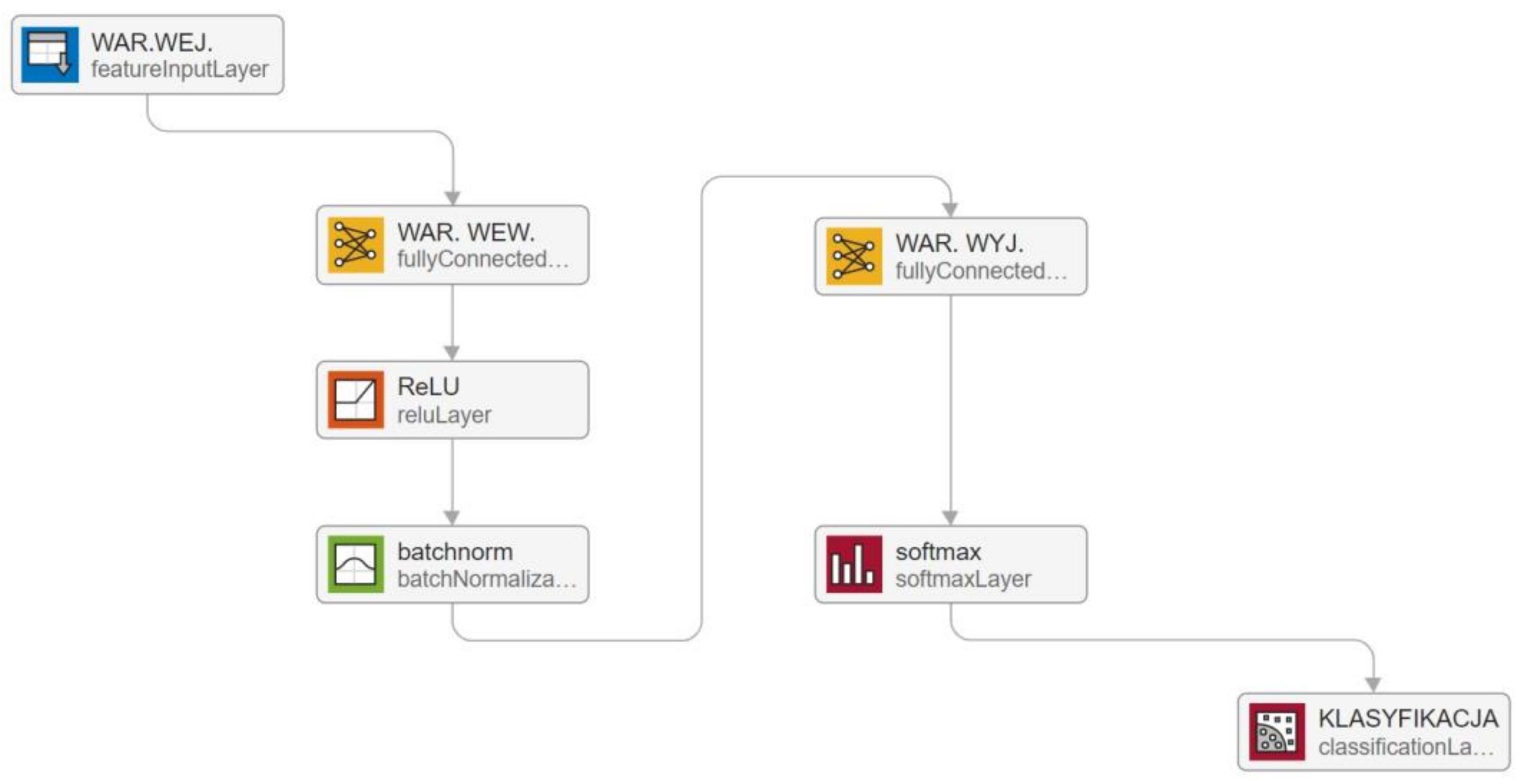
5. Structure of the Neural Network Used in the Classification System
- Pump in working order;
- Pump at its end of life;
- Worn-out pump.
- 5 neurons in the input layer;
- 3 neurons in the classification layer;
- 12 neurons in the hidden layer.
Network Training—Learning Parameters
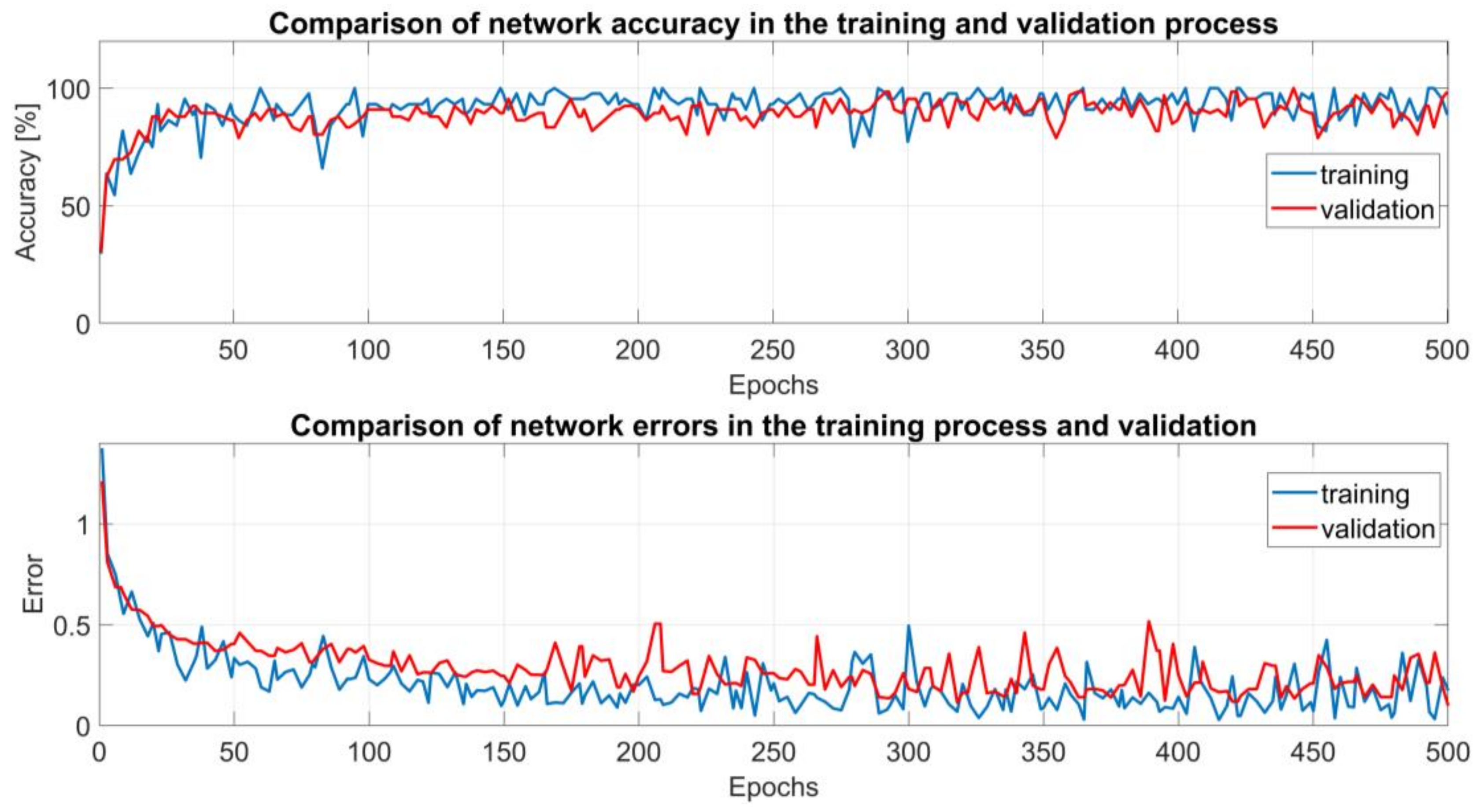
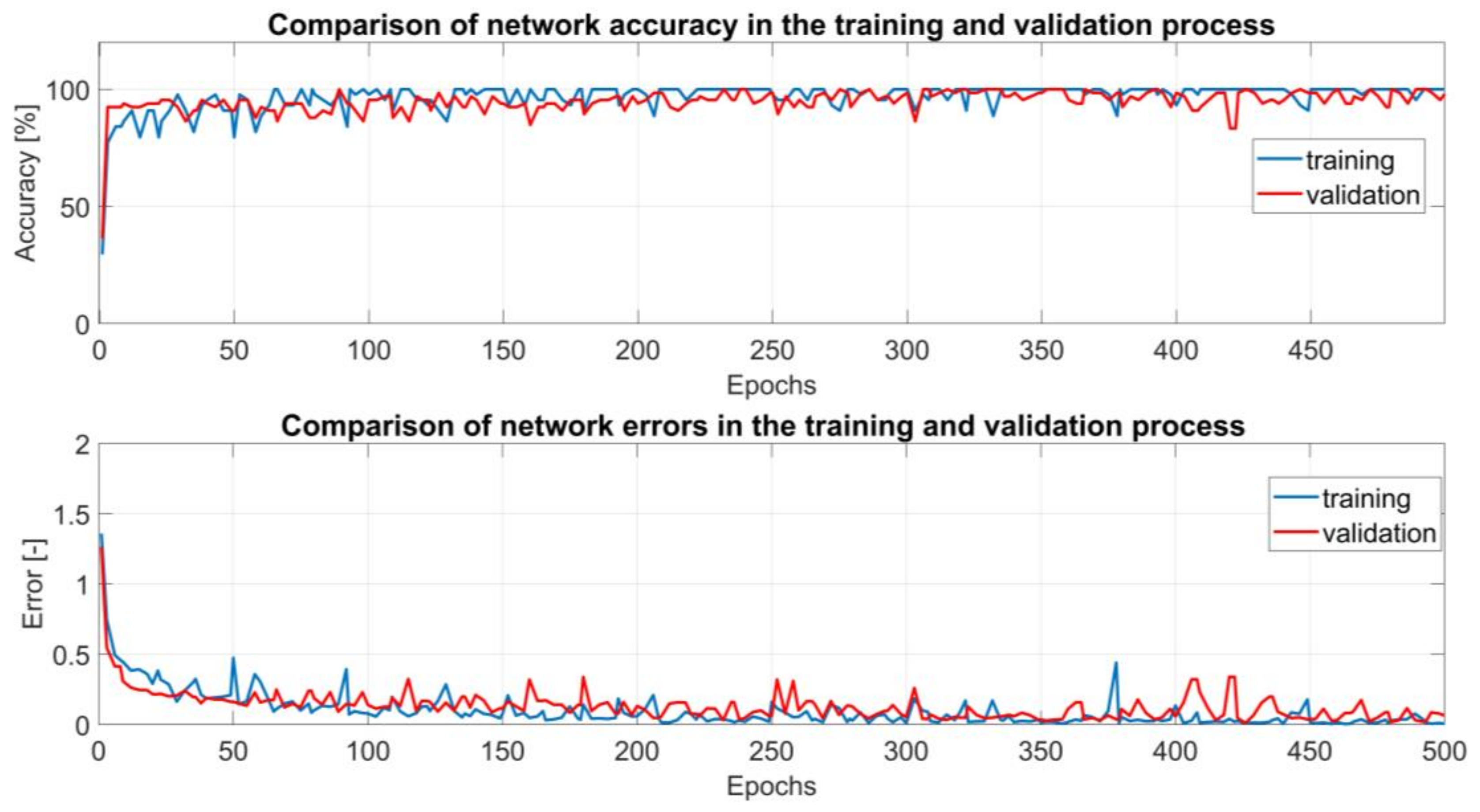
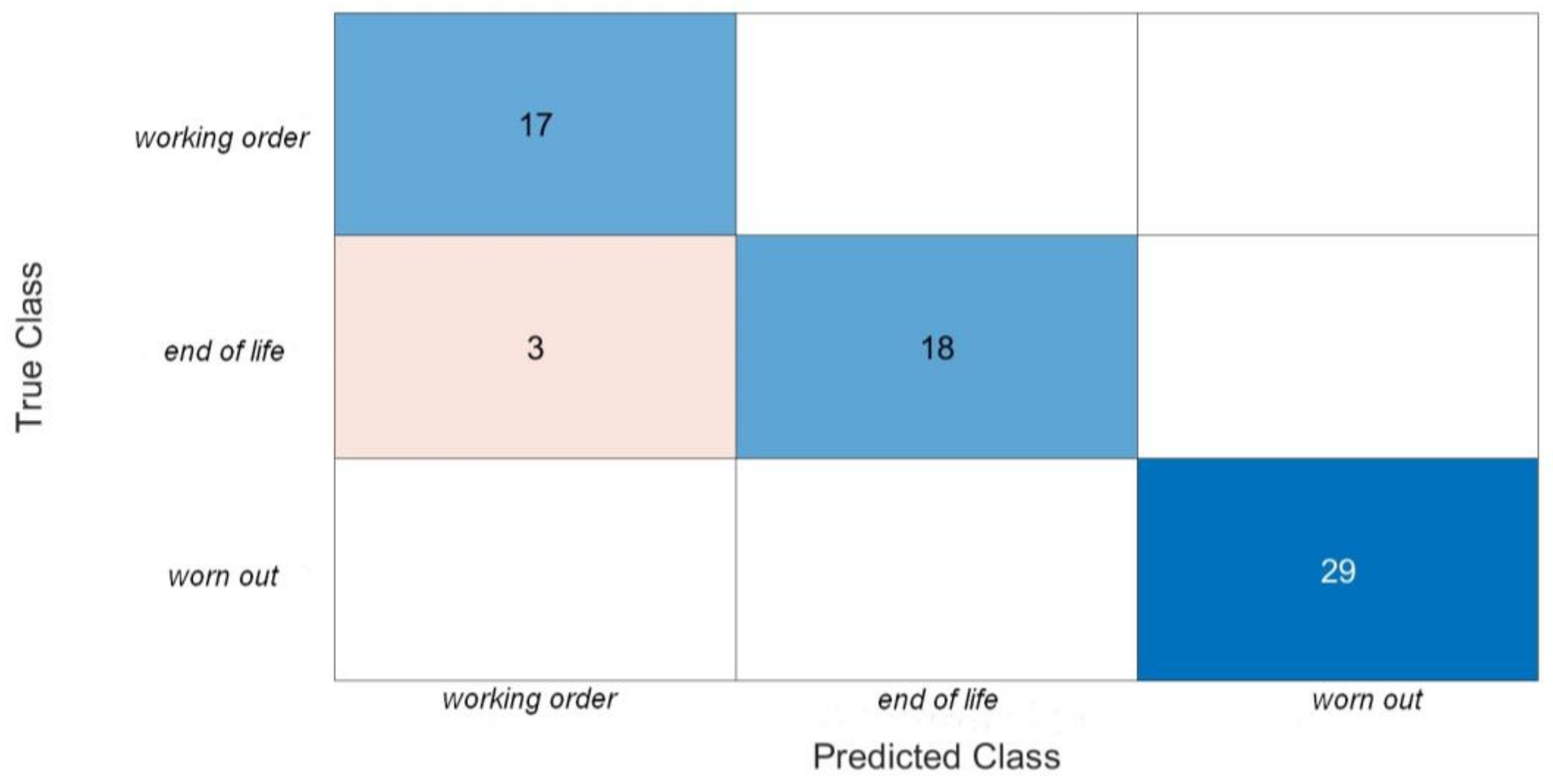
6. Analysis of Obtained Results and Final Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Merritt, H.E. Hydraulic Control Systems; John Wiley & Sons: New York, NY, USA, 1967. [Google Scholar]
- Manring, N.D.; Fales, R.C. Hydraulic Control Systems, 2nd ed.; John Wiley & Sons: New York, NY, USA, 2019. [Google Scholar]
- Manring, N. Fluid Power Pumps and Motors: Analysis, Design and Control; McGraw Hill Professional: New York, NY, USA, 2013. [Google Scholar]
- Watton, J. Modelling, Monitoring and Diagnostic Techniques for Fluid Power Systems; Springer: Berlin, Germany, 2007. [Google Scholar]
- Konieczny, J.; Stojek, J. Use of the K-Nearest Neighbour Classifier in Wear Condition Clssification of a Positive Displacement Pump. Sensors 2021, 21, 6247. [Google Scholar] [CrossRef]
- Bensaad, D.; Soualhi, A.; Guillet, F. A new leaky piston identification method in an axial piston pump based on the extended Kalman filter. Measurement 2019, 148, 106921. [Google Scholar] [CrossRef]
- Dabrowska, R.; Stetter, H.; Sasmito, H.; Kleinmann, S. Extended Kalman filter algorithm for advanced diagnosis of positive displacement pumps. In Proceedings of the 8th IFAC Symposium on Fault Detection, Supervision and Safety of Technical Processes (SAFEPROCESS), Mexico City, Mexico, 29–31 August 2012. [Google Scholar]
- Grewal, M.S.; Andrews, A.P. Kalman Filtering Theory and Practice Using MATLAB; John Wiley & Sons: New York, NY, USA, 2008. [Google Scholar]
- Asl, R.M.; Hagh, Y.S.; Simani, S.; Handroos, H. Adaptive square-root unscented Kalman filter: An experimental study of hydraulic actuator state estimation. Mech. Syst. Signal Process. 2019, 132, 670–691. [Google Scholar]
- Bahrami, M.; Naraghi, M.; Zareinejad, M. Adaptive super-twisting observer for fault reconstruction in electro-hydraulic systems. ISA Trans. 2018, 76, 235–245. [Google Scholar] [CrossRef] [PubMed]
- Stojek, J. Application of time-frequency analysis for diagnostics of valve plate wear in axial-piston pump. Arch. Mech. Eng. 2010, 57, 309–322. [Google Scholar] [CrossRef]
- Goharrizi, A.Y.; Sepehri, N.A. Wavelet-Based Approach for External Leakage Detection and Isolation from Internal Leakage in Valve-Controlled Hydraulic Actuators. IEEE Trans. Ind. Electron. 2011, 58, 4374–4384. [Google Scholar] [CrossRef]
- Goharrizi, A.Y.; Sepehri, N. Internal Leakage Detection in Hydraulic Actuators Using Empirical Mode Decomposition and Hilbert Spectrum. IEEE Trans. Instrum. Meas. 2012, 61, 368–378. [Google Scholar] [CrossRef]
- Jiang, W.; Zheng, Z.; Zhu, Y.; Li, Y. Demodulation for hydraulic pump fault signals based on local mean decomposition and improved adaptive multiscale morphology analysis. Mech. Syst. Signal Process. 2015, 58–59, 179–205. [Google Scholar] [CrossRef]
- Yang, J.; Xie, G.; Yang, Y.; Zhang, Y.; Liu, W. Deep model integrated with data correlation analysis for multiple intermittent faults diagnosis. ISA Trans. 2019, 95, 306–319. [Google Scholar] [CrossRef]
- Hajnayeb, A.; Ghasemloonia, A.; Khadem, S.E.; Moradi, M.H. Application and comparison of an ANN-based feature selection method and the genetic algorithm in gearbox fault diagnosis. Exp. Syst. Appl. 2011, 38, 10205–10209. [Google Scholar] [CrossRef]
- Pan, Z.Z.; Meng, Z.; Chen, Z.J.; Gao, W.Q.; Shi, Y. A two-stage method based on extreme learning machine for predicting the remaining useful life of rollingelement bearings. Mech. Syst. Signal. 2020, 144, 106899. [Google Scholar] [CrossRef]
- Ji, X.; Ren, Y.; Tang, H.; Shi, C.; Xiang, J. An intelligent fault diagnosis approach based on Dempster-Shafer theory for hydraulic valves. Measurement 2020, 165, 108129. [Google Scholar] [CrossRef]
- Zhao, R.; Yan, R.; Chen, Z.; Mao, K.; Wang, P.; Gao, R.X. Deep learning and its applications to machine health monitoring. Mech. Syst. Signal Process. 2019, 115, 213–237. [Google Scholar] [CrossRef]
- Jegadeeshwaran, R.; Sugumaran, V. Fault diagnosis of automobile hydraulic brake system using statistical features and support vector machines. Mech. Syst. Signal Process. 2015, 52–53, 436–446. [Google Scholar] [CrossRef]
- Lan, Y.; Hu, J.; Huang, J.; Niu, L.; Zeng, X.; Xiong, X.; Wu, B. Fault diagnosis on slipper abrasion of axial piston pump based on Extreme Learning Machine. Measurement 2018, 124, 378–385. [Google Scholar] [CrossRef]
- Ji, X.; Ren, Y.; Tang, H.; Xiang, J. DSmT-based three-layer method using multi-classifier to detect faults in hydraulic systems. Mech. Syst. Signal Process. 2021, 153, 107513. [Google Scholar] [CrossRef]
- Tiwari, R.; Bordoloi, D.J.; Dewangan, A. Blockage and cavitation detection in centrifugal pumps from dynamic pressure signal using deep learning algorithm. Measurement 2021, 173, 108676. [Google Scholar] [CrossRef]
- Wang, S.; Xiang, J.; Zhong, Y. Hesheng Tang: A data indicator-based deep belief networks to detect multiple faults in axial piston pumps. Mech. Syst. Signal Process. 2018, 112, 154–170. [Google Scholar] [CrossRef]
- Joshi, A.V. Machine Learning and Artificial Intelligence; Springer Nature: Cham, Switzerland, 2020. [Google Scholar]
- Li, X.; Xu, Y.; Li, N.; Yang, B.; and Lei, Y. Remaining Useful Life Prediction With Partial Sensor Malfunctions Using Deep Adversarial Networks. IEEE/CAA J. Autom. Sin. 2023, 10, 121–134. [Google Scholar] [CrossRef]
- Peng, H.C.; Long, F.; Ding, C. Feature Selection Based on Mutual Information: Criteria of Max-Dependency, Max-Relevance, and Min-Redundancy. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1226–1238. [Google Scholar]
- Guillon, M. Teoria i Obliczanie Układów Hydraulicznych; Wydawnictwo Naukowo Techniczne: Warszawa, Poland, 1966. [Google Scholar]
- Ma, J.; Chen, J.; Li, J.; Li, Q.; Ren, C. Wear analysis of swash plate/slipper pair of axis piston hydraulic pump. Tribol. Int. 2015, 90, 467–472. [Google Scholar] [CrossRef]
- Lyu, F.; Zhang, J.; Sun, G.; Xu, B.; Pan, M.; Huang, X.; Xu, H. Research on wear prediction of piston/cylinder pair in axial piston pumps. Wear 2020, 456–457, 203338. [Google Scholar] [CrossRef]
- Roberts, M.J. Signals and Systems Analysis Using Transform Methods and MATLAB; McGraw-Hill Higher Education: New York, NY, USA, 2004. [Google Scholar]
- Esfandiari, R.S. Numerical Methods for Engineers and Scientists Using MATLAB, 2nd ed.; CRC Press: Boca Raton, FL, USA; Taylor & Francis Group: Boca Raton, FL, USA, 2017. [Google Scholar]
- Bin, G.F.; Gao, J.J.; Li, X.J.; Dhillon, B.S. Early fault diagnosis of rotating machinery based on wavelet packets—Empirical mode decomposition feature extraction and neural network. Mech. Syst. Signal Process. 2012, 27, 696–711. [Google Scholar] [CrossRef]
- Kroese, D.P.; Botev, Z.I.; Taimre, T.; Vaisman, R. Data Science and Machine Learning: Mathematical and Statistical Methods; CRC Press: Boca Raton, FL, USA; Taylor & Francis Group: Boca Raton, FL, USA, 2017. [Google Scholar]
- Bhattacharyya, S.; Bhaumik, H.; Mukherjee, A.; De, S. Machine Learning for a Big Data Analysis; Walter de Gruyter: Berlin, Germany, 2019. [Google Scholar]
- Leis, J.W. Digital Signal Processing Using MATLAB for Students and Researchers; John Wiley & Sons: New York, NY, USA, 2011. [Google Scholar]
- Darbellay, G.A.; Vajda, I. Estimation of the information by an adaptive partitioning of the observation space. IEEE Trans. Inf. Theory 1999, 45, 4. [Google Scholar] [CrossRef]
- Samanta, B. Gear Fault Detection Using Artificial Neural Networks and Support Vector Machines with Genetic Algorithms. Mech. Syst. Signal Process. 2004, 18, 625–644. [Google Scholar] [CrossRef]
- Meyes, R.; Lu, M.; de Puiseau, C.W.; Meisen, T. Ablation studies in artificial neural networks. arXiv 2019, arXiv:1901.08644. [Google Scholar]
- Available online: https://www.mathworks.com/ (accessed on 1 September 2021).
- Zhu, Y.; Li, G.; Wanga, R.; Tanga, S.; Su, H.; Cao, K. Intelligent fault diagnosis of hydraulic piston pump combining improved LeNet-5 and PSO hyperparameter optimization. Appl. Acoust. 2021, 183, 108336. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference for Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]



| No. | Expression: | Feature: | Description: |
|---|---|---|---|
| 1 | Mean | sum of all data divided by the number of data | |
| 2 | where | Standard deviation | square root of variance; the variance was estimated using a consistent and unbiased estimator |
| 3 | Root mean square | square root of the arithmetic mean of the data squared | |
| 4 | Kurtosis | measure of the shape of feature distribution | |
| 5 | Skewness | defines the degree to which the distribution differs from the normal distribution | |
| 6 | Shape factor | root mean square of the signal divided by the mean value of the signal | |
| 7 | Impulse Factor | maximum absolute value of the signal divided by the mean absolute value of the signal | |
| 8 | Crest Factor | maximum absolute value in the data divided by the root mean square of the data | |
| 9 | Clearance Factor | maximum absolute value of the signal divided by the square root of the signal amplitude | |
| 10 | max PSD | Peak amplitude of PSD | maximum value of the power spectral density |
| 11 | max Freq. | Peak frequency of PSD | frequency of the maximum value of power spectral density |
| xi—i-th measurement data point, n—total number of data in the measurement | |||
| Feature | MIQX Coefficient Value |
|---|---|
| XT_PeakFreq | 0.37 |
| YW_PeakAmp | 0.31 |
| YT_CreastFactor | 0.05 |
| XW_RMS | 0.015 |
| YR_Skewness | 0.015 |
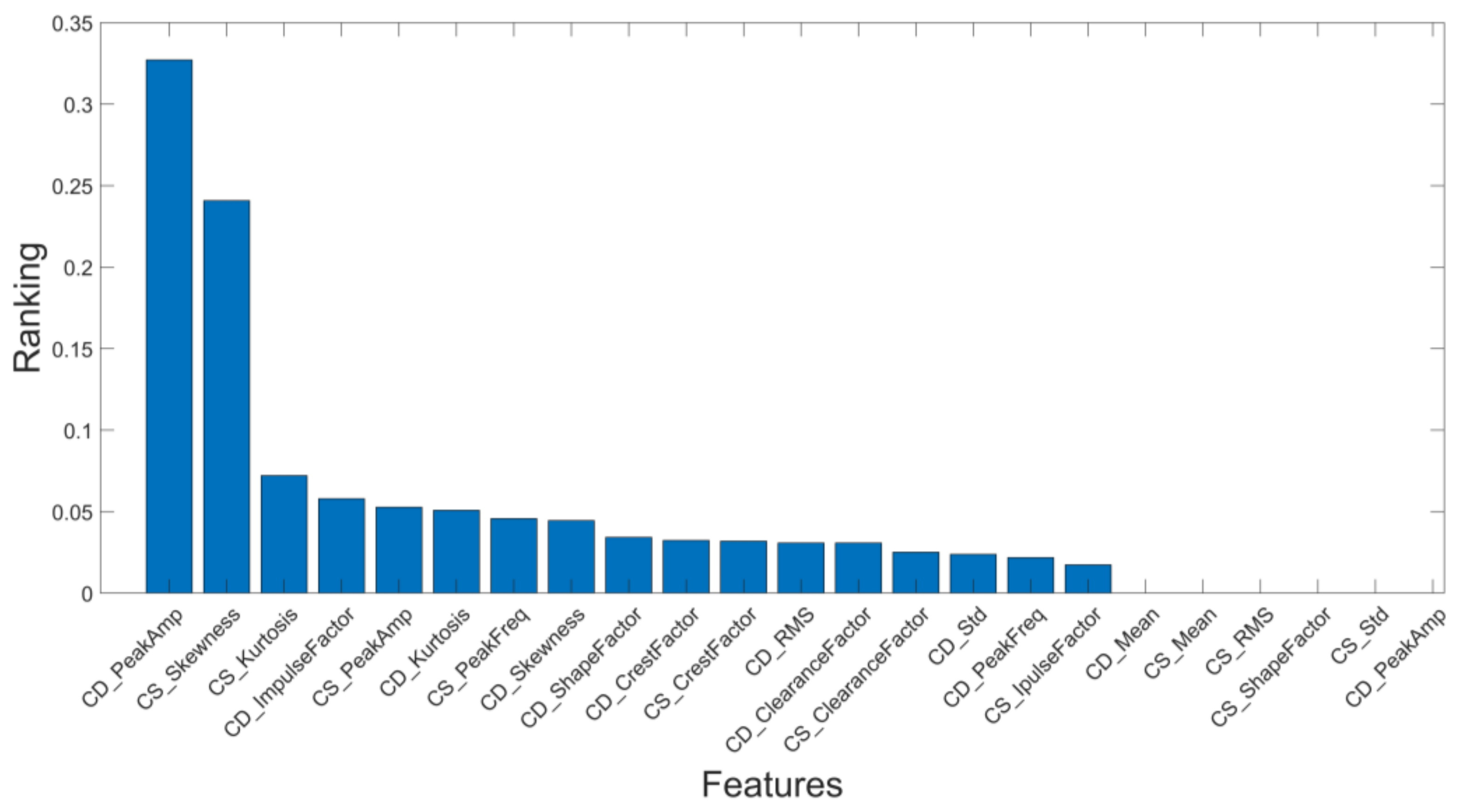
| Feature | MIQX Coefficient Value |
|---|---|
| CD_PeakAmp | 0.33 |
| CS_Skewness | 0.24 |
| CS_Kurtosis | 0.07 |
| CD_ImpulseFactor | 0.06 |
| CS_PeakAmp | 0.05 |
| Network Parameters | ||||
|---|---|---|---|---|
| No. | Name | Type | Number of Activated Variables | Variables Subject to Learning |
| 1 | WAR. WEJ. | Input layer | 5 | - |
| 2 | WAR. WEW. | Inner layer | 12 | 12 × 5 (weights), 12 × 1 (load) |
| 3 | ReLU | Activation | 12 | - |
| 4 | Batchnorm | Data normalization | 12 | 12 × 1 (offset), 12 × 1 (scaling) |
| 5 | WAR. WYJ. | Output layer | 3 | 3 × 12 (weights), 3 × 1 (load) |
| 6 | Softmax | Smoothing | 3 | - |
| 7 | KLASYFIKACJA | Classification | - | - |
| No. | Parameter Name | Parameter Value |
|---|---|---|
| 1 | Gradient Decay Factor | 0.95 |
| 2 | Squared Gradient Decay Factor | 0.99 |
| 3 | Epsilon | 1 × 10−8 |
| 4 | Initial Learn Rate | 1 × 10−3 |
| 5 | Learn Rate Schedule | ‘none’ |
| 6 | Learn Rate Drop Factor | 0.1 |
| 7 | Learn Rate Drop Period | 10 |
| 8 | L2Regularization | 1 × 10−3 |
| 9 | Gradient Threshold Method | ‘l2norm’ |
| 10 | Gradient Threshold | Inf. |
| 11 | Max Epochs | 500 |
| 12 | MiniBatch Size | 44 |
| 13 | Verbose | 1 |
| 14 | Verbose Frequency | 50 |
| 15 | Validation Data | 66 × 6 table |
| 16 | Validation Frequency | 20 |
| 17 | Validation Patience | Inf. |
| 18 | Shuffle | every epoch |
| 20 | Execution Environment | gpu |
| Diagnostic Signal Type | Method of Determining Features | Accuracy | Error | ||
|---|---|---|---|---|---|
| Training (%) | Validation (%) | Training (-) | Validation (-) | ||
| Vibrations | MRMR | 94 | 93.9 | 0.17 | 0.16 |
| Static and dynamic pressure | MRMR | 98.7 | 96.7 | 0.07 | 0.11 |
| Type of Diagnostic Signal | Method of Determining Features | Accuracy of acc Classifier (%) |
|---|---|---|
| Vibrations | MRMR | 95.5 |
| Static and dynamic pressure | MRMR | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Konieczny, J.; Łatas, W.; Stojek, J. Classification of Wear State for a Positive Displacement Pump Using Deep Machine Learning. Energies 2023, 16, 1408. https://doi.org/10.3390/en16031408
Konieczny J, Łatas W, Stojek J. Classification of Wear State for a Positive Displacement Pump Using Deep Machine Learning. Energies. 2023; 16(3):1408. https://doi.org/10.3390/en16031408
Chicago/Turabian StyleKonieczny, Jarosław, Waldemar Łatas, and Jerzy Stojek. 2023. "Classification of Wear State for a Positive Displacement Pump Using Deep Machine Learning" Energies 16, no. 3: 1408. https://doi.org/10.3390/en16031408
APA StyleKonieczny, J., Łatas, W., & Stojek, J. (2023). Classification of Wear State for a Positive Displacement Pump Using Deep Machine Learning. Energies, 16(3), 1408. https://doi.org/10.3390/en16031408








