CPSOGSA Optimization Algorithm Driven Cascaded 3DOF-FOPID-FOPI Controller for Load Frequency Control of DFIG-Containing Interconnected Power System
Abstract
:1. Introduction
- A novel cascaded 3DOF-FOPID-FOPI controller is proposed for the first time to solve the load frequency control problem of a two-area interconnected electric power system.
- The application of the CPOSGSA algorithm is extended to the load frequency control of a two-area interconnected power system through the optimal selection of gains and parameters of the cascade controller by the superior performance CPSOGSA algorithm.
- The DFIG power fluctuations due to stochastic wind speed are considered in addition to load perturbations in the area interconnected power system to verify the control performance of the controller in a more realistic scenario.
- The robustness of the proposed cascaded fractional-order controller is well illustrated by performing a sensitivity analysis under various conditions.
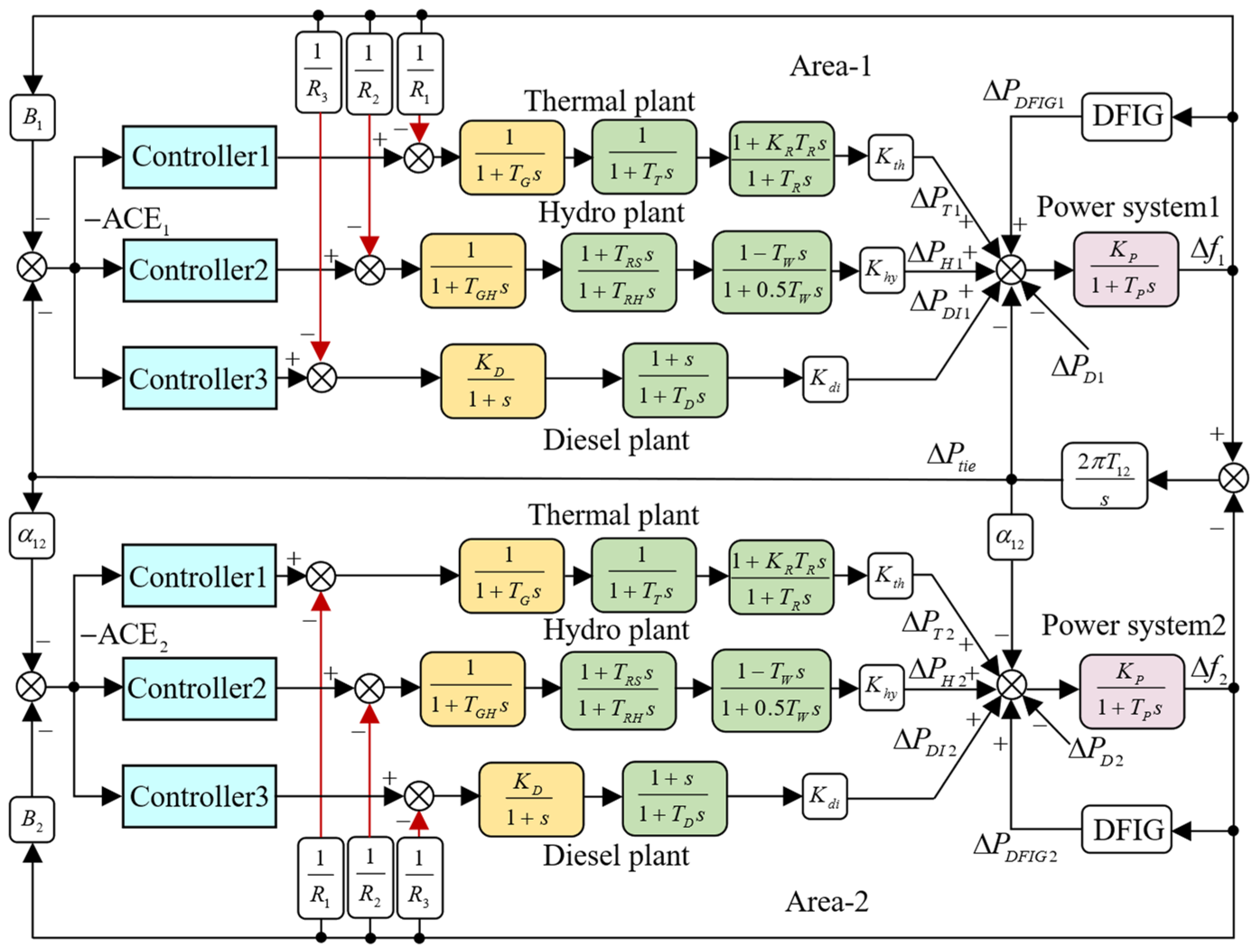
2. Systems Investigated
DFIG and Its Additional Frequency Response Model
3. Cascade Fractional Order Controller Design
3.1. Implementation of Fractional Calculus
3.2. Cascade 3DOF-FOPID-FOPI Controller
3.2.1. 3DOF-FOPID Controller
3.2.2. FOPI Controller
4. The Proposed CPSOGSA Algorithm
4.1. Particle Swarm Optimization
4.2. Gravitational Search Algorithm
4.3. Improved PSOGSA Algorithm under Chaotic Map Optimization (CPSOGSA)
5. Simulation Analysis
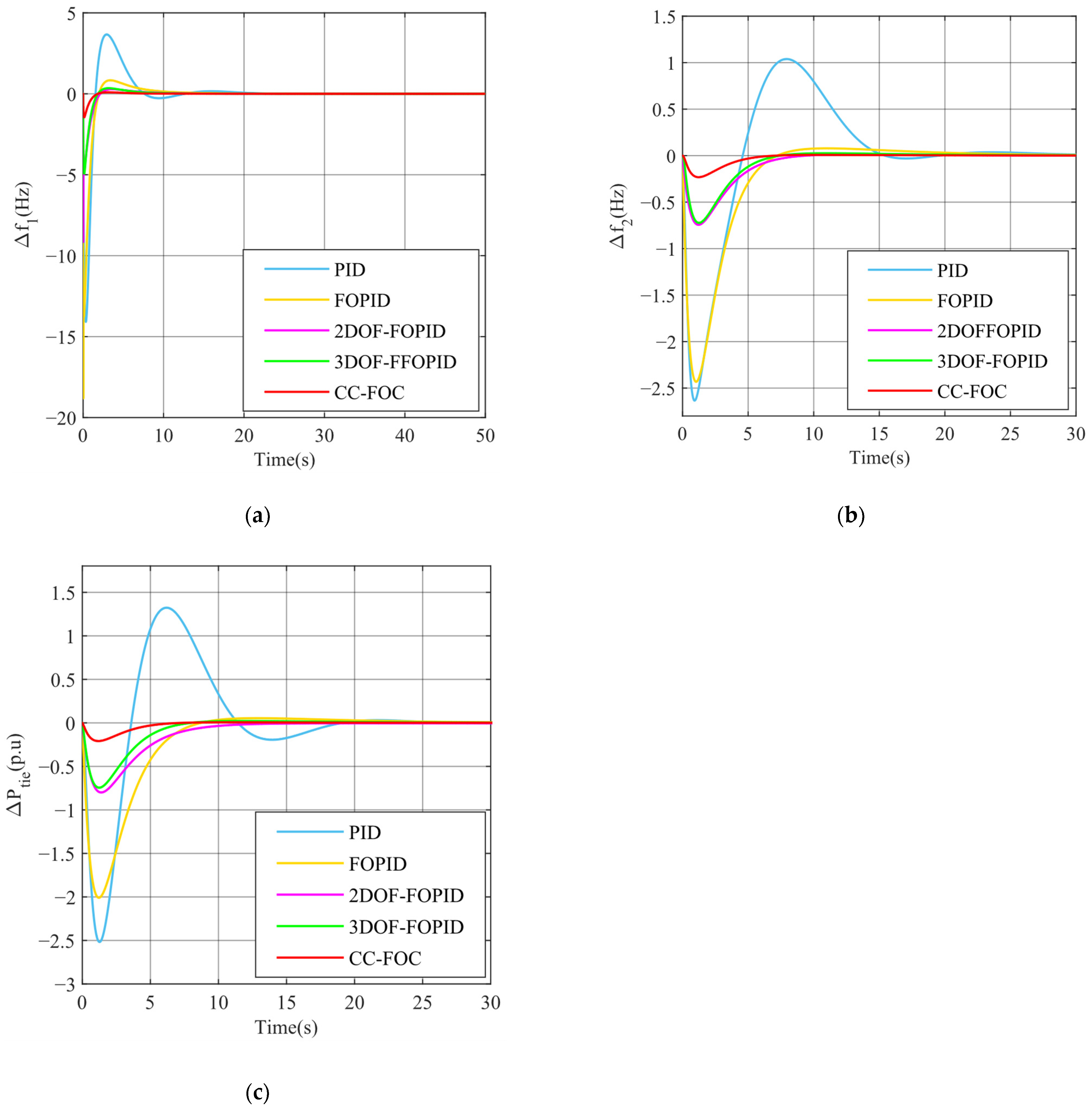
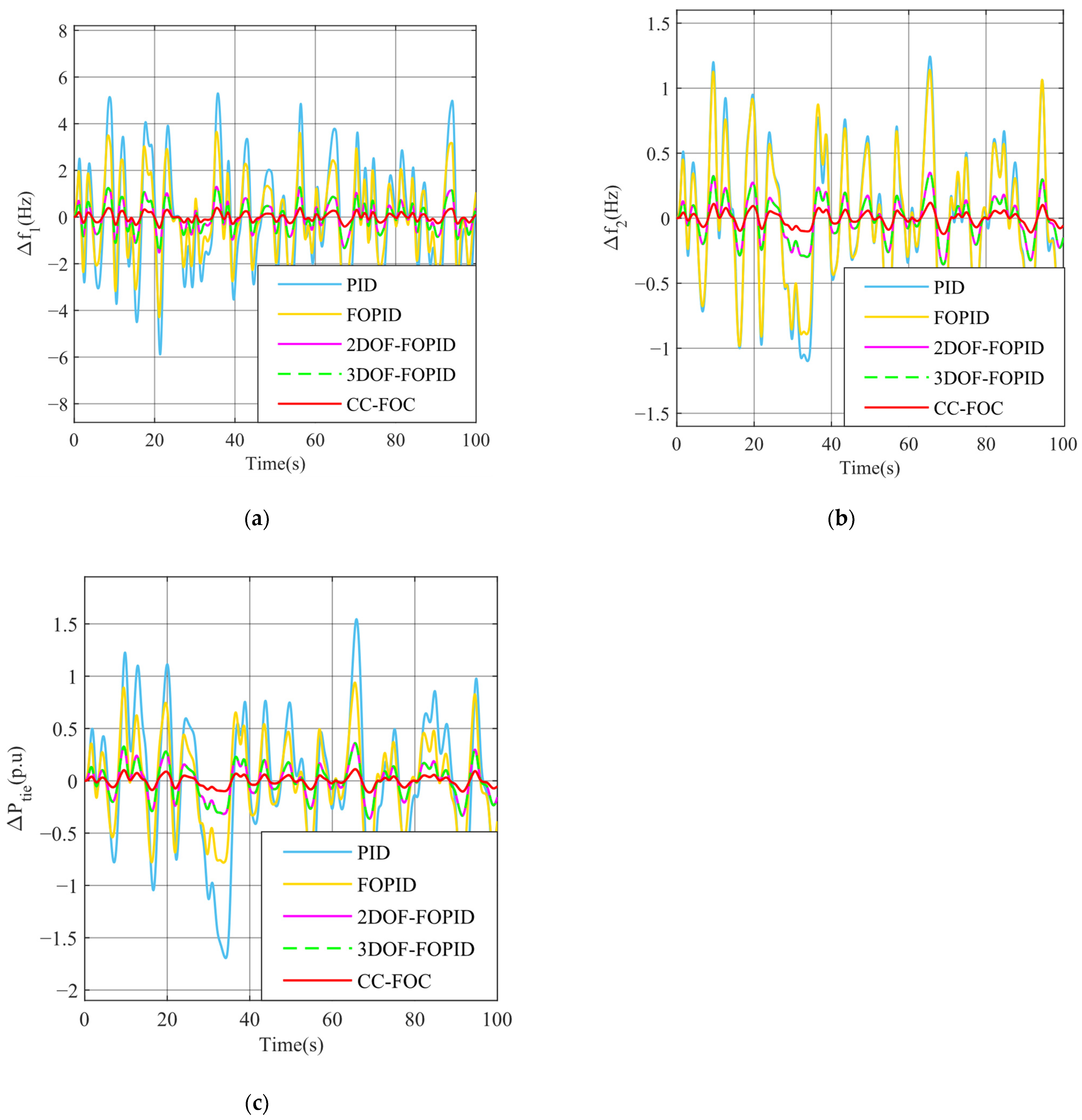
5.1. Scenario 1 Effect of Different Load Perturbations
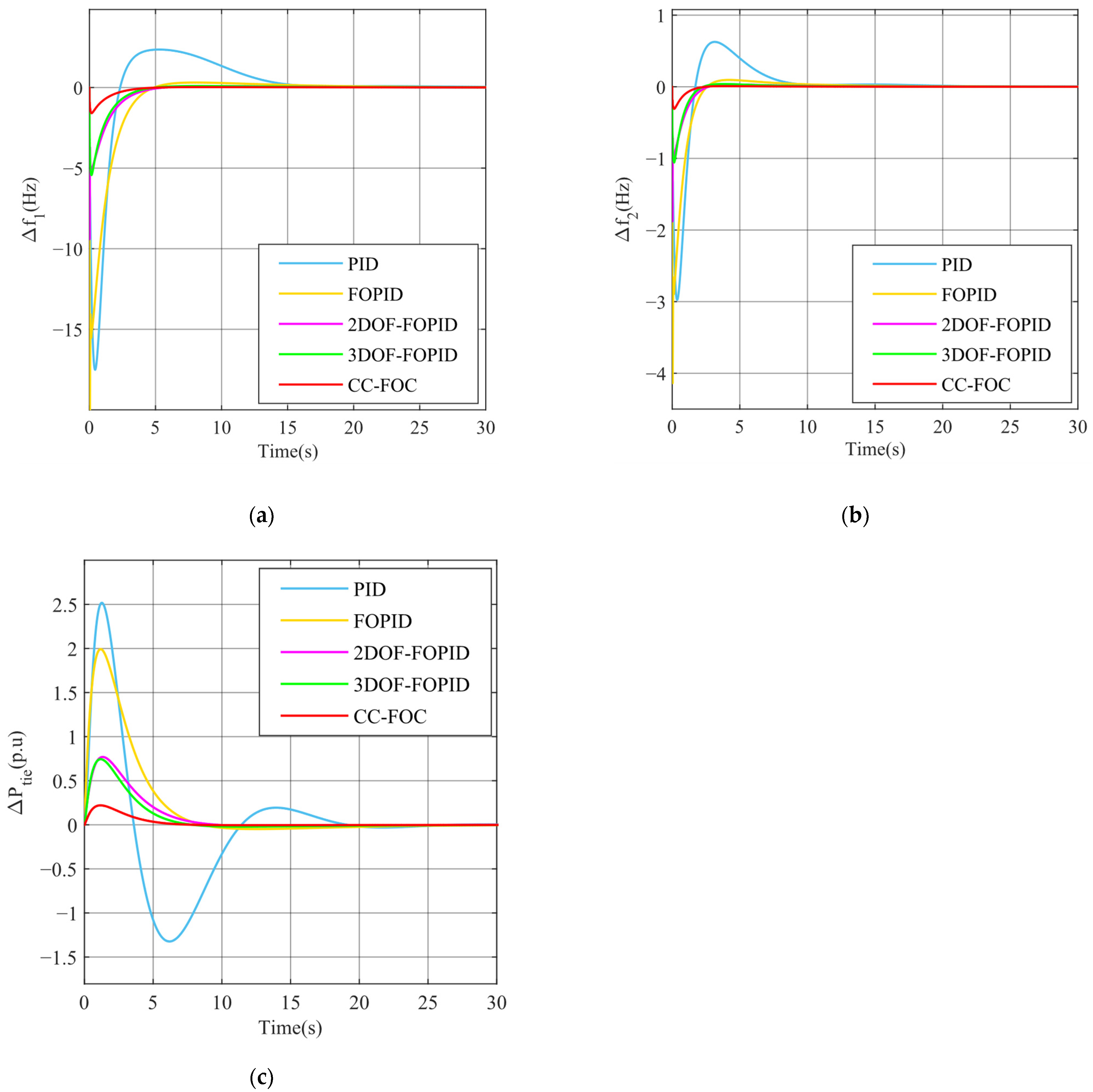
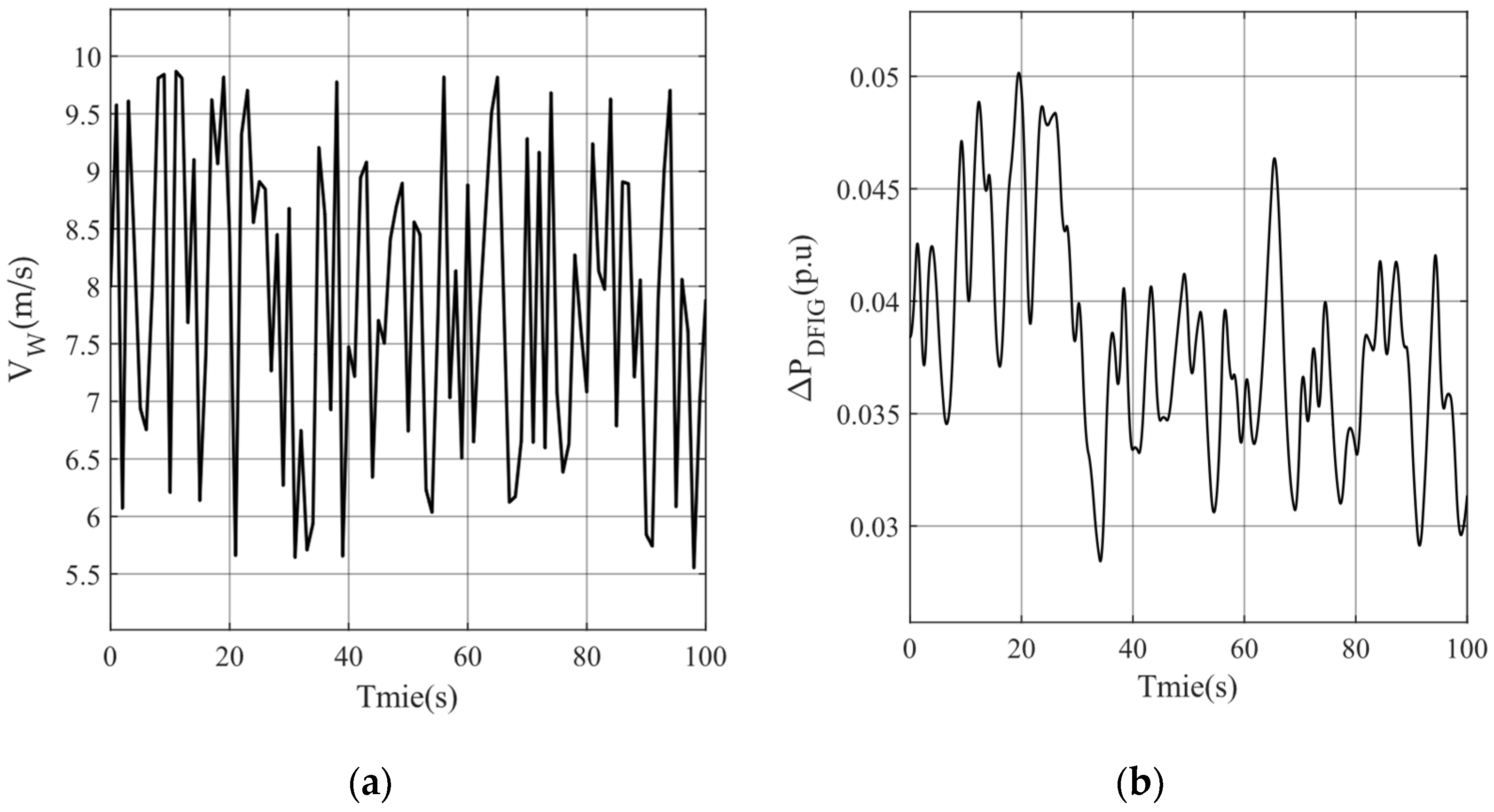
5.2. Scenario 2 Wind Speed Fluctuations
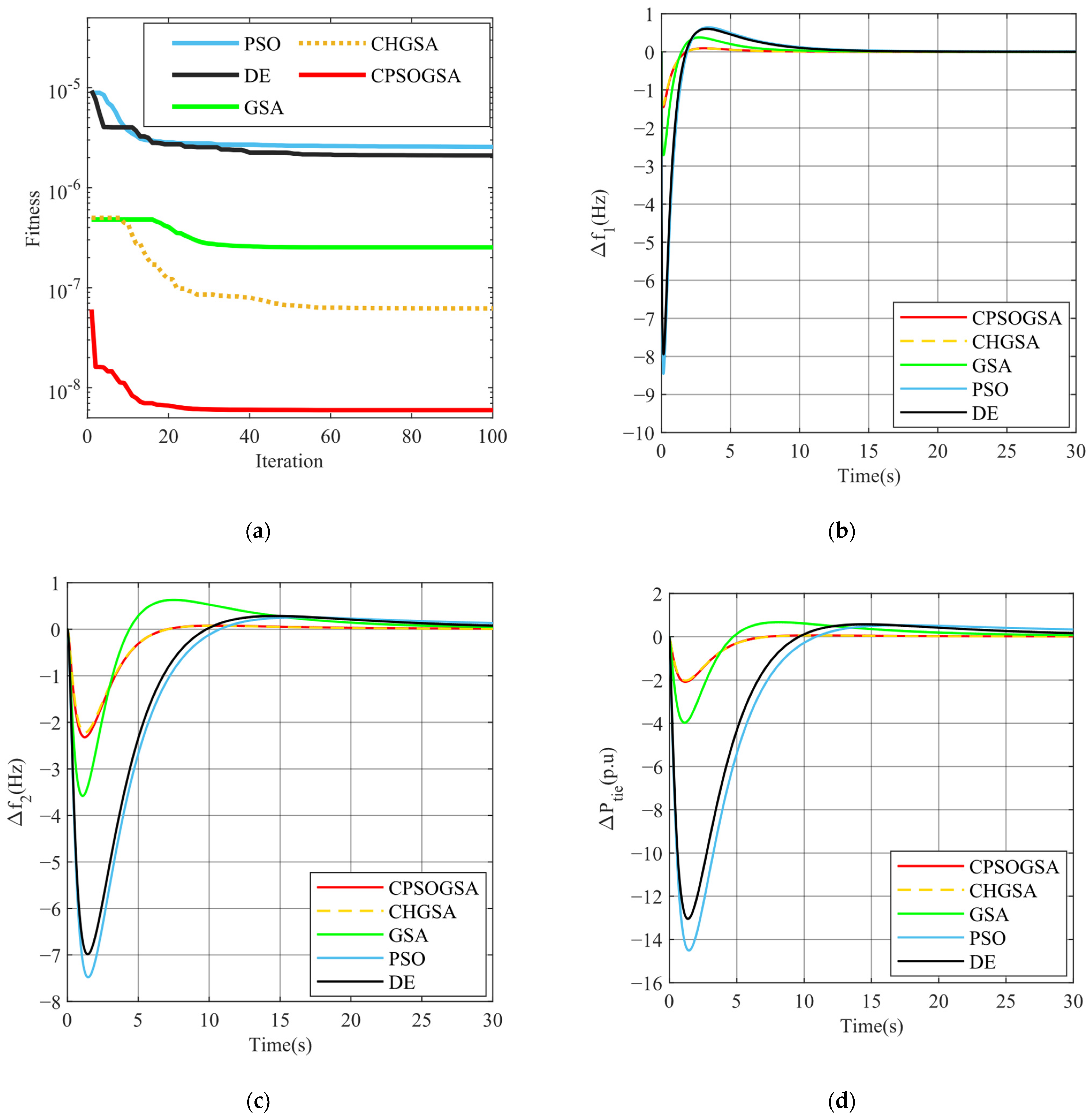
5.3. Scenario 3 Comparison of Different Optimization Algorithms
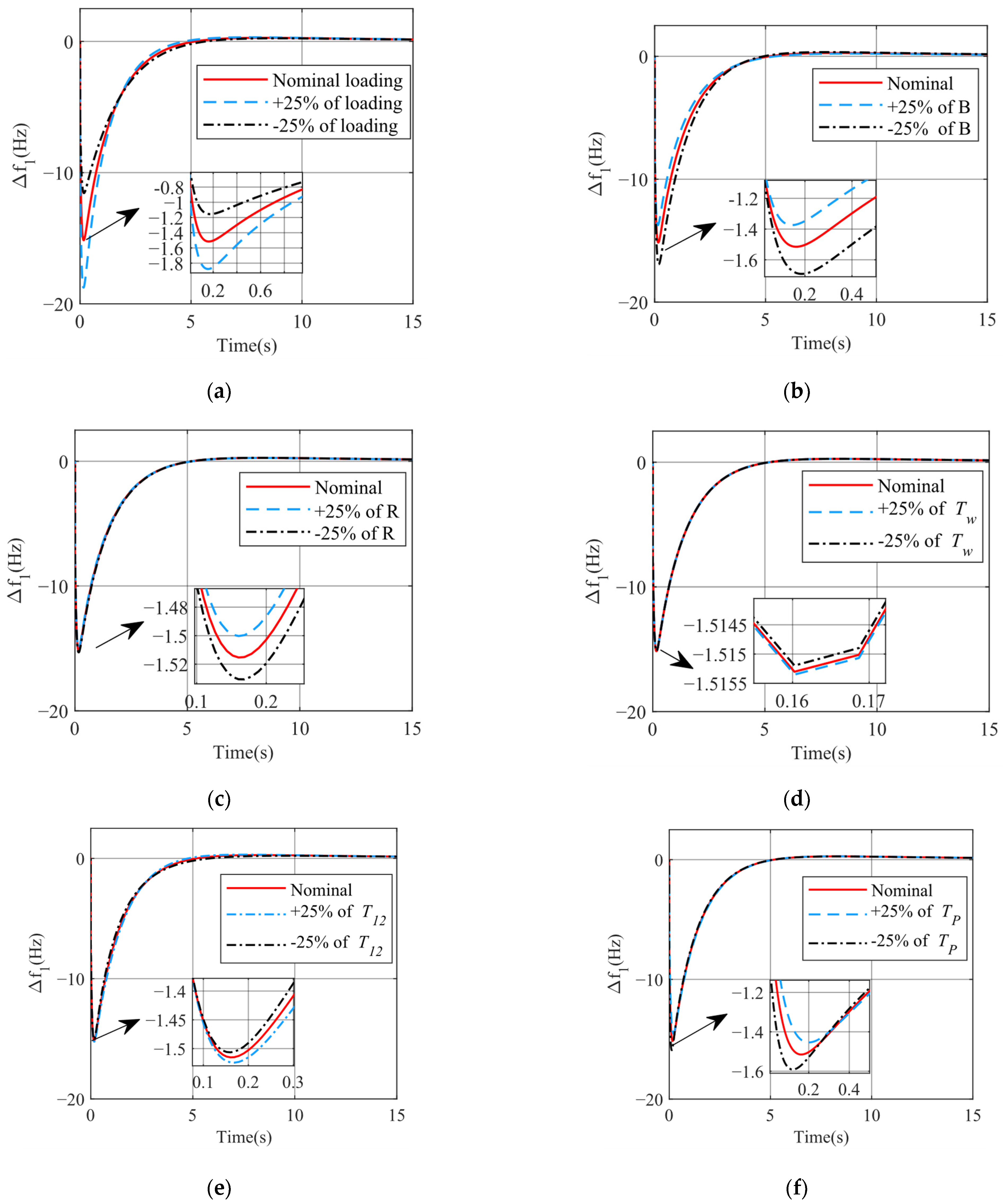
5.4. Scenario 4 Load Perturbation and Internal Parameter Changes
6. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CC-FOC | Cascade fractional-order controller |
| CPSOGSA | Improved particle swarm optimization and gravitational search algorithm under chaotic map optimization |
| DE | Differential evolution |
| DFIG | Doubly-fed induction generator |
| FOPI | Fractional-order proportional-integral |
| GSA | Gravitational search algorithm |
| ITSE | Time multiplied squared error |
| LFC | Load frequency control |
| PSO | Particle swarm optimization |
| PID | Proportional-integral-differential |
| 2DOF-FOPID | Two-degree-of-freedom fractional-order proportional-integral-differential |
| 3DOF-FOPID | Three-degree-of-freedom fractional-order proportional-integral-differential |
Appendix A
References
- Olabi, A.G.; Abdelkareem, M.A. Renewable energy and climate change. Renew. Sustain. Energy Rev. 2022, 158, 112111. [Google Scholar] [CrossRef]
- Cao, M.; Xu, Q.; Qin, X.; Cai, J. Battery energy storage sizing based on a model predictive control strategy with operational constraints to smooth the wind power. Int. J. Electr. Power Energy Syst. 2020, 115, 105471. [Google Scholar] [CrossRef]
- Tavakkoli, M.; Fattaheian-Dehkordi, S.; Pourakbari-Kasmaei, M.; Liski, M.; Lehtonen, M. An Approach to Divide Wind Power Capacity Between Day-Ahead Energy and Intraday Reserve Power Markets. IEEE Syst. J. 2022, 16, 1123–1134. [Google Scholar] [CrossRef]
- Du, M.; Niu, Y.; Hu, B.; Zhou, G.; Luo, H.; Qi, X. Frequency regulation analysis of modern power systems using start-stop peak shaving and deep peak shaving under different wind power penetrations. Int. J. Electr. Power Energy Syst. 2021, 125, 106501. [Google Scholar] [CrossRef]
- Bevrani, H.; Golpîra, H.; Messina, A.R.; Hatziargyriou, N.; Milano, F.; Ise, T. Power system frequency control: An updated review of current solutions and new challenges. Electr. Power Syst. Res. 2021, 194, 107114. [Google Scholar] [CrossRef]
- Khalid, J.; Ramli, M.A.M.; Khan, M.S.; Hidayat, T. Efficient Load Frequency Control of Renewable Integrated Power System: A Twin Delayed DDPG-Based Deep Reinforcement Learning Approach. IEEE Access 2022, 10, 51561–51574. [Google Scholar] [CrossRef]
- Mi, Y.; Chen, B.; Cai, P.; He, X.; Liu, R.; Yang, X. Frequency control of a wind-diesel system based on hybrid energy storage. Prot. Control Mod. Power Syst. 2022, 7, 31. [Google Scholar] [CrossRef]
- Kalyan, C.N.S.; Goud, B.S.; Reddy, C.R.; Bajaj, M.; Sharma, N.K.; Alhelou, H.H.; Siano, P.; Kamel, S. Comparative Performance Assessment of Different Energy Storage Devices in Combined LFC and AVR Analysis of Multi-Area Power System. Energies 2022, 15, 629. [Google Scholar] [CrossRef]
- Mi, Y.; Hao, X.Z.; Liu, Y.J.; Fu, Y.; Wang, C.S.; Wang, P.; Loh, P.C. Sliding mode load frequency control for multi-area time-delay power system with wind power integration. IET Gener. Transm. Distrib. 2017, 11, 4644–4653. [Google Scholar] [CrossRef]
- Fan, W.; Hu, Z.; Veerasamy, V. PSO-Based Model Predictive Control for Load Frequency Regulation with Wind Turbines. Energies 2022, 15, 8219. [Google Scholar] [CrossRef]
- Vafamand, N.; Arefi, M.M.; Asemani, M.H.; Dragičević, T. Decentralized Robust Disturbance-Observer Based LFC of Interconnected Systems. IEEE Trans. Ind. Electron. 2022, 69, 4814–4823. [Google Scholar] [CrossRef]
- Adibi, M.; Woude, J.v.d. Secondary Frequency Control of Microgrids: An Online Reinforcement Learning Approach. IEEE Trans. Autom. Control 2022, 67, 4824–4831. [Google Scholar] [CrossRef]
- Ali, M.; Kotb, H.; Aboras, K.M.; Abbasy, N.H. Design of Cascaded PI-Fractional Order PID Controller for Improving the Frequency Response of Hybrid Microgrid System Using Gorilla Troops Optimizer. IEEE Access 2021, 9, 150715–150732. [Google Scholar] [CrossRef]
- Rostami, Z.; Ravadanegh, S.N.; Kalantari, N.T.; Guerrero, J.M.; Vasquez, J.C. Dynamic Modeling of Multiple Microgrid Clusters Using Regional Demand Response Programs. Energies 2020, 13, 4050. [Google Scholar] [CrossRef]
- Khadanga, R.K.; Nayak, S.R.; Panda, S.; Das, D.; Prusty, B.R.; Sahu, P.R. A Novel Optimal Robust Design Method for Frequency Regulation of Three-Area Hybrid Power System Utilizing Honey Badger Algorithm. Int. Trans. Electr. Energy Syst. 2022, 2022, 6017066. [Google Scholar] [CrossRef]
- Patan, M.K.; Raja, K.; Azaharahmed, M.; Prasad, C.D.; Ganeshan, P. Influence of Primary Regulation on Frequency Control of an Isolated Microgrid Equipped with Crow Search Algorithm Tuned Classical Controllers. J. Electr. Eng. Technol. 2021, 16, 681–695. [Google Scholar] [CrossRef]
- Chen, G.; Li, Z.; Zhang, Z.; Li, S. An Improved ACO Algorithm Optimized Fuzzy PID Controller for Load Frequency Control in Multi Area Interconnected Power Systems. IEEE Access 2020, 8, 6429–6447. [Google Scholar] [CrossRef]
- Kamarposhti, M.A.; Shokouhandeh, H.; Alipur, M.; Colak, I.; Zare, H.; Eguchi, K. Optimal Designing of Fuzzy-PID Controller in the Load-Frequency Control Loop of Hydro-Thermal Power System Connected to Wind Farm by HVDC Lines. IEEE Access 2022, 10, 63812–63822. [Google Scholar] [CrossRef]
- Tabak, A. Fractional order frequency proportional-integral-derivative control of microgrid consisting of renewable energy sources based on multi-objective grasshopper optimization algorithm. Trans. Inst. Meas. Control 2021, 44, 378–392. [Google Scholar] [CrossRef]
- Ebrahim, M.A.; Becherif, M.; Abdelaziz, A.Y. PID-/FOPID-based frequency control of zero-carbon multisources-based interconnected power systems underderegulated scenarios. Int. Trans. Electr. Energy Syst. 2021, 31, e12712. [Google Scholar] [CrossRef]
- Agwa, A.M.; Abdeen, M.; Shaaban, S.M. Optimal FOPID Controllers for LFC Including Renewables by Bald Eagle Optimizer. CMC-Comput. Mater. Contin. 2022, 73, 5525–5541. [Google Scholar] [CrossRef]
- Pahadasingh, S.; Jena, C.; Panigrahi, C.K. Load Frequency Control Incorporating Electric Vehicles Using FOPID Controller with HVDC Link. In Proceedings of the Innovation in Electrical Power Engineering, Communication, and Computing Technology, Singapore, 22 February 2020; pp. 181–203. [Google Scholar]
- Mohapatra, T.K.; Dey, A.K.; Sahu, B.K. Employment of quasi oppositional SSA-based two-degree-of-freedom fractional order PID controller for AGC of assorted source of generations. IET Gener. Transm. Distrib. 2020, 14, 3365–3376. [Google Scholar] [CrossRef]
- Nayak, J.R.; Shaw, B.; Sahu, B.K. Implementation of hybrid SSA-SA based three-degree-of-freedom fractional-order PID controller for AGC of a two-area power system integrated with small hydro plants. IET Gener. Transm. Distrib. 2020, 14, 2430–2440. [Google Scholar] [CrossRef]
- Sahu, P.C.; Prusty, R.C.; Panda, S. Active power management in wind/solar farm integrated hybrid power system with AI based 3DOF-FOPID approach. Energy Sources Part A: Recovery Util. Environ. Eff. 2021, 1–21. [Google Scholar] [CrossRef]
- Ali, M.; Kotb, H.; Kareem AboRas, M.; Nabil Abbasy, H. Frequency regulation of hybrid multi-area power system using wild horse optimizer based new combined Fuzzy Fractional-Order PI and TID controllers. Alex. Eng. J. 2022, 61, 12187–12210. [Google Scholar] [CrossRef]
- Guha, D.; Roy, P.K.; Banerjee, S. Equilibrium optimizer-tuned cascade fractional-order 3DOF-PID controller in load frequency control of power system having renewable energy resource integrated. Int. Trans. Electr. Energy Syst. 2021, 31, e12702. [Google Scholar] [CrossRef]
- Barakat, M. Novel chaos game optimization tuned-fractional-order PID fractional-order PI controller for load–frequency control of interconnected power systems. Prot. Control Mod. Power Syst. 2022, 7, 16. [Google Scholar] [CrossRef]
- Choudhary, R.; Rai, J.N.; Arya, Y. Cascade FOPI-FOPTID controller with energy storage devices for AGC performance advancement of electric power systems. Sustain. Energy Technol. Assess. 2022, 53, 102671. [Google Scholar] [CrossRef]
- Guha, D.; Roy, P.K.; Banerjee, S. Frequency Control of a Wind-diesel-generator Hybrid System with Squirrel Search Algorithm Tuned Robust Cascade Fractional Order Controller Having Disturbance Observer Integrated. Electr. Power Compon. Syst. 2022, 50, 814–839. [Google Scholar] [CrossRef]
- Duman, S.; Li, J.; Wu, L.; Guvenc, U. Optimal power flow with stochastic wind power and FACTS devices: A modified hybrid PSOGSA with chaotic maps approach. Neural Comput. Appl. 2020, 32, 8463–8492. [Google Scholar] [CrossRef]
- Gan, K.; Sun, S.; Wang, S.; Wei, Y. A secondary-decomposition-ensemble learning paradigm for forecasting PM2.5 concentration. Atmos. Pollut. Res. 2018, 9, 989–999. [Google Scholar] [CrossRef]
- Celik, E. Design of new fractional order PI–fractional order PD cascade controller through dragonfly search algorithm for advanced load frequency control of power systems. Soft Comput. 2021, 25, 1193–1217. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the Icnn95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995. [Google Scholar]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. GSA: A Gravitational Search Algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Yang, X.-S. Chaotic bat algorithm. J. Comput. Sci. 2014, 5, 224–232. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H. Chaotic gravitational constants for the gravitational search algorithm. Appl. Soft Comput. 2017, 53, 407–419. [Google Scholar] [CrossRef]


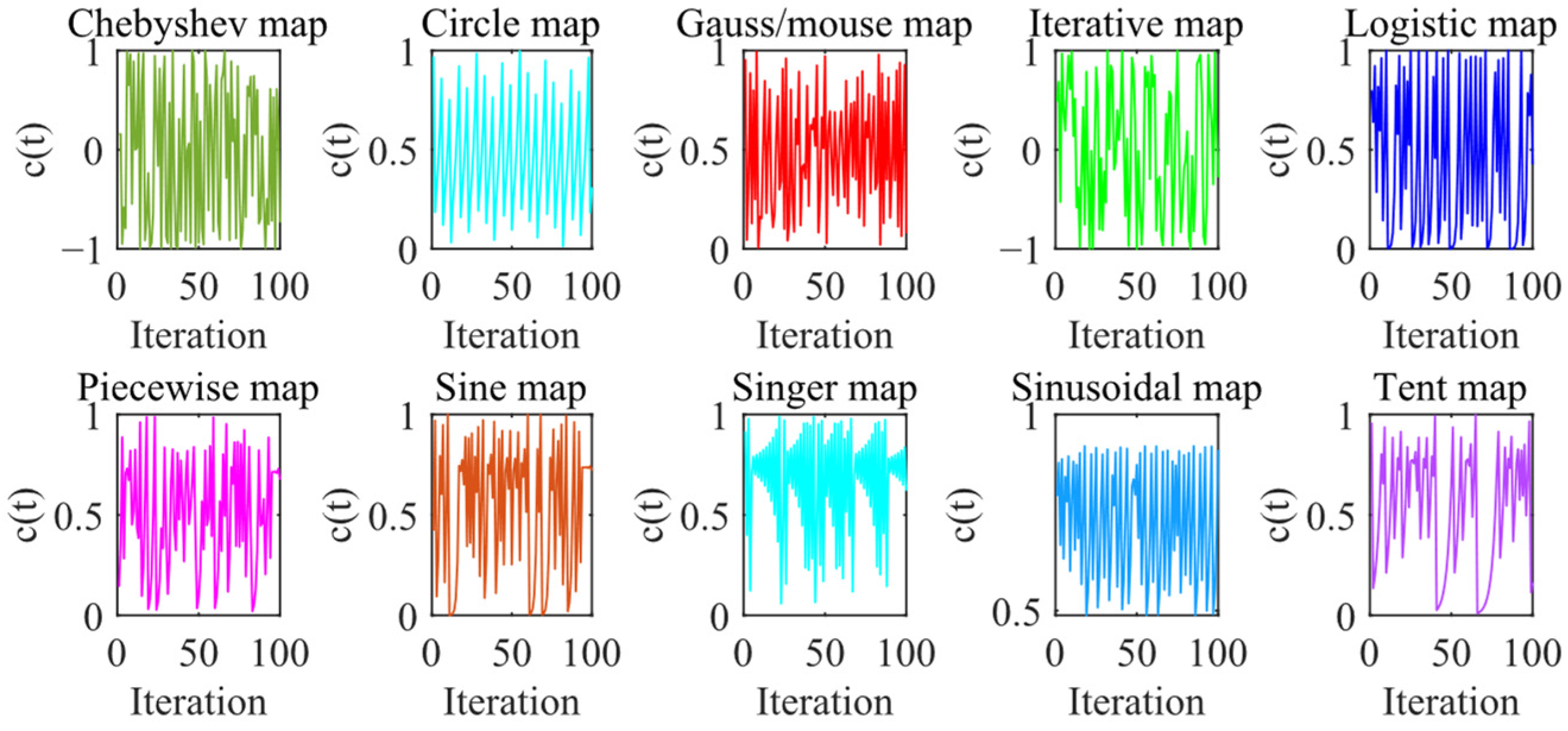

| No. | Chaotic Map | Function | Range |
|---|---|---|---|
| 1 | Chebyshev | [−1, 1] | |
| 2 | Circle | [0, 1] | |
| 3 | Gauss/Mouse | [0, 1] | |
| 4 | Iterative | [−1, 1] | |
| 5 | Logistic | [0, 1] | |
| 6 | Piecewise | [0, 1] | |
| 7 | Sine | [0, 1] | |
| 8 | Singer | [0, 1] | |
| 9 | Sinusoidal | [0, 1] | |
| 10 | Tent | [0, 1] |
| Controller | Unit | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PID | thermal | 2 | 0 | 2 | |||||||||
| hydro | 2 | 0 | 2 | ||||||||||
| diesel | 2 | 2 | 2 | ||||||||||
| FOPID | thermal | 2 | 2 | 2 | 0 | 0.9036 | |||||||
| hydro | 0.1677 | 1.8687 | 2 | 0 | 0 | ||||||||
| diesel | 2 | 2 | 2 | 0 | 0 | ||||||||
| 2DOF-FOPID | thermal | 1.9112 | 2 | 2 | 0 | 0.2920 | 0.0402 | 2.9999 | |||||
| hydro | 0.9487 | 0 | 0 | 0.0037 | 0.5265 | 0.3364 | 0 | ||||||
| diesel | 2 | 2 | 2 | 0.0845 | 0.3382 | 3 | 3 | ||||||
| 3DOF-FOPID | thermal | 1.9999 | 2 | 2 | 0 | 1 | 2.9910 | 3 | 1 | 46.5761 | |||
| hydro | 1.2494 | 1.9858 | 0.1133 | 1 | 0.5932 | 2.2241 | 2.9977 | 0.9536 | 188.0323 | ||||
| diesel | 2 | 2 | 2 | 0.0857 | 0 | 3 | 2.9998 | 1 | 143.5195 | ||||
| CC-FOC | thermal | 2 | 0 | 2 | 0.9913 | 0.9186 | 3 | 3 | 0.0836 | 64.6058 | 2 | 2 | 0.0386 |
| hydro | 2 | 0.0646 | 0 | 0.8879 | 0.9994 | 0 | 2.993 | 0 | 108.3272 | 0.3344 | 0 | 0.6158 | |
| diesel | 1.9994 | 1.9992 | 1.9996 | 0.1592 | 0 | 2.9972 | 2.9975 | 1 | 104.8120 | 2 | 2 | 0 |
| Controller | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| PID | −1.41 | 0.3 | 10.78 | −0.26 | 0.1 | 13.2 | −0.25 | 0.132 | 10.5 | 2.88 |
| FOPID | −1.88 | 0.0837 | 8.66 | −0.24 | 0.0078 | 5.46 | −0.2 | 0.005 | 6.21 | 0.79 |
| 2DOF-FOPID | −0.91 | 0.0286 | 5.45 | −0.074 | 0.001 | 4.65 | −0.08 | 0 | 5.65 | 0.122 |
| 3DOF-FOPID | −0.49 | 0.0347 | 5.35 | −0.0723 | 0.0026 | 4.25 | −0.0745 | 0.00223 | 4.45 | 0.098 |
| CC-FOC | −0.1452 | 0.0096 | 1.276 | −0.0230 | 0.0008 | 1.976 | −0.0209 | 0.0006 | 1.576 | 0.0078 |
| Controller | % Change | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| (Hz) | (Hz) | (sec) | (Hz) | (Hz) | (sec) | (Hz) | (Hz) | (sec) | |||
| Nominal | 0 | −0.1452 | 0.0096 | 1.276 | −0.0230 | 0.0008 | 1.976 | −0.0209 | 0.0006 | 1.576 | 0.0077 |
| Loading condition | +25 | −0.1816 | 0.0119 | 1.327 | −0.0290 | 0.0009 | 2.505 | −0.0261 | 0.0008 | 2.255 | 0.0122 |
| −25 | −0.1089 | 0.0071 | 1.142 | −0.0017 | 0.0006 | 1.192 | −0.0156 | 0.0005 | 1.142 | 0.0044 | |
| = 0.5390 | +25 | −0.1327 | 0.0087 | 1.255 | −0.0192 | 0.0006 | 1.505 | −0.0194 | 0.0006 | 1.455 | 0.0066 |
| = 0.3234 | −25 | −0.1610 | 0.0105 | 1.254 | −0.0286 | 0.0010 | 2.339 | −0.0226 | 0.0071 | 1.789 | 0.0094 |
| = 3 | +25 | −0.1439 | 0.0094 | 1.279 | −0.0227 | 0.0078 | 1.929 | −0.0207 | 0.0064 | 1.529 | 0.0077 |
| = 1.8000 | −25 | −0.1466 | 0.0096 | 1.277 | −0.0236 | 0.0081 | 2.027 | −0.0210 | 0.0065 | 1.627 | 0.0079 |
| = 1.25 | +25 | −0.1453 | 0.0095 | 1.277 | −0.0232 | 0.0079 | 1.977 | −0.0209 | 0.0065 | 1.577 | 0.0078 |
| = 0.75 | −25 | −0.1453 | 0.0095 | 1.278 | −0.0232 | 0.0078 | 1.978 | −0.0208 | 0.0065 | 1.578 | 0.0078 |
| = 0.0541 | +25 | −0.1446 | 0.0087 | 1.177 | −0.0266 | 0.0093 | 2.133 | −0.0239 | 0.0076 | 1.813 | 0.0074 |
| = 0.0325 | −25 | −0.1459 | 0.0100 | 1.326 | −0.0192 | 0.0061 | 1.476 | −0.0173 | 0.0049 | 1.527 | 0.0083 |
| = 14.3625 | +25 | −0.1384 | 0.0966 | 1.285 | −0.0233 | 0.0080 | 2.025 | −0.0233 | 0.0804 | 1.628 | 0.0084 |
| = 8.6175 | −25 | −0.1540 | 0.0947 | 1.243 | −0.0230 | 0.0078 | 1.925 | −0.0207 | 0.0065 | 1.534 | 0.0076 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, S.; Zeng, Y.; Qian, J.; Yang, F.; Li, Y. CPSOGSA Optimization Algorithm Driven Cascaded 3DOF-FOPID-FOPI Controller for Load Frequency Control of DFIG-Containing Interconnected Power System. Energies 2023, 16, 1364. https://doi.org/10.3390/en16031364
Xie S, Zeng Y, Qian J, Yang F, Li Y. CPSOGSA Optimization Algorithm Driven Cascaded 3DOF-FOPID-FOPI Controller for Load Frequency Control of DFIG-Containing Interconnected Power System. Energies. 2023; 16(3):1364. https://doi.org/10.3390/en16031364
Chicago/Turabian StyleXie, Shihao, Yun Zeng, Jing Qian, Fanjie Yang, and Youtao Li. 2023. "CPSOGSA Optimization Algorithm Driven Cascaded 3DOF-FOPID-FOPI Controller for Load Frequency Control of DFIG-Containing Interconnected Power System" Energies 16, no. 3: 1364. https://doi.org/10.3390/en16031364
APA StyleXie, S., Zeng, Y., Qian, J., Yang, F., & Li, Y. (2023). CPSOGSA Optimization Algorithm Driven Cascaded 3DOF-FOPID-FOPI Controller for Load Frequency Control of DFIG-Containing Interconnected Power System. Energies, 16(3), 1364. https://doi.org/10.3390/en16031364






