Diminishing Active Power Loss and Improving Voltage Profile Using an Improved Pathfinder Algorithm Based on Inertia Weight
Abstract
1. Introduction
- Inertia weight () was added to the parameter of the PFA (i.e., the vibration coefficient (ε) and fluctuation coefficient (A)) to improve the random walk of prey. The that was added to ε and A enhanced the ability to transit between exploration and exploitation and was proposed to solve the ORPD problem to diminish active power loss and to overcome the challenges of the PFA in reducing the searching ability when the problem becomes complex for the reliability and effective operation of the power systems.
- The penalty function combined with the objective function for better performance by including the load bus voltage, reactive power generation, and apparent power flow to avoid violation.
- The results obtained from the proposed IPFA with other algorithms showed that the proposed IPFA provided superior results compared with others.
2. Problem Formulation
2.1. Equality Constraints
2.2. Inequality Constraints
2.2.1. Generator Constraints
2.2.2. Reactive Power Compensation Limits
2.2.3. Transformer Tap Ratio Constraints
2.2.4. Line Flow Limits
3. Pathfinder Algorithm
3.1. Proposed Improved PFA (IPFA)
3.2. Implementation of the IPFA to the ORPD Problem
- Parameter initialization (size of the population, number of iterations, search space size, and system data).
- Run Newton–Raphson (NR) LF and calculate the fitness.
- Update counter (i.e., k = k + 1).
- Allow the swarms to randomly move using Equation (16).
- Determine the total power loss using Equation (11).
- Use Equations (24) and (25) to update and move the pathfinder and follower to the next position.
- Check the control variable if it is in a permissible range.
- Then select and store the best value.
- Are the stopping criteria satisfied? If not, go back to step 2; if YES, go to step 10.
- Display the result and end.
4. Result and Discussion
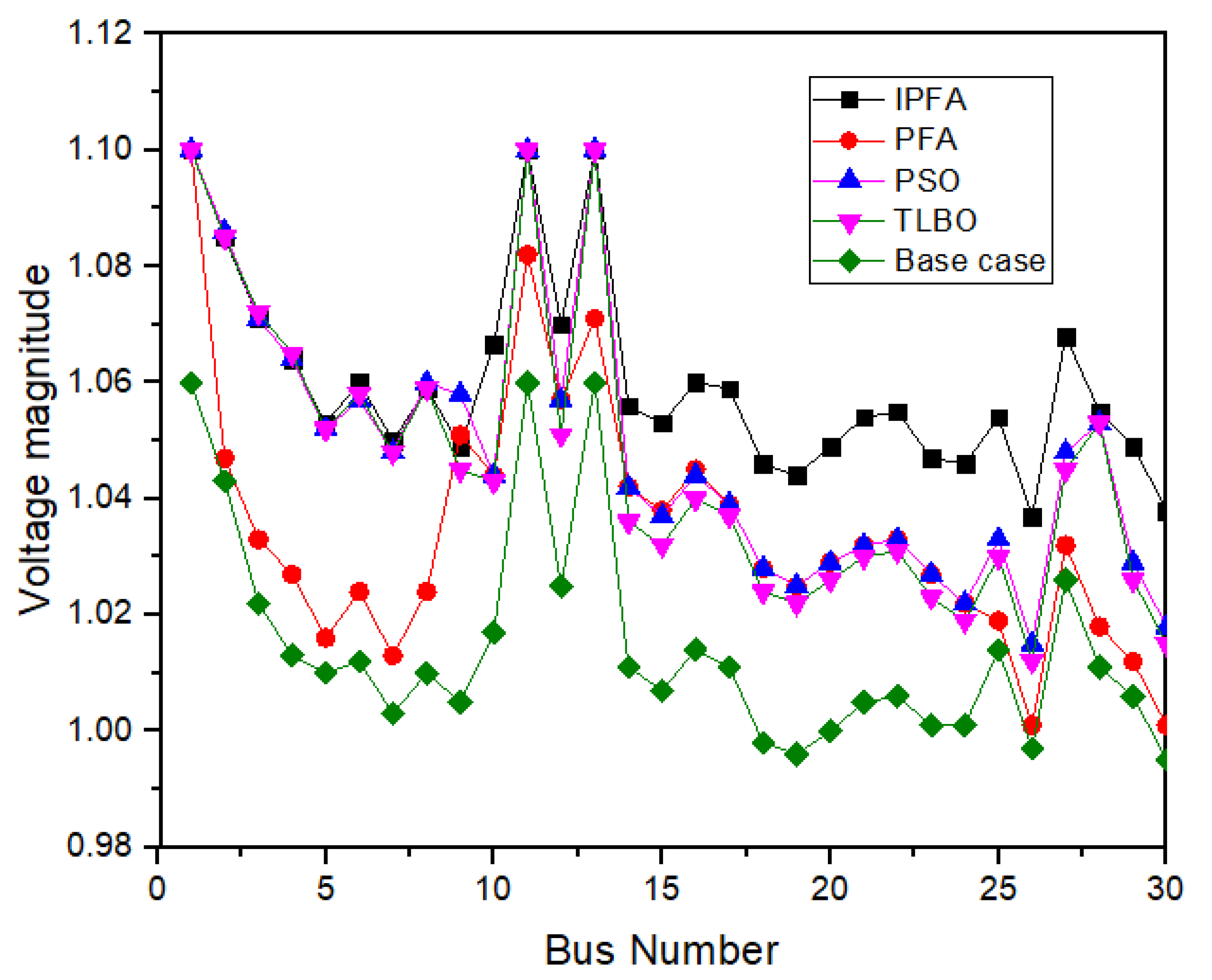
4.1. IEEE 30 Bus System
4.2. IEEE 118 Bus System


| Algorithms | Best MW | Worst MW | Mean MW | STD | % Save |
|---|---|---|---|---|---|
| IPFA | 115.048 | 118.758 | 116.903 | 2.62337 | 13.41 |
| PFA | 120.1287 | 123.425 | 121.7769 | 2.3308 | 9.58 |
| PSO | 117.9129 | 123.873 | 120.8930 | 4.2144 | 9.75 |
| TLBO | 118.0524 | 119.895 | 118.9737 | 1.30291 | 11.15 |
| MFO [23] | 116.4254 | - | - | - | 12.37 |
| HICA-PSO [42] | 127.82 | - | - | - | - |
| GSA [30] | 127.76 | - | - | - | 3.84 |
| FA-APTFPSO#4 [6] | 129.8815 | 146.6919 | 136.9296 | 4.2154 | 46.60 |
| ALC-PSO [26] | 121.53 | 132.99 | - | 91 × 10-10 | - |
| CPVEIHBMO [44] | 124.098 | - | - | - | 6.60 |
| GWO [27] | 120.65 | - | - | - | 9.19 |
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Symbols | Meaning |
| is the active power loss | |
| is the k branch | |
| is the overall number of transmission losses | |
| k | is the branch between bus i and j |
| is the voltage angle between bus i and j | |
| are the voltages at the ith and jth bus, respectively | |
| is the overall number of buses/nodes | |
| are the active and reactive power generations, respectively | |
| are the active and reactive load power demands at the ith bus, respectively | |
| is the mutual susceptance | |
| is the overall number of generators | |
| is the overall number of reactive power compensation | |
| is the overall number of transformers | |
| are random variables equal to , respectively | |
| is the vector position of the pathfinder | |
| is the current iteration | |
| are the positioned vectors of members i and j | |
| and | are randomly chosen between (1,2) in each iteration |
| are the random variables between (0,1) | |
| is the total number of iterations | |
| is the distance between two members | |
| are the random vectors between (−1, 1) | |
| A and | are the fluctuation and vibration coefficients, respectively |
| and | are the maximum and minimum inertia weights, respectively |
| z | is the current iteration |
| is the inertia weight | |
| are the maximum and minimum of the generator voltage, respectively | |
| are the maximum and minimum of the reactive power generated, respectively | |
| are the maximum and minimum active power generated, respectively | |
| are the maximum and minimum of the reactive power compensation, respectively | |
| are the maximum and minimum of the transformer tabs setting, respectively | |
| are the maximum and minimum of the load bus voltage, respectively | |
| is the apparent line flow | |
| is the maximum apparent line flow |
References
- Roy, R.; Das, T.; Mandal, K.K. Optimal reactive power dispatch using a novel optimization algorithm. J. Electr. Syst. Inf. Technol. 2021, 8, 1–24. [Google Scholar] [CrossRef]
- Sahli, Z.; Hamouda, A.; Bekrar, A.; Trentesaux, D. Reactive power dispatch optimization with voltage profile improvement using an efficient hybrid algorithm. Energies 2018, 11, 2134. [Google Scholar] [CrossRef]
- Adegoke, S.A.; Sun, Y. Power system optimization approach to mitigate voltage instability issues: A review. Cogent Eng. 2023, 10, 2153416. [Google Scholar] [CrossRef]
- Polprasert, J.; Ongsakul, W.; Dieu, V.N. Optimal reactive power dispatch using improved pseudo-gradient search particle swarm optimization. Electr. Power Components Syst. 2016, 44, 518–532. [Google Scholar] [CrossRef]
- Muhammad, Y.; Khan, R.; Raja, M.A.Z.; Ullah, F.; Chaudhary, N.I.; He, Y. Solution of optimal reactive power dispatch with FACTS devices: A survey. Energy Rep. 2020, 6, 2211–2229. [Google Scholar] [CrossRef]
- Nasouri Gilvaei, M.; Jafari, H.; Jabbari Ghadi, M.; Li, L. A novel hybrid optimization approach for reactive power dispatch problem considering voltage stability index. Eng. Appl. Artif. Intell. 2020, 96, 103963. [Google Scholar] [CrossRef]
- Ettappan, M.; Vimala, V.; Ramesh, S.; Kesavan, V.T. Optimal reactive power dispatch for real power loss minimization and voltage stability enhancement using Artificial Bee Colony Algorithm. Microprocess. Microsyst. 2020, 76, 103085. [Google Scholar] [CrossRef]
- Sayah, S. Modified differential evolution approach for practical optimal reactive power dispatch of hybrid AC–DC power systems. Appl. Soft Comput. J. 2018, 73, 591–606. [Google Scholar] [CrossRef]
- Alam, M.S.; De, M. Optimal reactive power dispatch using hybrid loop-genetic based algorithm. In Proceedings of the 2016 National Power Systems Conference (NPSC), Bhubaneswar, India, 19–21 December 2016; pp. 1–6. [Google Scholar]
- Khaled, U.; Eltamaly, A.M.; Beroual, A. Optimal power flow using particle swarm optimization of renewable hybrid distributed generation. Energies 2017, 10, 1013. [Google Scholar] [CrossRef]
- Barakat, A.F.; El-Sehiemy, R.A.; Elsayd, M.I.; Osman, E. An Enhanced Jaya Optimization Algorithm (EJOA) for Solving Multi-Objective ORPD Problem. In Proceedings of the 2019 International Conference on Innovative Trends in Computer Engineering (ITCE), Aswan, Egypt, 2–4 February 2019; pp. 479–484. [Google Scholar]
- Das, T.; Roy, R.; Mandal, K.K. Optimal Reactive Power Dispatch Incorporating Solar Power Using Jaya Algorithm; Springer: Singapore, 2020. [Google Scholar]
- Nguyen, T.T.; Vo, D.N.; Van Tran, H.; Van Dai, L. Optimal Dispatch of Reactive Power Using Modified Stochastic Fractal Search Algorithm. Complexity 2019, 2019, 4670820. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Vo, D.N. Improved Social Spider Optimization Algorithm for Optimal Reactive Power Dispatch Problem with Different Objectives; Springer: London, UK, 2020. [Google Scholar]
- Li, Z.; Cao, Y.; Van Dai, L.; Yang, X.; Nguyen, T.T. Finding solutions for optimal reactive power dispatch problem by a novel improved antlion optimization algorithm. Energies 2019, 12, 2968. [Google Scholar] [CrossRef]
- Abdel-Fatah, S.; Ebeed, M.; Kamel, S. Optimal Reactive Power Dispatch Using Modified Sine Cosine Algorithm. In Proceedings of the 2019 International Conference on Innovative Trends in Computer Engineering (ITCE), Aswan, Egypt, 2–4 February 2019; pp. 510–514. [Google Scholar]
- Biswas, P.P.; Suganthan, P.N.; Mallipeddi, R.; Amaratunga, G.A.J. Optimal reactive power dispatch with uncertainties in load demand and renewable energy sources adopting scenario-based approach. Appl. Soft Comput. J. 2019, 75, 616–632. [Google Scholar] [CrossRef]
- Üney, M.Ş.; Çetinkaya, N. New metaheuristic algorithms for reactive power optimization. Teh. Vjesn. 2019, 26, 1427–1433. [Google Scholar]
- Barakat, A.F.; El-Sehiemy, R.A.; Elsayd, M.I.; Osman, E. Solving reactive power dispatch problem by using JAYA optimization algorithm. Int. J. Eng. Res. Africa 2018, 36, 12–24. [Google Scholar] [CrossRef]
- Shaheen, A.M.; El-Sehiemy, R.A.; Farrag, S.M. Integrated Strategies of Backtracking Search Optimizer for Solving Reactive Power Dispatch Problem. IEEE Syst. J. 2018, 12, 424–433. [Google Scholar] [CrossRef]
- Medani, K.; Ben Oualid, S.S.; Bekrar, A. Whale optimization algorithm based optimal reactive power dispatch: A case study of the Algerian power system. Electr. Power Syst. Res. 2018, 163, 696–705. [Google Scholar] [CrossRef]
- Heidari, A.A.; Ali Abbaspour, R.; Rezaee Jordehi, A. Gaussian bare-bones water cycle algorithm for optimal reactive power dispatch in electrical power systems. Appl. Soft Comput. J. 2017, 57, 657–671. [Google Scholar] [CrossRef]
- Ng Shin Mei, R.; Sulaiman, M.H.; Mustaffa, Z.; Daniyal, H. Optimal reactive power dispatch solution by loss minimization using moth-flame optimization technique. Appl. Soft Comput. J. 2017, 59, 210–222. [Google Scholar] [CrossRef]
- Mouassa, S.; Bouktir, T.; Salhi, A. Ant lion optimizer for solving optimal reactive power dispatch problem in power systems. Eng. Sci. Technol. Int. J. 2017, 20, 885–895. [Google Scholar] [CrossRef]
- Mukherjee, A.; Mukherjee, V. Chaotic krill herd algorithm for optimal reactive power dispatch considering FACTS devices. Appl. Soft Comput. J. 2016, 44, 163–190. [Google Scholar] [CrossRef]
- Singh, R.P.; Mukherjee, V.; Ghoshal, S.P. Optimal reactive power dispatch by particle swarm optimization with an aging leader and challengers. Appl. Soft Comput. J. 2015, 29, 298–309. [Google Scholar] [CrossRef]
- Sulaiman, M.H.; Mustaffa, Z.; Mohamed, M.R.; Aliman, O. Using the gray wolf optimizer for solving optimal reactive power dispatch problem. Appl. Soft Comput. J. 2015, 32, 286–292. [Google Scholar] [CrossRef]
- Ghasemi, M.; Ghanbarian, M.M.; Ghavidel, S.; Rahmani, S.; Mahboubi Moghaddam, E. Modified teaching learning algorithm and double differential evolution algorithm for optimal reactive power dispatch problem: A comparative study. Inf. Sci. 2014, 278, 231–249. [Google Scholar] [CrossRef]
- Le Dinh, L.; Vo Ngoc, D.; Vasant, P. Artificial bee colony algorithm for solving optimal power flow problem. Sci. World J. 2013, 2013, 159040. [Google Scholar] [CrossRef]
- Duman, S.; Güvenç, U.; Sönmez, Y.; Yörükeren, N. Optimal power flow using gravitational search algorithm. Energy Convers. Manag. 2012, 59, 86–95. [Google Scholar] [CrossRef]
- Zandi, Z.; Afjei, E.; Sedighizadeh, M. Reactive power dispatch using Big Bang-Big Crunch optimization algorithm for voltage stability enhancement. In Proceedings of the 2012 IEEE International Conference on Power and Energy (PECon), Kota Kinabalu Sabah, Malaysia, 2–5 December 2012; pp. 239–244. [Google Scholar]
- Mahadevan, K.; Kannan, P.S. Comprehensive learning particle swarm optimization for reactive power dispatch. Appl. Soft Comput. J. 2010, 10, 641–652. [Google Scholar] [CrossRef]
- Yapici, H. Solution of optimal reactive power dispatch problem using pathfinder algorithm. Eng. Optim. 2021, 53, 1946–1963. [Google Scholar] [CrossRef]
- Adegoke, S.A.; Sun, Y. Optimum Reactive Power Dispatch Solution using Hybrid Particle Swarm Optimization and Pathfinder Algorithm. Int. J. Comput. 2022, 21, 403–410. [Google Scholar] [CrossRef]
- Yapici, H.; Cetinkaya, N. A new meta-heuristic optimizer: Pathfinder algorithm. Appl. Soft Comput. J. 2019, 78, 545–568. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R. A Modified Particle Swarm Optimizer. IEEE Int. Conf. Evol. Comput. 1998, 69–73. [Google Scholar] [CrossRef]
- Htay, T.T.; Mon, K.K.; Lin, O.Z. Optimal reactive power dispatch using particle swarm optimization algorithm for Yangon distribution network. IOP Conf. Ser. Earth Environ. Sci. 2020, 13, 101726. [Google Scholar] [CrossRef]
- Liang, C.H.; Chung, C.Y.; Wong, K.P.; Duan, X.Z.; Tse, C.T. Study of differential evolution for optimal reactive power flow’. IET Gener. Transm. Distrib. 2007, 1, 253–260. [Google Scholar] [CrossRef]
- Pandya, S.; Roy, R. Particle Swarm Optimization Based Optimal Reactive Power Dispatch. In Proceedings of the 2015 IEEE International Conference on Electrical, Computer and Communication Technologies (ICECCT), Coimbatore, India, 5–7 March 2015. [Google Scholar]
- Subbaraj, P.; Rajnarayanan, P.N. Optimal reactive power dispatch using self-adaptive real coded genetic algorithm. Electr. Power Syst. Res. 2009, 79, 374–381. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y.; Li, B. A hybrid artificial bee colony assisted differential evolution algorithm for optimal reactive power flow. Int. J. Electr. Power Energy Syst. 2013, 52, 25–33. [Google Scholar] [CrossRef]
- Mehdinejad, M.; Mohammadi-Ivatloo, B.; Dadashzadeh-Bonab, R.; Zare, K. Solution of optimal reactive power dispatch of power systems using hybrid particle swarm optimization and imperialist competitive algorithms. Int. J. Electr. Power Energy Syst. 2016, 83, 104–116. [Google Scholar] [CrossRef]
- Fernández-Porras, P.; Panteli, M.; Quirós-Tortós, J. Intentional controlled islanding: When to island for power system blackout prevention. IET Gener. Transm. Distrib. 2018, 12, 3542–3549. [Google Scholar] [CrossRef]
- Ghasemi, A.; Valipour, K.; Tohidi, A. Multi objective optimal reactive power dispatch using a new multi objective strategy. Int. J. Electr. Power Energy Syst. 2014, 57, 318–334. [Google Scholar] [CrossRef]



| Parameter Name | Value |
|---|---|
| Number of iterations | 200 and 300 |
| Particle number | 50 |
| 0.9 | |
| 0.4 | |
| A | A |
| Variables | Upper Limits (p.u) | Lower Limits (p.u) |
|---|---|---|
| The voltage of the load bus | 1.1 | 0.9 |
| Transformer tab | 1.1 | 0.9 |
| Shunt compensator | 0.04 | 0 |
| IEEE Test Systems | 30 Bus System | 118 Bus System |
|---|---|---|
| Number of buses | 30 | 118 |
| Generators | 6 | 54 |
| Transformers | 4 | 9 |
| Shunt compensator | 2 | 14 |
| Control variables | 12 | 77 |
| Base case power loss (MW) | 17.89 | 132.86 |
| Algorithms | Best MW | Worst MW | Mean | STD | % of Loss Reduction |
|---|---|---|---|---|---|
| IPFA | 16.035 | 17.053 | 16.544 | 0.71983 | 10.37 |
| PFA | 17.4469 | 17.982 | 17.71445 | 0.37844 | 2.52 |
| PSO | 16.1568 | 18.214 | 17.206 | 1.42553 | 9.58 |
| TLBO | 16.1607 | 17.983 | 17.07185 | 1.28856 | 9.67 |
| DE [41] | 16.2184 | 16.6060 | - | 0.0895 | - |
| DE-ABC [41] | 16.2163 | 16.2164 | - | 2.34 × 10-5 | - |
| ABC [41] | 16.2325 | 17.693 | - | 0.34919 | - |
| PSO [39] | 16.1810 | - | - | - | - |
| DE [38] | 16.4939 | - | - | - | - |
| EP [40] | 16.3896 | - | - | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adegoke, S.A.; Sun, Y. Diminishing Active Power Loss and Improving Voltage Profile Using an Improved Pathfinder Algorithm Based on Inertia Weight. Energies 2023, 16, 1270. https://doi.org/10.3390/en16031270
Adegoke SA, Sun Y. Diminishing Active Power Loss and Improving Voltage Profile Using an Improved Pathfinder Algorithm Based on Inertia Weight. Energies. 2023; 16(3):1270. https://doi.org/10.3390/en16031270
Chicago/Turabian StyleAdegoke, Samson Ademola, and Yanxia Sun. 2023. "Diminishing Active Power Loss and Improving Voltage Profile Using an Improved Pathfinder Algorithm Based on Inertia Weight" Energies 16, no. 3: 1270. https://doi.org/10.3390/en16031270
APA StyleAdegoke, S. A., & Sun, Y. (2023). Diminishing Active Power Loss and Improving Voltage Profile Using an Improved Pathfinder Algorithm Based on Inertia Weight. Energies, 16(3), 1270. https://doi.org/10.3390/en16031270







