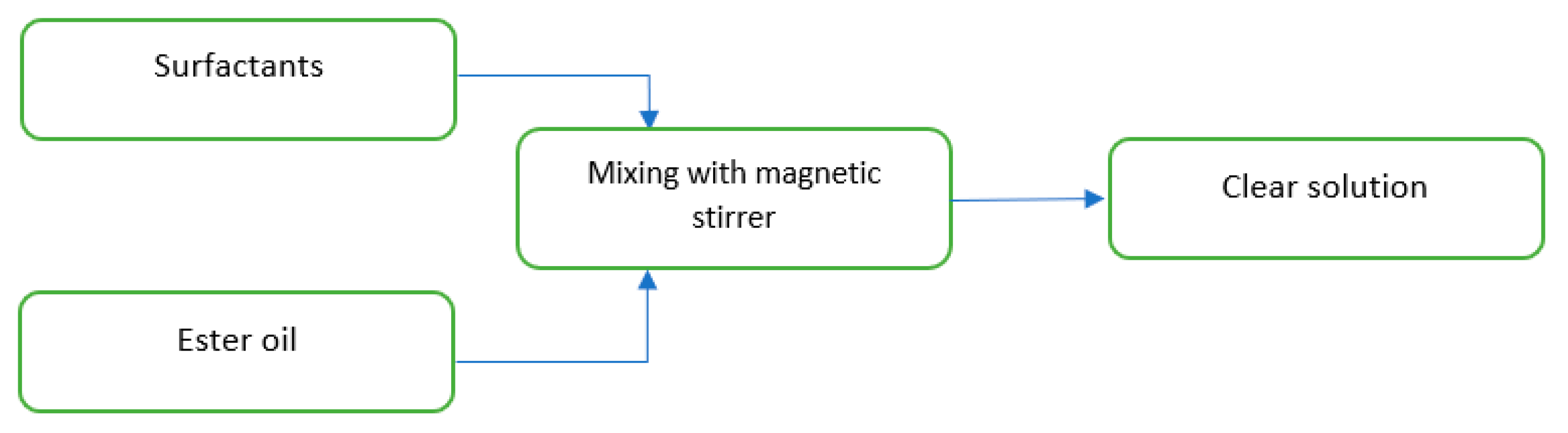
Figure 2.
Used magnetic stirrer with example sample.
Figure 2.
Used magnetic stirrer with example sample.
Figure 3.
Method of making tested solutions.
Figure 3.
Method of making tested solutions.
Figure 4.
Used breakdown voltage tester.
Figure 4.
Used breakdown voltage tester.
Figure 5.
Spherical electrodes in an empty tank.
Figure 5.
Spherical electrodes in an empty tank.
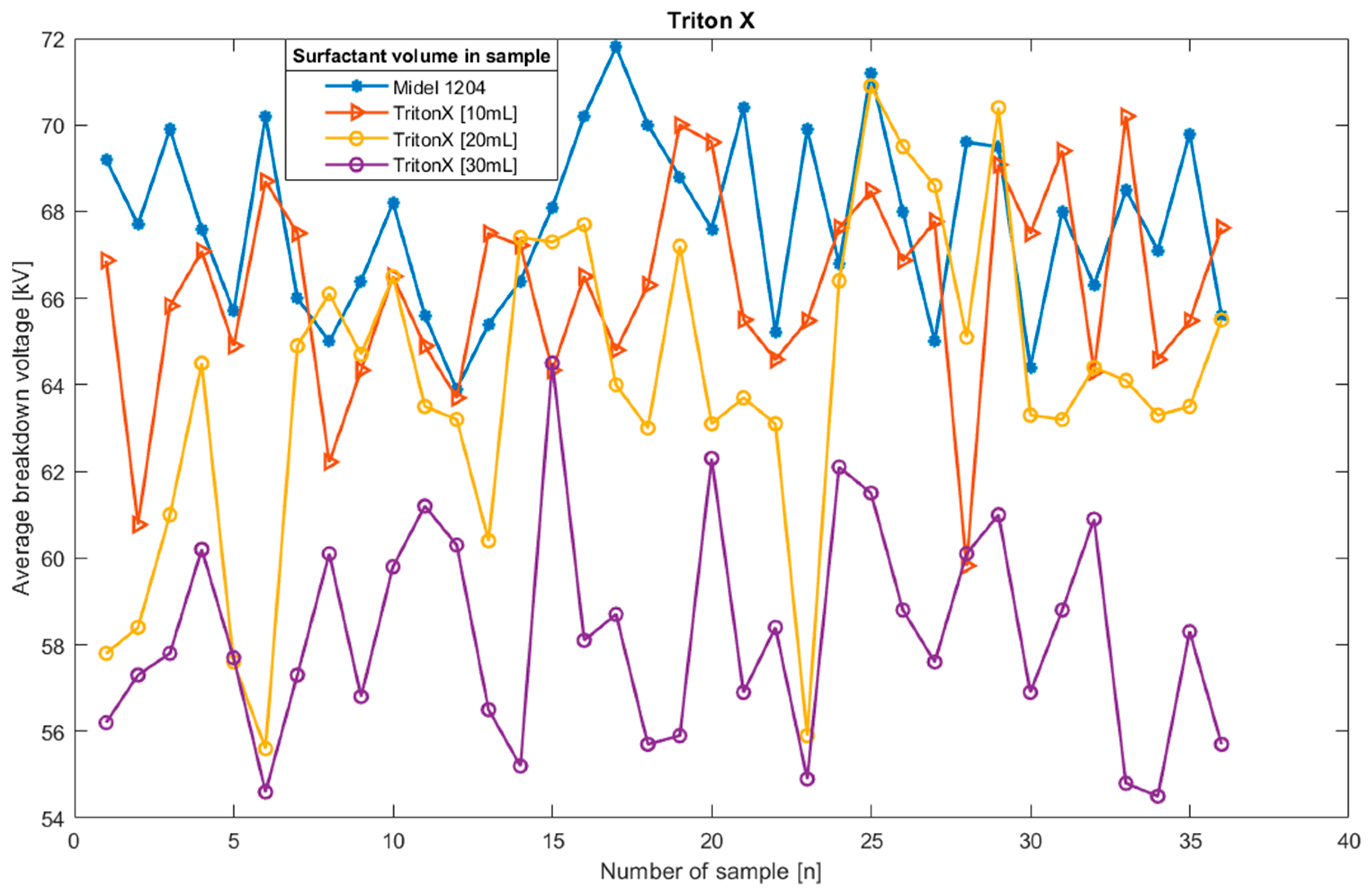
Figure 6.
Average breakdown voltage plot for oil sample Midel 1204 with different concentrations of surfactant Triton X.
Figure 6.
Average breakdown voltage plot for oil sample Midel 1204 with different concentrations of surfactant Triton X.
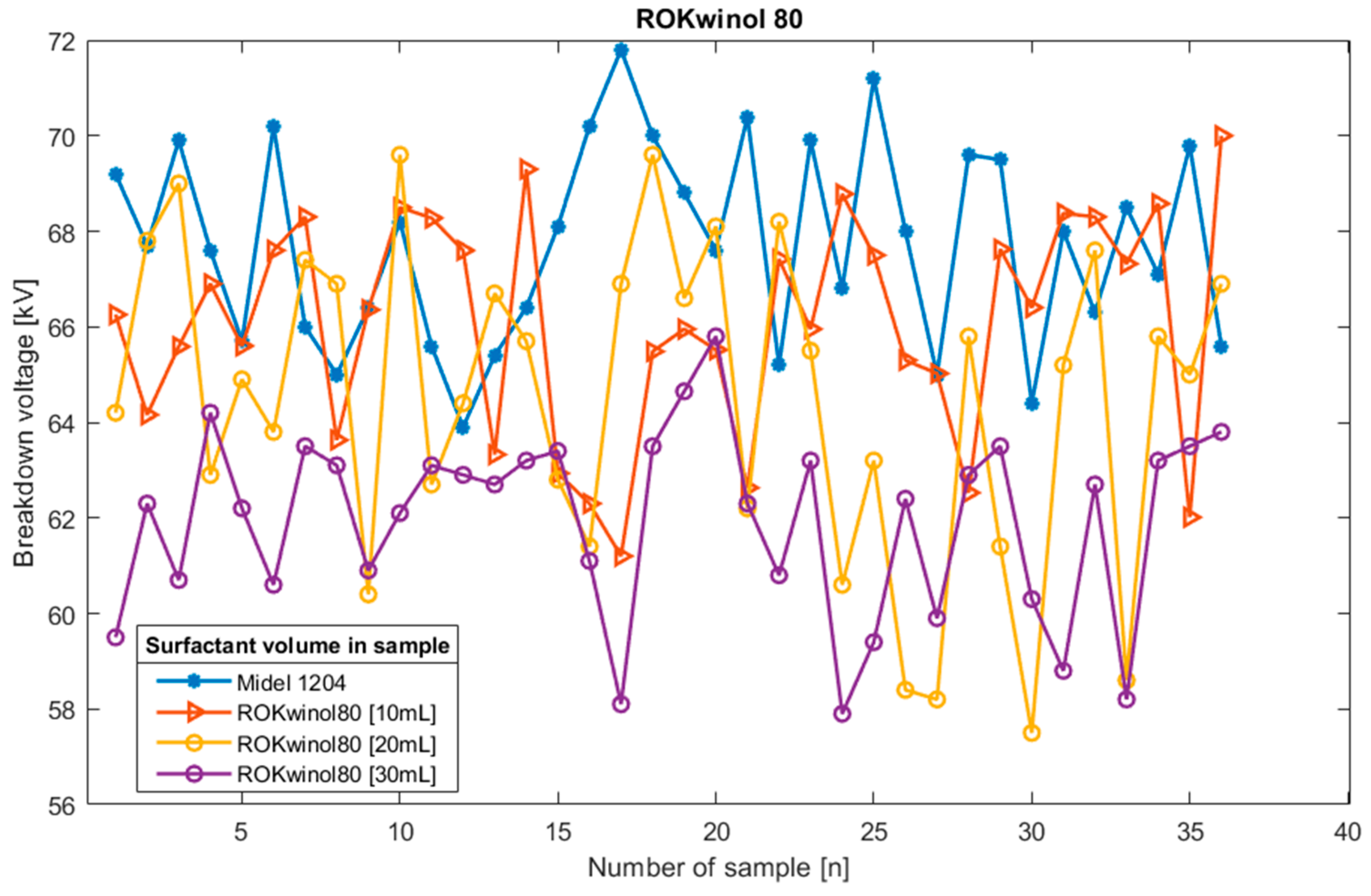
Figure 7.
Breakdown voltage plot for oil sample Midel 1204 with different concentrations of surfactant ROKwino l80.
Figure 7.
Breakdown voltage plot for oil sample Midel 1204 with different concentrations of surfactant ROKwino l80.
Figure 8.
Breakdown voltage plot for oil sample Midel 1204 with different concentrations of surfactant oleic acid.
Figure 8.
Breakdown voltage plot for oil sample Midel 1204 with different concentrations of surfactant oleic acid.
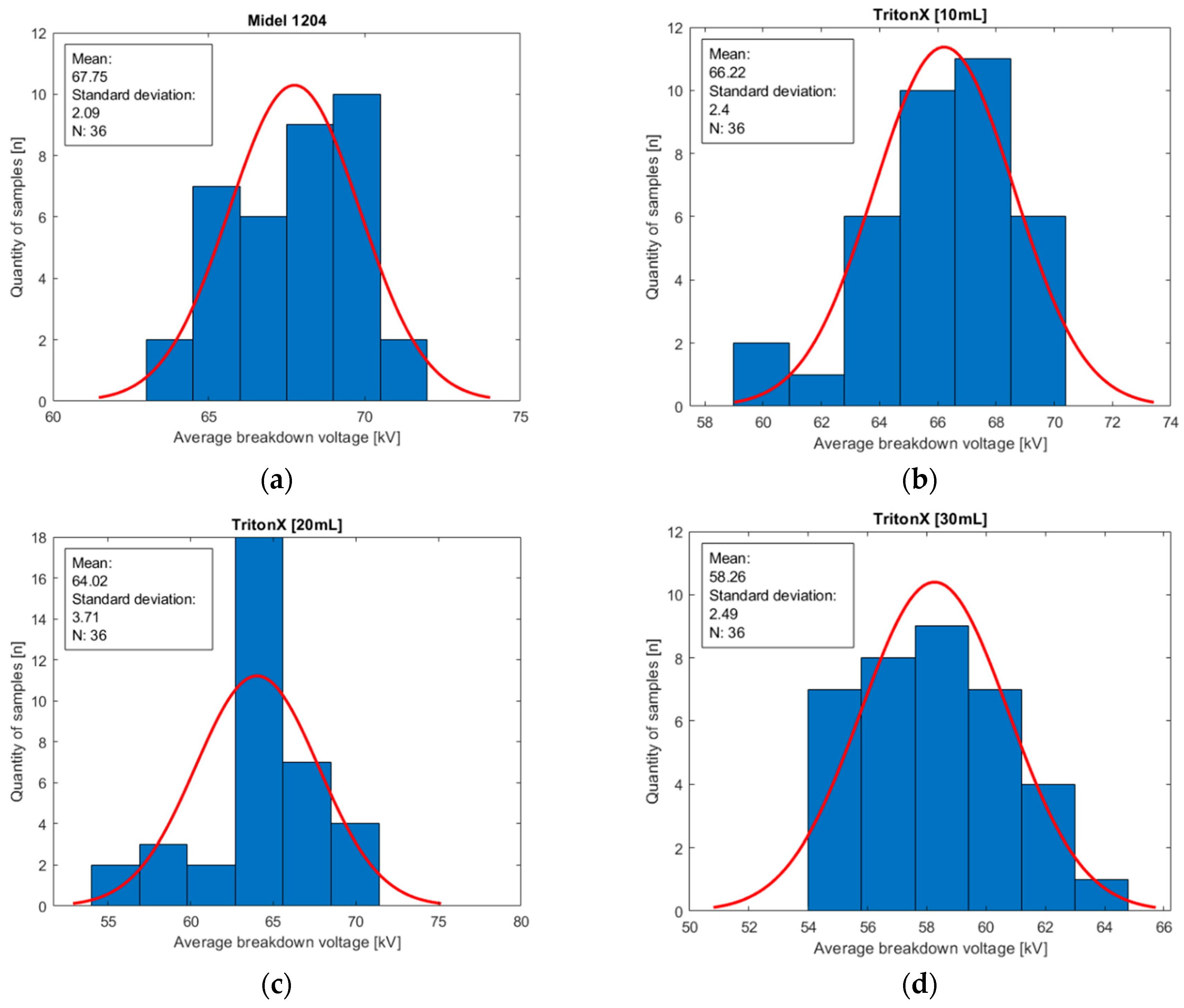
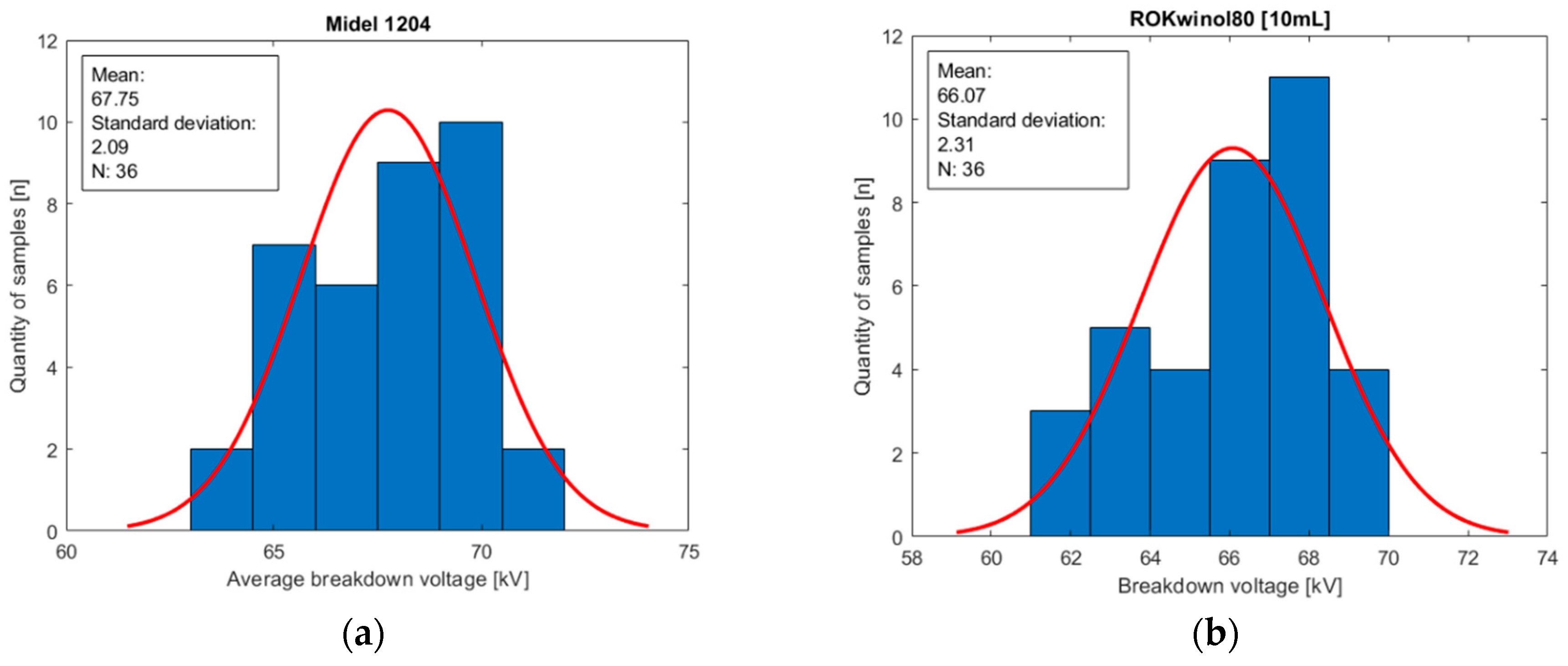
Figure 9.
Histograms of oil population Midel 1204 with different concentrations of surfactant Triton X: (a) base sample of Midel 1204; (b) 10 mL of surfactant Triton X in a sample; (c) 20 mL of surfactant Triton X in a sample; (d) 30 mL of surfactant Triton X in a sample.
Figure 9.
Histograms of oil population Midel 1204 with different concentrations of surfactant Triton X: (a) base sample of Midel 1204; (b) 10 mL of surfactant Triton X in a sample; (c) 20 mL of surfactant Triton X in a sample; (d) 30 mL of surfactant Triton X in a sample.
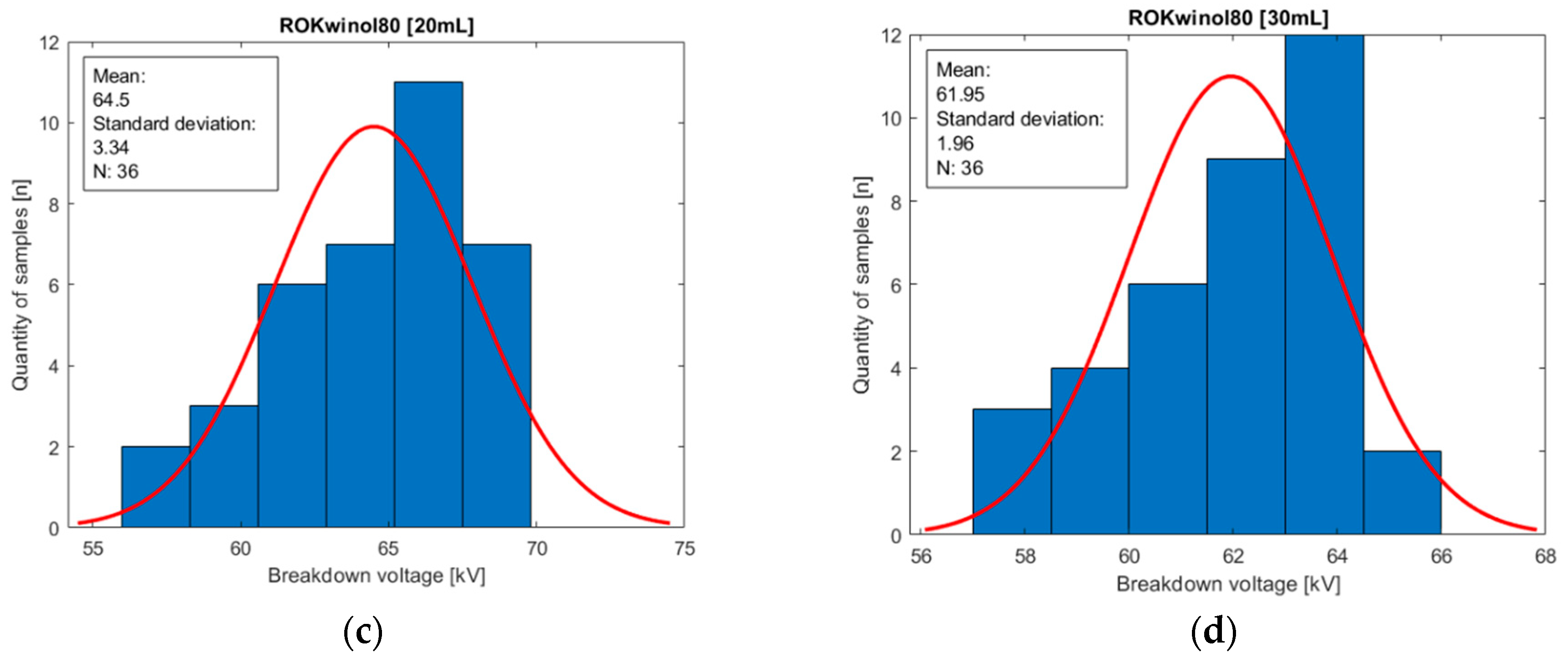
Figure 10.
Histograms of oil population Midel 1204 with different concentrations of surfactant ROKwino l80: (a) base sample of Midel 1204; (b) 10 mL of surfactant ROKwino l80 in a sample; (c) 20 mL of surfactant ROKwino l80 in a sample; (d) 30 mL of surfactant ROKwino l80 in a sample.
Figure 10.
Histograms of oil population Midel 1204 with different concentrations of surfactant ROKwino l80: (a) base sample of Midel 1204; (b) 10 mL of surfactant ROKwino l80 in a sample; (c) 20 mL of surfactant ROKwino l80 in a sample; (d) 30 mL of surfactant ROKwino l80 in a sample.
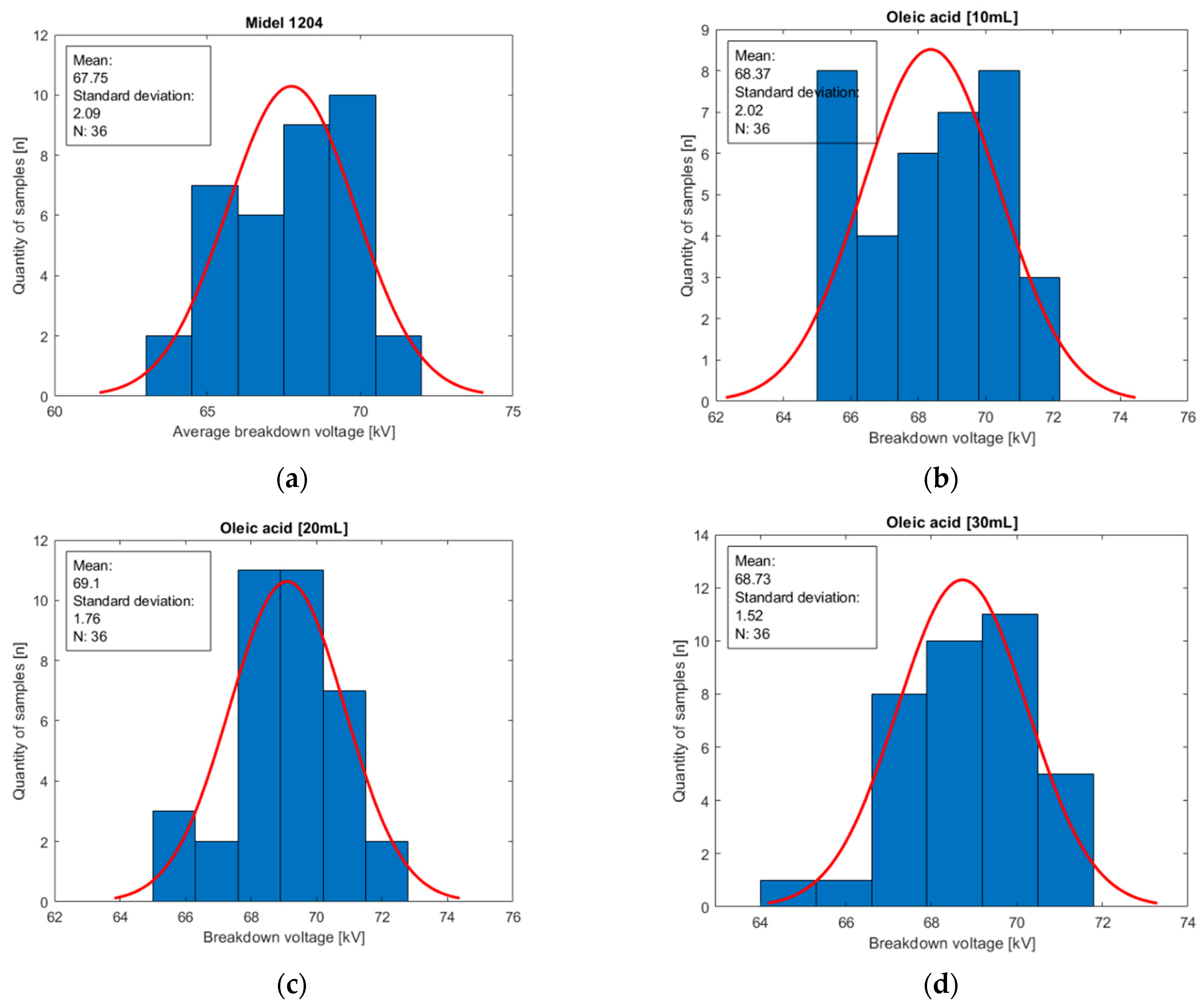
Figure 11.
Histograms of oil population Midel 1204 with different concentrations of surfactant oleic acid: (a) base sample of Midel 1204; (b) 10 mL of surfactant oleic acid in a sample; (c) 20 mL of surfactant oleic acid in a sample; (d) 30 mL of surfactant oleic acid in a sample.
Figure 11.
Histograms of oil population Midel 1204 with different concentrations of surfactant oleic acid: (a) base sample of Midel 1204; (b) 10 mL of surfactant oleic acid in a sample; (c) 20 mL of surfactant oleic acid in a sample; (d) 30 mL of surfactant oleic acid in a sample.
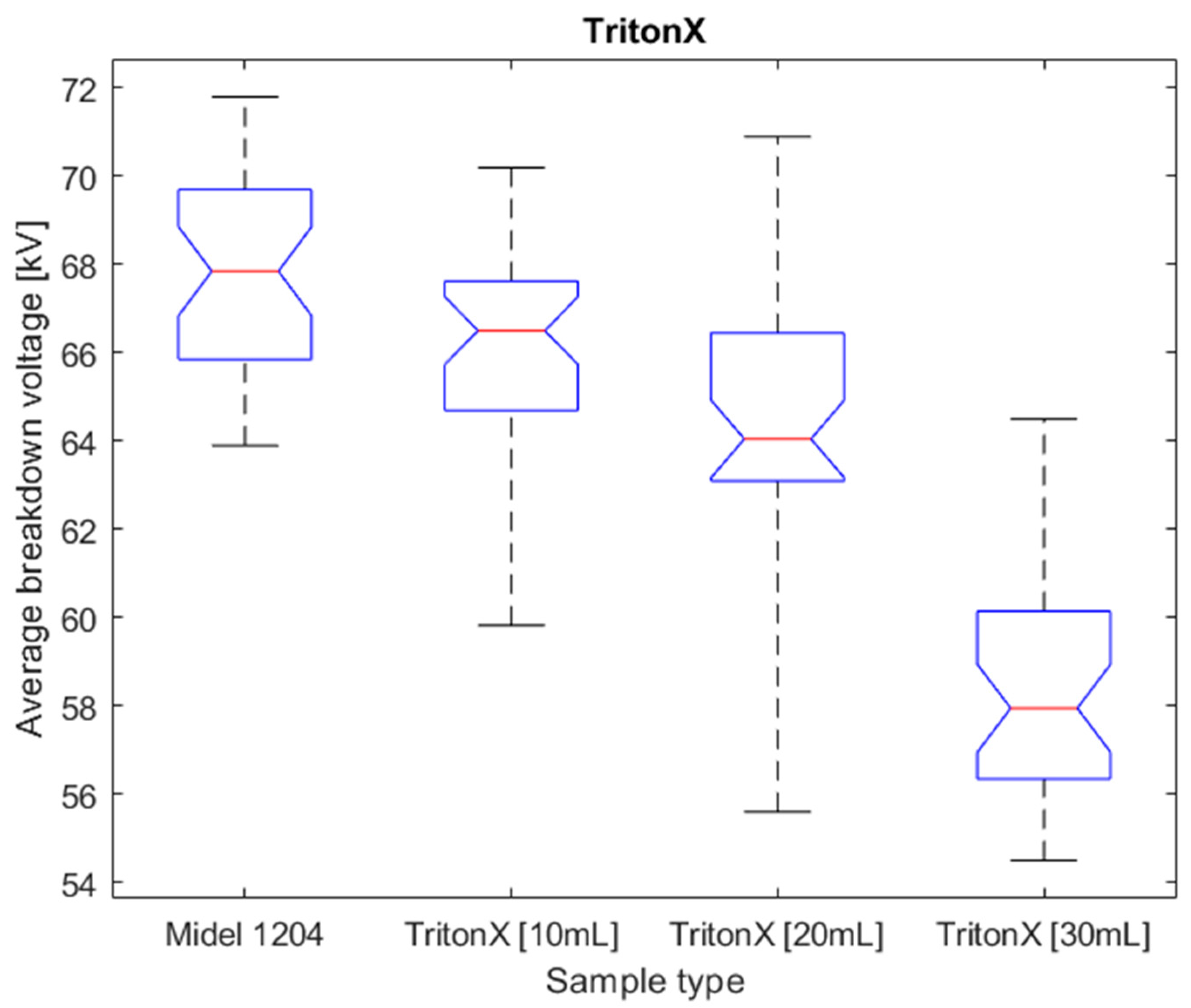
Figure 12.
Box plot for surfactant population of Triton X.
Figure 12.
Box plot for surfactant population of Triton X.
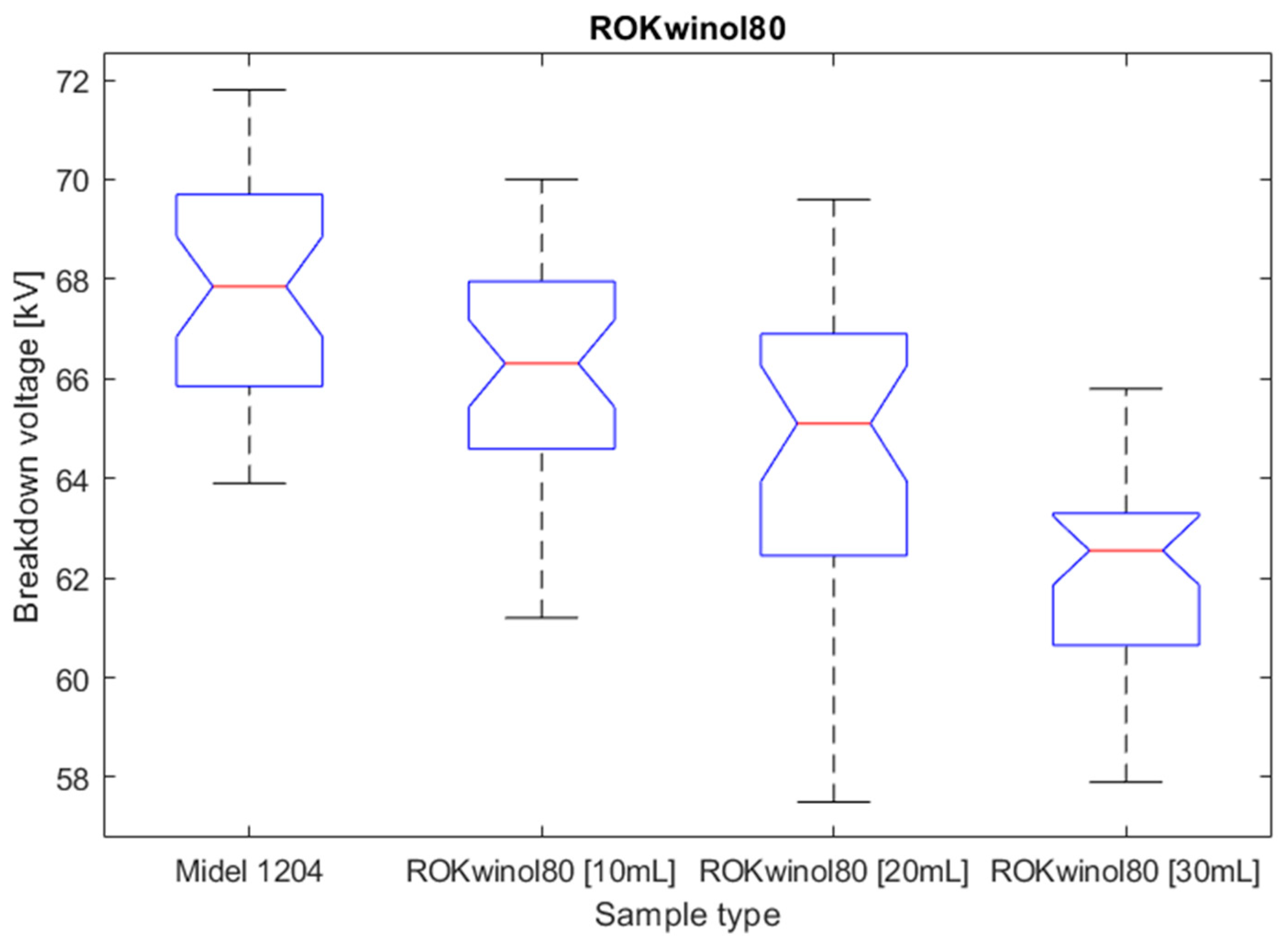
Figure 13.
Box plot for surfactant population of ROKwino l80.
Figure 13.
Box plot for surfactant population of ROKwino l80.
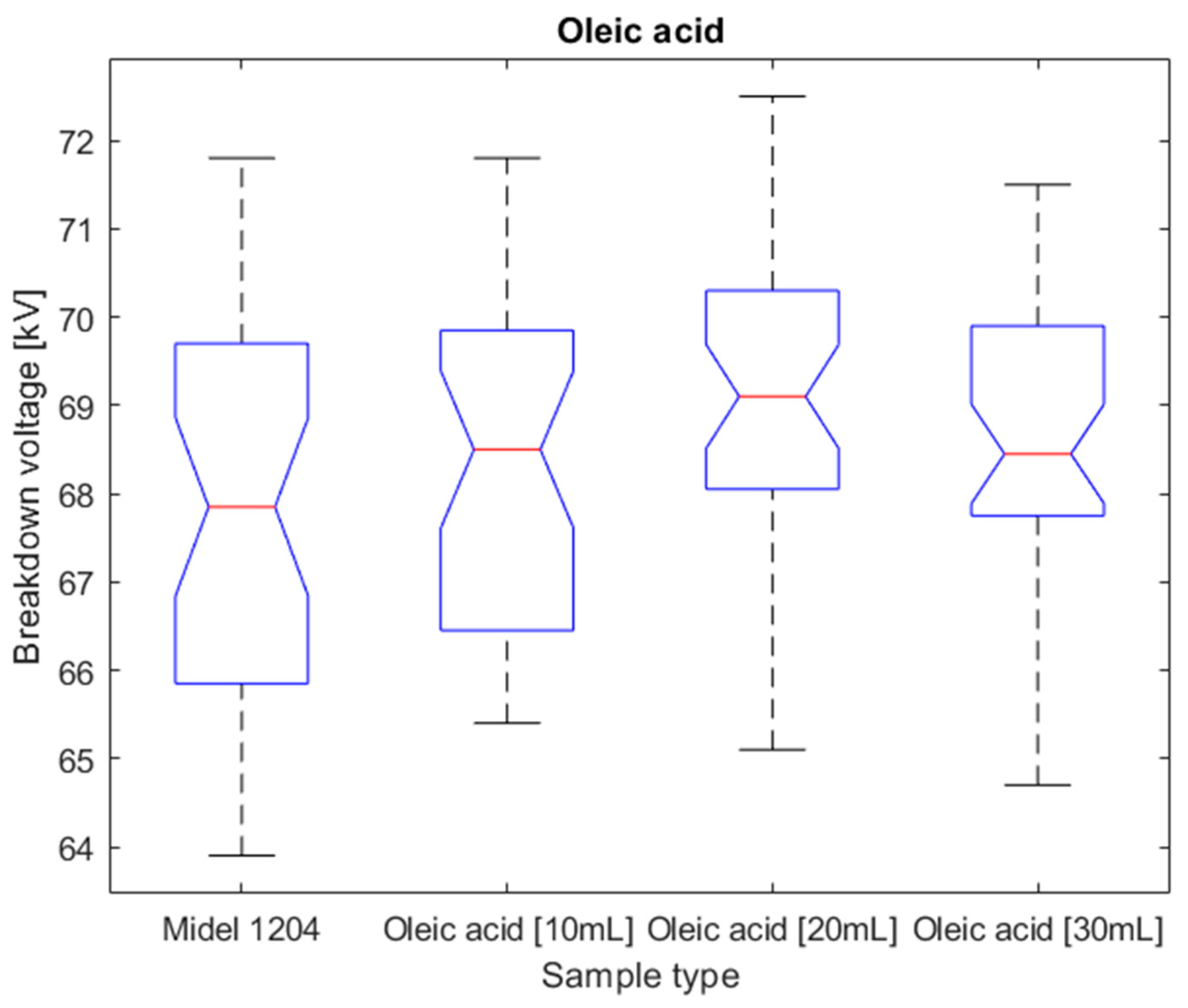
Figure 14.
Box plot for surfactant population of oleic acid.
Figure 14.
Box plot for surfactant population of oleic acid.
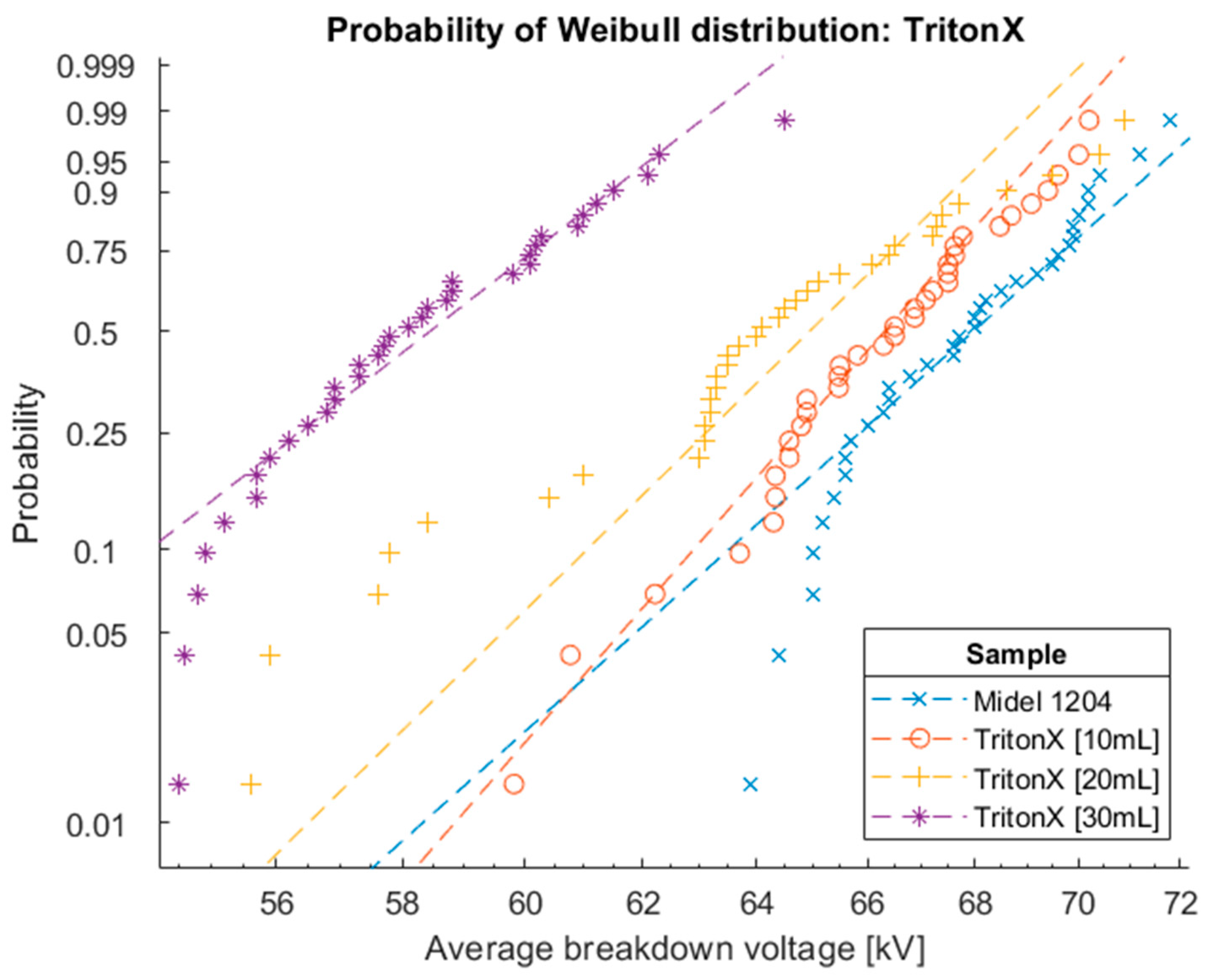
Figure 15.
Cumulation distribution functions for Weibull distribution of oil Midel 1204 with different concentrations of surfactant Triton X.
Figure 15.
Cumulation distribution functions for Weibull distribution of oil Midel 1204 with different concentrations of surfactant Triton X.
Figure 16.
Cumulation distribution functions for Weibull distribution of oil Midel 1204 with different concentrations of surfactant ROKwino l80.
Figure 16.
Cumulation distribution functions for Weibull distribution of oil Midel 1204 with different concentrations of surfactant ROKwino l80.
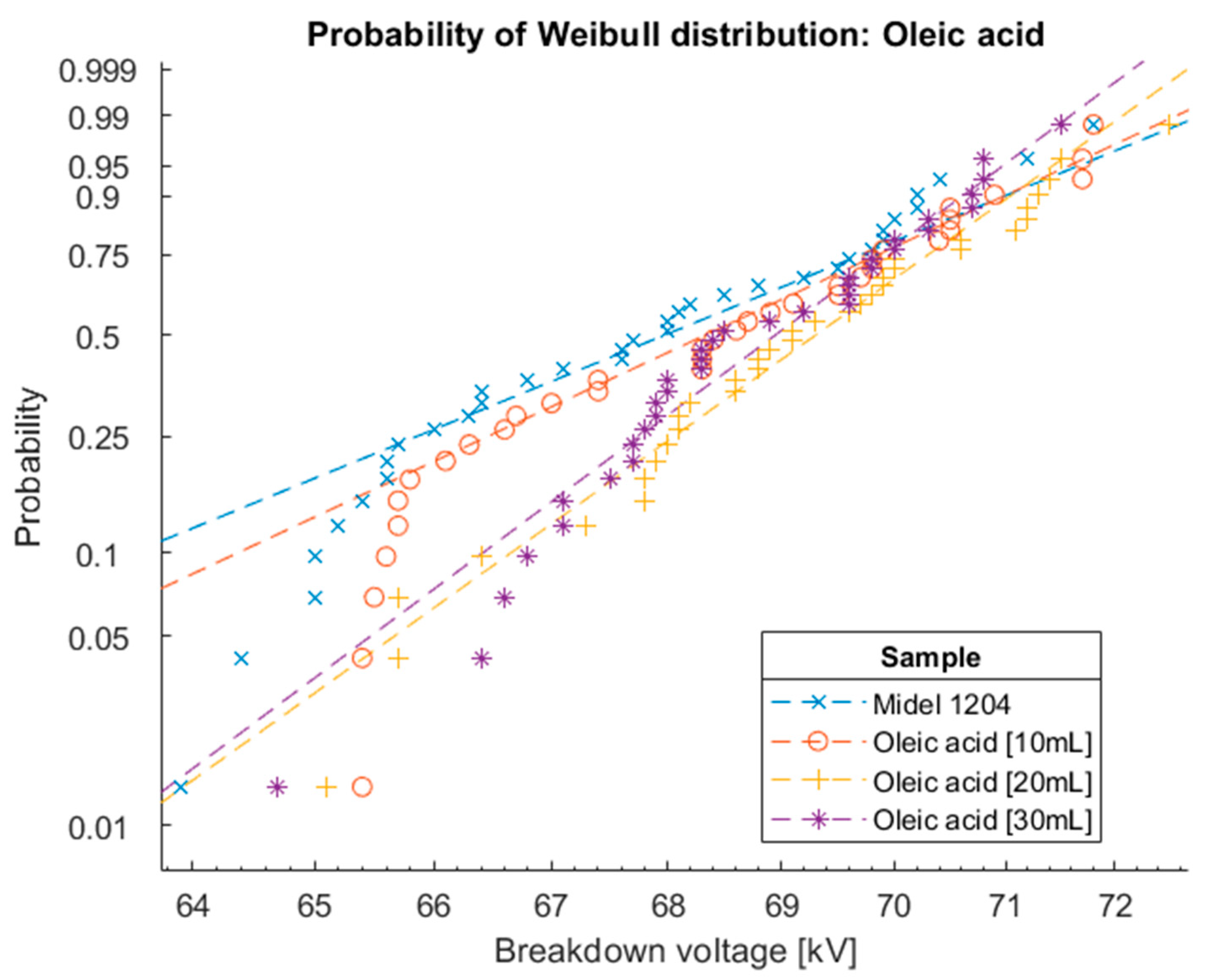
Figure 17.
Cumulation distribution functions for Weibull distribution of oil Midel 1204 with different concentrations of surfactant oleic acid.
Figure 17.
Cumulation distribution functions for Weibull distribution of oil Midel 1204 with different concentrations of surfactant oleic acid.
Figure 18.
Post hoc Bonferroni test for oil Midel 1204 with different concentrations of surfactant Triton X.
Figure 18.
Post hoc Bonferroni test for oil Midel 1204 with different concentrations of surfactant Triton X.
Figure 19.
Post hoc Bonferroni test for oil Midel 1204 with different concentrations of surfactant ROKwino l80.
Figure 19.
Post hoc Bonferroni test for oil Midel 1204 with different concentrations of surfactant ROKwino l80.
Figure 20.
Post hoc Bonferroni test for oil Midel 1204, with different concentrations of surfactant oleic acid.
Figure 20.
Post hoc Bonferroni test for oil Midel 1204, with different concentrations of surfactant oleic acid.
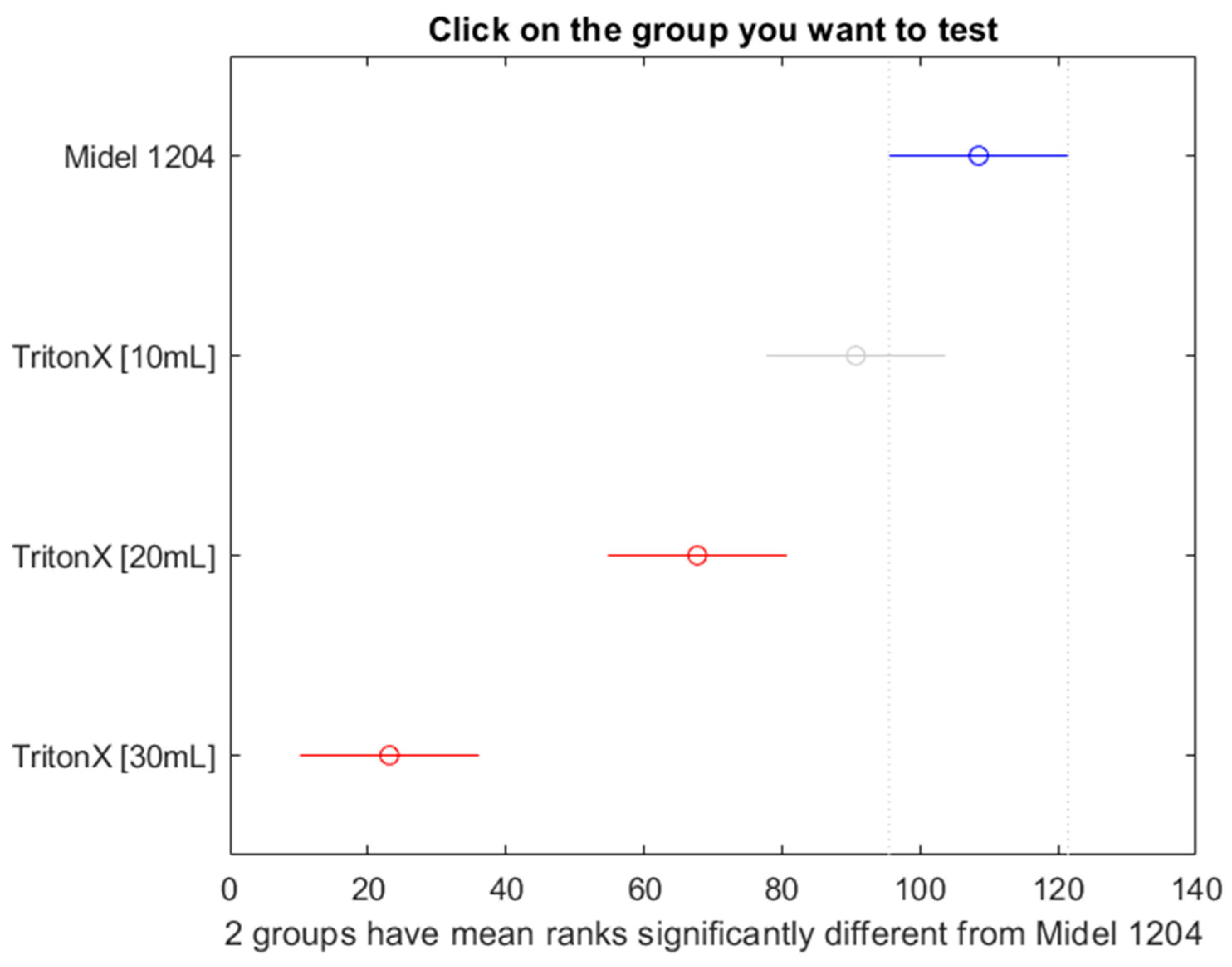
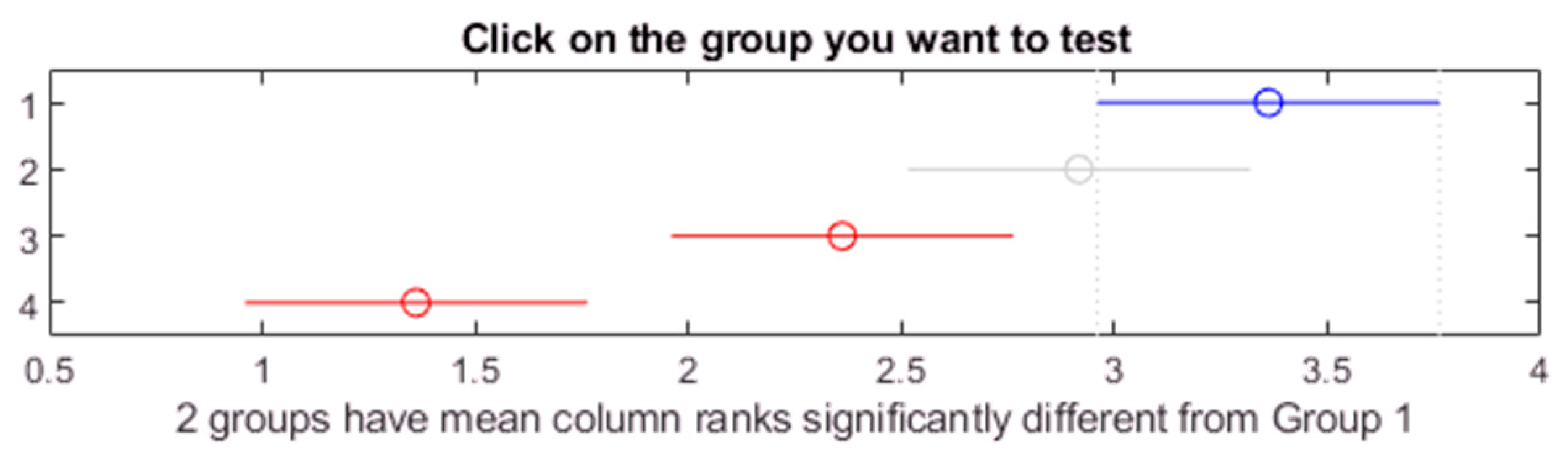
Figure 21.
Post hoc Bonferroni test for oil Midel 1204 with different concentrations of surfactant Triton X.
Figure 21.
Post hoc Bonferroni test for oil Midel 1204 with different concentrations of surfactant Triton X.
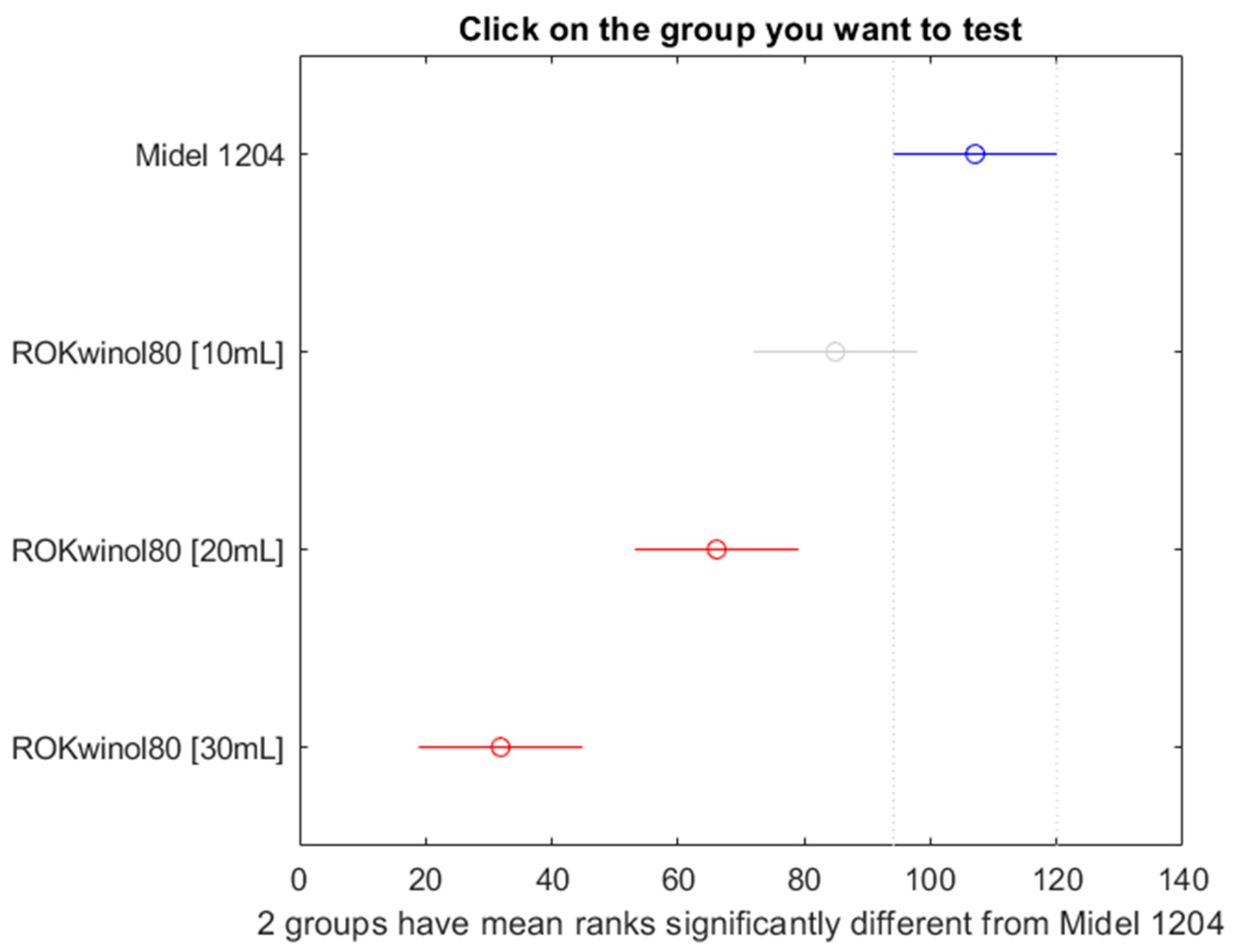
Figure 22.
Post hoc Bonferroni test for oil Midel 1204 with different concentrations of surfactant ROKwino l80.
Figure 22.
Post hoc Bonferroni test for oil Midel 1204 with different concentrations of surfactant ROKwino l80.
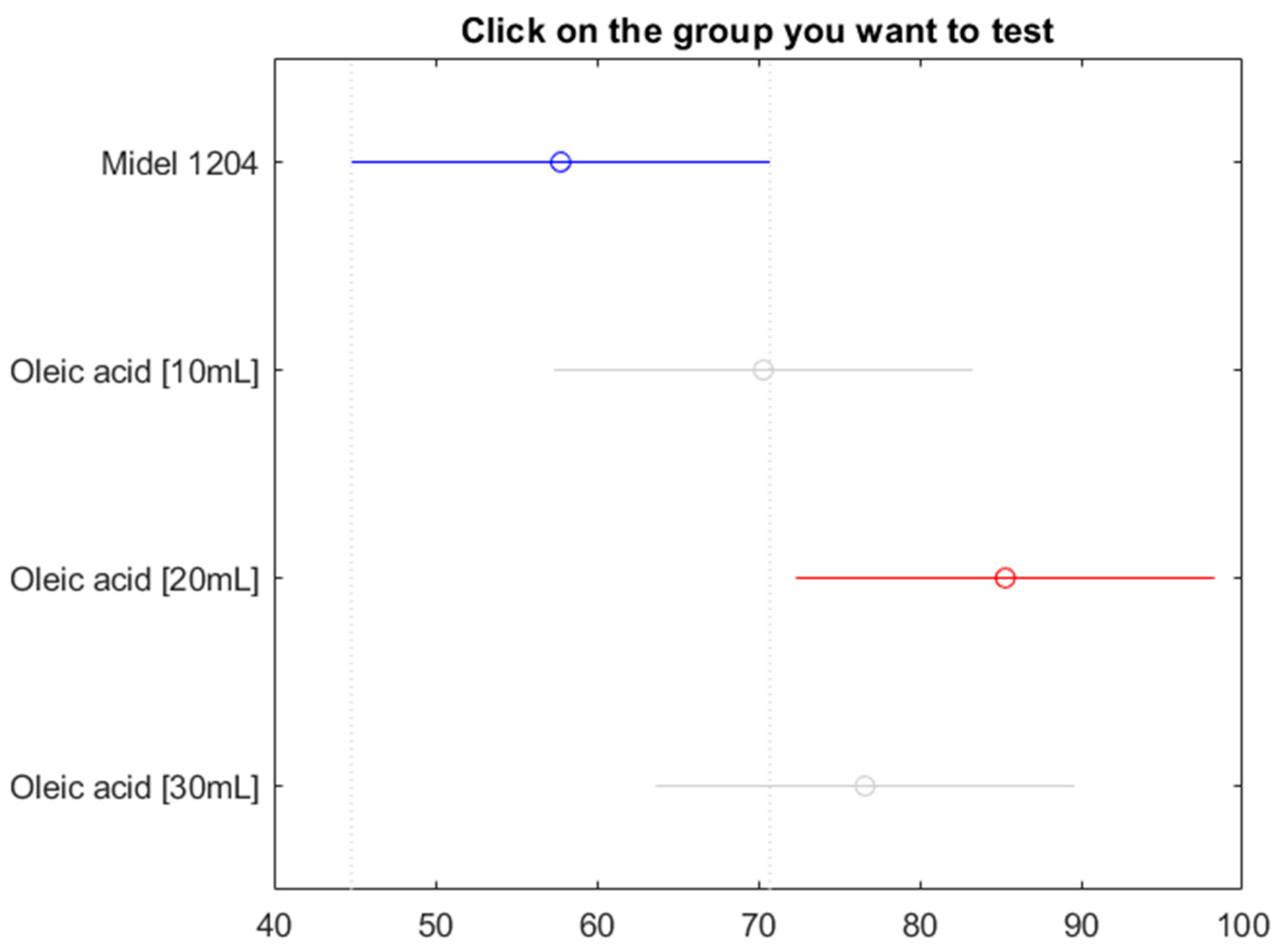
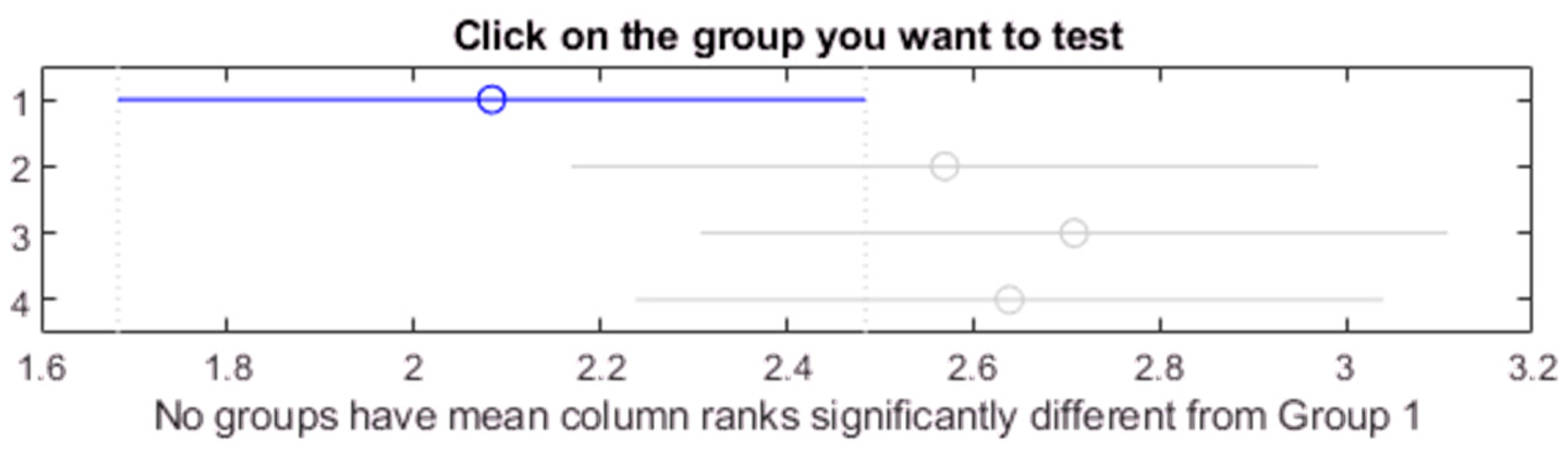
Figure 23.
Post hoc Bonferroni test for oil Midel 1204 with different concentrations of surfactant oleic acid.
Figure 23.
Post hoc Bonferroni test for oil Midel 1204 with different concentrations of surfactant oleic acid.
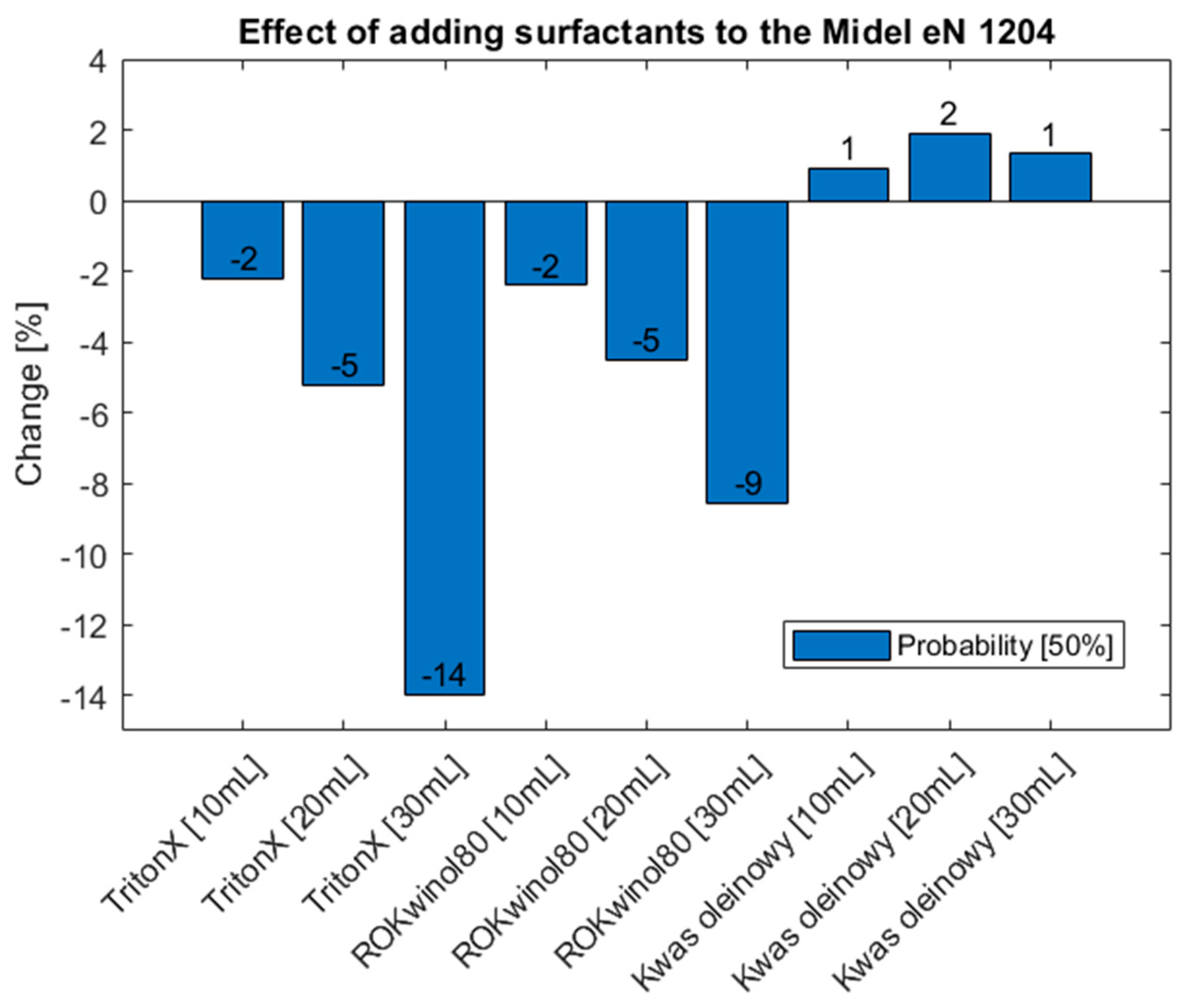
Figure 24.
Percentage change of probability compared with a base sample of oil MIDEL eN 1204.
Figure 24.
Percentage change of probability compared with a base sample of oil MIDEL eN 1204.
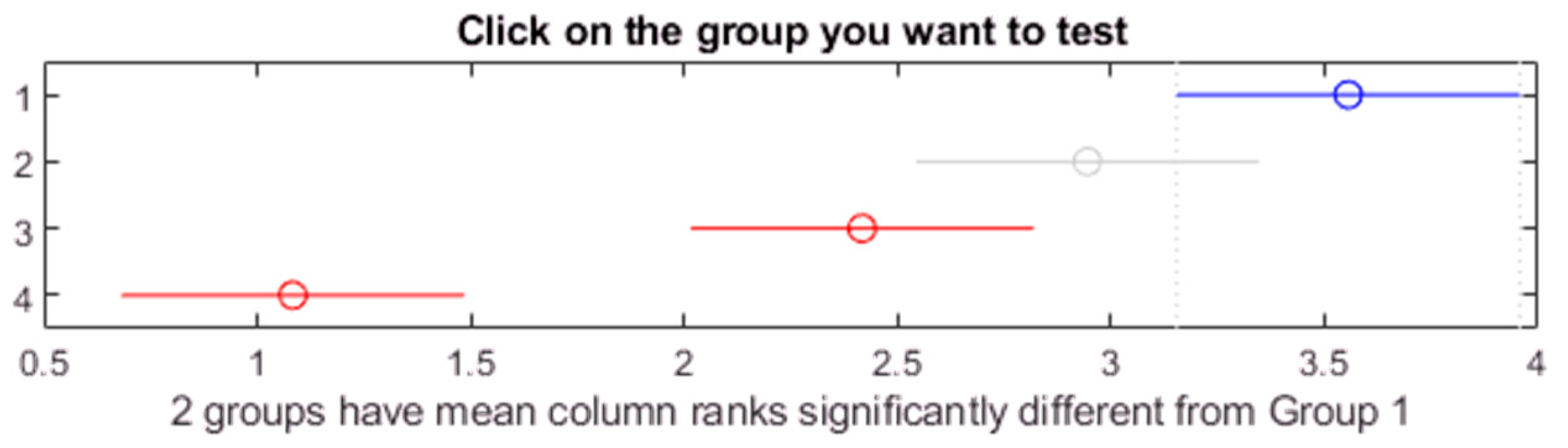
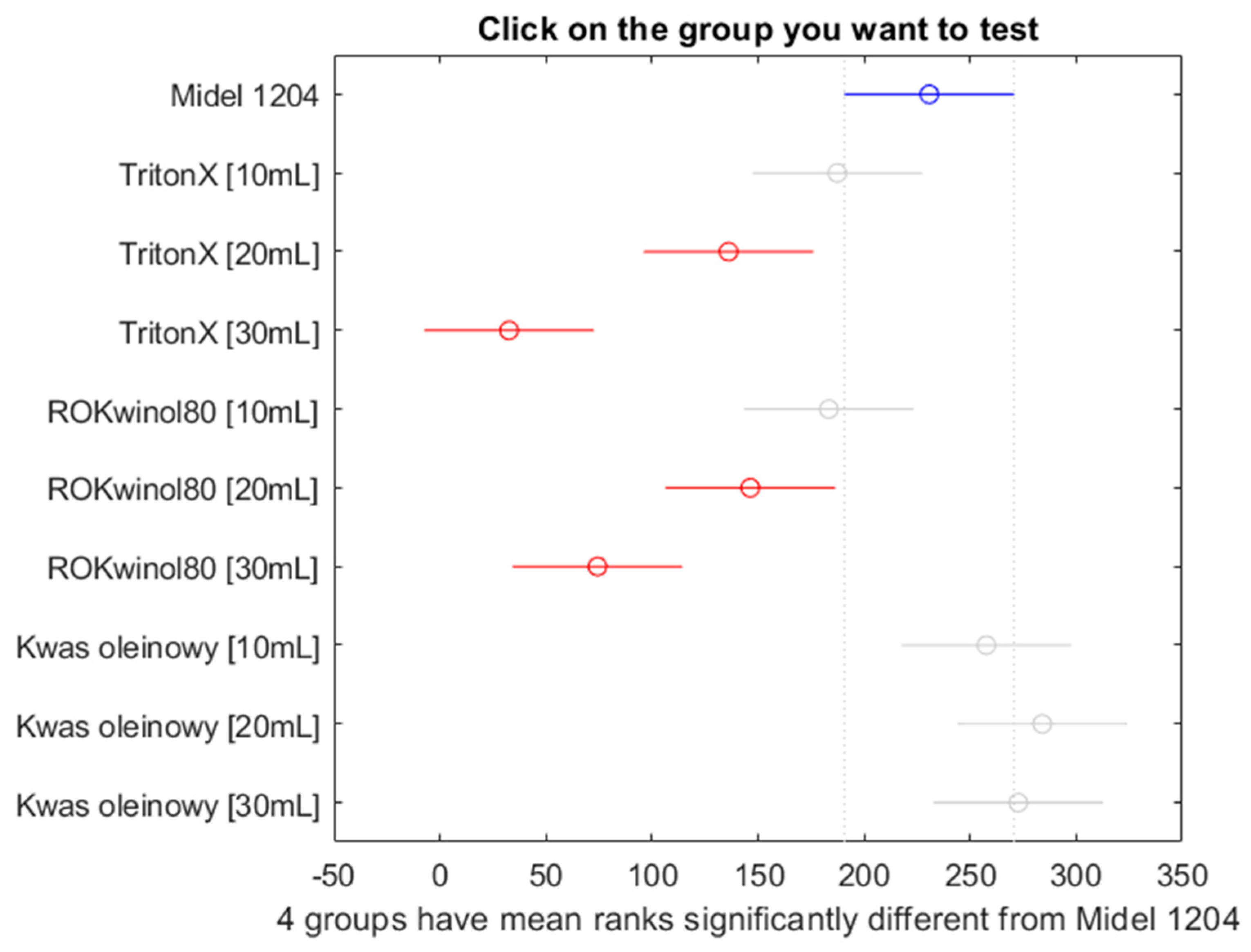
Figure 25.
Post hoc Bonferroni test of Kruskal-Wallis test for all samples.
Figure 25.
Post hoc Bonferroni test of Kruskal-Wallis test for all samples.
Figure 26.
ROKwino l80 samples after conducting breakdown voltage tests. S7—ROKwino l80 ≈ 1%, S9—ROKwino l80 ≈ 2%, S11—ROKwino l80 ≈ 3%.
Figure 26.
ROKwino l80 samples after conducting breakdown voltage tests. S7—ROKwino l80 ≈ 1%, S9—ROKwino l80 ≈ 2%, S11—ROKwino l80 ≈ 3%.
Table 1.
Chosen requirements for population distribution.
Table 1.
Chosen requirements for population distribution.
| Effect Size d | Statistical Significance alpha | Power of a Test p | Sample Size
N |
|---|
| 0.5 | 0.05 | 0.8 | 2:40 |
Table 2.
Electrical properties of natural ester oil MIDEL eN 1204 [
8].
Table 2.
Electrical properties of natural ester oil MIDEL eN 1204 [
8].
| Property | Standard Test Method ASTM D6871 | Standard Test Method IEC 62770 | MIDEL eN 1204 |
|---|
| Dielectric breakdown [kV] | ≥30 | - | ≥30 |
| Dielectric breakdown [kV] at: | | | |
| 1 mm gap | ≥20 | - | 45 |
| 2 mm gap | ≥35 | - | 57 |
| 2.5 mm gap | ≥35 | ≥35 | >75 |
| Gassing tendency [μL/min] | ≤0 | - | −46.1 |
| Power factor at 25 °C [%] | ≤0.2 | - | ≤0.2 |
| Power factor at 100 °C [%] | ≤4 | - | ≤4.0 |
| Dissipation factor at 90 °C [tg δ] | - | ≤0.05 | <0.03 |
Table 3.
Characteristic values of concentrations distribution for all samples.
Table 3.
Characteristic values of concentrations distribution for all samples.
| Sample | Mean Breakdown Voltage [kV] | Standard Deviation [kV] | Max Breakdown Voltage [kV] | Min Breakdown Voltage [kV] | Kurtosis | Skewness |
|---|
| Midel 1204 | 67.75 | 2.09 | 71.8 | 63.9 | 2 | 0.01 |
| Triton X [10 mL] | 66.22 | 2.40 | 70.2 | 59.80 | 3 | −0.60 |
| Triton X [20 mL] | 64.02 | 3.71 | 70.9 | 55.6 | 3 | −0.48 |
| Triton X [30 mL] | 58.26 | 2.49 | 64.5 | 54.5 | 2 | 0.40 |
| ROKwino l80 [10 mL] | 66.07 | 2.31 | 70 | 61.2 | 2 | −0.44 |
| ROKwino l80 [20 mL] | 64.5 | 3.34 | 69.6 | 57.5 | 2 | −0.49 |
| ROKwino l80 [30 mL] | 61.95 | 1.96 | 65.8 | 57.9 | 2 | −0.53 |
| Oleic acid [10 mL] | 68.37 | 2.09 | 71.8 | 63.9 | 2 | −0.02 |
| Oleic acid [20 mL] | 69.1 | 2.02 | 71.8 | 65.4 | 2 | −0.35 |
| Oleic acid [30 mL] | 68.73 | 1.76 | 72.5 | 65.1 | 3 | −0.32 |
Table 4.
Tests of normality distributions for all samples.
Table 4.
Tests of normality distributions for all samples.
| Sample | Probability p | Test Statistic | H0: Normal Distribution |
|---|
| Midel 1204 | 0.3224 | 0.9658 | Rejected |
| Triton X [10 mL] | 0.2031 | 0.9613 | Rejected |
| Triton X [20 mL] | 0.1156 | 0.9528 | Rejected |
| Triton X [30 mL] | 0.3613 | 0.9675 | Rejected |
| ROKwino l80 [10 mL] | 0.1097 | 0.9507 | Rejected |
| ROKwino l80 [20 mL] | 0.1339 | 0.9534 | Rejected |
| ROKwino l80 [30 mL] | 0.0392 | 0.9364 | Accepted |
| Oleic acid [10 mL] | 0.0387 | 0.9362 | Accepted |
| Oleic acid [20 mL] | 0.4986 | 0.9725 | Rejected |
| Oleic acid [30 mL] | 0.4349 | 0.9703 | Rejected |
Table 5.
Tests of Weibull distributions for all samples.
Table 5.
Tests of Weibull distributions for all samples.
| Sample | Probability p | Test Statistic | H0: Normal Distribution |
|---|
| Midel 1204 | 0.1701 | 0.5361 | Accepted |
| Triton X [10 mL] | 0.5872 | 0.3102 | Accepted |
| Triton X [20 mL] | 0.1508 | 0.5568 | Accepted |
| Triton X [30 mL] | 0.0584 | 0.7180 | Accepted |
| ROKwino l80 [10 mL] | 0.4649 | 0.3568 | Accepted |
| ROKwino l80 [20 mL] | 0.8694 | 0.2111 | Accepted |
| ROKwino l80 [30 mL] | 0.15 | 0.5635 | Accepted |
| Oleic acid [10 mL] | 0.1701 | 0.5361 | Accepted |
| Oleic acid [20 mL] | 0.1190 | 0.5972 | Accepted |
| Oleic acid [30 mL] | 0.4996 | 0.3429 | Accepted |
Table 6.
Values of shape factor and scale parameter for the Weibull probability plots.
Table 6.
Values of shape factor and scale parameter for the Weibull probability plots.
| Sample | Scale Parameter A | Shape Factor B |
|---|
| Midel 1204 | 68.7504 | 36.0394 |
| Triton X [10 mL] | 67.3056 | 33.1768 |
| Triton X [20 mL] | 65.6858 | 20.2204 |
| Triton X [30 mL] | 59.4716 | 23.4257 |
| ROKwino l80 [10 mL] | 67.1267 | 35.1369 |
| ROKwino l80 [20 mL] | 65.9936 | 24.0057 |
| ROKwino l80 [30 mL] | 62.8415 | 38.3968 |
| Oleic acid [10 mL] | 69.3374 | 38.1816 |
| Oleic acid [20 mL] | 69.9191 | 45.3652 |
| Oleic acid [30 mL] | 69.4408 | 52.4621 |
Table 7.
Selected probabilities of Weibull distribution for all samples.
Table 7.
Selected probabilities of Weibull distribution for all samples.
| Probability [%] | The Average Breakdown Voltage of Midel 1204 [kV] | Type and Volume of Surfactant | The Breakdown Voltage of Sample [kV] | Change [%] |
|---|
| 1 | 61 | Triton X [10 mL] | 58.59 | −3.17 |
| Triton X [20 mL] | 52.32 | −13.54 |
| Triton X [30 mL] | 48.87 | −19.24 |
| ROKwino l80 [10 mL] | 58.89 | −2.68 |
| ROKwino l80 [20 mL] | 54.49 | −9.96 |
| ROKwino l80 [30 mL] | 55.75 | −7.88 |
| Oleic acid [10 mL] | 61.47 | 1.58 |
| Oleic acid [20 mL] | 63.18 | 4.40 |
| Oleic acid [30 mL] | 63.61 | 5.12 |
| 10 | 65 | Triton X [10 mL] | 62.89 | −2.63 |
| Triton X [20 mL] | 58.77 | −9.01 |
| Triton X [30 mL] | 54.02 | −16.36 |
| ROKwino l80 [10 mL] | 62.96 | −2.52 |
| ROKwino l80 [20 mL] | 60.09 | −6.67 |
| ROKwino l80 [30 mL] | 59.26 | −8.24 |
| Oleic acid [10 mL] | 65.37 | 1.21 |
| Oleic acid [20 mL] | 66.54 | 3.01 |
| Oleic acid [30 mL] | 66.53 | 3.00 |
| 50 | 68 | Triton X [10 mL] | 66.57 | −2.19 |
| Triton X [20 mL] | 64.51 | −5.21 |
| Triton X [30 mL] | 58.55 | −13.97 |
| ROKwino l80 [10 mL] | 66.43 | −2.39 |
| ROKwino l80 [20 mL] | 64.99 | −4.50 |
| ROKwino l80 [30 mL] | 62.24 | −8.54 |
| Oleic acid [10 mL] | 68.67 | 0.91 |
| Oleic acid [20 mL] | 69.36 | 1.91 |
| Oleic acid [30 mL] | 68.96 | 1.33 |
Table 8.
Results of Kruskal–Wallis test for oil Midel 1204 with different concentrations of surfactant Triton X.
Table 8.
Results of Kruskal–Wallis test for oil Midel 1204 with different concentrations of surfactant Triton X.
| Source | Sums of Squares | Degrees of Freedom | Means of Squares | Chi-sq Statistic | p > Chi-sq |
|---|
| Columns | 147,154 | 3 | 49,051.5 | 84.58 | 3.19 × 10−18 |
| Error | 101,640 | 140 | 726 | - | - |
| Total | 240,795 | 143 | - | - | - |
Table 9.
Results of Kruskal–Wallis test for oil Midel 1204 with different concentrations of surfactant ROKwino l80.
Table 9.
Results of Kruskal–Wallis test for oil Midel 1204 with different concentrations of surfactant ROKwino l80.
| Source | Sums of Squares | Degrees of Freedom | Means of Squares | Chi-sq Statistic | p > Chi-sq |
|---|
| Columns | 109,483 | 3 | 36,495 | 62.93 | 1.39 × 10−13 |
| Error | 139,289 | 140 | 995 | - | - |
| Total | 248,773 | 143 | - | - | - |
Table 10.
Results of Kruskal–Wallis test for oil Midel 1204 with different concentrations of surfactant oleic acid.
Table 10.
Results of Kruskal–Wallis test for oil Midel 1204 with different concentrations of surfactant oleic acid.
| Source | Sums of Squares | Degrees of Freedom | Means of Squares | Chi-sq Statistic | p > Chi-sq |
|---|
| Columns | 14,500 | 3 | 4833 | 8.34 | 0.0395 |
| Error | 234,184 | 140 | 1672 | - | - |
| Total | 248,684 | 143 | - | - | - |
Table 11.
Multiple comparison results of the Kruskal–Wallis test between all samples.
Table 11.
Multiple comparison results of the Kruskal–Wallis test between all samples.
| Sample A | Sample B | Lower Limit | Difference | Upper Limit | Probability p |
|---|
| Midel 1204 | Triton X [10 mL] | −8.13 | 17.81 | 43.74 | 0.4200 |
| Midel 1204 | Triton X [20 mL] | 14.83 | 40.76 | 66.70 | 0.0002 |
| Midel 1204 | Triton X [30 mL] | 59.44 | 85.38 | 111.31 | 2.29 × 10−17 |
| Triton X [10 mL] | Triton X [20 mL] | −2.98 | 22.96 | 48.90 | 0.1171 |
| Triton X [10 mL] | Triton X [30 mL] | 41.63 | 67.57 | 93.51 | 3.77 × 10−11 |
| Triton X [20 mL] | Triton X [30 mL] | 18.67 | 44.61 | 70.55 | 3.41 × 10−5 |
| Midel 1204 | ROKwino l80 [10 mL] | −3.77 | 22.17 | 48.10 | 0.1448 |
| Midel 1204 | ROKwino l80 [20 mL] | 15.02 | 40.96 | 66.90 | 0.0001 |
| Midel 1204 | ROKwino l80 [30 mL] | 49.27 | 75.21 | 101.15 | 1.20 × 10−13 |
| ROKwino l80 [10 mL] | ROKwino l80 [20 mL] | −7.15 | 18.79 | 44.73 | 0.03356 |
| ROKwino l80 [10 mL] | ROKwino l80 [30 mL] | 27.10 | 53.04 | 78.98 | 4.10 × 10−7 |
| ROKwino l80 [20 mL] | ROKwino l80 [30 mL] | 8.31 | 34.25 | 60.19 | 0.0029 |
| Midel 1204 | Oleic acid [10 mL] | −38.49 | −12.56 | 13.38 | 1.00000 |
| Midel 1204 | Oleic acid [20 mL] | −53.47 | −27.54 | −1.61 | 0.0304 |
| Midel 1204 | Oleic acid [30 mL] | −44.78 | −18.85 | 7.08 | 0.3310 |
| Oleic acid [10 mL] | Oleic acid [20 mL] | −40.92 | −14.99 | 10.95 | 0.7640 |
| Oleic acid [10 mL] | Oleic acid [30 mL] | −32.22 | −6.29 | 19.64 | 1.0000 |
| Oleic acid [20 mL] | Oleic acid [30 mL] | −17.24 | 8.69 | 34.63 | 1.0000 |
Table 12.
Results of Friedman test for oil Midel 1204 with different concentrations of surfactant Triton X.
Table 12.
Results of Friedman test for oil Midel 1204 with different concentrations of surfactant Triton X.
| Source | Sums of Squares | Degrees of Freedom | Means of Squares | Chi-sq Statistic | p > Chi-sq |
|---|
| Columns | 120 | 3 | 39.90 | 71.83 | 1.728 × 10−15 |
| Error | 60 | 105 | 0.57 | - | - |
| Total | 180 | 143 | - | - | - |
Table 13.
Results of Friedman test for oil Midel 1204 with different concentrations of surfactant ROKwinol 80.
Table 13.
Results of Friedman test for oil Midel 1204 with different concentrations of surfactant ROKwinol 80.
| Source | Sums of Squares | Degrees of Freedom | Means of Squares | Chi-sq Statistic | p > Chi-sq |
|---|
| Columns | 80.33 | 3 | 26.77 | 48.20 | 1.93 × 10−10 |
| Error | 99.66 | 105 | 0.95 | - | - |
| Total | 180 | 143 | - | - | - |
Table 14.
Results of Friedman test for oil Midel 1204 with different concentrations of surfactant oleic acid.
Table 14.
Results of Friedman test for oil Midel 1204 with different concentrations of surfactant oleic acid.
| Source | Sums of Squares | Degrees of Freedom | Means of Squares | Chi-sq Statistic | p > Chi-sq |
|---|
| Columns | 8.68 | 3 | 2.89 | 5.22 | 0.1562 |
| Error | 170.82 | 105 | 1.62 | | |
| Total | 179.50 | 143 | | | |
Table 15.
Multiple comparison results of the Friedman test between all samples.
Table 15.
Multiple comparison results of the Friedman test between all samples.
| Sample A | Sample B | Lower Limit | Difference | Upper Limit | Probability p |
|---|
| Midel 1204 | Triton X [10 mL] | −8.13 | 17.81 | 43.74 | 0.4200 |
| Midel 1204 | Triton X [20 mL] | 14.83 | 40.76 | 66.70 | 0.0002 |
| Midel 1204 | Triton X [30 mL] | 59.44 | 85.38 | 111.31 | 2.29 × 10−17 |
| Triton X [10 mL] | Triton X [20 mL] | −2.98 | 22.96 | 48.90 | 0.1171 |
| Triton X [10 mL] | Triton X [30 mL] | 41.63 | 67.57 | 93.51 | 3.77 × 10−11 |
| Triton X [20 mL] | Triton X [30 mL] | 18.67 | 44.61 | 70.55 | 3.41 × 10−5 |
| Midel 1204 | ROKwino l80 [10 mL] | −0.36 | 0.44 | 1.25 | 0.8647 |
| Midel 1204 | ROKwino l80 [20 mL] | 0.20 | 1.00 | 1.80 | 0.0060 |
| Midel 1204 | ROKwino l80 [30 mL] | 1.20 | 2.00 | 2.80 | 2.96 × 10−10 |
| ROKwino l80 [10 mL] | ROKwino l80 [20 mL] | −0.25 | 0.56 | 1.36 | 0.4073 |
| ROKwino l80 [10 mL] | ROKwino l80 [30 mL] | 0.75 | 1.56 | 2.36 | 1.9 × 10−6 |
| ROKwino l80 [20 mL] | ROKwino l80 [30 mL] | 0.20 | 1.00 | 1.80 | 0.0060 |
| Midel 1204 | Oleic acid [10 mL] | −1.29 | −0.49 | 0.32 | 0.6579 |
| Midel 1204 | Oleic acid [20 mL] | −1.43 | −0.63 | 0.18 | 0.2382 |
| Midel 1204 | Oleic acid [30 mL] | −1.36 | −0.56 | 0.25 | 0.4050 |
| Oleic acid [10 mL] | Oleic acid [20 mL] | −0.94 | −0.14 | 0.66 | 1.0000 |
| Oleic acid [10 mL] | Oleic acid [30 mL] | −0.87 | −0.07 | 0.73 | 1.0000 |
| Oleic acid [20 mL] | Oleic acid [30 mL] | −0.73 | 0.07 | 0.87 | 1.0000 |