The Transient Cooling Performance of a Compact Thin-Film Thermoelectric Cooler with Horizontal Structure
Abstract
:1. Introduction
2. The Multi-Physics Field Model of Thin-Film Thermoelectric Coolers
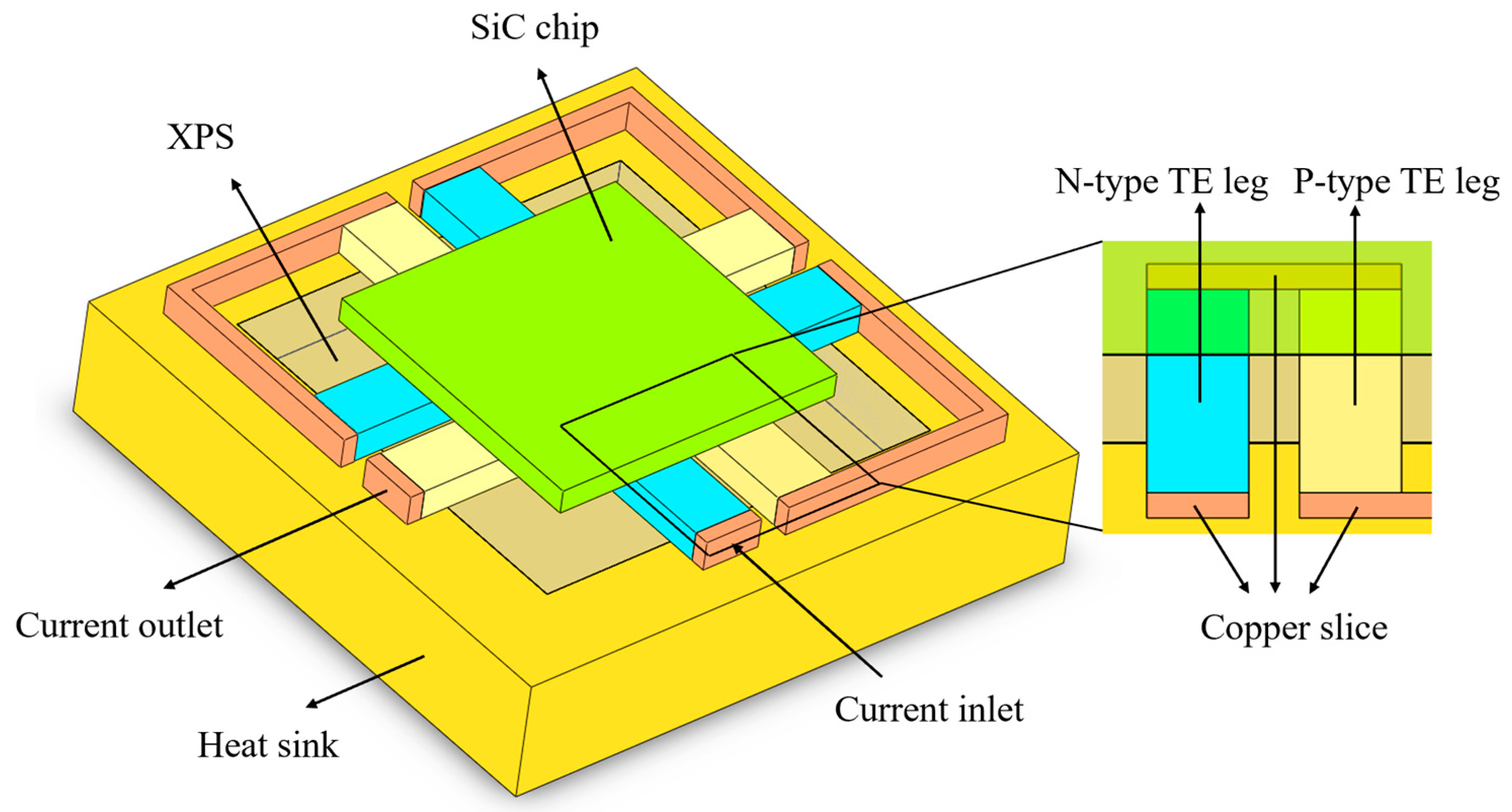
2.1. Physical Model of the Thin-Film Thermoelectric Cooler
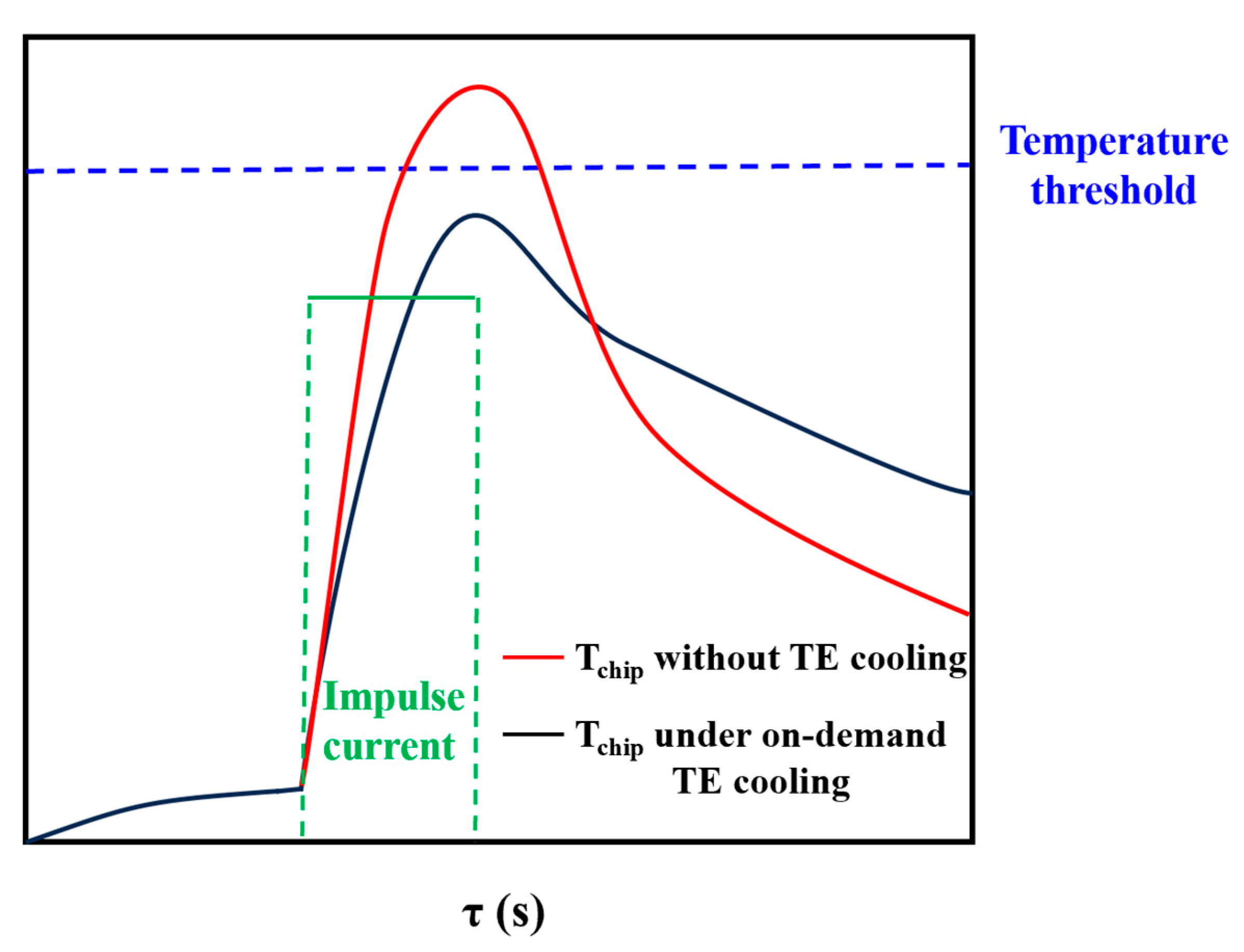
2.2. On-Demand Cooling
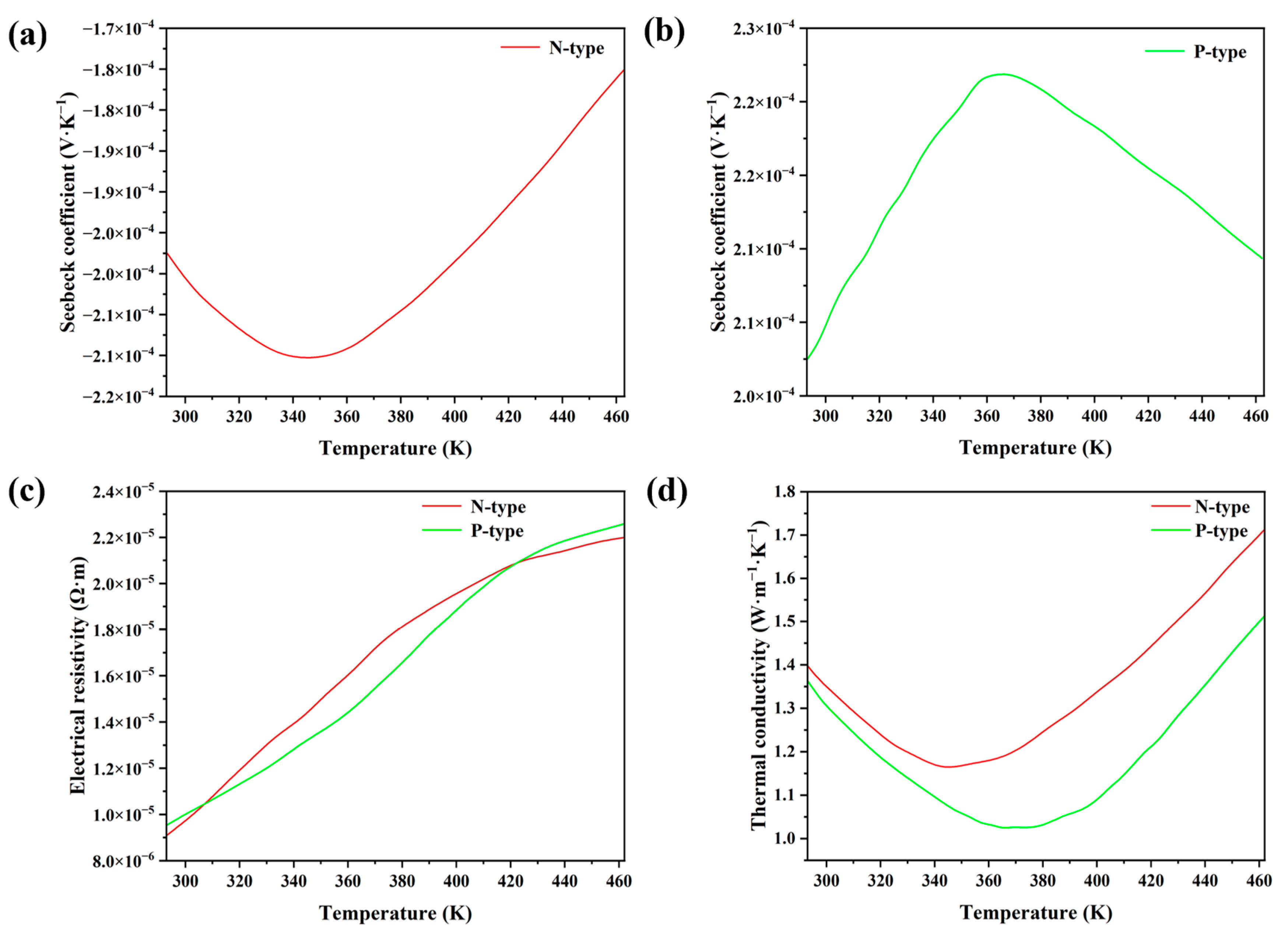
2.3. Governing Equations
2.4. Boundary Conditions
- (1)
- All the surfaces were set to be thermally insulated except for the hot and cold sides of the TEC and the bottom face of the heat sink.
- (2)
- Radiative heat transfer on all surfaces was neglected.
- (3)
- Parameters of the materials except thermoelectric materials were set not to vary with external factors such as temperature.
- (4)
- All the materials of the device were isotropic.
- (5)
- The SiC chip and the surface of the heat sink were electrical-insulating.
2.5. Numeral Method
3. Results and Discussions
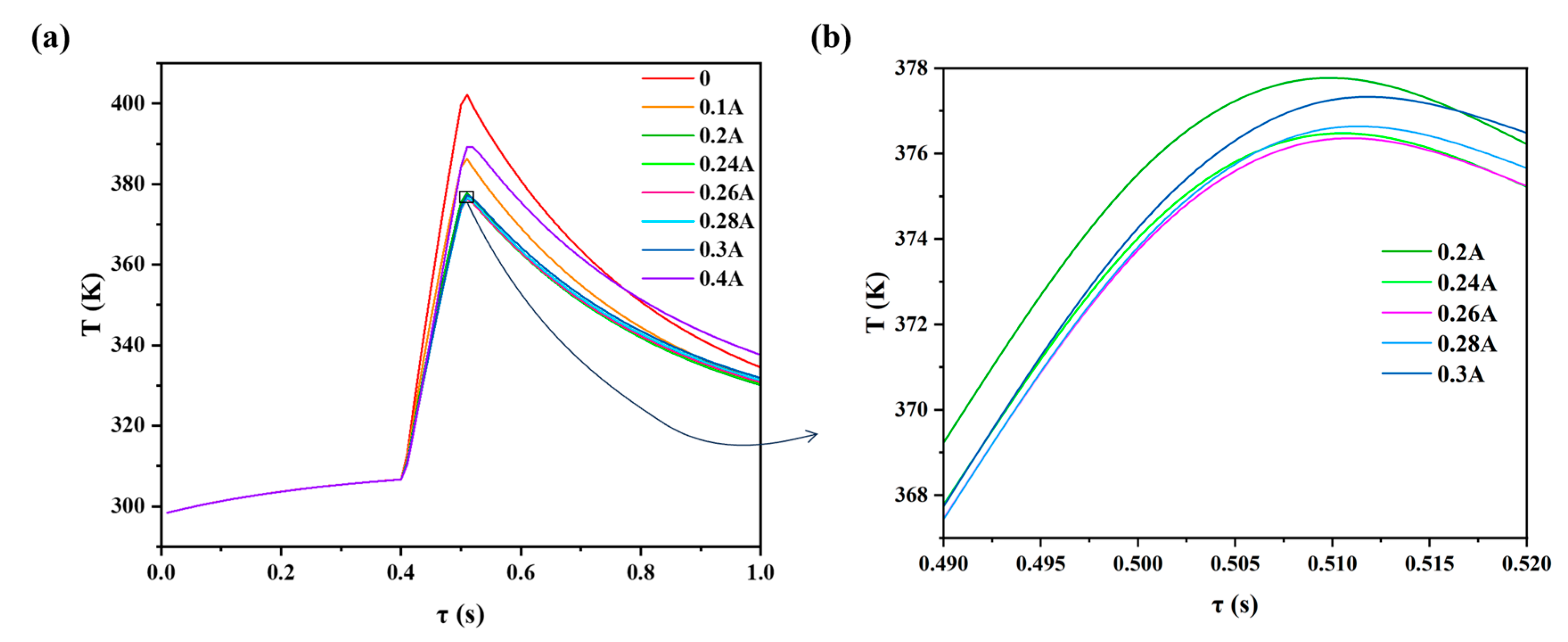
3.1. Effect of the Amplitude of Impulse Current
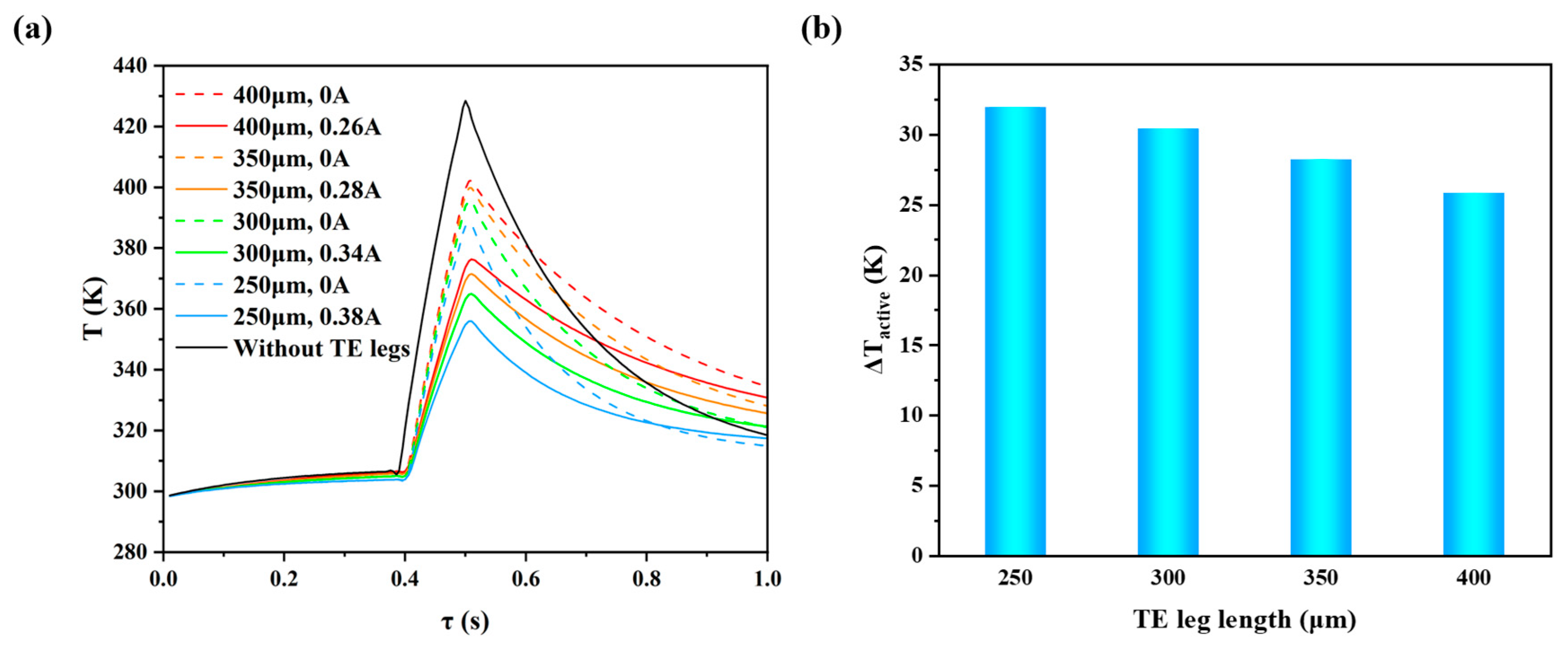
3.2. Effect of the Length of the Thermoelectric Legs
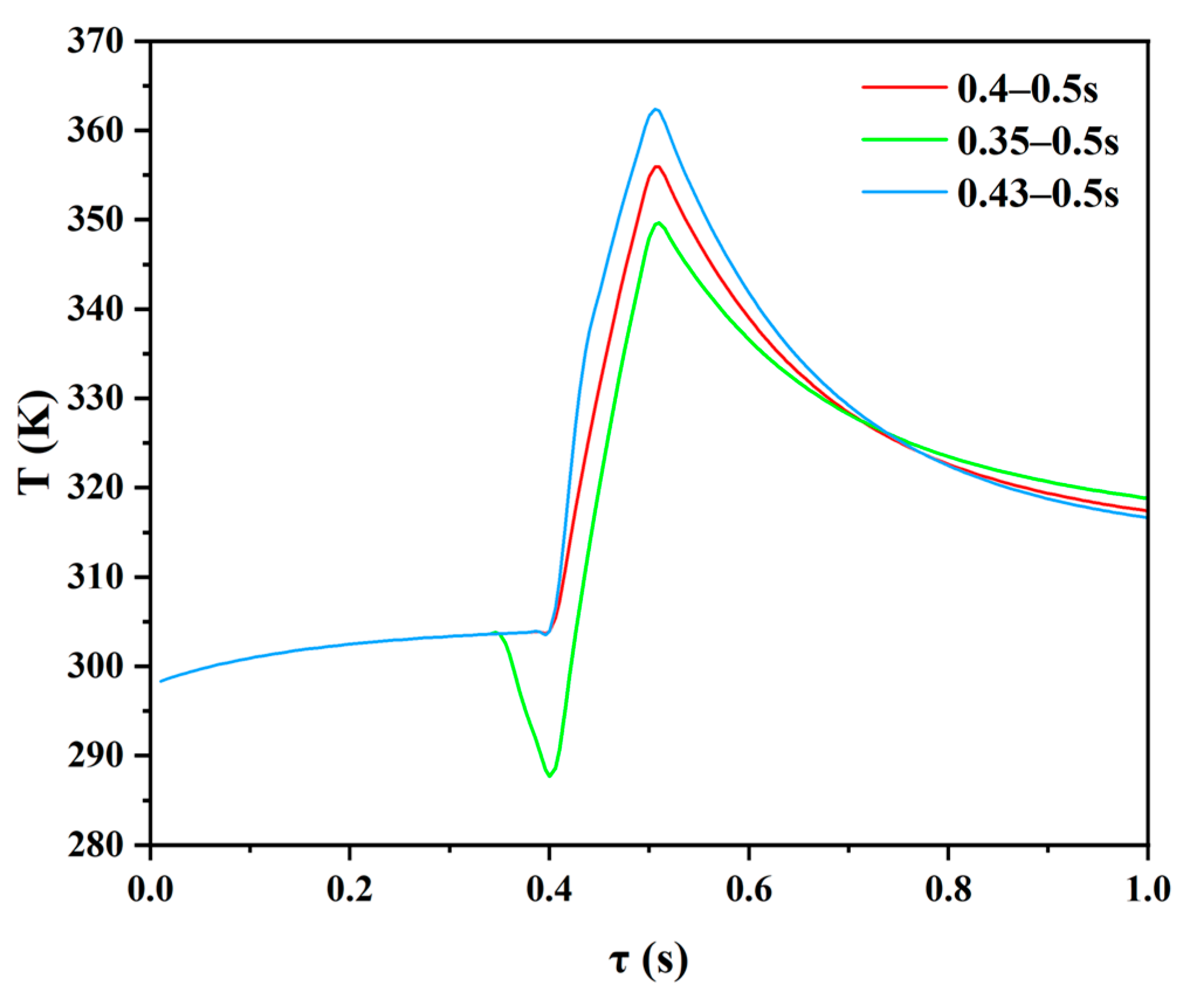
3.3. Effect of Imposing Time of the Current
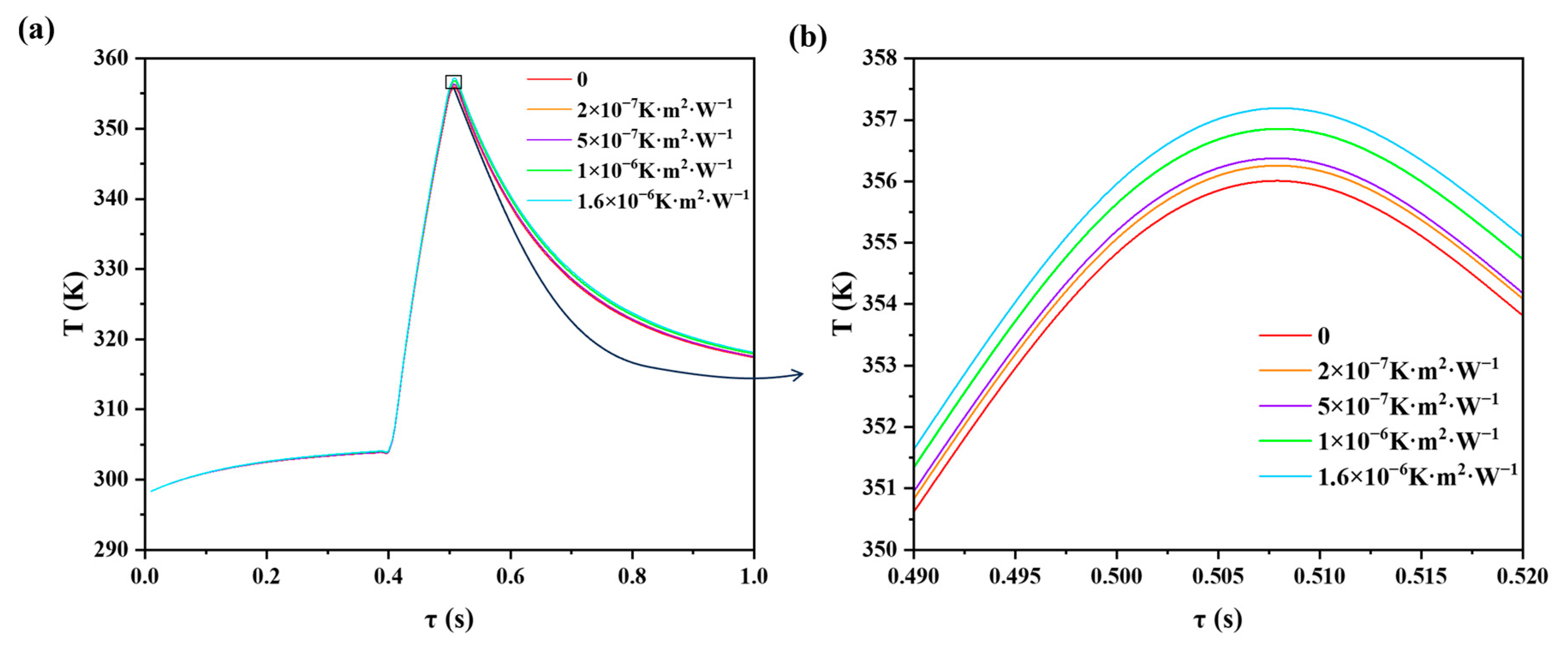
3.4. Effect of Contact Thermal Resistance
4. Conclusions
- (1)
- When the amplitude of the impulse current was gradually increased from 0 to 0.38 A, the cooling performance of the TEC was gradually enhanced, and a temperature drop of up to 25.85 K could be achieved, which contributed to keeping the chip running stably and efficiently. However, when the amplitude of the impulse current exceeded 0.26 A and continued to increase, the transient cooling performance decreased instead. When the amplitude was too large, the final temperature was even higher than that when the current was absent.
- (2)
- When the TE leg length was increased from 250 to 400 μm, the peak temperature under passive cooling gradually increased from 387.83 to 402.19 K, and the temperature drop of active cooling decreased from 31.91 to 25.85 K. The increase in the length of the TE legs was detrimental to both passive and active cooling.
- (3)
- Extending the current imposing time appropriately was conducive to further reducing the peak temperature of the chip while increasing the amplitude of the impulse current and delaying the current imposing time was unfeasible.
- (4)
- When contact thermal resistance was increased from 0 to 1.6 × 10−6 W·m2·K−1, the peak temperature increased by only 1.2 K. The contact thermal resistance had a small effect on the transient cooling performance of the TEC if the contact thermal resistance was less than 1.6 × 10−6 W·m2·K−1.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclatures
| Symbols | |
| cp | Specific heat (J·kg−1·K−1) |
| Electric field intensity (V·m−1) | |
| Current density (A∙m−2) | |
| k | Thermal conductivity of the thermoelectric material (W∙m−1∙K−1) |
| Heat flux density (W·m−2) | |
| Intensity of the internal heat source (W·m−3) | |
| R | Electrical resistance of the thin-film TEC (Ω) |
| T | Temperature (K) |
| Temperature difference (K) | |
| ΔTactive | The temperature drop of active cooling (K) |
| Temperature gradient (K∙m−1) | |
| α | Seebeck coefficient (V∙K−1) |
| Mass density (kg·m−3) | |
| Electrical resistivity of the thermoelectric material (Ω∙m) | |
| Abbreviations | |
| TE | Thermoelectric |
| TEC | Thermoelectric cooler |
| ZT | Figure of merit |
References
- Xiu, L. Time Moore: Exploiting Moore’s Law From The Perspective of Time. IEEE Solid-State Circuits Mag. 2019, 11, 39–55. [Google Scholar] [CrossRef]
- Ming, T.; Chen, S.; Yan, Y.; Gong, T.; Wan, J.; Wu, Y. The simulated cooling performance of a thin-film thermoelectric cooler with coupled-thermoelements connected in parallel. Heliyon 2022, 8, e10025. [Google Scholar] [CrossRef] [PubMed]
- Xie, J.L.; Tan, Y.B.; Wong, T.N.; Duan, F.; Toh, K.C.; Choo, K.F.; Chan, P.K.; Chua, Y.S. Multi-nozzle array spray cooling for large area high power devices in a closed loop system. Int. J. Heat Mass Transf. 2014, 78, 1177–1186. [Google Scholar] [CrossRef]
- Zhang, N.; Jiao, B.; Ye, Y.; Kong, Y.; Du, X.; Liu, R.; Cong, B.; Yu, L.; Jia, S.; Jia, K. Embedded cooling method with configurability and replaceability for multi-chip electronic devices. Energy Convers. Manag. 2022, 253, 115124. [Google Scholar] [CrossRef]
- Xiong, K.; Meng, L.; Wang, S. Design, fabrication, investigation and analysis of a novel flat evaporator loop heat pipe for cooling high heat flux server chips. Appl. Therm. Eng. 2022, 201, 117775. [Google Scholar] [CrossRef]
- Wang, P.; Bar-Cohen, A. On-chip hot spot cooling using silicon thermoelectric microcoolers. J. Appl. Phys. 2007, 102, 034503. [Google Scholar] [CrossRef]
- Nandihalli, N. Thermoelectric films and periodic structures and spin Seebeck effect systems: Facets of performance optimization. Mater. Today Energy 2022, 25, 100965. [Google Scholar] [CrossRef]
- Chen, X.; Dai, W.; Wu, T.; Luo, W.; Yang, J.; Jiang, W.; Wang, L. Thin Film Thermoelectric Materials: Classification, Characterization, and Potential for Wearable Applications. Coatings 2018, 8, 244. [Google Scholar] [CrossRef]
- Chen, W.; Shi, X.; Zou, J.; Chen, Z. Thermoelectric coolers for on-chip thermal management: Materials, design, and optimization. Mater. Sci. Eng. R Rep. 2022, 151, 100700. [Google Scholar] [CrossRef]
- Ding, J.; Zhao, W.; Jin, W.; Di, C.; Zhu, D. Advanced Thermoelectric Materials for Flexible Cooling Application. Adv. Funct. Mater. 2021, 31, 2010695. [Google Scholar] [CrossRef]
- Rao, A.; Ji, X.; Tritt, M. Properties of nanostructured one-dimensional and composite thermoelectric materials. MRS Bull. 2006, 31, 218–223. [Google Scholar] [CrossRef]
- Mao, J.; Chen, G.; Ren, Z. Thermoelectric cooling materials. Nat. Mater. 2020, 20, 454–461. [Google Scholar] [CrossRef] [PubMed]
- Venkatasubramanian, R.; Siivola, E.; Colpitts, T.; O’Quinn, B. Thin-film thermoelectric devices with high room-temperature figures of merit. Nature 2001, 413, 597–602. [Google Scholar] [CrossRef] [PubMed]
- Manno, M.V. On-Chip Thermoelectric Hotspot Cooling. Ph.D. Thesis, University of Maryland, College Park, MD, USA, 2015. [Google Scholar]
- Zhu, W.; Deng, Y.; Wang, Y.; Wang, A. Finite element analysis of miniature thermoelectric coolers with high cooling performance and short response time. Microelectron. J. 2013, 44, 860–868. [Google Scholar] [CrossRef]
- Lara Ramos, D.; Barati, V.; Garcia, J.; Reith, H.; Li, G.; Pérez, N.; Schierning, G.; Nielsch, K. Design Guidelines for Micro-Thermoelectric Devices by Finite Element Analysis. Adv. Sustain. Syst. 2019, 3, 1800093. [Google Scholar] [CrossRef]
- Alexandrov, B.; Sullivan, O.; Song, W.J.; Yalamanchili, S.; Kumar, S.; Mukhopadhyay, S. Control Principles and On-Chip Circuits for Active Cooling Using Integrated Superlattice-Based Thin-Film Thermoelectric Devices. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2014, 22, 1909–1919. [Google Scholar] [CrossRef]
- Gao, Y.; Shi, C.; Wang, X. Numerical analysis for transient supercooling effect of pulse current shapes on a two-stage thermoelectric cooler. Appl. Therm. Eng. 2019, 163, 114416. [Google Scholar] [CrossRef]
- Wu, Y.; Yang, J.; Chen, S.; Zuo, L. Thermo-element geometry optimization for high thermoelectric efficiency. Energy 2018, 147, 672–680. [Google Scholar] [CrossRef]
- Zhou, Q.; Bian, Z.; Shakouri, A. Pulsed cooling of inhomogeneous thermoelectric materials. J. Phys. D Appl. Phys. 2007, 40, 4376–4381. [Google Scholar] [CrossRef]
- Snyder, G.J.; Fleurial, J.P.; Caillat, T.; Yang, R.; Chen, G. Supercooling of Peltier cooler using a current pulse. J. Appl. Phys. 2002, 92, 1564–1569. [Google Scholar] [CrossRef]
- Yang, R.; Chen, G.; Ravi Kumar, A.; Snyder, G.J.; Fleurial, J.-P. Transient cooling of thermoelectric coolers and its applications for microdevices. Energy Convers. Manag. 2005, 46, 1407–1421. [Google Scholar] [CrossRef]
- Hao, J.; Qiu, H.; Ren, J.; Ge, Z.; Chen, Q.; Du, X. Multi-parameters analysis and optimization of a typical thermoelectric cooler based on the dimensional analysis and experimental validation. Energy 2020, 205, 118043. [Google Scholar] [CrossRef]
- Wang, T.; Wu, H.; Gao, D.; Zhang, K.; Meng, J. Achieving Better Super-cooling in a Two-Stage Transient Thermoelectric Device with Constraint-Free Pulse Current by Multi-Objective Optimization. J. Therm. Sci. 2021, 30, 1349–1362. [Google Scholar] [CrossRef]
- Liu, D.; Cai, Y.; Zhao, F.-Y. Optimal design of thermoelectric cooling system integrated heat pipes for electric devices. Energy 2017, 128, 403–413. [Google Scholar] [CrossRef]
- Jeong, E.S. A new approach to optimize thermoelectric cooling modules. Cryogenics 2014, 59, 38–43. [Google Scholar] [CrossRef]
- Qiu, C.; Shi, W. Comprehensive modeling for optimized design of a thermoelectric cooler with non-constant cross-section: Theoretical considerations. Appl. Therm. Eng. 2020, 176, 115384. [Google Scholar] [CrossRef]
- Nimmagadda, L.A.; Sinha, S. Thermoelectric Property Requirements for On-Chip Cooling of Device Transients. IEEE Trans. Electron Devices 2020, 67, 3716–3721. [Google Scholar] [CrossRef]
- Watzman, S.J.; Duine, R.A.; Tserkovnyak, Y.; Boona, S.R.; Jin, H.; Prakash, A.; Zheng, Y.; Heremans, J.P. Magnon-drag thermopower and Nernst coefficient in Fe, Co, and Ni. Phys. Rev. B 2016, 94, 144407. [Google Scholar] [CrossRef]
- Adams, M.J.; Verosky, M.; Zebarjadi, M.; Heremans, J.P. Active Peltier Coolers Based on Correlated and Magnon-Drag Metals. Phys. Rev. Appl. 2019, 11, 054008. [Google Scholar] [CrossRef]
- Rowe, D.; Kuznetzov, Z.; Kuznetsova, L.; Min, G. Electrical and thermal transport properties of intermediate-valence YbAl3. J. Phys. D Appl. Phys. 2002, 35, 2183–2186. [Google Scholar] [CrossRef]
- Ren, Z.; Kim, J.C.; Lee, J. Transient Cooling and Heating Effects in Holey Silicon-Based Lateral Thermoelectric Devices for Hot Spot Thermal Management. IEEE Trans. Compon. Packag. Manuf. Technol. 2021, 11, 1214–1222. [Google Scholar] [CrossRef]
- Sun, D.; Shen, L.; Sun, M.; Yao, Y.; Chen, H.; Jin, S. An effective method of evaluating the device-level thermophysical properties and performance of micro-thermoelectric coolers. Appl. Energy 2018, 219, 93–104. [Google Scholar] [CrossRef]
- Gong, T.; Gao, L.; Wu, Y.; Tan, H.; Qin, F.; Xin, X.; Shen, L.; Li, J.; Ming, T. A Model to Evaluate the Device-Level Performance of Thermoelectric Cooler with Thomson Effect Considered. J. Therm. Sci. 2022, 31, 712–726. [Google Scholar] [CrossRef]
- Wu, Y.; Chen, S.; Gong, T.; Shi, T.; Zuo, L.; Yan, Y.; Fang, Y.; Ming, T. A Strategy to Reduce the Peak Temperature of the Chip Working under Dynamic Power Using the Transient Cooling Effect of the Thin-Film Thermoelectric Cooler. J. Therm. Sci. 2022, 31, 1094–1105. [Google Scholar] [CrossRef]
- Rohsenow, W.M.; Hartnett, J.P.; Cho, Y.I. (Eds.) . Handbook of Heat Transfer; Osborne McGraw-Hill: New York, NY, USA, 1973. [Google Scholar]
- Chen, G. Nanoscale Energy Transport and Conversion: A Parallel Treatment of Electrons, Molecules, Phonons, and Photons; Oxford University Press: Oxford, UK, 2005. [Google Scholar]
- Xu, G.; Duan, Y.; Chen, X.; Ming, T.; Huang, X. Influence of interface contact effects on performance of different scale thermoelectric coolers. Appl. Therm. Eng. 2020, 169, 114933. [Google Scholar] [CrossRef]

| Material | Thermal Conductivity (W·m−1·K−1) | Electrical Resistivity (Ω·m) | Specific Heat (J·kg−1·K−1) |
|---|---|---|---|
| Cu | 398 | 1.8 × 10−7 | 390 |
| SiC | 450 | - | 1200 |
| Cu alloy | 401 | - | 398 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ming, T.; Liu, L.; Zhang, P.; Yan, Y.; Wu, Y. The Transient Cooling Performance of a Compact Thin-Film Thermoelectric Cooler with Horizontal Structure. Energies 2023, 16, 8109. https://doi.org/10.3390/en16248109
Ming T, Liu L, Zhang P, Yan Y, Wu Y. The Transient Cooling Performance of a Compact Thin-Film Thermoelectric Cooler with Horizontal Structure. Energies. 2023; 16(24):8109. https://doi.org/10.3390/en16248109
Chicago/Turabian StyleMing, Tingzhen, Lijun Liu, Peng Zhang, Yonggao Yan, and Yongjia Wu. 2023. "The Transient Cooling Performance of a Compact Thin-Film Thermoelectric Cooler with Horizontal Structure" Energies 16, no. 24: 8109. https://doi.org/10.3390/en16248109
APA StyleMing, T., Liu, L., Zhang, P., Yan, Y., & Wu, Y. (2023). The Transient Cooling Performance of a Compact Thin-Film Thermoelectric Cooler with Horizontal Structure. Energies, 16(24), 8109. https://doi.org/10.3390/en16248109








