Construction and Estimation of Battery State of Health Using a De-LSTM Model Based on Real Driving Data

Abstract

Electric vehicles (EVs) have considerable potential in promoting energy efficiency and carbon neutrality. State of health (SOH) estimations for battery systems can be effective for avoiding accidents involving EVs. However, existing methods have rarely been developed using real driving data. The complex working environments of EVs and their limited data acquisition capability increase the challenges for estimating SOH. In this study, a novel battery SOH definition for EVs was established by analyzing and extracting six potential SOH indicators from driving data. The definition proposed using the entropy weight method (EWM) described the degradation trend for different EV batteries. Combined with a denoising autoencoder, a novel long short-term memory neural network model was established for SOH prediction. It can learn robust features using noisy input data without being affected by different environments or driver behaviors. The network achieved a maximum mean absolute percentage error (MAPE) of 0.8827% and root mean square error (RMSE) of 0.9802%. The results have shown that the proposed method has a higher level of accuracy and is more robust than existing methods in the field.

1. Introduction

In the context of the energy crisis and global warming, the development of clean energy has attracted widespread attention from governments. In recent years, electric vehicles (EVs) have played a key role in politics, economics, and technology. Lithium-ion batteries (LIBs) are widely used in electric vehicles because of their long cycle lives, low self-discharge rates, and high energy densities. However, with battery operation, LIBs undergo performance degradation owing to irreversible physicochemical reactions, such as increased internal resistance, decreased electrolytes, and thickened solid electrolyte interphase (SEI) [1]. The health status of LIBs is a key parameter in evaluating their performance. Therefore, estimating battery aging and performance has attracted considerable attention. As a key indicator of battery status, an accurate estimation of the state of health (SOH) can avoid severe accidents effectively and provide a valid reference for vehicle services. The recovery of traction batteries used in EVs has become a novel research topic [2] in recent years, indicating that SOH estimation is an important element for related studies.

SOH is defined as the ratio of the existing value to the original value. It is commonly accepted in industry that battery capacity and ohmic resistance are used to express the SOH. The end-of-life (EOL) of batteries is defined by the remaining capacity and internal resistance. When the remaining capacity drops below 80% of the original value or the internal resistance is doubled, the battery no longer meets the performance requirements for EVs [3]. Therefore, SOH estimation is of considerable importance for the appropriate use of EV batteries and determining EV battery EOL.

In the present study, the SOH estimation methods were generally performed by analyzing the historical data of the battery, which allows the SOH to be determined. Several approaches have been dedicated to SOH estimation, and researchers [4] have divided these methods into model-based, data-driven, hybrid, and other methods. However, most of these studies were based on battery cycling experiments, and few studies estimated the SOH using real driving data.

Model-based SOH estimation methods have been widely adopted in industrial applications. Equivalent circuit models (ECM) [5] and electrochemical models [6] were combined with least-squares (LS)-based algorithms, which provided a robust online parameter identification method for estimating the SOH. In Ref. [7], the authors proposed a multi-adaptive forgetting factor recursive least-squares method to estimate the open-circuit voltage (OCV) and internal resistance of the battery. The simplicity of the algorithm was ensured, while accurately capturing real-time battery parameter changes. Combined with the ECM, the Kalman Filter-based algorithm [8] and observers [9] could provide an online joint estimation of the SOC and SOH with excellent real-time performance and convincing accuracy.

Data-driven methods have treated batteries as black-box models, followed by the extraction and condensation of data for model building. In [10], the authors selected the battery discharge time under a constant voltage drop as a feature and established a wavelet kernel relevance vector machine (RVM) model to achieve high-precision online SOH estimation. Chen [11] proposed an extreme learning machine (ELM) framework to estimate the SOH using a small amount of data. However, extracting the health features is a critical step that directly affects algorithm performance. Convolutional neural networks (CNN) with a specific computational process could learn the features by kernels without feature engineering. In Ref. [12], the authors combined the concepts of transfer learning and ensemble learning to propose a SOH estimation method with a higher level of accuracy and robustness for estimating the capacity of different batteries. The structures and hyperparameters of different data-driven models could strongly affect the algorithm performance [13].

Researchers have explored the feasibility of hybrids and other methods. Hybrid methods, combined with different methods or models, can achieve more effective outcomes. In Ref. [14], a model comprising a hybrid battery model and a sliding-mode observer was used to achieve reliable SOC and capacity estimation. The authors in Ref. [15] combined a metabolic grey model and multi-output Gaussian process regression to establish a data-fusion method for SOH and remaining useful life (RUL) prediction. Other methods that measure or analyze the generative information during battery cycling are relatively simple and efficient approaches for exploring the degradation of battery performance. In Ref. [16], the authors proposed an enhanced Coulomb counting method that could accurately estimate the SOC and SOH. Incremental capacity analysis (ICA) [17] and differential voltage analysis (DVA) [18] are representative evaluation methods that are not limited to specific battery types. The ICA is commonly accepted for the SOH estimation of batteries because of its simple calculation process and the significance of the battery aging mechanism.

Recently, several studies have proposed rapid SOH estimation methods based on actual driving data. In Ref. [19], the authors used real vehicle operating data, and a battery aging method combined with a dual-polarization equivalent circuit (DPEC). A recursive least-squares method (RLS) was proposed to predict the internal resistance. In Ref. [20], the authors applied discrete incremental capacity analysis to real driving data and proposed a processing method for real driving data. Meanwhile, clustering analysis provided a comparison of the SOH information for the same EVs type. However, in real EVs, there may not always be a complete charging and discharging process for the battery packs. Drivers’ habits can result in different depths of charging and discharging of battery packs. Data-driven methods are widely accepted owing to their powerful analytical capabilities for handling large-scale driving data. In Ref. [21], the authors established a prediction model based on a support vector machine (SVM). The algorithm only requires partial charging curves, making a rapid on-board diagnosis of the SOH realistic. The degradation of real vehicle batteries is a complex process. How to capture the information related to battery decline in huge data and accurately track the decline trend is a difficult task. Long short-term memory neural network (LSTM) is a special kind of recurrent neural network (RNN), which can effectively deal with long-term dependency problems and is suitable for time series tasks. Many researchers have tried to use LSTM to solve the battery parameter prediction problem. In Ref. [22], the authors present the LSTM model to perform real-time multi-forward-step SOC prediction for battery systems. Since the remaining useful life (RUL) is also difficult to predict when the predicted dataset is different from the training dataset in terms of the mapping of operating conditions, the authors [23] propose novel RUL prediction techniques based on long short-term memory network. Considering the influence of complex and changeable driving conditions, the authors [24] summarized eight potential battery health indicators. Subsequently, a variable-length input LSTM model for different driving conditions was constructed for SOH prediction, which can be used for full-climate vehicle applications.

However, there are still some challenges from prior studies. First, the raw driving data are of relatively poor quality owing to the limitations of the acquisition equipment. Most of the current prediction studies of SOH/RUL based on experimental environmental data ignore the noise problem of real driving data, so data processing and model robustness are very important to ensure prediction accuracy. Secondly, many prediction approaches have been established based on single-cell experiments. This means that the different discharge/charge characteristics and working temperatures of different cells may lead to a more complex SOH degradation process in battery packs [25]. Effectively evaluating vehicle battery pack degradation remains a challenge. Finally, the battery packs of EVs are affected by the environment and driving behavior, and methods for analyzing their impacts on the estimation results are still lacking.

To achieve a rapid and accurate SOH estimation of real vehicle batteries, this study aimed to extract potential SOH indicators and establish a novel SOH definition for battery packs using real driving data. In the proposed method, a data-driven model was used to provide an SOH prediction result that is immune to noise. The proposed method has addressed the effects of ambient temperature on batteries and provided battery SOH prediction results for different vehicles. The main structure of this paper is shown in Figure 1. The remainder of this paper is organized as follows. The processing method for real driving data is presented in Section 2. Section 3 introduces a fusion evaluation indicator for battery pack SOH and has demonstrated its feasibility. In Section 4, a novel data-driven model for SOH prediction is presented. Section 5 summarizes and analyzes the estimation results and provides the conclusion of the study.

2. Data Processing for Real Driving Data

2.1. Data Preprocessing

In this study, real driving data were used to evaluate the SOH of EV battery packs. The data were obtained from the National Big Data Alliance of New Energy Vehicles (NDANEV) and collected from the National Monitoring and Management Platform for New Energy Vehicles (NEVs) (http://www.ncbdc.top/, accessed on 20 December 2020). Historical data from ten purely electric commercial vehicles located in Beijing and Shanghai were processed. After removing the warning data samples, the original data from each vehicle (Vehicle 1–Vehicle 10) were sorted according to the collection time. The number of samples for each vehicle after filtering is listed in

Table 1. The number of samples for each vehicle.

Vehicle	Original Records	Filtered Records
1	8,369,972	5,618,887
2	560,297	560,221
3	450,596	450,528
4	374,026	369,351
5 (discarded)	7487	7487
6	1,668,507	1,665,611
7	1,635,071	1,629,541
8	1,224,282	1,220,165
9	605,133	604,653
10	407,840	407,776

. Vehicle 5 was discarded because it had fewer samples than the other vehicles. To analyze the potential impact of environmental factors, the ambient temperature data of Beijing and Shanghai were obtained from Weather Underground (https://www.wunderground.com/, accessed on 20 December 2020) with hourly sampling intervals.

2.2. Segmentation of Charging and Driving Data

The original data are highly complex because the vehicles have different states, including the parking–charging state, driving–charging state, uncharged state, charging completion state, abnormal state, and invalid state. The battery parameters of the different states vary significantly, which means that the data first required segmentation. During parking–charging and driving, the battery charging and discharging behaviors were relatively complete, the battery SOC changes were relatively uniform and continuous, the battery state was stable, and the main parameters, such as current, voltage, and temperature, changed relatively smoothly. Moreover, the research object of this paper is a commercial vehicle, which is usually in a constant driving and charging process. Therefore, it is reasonable to use driving segments and parking and charging segments to approximate the battery degradation of real vehicles in this paper. Therefore, parking–charging and driving data from the electric vehicles were separated from the raw data for further analysis. However, it would be difficult to delineate the complete segments accurately only using information on the vehicle status and charging status. The vehicle speed is a more accurate description of the status of vehicles, and the positive and negative values of the battery current can indicate the charging or discharging situation. Therefore, the vehicle speed, battery current, and vehicle status were selected as the filtration criteria for the charging data. The energy recovery system for electric vehicles can also charge its battery during the braking process. However, it is difficult to analyze the battery health status in this manner. Therefore, braking energy recovery data need to be excluded.

In summary, the filtering criteria for the parking charging data were as follows: the value of the battery current data was negative, the charging status was parking–charging, and the vehicle was in a parking state. Given the frequent starting and stopping of vehicles, the filtering criteria of the driving data cannot use the vehicle speed as the only distinction criterion, that is, the value of the battery current is non-negative, and the vehicle is starting. The filtering criteria for the different data types are listed in

Table 2. The filtering criteria of parking charging and driving segments.

Segment Type	Filtering Criteria
Parking–charging	Battery current < 0, charging status = stop charging, vehicle Speed = 0
Driving	Battery current ≥ 0, vehicle status = starting

.

After differentiating between vehicle charging and driving data, the data were divided into independent charging and driving segments for further analysis. The SOC value was used as the slice point for independent segments. Therefore, it is necessary to continuously maintain the charging and driving segments. If the length of the fragment is less than 30 or the value of the SOC range within the fragment is less than 20, the segments with little information should be excluded. Segments with abnormal voltage and current data need to be excluded to retain valid segments with sufficient information. The requirements for the data segments are as follows.

Considering that a real vehicle follows the driver’s decisions to start and stop, it will be detrimental to conduct further analysis if the vehicle stopping time is too long. Therefore, the segments were resliced according to the time interval between two adjacent samples. The time interval between two adjacent data samples was more than 15 min, which may have been because of the absence of samples or parking from the traffic conditions. Parking data in the segment with longer timescales need to be excluded, and, for further processing, the segment should be regarded as two independent segments. Subsequently, these segments must be filtered again according to the requirements shown in

Table 3. The requirements for parking charging and driving segments.

Requirements of Segments	Criteria
Length	Segment length > 30
SOC	Range of SOC variation > 20
Voltage and current	No abnormal variations

.

2.3. Outliers and Missing Value Processing

The charging and driving segments were obtained by processing the raw data. During the processes for data acquisition, transmission, and storage, some problems may occur, such as instability of sensors, changes in data acquisition environments, and external interference. The data collected may deviate from the normal range and affect further analyses. Therefore, in this study, the boxplot method was used to detect the outliers for all parameters in the charging and driving segments. All the outliers were treated as missing values and replaced with blank points so that outlier data could be processed along with the missing data.

The data used in this study were remotely collected and transmitted while the vehicle was operating. During the transmission process from the test vehicle to the data storage device, many factors may lead to missing values, such as sensor failures during data acquisition, weather interference, building blockage during the data transmission process, and memory or hardware failures of the data storage devices.

Therefore, it is necessary to fill in blank samples to obtain continuous variations in battery information. According to GB/T 32960.2-2016 [26], the maximum data acquisition interval should not exceed 30 s. Therefore, Lagrange interpolation was used to make the time interval between two adjacent data points within the fragment approximately 10 to 20 s.

We completed the processing of the charging and driving segments and then proceeded with further analysis. After data processing and filtering, we obtained 445 complete driving/charging cycles for Vehicle 1. The parameters of the driving and charging segments are shown in Figure 2.

3. SOH Construction Method

With continuous chemical reactions inside the battery, the aging of electrode materials, electrolytes, and the diaphragm leads to the deterioration of battery performance. Most current studies use battery characteristic parameters to define the SOH, which is commonly defined as the ratio of battery capacity to nominal capacity under certain conditions. The use of SOH based on capacity has been widely accepted in electric vehicles. Another extensively used SOH definition method uses the internal resistance of a battery to characterize changes in battery health [27]. The two definitions of the SOH are as follows:

$$\begin{array}{c}{SOH}_{Capacity}=\frac{C_{now}}{C_{new}}\times 100\%\end{array}$$

(1)

$$\begin{array}{c}{SOH}_{InternalResistance}=\frac{R_{EOL}-R_{now}}{R_{EOL}-R_{new}}\times 100\%\end{array}$$

(2)

where $C_{new}$ represents the capacity of the new battery, $C_0$ is the nominal capacity of the battery, $R_{now}$ is the internal resistance at the current time, $R_{new}$ is nominal battery internal resistance, and $R_{EOL}$ is the internal resistance at the end of battery life.

However, given that the battery capacity and internal resistance of electric vehicles are difficult to measure, it is difficult to apply traditional capacity and internal resistance definition methods to accurately describe the SOH of battery packs. However, the present methods for defining the SOH are still not available for real EVs because of the following problems:

The battery SOH estimation algorithm depends on the SOC, and the tabulated SOC is calculated by the nominal capacity value, which leads to certain errors in the calculation results. An estimation algorithm based on internal resistance requires a high-precision battery model, which has high requirements for BMS computing capability. However, conducting capacity or internal resistance tests for real electric vehicles in certain laboratory environments can be relatively difficult. This implies that it is difficult to acquire the real value of the SOH of battery packs.

Differences in material processes and other aspects will result in differences in the voltage or internal resistance of cells and, therefore, will have an impact on the overall performance of vehicle batteries. This means that the degradation trends of different cells are not the same. However, most current methods are used to describe the SOH of a single cell, and cannot effectively describe the inconsistency of cells in battery packs. Given that vehicles operate in different regions, battery packs in different ambient climates may have different degradation tendencies.

Finally, different drivers showed different behaviors. Frequent starting and stopping of the vehicle and charging habits may have different effects on the battery pack cycling life.

3.1. Extraction of SOH Indicators

Based on these problems, a detailed indicator is considered to determine the SOH of a battery pack in a real vehicle. In addition, a novel SOH evaluation method has been proposed to define the SOH for real vehicle battery packs. In the following section, we presented six potential battery health indicators and their calculation methods. It was assumed that the battery health conditions remained constant within a certain segment.

(1)

Mileage capability (MC).

The traffic conditions and driving behaviors of different vehicles are irregular during actual operation. The charge and discharge rate [28,29] and depth of discharge [30] (DOD) have certain impacts on the battery SOH. Therefore, the decreasing trend of miles that can be driven per SOC could reflect the discharge performance of the battery packs. Mileage capability is expressed as follows:

$$\begin{array}{c}{SOH}_{MC}=\frac{{Mileage}_{ed}-{Mileage}_{sd}}{{SOC}_{sd}-{SOC}_{ed}}\end{array}$$

(3)

where ${Mileage}_{ed}$ is mileage at the end of a driving segment, ${Mileage}_{sd}$ is mileage at the start of the segment, ${SOC}_{ed}$ is the SOC at the end of the segment, and ${SOC}_{sd}$ is the SOC at the start of the segment.

(2)

Capacity analysis (CA).

Battery capacity remains an essential indicator for describing the health status of a battery and can be calculated from the Ampere integral. However, this requires highly accurate SOC measurement values, which leads to practical difficulties for EVs. The calculated capacity resulting from the discharging segments may lead to errors because of unstable discharging currents. Hence, capacity was only obtained from the charging segments. The method was simplified while calculating battery capacity as accurately as possible. In this section, we selected the charging segments according to the driver’s charging habits, that is, a low or high charging rate. Some drivers are accustomed to using fast charging to save time, for example, Vehicle 7, and use slow charging a few times, then the fast charging segments are used for calculation. Since we do not know the nominal battery capacity of each vehicle in advance, the traditional method of defining SOH using capacity cannot be applied. Therefore, we can capture the information of the battery capacity’s decline trend to characterize the SOH as accurately as possible. It is difficult and challenging compared to the traditional capacity definition method.

$$\begin{array}{c}{SOH}_{CA}=\frac{{\int }_{sc}^{ec}Idt}{{SOC}_{sc}-{SOC}_{ec}}\end{array}$$

(4)

where ${SOC}_{ec}$ and SOC at the end of the segment, ${SOC}_{sc}$ is SOC at the start of the segment, respectively. $I$ is the current in real time.

(3)

Internal resistance (IR).

As widely used battery health status indicators, batteries exhibit different internal resistance characteristics at different SOC, ambient temperatures, and charging/discharging rates [31]. To avoid inaccurate calculations, the resistance was obtained by selecting the SOC in the range 70–90. The completed part of the charging segment and the beginning of the driving segment were selected for calculation.

$$\begin{array}{c}{SOH}_{IR}=\frac{U_t-U_{t-1}}{I_t-I_{t-1}}\end{array}$$

(5)

$U_t$ and $I_t$ are the battery terminal voltages and currents at the charging and driving segments, and $U_{t-1}$ and $I_{t-1}$ are the battery terminal voltages and currents, respectively, at the previous sampling time.

(4)

Charging time from 50 SOC to 60 s SOC.

Different drivers may prefer rapid or slow charging at different battery discharge depths according to their charging habits. For example, fast charging is preferred 463 times during the 513 charging cycles of Vehicle 7. Therefore, the ${SOH}_{CT10}$ of this vehicle is calculated using the fast charging segments.

$$\begin{array}{c}{SOH}_{CT10}={T_{60}-T}_{50}\end{array}$$

(6)

where $T_{50}$ indicates the charging time point when the SOC reaches 50, and $T_{60}$ indicates the charging time point when the SOC reaches 60.

(5)

Cell voltage differences (CVD).

With the increasing inconsistency between individual cells during the battery pack aging process, the degree of battery aging between different cells significantly affects the SOH of the battery [32]. Therefore, the maximum cell voltage and cell temperature differences were selected as indicators to describe the cell inconsistencies of the packs.

$$\begin{array}{c}{SOH}_{CVD}=\frac{1}{n}{\displaystyle \sum _{i=1}^n}({maxCV}_i-{minCV}_i)\end{array}$$

(7)

where ${maxCV}_i$ denotes the maximum cell voltage sequence of the $i$-th segment, ${minCV}_i$ is the minimum cell voltage sequence of the $i$-th segment, and $n$ is the number of records in the $i$-th segment.

(6)

Cell temperature differences (CTD)

$$\begin{array}{c}{SOH}_{CTD}=\frac{1}{n}{\displaystyle \sum _{i=1}^n}({maxCT}_i-{minCT}_i)\end{array}$$

(8)

where ${maxCV}_i$ denotes the maximum cell temperature sequence of the $i$-th segment, ${minCV}_i$ is the minimum cell temperature sequence of the $i$-th segment, and $n$ is the number of records in the $i$-th segment.

Among the six indicators listed in Figure 3, ${SOH}_{MC}{, SOH}_{CA}$, ${{SOH}_{IR}, SOH}_{CT10}$ mainly describe the battery performance in the charging and discharging process. ${SOH}_{CVD},{ SOH}_{CTD}$ are used to describe the inconsistency changes between the cells in the battery pack. For the indicator ${SOH}_{CT10}$ of the driving segments, the neighboring charging segments are used for filling, and the same applies to the ${SOH}_{MC}$ of the charging segments, to ensure that the number of indicators is the same. The six indicators calculated for Vehicle 7 and Vehicle 8 are shown as an example in Figure 3. The linear fit of each indicator curve was also analyzed to facilitate observing changes. There are sharp fluctuations in all indicators with the increase in charge/discharge cycles. This may be because of the combined effect of multiple influencing factors such as ambient climates, traffic conditions, and human factors. There was not a clear decreasing trend of ${SOH}_{MC}$ because of the driving habits of different drivers and traffic conditions. The fitted straight lines of ${SOH}_{IR}$ and ${SOH}_{CTD}$ do not have trends that are as pronounced as ${SOH}_{CA}$ and ${SOH}_{CVD}$. In terms of the actual operations, the indicators do not always vary within a definite time range. In this context, a single SOH indicator may not be able to accurately describe the battery health status. There are likely to be substantially different SOH decline trends for different vehicles because each indicator is influenced by multiple variables. The battery capacity, internal resistance, and cell temperature are affected by the ambient temperature. Considering the joint effect of different factors, a detailed evaluation method for SOH needs to be developed for different vehicles.

3.2. Construction of SOH Using Entropy Weight Method (EWM)

Entropy is used to measure the level of disorganization of a system. The lesser the degree of variation of an indicator, the smaller the amount of information reflected, that is, information entropy. Similarly, the greater the amount of information provided by the indicator, the greater the role it plays in detailed evaluation, and the greater the impact the indicator has on the detailed evaluation, that is, the weight [33]. The entropy method is a weighting method that can be used to measure the linear dependence between a random variable and a set of random variables. Li [34] used the entropy weight method to evaluate the significance of health indicators extracted from the IC curve, and the grey correlation was used to evaluate the SOH of the battery. Therefore, the information entropy was calculated to obtain the weights of each indicator and provide a basis for a detailed evaluation. The main steps of the entropy weight method are as follows.

(1)

Data normalization

$$\begin{array}{c}{Y}_{ij}=\frac{X_{ij}-\min \left\{x_{1j},x_{2j},\cdots x_{nj}\right\}}{max\left\{x_{1j},x_{2j},\cdots x_{nj}\right\}-\mathrm{m}\mathrm{i}\mathrm{n}\{x_{1j},x_{2j},\cdots x_{nj}\}}\end{array}$$

(9)

$$\begin{array}{c}{Y}_{ij}=\frac{\max \left\{x_{1j},x_{2j},\cdots x_{nj}\right\}-X_{ij}}{max\left\{x_{1j},x_{2j},\cdots x_{nj}\right\}-\mathrm{m}\mathrm{i}\mathrm{n}\{x_{1j},x_{2j},\cdots x_{nj}\}}\end{array}$$

(10)

$$\begin{array}{c}{p}_{ij}=\frac{Y_{ij}}{\sum _{i=1}^n{Y}_{ij}}\end{array}$$

(11)

Equations (1) and (2) are applied to the forward and inverse indicators, respectively. Where n denotes the number of indicators. Where $X_{ij}$ denotes the $i$-th parameter of the $\mathrm{j}$th indicator, $max\left\{x_{1j},x_{2j},\cdots x_{nj}\right\}$ is the maximum value in the indicator series. $min\{x_{1j},x_{2j},\cdots x_{nj}\}$ is the minimum value of the indicator series, and $Y_{ij}$ is the standardized result of the indicator. Weight $p_{ij}$ is the $\mathrm{j}$-th indicator in the $\mathrm{i}$-th indicator and is obtained from Equation (3).

(2)

Information entropy calculation

$$\begin{array}{c}{E}_j=k\sum _{i=1}^n{p}_{ij }\ln p_{ij }\end{array}$$

(12)

where $p_{ij }$ is the weight of the standardized value of the$i$-th parameter of the $\mathrm{j}$-th indicator, $E_j$ is the entropy value of the j-th indicator. To ensure that information entropy takes a value in the range [0, 1], the value of $k$ is generally taken as $\frac{1}{\ln n}$.

(3)

Calculation of weights

$$\begin{array}{c}{G}_j={1-E}_j\end{array}$$

(13)

$$\begin{array}{c}{W}_j=\frac{G_j}{k\sum _{j=1}^k{E}_j}\end{array}$$

(14)

where $k$ is a constant, and $G_j$ denotes the degree of differentiation of the $\mathrm{j}$-th indicator values. The greater the data variation, the greater the $G_j$ and, therefore, the greater the weight of the indicator. The smaller the data variation, the smaller the $G_j$, and, therefore, the smaller the weight of the indicator. If the data are consistent for a certain indicator condition, the coefficient of variation is zero.

(4)

Evaluation results

$$\begin{array}{c}{S}_j=W_j\times Y_{ij}\end{array}$$

(15)

where $S_j$ is the composite evaluation result.

According to information theory, weights reflect the importance of an indicator. We subjectively listed six indicators that correlate with the life of a power battery pack. Before the calculation, the positive and negative values of the six indicators are distinguished according to their numerical variation characteristics. Therefore, ${SOH}_{MC},{ SOH}_{CA}{, SOH}_{CT10}$ are selected as positive indicators, whereas ${SOH}_{IR}, {SOH}_{CVD}, {SOH}_{CTD}$ are selected as negative indicators. Therefore, the new SOH calculation equation is as follows:

$$\begin{array}{c}{SOH}_{new}=W_{MC}{SOH}_{MC}+{W_{CA}SOH}_{CA+}{W_{IR}SOH}_{IR}+{{W_{CT10}SOH}_{CT10}+W_{CVD}SOH}_{CVD}+{W_{CTD}SOH}_{CTD}\end{array}$$

(16)

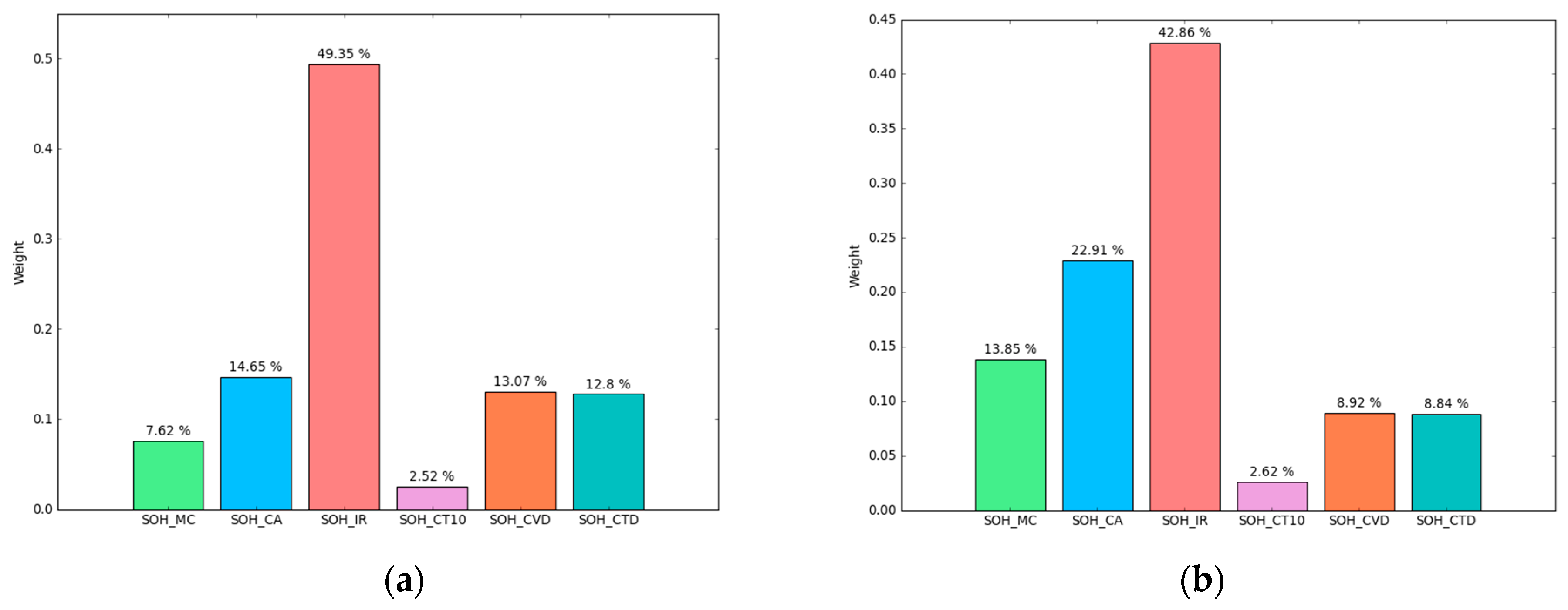
According to the proposed method, Vehicle 3 in Shanghai and Vehicle 8 in Beijing were regarded as examples for comparison and analysis. The weights of each health indicator of the two vehicles are given in Figure 4a,b. The internal resistance and capacity indicators account for more than 60% of the detailed evaluation system. The ${SOH}_{MC}$ is more variable because of the influence of restricted driver behaviors and traffic conditions. The mileage indicator has different weight in evaluating SOH of different vehicles. The ${SOH}_{CVD}, {SOH}_{CTD}$ have approximately the same percentage in the evaluation system. The ${SOH}_{CT10}$ has little impact on the overall evaluation system. It can be seen that a diversity of SOH evaluation methods is necessary for different vehicles.

3.3. Effect of Ambient Temperature

The electric vehicles used in Beijing and Shanghai have different working environments. Figure 5 shows the calculated SOH results and the ambient temperature curves. The SOH results do not follow a strictly linear trend. There are many reasons for this phenomenon, including temperature fluctuations, sudden changes in discharge current, changes in vehicle driving speed, and the power consumption of onboard electronics. Therefore, the SOH values obtained from the calculations needs to be corrected. In this section, the ambient temperature data were analyzed to avoid calculation errors.

The battery health status under different ambient temperatures shows an Arrhenius relationship with temperature [35]. Vehicles 1, 7, 8, and 10 were in Beijing, and Vehicles 2, 3, 4, 6, and 9 were in Shanghai. After completing the outlier processing of the ambient temperature data, resampling was performed and spliced with the data from each vehicle. Figure 5 shows that there were similar short-term fluctuations in the raw SOH as the seasonal ambient temperature changed. The higher the temperature, the faster the internal reaction rate of the battery and the more evident the change in the battery SOH. The lower the temperature, the slower the change in the battery SOH. However, the effect of ambient temperature was limited to small short-term fluctuations in the SOH curve. In the case of a more stable long-term trend of battery decline, the ambient temperature did not affect the long-term decline trend of the battery.

Therefore, the ambient temperature is used as the main factor for correcting the SOH previously calculated. To exclude the influence of other factors, such as battery charging and discharging cycles, cycling data within 15 cycles and an average battery current close to the global average current were selected for modeling. The average SOH value of the battery with an average temperature close to 25 °C was selected as the baseline noted as ${\mathrm{S}\mathrm{O}\mathrm{H}}_{\mathrm{t}0}$. Based on ${\mathrm{S}\mathrm{O}\mathrm{H}}_{\mathrm{t}0}$, the ratio of ${\mathrm{S}\mathrm{O}\mathrm{H}}_{\mathrm{t}}$ to ${\mathrm{S}\mathrm{O}\mathrm{H}}_{\mathrm{t}0}$ at different battery temperatures was obtained to express the temperature correction coefficient. It was assumed that the characteristics of the individual cells were not significantly different from those before they were formed into a battery pack. The average temperature $\overline{T}$ and the temperature correction factor $K_T(t)$ were calculated as follows:

$$\begin{array}{c}t=\frac{T_{max}-T_{min} }{2}\end{array}$$

(17)

$$\begin{array}{c}{K}_T\left(t\right)=\frac{{SOH}_T(t) }{{SOH}_{t_0}}\end{array}$$

(18)

where $T_{max}$, $T_{min}$ represent the maximum and minimum temperatures of the cell in a certain section, and $t$ represents the average temperature. $K_T(t)$ is the temperature correction coefficient, ${SOH}_T(t)$ is the SOH at different temperatures, ${SOH}_{t_0}$ is the baseline SOH, and $t$ is the average temperature.

According to the relationship between the correction coefficients and the temperature, the results were fitted using the exponential fitting method, as shown in Figure 6a,b. The corresponding expressions for the correction coefficients and temperature correction equations were obtained as follows:

$$\begin{array}{c}{K}_{T3}\left(t\right)={-0.49261\times e}^{-0.02573t}+1.25641\end{array}$$

(19)

$$\begin{array}{c}{K}_{T8}\left(t\right)={-124.13\times e}^{-1.3651\times {10}^{-5}t}+125.06\end{array}$$

(20)

$$\begin{array}{c}{SOH}_{TC}=\frac{{SOH}_T }{K_T\left(t\right)}\end{array}$$

(21)

where ${SOH}_T$ indicates the SOH without temperature correction, and ${SOH}_{TC}$ indicates the SOH after temperature correction. The relationship between the SOH increment before and after temperature correction and the battery charging and discharging cycles is shown in Figure 6c,d. The increase in SOH varies cyclically with time, which is in line with the constant change in battery temperature as the temperature changes throughout the year. The starting time of Vehicle 3 was operated from 2 May 2018 to 10 December 2019, and Vehicle 8 was operated from 9 March 2018 to 8 September 2019. Given the lower temperatures in fall and winter, with ambient temperatures below 25 °C in most cases, the corrected increase was larger, and higher ambient temperatures in spring and summer resulted in a smaller corrected increase.

The SOH results after temperature correction for the two vehicles are shown in Figure 6e,f. Given that the acquisition data of Vehicle 3 were far fewer than those of Vehicle 8, it showed a larger fluctuation range. With the long-term trend, the corrected results were more compatible with the actual battery SOH degradation trend.

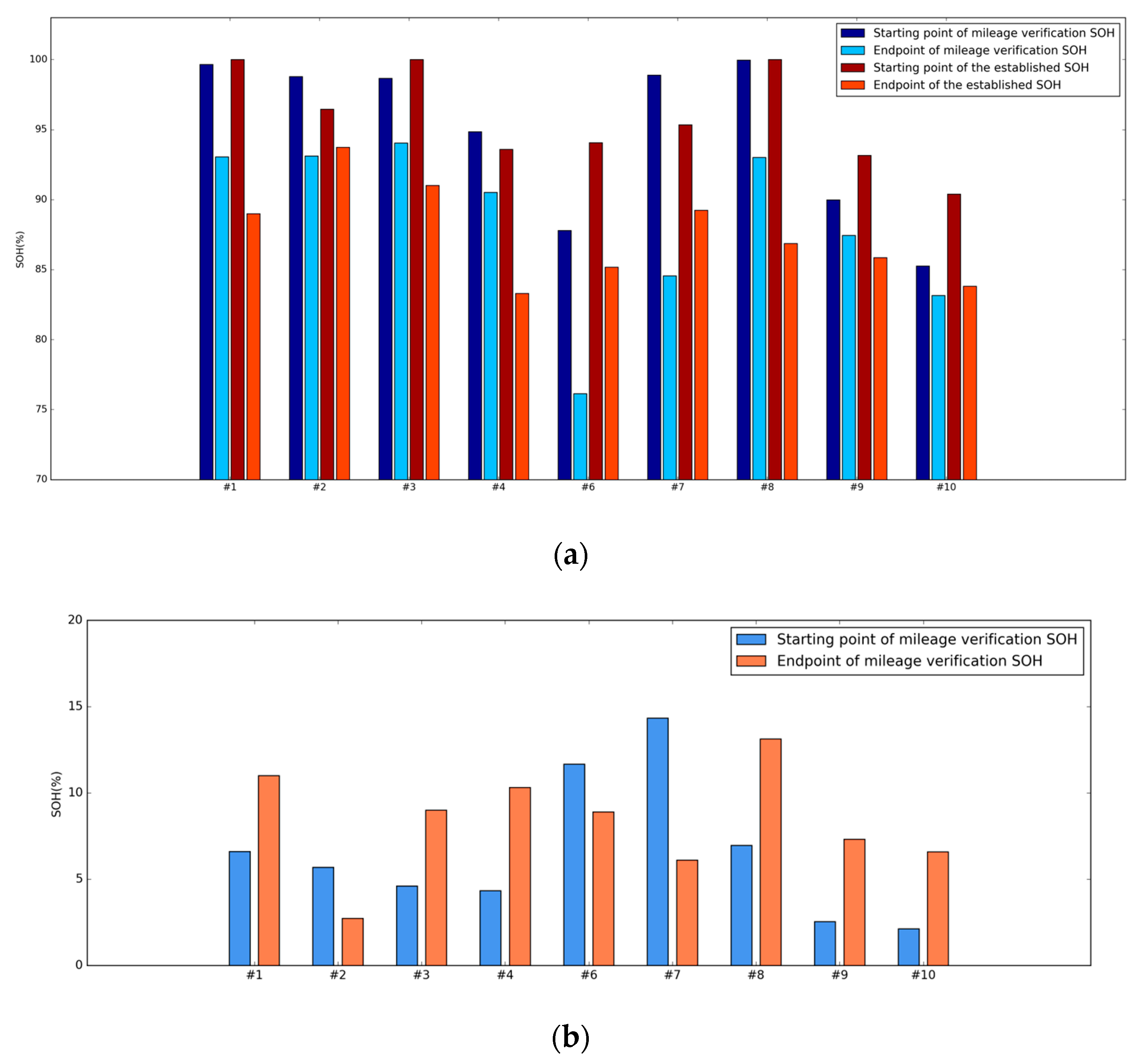
To date, there has been no accurate method developed for measuring the SOH of EV battery packs. Without battery information, it is difficult to obtain the health statuses of real vehicle battery packs. To verify the feasibility of the proposed method, driving mileage was treated as an approximate evaluation method for reference. The SOH calculated from the mileage of each vehicle was obtained according to literature [22]. The 150,000 km range was treated as the full life cycle driving range of the EVs. The SOH validation equation is as follows:

$$\begin{array}{c}SOH=100\%-\frac{Mileage}{150000}\times \left(100\%-80\%\right)\end{array}$$

(22)

The verification results for this SOH with mileage are shown in Figure 7. The calculated results had approximately the same starting point as the validated SOH, and the SOH loss was greater. The potential reasons for this were the real driving data of commercial electric vehicles used for the analysis in this study and the fact that the vehicles required frequent charging or driving to meet passenger demands. Therefore, compared with private vehicles, more time spent driving miles daily will result in more rapid battery degradation. Among the multiple aging modes of batteries, the cycling life accounts for a larger proportion of the battery storage life of commercial electric vehicles. Therefore, it is appropriate to consider cycling life as the main cause of battery degradation. Therefore, the proposed SOH calculation method accurately describes the health states of different electric vehicle batteries. Comparing this model with other studies using the same data source proves the suitability of this indicator.

4. SOH Estimation Based on De-LSTM

Long short-term memory [36] (LSTM) was developed to solve the long-term dependency problem of general RNNs (recurrent neural networks). The LSTM replaces the hidden layer unit in the RNN with a recurrent memory unit with special memory functions. This enables it to selectively retain or delete historical information through input, forgetting, and output gates, therefore, ensuring that the gradient remains after a long period of data learning.

Before training the neural network model begins, a denoising autoencoder (DAE) [37] is added to the neural network to improve the stability and robustness of the model and enhance its generalization ability. The denoising autoencoder is an unsupervised method that adds noise to the input data based on the autoencoder (AE) to learn the original data superimposed with noise, and the decoding learns the features with strong robustness.

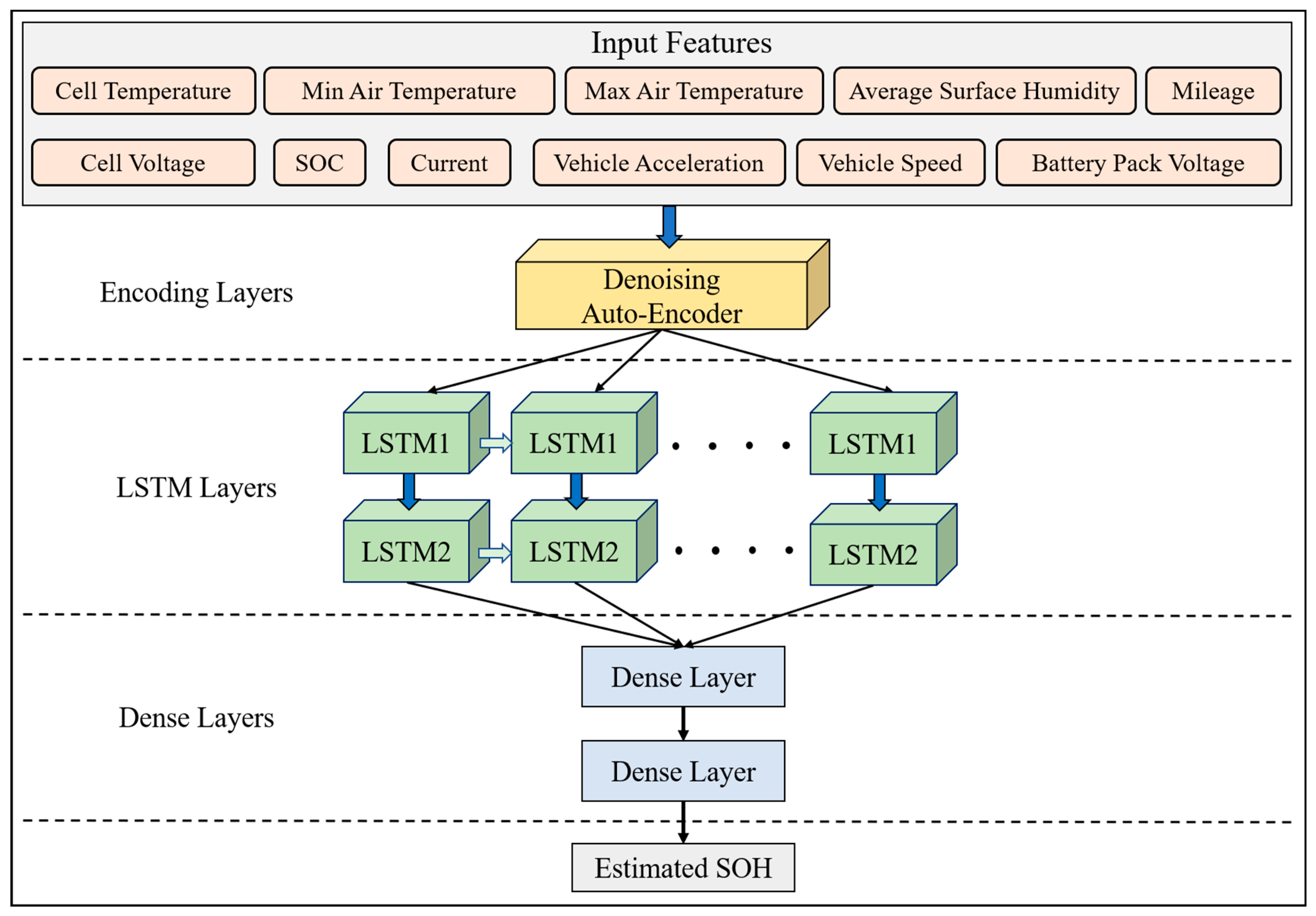
To address the problems of existing methods, we built a denoising long short-term memory neural network (De-LSTM) with a variable length input. The De-LSTM mechanism is shown in Figure 8. The denoising auto-encoder has two functions, that is, adding noise encoding to the data and decoding it to restore the real data. The normalized data input sequence is represented by $X_n$, and Gaussian noise is superimposed to obtain $X_{ns}$. The data dimensions are then mapped back to the original dimensions using the decoding layer.

$$\begin{array}{c}Y=\mathsf{\sigma }\left(W^T{X}_{ns}+\mathrm{b}\right)\end{array}$$

(23)

$$\begin{array}{c}\widehat{X_{ns}}={\mathsf{\sigma }}^{\prime }\left(W^{\prime }Y+b^{\prime }\right)\end{array}$$

(24)

where $\mathsf{\sigma },\mathrm{W},\mathrm{b}$, and $\mathrm{Y}$ denote the activation function, weight matrix, bias matrix, and coded output matrix of the encoder, respectively. ${\mathsf{\sigma }}^{\prime },W^{\prime },b^{\prime }$, and $\widehat{X_{ns}}$ denote the activation function, weight matrix, bias matrix, and decoded output matrix of the decoder, respectively.

Subsequently, the decoded data are fed into the LSTM neural network to establish the mapping from the input sequence to the output sequence using the following computational equations:

$$\begin{array}{c}{f}_t=\sigma \left(W_f\left[h_{t-1}, x_t\right]+b_f\right)\end{array}$$

(25)

$$\begin{array}{c}{i}_t=\sigma \left(W_i\left[h_{t-1}, x_t\right]+b_i\right)\end{array}$$

(26)

$$\begin{array}{c}\widetilde{C_t}=\tanh \left(W_C\left[h_{t-1}, x_t\right]+b_C\right)\end{array}$$

(27)

$$\begin{array}{c}{C}_t=f_t\ast C_t+i_t\ast \widetilde{C_t}\end{array}$$

(28)

$$\begin{array}{c}{o}_t=\sigma \left(W_o\left[h_{t-1}, x_t\right]+b_o\right)\end{array}$$

(29)

$$\begin{array}{c}{h}_t=o_t\ast \tanh \left(C_t\right)\end{array}$$

(30)

where $h_{t-1}$ is the past parameter, $x_t$ is the current input parameter, $W$ is the weight, $b$ is the bias, $f_t$ is the value of the forget gate, and $i_t$ and $\widetilde{C_t}$ are the values calculated using the sigmoid and activation functions, respectively. $C_t$ is the value updated in the cell state, $o_t$ is the value of the output gate, and $h_t$ is the output.

To train the model, the charging and driving segments obtained in the second section were processed to extract the input features of the model. A detailed consideration of the generative information of the battery and external environment information is required to extract features strongly correlated with the SOH. Vehicle speed and acceleration can represent a driver’s driving habits and approximate the influence of battery health caused by the usability factors of the battery. Ambient temperature and average surface humidity can approximately reflect the impact of battery degradation on environmental factors. Therefore, ten input features were determined. These were the vehicle speed, acceleration, battery current, battery pack voltage, SOC, battery cell temperature, battery cell voltage, maximum and minimum ambient temperatures, and average surface humidity.

To express the time series dependence of the predicted objects, each input sample needs to contain features at multiple time steps. For each charge/discharge cycle, the sequence of the battery health characteristics of the previous ($time\_steps$-1) cycle was added to the sequence of the battery health characteristics of that cycle ($time\_steps$ is the time sequence step length). Therefore, the long-term dependence of the battery decline trend is captured by the learning ability of the LSTM model.

K-fold cross-validation [38] was used to repeatedly use the divided data in different combinations. This was used to effectively avoid the problem of poor training effect and the difficulty of the validation data in accurately reflecting the generalization error caused by the insufficient amount of data. Meanwhile, the impact of different division methods on the model performance was avoided when dividing the training and validation sets. To prevent the neural network model from overfitting, L2 regularization and dropout were added to the designed network to reduce the sensitivity of the network to specific features and improve the model generalization performance [39]. An overview of the battery SOH estimation structure based on the De-LSTM is shown in Figure 9. After denoising the original input features using an autoencoder, a two-layer LSTM was used to capture the relationship between the input and output. The prediction results were then obtained through two fully connected layers and an output layer.

5. Results and Discussion

In the designed neural network, 10%, 20%, and 30% of the data segments were divided into test data. The hyperparameters were set as follows: epoch = 120 and batch size = 22. The relus appear to be inappropriate for RNNs because of their large outputs [40] so Adam [41] was chosen as the optimizer in this paper, and the learning rate was set to 0.001. In the proposed network, tanh was used as the activation function. To verify the robustness of this model, zero-mean white Gaussian noise with a mean standard deviation of 5% was added to all input data sequences. The noise level was higher than that of the acceptable sensor in most industries [42]. Three metrics were selected to evaluate the SOH prediction results, namely the mean absolute percentage error (MAPE), root mean square error (RMSE), and relative error (RE). The metric definition is as follows:

$$\begin{array}{c}\mathrm{MAPE}=\frac{100\%}{\mathrm{n}} {\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}}\frac{\left|\widetilde{{\mathrm{y}}_{\mathrm{i}}}-{\mathrm{y}}_{\mathrm{i}}\right|}{{\mathrm{y}}_{\mathrm{i}}}\end{array}$$

(31)

$$\begin{array}{c}\mathrm{RMSE}=\sqrt{\frac{1}{\mathrm{n}}{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}}{\left({\mathrm{y}}_{\mathrm{i}}-\widetilde{y_i}\right)}^2} \end{array}$$

(32)

$$\begin{array}{c}\mathrm{RE}=\frac{\left|\tilde{\mathrm{y}}-\mathrm{y}\right|}{\mathrm{y}}\end{array}$$

(33)

where $n$ is the sequence length, $y$ is the true value, and $\tilde{y}$ is the predicted value.

The SOH prediction results and errors for nine vehicles are shown in Figure 10. The De-LSTM model with its unique long- and short-term memory mechanism can reflect the time series dependence of the battery aging process. The auto-encoder can achieve a higher level of performance with the data reconstruction mechanism, while mitigating noise, outliers, and the influence of early data. The De-LSTM model can then obtain accurate prediction results under noisy data and effectively track the local and global characteristics of the aging process of different batteries. The model achieved satisfactory results for various batteries under different environments. The RMSE, MAE, and RE result of training/prediction proportion of 90%:10% were less than 0.9802%, 0.8827%, and 0.0106, respectively. The comparison results for different test set sizes are shown in Figure 11. It can be seen that the training/prediction proportion of 90%:10% has the highest accuracy and the model has lower RMSE and MRE in different training/prediction proportions.

The comparison results of the De-LSTM, LSTM, and GRU models with the same structure and parameters are shown in Figure 12. Vehicle 7, which had the most accurate prediction results, and Vehicle 6, which had the lowest level of accuracy, were considered as examples. Owing to the effect of noise in the acquisition data, training on the original data has a potential impact on the long-term performance of the model. The DAE can reconstruct noisy input features in low dimensions, which provides more robust features for the LSTM layers. Compared to LSTM and GRU, De-LSTM had a higher prediction accuracy, as shown in Figure 12, for the MSE and RE results.

The results of this study were compared with the algorithms of other studies in

Table 4. Comparison of errors for existing studies.

Method	Refs.	Battery Chemistry	Research Data	Mode of Operation	Estimation Precision
ECM based	[2]	Li-ion	Laboratory experiment	Online	MAX = 3%
Coulomb counting	[3]	Li-ion	Laboratory experiment	Online	Errors = 1.08%
EKF	[10]	Li-ion	Laboratory experiment	Online	Max = 3%
UKF	[43]	Li-ion	Laboratory experiment	Online	RMSE < 4%
SVM	[19]	LiNiCoMn	Laboratory experiment	Online	Max < 3%
Catboost	[17]	NCA/NMC/LFP	Real-world EVs	Offline	MAPE < 2.74% RMSE < 1.12
KF + linear regression	[13]	LiNMC	Laboratory experiment	Offline	MAX = 2.12%
RVM + UKF	[44]	LIBs	Laboratory experiment	Online	RMSE < 3%
GPR	[45]	LIBs	Laboratory experiment	Online	Accuracy = 2.2%
RNN	[46]	Li-ion	Laboratory experiment	Online	MSE < 5%
LSTM in this study		Various types of power battery	Real-world EVs for different Application Scenarios	Online	RMSE < 1.2207% MAPE < 1.0514% RE < 0.0172
De-LSTM in this study		Various types of power battery	Real-world EVs for different Application Scenarios	Online	RMSE < 0.9802% MAPE < 0.8827% RE < 0.0106

. The quality of the real vehicle driving data was poorer in this study. Compared with previous studies, the proposed SOH evaluation method provides a more detailed measure of the battery health status, and the De-LSTM model performs more effectively on noisy input data. The model presented in this paper has better accuracy and robustness compared to previous studies, and especially for real vehicle battery SOH in different environments, it is more valuable. Moreover, because of the different amounts of data collected from different vehicles, the model may not learn the complete SOH degradation trend if the amount of training data is excessively small, which may cause large errors. Based on the electric vehicle big data platform, the feasibility of applying the method in different vehicles and scenarios can be further improved. The model can be further trained to optimize the model structure and hyper parameters through a large database.

6. Conclusions

6.1. Summary of This Study

This study has proposed a robust and highly accurate method for estimating the state of health of EV batteries based on driving data collected from real vehicles. A detailed battery state of health evaluation criterion is established using the entropy weight method, which provides a new direction for estimating the SOH of real EVs. In addition to using battery capacity and internal resistance to indicate battery degradation, we incorporated vehicle drivability, charging time, and voltage and temperature differences between cells to provide a more comprehensive representation of battery degradation. After analyzing the feasibility of this SOH indicator, we discuss the effect of ambient temperature on the calculation of the indicator and make corrections. The results show that the offline trained model performs accurate state of health prediction results on nine different electric vehicle data. Furthermore, the denoising encoder in our data-driven model can effectively deal with the noise problem in data sampling. Besides the generative parameters of the battery system, some external factors such as ambient weather and driving behavior are also used as inputs for model training to improve the generalization ability. With a sufficient amount of data, the trained model not only achieves effective health state prediction, but also obtains battery degradation trends based on partial charging and discharging segments.

6.2. Outlook of Future Research

The battery state of health estimation method for electric vehicles researched in this paper can effectively alleviate the public’s anxiety about the battery’s usage status and establish a foundation for energy conservation and emission reduction as well as the development of the new energy vehicle market. In the future, the evaluation method should be complemented by the refinement of multiple environmental factors and driving behaviors. The structure and hyperparameters of the state of health prediction model will be optimized using data from different vehicles. On the basis of a big data platform for electric vehicles, the SOH evaluation method and prediction model developed have broad prospects for various applications. In conjunction with the development of a policy on the secondary utilization of batteries, more sophisticated models will be developed to provide technical support in the future.