Phase-Field Modeling of Coupled Thermo-Hydromechanical Processes for Hydraulic Fracturing Analysis in Enhanced Geothermal Systems
Abstract
:1. Introduction
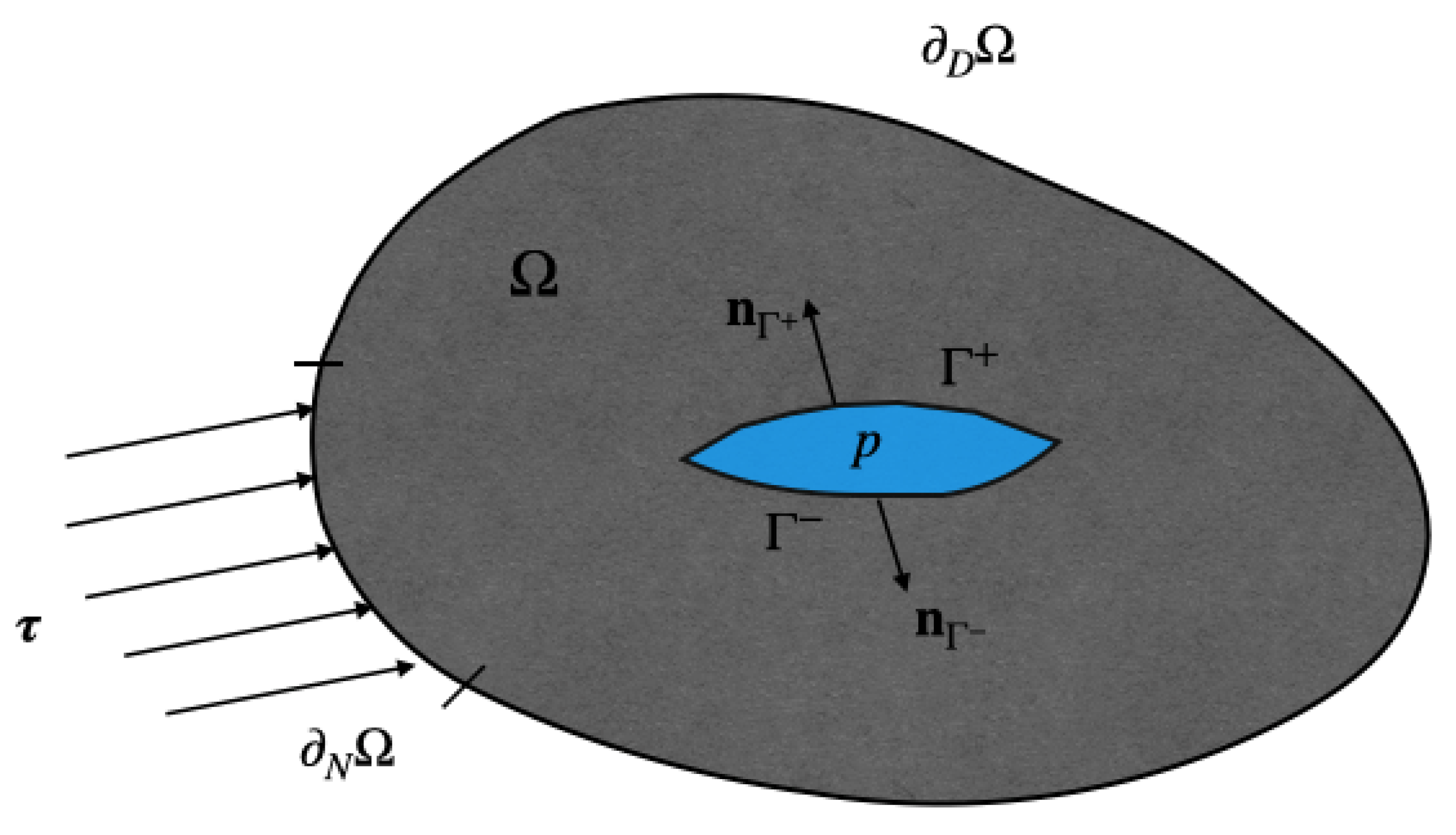
2. Mathematical Model
2.1. Mechanical Equilibrium and Phase-Field Equations
2.2. Mass Balance and Momentum Balance Equations
2.3. Energy Balance Equation
2.4. System of Equations and Coupling Technique
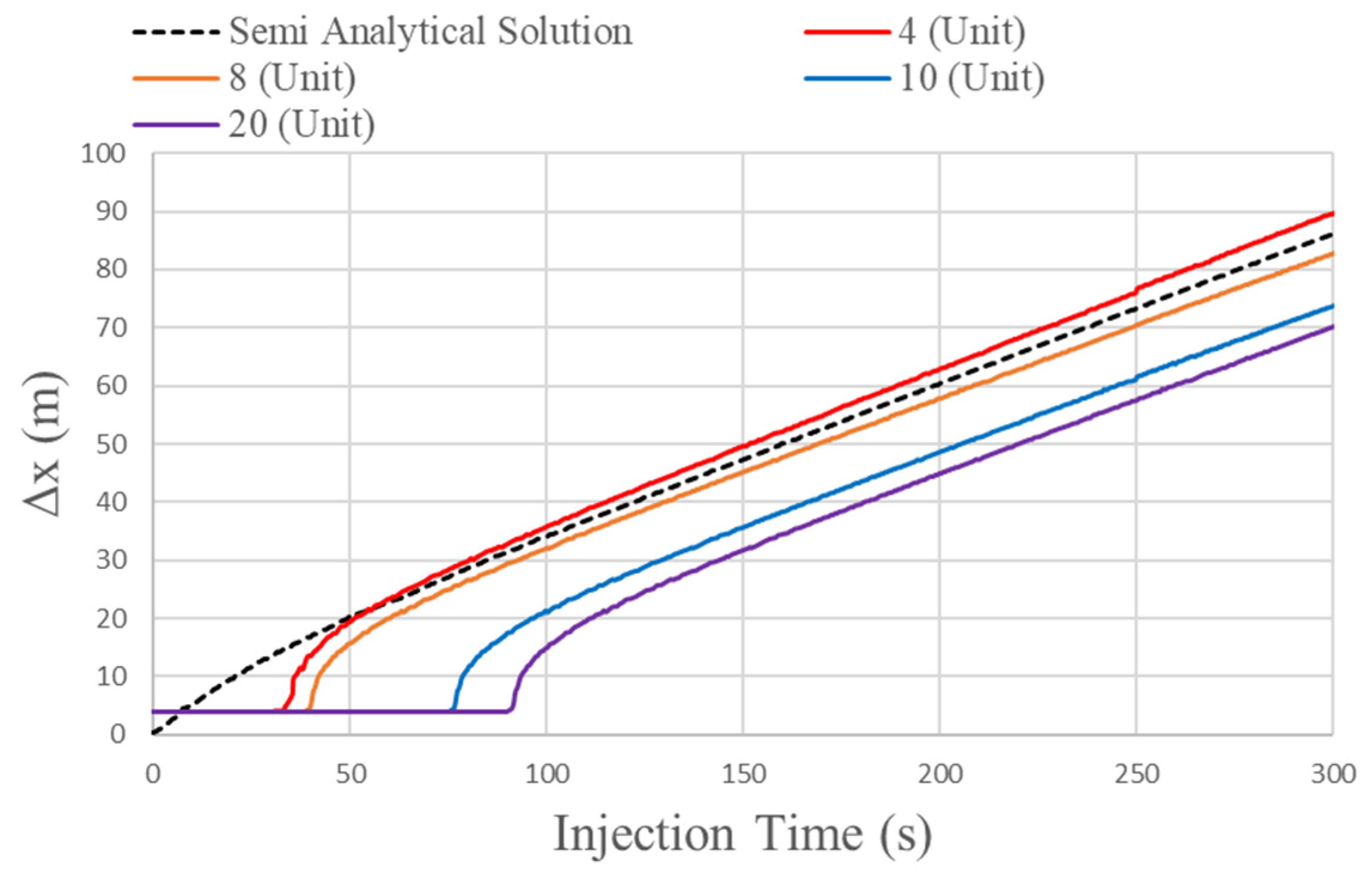
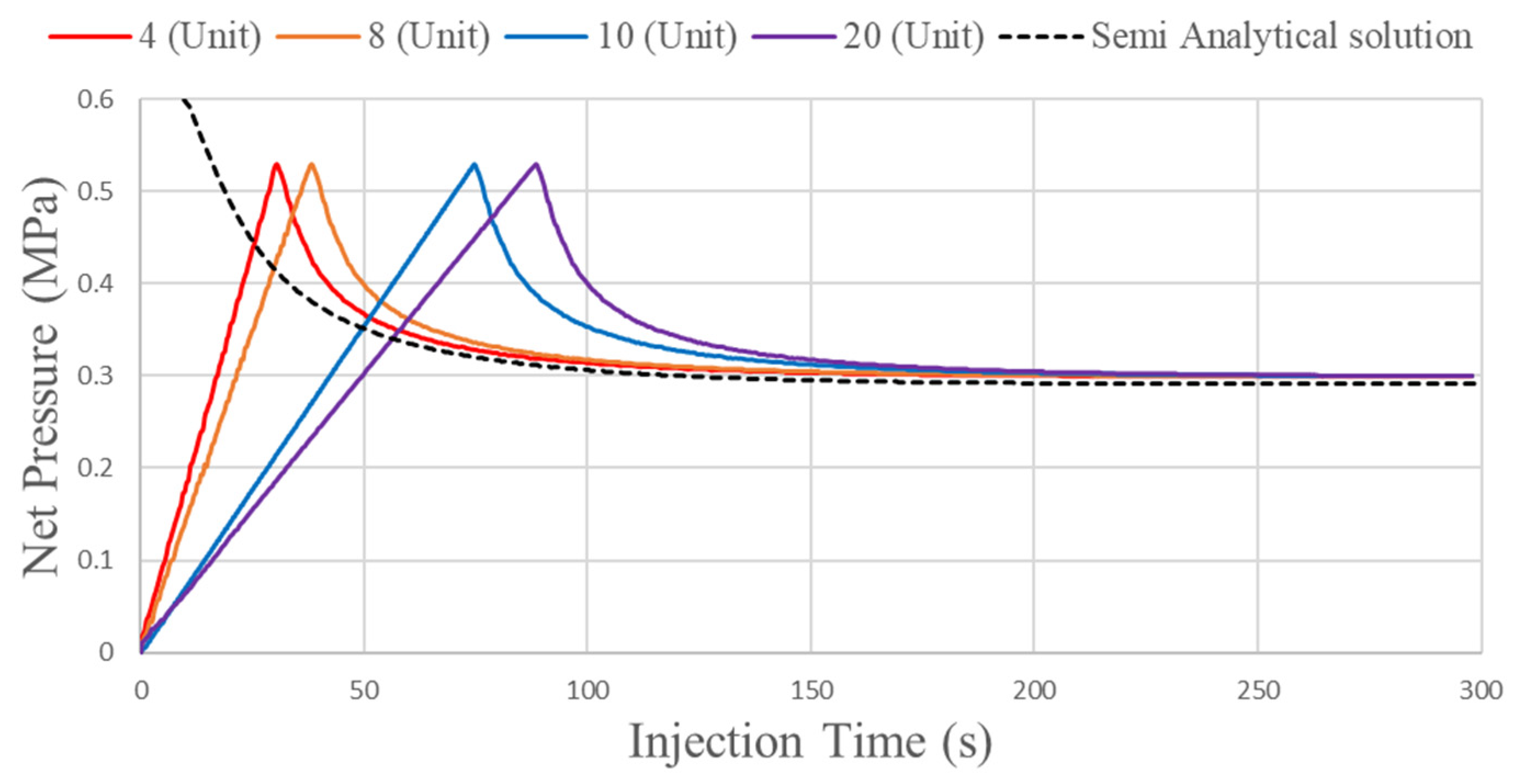
2.5. Verification
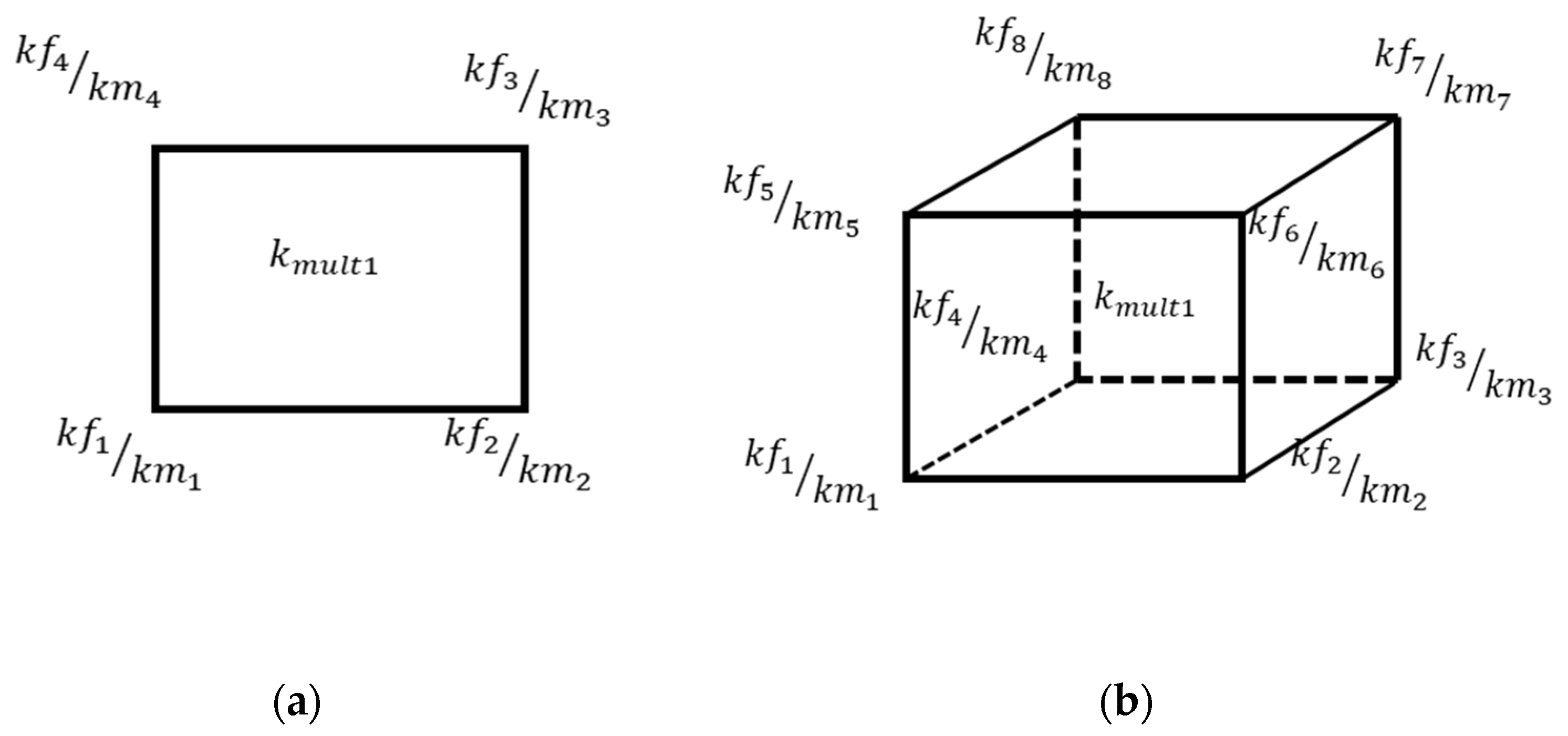
2.6. Geometric and Numerical Model Division
2.7. Model Parameters
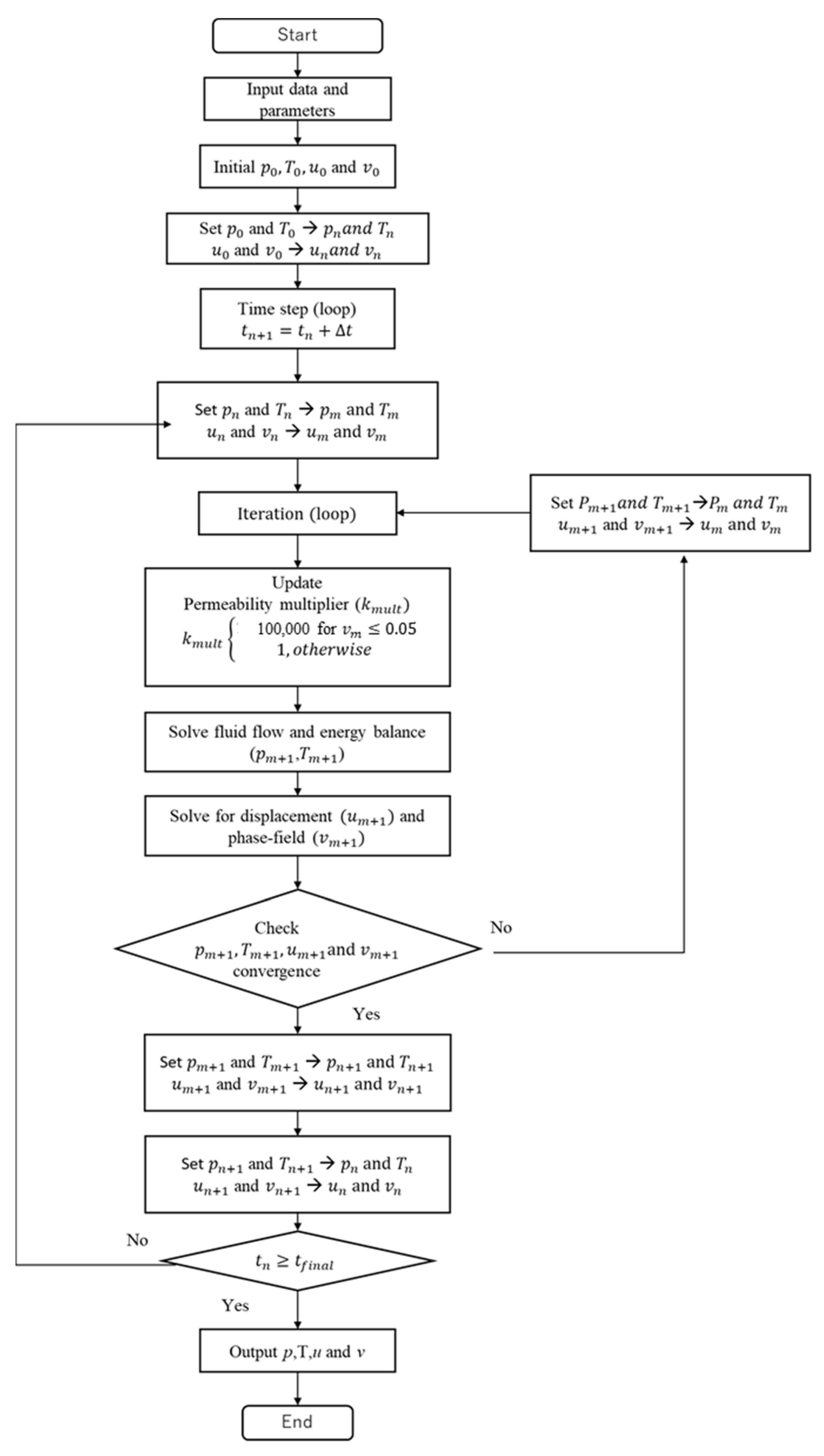
2.8. Simulation Scheme
3. Results
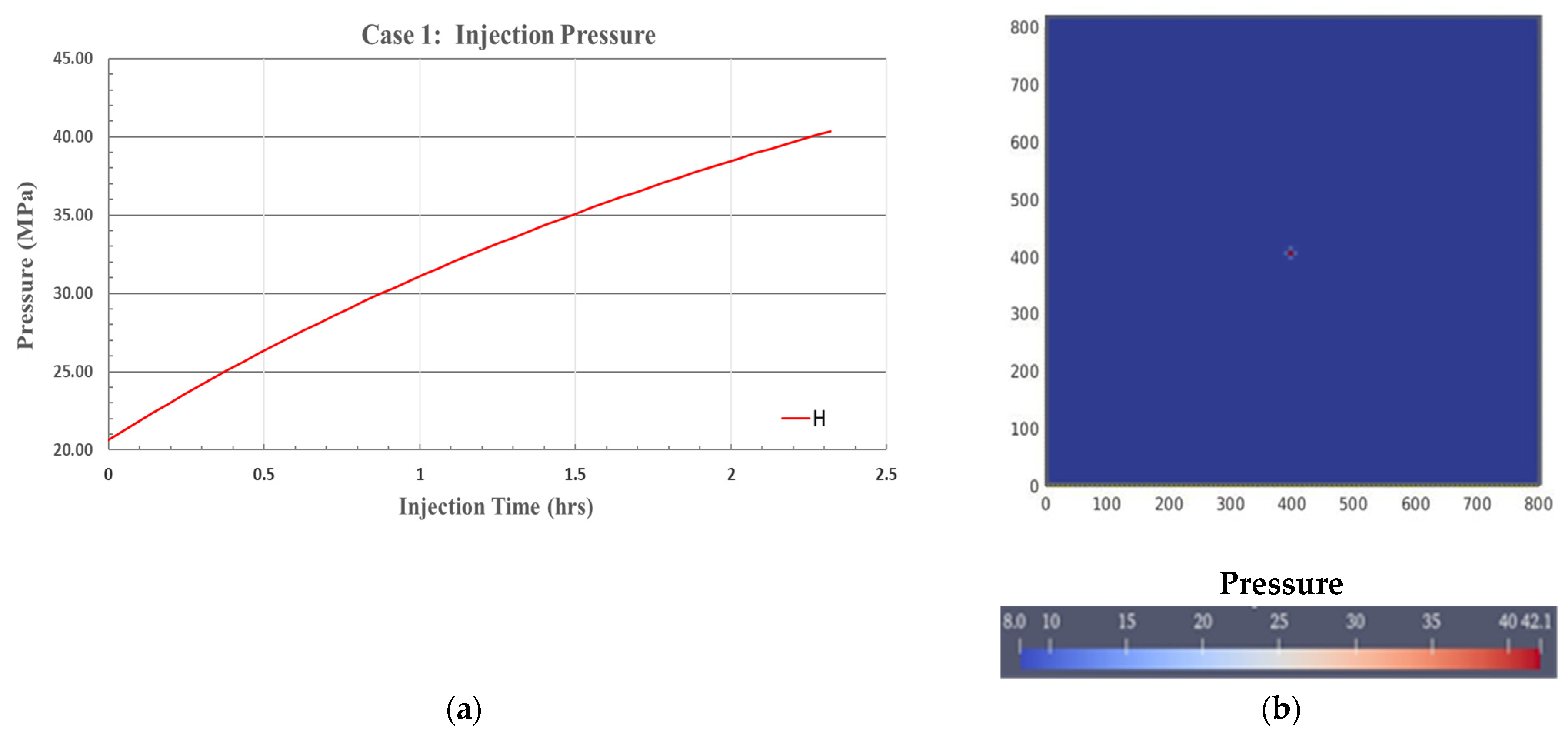
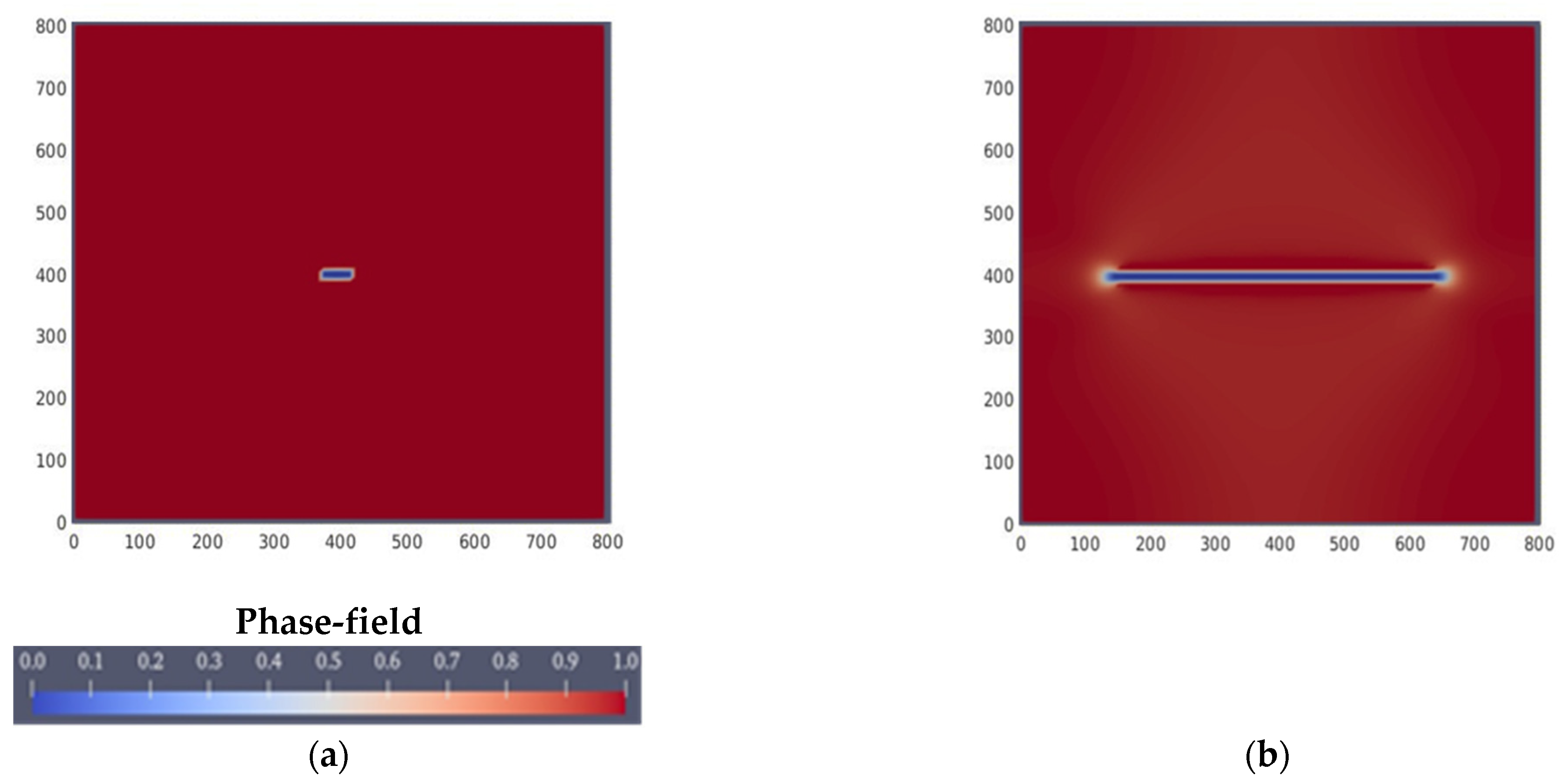
3.1. Case 1: Hydro Simulation
3.2. Case 2: Hydromechanical Simulation
3.3. Case 3: Thermo-Hydromechanical Simulation
3.4. Case 4: Thermo-Hydromechanical Simulation in a Naturally Fractured Formation
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| X | Distance (m) |
| Δt | Time interval (s) |
| E | Young’s modulus (GPa) |
| v | Poisson’s ratio |
| Fracture toughness (Pa·m) | |
| Φ | Porosity |
| Fluid source terms () | |
| µ | Fluid viscosity (Pa·s) |
| Bulk modulus fluid (GPa) | |
| b | Body force (N/kg) |
| τ | External forces (N) |
| Effective stress (Pa) | |
| Rock density (kg/) | |
| Water density (kg/) | |
| Water viscosity (Pa·s) | |
| Average thermal conductivity (W/(m·K) | |
| Specific heat of fluid (J/kg) | |
| Specific internal energy (KJ/kg) | |
| Porosity compressibility (/Pa) | |
| β | Thermal expansion (°C) |
References
- Shere, J. Renewable: The World—Changing Power of Alternative Energy; St. Martin’s Press: New York, NY, USA, 2013. [Google Scholar]
- IRENA. Renewable Capacity Statics 2018; International Renewable Energy Agency (IRENA): Abu Dhabi, United Arab Emirates, 2018. [Google Scholar]
- Tiwari, G.N.; Ghosal, M.K. Renewable Energy Resources: Basic Principles and Applications; Alpha Science Int’l Ltd.: New Delhi, India, 2005. [Google Scholar]
- Gudmundsson, G.H. Transmission of basal variability to a glacier surface. J. Geophys. Res. Solid Earth 2003, 108, 1–19. [Google Scholar] [CrossRef]
- Batchelor, A.S. The Stimulation of a Hot Dry Rock Geothermal Reservoir in the Cornubian Granite, England. In Proceedings of the Eighth Workshop Geothermal Reservoir Engineering, Cornwall, UK, 1 January 1982. [Google Scholar]
- Kelkar, S.; Lewis, K.; Hickman, S.; Davatzes, N.; Moos, D.; Zyvoloski, G. Modeling Coupled Ther-mal-Hydrological-Mechanical Processes During Shear Stimulation of an EGS Well. In Proceedings of the Thirty-Seventh Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 30 January–1 February 2012; Volume 1988, pp. 1–8. [Google Scholar]
- Tester, J.W.; Anderson, B.J.; Batchelor, A.S.; Blackwell, D.D.; DiPippo, R.; Drake, E.M.; Garnish, J.; Livesay, B.; Moore, M.C.; Nichols, K.; et al. Impact of enhanced geothermal systems on US energy supply in the twenty-first century. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2007, 365, 1057–1094. [Google Scholar] [CrossRef] [PubMed]
- Zoback, M.D. Reservoir Geomechanics; Cambridge University Press: Cambridge, MA, USA, 2007. [Google Scholar] [CrossRef]
- Adachi, J.; Siebrits, E.; Peirce, A.; Desroches, J. Computer simulation of hydraulic fractures. Int. J. Rock Mech. Min. Sci. 2007, 44, 739–757. [Google Scholar] [CrossRef]
- Yi, G.; Yu, T.; Bui, T.Q.; Ma, C.; Hirose, S. SIFs evaluation of sharp V-notched fracture by XFEM and strain energy approach. Theor. Appl. Fract. Mech. 2017, 89, 35–44. [Google Scholar] [CrossRef]
- Zarrinzadeh, H.; Kabir, M.; Varvani-Farahani, A. Static and dynamic fracture analysis of 3D cracked orthotropic shells using XFEM method. Theor. Appl. Fract. Mech. 2020, 108, 102648. [Google Scholar] [CrossRef]
- McClure, M.; Babazadeh, M.; Shiozawa, S.; Huang, J. Fully coupled hydromechanical simulation of hydraulic fracturing in three-dimensional discrete fracture networks. Soc. Pet. Eng.-SPE Hydraul. Fract. Technol. Conf. 2016, 21, 1302–1320. [Google Scholar] [CrossRef]
- Gu, H.; Weng, X. Criterion for fractures crossing frictional interfaces at non-orthogonal angles. In Proceedings of the 44th U.S. Rock Mechanics Symposium and 5th U.S.-Canada Rock Mechanics Symposium, Salt Lake City, UT, USA, 27 June 2010. [Google Scholar]
- Bourdin, B.; Francfort, G.; Marigo, J.-J. Numerical experiments in revisited brittle fracture. J. Mech. Phys. Solids 2000, 48, 797–826. [Google Scholar] [CrossRef]
- Francfort, G.; Marigo, J.-J. Revisiting brittle fracture as an energy minimization problem. J. Mech. Phys. Solids 1998, 46, 1319–1342. [Google Scholar] [CrossRef]
- Alessi, R.; Marigo, J.-J.; Maurini, C.; Vidoli, S. Coupling damage and plasticity for a phase-field regularisation of brittle, cohesive and ductile fracture: One-dimensional examples. Int. J. Mech. Sci. 2018, 149, 559–576. [Google Scholar] [CrossRef]
- Carrara, P.; Ambati, M.; Alessi, R.; De Lorenzis, L. A framework to model the fatigue behavior of brittle materials based on a variational phase-field approach. Comput. Methods Appl. Mech. Eng. 2019, 361, 112731. [Google Scholar] [CrossRef]
- Bourdin, B.; Chukwudozie, C.P.; Yoshioka, K. A Variational Approach to the Numerical Simulation of Hydraulic Fracturing. Proc.-SPE Annu. Tech. Conf. Exhib. 2012, 2, 1442–1452. [Google Scholar] [CrossRef]
- Hofacker, M.; Miehe, C. Continuum phase field modeling of dynamic fracture: Variational principles and staggered FE implementation. Int. J. Fract. 2012, 178, 113–129. [Google Scholar] [CrossRef]
- Wick, T.; Singh, G.; Wheeler, M.F. Fluid-Filled Fracture Propagation With a Phase-Field Approach and Coupling to a Reservoir Simulator. SPE J. 2016, 21, 0981–0999. [Google Scholar] [CrossRef]
- Wilson, Z.A.; Landis, C.M. Phase-field modeling of hydraulic fracture. J. Mech. Phys. Solids 2016, 96, 264–290. [Google Scholar] [CrossRef]
- Heider, Y.; Markert, B. Simulation of hydraulic fracture of porous materials using the phase-field modeling approach. Pamm 2016, 16, 447–448. [Google Scholar] [CrossRef]
- Chukwudozie, C.; Bourdin, B.; Yoshioka, K. A variational phase-field model for hydraulic fracturing in porous media. Comput. Methods Appl. Mech. Eng. 2019, 347, 957–982. [Google Scholar] [CrossRef]
- Zhou, S.; Zhuang, X.; Rabczuk, T. Phase-field modeling of fluid-driven dynamic cracking in porous media. Comput. Methods Appl. Mech. Eng. 2019, 350, 169–198. [Google Scholar] [CrossRef]
- Yoshioka, K.; Yoshioka, K.; Bourdin, B.; Bourdin, B. A variational hydraulic fracturing model coupled to a reservoir simulator. Int. J. Rock Mech. Min. Sci. 2016, 88, 137–150. [Google Scholar] [CrossRef]
- Olasolo, P.; Juárez, M.; Morales, M.; D’amico, S.; Liarte, I. Enhanced geothermal systems (EGS): A review. Renew. Sustain. Energy Rev. 2016, 56, 133–144. [Google Scholar] [CrossRef]
- Xia, Y.; Plummer, M.; Podgorney, R.; Ghassemi, A. An Assessment of Some Design Constraints on Heat Production of a 3D Conceptual EGS Model Using an Open-Source Geothermal Reservoir Simulation Code. In Proceedings of the Forty-First Workshop on Geothermal Reservoir Engineering, Stanford University, Stanford, CA, USA, 22–24 February 2016. [Google Scholar]
- Hu, L.; Winterfeld, P.H.; Fakcharoenphol, P.; Wu, Y.-S. A novel fully-coupled flow and geomechanics model in enhanced geothermal reservoirs. J. Pet. Sci. Eng. 2013, 107, 1–11. [Google Scholar] [CrossRef]
- Haris, M.; Hou, M.Z.; Feng, W.; Luo, J.; Zahoor, M.K.; Liao, J. Investigative Coupled Thermo-Hydro-Mechanical Modelling Approach for Geothermal Heat Extraction through Multistage Hydraulic Fracturing from Hot Geothermal Sedimentary Systems. Energies 2020, 13, 3504. [Google Scholar] [CrossRef]
- Pandey, S.; Chaudhuri, A.; Kelkar, S. A coupled thermo-hydro-mechanical modeling of fracture aperture alteration and reservoir deformation during heat extraction from a geothermal reservoir. Geothermics 2016, 65, 17–31. [Google Scholar] [CrossRef]
- Rinaldi, A.P.; Rutqvist, J.; Sonnenthal, E.L.; Cladouhos, T.T. Coupled THM modeling of hydroshearing stimulation in tight fractured volcanic rock. Transp. Porous Media 2015, 108, 131–150. [Google Scholar] [CrossRef]
- Xie, L.; Min, K.B. Initiation and propagation of fracture shearing during hydraulic stimulation in enhanced geothermal system. Geothermics 2016, 59, 107–120. [Google Scholar] [CrossRef]
- Yuan, Y.; Xu, T.; Moore, J.; Lei, H.; Feng, B. Coupled thermo–hydro–mechanical modeling of hydro-shearing stimulation in an enhanced geothermal system in the raft river geothermal field, USA. Rock Mech. Rock Eng. 2020, 53, 5371–5388. [Google Scholar] [CrossRef]
- Li, S.; Zhang, D. Three-Dimensional Thermoporoelastic Modeling of Hydrofracturing and Fluid Circulation in Hot Dry Rock. J. Geophys. Res. Solid Earth 2023, 128, e2022JB025673. [Google Scholar] [CrossRef]
- Krogstad, S.; Lie, K.A.; Møyner, O.; Nilsen, H.M.; Raynaud, X.; Skaflestad, B. MRST-AD—An Open-Source Framework for Rapid Prototyping and. In Proceedings of the SPE Reservoir Simulation Symposium, Houston, TX, USA, 23–25 February 2015. [Google Scholar]
- Yoshioka, K.; Parisio, F.; Naumov, D.; Lu, R.; Kolditz, O.; Nagel, T. Comparative verification of discrete and smeared numerical approaches for the simulation of hydraulic fracturing. GEM—Int. J. Geomath. 2019, 10, 13. [Google Scholar] [CrossRef]
- Griffith, A.A., VI. The phenomena of rupture and flow in solids. Philos. Trans. R. Soc. Lond. Ser. A 1921, 221, 163–198. [Google Scholar]
- Bourdin, B.; Francfort, G.A.; Marigo, J.-J. The Variational Approach to Fracture. J. Elast. 2008, 91, 5–148. [Google Scholar] [CrossRef]
- Faust, C.R.; Mercer, J.W. Geothermal reservoir simulation: 2. Numerical Solution Technique for Liquid- and Vapor-Dominated Hydrothermal Systems. Water Resour. Res. 1979, 15, 31–46. [Google Scholar] [CrossRef]
- Coats, K.H. Geothermal Reservoir Modeling. In Proceedings of the SPE Annual Fall Technical Conference and Exhibition, Denver, CO, USA, 9–12 October 1977. [Google Scholar]
- Al-Shemmeri, T.T. Engineering Fluid Mechanics Solution Manual; Bookboon: London, UK, 2012. [Google Scholar]
- Praditia, T.; Helmig, R.; Hajibeygi, H. Multiscale formulation for coupled flow-heat equations arising from single-phase flow in fractured geothermal reservoirs. Comput. Geosci. 2018, 22, 1305–1322. [Google Scholar] [CrossRef]
- Garagash, D.I. Plane-strain propagation of a fluid-driven fracture during injection and shut-in: Asymptotics of large toughness. Eng. Fract. Mech. 2006, 73, 456–481. [Google Scholar] [CrossRef]
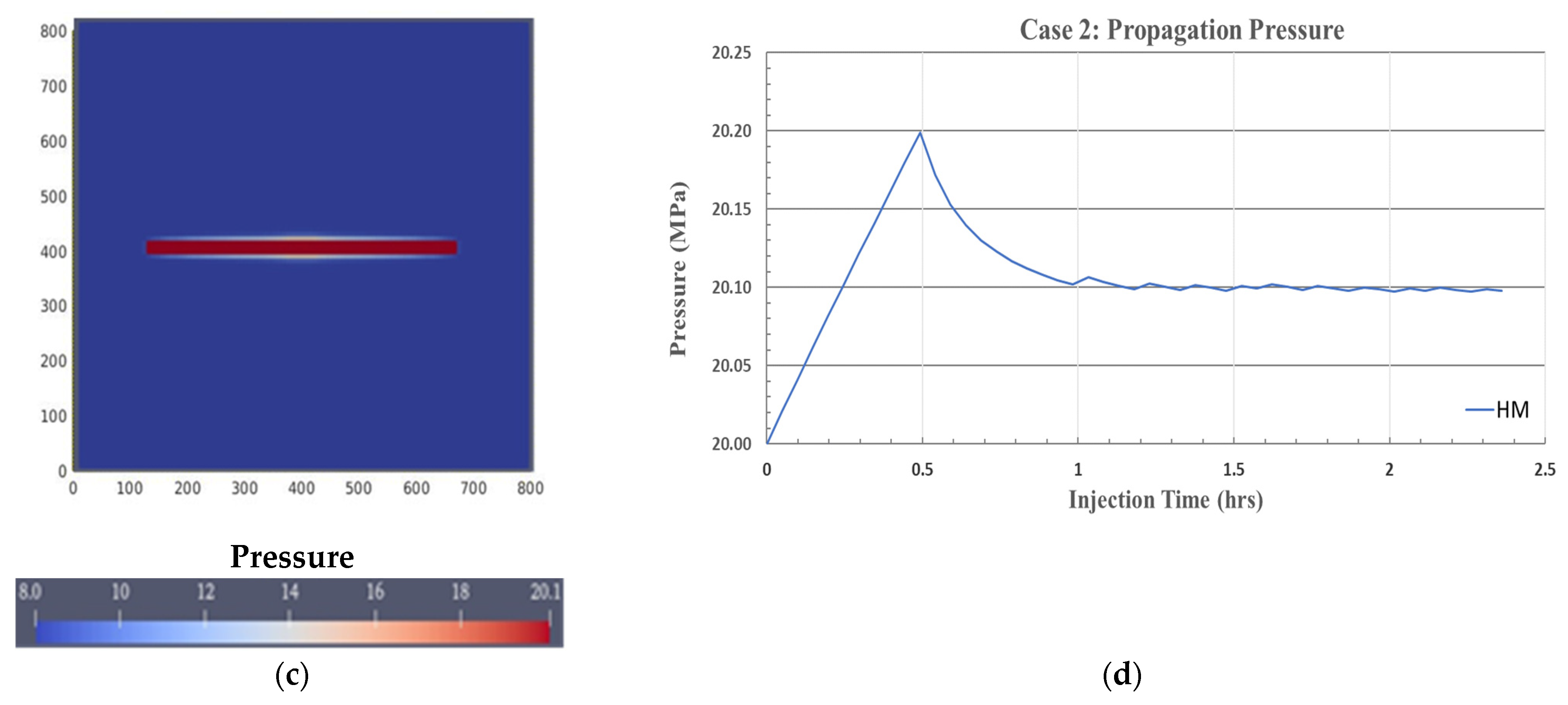

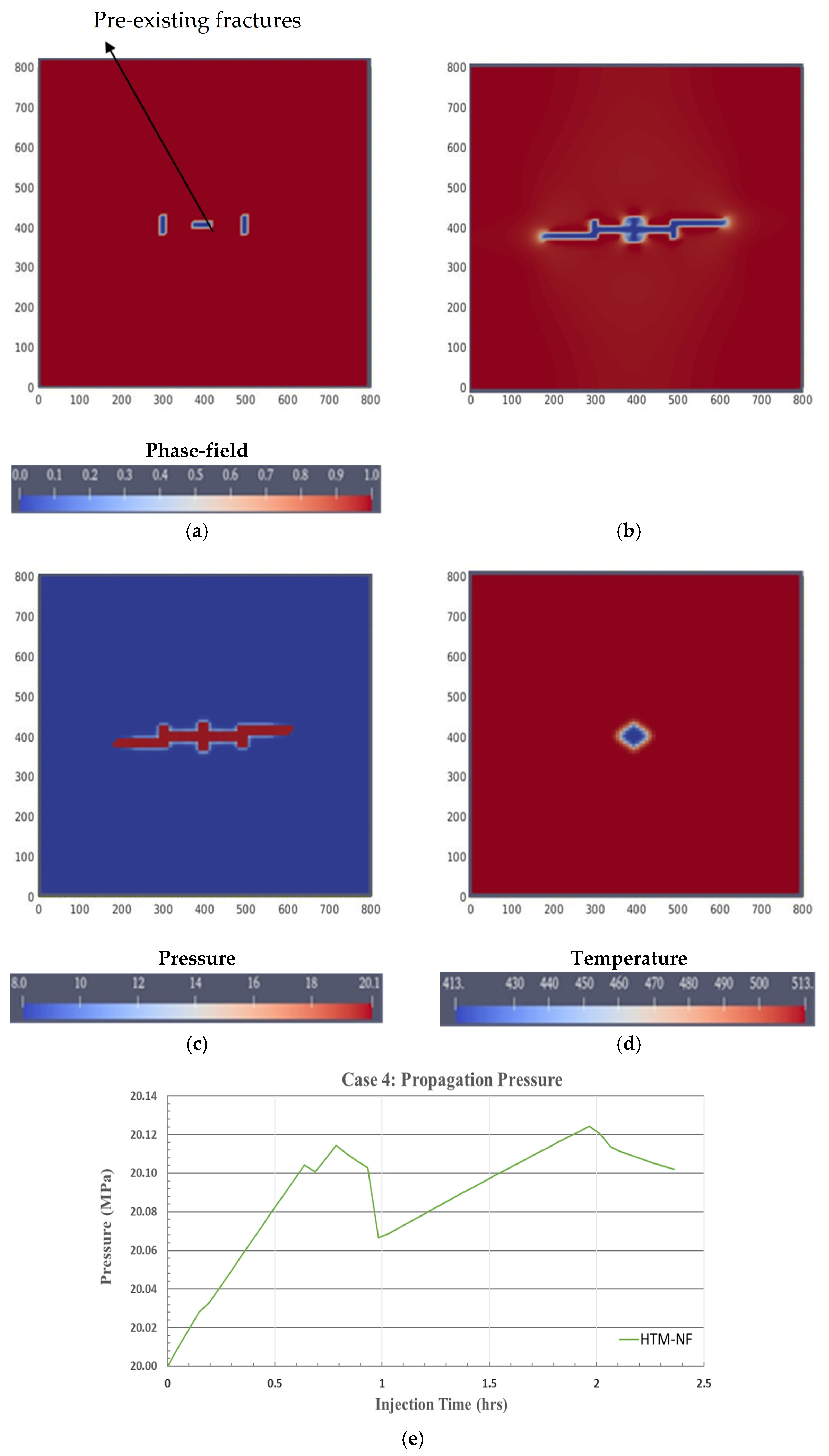
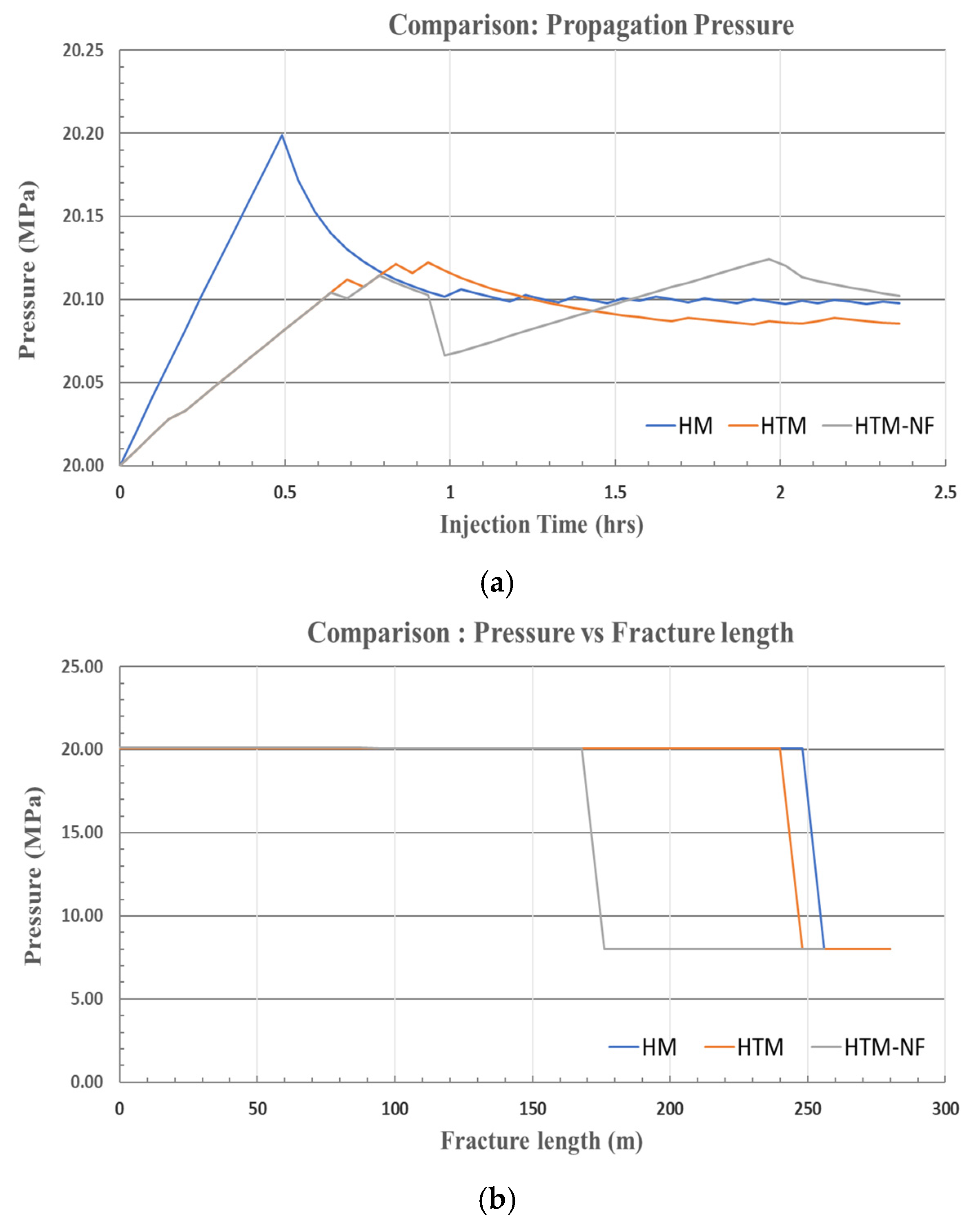
| Parameter | Value |
|---|---|
| Distance (x) | 100 m |
| Time interval (Δt) | 0.283 s |
| Young’s modulus (E) | 17 GPa |
| Poisson’s ratio (v) | 0.2 |
| Fracture toughness () | 100 Pa·m |
| Porosity (Φ) | 0.2 |
| Fluid source term () | 5 × |
| Fluid viscosity (µ) | 4 × Pa∙s |
| Bulk modulus fluid () | 0.625 GPa |
| Parameter | Value |
|---|---|
| Rock density () | 2500 kg/ [28] |
| Water density () | Computed using the simplified Coats model [41] |
| Water viscosity () | Computed from the correlation proposed [40] |
| Average thermal conductivity () | 1.0 W/(m·K) |
| Specific heat of fluid () | 4200 J/kg |
| Specific internal energy () | 420 KJ/kg |
| Porosity compressibility () | 1.0 /Pa |
| Porosity () | 0.1 |
| Thermal expansion () | 7.5 × |
| Matrix permeability (k) | 0.01 mD |
| Fracture toughness () | 80 Pa·m |
| Biot’s coefficient () | 1.0 |
| Poisson’s ratio () | 0.1 |
| Young’s modulus (E) | 12 GPa |
| Maximum horizontal stress ( | 20.5 MPa |
| Minimum horizontal stress ( | 20 MPa |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Putra, V.; Furui, K. Phase-Field Modeling of Coupled Thermo-Hydromechanical Processes for Hydraulic Fracturing Analysis in Enhanced Geothermal Systems. Energies 2023, 16, 7942. https://doi.org/10.3390/en16247942
Putra V, Furui K. Phase-Field Modeling of Coupled Thermo-Hydromechanical Processes for Hydraulic Fracturing Analysis in Enhanced Geothermal Systems. Energies. 2023; 16(24):7942. https://doi.org/10.3390/en16247942
Chicago/Turabian StylePutra, Vaya, and Kenji Furui. 2023. "Phase-Field Modeling of Coupled Thermo-Hydromechanical Processes for Hydraulic Fracturing Analysis in Enhanced Geothermal Systems" Energies 16, no. 24: 7942. https://doi.org/10.3390/en16247942
APA StylePutra, V., & Furui, K. (2023). Phase-Field Modeling of Coupled Thermo-Hydromechanical Processes for Hydraulic Fracturing Analysis in Enhanced Geothermal Systems. Energies, 16(24), 7942. https://doi.org/10.3390/en16247942





