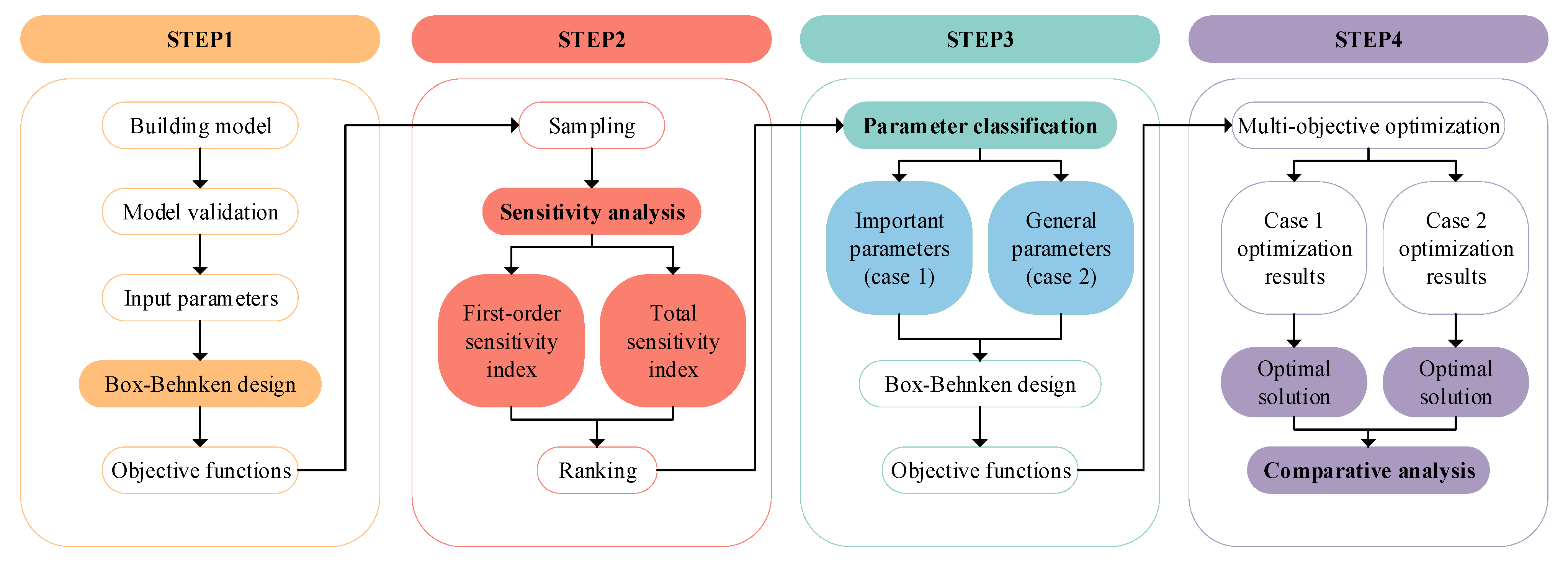
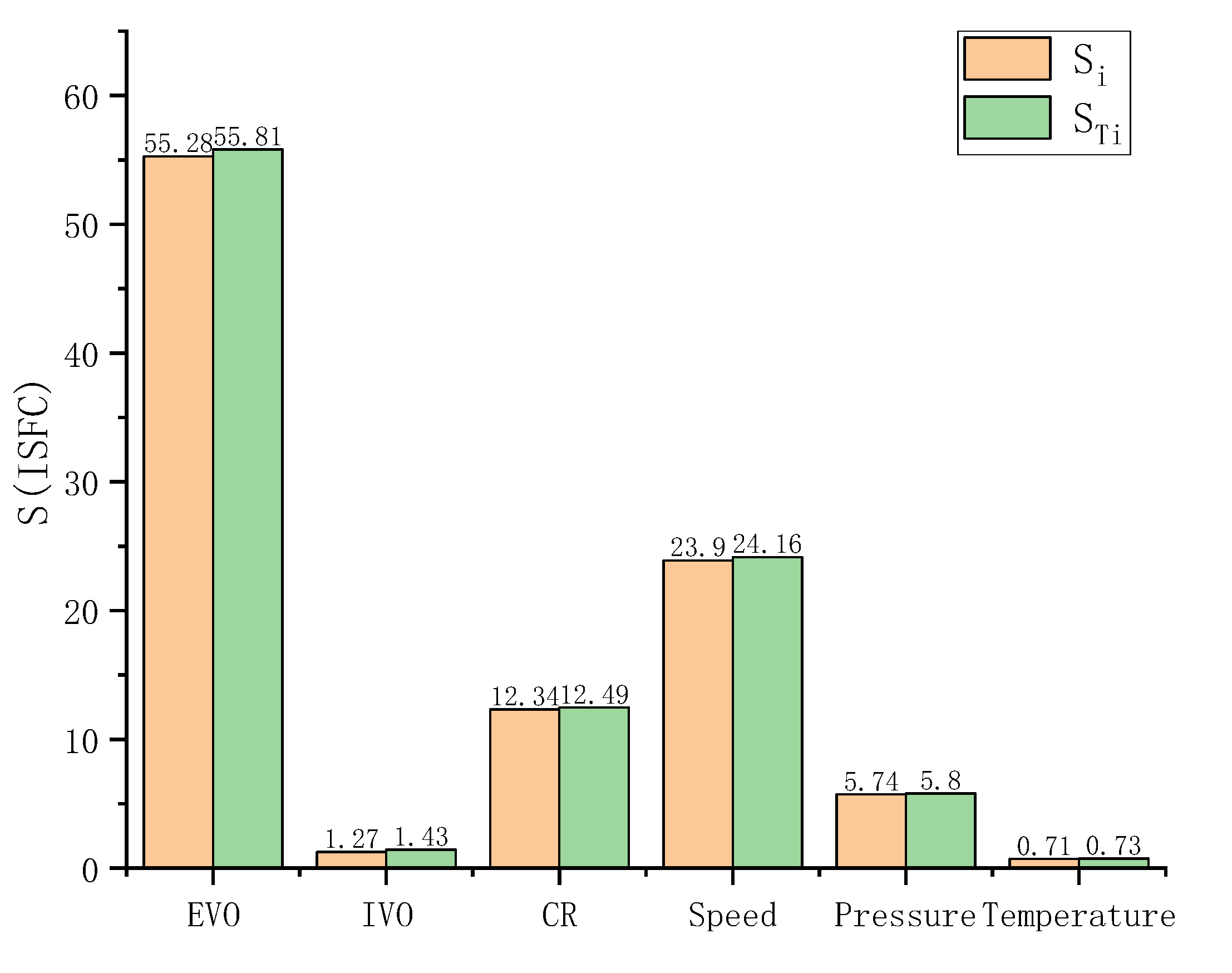3.1. Sensitivity Analysis
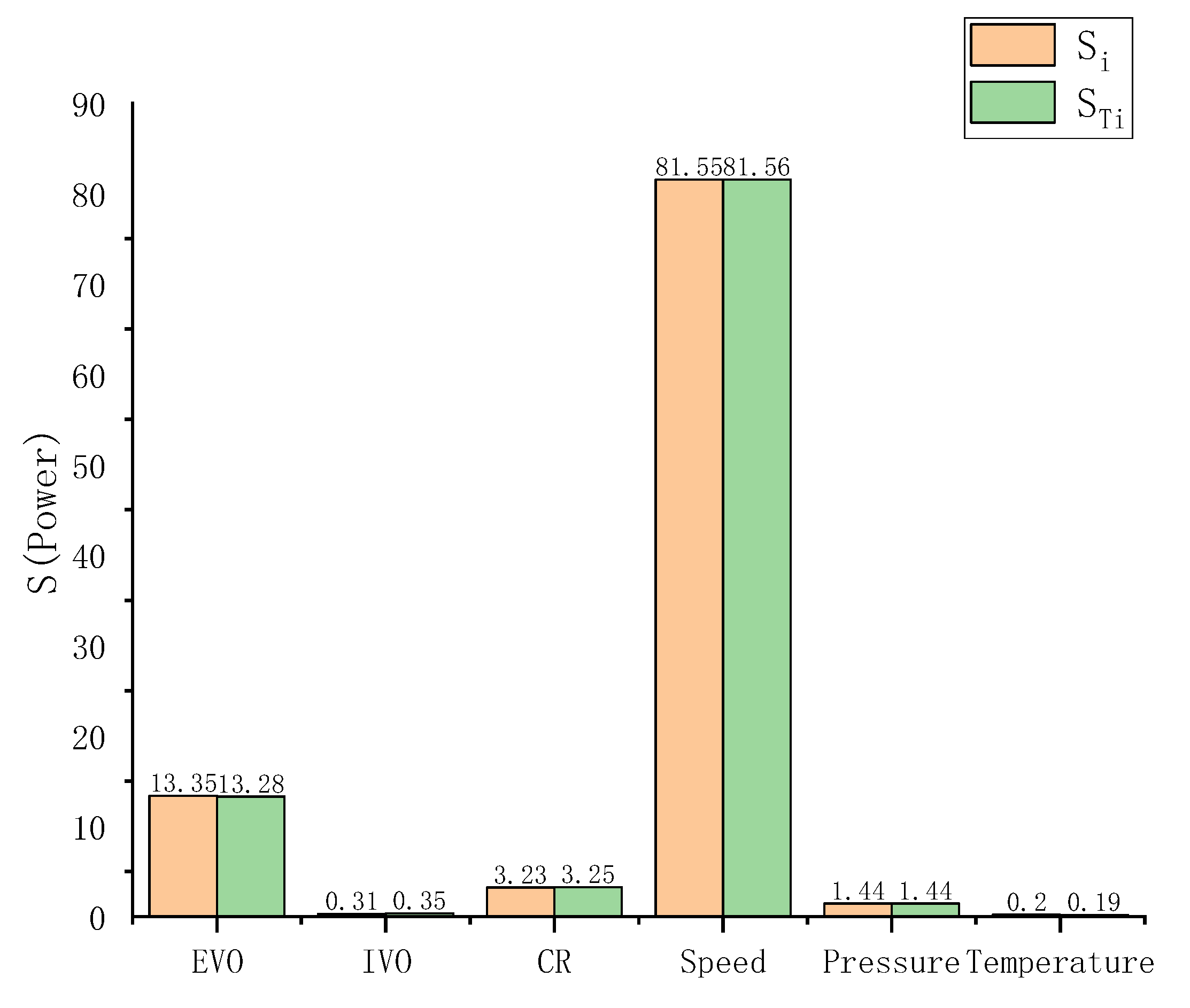
Figure 6 illustrates the first-order and total-order sensitivity indices to power for the six parameters evaluated by applying the Sobol method. The parameter with the largest effect on power is the engine speed. The first- and total-order sensitivity indices are 81.55% and 81.56%, respectively. The next most influential parameter is EVO with first- and total-order sensitivity indices of 13.35% and 13.28%, respectively. All other parameters have first-order and total-order sensitivity indices of less than 5% and have relatively little effect.
The first-order and total-order sensitivity indices of the six parameters of ISFC are shown in
Figure 7. EVO is the most important parameter with first-order and total-order sensitivity indices of 55.28% and 55.81%, respectively. Next, engine speed also has a significant effect. Both the first- and total-order sensitivity indices of CR and intake pressure are also greater than 5%, again possessing a non-negligible influence effect.
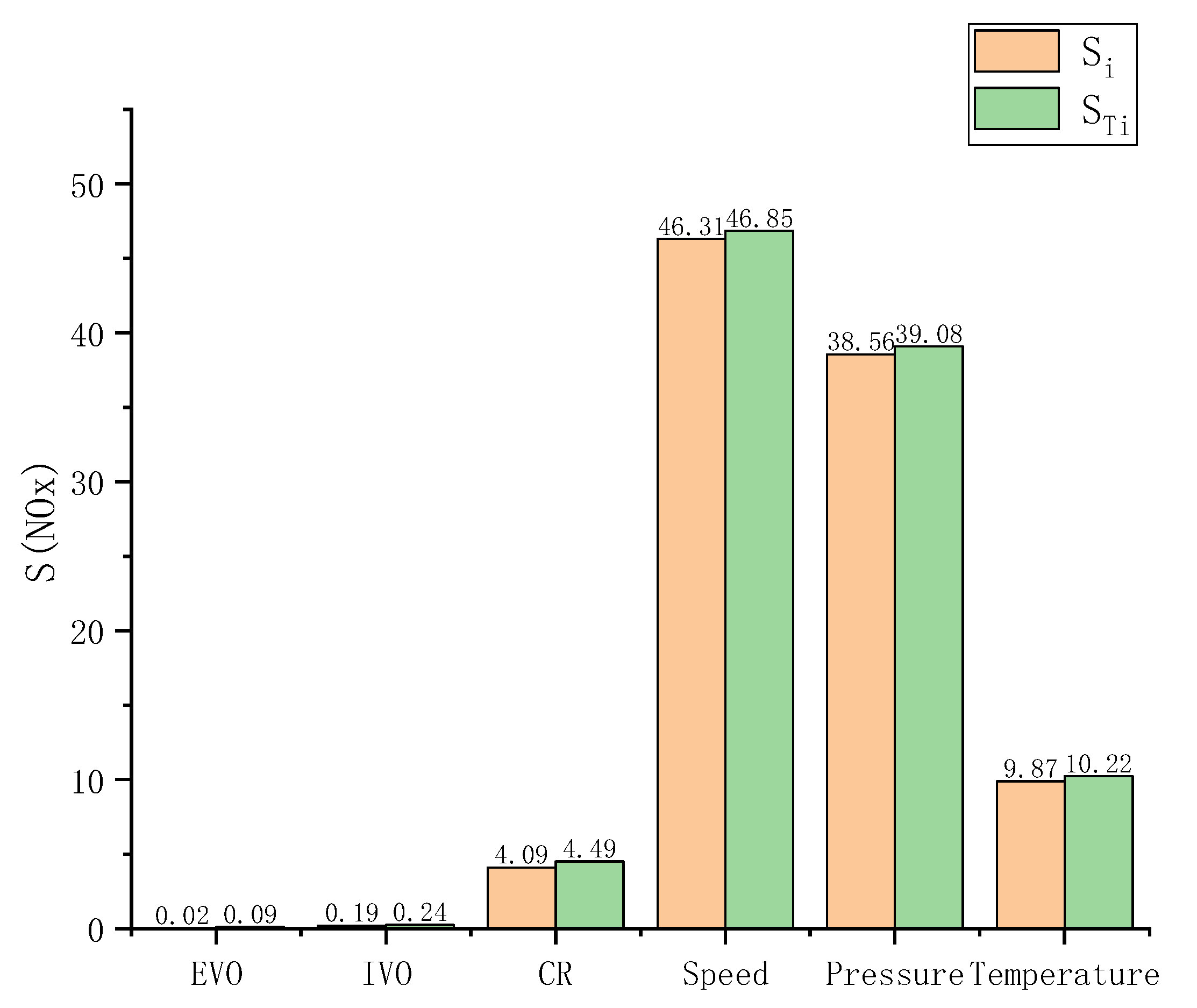
The first-order and total-order sensitivity indices of the parameters for NOx are shown in
Figure 8. The engine speed has the largest influence, with first-order and total-order sensitivity indices of 46.31% and 46.35%, while the difference between the sensitivity indices of intake pressure and engine speed is only less than 10%, and the first-order and total-order sensitivity indices of intake pressure are 38.56% and 39.08%, respectively. The relative influence of intake air temperature and CR is limited, while that of EVO and IVO is almost negligible.
The degree of influence of different control parameters on the performance parameters varies considerably. The six control parameters are divided into two groups, one for the parameters with high influence (Case1) and one for the parameters with low influence (Case2). The parameters selected for Case1 are engine speed, EVO and intake pressure, while the parameters selected for Case2 are IVO, CR and intake temperature. The range of parameter variation is shown in
Table 3.
3.2. RSM Results
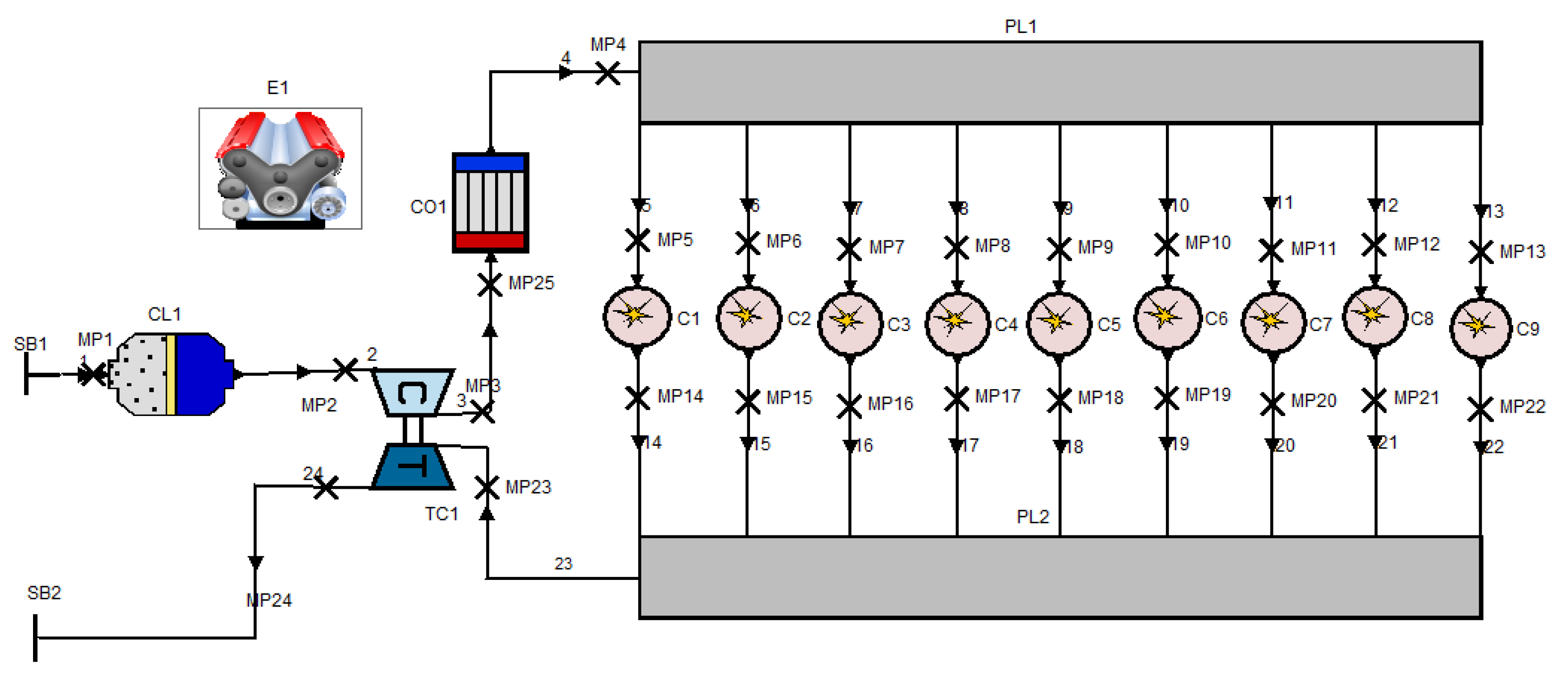
Based on the BBD method, the experimental design was carried out for Case1 and Case2, respectively, and numerical simulation tests were conducted using AVL-BOOST. The response surface functions for
Power,
ISFC and
NOx were obtained by analyzing the experimental results. The response surface functions obtained for Case1 based on the coding factors are shown in Equations (7)–(9), where
A,
B and
C represent EVO, rotational speed and inlet pressure, respectively. The response surface functions obtained for Case2 are shown in Equations (10)–(12), where
E,
F and
G represent IVO, CR and inlet temperature, respectively.
In order to demonstrate the effectiveness of the combined RSM and MOPSO optimization method, the constructed response surface functions were evaluated.
Table 4 shows that
R2 is very high (
R2 > 0.99), which indicates that the input data is effectively used to fit the response surface function. The value of
R2adj is somewhat reduced compared to
R2. This is because whenever more variables are added, whether or not there is a relationship between the added variables and the output variables, then
R2 either remains constant or increases.
R2adj counteracts the effect of the number of samples on R
2 and therefore reflects the significance of the eigenvalues [
28].
R2pred represents the magnitude of the response surface function’s predictive ability with respect to the data [
29]. The fact that the
R2,
R2adj, and
R2pred for Case1 and Case2 are all greater than 0.9 proves that the response surface function has good predictive ability.
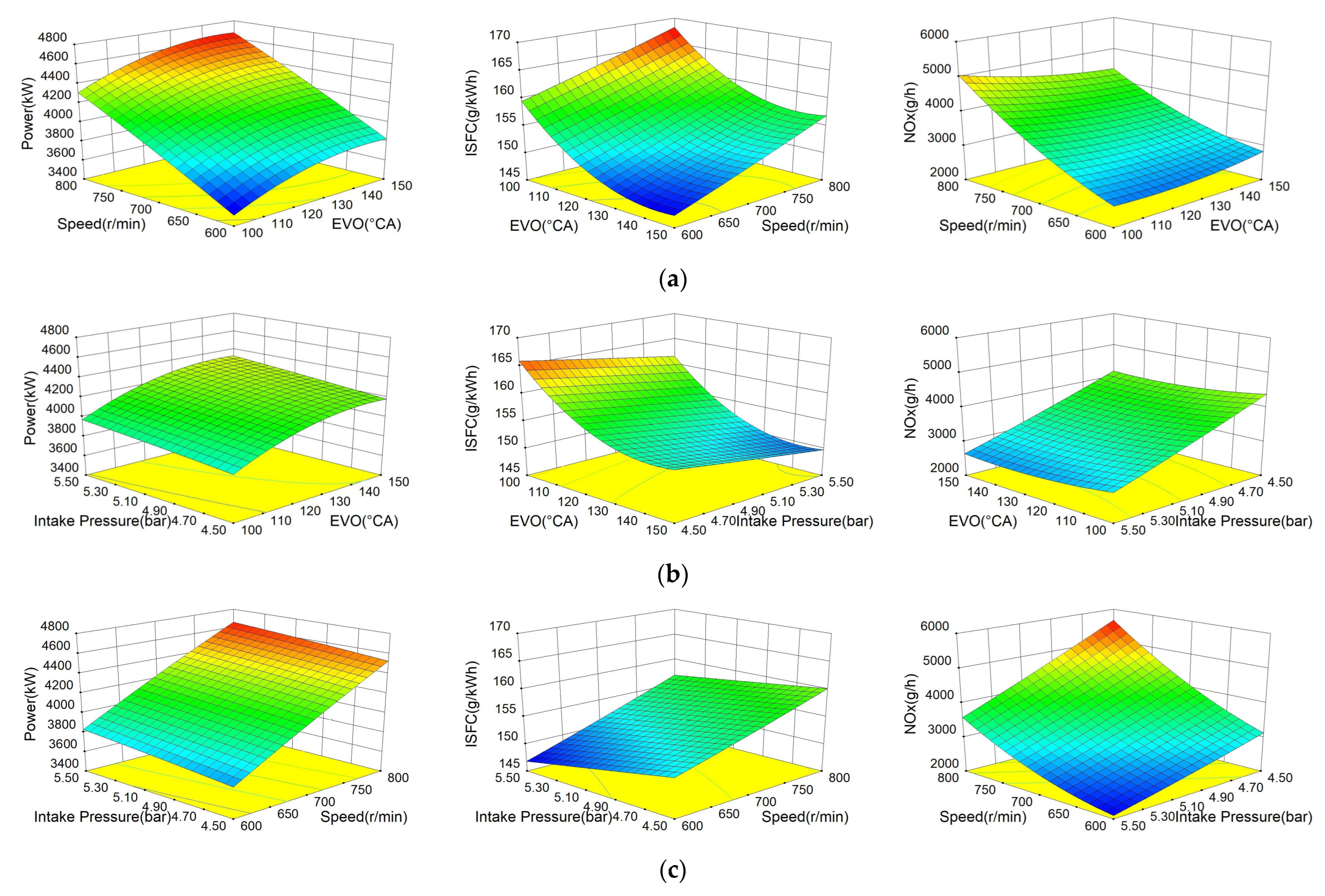
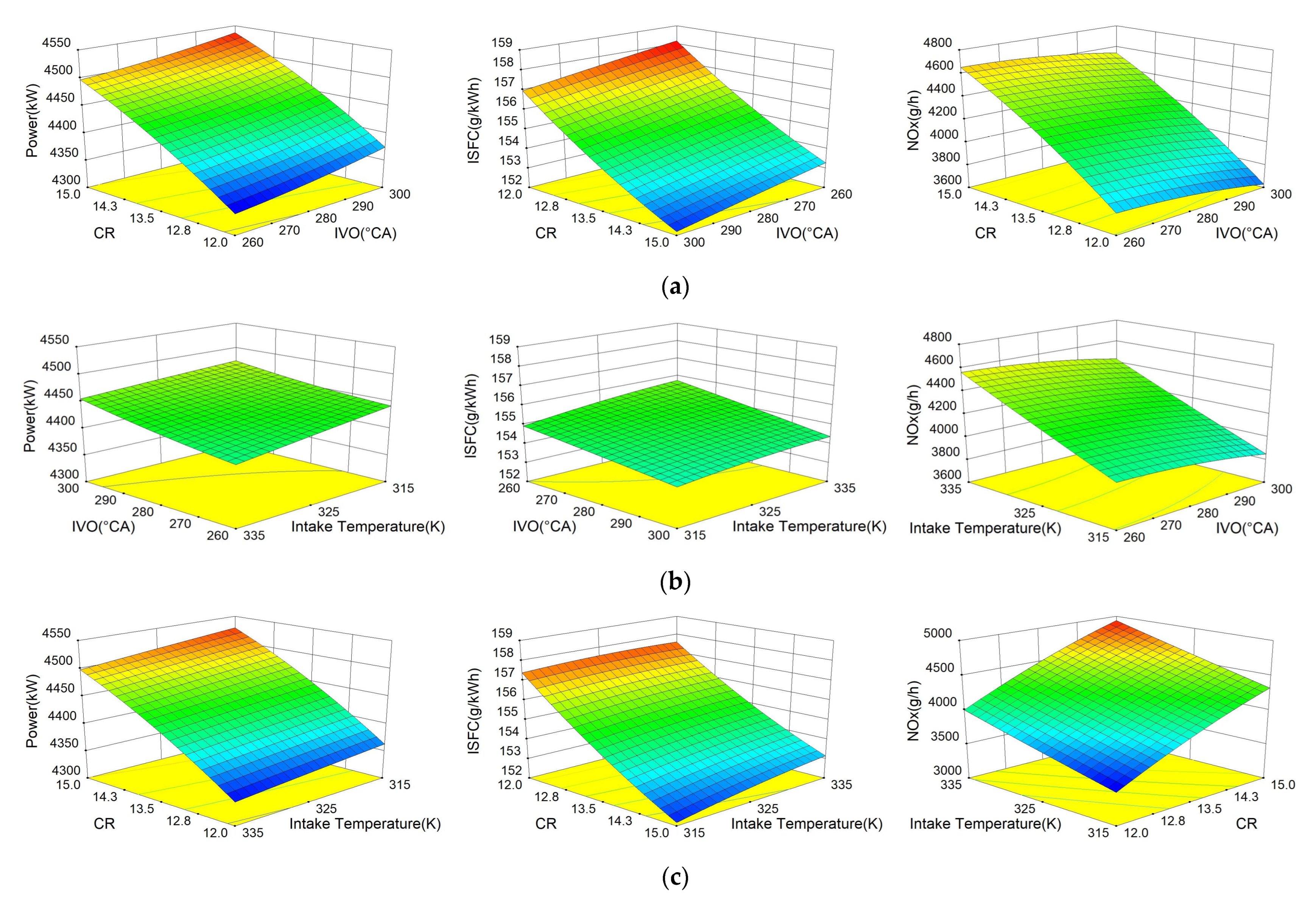
Figure 8 and
Figure 9 show the response surface plots for Case1 and Case2, respectively.
As shown in
Figure 8, with the increase in engine speed, the engine output power increases significantly; this is because the engine cycle injection volume and gas supply are certain, and the increase in speed makes the number of engine cycles per unit time increase, resulting in a significant increase in engine output power. The early EVO (100–110° CA) causes the high pressure gas in the combustion chamber to be released into the exhaust pipe in advance, resulting in an insufficient release of gas energy, and therefore lower engine power. Appropriately delayed EVO (110–130° CA) allows the gas energy in the combustion chamber to be fully utilized to push the piston to do work. However, excessively late EVO (130–150° CA) has a low effect on power because the gas energy in the combustion chamber has been fully utilized and there is little gas energy left before EVO to provide more output energy. Increasing the intake pressure increases the in-cylinder pressure during combustion, increasing the work capacity of the gas in the cylinder, so output power is increased.
As shown in
Figure 9, mechanical losses due to friction losses increase at high engine speeds, and therefore ISFC increases. The effect of EVO on ISFC is due to the same reason as that on power. Excessive early opening of the exhaust valve results in insufficient utilization of gas energy, which increases ISFC. Delaying EVO resulted in full gas energy release and reduced ISFC, while the increase in inlet pressure increased the oxygen content in the combustion chamber, which facilitated the rapid development of oxidative reactions in the combustion process. The rapid oxidation reaction reduces the combustion loss; therefore, the increased intake pressure can reduce the ISFC [
30].
As shown in
Figure 9, the increase in engine speed leads to a significant increase in NOx emissions. This is because the increase in rotational speed leads to an increase in the in-cylinder temperature increase rate and drastic temperature changes. The maximum in-cylinder temperature during combustion is increased. The NOx generation is mainly affected by the in-cylinder temperature, and the NOx emission increases exponentially as the in-cylinder temperature increases [
31]. Therefore, increasing the engine speed leads to a significant increase in NOx emissions [
32]. Delaying EVO allows a small amount of in-cylinder gas to remain in the combustion chamber, reducing the efficiency of the air exchange. The reduction in the amount of fresh air results in a lower maximum in-cylinder temperature for the combustion process, which results in lower NOx emissions [
33]. The increase in intake pressure leads to an increase in the mass of the in-cylinder mass, which increases the total heat capacity of the in-cylinder mass. After the exothermic combustion of the fuel, the increase in the total heat capacity leads to a decrease in the in-cylinder temperature, which destroys the main conditions for the generation of NOx and reduces NOx emissions.
As shown in
Figure 10, the increase in CR is accompanied by a significant increase in output power. The high compression ratio implies a reduction in the volume of the combustion chamber, which allows the combustion process to develop rapidly, increasing the in-cylinder burst pressure and thus increasing the output power. Although high CR increases the output power, the rapid development of the combustion process increases the in-cylinder pressure on one hand and the in-cylinder temperature on the other hand, which leads to a surge in NOx emissions [
34]. ISFC increases under low CR conditions. This is because the output power obtained by consuming the same mass of fuel is lower under low CR conditions, which leads to the output of the same power at the cost of more fuel under low CR conditions.
In the image on IVO in
Figure 10, it can be seen that delayed IVO increases the output power, but the increase is limited. Delayed IVO improves the in-cylinder excess air mass, which allows the natural gas to be burned under lean conditions and improves the fuel combustion conditions to some extent [
35]. Therefore, delayed IVO can increase the power output while ISFC is reduced by a small amount. NOx production depends on the temperature of the combustion process and the oxygen concentration in the combustion chamber. The delayed IVO increases the oxygen concentration in the combustion chamber, but the total heat capacity of the cylinder increases at the same time. In this case, the increased total heat capacity of the cylinder reduces the temperature of the cylinder. At this time, the degree of influence of the in-cylinder temperature on NOx generation is higher than the degree of influence of oxygen concentration on NOx generation [
36]. Therefore, the delayed IVO reduces NOx emissions.
From
Figure 10 it can be seen that the output power varies inversely with the intake air temperature. High intake temperature leads to lower output power, which increases ISFC and reduces fuel economy. For NOx emissions, the increase in intake air temperature raises the in-cylinder temperature and promotes NOx production. Therefore, NOx emissions are proportional to the intake air temperature.
The extent of the effects of EVO, IVO, CR, engine speed, intake temperature and intake pressure on power, ISFC and NOx emissions in
Figure 9 and
Figure 10 are consistent with the conclusions obtained in the sensitivity analysis. The feasibility of the Sobol sensitivity analysis method is verified.
3.3. Optimization Results
Based on the Case1 and Case2 response functions obtained in RSM, the optimization was performed using the MOPSO algorithm. The MOPSO algorithm developed in the Matlab environment minimizes the optimization objectives of ISFC and NOx emissions. The optimization objective power function is solved for the maximum value. The number of individuals for the population is set to 100 and the number of iterations is 100.
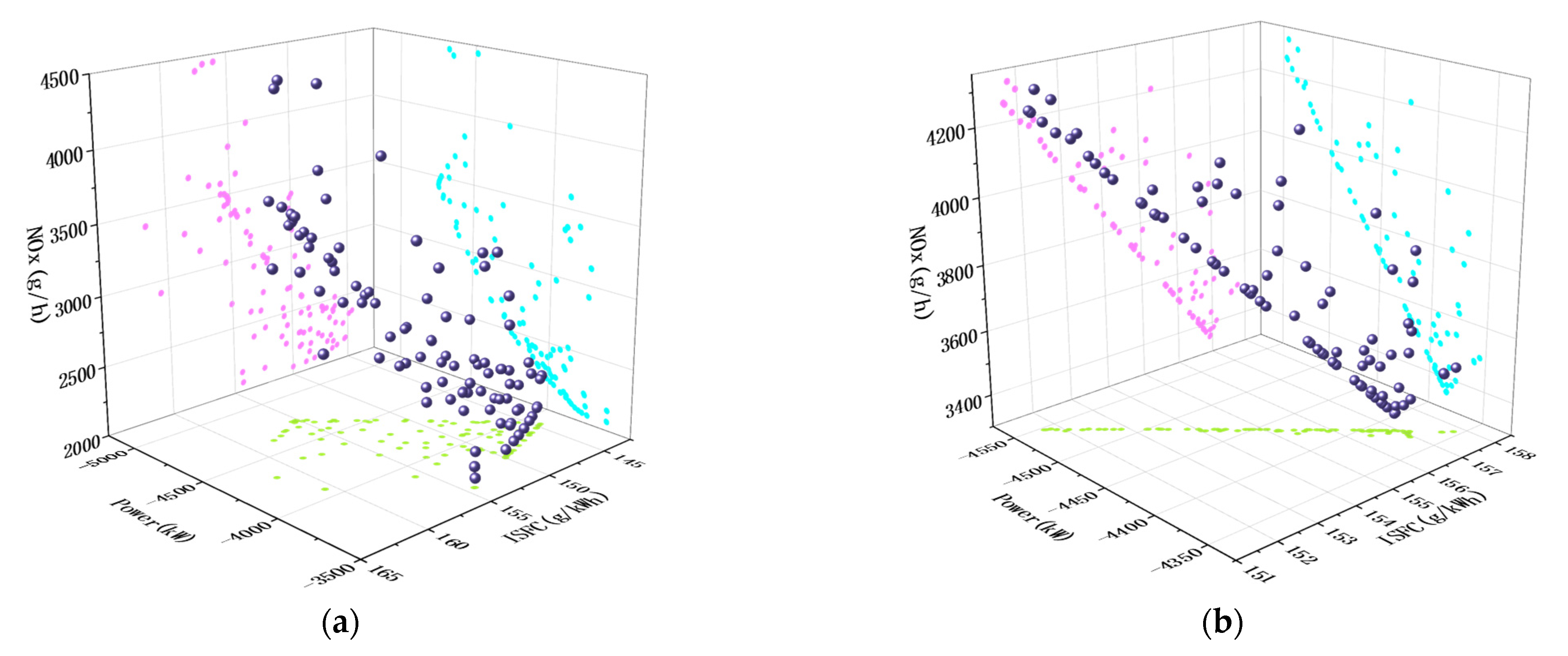
The Case1 optimization results based on engine speed, EVO and intake pressure decision variables are shown in
Figure 11a. The optimization results of Case2 based on IVO, CR and intake temperature decision variables are shown in
Figure 11b. The optimized solution sets of Case1 have good diversity and are evenly distributed. The distribution ranges of the optimized solution sets of Case1 and Case2 are shown in
Table 5. The optimized solution sets of Case1 have a better breadth and a larger coverage of the solution sets compared to Case2. The optimization results of Case2, on the other hand, more clearly reflect the trade-off relationship between the optimization objectives, but lack diversity and have a poor degree of uniform distribution. There is a linear relationship between power and ISFC, with a decrease in ISFC, an increase in fuel economy and an increase in fuel work capacity. The trade-off relationship between ISFC and NOx is in line with the results of Liu et al. [
37].
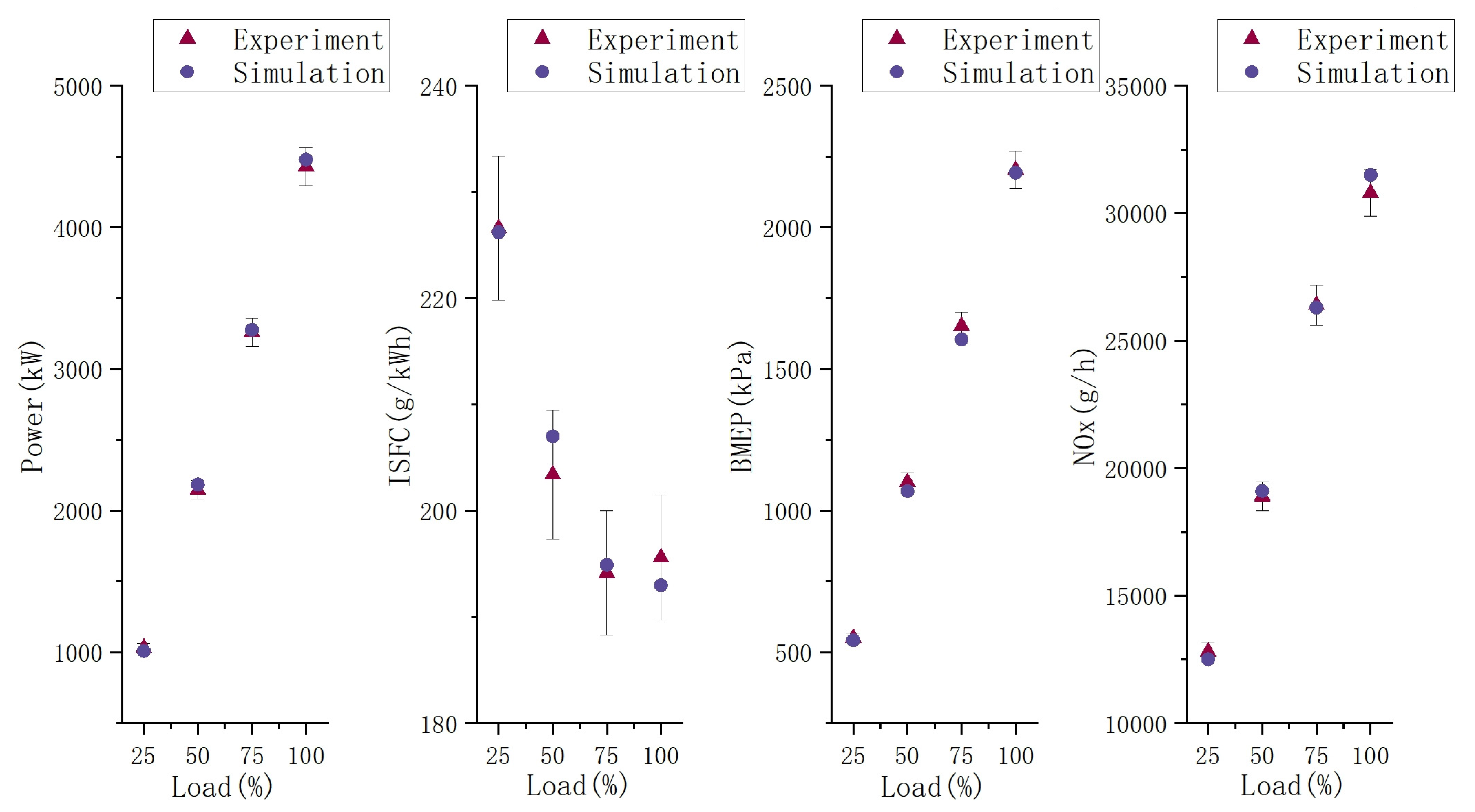
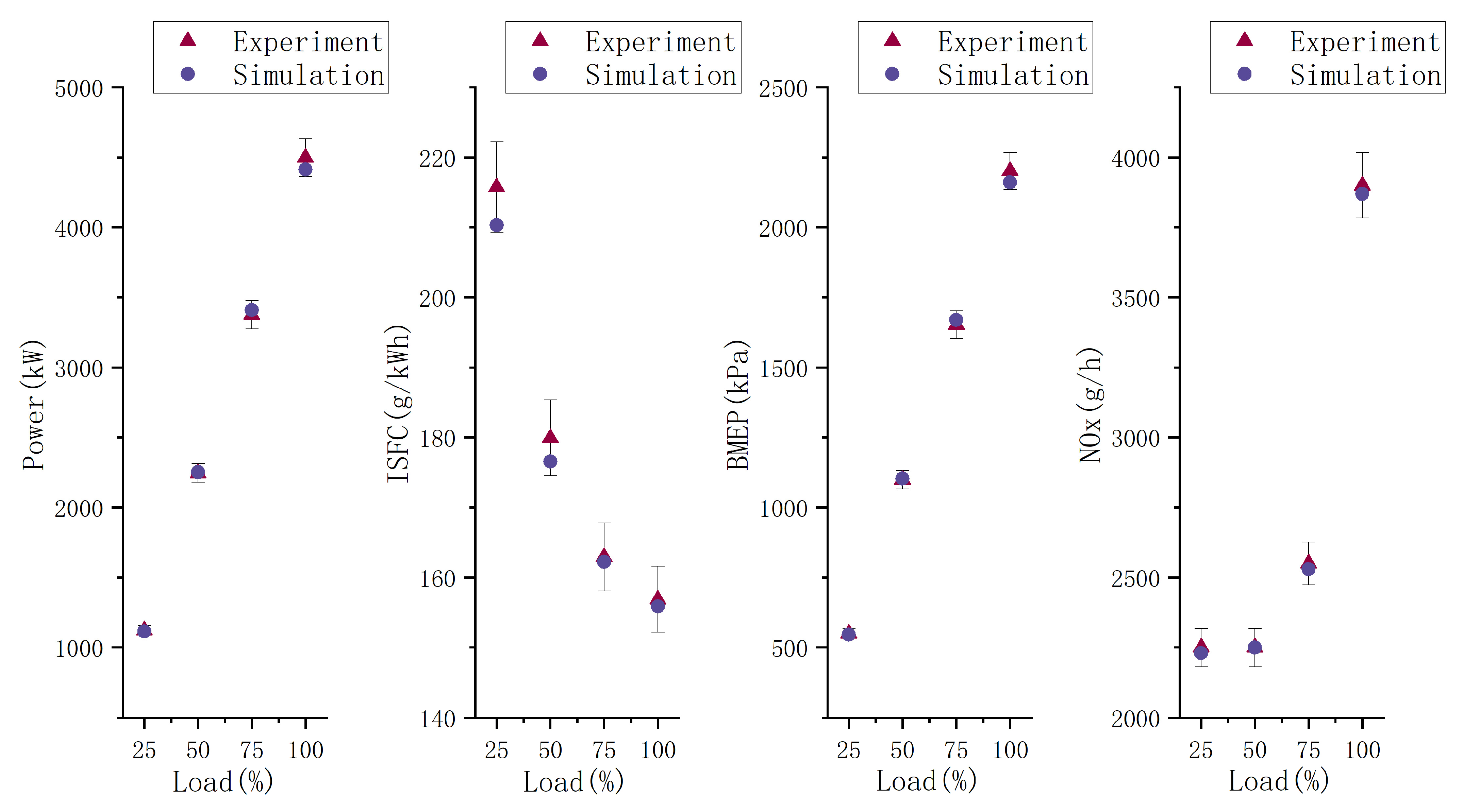
The set of optimization solutions obtained using the MOPSO algorithm demonstrates the trade-offs between the optimization objectives and provides diverse solutions. However, there is a non-dominated relationship between the solutions, so it is difficult to select the best solution from them. The solution with higher power in the non-dominated solution set is preferred due to economic considerations when sailing the ship. The optimal solution for Case1 was selected to have an EVO of 146.2° CA, a rotational speed of 800 r/min and an intake pressure of 5.5 MPa, which resulted in an engine power of 4734.4 kW, an ISFC of 155.2 g/kWh and NOx emissions of 3435 g/h. For Case2, the optimal solution had an IVO of 300° CA, a CR of 15 and an inlet temperature of 315 K. The optimal solution was selected to have a power of 4734.4 kW, an ISFC of 155.2 g/kWh and emissions of 3435 g/h. At an intake temperature of 315 K, the engine output is 4546.8 kW, ISFC is 151.7 g/kWh and NOx emissions are 4254 g/h.
As shown in
Table 6, Case1 optimization resulted in a significant increase in output power and a slight decrease in ISFC, while NOx emissions were significantly reduced. Case2 optimization increased output power to some extent, but NOx emissions were significantly increased, while ISFC was reduced a little.
Therefore, the selection of optimization parameters during engine optimization has a significant impact on the final optimization results. Selecting parameters that have a high impact on the optimization objective can lead to better performance in the final optimization results. On the other hand, the selection of parameters that have little influence on the optimization objective not only does not lead to better optimization results, but also worsens the performance and emission performance of the engine.