Abstract
In the modern era, where the global energy sector is transforming to meet the decarbonization goal, cutting-edge information technology integration, artificial intelligence, and machine learning have emerged to boost energy conversion and management innovations. Incorporating artificial intelligence and machine learning into energy conversion, storage, and distribution fields presents exciting prospects for optimizing energy conversion processes and shaping national and global energy markets. This integration rapidly grows and demonstrates promising advancements and successful practical implementations. This paper comprehensively examines the current state of applying artificial intelligence and machine learning algorithms in energy conversion and management evaluation and optimization tasks. It highlights the latest developments and the most promising algorithms and assesses their merits and drawbacks, encompassing specific applications and relevant scenarios. Furthermore, the authors propose recommendations to emphasize the prioritization of acquiring real-world experimental and simulated data and adopting standardized, explicit reporting in research publications. This review paper includes details on data size, accuracy, error rates achieved, and comparisons of algorithm performance against established benchmarks.
1. Introduction
Over the past decades, there has been a great effort to slow global warming. In 1992, industrialized countries and transitioning economies pledged to capping and diminishing greenhouse gases (GHG) by signing the Kyoto Protocol [1]. In 2015, climate change mitigation, adaptation, and financing goals were set at the Paris Accord, the UN Climate Change Conference in Paris (COP21), by 196 countries to restrict global temperature increases lower than 2.0 °C, preferably to only 1.5 °C [2]. In 2021, at the UN Climate Change Conference in Glasgow (COP26), 197 countries concurred to maintain the 1.5 °C goal through the Glasgow Climate Pact; the resolution aimed to materialize the 2015 Paris Agreement. Additionally, the Pact doubled the financial contributions and asked countries to prepare increasingly ambitious climate commitments ahead of the COP27 in Egypt in 2022 [3]. Nonetheless, these Pacts are not ambitious enough to achieve the climate goals in what is often referred to as the pivotal decade of 2020–2030 [3]. Some reports proclaim that net zero emissions could be reached by 2070 if serious and extensive measures to ban fossil fuels and promote renewable energy production are followed [4]. Achieving net zero CO2 emissions goal requires faster progress in implementing new technologies for energy conversion, distribution, and use [5,6,7,8,9,10,11]. There is also a need to accelerate the progress in the hydrogen economy to ensure rapid technology adoption across countries [7].
One of the significant technological improvements in the past decades, especially in forecasting, prediction, optimization, description, and clustering, has been the development, implementation, and improvement of artificial intelligence (AI) and machine learning (ML) algorithms. According to McKinsey & Company (Chicago, IL, USA) research institute, AI could potentially create a surplus of global economic activity of approximately USD 13 trillion by 2030. By 2030, it is predicted that 70% of firms will adopt at least one kind of AI technology [12].
AI (including perception, neural networks, ML, knowledge representation, etc.) has been driving revolutions in diverse areas; for example, autonomously driven vehicles, robotic manipulators, image analysis, computer vision, art creation, natural language processing, time series analysis, target online advertisement, etc. [13]. This has become realistic because of the growth in the availability and storage of digital data [14]. As the size of structured data increases, the ability of algorithms to perform better tends to increase. In October 2022, the European Commission announced an action plan to digitize the energy system to create data-sharing frameworks, data centers, and energy data space [15]. These developments have made artificial intelligence algorithms/methods a promising tool for modeling, forecasting, and optimizing energy conversion processes to improve the overall effectiveness of the energy sectors.
From now on, we will slightly distinguish between AI and ML algorithms and methods. In this paper, ML algorithms are considered as a subset of AI algorithms. AI is defined as any smart system or machine that conducts tasks that would typically need human supervision or intelligence. ML is a subset of algorithms under AI that use statistical methods to learn from data and can make decisions based on observed patterns. Deep learning (DL), which will be spoken about in further detail later, is a subset of ML, where the main distinction arrives from the use of artificial neural networks (ANNs) to have smart systems train themselves through large amounts of data and perform various complex tasks.
This paper includes a bibliographic study on AI and ML approaches in the energy sector and a review of AI algorithms and methods in the context of energy conversion. The VOSViewer software is used for the visualization of obtained data via keywords. The generated clusters are described and analyzed in detail. “Hot” research topics are discovered based on the horizontal timeline clustering from CiteSpace [16].
All in all, this paper aims to answer questions related to the use of AI and ML in energy conversion and management, as well as discuss the observable popularity and trends of particular AI algorithms. After the introduction, in Section 2, the reader will find the details of the Materials and Methods taken to carry out this bibliometric analysis. In Section 3 and Section 4, the following main guiding questions are answered:
- Are AI techniques being applied in energy conversion and management fields? If so, which algorithms and for what tasks (Section 3.1 and Section 3.2)?
- What kind of data and data size are researchers in this field using? Are they relying on simulated data or using real-life data to train and test their AI models? Are papers doing a good job at reporting their data? What tools are they using to conduct these studies? What are the data and algorithms’ memory requirements (Section 3.3, Section 3.4 and Section 3.5)?
- What are the trending AI algorithms? How effective or accurate are they? What are their strengths and limitations (Section 4)?
By providing this review, this paper aims to inform energy conversion and management researchers on AI and ML techniques that may be applicable to their fields of study. A second aim is to promote interdisciplinary collaboration between energy and data science researchers, as AI and ML techniques may offer ways to improve energy conversion tasks and ultimately improve the changes to reach net zero emissions.
2. State of the Art
2.1. Bibliographic Study
The evaluated publications are ranked based on selected criteria, and the most used algorithms in the top rankings are discussed thoroughly. The data and algorithms used in the documents are compared quantitatively; the benefits and limitations of the AI methods and approaches are addressed and explained. The systematic research process consists of three phases, shown in Figure 1.

Figure 1.
The methodology approach in this research.
The research in energy conversion (systems and processes) is growing continuously. It relates to fast progress in the following subfields: renewable energy, alternative fuels, hydrogen economy, decarbonization, energy storage, application of new and advanced thermodynamic cycles, etc.
From approximately 120 thousand documents identified in Scopus using the keywords “machine learning”, “artificial intelligence”, “supervised learning”, “unsupervised learning”, “deep learning”, “reinforcement learning”, and “neural network” (95% are written in English), the authors selected the energy-related papers (35%). Further, this list was limited to around 600 publications where the application to energy conversion and energy management is discussed intensively. The use of AI in energy conversion first appeared in 1994 [17]. However, there is still a lack of standardization in writing data science terms in conjunction with different fields of application, including energy conversion and management.
The following publications that reviewed the application of AI in some energy sectors should be mentioned explicitly. Artificial neural network, support vector machine (SVM) regression, and k-nearest neighbors (KNN) algorithms were used to predict and model bioenergy production from waste and optimize biohydrogen production [18]. A global study on oil and gas wells revealed that ML is a significant cluster in the literature and is utilized in all aspects, with research directions focusing on crude oil intelligent exploration, intelligent drilling, and smart oil fields [19]. Feature and pattern recognition algorithms are successfully applied to the fault diagnosis of wind turbines with 100% accuracy and a fault diagnosis improvement of approximately 90% [20]. Optimizing electrochemical energy conversion devices, such as fuel cells, requires using a variety of algorithms, including image recognition convolutional neural networks, to identify the optimal ink structures of catalyst layers [21]. Artificial neural networks have intensively emerged in wind energy conversion systems (WECS) applications, specifically in wind speed forecasting, wind power control, and diagnosis classification [22]. One comprehensive study [23] identified the role and progress of AI in renewable energy-related topics, for example:
- Wind Energy: backpropagation neural networks were effective for wind farm operational planning;
- Solar Energy: modeling and controlling photovoltaic systems using backpropagation neural networks;
- Geothermal Energy: artificial neural networks are key tools for geothermal well drilling plans, their control, and optimization;
- Hydroenergy: hydropower plant design and control implement fuzzy, ANN, adaptive neuro-fuzzy inference system (ANFIS), and genetic algorithms for optimization;
- Ocean Energy: ocean engineering and forecasting rely heavily on ANFIS, back propagation neural networks, and autoregressive moving average models;
- Bioenergy: categorization of biodiesel fuel using KNN, SVM, and similar classification algorithms, as well as a hybrid system, combining the elements of a fuzzy logic and ANN, is employed to enhance the heat transfer efficiency and cleaning processes of a biofuel boiler;
- Hybrid Renewable Energy: ANFIS is utilized in hybrid AI techniques to enhance the performance of hybrid photovoltaic–wind–battery systems and ultimately reduce production costs, as well for the modeling of biodiesel systems, solar radiation, and wind power analysis and wavelet decomposition; ANNs and autoregressive methods are used in solar radiation analysis; SVR+ARIMA ( autoregressive integrated moving average) for the tidal ongoing analysis; improved and hybrid ANNs in photovoltaic system load analysis; and data-mining method-based systematic energy control system.
The graphical bibliometric analysis of Scopus database data was performed using the VOSViewer Software 1.6.18 [24]. This software enables the assembly of data for conducting comprehensive bibliometric map analyses. By utilizing an intelligent local shifting algorithm designed for community detection based on large-scale modularity, VOSViewer generates a cluster map that facilitates the interpretation of research categories and the connections between documents [25]. Figure 2 shows the interconnections between the keywords associated with AI and ML in the field of energy conversion and management. To create this map in the VOSViewer, the CSV file downloaded from Scopus, based on the final query chosen by the authors of this paper, which searched for research work with keywords related to energy conversion, AI, and ML, was loaded into the system. Then, the type of analysis was chosen to be co-occurrence-based on the authors’ keywords. The minimum number of co-occurrences threshold was chosen to be three. The results show that keywords are interconnected by seven clusters. The center clusters (ANN, ML, deep learning cluster, optimization algorithm, and the neural network) are the most interconnected and relate to overarching broad machine learning topics. ANNs form their own cluster not only because it is the most widely used algorithm but also due to its ability to perform various tasks with reliably high accuracy. The remaining clusters deal with particular energy conversion systems. Wind energy is the most abundant application in the set of the selected publications, as it holds its cluster. Wave energy also forms its own cluster with a relatively minor representation. It is seen that the wind and wave energy conversion utilize different approaches, as there is not much direct overlap between their clusters. It is evident from these initial maps that research topics are divided into energy topics, tasks within those topics, and the algorithm being applied. Upon closer inspection, energy tasks and topics are connected by different algorithms. Further, the most appropriate algorithm and showcases better data quality and performance for specific energy topics and task pairs will be evaluated.
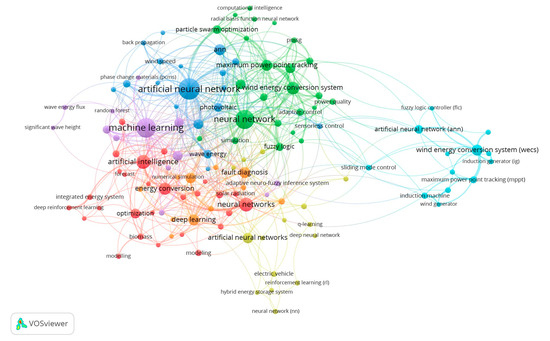
Figure 2.
Bibliometric map of the interconnection of keywords associated with energy conversion and management and ML/AI (VOSViewer software).
2.2. Document Information Extraction
In this review paper, the authors used PDFMiner of Python to extract the text from the selected publications (around 600 PDF files), and analyze the text to extract key data points using their version of a named entity recognition algorithm. However, the intricacies of this algorithm go beyond the scope of this paper. Nevertheless, a brief explanation follows. The extraction of each category was performed by the iterative creation of a hierarchical dictionary that captured at least 90% of the features automatically. Then, the extracted features for each paper were confirmed manually through a double pass to ensure the reduction in errors. The extracted key data points include the following:
- Algorithm: the highlighted algorithm used in the publication;
- Energy Topic: the energy conversion domain the publication relates to (i.e., different kinds of renewable energy, nonrenewable energy, energy conversion systems, etc.);
- Energy Task: the specific task highlighted within an energy-related topic (i.e., forecasting, optimization, etc.);
- Energy Domain: the primary energy resource the publication relates to (i.e., wind, solar, natural gas, etc.);
- Data Size: the number of total observations in the dataset used in the publication;
- Data Type: the origin and nature of the data used (i.e., real data (panel data), simulated data (data created through mathematical and computer simulators), time series (data with dates and/or time), images, etc.);
- Performance Measure: the score of accuracy, error, or percentage improvement achieved by the algorithm;
- Performance Measure Type: the name of the performance measure (i.e., root-mean-square error (RMSE), mean squared error (MSE), mean absolute error, R-squared, etc.);
- Comparative Benchmark Performance: the percentage improvement achieved by the highlighted algorithm either over the traditional non-AI method or the next-best AI method;
- Tools Used: the programming language or software applied to achieve the reported results (i.e., MATLAB, Python, etc.);
- Device Memory: the number of GB in the RAM (random-access memory) of the device used to produce numerical data in the publications.
2.3. Overview of ML and AI Algorithms
AI is intelligence demonstrated by machines and computers and is marked by its ability to perceive, synthesize, and infer patterns from images, data, and other types of structured or unstructured information. Artificial intelligence takes on various forms, encompassing speech recognition, computer vision, language translation, categorizing datasets, and other transformations of input-to-output relationships. The Oxford English Dictionary of Oxford University Press describes AI as “the theory and development of computer systems able to perform tasks that normally require human intelligence, such as visual perception, speech recognition, decision-making, and translation between languages” [26].
Although artificial intelligence and machine learning are often used synonymously, ML is recognized as a component within the broader domain of AI. ML algorithms construct a model using sample data, referred to as training data, in order to make predictions. These predictions can involve classification, regression, or decisions regarding new and unseen data, which are typically referred to as test data. In 1959, Arthur Samuel first introduced the expression machine learning [27], with his famous question: “How can computers learn to solve problems without being explicitly programmed?”
2.3.1. AI: Beginning, Winter, and Revival
The origins of artificial intelligence are frequently associated with Alan Turing’s concept of computation. This theory proposed that a machine, capable of manipulating symbols as basic as 0 and 1, could replicate any possible form of mathematical reasoning. This idea eventually gave rise to the Turing machine computational model [28]. AI was established as a field of research in 1956 at a workshop at Dartmouth College. Small successes followed this workshop, as its leaders and their students began developing computer programs that managed to learn game strategies for checkers, solve word problems in algebra, provide logical theorems, and speak English. By the mid-1960s, research in the United States was receiving substantial funding from the Department of Defense, and research facilities had been set up on a global scale [29].
However, AI momentum began to slow down around 1974 because of Sir James Lighthill’s critical stance [30], which disparaged AI researchers for not addressing the anticipated combinatorial explosion when solving real-world problems. Moreover, pressure escalated from the U.S. Congress to fund more fruitful projects. Frustrated, the U.S. and U.K. governments stopped investigative research in AI. The following few years would be known as the “AI winter”, a period when subsidy for AI undertakings was scarce [17].
In the early 1980s, the commercial success of expert systems revived exploratory interest in AI research, which simulated human experts’ knowledge and analytical skills [31]. In 1985, the AI market had surpassed a billion U.S. dollars in value. Concurrently, the fifth-generation computer project in Japan served as a catalyst, prompting the governments of the United States and the United Kingdom to reinstate funding for AI research in academia [29]. However, in 1987, the Lisp machine market experienced a collapse, leading to another extended period of stagnation for the field of AI, often referred to as a “winter” [29].
Gradually, AI rebuilt its reputation in the late 1990s by uncovering specific solutions to specific problems. This enabled scientists to generate confirmable findings, utilize a broader range of mathematical approaches, and engage in interdisciplinary cooperation [29]. As of the year 2000, the solutions created by AI experts had gained extensive adoption [32].
These modest advances began to multiply significantly as more powerful computers, enhancements in algorithms, and increased access to extensive datasets paved the way for substantial progress in machine learning and perception, yielding remarkable outcomes [33]. Jack Clark from Bloomberg believes 2015 was a landmark year for artificial intelligence due to the increase in cloud computing infrastructure and increased research tools and datasets that made neural networks and other AI implementations increasingly affordable [34]. Research into AI increased by 50% between 2015 and 2019 [35].
The following subsections discuss the different groups of AI algorithms currently available.
2.3.2. Supervised and Unsupervised Learning Algorithms
Machine learning revolves around the development of algorithms that enable a computer to acquire “intelligence”. Learning involves identifying statistical patterns or other data-related regularities. The initial two categories of machine learning algorithms include the following:
- Supervised learning produces a function that maps inputs to estimated outputs by providing the algorithm input–output pairs during training. Supervised learning algorithms are also mainly used for regression problems [36]. These include, but are not limited to, decision trees, random forest, linear and logistic regression, support vector machine, ANN, and other neural network algorithms that use a labeled training set.
- Unsupervised learning algorithms analyze a dataset comprising solely inputs and discern data structures by examining shared characteristics among data points. Unsupervised learning algorithms are commonly used for grouping or clustering data points. Summarizing and explaining data features are other tasks for these algorithms [36], which include, but are not limited to, k-means clustering, principal component analysis, and hierarchical clustering. There also exists semi-unsupervised learning, where only a small part of the training dataset is labeled.
2.3.3. Reinforcement Learning Algorithms
The third paradigm of ML is reinforcement learning (RL). This group of algorithms is quite different from others. RL was inspired by the psychological principle of how animals learn by interacting with the environment. RL algorithms have three main components: an agent, an environment, and a goal. The agent will choose from a set of possible actions, which will then cause a new state and reward from the environment, which is then shown to the agent. Based on this information, the agent will learn whether its action successfully achieved its goal. After a sufficient amount of iterations and trial-and-error events, the agent should become intelligent in relation to the action it chooses in this specific environment by maximizing/minimizing the rewards; this final framework of acting learned is called the policy. Unlike supervised learning, RL does not need input–output pairs or explicitly told directions on how to behave. Instead, RL algorithms learn independently by balancing exploration (of uncharted options) and exploitation (of currently successful strategies). In other words, a good RL algorithm will learn a policy that is prepared for all scenarios. A good RL algorithm will do its best to explore the space of possible strategies and learn how to act. The environment is typically specified as a Markov decision process, with some RL algorithms also including dynamic programming approaches [37].
Different RL algorithms take different approaches to calculating the states and rewards over time, known as the state-value function, sometimes prioritizing newer information over earlier information, and also have different approaches to how agents choose actions, some allowing for more exploration based on a coefficient at the beginning than the end, as well as different approaches to policy definition. These include, but are not limited to, Monte Carlo, Q-learning, state–action–reward–state–action, soft actor critic (SAC), and deep deterministic policy gradient.
2.3.4. Other Types of Algorithms
Not all AI algorithms fall under the abovementioned paradigms and may have noteworthy characteristics. The dimensionality reduction decreases the number of features under consideration by narrowing the set of features to the ones that explain the majority of the variance in the output variable, ultimately reducing the complexity or noise of the dataset. The most commonly known algorithm is principal component analysis [38].
Moreover, optimization algorithms (genetic algorithm, grey wolf optimizer, gradient descent algorithm, etc.) also have their paradigm. These algorithms use stochastic and heuristic principles to search a plausible space for the solution that optimizes a particular function, with or without constraints.
Machine learning also has fields such as natural language processing, which deals with analyzing, treating, and predicting text and graph-based algorithms, and neural networks, which transform data into network graphs, which can be analyzed based on centrality, similarity, etc.
Deep learning involves neural network algorithms that increase the number of layers within the “hidden ers” of artificial neural networks to achieve deeper learning, as opposed to shallow networks with a minimum amount of layers [29]. These tend to vary in structure and will be discussed further.
3. Machine Learning and Artificial Intelligence in Research on Energy Conversion
To around 600 sources that were selected using the Scopus database, the authors applied additional filters to review the different facets of sources thoroughly; for example, double submissions to different journals, review papers, paywall documents, etc. Five hundred thirty documents were identified for further evaluation. Around 40% of them relied on simulated or numerical data. The complexity of an algorithm can only be fully realized when the data available are sufficiently large and representative of the environment ultimately meant to be studied. Simulated and numerical models are an effective way to test out new algorithms or concepts and generate as much data as possible. These data could be considered as “low-quality” because they may fail to capture all the intricacies of the inherent model in nature; relying on synthetic data could lead to failures when scaling a model into reality [39].
Other important attributes collected for each paper were the data size, performance measure, and benchmark performance measure of the main algorithm being used. This paper notes data size as the number of rows in a frame, that is, the total number of samples used for training, validation, and/or testing. Performance measures were collected in the form that each individual document presented to them. For instance, papers related to forecasting usually used RMSE as an error measure of the proposed algorithm. Lastly, benchmark performance measures were considered as the percentage improvement provided by the algorithm in comparison to either a non-ML traditional approach or the next-best ML or traditional model; this depended on what each individual paper reported, which at times would be explicitly reported and other times had to be manually calculated by the authors. The benchmark performance measures are an effective way to compare across papers. From the 530 selected documents, approximately 65% explicitly demonstrated the data size of the utilized dataset and a performance measure; approximately 47% also explicitly reported a calculated benchmark performance measure. In 36% of the sources, a real dataset has been explicitly mentioned or made possible to find or calculate it, a performance measure of the proposed algorithm, and a benchmark comparison of the proposed algorithm.
The authors tried to develop the interconnection of keywords for the set of the publications with real data, indicate a performance measure, and compare against a benchmark. Unfortunately, this attempt was unsuccessful because the keywords (used by the authors of the evaluated publications) tend not to be very specific.
The six clusters were generated to have a more accurate picture (Figure 3). As ANN is the most popular algorithm used over the years, it has the largest node in cluster “red” with a total of 76 inter-occurrences. ANNs are used for forecasting, load control, and optimization tasks in wind and wave energy, photovoltaic systems, solar energy conversion systems, mixed renewable energy, and energy storage. This nonlinear learning algorithm is the widest applied due to its relatively accurate learning capabilities, performance, and accessibility to nonexperts [40,41]. The popularity of ANNs took place between the years 2014 and 2020, with works on photovoltaic systems and wind speed forecasting more in the past, while works on wave height and energy and overall solar energy conversion forecasting more recently. The adoption of ANNs to energy conversion tasks follows two years after the groundbreaking performance of AlexNet (a convolutional neural network presented by the Canadian team in the ImageNet competition 2012). This event allowed deep learning to be widely adopted and attractive due to its outstanding learning capability and low error [42].
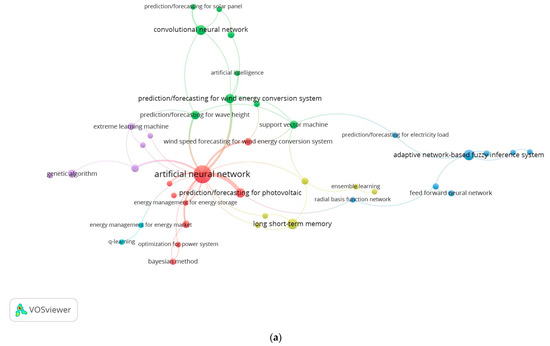
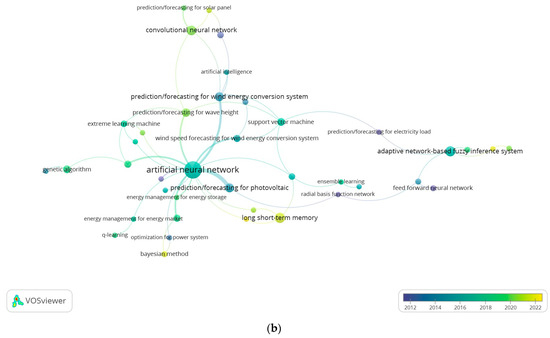
Figure 3.
Bibliometric (a) and year-based (b) maps of the interconnection of unique keywords related to energy conversion and ML/AI in documents that include real data, data size, performance measure, and a comparison benchmark (VOSViewer software).
Cluster “green” surrounds the use of convolutional neural networks (CNNs), recurrent neural networks (RNNs), backpropagation neural networks (BPNNs), and SVMs. With 26 occurrences, these advanced deep learning algorithms, architectures, and support vector machines are applied for forecasting the effectiveness of solar panels, wave height and wave energy conversion, and the effectiveness of windmills. The interest in wave height forecasting is recent, as of 2020–2022. This is evident with more advanced deep learning algorithms (for example, CNNs, RCNNs) and backpropagation neural networks.
The ANFIS is the central node of cluster “blue”, alongside other algorithm nodes, such as feedforward neural network, big data techniques, and radial basis function network. ANFIS, the one with 13 out of 18 occurrences, is utilized for doubly fed induction generator control for wind energy conversion, prediction of oscillating water columns, and maximum power point tracking for photo voltaic cells. The ANFIS algorithm brought about high performance in some instances, and its popularity among these publications was seen from 2016 to 2018. More creative uses of algorithm techniques are being applied. For instance, big data techniques are being used to predict and forecast wave energy converters [43].
Cluster “yellow” has 16 occurrences dealing with solar radiation forecasting (which began recently), fault diagnosis for photovoltaics, energy management for solar power, and estimation of the storage options using lithium-ion batteries. The main algorithm node of this cluster is the long short-term memory (LSTM) algorithm. A hint at the direction of prediction tasks is the use of the LSTM algorithm.
Optimization tasks comprise most of the nine occurrences in cluster “purple”. The genetic optimization algorithm is used for optimization problems related to biomass conversion and forecasting in wave energy systems. The other part of the cluster is the extreme learning machine, a form of a feedforward neural network used for optimization in energy harvesting and renewable energy forecasting tasks. Most of these publications date to the period 2018–2020.
Cluster “turquoise” is the smallest, with only two occurrences. This cluster stands alone as it is related to energy management in energy markets using a reinforcement learning algorithm called Q-learning. Reinforcement learning algorithms have been the algorithms of choice in recent studies related to energy management and smart grids.
All in all, clusters “red”, “green”, and “blue” represent a majority of the publications that use real data and direct measures. While clusters “yellow”, “purple”, and “turquoise” provide insights into newer algorithms being explored for different tasks and topics than before.
Publications have different aims and are at different stages of research. Documents that do not report either a performance measure or a benchmark measure may be aiming to explain a new theoretical approach; these tend to declare that the next steps would be to conduct empirical research on the proposed method framework. Such studies may be at an early theory exploration stage of a topic. A publication that reports a performance measure but does not mention a benchmark performance measure could aim to explore the plausibility of a new method; these papers tend to cite in their limitations that the next step would be to benchmark. These studies have begun the implementation phase. Nonetheless, a study that explicitly reports data size, the origin of the quality of the data, a performance measure of the primary algorithm, and a benchmark algorithm means this study is at the end of its cycle, at the confirmation phase. These publications are particularly interesting, as they discovered the capabilities of ML/AI algorithms within the field of energy conversion.
3.1. Most Researched Topics, Tasks, and Domains
The top topics reported in the evaluated publications are shown in Figure 4. For almost 30 years (Figure 4a), maximum power point tracking in wind energy has been the most popular topic, followed by other wind energy-related topics such as forecasting and doubly fed induction generator optimization and management. The wave energy domain consists of forecasting for wave height and wave energy converters. The third most popular domain is solar energy forecasting and optimization. The most explored topics in recent years (Figure 4b) are dedicated to estimating and predicting lithium-ion battery storage. Wind, wave, and solar energy topics remain relevant.

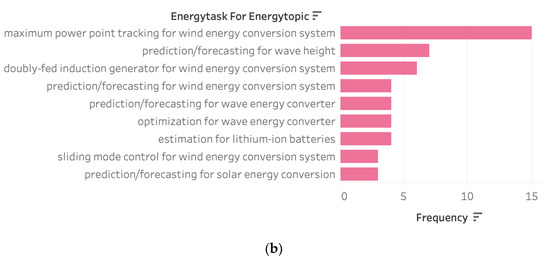
Figure 4.
Most popular energy conversion tasks and topics: (a) 1994–2022; (b) 2020–2022.
3.2. Most Popular Algorithms
The most widely used AI and ML algorithms applied to energy conversion are reported in Figure 5. The standard artificial neural network is the most popular, followed by the adaptive network-based fuzzy inference system (ANFIS) algorithm, genetic algorithm, long short-term memory (LSTM), recurrent neural network (RNN), Q-learning, and convolutional neural network (CNN). These algorithms are mostly deep learning algorithms, except for genetic algorithms and Q-learning, which are optimization and reinforcement learning algorithms, respectively. Their popularity is not surprising as they offer remarkably high accuracy, low error rates, and vast overall improvement to traditional methods.
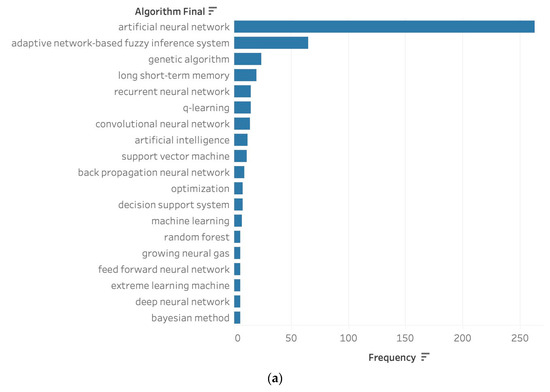
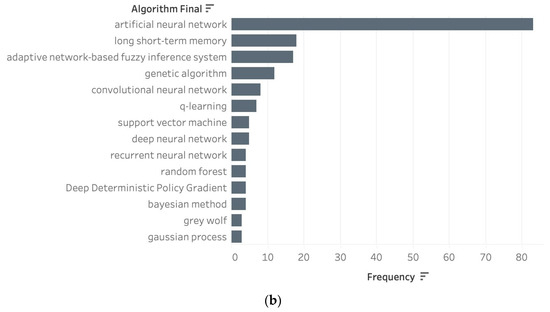
Figure 5.
Most popular algorithms: (a) 1994–2022; (b) 2020–2022.
The emergence of the LSTM and CNN algorithm popularity in recent years is evident (Figure 5b). Moreover, more complex forms of reinforcement learning, such as deep deterministic policy gradient (DDPG) algorithms, are being applied. ML algorithms such as SVM, random forest, and Gaussian process regression are being explored as well. Machine learning offers high computation speed and little memory requirements with the accuracy similar to that of its deep learning counterparts.
3.3. Simulated Data vs. Real Data
Of the already mentioned selected papers, 42% reported simulated data, 18%—data size, 22%—benchmarked performance measures, and 11% reported both.
The distribution of data sizes in the publications with simulated data (Figure 6a) has high outliers in comparison to the publications with real data, especially when noting that the maximum data size for simulated works was 10 million samples. Both sets seem to have similar medians, means, and deviations, with the real dataset having on average 2000 more samples.
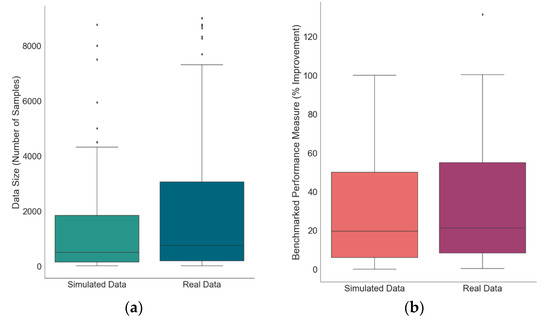
Figure 6.
Comparison between simulated and real data: (a) data size; (b) benchmarked performance measure.
The distribution of benchmarked performance measures in the publications with real data (Figure 6b) has higher outliers than the publications with simulated data, especially when noting that the maximum for improvement provided by a publication using real data was 92 times the status quo. Overall, it seems that studies with real data manage to provide a more significant percentage improvement than simulated data studies.
3.4. Tools
Here, the authors analyzed the programming languages or the software used. Table 1 shows that the most used are MATLAB/SIMULINK and Python. MATrix LABoratory, better known as MATLAB, created by MathWorks, is a versatile programming language and numeric computation environment. It facilitates operations on matrices, visualization of functions and data, algorithm implementation, development of user interfaces, and integration with programs in different languages. As a widely adopted platform in the field of AI, particularly for implementing optimization algorithms. MATLAB enjoys significant popularity in academic settings. As of 2020, it has more than 4 million users globally [44]. Most publications that mentioned the use of MATLAB also mentioned MATLAB’s SIMULINK a programming environment for simulating multidomain dynamical systems [44]. Almost every paper that reports the simulation results makes use of this environment. Python stands as a high-level, versatile programming language characterized by a design philosophy that prioritizes code readability and independent library development. With 8.2 million worldwide developers using Python, it has gained popularity recently and wide adoption in industry [45]. However, it was observed that most publications do not provide information about used software and/or programming languages.

Table 1.
Frequency of programming languages and range of years of usage.
3.5. Memory Requirements
As algorithms grow in complexity, and data become larger, with data availability increasing over time, the discussion of the memory requirements is essential. The memory requirements of a data science project, measured in GB RAM, can be broken down into two main components: the inherited complexity performed by the algorithm and the size of the data, that is, the length and width of the dataset. Random-access memory (RAM) is a type of computer memory that is dynamically read and modified in any sequence, commonly employed for the storage of operational data and machine code, and often becomes problematic when algorithms are complex and/or data are too big. Only 4% of the publications mentioned the GB RAM capacity of the device or online platform used. If the memory requirement was not mentioned explicitly, then the authors assigned a default memory requirement based on the type of algorithm applied. For instance, for reinforcement learning and supervised machine learning algorithms, it is recommended to have at least 8 GB RAM, and for deep learning algorithms, typically 16 GB RAM.
3.6. Research Hotspots and Direction
A clustering analysis was also conducted using the CiteSpace software (Basic version 6.2.R6, 2022). Figure 7 shows the 13 main clusters, sorted in descending relevance, based on the number of member references. The modularity of this network is 0.5594, and the mean silhouettes are 0.8045, according to the agglomeration cluster. It indicates that the research direction of energy conversion and artificial intelligence application is defined well enough.
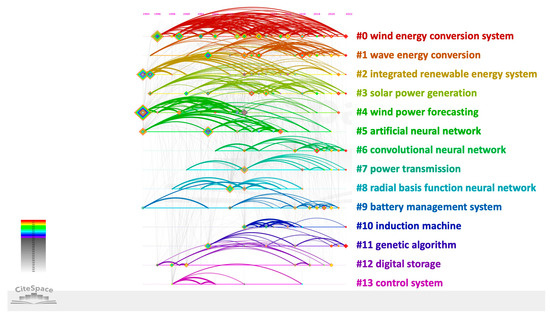
Figure 7.
Clusters with a timeline view of keywords using CiteSpace software.
The following research clusters were formed using the highest frequency of the keywords:
- Wind Energy Conversion Systems (#0, #4). These two clusters were merged in the analysis as they both describe wind energy conversion. The highest frequency keywords include wind power (141 sources), controller (64 sources), wind turbine (57 sources), maximum power point tracker (41 sources), and neural network (284 sources). In 2016, using MATLAB simulations, a new control technique was introduced using neural networks and fuzzy logic controllers applied to a grid-connected doubly fed induction generator to maximize turbine power output. Based on the simulation findings, the neuron controller significantly reduced the response time while constraining and surpassing peak values compared to the fuzzy logic controller [46]. Moreover, a novel combined maximum power point tracking (MPPT)-pitch angle robust control system of a variable-speed wind turbine using ANNs was reported; the simulations showed a 75% improvement in power generation in comparison to typical controllers [47]. Following this work, others discussed the merge of adaptive neuro-fuzzy controllers and their improved performance on MPPT in WECS [48,49]. Soft computing approaches using optimization were and continue to be explored for MPPT problems. For instance, particle swarm optimization (PSO) tracks the maximum power point without measuring the rotor speed, reducing the controller’s computation needs [50]. As for forecasting, 6400 min of wind measurement arrays were used to achieve a 14% improvement in the accuracy of wind power 12-step ahead forecasting using RNNs [51]. Later, ANNs were used to forecast 120 steps ahead, achieving 27% higher accuracy than the benchmark [52]. Forecasting for WECS and other systems heavily relies on neural networks, as they are robust and accurate. The continuous growth in this field is evident by the consistent links throughout the years of this field. Interest in this cluster continues to grow and be active. However, research on wind power forecasting has become scarce since 2009.
- Wave Energy Conversion Systems (#1). The highest frequency keywords include forecasting (116 sources), wave energy (42 sources) and converters (33 sources), deep neural network (24 sources), and significant wave height (4 sources). Influential data science works in wave energy began catching attention in 2015. Due to the computational complexity associated with analyzing wave energy converter arrays and the escalating computational demands as the number of devices in the system grows, initial significant research efforts focused on finding optimal configurations for these arrays. For instance, a combination of optimization strategies was applied. The suggested methodology involved a statistical emulator to forecast array performance. This was followed by the application of a novel active learning technique that simultaneously explored and concentrated on key areas of interest within the problem space. Finally, a genetic algorithm was employed to determine the optimal configurations for these arrays [53]. These methods were tested on 40 wave energy converters with 800 data points and proved to be extremely fast and easily scalable to arrays of any size [53]. Studies focused on control methods to optimize energy harvesting of a sliding-buoy wave energy converter were reported in [54], using an algorithm based on a learning vector quantitative neural network. Later, the optimization approach became more popular in publications on forecasting for wave energy converters. A multi-input convolutional neural network-based algorithm was applied in [55] to predict power generation using a double-buoy oscillating body device, beating out the conventional supervised artificial network and regression models by a 16% increase in accuracy. It also emphasized the significance of larger datasets, pointing out that increasing the size of the dataset could capture more details from the training images, resulting in improved model-fitting performance [55]. More recent works on forecasting focus on significant wave height prediction using experimental meteorology data and hybrid decomposition and CNNs methods, ultimately achieving 19.0–25.4% higher accuracy [56,57]. Interest in this cluster continues to grow.
- Integrated Renewable Energy System Management (#2). This cluster combines the publications related to the management of integrated renewable energy systems [58], power generation using the organic Rankine cycle [59] and power systems outage outages [60], biomass energy conversion [61,62], and hybrid systems [63] using knowledge-based design tools, mixed-integer linear programming, genetic algorithm, decision support systems, and ANNs. These topics were abundant in the late 1990s and 2005–2015. However, more recent publications on these topics are scarce.
- Solar Power Generation (#3). Containing keywords related to photovoltaics and their systems (29 sources), general solar power (29 sources), and solar–thermal energy conversion (44 sources), this cluster is consistently growing and active. Early works in this cluster focused on power forecasting for photovoltaics since insolation is not constant and meteorological conditions influence output. Ref. [64] reports the choice of the radial basis function neural network (RBFNN) for its structural simplicity and universal approximation property and RNN for it is a good tool for time series data forecasting for 24-hour ahead forecasting with RMSE as low as 0.24. As the solar cells market grew favorably in 2009, publications also explored the feasibility of ANNs for MPPT of crystalline-Si and non-crystalline-Si photovoltaic modules with high accuracy, MSE as low as 0.05 [65,66]. It also explored temperature-based modeling without meteorological sensors using gene expression programming for the first time and other AI models such as ANNs and ANFIS. The ANNs reduced RMSE error by 19.05% compared to the next-best model [67]. Similar studies were conducted using a hybrid ANN with Levenberg–Marquardt algorithm on solar farms with a 99% correlation between predictions and test values [68]. Other than forecasting tasks, publications also range on topics like smart fault-tolerant systems using ANNs for inverters [69] to MPPT of a three-phase grid-connected photovoltaic system using particle swarm optimization-based ANFIS [70]. More recent papers focus on using more attribute-rich data to perform short-term forecasting of solar power generation for a smart energy management system using ANNs [71], gradient boosting machine algorithms [72], and a more complex multi-step CNN stacked LSTM technique [73] with great accuracy. The emergence of complex boosting techniques is interesting because these algorithms tend to learn faster and in a computationally less costly way than NNs but with similar accuracy.
- Deep Learning Algorithms (#5, #6, #8). These clusters were grouped into one because of the popular deep learning algorithms. The artificial neural network (#5) showcases many vertical links; ANNs are popular across almost all energy conversion tasks and domains for their ability to learn and model nonlinear relationships. In [74], ANN algorithms are used to model a diesel engine with waste cooking biodiesel fuel to predict the brake power, torque, specific fuel consumption, and exhaust emissions, ultimately achieving an MSE as low as 0.0004. An application of an ANN with Levenberg–Marquardt learning algorithm technique for predicting hourly wind speed was reported in [75]. ANNs were popular in the early years of adoption until 2015. Recent studies, where ANNs are the highlighted algorithm, tend to be newer areas of exploration in energy conversion and data sciences. For instance, using 36,100 experimental data points of combustion metrics to control combustion physics-derived models, a 2.9% decrease in MAPE was achieved using ANNs. [76]. However, in most recent studies, ANNs are used as the benchmark of comparison for a more complex or efficient method.
The second most recent cluster is #6, convolutional neural networks (CNNs). This deep neural network algorithm has recently gained consistent momentum in energy conversion publications. In 2018, in induction motor bearing fault diagnosis, a CNN structure increased accuracy by 16.36% compared to SVM, random forest, and K-means clustering using 448 data samples [77]. CNNs are used across different topics, evident by their vertical links across clusters. For instance, a CNN structure achieved 98.95% accuracy using 960 data points as a detection algorithm for inter-turn short-circuit faults, demagnetization faults, and hybrid faults (a combination of both) in interior permanent magnet synchronous machines [78]. CNNs are powerful tools in the wave energy conversion prediction field, one of the most promising renewable resources [55]. Ref. [79] explored a constant frequency control algorithm based on a deep learning prediction model to improve the steady-state accuracy of the hydraulic motor speed. This paper proposed a prediction model based on empirical wavelet transform LSTM-CNN, which improved the prediction accuracy by 12.26% compared to the short-term memory neural network. CNNs consistently outperforms its predecessor algorithms, such as ANNs, LSTM, and ANFIS.
As for cluster #8, RBFNN and ANFIS algorithms are used across domains. RBFNNs are ANNs that use radial basis functions as the activation functions of the neural network, which is modeled after the Takagi–Sugeno fuzzy inference system [80]. Studies used RBFNNs to optimize the control of power with a stable voltage at the generator terminals using two controllers [81,82] and to improve the accuracy of the predicted output I–V and P–V curves [83], with MSE score reduction as low as 10%. As for the adaptive neuro-fuzzy inference system algorithms, they are used across domains. For instance, ANFIS is used for a controller for static VAR compensator, used in power networks integrated with WECS, to address the torque oscillation problem, which achieved 20% efficiency over the benchmark approach [84], for short-term wind power forecasting and enhanced by particle swarm optimization [85], and as an adaptive sliding mode controller to regulate the extracted power of wind turbine at its constant rated power [86]. The publications in this cluster heavily overlap with clusters #5 and #6. These algorithms were intensively applied from 2002 to 2016. However, RBFNN and ANFIS algorithms seem to have been overtaken by the interest in CNNs, since their convolutional nature allows them to automatically detect the important features inherent in the data without any human supervision, which leads to higher accuracy or optimization.
- Electric Power Transmission (#7). This cluster contains research related to the stability and management of unified power flow controllers (UPFC), electrical grids, and transmission lines. In 2008, IEEE held a conference titled “Conversion and Delivery of Electrical Energy in the 21st Century”; several noteworthy publications are included in this cluster. A Lyapunov-based adaptive neural network UPFC was applied to improve power system transient stability [87]. Outage possibilities in the electric power distribution utility are modeled using a para-consistent logic and paraconsistent analysis nodes [60]. Linear matrix inequality optimization algorithms were used to design output feedback power system stabilizers, which ultimately improved efficiency by 68%, compared to the standard controller [88]. A first look at the utility of reinforcement learning was explored by applying a Q-learning method-based on-line self-tuning control methodology to solve the automatic generation control under NERC’s new control performance standards, which achieved all proposed constraints and achieved a 6% reduction in error compared to the traditional controller [89]. After a gap of inactivity in this cluster, a resurgence of these topics began in 2020, focusing heavily on reinforcement learning for smart grid control and more thorough agent, environment, and state definition. A Q-learning agent power system stabilizer is designed for a grid-connected doubly fed induction generator-based wind system to optimize control gains online when wind speed varies, amounting to a nine-time more stable controller [90]. The use of an advanced deep reinforcement learning approach is applied to energy scheduling strategy to optimize multiple targets, including minimizing operational costs and ensuring power supply reliability of an integrated power, heat, and natural-gas system consisting of energy coupling units and wind power generation interconnected via a power grid using a robust 60,000 data points and achieving 21.66% efficiency over particle swarm optimization and outperforming a deep Q-learning agent [91]. As energy systems become increasingly integrated with more complex sourcing and distribution, the interest in this field of publications will continue to grow.
- Battery/Charging Management System (#9). This cluster relates to electric vehicle charging, scheduling, and lithium-ion battery management. In dynamic wireless power transfer systems for electric vehicle charging, the degree of LTM significantly affects energy efficiency and transfer capability. An ANN-based algorithm was propositioned to estimate the LTM value; i.e., the controller would have the ability to establish an adjusted reference value for the primary coil current, offsetting the decrease in energy transfer capacity due to LTM, thus leading to a 32% increase in the value of the transferred energy [92]. A neural network energy management controller (NN-EMC) is designed and applied to a hybrid energy storage system using the multi-source inverter (MSI). The primary objective is to manage the distribution of current between a Li-ion battery and an ultracapacitor by actively manipulating the operational modes of the MSI. Moreover, dynamic programming (DP) was used to optimize the solution to limit battery wear and the input source power loss. This DP-NN-EMC solution was evaluated against the battery-only energy storage system and the hybrid energy storage system MSI with 50% discharge duty cycle. Both the battery RMS current and peak battery current have been found to be reduced by 50% using the NN-EMC compared to the battery-only energy storage system for a large city drive cycle [93]. Battery/ultracapacitor hybrid energy storage systems have been widely studied in electric vehicles to achieve a longer battery life. Ref. [94] presents a hierarchical energy management approach that incorporates sequential quadratic programming and neural networks to optimize a semi-active battery/ultracapacitor hybrid energy storage system. The goal is to reduce both battery wear and electricity expenses. An industrial multi-energy scheduling framework is proposed to optimize the usage of renewable energy and reduce energy costs. The proposed method addresses the management of multi-energy flows in industrial integrated energy systems [95]. This field borrows from a diverse set of algorithms.
- Induction Machine, Digital Storage, and Control System (#10, #12, #13). These three clusters have lost momentum and become unexplored in recent years. Regarding the induction machine, a sensorless vector-control strategy for an induction generator operating in a grid-connected variable speed wind energy conversion system was presented using an RNN, offering a 4.5% improvement upon the benchmark [96]. Cluster #12 combines the publications related to the accurate modeling of state-of-charge and battery storage using ANNs and RNNs [97,98,99]. Cluster #13 includes the publications related to maximum point tracking in wind energy conversion systems using neural network controllers [100,101,102] and energy maximization using neural networks, such as learning vector quantitative neural networks, on a sliding-buoy wave energy converter [54].
- Genetic Algorithm (#11). This cluster deals primarily with the application of the genetic algorithm to various energy conversion systems, as well as other optimization techniques. A genetic algorithm solves both constrained and unconstrained optimization problems, similar to how genetics evolve in nature through natural selection and biological evolution. The genetic algorithm revises a population of individual solutions as it explores different solutions. [103]. Evident on the timeline of this cluster is the consistent use of this optimization technique throughout the years; optimization techniques are often part of a typical data science project pipeline, where the data science algorithm transforms inputs into outputs, and the optimization tools can be used to optimize the inputs, outputs, or algorithm itself. Thus, ANNs or other neural networks are often paired up with the genetic algorithm. A review of how the genetic algorithm is often used to optimize the input space of ANN models and investigate the effects of various factors on fermentative hydrogen production was reported in [104]. A multi-objective genetic algorithm was employed to derive a Pareto optimal collection of solutions for geometrical attributes of airfoil sections designed for 10-meter blades of a horizontal axis wind turbine. The process utilized ANN-modelled objective functions and was discussed in [105]. Ref. [106] reported the high performance and durability of a direct internal reforming solid oxide fuel cell by coupling a deep neural network with a multi-objective genetic algorithm, improving the high-power density by 190% while significantly reducing carbon deposition. A similar approach was undertaken to maximize the exergy efficiency and minimize the total cost of a geothermal desalination system [107].
4. Strengths and Weaknesses
4.1. Ranking Publications
Table 2 shows a ranking matrix. The rankings were determined based on the average score of the publications on each criterion. A score of “5” indicates excellence in particular criteria, whereas “0” indicates that a publication did not excel in specific criteria; integer scores between 0 and 5 were assigned based on this scale of excellence, where a higher score indicates higher performance in that criteria.

Table 2.
Ranking matrix.
A discussion of the algorithms used in the publications ranked as top 40, a total of 88 publications (since there were publications with the same total score) or approximately the top 10% of the publications, based on the ranking matrix criteria in Table 2, follows with an in-depth look at the strengths and weaknesses of each algorithm. These publications represent the publications with the largest datasets, use of non-simulated real data, quantifiable performance achieved, recent publication date, high number of citations, preferred algorithm types, and without much memory limitations. Based on the weights of the ranking matrix, it is clear that the quality of the data and the performance of the model were the most important criteria.
4.2. Artificial Neural Networks
Artificial neural networks (ANNs) are computational modeling algorithms that have emerged recently and have become a staple in many disciplines for modeling complex real-world nonlinear problems. Twenty-two publications were identified among the five hundred thirty. ANNs consist of intricately connected adaptable basic processing elements known as artificial neurons or nodes. They are proficient in executing highly concurrent computations for data processing and knowledge representation, drawing inspiration from the functioning of the human brain [40,41]. The general structure of an ANN is shown in Figure 8. The input to the ANN is each row of data with its diverse columns fed as individual inputs into the neurons of the input layer. Neurons are the basic building blocks of ANNs. They act like tiny decision makers. Let us assume that all data points consist of five columns (features or explanatory variables); then, there would be five input layer neurons. If our input consisted of 28 × 28-pixel images, with a total of 784 pixels per picture, then there would be a total of 784 input layer neurons. Neurons in the input layer are connected to neurons in the next layer through weights. Weights are like knobs that adjust the strength of the connection between neurons. The network learns to adjust these weights during training. Each input neuron’s value is then multiplied by the initial weights, which are initialized randomly, and summed, adding to the numerical bias initially assigned to the hidden layer neurons (i.e., ). The hidden layers are the layers in between the input and output layers. There can be one or more hidden layers. These layers are where most of the computation happens. Neurons in the hidden layers take input from the previous layer, apply mathematical operations, and pass the result to the next layer. Subsequently, these computed values undergo evaluation by activation functions, commonly referred to as threshold functions. Each neuron also has an “activation function.” This function determines whether the neuron should fire or not based on the information it receives. Common activation functions include the sigmoid and ReLU (rectified linear unit) functions. This assessment governs the activation status of the neuron, and the cumulative result influences either the subsequent hidden layer or, in the cases where there is only one hidden layer, the final output. The final layer is the output layer. It produces the network’s prediction or classification based on the information processed in the hidden layers. This process called forward propagation, is repeated until the final weights determine the initial output (i.e., y). The network will then measure the error of the prediction based on the expected output, in a supervised way, that is, by comparing it to the provided real output value. A “loss function” calculates the difference between the network’s predictions and the actual answers to measure how well the network is performing. The goal is to minimize this difference. The choice of a loss function depends on the type of problem you are trying to solve. Mean squared error (MSE) is a popular choice for regression problems where the outcome variable is a continuous value. Cross-entropy is to classification as MSE is to regression, with two types for binary and multi-class classification problems. There are plenty more loss functions that can be chosen based on the specific task. These steps are repeated, and by continuously training on the remaining training dataset, the network will adjust its weights until it reaches a strong level of prediction, a minimized loss function; this training process of adjustment is called backpropagation [108]. This overall process is what is sometimes defined as learning. Lastly, the trained ANN will be applied to unseen data, typically referred to as test data, to judge its performance. Several evaluation metrics are commonly used. The choice of evaluation metrics depends on the type of task your ANN is designed for (e.g., classification or regression).
Within artificial systems, learning is conceived as the process of adapting the neural system in reaction to external inputs aimed at accomplishing a particular task, such as classification or regression. This adaptation entails alterations to the network’s structure, encompassing adjustments to link weights, the addition or removal of connection links, and modifications to the activation function rules of individual neurons. Learning in ANNs takes place through an iterative process as the network encounters training samples, mirroring the way humans acquire knowledge through experience. An ANN-based system is considered to have learned when it can effectively manage imprecise, ambiguous, noisy, and probabilistic data without exhibiting significant performance degradation and can apply its acquired knowledge to unfamiliar tasks [40]. ANNs can be used for pattern recognition, clustering, function approximation or modeling, forecasting, optimization, association, and control. Some standardized pre-processing of data before the application of ANNs or other algorithms includes, but is not limited to, noise removal, reducing input dimensionality, and data transformation [109,110], treatment of nonnormally distributed data, data inspection, and deletion of outliers [111,112]. It is advisable to employ data normalization to avoid the dominance of larger values over smaller ones and the premature favoring of hidden nodes, which can impede the learning process [113].
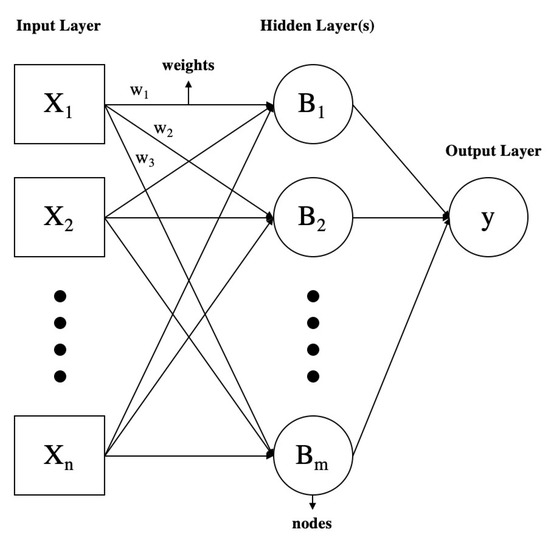
Figure 8.
The general structure of an ANN (from [114]).
Within the studied publications, ANNs are most notably used in the modeling of photovoltaic modules [115], short-term wind power forecasting [116], and real-time electricity price prediction [117], providing between 20.0 and 99.5% improved performance on the benchmark method using between 63,000 and 262,000 real data samples.
4.2.1. Strengths
The appeal of ANNs stems from their distinctive information processing attributes, including nonlinearity, extensive parallelism, resilience, tolerance to faults and failures, learning capabilities, adeptness in managing imprecise and fuzzy data, and their capacity to generalize. In other words, ANNs, and other deep learning algorithms do not require the data to undergo human pre-processing, which could introduce many issues, including bias [118]. These characteristics are desirable because
- nonlinearity allows for a great fit to almost any dataset,
- noise-insensitivity provides accurate prediction in the presence of slight errors in data, which are common,
- high parallelism allows for fast processing and hardware failure-tolerance,
- the system may modify itself in the face of a changing environment and data by training the neural network once again, and
- its ability to generalize enables the application of the model to unlearned and new data.
ANNs achieve nonlinearity through the use of the nonlinear activation functions (e.g., sigmoid, ReLU, tanh) within their neurons. These activation functions introduce nonlinearity into the network, allowing ANNs to capture complex and nonlinear relationships in the data. ANNs are inherently robust to noise to some extent due to their architecture. During training, the network learns to assign different weights to input features and connections. These weighted averages can help to mitigate the impact of noisy data points during prediction. Moreover, ANNs leverage parallelism efficiently. Neurons in the hidden layers of the network can perform computations independently, allowing for high parallelism. Lastly, ANNs are great at generalization thanks to their dropout and weight decay techniques which avoid overfitting. These regularization methods encourage the network to focus on the most important features and reduce sensitivity to noise in the data [118].
4.2.2. Weaknesses
As discussed, ANNs are powerful tools with wide-ranging applications. However, ANNs have important limitations that should be considered.
These include the following:
- ANNs’ success depends on both the quality and quantity of the data;
- A lack of decisive rules or guidelines for optimal ANN architecture design;
- A prolonged training time, which could extend from hours to months;
- The inability to comprehensibly explain the process through which the ANN made a given output, often criticized for being black boxes;
- There are parameters that require optimizing, which are at times not intuitively apparent [119].
While there are common architectural choices (e.g., the number of layers and neurons), there is no one-size-fits-all guideline for designing an optimal ANN architecture. Determining the right architecture requires empirical experimentation and domain expertise, which can be time-consuming and resource-intensive. Training deep ANNs, especially for complex tasks, can be computationally expensive and time-consuming. Training on large datasets with deep architectures may require significant computational resources, including GPUs or TPUs, and can take hours or even days to complete. ANNs can be seen as “black box” models, making it challenging to understand and interpret their internal workings. This lack of explainability can be a significant drawback, especially in applications where transparency and interpretability are crucial. To mitigate these weaknesses, researchers and practitioners are actively working on developing techniques and tools for data-efficient learning, automated architecture search, model explainability, and transfer learning [119].
4.3. Ensemble Learning: XGBoost, Random Forest, Support Vector Machine, Decision Trees
Ensemble learning involves the utilization of multiple learning algorithms in tandem to enhance predictive performance beyond what can be achieved individually by each constituent of the ensemble method [120]. Six publications out of the five hundred thirty were identified. For instance, a popular ensemble algorithm is the random forest algorithm, which can be used for classification and regression problems. Random algorithms are constructed by a multitude of decision trees at training time. Decision trees are a flowchart-like structure in which each internal node represents a “decision” on an attribute (e.g., whether a dice will roll an odd or even number, marked at times by probability), each branch represents the outcome of the decision, and each leaf node represents a class label (the decision taken or label assigned to those samples at the leaf after computing all attributes). The decisions can be represented by inequality or equivalent tests. The paths from root to leaf represent classification rules. For classification purposes, the random forest algorithm’s output corresponds to the class favored by the majority of trees. In regression tasks, the output represents the average prediction derived from the individual trees [120]. Random decision forests correct for decision trees’ habit of overfitting to their training set [121]. Overfitting is a major concern in supervised learning tasks. It occurs when the model learns the data in the training process too closely, yielding a great accuracy or low error rate, but then the model runs the risk of performing poorly with unseen data. Random forest algorithms generally outperform decision trees, but their accuracy tends to be lower than that of gradient-boosted tree algorithms, such as the regularized gradient-boosting frameworks provided by the XGBoost software library(Extreme Gradient Boosting, ver.2.0.2). Boosting algorithms aim to incrementally build an ensemble by training each following model instance to emphasize the training instances the previous models classified or predicted poorly [122]. Gradient boosting algorithms aim to use stochastic gradient descent or similar optimization algorithms to reduce the overall prediction error of the iterative models. It is achieved by adding a new estimator, a residual, to the previous model to attempt to correct the predecessor’s errors. This estimator is calculated from the negative gradient of the loss function, which tends to be MSE for regression problems and cross-entropy loss/log loss for classification problems [121]. XGBoost, unlike other gradient descent algorithms, uses a second-order Taylor approximation in the loss function to make the connection to Newton–Raphson method, which is a root-finding algorithm. XGBoost provides an excellent approximation of the residuals iteratively, ultimately creating a strong ensemble learner [123].
Lastly, the SVM algorithm is sometimes a great candidate as a replacement for decision trees in ensemble methods where multiple SVM learners are used. SVMs are supervised learning models used for regression and classification problems. In summary, a linear SVM attempts to classify a training set by trying to find a maximum-margin hyperplane that divides the training vectors into classes, most notably in binary classification problems. Different SVM variations exist, including nonlinear SVMs [124].
Within the selected publications, SVMs are most notably used in conjunction with deep neural networks to estimate the lithium-ion battery state [125], wind turbine event detection [126], and short-term wind speed forecasting [127], providing between 33 and 77.37% improved performance on the benchmark method. RFs were used for intelligent fault diagnosis for photovoltaic units using array voltage and string currents [128] and explaining the hydrogen adsorption properties of defective nitrogen-doped carbon nanotubes [129], with an average of 99% accuracy. Lastly, XGBoost and other adaptive boosting and deep learning hybrid techniques were used for intra-day solar irradiance fore casting in tropical high variability regions [130] and for wave energy forecasting [131], achieving between 25 and 29.3% improved performance compared to the benchmark models using between 25,000 and 52,000 real data samples.
4.3.1. Strengths
The ensemble learning methods are solid tools for linear and nonlinear classification and regression problems. RFs and XGBoost algorithms provide high accuracy or low error rates. Ensemble learning methods are able to accomplish such performance by combining predictions of multiple individual models (decision trees for RFs and XGBoost) to make more accurate predictions. The base model of these two models are Decision Trees (DTs), which are usually prone to high variance because they are sensitive to small variations in training data. RFs and XGBoost mitigate this by averaging or combining the results of multiple trees, which reduces variance bias and ultimately makes predictions more stable. By combining multiple trees, RFs, and XGBoost can approximate complex decision boundaries, that is, nonlinearity in the data, allowing them to model a wide range of data patterns effectively. Gradient boosting algorithms, such as XGBoost, reduce bias and variance while increasing accuracy compared to RFs [122]. SVMs are often the linear regressor or classifier of choice for binary problems, as they provide high accuracy with low computation costs. Ensemble methods of SVMs build on this strength to tackle nonlinear problems. Compared to ANNs, ensemble methods are computationally less costly and have faster training and prediction times.
4.3.2. Weaknesses
Ensemble methods require extensive parameter tuning to discover the best rendition of the ensemble NING method. Algorithms do exist to tackle this issue, such as GridSearch, which is often built into the ARY and packages that house these algorithms in software [123]. While all algorithms risk overfitting, and ensemble methods are not an exception, XGBoost borrows some concepts from bootstrap aggregating algorithms to reduce overfitting. Bootstrap aggregating, often referred to as bagging, generates m samples, from large enough datasets these subsamples, known as bootstraps, tend to be 63.2% the size of the original dataset from a given training set by sampling with replacement; this ensures that each bootstrap is independent of its peers. Then, m total models are fit to the m bootstraps, one model for each, and their outputs are then averaged. This process minimizes overfitting thanks to the multiplicity of the samples and their independence. With these methods is the necessity for manual featurization, which is not necessary in neural network frameworks.
While ensemble methods are less computationally costly than deep neural networks, ensemble methods have lower accuracy than deep neural networks. Thus, when researchers seek higher accuracy than that provided by ensemble methods, they often fall back on deep neural networks and use ensemble methods as the benchmark.
4.4. Long Short-Term Memory
A recurrent neural network (RNN) is a type of ANN characterized by the presence of cyclic connections, which enable the information from certain nodes to impact the subsequent input received by those very nodes. As such, RNNs exhibit temporal dynamic behavior, which makes RNNs distinctly applicable for a time series analysis [132]. RNNs are said to have both short-term and long-term “memory”. Built upon the foundation of feedforward neural networks, RNNs harness their internal memory to effectively handle input sequences of varying lengths [133].
Long short-term memory (LSTM) networks feature an enhanced iteration of the RNN architecture, meticulously engineered to capture temporal sequences and their extended relationships with greater accuracy compared to conventional RNNs. In a sense, the LSTM architecture stores short-term memory longer than that of RNNs. In some instances, this is crucial; long-term dependencies are sometimes required to predict the current output. Thus, an ideal algorithm dealing with problems that require long-term dependencies can decide which parts of the context need to be carried forward and how much of the past needs to be “forgotten”. This vanishing gradient problem is one that the LSTM tries to address and almost remove completely by applying a hidden layer known as a gated unit or gated cell. The gated cell comprises four layers that interact with one another to produce both a numerical output of the cell and the cell state. These two outputs are then passed onto the next hidden layer. While RNNs have only a single neural net layer of tanh, a classification function with two outputs, LSTM networks have three logistic sigmoid gates and one tanh layer. These gates act as filters, selectively regulating the passage of information through the cell. They decide what portion of the data is relevant for the subsequent cell and what should be disregarded. Typically, the output falls within the 0–1 range, where 0 signifies the exclusion of all information, while 1 signifies the inclusion of all information.
Each LSTM cell has three inputs ht−1, Ct−1, and xt and two outputs ht and Ct. For a given time t, ht is the hidden state, Ct is the cell state or memory, xt is the current data point or input. The first sigmoid layer inputs are ht−1 and xt. This component is referred to as the forget gate because its output determines the extent to which information from the previous cell should be retained. The output of the forget gate is a value between 0 and 1, which is then element-wise multiplied with the previous cell state Ct−1. As for the second sigmoid layer, it is the input gate, which chooses what new information makes it to the cell. It takes two inputs ht−1 and xt, the previous hidden state and the current data point. The tanh layer creates a vector Ct of the new candidate values. These second sigmoid layer and the tanh layer determine the information to be stored in the cell state. Their point-wise multiplication determines the amount of information to be added to the cell state. The outcome of the input gate is combined with the outcome of the forget gate, which is multiplied by the previous cell state, resulting in the generation of the current cell state Ct. Subsequently, the cell’s output is computed by utilizing the third sigmoid layer and the tanh layer. The former determines the portion of Ct that will be incorporated into the output, while the latter adjusts the output within the [−1, 1] range. Finally, these results undergo point-wise multiplication to produce the final output ht of the cell [134,135,136].
LSTM networks were designed to be even better suited than RNNs for classifying, processing, and making predictions based on time series data. In recent years, notable publications revealed that using the LSTM algorithm for the prediction and evaluation of a solid oxide fuel cell (SOFC) system’s operating state [137], learning the congestion level of a power distribution system which designates the loading of a distribution feeder [138], and fouling prediction in heat exchangers to avoid inefficiencies and shutdowns [139], provided improved performance compared to the benchmark autoregressive integrated moving average and regression algorithms by between 19.1 and 200% using 629,873, 86,400, and 23,040 real data samples, respectively.
4.4.1. Strengths
LSTM networks are particularly adept at tasks involving the classification, analysis, and prediction of time series data, as they can effectively handle situations where significant events within the time series may have variable and unanticipated time intervals between them. Moreover, LSTM networks are well-suited for tasks requiring the importance of long-term dependencies. Relative insensitivity to large gaps is the distinguishing advantage of LSTM networks over RNNs, achieved by dealing with the vanishing gradient problem almost completely [136].
4.4.2. Weaknesses
All in all, LSTM networks are one of the best options for tackling problems that require long-term dependencies. However, the LSTM architecture fails to remove the vanishing gradient completely. The primary factor is that data transfer between cells remains a necessity for their processing. Future research for the enhancement of RNNs may focus on addressing this challenge, as there is a quest among developers for a model capable of retaining past information over extended durations beyond what LSTM networks currently provide. Moreover, LSTM networks also require substantial resources and time to train and become implementation-ready. It is due to the high memory-bandwidth required because of the linear layers present in each cell. Thus, LSTM networks may become relatively inefficient because of their high bandwidth. Thirdly, LSTM networks become affected by different random weight initialization, preferring small weight initialization instead. This parameter does make finding the best LSTM model complex. Lastly, LSTM networks are prone to overfitting. The dropout method is typically used in RNNs to solve overfitting; it makes the model generalize more by probabilistically excluding the activation and weight updates of input and recurrent connections to LSTM units while training the network. However, this method is difficult to apply successfully [134,135,136].
4.5. Convolutional Neural Network
Convolutional neural networks (CNNs) represent a specific category of ANNs that employ a mathematical operation known as convolution instead of the conventional matrix multiplication in at least one of their hidden layers. Five publications were identified. These networks are purposefully crafted for the manipulation of pixel information and find application in tasks like image identification and manipulation. However, their utility extends beyond this domain, encompassing various other functions like prediction, modeling, clustering, and data analysis [140]. Similar to ANNs, CNNs have input, hidden, and output layers. The main distinction comes in the ability of the hidden layers to perform convolutions.
Usually, convolution entails the dot product between the convolution kernel and the input matrix of the layer. The activation function frequently employed for this product is ReLU. While the convolution kernel moves across the input matrix, it produces a feature map that subsequently feeds into the next layer. Subsequent layers may include pooling layers, fully connected layers, and normalization layers, among others [141]. Pooling layers reduce the data dimensions by combining the outputs of neuron clusters at one layer into a single neuron in the next layer. Local pooling combines small clusters, while global pooling acts on all the neurons of the feature map [142]. There are primarily two types of pooling in practice: max pooling selects the highest value within each local group of neurons in the feature map, whereas average pooling calculates the mean value [143]. Fully connected layers link every node in one layer to every node in another layer [141]. Between 2018 and 2022, the most notable publications in energy conversion used CNNs to forecast fuel cells power generation accurately [144], ocean wave power prediction [145], and solar panel output forecasting [146], which provided an 11–60% improvement on the benchmark using between 17,000 and 77,000 real data samples.
4.5.1. Strengths
CNNs share all the same advantages as ANNs, but their main distinctive advantage is their superior capabilities related to the 2D structure of an input image. It is achieved through its neighboring connections and tied weights coupled by diversity in convolutional, pooling, fully connected, and normalizing layers, which enables further translation of variant characteristics.
4.5.2. Weaknesses
CNNs share similar limitations with ANNs. These include the following:
- CNNs’ success also depends on both the quality and quantity of the data;
- A lack of decisive rules or guidelines for optimal CNN architecture design, although different architectures have been studied and show promising results;
- A prolonged training time, which could extend from hours to months;
- The explainability of CNNs outputs is also limited;
- There are parameters and choices in layers that require optimizing, sometimes leading to trial and error until the desired accuracy or error rate is reached.
4.6. Adaptive Network-Based Fuzzy Inference System
Developed in the early 1990s, the ANFIS algorithm is a kind of ANN that is based on Takagi–Sugeno fuzzy inference system [147]. Only four publications were identified. In juxtaposition to Boolean logic, which categorically assigns truth values to variables as either 1 or 0, a fuzzy logic constitutes a variant of a many-valued logic wherein the truth value of variables can manifest as any real number falling within the continuous interval between 0 and 1. Through this mechanism, the notion of partial veracity becomes viable, wherein the veracity level is capable of encompassing a spectrum that extends from absolute verity (1) to absolute falsity (0). These come in many forms, including IF-THEN clauses [148]. Thus, a fuzzy logic allows models to recognize, represent, manipulate, interpret, and use data and information that can be vague and lack certainty [80]. ANFIS amalgamates neural network and fuzzy logic paradigms, thereby endowing the ANFIS algorithm with the prospect of harnessing the advantages inherent in both paradigms within a unified framework. The inference system comprises a collection of fuzzy “if-then” rules, equipped with the capacity for learning and approximating nonlinear functions. [149]. ANFIS is considered a universal estimator for these capabilities [150]. The ANFIS algorithm may be optimized by pairing it with the best parameters obtained by a genetic algorithm [151].
The architecture of the ANFIS model is made up of five layers. The initial layer plays a distinctive role in distinguishing an ANFIS network from conventional neural networks. Within the fuzzification layer, the input values are processed to ascertain their respective membership functions. The computation of membership degrees for each function is achieved through the utilization of the premise parameter set, thereby transforming the inputs into fuzzy values. In regular neural networks, the first sigmoid layer normalizes inputs to values between 0 and 1 to pre-process the data. An ANFIS neural network does not use a sigmoid function to pre-process the data. Instead, the fuzzification layer performs the pre-processing by turning the inputs into fuzzy values [152].
Between 2019 and 2022, the most notable publications in energy conversion used ANFIS to create probabilistic wind turbine power curve models to quantify the uncertainties of energy conversion and highly scattered relationships of actual wind speed to power [153], investigate the effectiveness of proton exchange membrane fuel cell historical behavior and their operating mode on future performance at both static and nonstatic conditions [154], and predict the whole range of graphene oxide nanoparticle data [155], which provided a 24–163% improvement on the benchmark using 50,256, 1100, and 10,530 real data points.
4.6.1. Strengths
The ANFIS algorithm has several advantages [149,150,151,152]:
- Capability to capture the nonlinear structure of a process;
- Strong adaption capability;
- Rapid learning capacity, thanks to its parallel computation capabilities;
- Fewer adjustable parameters than ANNs;
- Universal application.
ANFIS captures nonlinear structures by combining the adaptability of neural networks with the interpretability of fuzzy logics. It adjusts membership functions, rule weights, and neural network parameters during training to fit the data’s nonlinear patterns. The “adaptive” aspect of ANFIS comes from its ability to adjust the parameters of its membership functions and fuzzy rules using a learning algorithm. Commonly used learning algorithms include gradient descent or least-squares methods. These algorithms iteratively update the parameters to minimize the error between the actual and predicted output. ANFIS can also incorporate a neural network component, which is typically a single-layer feedforward neural network. This neural network takes the intermediate fuzzy outputs from the fuzzy inference step and further processes them. Neural networks are inherently capable of approximating nonlinear functions, and this component enhances ANFIS’s ability to capture complex nonlinear relationships. This hybrid approach allows ANFIS to effectively model complex relationships in processes or data while maintaining transparency and interpretability through its fuzzy rule base. These features make ANFIS a consistently used algorithm in the energy field, most notably in energy system management, thanks to its easy integration with other control design methods [149,150,151,152].
4.6.2. Weaknesses
Given that the ANFIS algorithm is efficient, accurate, and adaptable, its main potential disadvantage is the potentiality of overfitting. Another consideration is that an ANFIS network may not achieve as high accuracy due to its universal application as a CNN with images or an LSTM network with time series. Thus, ANFIS networks come in handy as a first-choice exploration and a benchmark, as well as for problems with difficult-to-map nonlinear processes.
4.7. Reinforcement Learning: Q-learning, Deep Deterministic Policy Gradient, Actor Critic
The top-ranked reinforcement learning algorithm publications utilized Q-learning, SAC, and DDPG agents in the energy conversion set of documents collected. As mentioned earlier, reinforcement learning algorithms concern a learning agent and its environment and the set of actions taken by the agent per a set of states, which yield different rewards. The ultimate goal of the agent is to finalize the final total reward. Estimation of the expected value of the total rewards from particular actions at particular states is where reinforcement learning algorithms differentiate. Only four publications were identified.
Q-learning is a subset of reinforcement learning algorithms that aims to learn the value of an action in a particular state. The agent will initialize a table of actions and potential states at 0. Through the training, the agent will update the expected value of every action in each particular state, known as Q values. This table ultimately determines how an agent acts given a certain state and its set of actions to maximize its total reward. At the heart of the method for computing these Q values lies a Bellman equation, which involves a straightforward update process known as value iteration. This update combines the current value with new information using a weighted average. Q-learning algorithms are capable of addressing challenges involving uncertain transitions and rewards in a problem domain, all without necessitating extensive adjustments or adaptations [156].
A fundamental contrast between Q-learning and DDPG (deep deterministic policy gradient) agents lies in the nature of their state and action spaces. Specifically, DDPG agents navigate within continuous state and action spaces, while Q-learning agents operate in discrete counterparts. Furthermore, DDPG employs a dual learning paradigm wherein it simultaneously trains a Q-function and a policy. This training process is reliant on off-policy data and the application of the Bellman equation, with the Q-function serving as a foundation for informing the policy learning process and vice versa. Presuming that the Q-function is differentiable concerning the action argument allows for a gradient-based learning approach. Thus, the DDPG tends to be an excellent option for problems with continuous spaces [157].
Developed in collaboration between Google and UC Berkeley, the SAC algorithm is an off-policy RL algorithm based on a maximum entropy approach. The maximum entropy reinforcement learning framework aims to achieve the optimal policy by maximizing the expected return and the expected entropy itself [158]. In other words, a primary distinction between the Q-learning/DDPG and SAC algorithms is that the former consists of a critic, which aims at updating state-action values; in contrast, the SAC algorithm consists of a critic and an actor who takes action and explores the space based on the critic’s insights, which ultimately also informs the critic.
From 2018 to 2022, prominent research works in the realm of energy conversion to a rage extent employed Q-learning to oversee the efficient energy management of a hybrid energy storage system that incorporates supercapacitors and undersea storage. These systems were designed for the purpose of integrating wave energy conversion into the electrical grid [159]. DDPG was employed to develop a dynamic energy conversion and management model for an integrated electricity and natural gas system [160]. The soft actor critic algorithm was applied in the context of energy scheduling strategy with the aim of optimizing various objectives. These objectives encompassed the reduction in operational expenses and the guarantee of a dependable power supply [91], which provided a 21–69% improvement on the benchmark.
4.7.1. Strengths
Q-learning algorithms are greatly adaptive to stochastic changes in states and rewards [156]. DDPG agents adopt the remarkable adaptability and predictive power of Q-learning algorithms and apply them to continuous spaces, which leads to DDPG algorithms having wider adaptability across problems [157]. SAC agents provide improved stability concerning the hyperparameters and outperform prior on-policy and off-policy methods in sample efficiency and asymptotic performance. Therefore, real-world applications of SAC are more stable. By avoiding parameter tuning and having sample efficiency, the SAC algorithm tends to have a computational efficiency advantage over the Q-learning and DDPG agents [158].
These algorithms have potential in areas where an intelligent system controller or manager is being implemented, for instance, in a smart electrical grid management strategy.
4.7.2. Weaknesses
As foreshadowed earlier, Q-learning and DDPG are computationally very expensive, especially in comparison to the SAC algorithm. A weakness of reinforcement learning algorithms is their currently limited application space. For these algorithms to be used, the specific problem task must be one where the environment must be modeled or fit into the paradigms of states, actions, actors, critics, and environment.
4.8. Other Algorithms Worth Mentioning: Graph Neural Networks and Regression Methods
Other algorithms were also present in the top-rated publications but with only one or two publications. The authors wanted to highlight two. Twenty-one publications were identified out of the five hundred thirty.
The first is a graph neural networks (GNNs). In the realm of artificial intelligence and machine learning, where innovation continually reshapes our understanding of complex data structures, GNNs have emerged as a powerful tool. These networks represent a pioneering paradigm shift, enabling us to harness the latent insights within interconnected data, such as social networks, molecular structures, recommendation systems, etc. Graphs, a versatile data representation, inherently describe relationships and dependencies among entities. By 2021, GNNs have garnered increasing attention due to their remarkable performance. GNNs exhibit the capability to capture intricate dependencies within various data modalities, such as graphs, images, and structural data, by facilitating information propagation through message passing among the nodes of the graphs. Notably, unlike CNNs, GNNs preserve a state that encapsulates information derived from their local neighborhood, allowing for arbitrary depth of information retention. Moreover, no other neural networks can handle graph input data like GNNs [161]. Thus, unique problems can sometimes be solved by GNNs. For instance, within the set of the energy conversion publications of this paper, a graph convolutional neural network (GCNN) is used in 92,219 entries of inorganic crystal data to chart lattice thermal conductivity, with a R2 of 0.85; in comparison to random forests, GNNs did not require any ad hoc physics-based featurization, rendering more robust outcomes [162].
The second is regression methods. While standard regression models typically do not achieve as high performance as neural networks, especially on nonlinear processes where featurization does not work, regression methods are sometimes enough for particular problems or crucial components of a more complex algorithm, such as neural networks. Moreover, regression models are extensively less computationally expensive than neural networks. In the context of the energy conversion studies detailed in this paper, the lasso regression model was applied to discern the associations among wave parameters. It was employed to identify and opt for the most suitable approach for transforming wave parameters in coastal Irish Waters. This endeavor culminated in the attainment of a remarkably low RMSE value, specifically amounting to 0.17 [163]. Also, a multivariate polynomial regression model is implemented to produce a light-dependent resistor-based solar tracker that can learn and improve its action from daily interaction with the environment, which achieved a 0.0806 RMSE score [164]. Regression is a classic model that researchers should not neglect, as this tool is efficient and sometimes sufficient.
The synergy between advanced computational techniques and developments in the energy sector is supposed to ignite promising success in energy efficiency, sustainability, and reliability in the production, distribution, and sustainable use of energy resources.
5. Conclusions
Machine learning and artificial intelligence algorithms have found application in specific tasks within the domain of energy conversion and management.
Research in this field reveals that the ratio of publications utilizing real-world data to the publications utilizing simulated data is 3:2. As expected, papers relying on real data exhibit superior algorithm performance compared to established benchmarks and often involve larger datasets. Researchers must prioritize the use of real data and exert creative ways to build datasets. A model may only be deemed reliable if it was trained or developed through the use of real-world data. While simulated datasets are great for exploratory research, true advancements in any field will only be achieved through findings and models from large and real datasets. Moreover, the authors recommend adopting standardized and transparent reporting practices regarding data size, accuracy, error rates, and benchmark performance in research papers. All papers that are empirical should explicitly state the origin of the dataset, dimensions, and features of the dataset, chosen models, coding environment used, memory requirements of the process, loss function, performance metric, and achieved performance improvement relative to a benchmark. Such practices enable other researchers to comprehend the findings’ implications better and facilitate adopting, comparing, replicating, and implementing favorable algorithms. The authors found it shocking to discover that 29.37% of the studied works did not publish their performance metrics, 38.94% did not provide a benchmark within their study to compare the algorithm implemented, 32.01% did not report the size of the data, and the majority did not mention the coding program used or the memory requirement of their process.
While MATLAB is a comfortable choice for implementing coding programs, energy researchers should consider the adoption of Python as a preferred coding language. Python has wider adoption and community support, a rich ecosystem of high-performance libraries, ease of use and readability, and wider industry adoption.
Top-ranked papers and a timeline clustering analysis illustrate continuous growth in the publications related to wind energy conversion systems, wave energy conversion systems, solar power, and electric power transmission. These publications frequently delve into the application of convolutional neural networks, hybrid approaches using genetic algorithms, ensemble learning, reinforcement learning, long short-term memory algorithms, hybrid models incorporating regression methods, and graph neural networks for various tasks, such as classification, regression, optimization, or system management. Widespread adoption and utilization of these techniques hinge on integrating mathematical and computer science expertise into the energy field. The application of artificial intelligence techniques has demonstrated exponential growth in recent years and holds significant potential for the future.
In conclusion, artificial intelligence is poised to become an integral part of research in energy conversion systems and the entire energy sector, offering numerous opportunities to enhance their energetic, economic, and environmental performance and, therefore, contribute to the goals of sustainability. As shown in this body of work, AI can provide significant benchmark performance improvement compared to traditional or non-AI methods for various tasks in energy conversion; the authors encourage energy researchers to make it standard practice to reach out or collaborate with their institution’s data, computer science, and mathematics experts when performing any task to see if there is room to include AI methods. The authors hope to convince energy research departments about the beneficial possibilities of increasingly adopting the use of Python, trending AI methods, large and real datasets, and analogous standard reporting practice, as the one described above.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| AI | artificial intelligence |
| ANN | artificial neural network |
| ANFIS | adaptive neuro-fuzzy inference system |
| ARIMA | autoregressive integrated moving average |
| BPNN | backpropagation neural network |
| CNN | convolutional neural network |
| DDPG | deep deterministic policy gradient |
| GNN | graph neural network |
| LSTM | long short-term memory |
| LTM | lateral misalignment |
| ML | machine learning |
| MPPT | maximum power point tracking |
| MSE | mean squared error |
| NN-EMC | neural network energy management controller |
| RAM | random access memory |
| RBFNN | radial basis function neural network |
| RL | reinforcement learning |
| RMS | root mean square |
| RMSE | root-mean-square error |
| RNN | recurrent neural network |
| SAC | soft actor critic |
| SVM | support vector machine |
| UPFC | unified power flow controller |
| WECS | wind energy conversion systems |
References
- Karsten Würth. What is the Kyoto Protocol? Available online: https://unfccc.int/kyoto_protocol (accessed on 7 November 2022).
- UNFCCC. The Paris Agreement. Available online: https://unfccc.int/process-and-meetings/the-paris-agreement/the-paris-agreement (accessed on 7 November 2022).
- OP26 Outcomes. UN Climate Change Conference UK 2021. 2021. Available online: https://ukcop26.org/the-conference/cop26-outcomes/ (accessed on 7 November 2022).
- IEA. Net Zero Roadmap: A Global Pathway to Keep the 1.5 °C Goal in Reach. 2023. Available online: www.iea.org (accessed on 7 October 2023).
- IEA. Clean Energy Innovation, IEA. 2020. Available online: https://www.iea.org/reports/clean-energy-innovation (accessed on 7 November 2022).
- IEA. Global Hydrogen Review. International Energy Agency, Paris, 2021. Available online: https://www.iea.org/reports/global-hydrogen-review-2021 (accessed on 7 November 2022).
- Incer-Valverde, J.; Patino-Arevalo, L.J.; Tsatsaronis, G.; Morosuk, T. Hydrogen-driven Power-to-X: State of the art and multicriteria evaluation of a study case. Energy Convers. Manag. 2022, 266, 115814. [Google Scholar] [CrossRef]
- IEA. Energy Technology Perspectives 2020. International Energy Agency, Paris. 2020. Available online: https://www.iea.org/reports/energy-technology-perspectives-2020 (accessed on 7 November 2022).
- BloombergNEF. Hydrogen Economy Outlook. Key Messages; Bloomberg Finance L.P: New York, NY, USA, 2020. [Google Scholar]
- IEA. The Future of Hydrogen. International Energy Agency, Paris, 2019. Available online: https://www.iea.org/reports/the-future-of-hydrogen (accessed on 7 November 2022).
- IRENA. The Future of Hydrogen; International Renewable Energy Agency: Abu Dhabi, United Arab Emirates, 2019. [Google Scholar]
- Jacques, B. Notes from the AI Frontier: Modeling the Impact of AI on the World Economy, McKinsey Company. McKinsey Company. 2019. Available online: https://www.mckinsey.com/featured-insights/artificial-intelligence/notes-from-the-AI-frontier-modeling-the-impact-of-ai-on-the-world-economy (accessed on 8 November 2022).
- Xu, Y.; Liu, X.; Cao, X.; Huang, C.; Liu, E.; Qian, S.; Liu, X.; Wu, Y.; Dong, F.; Qiu, J.; et al. Artificial intelligence: A powerful paradigm for scientific research. Innovation 2021, 2, 100179. [Google Scholar] [CrossRef] [PubMed]
- EETimes. Digital Data Storage Is Undergoing Mind-Boggling Growth. EETimes. 2016. Available online: https://www.eetimes.com/digital-data-storage-is-undergoing-mind-boggling-growth/ (accessed on 8 November 2022).
- European Commission. Digitalising the Energy System—EU Action Plan; European Commission: Brussels, Belgium, 2022. [Google Scholar]
- Chen, C. A Practical Guide for Mapping Scientific Literature; Nova Science Publishers: Hauppauge, NY, USA, 2016. [Google Scholar]
- Crevier, D. AI: The Tumultuous Search for Artificial Intelligence; BasicBooks: New York, NY, USA, 1993. [Google Scholar]
- Sharma, A.K.; Ghodke, P.K.; Goyal, N.; Nethaji, S.; Chen, W.-H. Machine learning technology in biohydrogen production from agriculture waste: Recent advances and future perspectives. Bioresour. Technol. 2022, 364, 128076. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Du, Y.; Han, S.; Qiu, Q. Global progress in oil and gas well research using bibliometric analysis based on Vosviewer and Citespace. Energies 2022, 15, 5447. [Google Scholar] [CrossRef]
- Chang, C.C.W.; Ding, T.J.; Ping, T.J.; Ariannejad, M.; Chao, K.C.; Samdin, S.B. Fault detection and anti-icing technologies in wind energy conversion systems: A review. Energy Rep. 2022, 8, 28–33. [Google Scholar] [CrossRef]
- Ding, R.; Zhang, S.; Chen, Y.; Rui, Z.; Hua, K.; Wu, Y.; Li, X.; Duan, X.; Wang, X.; Li, J.; et al. Application of machine learning in optimizing proton exchange membrane fuel cells: A review. Energy AI 2022, 9, 100170. [Google Scholar] [CrossRef]
- Alshehri, J.; Alzahrani, A.; Khalid, M. Wind energy conversion systems and artificial neural networks: Role and applications. In Proceedings of the 2019 IEEE Innovative Smart Grid Technologies—Asia (ISGT Asia), Chengdu, China, 21–24 May 2019; pp. 1777–1782. [Google Scholar]
- Ashfaq, A.; Kamran, M.; Rehman, F.; Sarfaraz, N.; Ilyas, H.U.; Riaz, H.H. Role of artificial intelligence in renewable energy and its scope in future. In Proceedings of the 2022 5th International Conference on Energy Conservation and Efficiency (ICECE), Lahore, Pakistan, 16–17 March 2022; pp. 1–6. [Google Scholar]
- van Eck, N.J.; Waltman, L. Software survey: VOSViewer, a computer program for bibliometric mapping. Scientometrics 2009, 84, 523–538. [Google Scholar] [CrossRef]
- Waltman, L.; van Eck, N.J. A smart local moving algorithm for large-scale modularity-based community detection. Eur. Phys. 2013, 86, 471. [Google Scholar] [CrossRef]
- OED Online. Artificial Intelligence; Oxford University Press: Oxford, UK, 2022. [Google Scholar]
- Mitchell, T. Machine Learning; McGraw Hill: New York, NY, USA, 1997. [Google Scholar]
- Sipser, M. Introduction to the Theory of Computation, 3rd ed.; Cengage Learning: Boston, MA, USA, 2013. [Google Scholar]
- McCorduck, P. Machines Who Think, 2nd ed.; A. K. Peters: Natick, MA, USA, 2004. [Google Scholar]
- Lighthill, J. Artificial Intelligence: A Paper Symposium; Science Research Council: London, UK, 1973. [Google Scholar]
- Nilsson, N.J.; Nilsson, N.J. Artificial Intelligence: A New Synthesis; Morgan Kaufmann: San Francisco, CA, USA, 1998. [Google Scholar]
- National Research Council. Funding A Revolution: Government Support for Computing Research; National Academies Press: Washington, DC, USA, 1999. [Google Scholar]
- Ask the AI Experts: What’s Driving Today’s Progress in AI? McKinsey Company. 2018. Available online: https://www.mckinsey.com/capabilities/quantumblack/our-insights/ask-the-ai-experts-whats-driving-todays-progress-in-ai (accessed on 8 November 2022).
- Clark, J. Why 2015 was a breakthrough year in artificial intelligence. Bloom. Technol. 2015, 18. Available online: https://www.pinterest.com/pin/106467978669157536/ (accessed on 8 November 2022).
- Lewis, J.; Schneegans, S.; Straza, T. UNESCO Science Report: The Race Against Time for Smarter Development; UNESCO: Paris, France, 2021; Volume 2021. [Google Scholar]
- Tucker, A.B. Computer Science Handbook; Chapman and Hall/CRC: Newton, MA, USA/Boca Raton, FL, USA, 2004. [Google Scholar]
- van Otterlo, M.; Wiering, M. Reinforcement learning and markov decision processes. In Reinforcement Learning; Springer: Berlin/Heidelberg, Germany, 2012; pp. 3–42. [Google Scholar]
- Roweis, S.T.; Saul, L.K. Nonlinear dimensionality reduction by locally linear embedding. Science 2000, 290, 2323–2326. [Google Scholar] [CrossRef]
- European Union Agency for Fundamental Rights (FRA). Data Quality and Artificial Intelligence—Mitigating Bias and Error to Protect Fundamental Rights; European Union Agency for Fundamental Rights (FRA): Vienna, Austria, 2019. [Google Scholar]
- Schalkoff, R.J. Artificial Neural Networks; McGraw-Hill Higher Education: New York, NY, USA, 1997. [Google Scholar]
- Hecht-Nielsen, R. Neurocomputing; Addison-Wesley Longman Publishing: Boston, MA, USA, 1989. [Google Scholar]
- Li, F.-F. Large Scale Visual Recognition Challenge 2012 (ILSVRC2012). ImageNet. 2012. Available online: https://www.image-net.org/challenges/LSVRC/2012/results.html/ (accessed on 8 November 2022).
- Seo, D.; Huh, T.; Kim, M.; Hwang, J.; Jung, D. Prediction of air pressure change inside the chamber of an oscillating water column–wave energy converter using machine-learning in big data platform. Energies 2021, 14, 2982. [Google Scholar] [CrossRef]
- MathWorks. MATLAB. Available online: https://www.mathworks.com/products/matlab.html (accessed on 8 November 2022).
- Python Software Foundation. Python. Available online: https://www.python.org/ (accessed on 8 November 2022).
- Medjber, A.; Guessoum, A.; Belmili, H.; Mellit, A. New neural network and fuzzy logic controllers to monitor maximum power for wind energy conversion system. Energy 2016, 106, 137–146. [Google Scholar] [CrossRef]
- Dahbi, A.; Nait-Said, N.; Nait-Said, M.-S. A novel combined mppt-pitch angle control for wide range variable speed wind turbine based on neural network. Int. J. Hydrogen Energy 2016, 41, 9427–9442. [Google Scholar] [CrossRef]
- Moradi, H. Sliding mode type-2 neuro-fuzzy power control of grid-connected DFIG for wind energy conversion system. IET Renew. Power Gener. 2019, 13, 2435. [Google Scholar] [CrossRef]
- Chhipa, A.A.; Kumar, V.; Joshi, R.R.; Chakrabarti, P.; Jasinski, M.; Burgio, A.; Leonowicz, Z.; Jasinska, E.; Soni, R.; Chakrabarti, T. Adaptive neuro-fuzzy inference system-based maximum power tracking controller for variable speed WECS. Energies 2021, 14, 6275. [Google Scholar] [CrossRef]
- Ali Zeddini, M.; Pusca, R.; Sakly, A.; Faouzi Mimouni, M. Pso-based mppt control of wind-driven self-excited induction generator for pumping system. Renew. Energy 2016, 95, 162–177. [Google Scholar] [CrossRef]
- Kariniotakis, G.N.; Stavrakakis, G.S.; Nogaret, E.F. Wind power forecasting using advanced neural networks models. IEEE Trans. Energy Convers. 1996, 11, 762–767. [Google Scholar] [CrossRef]
- Alexiadis, M.C.; Dokopoulos, P.S.; Sahsamanoglou, H.S. Wind speed and power forecasting based on spatial correlation models. IEEE Trans. Energy Convers. 1999, 14, 836–842. [Google Scholar] [CrossRef]
- Sarkar, D.; Contal, E.; Vayatis, N.; Dias, F. Prediction and optimization of wave energy converter arrays using a machine learning approach. Renew. Energy 2016, 97, 504–517. [Google Scholar] [CrossRef]
- Tri, N.M.; Truong, D.Q.; Thinh, D.H.; Binh, P.C.; Dung, D.T.; Lee, S.; Park, H.G.; Ahn, K.K. A novel control method to maximize the energy-harvesting capability of an adjustable slope angle wave energy converter. Renew. Energy 2016, 97, 518–531. [Google Scholar] [CrossRef]
- Ni, C.; Ma, X. Prediction of wave power generation using a convolutional neural network with multiple inputs. Energies 2018, 11, 2097. [Google Scholar] [CrossRef]
- Yang, S.; Deng, Z.; Li, Z.; Zheng, C.; Xi, L.; Zhuang, J.; Zhang, Z.; Zhang, Z. A novel hybrid model based on stl decomposition and one-dimensional convolutional neural networks with positional encoding for significant wave height forecast. Renew. Energy 2021, 173, 531–543. [Google Scholar] [CrossRef]
- Huang, W.; Dong, S. Improved short-term prediction of significant wave height by decomposing deterministic and stochastic components. Renew. Energy 2021, 177, 743–758. [Google Scholar] [CrossRef]
- Ramakumar, R.; Abouzahr, I.; Krishnan, K.; Ashenayi, K. Design scenarios for integrated renewable energy systems. IEEE Trans. Energy Convers. 1995, 10, 736–746. [Google Scholar] [CrossRef]
- Wu, C.; Burke, T.J. Intelligent computer aided optimization on specific power of an otec rankine power plant. Appl. Therm. Eng. 1998, 18, 295–300. [Google Scholar] [CrossRef]
- Da Silva Filho, J.I.; Rocco, A. Power systems outage possibilities analysis by paraconsistent logic. In Proceedings of the 2008 IEEE Power and Energy Society General Meeting—Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008; pp. 1–6. [Google Scholar]
- Frombo, F.; Minciardi, R.; Robba, M.; Rosso, F.; Sacile, R. Planning woody biomass logistics for energy production: A strategic decision model. Biomass Bioenergy 2009, 33, 372–383. [Google Scholar] [CrossRef]
- Rentizelas, A.A.; Tatsiopoulos, I.P.; Tolis, A. An optimization model for multi-biomass tri-generation energy supply. Biomass Bioenergy 2009, 33, 223–233. [Google Scholar] [CrossRef]
- Zhou, Y.; Zheng, S.; Zhang, G. Machine learning-based optimal design of a phase change material integrated renewable system with on-site pv, radiative cooling and hybrid ventilations—Study of modelling and application in five climatic regions. Energy 2020, 192, 116608. [Google Scholar] [CrossRef]
- Yona, A.; Senjyu, T.; Saber, Z.Y.; Funabashi, T.; Sekine, H.; Kim, C.-H. Application of neural network to 24-hour-ahead generating power forecasting for pv system. In Proceedings of the 2008 IEEE Power and Energy Society General Meeting—Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008; pp. 1–6. [Google Scholar]
- Syafaruddin, S.; Hiyama, T.; Karatepe, E. Feasibility of artificial neural network for maximum power point estimation of non crystalline-si photovoltaic modules. In Proceedings of the 2009 15th International Conference on Intelligent System Applications to Power Systems, Curitiba, Brazil, 8–12 November 2009; pp. 1–6. [Google Scholar]
- Celik, A.N. Artificial neural network modelling and experimental verification of the operating current of mono-crystalline photovoltaic modules. Solar Energy 2011, 85, 2507–2517. [Google Scholar] [CrossRef]
- Landeras, G.; López, J.J.; Kisi, O.; Shiri, J. Comparison of gene expression programming with neuro-fuzzy and neural network computing techniques in estimating daily incoming solar radiation in the Basque country (northern Spain). Energy Convers. Manag. 2012, 62, 1–13. [Google Scholar] [CrossRef]
- Çelik, Ö.; Teke, A.; Yıldırım, H.B. The optimized artificial neural network model with Levenberg–Marquardt algorithm for global solar radiation estimation in eastern Mediterranean region of Turkey. J. Clean. Prod. 2016, 116, 1–12. [Google Scholar] [CrossRef]
- Stonier, A.A.; Lehman, B. An intelligent-based fault-tolerant system for solar-fed cascaded multilevel inverters. IEEE Trans. Energy Convers. 2018, 33, 1047–1057. [Google Scholar] [CrossRef]
- Andrew-Cotter, J.; Uddin, M.N.; Amin, I.K. Particle swarm optimization based adaptive neuro-fuzzy inference system for mppt control of a three-phase grid-connected photovoltaic system. In Proceedings of the 2019 IEEE International Electric Machines Drives Conference (IEMDC), San Diego, CA, USA, 12–15 May 2019; pp. 2089–2094. [Google Scholar]
- Rao, C.K.; Sahoo, S.K.; Yanine, F.F. Forecasting electric power generation in a photovoltaic power systems for smart energy management. In Proceedings of the 2022 International Conference on Intelligent Controller and Computing for Smart Power (ICICCSP), Hyderabad, India, 21–23 July 2022; pp. 1–6. [Google Scholar]
- Theocharides, S.; Venizelou, V.; Makrides, G.; Georghiou, G.E. Day-ahead forecasting of solar power output from photovoltaic systems utilising gradient boosting machines. In Proceedings of the 2018 IEEE 7th World Conference on Photovoltaic Energy Conversion (WCPEC) (A Joint Conference of 45th IEEE PVSC, 28th PVSEC 34th EU PVSEC), Waikoloa, HI, USA, 10–15 June 2018; pp. 2371–2375. [Google Scholar]
- Michael, N.E.; Mishra, M.; Hasan, S.; Al-Durra, A. Short-term solar power predicting model based on multistep cnn stacked lstm technique. Energies 2022, 15, 2150. [Google Scholar] [CrossRef]
- Ghobadian, B.; Rahimi, H.; Nikbakht, A.M.; Najafi, G.; Yusaf, T.F. Diesel engine performance and exhaust emission analysis using waste cooking biodiesel fuel with an artificial neural network. Renew. Energy 2009, 34, 976–982. [Google Scholar] [CrossRef]
- Cheggaga, N. New neural networks strategy used to improve wind speed forecasting. Wind. Eng. 2013, 37, 369–379. [Google Scholar] [CrossRef]
- Mishra, C.; Subbarao, P.M.V. Machine Learning Integration With Combustion Physics to Develop a Composite Predictive Model for Reactivity Controlled Compression Ignition Engine. J. Energy Resour. Technol. 2021, 144, 042302. [Google Scholar] [CrossRef]
- Pandarakone, S.E.; Masuko, M.; Mizuno, Y.; Nakamura, H. Deep neural network based bearing fault diagnosis of induction motor using fast Fourier transform analysis. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 23–27 September 2018; pp. 3214–3221. [Google Scholar]
- Jeong, H.; Lee, H.; Kim, S.W. Classification and detection of demagnetization and inter-turn short circuit faults in IPMSMs by using convolutional neural networks. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 23–27 September 2018; pp. 3249–3254. [Google Scholar]
- Wei, H.; Su, W.; Shi, J. Research on variable speed constant frequency energy generation based on deep learning for disordered ocean current energy. Energy Rep. 2022, 8, 13824–13836. [Google Scholar] [CrossRef]
- Babuška, R. Fuzzy Modeling for Control; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 12. [Google Scholar]
- Kamalasadan, S. An intelligent coordinated design for excitation and speed control of synchronous generators based on supervisory loops. In Proceedings of the 2008 IEEE Power and Energy Society General Meeting—Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008; pp. 1–8. [Google Scholar]
- Kamalasadan, S. A new high performance intelligent speed controller for induction motor based on supervisory loops. In Proceedings of the 2008 IEEE Power and Energy Society General Meeting—Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008; pp. 1–7. [Google Scholar]
- Bonanno, F.; Capizzi, G.; Graditi, G.; Napoli, C.; Tina, G.M. A radial basis function neural network based approach for the electrical characteristics estimation of a photovoltaic module. Appl. Energy 2012, 97, 956–961. [Google Scholar] [CrossRef]
- Huang, H.; Chung, C.-Y. Adaptive neuro-fuzzy controller for static var compensator to damp out wind energy conversion system oscillation. IET Gener. Transm. Distrib. 2013, 7, 200–207. [Google Scholar] [CrossRef]
- Chang, W.-Y. Short-term wind power forecasting using the enhanced particle swarm optimization based hybrid method. Energies 2013, 6, 4879–4896. [Google Scholar] [CrossRef]
- Dastres, H.; Mohammadi, A.; Shamekhi, M. A neural network based adaptive sliding mode controller for pitch angle control of a wind turbine. In Proceedings of the 2020 11th Power Electronics, Drive Systems, and Technologies Conference (PEDSTC), Tehran, Iran, 4–6 February 2020; pp. 1–6. [Google Scholar]
- Chu, C.-C.; Tsai, H.-C. Application of Lyapunov-based adaptive neural network upfc damping controllers for transient stability enhancement. In Proceedings of the 2008 IEEE Power and Energy Society General Meeting—Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008; pp. 1–6. [Google Scholar]
- Soliman, M.; Emara, H.; Elshafei, A.; Bahgat, A.; Malik, O.P. Robust output feedback power system stabilizer design: An lmi approach. In Proceedings of the 2008 IEEE Power and Energy Society General Meeting—Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008; pp. 1–8. [Google Scholar]
- Tao, Y.; Bin, Z. A novel self-tuning cps controller based on q-learning method. In Proceedings of the 2008 IEEE Power and Energy Society General Meeting—Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008; pp. 1–6. [Google Scholar]
- Kosuru, R.; Chen, P.; Liu, S. A reinforcement learning based power system stabilizer for a grid connected wind energy conversion system. In Proceedings of the 2020 IEEE Electric Power and Energy Conference (EPEC), Edmonton, AB, Canada, 9–10 November 2020; pp. 1–5. [Google Scholar]
- Zhang, B.; Hu, W.; Cao, D.; Li, T.; Zhang, Z.; Chen, Z.; Blaabjerg, F. Soft actor–critic-based multi-objective optimized energy conversion and management strategy for integrated energy systems with renewable energy. Energy Convers. Manag. 2021, 243, 114381. [Google Scholar] [CrossRef]
- Tavakoli, R.; Pantic, Z. Ann-based algorithm for estimation and compensation of lateral misalignment in dynamic wireless power transfer systems for ev charging. In Proceedings of the 2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 1–5 October 2017; pp. 2602–2609. [Google Scholar]
- Ramoul, J.; Chemali, E.; Dorn-Gomba, L.; Emadi, A. A neural network energy management controller applied to a hybrid energy storage system using multi-source inverter. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 23–27 September 2018; pp. 2741–2747. [Google Scholar]
- Lu, Y.; Liu, W.; Wu, Y.; Huang, J.; Liao, H.; Liu, Y.; Peng, J.; Huang, Z. A hierarchical energy management strategy for battery/ultracapacitor hybrid energy storage systems via supervised learning. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Virtual, 11–15 October 2020; pp. 3698–3703. [Google Scholar]
- Xu, Z.; Han, G.; Liu, L.; Martínez-García, M.; Wang, Z. Multi-energy scheduling of an industrial integrated energy system by reinforcement learning-based differential evolution. IEEE Trans. Green Commun. Netw. 2021, 5, 1077–1090. [Google Scholar] [CrossRef]
- Chen, C.H.; Hong, C.-M.; Cheng, F.-S. Intelligent speed sensorless maximum power point tracking control for wind generation system. Int. J. Electr. Power Energy Syst. 2012, 42, 399–407. [Google Scholar] [CrossRef]
- Soliman, H.; Davari, P.; Wang, H.; Blaabjerg, F. Capacitance estimation algorithm based on dc-link voltage harmonics using artificial neural network in three-phase motor drive systems. In Proceedings of the 2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 1–5 October 2017; pp. 5795–5802. [Google Scholar]
- Giraud, F.; Salameh, Z.M. Neural network modeling of the gust effects on a grid-interactive wind energy conversion system with battery storage. Electr. Power Syst. Res. 1999, 50, 155–161. [Google Scholar] [CrossRef]
- Zhao, R.; Kollmeyer, P.J.; Lorenz, R.D.; Jahns, T.M. A compact unified methodology via a recurrent neural network for accurate modeling of lithium-ion battery voltage and state-of-charge. In Proceedings of the 2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 1–5 October 2017; pp. 5234–5241. [Google Scholar]
- Eskander, M.N. Neural network controller for a permanent magnet generator applied in a wind energy conversion system. Renew. Energy 2002, 26, 463–477. [Google Scholar] [CrossRef]
- Abdesh, M.; Khan, S.K.; Azizur Rahman, M. An adaptive self-tuned wavelet controller for ipm motor drives. In Proceedings of the 2008 IEEE Power and Energy Society General Meeting—Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008; pp. 1–4. [Google Scholar]
- Lakshmi, M.J.; Babu, Y.S.K.; Babu, P.M. PMSG based wind energy conversion system for maximum power extraction. In Proceedings of the 2016 Second International Conference on Computational Intelligence Communication Technology (CICT), Ghaziabad, India, 12–13 February 2016; pp. 366–371. [Google Scholar]
- Mitchell, M. An Introduction to Genetic Algorithms; MIT Press: Cambridge, MA, USA, 1996. [Google Scholar]
- Nath, R.; Das, D. Modeling and optimization of fermentative hydrogen production. Bioresour. Technol. 2011, 102, 8569–8581. [Google Scholar] [CrossRef] [PubMed]
- Mortazavi, S.M.; Soltani, M.R.; Motieyan, H. A pareto optimal multi-objective optimization for a horizontal axis wind turbine blade airfoil sections utilizing exergy analysis and neural networks. J. Wind. Eng. Ind. Aerodyn. 2015, 136, 62–72. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, C.; Zhao, S.; Wang, J.; Zu, B.; Han, M.; Du, Q.; Ni, M.; Jiao, K. Coupling deep learning and multi-objective genetic algorithms to achieve high performance and durability of direct internal reforming solid oxide fuel cell. Appl. Energy 2022, 315, 119046. [Google Scholar] [CrossRef]
- Farsi, A.; Rosen, M.A. Multi-Objective Optimization of a Geothermal Steam Turbine Combined with Reverse Osmosis and Multi-Effect Desalination for Sustainable Freshwater Production. J. Energy Resour. Technol. 2022, 144, 052102. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning Internal Representations by Error Propagation; Technical Report; California University San Diego La Jolla Institute for Cognitive Science: San Diego, CA, USA, 1985. [Google Scholar]
- Dowla, F.U.; Dowla, F.J.; Rogers, L.L.; Rogers, L.L. Solving Problems in Environmental Engineering and Geosciences with Artificial Neural Networks; MIT Press: Cambridge, MA, USA, 1995. [Google Scholar]
- Swingler, K. Applying Neural Networks: A Practical Guide; Morgan Kaufmann: Burlington, MA, USA, 1996. [Google Scholar]
- Masters, T. Practical Neural Network Recipes in C++; Academic Press Professional: Cambridge, MA, USA, 1993. [Google Scholar]
- Stein, R. Preprocessing data for neural networks. AI Expert 1993, 8, 1–32. [Google Scholar]
- Hassoun, M.H. Fundamentals of Artificial Neural Networks; MIT Press: Cambridge, MA, USA, 1995. [Google Scholar]
- Sairamya, N.J.; Susmitha, L.; George, S.T.; Subathra, M.S.P. Hybrid approach for classification of electroencephalographic signals using time–frequency images with wavelets and texture features. In Intelligent Data Analysis for Biomedical Applications; Hemanth, D.J., Gupta, D., Balas, V.E., Eds.; Intelligent Data-Centric Systems; Academic Press: Cambridge, MA, USA, 2019; Chapter 12; pp. 253–273. [Google Scholar]
- Lopez-Guede, J.M.; Ramos-Hernanz, J.A.; Zulueta, E.; Fernadez-Gamiz, U.; Oterino, F. Systematic modeling of photovoltaic modules based on artificial neural networks. Int. J. Hydrogen Energy 2016, 41, 12672–12687. [Google Scholar] [CrossRef]
- Mansoor, M.; Ling, Q.; Zafar, M.H. Short term wind power prediction using feedforward neural network (FNN) trained by a novel sine-cosine fused chimp optimization algorithm (SCHOA). In Proceedings of the 2022 5th International Conference on Energy Conservation and Efficiency (ICECE), Lahore, Pakistan, 16–17 March 2022; pp. 1–6. [Google Scholar]
- Ullah, M.H.; Paul, S.; Park, J.-D. Real-time electricity price forecasting for energy management in grid-tied MTDC microgrids. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 23-27 September 2018; pp. 73–80. [Google Scholar]
- Jain, A.K.; Mao, J.; Mohiuddin, K.M. Artificial neural networks: A tutorial. Computer 1996, 29, 31–44. [Google Scholar] [CrossRef]
- Basheer, I.A.; Hajmeer, M. Artificial neural networks: Fundamentals, computing, design, and application. J. Microbiol. Methods 2000, 43, 3–31. [Google Scholar] [CrossRef] [PubMed]
- Polikar, R. Ensemble based systems in decision making. IEEE Circuits Syst. Mag. 2006, 6, 21–45. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: Berlin/Heidelberg, Germany, 2009; Volume 2. [Google Scholar]
- Breiman, L. Bias, Variance, and Arcing Classifiers; Technical Report, Tech. Rep. 460; Statistics Department, University of California: Berkeley, CA, USA, 1996. [Google Scholar]
- Chen, T.; He, T.; Benesty, M.; Khotilovich, V. Package ‘XGBOOST’. R Version 2019, 90, 1–66. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Shrivastava, P.; Soon, T.K.; Idris, M.Y.B.; Mekhilef, S.; Adnan, S.B.R.S. Lithium-ion battery state of energy estimation using deep neural network and support vector regression. In Proceedings of the 2021 IEEE 12th Energy Conversion Congress & Exposition-Asia (ECCE-Asia), Singapore, 24–27 May 2021; pp. 2175–2180. [Google Scholar]
- Hu, C.; Albertani, R. Wind turbine event detection by support vector machine. Wind Energy 2021, 24, 672–685. [Google Scholar] [CrossRef]
- Ahmed, S.; Khalid, M.; Akram, U. A method for short-term wind speed time series forecasting using support vector machine regression model. In Proceedings of the 2017 6th International Conference on Clean Electrical Power (ICCEP), Santa Margherita Ligure, Italy, 27–29 June 2017; pp. 190–195. [Google Scholar]
- Chen, Z.; Han, F.; Wu, L.; Yu, J.; Cheng, S.; Lin, P.; Chen, H. Random forest based intelligent fault diagnosis for pv arrays using array voltage and string currents. Energy Convers. Manag. 2018, 178, 250–264. [Google Scholar] [CrossRef]
- Kronberg, R.; Lappalainen, H.; Laasonen, K. Hydrogen adsorption on defective nitrogen-doped carbon nanotubes explained via machine learning augmented dft calculations and game-theoretic feature attributions. J. Phys. Chem. C 2021, 125, 15918–15933. [Google Scholar] [CrossRef]
- Dong, Z.; Yang, D.; Yan, J.; Yu, C. Deep learning solution for intra-day solar irradiance fore casting in tropical high variability regions. In Proceedings of the 2018 IEEE 7th World Conference on Photovoltaic Energy Conversion (WCPEC) (A Joint Conference of 45th IEEE PVSC, 28th PVSEC 34th EU PVSEC), Waikoloa, HI, USA, 10–15 June 2018; pp. 2736–2741. [Google Scholar]
- Pani, N.K.K.; Jha, V.A.; Bai, L.; Cheng, L.; Zhao, T. A hybrid machine learning approach to wave energy forecasting. In Proceedings of the 2021 North American Power Symposium (NAPS), College Station, TX, USA, 14–16 November 2021. [Google Scholar]
- Tealab, A. Time series forecasting using artificial neural networks methodologies: A systematic review. Future Comput. Inform. J. 2018, 3, 334–340. [Google Scholar] [CrossRef]
- Dupond, S. A thorough review on the current advance of neural network structures. Annu. Rev. Control. 2019, 14, 200–230. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to forget: Continual prediction with LSTM. Neural Comput. 2000, 12, 2451–2471. [Google Scholar] [CrossRef] [PubMed]
- Gers, F.A.; Schraudolph, N.N.; Schmidhuber, J. Learning precise timing with LSTM recurrent networks. J. Mach. Learn. Res. 2002, 3, 115–143. [Google Scholar]
- Rao, M.; Wang, L.; Chen, C.; Xiong, K.; Li, M.; Chen, Z.; Dong, J.; Xu, J.; Li, X. Data-driven state prediction and analysis of sofc system based on deep learning method. Energies 2022, 15, 3099. [Google Scholar] [CrossRef]
- Ucer, E.; Kisacikoglu, M.; Gurbuz, A.; Rahman, S.; Yuksel, M. A machine learning approach for understanding power distribution system congestion. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Virtual, 11–15 October 2020; pp. 1977–1983. [Google Scholar]
- Soualhi, M.; El Koujok, M.; Nguyen, K.T.P.; Medjaher, K.; Ragab, A.; Ghezzaz, H.; Amazouz, M.; Ouali, M.-S. Adaptive prognostics in a controlled energy conversion process based on long-and short-term predictors. Appl. Energy 2021, 283, 116049. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016; Available online: http://www.deeplearningbook.org (accessed on 8 November 2022).
- Hassoun, M.H. Guide to Convolutional Neural Networks: A Practical Application to Traffic-Sign Detection and Classification; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Ciresan, D.; Meier, U.; Masci, J.; Gambardella, L.M.; Schmidhuber, J. Flexible, High Performance Convolutional Neural Networks for Image Classification. In Proceedings of the Twenty-Second International Joint Conference on Artificial Intelligence, Barcelona, Spain, 16–22 July 2011; pp. 1237–1242. [Google Scholar]
- Ciresan, D.C.; Meier, U.; Schmidhuber, J. Multi-column deep neural networks for image classification. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 3642–3649. [Google Scholar]
- Chou, J.-S.; Cheng, T.-C.; Liu, C.-Y.; Guan, C.-Y.; Yu, C.-P. Metaheuristics-optimized deep learning to predict generation of sustainable energy from rooftop plant microbial fuel cells. Int. J. Energy Res. 2022, 46, 21001–21027. [Google Scholar] [CrossRef]
- Bento, P.; Pombo, J.; do Rosario Calado, M.; Mariano, S. Ocean wave power forecasting using convolutional neural networks. IET Renew. Power Gener. 2021, 15, 3341–3353. [Google Scholar] [CrossRef]
- Sun, Y.; Venugopal, V.; Brandt, A.R. Convolutional neural network for short-term solar panel output prediction. In Proceedings of the 2018 IEEE 7th World Conference on Photovoltaic Energy Conversion (WCPEC) (A Joint Conference of 45th IEEE PVSC, 28th PVSEC & 34th EU PVSEC), Waikoloa, HI, USA, 10–15 June 2018; pp. 2357–2361. [Google Scholar]
- Jang, J.-S.R. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Novák, V.; Perfilieva, I.; Močkoř, J. Mathematical Principles of Fuzzy Logic; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Abraham, A. Adaptation of fuzzy inference system using neural learning. In Fuzzy Systems Engineering; Springer: Berlin/Heidelberg, Germany, 2005; pp. 53–83. [Google Scholar]
- Jang, J.-S.R.; Sun, C.-T.; Mizutani, E. Neuro-fuzzy and soft computing—A computational approach to learning and machine intelligence. IEEE Trans. Autom. Control 1997, 42, 1482–1484. [Google Scholar] [CrossRef]
- Tahmasebi, P.; Hezarkhani, A. A hybrid neural networks-fuzzy logic-genetic algorithm for grade estimation. Comput. Geosci. 2012, 42, 18–27. [Google Scholar] [CrossRef] [PubMed]
- Jang, J.-S.R. Self-learning fuzzy controllers based on temporal backpropagation. IEEE Trans. Neural Netw. 1992, 3, 714–723. [Google Scholar] [CrossRef] [PubMed]
- Yan, J.; Zhang, H.; Liu, Y.; Han, S.; Li, L. Uncertainty estimation for wind energy conversion by probabilistic wind turbine power curve modelling. Appl. Energy 2019, 239, 1356–1370. [Google Scholar] [CrossRef]
- He, K.; Zhang, C.; He, Q.; Wu, Q.; Jackson, L.; Mao, L. Effectiveness of pemfc historical state and operating mode in pemfc prognosis. Int. J. Hydrogen Energy 2020, 45, 32355–32366. [Google Scholar] [CrossRef]
- Bai, J.; Kadir, D.H.; Fagiry, M.A.; Tlili, I. Numerical analysis and two-phase modeling of water graphene oxide nanofluid flow in the riser condensing tubes of the solar collector heat exchanger. Sustain. Energy Technol. Assess. 2022, 53, 102408. [Google Scholar]
- Melo, F.S. Convergence of Q-Learning: A Simple Proof; Technical Report; Institute of Systems and Robotics: Lisbon, Portugal, 2001; pp. 1–4. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Haarnoja, T.; Zhou, A.; Hartikainen, K.; Tucker, G.; Ha, S.; Tan, J.; Kumar, V.; Zhu, H.; Gupta, A.; Abbeel, P. Soft actor-critic algorithms and applications. arXiv 2018, arXiv:1812.05905. [Google Scholar]
- Forestieri, J.N.; Farasat, M. Integrative sizing/real-time energy management of a hybrid supercapacitor/undersea energy storage system for grid integration of wave energy conversion systems. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 8, 3798–3810. [Google Scholar] [CrossRef]
- Zhang, B.; Hu, W.; Li, J.; Cao, D.; Huang, R.; Huang, Q.; Chen, Z.; Blaabjerg, F. Dynamic energy conversion and management strategy for an integrated electricity and natural gas system with renewable energy: Deep reinforcement learning approach. Energy Convers. Manag. 2020, 220, 113063. [Google Scholar] [CrossRef]
- Zhou, J.; Cui, G.; Hu, S.; Zhang, Z.; Yang, C.; Liu, Z.; Wang, L.; Li, C.; Sun, M. Graph neural networks: A review of methods and applications. AI Open 2020, 1, 57–81. [Google Scholar] [CrossRef]
- Zhu, T.; He, R.; Gong, S.; Xie, T.; Gorai, P.; Nielsch, K.; Grossman, J.C. Charting lattice thermal conductivity for inorganic crystals and discovering rare earth chalcogenides for thermoelectrics. Energy Environ. Sci. 2021, 14, 3559–3566. [Google Scholar] [CrossRef]
- Barker, A.; Murphy, J. Machine learning approach for optimal determination of wave parameter relationships. IET Renew. Power Gener. 2017, 11, 1127–1135. [Google Scholar] [CrossRef]
- Gaafar, E.G.M.; Sidahmed, B.A.M.; Nawari, M.O. The improvement of ldr based solar tracker’s action using machine learning. In Proceedings of the 2019 IEEE Conference on Energy Conversion (CENCON), Yogyakarta, Indonesia, 16-17 October 2019; pp. 230–235. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).