Balancing of Low-Voltage Supply Network with a Smart Utility Controller Leveraging Distributed Customer Energy Sources
Abstract
:1. Introduction
2. Related Work and Contribution of This Research
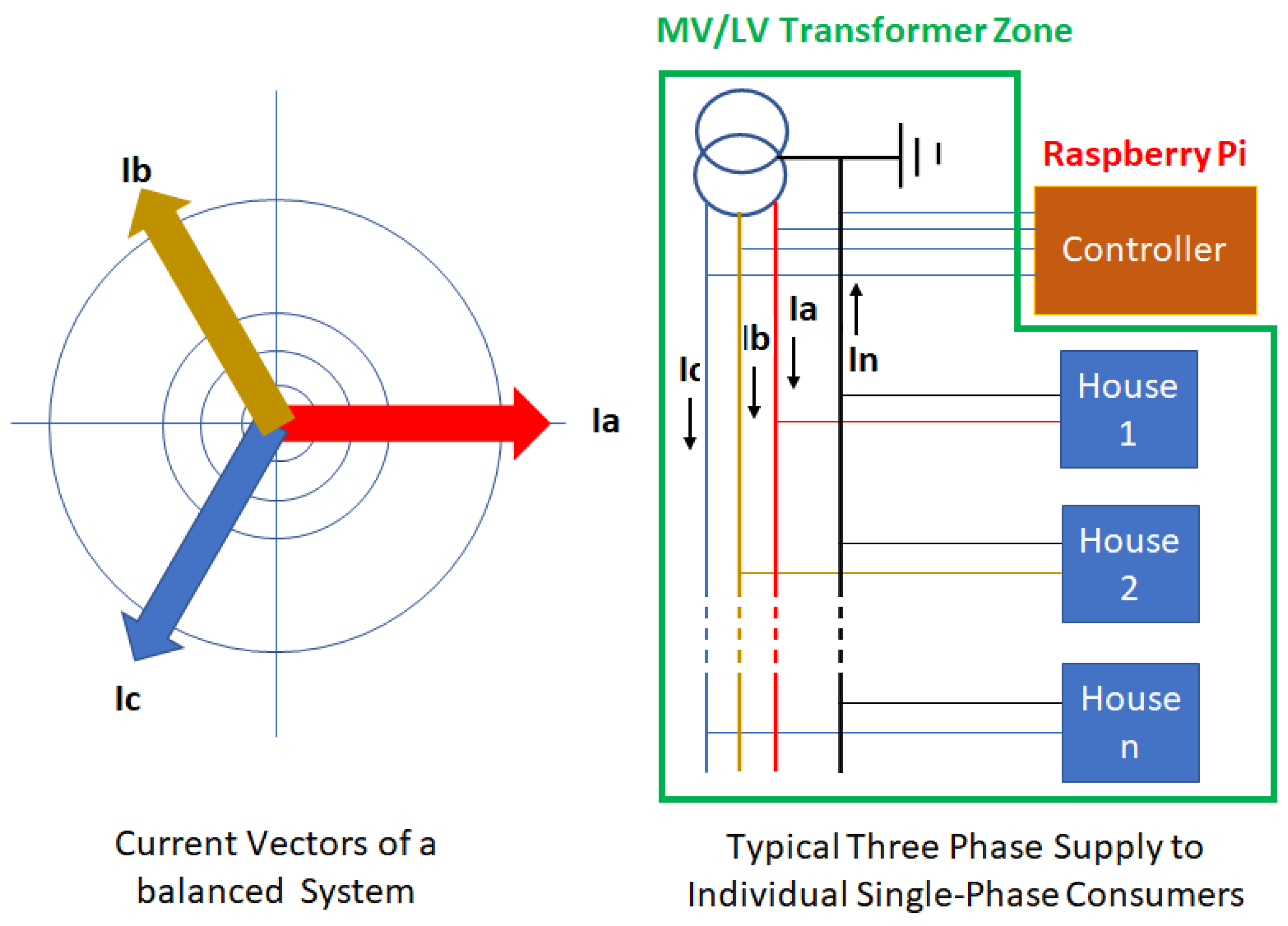
2.1. Balancing of Phases in Low-Voltage Networks
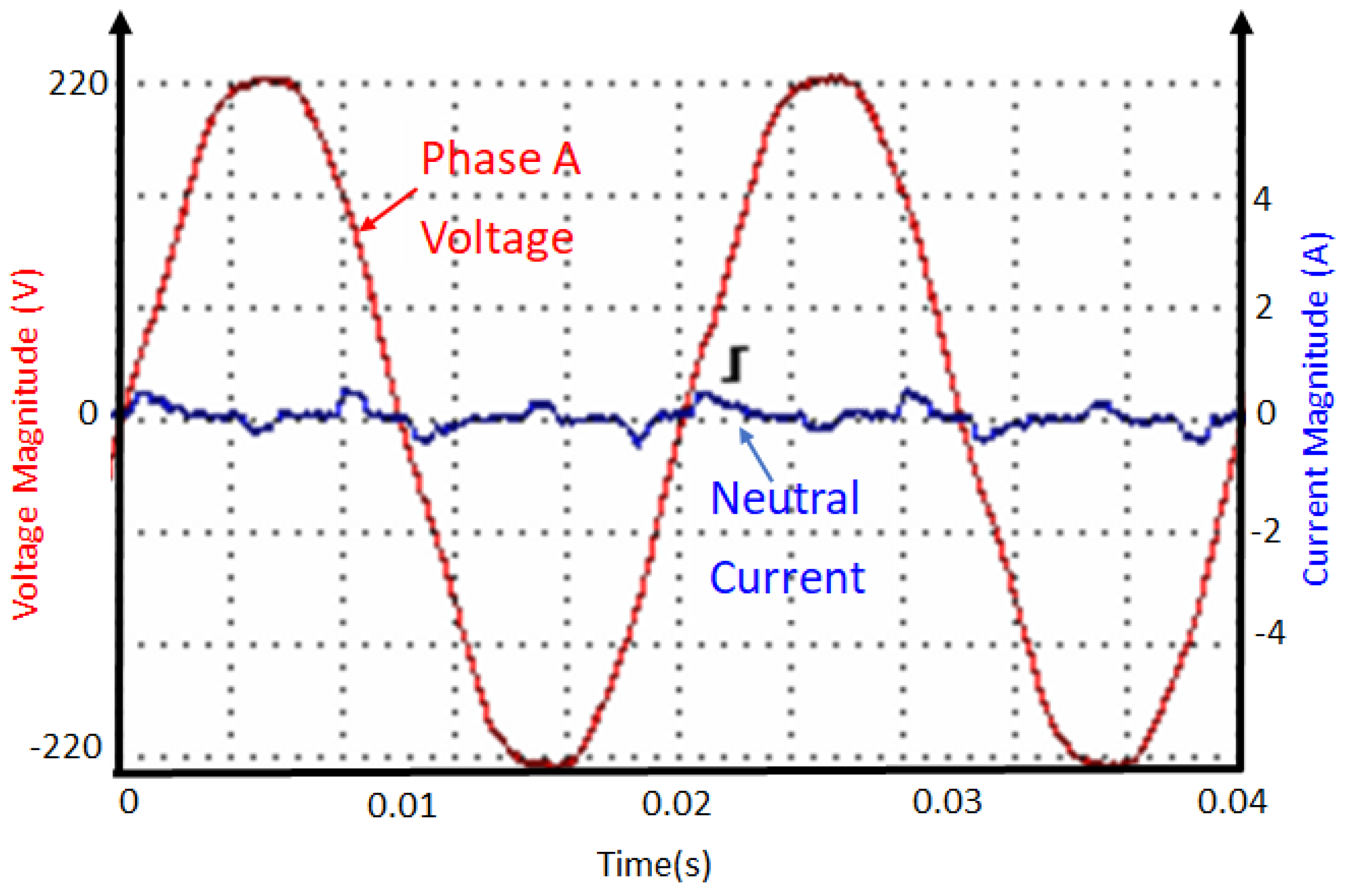
2.2. Consequences of Unbalanced System
2.3. Monitoring of Low-Voltage Networks
2.4. Understanding Inverter Communication
2.5. Smart Grid Communication Networks and Protocols
- Power-line carrier (PLC), which provides two-way communication through existing LV network infrastructure.
- LoRa, which is a wireless technology that provides secure, low-power data transmission over long distances.
- ZigBee, which is a wireless communication protocol specifically designed to facilitate low-power, short-range connectivity between devices.
2.6. Comparable Energy Systems
3. Case Study
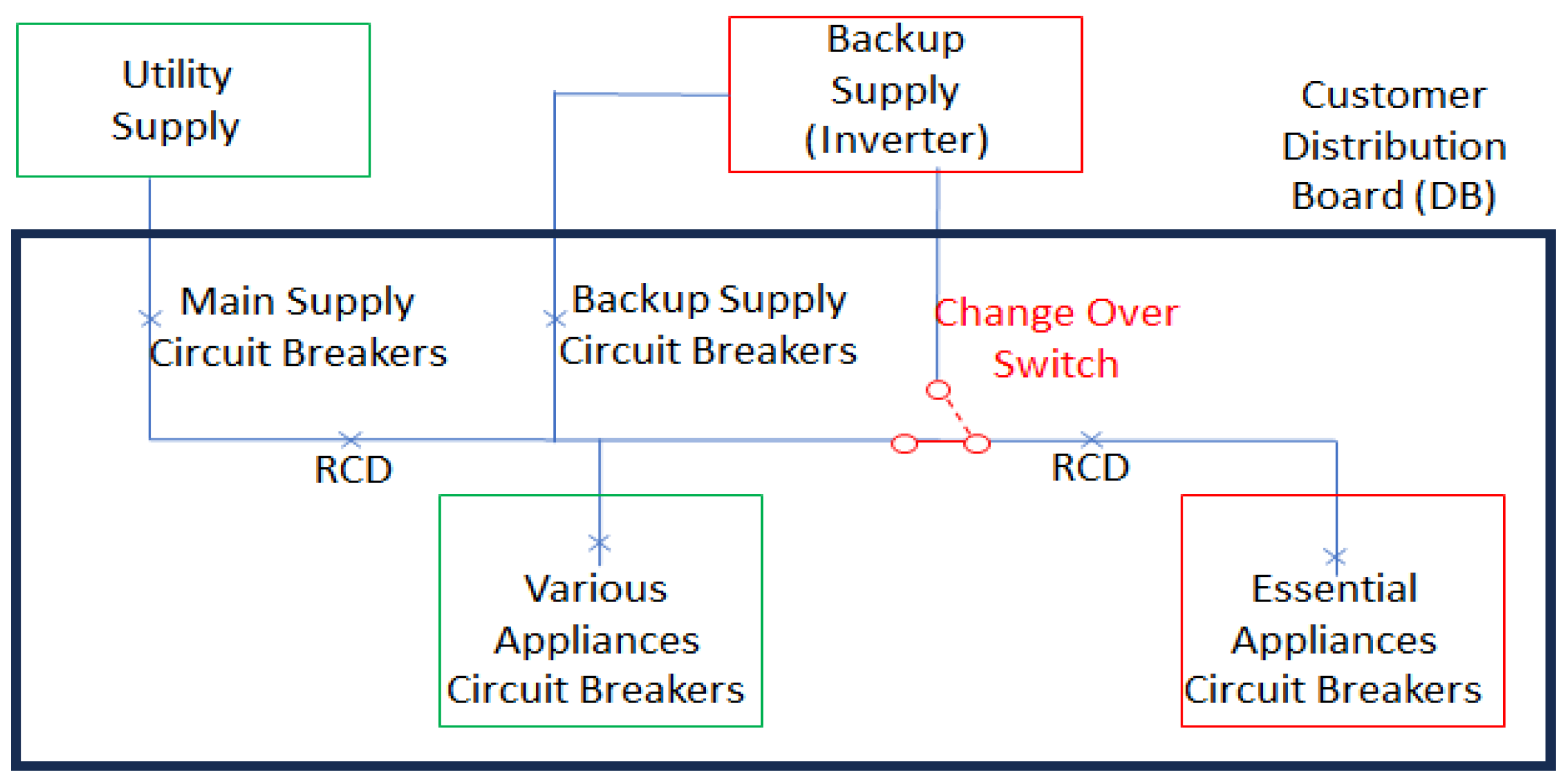
3.1. Description of a Typical LV Customer Installation
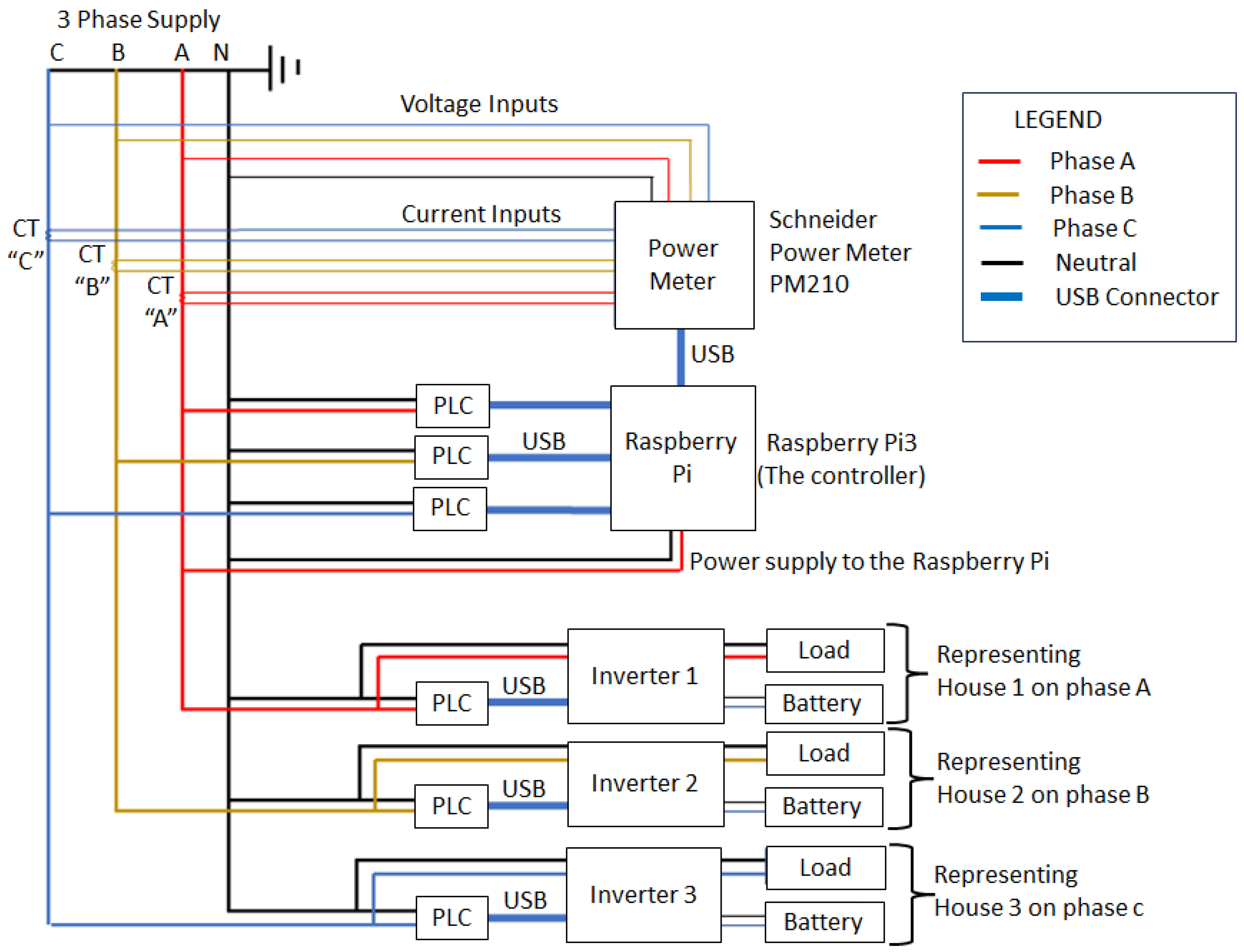
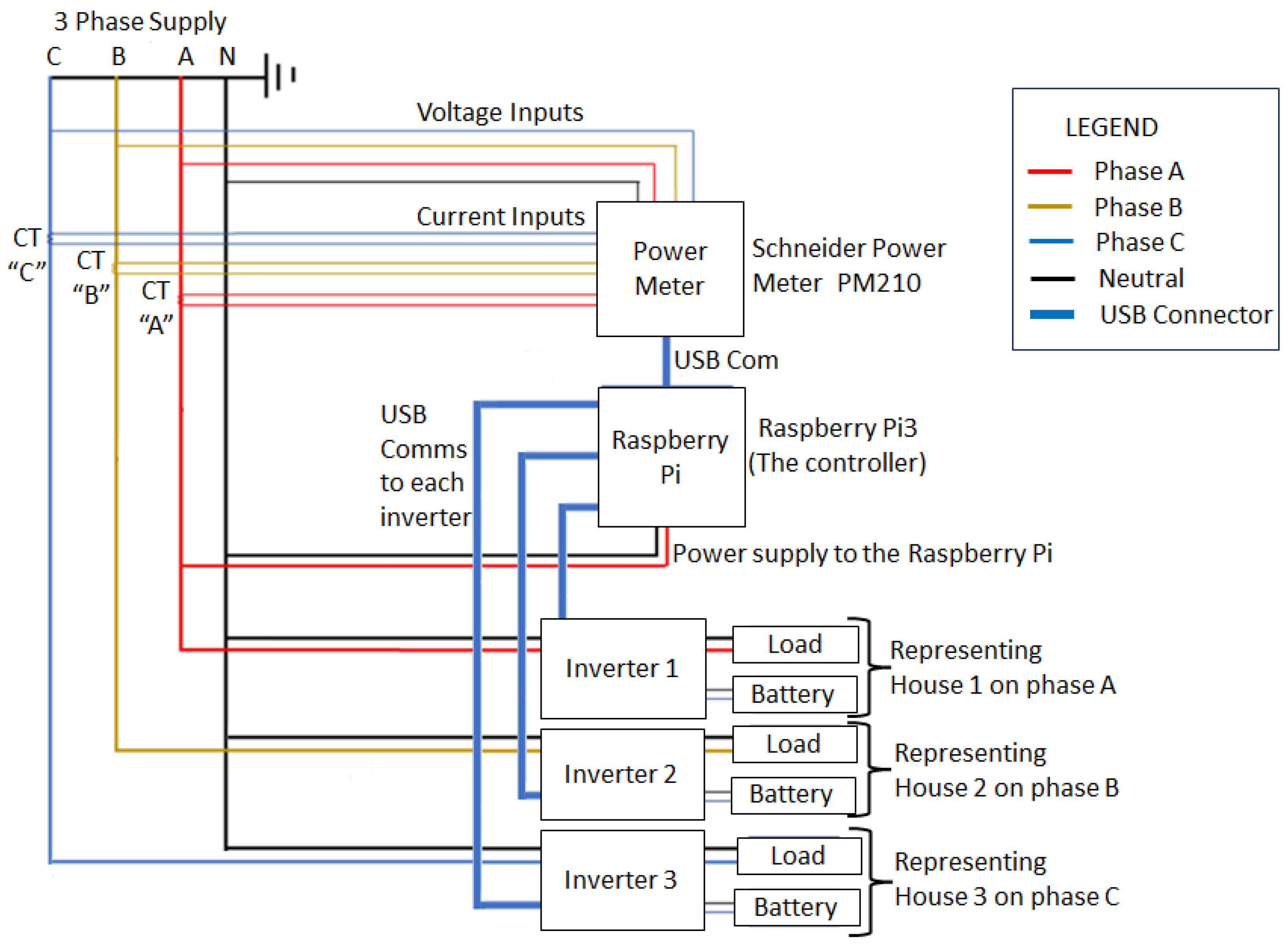
3.2. Description of Devices Used in the Laboratory
- Rapberry Pi;
- Schneider Powerlogic meter;
- Mercer hybrid inverter.
3.2.1. The Raspberry Pi
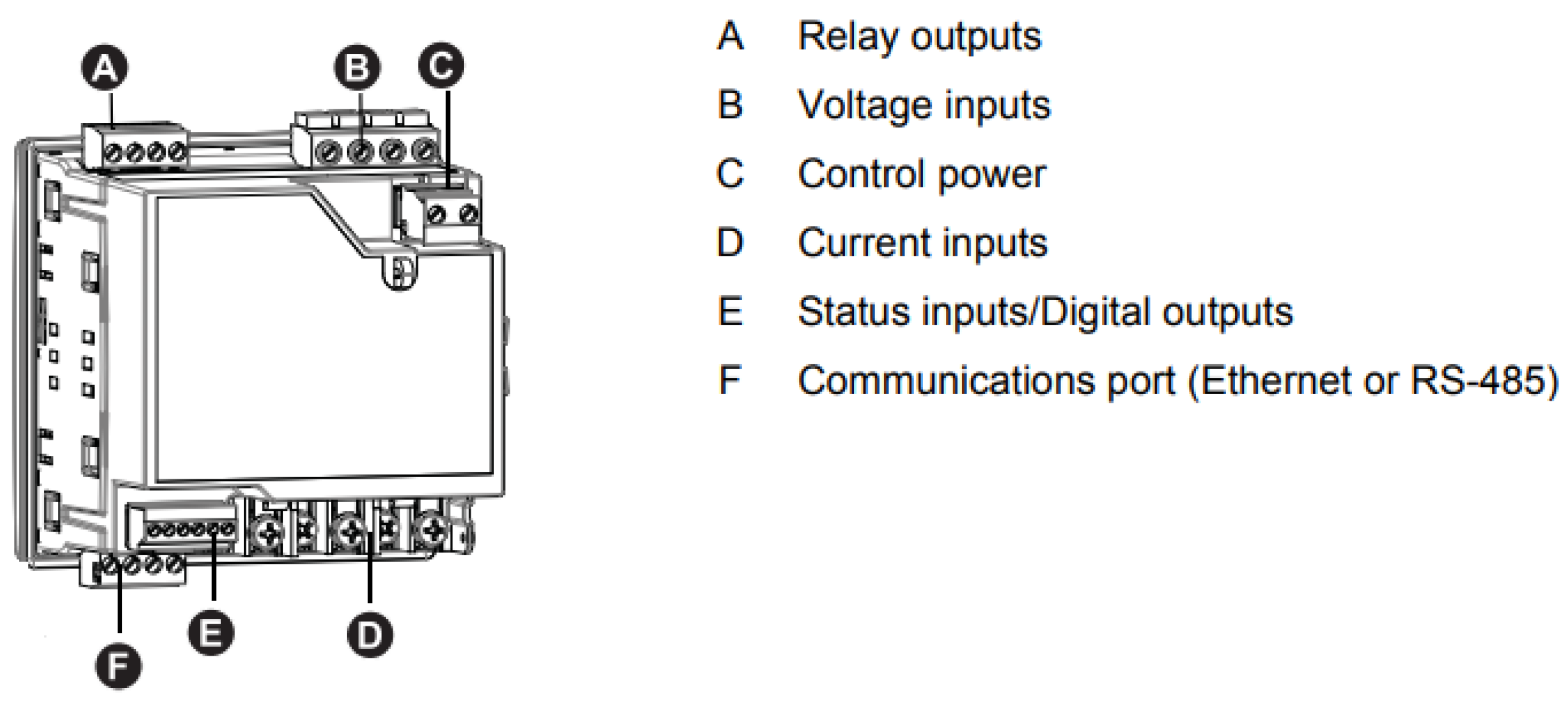
3.2.2. The Power Meter
3.2.3. The Hybrid Inverter
3.3. Laboratory Installation and Setup
3.4. Methodology to Estimate Level of Improvement Due to the Implementation of the Utility Controller
- Establishment of the problems that are created by the normal operation: uncontrolled inverter system.
- Identification of control parameters that are more effective for ensuring stability and high performance of the network.
- Design of a controller for the lab system.
- Evaluation of the effectiveness of the controller.
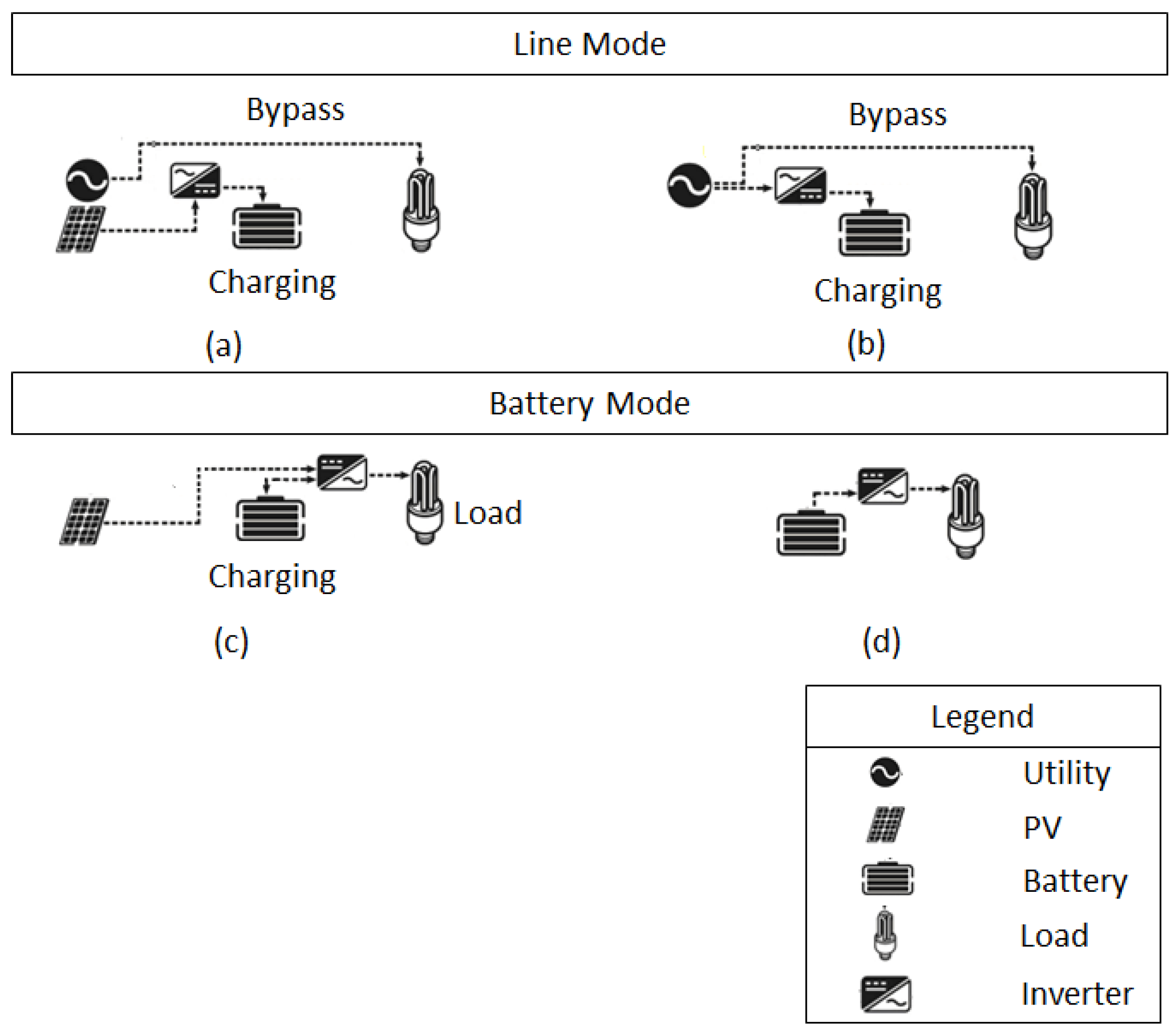
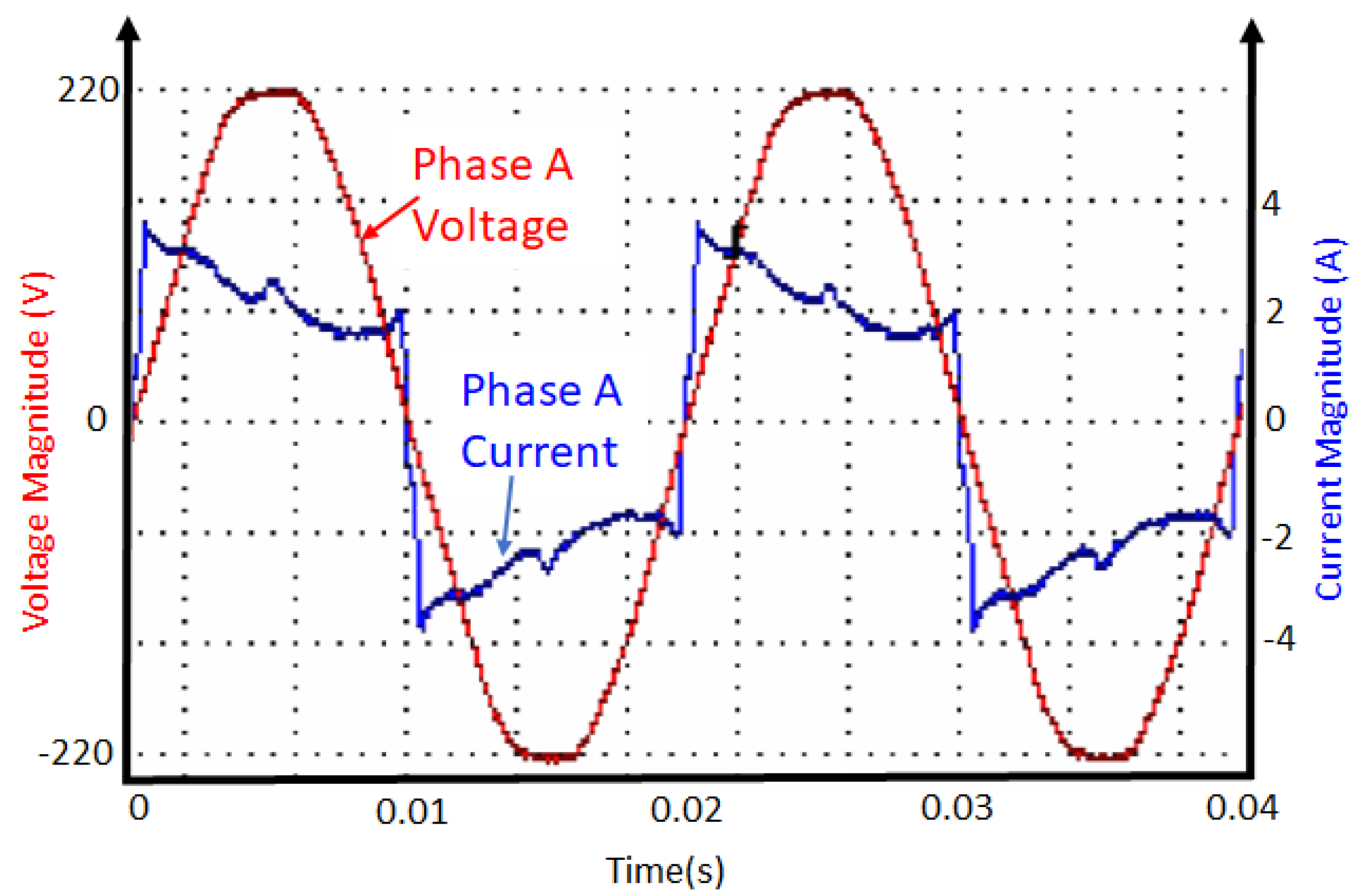
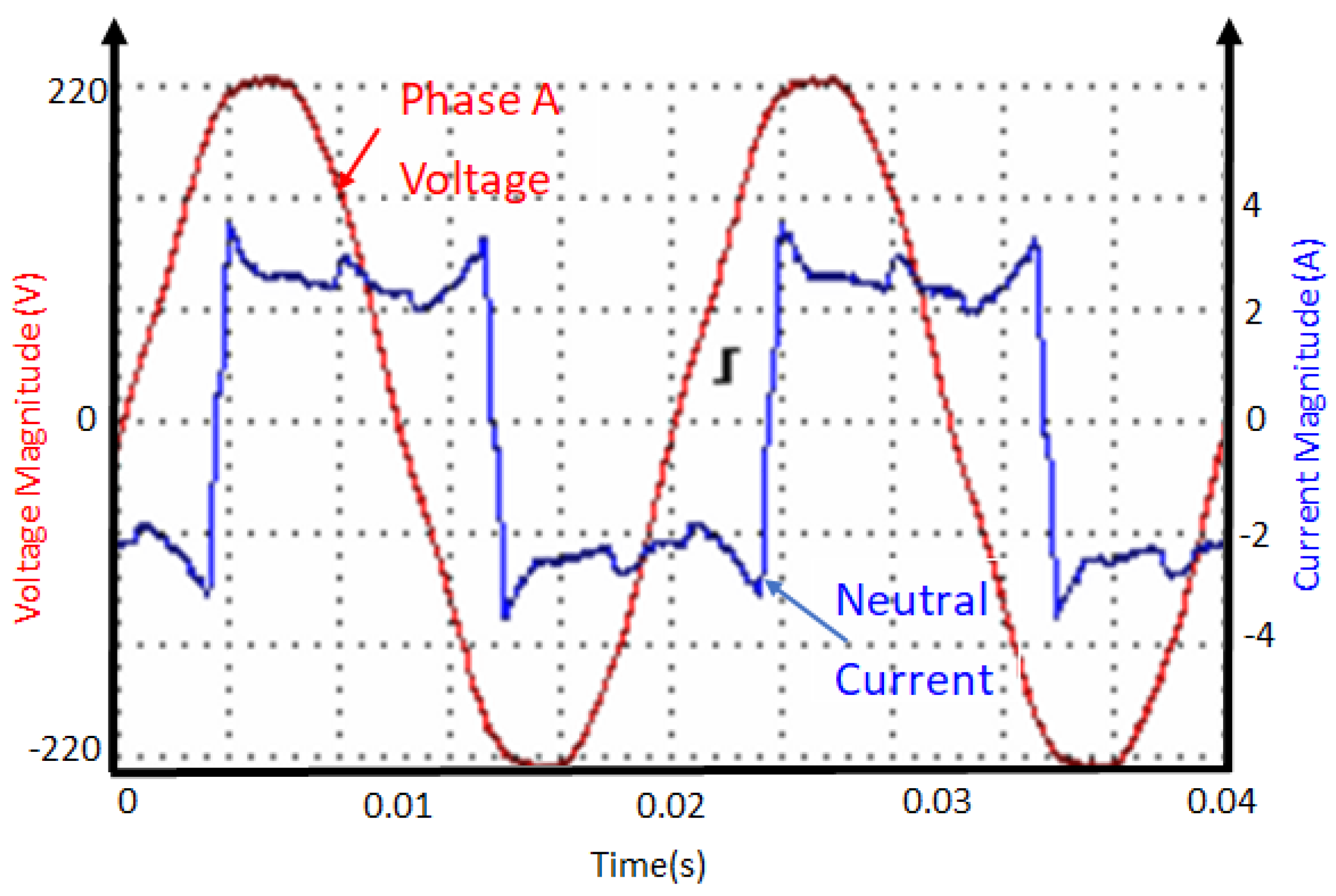
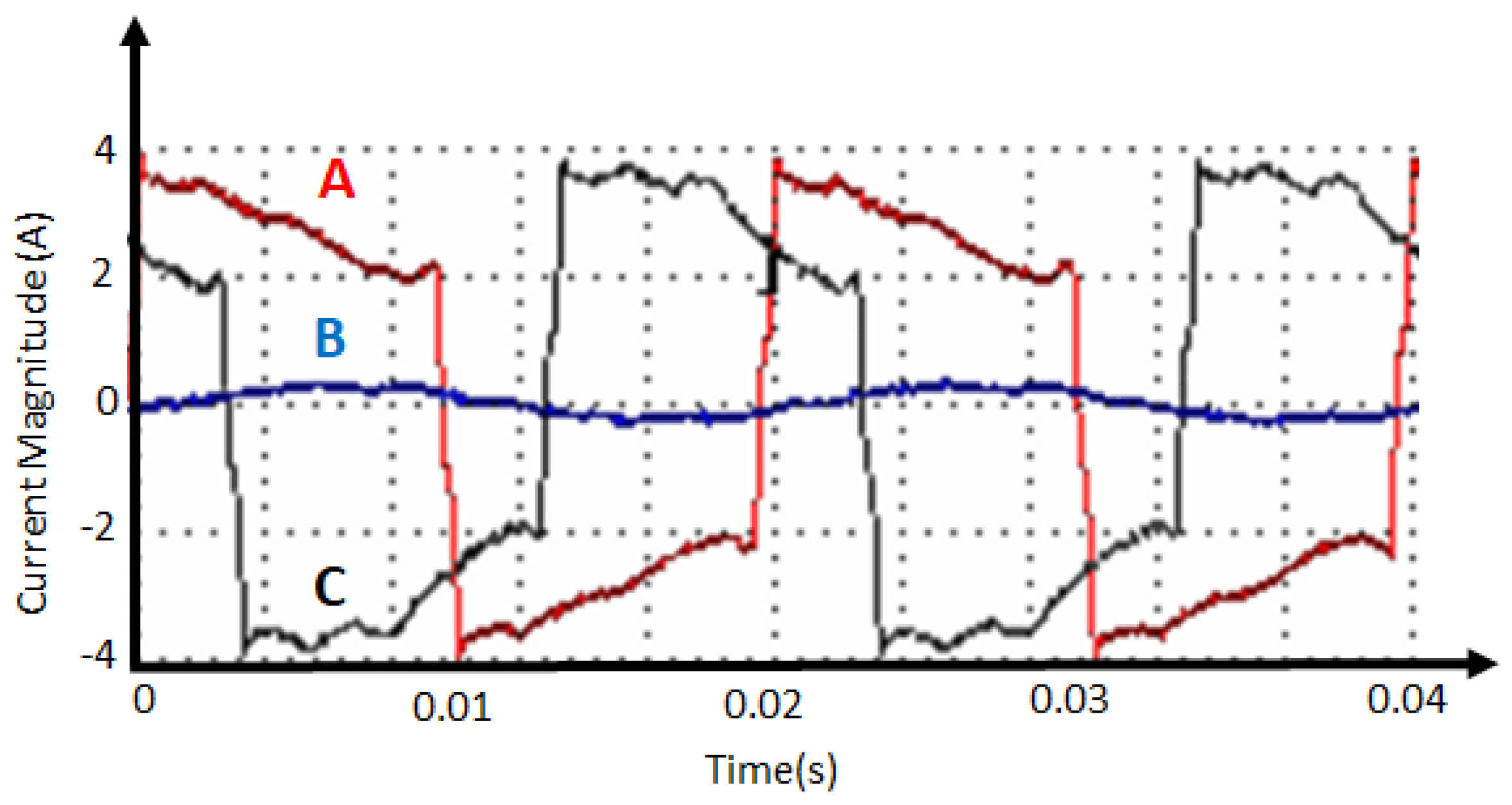
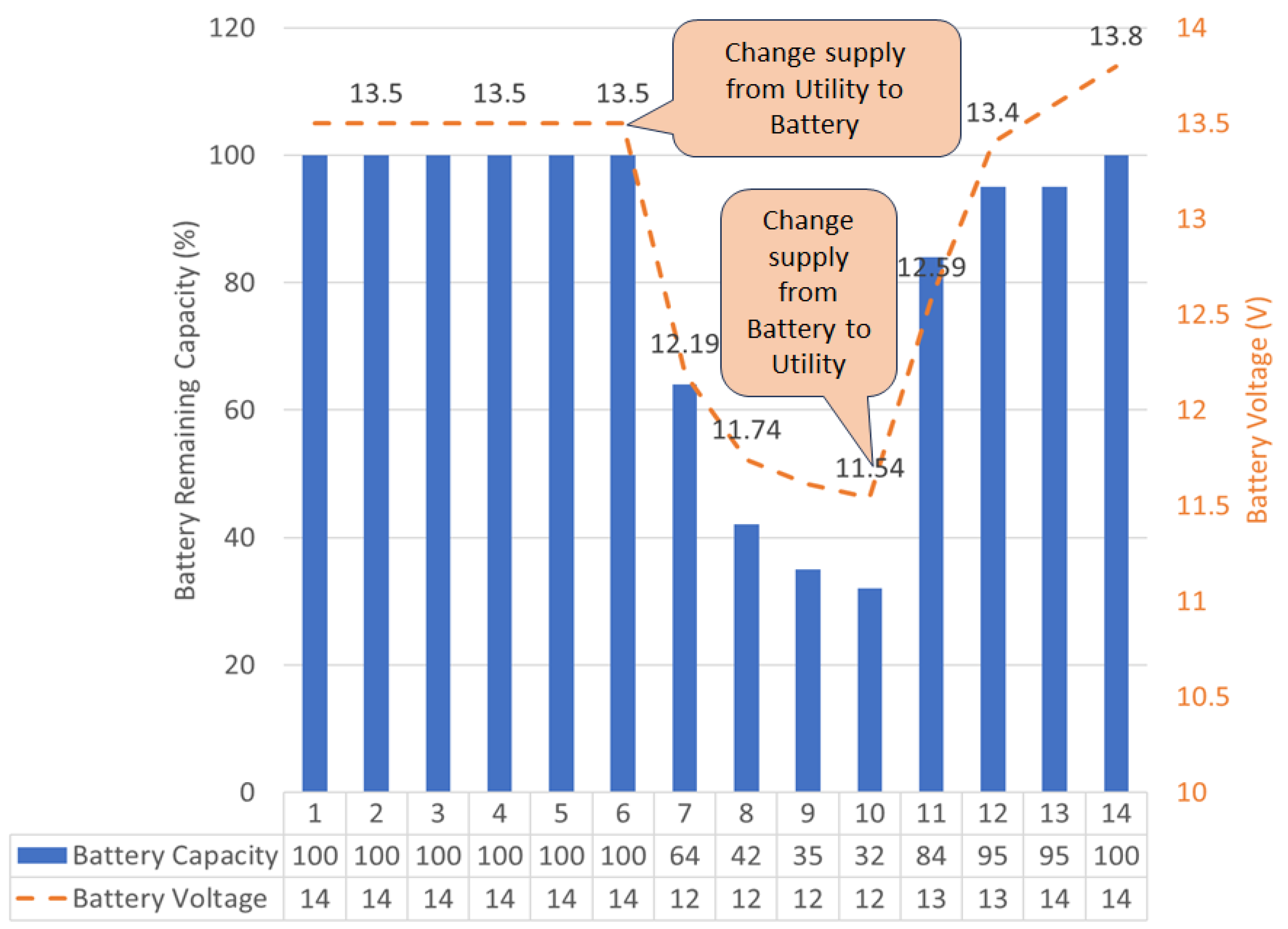
3.5. Base-Case Scenario: Uncontrolled System
- The AC output load is supplied directly from the utility.
- The AC output load is supplied directly from the PV panels. This mode is not utilized in this study.
- The AC output load is supplied directly from the battery.
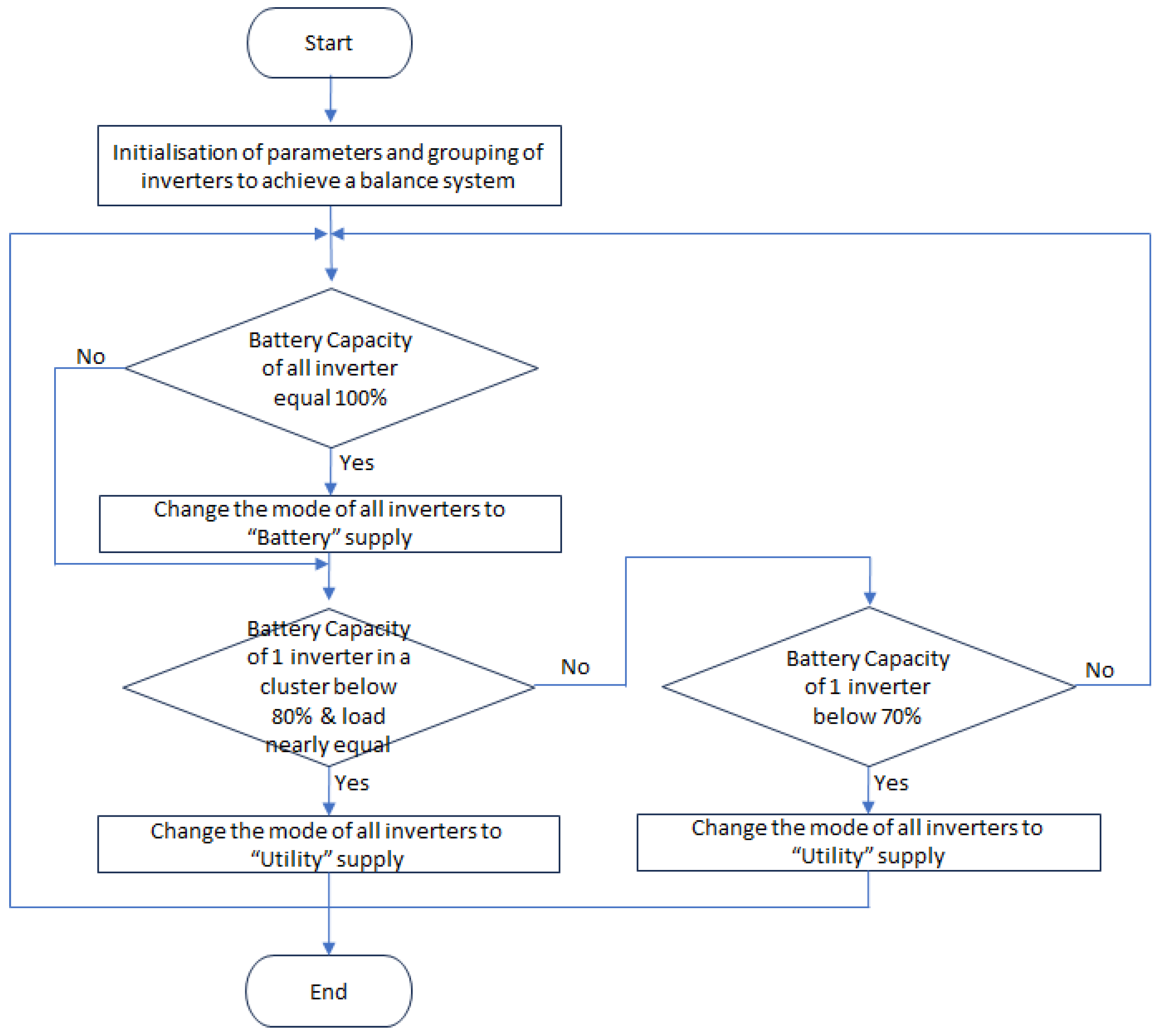
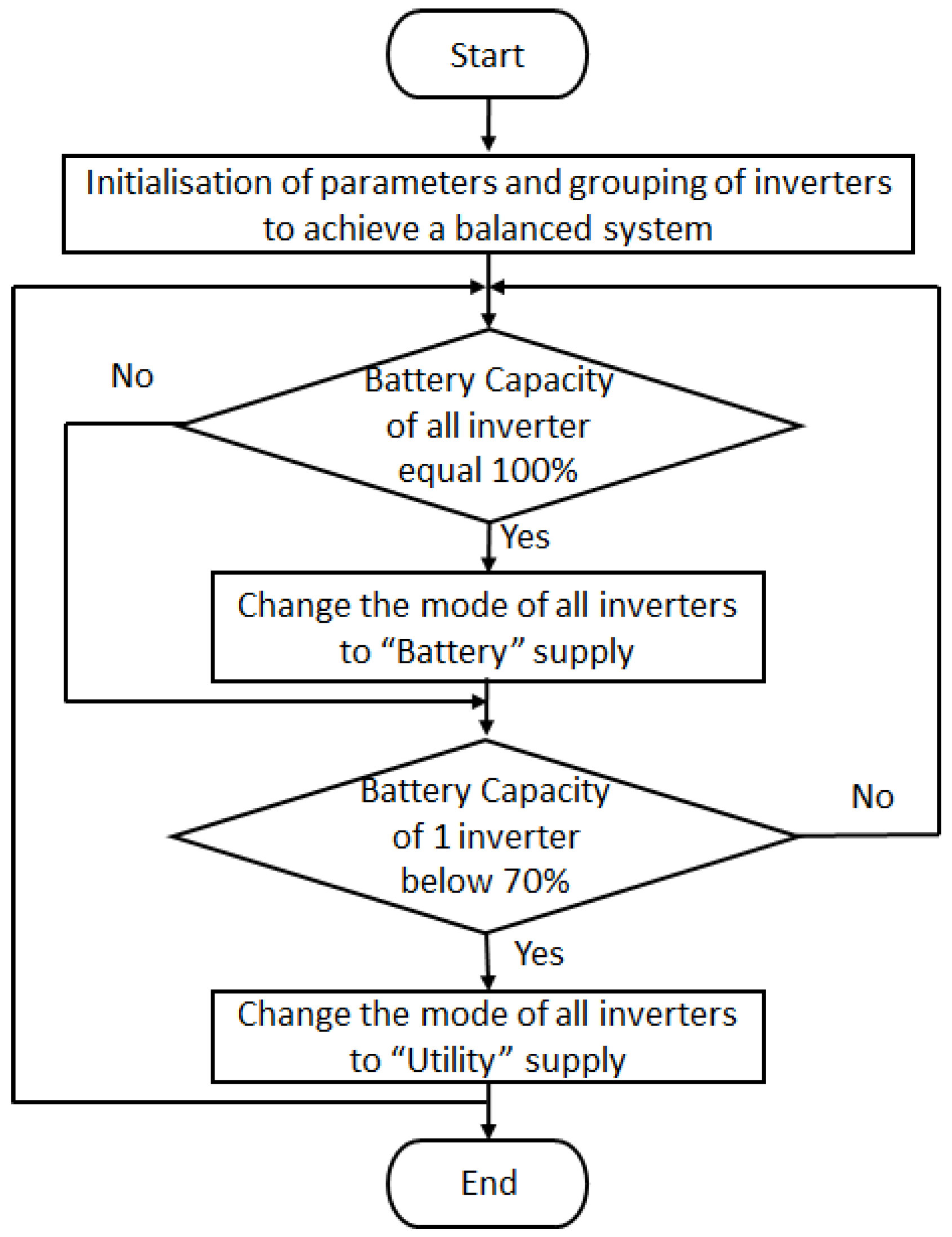
3.6. Design of the Controller
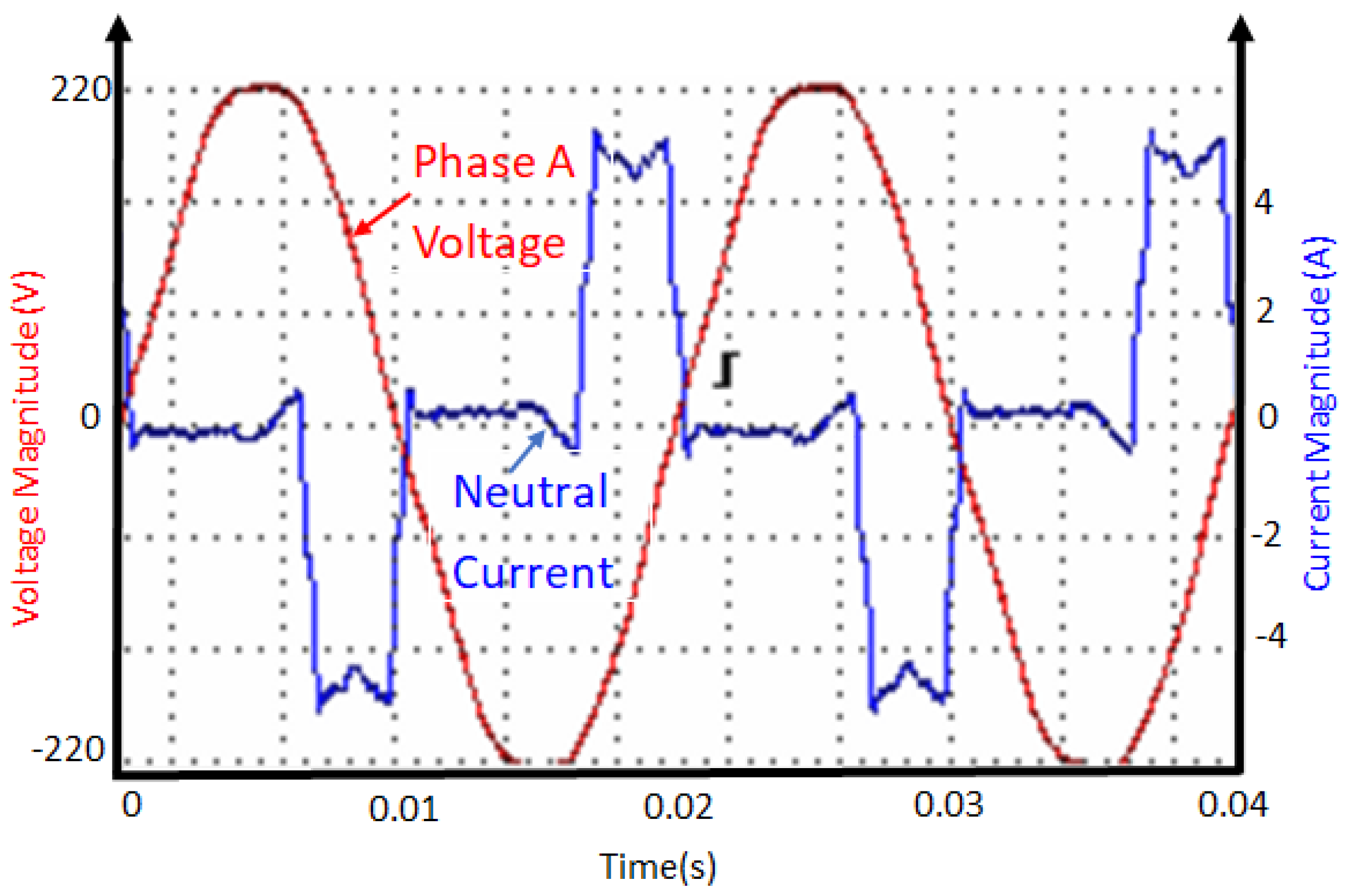
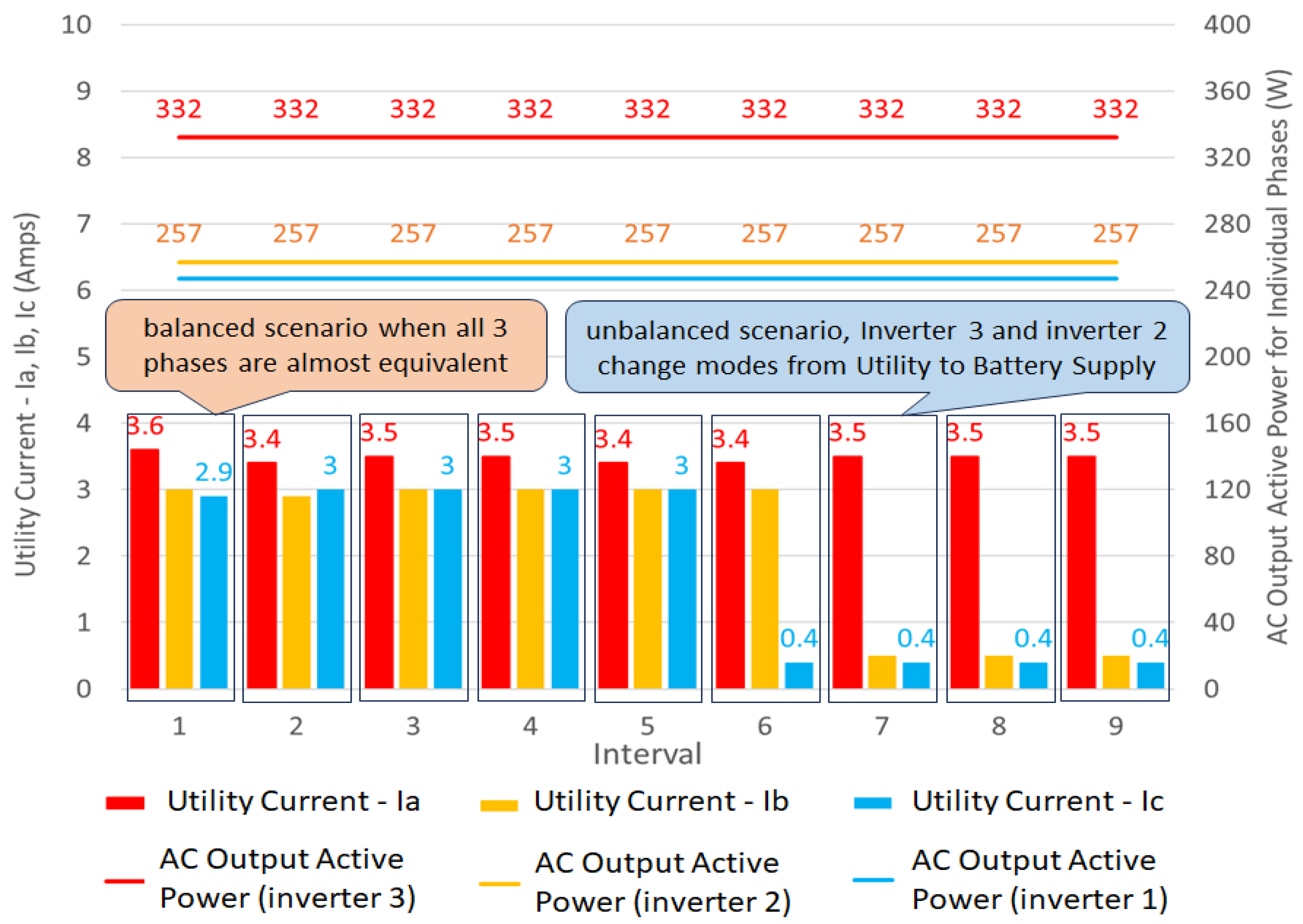
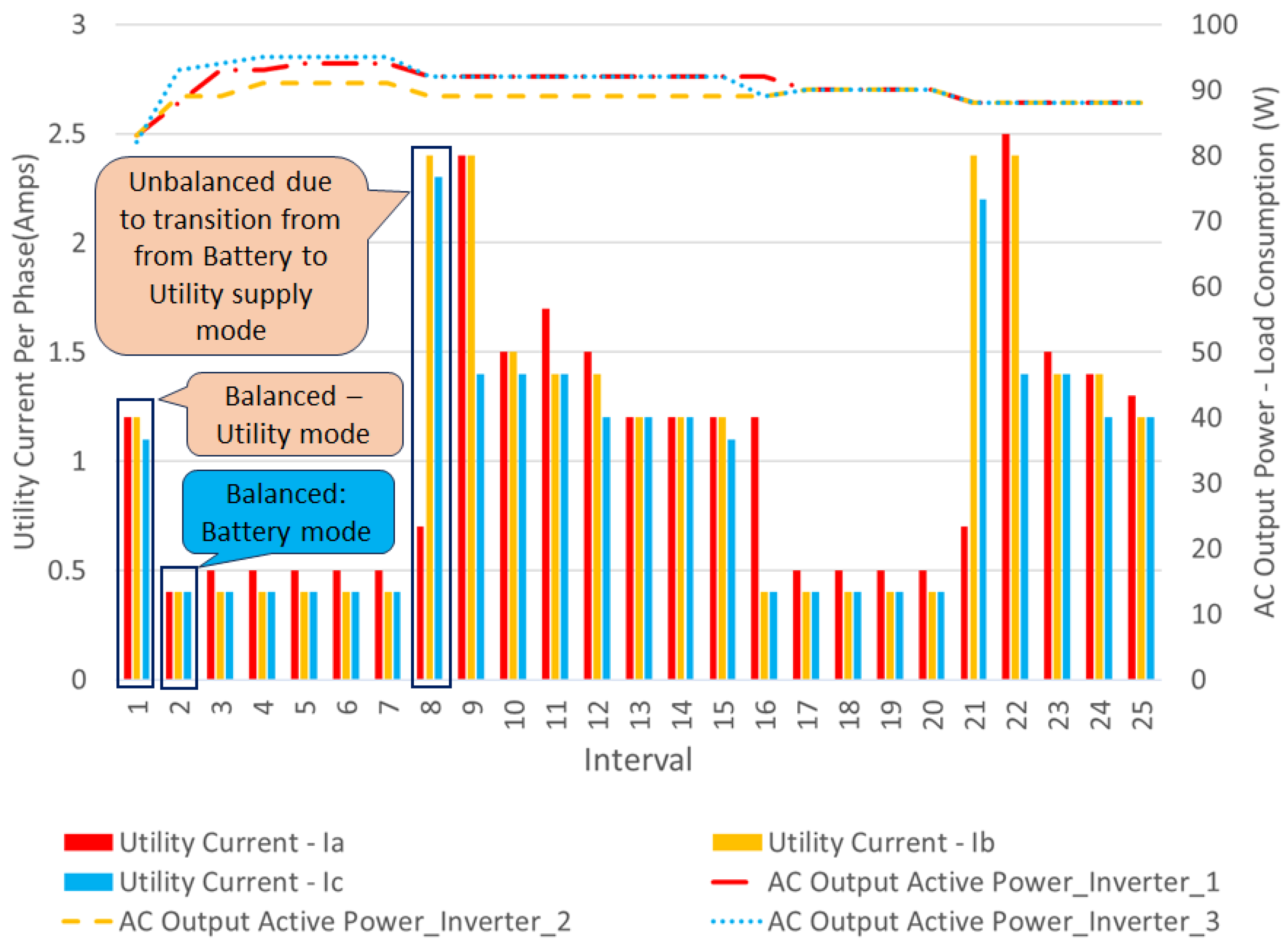
3.7. Controlled System
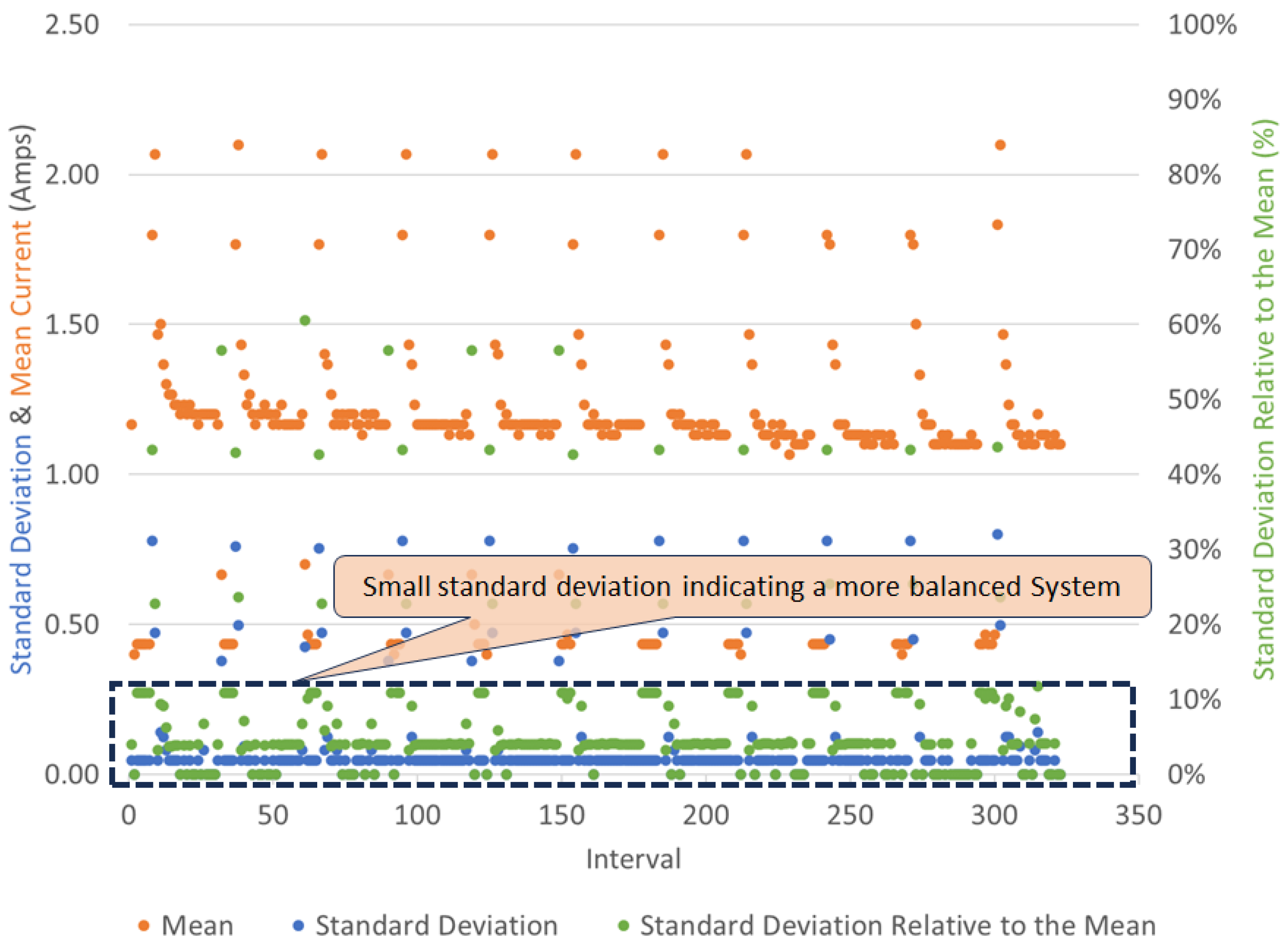
3.8. Evaluation of the Effectiveness of the Controller
3.9. Cyber Attack on Communication Networks
4. Conclusions and Recommendations
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ADMD | After diversity maximum demand |
| Ah | Amp-hour |
| BPSO | Binary particle swarm optimization |
| CAN Bus | Controller area network |
| COTS | Commercial off-the-shelf |
| CRC | Cyclic redundancy check |
| CT | Current transformer |
| DC | Direct current |
| DERs | Distributed energy resources |
| DSO | Distribution system operator |
| DSSE | Distribution system state estimation |
| HV | High voltage |
| HVAC | Heating, ventilation and air conditioning |
| ICT | Information and communication technology |
| kVA | Kilovolt-ampere |
| kW | Killowatt |
| LP-WAN | Low-power wide-area network |
| LV | Low voltage |
| LVDG | Low-voltage distribution grid |
| MV | Medium voltage |
| MVDG | Medium-voltage distribution grid |
| NMD | Notified maximum demand |
| NRS | National regulatory standards |
| PLC | Power line carrier |
| PLT | Power line telecommunication |
| PMUs | Phasor measurement units |
| PV | Photovotaic |
| RF | Radio frequency |
| RMSI | Root mean squares of currents |
| RMSV | Root mean squares of voltages |
| SCADA | Supervisory control and data acquisition |
| SSEGs | Small-scale embedded generators |
| USB | Universal serial bus |
| WLS | Weighted least-squares |
Appendix A
References
- Liu, B.; Meng, K.; Dong, Z.Y.; Wong, P.K.; Li, X. Load balancing in low-voltage distribution network via phase reconfiguration: An efficient sensitivity-based approach. IEEE Trans. Power Deliv. 2020, 36, 2174–2185. [Google Scholar]
- Grigoras, G.; Neagu, B.C.; Gavrilas, M.; Tristiu, I.; Bulac, C. Optimal phase load balancing in low voltage distribution networks using a smart meter data-based algorithm. Mathematics 2020, 8, 549. [Google Scholar]
- Grigoras, G.; Neagu, B.C.; Scarlatache, F.; Noroc, L.; Chelaru, E. Bi-level phase load balancing methodology with clustering-based consumers’ selection criterion for switching device placement in low voltage distribution networks. Mathematics 2021, 9, 542. [Google Scholar]
- Altawil, I.; Obeidat, E.; Mahafzah, K.A.; Albatianeh, Z. Salp swarm algorithm for optimal load balancing in low voltage networks. Int. J. Power Electron. Drive Syst. (IJPEDS) 2022, 13, 2506–2514. [Google Scholar]
- Yan, R.; Saha, T.K. Investigation of voltage imbalance due to distribution network unbalanced line configurations and load levels. IEEE Trans. Power Syst. 2012, 28, 1829–1838. [Google Scholar]
- Ballestín-Fuertes, J.; Sanz-Osorio, J.F.; Muñoz-Cruzado-Alba, J.; Puyal, E.L.; Leiva, J.; Rivero, J.R. Four-legs D-STATCOM for current balancing in low-voltage distribution grids. IEEE Access 2021, 10, 779–788. [Google Scholar]
- Bina, M.T.; Kashefi, A. Three-phase unbalance of distribution systems: Complementary analysis and experimental case study. Int. J. Electr. Power Energy Syst. 2011, 33, 817–826. [Google Scholar]
- Von Jouanne, A.; Banerjee, B. Assessment of voltage unbalance. IEEE Trans. Power Deliv. 2001, 16, 782–790. [Google Scholar]
- NRS Standard 048-2; Electricity Supply—Quality of Supply Part 2: Voltage Characteristics, Compatibility Levels, Limits and Assessment Methods (Edition 3). South African National Standard (NRS): Pretoria, South Africa, 2007. Available online: https://ukzn-iis-02.ukzn.ac.za/san/NRS048-2.pdf (accessed on 12 October 2023).
- Du, Y.; Chen, J.; Li, H.; Yin, J.; Shao, M.; Guo, H. Discussion on the evaluation method of current unbalance compensation effect of three-phase unbalanced load adjusting device in distribution network. In Proceedings of the 2021 China International Conference on Electricity Distribution (CICED), Shanghai, China, 6–9 April 2021; pp. 230–234. [Google Scholar]
- Dey, N.; Chakraborty, A. Neutral Current and Neutral Voltage in Three Phase Four Wire Distribution System of a Technical Institution. Int. J. Comput. Appl. 2013, 72, 1–7. [Google Scholar]
- Kotsonias, A.; Asprou, M.; Hadjidemetriou, L.; Kyriakides, E. Enhancing the State Estimation for Low Voltage Distribution Grids. In Proceedings of the 2020 IEEE PES Innovative Smart Grid Technologies Europe (ISGT-Europe), Hague, The Netherlands, 26–28 October 2020; pp. 914–918. [Google Scholar]
- Kotsonias, A.; Asprou, M.; Hadjidemetriou, L.; Kyriakides, E. State estimation for distribution grids with a single-point grounded neutral conductor. IEEE Trans. Instrum. Meas. 2020, 69, 8167–8177. [Google Scholar]
- Armendariz, M.; Chenine, M.; Nordström, L.; Al-Hammouri, A. A co-simulation platform for medium/low voltage monitoring and control applications. In Proceedings of the ISGT 2014, Kuala Lumpur, Malaysia, 20–23 May 2014; pp. 1–5. [Google Scholar]
- Krcal, V.; Topolanek, D.; Vycital, V.; Vaculik, J. Indication of abnormal operation conditions in a mesh network based on data from distributed measurement. In Proceedings of the CIRED 2021—The 26th International Conference and Exhibition on Electricity Distribution, Online, 20–23 September 2021; Volume 2021, pp. 1567–1571. [Google Scholar]
- Armendariz, M.; Babazadeh, D.; Nordström, L.; Barchiesi, M. A method to place meters in active low voltage distribution networks using BPSO algorithm. In Proceedings of the 2016 Power Systems Computation Conference (PSCC), Genoa, Italy, 20–24 June 2016; pp. 1–7. [Google Scholar]
- Kwapisz, A. Utilization of the monitoring system for MV/LV transformers in smart grid application. In Proceedings of the 2016 Electric Power Networks (EPNet), Szklarska Poreba, Poland, 19–21 September 2016; pp. 1–4. [Google Scholar]
- Chaves, T.R.; Martins, M.A.I.; Pacheco, B.A. MV/LV Overhead Transformer Monitoring and Hot Spot Temperature Estimation. In Proceedings of the 2020 Intermountain Engineering, Technology and Computing (IETC), Orem, UT, USA, 14–15 May 2022; pp. 1–5. [Google Scholar]
- Ge, W.; Luo, H.; Zhao, H.; Gao, Q.; Zhou, G.; Ma, Y.; Fu, L. Research on communication technology of power monitoring system based on medium voltage power line carrier and low power wide area network. In Proceedings of the 2017 IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 26–28 November 2017; pp. 1–4. [Google Scholar]
- Baimel, D.; Tapuchi, S.; Baimel, N. Smart grid communication technologies-overview, research challenges and opportunities. In Proceedings of the 2016 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Capri, Italy, 22–24 June 2016; pp. 116–120. [Google Scholar]
- Lasagani, K.; Iqbal, T.; Mann, G.K. Data Logging and Control of a Remote Inverter Using LoRa and Power Line Communication. Energy Power Eng. 2018, 10, 351–365. [Google Scholar]
- Lin, Y.; Barooah, P.; Meyn, S.; Middelkoop, T. Experimental evaluation of frequency regulation from commercial building HVAC systems. IEEE Trans. Smart Grid 2015, 6, 776–783. [Google Scholar]
- de Araujo Passos, L.A.; van den Engel, P.; Baldi, S.; De Schutter, B. Dynamic optimization for minimal HVAC demand with latent heat storage, heat recovery, natural ventilation, and solar shadings. Energy Convers. Manag. 2023, 276, 116573. [Google Scholar]
- Standard 10142-1; The Wiring of Premises—Part 1: Low-Voltage Installations. SANS: Pretoria, South Africa, 2017.
- Proedrou, E. A comprehensive review of residential electricity load profile models. IEEE Access 2021, 9, 12114–12133. [Google Scholar]
- Claeys, R.; Cleenwerck, R.; Knockaert, J.; Desmet, J. Stochastic generation of residential load profiles with realistic variability based on wavelet-decomposed smart meter data. Appl. Energy 2023, 350, 121750. [Google Scholar]
- Stephen, B.; Mutanen, A.J.; Galloway, S.; Burt, G.; Järventausta, P. Enhanced load profiling for residential network customers. IEEE Trans. Power Deliv. 2013, 29, 88–96. [Google Scholar]
- Bizzozero, F.; Gruosso, G.; Vezzini, N. A time-of-use-based residential electricity demand model for smart grid applications. In Proceedings of the 2016 IEEE 16th International Conference on Environment and Electrical Engineering (EEEIC), Florence, Italy, 7–10 June 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Sajjad, I.A.; Chicco, G.; Napoli, R. Effect of aggregation level and sampling time on load variation profile—A statistical analysis. In Proceedings of the MELECON 2014—2014 17th IEEE Mediterranean Electrotechnical Conference, Beirut, Lebanon, 13–16 April 2014; pp. 208–212. [Google Scholar]
- Elombo, A.I.; Morstyn, T.; Apostolopoulou, D.; McCulloch, M.D. Residential load variability and diversity at different sampling time and aggregation scales. In Proceedings of the 2017 IEEE AFRICON, Cape Town, South Africa, 18–20 September 2017; pp. 1331–1336. [Google Scholar]
- Zarzycki, K.; Chaber, P.; Cabaj, K.; Ławryńczuk, M.; Marusak, P.; Nebeluk, R.; Plamowski, S.; Wojtulewicz, A. Forgery Cyber-Attack Supported by LSTM Neural Network: An Experimental Case Study. Sensors 2023, 23, 6778. [Google Scholar]
- Kravchik, M.; Shabtai, A. Detecting cyber attacks in industrial control systems using convolutional neural networks. In Proceedings of the 2018 Workshop on Cyber-Physical Systems Security and Privacy, Toronto, ON, Canada, 19 October 2018; pp. 72–83. [Google Scholar]
- Alladi, T.; Chamola, V.; Zeadally, S. Industrial control systems: Cyberattack trends and countermeasures. Comput. Commun. 2020, 155, 1–8. [Google Scholar]













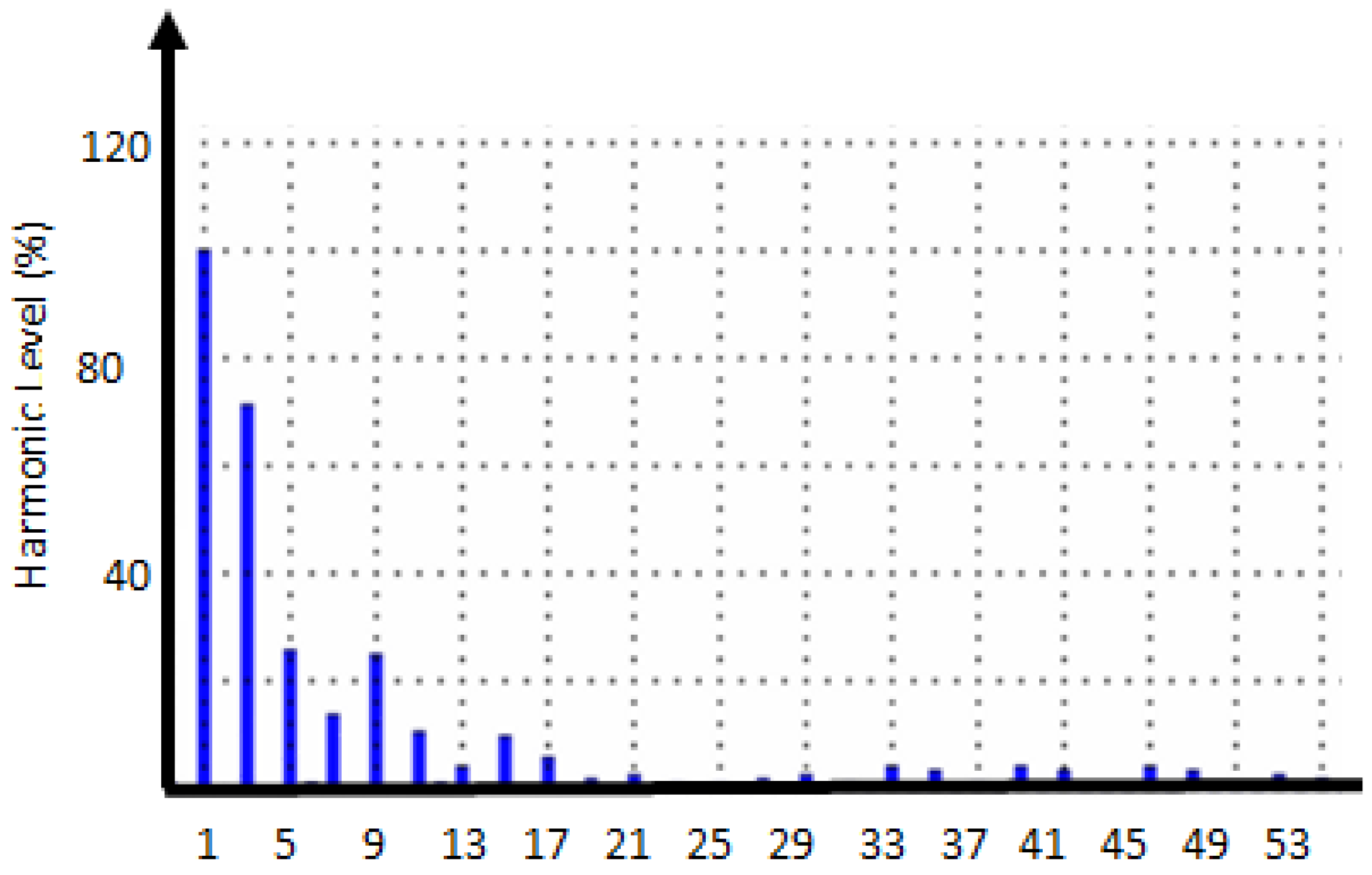

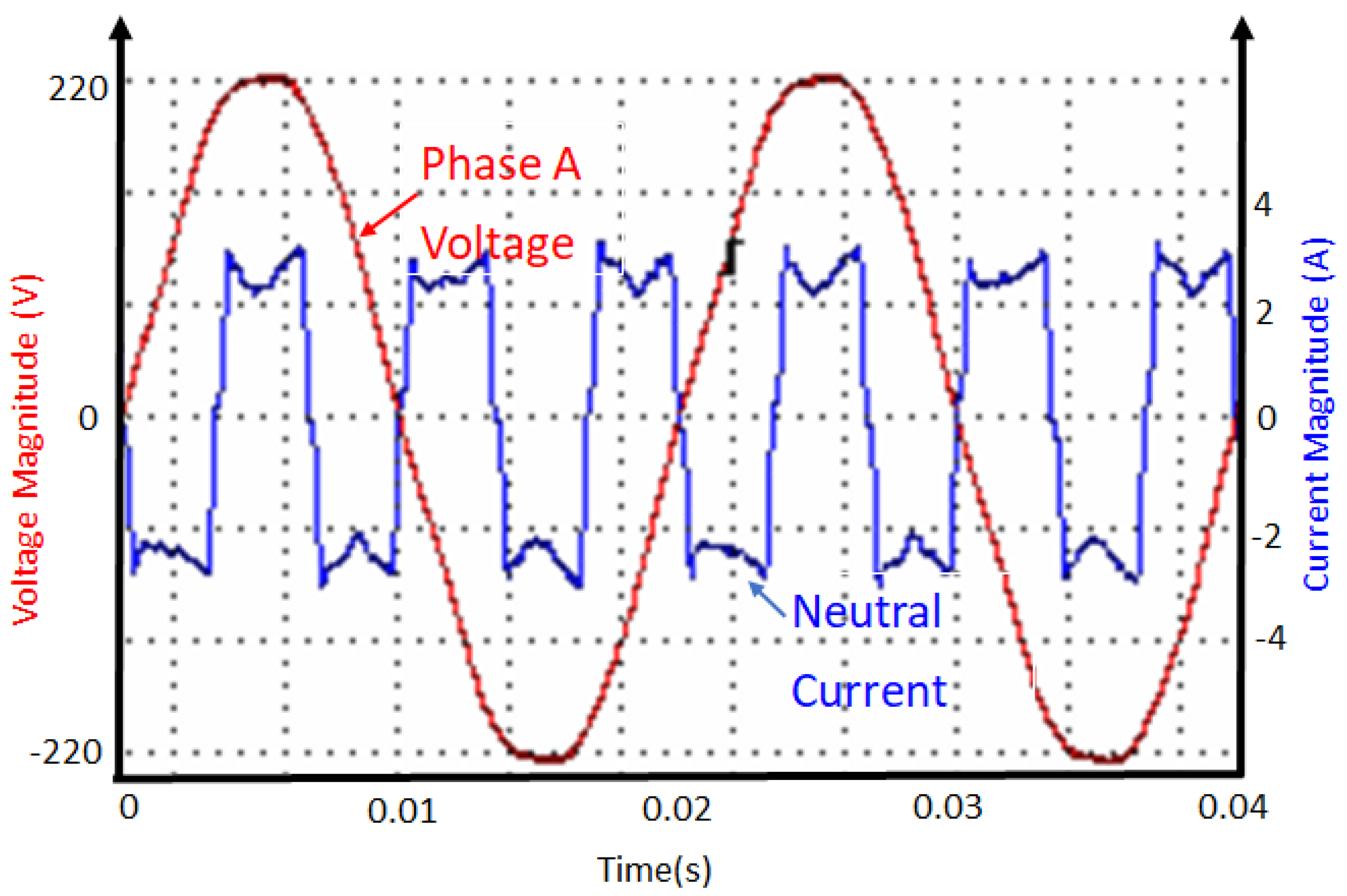
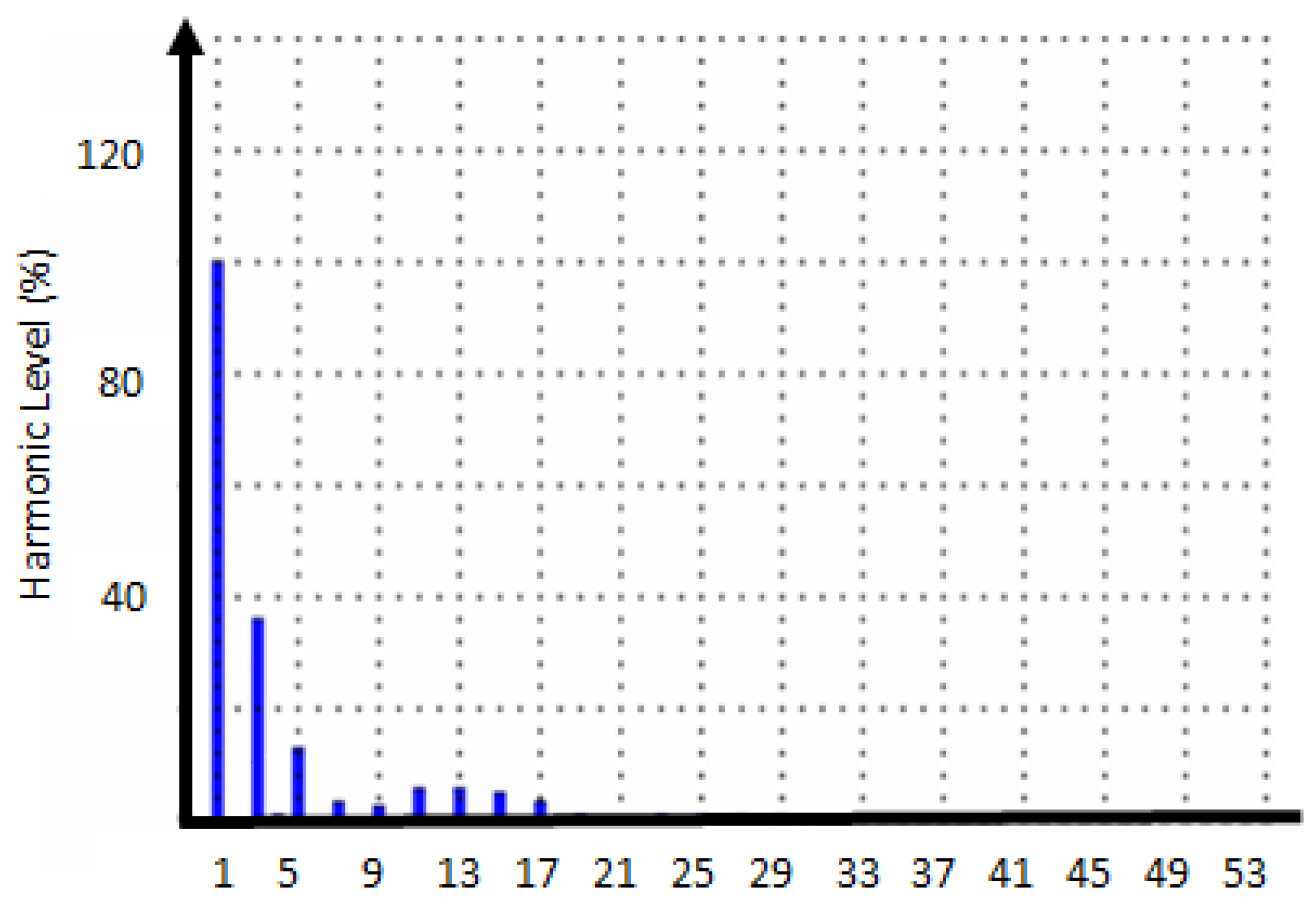
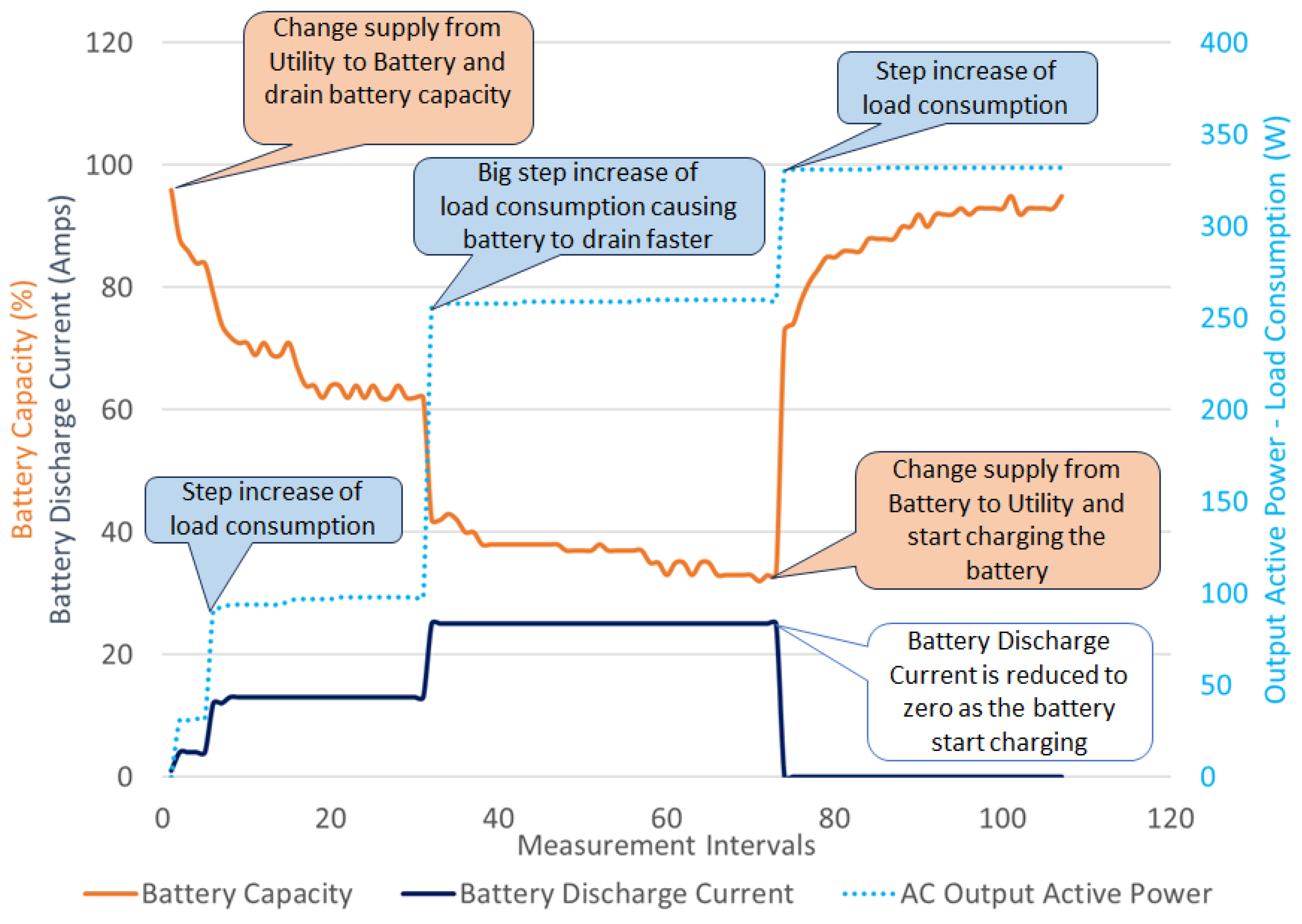


| Number of Phases | Service Circuit Breaker Size (A) | NMD (kVA) | Generation Limit (kVA) |
|---|---|---|---|
| 1 | 20 | 4.6 | 1.2 |
| 1 | 60 | 13.8 | 3.4 |
| 1 | 80 | 18.4 | 4.6 |
| 3 | 60 | 41.6 | 10.4 |
| 3 | 80 | 55.4 | 13.8 |
| Inverter Internal Parameter | Unit Measure |
|---|---|
| Grid Voltage | V |
| Grid Frequency | Hz |
| AC Output Voltage | V |
| AC Output Frequency | Hz |
| AC Output Apparent Power | VAr |
| AC Output Active Power | kW |
| Output Load Percentage | % |
| Bus Voltage | V |
| Battery Voltage | V |
| Battery Charging Current | A |
| Battery Capacity | % |
| Inverter Heat Sink Temperature | Deg C |
| PV Input Current | A |
| PV Input Voltage | V |
| Battery Discharge Current | A |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mtolo, D.; Dorrell, D.; Pillay Carpanen, R. Balancing of Low-Voltage Supply Network with a Smart Utility Controller Leveraging Distributed Customer Energy Sources. Energies 2023, 16, 7707. https://doi.org/10.3390/en16237707
Mtolo D, Dorrell D, Pillay Carpanen R. Balancing of Low-Voltage Supply Network with a Smart Utility Controller Leveraging Distributed Customer Energy Sources. Energies. 2023; 16(23):7707. https://doi.org/10.3390/en16237707
Chicago/Turabian StyleMtolo, Dumisani, David Dorrell, and Rudiren Pillay Carpanen. 2023. "Balancing of Low-Voltage Supply Network with a Smart Utility Controller Leveraging Distributed Customer Energy Sources" Energies 16, no. 23: 7707. https://doi.org/10.3390/en16237707
APA StyleMtolo, D., Dorrell, D., & Pillay Carpanen, R. (2023). Balancing of Low-Voltage Supply Network with a Smart Utility Controller Leveraging Distributed Customer Energy Sources. Energies, 16(23), 7707. https://doi.org/10.3390/en16237707







