Scalable Inverse Uncertainty Quantification by Hierarchical Bayesian Modeling and Variational Inference
Abstract
:1. Introduction
2. Materials and Methods
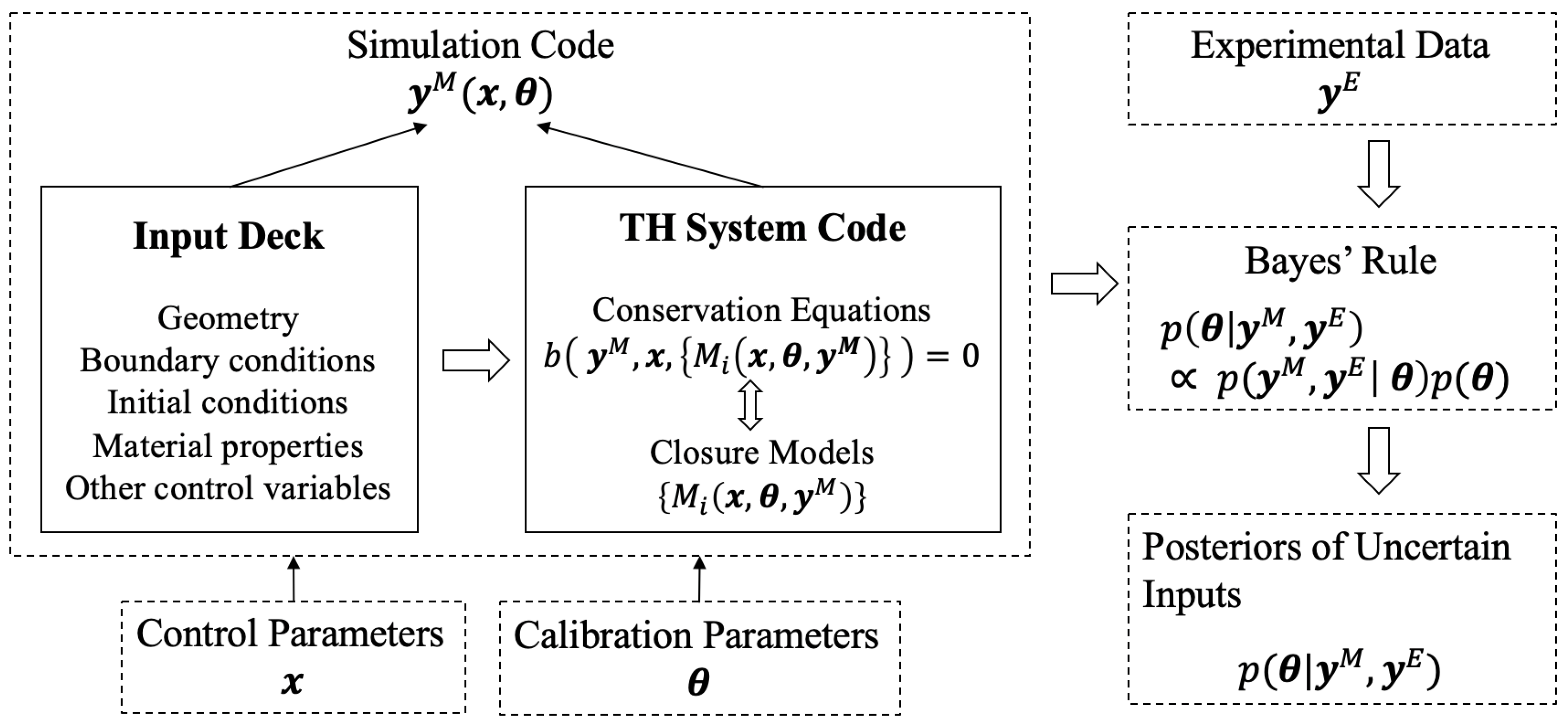
2.1. Bayesian IUQ Framework Overview
- Problem Definition. Identify the problem being studied and choose relevant experimental data and simulation codes. In this work, we utilize the BFBT (BWR Full-size Fine-mesh Bundle Test) benchmark data [36] and build the corresponding models using TRACE. Details of the experimental data and the simulation codes will be introduced in the following session.
- Sensitivity Analysis. In this step, we aim to identify the key and influential input parameters. For the chosen TH codes, these input parameters are typically multipliers for the coefficients in closure equations, such as single-phase/two-phase heat transfer coefficients, interfacial drag coefficients, etc. This identification can be accomplished through two successive SA steps. Initially, a relatively straightforward perturbation method is applied to all parameters to identify those that are active in the model. Following this, a more precise SA method, known as Sobol indices, is employed to determine the influential parameters within a constrained variable space. In the field of nuclear TH, a variety of SA techniques have been effectively employed. These include Subset Simulation, Line Sampling [44], Sobol indices [45,46], Pearson correlation coefficient, elementary effects method [47], adjoint method [48] etc.
- Surrogate Model. Surrogate models are approximations of the input/output relation of the original computer model. They are developed using a limited set of full model simulations (known as the training set) combined with a learning algorithm. Typical MCMC sampling algorithms takes at least thousands of samples, thus if the simulation codes are computationally expensive, it would be impossible to to conduct the computation efficiently. In this scenario, we can use a surrogate model, also referred to as emulators or metamodels, to replace the computationally prohibitive simulation code. Many learning algorithms are available and have been successfully applied to TH applications, such as, Polynomial Regression (PR) [43], Gaussian Process (GP) [41,49], Artificial Neural Networks [50,51,52], etc.
- Hierarchical Bayesian Model. Once the problem is clearly defined and the uncertain inputs are identified, a hierarchical Bayesian model is formulated accordingly. The hierarchical structure should be defined based on the group effects in the experimental data. This step also involves establishing the likelihood function and formulating the posterior distributions.
- Posterior Exploration. In this step, inference algorithms such as MCMC and VI are employed compute the approximate posterior distributions of the parameters.
- Posterior Predictive Check (PPC). PPC is the process of comparing the observed experimental data to the posterior predictions of the model. The core concept is that if the posterior parameter distributions are good approximations of the “true” underlying distributions, then the predicted data from the model should actually “look like” real observed data. If the patterns in the predicted data do not mirror the patterns in the observed data, then we are motivated to invent models that can produce the QoIs [53]. PPC provides a great way to confirm the the obtained posteriors.
- Forward UQ (FUQ). In applications where we are interested in the uncertainty ranges of QoIs, the derived posterior distributions are propagated through the simulation model. This FUQ process is expected to produce more accurate model prediction uncertainties by using the PMP uncertainties quantified from IUQ.
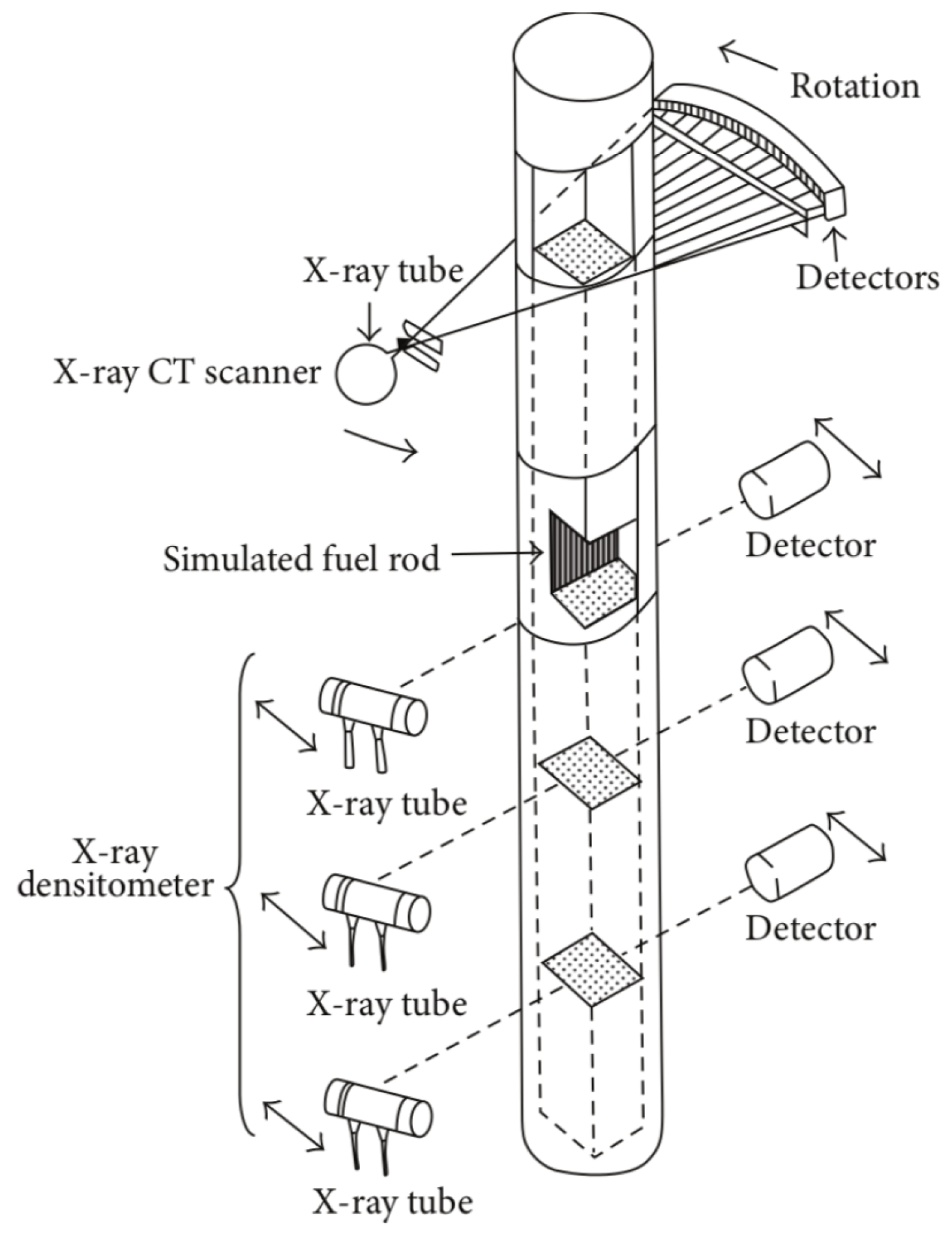
2.2. TRACE PMPs and BFBT Benchmark Data
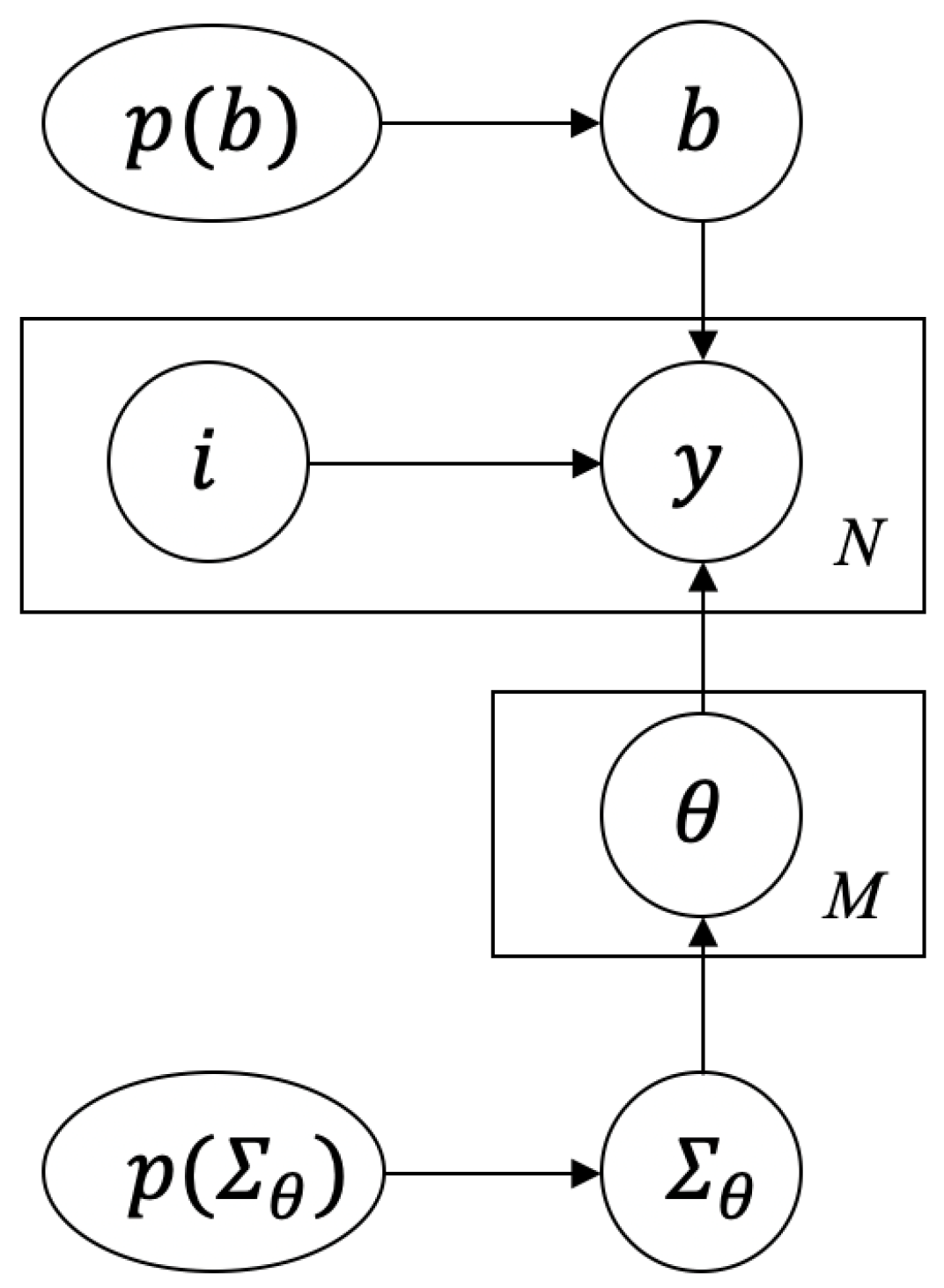
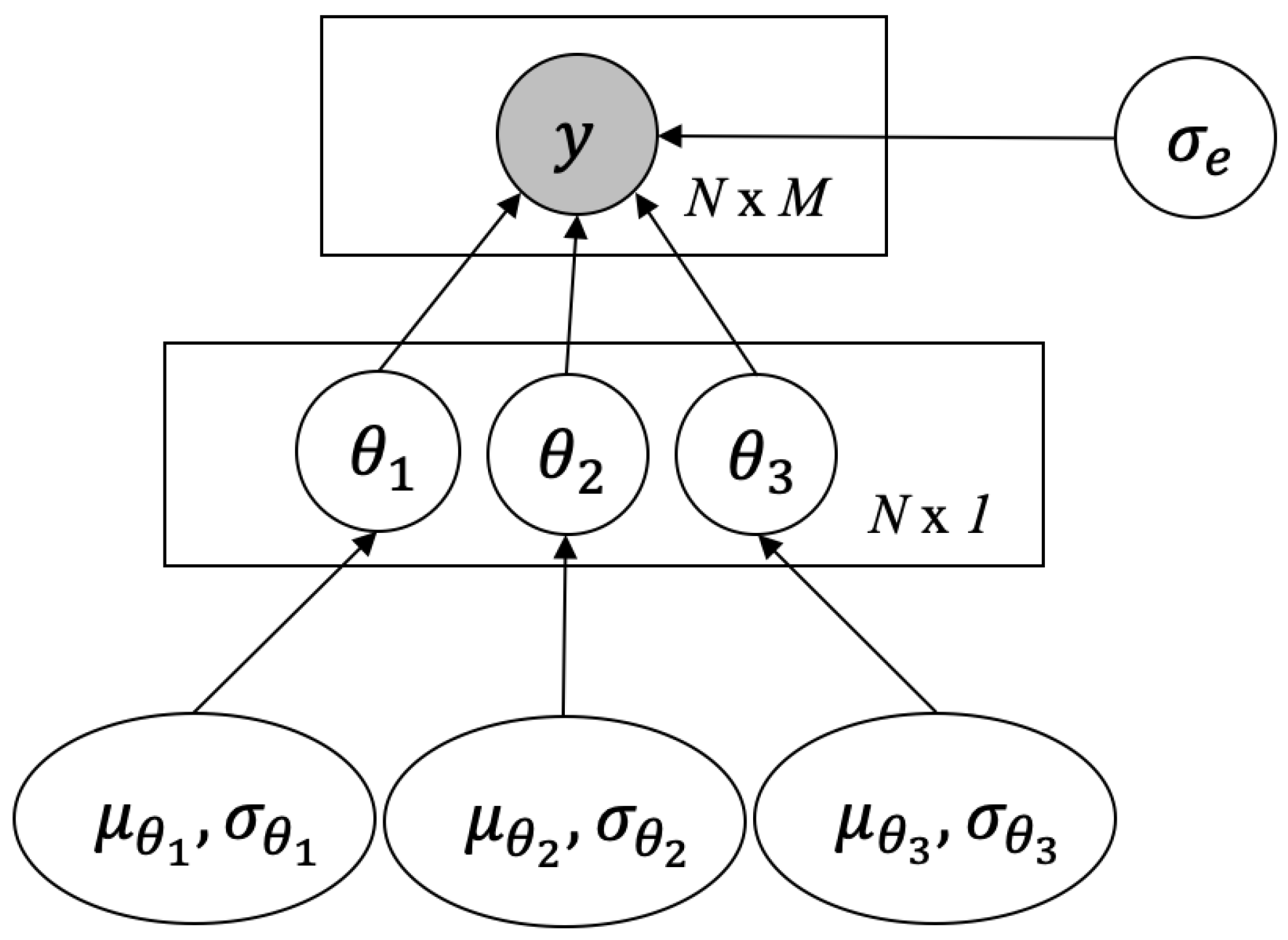
2.3. Hierarchical Bayesian Model
- Draw global variables and .
- Draw group-specific variables according to
- Draw observed data point .
2.4. Markov Chain Monte Carlo
2.5. Variational Inference
3. Results
3.1. Synthetic Data Example
3.1.1. Problem Definition
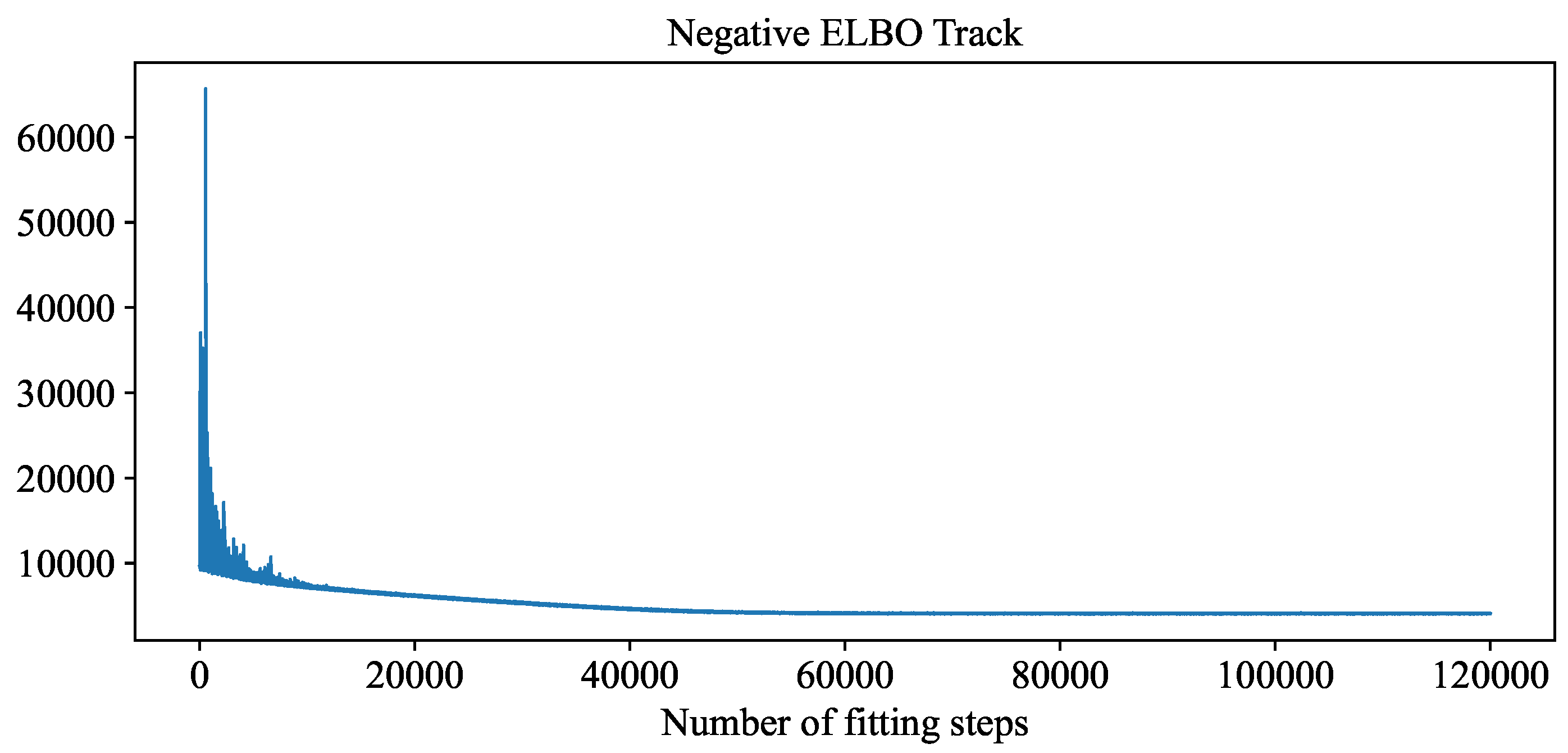
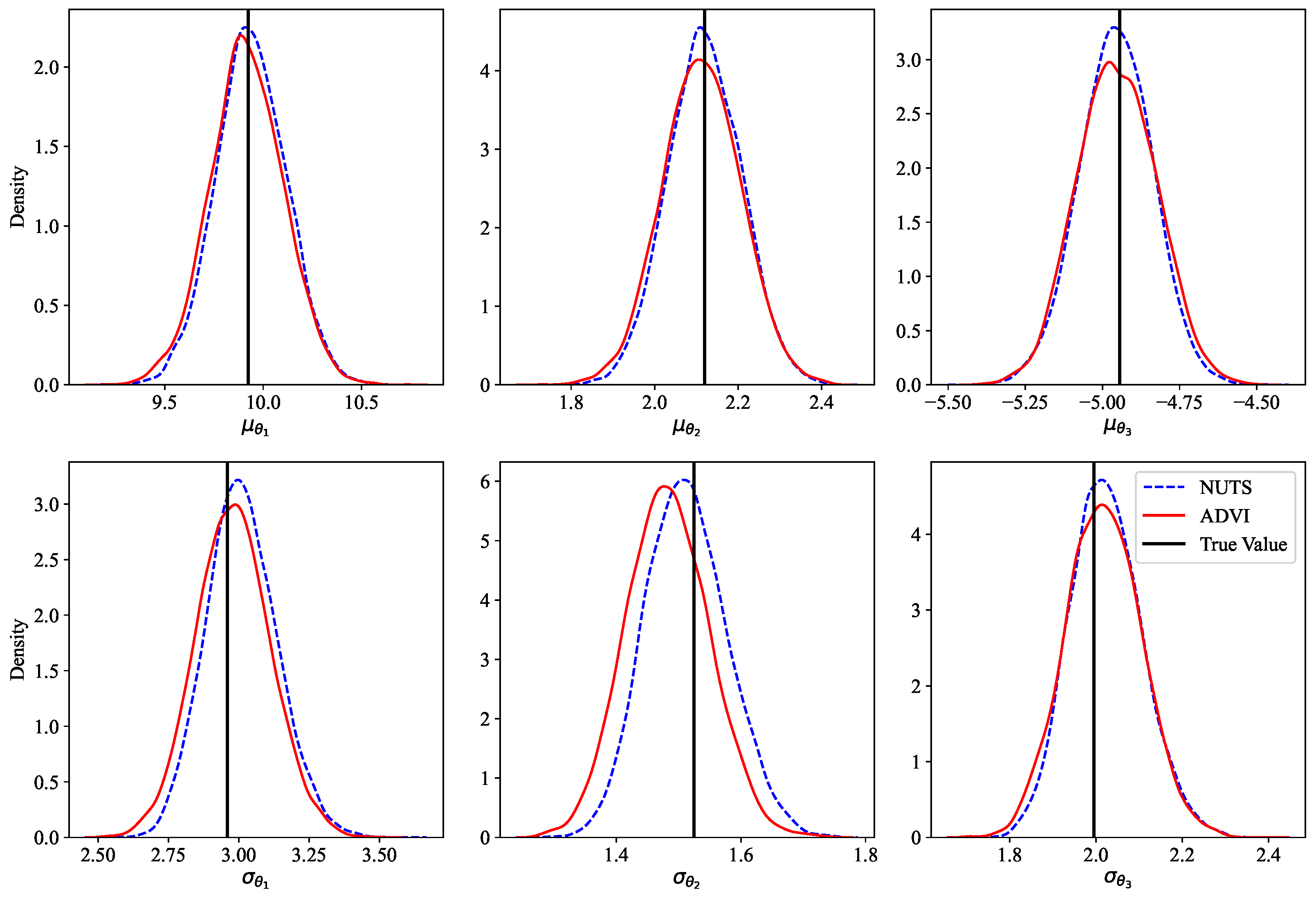
3.1.2. Results and Discussions
- Draw samples of global variables, (), from their prior distributions. We use wide uniform distributions as priors to reflect our ignorance of knowledge.
- For and , draw samples of group-specific parameters .
3.2. Nuclear Thermal-Hydraulics Application
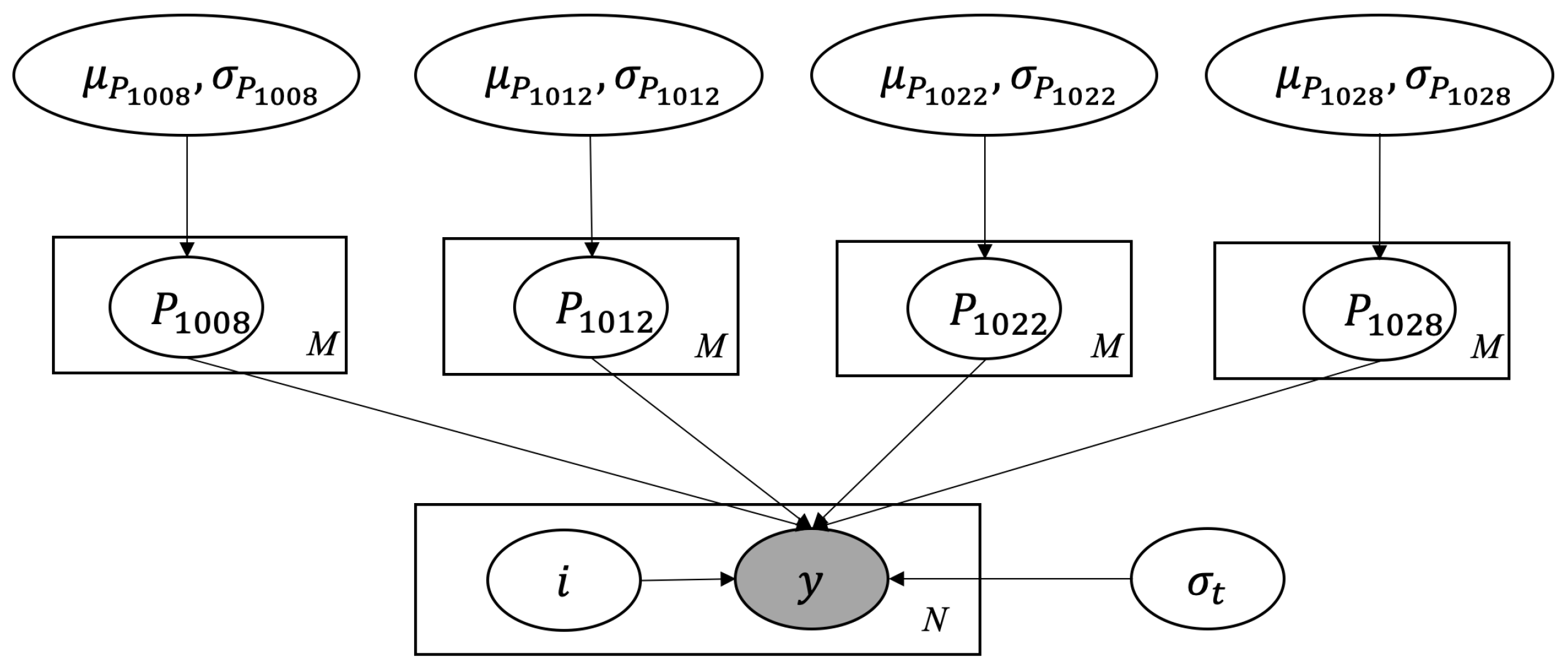
3.2.1. Problem Definition
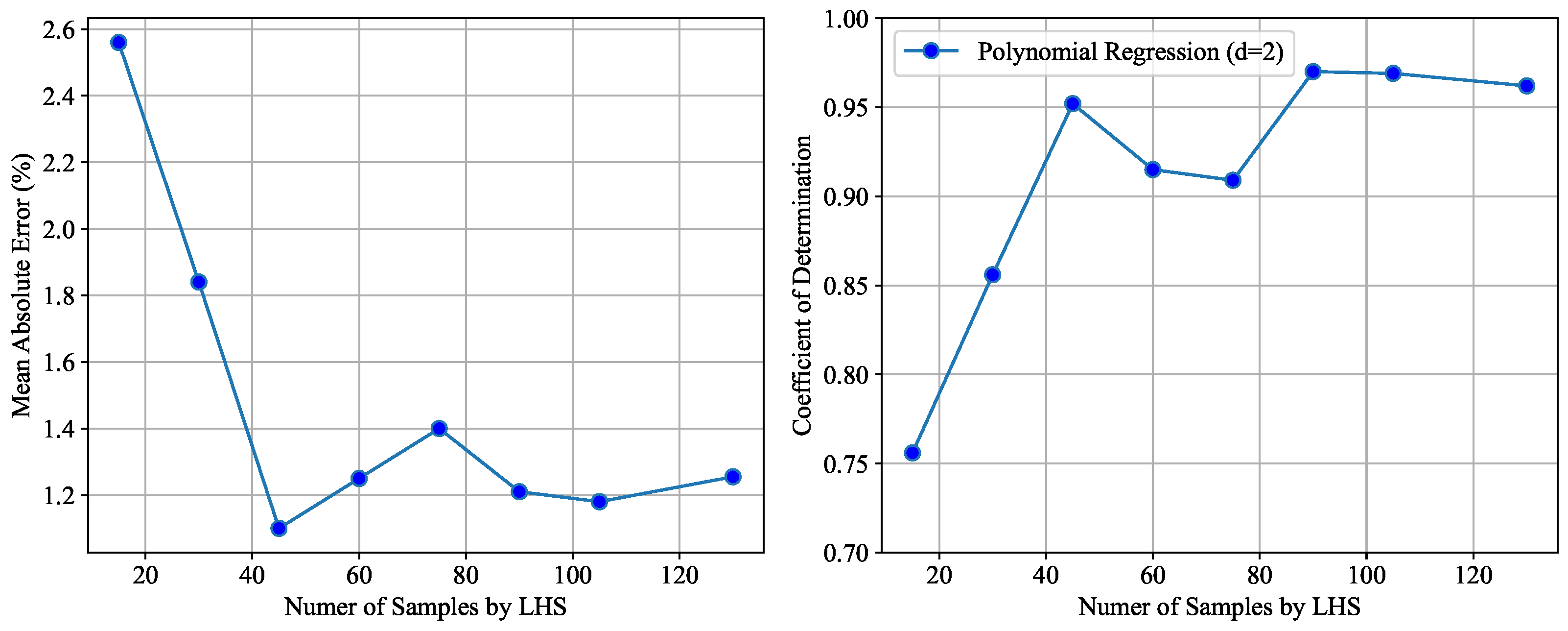
3.2.2. Sensitivity Analysis and Surrogate Model
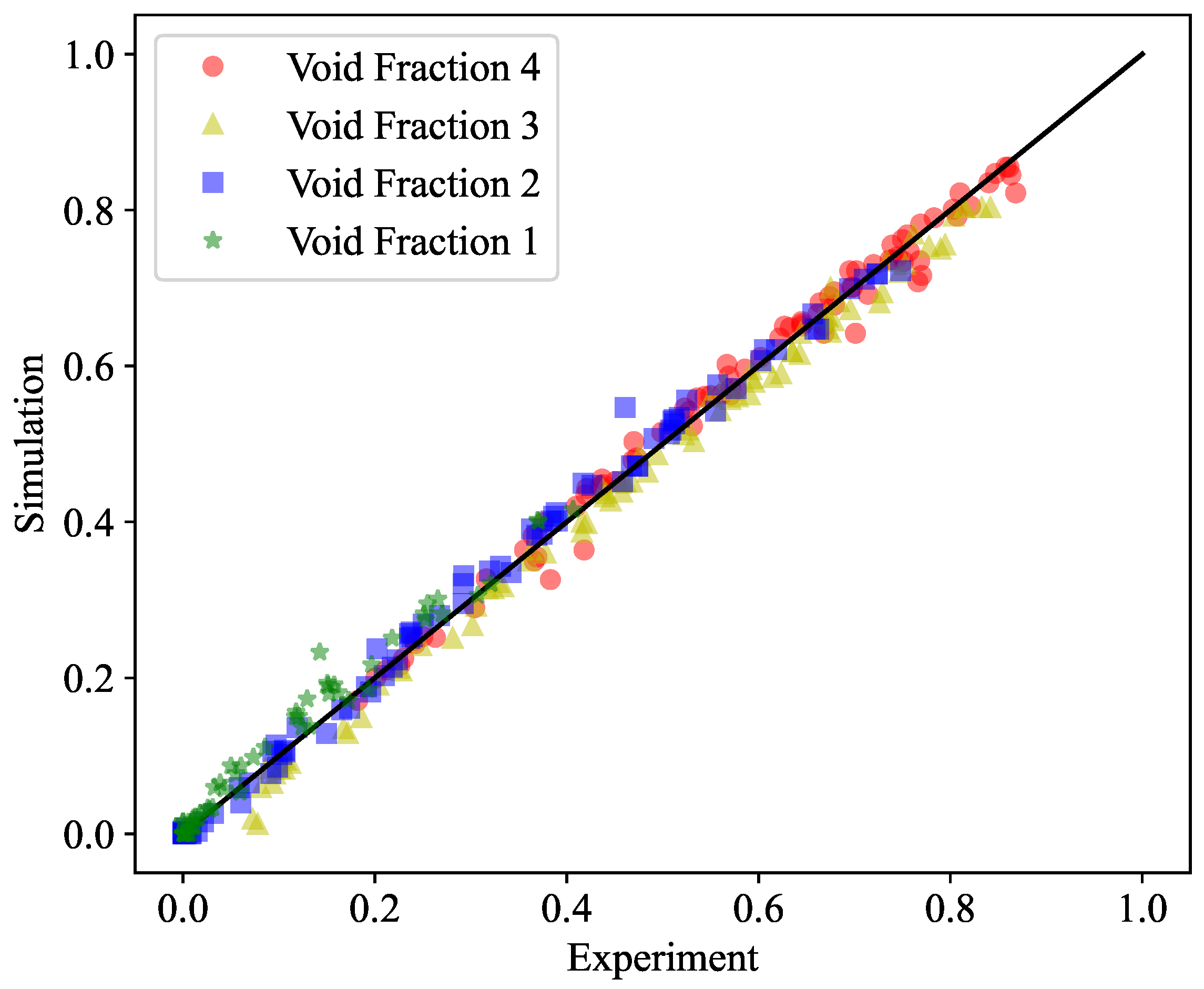
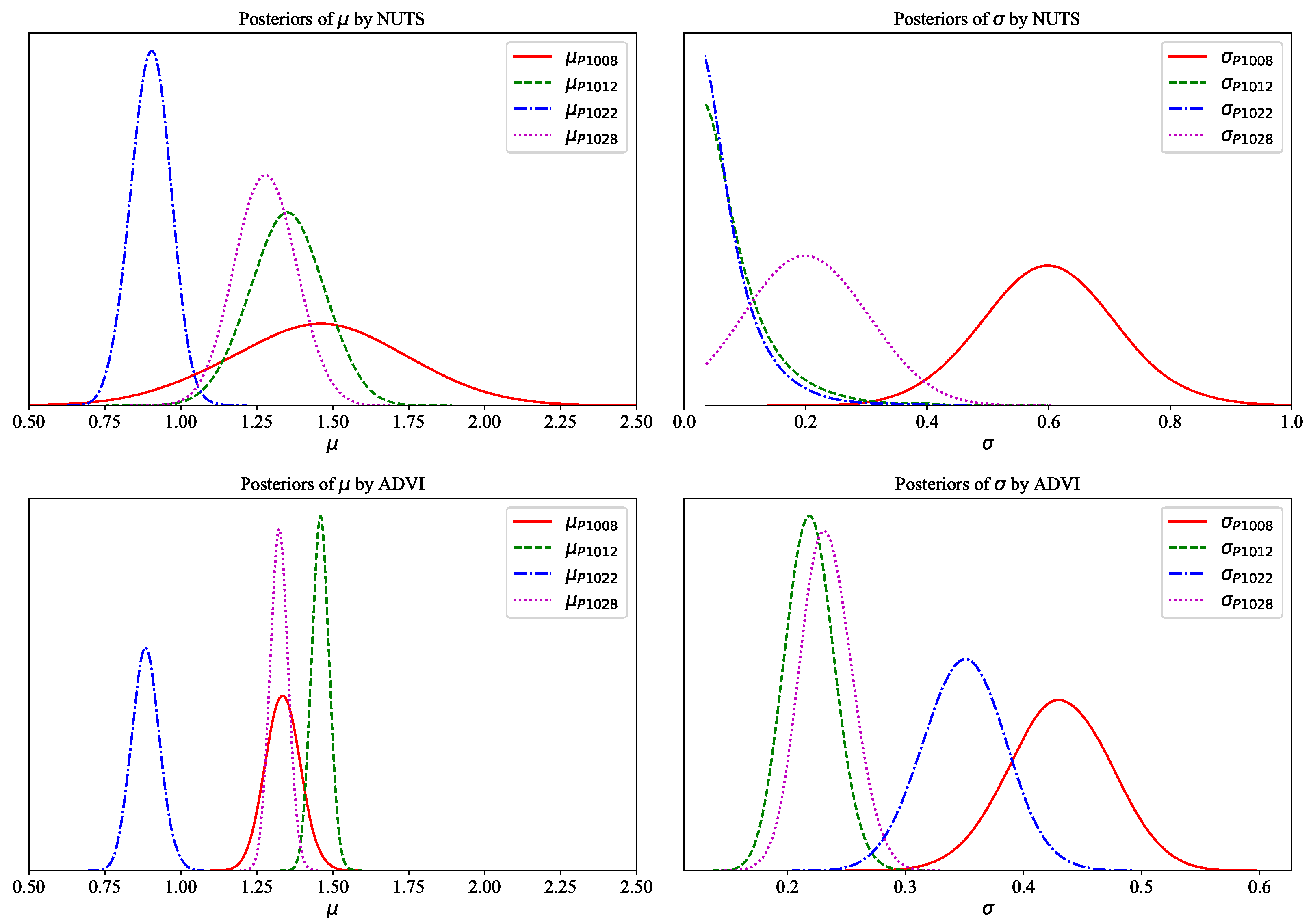
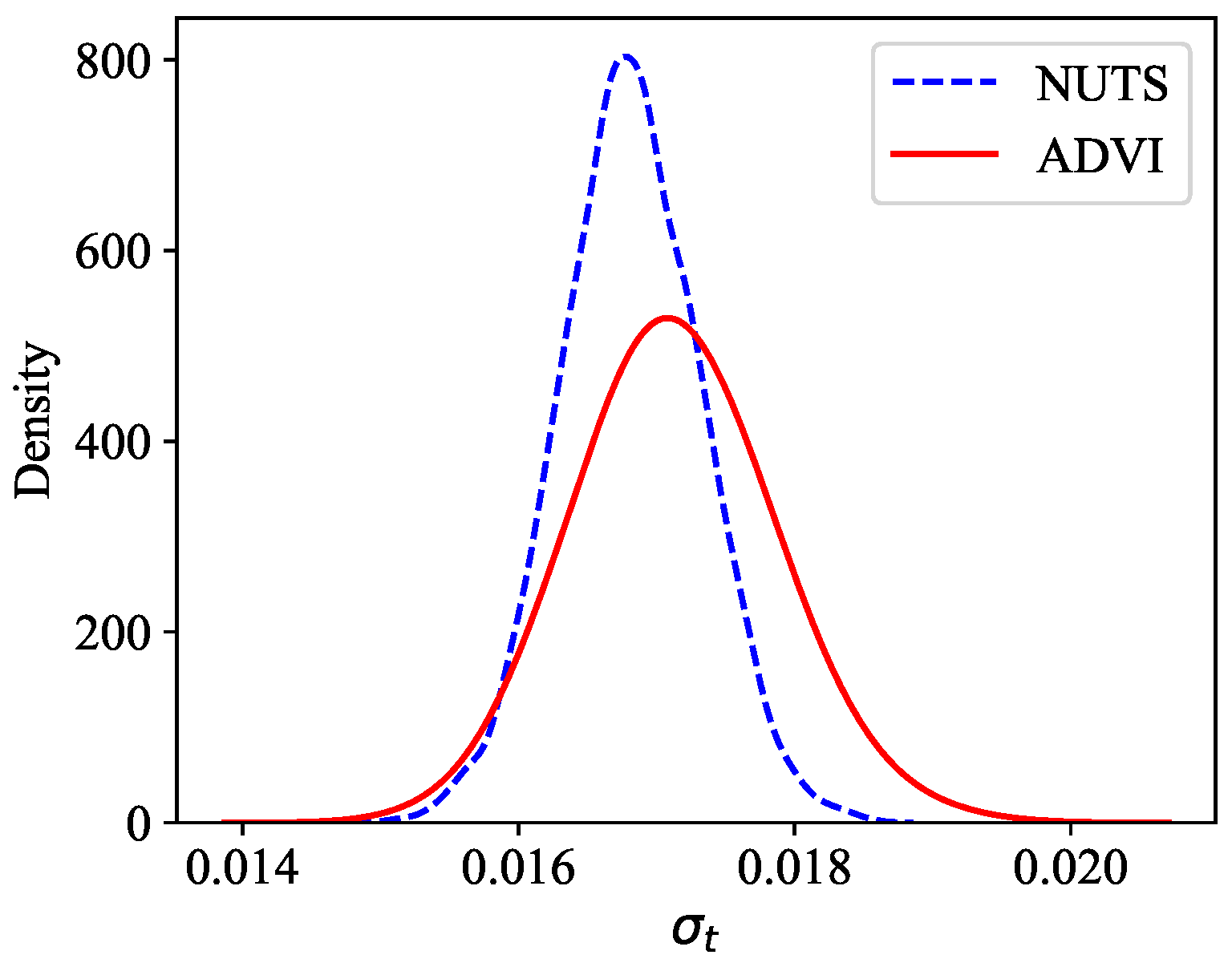
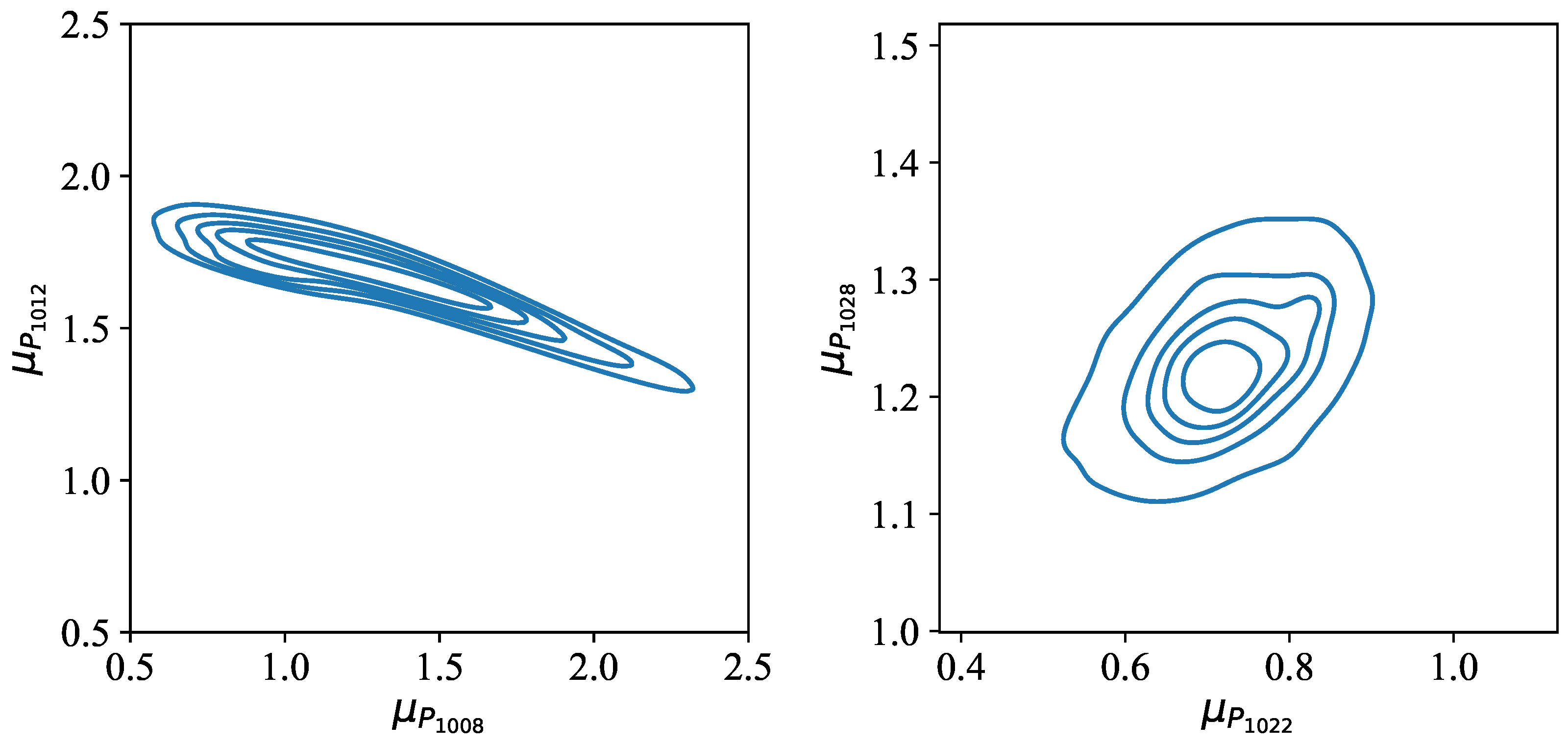
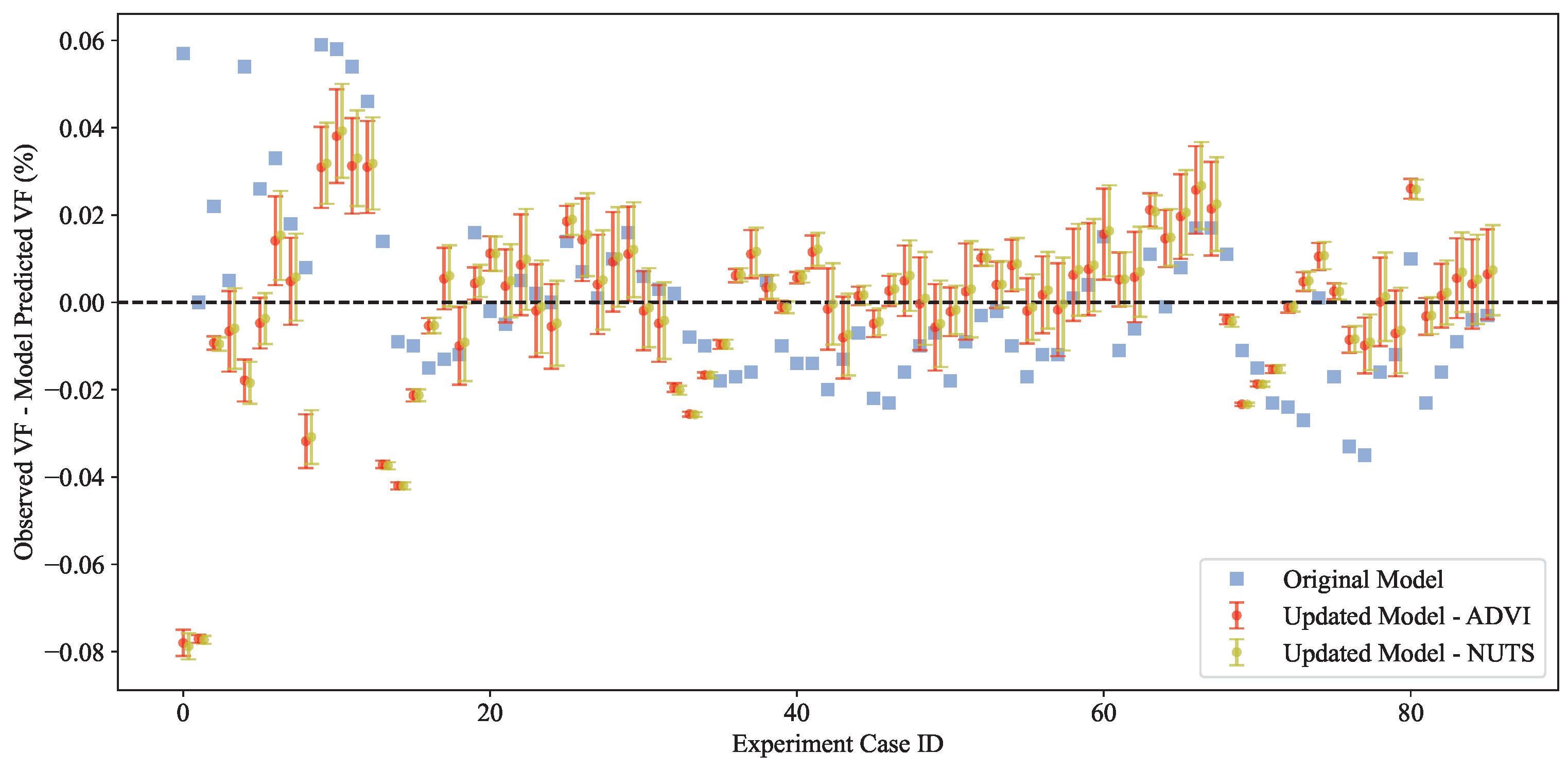
3.2.3. Results
4. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ADVI | Automatic Differentiation Variational Inference |
| BFBT | BWR Full-size Fine-mesh Bundle Test |
| ELBO | Evidence Lower Bound |
| FUQ | Forward Uncertainty Quantification |
| GP | Gaussian Process |
| IET | Integral-effect test |
| IUQ | Inverse Uncertainty Quantification |
| KDE | Kernel Density Estimate |
| LHS | Latin Hypercube Sampling |
| MAE | Mean Absolute Error |
| MCMC | Markov Chain Monte Carlo |
| NUTS | No-U-Turn-Sampler |
| PMP | Physical Model Parameters |
| PPC | Posterior Predictive Check |
| PR | Polynomial Regression |
| QoI | Quantity-of-Interest |
| SET | Separate-Effect Test |
| TH | Thermal-Hydraulics |
| UQ | Uncertainty Quantification |
| VBMC | Variational Bayesian Monte Carlo |
| VF | Void Fraction |
| VI | Variational Inference |
| VVUQ | Verification, Validation, and Uncertainty Quantification |
References
- Wu, X.; Xie, Z.; Alsafadi, F.; Kozlowski, T. A comprehensive survey of inverse uncertainty quantification of physical model parameters in nuclear system thermal–hydraulics codes. Nucl. Eng. Des. 2021, 384, 111460. [Google Scholar] [CrossRef]
- Kennedy, M.C.; O’Hagan, A. Bayesian calibration of computer models. J. R. Stat. Soc. Ser. B Statistical Methodol. 2001, 63, 425–464. [Google Scholar] [CrossRef]
- Bui, A.; Williams, B.; Dinh, N. Advanced Calibration and Validation of a Mechanistic Model of Subcooled Boiling Two-Phase Flow. In Proceedings of the International Congress on Advances in Nuclear Power Plants, Charlotte, NC, USA, 6–9 April 2014. [Google Scholar]
- Damblin, G.; Gaillard, P. Bayesian inference and non-linear extensions of the CIRCE method for quantifying the uncertainty of closure relationships integrated into thermal-hydraulic system codes. Nucl. Eng. Des. 2020, 359, 110391. [Google Scholar] [CrossRef]
- Skorek, T.; de Crécy, A.; Kovtonyuk, A.; Petruzzi, A.; Mendizábal, R.; de Alfonso, E.; Reventós, F.; Freixa, J.; Sarrette, C.; Kyncl, M.; et al. Quantification of the uncertainty of the physical models in the system thermal-hydraulic codes–PREMIUM benchmark. Nucl. Eng. Des. 2019, 354, 110199. [Google Scholar] [CrossRef]
- Baccou, J.; Zhang, J.; Fillion, P.; Damblin, G.; Petruzzi, A.; Mendizábal, R.; Reventós, F.; Skorek, T.; Couplet, M.; Iooss, B.; et al. SAPIUM: A Generic Framework for a Practical and Transparent Quantification of Thermal-Hydraulic Code Model Input Uncertainty. Nucl. Sci. Eng. 2020, 194, 721–736. [Google Scholar] [CrossRef]
- Ghione, A.; Sargentini, L.; Damblin, G.; Fillion, P.; Baccou, J.; Sueur, R.; Iooss, B.; Petruzzi, A.; Zeng, K.; Zhang, J.; et al. Applying the SAPIUM guideline for Input Uncertainty Quantification: The ATRIUM project. In Proceedings of the 20th International Topical Meeting on Nuclear Reactor Thermal Hydraulics (NURETH-20), Washington, DC, USA, 20–25 August 2023. [Google Scholar]
- Liu, Y.; Hu, R.; Zou, L.; Nunez, D. SAM-ML: Integrating data-driven closure with nuclear system code SAM for improved modeling capability. Nucl. Eng. Des. 2022, 400, 112059. [Google Scholar] [CrossRef]
- Damblin, G.; Bachoc, F.; Gazzo, S.; Sargentini, L.; Ghione, A. A generalization of the CIRCE method for quantifying input model uncertainty in presence of several groups of experiments. arXiv 2023, arXiv:2306.02762. [Google Scholar] [CrossRef]
- Xie, Z.; Alsafadi, F.; Wu, X. Towards improving the predictive capability of computer simulations by integrating inverse Uncertainty Quantification and quantitative validation with Bayesian hypothesis testing. Nucl. Eng. Des. 2021, 383, 111423. [Google Scholar] [CrossRef]
- Helleckes, L.M.; Osthege, M.; Wiechert, W.; von Lieres, E.; Oldiges, M. Bayesian calibration, process modeling and uncertainty quantification in biotechnology. PLoS Comput. Biol. 2022, 18, e1009223. [Google Scholar] [CrossRef]
- Mosser, L.; Zabihi Naeini, E. A comprehensive study of calibration and uncertainty quantification for Bayesian convolutional neural networks—An application to seismic data. Geophysics 2022, 87, IM157–IM176. [Google Scholar] [CrossRef]
- Ye, J.; Mahmoudi, M.; Karayagiz, K.; Johnson, L.; Seede, R.; Karaman, I.; Arroyave, R.; Elwany, A. Bayesian calibration of multiple coupled simulation models for metal additive manufacturing: A Bayesian network approach. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part B Mech. Eng. 2022, 8, 011111. [Google Scholar] [CrossRef]
- Bae, J.H.; Chang, K.; Lee, G.H.; Kim, B.C. Bayesian inference of cavitation model coefficients and uncertainty quantification of a Venturi flow simulation. Energies 2022, 15, 4204. [Google Scholar] [CrossRef]
- Zeng, F.; Zhang, W.; Li, J.; Zhang, T.; Yan, C. Adaptive model refinement approach for bayesian uncertainty quantification in turbulence model. AIAA J. 2022, 60, 3502–3516. [Google Scholar] [CrossRef]
- Wang, H.; Fu, T.; Du, Y.; Gao, W.; Huang, K.; Liu, Z.; Chandak, P.; Liu, S.; Van Katwyk, P.; Deac, A.; et al. Scientific discovery in the age of artificial intelligence. Nature 2023, 620, 47–60. [Google Scholar] [CrossRef]
- Dong, G.; Cai, L.; Datta, D.; Kumar, S.; Barnes, L.E.; Boukhechba, M. Influenza-like symptom recognition using mobile sensing and graph neural networks. In Proceedings of the Conference on Health, Inference, and Learning, Virtual Event, USA, 8–10 April 2021; pp. 291–300. [Google Scholar]
- Dong, G.; Tang, M.; Cai, L.; Barnes, L.E.; Boukhechba, M. Semi-supervised graph instance transformer for mental health inference. In Proceedings of the 2021 20th IEEE International Conference on Machine Learning and Applications (ICMLA), Pasadena, CA, USA, 13–16 December 2021; pp. 1221–1228. [Google Scholar]
- Chen, S.; Kong, N.; Sun, X.; Meng, H.; Li, M. Claims data-driven modeling of hospital time-to-readmission risk with latent heterogeneity. Health Care Manag. Sci. 2019, 22, 156–179. [Google Scholar] [CrossRef]
- Wu, J.; Tao, R.; Zhao, P.; Martin, N.F.; Hovakimyan, N. Optimizing nitrogen management with deep reinforcement learning and crop simulations. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 1712–1720. [Google Scholar]
- Ma, C.; Peng, Y.; Wu, L.; Guo, X.; Wang, X.; Kong, X. Application of machine learning techniques to predict the occurrence of distraction-affected crashes with phone-use data. Transp. Res. Rec. 2022, 2676, 692–705. [Google Scholar] [CrossRef]
- Meng, Y.; Wu, L.; Ma, C.; Guo, X.; Wang, X. A comparative analysis of intersection hotspot identification: Fixed vs. varying dispersion parameters in negative binomial models. J. Transp. Saf. Secur. 2022, 14, 305–322. [Google Scholar] [CrossRef]
- Li, Z.; Kong, X.; Zhang, Y. Exploring factors associated with crossing assertiveness of pedestrians at unsignalized intersections. Transp. Res. Rec. 2023, 2677, 182–198. [Google Scholar] [CrossRef]
- Xue, B.; Li, D.; Lu, C.; King, C.R.; Wildes, T.; Avidan, M.S.; Kannampallil, T.; Abraham, J. Use of machine learning to develop and evaluate models using preoperative and intraoperative data to identify risks of postoperative complications. JAMA Netw. Open 2021, 4, e212240. [Google Scholar] [CrossRef]
- Xue, B.; Jiao, Y.; Kannampallil, T.; Fritz, B.; King, C.; Abraham, J.; Avidan, M.; Lu, C. Perioperative predictions with interpretable latent representation. In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 14–18 August 2022; pp. 4268–4278. [Google Scholar]
- Hu, J.; Xu, Y.; Tang, Z. DAN-PD: Domain adaptive network with parallel decoder for polyp segmentation. Comput. Med Imaging Graph. 2022, 101, 102124. [Google Scholar] [CrossRef]
- Li, Z.; Tang, Z.; Hu, J.; Wang, X.; Jia, D.; Zhang, Y. NST: A nuclei segmentation method based on transformer for gastrointestinal cancer pathological images. Biomed. Signal Process. Control 2023, 84, 104785. [Google Scholar] [CrossRef]
- Li, Z.; Wei, Z.; Zhang, Y.; Kong, X.; Ma, C. Applying an interpretable machine learning framework to study mobility inequity in the recovery phase of COVID-19 pandemic. Travel Behav. Soc. 2023, 33, 100621. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Lu, L.; Xiang, Y.; Lu, Q.; Li, M. A data heterogeneity modeling and quantification approach for field pre-assessment of chloride-induced corrosion in aging infrastructures. Reliab. Eng. Syst. Saf. 2018, 171, 123–135. [Google Scholar] [CrossRef]
- Chen, S.; Wu, J.; Hovakimyan, N.; Yao, H. ReConTab: Regularized Contrastive Representation Learning for Tabular Data. arXiv 2023, arXiv:2310.18541. [Google Scholar]
- Robertson, G.; Sjöstrand, H.; Andersson, P.; Hansson, J.; Blair, P. Treating model inadequacy in fuel performance model calibration by parameter uncertainty inflation. Ann. Nucl. Energy 2022, 179, 109363. [Google Scholar] [CrossRef]
- Wang, C.; Wu, X.; Kozlowski, T. Inverse Uncertainty Quantification by Hierarchical Bayesian Modeling and Application in Nuclear System Thermal-Hydraulics Codes. arXiv 2023, arXiv:2305.16622. [Google Scholar]
- Wang, C. A Hierarchical Bayesian Calibration Framework for Quantifying Input Uncertainties in Thermal-Hydraulics Simulation Models. Ph.D. Thesis, University of Illinois at Urbana-Champaign, Champaign, IL, USA, 2020. [Google Scholar]
- Kingma, D.P.; Salimans, T.; Welling, M. Variational dropout and the local reparameterization trick. arXiv 2015, arXiv:1506.02557. [Google Scholar]
- Che, Y.; Wu, X.; Pastore, G.; Li, W.; Shirvan, K. Application of Kriging and Variational Bayesian Monte Carlo method for improved prediction of doped UO2 fission gas release. Ann. Nucl. Energy 2021, 153, 108046. [Google Scholar] [CrossRef]
- Neykov, B.; Aydogan, F.; Hochreiter, L.; Ivanov, K.; Utsuno, H.; Kasahara, F.; Sartori, E.; Martin, M. NUPEC BWR full-size fine-mesh bundle test (BFBT) benchmark. OECD Pap. 2006, 6, 1–132. [Google Scholar] [CrossRef]
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Dunson, D.B.; Vehtari, A.; Rubin, D.B. Bayesian Data Analysis; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Wang, C.; Wu, X.; Kozlowski, T. Surrogate-based Bayesian Calibration of Thermal-Hydraulics Models based on PSBT Time-dependent Benchmark Data. In Proceedings of the PANS Best Estimate Plus Uncertainty International Conference (BEPU-2018), Real Collegio, Lucca, Italy, 13–19 May 2018. [Google Scholar]
- Wang, C.; Wu, X.; Borowiec, K.; Kozlowski, T. Bayesian calibration and uncertainty quantification for TRACE based on PSBT benchmark. Trans. Am. Nucl. Soc. 2018, 118, 419–422. [Google Scholar]
- Liu, F.; Bayarri, M.; Berger, J. Modularization in Bayesian analysis, with emphasis on analysis of computer models. Bayesian Anal. 2009, 4, 119–150. [Google Scholar]
- Wang, C.; Wu, X.; Kozlowski, T. Gaussian Process–Based Inverse Uncertainty Quantification for TRACE Physical Model Parameters Using Steady-State PSBT Benchmark. Nucl. Sci. Eng. 2019, 193, 100–114. [Google Scholar] [CrossRef]
- Wang, C.; Wu, X.; Kozlowski, T. Surrogate-Based Inverse Uncertainty Quantification of TRACE Physical Model Parameters Using Steady-State PSBT Void Fraction Data. In Proceedings of the 17th International Topical Meeting on Nuclear Reactor Thermal Hydraulics (NURETH 17), Xi’an, China, 3–8 September 2017; pp. 3–8. [Google Scholar]
- Wang, C.; Wu, X.; Kozlowski, T. Inverse Uncertainty Quantification by Hierarchical Bayesian Inference for TRACE Physical Model Parameters based on BFBT benchmark. In Proceedings of the 18th International Topical Meeting on Nuclear Reactor Thermal Hydraulics (NURETH-18), Portland, OR, USA, 18–23 August 2019. [Google Scholar]
- Zio, E.; Pedroni, N. Monte Carlo simulation-based sensitivity analysis of the model of a thermal–hydraulic passive system. Reliab. Eng. Syst. Saf. 2012, 107, 90–106. [Google Scholar] [CrossRef]
- Wang, C.; Wu, X.; Kozlowski, T. Sensitivity and Uncertainty Analysis of TRACE Physical Model Parameters Based on PSBT Benchmark Using Gaussian Process Emulator. In Proceedings of the 17th International Topical Meeting on Nuclear Reactor Thermal Hydraulics (NURETH 17), Xi’an, China, 3–8 September 2017; pp. 3–8. [Google Scholar]
- Perret, G.; Wicaksono, D.; Clifford, I.D.; Ferroukhi, H. Global Sensitivity Analysis and Bayesian Calibration on a Series of Reflood Experiments with Varying Boundary Conditions. Nucl. Technol. 2022, 208, 711–722. [Google Scholar] [CrossRef]
- Li, D.; Jiang, P.; Hu, C.; Yan, T. Comparison of local and global sensitivity analysis methods and application to thermal hydraulic phenomena. Prog. Nucl. Energy 2023, 158, 104612. [Google Scholar] [CrossRef]
- Cacuci, D.; Ionescu-Bujor, M. Adjoint sensitivity analysis of the RELAP5/MOD3. 2 two-fluid thermal-hydraulic code system—I: Theory. Nucl. Sci. Eng. 2000, 136, 59–84. [Google Scholar] [CrossRef]
- Khan, A.H.; Omar, S.; Mushtary, N.; Verma, R.; Kumar, D.; Alam, S. Digital Twin and Artificial Intelligence Incorporated With Surrogate Modeling for Hybrid and Sustainable Energy Systems. arXiv 2022, arXiv:2210.00073. [Google Scholar]
- Liu, Y.; Dinh, N.; Sato, Y.; Niceno, B. Data-driven modeling for boiling heat transfer: Using deep neural networks and high-fidelity simulation results. Appl. Therm. Eng. 2018, 144, 305–320. [Google Scholar] [CrossRef]
- Ayodeji, A.; Amidu, M.A.; Olatubosun, S.A.; Addad, Y.; Ahmed, H. Deep learning for safety assessment of nuclear power reactors: Reliability, explainability, and research opportunities. Prog. Nucl. Energy 2022, 151, 104339. [Google Scholar] [CrossRef]
- Zio, E.; Apostolakis, G.E.; Pedroni, N. Quantitative functional failure analysis of a thermal–hydraulic passive system by means of bootstrapped Artificial Neural Networks. Ann. Nucl. Energy 2010, 37, 639–649. [Google Scholar] [CrossRef]
- Kruschke, J. Doing Bayesian Data Analysis: A Tutorial with R, JAGS, and Stan, 2nd ed.; Academic: Burlinton, MA, USA, 2015. [Google Scholar]
- Wu, X.; Wang, C.; Kozlowski, T. Kriging-based surrogate models for uncertainty quantification and sensitivity analysis. In Proceedings of the MC-2017, International Conference on Mathematics Computational Methods Applied to Nuclear Science Engineering, Jeju, Republic of Korea, 16–20 April 2017. [Google Scholar]
- Wu, X.; Wang, C.; Kozlowski, T. Global sensitivity analysis of trace physical model parameters based on bfbt benchmark. In Proceedings of the MC-2017, International Conference on Mathematics Computational Methods Applied to Nuclear Science Engineering, Jeju, Republic of Korea, 16–20 April 2017. [Google Scholar]
- NRC, US. TRACE V5. 0 Theory Manual, Field Equations, Solution Methods and Physical Models; United States Nuclear Regulatory Commission: Rockville, MD, USA, 2008.
- Hoffman, M.D.; Gelman, A. The No-U-Turn sampler: Adaptively setting path lengths in Hamiltonian Monte Carlo. J. Mach. Learn. Res. 2014, 15, 1593–1623. [Google Scholar]
- Cocci, R.; Damblin, G.; Ghione, A.; Sargentini, L.; Lucor, D. Extension of the CIRCE methodology to improve the Inverse Uncertainty Quantification of several combined thermal-hydraulic models. Nucl. Eng. Des. 2022, 398, 111974. [Google Scholar] [CrossRef]
- Blei, D.M.; Kucukelbir, A.; McAuliffe, J.D. Variational inference: A review for statisticians. J. Am. Stat. Assoc. 2017, 112, 859–877. [Google Scholar] [CrossRef]
- Kucukelbir, A.; Tran, D.; Ranganath, R.; Gelman, A.; Blei, D.M. Automatic differentiation variational inference. J. Mach. Learn. Res. 2017, 18, 1–45. [Google Scholar]
- Salvatier, J.; Wiecki, T.V.; Fonnesbeck, C. Probabilistic programming in Python using PyMC3. PeerJ Comput. Sci. 2016, 2, e55. [Google Scholar] [CrossRef]
- Kucukelbir, A.; Ranganath, R.; Gelman, A.; Blei, D. Automatic variational inference in Stan. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; pp. 568–576. [Google Scholar]
- Challis, E.; Barber, D. Gaussian Kullback-Leibler Approximate Inference. J. Mach. Learn. Res. 2013, 14, 2239–2286. [Google Scholar]
- Saltelli, A.; Annoni, P.; Azzini, I.; Campolongo, F.; Ratto, M.; Tarantola, S. Variance based sensitivity analysis of model output. Design and estimator for the total sensitivity index. Comput. Phys. Commun. 2010, 181, 259–270. [Google Scholar] [CrossRef]
- Iwanaga, T.; Usher, W.; Herman, J. Toward SALib 2.0: Advancing the accessibility and interpretability of global sensitivity analyses. Socio-Environ. Syst. Model. 2022, 4, 18155. [Google Scholar] [CrossRef]
- Aly, Z.; Casagranda, A.; Pastore, G.; Brown, N.R. Variance-based sensitivity analysis applied to the hydrogen migration and redistribution model in Bison. Part II: Uncertainty quantification and optimization. J. Nucl. Mater. 2019, 523, 478–489. [Google Scholar] [CrossRef]
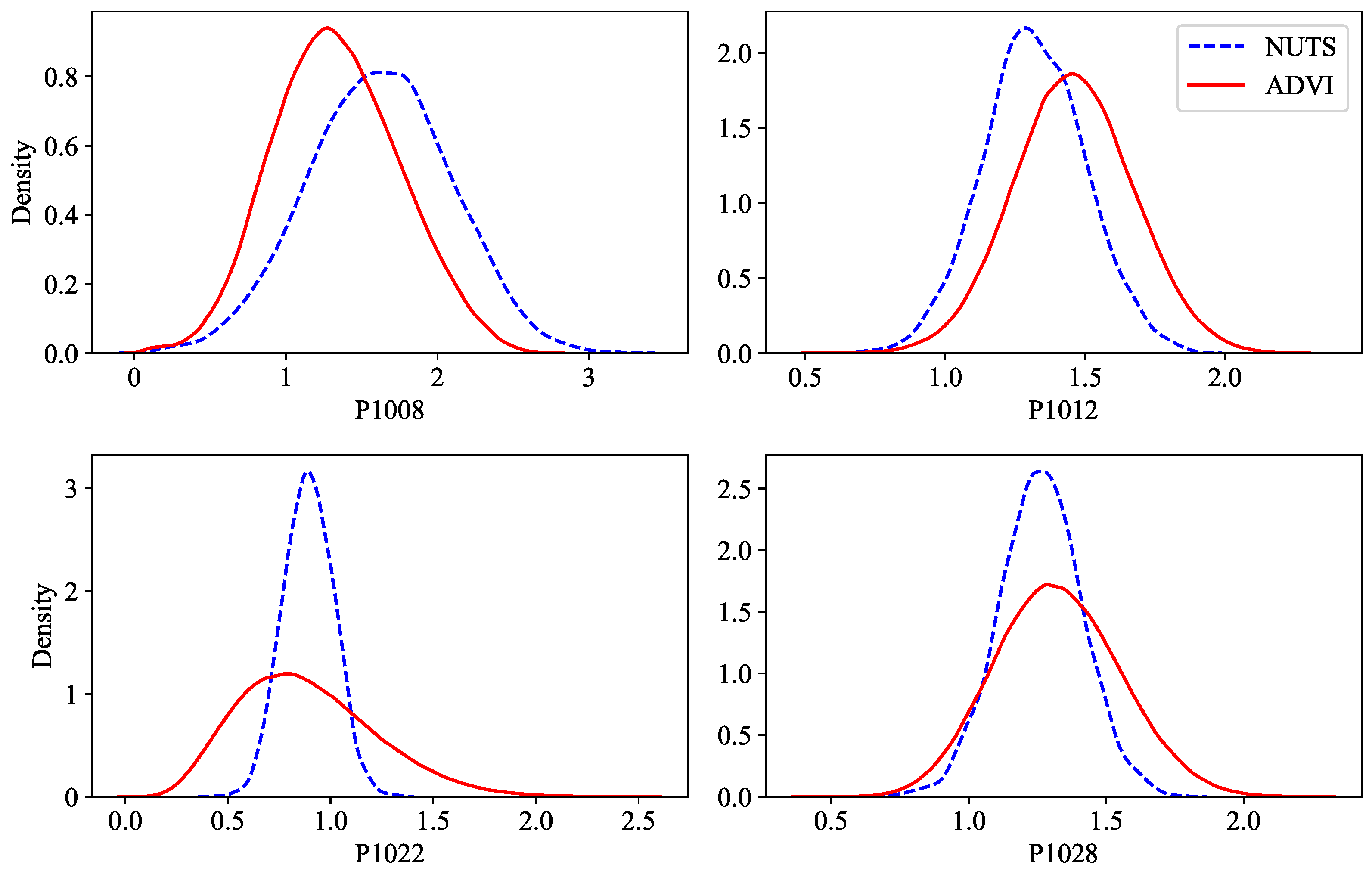
| ADVI | NUTS | |
|---|---|---|
| Number of fitting/sampling steps required | 120,000 | 6000 |
| Computational time | 12 s | 50 s |
| Parameter | Definition |
|---|---|
| Single phase liquid to wall heat transfer coefficient | |
| Subcooled boiling heat transfer coefficient | |
| Wall drag coefficient | |
| Interfacial drag (bubbly/slug Rod Bundle–Bestion) coefficient |
| Parameters | Distributions | Dist. Parameter 1 | Dist. Parameter 2 |
|---|---|---|---|
| Uniform | |||
| Uniform | |||
| Normal |
| Parameters | NUTS | ADVI | ||
|---|---|---|---|---|
| ADVI | NUTS | |
|---|---|---|
| Number of fitting/sampling steps required | 300,000 | 100,000 |
| Computational time | 58 s | 1520 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Wu, X.; Xie, Z.; Kozlowski, T. Scalable Inverse Uncertainty Quantification by Hierarchical Bayesian Modeling and Variational Inference. Energies 2023, 16, 7664. https://doi.org/10.3390/en16227664
Wang C, Wu X, Xie Z, Kozlowski T. Scalable Inverse Uncertainty Quantification by Hierarchical Bayesian Modeling and Variational Inference. Energies. 2023; 16(22):7664. https://doi.org/10.3390/en16227664
Chicago/Turabian StyleWang, Chen, Xu Wu, Ziyu Xie, and Tomasz Kozlowski. 2023. "Scalable Inverse Uncertainty Quantification by Hierarchical Bayesian Modeling and Variational Inference" Energies 16, no. 22: 7664. https://doi.org/10.3390/en16227664
APA StyleWang, C., Wu, X., Xie, Z., & Kozlowski, T. (2023). Scalable Inverse Uncertainty Quantification by Hierarchical Bayesian Modeling and Variational Inference. Energies, 16(22), 7664. https://doi.org/10.3390/en16227664





