Abstract
Emission reduction in the main greenhouse gas, CO2, can be achieved efficiently via CO2 geological storage and utilization (CCUS) methods such as the CO2 enhanced oil/water/gas recovery technique, which is considered to be an important strategic technology for the low-carbon development of China’s coal-based energy system. During the CCUS, the thermodynamic properties of the CO2–water–rock system, such as the interfacial tension (IFT) and wettability of the caprock, determine the injectability, sealing capacity, and safety of this scheme. Thus, researchers have been conducting laboratory experiments and modeling work on the interfacial tension between CO2 and the water/brine, wettability of caprocks, the solubility of gas–liquid binary systems, and the pH of CO2-saturated brine under reservoir temperature and pressure conditions. In this study, the literature related to the thermodynamic properties of the CO2–water–rock system is reviewed, and the main findings of previous studies are listed and discussed thoroughly. It is concluded that limited research is available on the pH of gas-saturated aqueous solutions under CO2 saline aquifer storage conditions, and less emphasis has been given to the wettability of the CO2–water/brine–rock system. Thus, further laboratory and modeling research on the wettability alternations of caprock in terms of molecular dynamics is required to simulate this phenomenon at the molecular level. Moreover, simplified IFT and solubility prediction models with thermodynamic significance and high integrity need to be developed. Furthermore, interaction mechanisms coupling with multi-factors associated with the gas–liquid–solid interface properties and the dissolution and acidification process need to be explored in future work.
1. Introduction
Recently, countries worldwide have announced their goal of attaining a carbon peak and neutralization to tackle climate change caused by anthropogenic CO2 emissions into the atmosphere using vast amounts of fossil fuel energy. In science, coal, oil, and gas still constitute a large percentage of the energy supply and conception chain, and the technical path of carbon emission reduction while ensuring that a safe energy supply is attracting increased attention in the field of energy usage. The growth in the proportion of renewable energy sources, such as wind and solar power, in the energy supply and conceptions chain, as well as the development of carbon capture, storage, and utilization (CCUS), are recognized as the key factors in achieving net zero carbon emissions [1,2]. Currently, deep saline aquifers are considered the most promising and effective method of CO2 emission reduction via CO2 geological storage because of their large capacity, which is estimated to be approximately 1000–10,000 GT, which is more than the total amount of anthropocentric CO2 emissions produced this century. Another promising option is CO2 storage in offshore reservoirs because of their vast uptake capacity and low risk of leakage into offshore aquifers [3].
Since 2000, China has been developing CCUS technology, which is considered to be one of the most important strategic technologies for the low-carbon development of China’s coal-based energy system. According to the 2021 China CCUS Annual Report, about 5.1 GT and 9.0 GT CO2 can be sequestered in China via CO2-Enhanced Oil Recovery (CO2-EOR) [4] and CO2-Enhanced Gas Recovery (CO2-EGR) technologies, respectively [5]. Additionally, by utilizing depleted gas reservoirs, approximately 15.3 GT CO2 can be stored, while injection into deep saline aquifers offers an even greater sequestration potential, estimated at around 2420 GT [5]. However, the implementation of domestic CO2 geological utilization and storage technology currently faces significant challenges, including high energy consumption for carbon capture, source–sink mismatches, unclear long-term sequestration mechanisms, and underdeveloped leakage monitoring and emergency response systems. Moreover, domestic CCUS technology must integrate cutting-edge scientific and technological advancements from both local and international sources to establish industrial clusters that encompass CO2 emission sources, capture, and geological storage, thereby creating a comprehensive and effective carbon emission reduction strategy.
At present, storage-related research has yielded promising results; however, demonstration projects and widespread applications are lacking. Thus, there is an urgent need to address key scientific questions concerning capture and storage, scale up the development of CO2 geological utilization and storage technology, and ultimately provide a solid technical foundation for the low-carbon, clean, and efficient use of coal and other fossil energy sources, contributing to national energy security. One major reason for the launch of new CCUS projects is public concern about the environmental impacts and risks related to CCUS projects, which may directly influence the decision-making process during CCUS site selection [6]. Technical support is required for the development of CCUS, as expected, in terms of technologies supporting CO2 saline aquifer storage, since leakage from the sealing site determines the flexibility of this scheme. Fundamental research on carbon migration in reservoirs, which is influenced by the thermodynamic properties of fluids, is essential to deepen the understanding of the mechanisms influencing CO2 saline aquifer storage.
There are four main trapping mechanisms in the geological carbon storage process, including residual trapping, also known as capillary trapping, structural trapping, and solubility and mineral trapping, as shown in the Figure 1 [7,8,9]. Structural or hydrodynamic trapping plays an important role at the beginning of the injection of CO2 into saline aquifers, where the injected CO2 can be trapped and sealed via a low-permeability caprock or shale above the saline aquifers [10]. However, the trapped CO2 is likely to escape into the atmosphere along the fractures of the caprock, leading to failure during structural trapping. Thus, structural integrity is crucial for the successful structural trapping of CO2. In contrast, capillary trapping relies less on structural integrity, and the trapping of migrating CO2 in pores can be achieved via snap-off effects [11]. Capillary trapping mechanisms have been widely studied because of their reliability, strong adaptability, and long-term efficiency during the CO2 saline aquifers storage process [12]. It was found that the efficiency of capillary trapping is determined by the threshold capillary pressure, which, in turn, is a function of the interface properties of the CO2-water-rock system, which determines the fluid distribution on the surface of the reservoir rocks [13]. Thus, the reservoir wettability and interfacial tension (IFT) between the CO2 and reservoir brines are important thermodynamic properties of fluids that determine the injectability, sealing capacity, and safety of the CO2 saline aquifer storage scheme.
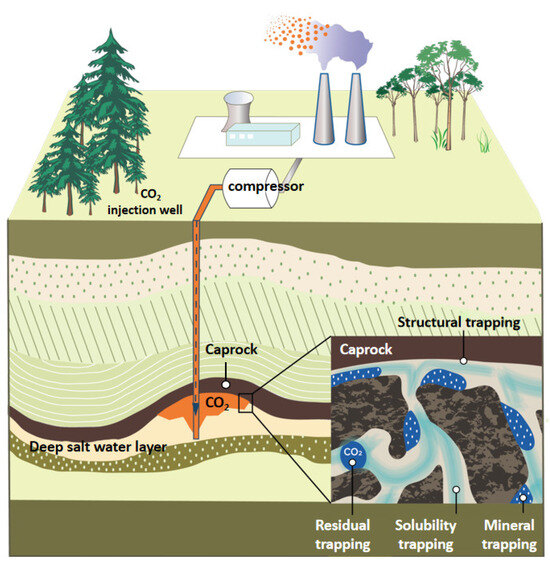
Figure 1.
The main trapping mechanisms used in CO2 geological storage: structural trapping, residual trapping, solubility trapping, and mineral trapping (The blue line represents the direction of CO2 injection).
Meanwhile, injected CO2 dissolves in reservoir fluids and leads to a density gradient between different areas in the water layer [14], which eventually leads to the convective mixing of CO2 and reservoir fluids. Then, the dissolution rate of CO2 into the reservoir fluids is further increased due to the density gradient, resulting in CO2 solubility trapping in the water layer of the reservoir [15]. During the process of CO2 storage in saline aquifers, the process of CO2 dissolving into reservoir brine lasts for most of the time. Thus, the solubility trapping mechanism plays a major role in this scheme. Moreover, the mutual solubility between CO2 and reservoir fluids influences the long-term safe storage of CO2 as well as the solid–liquid–gas interactions at the injected reservoir site [16]. Therefore, it is essential to investigate the mutual solubility of CO2 and reservoir fluids during phase equilibrium under CO2 saline aquifer storage conditions [17].
Owing to the slow chemical reactions with the reservoir rocks, the dissolved CO2 is mineralized, which is known as mineralization trapping and is the most important trapping mechanism involved in CO2 saline aquifer storage [18]. However, the dissolution of CO2 into the reservoir fluids lowers the pH of the reservoir. The erosion of reservoir rocks and caprocks caused by the low pH of the reservoir results in the leakage of sealed CO2 from the caprocks [19]. Generally, the pH of CO2-saturated brine plays a key role in estimating the CO2 storage capacity of the reservoir during mineralization trapping [20,21]. Therefore, fundamental research on the pH of CO2-saturated brine during the CO2 saline aquifer storage scheme may lead to stimulation failure or cause high risks in the operation process [22,23]. In addition to the main trapping mechanisms mentioned here, other CO2 trapping mechanisms [24], such as hydrodynamic and carbon adsorption trapping and CO2 trapping via changes in the partial capillary pressure [25] or permeability [26], have been studied.
The sealing site for the CCS covers extremely high temperatures and pressures, where CO2 is in a supercritical state ( 304.2 K and 7.4 MPa) and the salinity of the potential sealing site could be greater than 100 g/L [27,28,29]. The CO2 phase diagram shown in Figure 2 illustrates that the injected CO2 changes its phase from liquid/vapor to supercritical in the reservoir [30]. According to previous research, the CO2 phase state determines its properties, leading to a change in the thermodynamic properties of reservoir fluids saturated with injected CO2 [30]. Therefore, the laboratory apparatus must be designed to withstand the extremely high pressure, temperature, and corrosion associated with the high salt concentration.
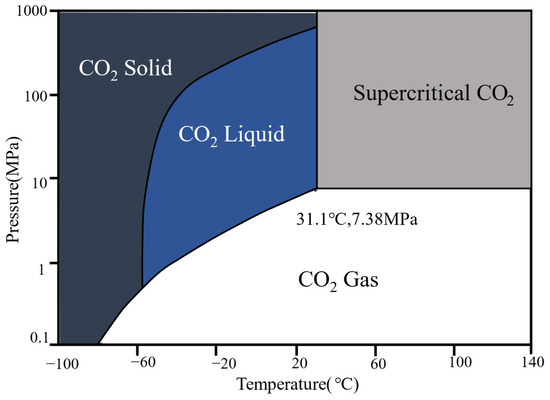
Figure 2.
Pressure–temperature-dependent CO2 phases [30].
After CO2 is injected into a porous medium, a series of physical and chemical changes occur in the rock strata and brine [31]. These changes upset the balance between the existing rock strata and brine, resulting in a change in the trapping efficiency, as shown in Figure 3 [31].
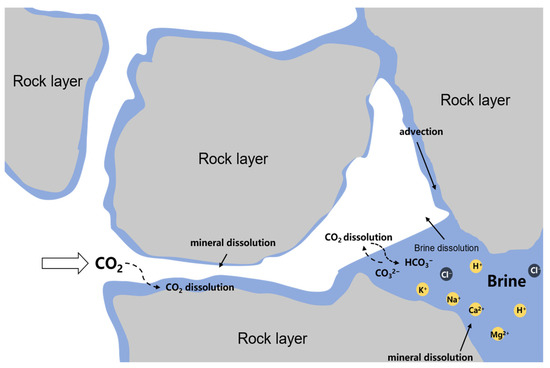
Figure 3.
The injected CO2 and saline water migration diagram at the pore scale during the CO2 saline aquifer storage process [31].
Thus, fundamental research on the thermodynamic properties of gas–liquid–solid systems is important for estimating the safe and long-term storage of CO2 saline aquifers. Thus, in this study, the experimental and predicted thermodynamic properties, such as the interfacial tension, wettability, pH, and solubility of the CO2-brine-rock system, were reviewed carefully. Experimental and modeling methods were compared, methods for obtaining thermodynamic properties of a gas–liquid–solid system with high integrity were proposed, and trapping mechanisms were clarified. The results of this review provide theoretical support for the feasibility of a long-lasting and safe CO2–saline aquifer storage scheme to provide a solid technical foundation for the low-carbon, clean, and efficient use of coal and other fossil energy sources, contributing to national energy security.
2. Thermodynamic Properties
2.1. Interfacial Tension between CO2 and Water/Brine
The threshold capillary pressure that determines the efficiency of residual trapping is a function of the wettability and the interfacial tension (IFT) between the CO2 and reservoir brines, as described by the standard Young–Laplace equation, as shown in Equation (1) [13,32]. This threshold capillary pressure characterizes the penetration ability of the non-wetting phase (CO2) into the macropores and throats of the reservoir rock that were originally water saturated. Research findings suggest that lower IFT leads to enhanced CO2 capillary trapping, as it reduces the capillary pressure required for CO2 capture within pore spaces, thereby improving storage efficiency. Due to the complexity of the actual reservoir, the wettability of the sealing site can be represented by measuring the contact angles (CAs) of the CO2-brine-rock system. Thus, the laboratory and modelling work of CO2–brine IFTs and rock CAs have been reviewed, and the key findings are highlighted in this section.
where Pcth is the threshold capillary pressure of brine/water-saturated caprock (mN·m−1) is the IFT between water/brine and CO2, θ is the CA between the brine/water and rocks in a CO2 atmosphere, and R is the maximum radius of cylindrical caprocks.
Different methods exist for measuring the IFT between gases and liquids. Among these, the pendent drop method, which is based on the axisymmetric drop shape analysis (ADSA) technique, is widely used because of its high accuracy and efficiency. Pictures of the pendent drop of the desired solution were captured using a CCD camera at a high resolution under the evaluated temperature and pressure conditions. However, the accuracy of the calculated IFTs based on this method strongly depends on the density difference between the gas and liquid, as illustrated in Equation (2).
where g is the gravity constant; γ is the IFT; Δρ is the density difference; H is the shape facture, which is related to the drop shape parameters; and De is the horizontal diameter of the drop. Therefore, the accuracy of the obtained density difference determines the integrity of the IFT values measured using the pendent drop method.
Numerous experimental studies have been conducted on the IFT between CO2 and reservoir fluids using the pendent drop method based on the ADSA technique [32,33,34,35]. Initially, most laboratory studies were conducted on CO2 + water binary systems under reservoir conditions. Then, considering the effects of actual reservoir brine’s ionic strengths and types on the IFT between the CO2-brine system, the IFTs of the CO2 + brine binary system consistent with the reservoir conditions were measured, where temperatures and pressures ranged from 278 to 423 K and 0.1–70 MPa, respectively [32,33,34,36,37,38]. However, owing to the differences in the experimental procedures and methods, disparities and contradictions exist in the experimental results, which has led to doubts regarding the accuracy and reliability of the IFT data in the literature [39]. Accurate determination of the density difference between CO2 and water/brine is critical to the IFT measurement results based on ADSA, as shown in Equation (1) [13]. Due to the mutual dissolution of CO2 and water/brine, the density of the two-phase equilibrium must be considered when measuring the two-phase IFT [40]. Thus, the difference between density difference determination methods also leads to a disparity in the IFTs reported in the literature. It is found that the IFT of the CO2 + brine system increases with molalities, and those with divalent ion is twice larger than the monovalent ions at the same temperature, pressure, and molality conditions [41]. The measurement time also influenced the accuracy of the measured IFT data [39]. Larger errors were observed in the obtained data when waiting too long for the measurement, where the drop shape presented less integrity. The poor results (excessively small IFT) in Chun’s [36] work resulted from waiting for days for the system to reach phase equilibrium, as observed in previous literature [39].
To supplement the IFT database between CO2 and water/brines, the research scope was extended to higher temperatures and pressures via modelling methods. The molecular dynamics (MD) method was developed to better understand the relationship between the surface strength and IFT for the CO2 + H2O binary system; however, a relatively high deviation between the predicted and experimental values was found [42,43,44]. In recent years, an artificial neural network (ANN) method was presented to estimate the IFTs for a CO2 + water/brine binary system [45,46,47,48,49]. The ANN method exhibited a high level of accuracy with respect to different systems, while it was strongly dependent on the experimental data; thus, the estimation is restricted to the experimental conditions and cannot be extended to predictions beyond the experimental temperature and pressure ranges with high integrity. In previous work conducted by Chow [50], a theoretical model uses of square gradient theory (SGT) applied to the ‘statistical associating fluid-theory variable-range Mie’ (SAFT-VR-Mie) Equation of State (EoS) was developed for the IFTs of the CO2 + H2O/CO2 binary system and the CO2 + N2/Ar + H2O ternary system. The model exhibited a high level of integrity for the CO2 + H2O/brine binary system. The SAFT theory proposed by Chapman et al. [51,52] is one of the most successful models for modern algebraic descriptions of chain fluids and has been applied to estimate the thermodynamic and phase equilibrium properties of complex fluid mixtures in recent years [53,54,55,56,57]. However, the SAFT EoS is too complicated and requires too many factors and parameters. Most recently, Jerauld et al. [58] proposed a revised correlation method for the accurate estimation of the CO2-brine IFT based on over 1600 data points from the literature and concluded that the Kashefi [59] method has better qualitative behavior and improves predictions with an AARE of approximately 5%. Neural network- and machine learning-based models have high computing speeds, strong adaptability, and a fault-tolerant ability; however, the normalization method lacks thermodynamic meaning. Moreover, the thermodynamic relationships between the main CO2 trapping mechanisms in terms of solubility and IFT for the CO2 + H2O/brine binary system need to be elaborated in detail [27]. A detailed literature review is provided in the following Table 1 and Table 2.

Table 1.
Literature review for the CO2-pure solution IFTs.

Table 2.
Literature review for the CO2-brine IFTs.
It was concluded that the interfacial characteristics of rock–fluid systems have a significant influence on the efficiency of CO2 capillary trapping during saline aquifer sequestration [73]. Thus, in previous studies, the IFT between CO2 and brine of different concentrations under reservoir pressure and temperature conditions has been investigated systematically. The results indicate that the IFT of the CO2-brine binary system depends on the temperature, pressure, and molality [13,40,74]. According to previous research, the CO2-brine IFT has a very limited pressure dependence tendency after the pseudo-plateau is reached. As for the salt concentrations, a linear relationship exists between the average increase in the CO2-brine IFT and the brine molality [32,40]. According to previous research, this can be expressed using the following equations [80]:
The details of this method were discussed in a previous study [32]. The parameters for a1–3 and b1–6 were obtained by fitting the predicted results to the experimental data, and the coefficients used to model the CO2-brine IFT are listed in Table 3.

Table 3.
Coefficients used to model the CO2-brine IFTs.
Then, a modified empirical correlation based on experimental data was presented in Figure 4, where Δγ is the deviation between the experimental and estimated values for the CO2-brine IFT. The modified empirical correlation uses only a few regression coefficients with a relatively low error for most of the experimental data with around 600 data points. The prediction results reached good agreement with the experiment, as shown in Figure 4. Thus, IFTs between CO2-brine can be estimated via the modified empirical correlation based on the linear relations of Δγ and salinity, covering a wide range of temperatures (373–423 K), pressures (3–30 MPa), and ionic strengths (0–4.9 mol·kg−1) for brines containing Na+, K+, Ca2+, and Mg2+.
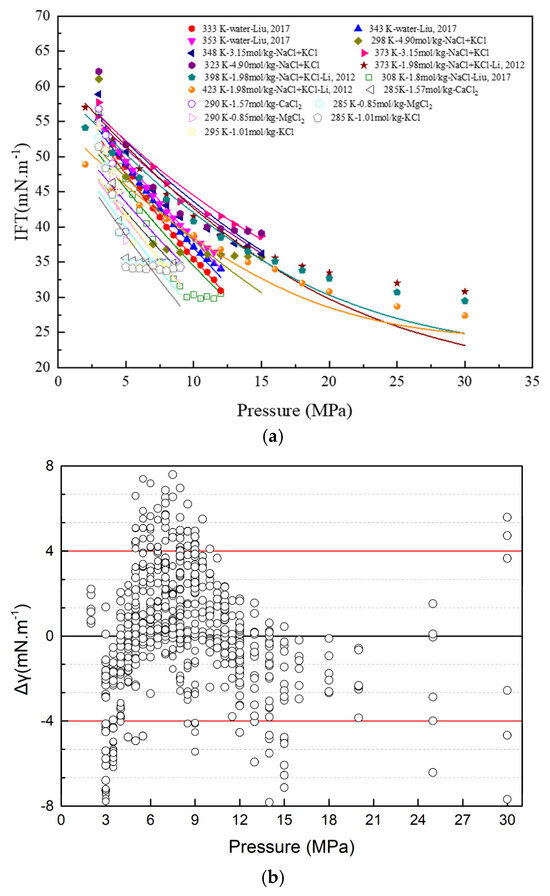
Figure 4.
Diagram for linear fitting and experiment (a): lines are fitting values based on the modified empirical correlation based on experimental data and dots are data from the experiment, and distribution of deviations of the calculated IFT from the measured IFT (b).
However, to predict the IFTs when the isotherms reached a plateau, the empirical correlations based on the linear relation method yielded larger deviations (Δγ larger than ±4 mN·m−1) than expected, as shown in Figure 4. Moreover, a large discontinuity in the slope for the IFTs against temperature at a constant pressure when passing from the liquid/vapor to the super-critical/liquid region was observed. Therefore, a model that is smooth and continuous in slope and successfully fits the IFT data corresponding to the CO2 geological storage conditions, especially those covering the CO2 phase-change region with thermodynamic significance, needs to be developed in future work. The following conclusions are relevant based on the results discussed above:
- Different methods exist to measure the IFT between gases and liquids. Among these, the pendent drop method, which is based on the axisymmetric drop shape analysis (ADSA) technique, is widely used because of its high accuracy and efficiency.
- An accurate measurement of the IFT in CO2 reservoir brines at the evaluated high-temperature and pressure ranges corresponding to actual reservoir conditions relies on the integrity of the experimental apparatus and approach.
- Because of the temperature and pressure limitations of the desired experimental apparatus, a prediction model for the IFT between CO2 and reservoir brines in accordance with the actual reservoir conditions covering a wide range of temperatures, pressures, ionic types, and strengths is essential.
- The results indicate that the IFT of the CO2-brine binary system depends on the temperature, pressure, and molality. However, the pressure has a limited influence on the CO2-brine IFT after the pseudo-plateau has been reached.
A simplified IFT prediction model with thermodynamic significance and high integrity for predicting IFTs when a pseudo-plateau is reached needs to be developed. And the model needs to cover a wide range of temperatures and pressures corresponding to the CO2 geological storage conditions in future work.
2.2. Wettability of the CO2-Water/Brine-Rock System
Multiphase flows in porous media are of great importance in many industrial processes in terms of geological CO2 sequestration and utilization, including enhanced oil/gas/water recovery [81,82]. The effects of fluid properties and flow conditions have been widely studied in previous research, whereas less emphasis has been given to the wettability of the CO2–water/brine–rock system, which is a key parameter influencing the storage capacity and security of the CO2 geological storage scheme [83].
The seepage characteristics of reservoir fluids are a function of wettability because the fluid distribution in the pore space of reservoir rocks is governed by rock wettability [81]. Therefore, it is important to accurately measure the rock wettability under CO2 geological storage conditions. The wettability of the CO2-water/brine–rock system was estimated by measuring the contact angles of individual rock sample surfaces under reservoir conditions using conventional methods, including the ADSA [62,73]. However, conventional contact angle and tomographic imaging methods have serious limitations [83]. The measurement methods are diverse, and the methods that have been commonly used in recent years are summarized in Table 4, and Figure 5 shows how the static normal contact angle changes with pressure.


Table 4.
Literature review on the investigation of the wettability of CO2-brine-rock systems.
Table 4.
Literature review on the investigation of the wettability of CO2-brine-rock systems.
| Method | Analysis Mode | Resources | Schematic |
|---|---|---|---|
| Sessile drop | Experimental, manual/automatic analysis | Bikkina et al. (2011) [84] Iglauer et al. (2014) [85] Liu et al. (2015) [71] Mutailipu et al. (2019) [32] | 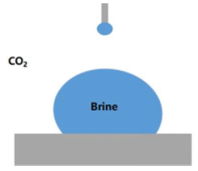 |
| Captive bubble | Experimental, manual/automatic analysis | Chiquet et al. (2007) [86] Broseta et al. (2012) [87] Farokhpoor et al. (2013) [88] Shojai Kaveh et al. (2016) [89] | 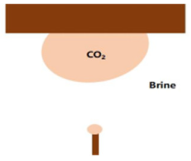 |
| Sessile drop/Captive bubble on a titled plate | Experimental, manual/automatic analysis | Saraji et al. (2013) [62] Arif et al. (2016) [73] Arif et al. (2017) [77] | 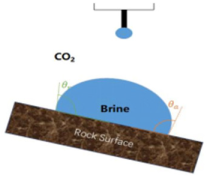 |
| Capillary meniscus analysis | Experimental, image analysis | Li et al. (2014) [90] Hobeike et al. (2017) [91] Al-Zaidi et al. (2018) [92] | 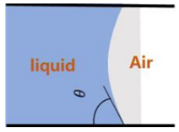 |
| 2D micromodel | Injected fluid imaged via microscope/analyzed using ImageJ | Chalbaud et al. (2009) [13] Kim et al. (2012) [93] Zhao et al. (2016) [82] |  |
| 3D μ-CT imaging | CT-scan under dynamic condition/image analyzed using an algorithm | Andrew et al. (2013) [94] Lv et al. (2017) [95] Iglauer et al. (2018) [96] |  |
| Molecular dynamics (MD)simulation | High power computing/numerical solution of force field algorithm | Iglauer et al. (2012) [97] Liang et al. (2017) [98] Wang et al. (2022) [99] |  |
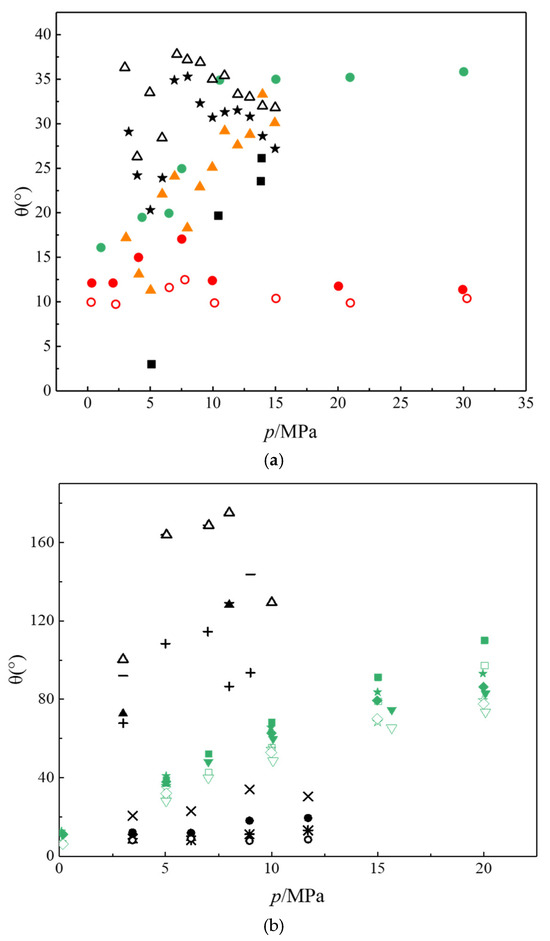
Figure 5.
Contact angle as a pressure function of experimental data. Symbols represent experimental data. Black represents the CO2-water/saltwater-quartz. Red represents the CO2-water/saltwater–calcite. Orange represents CO2-water/saltwater-Berea. Green represents CO2-water/saltwater–Muscovite mica. (a) Static contact angle. ■, DI water-CO2, 296 K [85]; ●, Freshwater-CO2, ○, NaCl (0.8 mol·kg−1)-CO2, ●, NaCl (0.8 mol·kg−1)-CO2, 309.15 K [88]; ▲, NaCl (1.98 mol·kg−1)-CO2, ∆, Water-CO2, ★, NaCl (1.98 mol·kg−1)-CO2, 373 K [32]. (b) Dynamic contact angle. Solid points and × and + represent advanced angles. Hollow points and * and—represent receding angles. ■□, Water-CO2, 308 K, ▼▽, Water-CO2, 323 K [73]; ★☆, MgCl2 (20%wt)-CO2, ◆◇, CaCl2 (20%wt)-CO2, 323 K [77]; ×*, Water-CO2, 333.15 K, ●○, Water-CO2, 308.15 K [62]; ▲∆, NaCl (0.102 mol/L)-CO2, +—NaCl (1 mol/L)-CO2, 313.15 K [71].
The wettability alteration of caprocks as a function of the temperature and pressure in the presence of supercritical CO2 has been systematically investigated in previous studies. The wettability of the CO2-brine-mica/quartz system barely changes and remains wet, regardless of the conditions observed [86]. The substrates remained hydrophilic in most of the experimental temperature, pressure, and salinity ranges, whereas a sudden increase in the CAs (5–13°) was observed when CO2 was converted from the subcritical to the supercritical region for different rock samples in our previous work [32]. Alterations in the wettability of the caprock in the presence of supercritical CO2 have also been reported in other studies [62,71,86,87]. Based on previous research, wettability alternations of the caprock should be taken into consideration for accurate estimation of the CO2 storage capacity of a potential sequestration site. The wettability of rock/CO2/brine and rock/oil/CO2-enriched brine systems has been analyzed critically, and a future outlook was proposed in previous literature [100]. Until very recently, only limited investigations have been conducted regarding the CAs between reservoir rocks and water or brine, although wettability has a profound influence on fluid–fluid interactions in the presence of a solid surface under CO2 storage conditions [82].
Traditional contact angle measurements overlook the 3D pore geometry, surface roughness, and chemical heterogeneity, making them more prone to error. Hence, a micro-computed tomography (CT) scanner method was used to measure the local CAs of a CO2-brine–glass beads system at the pore scale [95,101]. However, there are obvious limitations and disadvantages associated with using the CT method. It is expensive, time-consuming, and the medical CT resolution is too low, resulting in only averaged saturations being measured, and this curvature measurement may be biased owing to its voxelized nature [82]. To overcome some of the abovementioned limitations and to deepen the fundamental understanding of the flow processes of supercritical CO2 via brine-saturated porous media, Nuclear Magnetic Resonance (NMR) with molecular resolution has recently been used to measure CO2-rock wettability in recent work [83]. Despite recent advances in our ability to accurately measure the wettability under reservoir conditions and engineer wettability in the subsurface, the complex physics of wetting continues to challenge our microscopic and macroscopic descriptions [82], owing to measurement disparities, variation in the sample type, roughness, contamination, and cleaning procedures [73,77,84,87]. Stefan et al. [85] proposed that the broad spread of CA data in the literature was caused by surface contamination. Thus, establishing a practical cleaning procedure for the surfaces of sample substrates is of vital importance for the accurate measurement of rock wettability [32,62,84,85,88].
Overall, the data on CO2-brine IFTs and rock CAs from laboratory studies are inadequate and contain discrepancies. Most of the experimental studies discussed above used the pendent drop method based on the ADSA method. Thus, experimental errors, inconsistent measurement procedures, and errors in the subsequent analytical techniques could explain these disparities. Therefore, to obtain adequate data with high integrity for CO2-brine IFTs and rock CAs corresponding to reservoir conditions, further laboratory and modelling research in terms of molecular dynamics and simplified equations of state is required, and the thermodynamic relations between interphase properties need to be elaborated in particular.
Based on the results discussed above, the following conclusions are relevant:
- Conventional methods in terms of the contact angle and tomographic imaging measurements have serious limitations.
- The disparity in the CA results in the reported data can be attributed to the differences in the experimental procedures, substrates, roughness, and cleaning procedures used for the substrate surfaces.
- The effects of the ionic strength and ionic type on the CAs of different substrates need to be further investigated to verify the effects of salinity on CAs.
- Alternation in the wettability of the caprock in the presence of supercritical CO2 has been observed, and a molecular dynamics method should be implemented to simulate this phenomenon at the molecular level.
2.3. The Mutual Solubility between CO2 and Water/Brine
Solubility capture is one of the main long-term carbon capture mechanisms, accounting for approximately 20% of the total capture amount at the initial stage of injection. It can capture up to 90% of the CO2 injection amount [11,102]. Thus, the mutual solubility between CO2 and reservoir fluids is one of the key thermodynamic properties that determines the flexibility of the CO2 saline aquifer sequestration scheme. Over the years, solubility data for CO2 + H2O systems have been reviewed and analyzed [103]. Laboratory solubility data for a CO2 + H2O system covering a wide range of temperatures and pressures are available in the previously published literature [104,105,106]. Recently, empirical equations and estimation models for water-saturated CO2 were developed based on experimental data available in the literature [107,108]. Then, modeling for the estimation of mutual solubility in the CO2 + H2O binary system was conducted [109,110,111,112,113].In addition, estimation methods of the p-T-x properties of the CO2 + H2O binary system were proposed by others [114,115].
Considering the effects of salinity on solubility, solubility estimation models based on the hybrid GE equation of state (EoS) [116], Anderko–Pitzer EOS [117], Pitzer EoS [118,119], PC-SAFT EoS [120], mixed solvent electrolyte (MSE) model, and Soave–Redlich–Kwong (SRK) EoS [121] were developed by previous researchers. Mutual solubility research on the CO2 + brine/complex brine binary system containing ions such as Na+, K+, Mg2+, and Ca2+ as well as Cl1−, SO2−4 for a temperature (T) of 273 K < T < 469 K, a molality (m) of 0 mol·kg−1 < m < 5.0 mol·kg−1, and pressure (p) of up to 104 MPa has been carried out over the years and is presented in Table 5 and Figure 6. Hou et al. [17] performed mutual solubility measurements on the CO2 + H2O binary system, and considering the effects of the dissolved salts, vapor–liquid equilibria were measured for the CO2 + H2O + NaCl/KCl system using the same analytical apparatus [17]. Duan’s model [122] was found to be broadly satisfactory for measuring the solubility of CO2 in NaCl (aq) but performed poorly for assessing the solubility of CO2 in KCl (aq). Ratnakar et al. [123] developed a method that uses an ionic strength-based mixing rule and extended the well-known Setschenow relation to capture the impact of a mixture of salts containing mono- or multivalent ions to predict the gas solubility in brine solutions with single or mixed salts. Then, Zhao et al. [124] used the Setschenow coefficient of ions to calculate the solubility of CO2 in mixed salt solutions. Most recently, Sun et al. [106] proposed a simple model for the prediction of mutual solubility in CO2 + H2O and CO2 + brine systems.
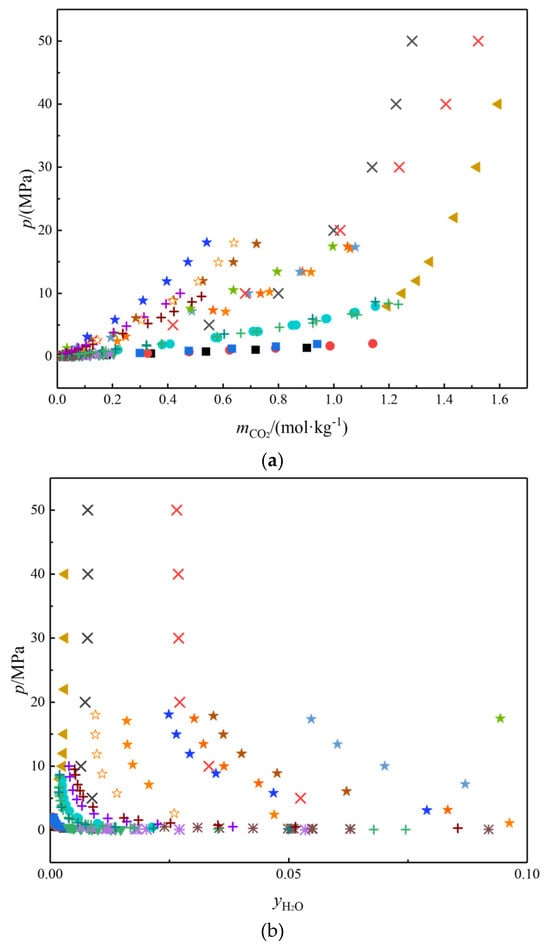
Figure 6.
Experimental mutual solubility. Symbols represent experimental data. (a) Pressure p plotted against molality mCO2 of CO2 in the aqueous phase; (b) pressure p plotted against mole fraction yH2O of water in the non-aqueous phase. ■, 274.15 K; ■, 282.15 K [125]; ●, 278.22 K; ● 318.23 K [126]; ▼, 288 K [127]; *, 298.2 K; *, 323.2 K [102]; ◄, 308.15 K [128]; ★, 373.15 K; ★, 398.15 K; ★, 423.15 K; ★, 448.15 K; ☆, 373.15 K, mNaCl = 2.5 mol·kg−1; ★, 423.15 K, mNaCl = 4 mol·kg−1; ★, 423.15 K, mKCl = 2.5 mol·kg−1 [17]; +, 313 K, mNaCl = 0.52 mol·kg−1; +, 313 K, mNaCl = 4.34 mol·kg−1; +, 353 K, mKCl = 0.5 mol·kg−1; +, 313 K, mKCl = 1 mol·kg−1; +, 353 K, mKCl = 4 mol·kg−1 [129]; mNaHCO3 = 0.8 mol·kg−1; ×, 348.15 K; ×, 398.15 K [130].
In the meantime, a well-developed model was proposed by Spycher and Pruess [131] to calculate the composition of the compressed CO2 and liquid H2O phases at equilibrium based on a noniterative procedure to evaluate the feasibility of CO2 geologic sequestration for temperatures between 285 K and 383 K and pressures of up to 60 MPa (i.e., 285 K ≤ T ≤ 383 K; p ≤ 60 MPa) by equating chemical potentials and using the Redlich–Kwong EoS. Because the equilibrium constant K (i.e., directly related to the standard Gibbs free energy of the reaction as ∆G0 = −RT ln K) is a more fundamental thermodynamic property than Henry’s law constant H, and because the formulation can be more easily extended to a non-ideal aqueous phase (i.e., resulting from the addition of salts) than formulations involving Henry’s law constant, K instead of H was used in their solubility model. In 2005, their [132] solubility model was extended to include the effect of chloride salts in the aqueous phase by combining the activity coefficient formulations of Duan and Sun [119] and Rumpf et al. [133] with their solubility correlations with an accuracy within the experimental uncertainty for solutions of up to 6 mol·kg−1 NaCl and 4 mol·kg−1 CaCl2. Then, Spycher and Pruess extended the temperature range of their solubility model up to 573 K (285 K ≤ T ≤ 573 K; p ≤ 60 MPa) in 2010 [134]. The Redlich and Wong equation [135] was used in the Spycher and Pruess [134] solubility model. Nevertheless, the basic Redlich–Kwong [136] equation can only be applied to a few rather simple fluids. This is because the parameters of the equation are based entirely on the two critical constants, namely the critical temperature (Tc) and the critical pressure (pc), and do not involve the acentric factor. The equation of Peng and Robinson [137] is structurally similar to the Redlich and Kwong [135] equation, but it contains an acentric factor for its application to a pure fluid. The content related to the equation of state can be found in the literature [138,139].
Therefore, to better estimate the phase equilibrium properties of mixtures composed of interacting molecules, the interaction parameter Kij based on the EoS and mixing rules can be correlated with the modified Peng–Robinson [137] EoS and the mixing rules of Panagiotopoulos and Reid [140]. Furthermore, in the Spycher and Pruess [134] model, different coefficients and parameters were developed for temperatures of above 373 K and below 373 K, such as the Margules expression and the equilibrium constant K. The activity coefficients used for the effects of different chloride salts in the brine system were the same, although it has been proven that the ion type has a significant influence on the mutual solubility of the CO2 + brine binary system. Thus, to develop a more reliable and simplified solubility model covering the P–T range of interest for applications to geologic CO2 sequestration, the original solubility model of Spycher and Pruess needs to be further modified by replacing the Redlich–Kwong [135] EoS with the Peng–Robinson [137], and the calculation methods of the mole fraction, equilibrium constant, and fugacity coefficient also needed to be optimized. According to the literature review presented in Table 5, it can be concluded that the main methods for modeling the solubility of liquid or gas phases include an EoS that is usually based on φ-φ [108,112] or γ-φ [17,129,134] equations.

Table 5.
Literature data for CO2-H2O/brine mutual solubility system.
Table 5.
Literature data for CO2-H2O/brine mutual solubility system.
| References | Aqueous Phase | m/ (mol·kg−1) | Temperature T/K | Pressure p/MPa |
|---|---|---|---|---|
| Bamberger et al. (2000) [112] | H2O | 0 | 323.2–353.1 | 4–14.2 |
| Servio et al. (2001) [141] | H2O | 0 | 278.05–283.15 | 2–3.7 |
| Anderson et al. (2002) [125] | H2O | 0 | 274.15–288.15 | 0.07–2.2 |
| Kiepe et al. (2002) [129] | H2O | 0 | 313.2–393.17 | 0.09–10 |
| Valtz et al. (2004) [126] | H2O | 0 | 278.2–318.2 | 0–8 |
| Chapoy et al. (2004) [108] | H2O | 0 | 274.14–351.31 | 0.19–7.31 |
| Iwai et al. (2004) [136] | H2O | 0 | 313.2 | 15 |
| Zhang et al. (2005) [142] | H2O | 0 | 304–313 | 1–4.6 |
| Dalmolin et al. (2006) [127] | H2O | 0 | 288–323 | 0.1–0.5 |
| Qin et al. (2008) [143] | H2O | 0 | 323.6–324.1 | 0.03–0.05 |
| Pereira et al. (2009) [102] | H2O | 0 | 298.2–323.2 | 0.05–0.6 |
| Martin et al. (2009) [144] | H2O | 0 | 353–393 | 10–30 |
| Han et al. (2009) [145] | H2O | 0 | 313.2–343.2 | 4.3–17.3 |
| Dell’Era et al. (2010) [146] | H2O | 0 | 298.48–298.63 | 0.2–0.8 |
| Ferrentino et al. (2010) [147] | H2O | 0 | 308.15–323.15 | 5.5–15 |
| Ruffine et al. (2010) [148] | H2O | 0 | 333 | 4.8–11.5 |
| Liu et al. (2011) [149] | H2O | 0 | 308.15–323.15 | 2–16 |
| Tabasinejad et al. (2011) [150] | H2O | 0 | 422.98–478.35 | 3.9–103.4 |
| Schüler et al. (2012) [151] | H2O | 0 | 308–333 | 0.101 |
| Liu et al. (2012) [152] | H2O | 0 | 308.15–318.15 | 8–16 |
| Hou et al. (2013) [17] | H2O | 0 | 298.15–448.15 | 1–18 |
| Serpa et al. (2013) [153] | H2O | 0 | 298–323 | 0.1–0.4 |
| Wang et al. (2013) [154] | H2O | 0 | 313.15–373.15 | 9–17.6 |
| Tong et al. (2013) [155] | H2O | 0 | 374.1–323.2 | 7.2–27.3 |
| Jiang et al. (2014) [156] | H2O | 0 | 333.15–373.15 | 8–18 |
| Bastami et al. (2014) [157] | H2O | 0 | 328.15–375.15 | 6.8–20.7 |
| Al Ghafri et al. (2014) [158] | H2O | 0 | 323.15 | 2–18.7 |
| Krotov et al. (2014) [159] | H2O | 0 | 353.3 | 0.6–9.7 |
| Meyer et al. (2015) [160] | H2O | 0 | 283.15–333.19 | 0–5 |
| Muromachi et al. (2015) [161] | H2O | 0 | 286.15–298.15 | 0.2–4.0 |
| Tang et al. (2015) [128] | H2O | 0 | 308.15–468.15 | 7.9–41 |
| Foltran et al. (2015) [162] | H2O | 0 | 313.15 | 8–12.5 |
| Rumpf et al. (1994) [133] | NaCl | 4–6 | 313–433 | 0.5–9.6 |
| Kiepe et al. (2002) [98,129] | NaCl | 0.5–4.3 | 313–352 | 0.1–10 |
| Bando et al. (2003) [163] | H2O/NaCl | 0–0.55 | 303–333 | 10–20 |
| Kiepe et al. (2002) [98,129] | KCl | 0.5–4.0 | 313–353 | 0.1–10.5 |
| Hou et al. (2013) [17] | NaCl/KCl | 2.5–4.0 | 323–423 | 2.6–18.2 |
| Tong et al. (2013) [155] | Complex brine | 1–5 | 310–425 | 1.2–34.9 |
| Hoballah et al. (2017) [130] | NaHCO3 | 0.8 | 348–398 | 5–50 |
Based on the results discussed above, the following conclusions are relevant:
- Empirical equations and estimation models for CO2 + H2O systems have been widely implemented to calculate the solubility of water-saturated CO2; however, they have limitations in estimating the solubility of H2O in compressed CO2.
- There are still too many parameters in the Duan et al. model, and most importantly, it is not intended to compute the solubility of H2O in a compressed CO2 gas phase and does not distinguish between ions of the same charge.
- Although the Krichevsky–Kasarnovsky (KK) approach provides a reasonably good representation of the data, it either fails to fit the data or yields an unphysically negative slope at higher temperatures.
- The well-developed Spycher and Pruess model is widely used to develop a more reliable and simplified model for determining the mutual solubility between CO2 and brines containing different ionic species and of different strengths.
- In the Spycher and Pruess model, different coefficients and parameters have been developed for temperatures above 373 K and below 373 K, such as the Margules expression and equilibrium constant K, which have no thermodynamic meaning. Furthermore, the activity coefficients used to determine the effects of different chloride salts in the brine system were the same. The interaction parameter Kij, based on the EoS and mixing rules, can still be correlated with the modified Peng–Robinson and the mixing rules of Panagiotopoulos and Reid.
The main methods used for modelling the solubility of liquid or gas phases include an EoS that is usually based on φ-φ or γ-φ equations. Previous solubility models were either limited to a certain range of temperatures or pressures, or were too complex. Most importantly, until very recently, limited research has been available for the simultaneous calculation of the mutual solubility of the CO2-rich phase and the H2O-rich phase with high integrity for the application of the CO2 saline aquifer storage scheme. Furthermore, the interaction mechanism coupling with multiple factors of the gas–liquid–solid interface properties and the dissolution and acidification process needs to be explored in future work.
2.4. pH of CO2-Saturated Brine
Modeling and experimental research have been carried out over the years to estimate the pH of the CO2-saturated brine system. In general, electrometric or optical methods are used to measure the pH of CO2-saturated brine or water, where the former is based on the electrode system [164], and the latter is based on UV–vis spectrophotometry [165,166,167]. Careful calibration of the measurement system is essential for both measurement approaches.
Previous studies on the pH of CO2-saturated aqueous solutions have mainly focused on water [168,169,170,171,172], seawater [173], and NaCl brines [174,175,176,177,178,179,180,181,182]. However, reservoir brines contain Na+, Cl−, K+, Ca2+, Mg2+, SO42−, HCO3−, and CO32−, which are expected to significantly influence the fluid properties [76,130,183]. Measurements of brines containing salts other than, or in addition to, NaCl were performed by Stefansson et al. [184], who studied complex systems containing Na2CO3, NaHCO3, NaOH, HCl, and NaCl, and by Li et al. [182], who studied both NaCl and NaHCO3 brines. An updated literature review on the pH measurement of CO2-saturated aqueous solutions is presented in our previous work [23]. According to a review of the previous literature [23,168,171,172,173,174,175,177,180,182,185], it can be concluded that the electrometric method is often used to measure the pH of CO2-saturated aqueous solutions covering a wide range of temperatures and pressures (pressures up to 35 MPa), due to its reliability and stability under reservoir conditions. While Toews et al. [169] and Parton et al. [170] measured the pH of the CO2-H2O system for the temperatures and pressures ranging from 298 to 343 K and from 7 to 20 MPa, respectively, via optical methods. Then, Shao et al. [179] used an optical method to measure the pH of a CO2-NaCl system for temperatures and pressures ranging from 298 to 366 K and from 0 to 20 MPa, respectively, while the pressure was 0.1 MPa for the same measurement system in Millero et al.’s work [178]. Also, in Stefansson et al.’s [184] work, the optical method was used to measure the pH of a CO2-saturated complex brine system at a low pressure range (pressures ranging from 1 to 2 MPa).
Typically, geochemical simulators such as PHREEQC [186] and EQ3NR [187] have been used to model the pH of gas-saturated aqueous solutions. These models implement the Pitzer model to calculate the activity coefficients of solutes in the aqueous phase, the correlations of Henry’s constant and an equation of state for gaseous components, and the correlations of standard equilibrium constants for aqueous-phase chemical reactions [188,189,190]. In a previous study on NaCl and NaHCO3, as well as KCl brines, the Pitzer model accounted well for the measured pH over a wide range of temperatures, pressures, and ionic strengths [23,182]. This type of model offers a convenient route for predicting the pH of complex brines with dissolved CO2; however, additional validation is required for brines other than NaCl (aq). Prior to estimating the pH, the solubility of gas-saturated aqueous solutions is calculated first in the PHREEQC; thus, the two important thermodynamic properties (pH and solubility) of gas-saturated aqueous solutions can be evaluated via geochemical simulators such as PHREEQC. However, there are limited studies available in the literature to investigate the thermodynamic relations between the pH and solubility of gas-saturated aqueous solutions.
Given the lack of experimental data, it is important to measure the pH of CO2-saturated brines other than NaCl (aq) over wide ranges of temperatures, pressures, and molalities. The range of investigated conditions should include those relevant to CO2 storage in deep-saline aquifers. In previous work, the pH of CO2-saturated aqueous KCl solutions was measured over wide ranges of temperature and pressure and at salt molalities of 2 mol·kg−1 and 4 mol·kg−1 [23]. It was observed that the influence of KCl on the pH under conditions of a constant temperature and CO2 partial pressure was different from that of NaCl, with the pH in the former being slightly higher. However, this difference in behavior is probably only significant in brines with high f K+ molalities [23]. The Pitzer model combined with the MacInnes convention [191], as implemented in PHREEQC version 3.5.0, provides a generally good prediction of the pH of the CO2-saturated aqueous KCl solutions [23]. Hence, previous work served to validate a geochemical simulator based on the Pitzer model for the prediction of pH in systems involving CO2 dissolved in water, NaCl (aq), NaHCO3 (aq), and KCl (aq) [23,172,182]. The influence of divalent cations on the pH of CO2-saturated aqueous solutions might be different from that of monovalent cations; thus, the model requires further validation for systems involving CO2 dissolved in brine containing other types of ionic ions, such as Ca2+ and Mg2+. To the best of our knowledge, there are no publications on the pH of a saturated CO2-CaCl2 solution and a saturated CO2-MgCl2 solution under high-temperature and high-pressure conditions. Therefore, the aim of future research on the pH of saturated CO2-brine is to validate the integrity of geochemical simulators based on the Pitzer model.
Based on the results discussed above, the following conclusions are relevant:
- Very limited research is available for the pH of gas-saturated aqueous solutions under CO2 saline aquifer storage conditions, although it is considered to be one of the most important parameters of reservoir fluids.
- In general, electrometric or optical methods are used to measure the pH of CO2-saturated brine or water. On the basis of the literature review, it can be concluded that the electrometric method is often used to measure the pH of CO2-saturated aqueous solutions covering a wide range of temperatures and pressures (pressures of up to 35 MPa) due to its reliability and stability under reservoir conditions.
- Geochemical simulators based on the Pitzer model offer a convenient route for predicting the pH of complex brines with dissolved CO2. However, additional validation is required for brines other than NaCl (aq).
- The pH and solubility of gas-saturated aqueous solutions can be evaluated via geochemical simulators such as PHREEQC. However, there are limited studies available in the literature to investigate the thermodynamic relations between the pH and solubility of gas-saturated aqueous. The mechanisms of dissolution and acidizing during the CO2 saline aquifer storage process need to be studied systematically, and thermodynamics relations between the pH and solubility of gas-saturated aqueous solutions need to be clarified.
- Given the lack of experimental data, it is important to measure the pH of CO2-saturated brines other than NaCl (aq) over wide ranges of temperatures, pressures, and molality. The range of investigated conditions should include those relevant to CO2 storage in deep-saline aquifers. The results of these experiments were compared with calculations based on the Pitzer model to validate the geochemical simulators based on the Pitzer model.
3. Influence of Interface Properties on the Pore-Scale Multi-Phase Flow
3.1. Core Flooding Experiment and Modelling
The CO2-water displacement process at the pore scale can be investigated via laboratory core flooding experiments under reservoir conditions using X-ray CT scanning technology [148,192,193,194]. The effects of different samples and flow rates on the CO2/brine displacement efficiency have been studied [195,196]. Laboratory core flooding experimental systems and apparatus for CO2 geological sequestration developed over the past decade have been reviewed carefully in previously published literature [197]. Meanwhile, the laboratory experiments have been replicated by implementing numerical models that can accurately interpolate the CO2/brine relative permeability by matching the experimental data. Subsequently, a 2D semi-analytical model was developed to predict the brine displacement efficiency over a wide range of capillary numbers [198]. Magnetic resonance imaging (MRI) has been widely used to study the migration of injected CO2 in porous media [199]. A multiphase flow experimental system based on MRI was used to study the multiphase flow and displacement process of CO2 during the storage of saline water layers. The local porosity of a single layer can be obtained using the MRI method so that the internal pore structure of porous media can be comprehensively analyzed, and the visual detection of multiphase seepage in porous media can be realized. In addition, MRI phase migration velocimetry can accurately and quantitatively analyze the flow velocity and mass transfer of multiphase seepage in porous media [200].
The flow of carbon dioxide is affected by the anisotropy of the porosity and permeability of the porous media; therefore, it is necessary to reasonably analyze the pore structure of the sealed formation during the process of carbon dioxide storage. Recently, a pore-scale fluid flow method based on pore network models from sample X-ray computed tomography (micro-CT) was developed to analyze the CO2/brine displacement process [71,201]. Pore network models have been widely used to analyze the core structure and multiphase flow simulation of oil/water to enhance oil recovery [202,203,204,205]. Currently, pore network multi-phase flow simulation models are being implemented in research on the CO2/brine seepage characteristics of reservoir rock samples to provide a fundamental understanding of the CO2/brine displacement process in porous media under CO2 reservoir storage conditions. Other models applied in the research of multiphase flow problems include the Lattice Boltzmann model (LBM) of multiphase flow system [206], the Shan–Chen (S-C) model [207], the four-parameter random growth method (QSGS) [208], the generalized Lattice Boltzmann model (GLBM) [209], and the Homogenized Lattice Boltzmann model (HLBM) [210]. However, limited pore-scale numerical simulations are available in the literature.
On the other hand, the thermodynamic properties, such as the interfacial tension, wettability, and density of the gas–liquid–solid system, are important parameters of pore network multi-phase flow simulation models. Different equations have been developed to consider the heterogeneity of wettability in pore network multi-phase flow simulation models [204,211]. The effects of fluid properties and flow conditions have been widely studied in previous research, whereas less emphasis has been given to the wettability of the CO2–water/brine–rock system, which is a key parameter that influences the storage capacity and security of the CO2 geological storage scheme. The influence of the thermodynamic properties on muti-phase flow in porous media is discussed in this section in terms of the wettability and interface properties via pore network multi-phase flow simulation models.
3.2. Effects of Wettability
In general, the wettability of a given rock/fluid system controls the pore-scale arrangement of fluids within the rock pore space, which, in turn, affects the micro- and reservoir-scale multiphase flow properties [212]. Previous studies in this area have focused on water-driven oil repellency. Morrow et al. [213] found, by using different methods, that when the rock wettability changes from hydrophilic to neutral or even lipophilic, the water percolation resistance increases significantly, the oil percolation resistance decreases, and the oil repellency efficiency tends to increase, with the highest repellency efficiency occurring for weakly water-wet rock samples. Furthermore, it is proposed that for low-permeability reservoirs, the shift in wettability from hydrophilic to neutral is an important mechanism for improving the recovery rate.
The relative permeability of bead-filled porous media with altered wetting conditions was also investigated in recent years by Landry et al. [214] based on the Lattice Boltzmann method. They found that changes in the surface wettability did not significantly affect the relative permeability of the wetted phase but resulted in a significant decrease in the relative permeability of the non-wetted phase [214]. Hwang et al. [215] investigated the effect of the fracture wettability on the capillary pressure and relative permeability profiles. They found that a larger proportion of non-water-wetted solid surfaces led to a higher relative water permeability for a given water saturation level [215]. Guo et al. [216] focused on the effect of wettability inhomogeneity on percolation and found that, under both homogeneous and inhomogeneous wetting conditions, the inhalation process increased the relative permeability of water and decreased the relative permeability of scCO2 compared to the repulsion process.
Thus, the wetting properties of the reservoir must be considered when studying its seepage characteristics to ensure the flexibility of the CO2 deep saline aquifer storage scheme [13]. Investigations of the seepage characteristics of the CO2-brine two-phase flow under CO2 deep saline aquifer storage conditions have been carried out for years via both laboratory experiments and numerical simulations in terms of relative permeability and capillary pressure.
Recently, researchers measured the contact angles between brine, dense CO2, and minerals representative of shales, such as mica and quartz [86,217]. They reported that the water-wettability of these minerals barely changed. Perrin and Benson [195] studied the CO2-brine displacement process in rock samples at various flow rates. They observed that the CO2-brine displacement efficiency depended on the heterogeneity of the cores and the flow rates. However, only limited laboratory experiments have been conducted regarding the wettability of reservoir rocks under CO2 storage conditions owing to the complexity of the experimental process. With the fast development of pore-scale numerical simulations, the effect of the wettability on fluid flow in porous media can be investigated via pore network models combined with X-ray computed tomography (micro-CT) [202,203,204,205,218,219]. Chen and Liu measured the percolation properties of a CO2-brine two-phase flow in porous media via pore network modeling [71,201]. It is believed that a two-phase flow simulation based on pore network modeling is a reliable, efficient, and economical method for investigating the reservoir CO2 storage capacity.
In a previous study, the pore network flow simulation model was used to study the influences of the thermodynamic properties and pore structure on the CO2-brine seepage characteristics at 323 K and 12.4 MPa with a 6 g/L NaCl solution, providing a fundamental understanding of the CO2-brine displacement process under CO2 reservoir storage conditions [220]. The results indicate that changing the rock-wetting behavior and interactions between the fluid and gas–rock has a significant effect on the gas-flooding process compared to water flooding as the temperature and pressure increase. To better understand the influence of wettability on the fluid flow in porous media, the CO2-brine two-phase flow behavior in homogenous Berea sandstone was investigated using the pore network flow simulation method [221]. A single wetting system was used for the flow simulation, and the sample was considered to be homogeneously wetted Berea sandstone. The results indicate that the fluid flow of gas and water is much better in a strongly water-wet system than in a completely CO2-wet system, and the entire system was in a stable displacement state.
However, most natural reservoir cores are heterogeneous wetting porous media, and their pore spaces are partly water-wet and partly hydrophilic. Thus, it is of great significance to study the effects of wettability heterogeneity on the gas–water flow under reservoir conditions. In our previous work, the influence of wettability on the CO2-brine two-phase flow behavior in a Berea sandstone sample was studied using a pore network numerical flow simulation method [222]. The results indicate that the heterogeneity of wettability has a significant influence on the CO2-brine two-phase flow behaviour during water flooding. When the non-wetting proportion of the system increases, the system becomes more CO2 wet, and the liquidity of the aqueous phase is enhanced; in the end, more CO2 is displaced by the aqueous phase. Therefore, saline with strong water-wetting properties might be the best site for CO2 storage because of the better CO2 flow characteristics of strong water-wetting porous media [222].
It seems that the numerical simulation based on pore network extraction is an efficient and economical method for studying the gas–water seepage characteristics under CO2 reservoir storage conditions, especially for investigating the influence of wettability on the fluid flow in porous media. However, the integrity of this method needs to be validated by combining it with the results of laboratory core flooding experiments.
3.3. Effects of Interphase Properties
In addition to the wettability, the influence of the thermodynamic properties, such as the interfacial tension, fluid flow rate, and viscosity, on multiphase flow in porous media is also a popular research topic. Gu et al. [223] experimentally determined that residual brine saturation is a function of the viscous force at a certain flow rate. As the flow rate increased, the residual brine saturation decreased, and the endpoint CO2 relative permeability increased. Lyi et al. [224] used the ANSYS-CFD technique to establish a numerical model for hot water injection in oil-bearing sandstone cores. It was found that the permeability (relative) of the oil flow curve was strongly influenced by the flow rate, whereas water had little or no effect on the relative permeability. A fully implicit isothermal compositional pore network model for gas and condensate flows was proposed by Reis et al. [225], which predicts the positive effect of flow on the relative permeability curve, and a higher relative permeability is expected at lower levels of IFT. Using an experimental method, Henderson et al. [226] found that the relative permeability of both phases increased with an increasing flow rate under both steady- and unsteady-state conditions. Increasing the value of the interphase IFT decreased the relative permeability of the gas phase more than that of the condensate phase.
The experimental data were analyzed by Balogun et al. [227] using the nonstationary water drive method and numerical calculations by history fitting, and it was found that the relative permeability curve increased for high-viscosity oil and decreased for low-viscosity oil as the flow rate increased. Esmaeili et al. [228] used the Johnson, Bossler, and Neumann (JBN) method and a history matching method to calculate the relative permeability of isothermal oil drive test results. The results showed that the relative oil-water permeability was almost insensitive to the viscosity ratio. Bennion et al. [229] found that the better the viscosity ratio between water and CO2 (the more favorable), the better the replacement effect. Later, it was found that the IFT may play a more important role in the variation in the relative permeability and endpoint saturation characteristics than the viscosity ratio [230].
Babadagli [231] suggested that a decrease in the IFT during the imbcycle process leads to a decrease in the capillary pressure, which in turn facilitates percolation. Jamialahmadi et al. [232] later confirmed this conclusion using the free-energy Lattice Boltzmann method. The effect of gas–tension was found after extensive experimental studies by Bennion et al. [230]: the relative permeability of a given system increases with a decreasing IFT. Later, Gu et al. [223] reconfirmed this conclusion; the curves of both phases shifted toward an increase in brine saturation as the IFT increased. Using an ideal pore-scale numerical model, Iyi et al. [233] analyzed the VOF and found that, under all wettability conditions, the repulsion efficiency could be improved by sufficiently reducing the IFT between fluid phases. By reducing the IFT and changing the wettability to a water-wet state, recovery could be improved.
Based on the results discussed above, the following conclusions are relevant:
The effects of thermodynamic properties on pore-scale multi-phase flow can be investigated via pore flooding experiments based on X-ray computed tomography (micro-CT) and pore-scale numerical simulations. The latter is widely used because of its high efficiency and economy. However, the pore-scale simulation model can be modified in combination with laboratory research to explore the influence of interface properties on multiphase flow in porous media.
Limited pore-scale numerical simulations are available in the literature. On the other hand, thermodynamic properties, such as the IFT and wettability of the gas–liquid–solid system, are important parameters of pore network multi-phase flow simulation models. The effects of fluid properties and flow conditions have been widely studied in previous research, whereas less emphasis has been given to the wettability of the CO2–water/brine–rock system, which is a key parameter influencing the storage capacity and security of the CO2 geological storage scheme.
The multi-dimensional and multi-scale gas–liquid flow visualization experiment, as well as pore-scale seepage numerical modeling coupling with multi-parameters, need to be carried out. The variation and the interaction mechanism of pore seepage features caused by the physical and chemical interactions of the multi-phase interface properties need to be clarified in future work to provide a theoretical base and technical guidance on the achievement of the CO2 geological storage and utilization project with high integrity and efficiency.
4. Conclusions
A detailed review devoted to the consideration and analysis of literature sources for the last 15 years on thermodynamic properties in the gas–liquid–solid system in the process of geological storage of carbon dioxide is presented in this study. After reviewing the previous literature, the following conclusion can be drawn:
- (1)
- A simplified IFT prediction model with thermodynamic significance and high integrity for predicting IFTs when a pseudo-plateau is reached needs to be developed in future work to cover a wide range of temperatures and pressures corresponding to CO2 geological storage conditions.
- (2)
- Further laboratory and modelling research on the wettability alternations of caprock in terms of the molecular dynamics and simplified equations of state is required, and the thermodynamic relations between interphase properties need to be elaborated in particular.
- (3)
- The main methods for modelling the mutual solubility of liquid or gas phases include EoS, which is usually based on φ-φ or γ-φ equations. Until very recently, limited research has been available on the simultaneous calculation of the mutual solubility of the CO2-rich phase and the H2O-rich phase with high integrity for the application of the CO2 saline aquifer storage scheme. Furthermore, interaction mechanism coupling with multi-factors associated with the gas–liquid–solid interface properties and the dissolution and acidification process need to be explored in future work.
- (4)
- Very limited research is available on the pH of gas-saturated aqueous solutions under CO2 saline aquifer storage conditions. Given the lack of experimental data, it is important to measure the pH of CO2-saturated brines other than NaCl (aq) over wide ranges of temperature, pressure, and molality relevant to CO2 storage in deep-saline aquifers in future work.
- (5)
- Multi-dimensional and multi-scale gas–liquid flow visualization experiments, as well as pore-scale seepage numerical modeling coupling with multi-parameters, need to be carried out. The variation and the interaction mechanism of pore seepage features caused by the physical and chemical interactions of the multi-phase interface properties need to be clarified in future work to provide a theoretical base for and technical guidance on the achievement of the CCUS project with high integrity and efficiency.
The main findings of this study can provide a reference for future research on the interface properties of gas–liquid–solid systems and can illustrate the mechanisms of pore-scale multi-phase flow during the CO2 geological storage and utilization process to provide a solid technical foundation for the low-carbon, clean, and efficient use of coal and other fossil energy sources, thereby contributing to national energy security.
Author Contributions
Investigation, M.M., Q.X., T.L., Y.Y. and F.X.; resources, M.M., Q.X., T.L., Y.Y. and F.X.; data curation, Q.X., T.L., Y.Y. and F.X.; writing—original draft preparation, M.M.; writing—review and editing, M.M.; visualization, Q.X., T.L., Y.Y. and F.X.; supervision, M.M.; project administration, M.M.; funding acquisition, M.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by funding from a Special Project for the key Research and Development Program of Xinjiang Autonomous Region (grant number 2022B01033-2), Central guide the development of local technology specific fund (grant number ZYYD2022C16), National Natural Science Foundation of China, China (grant numbers 52366010), Xinjiang Autonomous Region Innovation Environment (talents, base) construction special project-youth fund for natural science (grant number 2021D01C089), Dr. Tianchi Project (grant number TCBS202006).
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Peridas, G.; Mordick Schmidt, B. The role of carbon capture and storage in the race to carbon neutrality. Electr. J. 2021, 34, 106996. [Google Scholar] [CrossRef]
- Zhao, K.; Jia, C.; Li, Z.; Du, X.; Wang, Y.; Li, J.; Yao, Z.; Yao, J. Recent Advances and Future Perspectives in Carbon Capture, Transportation, Utilization, and Storage (CCTUS) Technologies: A Comprehensive Review. Fuel 2023, 351, 128913. [Google Scholar] [CrossRef]
- Golomb, D.; Pennell, S. Ocean sequestration of carbon dioxide (CO2). In Developments and Innovation in Carbon Dioxide (CO2) Capture and Storage Technology; Woodhead Publishing: Sawston, UK, 2010; Volume 2, pp. 304–323. [Google Scholar]
- Bello, A.; Ivanova, A.; Cheremisin, A. A Comprehensive Review of the Role of CO2 Foam EOR in the Reduction of Carbon Footprint in the Petroleum Industry. Energies 2023, 16, 1167. [Google Scholar] [CrossRef]
- Cai, B.F.; Li, Q.; Zhang, X.; Cao, C.; Cao, L.B.; Chen, W.H. China Carbon Dioxide Capture, Utilization, and Storage (CCUS) Annual Report (2021)—Research Path of China CCUS; China 21st Century Agenda Management Center: Beijing, China, 2021. [Google Scholar]
- Cai, B.; Li, Q.; Liu, G.; Liu, L.; Jin, T.; Shi, H. Environmental concern-based site screening of carbon dioxide geological storage in China. Sci. Rep. 2017, 7, 7598. [Google Scholar] [CrossRef] [PubMed]
- Krevor, S.; Blunt, M.J.; Benson, S.M.; Pentland, C.H.; Reynolds, C.; Al-Menhali, A.; Niu, B. Capillary trapping for geologic carbon dioxide storage—From pore scale physics to field scale implications. Int. J. Greenh. Gas Control 2015, 40, 221–237. [Google Scholar] [CrossRef]
- Bradshaw, J.; Bachu, S.; Bonijoly, D.; Burruss, R.; Holloway, S.; Christensen, N.P.; Mathiassen, O.M. CO2 storage capacity estimation: Issues and development of standards. Int. J. Greenh. Gas Control 2007, 1, 62–68. [Google Scholar] [CrossRef]
- Afolayan, B.; Mackay, E.; Opuwari, M. Dynamic modeling of geological carbon storage in an oil reservoir, Bredasdorp Basin, South Africa. Sci. Rep. 2023, 13, 16573. [Google Scholar] [CrossRef]
- Sminchak, J.; Neeraj, G.; Charles, B.; Perry, B. Issues Related to Seismic Activity Induced by the Injection of CO2 in Deep Saline Aquifers; National Energy Technology Laboratory: Pittsburgh, PA, USA; Morgantown, WV, USA, 2001. [Google Scholar]
- Macminn, C.W.; Szulczewski, M.L.; Juanes, R. CO2 migration in saline aquifers. Part 1. Capillary trapping under slope and groundwater flow. J. Fluid Mech. 2010, 662, 329–351. [Google Scholar] [CrossRef]
- Teng, Y.; Jiang, L.; Liu, Y.; Wang, D.; Song, Y. MRI study on CO2 capillary trap and drainage behavior in sandstone cores under geological storage temperature and pressure. Int. J. Heat Mass Transf. 2018, 119, 678–687. [Google Scholar] [CrossRef]
- Chalbaud, C.; Robin, M.; Lombard, J.; Martin, F.; Egermann, P.; Bertin, H. Interfacial tension measurements and wettability evaluation for geological CO2 storage. Adv. Water Resour. 2009, 32, 98–109. [Google Scholar] [CrossRef]
- Teng, Y.; Wang, P.; Jiang, L.; Liu, Y.; Song, Y.; Wei, Y. An experimental study of density-driven convection of fluid pairs with viscosity contrast in porous media. Int. J. Heat Mass Transf. 2020, 152, 119514. [Google Scholar] [CrossRef]
- Irfan, M.F.; Bisson, T.M.; Bobicki, E.; Arguelles-Vivas, F.; Xu, Z.; Liu, Q.; Babadagli, T. CO2 storage in saline aquifers by dissolution and residual trapping under supercritical conditions: An experimental investigation. Colloids Surf. A Physicochem. Eng. Asp. 2018, 548, 37–45. [Google Scholar] [CrossRef]
- Rosenbauer, R.J.; Thomas, B. Carbon dioxide (CO2) sequestration in deep saline aquifers and formations. In Developments and Innovation in Carbon Dioxide (CO2) Capture and Storage Technology; Woodhead Publishing: Sawston, UK, 2010; Volume 2, pp. 57–103. [Google Scholar]
- Hou, S.-X.; Maitland, G.C.; Trusler, J.P.M. Phase equilibria of (CO2 + H2O + NaCl) and (CO2 + H2O + KCl): Measurements and modeling. J. Supercrit. Fluids 2013, 78, 78–88. [Google Scholar] [CrossRef]
- Al-Bazali, T.; Zhang, J.; Chenevert, M.E.; Sharma, M. Measurement of the Sealing Capacity of Shale Caprocks; SPE Annual Technical Conference and Exhibition: Houston, TX, USA, 2005. [Google Scholar] [CrossRef]
- Kaszuba, J.P.; Janecky, D.R.; Snow, M.G. Carbon dioxide reaction processes in a model brine aquifer at 200 °C and 200 bars: Implications for geologic sequestration of carbon. Appl. Geochem. 2003, 18, 1065–1080. [Google Scholar] [CrossRef]
- Druckenmiller, M.L.; Maroto-Valer, M.M. Carbon sequestration using brine of adjusted pH to form mineral carbonates. Fuel Process. Technol. 2005, 86, 1599–1614. [Google Scholar] [CrossRef]
- Morse, J.W.; Arvidson, R.S. The dissolution kinetics of major sedimentary carbonate minerals. Earth Sci. Rev. 2002, 58, 51–84. [Google Scholar] [CrossRef]
- Alkhaldi, M.H.; Nasr-El-Din, H.A.; Sarma, H.K. Kinetics of the Reaction of Citric Acid with Calcite. SPE J. 2010, 15, 704–713. [Google Scholar] [CrossRef]
- Mutailipu, M.; Liu, Y.; Song, Y.; Trusler, J.P.M. The pH of CO2–saturated aqueous KCl solutions at temperatures between 298 K and 423 K at pressures up to 13.5 MPa. Chem. Eng. Sci. 2021, 234, 116434. [Google Scholar] [CrossRef]
- Saadatpoor, E.; Bryant, S.L.; Sepehrnoori, K. New trapping mechanism in carbon sequestration. Transp. Porous Media 2010, 82, 3–17. [Google Scholar] [CrossRef]
- Krevor, S.C.M.; Pini, R.; Li, B.; Benson, S.M. Capillary heterogeneity trapping of CO2 in a sandstone rock at reservoir conditions. Geophys. Res. Lett. 2011, 38, L15401. [Google Scholar] [CrossRef]
- Luhmann, A.J.; Kong, X.Z.; Tutolo, B.M.; Ding, K.; Saar, M.O.; Seyfried, W.E., Jr. Permeability reduction produced by grain reorganization and accumulation of exsolved CO2 during geologic carbon sequestration: A new CO2 trapping mechanism. Environ. Sci. Technol. 2012, 47, 242–251. [Google Scholar] [CrossRef] [PubMed]
- Trusler, J.P.M. Thermophysical Properties and Phase Behavior of Fluids for Application in Carbon Capture and Storage Processes. Annu. Rev. Chem. Biomol. Eng. 2017, 8, 381–402. [Google Scholar] [CrossRef] [PubMed]
- Ebigbo, A.; Class, H.; Helmig, R. CO2 leakage through an abandoned well: Problem-oriented benchmarks. Comput. Geosci. 2007, 11, 103–115. [Google Scholar] [CrossRef]
- Chadwick, A.; Arts, R.J.; Bernstone, C.; May, F.; Thibeau, S.; Zweigel, P. Best practice for the storage of CO2 in saline aquifers. Br. Geol. Surv. Occas. Publ. 2008, 14, 267. [Google Scholar]
- Espinoza, D.N.; Kim, S.H.; Santamarina, J.C. CO2 geological storage—Geotechnical implications. KSCE J. Civ. Eng. 2011, 15, 707–719. [Google Scholar] [CrossRef]
- Amshoff, P.; Weger, T.; Ostertag-Henning, C. Dissolution kinetics of CO2 and CO2-SO2 mixtures in water and brine at geological storage conditions of 16 MPa and 333 K. Int. J. Greenh. Gas Control 2018, 79, 173–180. [Google Scholar] [CrossRef]
- Mutailipu, M.; Liu, Y.; Jiang, L.; Zhang, Y. Measurement and estimation of CO2–brine interfacial tension and rock wettability under CO2 sub- and super-critical conditions. J. Colloid Interface Sci. 2019, 534, 605–617. [Google Scholar] [CrossRef]
- Jho, C.; Nealon, D.; Shogbola, S.; King, A.D. Effect of pressure on the surface tension of water: Adsorption of hydrocarbon gases and carbon dioxide on water at temperatures between 0 and 50 °C. J. Colloid Interface Sci. 1978, 65, 141–154. [Google Scholar] [CrossRef]
- Hebach, A.; Oberhof, A.; Dahmen, N.; Kögel, A.; Ederer, H.; Dinjus, E. Interfacial tension at elevated pressures measurements and correlations in the water + carbon dioxide system. J. Chem. Eng. Data 2002, 47, 1540–1546. [Google Scholar] [CrossRef]
- Kuang, N.; Yang, S.; Yuan, Z.; Wang, M.; Zhang, Z.; Zhang, X.; Wang, M.; Zhang, Y.; Li, S.; Wu, J. Study on oil and gas amphiphilic surfactants promoting the miscibility of CO2 and crude oil. ACS Omega 2021, 6, 27170–27182. [Google Scholar] [CrossRef]
- Chun, B.S.; Wilkinson, G.T. Interfacial Tension in High-Pressure Carbon Dioxide Mixtures. Ind. Eng. Chem. Res. 1995, 34, 4371–4377. [Google Scholar] [CrossRef]
- Akutsu, T.; Yamaji, Y.; Yamaguchi, H.; Watanabe, M.; Smith, R.L., Jr.; Inomata, H. Interfacial tension between water and high pressure CO2 in the presence ofhydrocarbon surfactants. Fluid Phase Equilibria 2007, 157, 163–168. [Google Scholar] [CrossRef]
- Kvamme, B.; Kuznetsova, T.; Hebach, A.; Oberhof, A.; Lunde, E. Measurements and modelling of interfacial tension for water + carbon dioxide systems at elevated pressures. Comput. Mater. Sci. 2007, 38, 506–513. [Google Scholar] [CrossRef]
- Georgiadis, A.; Llovell, F.; Bismarck, A.; Blas, F.J.; Galindo, A.; Maitland, G.C.; Trusler, J.P.M.; Jackson, G. Interfacial tension measurements and modelling of (carbon dioxide + n-alkane) and (carbon dioxide + water) binary mixtures at elevated pressures and temperatures. J. Supercrit. Fluids 2010, 55, 743–754. [Google Scholar] [CrossRef]
- Li, X.S.; Boek, E.; Maitland, G.C.; Trusler, J.P.M. Interfacial Tension of (Brines + CO2): (0.864 NaCl + 0.136 KCl) at Temperatures between (298 and 448) K, Pressures between (2 and 50) MPa, and Total Molalities of (1 to 5) mol.kg(−1). J. Chem. Eng. Data 2012, 57, 1078–1088. [Google Scholar] [CrossRef]
- Aggelopoulos, C.; Robin, M.; Vizika, O. Interfacial tension between CO2 and brine (NaCl + CaCl2) at elevated pressures and temperatures: The additive effect of different salts. Adv. Water Resour. 2011, 34, 505–511. [Google Scholar] [CrossRef]
- Nielsen, L.C.; Bourg, I.C.; Sposito, G. Predicting CO2-water interfacial tension under pressure and temperature conditions of geologic CO2 storage. Geochim. Cosmochim. Acta 2012, 81, 28–38. [Google Scholar] [CrossRef]
- da Rocha, S.R.P.; Johnston, K.P.; Westacott, R.E.; Rossky, P.J. Molecular structure of the water-supercritical CO2 interface. J. Phys. Chem. B 2001, 105, 12092–12104. [Google Scholar] [CrossRef]
- Kuznetsova, T.; Kvamme, B. Thermodynamic properties and interfacial tension of a model water-carbon dioxide system. Phys. Chem. Chem. Phys. 2002, 4, 937–941. [Google Scholar] [CrossRef]
- Li, Z.; Wang, S.; Li, S.; Liu, W.; Li, B.; Lv, Q.-C. Accurate Determination of the CO2−Brine Interfacial Tension Using Graphical Alternating Conditional Expectation. Energy Fuels 2014, 28, 624–635. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Feng, Q.H.; Wang, S.H.; Zhang, X.M.; Wang, S.L. Estimation of CO2-brine interfacial tension using an artificial neural network. J. Supercrit. Fluids 2016, 107, 31–37. [Google Scholar] [CrossRef]
- Partovi, M.; Mosalanezhad, M.; Lotfi, S.; Barati-Harooni, A.; Najafi-Marghmaleki, A.; Mohammadi, A.H. On the estimation of CO2-brine interfacial tension. J. Mol. Liq. 2017, 243, 265–272. [Google Scholar] [CrossRef]
- Liu, X.; Mutailipu, M.; Zhao, J.; Liu, Y. Comparative Analysis of Four Neural Network Models on the Estimation of CO2–Brine Interfacial Tension. ACS Omega 2021, 6, 4282–4288. [Google Scholar] [CrossRef] [PubMed]
- Song, Y.; Sung, W.; Jang, Y.; Jung, W. Application of an artificial neural network in predicting the effectiveness of trapping mechanisms on CO2 sequestration in saline aquifers. Int. J. Greenh. Gas Control 2020, 98, 103042. [Google Scholar] [CrossRef]
- Chow, Y.T.F.; Eriksen, D.K.; Galindo, A.; Haslam, A.J.; Jackson, G.; Maitland, G.C.; Trusler, J.P.M. Interfacial tensions of systems comprising water, carbon dioxide and diluent gases at high pressures: Experimental measurements and modelling with SAFT-VR Mie and square-gradient theory. Fluid Phase Equilibria 2016, 407, 159–176. [Google Scholar] [CrossRef]
- Chapman, W.G.; Gubbins, K.E.; Jackson, G.; Radosz, M. SAFT: Equation-of-state solution model for associating fluids. Fluid Phase Equilibria 1989, 52, 31–38. [Google Scholar] [CrossRef]
- Walter, G.; Chapman, K.E.G.; Jackson, G.; Radosz, M. New Reference Equation of State for Associating Liquids. Ind. Eng. Chem. Res. 1990, 29, 1709–1721. [Google Scholar]
- Müller, E.A.; Gubbins, K.E. Molecular-Based Equations of State for Associating Fluids: A Review of SAFT and Related Approaches. Ind. Eng. Chem. Res. 2001, 40, 2193–2211. [Google Scholar] [CrossRef]
- Economou, I.G. Statistical Associating Fluid Theory: A Successful Model for the Calculation of Thermodynamic and Phase Equilibrium Properties of Complex Fluid Mixtures. Ind. Eng. Chem. Res. 2002, 41, 953–962. [Google Scholar] [CrossRef]
- Paricaud, P.; Galindo, A.; Jackson, G. Recent advances in the use of the SAFT approach in describing electrolytes, interfaces, liquid crystals and polymers. Fluid Phase Equilibria 2002, 194–197, 87–96. [Google Scholar] [CrossRef]
- Tan, S.P.; Adidharma, H.; Radosz, M. Recent Advances and Applications of Statistical Associating Fluid Theory. Ind. Eng. Chem. Res. 2008, 47, 8063–8082. [Google Scholar] [CrossRef]
- McCabe, C.; Galindo, A. Chapter 8 SAFT Associating Fluids and Fluid Mixtures. In Applied Thermodynamics of Fluids; The Royal Society of Chemistry: London, UK, 2010; pp. 215–279. [Google Scholar] [CrossRef]
- Jerauld, G.R.; Korrani, A.K.N. Revised Correlation for Accurate Estimation of CO2-Brine Interfacial Tension at Reservoir Conditions. In Proceedings of the SPE Improved Oil Recovery Conference, Virtual, 25–29 April 2022. [Google Scholar] [CrossRef]
- Kashefi, K. Measurement and Modelling of Interfacial Tension and Viscosity of Reservoir Fluids; Heriot-Watt University: Edinburgh, UK, 2012. [Google Scholar]
- Chiquet, P.; Daridon, J.-L.; Broseta, D.; Thibeau, S. CO2/water interfacial tensions under pressure and temperature conditions of CO2 geological storage. Energy Convers. Manag. 2007, 48, 736–744. [Google Scholar] [CrossRef]
- Bikkina, P.K.; Shoham, O.; Uppaluri, R. Equilibrated Interfacial Tension Data of the CO2–Water System at High Pressures and Moderate Temperatures. J. Chem. Eng. Data 2011, 56, 3725–3733. [Google Scholar] [CrossRef]
- Saraji, S.; Goual, L.; Piri, M.; Plancher, H. Wettability of Supercritical Carbon Dioxide/Water/Quartz Systems: Simultaneous Measurement of Contact Angle and Interfacial Tension at Reservoir Conditions. Langmuir 2013, 29, 6856–6866. [Google Scholar] [CrossRef]
- Khosharay, S.; Varaminian, F. Experimental and modeling investigation on surface tension and surface properties of (CH4 + H2O), (C2H6 + H2O), (CO2 + H2O) and (C3H8 + H2O) from 284.15 K to 312.15 K and pressures up to 60 bar. Int. J. Refrig. 2014, 47, 26–35. [Google Scholar] [CrossRef]
- Pereira, L.M.C.; Chapoy, A.; Burgass, R.; Oliveira, M.B.; Coutinho, J.A.P.; Tohidi, B. Study of the impact of high temperatures and pressures on the equilibrium densities and interfacial tension of the carbon dioxide/water system. J. Chem. Thermodyn. 2016, 93, 404–415. [Google Scholar] [CrossRef]
- Liu, Y.; Li, H.A.; Okuno, R. Measurements and Modeling of Interfacial Tension for CO2/CH4/Brine Systems under Reservoir Conditions. Ind. Eng. Chem. Res. 2016, 55, 12358–12375. [Google Scholar] [CrossRef]
- Sutjiadi-Sia, Y.; Jaeger, P.; Eggers, R. Interfacial phenomena of aqueous systems in dense carbon dioxide. J. Supercrit. Fluids 2008, 46, 272–279. [Google Scholar] [CrossRef]
- Chow, Y.T.F.; Maitland, G.C.; Trusler, J.P.M. Martin Interfacial tensions of the (CO2 + N2 + H2O) system at temperatures of (298 to 448) K and pressures up to 40 MPa. J. Chem. Thermodyn. 2016, 93, 392–403. [Google Scholar] [CrossRef]
- Yang, D.; Tontiwachwuthikul, P.; Gu, Y. Interfacial Interactions between Reservoir Brine and CO2 at High Pressures and Elevated Temperatures. Energy Fuels 2005, 19, 216. [Google Scholar] [CrossRef]
- Chalbaud, C.A.; Robin, M.; Egermann, P. Interfacial tension data and correlations of brine-CO2 systems under reservoir conditions. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 24–27 September 2006; Society of Petroleum Engineers: Houston, TX, USA, 2006. [Google Scholar]
- Bachu, S.; Bennion, D.B. Interfacial Tension between CO2, Freshwater, and Brine in the Range of Pressure from (2 to 27) MPa, Temperature from (20 to 125) degrees C, and Water Salinity from (0 to 334 000) mg·L−1. J. Chem. Eng. Data 2009, 54, 765–775. [Google Scholar] [CrossRef]
- Liu, Y.; Mutailipu, M.; Jiang, L.L.; Zhao, J.F.; Song, Y.C.; Chen, L.Y. Interfacial tension and contact angle measurements for the evaluation of CO2-brine two-phase flow characteristics in porous media. Environ. Prog. Sustain. Energy 2015, 34, 1756–1762. [Google Scholar] [CrossRef]
- Liu, Y.; Tang, J.; Wang, M.; Wang, Q.; Tong, J.; Zhao, J.; Song, Y. Measurement of interfacial tension of CO2 and NaCl aqueous solution over wide temperature, pressure, and salinity ranges. J. Chem. Eng. Data 2017, 62, 1036–1046. [Google Scholar] [CrossRef]
- Arif, M.; Al-Yaseri, A.Z.; Barifcani, A.; Lebedev, M.; Iglauer, S. Impact of pressure and temperature on CO2-brine-mica contact angles and CO2-brine interfacial tension: Implications for carbon geo-sequestration. J. Colloid Interface Sci. 2016, 462, 208–215. [Google Scholar] [CrossRef] [PubMed]
- Pereira, L.M.C.; Chapoy, A.; Burgass, R.; Tohidi, B. Interfacial tension of CO2 + brine systems: Experiments and predictive modelling. Adv. Water Resour. 2017, 103, 64–75. [Google Scholar] [CrossRef]
- Yekeen, N.; Padmanabhan, E.; Abdulelah, H.; Irfan, S.A.; Okunade, O.A.; Khan, J.A.; Negash, B.M. CO2/brine interfacial tension and rock wettability at reservoir conditions: A critical review of previous studies and case study of black shale from Malaysian formation. J. Pet. Sci. Eng. 2021, 196, 107673. [Google Scholar] [CrossRef]
- Aggelopoulos, C.A.; Robin, M.; Perfetti, E.; Vizika, O. CO2/CaCl2 solution interfacial tensions under CO2 geological storage conditions: Influence of cation valence on interfacial tension. Adv. Water Resour. 2010, 33, 691–697. [Google Scholar] [CrossRef]
- Arif, M.; Jones, F.; Barifcani, A.; Iglauer, S. Electrochemical investigation of the effect of temperature, salinity and salt type on brine/mineral interfacial properties. Int. J. Greenh. Gas Control 2017, 59, 136–147. [Google Scholar] [CrossRef]
- Wang, H.; Luo, M.; Lun, Z.; Lv, C.; Zhao, C.H.; Zhao, Q.-N.; Lang, D. Determination and Comparison of Interfacial Interactions between CO2, Crude Oil, and Brine at Reservoir Conditions. Energy Fuels 2018, 32, 8187–8192. [Google Scholar] [CrossRef]
- Amooie, M.A.; Hemmati-Sarapardeh, A.; Karan, K.; Husein, M.M.; Soltanian, M.R.; Dabir, B. Data-driven modeling of interfacial tension in impure CO2-brine systems with implications for geological carbon storage. Int. J. Greenh. Gas Control 2019, 90, 102811. [Google Scholar] [CrossRef]
- Mutailipu, M. Gas-Liquid-Solid Interface Properties and Their Effect on the Seepage Characteristics under CO2 Geological Storage Conditions. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2020. [Google Scholar]
- Blunt, M.J. (Ed.) Multiphase Flow in Permeable Media: A Pore-Scale Perspective. In Multiphase Flow in Permeable Media: A Pore-Scale Perspective; Cambridge University Press: Cambridge, UK, 2017; pp. i–iv. [Google Scholar]
- Zhao, B.; MacMinn, C.W.; Juanes, R. Wettability control on multiphase flow in patterned microfluidics. Proc. Natl. Acad. Sci. USA 2016, 113, 10251–10256. [Google Scholar] [CrossRef] [PubMed]
- Baban, A.; Al-Yaseri, A.; Keshavarz, A.; Amin, R.; Iglauer, S. CO2–brine–sandstone wettability evaluation at reservoir conditions via Nuclear Magnetic Resonance measurements. Int. J. Greenh. Gas Control 2021, 111, 103435. [Google Scholar] [CrossRef]
- Bikkina, P.K. Contact angle measurements of CO2–water–quartz/calcite systems in the perspective of carbon sequestration. Int. J. Greenh. Gas Control 2011, 5, 1259–1271. [Google Scholar] [CrossRef]
- Iglauer, S.; Salamah, A.; Sarmadivaleh, M.; Liu, K.; Phan, C. Contamination of silica surfaces: Impact on water–CO2–quartz and glass contact angle measurements. Int. J. Greenh. Gas Control 2014, 22, 325–328. [Google Scholar] [CrossRef]
- Chiquet, P.; Broseta, D.; Thibeau, S. Wettability alteration of caprock minerals by carbon dioxide. Geofluids 2007, 7, 112–122. [Google Scholar] [CrossRef]
- Broseta, D.; Tonnet, N.; Shah, V. Are rocks still water-wet in the presence of dense CO2 or H2S? Geofluids 2012, 12, 280–294. [Google Scholar] [CrossRef]
- Farokhpoor, R.; Bjørkvik, B.J.A.; Lindeberg, E.; Torsæter, O. Wettability behaviour of CO2 at storage conditions. Int. J. Greenh. Gas Control 2013, 12, 18–25. [Google Scholar] [CrossRef]
- Shojai Kaveh, N.; Barnhoorn, A.; Wolf, K.H. Wettability evaluation of silty shale caprocks for CO2 storage. Int. J. Greenh. Gas Control 2016, 49, 425–435. [Google Scholar] [CrossRef]
- Li, X.; Fan, X.; Brandani, S. Difference in pore contact angle and the contact angle measured on a flat surface and in an open space. Chem. Eng. Sci. 2014, 117, 137–145. [Google Scholar] [CrossRef]
- Hobeika, N.; Bouriat, P.; Touil, A.; Broseta, D.; Brown, R.; Dubessy, J. Help from a Hindrance: Using Astigmatism in Round Capillaries to Study Contact Angles and Wetting Layers. Langmuir 2017, 33, 5179–5187. [Google Scholar] [CrossRef]
- Al-Zaidi, E.; Fan, X. Effect of aqueous electrolyte concentration and valency on contact angle on flat glass surfaces and inside capillary glass tubes. Colloids Surf. A Physicochem. Eng. Asp. 2018, 543, 1–8. [Google Scholar] [CrossRef]
- Kim, Y.; Wan, J.; Kneafsey, T.J.; Tokunaga, T.K. Dewetting of Silica Surfaces upon Reactions with Supercritical CO2 and Brine: Pore-Scale Studies in Micromodels. Environ. Sci. Technol. 2012, 46, 4228–4235. [Google Scholar] [CrossRef] [PubMed]
- Andrew, M.; Bijeljic, B.; Blunt, M.J. Pore-scale imaging of geological carbon dioxide storage under in situ conditions. Geophys. Res. Lett. 2013, 40, 3915–3918. [Google Scholar] [CrossRef]
- Lv, P.; Liu, Y.; Wang, Z.; Liu, S.; Jiang, L.; Chen, J.; Song, Y. In Situ Local Contact Angle Measurement in a CO2–Brine–Sand System Using Microfocused X-ray CT. Langmuir 2017, 33, 3358–3366. [Google Scholar] [CrossRef] [PubMed]
- Iglauer, S.; Lebedev, M. High pressure-elevated temperature X-ray micro-computed tomography for subsurface applications. Adv. Colloid Interface Sci. 2018, 256, 393–410. [Google Scholar] [CrossRef]
- Iglauer, S.; Mathew, M.S.; Bresme, F. Molecular dynamics computations of brine–CO2 interfacial tensions and brine–CO2–quartz contact angles and their effects on structural and residual trapping mechanisms in carbon geo-sequestration. J. Colloid Interface Sci. 2012, 386, 405–414. [Google Scholar] [CrossRef]
- Liang, Y.; Tsuji, S.; Jia, J.; Tsuji, T.; Matsuoka, T. Modeling CO2-Water-Mineral Wettability and Mineralization for Carbon Geosequestration. Acc. Chem. Res. 2017, 50, 1530–1540. [Google Scholar] [CrossRef]
- Wang, Z.; Yu, C.; Zhao, J.; Guo, P.; Liu, H. Molecular dynamics simulation for quantitative characterization of wettability transition on silica surface. J. Mater. Res. Technol. 2022, 19, 4371–4380. [Google Scholar] [CrossRef]
- Arif, M.; Abu-Khamsin, S.A.; Iglauer, S. Wettability of rock/CO2/brine and rock/oil/CO2-enriched-brine systems: Critical parametric analysis and future outlook. Adv. Colloid Interface Sci. 2019, 268, 91–113. [Google Scholar] [CrossRef]
- Lv, P.; Liu, Y.; Jiang, L.; Song, Y.; Wu, B.; Zhao, J.; Zhang, Y. Experimental determination of wettability and heterogeneity effect on CO2 distribution in porous media. Greenh. Gases Sci. Technol. 2016, 6, 401–415. [Google Scholar] [CrossRef]
- Siqueira Campos, C.E.P.; Villardi, H.G.D.A.; Pessoa, F.L.P.; Uller, A.M.C. Solubility of Carbon Dioxide in Water and Hexadecane: Experimental Measurement and Thermodynamic Modeling. J. Chem. Eng. Data 2009, 54, 2881–2886. [Google Scholar] [CrossRef]
- Scott, R.; Konynenburg, P.V. Static properties of solutions. Van der Waals and related models for hydrocarbon mixtures. Discuss. Faraday Soc. 1970, 49, 10. [Google Scholar] [CrossRef]
- Crovetto, R. Evaluation of Solubility Data of the System CO2-H2O from 273 K to the Critical Point of Water. J. Phys. Chem. Ref. Data 1991, 20, 575–589. [Google Scholar] [CrossRef]
- Carroll, J.; Slupsky, J.D.; Mather, A.E. The Solubility of Carbon Dioxide in Water at Low Pressure. J. Phys. Chem. Ref. Data 1991, 20, 1201–1209. [Google Scholar] [CrossRef]
- Sun, X.; Wang, Z.; Li, H.; He, H.; Sun, B. A simple model for the prediction of mutual solubility in CO2-brine system at geological conditions. Desalination 2021, 504, 114972. [Google Scholar] [CrossRef]
- Diamond, L.W.; Akinfiev, N.N. Solubility of CO2 in water from −1.5 to 100 °C and from 0.1 to 100 MPa: Evaluation of literature data and thermodynamic modelling. Fluid Phase Equilibria 2003, 208, 265–290. [Google Scholar] [CrossRef]
- Chapoy, A.; Mohammadi, A.H.; Chareton, A.; Tohidi, B.; Richon, D. Measurement and Modeling of Gas Solubility and Literature Review of the Properties for the Carbon Dioxide—Water System. Ind. Eng. Chem. Res. 2004, 43, 1794–1802. [Google Scholar] [CrossRef]
- King, M.B.; Mubarak, A.; Kim, J.D.; Bott, T.R. The mutual solubilities of water with supercritical and liquid carbon dioxides. J. Supercrit. Fluids 1992, 5, 296–302. [Google Scholar] [CrossRef]
- Shyu, G.; Hanif, N.S.M.; Hall, K.; Eubank, P.T. Carbon dioxide-water phase equilibria results from the Wong-San dler combining rules. Fluid Phase Equilibria 1997, 130, 73–85. [Google Scholar] [CrossRef]
- Duan, Z.; Møller, N.; Weare, J.H. An equation of state for the CH4-CO2-H2O system: II. Mixtures from 50 to 1000 °C and 0 to 1000 bars. Geochim. Cosmochim. Acta 1992, 56, 2619–2631. [Google Scholar] [CrossRef]
- Bamberger, A.; Sieder, G.; Maurer, G. High-pressure (vapor + liquid) equilibrium in binary mixtures of (carbon dioxide + water or acetic acid) at temperatures from 313 to 353 K. J. Supercrit. Fluids 2000, 17, 97–100. [Google Scholar] [CrossRef]
- Hu, J.; Duan, Z.; Zhu, C.; Chou, I.-M. PVTx properties of the CO2-H2O and CO2-H2O-NaCl systems below 647 K: Assessment of experimental data and thermodynamic models. Chem. Geol. 2007, 238, 249–267. [Google Scholar] [CrossRef]
- Coan, C.R.; King, A.D. Solubility of water in compressed carbon dioxide, nitrous oxide, and ethane: Evidence for hydration of carbon dioxide and nitrous oxide in the gas phase. J. Am. Chem. Soc. 1971, 93, 1857–1862. [Google Scholar]
- Carroll, J.J.; Mather, A.E. The system carbon dioxide-water and the Krichevsky-Kasarnovsky equation. J. Solut. Chem. 1992, 21, 607–621. [Google Scholar] [CrossRef]
- Orbey, H.; Sandler, S.I. Cubic Equations of State and Their Mixing Rules; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Bermejo, M.D.; Martín, A.; Florusse, L.J.; Peters, C.J.; Cocero, M.J. The influence of Na2SO4 on the CO2 solubility in water at high pressure. Fluid Phase Equilibria 2005, 238, 220–228. [Google Scholar] [CrossRef]
- Duan, Z.; Møller, N.; Weare, H. Equation of state for the NaCl-H2O-CO2 system: Prediction of phase equilibria and volu metric properties. Geochem. Cosmochem. Acta 1995, 59, 2869–2882. [Google Scholar] [CrossRef]
- Duan, Z.; Sun, R. An improved model calculating CO2 solubility in pure water and aqueous NaCl solutions from 273 to 533 K and from 0 to 2000 bar. Chem. Geol. 2003, 193, 257–271. [Google Scholar] [CrossRef]
- Yan, Y.Z.; Chen, C.C. Thermodynamic modeling of CO2 solubility in aqueous solutions of NaCl and Na2SO4. J. Supercrit. Fluids 2010, 55, 623–634. [Google Scholar] [CrossRef]
- Springer, R.D.; Wang, Z.; Anderko, A.; Wang, P.; Felmy, A.R. A thermodynamic model for predicting mineral reactivity in supercritical carbon dioxide: I. Phase behavior of carbon dioxide–water–chloride salt systems across the H2O-rich to the CO2-rich regions. Chem. Geol. 2012, 322/323, 151–171. [Google Scholar] [CrossRef]
- Duan, Z.; Sun, R.; Zhu, C.; Chou, I.M. An improved model for the calculation of CO2 solubility in aqueous solutions containing Na+, K+, Ca2+, Mg2+, Cl−, and SO42−. Mar. Chem. 2006, 98, 131–139. [Google Scholar] [CrossRef]
- Ratnakar, R.R.; Venkatraman, A.; Kalra, A.; Dindoruk, B. On the prediction of gas solubility in brine solutions with single or mixed salts: Applications to gas injection and CO2 capture/sequestration. J. Nat. Gas Sci. Eng. 2020, 81, 103450. [Google Scholar] [CrossRef]
- Zhao, H.; Dilmore, R.; Allen, D.E.; Hedges, S.W.; Soong, Y.; Lvov, S.N. Measurement and modeling of CO2 solubility in natural and synthetic formation brines for CO2 sequestration. Environ. Sci. Technol. 2015, 49, 1972–1980. [Google Scholar] [CrossRef] [PubMed]
- Anderson, G.K. Solubility of Carbon Dioxide in Water under Incipient Clathrate Formation Conditions. J. Chem. Eng. Data 2002, 47, 219–222. [Google Scholar] [CrossRef]
- Valtz, A.; Chapoy, A.; Coquelet, C.; Paricaud, P.; Richon, D. Vapour–liquid equilibria in the carbon dioxide–water system, measurement and modelling from 278.2 to 318.2 K. Fluid Phase Equilibria 2004, 226, 333–344. [Google Scholar] [CrossRef]
- Dalmolin, I.; Skovroinski, E.; Biasi, A.; Corazza, M.L.; Dariva, C.; Oliveira, J.V. Solubility of carbon dioxide in binary and ternary mixtures with ethanol and water. Fluid Phase Equilibria 2006, 245, 193–200. [Google Scholar] [CrossRef]
- Tang, Y.; Bian, X.; Du, Z.; Wang, C. Measurement and prediction model of carbon dioxide solubility in aqueous solutions containing bicarbonate anion. Fluid Phase Equilibria 2015, 386, 56–64. [Google Scholar] [CrossRef]
- Kiepe, J.; Horstmann, S.; Fischer, K.; Gmehling, J. Experimental determination and prediction of gas solubility data for CO2 + H2O mixtures containing NaCl or KCl at temperatures between 313 and 393 K and pressures up to 10 MPa. Ind. Eng. Chem. Res. 2002, 41, 4393–4398. [Google Scholar] [CrossRef]
- Hoballah, R. On the Solubility of Acid and Sour Gases in Water and Brines under Reservoir Conditions. Ph.D. Thesis, Imperial College London, London, UK, 2017. [Google Scholar]
- Spycher, N.; Pruess, K.; Ennis-King, J. CO2-H2O mixtures in the geological sequestration of CO2. I. Assessment and calculation of mutual solubilities from 12 to 100 °C and up to 600 bar. Geochim. Cosmochim. Acta 2003, 67, 3015–3031. [Google Scholar] [CrossRef]
- Spycher, N.; Pruess, K. CO2-H2O mixtures in the geological sequestration of CO2. II. Partitioning in chloride brines at 12–100 °C and up to 600 bar. Geochim. Cosmochim. Acta 2005, 69, 3309–3320. [Google Scholar] [CrossRef]
- Rumpf, B.; Nicolaisen, H.; Öcal, C.; Maurer, G. Solubility of carbon dioxide in aqueous solutions of sodium chloride: Experimental results and correlation. J. Solut. Chem. 1994, 23, 431–448. [Google Scholar] [CrossRef]
- Spycher, N.; Pruess, K. A phase-partitioning model for CO2–brine mixtures at elevated temperatures and pressures: Application to CO2-enhanced geothermal systems. Transp. Porous Media 2010, 82, 173–196. [Google Scholar] [CrossRef]
- Redlich, O.; Kwong, J.N.S. On the Thermodynamics of Solutions. V. An Equation of State. Fugacities of Gaseous Solutions. Chem. Rev. 1949, 44, 233–244. [Google Scholar] [CrossRef]
- Iwai, Y.; Uno, M.; Nagano, H.; Arai, Y. Measurement of solubilities of palmitic acid in supercritical carbon dioxide and entrainer effect of water by FTIR spectroscopy. J. Supercrit. Fluids 2004, 28, 193–200. [Google Scholar] [CrossRef]
- Peng, D.Y.; Robinson, D.B. A New Two-Constant Equation of State. Ind. Eng. Chem. Res. 1976, 15, 59–64. [Google Scholar] [CrossRef]
- Valderrama, J.O. The state of the cubic equations of state. Ind. Eng. Chem. Res. 2003, 42, 1603–1618. [Google Scholar] [CrossRef]
- Assael, M.J.; Trusler, J.P.M.; Tsolakis, T.F. Thermophysical Properties of Fluids: An Introduction to Their Prediction; Imperial College Press: London, UK, 1996. [Google Scholar]
- Panagiotopoulos, A.Z.; Reid, R.C. New Mixing Rules for Cubic Equations of State for Highly Polar Asymmetric Mixtures; ACS Symposium Series; American Chemical Society: Washington, DC, USA, 1986; pp. 571–582. [Google Scholar] [CrossRef]
- Servio, P.; Englezos, P. Effect of temperature and pressure on the solubility of carbon dioxide in water in the presence of gas hydrate. Fluid Phase Equilibria 2001, 190, 127–134. [Google Scholar] [CrossRef]
- Zhang, G.; Wu, Y.; Ma, P.; Wu, G.; Li, D. Measurement and correlation of solubility of carbon monoxide and other gases solubility in phenol. Huagong Xuebao J. Chem. Ind. Eng. 2005, 56, 2039–2045. [Google Scholar]
- Qin, J.; Rosenbauer, R.J.; Duan, Z. Experimental measurements of vapor–liquid equilibria of the H2O + CO2 + CH4 ternary system. J. Chem. Eng. Data 2008, 53, 1246–1249. [Google Scholar] [CrossRef]
- Martín, Á.; Pham, H.M.; Kilzer, A.; Kareth, S.; Weidner, E. Phase equilibria of carbon dioxide + poly ethylene glycol + water mixtures at high pressure: Measurements and modelling. Fluid Phase Equilibria 2009, 286, 162–169. [Google Scholar] [CrossRef]
- Han, J.M.; Shin, H.Y.; Min, B.-M.; Han, K.-H.; Cho, A. Measurement and correlation of high pressure phase behavior of carbon dioxide + water system. J. Ind. Eng. Chem. 2009, 15, 212–216. [Google Scholar] [CrossRef]
- Dell’Era, C.; Uusi-Kyyny, P.; Pokki, J.-P.; Pakkanen, M.; Alopaeus, V. Solubility of carbon dioxide in aqueous solutions of diisopropanolamine and methyldiethanolamine. Fluid Phase Equilibria 2010, 293, 101–109. [Google Scholar] [CrossRef]
- Ferrentino, G.; Barletta, D.; Balaban, M.O.; Ferrari, G.; Poletto, M. Measurement and prediction of CO2 solubility in sodium phosphate monobasic solutions for food treatment with high pressure carbon dioxide. J. Supercrit. Fluids 2010, 52, 142–150. [Google Scholar] [CrossRef]
- Ruffine, L.; Trusler, J.P.M. Phase behaviour of mixed-gas hydrate systems containing carbon dioxide. J. Chem. Thermodyn. 2010, 42, 605–611. [Google Scholar] [CrossRef]
- Liu, Y.; Hou, M.; Yang, G.; Han, B. Solubility of CO2 in aqueous solutions of NaCl, KCl, CaCl2 and their mixed salts at different temperatures and pressures. J. Supercrit. Fluids 2011, 56, 125–129. [Google Scholar] [CrossRef]
- Tabasinejad, F.; Moore, R.G.; Mehta, S.A.; Fraassen, K.C.V.; Barzin, Y.; Rushing, J.A.; Newsham, K.E. Water Solubility in Supercritical Methane, Nitrogen, and Carbon Dioxide: Measurement and Modeling from 422 to 483 K and Pressures from 3.6 to 134 MPa. Ind. Eng. Chem. Res. 2011, 50, 4029–4041. [Google Scholar] [CrossRef]
- Schüler, N.; Hecht, K.; Kraut, M.; Dittmeyer, R. On the Solubility of Carbon Dioxide in Binary Water–Methanol Mixtures. J. Chem. Eng. Data 2012, 57, 2304–2308. [Google Scholar] [CrossRef]
- Liu, Y.; Hou, M.; Ning, H.; Yang, D.; Yang, G.; Han, B. Phase equilibria of CO2 + N2 + H2O and N2 + CO2 + H2O + NaCl + KCl + CaCl2 systems at different temperatures and pressures. J. Chem. Eng. Data 2012, 57, 1928–1932. [Google Scholar] [CrossRef]
- Serpa, F.S.; Vidal, R.S.; Filho, J.H.B.A.; Nascimento, J.F.D.; Ciambelli, J.R.P.; Figueiredo, C.M.S.; Salazar-Banda, G.R.; Santos, A.F.; Fortuny, M.; Franceschi, E.; et al. Solubility of carbon dioxide in ethane-1,2-diol–water mixtures. J. Chem. Eng. Data 2013, 58, 3464–3469. [Google Scholar] [CrossRef]
- Wang, Z.; Felmy, A.R.; Thompson, C.J.; Loring, J.S.; Joly, A.G.; Rosso, K.M.; Schaef, H.T.; Dixon, D.A. Near-infrared spectroscopic investigation of water in supercritical CO2 and the effect of CaCl2. Fluid Phase Equilibria 2013, 338, 155–163. [Google Scholar] [CrossRef]
- Tong, D.; Trusler, M.; Vega-Maza, D. Solubility of CO2 in aqueous solutions of CaCl2 or MgCl2 and in a synthetic formation brine at temperatures up to 423 K and pressures up to 40 MPa. J. Chem. Eng. Data 2013, 58, 2116–2124. [Google Scholar] [CrossRef]
- Jiang, C.Y.; Wu, J.F.; Sun, Z.J.; Pan, Q.M. Solubility of water in supercritical CO2. Huaxue Gongcheng Xi’an 2014, 42, 42–47. [Google Scholar]
- Bastami, A.; Allahgholi, M.; Pourafshary, P. Experimental and modelling study of the solubility of CO2 in various CaCl2 solutions at different temperatures and pressures. Pet. Sci. 2014, 11, 569–577. [Google Scholar] [CrossRef]
- Al Ghafri, S.Z.S.; Forte, E.; Galindo, A.; Maitland, G.C.; Trusler, J.P.M. Experimental and Modeling Study of the Phase Behavior of (Heptane + Carbon Dioxide + Water) Mixtures. J. Chem. Eng. Data 2015, 60, 3670–3681. [Google Scholar] [CrossRef]
- Krotov, D.G. Further Development of the group contribution equation of state VTPR for description of electrolyte and polymer systems. Ph.D. Thesis, Universität Oldenburg, Oldenburg, Germany, 2014. [Google Scholar]
- Meyer, C.W.; Harvey, A.H. Dew-point measurements for water in compressed carbon dioxide. AIChE J. 2015, 61, 2913–2925. [Google Scholar] [CrossRef]
- Muromachi, S.; Shijima, A.; Miyamoto, H.; Ohmura, R. Experimental measurements of carbon dioxide solubility in aqueous tetra-n-butylammonium bromide solutions. J. Chem. Thermodyn. 2015, 85, 94–100. [Google Scholar] [CrossRef]
- Foltran, S.; Vosper, M.E.; Suleiman, N.B.; Wriglesworth, A.; Ke, J.; Drage, T.C.; Poliakoff, M.; George, M.W. Understanding the solubility of water in carbon capture and storage mixtures: An FTIR spectroscopic study of H2O + CO2 + N2 ternary mixtures. Int. J. Greenh. Gas Control 2015, 35, 131–137. [Google Scholar] [CrossRef]
- Bando, S.; Takemura, F.; Nishio, M.; Hihara, E.; Akai, M. Solubility of CO2 in Aqueous Solutions of NaCl at (30 to 60) °C and (10 to 20) MPa. J. Chem. Eng. Data 2003, 48, 576–579. [Google Scholar] [CrossRef]
- Marion, G.M.; Millero, F.J.; Camões, M.F.; Spitzer, P.; Feistel, R.; Chen, C.T.A. pH of seawater. Mar. Chem. 2011, 126, 89–96. [Google Scholar] [CrossRef]
- Byrne, R.H.; Breland, J.A. High precision multiwavelength pH determinations in seawater using cresol red. Deep. Sea Res. Part A Oceanogr. Res. Pap. 1989, 36, 803–810. [Google Scholar] [CrossRef]
- Clayton, T.D.; Byrne, R.H. Spectrophotometric seawater pH measurements: Total hydrogen ion concentration scale calibration of m-cresol purple and at-sea results. Deep. Sea Res. Part I Oceanogr. Res. Pap. 1993, 40, 2115–2129. [Google Scholar] [CrossRef]
- Robert-Baldo, G.L.; Morris, M.J.; Byrne, R.H. Spectrophotometric determination of seawater pH using phenol red. Anal. Chem. 1985, 57, 2564–2567. [Google Scholar] [CrossRef]
- Meyssami, B.; Balaban, M.O.; Teixeira, A.A. Prediction of pH in Model Systems Pressurized with Carbon Dioxide. Biotechnol. Prog. 1992, 8, 149–154. [Google Scholar] [CrossRef]
- Toews, K.L.; Shroll, R.M.; Wai, C.M.; Smart, N.G. pH-Defining Equilibrium between Water and Supercritical CO2. Influence on SFE of Organics and Metal Chelates. Anal. Chem. 1995, 67, 4040–4043. [Google Scholar] [CrossRef]
- Parton, T.; Spilimbergo, S.; Elvassore, N.; Bertucco, A. UV–VIS spectroscopy for the determination of diffusion coefficient and pH in aqueous solutions/sc-CO2 systems. In Proceedings of the 4th International Symposium on High Pressure Process Technology and Chemical Engineering, Venice, Italy, 22–25 September 2002; pp. 447–452. [Google Scholar]
- Rosenqvist, J.; Kilpatrick, A.D.; Yardley, B.W.D. Solubility of carbon dioxide in aqueous fluids and mineral suspensions at 294 K and subcritical pressures. Appl. Geochem. 2012, 27, 1610–1614. [Google Scholar] [CrossRef]
- Peng, C.; Crawshaw, J.P.; Maitland, G.C.; Trusler, J.P.M.; Vega-Maza, D. The pH of CO2-saturated water at temperatures between 308 K and 423 K at pressures up to 15 MPa. J. Supercrit. Fluids 2013, 82, 129–137. [Google Scholar] [CrossRef]
- Kimuro, B.; Kusayanagi, T.; Yamaguchi, F.; Ohtsubo, K.; Morishita, M. Basic experimental results of liquid CO2 injection into the deep ocean. IEEE Trans. Energy Convers. 1994, 9, 732–735. [Google Scholar] [CrossRef]
- Crolet, J.; Bonis, M. pH measurements in aqueous CO2 solutions under high pressure and temperature. Corrosion 1983, 39, 39–46. [Google Scholar] [CrossRef]
- Schaef, H.T.; McGrail, B.P.; Marti, P.F. Direct Measurements of pH and Dissolved CO2 Concentrations in H2O-CO2-NaCl Mixtures to Supercritical Conditions. In Proceedings of the Carbon Sequestration Second Annual Conference, Alexandria, VA, USA, 5–8 May 2003. [Google Scholar]
- Schaef, T.H.; McGrail, P.B. Direct measurements of pH and dissolved CO2 in H2O-CO2 brine mixtures to supercritical conditions. In Greenhouse Gas Control Technologies 7; Elsevier Science Ltd.: Oxford, UK, 2005; pp. 2169–2173. [Google Scholar] [CrossRef]
- Hinds, G.; Cooling, P.; Wain, A.; Zhou, S.; Turnbull, A. Technical Note: Measurement of pH in Concentrated Brines. Corrosion 2009, 65, 635–638. [Google Scholar] [CrossRef]
- Millero, F.J.; DiTrolio, B.R.; Suarez, A.F.; Lando, G. Spectroscopic measurements of the pH in NaCl brines. Geochim. Cosmochim. Acta 2009, 73, 3109–3114. [Google Scholar] [CrossRef]
- Shao, H.; Thompson, C.J.; Cantrell, K.J. Evaluation of experimentally measured and model-calculated pH for rock–brine–CO2 systems under geologic CO2 sequestration conditions. Chem. Geol. 2013, 359, 116–124. [Google Scholar] [CrossRef]
- Truche, L.; Bazarkina, E.F.; Berger, G.; Caumon, M.-C.; Bessaque, G.; Dubessy, J. Direct measurement of CO2 solubility and pH in NaCl hydrothermal solutions by combining in-situ potentiometry and Raman spectroscopy up to 280 °C and 150 bar. Geochim. Cosmochim. Acta 2016, 177, 238–253. [Google Scholar] [CrossRef]
- Haghi, R.K.; Chapoy, A.; Peirera, L.M.C.; Yang, J.; Tohidi, B. pH of CO2 saturated water and CO2 saturated brines: Experimental measurements and modelling. Int. J. Greenh. Gas Control 2017, 66, 190–203. [Google Scholar] [CrossRef]
- Li, X.; Peng, C.; Crawshaw, J.P.; Maitland, G.C.; Trusler, J.P.M. The pH of CO2-saturated aqueous NaCl and NaHCO3 solutions at temperatures between 308 K and 373 K at pressures up to 15 MPa. Fluid Phase Equilibria 2018, 458, 253–263. [Google Scholar] [CrossRef]
- Hyde, A.M.; Zultanski, S.L.; Waldman, J.H.; Zhong, Y.L.; Shevlin, M.; Peng, F. General principles and strategies for salting-out informed by the Hofmeister series. Org. Process Res. Dev. 2017, 21, 1355–1370. [Google Scholar] [CrossRef]
- Stefánsson, A.; Bénézeth, P.; Schott, J. Carbonic acid ionization and the stability of sodium bicarbonate and carbonate ion pairs to 200 °C—A potentiometric and spectrophotometric study. Geochim. Cosmochim. Acta 2013, 120, 600–611. [Google Scholar] [CrossRef]
- Mohammadian, E.; Hadavimoghaddam, F.; Kheirollahi, M.; Jafari, M.; Chenlu, X.; Liu, B. Probing Solubility and pH of CO2 in aqueous solutions: Implications for CO2 injection into oceans. J. CO2 Util. 2023, 71, 102463. [Google Scholar]
- Parkhurst, D.L.; Appelo, C.A.J. Description of input and examples for PHREEQC version 3: A computer program for speciation, batch-reaction, one-dimensional transport, and inverse geochemical calculations. In U.S. Geological Survey Techniques and Methods, Book 6; U.S. Geological Survey: Denver, CO, USA, 2013; p. 519. [Google Scholar]
- Wolery, T.J. EQ3NR: A Computer Program for Geochemical Aqueous Speciation-Solubility Calculations User’s Guide and Documentation; U.S. Department of Energy Office of Scientific and Technical Information: Oak Ridge, TN, USA, 1983; p. 202. [Google Scholar]
- Pitzer, K.S. Thermodynamics of electrolytes. I. Theoretical basis and general equations. J. Phys. Chem. 1973, 77, 268–277. [Google Scholar] [CrossRef]
- Plummer, L.N.; Parkhurst, D.L.; Fleming, G.W.; Dunkle, S.A. A Computer Program Incorporating Pitzer’s Equations for Calculation of Geochemical Reactions in Brines; U.S. Geological Survey: Denver, CO, USA, 1988. [Google Scholar]
- Pitzer, K.S. (Ed.) Activity Coefficients in Electrolyte Solutions; CRC Press: Boca Raton, FL, USA, 1991. [Google Scholar]
- MacInnes, D.A. The Activities of the Ions of Strong Electrolytes. J. Am. Chem. Soc. 1919, 41, 1086–1092. [Google Scholar] [CrossRef]
- Bennion, B.; Bachu, S. Drainage and imbibition relative permeability relationships for supercritical CO2/Brine and H2S/Brine systems in intergranular sandstone, carbonate, shale, and anhydrite rock. SPE Reserv. Eval. Eng. 2008, 11, 487–496. [Google Scholar] [CrossRef]
- Perrin, J.C.; Benson, S. An Experimental Study on the Influence of Sub-Core Scale Heterogeneities on CO2 Distribution in Reservoir Rocks. Transp. Porous Media 2010, 82, 93–109. [Google Scholar] [CrossRef]
- Krevor, S.C.M.; Pini, R.; Zuo, L.; Benson, S.M. Relative permeability and trapping of CO2 and water in sandstone rocks at reservoir conditions. Water Resour. Res. 2012, 48, 16. [Google Scholar] [CrossRef]
- Perrin, J.-C.; Michael, K.; Chia-Wei, K.; Ljuba, M.; Ethan, C.; Sally, M., B. Core-scale experimental study of relative permeability properties of CO2 and brine in reservoir rocks. Energy Procedia 2009, 1, 3515–3522. [Google Scholar] [CrossRef]
- Farokhpoor, R.; Lindeberg, E.G.B.; Torsaeter, O.; Mork, M.B.; Mork, A. Permeability and relative permeability measurements for CO2-brine system at reservoir conditions in low permeable sandstones in Svalbard. Greenh. Gases 2014, 4, 36–52. [Google Scholar] [CrossRef]
- Sun, Y.; Li, Q.; Yang, D.; Liu, X. Laboratory core flooding experimental systems for CO2 geosequestration: An updated review over the past decade. J. Rock Mech. Geotech. Eng. 2016, 8, 113–126. [Google Scholar] [CrossRef]
- Kuo, C.-W.; Benson, S.M. Numerical and analytical study of effects of small scale heterogeneity on CO2/brine multiphase flow system in horizontal corefloods. Adv. Water Resour. 2015, 79, 1–17. [Google Scholar] [CrossRef]
- Wang, S.; Jiang, L.; Cheng, Z.; Liu, Y.; Zhao, J.; Song, Y. Experimental study on the CO2-decane displacement front behavior in high permeability sand evaluated by magnetic resonance imaging. Energy 2021, 217, 119433. [Google Scholar] [CrossRef]
- Wang, S.; Cheng, Z.; Jiang, L.; Song, Y.; Liu, Y. Quantitative study of density-driven convection mass transfer in porous media by MRI. J. Hydrol. 2021, 594, 125941. [Google Scholar] [CrossRef]
- Chen, L.Y.; Liu, Y.; Mutailipu, M. Based on the Pore Network Model of CO2-Water-Quartz System Two-Phase Flow Characteristics Study. Adv. Mater. Res. 2014, 962–965, 1289–1292. [Google Scholar] [CrossRef]
- Dong, H.; Fjeldstad, S.; Alberts, L.; Roth, S.; Bakke, S.; Øren, P.-E.; Numerical Rocks, A. Pore network modelling on carbonate: A comparative study of different micro-CT network extraction methods. In Proceedings of the International Symposium of the Society of Core Analysts, Abu Dhabi, United Arab Emirates, 29 October–2 November 2008; pp. 22–29. [Google Scholar]
- Dong, H.; Blunt, M. Pore-network extraction from micro-computerized-tomography images. Phys. Rev. E 2009, 80, 036307. [Google Scholar] [CrossRef]
- Valvatne, P.H.; Blunt, M.J. Predictive pore-scale modeling of two-phase flow in mixed wet media. Water Resour. Res. 2004, 40, W07406. [Google Scholar] [CrossRef]
- Zhao, X.C.; Blunt, M.J.; Yao, J. Pore-scale modeling: Effects of wettability on waterflood oil recovery. J. Pet. Sci. Eng. 2010, 71, 169–178. [Google Scholar] [CrossRef]
- Gunstensen, A.K.; Rothman, D.H.; Zaleski, S.; Zanetti, G. Lattice Boltzmann model of immiscible fluids. Phys. Rev. A 1991, 43, 4320–4327. [Google Scholar] [CrossRef] [PubMed]
- Shan, X.; Chen, H. Lattice Boltzmann model for simulating flows with multiple phases and components. Phys. Rev. E 1993, 47, 1815–1819. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Wang, J.; Pan, N.; Chen, S. Mesoscopic predictions of the effective thermal conductivity for microscale random porous media. Phys. Rev. E 2007, 75, 036702. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Chen, L.; Kang, Q.; Rahman, S.S. Apparent permeability prediction of organic shale with generalized lattice Boltzmann model considering surface diffusion effect. Fuel 2016, 181, 478–490. [Google Scholar] [CrossRef]
- Lautenschlaeger, M.P.; Weinmiller, J.; Kellers, B.; Danner, T.; Latz, A. Homogenized lattice Boltzmann model for simulating multi-phase flows in heterogeneous porous media. Adv. Water Resour. 2022, 170, 104320. [Google Scholar] [CrossRef]
- Blunt, M.J.; Bijeljic, B.; Dong, H.; Gharbi, O.; Iglauer, S.; Mostaghimi, P.; Paluszny, A.; Pentland, C. Pore-scale imaging and modelling. Adv. Water Resour. 2012, 51, 197–216. [Google Scholar] [CrossRef]
- Alhammadi, A.M.; AlRatrout, A.; Singh, K.; Bijeljic, B.; Blunt, M.J. In situ characterization of mixed-wettability in a reservoir rock at subsurface conditions. Sci. Rep. 2017, 7, 10753. [Google Scholar] [CrossRef]
- Morrow, N.R. Wettability and its effect on oil recovery. J. Pet. Technol. 1990, 42, 1476–1484. [Google Scholar] [CrossRef]
- Landry, C.; Karpyn, Z.; Ayala, O. Relative permeability of homogenous-wet and mixed-wet porous media as determined by pore-scale lattice Boltzmann modeling. Water Resour. Res. 2014, 50, 3672–3689. [Google Scholar] [CrossRef]
- Hwang, S.I.; Lee, K.P.; Lee, D.S.; Powers, S.E. Effects of fractional wettability on capillary pressure–saturation–relative permeability relations of two-fluid systems. Adv. Water Resour. 2006, 29, 212–226. [Google Scholar] [CrossRef]
- Guo, R.; Dalton, L.; Crandall, D.; McClure, J.; Wang, H.; Li, Z.; Chen, C. Role of heterogeneous surface wettability on dynamic immiscible displacement, capillary pressure, and relative permeability in a CO2-water-rock system. Adv. Water Resour. 2022, 165, 104226. [Google Scholar] [CrossRef]
- Mahadevan, J. Comments on the paper titled “Contact angle measurements of CO2–water-quartz/calcite systems in the perspective of carbon sequestration”: A case of contamination? Int. J. Greenh. Gas Control 2012, 7, 261–262. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, J.; Zhang, Y.; Wang, D.; Li, Y.; Song, Y. Analysis of the influence of wettability on permeability in hydrate-bearing porous media using pore network models combined with computed tomography. J. Nat. Gas Sci. Eng. 2015, 26, 1372–1379. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, J.; Zhang, Y.; Wang, D.; Li, Y.; Song, Y. Analysis of the effect of particle size on permeability in hydrate-bearing porous media using pore network models combined with CT. Fuel 2016, 163, 34–40. [Google Scholar] [CrossRef]
- Mutailipu, M.; Liu, Y.; Wu, B.; Song, Y.; Wang, D.; Ai, L. Gas-Water Two Phase Flow Simulation Based on Pore Network Model for Reservoir Rocks. Energy Procedia 2017, 142, 3214–3219. [Google Scholar] [CrossRef]
- Mutailipu, M.; Liu, Y.; Wu, B. Simulation of wettability effects on gas-water flow in porous media. In Proceedings of the 16th International Heat Transfer Conference, Beijing, China, 10–15 August 2018. [Google Scholar]
- Mhriay, M.; Ying, T.; Peng, L.; Yu, L.; Yong, S. Numerical simulation of gas-water flow in heterogeneous wetting porous media. In Proceedings of the 4th Green House Gas Technology, Melbourne, Australia, 21–25 October 2018. [Google Scholar]
- Gu, S.J.; Lee, J.; Ki, S.; Huh, D.G.; Park, C.H. Effects of viscosity ratio, interfacial tension and flow rate on hysteric relative permeability of CO2/brine systems. Energy Oxf. 2017, 133, 62–69. [Google Scholar]
- Iyi, D.; Balogun, Y.; Oyeneyin, B.; Faisal, N. A numerical study of the effects of temperature and injection velocity on oil-water relative permeability for enhanced oil recovery. Int. J. Heat Mass Transf. 2022, 191, 122863. [Google Scholar] [CrossRef]
- Reis, P.; Carvalho, M.S. Pore-Scale Compositional Modeling of Gas-Condensate Flow: Effects of Interfacial Tension and Flow Velocity on Relative Permeability. J. Pet. Sci. Eng. 2021, 202, 108454. [Google Scholar] [CrossRef]
- Henderson, G.D.; Danesh, A.; Tehrani, D.H.; Peden, J.M. The effect of velocity and interfacial tension on relative permeability of gas condensate fluids in the wellbore region. J. Pet. Sci. Eng. 1997, 17, 265–273. [Google Scholar] [CrossRef]
- Balogun, Y.; Iyi, D.; Faisal, N.; Oyeneyin, B.; Oluyemi, G.; Mahon, R. Experimental investigation of the effect of temperature on two-phase oil-water relative permeability. J. Pet. Sci. Eng. 2021, 203, 108645. [Google Scholar] [CrossRef]
- Esmaeili, S.; Modaresghazani, J.; Sarma, H.; Harding, T.G.; Maini, B.B.J.F. Effect of temperature on relative permeability–Role of viscosity ratio. Fuel 2020, 278, 118318. [Google Scholar] [CrossRef]
- Bennion, B.; Bachu, S. Relative Permeability Characteristics for Supercritical CO2 Displacing Water in a Variety of Potential Sequestration Zones in the Western Canada Sedimentary Basin. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 9–12 October 2005. [Google Scholar]
- Bennion, D.B.; Bachu, S. Dependence on Temperature, Pressure, and Salinity of the IFT and Relative Permeability Displacement Characteristics of CO2 Injected in Deep Saline Aquifers. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 24–27 September 2006. [Google Scholar]
- Babadagli, T. Analysis of oil recovery by spontaneous imbibition of surfactant solution. Oil Gas Sci. Technol. 2005, 60, 697–710. [Google Scholar] [CrossRef]
- Mohammad, J.; Javad, A. Investigating the effect of interfacial tension and contact angle on capillary pressure curve, using free energy Lattice Boltzmann Method. J. Nat. Gas Sci. Eng. 2016, 35, 1146–1157. [Google Scholar]
- Iyi, D.; Balogun, Y.; Oyeneyin, B.; Faisal, N. Numerical Modelling of the Effect of Wettability, Interfacial Tension and Temperature on Oil Recovery at Pore-Scale level. J. Pet. Sci. Eng. 2021, 201, 108453. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).