Prediction of Dynamic Temperature and Thermal Front in a Multi-Aquifer Thermal Energy Storage System with Reinjection

Abstract

The accurate temperature and thermal front prediction in aquifer thermal energy storage systems during reinjection are crucial for optimal management and sustainable utilization. In this paper, a novel two-way fully coupled thermo–hydro model was developed to investigate the dynamic thermal performance and fronts for multiple aquifer thermal energy storage systems. The model was validated using a typical model, and the evolution characteristics of wellbore temperature before and after the breakthrough of the hydraulic front and thermal front were deeply studied. Sensitivity analysis was conducted to delineate the influence of various reservoir and reinjection factors on the thermal extraction temperature (TET). The results revealed that thermal conductivity significantly impacts the thermal extraction rate among the various reservoir factors. In contrast, volumetric heat capacity has the weakest influence and negatively correlates with the TET. Concerning the reinjection factors, the effect of the reinjection volume rate on the TET was significantly more significant than the reinjection temperature. Furthermore, the correlation between the TET and different properties was observed to be seriously affected by the exploitation period. The coupled model presented in this study offers insight into designing the exploitation scheme in deep reservoirs and geothermal resources.

1. Introduction

Geothermal energy is considered as one of the most promising sustainable, renewable, and clean energy resources, widely used for electricity generation, space heating, and greenhouse applications [1,2]. In recent years, aquifer thermal energy storage (ATES) has emerged as a promising alternative for preserving excess thermal energy for future demand, owing to its advantages of enormous storage capacity, easy implementation, environmental friendliness, and good economic benefits [3,4,5]. Reinjection has become a standard ATES system management strategy, which helps to enhance energy extraction efficiency and maintain reservoir pressure [6]. Accurately predicting temperature behavior and front propagation in ATES reinjection systems is vital for various applications, making it crucial for decision makers and geothermal engineers in terms of optimal design and sustainable utilization.

Field experiments are costly to perform [7]. However, it is crucial to determine the long-term performance of ATES systems before reinjection. Simulation technology of fluid flow and heat transfer processes has been integral to scientific research and applications over the past decades [8]. Despite the many efforts made to develop accurate numerical models, even with many simulations of geothermal systems being widely applied in over 100 fields worldwide [6], the complex nature of this issue still motivates several studies [9]. For example, how to accurately obtain the transient changes in various physical properties and effectively couple the seepage and temperature fields.

Significant advancements have been made in temperature modeling for fluid flow and heat transfer since the pioneering work of Lauwerier et al., who focused on simulating temperature distribution during the long-term injection of hot fluid to improve recovery percentages [10]. Gringarten and Sauty et al. then presented a non-steady state mathematical model to describe transient temperature behavior during the reinjection of heat-depleted water into aquifers, building upon Lauwerier, Carslaw, and Jaeger’s one-dimensional mass flow conceptual study [10,11,12,13]. Chen and Reddell developed an analytical solution to describe temperature behavior during thermal injection into a confined aquifer, whether steady or unsteady [14]. Their study also discussed temperature distribution in aquifer thermal energy storage (ATES) and petroleum engineering. In the 1990s, Molson et al. proposed a 3D finite element fully coupled model for simulating low-temperature groundwater flow and thermal energy transport [15]. Mongelli and Pagliarulo provided a simple model of groundwater flowing parallel to the terrestrial heat flow, allowing for calculating temperature distribution and determining the extent and magnitude of the zone of influence. [16]. Cheng et al. derived a multi-dimensional heat flow model for heat extraction by circulating water in a geothermal reservoir [17]. Boyadjiev et al. investigated temperature profiles in a porous medium and extended the Lauwerier model [10] to include fractional extensions [18]. Yang and colleagues proposed steady-state/transient temperature models that use Laplace transforms to describe ATES temperature behavior [19,20,21,22]. More recently, Lee derived a coupled hydrogeological numerical model for groundwater flow and heat transport, enabling the analysis of ATES thermal behavior and recovery temperatures [1]. Ganguly created a precise integral solution for a quasi-2D heat flow model in a complex geothermal reservoir. It considers advection, longitudinal conduction, and heat transfer to surrounding rock layers driven by vertical temperature differences [23].

In addition, numerical simulation software is widely used in this field. However, controlling the parameters and computational procedures can be complex, similar to a black box operation [24,25,26]. Computational schemes that are faster and more accurate have been developed in reservoir simulation, while other numerical simulation codes are still under development [7]. The term “black box” refers to situations in numerical simulation where a model’s internal mechanisms are unknown to the user. Users can only input data and observe output results without understanding the specific operational processes within the model. In such cases, it becomes challenging for users to assess the accuracy and reliability of the model. Consequently, issues are related to low interpretability, validation difficulties, and debugging challenges. There are various types of software available for numerical simulation, including commercial software (such as ANSYS and COMSOL), open-source software (like OpenFOAM), and general-purpose software (such as MATLAB and Python), among others. Commercial software can provide various functionalities and professional technical support, making it suitable for addressing various complex problems. However, its high cost may render it less practical for small teams and researchers. On the other hand, open-source software is advantageous due to its cost-free nature, open-source code, and strong community support, offering a high degree of flexibility. Nevertheless, it often comes with a steep learning curve, necessitating users to possess a certain level of programming and numerical computing expertise. General-purpose software like MATLAB and Python offers flexibility and can be employed for diverse mathematical modeling and simulation tasks, benefiting from extensive scientific computing libraries. However, they may not perform as well as specialized finite element software in handling complex problems in specific domains.

Despite these advances, few studies have been conducted on simultaneously estimating temperature profiles and predicting hydrodynamic and thermal fronts. The hydrodynamic front is where the injected fluid moves at a particular moment in ATES; the thermal front represents the position where the fluid interface temperature equals the injected fluid temperature at a specific moment. For example, in the geothermal doublet development process, one well is used for injection, while another is used for production. The reinjection of fluids tends to be much colder than the ATES system, which can cool the fluid produced from nearby wells. The premature breakthrough of hydrodynamic and thermal fronts can also cause operational problems, such as plant output running below design, added makeup wells costs, and field operations modifications [27]. Therefore, it is essential to determine the propagation of hydrodynamic and thermal fronts in an ATES system. This study will establish a fully coupled model to qualitatively evaluate the relationship between temperature and hydrodynamic/thermal front. Dynamic sensitivity analysis of production temperature was carried out from the space–time perspective.

Several researchers have studied the advancement of hydrodynamic and thermal fronts in ATES through field experiments or theoretical approaches. Bodvarsson’s early work in porous media highlighted two key findings: (a) the thermal front lags behind the hydrodynamic front by a constant related to volumetric heat capacities, and (b) a sudden temperature change occurs at the thermal front [28]. Later, Molz et al. performed two experiments to study heat storage in aquifers and utilized test data to calibrate mathematical models that account for the interconnected processes of fluid flow and heat transfer in ATES systems [29,30].

Lippmann, Satman, Gringarten, Tsang, and others delved into the advancement of hydrodynamic and thermal fronts in various contexts, including fractured porous media. They recognized that numerical codes are essential for modeling complex, heterogeneous systems [12,31,32,33]. Researchers also examined multiphase geothermal systems with varying formation properties, developing numerous numerical codes [34,35,36]. Stopa and Wojnarowski introduced a solution and equation that incorporate fluid thermal properties changing with temperature to estimate the velocity of the thermal front in geothermal reservoirs [37]. Ascencio developed a theoretical temperature model for cold water reinjection in naturally fractured systems, revealing several parameters’ influence on the thermal front movement rate [38]. In more recent work, Abbasi and their research team proposed an exact analytical solution to describe transient temperature profiles and the advancement of the thermal front [6,39]. Additionally, Shi developed a coupled thermal-hydraulic-mechanical model to investigate heat extraction performance and thermal breakthrough [2].

Although great successes have been achieved for decades, various simulation technology has been used to model ATES’s transient temperature distribution and fronts analysis. Most of the mentioned studies ignore the impacts of the complex wellbore configuration and multiple adjacent formations, leading to a lack of consideration for the thermal interaction involving the wellbore, adjacent formations, and the Multiple Aquifers Thermal Energy Storage (MATES) system. The depth-dependent downward velocity of tubing fluid and the temperature-dependent thermal properties of downhole fluid were also not highly valued. In addition, few scholars have studied the relationship between temperature and fronts qualitatively or quantitatively. Thus, there is little research relating temperature inside the tubing with the MATES system’s hydrodynamic front or thermal front. This study will provide insight into designing the exploitation scheme in deep reservoirs and geothermal resources.

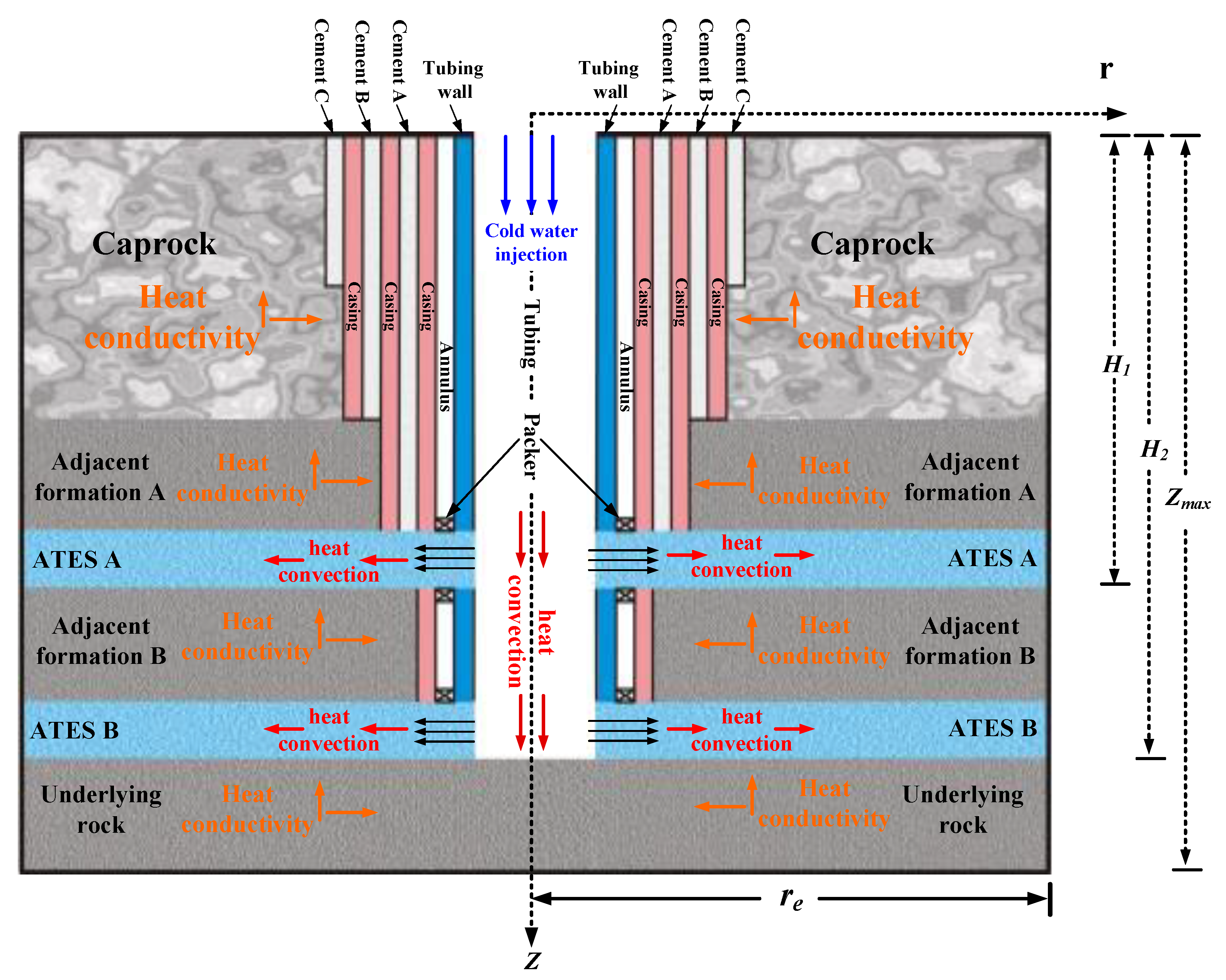
2. Heat Transfer Model

Figure 1 illustrates the 2D temperature model in cylindrical coordinates for the MATES system during cold water reinjection (e.g., injecting fluids into sandstone formations with large porosity and permeability), and the heat transfer process is depicted in the schematic diagram. To facilitate the research, the complex configuration of the MATES system is divided into three layers in the horizontal direction: the tubing with fluid flow, the tubing–casing annulus with static fluid, and the tubing wall, casing, cement ring, and formations that are divided into multiple layers based on different casing programs. Moreover, in the vertical direction, the MATES system can be divided into two parts: impermeable formations, including the caprock, the underlying rock, and the adjacent rocks, and aquifers. The heat transfer characteristics can be summarized as: (a) The ATES region is primarily characterized by horizontal thermal convection; (b) The region inside the tubing primarily involves vertical thermal convection; (c) Other areas and boundary locations are characterized by heat conduction.

In addition, in this fully coupled thermal-hydraulic model, the major assumptions and approximations are as follows [8,40,41]:

(a)

Undisturbed geothermal temperature of the downhole is a known function of depth, and the vertical borehole radius remains unchanged with depth.

(b)

The reinjection well thoroughly penetrates the MATES system, and the fluid flow is steady state.

(c)

MATES fluid flows are considered planar radial flow.

(d)

Fitting functions of the thermo–physical parameters with different temperatures are suitable for the coupled thermal-hydraulic model.

2.1. Two-Way Fully Coupled Mathematical Model

Based on the heat flow process of the model, the governing equation for the temperature field was derived. This research used the implicit finite difference method to solve the transient temperature distribution, and the different discrete schemes of the model are presented in Appendix A. Furthermore, the downhole mesh generation method is also illustrated in Appendix A.

2.1.1. Heat Transfer Model Inside the Tubing

During the reinjection process, the dominant heat transfers of the tubing fluid are considered to be continuous medium conduction and convection. Moreover, while the vertical component of the tubing fluid’s downward seepage velocity is taken into consideration, the radial part is neglected. Therefore, the heat transfer equation inside the tubing can be expressed as [8]:

$$\frac{1}{\mathrm{r}}\frac{\mathsf{\partial }}{\mathsf{\partial }\mathrm{x}}\left({\mathrm{r}\mathsf{\lambda }}_{\mathrm{w}}\frac{\mathsf{\partial }\mathrm{T}}{\mathsf{\partial }\mathrm{x}}\right)+\frac{\mathsf{\partial }}{\mathsf{\partial }\mathrm{z}}\left({\mathsf{\lambda }}_{\mathrm{w}}\frac{\mathsf{\partial }\mathrm{T}}{\mathsf{\partial }\mathrm{z}}\right)-\frac{\mathsf{\partial }}{\mathsf{\partial }\mathrm{z}}\left({\mathsf{\rho }}_{\mathrm{w}}{\mathrm{c}}_{\mathrm{w}}{\mathrm{v}}_{\mathrm{z}}\mathrm{T}\right)=\frac{\mathsf{\partial }}{\mathsf{\partial }\mathrm{t}}\left({\mathsf{\rho }}_{\mathrm{w}}{\mathrm{c}}_{\mathrm{w}}\mathrm{T}\right)$$

(1)

where T is the temperature at a specific reinjection time, λ_w is the thermal conductivity of the water, ρ_w is the density of water, c_w is the specific heat capacity of water, and v_z denotes the downward seepage velocity of the tubing fluid.

The downward seepage velocity of the tubing fluid is proportional to volume flow; thus, the tubing fluid’s downward seepage velocity (v_z) can be defined as:

$${\mathrm{v}}_{\mathrm{z}}=\{\begin{array}{c} \frac{{\mathrm{q}}_{\mathrm{in}}}{{\mathsf{\pi }\mathrm{r}}_{\mathrm{ti}}^2}, \mathrm{if} 0<{\mathrm{Z}}_{\mathrm{i}}\le {\mathrm{H}}_1\\ \frac{{\mathrm{q}}_{\mathrm{in}}}{{\mathsf{\pi }\mathrm{r}}_{\mathrm{ti}}^2}\left(1-{\mathrm{P}}_{\mathrm{A}}\right), \mathrm{if} {\mathrm{H}}_1<{\mathrm{Z}}_{\mathrm{i}}\le {\mathrm{H}}_2\\ \end{array}$$

(2)

where q_in is the total volumetric reinjection rate, r_ti is the inside radius of the tubing, P_A is the ratio of the volumetric reinjection rate of ATES A to the total volumetric reinjection rate, H₁ is the depth of the bottom of the ATES A, and H₂ is the depth of the bottom of the ATES B.

2.1.2. Heat Transfer Model from the Impermeable Formations to the Tubing Wall

For impermeable formations, heat conduction dominates heat transfer rather than convection. In addition, the tubing–casing annulus is assumed to fill with stagnant water, and thermal radiation effects are ignored. Thus, the transient temperature field governing equation for tubing, annulus, casing, cement, and impermeable formations can be given by [42]:

$$\frac{1}{\mathrm{r}}\frac{\mathsf{\partial }}{\mathrm{r}\mathsf{\partial }\mathrm{x}}\left({\mathrm{r}\mathsf{\lambda }}_{\mathrm{s}}^{*}\frac{\mathsf{\partial }\mathrm{T}}{\mathrm{r}\mathsf{\partial }\mathrm{x}}\right)+\frac{\mathsf{\partial }}{\mathsf{\partial }\mathrm{z}}\left({\mathsf{\lambda }}_{\mathrm{s}}^{*}\frac{\mathsf{\partial }\mathrm{T}}{\mathsf{\partial }\mathrm{z}}\right)=\frac{\mathsf{\partial }}{\mathsf{\partial }\mathrm{t}}\left({\left(\mathsf{\rho }\mathrm{c}\right)}_{\mathrm{s}}^{*}\mathrm{T}\right)$$

(3)

where

$${\mathsf{\lambda }}_{\mathrm{s}}^{*}={\mathsf{\lambda }}_{\mathrm{s}}^{1-\varnothing }{\mathsf{\lambda }}_{\mathrm{w}}^{\varnothing }$$

(4)

$${\left(\mathsf{\rho }\mathrm{c}\right)}_{\mathrm{s}}^{*}=\varnothing {\mathsf{\rho }}_{\mathrm{w}}{\mathrm{c}}_{\mathrm{w}}+\left(1-\varnothing \right){\mathsf{\rho }}_{\mathrm{s}}{\mathrm{c}}_{\mathrm{s}}$$

(5)

where ${\mathsf{\lambda }}_{\mathrm{s}}^{*}$ is the equivalent thermal conductivity of impermeable media, ${\left(\mathsf{\rho }\mathrm{c}\right)}_{\mathrm{s}}^{*}$ is the equivalent volumetric heat capacity of impermeable media, λ_s is the thermal conductivity of impermeable media, λ_w is the thermal conductivity of the water, ∅ is the porosity, ρ_w is the density of water, c_w is the specific heat capacity of water, ρ_s is the density of impermeable media, and c_s is the specific heat capacity of the impermeable media.

2.1.3. Heat Transfer Model of the MATES System

Heat conduction and convection dominated the heat transfer of the MATES system. Thus, the temperature field equation of the MATES system can be expressed as [8]:

$$\frac{1}{\mathrm{r}}\frac{\mathsf{\partial }}{\mathrm{r}\mathsf{\partial }\mathrm{x}}\left({\mathrm{r}\mathsf{\lambda }}_{\mathrm{m}}^{*}\frac{\mathsf{\partial }\mathrm{T}}{\mathrm{r}\mathsf{\partial }\mathrm{x}}\right)+\frac{\mathsf{\partial }}{\mathsf{\partial }\mathrm{z}}\left({\mathsf{\lambda }}_{\mathrm{m}}^{*}\frac{\mathsf{\partial }\mathrm{T}}{\mathsf{\partial }\mathrm{z}}\right)-\frac{\mathsf{\partial }}{\mathrm{r}\mathsf{\partial }\mathrm{x}}\left({\left(\mathsf{\rho }\mathrm{cv}\right)}_{\mathrm{r}}\mathrm{T}\right)=\frac{\mathsf{\partial }}{\mathsf{\partial }\mathrm{t}}\left({\left(\mathsf{\rho }\mathrm{c}\right)}_{\mathrm{m}}^{*}\mathrm{T}\right)$$

(6)

where

$${\mathsf{\lambda }}_{\mathrm{m}}^{*}={\mathsf{\lambda }}_{\mathrm{m}}^{1-\varnothing }{\mathsf{\lambda }}_{\mathrm{w}}^{\varnothing }$$

(7)

$${\left(\mathsf{\rho }\mathrm{c}\right)}_{\mathrm{m}}^{*}=\varnothing {\mathsf{\rho }}_{\mathrm{w}}{\mathrm{c}}_{\mathrm{w}}+\left(1-\varnothing \right){\mathsf{\rho }}_{\mathrm{m}}{\mathrm{c}}_{\mathrm{m}}$$

(8)

$${\left(\mathsf{\rho }\mathrm{cv}\right)}_{\mathrm{r}}={\mathsf{\rho }}_{\mathrm{w}}{\mathrm{c}}_{\mathrm{w}}{\mathrm{v}}_{\mathrm{wr}}\left(\mathrm{r}\right)$$

(9)

where ${\mathsf{\lambda }}_{\mathrm{m}}^{*}$ is the equivalent thermal conductivity of the aquifers, ${\left(\mathsf{\rho }\mathrm{c}\right)}_{\mathrm{m}}^{*}$ is the equivalent volumetric heat capacity of aquifers, λ_m is the thermal conductivity of the aquifers, ∅ is the porosity, ρ_w is the density of water, c_w is the specific heat capacity of water, ρ_m is the density of matrix in ATES, c_m is the specific heat capacity of the matrix in ATES, and v_wr(r) is the radial seepage velocity of the fluid in ATES.

The fluid flows of the MATES system are considered planar radial flow. Therefore, the fluid seepage velocity (v_wr) in Equation (9) is the function of the radial position:

$${\mathrm{v}}_{\mathrm{wr}}\left(\mathrm{r}\right)={\mathrm{q}}_{in}/\left(2{\mathsf{\pi }\mathrm{rh}}_m\varnothing \right)$$

(10)

where v_wr(r) is the radial seepage velocity of the fluid in ATES, q_in is the total volumetric reinjection rate, r is the radial distance from the borehole axis, h_m is the aquifer thickness, and ∅ is the porosity.

2.1.4. Initial and Boundary Conditions of the Model

Downhole initial (undisturbed) geothermal temperature is assumed to be a known function of depth. Thus, the initial condition can be written as:

$$\mathrm{T}{|}_{\mathrm{t}=0}={\mathrm{T}}_{\mathrm{sur}}+{\mathrm{g}}_{\mathrm{T}}\mathrm{z}$$

(11)

where T_sur is the initial surface temperature, g_T is the undisturbed geothermal gradient, and z is the vertical depth from surface.

In the radial direction, the borehole axis features an adiabatic boundary condition described as Equation (12); the coupled boundary conditions at interfaces between the tubing fluid and the tubing wall, the tubing fluid and the MATES system can be given by Equations (13) and (14), respectively. The outer boundary of the downhole temperature is assumed to be equal to the (undisturbed) geothermal temperature. Therefore, the outer boundary condition of the model can be defined by Equation (15).

$${\mathsf{\lambda }}_{\mathrm{w}}\frac{\mathsf{\partial }\mathrm{T}}{\mathsf{\partial }\mathrm{r}}{|}_{\mathrm{r}=0}=0$$

(12)

$$\{\begin{array}{c}{\mathrm{h}}_{\mathrm{c}}\left({\mathrm{T}}_{\mathrm{bf}}-{\mathrm{T}}_{\mathrm{bw}}\right)=-{\mathsf{\lambda }}_{\mathrm{s}}^{*}\frac{\mathsf{\partial }\mathrm{T}}{\mathsf{\partial }\mathrm{r}}{|}_{\mathrm{r}={\mathrm{r}}_{\mathrm{ti}}}\\ {\mathrm{T}}_{\mathrm{bf}}{|}_{\mathrm{r}={\mathrm{r}}_{\mathrm{ti}}}={\mathrm{T}}_{\mathrm{bw}}{|}_{\mathrm{r}={\mathrm{r}}_{\mathrm{ti}}} \end{array}$$

(13)

$$\{\begin{array}{c}{\mathsf{\lambda }}_{\mathrm{w}}\frac{\mathsf{\partial }\mathrm{T}}{\mathsf{\partial }\mathrm{r}}{|}_{\mathrm{r}={\mathrm{r}}_{\mathrm{ti}}}+\left|{\left(\mathsf{\rho }\mathrm{cv}\right)}_{\mathrm{r}}\right|\left({\mathrm{T}}_{\mathrm{tm}}-{\mathrm{T}}_{\mathrm{tw}}\right){|}_{\mathrm{r}={\mathrm{r}}_{\mathrm{ti}}}={\mathsf{\lambda }}_{\mathrm{s}2}^{*}\frac{\mathsf{\partial }\mathrm{T}}{\mathsf{\partial }\mathrm{r}}{|}_{\mathrm{r}={\mathrm{r}}_{\mathrm{ti}} } \\ {\mathrm{T}}_{\mathrm{tw}}{|}_{\mathrm{r}={\mathrm{r}}_{\mathrm{ti}}}={\mathrm{T}}_{\mathrm{tm}}{|}_{\mathrm{r}={\mathrm{r}}_{\mathrm{ti}}} \end{array}$$

(14)

$$\mathrm{T}{|}_{\mathrm{r}={\mathrm{r}}_{\mathrm{e}}}={\mathrm{T}}_{\mathrm{sur}}+{\mathrm{g}}_{\mathrm{T}}\mathrm{z}$$

(15)

where

$${\mathrm{h}}_{\mathrm{c}}=0.023\frac{{\mathsf{\lambda }}_{\mathrm{w}}}{\mathrm{L}}{\mathrm{R}}_{\mathrm{ef}}^{0.8}{\mathrm{P}}_{\mathrm{rf}}^{\mathrm{n}}$$

(16)

where h_c is the convection heat transfer coefficient, T_bf is the fluid temperature at the tubing/tubing wall interface, T_bw is the tubing wall temperature at the tubing/tubing wall interface, r_ti is the inside radius of the tubing, T_tm is the temperature of the ATES at the interface between the tubing and the ATES, T_tw is the tubing fluid temperature at the interface between the tubing and the ATES, r_e is the radial distance from the borehole axis to the reservoir limit, L is the characteristic length, R_ef is the Reynolds number, P_rf is the Prandtl number, and n = 0.4 for the fluid being heated, n = 0.3 for the fluid being cooled. Here, we let n = 0.3.

In the longitudinal direction, we assumed that no heat transfer is occurring at the model’s top and bottom; thus, their boundary conditions can be described as Equations (17)–(20), respectively. In addition, the coupled boundary condition at interfaces between the aquifers and adjacent formations can be defined by Equation (21).

$${\mathsf{\lambda }}_{\mathrm{w}}\frac{\mathsf{\partial }\mathrm{T}}{\mathsf{\partial }\mathrm{z}}{|}_{\mathrm{z}=0\left(\mathrm{r}\le {\mathrm{r}}_{\mathrm{ti}}\right)}=0$$

(17)

$${\mathsf{\lambda }}_{\mathrm{s}}^{*}\frac{\mathsf{\partial }\mathrm{T}}{\mathsf{\partial }\mathrm{z}}{|}_{\mathrm{z}=0\left({\mathrm{r}}_{\mathrm{ti}}<\mathrm{r}\le {\mathrm{r}}_{\mathrm{e}}\right)}=0$$

(18)

$${\mathsf{\lambda }}_{\mathrm{w}}\frac{\mathsf{\partial }\mathrm{T}}{\mathsf{\partial }\mathrm{z}}{|}_{\mathrm{z}={\mathrm{z}}_{\max }}\left(\mathrm{r}\le {\mathrm{r}}_{\mathrm{ti}}\right)=0$$

(19)

$${\mathsf{\lambda }}_{\mathrm{s}}^{*}\frac{\mathsf{\partial }\mathrm{T}}{\mathsf{\partial }\mathrm{z}}{|}_{\mathrm{z}={\mathrm{z}}_{\max }}\left({\mathrm{r}}_{\mathrm{ti}}<\mathrm{r}\le {\mathrm{r}}_{\mathrm{e}}\right)=0$$

(20)

$$\{\begin{array}{c}{\mathsf{\lambda }}_{\mathrm{s}}^{*}\frac{\mathsf{\partial }\mathrm{T}}{\mathsf{\partial }\mathrm{z}}{|}_{\mathrm{z}={\mathrm{z}}_{\mathrm{b}}}\left({\mathrm{r}}_{\mathrm{ti}}<\mathrm{r}\le {\mathrm{r}}_{\mathrm{e}}\right)={\mathsf{\lambda }}_{\mathrm{m}}^{*}\frac{\mathsf{\partial }\mathrm{T}}{\mathsf{\partial }\mathrm{z}}{|}_{\mathrm{z}={\mathrm{z}}_{\mathrm{b}}} \left({\mathrm{r}}_{\mathrm{ti}}<\mathrm{r}\le {\mathrm{r}}_{\mathrm{e}} \right) \\ {\mathrm{T}}_{\mathrm{bm}}{|}_{\mathrm{z}={\mathrm{z}}_{\mathrm{b}}}={\mathrm{T}}_{\mathrm{bs}}{|}_{\mathrm{z}={\mathrm{z}}_{\mathrm{b}}} \end{array}$$

(21)

where r_ti is the inside radius of the tubing, r_e is the radial distance from the borehole axis to the reservoir limit, z_max is the total well depth from surface, z_b is the depth of boundaries between the aquifers and the adjacent formations, T_bm is the temperature of aquifers at interfaces between the aquifers and the adjacent formations, and T_bs is the temperature of adjacent formations at interfaces between the aquifers and the adjacent formations.

2.1.5. Fluid Thermo–Physical Properties with Different Temperature

Regression analysis was used to study the thermo–physical properties of the fluid at different temperatures. The density (ρ_w(T)), specific heat capacity (c_w(T)), and thermal conductivity (λ_w(T)) empirical formulas can be defined by Equations (22), (23) and (24), respectively. Further details on the data source and regression analysis of different parameters are presented in Appendix B.

$${\mathsf{\rho }}_{\mathrm{w}}\left(\mathrm{T}\right)=-0.0027{\mathrm{T}}^2-0.1395\mathrm{T}+1005.4$$

(22)

$${\mathrm{c}}_{\mathrm{w}}\left(\mathrm{T}\right)=0.0001{\mathrm{T}}^3-0.036{\mathrm{T}}^2-3.1\mathrm{T}+4103.9$$

(23)

$${\mathsf{\lambda }}_{\mathrm{w}}\left(\mathrm{T}\right)=7.8889\times {10}^{-6}{\mathrm{T}}^2+0.002\mathrm{T}+0.5603$$

(24)

2.1.6. Derivation of Hydrodynamic Front and Thermal Front Migration Model

The fluid flows of MATES system are considered as planar radial flow in this model, and the fluid seepage velocity (v_wr) of MATES system can be obtained from Equation (10). Thus, the hydrodynamic breakthrough time (${\mathrm{t}}_{\mathrm{HB}}$) can be derived by:

$${\mathrm{t}}_{\mathrm{HB}}={{\displaystyle \int }}_{{\mathrm{r}}_{\mathrm{ti}}}^{{\mathrm{r}}_{\mathrm{e}}}\frac{\mathrm{dr}}{{\mathrm{v}}_{\mathrm{wr}}\left(\mathrm{r}\right)}={\frac{{\mathsf{\pi }\mathrm{r}}^2\mathrm{h}\varnothing }{\varnothing }|}_0^{{\mathrm{r}}_{\mathrm{e}}}=\frac{\mathsf{\pi }\mathrm{h}\varnothing \left({\mathrm{r}}_{\mathrm{e}}^2-{\mathrm{r}}_{\mathrm{ti}}^2\right)}{{\mathrm{q}}_{\mathrm{in}}}$$

(25)

Based on the conservation of mass and energy theory for single-phase fluid in porous media, the thermal breakthrough time is delayed by a constant value relative to the hydrodynamic breakthrough time. Thus, it can be expressed as follows [37]:

$${\mathrm{t}}_{\mathrm{TB}}={\mathrm{t}}_{\mathrm{HB}}\left(1+{\mathrm{D}}_{\mathrm{T}}\right)$$

(26)

where

$${\mathrm{D}}_{\mathrm{T}}=\frac{\left(1-\varnothing \right){\mathsf{\rho }}_{\mathrm{m}}{\mathrm{c}}_{\mathrm{m}}}{\varnothing {\mathsf{\rho }}_{\mathrm{w}}{\mathrm{c}}_{\mathrm{w}}}$$

(27)

where ∅ is the porosity, ρ_m is the density of matrix in ATES, c_m is the specific heat capacity of the matrix in ATES, ρ_w is the density of water, and c_w is the specific heat capacity of water.

Incorporating Equation (25), the radial position (r_HF) of the hydrodynamic front with different reinjection times can be given by:

$${\mathrm{r}}_{\mathrm{HF}}=\sqrt{\frac{{\mathrm{q}}_{\mathrm{in}}\mathrm{t}}{\varnothing {\mathsf{\pi }\mathrm{h}}_m}+{\mathrm{r}}_{\mathrm{ti}}^2}$$

(28)

where q_in is the total volumetric reinjection rate, t is the reinjection time, ∅ is the porosity, h_m is the aquifer thickness, and r_ti is the inside radius of the tubing.

Although any contribution from adjacent strata is neglected, the radial position (r_TF) of the thermal front at different reinjection times can be computed using the equation proposed by Ascencio et al. [38]:

$${\mathrm{r}}_{\mathrm{TF}}=\sqrt{{\mathsf{\omega }}_{\mathrm{f}}}{\mathrm{r}}_{\mathrm{HF}}$$

(29)

where

$${\mathsf{\omega }}_{\mathrm{f}}=\frac{\varnothing {\mathsf{\rho }}_{\mathrm{w}}{\mathrm{c}}_{\mathrm{w}}}{{\left(\mathsf{\rho }\mathrm{c}\right)}_{\mathrm{m}}^{*}}$$

(30)

where ∅ is the porosity, ρ_w is the density of water, c_w is the specific heat capacity of water, and ${\left(\mathsf{\rho }\mathrm{c}\right)}_{\mathrm{m}}^{*}$ is the equivalent volumetric heat capacity of aquifers.

2.2. Model Validation

The proposed coupled model was programmed and compared with Li’s classical analytical model [20] to ensure the mathematical equations were accurately modeled without errors. The analytical model of Li and the proposed model were based on similar concepts and reinjection forms, making the simplified model (Figure 2a) suitable for verifying the accuracy of the mathematical derivation of the proposed model. The simplified model consisted of the wellbore, an aquifer with overlying and underlying rock, and its geometry parameters, ambient temperature, and reinjection conditions are given in

Table A1. Geometry properties, ambient temperature, and reinjection conditions.

Properties	Value
Outside radius of wellbore (rwb)/m	0.09
Reservoir limit (re)/m	184.36
Thickness of overlying (hover)/m	30
Thickness of aquifer (hm)/m	10
Thickness of underlying (hunder)/m	60
Total volumetric Reinjection rate (qin)/ m3/d	271.43
Reinjection temperature (Tin)/ °C	20
Surface temperature (Tsur)/°C	20
Geothermal gradient (gT)/°C/m	0.03

(Appendix C). The thermo–physical properties of both models were derived from the same data set, provided in

Table A2. Data used in model comparison.

	Material	Overlying Rock	Underlying Rock	Matrix of the Aquifer
Properties
Density/kg/m3		2450	2650	2550
Specific heat/[J/(Kg·°C)]		950	820	850
Thermal conductivity coefficient/[W/(m·°C)]		2.1	2.2	2.5
Porosity/%		-	-	15

(Appendix C).

Transient ATES temperature profiles of the proposed model and the analytical solution are presented in Figure 2b, with the temperature distribution trend matching well; this indicates the feasibility and accuracy of the mathematical derivation of the proposed thermal-hydraulic coupled model. The temperature difference between Li’s analytical model and the proposed model can be attributed to two main reasons: (1) the proposed model of the interconnected system considered the thermal interaction between the wellbore, impermeable formations, and ATES, such as radial heat transfer of wellbore fluids and longitudinal heat transfer of ATES; however, the analytical model emphasized mathematical derivation and solution without considering the above coupled heat transfer processes. (2) The proposed model highly valued the temperature-dependent thermo–physical properties of the fluid, while the analytical model assumed the thermo–physical properties of the fluid were spatially and temporally invariant.

3. Results and Discussion

Based on the discussion above, numerical solutions were utilized to simulate the temperature distribution and propagation of the hydrodynamic/thermal front. By combining the transient temperature and thermal front, the characteristics of wellbore temperature variation before and after thermal breakthrough were studied and discussed in detail. Furthermore, sensitivities were analyzed in two main categories: (a) reinjection parameters and (b) geological factors. The coefficients of variation of the outlet temperatures corresponding to various sensitivity parameters were also calculated. Appendix C includes the basic parameters used for calculation (see

Table A3. Downhole geometry parameters.

Radial Direction
Inside radius of tubing (rti)/m	0.050
Outside radius of tubing (rto)/m	0.055
Inside radius of casing (rci)/m	0.065
Inside radius of cement A (rai)/m	0.070
Outside radius of cement A (rab)/m	0.090
Outside radius of cement B (rbb)/m	0.110
Outside radius of cement C (rcb)/m	0.130
Reservoir limit (re)/m	518.92
Longitudinal direction
Interval of cement A/m	0–1030
Interval of cement B/m	0–1000
Interval of cement C/m	0–500
Interval of caprock/m	0–1000
Interval of adjacent formation A/ m	1000–1030
Interval of ATES A/ m	1030–1035
Interval of adjacent formation B/ m	1035–1065
Interval of ATES B/ m	1065–1070
Interval of underlying rock/ m	1070–1100

,

Table A4. Thermo–physical properties of various media.

	Material	Tubing (Casing)	Cements	Caprock	Adjacent Formations and Underlying Rock
Properties
Density/kg/m3		7900	2150	1920	2500
Specific heat/[J/(Kg·°C)]		460	2000	922	900
Thermal conductivity coefficient/[W/(m·°C)]		16.2	0.7	1.02	2.2

and

Table A5. Ambient temperature and reinjection conditions.

Ambient temperature
Surface temperature (Tsur)/°C	20
Geothermal gradient (gT)/°C/m	0.03
Reinjection conditions
Total volumetric Reinjection rate (qin) /m3/d	3121.48
Volumetric Reinjection rate of ATES A/m3/d	1560.74
Volumetric Reinjection rate of ATES B/m3/d	1560.74
Reinjection temperature/°C	20

), and the fluid’s transient thermo–physical parameters (ρ_w, c_w, and λ_w) were obtained by dynamically invoking Equations (22)–(24) described in Appendix B.

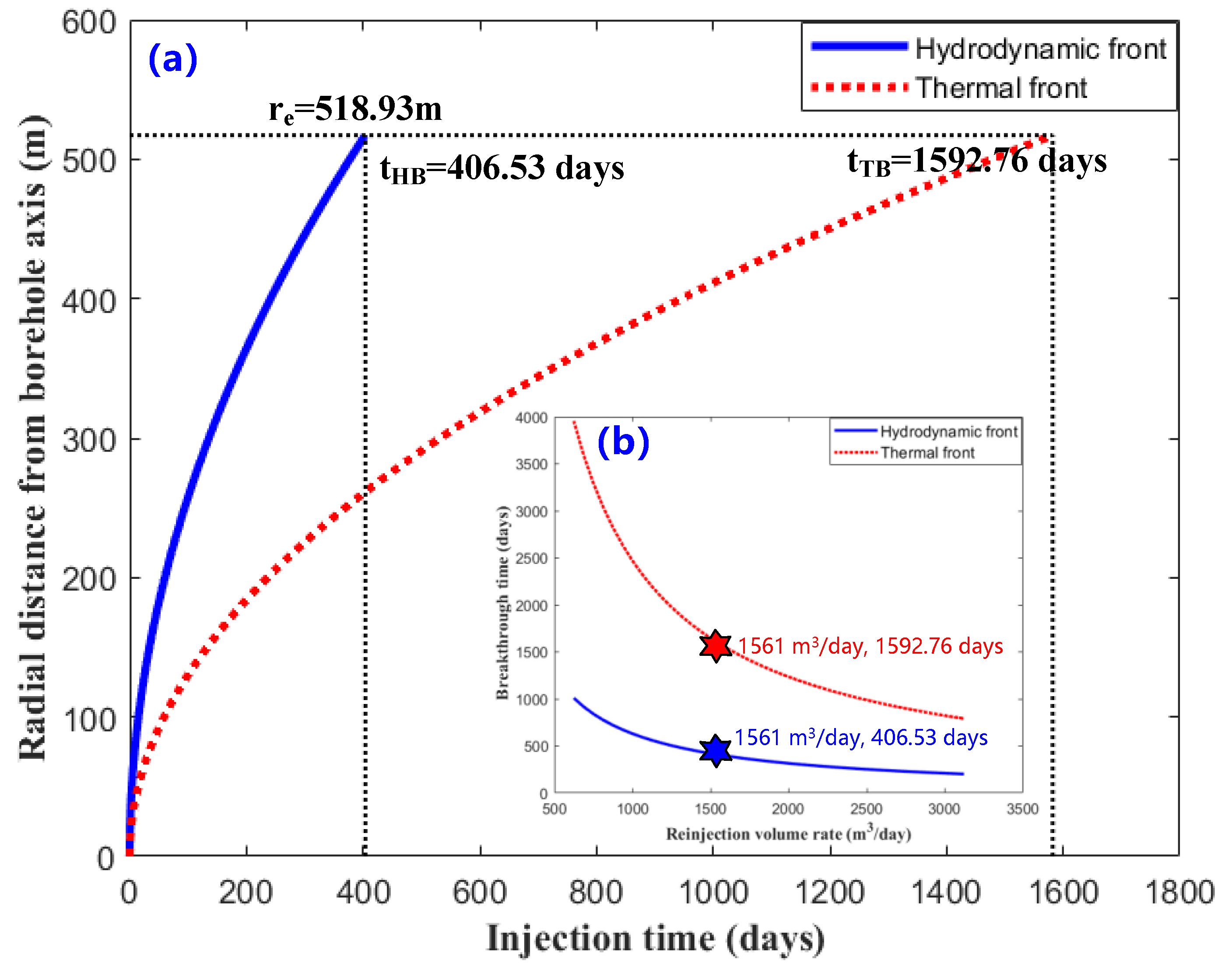
3.1. The Advancement Characteristic of the Hydrodynamic Front and Thermal Front

Using the model parameters of this study (Appendix C) and Equations (25)–(30), the radial position of the hydrodynamic and thermal fronts at different reinjection times is illustrated in Figure 3. The hydrodynamic and thermal fronts continue to advance with reinjection time. Still, the radial position of the fronts has a nonlinear relationship with reinjection time (Figure 3a). In the early injection stage, the fronts advance faster. In contrast, in the late stage of reinjection, the front migration is relatively slow. It is observed that the hydrodynamic breakthrough time and thermal breakthrough time are t_HB = 406.53 days and t_TB = 1592.76 days, respectively. Additionally, under the same conditions, we calculated the hydrodynamic front’s and thermal front’s breakthrough times at different reinjection volume rates (Figure 3b). The breakthrough times of the hydrodynamic and thermal front also showed a nonlinear relationship with the reinjection volume rate. Under the condition that q_in < 1000 m³/day, the hydrodynamic and thermal front’s breakthrough times vary significantly with the reinjection volume rate. When q_in > 1000 m³/day, the change in the reinjection volume rate has little influence on thermal breakthrough.

Furthermore, it is widely accepted that the location of the thermal front corresponds to the maximum radial temperature gradient. To investigate the suitability of the thermal front model derived in this study, the radial positions of fronts at different times were calculated using the above method. Figure 4 illustrates the ATES radial temperature gradient with varying times of reinjection before the hydrodynamic breakthrough. Notably, the radial position (R_max) of the maximum value of the radial temperature gradient correlates well with the calculated thermal front position (r_TF). The relative error (D_error) between r_TF and R_max can be expressed as$\mathrm{Derror} =\left|\left(\mathrm{Rmax} - \mathrm{rHF}\right)\right|/\mathrm{rHF}$. The relative errors for reinjection times of 5, 20, 45, and 100 days are 0.70%, 1.88%, 4.23%, and 5.94%, respectively. The detailed relative errors are presented in Figure 4b, where an increase in reinjection time leads to an increase in error. The most significant source of error may be the grid size (larger mesh sizes away from the wellbore) since the radial temperature gradient of thermal storage is based on the temperature values of grid nodes. Therefore, the front migration locations calculated using Equations (25)–(30) derived in this paper are relatively accurate, enabling further research on the relationship between transient temperature in tubing and the hydrodynamic/thermal front migration position, which can provide a basis for predicting the front using wellbore temperature.

3.2. Monitoring the Hydrodynamic/Thermal Breakthrough via the Temperature Inside the Tubing

Figure 5 displays the temperature distribution inside the tubing at the tubing/tubing wall interface (r = 0.04 m, 1000 m ≤ z ≤ 1100 m) with different reinjection times. The following observations can be made:

(1)

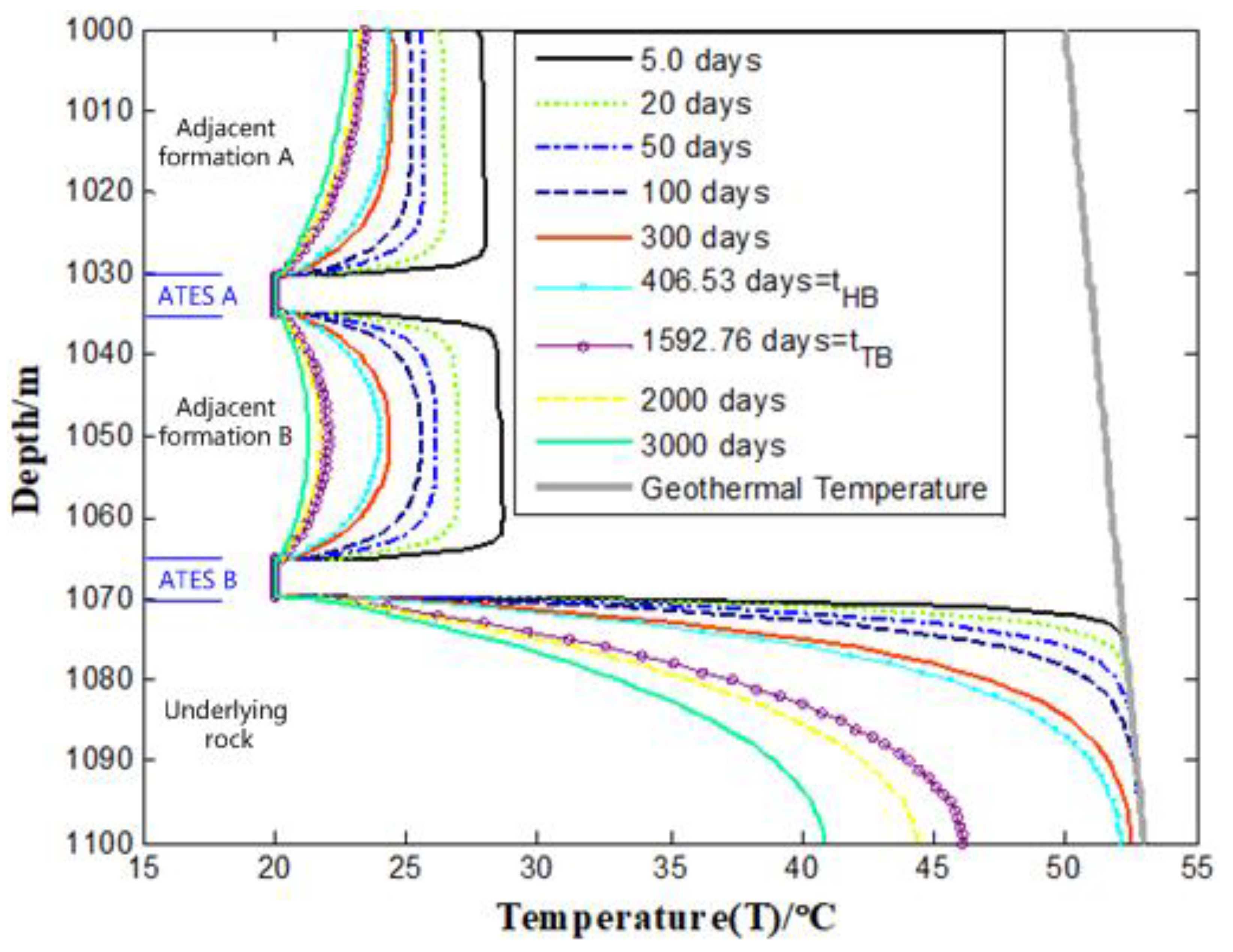
The tubing fluid in sections of adjacent formations A (1000 m ≤ z ≤ 1030 m) and B (1035 m ≤ z ≤ 1065 m) is continuously cooled by the injected fluid, with heat convection and conduction of wellbore fluid dominating the heat transfer, causing a gradual temperature decrease until it approaches the injected fluid temperature. However, for wellbore fluid in the underlying rock depth range (1070 m ≤ z ≤ 1100 m), longitudinal heat conduction dominates the heat transfer, resulting in a more gradual temperature decrease.

(2)

In sections of ATES A (1030 m ≤ z ≤ 1035 m) and B (1065 m ≤ z ≤ 1070 m), the fluid temperature in the tubing is equal to the reinjection temperature (Tin = 20℃) throughout the injection life. As a result, the longitudinal temperature gradient inside the tubing for ATES A and B sections almost always approaches zero. In contrast, the absolute value of the temperature gradient inside the tubing for the depth range of impermeable formations is larger.

(3)

Before hydrodynamic breakthrough time (tHB = 406.53 days), the tubing temperature changes significantly with reinjection time in sections of adjacent formations A and B, while the temperature changes little in the section of the underlying rock. However, after the thermal breakthrough time (tTB = 1592.76 days), the temperature change inside the tubing for the underlying rock section is more significant than that in adjacent formations A and B.

(4)

In the upper part of ATES A (1010–1020 m) and ATES B (1050–1060 m), before the thermal breakthrough, the temperature curve with depth shows a vertical distribution, with the temperature increase rate being almost zero. After the thermal breakthrough, the temperature increase rate is negative. Additionally, for the bottom hole (z = 1100 m), about 40 m away from the bottom of ATES B, the temperature is almost equal to the original formation temperature before the thermal breakthrough, which drops by 13% after the thermal breakthrough. Therefore, the temperature inside the tubing can be effectively used to monitor hydrodynamic or thermal breakthrough occurrences based on these observations.

3.3. Dynamic Thermal Performance Analysis of MATES

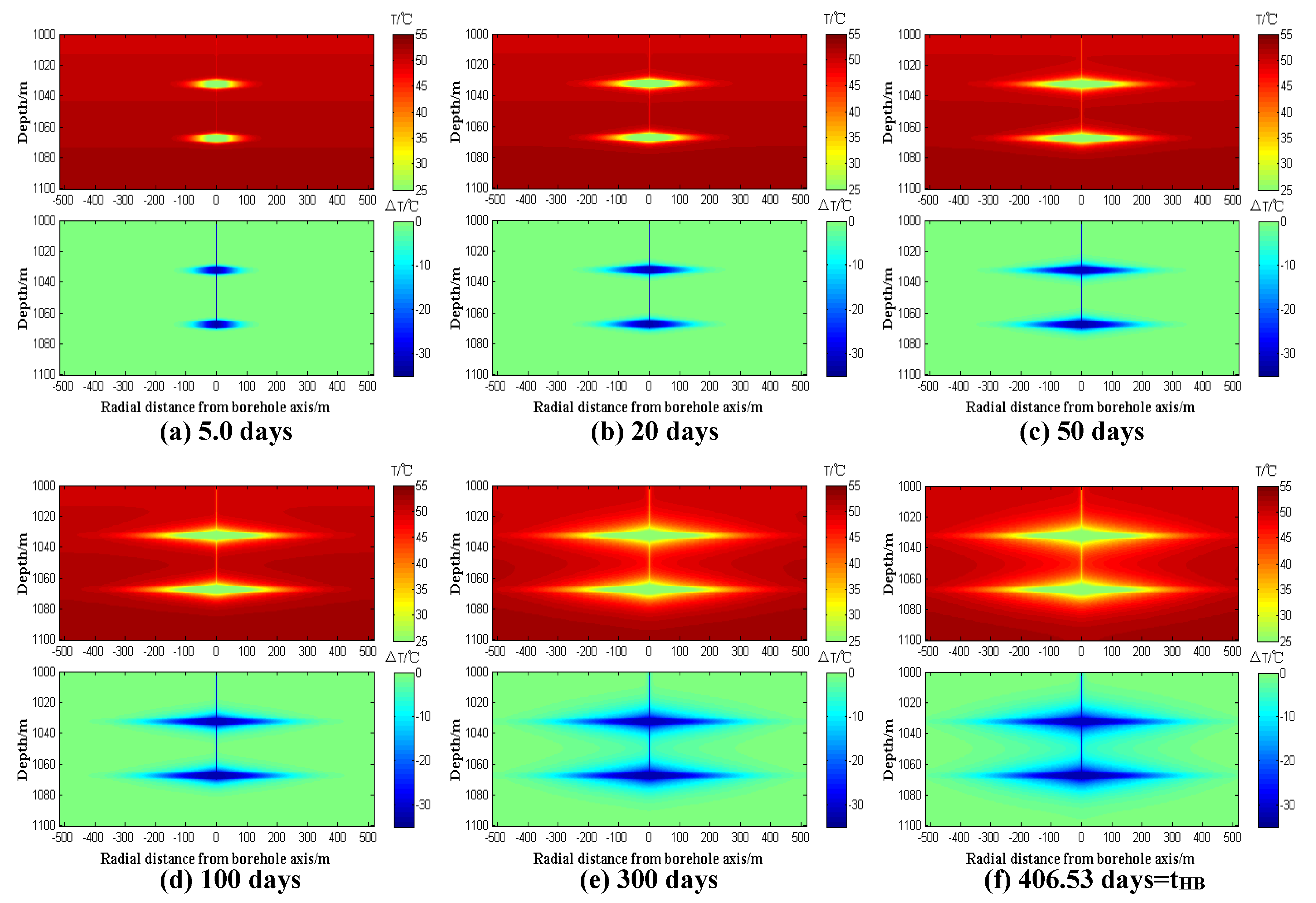
3.3.1. Spatial Distribution of the Downhole Transient Temperature (1000 m$\le \mathrm{z} \le$

1100 m, −518.93 m$\le \mathrm{r}\le$518.93 m)

Figure 6 illustrates the evolution of the downhole temperature distribution (1000 m ≤ z ≤ 1100 m, −518.93 m ≤ r ≤ 518.93 m) during the 3000-day reinjection period. The upper part of each subgraph (Figure 6a–i) displays the temperature distribution (T), while the lower part shows the temperature variation (∆T = T − T₀). The following observations can be made:

(1)

The temperature profile can easily determine the location of the ATES, as the spatial downhole temperature distribution resembles the shape of a “compass”; this is because the reinjection fluid of the ATES constantly migrates from the wellbore to the thermal reservoir boundary, leading to differences in cooling time for different radial positions of the ATES, resulting in varying temperatures. The temperature of the ATES near the wellbore decreases significantly, while the temperature of the ATES further from the wellbore decreases only slightly.

(2)

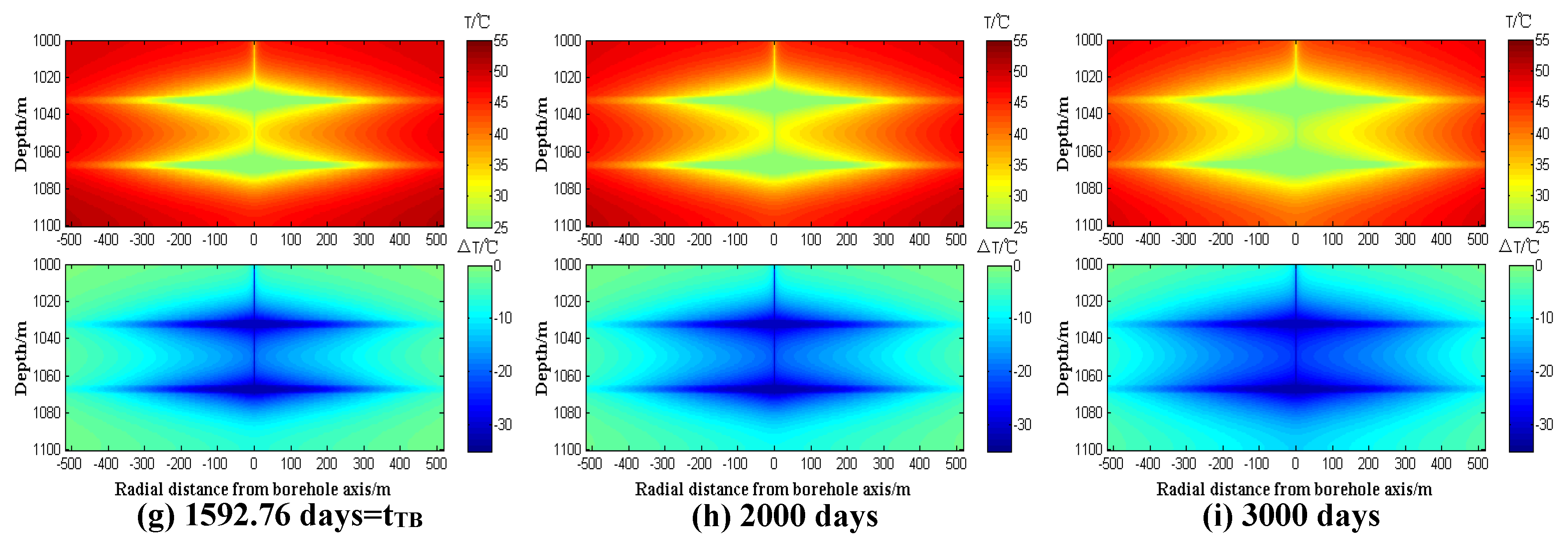
The ATES and the impermeable formations above and below are continuously cooled by the injected fluid, causing a gradual temperature decrease. As the hydrodynamic front advances, the range of cooled impermeable formations increases gradually. At the later stage of reinjection, the temperature of the ATES (1030 m ≤ z ≤ 1035 m, 1065 m ≤ z ≤ 1070 m) approaches that of the injected fluid. Moreover, Figure 6g–i reveals that during the entire reinjection life, the temperature of the ATES decreases gradually, but not indefinitely, with a “steady state” eventually reached.

(3)

When the hydraulic front breaks through (Figure 6f), the temperature of the heat storage boundary (R_e = 518 m) does not decrease significantly. However, the boundary temperature drops significantly when the thermal front breaks through. Additionally, the entire thermal reservoir (1030 m ≤ z ≤ 1035 m, 1065 m ≤ z ≤ 1070 m) is wholly cooled for about 3000 days (Figure 6i), about twice the thermal front breakthrough time, after which, the whole heat reservoir temperature is almost equal to that of the injected fluid.

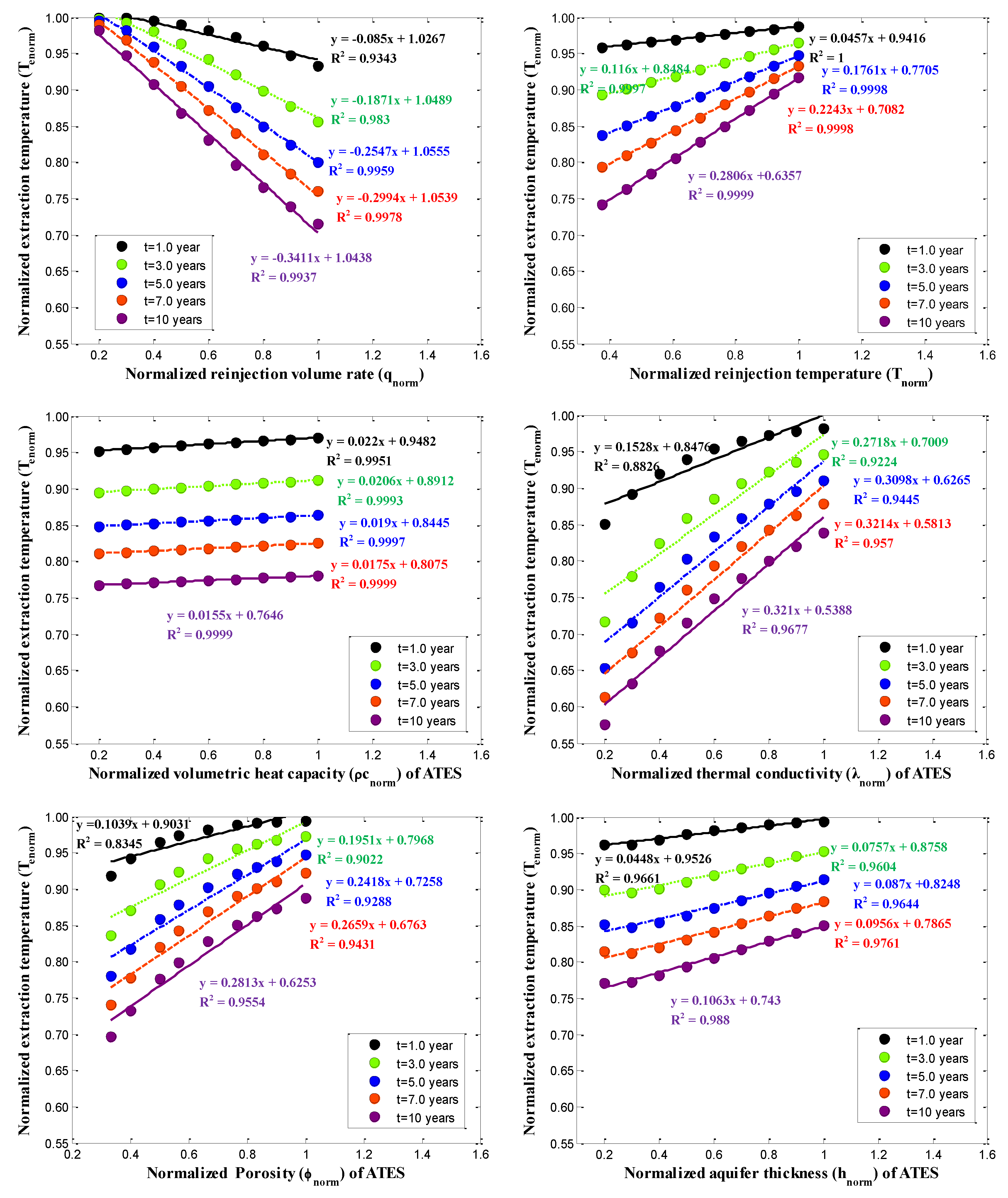
3.3.2. Sensitivity Analysis of ATES Thermal Extraction

To investigate the effects of different factors on thermal extraction temperature, we conducted a sensitivity analysis to provide a spatial and temporal dynamic evaluation of various parameters, such as reinjection volume rate (q_in), reinjection temperature (T_in), volumetric heat capacity ((ρc)_m), thermal conductivity (λ_m), porosity (∅_m), and aquifer thickness (h_m).

To compare the influence characteristics under the same conditions, we normalized the sensitive parameters, including q_in, T_in, (ρc)_m, λ_m, ∅_m, h_m, and thermal extraction temperature (T_e). Definitions for the various normalized parameters are presented in Equations (31)–(37).

$${\mathrm{T}}_{\mathrm{enorm}}={\mathrm{T}}_{\mathrm{e}}/{\mathrm{T}}_{\mathrm{a}}$$

(31)

where T_enorm is the normalized thermal extraction temperature, T_e is the thermal extraction temperature, and T_a is the initial ambient temperature.

The ATES thermal extraction temperature we focused on was at a depth of 1032.6 m. To calculate the ambient temperature (T_a), we used the formula Ta = T_sur + g_tZ, where T_sur represents the surface temperature, g_t is the geothermal gradient, and Z is the depth of interest. Assuming Tsur to be 20 °C and g_t to be 0.03 m/°C, we can compute T_a as $\mathrm{Ta}=20 °\mathrm{C}+0.03 \mathrm{m}/°\mathrm{C}\times 1032.6 \mathrm{m}=50.978 °\mathrm{C}$.

$${\mathrm{q}}_{\mathrm{norm}}={\mathrm{q}}_{\mathrm{in}}/\left(4071{ \mathrm{m}}^3/\mathrm{d}\right)$$

(32)

$${\mathrm{T}}_{\mathrm{norm}}={\mathrm{T}}_{\mathrm{in}}/\left(40 °\mathrm{C}\right)$$

(33)

$${\mathsf{\rho }\mathrm{c}}_{\mathrm{norm}}={\left(\mathsf{\rho }\mathrm{c}\right)}_{\mathrm{m}}/\left(3.0\times {10}^6 \mathrm{J}/\left({\mathrm{m}}^3·\mathrm{K}\right)\right)$$

(34)

$${\mathsf{\lambda }}_{\mathrm{norm}}={\mathsf{\lambda }}_{\mathrm{m}}/\left(3.0 \mathrm{W}/\left(\mathrm{m}·\mathrm{K}\right)\right)$$

(35)

$${\varnothing }_{\mathrm{norm}}={\varnothing }_{\mathrm{m}}/0.3$$

(36)

$${\mathrm{h}}_{\mathrm{norm}}={\mathrm{h}}_{\mathrm{m}}/\left(30 \mathrm{m}\right)$$

(37)

Figure 7 presents the normalized extraction temperatures for different normalized values of various parameters at different reinjection times. We conducted a linear regression analysis to study the relationship between normalized thermal extraction temperature and different normalized values of multiple parameters. Additionally, we defined “k_slope” as the slope of the fitting curves. Our observations indicate that all parameters, including T_in, (ρc)_m, λ_m, ∅_m, and hm, were positively correlated with thermal extraction temperature, except for qin. As reinjection time increased, the sensitivity of (ρc)_m to thermal extraction temperature decreased, unlike other parameters, including T_in, q_in, λ_m, ∅_m, and h_m. Among all the sensitivity factors studied, only the sensitivity of (ρc)_m to thermal extraction temperature decreased with reinjection time. K_slope fell from 0.022 to 0.0155 when reinjection time varied from 1.0 to 10.0 years, indicating that the impact of (ρc)_m on thermal extraction temperature can be disregarded in the later stages of reinjection time. Additionally, the K_slope of q_in was significantly greater than that of T_in for reinjection factors.

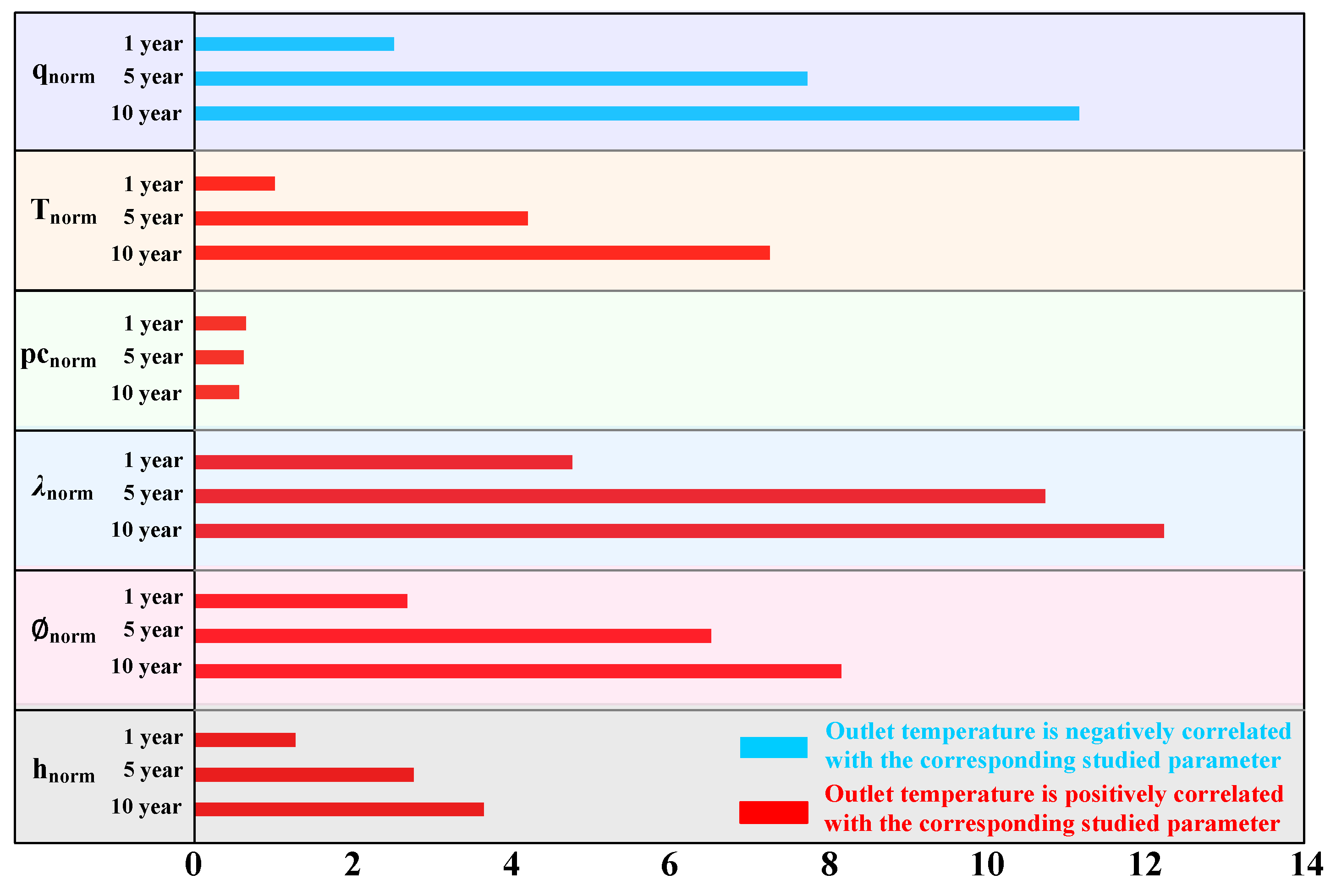
3.3.3. Comprehensive Comparison of Sensitivity Analysis

To comprehensively compare the influence degree of various parameters on the thermal extraction temperature in this study, based on the principle of mathematical statistics, we adopted the coefficient of variation as the index of sensitivity evaluation [43,44]:

$$C_v=\frac{s}{\left|\overline{y}\right|}$$

(38)

$$\mathrm{s}=\sqrt{\frac{1}{N}{{\displaystyle \sum }}_{i=1}^N{\left(y_i-\overline{y}\right)}^2}$$

(39)

where C_v is the coefficient of variation, s is the standard deviation of the sample data, $\left|\overline{y}\right|$ is the average of sample data, y_i represents a data sample, and N represents the number of sample data.

The coefficient of variation (C_v) represents the sensitivity of thermal extraction temperature to different influencing factors. A higher C_v value indicates a more significant influence of that factor on thermal extraction temperature. Figure 8 summarizes the results of the sensitivity comparison of the parameters studied. Among injection parameters, reinjection volume rate (q_in) influences the thermal extraction temperature the most. Regarding ATES attributes, thermal conductivity (λ_m) has the highest sensitivity within the studied parameter ranges, followed by porosity (∅_m). The reservoir volume heat capacity ((ρc)_m) and reservoir thickness (h_m) have relatively little impact on thermal extraction temperature. Therefore, thermal conductivity and porosity are essential for evaluating thermal reservoirs and extraction. In addition, the reinjection volume rate is a critical evaluation parameter among injection parameters. As reinjection time increases, the influence of different parameters on heat extraction temperature is more significant. Thus, the reinjection times significantly influence the correlations between thermal extraction temperature and thermo–physical properties. Therefore, reinjection time is also a critical factor to consider in heat storage development.

4. Conclusions

This study established a fully coupled model to qualitatively evaluate the relationship between temperature and hydrodynamic/thermal front. Dynamic sensitivity analysis of production temperature was carried out from the space–time perspective. The following conclusions have been drawn.

(a)

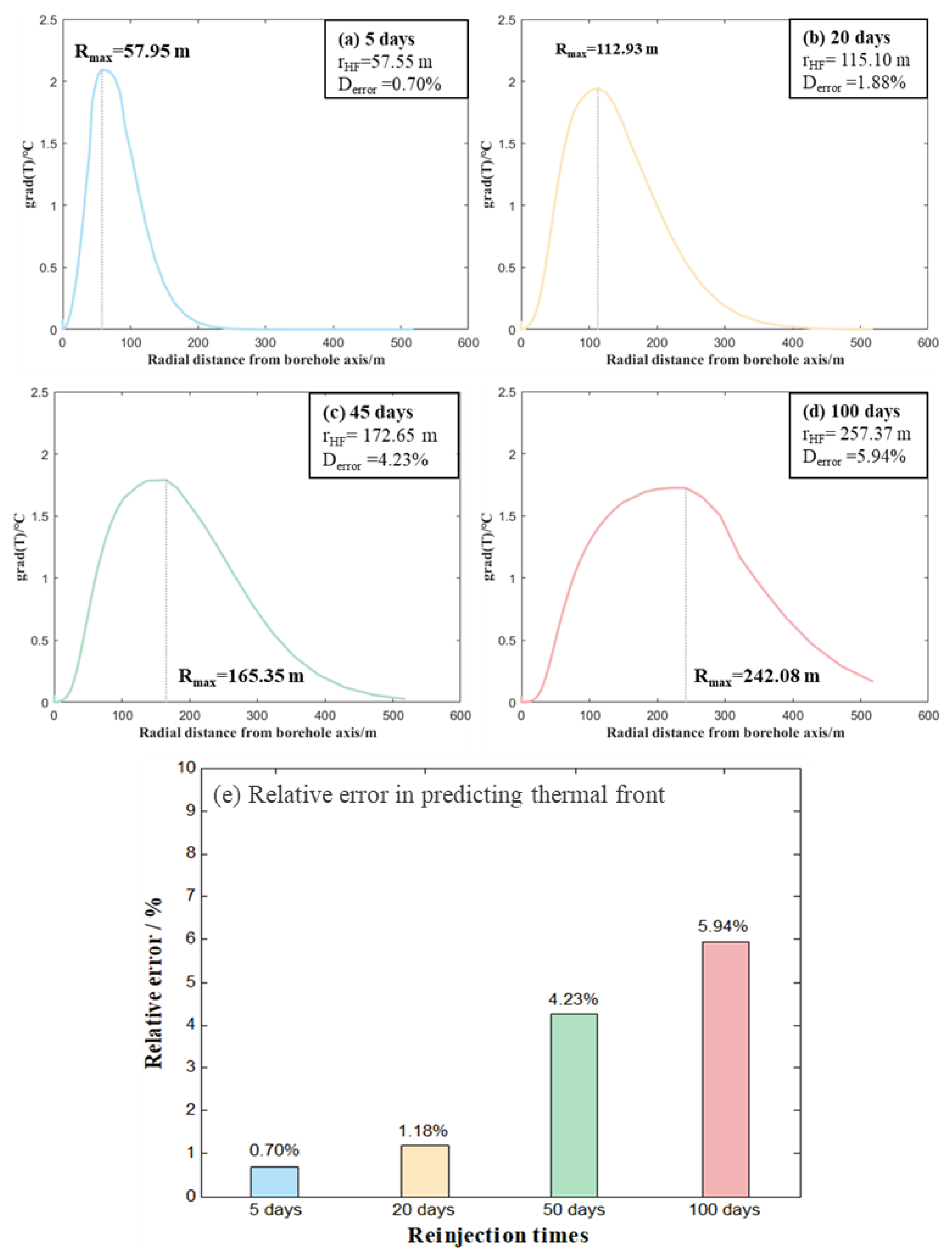
The accuracy of the thermal front migration calculation model for geothermal reservoirs with radial fluid seepage has been confirmed. The position of the hydraulic front can be used to accurately predict the position of the thermal front before the hydraulic breakthrough, as the radial position (R_max) of the maximum radial temperature gradient corresponds well with the calculated radial position (r_HF) of the thermal front. The relative error between R_max and r_HF ranges from 0.70% to 5.94%, providing a reliable basis for forecasting the thermal front position various times before hydraulic breakthrough.

(b)

The temperature increase rate in the upper parts of ATES A (1010–1020 m) and ATES B (1050–1060 m) is almost negligible. However, the temperature increase rate turns negative after the thermal breakthrough (t > t_TB = 1592.76 days). Furthermore, the temperature in the bottom hole (z = 1100 m), located approximately 40 m from the base of ATES B, remains close to the formation’s original temperature before the thermal breakthrough. Following the thermal breakthrough, the temperature drops by approximately 13%. These trends can serve as an indicator to detect hydrodynamic or thermal breakthroughs based on temperature monitoring inside the tubing.

(c)

The temperature gradient in the ATES section is close to zero (grad(T) = 0). Conversely, the temperature gradient in the impermeable formations section is more significant, allowing for identifying the location of the ATES or impermeable formations through analysis of the temperature inside the tubing.

(d)

The sensitivity analysis revealed that the normalized thermal extraction temperature variation with various normalized parameters is nearly linear. Furthermore, the following significant findings can be noted: (i) Among the reservoir factors (such as λ_m, (ρc)_m, ∅_m, and h_m of the ATES), λ_m holds the most significant influence on the thermal extraction rate. In contrast, (ρc)_m has the weakest impact. In contrast, q_in had a significantly higher impact on thermal extraction temperature than T_in, with only q_in showing a negative correlation with the thermal extraction temperature. (ii) Thermal conductivity and porosity are vital evaluation indices for assessing thermal reservoir development. Similarly, the reinjection volume rate is critical among the various injection parameters. As the reinjection time increases, the impact of different parameters on heat extraction temperature becomes more significant. Hence, the reinjection time must be meticulously considered in evaluating heat storage or heat extraction.

(e)

This study is applicable not only for single ATES but also for MATES, allowing us to consider the aquifer and adjacent formation as having multiple layers with dynamic thermo–physical properties. Moreover, the proposed coupled thermal-hydraulic model, as opposed to analytical or semi-analytical models, offers the capability to predict the complete dynamic temperature distribution within the wellbore of complex configuration and reservoirs under more realistic heat exchange conditions.

(f)

To make the model more closely resemble the natural geothermal geological environment, there are two main tasks for the next step: first, considering random fractures’ impact on temperature and the thermal front, and secondly, studying the relationship between transient temperatures at different positions within the wellbore and the fluid front/thermal front.