Economic Applicability of Solar Tracking Photovoltaic Systems in Commercial Buildings: Case Study in South Korean Climate

Abstract

This study investigated the applicability of a tracking photovoltaic (PV) system installed in the roof area of a commercial building. Because PVWatts is the only PV module with a tracking feature in EnergyPlus, its electricity generation was validated through comparisons with detailed PV modules in EnergyPlus. The tracking PV system generated 26.8–35.5% more electricity annually than a fixed system in the climate of Incheon (S. Korea). The load coverage analysis of the tracking PV system was conducted with the reference commercial building model in EnergyPlus. Approximately 14% of the total building electric demand, including heating, ventilation, and air-conditioning; lighting; and equipment, was met by one PV array. Finally, the life cycle cost analysis of the tracking PV system was conducted by considering the net present value, which includes the initial installation and operation costs. The initial investment was returned after approximately 8 years, assuming between two and six tracking PV arrays were installed. Moreover, up to 26.8% cost savings were achieved in 15 years compared to the case without any PV arrays.

1. Introduction

1.1. Background

International efforts have been made to cope with the global energy crisis. A Conference of the Parties session has been consistently held during climate change conferences, starting from 1997 in Tokyo (Japan) to most recently 2023 in Sharm el-Sheikh (Egypt) [1]. Moreover, Renewable Energy 100 (RE100) has recently been initiated by principal corporations and has had a great ripple effect globally [2]. Compared to other sectors such as transportation and industry, the building sector consumes approximately 50% of the total electric energy [3]; therefore, it warrants great attention. Specifically, electricity is considered the main energy source, and it can be utilized not only by buildings but also by other sectors, such as autonomous vehicles. Renewable energy including photovoltaic (PV), geothermal, and wind energy generates this electricity sustainably [4,5]. Moreover, PV systems have long been investigated regardless of the weather, including in hot and cold climates, such as India [6,7] and Canada [8], respectively. Various hybrid systems were developed from PV systems, including PV arrays integrated with a thermal collector to produce heat for hot water [9], a fuel cell hybrid system [10], and a PV–thermoelectric system [11]. A recent review investigated the technical challenges and potential future applications of PV arrays integrated with and attached to buildings [12].

The renewable portfolio standards (RPS) regulation was initiated in 2012 in S. Korea to enforce the minimum requirement for utilizing renewable energy in buildings [13,14]. The regulation is becoming stricter, with a target minimum rate of 32% in 2023 and 40% in 2030 for the public sector. To promote broader deployment, the government supports up to 80% of the installation cost, but this is limited to fixed PV systems. Moreover, among renewable energy sources, PV systems exhibit the most rapid rise in generation trends [15]. However, their contribution to the total electricity generation in S. Korea is only 4.1%, which is ranked 11th globally.

The solar angle is relevant to the electricity generation of PV systems, as experimentally investigated and evaluated in a previous study [16]. Utilizing a tracking feature is a good method for maximizing its efficiency and the resulting generation rate. However, tracking PV systems are rare in S. Korea due to the high initial cost of the investment and a lack of awareness. Moreover, a fixed system is regarded as more reliable in terms of its structure and maintenance. A systematic cost analysis with an improved generation rate for tracking PV systems as well as engineering efforts are needed to overcome the drawback discussed above.

1.2. Literature Review

Even a tracking system with only three positions exhibited 12–20% higher generation than a fixed system [17]. The experiment involved a standalone PV system with one axis and three positions, which was conducted over 13 months in Taipei (Taiwan). The emphasis was on not only the higher electricity generation of the tracking system but also the ease of implementation using a simple, robust design with easy control (only three positions) and the prevention of malfunction. Similarly, a double-axis PV system was tested in the climate of Mugla (Turkey) [18]. Notably, its generation rate was 17–42% higher than that of the fixed system. Moreover, a simulation model was validated and developed using the PVSYST program. The simulation results demonstrated that 33.8% higher electric generation could be achieved using the proposed tracking system compared to the fixed system. Another study demonstrated improved energy generation using a single-axis tracking PV system in a European climate (i.e., Italy) [19]. Over a month, the test results demonstrated that the deviation between the two systems was greater on a clear than a cloudy day. A dual-axis tracking PV system was simulated in a hot African climate (Nigeria), which corresponded to a low-latitude region [20]. Up to 30% more electricity was generated using the proposed dual-axis PV system compared to the optimally fixed system. The optimal tilt angle of a PV array was investigated for a PV system installed over the windows of multistory buildings [21]. This type of PV system was experimentally validated against the measurement data from the test cell and applied to the EnergyPlus simulation. An optimized tilt angle and PV width, as well as a cost analysis, were suggested for different regions in China. Another alternative to improve the performance of a PV array is using a reflector system [22]. A recent study revealed an up to 17.8% improvement in generation using this system. Systematic experiments with and without the reflector were conducted, and a validated simulation model was used to find the optimal configuration of this system.

The tracking system was investigated not only for the PV array but also for the solar collector [22]. The exergy efficiency of the movable solar air collector was tested against that of a conventional fixed system. Approximately 2.4 times higher efficiency was achieved using the proposed tracking system, as demonstrated through experimental and theoretical analysis. Moreover, an environmental–economic analysis (e.g., CO₂ emission) demonstrated that the environmental friendliness of the movable system was double that of the conventional system.

Previous studies conducted economic analyses of the PV system. One study claimed that the cost of the tracking system could be similar to that of a conventional system [17]. The proposed tracking system was small, so it could be mounted on walls, whereas the conventional system was installed on the roof using a sturdy frame to prevent structural problems. In another study, PV models of fixed and tracking systems, including those with single and dual axes, were evaluated from an economic perspective [20]. They utilized analytic simulation models to evaluate the levelized cost of electricity (LCOE) to determine the overall costs over a life span of electricity generation. Moreover, an LCC analysis focusing on the optimal tilt angle and PV width was conducted in various climates in China [12]. Although this study did not consider the movable PV, an optimized design of the PV was proposed, including the economic benefit based on extensive LCC analysis applying the net present value (NPV). Another recent study investigated the global economic potential of semi-transparent PV installed in a building as windows [23]. The life cycle analysis was performed by focusing on the energy payback time (EPBT) and greenhouse gas payback time (GPBT) based on the simulations calibrated with an experiment using the chamber test. The payback periods of both indicators were 13.8 and 10.4 years, which were less than the 25-year operation life of the system.

Many studies have utilized standalone simulation tools, such as PVsyst [6,18] and HOMER [6,7]. However, these have been limited to analyzing electricity generation without considering its usage in the building where the PV was installed. The building load coverage rate based on the PV generation should be evaluated for various applications: for instance, the generated electricity can be transferred to other consumers, traded, or sold. This can be achieved via building energy management in a smart grid.

1.3. Research Gap and Objectives

The literature review suggested that tracking PV has the potential to increase the low electricity generation in S. Korea, as revealed through simulations and experiments. Moreover, the economic analysis confirmed the superiority of tracking systems in terms of cost and environmental impact. However, a detailed life cycle cost (LCC) analysis comparing the tracking PV system to a fixed one and considering the electricity requirement of the target building where the PV is mounted in the S. Korean climate has rarely been conducted.

Therefore, this study investigated the improvements in generation rate from using the tracking system compared to the fixed system in a realistic scenario of commercial buildings in S. Korea. A popular building energy simulation tool, namely EnergyPlus, was utilized as the simulation test bed. To consider typical cases, a reference commercial building model was utilized. The existing PV modules (Sandia and TRNSYS models) in EnergyPlus were cross-evaluated using PVWatts [24], which has a tracking feature, after which an LCC analysis was conducted with and without the tracking feature, as shown in Figure 1.

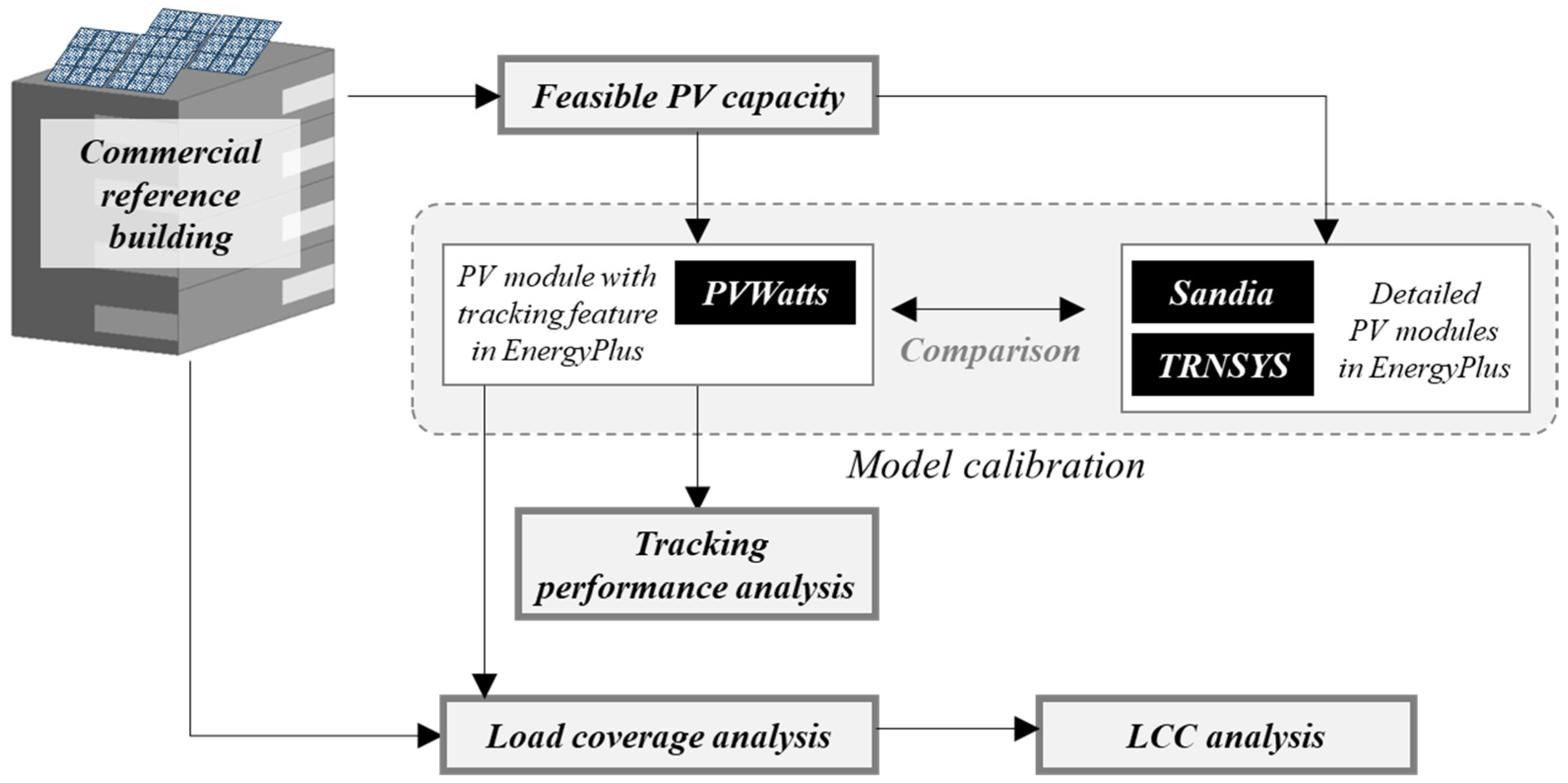
2. Simulation Case Study

A reference commercial building model developed in S. Korea was used in this study [25]. Typical Meteorological Year (TMY) 3 weather data of the target region (Incheon, S. Korea) were utilized. The typical schedule and internal heat gain profiles of the office building were the input.

2.1. Theoretical Background of PV Modules

PVWatts is a standalone PV simulator that is available as an application programming interface (API) as well as on the web [24]. It was developed in the National Renewable Energy Laboratory (NREL) in the US in 1998, and the newest version, 8.1, was developed in early 2023. The newest EnergyPlus version 22 adopted PVWatts version 5, which was developed in 2014 [26].

In general, PV electricity generation is calculated by multiplying the voltage and current at maximum power point tracking (MPPT) as follows: $P=V_{mp}·I_{mp}$.

The TRNSYS model is based on an equivalent one-diode model that generates the I–V (current and volt) curve and identifies the maximum point. The current is calculated by subtracting the diode current (I_d) from the light current (I_L).

$$I=I_L-I_d$$

(1)

The diode current (I_d) is determined from the Shockley equation:

$$I_d=I_0\left[\exp \left(\frac{q}{\mathsf{\gamma }\mathrm{k}{T}_c}\left(V+{IR}_s\right)\right)-1\right]$$

(2)

The diode reverse saturation current (I_o) is determined from the reference temperature, and the light current (I_L) is linearly calculated from the incident radiation:

$$\frac{I_o}{I_{o,ref}}={\left(\frac{T_c}{T_{c,ref}}\right)}^3$$

(3)

$$I_L=I_{L,ref}\frac{G_T}{G_{T,ref}}$$

(4)

Three conditions, namely the open-circuit, short circuit, and maximum power, are considered to determine I_L,ref, I_o,erf, γ, and R_s in Equation (2). The current (I_mp) and voltage (V_mp) are then iteratively determined from the MPPT along the I–V curve.

The Sandia model was developed in Sandia National Lab [27]. Similar to the TRNSYS model, it can generate the I–V curve from the short circuit current (I_sc), current and voltage at MPPT (I_mp, V_mp), open-circuit voltage (V_oc), half of the open-circuit voltage (I_x), and the average of open-circuit voltage and MPPT (I_xx). The current at the short circuit (I_sc) is calculated from the polynomial functions (f₁, f₂) of the solar spectrum through the airmass (AM_a) and the solar angle from the nominal (AOI) portion (f_d) of diffuse solar radiation (E_diff) and the difference between the reference outdoor (T₀) and inside cell (T_c) temperatures by applying a multiplier (α_ISC). The PV module temperature is calculated from the wind, and the cell inside temperature (T_c) can then be calculated.

$$I_{sc}=I_{sco}·f_1\left({AM}_a\right)·\left\{\frac{E_b·f_2\left(AOI\right)+f_d·E_{diff}}{E_0}\right\}·\left\{1+{\alpha }_{ISC}·\left(T_c-T_0\right)\right\}$$

(5)

The remaining variables are defined based on the empirical coefficients relating the effective solar radiation (E_e) and temperature (T_c, T_o) to the current (I_mp, I_x, I_xx) and voltage (V_mp, V_oc). Detailed information on the mathematical formulation can be found in the work of King et al. [27].

$$I_{mp}=I_{mpo}·\left\{C_o·E_e+C_1·{E_e}^2\right\}·\left\{1+{\alpha }_{IMP}·\left(T_c-T_0\right)\right\}$$

(6)

$$V_{mp}=V_{mpo}+C_2·N_s·\delta \left(T_C\right)·\ln \left(E_e\right)+C_3·N_3·{\left\{\delta \left(T_C\right)·\ln \left(E_e\right)\right\}}^2+{\beta }_{vmp}\left(E_e\right)·\left(T_c-T_0\right)$$

(7)

$$V_{oc}=V_{oco}+N_s·\delta \left(T_C\right)·\ln \left(E_e\right)+{\beta }_{voc}\left(E_e\right)·\left(T_c-T_0\right)$$

(8)

$$I_x=I_{xo}·\left\{C_4·E_e+C_5·{E_e}^2\right\}·\left\{1+{\alpha }_{Isc}·\left(T_c-T_0\right)\right\}$$

(9)

$$I_{xx}=I_{xxo}·\left\{C_6·E_e+C_7·{E_e}^2\right\}·\left\{1+{\alpha }_{Imp}·\left(T_c-T_0\right)\right\}$$

(10)

Unlike the TRNSYS and Sandia models, the PVWatts model is based on a simpler formulation. The module DC power (P_dc) is computed by multiplying the transmitted plane-of-array (POA) irradiance (I_tr) by the nameplate DC rating (P_dc0) of the module and the temperature difference between the reference (T_ref) and cell temperatures (T_cell).

$$P_{dc}=\frac{I_{tr}}{1000}{P}_{dc0}\left\{1+\gamma \left(T_{cell}-T_{ref}\right)\right\}$$

(11)

The transmitted POA irradiance (I_tr) is calculated by multiplying the POA irradiance (I_poa), which consists of the beam and diffuse (sky and ground-reflected) components, by the transmittance through the antireflective (AR) coating and glass (τ_AR and τ_glass). The angle between the solar rays and the panel is calculated from the aforementioned transmittance coefficients. A detailed explanation can be obtained from the manual [25] and its source [28,29].

$$I_{tr}=I_{poa}{\tau }_{AR}{\tau }_{glass}$$

(12)

2.2. Model Validation

PVWatts was adopted in EnergyPlus, which has a biaxial tracking feature, unlike existing PV modules, including the Sandia and TRNSYS models. Therefore, we calibrated the PVWatts module against the existing models. Notably, the Simple model, which is too simple, was excluded from the calibration. PV angles from 0 to 90° with 15° increments were considered. To simulate the tilted PV with the Simple, Sandia, and TRNSYS models in EnergyPlus, we built a dummy structure based on the X, Y, and Z coordinates by calculating the angle of the surface on which the PV models was installed.

The capacity of the PV module for all models was set to approximately 5 kW. Detailed properties of Sandia and TRNSYS models were set based on the default value from their original model in EnergyPlus. For example, I_sc and I_mp were set to 4.75 A and 4.45 A, and V_oc and V_mp were set to 21.4 V, and 17 V, respectively. Example files including “Generator_PVWatts” and “GeneratorswithPV” were used as references to configure the validation models.

In the initial comparison of the total and monthly electricity generation, consistent over-generation was observed in PVWatts compared to the two existing modules. This trend was observed in a daily and hourly comparison, which will be discussed later. Therefore, the constant of PV efficiency was manually calibrated with daily data. Accordingly, “system losses” of Generator:PVWatts in EnergyPlus was calibrated. The default value was 0.24, which denotes an efficiency of 0.76 (i.e., 76%). The initial comparison revealed that approximately 83% and 84% of the electricity was generated in the TRNSYS and Sandia models, respectively. Therefore, the efficiency of PVWatts needs to be reduced to similar proportions. The default efficiency of 0.76 decreased by 0.72 (0.76 × 0.835). Finally, the calibrated system losses were 0.28. The initial and calibrated PVWatts models are compared with the two models in Figure 2. Compared to the initial PVWatts model, the final model exhibited a good match with the detailed models in EnergyPlus.

The RMSE and cvRMSE of PVWatts and the existing models (Sandia and TRNSYS) are shown in Figure 3. For a fine scale, hourly data were layered on the daily comparison without further calibration. In both comparisons with Sandia and TRNSYS models, the daily evaluation exhibited a good match in the middle angle range (i.e., 30–45°), whereas the hourly evaluation exhibited the reverse trend. In the hourly comparison, the cvRMSE increases but is largely less than 10%, which is acceptable for the simulation case study.

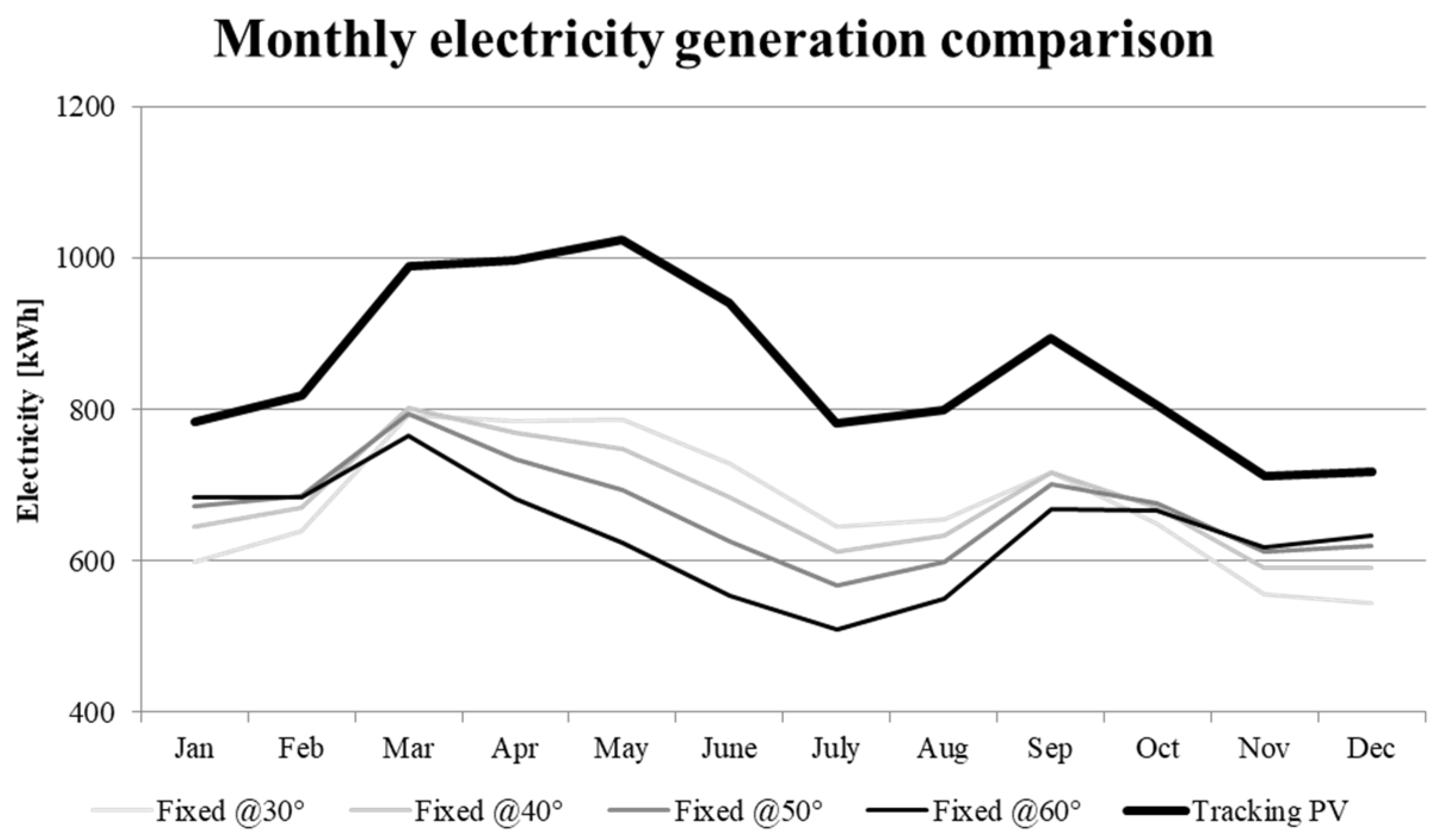
2.3. Tracking Performance Evaluation

In this section, the electricity generation performances of tracking and fixed PVs are evaluated using the calibrated PVWatts models. The capacity of the PV was set to 5 kW, which corresponds to an array area of approximately 31.25 m² [24]. The roof area occupied by the PV was conservatively set based on this array area. We assumed that five PV arrays could be installed on the roof (200 m²), which take up to 80% of the total area when considering the staircase and space for occupants. The maximum number of PVs that could be installed on the roof was six, which covers 93.5% of the roof area.

The electricity generation of the tracking PV was compared with that of a PV fixed at a tilt of 30–60° with 10° discernments, as shown in Figure 4. The deviation between tracking and fixed systems depended on the angle and month due to changing solar altitudes at different seasons. As expected, the fixed PV with a steep tilt was advantageous for winter and disadvantageous for summer. The maximum generation was achieved at 40°, whereas the minimum was achieved at 60°. Between 26.8% and 35.5%, more electricity generation was achieved annually using the tracking system than using the four fixed cases. This justifies applying the tracking system and forms the basis of the cost analysis discussed in Section 2.5.

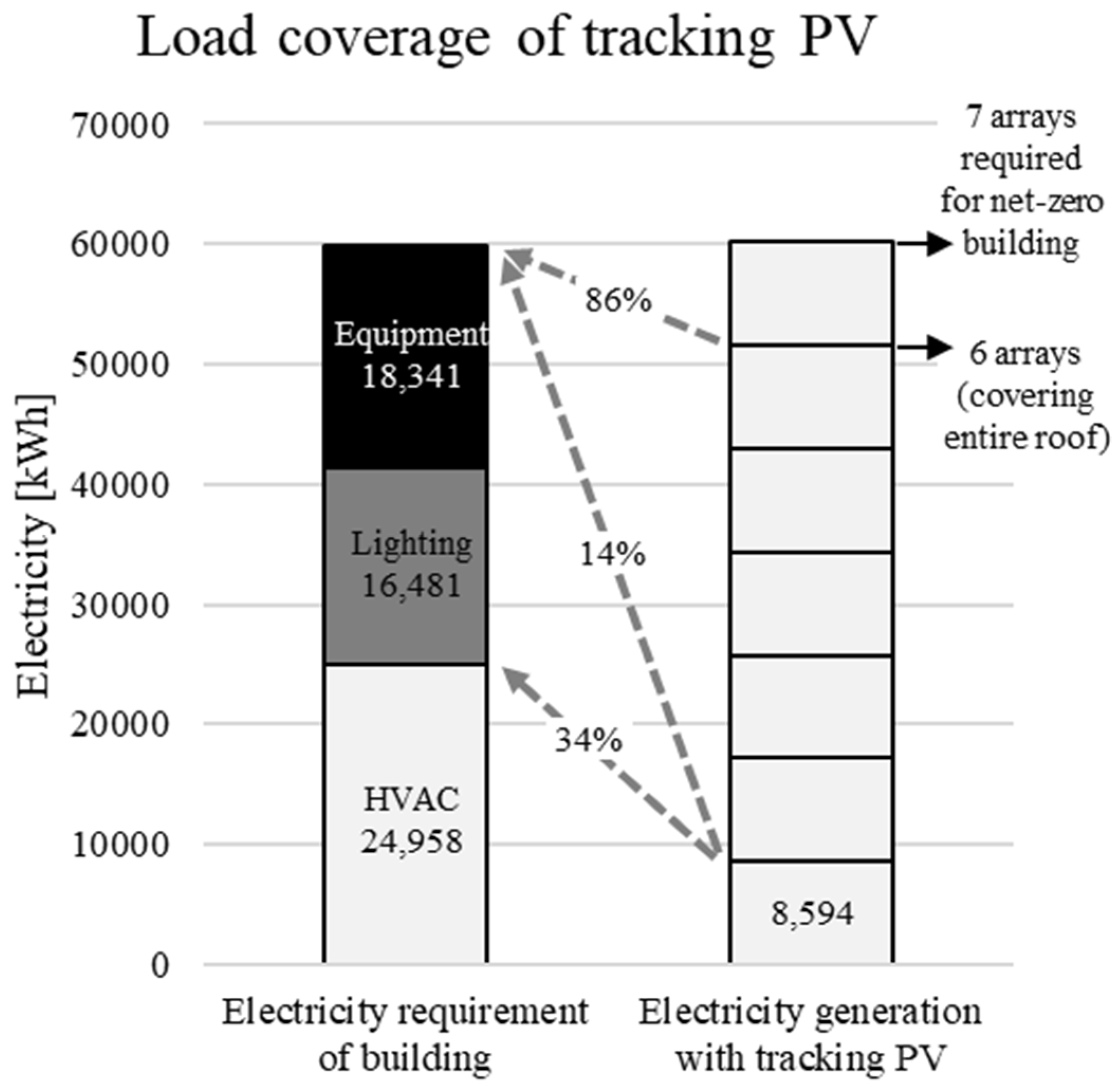
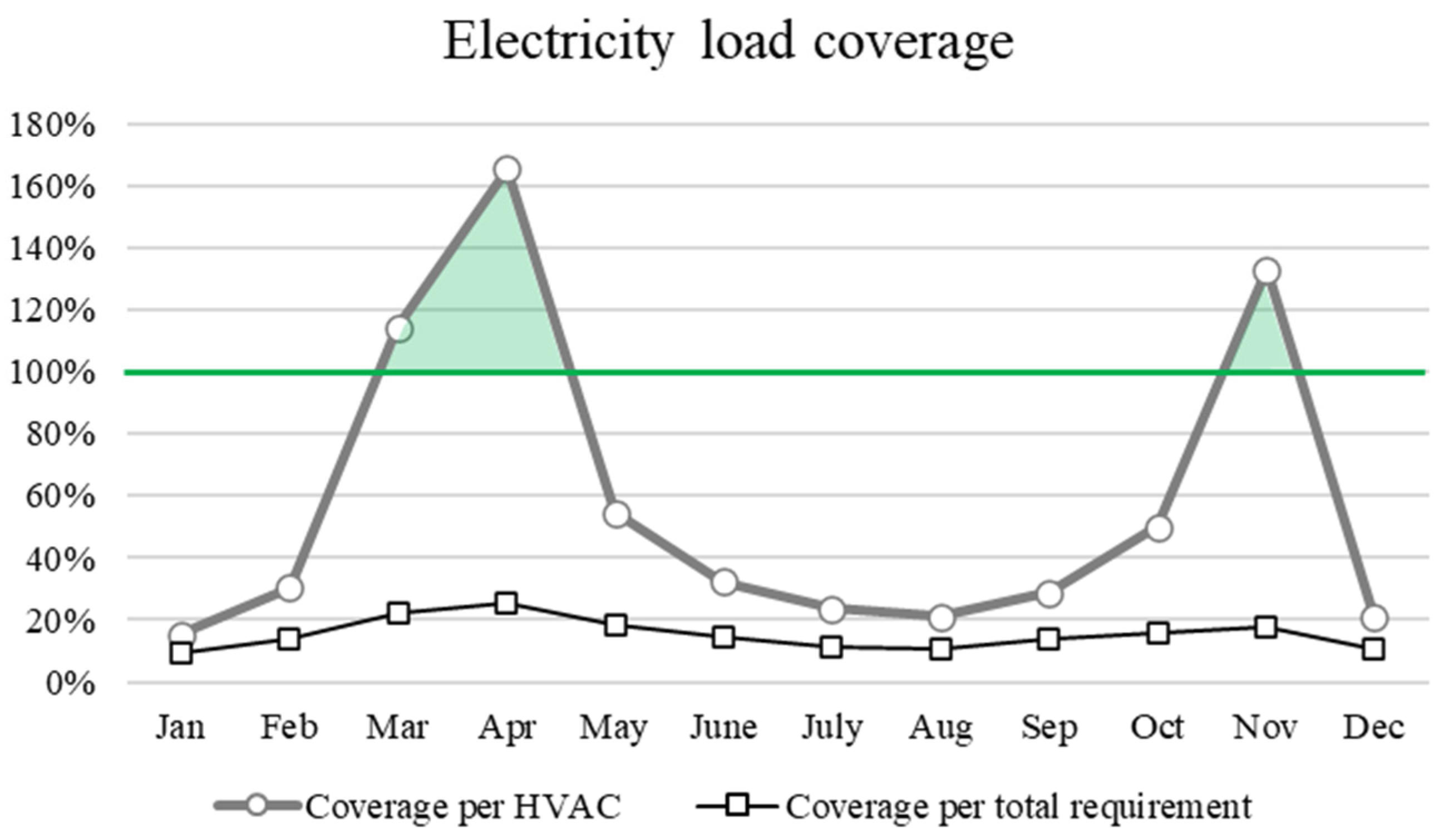
2.4. Building Load Coverage Analysis

For simulating the reference commercial building, we considered a typical office schedule, namely 9 a.m.–6 p.m. The heating, ventilation, and air-conditioning (HVAC) system was assumed as an ideal system, with only the pure heating and cooling load being calculated: ZoneHVAC:IdealLoadsAirSystem was applied in EnergyPlus. The COPs of the heating and cooling systems were set to 2.27 and 3.97, respectively, which are typical for HVAC systems, to calculate the electricity consumption.

The annual cooling and heating loads were 57,849 kWh and 23,577 kWh, and the corresponding electricity consumption levels were 14,572 kWh and 10,386 kWh, respectively. The electricity consumption levels of the lighting and equipment were 16,481 kWh and 18,341 kWh, respectively. The total building electricity requirement was 59,780 kWh, whereas the generation of one tracking PV was 8594 kWh. The HVAC took up 34% and 14% of the entire building load, as shown in Figure 5. As previously stated, six PV arrays could be installed, considering the roof area, which could produce 86% of the entire building load. However, seven PV arrays were required to satisfy the building requirement for net-zero energy. Therefore, further analysis is required, including an hourly load comparison because of time variations. However, the required load of the typical office building is expected to be well-matched with daytime electricity generation.

Figure 6 shows the monthly load requirement and generation from one tracking PV. Figure 7 shows the electricity load coverage of the PV generation per HVAC and the total electricity load of the building. When considering the electricity load of the entire building, the coverage is stable—from 15% to 20%. However, if only the thermal electricity load is considered, this exceeds 100% (green shade) during the intermediate season, during which the thermal load is insignificant compared to that during the warm and cool seasons.

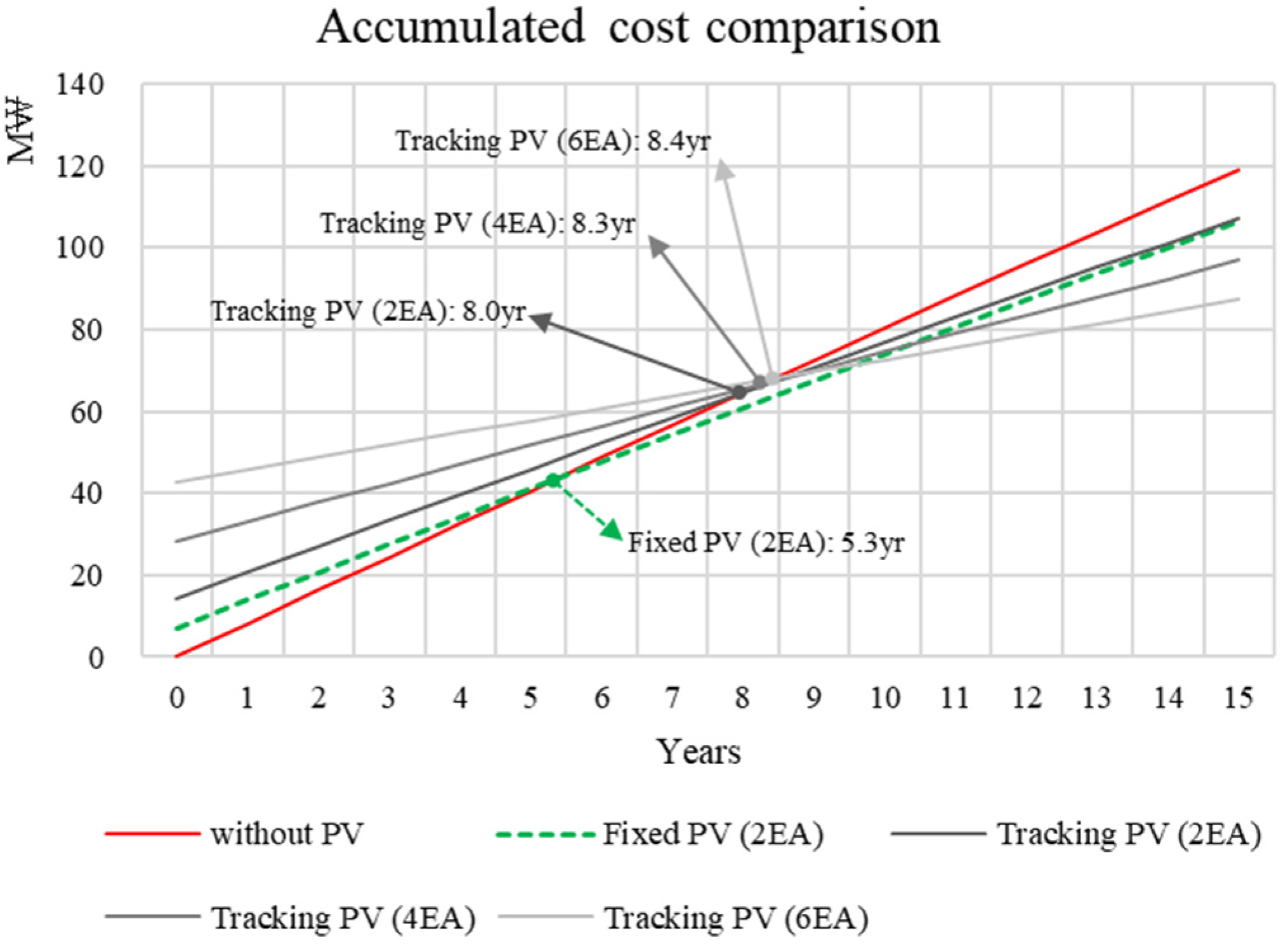
2.5. Life Cycle Cost Analysis

For the LCC analysis, we assumed arrays ranging from one to six, which covered approximately 94% of the entire roof area. The 2023 electricity cost structure of S. Korea was applied [30]. The demand charge was applied: for each month, 6610 ₩/kW was multiplied by the maximum electricity usage, including the HVAC, lighting, and equipment load. The seasonal prices applied for the summer, intermediate, and winter seasons were 124.4 ₩/kWh, 83.9 ₩/kWh, and 111 ₩/kWh, respectively. The net present value method was utilized to convert the future value into the current value, considering the inflation rate and increase rate in electricity cost. The average values from 2011 to 2022 were utilized. The average inflation rate was 1.867%, whereas the average electricity cost increase rate was 1.396%. Detailed rate information is presented in Appendix A (

Table A1. Inflation and electricity cost increase rate.

Year	11′	12′	13′	14′	15′	16′	17′	18′	19′	20′	21′	22′	Avg
Inflation rate	4	2.2	1.3	1.3	0.7	1	1.9	1.5	0.4	0.5	2.5	5.1	1.867
Electricity cost increase rate	4.75	4.9	4.7	0	0	0	−1.7	0	−0.5	0	0	4.6	1.396

,

Table A2. Monthly building electricity load and cost (cost unit: ₩).

	HVAC	Lighting	Equipment	Unit Electricity Cost	Total Electricity Cost
January	4247	1388.9	1552.75	111.0	797,928
February	2246	1267.29	1408.71	111.0	546,326
March	724	1440.51	1582.95	83.9	314,400
April	505	1295.39	1470.47	83.9	274,385
May	1573	1440.51	1582.95	83.9	385,670
June	2430	1382.77	1524.87	100.7	537,494
July	2769	1353.13	1528.55	100.7	568,987
August	3164	1440.51	1582.95	100.7	623,113
September	2607	1347	1500.67	83.9	457,657
October	1348	1388.9	1552.75	83.9	359,879
November	449	1382.77	1524.87	83.9	281,622
December	2897	1353.13	1528.55	111.0	641,387
Total	24,958	16,481	18,341	1139	5,788,848

,

Table A3. Monthly base utility cost (demand charge) (cost unit: ₩).

	No PV	Fixed PV	Tracking PV (No. of Array)
			1	2	3	4	5	6	7
January	431,459	431,459	431,459	431,459	431,459	431,459	431,459	431,459	431,459
February	328,371	328,371	328,371	328,371	328,371	328,371	328,371	328,371	328,371
March	201,438	201,438	201,438	201,438	201,438	201,438	201,438	201,438	201,438
April	109,476	99,167	92,880	77,454	68,990	67,400	65,810	64,220	62,630
May	124,278	114,609	106,469	90,654	81,384	73,634	69,016	64,399	59,781
June	143,386	134,203	126,678	112,516	107,464	102,411	97,359	92,306	87,254
July	160,123	149,035	143,371	128,199	117,908	109,193	102,764	98,901	95,038
August	164,139	152,276	147,421	131,983	119,530	112,019	108,098	104,178	100,257
September	148,943	137,673	132,643	119,705	113,946	110,122	106,298	102,473	98,649
October	131,762	122,247	118,234	108,673	99,781	94,411	92,837	91,262	89,687
November	105,786	102,299	102,299	102,299	102,299	102,299	102,299	102,299	102,299
December	404,669	404,669	404,669	404,669	404,669	404,669	404,669	404,669	404,669
Total	2,453,830	2,377,447	2,335,932	2,237,420	2,177,238	2,137,426	2,110,418	2,085,975	2,061,532

,

Table A4. Monthly total utility cost (cost unit: ₩).

	No PV	Fixed PV	Tracking PV (No. of Array)
			1	2	3	4	5	6	7
January	1,229,387	1,229,387	1,229,387	1,229,387	1,229,387	1,229,387	1,229,387	1,229,387	1,229,387
February	874,697	874,697	874,697	874,697	874,697	874,697	874,697	874,697	874,697
March	515,838	515,838	515,838	515,838	515,838	515,838	515,838	515,838	515,838
April	383,861	373,552	367,265	351,839	343,375	341,785	340,195	338,605	337,015
May	509,948	500,279	492,138	476,323	467,054	459,303	454,686	450,068	445,451
June	680,880	671,697	664,171	650,010	644,957	639,905	634,852	629,800	624,747
July	729,110	718,022	712,358	697,186	686,894	678,180	671,751	667,888	664,025
August	787,252	775,389	770,534	755,096	742,643	735,132	731,212	727,291	723,370
September	606,600	595,330	590,301	577,362	571,603	567,779	563,955	560,131	556,307
October	491,642	482,126	478,113	468,552	459,660	454,291	452,716	451,141	449,567
November	387,408	383,921	383,921	383,921	383,921	383,921	383,921	383,921	383,921
December	1,046,056	1,046,056	1,046,056	1,046,056	1,046,056	1,046,056	1,046,056	1,046,056	1,046,056
Total	8,242,678	8,166,295	8,124,780	8,026,268	7,966,086	7,926,274	7,899,266	7,874,823	7,850,381

and

Table A5. Monthly PV generation and corresponding cost.

	Monthly Cost of Electricity [₩/kWh]	Tracking PV			Fixed PV
		PV Generation [kWh]	Operation Consumption [kwh]	Net Generation Cost [₩]	PV Generation [kWh]	Net Generation Cost [₩]
January	111.0	656	10.85	71,667	532	102,201
February	111.0	686	9.80	75,078	560	105,278
March	83.9	828	10.85	68,601	680	100,132
April	83.9	834	10.50	69,119	660	98,466
May	83.9	858	10.85	71,038	650	97,688
June	100.7	787	10.50	78,195	597	103,279
July	100.7	655	10.85	64,897	532	96,663
August	100.7	669	10.85	66,298	546	98,079
September	83.9	748	10.50	61,875	612	94,426
October	83.9	674	10.85	55,610	564	90,437
November	83.9	597	10.50	49,178	491	84,304
December	111.0	601	10.85	65,467	486	97,036
Total	1139	8594	127.75	797,022	6909	1,167,989

).

The entire building electricity load, including the HVAC, lighting, and equipment, was calculated from the reference building model and summarized in

Table 1. LCC analysis with different numbers of PV arrays (cost unit: ₩).

	No. PV Array	Building Electricity Demand	Base Utility Cost (Demand Charge)	Annual Electricity Cost	Annual Unit PV Generation Cost	Annual Net Cost
No PV		5,788,848	2,453,830	8,242,678		8,242,678
Fixed PV	2		2,377,447	8,166,295	650,549	6,865,197
Tracking PV	1		2,335,932	8,124,780	797,022	7,327,758
	2		2,237,420	8,026,268		6,432,224
	3		2,177,238	7,966,086		5,575,020
	4		2,137,426	7,926,274		4,738,186
	5		2,110,418	7,899,266		3,914,156

. The annual electricity requirement was the same for all cases. However, the base utility cost was calculated with the peak demand for each month, which varies depending on the number of PVs. For this evaluation, hourly data of the building electricity load and PV electricity generation were used to estimate the peak electricity usage. Specifically, the electricity generation was extracted from the building electricity load. The annual net electricity cost was then calculated and used for the LCC analysis. The TMY3 weather file for the target region (Incheon, S. Korea) was repeatedly applied for 15 years for the LCC analysis.

Figure 8 shows the LCC analysis results for 15 years. The accumulated cost was calculated from the initial investment, including the product and installation costs. We identified between six and seven products with product and installation information, and their averaged values were used, that is, 3,570,000 ₩ and 3,520,000 ₩, respectively. For the fixed PV, the initial cost was approximately half that of the tracking PV. Therefore, the payback period was relatively short, that is, 5.3 years. The tracking PV with two, four, and six arrays required payback periods of 8.0 years, 8.3 years, and 8.4 years, respectively. However, in the 15-year evaluation, the total accumulated costs of fixed and tracking PV assuming two PV arrays were similar, namely 10.7% and 10.1% compared to that in the case without PV, respectively. Those with four and six arrays exhibited 18.7% and 26.8% savings, respectively.

3. Conclusions

This study evaluated the economic feasibility of the PV system with a tracking feature installed on a commercial building in the S. Korean climate. A systematic simulation was conducted to validate the PVWatts models in EnergyPlus against the existing detailed models to leverage the tracking feature. The validated PVWatts model was used to evaluate the electricity coverage analysis of the reference commercial building. The LCC analysis of the PV with and without the tracking feature was conducted to evaluate its economic applicability. The main findings are summarized as follows:

• The PVWatts model achieved higher electricity generation than the TRNSYS and Sandia models. Their deviations were constant, so efficiency reductions (e.g., 83.5%) were applied to validate the PVWatts model with the tracking feature.
• The electricity load coverage levels of one and six tracking PV arrays were 14% and 86% of the total electricity requirement, respectively. To achieve net-zero energy in buildings in S. Korea, seven tracking PVs need to be installed, which cover 109% of the roof area.
• The LCC analysis via the NPV method yielded a payback period of between 5.3 and 8.4 years for the tracking and fixed PV system. The total cost-saving percentage in the 15-year window compared to the case without PV was 18.7–26.8%.

4. Discussion and Limitations

In this study, LCC analysis did not consider economic support from the government, including tax exemption and initial cost subsidies. If this is applied, the payback period would be significantly reduced. Moreover, as many PV modules are installed on the roof, the modules can shade each other, especially when the solar altitude is low. This study did not consider this degradation in electricity generation from the PV system.

In addition, this study did not consider the maintenance cost of the PV system. For the long-term LCC analysis, this cost might impact the payback period as periodic monitoring and maintenance guarantee the production performance over the lifetime of the PV system [31]. However, defining regular maintenance schedules and the corresponding cost is complicated and challenging. Therefore, we did not consider this aspect in our study. For a more realistic analysis of the LCC of the PV system in building applications, those limitations should be addressed in future work.

This study focused on the tracking system of the PV module. However, overcoming the space limitation of the roof where the PV modules are installed should be investigated, to build integrated photovoltaic systems. Finally, the economic feasibility of the system can be further studied based on LCC analysis.