Enhancing the Performance and Efficiency of Two-Level Voltage Source Inverters: A Modified Model Predictive Control Approach for Common-Mode Voltage Suppression
Abstract
:1. Introduction
- A comprehensive introduction to the MPC strategy, an explanation of CMV, a discussion of the associated risks, and a presentation of the most prominent modified MPC strategies designed to enhance performance and suppress CMV.
- A new pre-selection strategy for voltage vectors (VVs) is designed based on statistical analyses. This strategy fully utilizes the six non-zero VVs of the 2L-VSI to completely restrict common-mode voltage CMV within ±udc/6. Additionally, it reduces the computational burden of the cost function and minimizes total harmonic distortions (THDs) and current ripples.
- Simulation and experimental results are presented to verify the effectiveness of the proposed strategy. Furthermore, to ensure the efficiency of the proposed method, the inverter’s performance was tested under various operating conditions, and the results are provided.
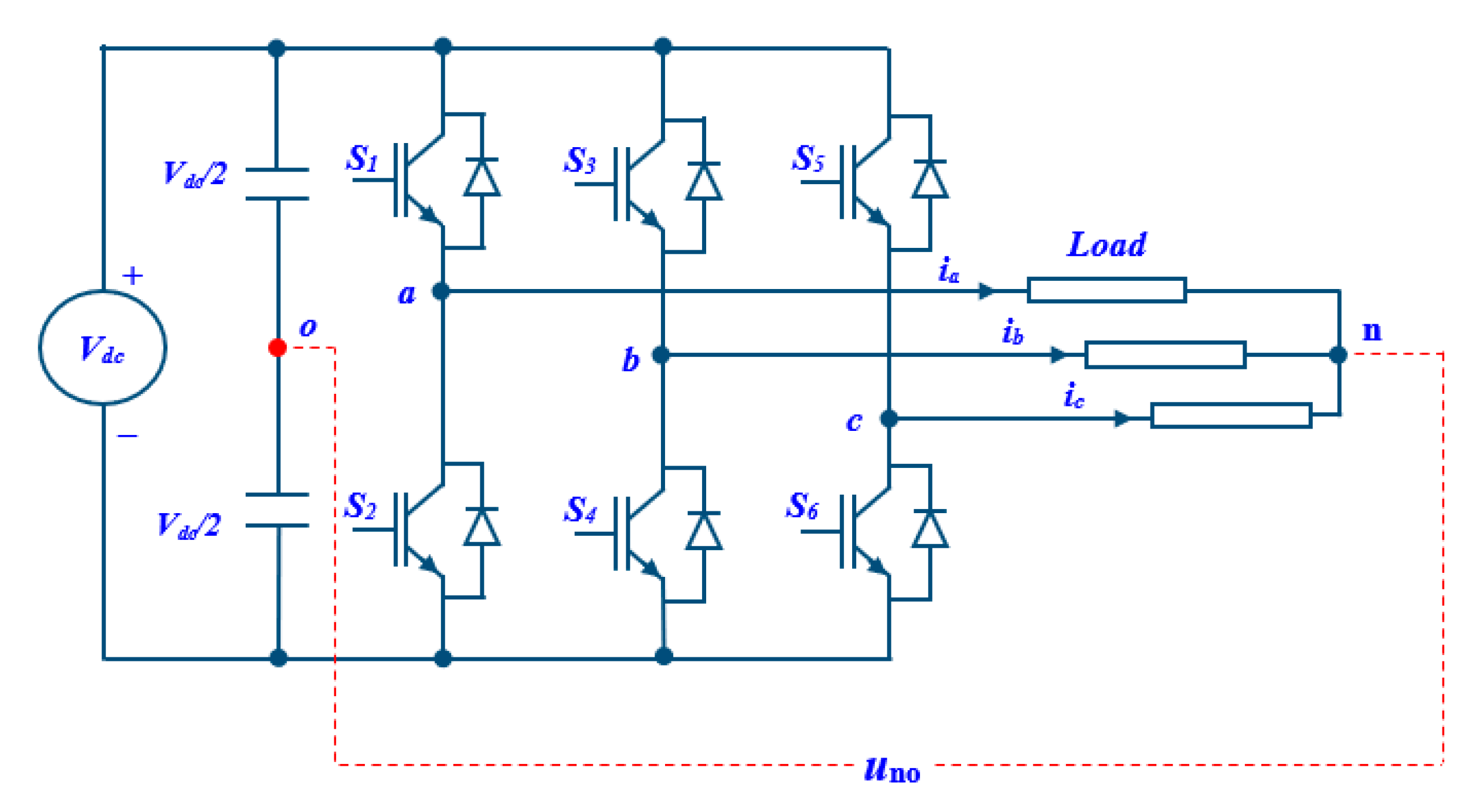
2. System under Study
2.1. Common-Mode Voltage
2.2. Modified Model Predictive Control (MPC) to Reduce the CMV
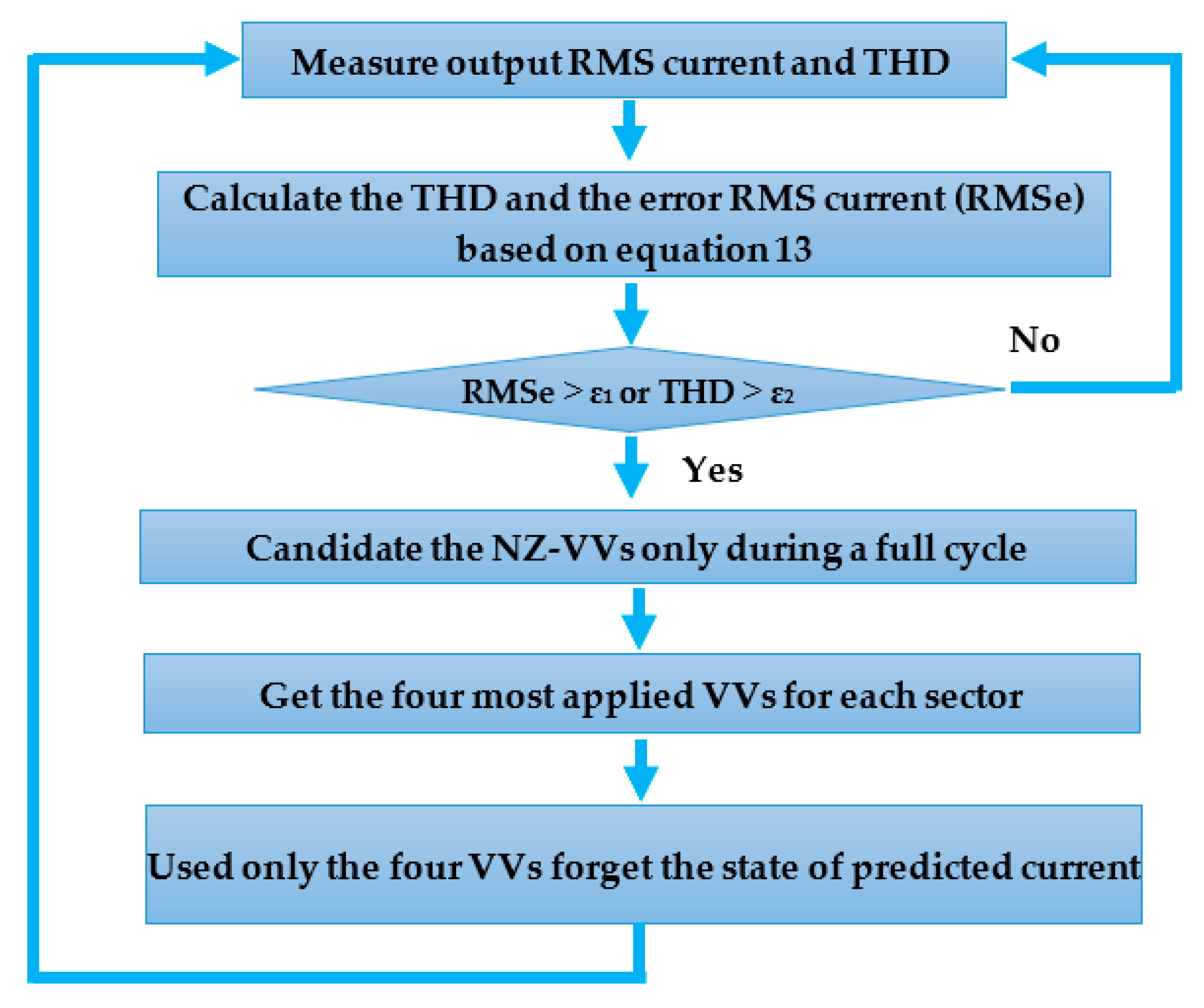
3. Proposed Strategy
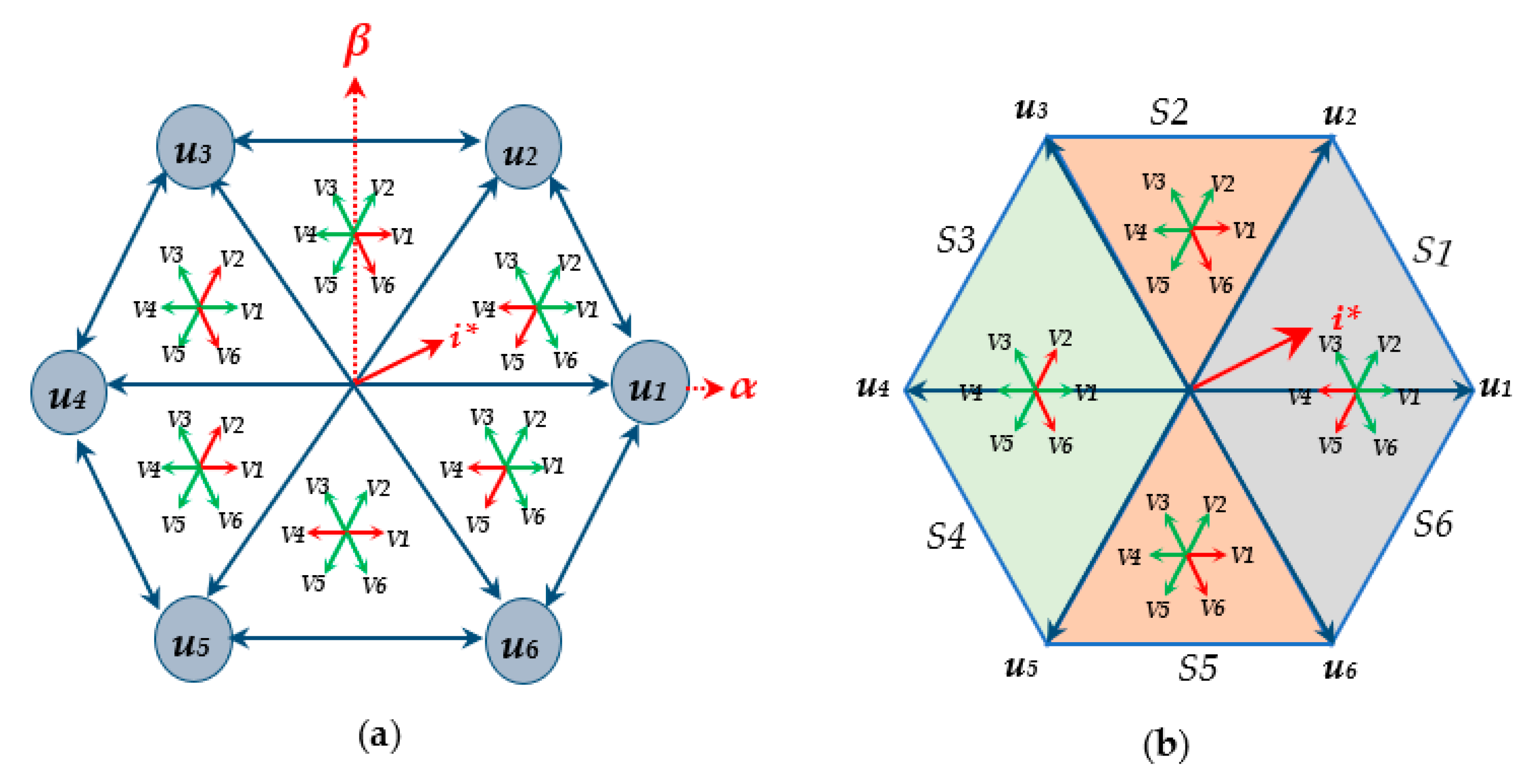
3.1. Statistics Results
- In the first sector (S1), the VVs u1, u2, u3, and u6 are the most applied, as shown in Figure 5a.
- In the second sector (S2), the VVs u2, u3, u4, and u5 are the most applied, as shown in Figure 5b.
- In the third sector (S3), the VVs u1, u3, u4, and u5 are the most applied, as shown in Figure 5c.
- In the fourth sector (S4), the VVs u3, u4, u5, and u6 are the most applied, as shown in Figure 5d.
- In the fifth sector (S5), the VVs u2, u3, u5, and u6 are the most applied, as shown in Figure 5e.
- In the sixth sector (S6), the VVs u1, u2, u3, and u6 are the most applied, as shown in Figure 5f.
3.2. Four VVs Symmetrical Strategy (4-VVsS)
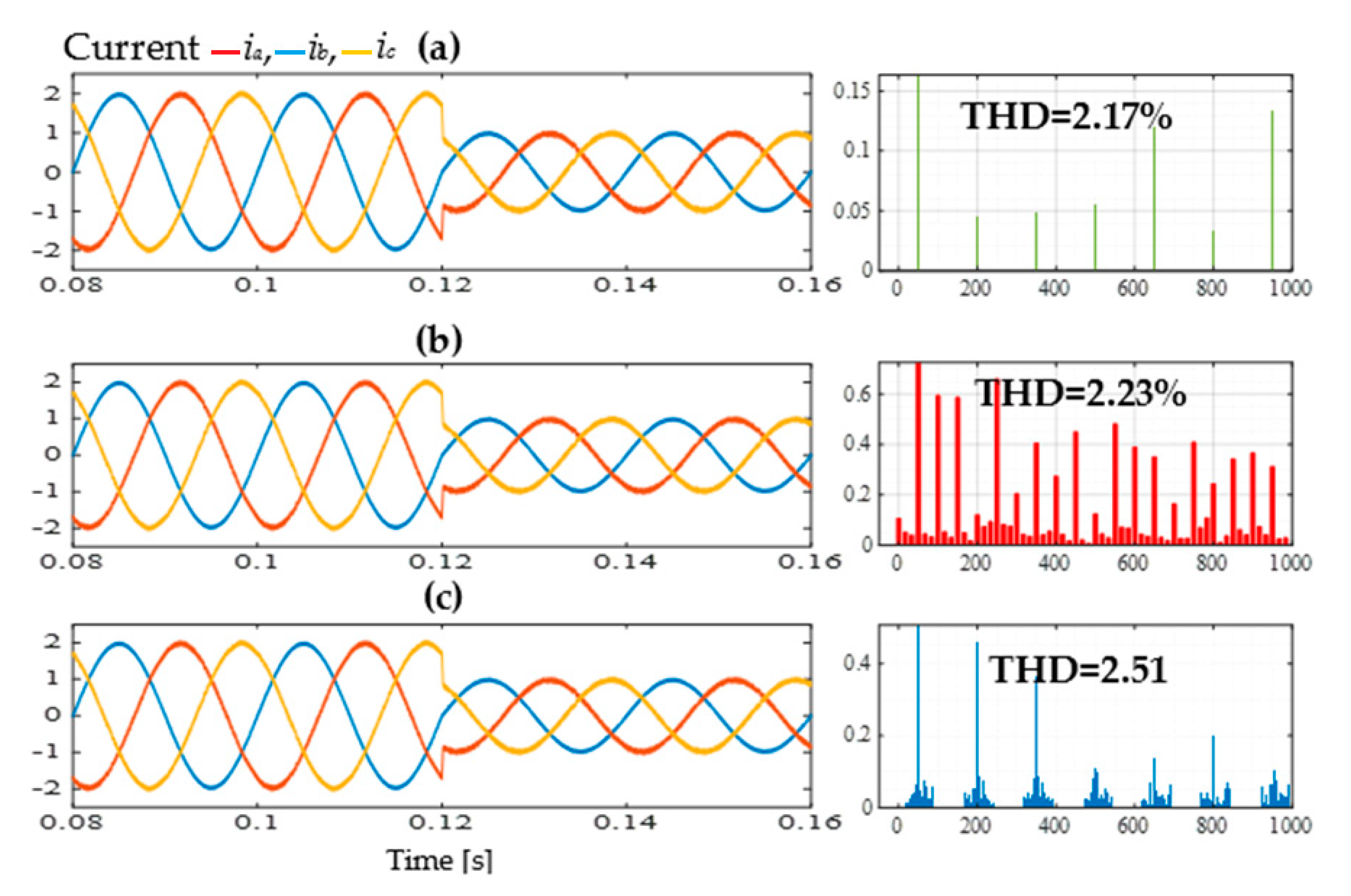
4. Simulation Results
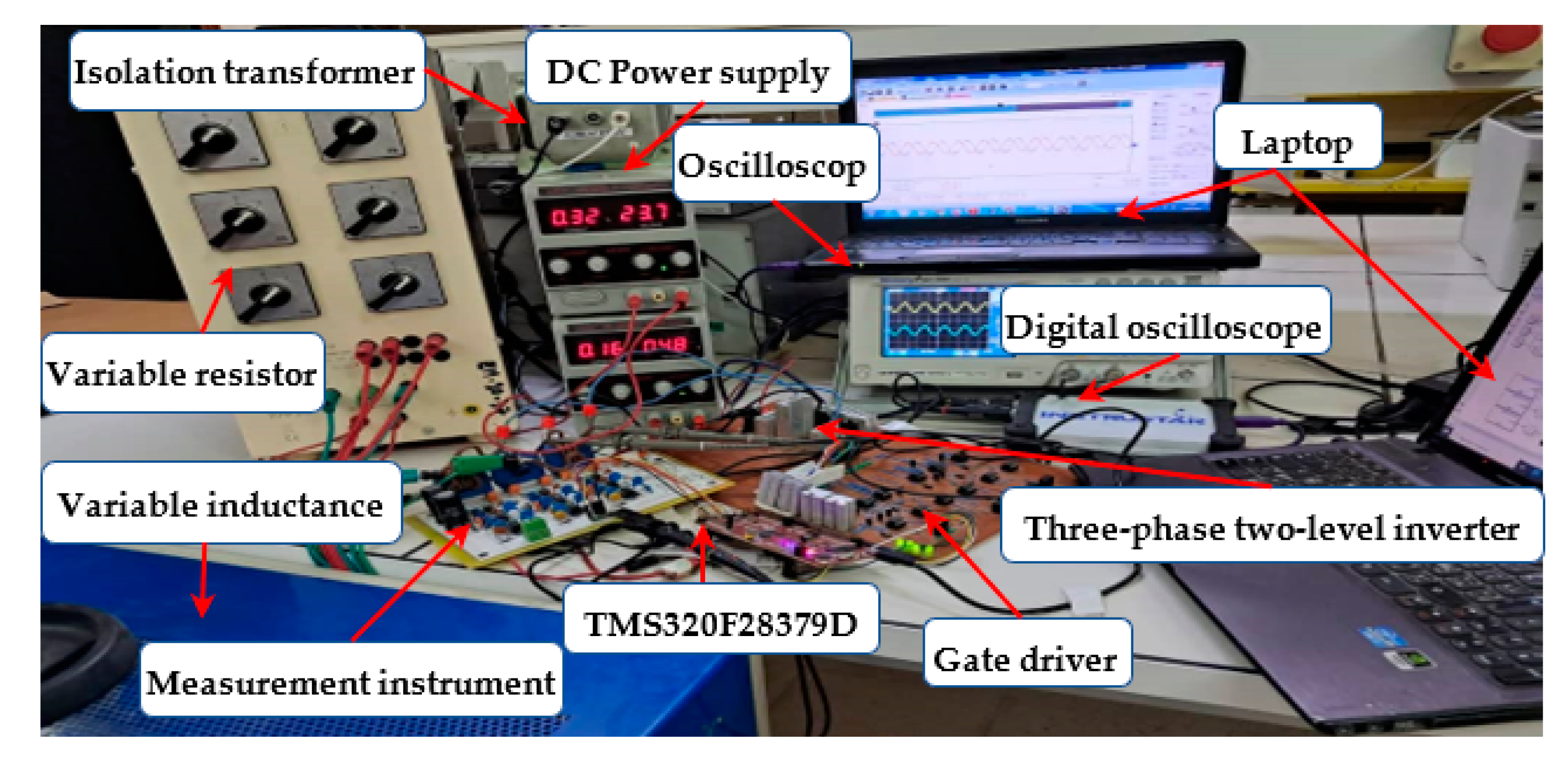
5. Experimental Evaluations
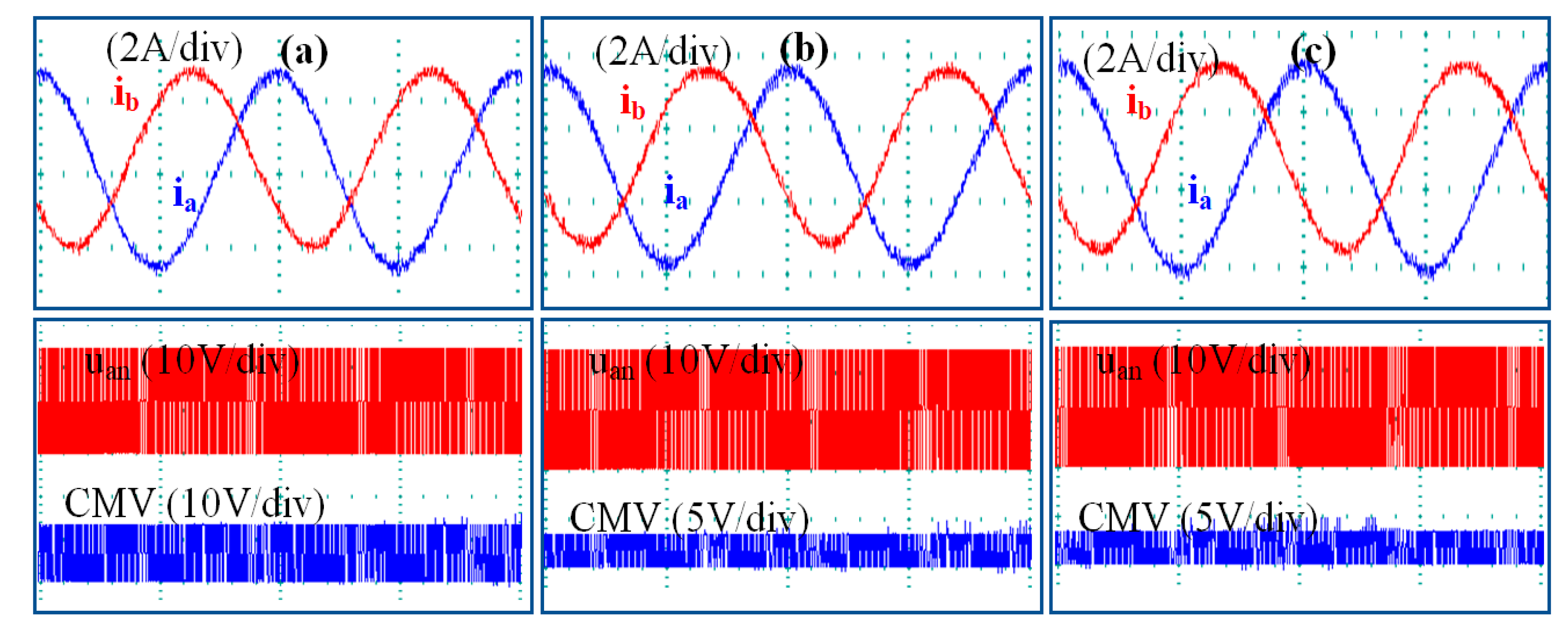
5.1. Steady-State Performance
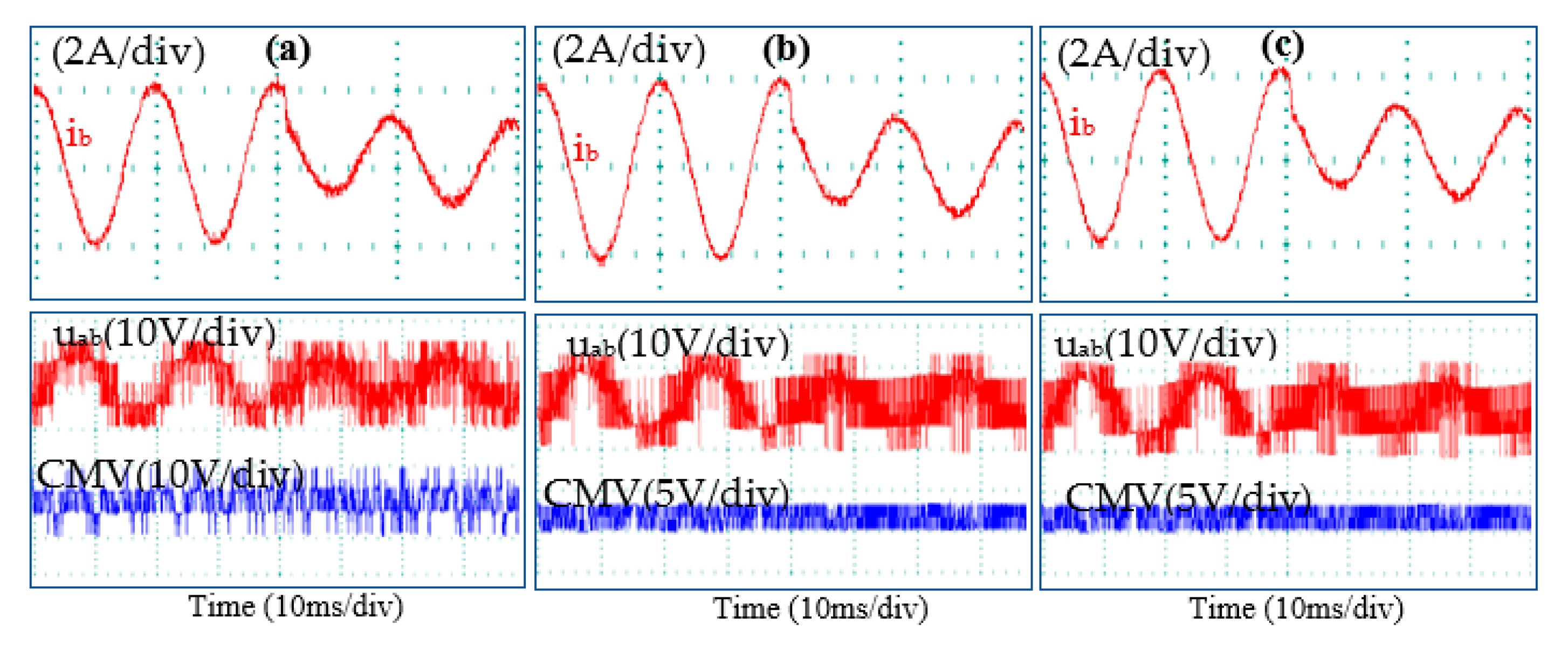
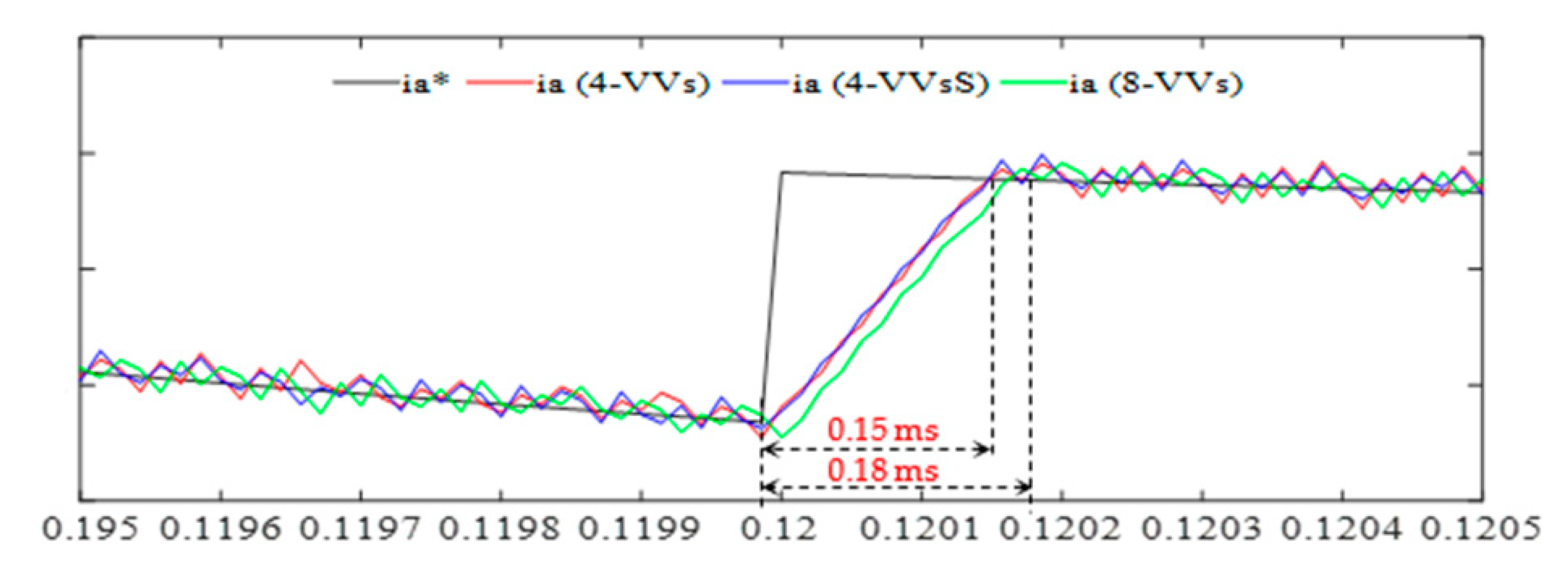
5.2. Dynamic Performance
6. Performance Tests
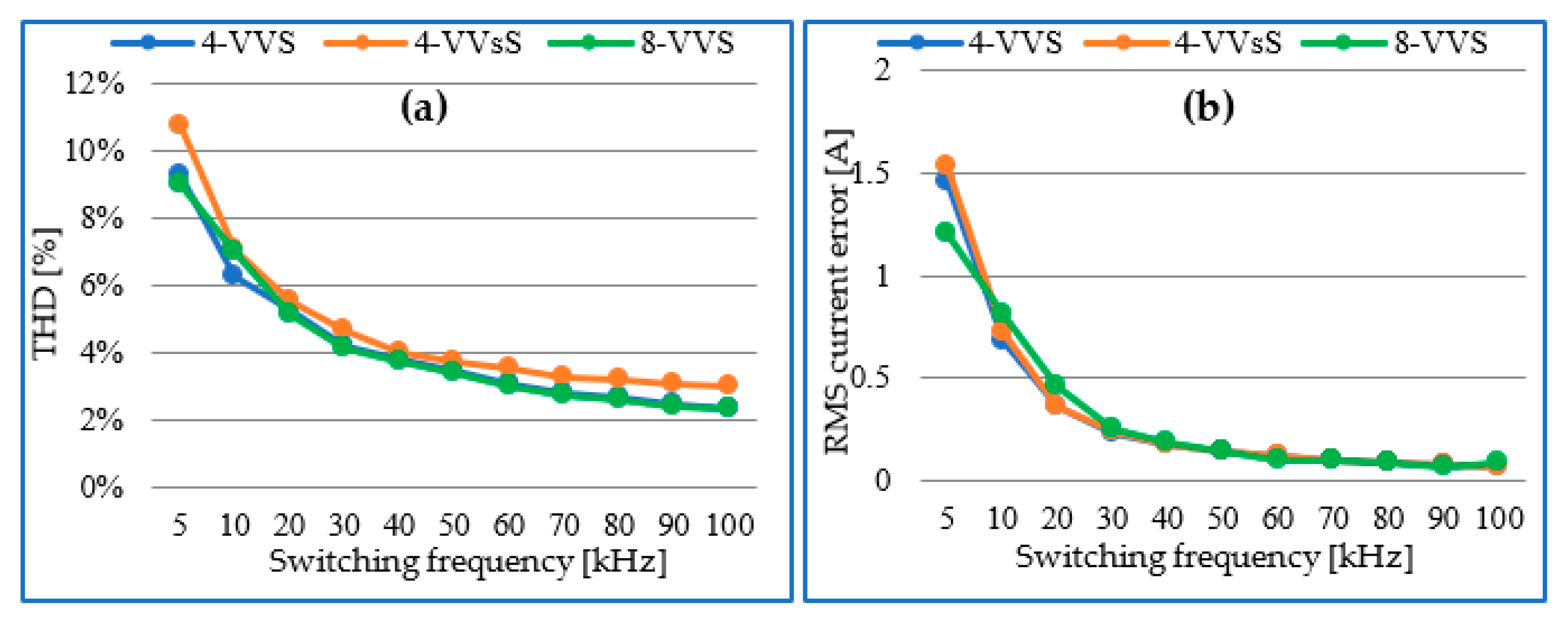
6.1. Switching Frequency
6.2. Inductance Variations
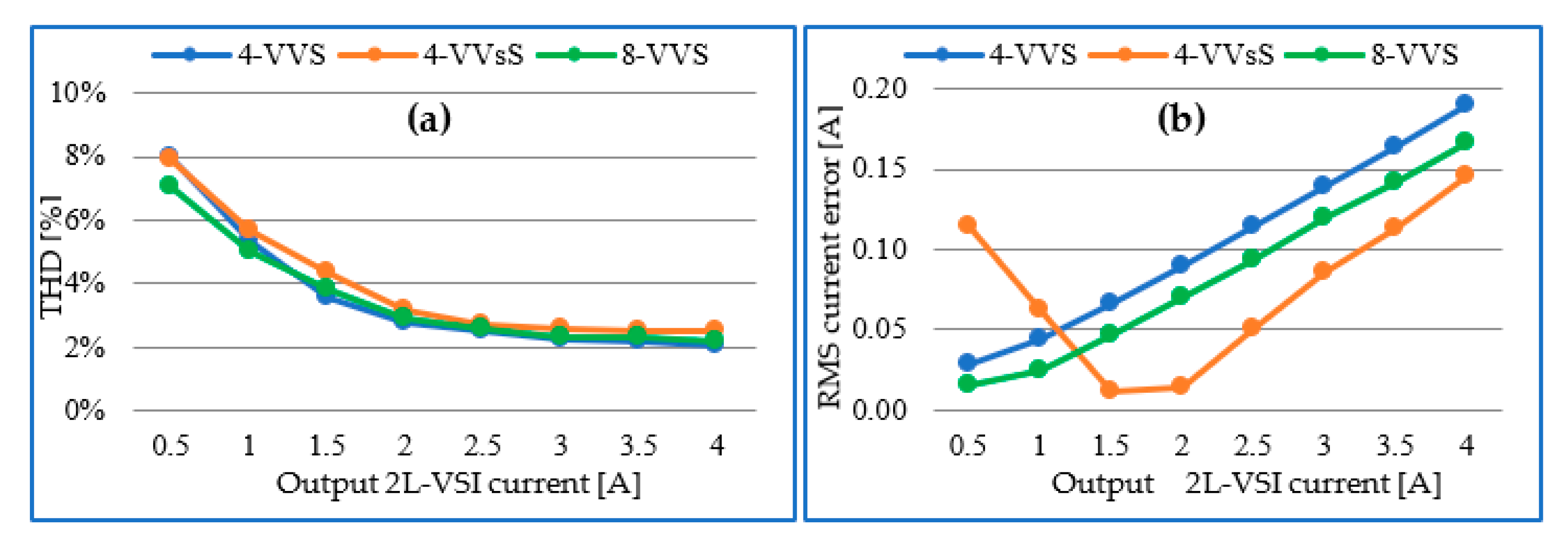
6.3. Output 2L-VSI Current Variation
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, R.; Wang, C.; Loh, P.C.; Yan, Q.; Xu, H.; Blaabjerg, F. A practical core-loss estimation method for three-phase three-level grid-connected inverters. IEEE Trans. Power Electron. 2019, 32, 6447–6462. [Google Scholar] [CrossRef]
- Abdulrahim, A.; Shokry, M. Efficient Implicit Model Predictive Control of Three-Phase Inverter with an Output LC Filter. J. Comput. Control Eng. 2021, 51, 28–38. [Google Scholar]
- Shao, S.; Li, J.; Li, Y.; Liu, Y. Modeling and control of a grid-connected photovoltaic system based on a three-phase voltage source inverter. IEEE Trans. Ind. Electron. 2015, 62, 7008–7018. [Google Scholar]
- Guo, L.; Jin, N.; Li, Y.; Luo, K. A Model Predictive Control Strategy with Sliding Mode Observer for Grid-Connected Inverter. IEEE Trans. Power Electron. 2015, 30, 6203–6213. [Google Scholar]
- Gui, Y.; Wang, X.; Wu, H.; Blaabjerg, F. Voltage Modulated Direct Power Control for a Weak Grid-Connected Voltage Source Inverters. IEEE Trans. Power Electron. 2019, 34, 11383–11395. [Google Scholar] [CrossRef]
- Yang, L.; Xia, Y.; Cai, X. Control strategies of grid-connected inverter systems with LCL filters: A review. IEEE Trans. Power Electron. 2016, 31, 3585–3603. [Google Scholar]
- Komurcugil, H.; Bayhan, S.; Abu-Rub, H. Variable- and fixed-switching-frequency-based hcc methods for grid-connected vsi with active damping and zero steady-state error. IEEE Trans. Ind. Electron. 2017, 64, 7009–7018. [Google Scholar] [CrossRef]
- Viswadev, R.; Arjun, M.; Ramana, V.V.; Venkatesa perumal, B.; Mishra, S. A novel AC current sensorless hysteresis control for grid-tie inverters. IEEE Trans. Ind. Electron. 2019, 66, 6237–6246. [Google Scholar] [CrossRef]
- Zine, M.; Chemsa, A.; Labiod, C.; Ikhlef, M.; Srairi, K.; Benbouzid, M. Coupled indirect torque control and maximum power point tracking technique for optimal performance of 12/8 switched reluctance generator-based wind turbines. Machines 2022, 10, 1046. [Google Scholar] [CrossRef]
- Harbi, I.; Lobo Heldwein, M.; Kennel, R.; Abdelrahem, M. Enhanced Fault-Tolerant Robust Deadbeat Predictive Control for Nine-Level ANPC-Based Converter. IEEE Access 2022, 10, 32133–32145. [Google Scholar] [CrossRef]
- Harbi, I.; Ahmed, M.; Hackl, C.M. Low-Complexity Dual-Vector Model Predictive Control for Single-Phase Nine-Level ANPC-Based Converter. IEEE Trans. Power Electron. 2023, 15, 567–578. [Google Scholar] [CrossRef]
- Zheng, W.; Xie, S.; Chen, S.; He, X. Model predictive control for three-phase four-wire grid-connected inverter based on space vector modulation. IEEE Trans. Power Electron. 2015, 30, 1237–1252. [Google Scholar]
- Bhattarai, B.; Ashour, M. Hysteresis current control with the state-space averaging technique for grid-connected inverter under unbalanced and nonlinear loads. IET Power Electron. 2018, 11, 2044–2054. [Google Scholar]
- Kwak, S.; Mun, S. Model Predictive Control Methods to Reduce Common-Mode Voltage for Three-Phase Voltage Source Inverters. IEEE Trans. Power Electron. 2014, 30, 5019–5035. [Google Scholar] [CrossRef]
- Chen, Y.; Xue, Y.; Blaabjerg, F. Model predictive control of three-phase inverters for grid-connected photovoltaic systems. IEEE Trans. Ind. Appl. 2019, 55, 6466–6476. [Google Scholar]
- Alizadeh, P.; Rezaei-Zare, A.; Yazdani, A. Model predictive control of three-phase inverters with predictive current control. IEEE Trans. Ind. Electron. 2018, 65, 4112–4122. [Google Scholar]
- Zarei, M.E.; Ramirez, D.; Prodanovic, M.; Venkataramanan, G. Multi-Vector Model Predictive Power Control for Grid Connected Converters in Renewable Power Plants. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 65, 46–57. [Google Scholar]
- Zhao, Z.; Zhong, Y.; Gao, H.; Yuan, L.; Lu, T. Hybrid selective harmonic elimination PWM for common-mode voltage reduction in three-level neutral-point-clamped inverters for variable speed induction drives. IEEE Trans. Power Electron. 2014, 29, 3024–3035. [Google Scholar] [CrossRef]
- Perez, M.; Aguilar, C.; Ortega, R. Predictive direct power control relying only on non-zero voltage vectors. IEEE Trans. Power Electron. 2017, 32, 5236–5246. [Google Scholar]
- Abu-Khader, A.; Abu-Siada, A.; Saidur, R. Predictive Current Control for Voltage Source Inverters Considering Dead-Time Effect. IEEE Trans. Ind. Electron. 2018, 65, 4236–4247. [Google Scholar]
- Ooi, B.T.; Liu, Y.; Gao, W. A model predictive control based common-mode voltage suppression strategy for voltage source inverter. IEEE Trans. Ind. Electron. 2016, 63, 6115–6125. [Google Scholar]
- Guo, L.; Jin, N.; Li, Y.; Luo, K. A New Adaptive Optimal Control Algorithm for the Permanent Magnet Synchronous Motor. IEEE Trans. Ind. Electron. 2017, 64, 6684–6694. [Google Scholar]
- Nguyen, T.D.; Phan, D.Q.; Dao, D.N.; Lee, H.H. Carrier phase-shift PWM to reduce common-mode voltage for three-level T-type NPC inverters. J. Power Electron. 2014, 14, 1197–1207. [Google Scholar] [CrossRef]
- Videt, A.; Le Moigne, P.; Idir, N.; Baudesson, P.; Cimetière, X. A new carrier-based PWM providing common-mode current reduction and DC-bus balancing for three-level inverters. IEEE Trans. Ind. Electron. 2008, 54, 3001–3011. [Google Scholar] [CrossRef]
- Preindl, M.; Schaltz, E.; Thøgersen, P. Switching Frequency Reduction Using Model Predictive Direct Current Control for High-Power Voltage Source Inverters. IEEE Trans. Ind. Electron. 2011, 58, 2826–2835. [Google Scholar] [CrossRef]
- Kouro, S.; Malinowski, M.; Gopakumar, K.; Franquelo, L.G.; Perez, M.A.; Leon, J.I. Recent advances and industrial applications of multilevel converters. IEEE Trans. Ind. Electron. 2010, 57, 2553–2580. [Google Scholar] [CrossRef]
- Haque, M.H.; Gaffar, A. Comparative analysis of control strategies for voltage source inverter in renewable energy systems: A review. Int. J. Renew. Energy Res. (IJRER) 2017, 7, 202–212. [Google Scholar]
- Nguyen, H.T.; Jung, J.W. Disturbance-Rejection-Based Model Predictive Control: Flexible-Mode Design With a Modulator for Three-Phase Inverters. IEEE Trans. Ind. Electron. 2021, 68, 4793–4803. [Google Scholar] [CrossRef]
- Hoseini, S.K.; Adabi, J.; Sheikholeslami, A. Predictive modulation schemes to reduce common-mode voltage in three-phase inverters-fed AC drive systems. IET Power Electron. 2014, 7, 840–849. [Google Scholar] [CrossRef]
- Tran, T.-T.; Gguyen, M.-K.; Duong, T.-D.; Choi, J.-H.; Lim, Y.-C.; Zare, F. A Switched-Capacitor-Voltage-Doubler Based Boost Inverter for Common-Mode Voltage Reduction. IEEE Trans. Power Electron. 2019, 7, 98618–98629. [Google Scholar] [CrossRef]
- Chen, Y.; Wu, Y.; Ruan, X. A Finite Control Set Model Predictive Control Method for Matrix Converter with Zero Common-Mode Voltage. IEEE Energy Convers. Congr. Expo. (ECCE) 2016, 6, 327–338. [Google Scholar]
- Shen, Y.; Wang, K.; Blaabjerg, F. Common-Mode Voltage Reduction in Grid-Connected Inverters: A Comprehensive Study. IEEE Trans. Power Electron. 2018, 33, 3786–3799. [Google Scholar]
- Moreira, M.D.C.; Torres, R.P.; Cabral, E.R.; Barreto, L.H.S.C. Common-Mode Voltage Reduction in Transformer less Single-Phase Photovoltaic Inverters. IEEE Trans. Power Electron. 2013, 30, 5019–5035. [Google Scholar]
- Giaouris, D.; Kladas, A.; Papanikolaou, N. Hybrid PWM technique for Common-Mode Voltage reduction in three-level neutral point clamped inverter. IEEE Trans. Power Electron. 2013, 28, 1784–1794. [Google Scholar]
- Guo, L.; Jin, N.; Gan, C.; Xu, L.; Wang, Q. An Improved Model Predictive Control Strategy to Reduce Common-Mode Voltage for 2-Level Voltage Source Inverters Considering Dead Time Effects. IEEE Trans. Ind. Electron. 2018, 66, 3561–3572. [Google Scholar] [CrossRef]






| State | S1 = 1 | S3 = 1 | S5 = 1 |
|---|---|---|---|
| S2 = 1 | |||
| S4 = 1 | |||
| S6 = 1 |
| S1 | S3 | S5 | Voltage Vectors (VVs) | Output Voltage of the 2L-VSI |
|---|---|---|---|---|
| 0 | 0 | 0 | u0 | 0 |
| 1 | 0 | 0 | u1 | |
| 1 | 1 | 0 | u2 | |
| 0 | 1 | 0 | u3 | |
| 0 | 1 | 1 | u4 | |
| 0 | 0 | 1 | u5 | |
| 1 | 0 | 1 | u6 | |
| 1 | 1 | 1 | u7 | 0 |
| State | Voltage Vectors (VVs) | uno |
|---|---|---|
| (000) | u0 | −Vdc/2 |
| (100) | u1 | −Vdc/6 |
| (110) | u2 | Vdc/6 |
| (010) | u3 | −Vdc/6 |
| (011) | u4 | Vdc/6 |
| (001) | u5 | −Vdc/6 |
| (101) | u6 | Vdc/6 |
| (111) | u7 | Vdc/2 |
| Sector | Candidate VVs | |||||
|---|---|---|---|---|---|---|
| u1 (100) | u2 (110) | u3 (010) | u4 (011) | u5 (001) | u6 (101) | |
| 4-VVs Strategy | ||||||
| Sector 1 | X | X | X | X | ||
| Sector 6 | X | X | X | X | ||
| Sector 3 | X | X | X | X | ||
| Sector 4 | X | X | X | X | ||
| Sector 5 | X | X | X | X | ||
| Sector 2 | X | X | X | X | ||
| 4-VVsS Strategy | ||||||
| Sector 1 | X | X | X | X | ||
| Sector 6 | X | X | X | X | ||
| Sector 3 | X | X | X | X | ||
| Sector 4 | X | X | X | X | ||
| Sector 5 | X | X | X | X | ||
| Sector 2 | X | X | X | X | ||
| Parameter | Numerical Value |
|---|---|
| DC-link voltage [V] | 24 |
| Sampling frequency [kHz] | 10 |
| Reference frequency [Hz] | 50 |
| Resistance load [Ω] | 3.4 |
| Inductance load [mH] | 20 |
| DC-link bus capacitor (C1, C2) [µF] | 3300 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Medekhel, L.; Hettiri, M.; Labiod, C.; Srairi, K.; Benbouzid, M. Enhancing the Performance and Efficiency of Two-Level Voltage Source Inverters: A Modified Model Predictive Control Approach for Common-Mode Voltage Suppression. Energies 2023, 16, 7305. https://doi.org/10.3390/en16217305
Medekhel L, Hettiri M, Labiod C, Srairi K, Benbouzid M. Enhancing the Performance and Efficiency of Two-Level Voltage Source Inverters: A Modified Model Predictive Control Approach for Common-Mode Voltage Suppression. Energies. 2023; 16(21):7305. https://doi.org/10.3390/en16217305
Chicago/Turabian StyleMedekhel, Lamine, Messaoud Hettiri, Chouaib Labiod, Kamel Srairi, and Mohamed Benbouzid. 2023. "Enhancing the Performance and Efficiency of Two-Level Voltage Source Inverters: A Modified Model Predictive Control Approach for Common-Mode Voltage Suppression" Energies 16, no. 21: 7305. https://doi.org/10.3390/en16217305
APA StyleMedekhel, L., Hettiri, M., Labiod, C., Srairi, K., & Benbouzid, M. (2023). Enhancing the Performance and Efficiency of Two-Level Voltage Source Inverters: A Modified Model Predictive Control Approach for Common-Mode Voltage Suppression. Energies, 16(21), 7305. https://doi.org/10.3390/en16217305







