Prediction of Thermal Conductivity of Litz Winding by Least Square Method and GA-BP Neural Network Based on Numerical Simulations
Abstract
:1. Introduction
2. Method
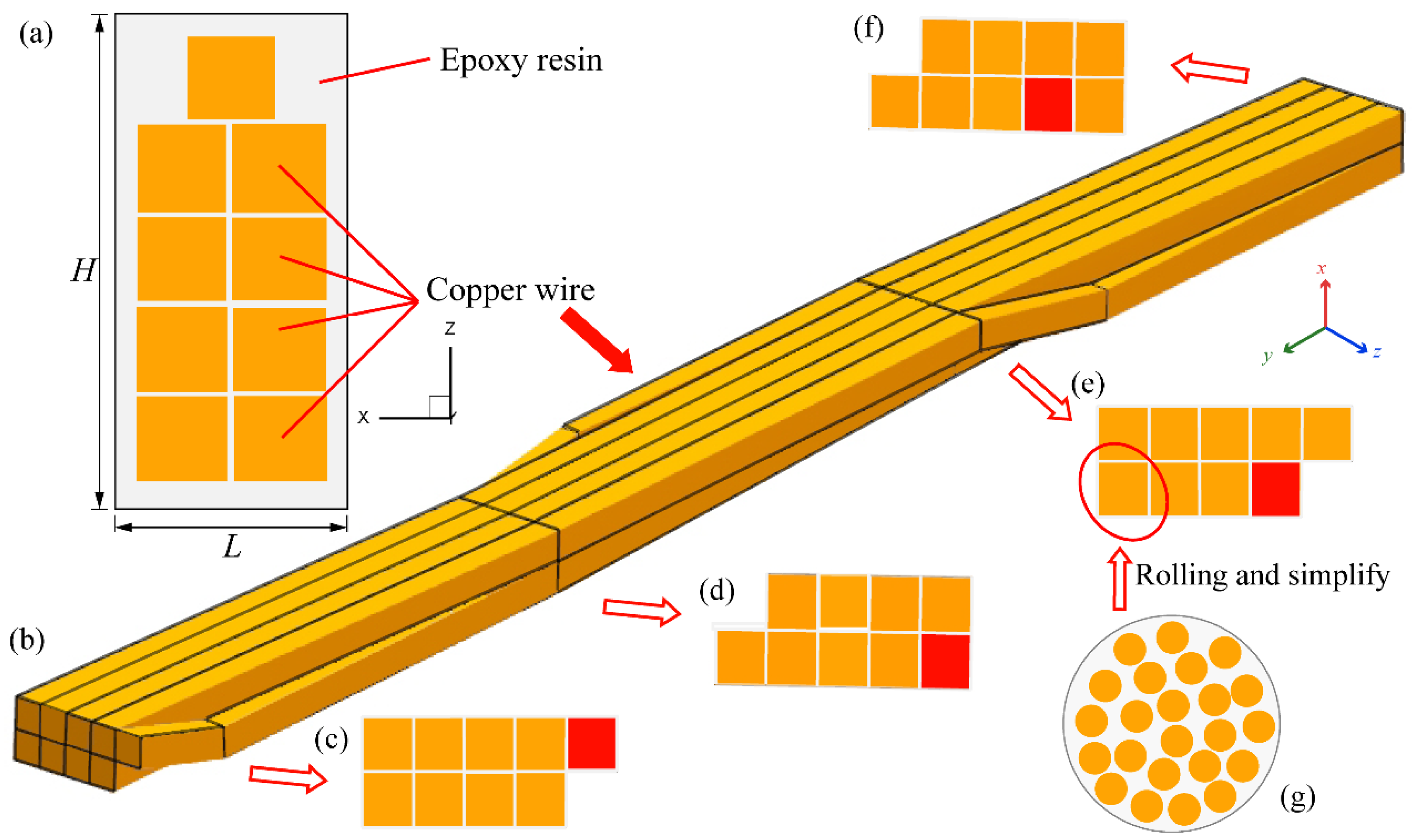
2.1. Physical Model
2.2. Materials
2.3. Simulation Method
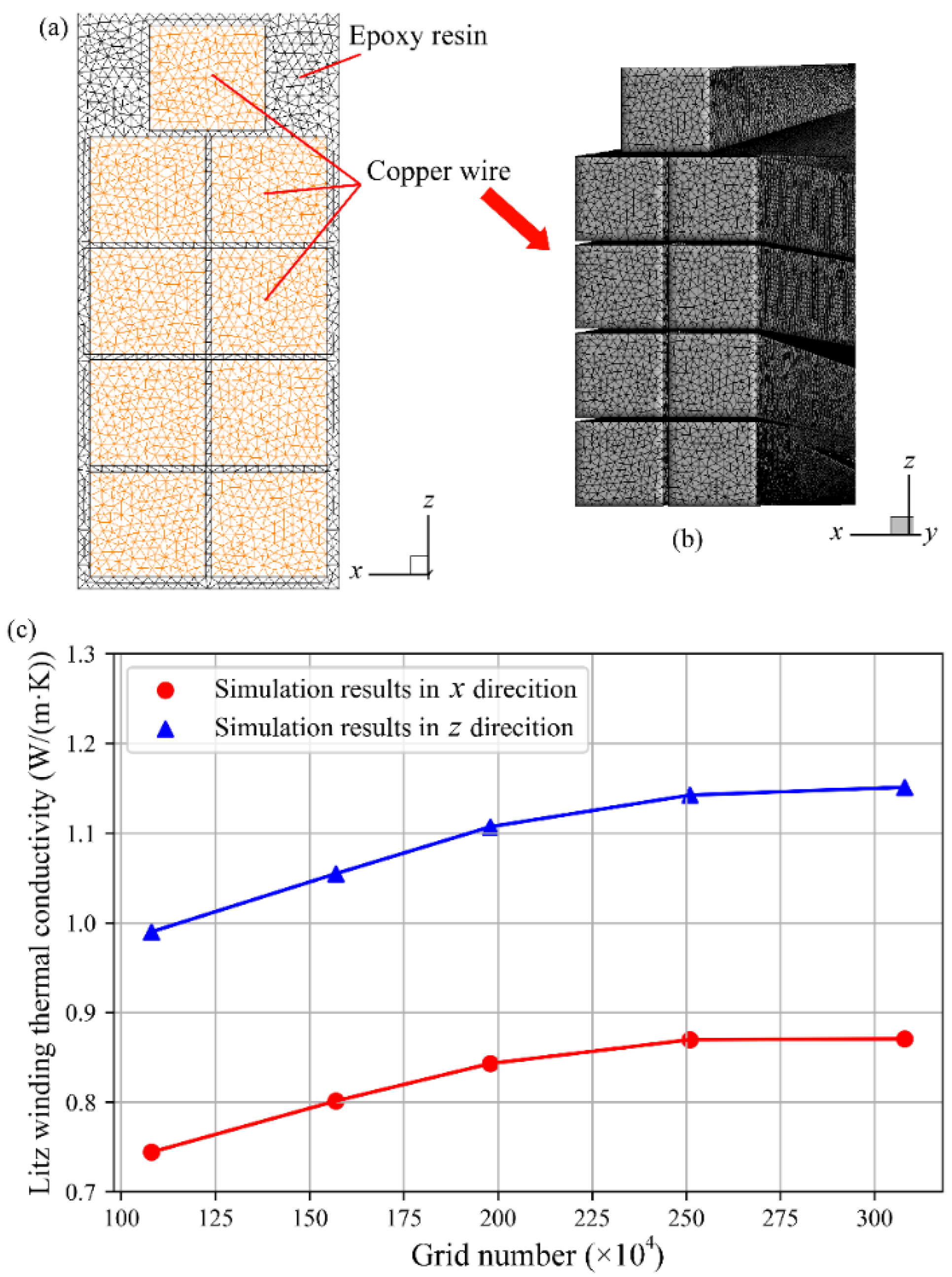
2.4. Grid Independence Test
3. Experimental Verification
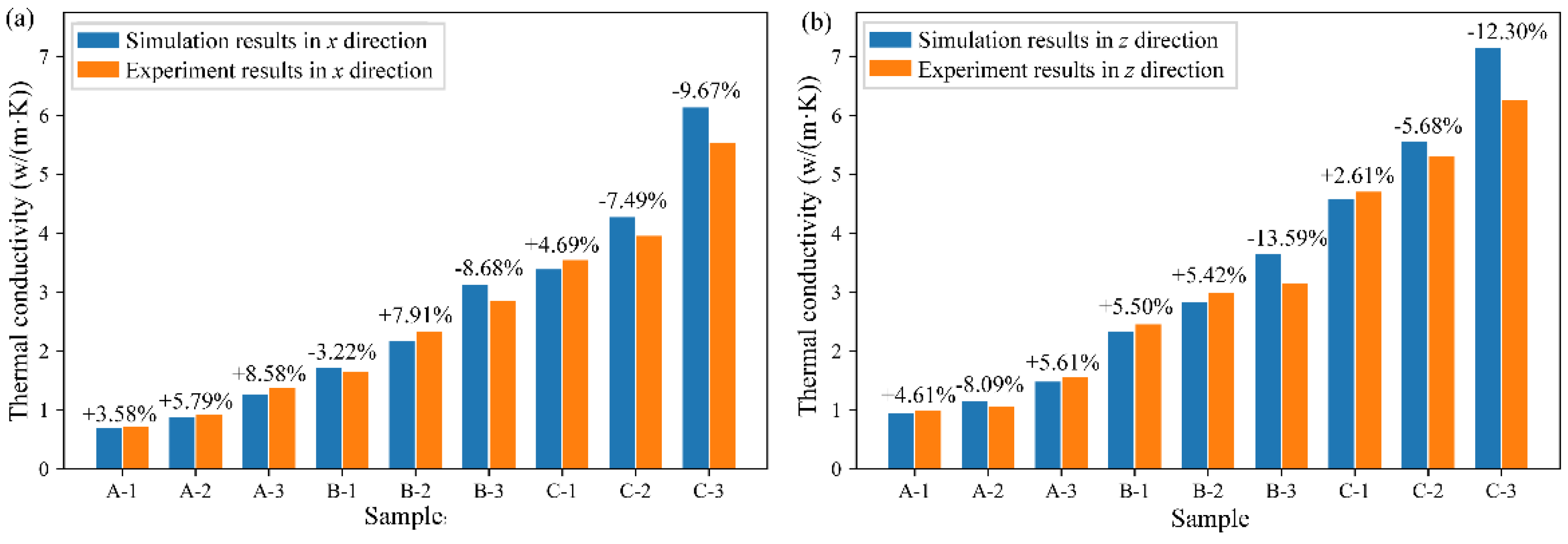
3.1. Sample Parameters
3.2. Hardware Setup and Test Procedure
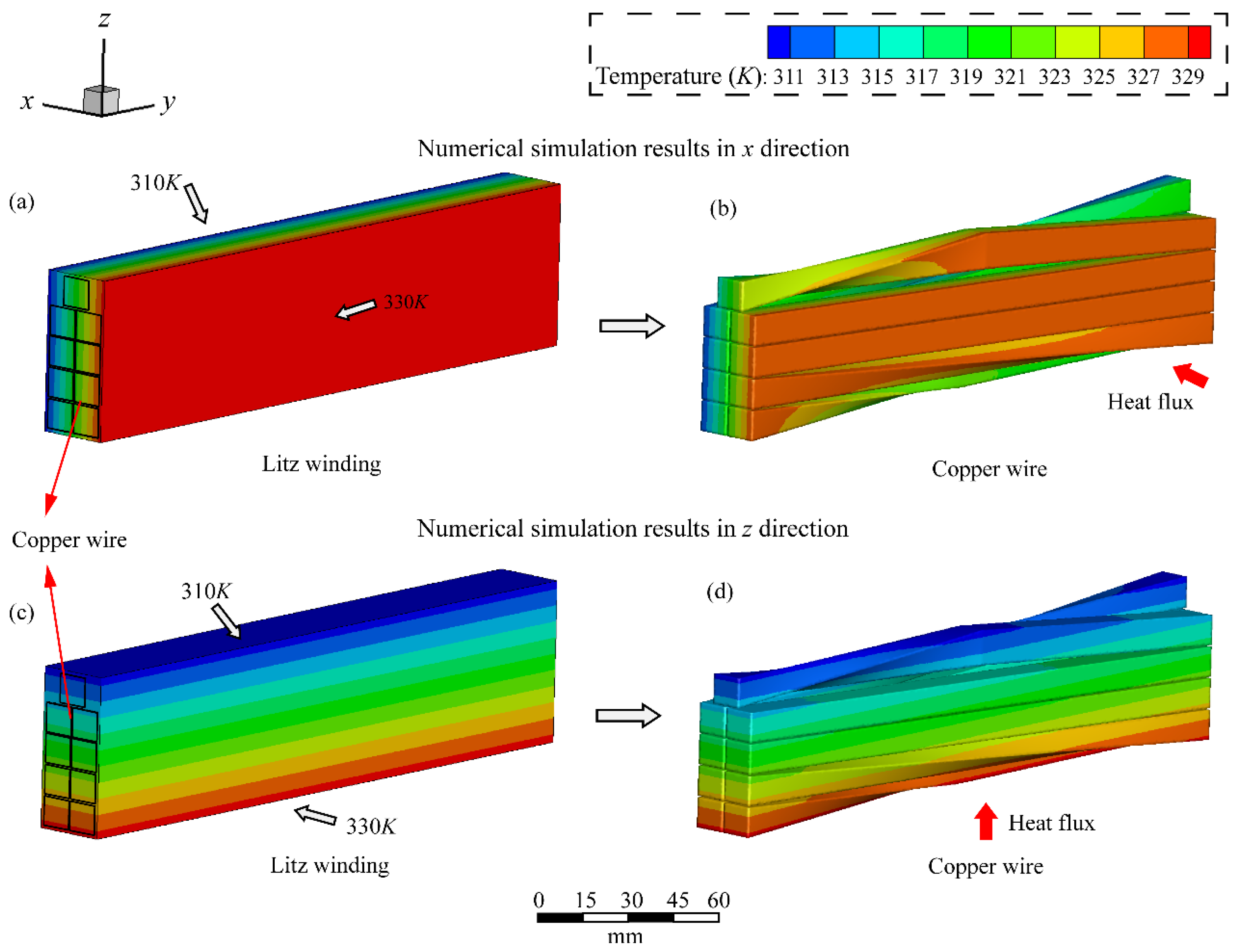
3.3. Validation of the Numerical Model
4. Results and Discussion
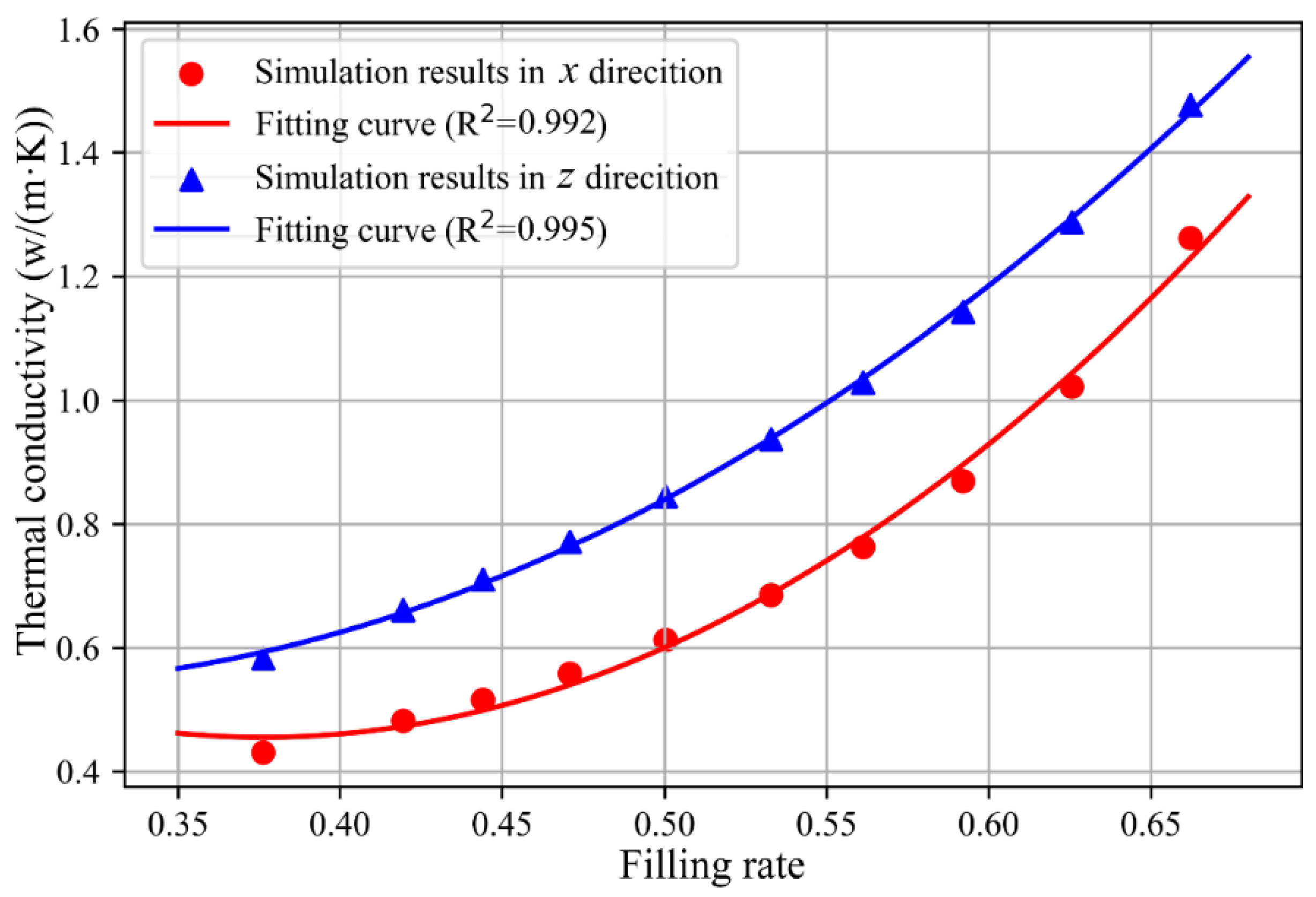
4.1. Effect of Filling Rate
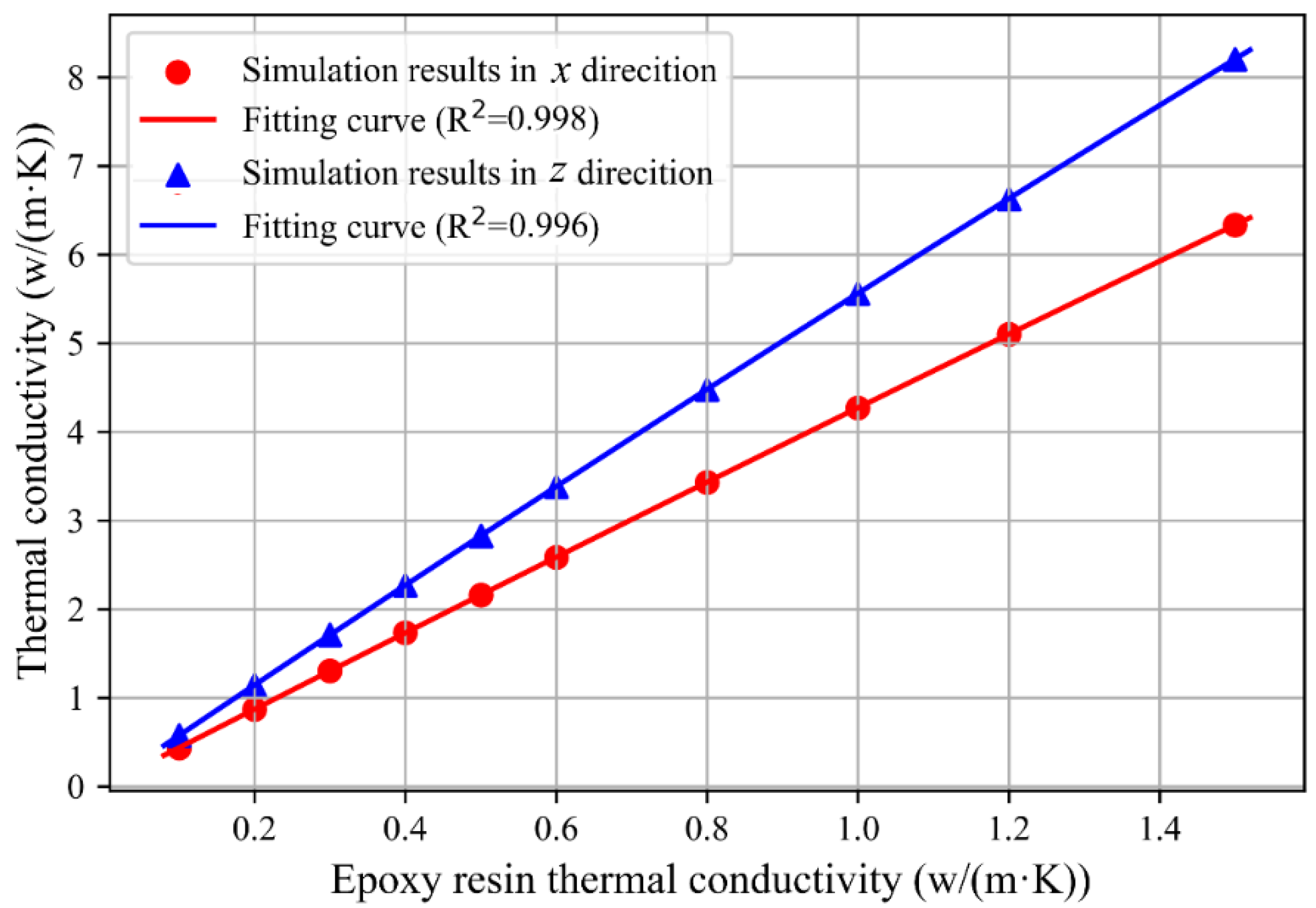
4.2. Effect of Epoxy-Resin Type
4.3. Joint Effect of Filling Rate and Epoxy-Resin Type
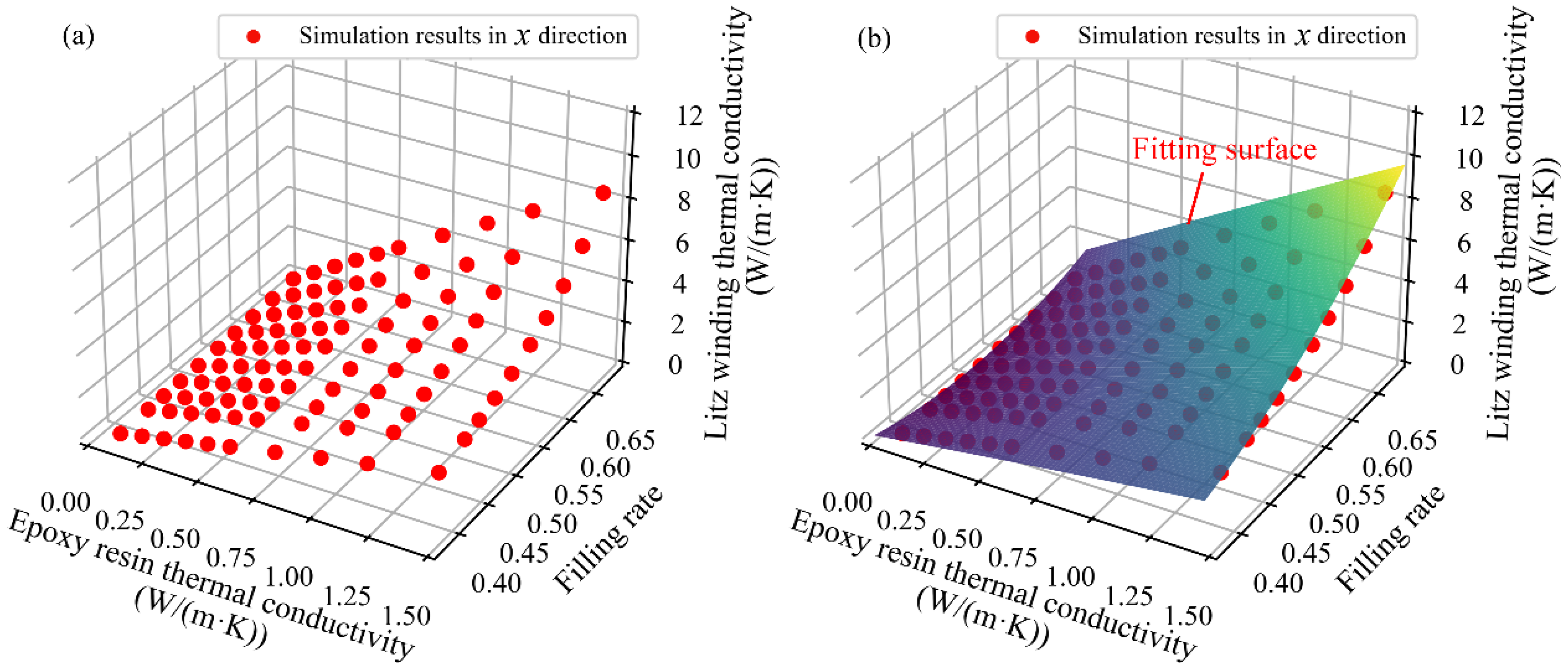
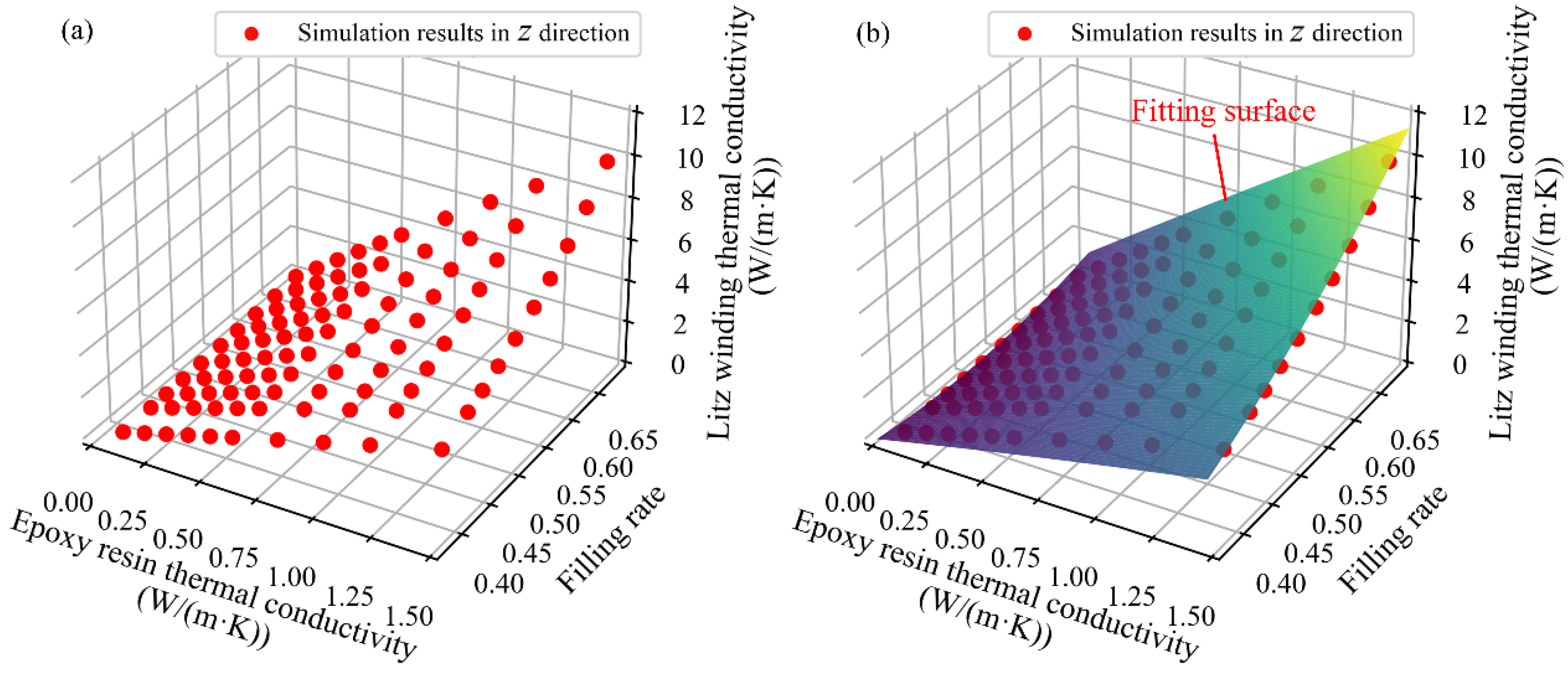
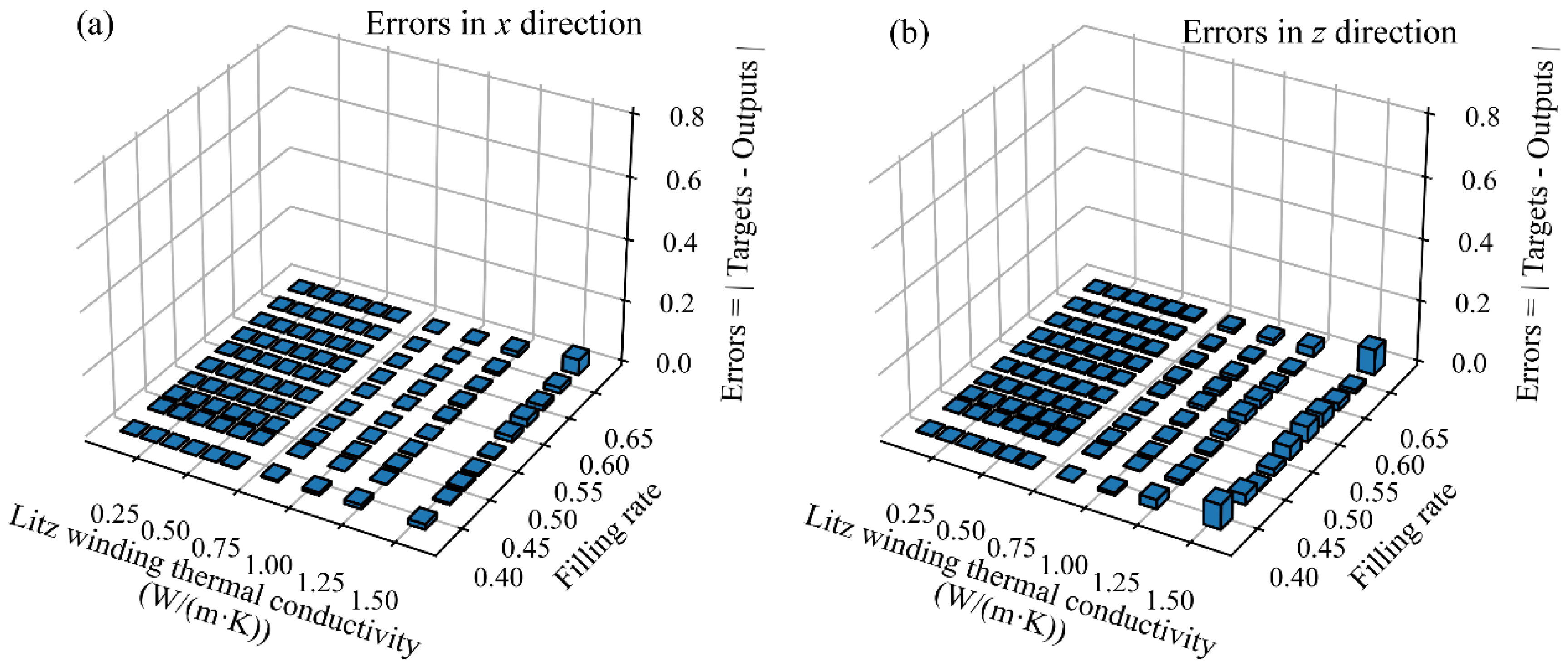
4.3.1. Prediction with the Least Square Method
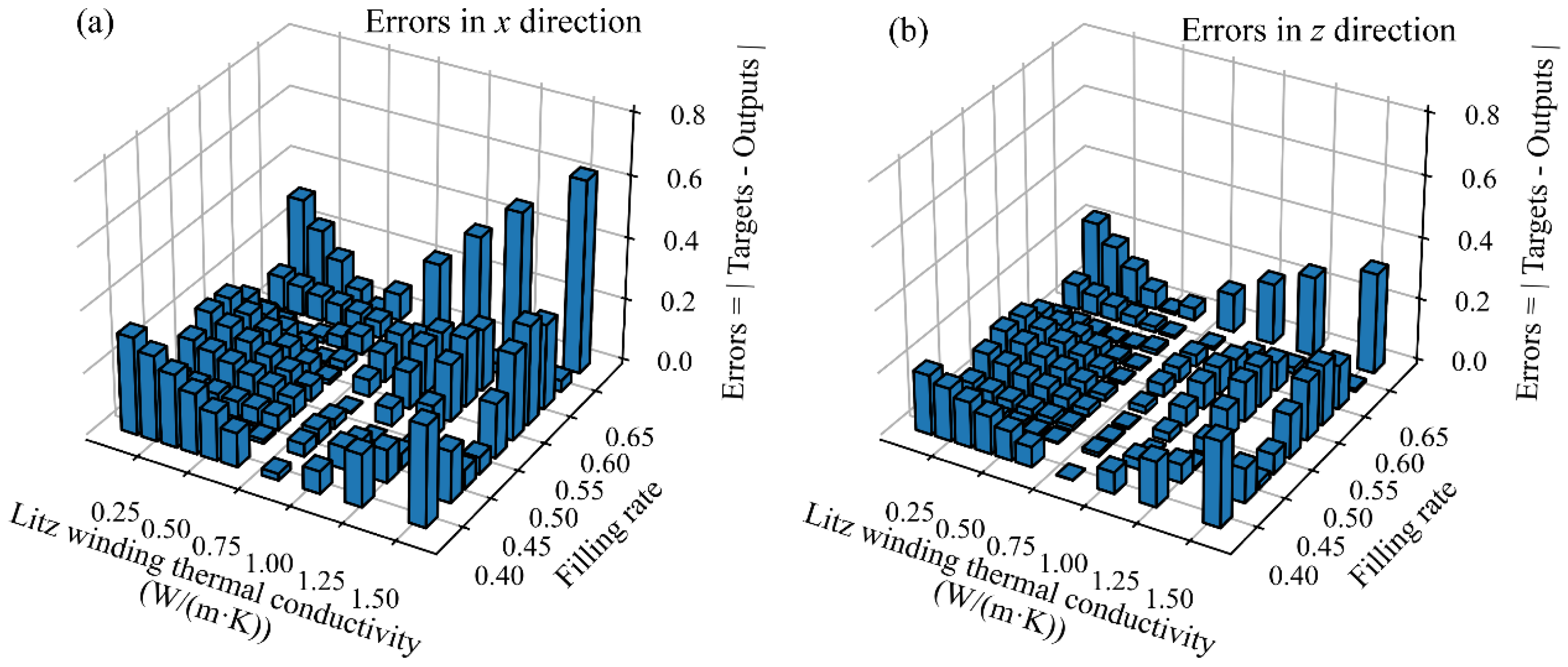
4.3.2. Prediction with GA-BP Neural Network
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kumar, D.; Gupta, R.A. A Comprehensive Review on BLDC Motor and Its Control Techniques. Int. J. Power Electron. 2021, 14, 292–335. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, B.; Fu, X.; Yan, S. Numerical Study on the Influence of Vortex Generator Arrangement on Heat Transfer Enhancement of Oil-Cooled Motor. Energies 2021, 14, 6870. [Google Scholar] [CrossRef]
- Sayed, E.; Abdalmagid, M.; Pietrini, G.; Sa’adeh, N.-M.; Callegaro, A.D.; Goldstein, C.; Emadi, A. Review of Electric Machines in More-/Hybrid-/Turbo-Electric Aircraft. IEEE Trans. Transp. Electrif. 2021, 7, 2976–3005. [Google Scholar] [CrossRef]
- Zhou, Y.; Dong, Q.; Niu, X.-J.; Xu, H.; Xiong, Q.; Su, H.; Zheng, J. A Pole Pair Segment of Oil-Cooling Air-Core Stator for a 2 MW Direct-Drive High Temperature Superconducting Wind Power Generator. J. Electr. Eng. Technol. 2021, 16, 3145–3155. [Google Scholar] [CrossRef]
- Inoue, S.; Akagi, H. A Bidirectional Isolated DC–DC Converter as a Core Circuit of the Next-Generation Medium-Voltage Power Conversion System. IEEE Trans. Power Electron. 2007, 22, 535–542. [Google Scholar] [CrossRef]
- Leibl, M.; Ortiz, G.; Kolar, J.W. Design and Experimental Analysis of a Medium-Frequency Transformer for Solid-State Transformer Applications. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 110–123. [Google Scholar] [CrossRef]
- Shen, W.; Wang, F.; Boroyevich, D.; Tipton IV, C.W. High-Density Nanocrystalline Core Transformer for High-Power High-Frequency Resonant Converter. IEEE Trans. Ind. Appl. 2008, 44, 213–222. [Google Scholar] [CrossRef]
- Sullivan, C.R. Optimal Choice for Number of Strands in a Litz-Wire Transformer Winding. IEEE Trans. Power Electron. 1999, 14, 283–291. [Google Scholar] [CrossRef]
- Carretero, C.; Acero, J.; Alonso, R. TM-TE Decomposition of Power Losses in Multi-Stranded Litz-Wires Used in Electronic Devices. Prog. Electromagn. Res. 2012, 123, 83–103. [Google Scholar] [CrossRef]
- Liu, X.; Gerada, D.; Xu, Z.; Corfield, M.; Gerada, C.; Yu, H. Effective Thermal Conductivity Calculation and Measurement of Litz Wire Based on the Porous Metal Materials Structure. IEEE Trans. Ind. Electron. 2020, 67, 2667–2677. [Google Scholar] [CrossRef]
- Sullivan, C.R.; Zhang, R.Y. Simplified Design Method for Litz Wire. In Proceedings of the 2014 IEEE Applied Power Electronics Conference and Exposition—APEC 2014, Long Beach, CA, USA, 25–29 March 2014; pp. 2667–2674. [Google Scholar]
- Jaritz, M.; Hillers, A.; Biela, J. General Analytical Model for the Thermal Resistance of Windings Made of Solid or Litz Wire. IEEE Trans. Power Electron. 2019, 34, 668–684. [Google Scholar] [CrossRef]
- Idoughi, L.; Mininger, X.; Bouillault, F.; Bernard, L.; Hoang, E. Thermal Model With Winding Homogenization and FIT Discretization for Stator Slot. IEEE Trans. Magn. 2011, 47, 4822–4826. [Google Scholar] [CrossRef]
- Yi, X.; Yang, T.; Xiao, J.; Miljkovic, N.; King, W.P.; Haran, K.S. Equivalent Thermal Conductivity Prediction of Form-Wound Windings with Litz Wire Including Transposition Effects. IEEE Trans. Ind. Appl. 2021, 57, 1440–1449. [Google Scholar] [CrossRef]
- Simpson, N.; Wrobel, R.; Mellor, P.H. Estimation of Equivalent Thermal Parameters of Impregnated Electrical Windings. IEEE Trans. Ind. Appl. 2013, 49, 2505–2515. [Google Scholar] [CrossRef]
- Wrobel, R.; Mellor, P.H. A General Cuboidal Element for Three-Dimensional Thermal Modelling. IEEE Trans. Magn. 2010, 46, 3197–3200. [Google Scholar] [CrossRef]
- Woodworth, A.A.; Jansen, R.; Duffy, K.; Nazhipour Author, P.; Shin, E.-S. Creating a Multifunctional Composite Stator Slot Material System to Enable High Power Density Electric Machines for Electrified Aircraft Applications. In Proceedings of the 2018 AIAA/IEEE Electric Aircraft Technologies Symposium (EATS), Cincinnati, OH, USA, 12–14 July 2018; pp. 1–8. [Google Scholar]
- Liu, H.P.; Hahne, J.J. High-Speed Compulsator Stator Thermal Management. IEEE Trans. Magn. 2003, 39, 357–361. [Google Scholar] [CrossRef]
- Huang, X.; Tan, Q.; Li, L.; Li, J.; Qian, Z. Winding Temperature Field Model Considering Void Ratio and Temperature Rise of a Permanent-Magnet Synchronous Motor with High Current Density. IEEE Trans. Ind. Electron. 2017, 64, 2168–2177. [Google Scholar] [CrossRef]
- Salinas López, G.; Expósito, A.D.; Muñoz-Antón, J.; Ramírez, J.Á.O.; López, R.P. Fast and Accurate Thermal Modeling of Magnetic Components by FEA-Based Homogenization. IEEE Trans. Power Electron. 2020, 35, 1830–1844. [Google Scholar] [CrossRef]
- Ke, J.; Wang, B.; Yang, Z. Application of GA and BP Neural Network in Heat Dissipation of Batteries. Mach. Des. Manuf. 2019, 11, 196–199. [Google Scholar] [CrossRef]
- Ivanova, A.; Migorski, S.; Wyczolkowski, R.; Ivanov, D. Numerical Identification of Temperature Dependent Thermal Conductivity Using Least Squares Method. Int. J. Numer. Methods Heat Fluid Flow 2019, 30, 3083–3099. [Google Scholar] [CrossRef]
- Jaritz, M.; Biela, J. Analytical Model for the Thermal Resistance of Windings Consisting of Solid or Litz Wire. In Proceedings of the 2013 15th European Conference on Power Electronics and Applications (EPE), Lille, France, 2–6 September 2013; pp. 1–10. [Google Scholar]
- Wrobel, R.; Ayat, S.; Baker, J.L. Analytical Methods for Estimating Equivalent Thermal Conductivity in Impregnated Electrical Windings Formed Using Litz Wire. In Proceedings of the 2017 IEEE International Electric Machines and Drives Conference (IEMDC), Miami, FL, USA, 21–24 May 2017; pp. 1–8. [Google Scholar]
- Chapman, B.L.W. Shielded gradients. And the general solution to the near field problem of electromagnet design. Magn. Reson. Mater. Biol. Phys. Med. 1974, 9, 146–151. [Google Scholar] [CrossRef] [PubMed]
- Gustafsson, S.E. Transient Plane Source Techniques for Thermal Conductivity and Thermal Diffusivity Measurements of Solid Materials. Rev. Sci. Instrum. 1991, 62, 797–804. [Google Scholar] [CrossRef]
- Dai, R.; Chandrasekaran, G.; Chen, J.; Jackson, C.; Liu, Y.; Nian, Q.; Kwon, B. Thermal Conductivity of Metal Coated Polymer Foam: Integrated Experimental and Modeling Study. Int. J. Therm. Sci. 2021, 169, 107045. [Google Scholar] [CrossRef]
- Kincaid, D.R.; Cheney, E.W. Numerical Analysis: Mathematics of Scientific Computing; American Mathematical Society: Providence, RI, USA, 2002. [Google Scholar]
- Huang, D.; Gong, R.-X.; Gong, S. Prediction of Wind Power by Chaos and BP Artificial Neural Networks Approach Based on Genetic Algorithm. J. Electr. Eng. Technol. 2015, 10, 41–46. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, N.; Wu, L.; Wang, Y. Wind Speed Forecasting Based on the Hybrid Ensemble Empirical Mode Decomposition and GA-BP Neural Network Method. Renew. Energy 2016, 94, 629–636. [Google Scholar] [CrossRef]
- Papari, M.M.; Yousefi, F.; Moghadasi, J.; Karimi, H.; Campo, A. Modeling Thermal Conductivity Augmentation of Nanofluids Using Diffusion Neural Networks. Int. J. Therm. Sci. 2011, 50, 44–52. [Google Scholar] [CrossRef]
- Liu, H.-M.; Zhao, Y.-L.; Cheng, Y.-M.; Wu, J.; Al Shurafa, M.A.M.; Liu, C.; Lee, I.-K. A New Power Supply Strategy for High Power Rectifying Units in Electrolytic Copper Process. J. Electr. Eng. Technol. 2022, 17, 1143–1156. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, Y. Adaptive RBF Neural Network Based on Sliding Mode Controller for Active Power Filter. Int. J. Power Electron. 2020, 11, 460–481. [Google Scholar] [CrossRef]
- Li, J.; Guo, B.; Shen, Y.; Li, D.; Huang, Y. A Modeling Approach for Energy Saving Based on GA-BP Neural Network. J. Electr. Eng. Technol. 2016, 11, 1289–1298. [Google Scholar] [CrossRef]


| Materials | Thermal Conductivity ) | Materials | Thermal Conductivity ) |
|---|---|---|---|
| Copper wire | 387.6 | Epoxy resin 6 | 0.6 |
| Epoxy resin 1 | 0.1 | Epoxy resin 7 | 0.8 |
| Epoxy resin 2 | 0.2 | Epoxy resin 8 | 1.0 |
| Epoxy resin 3 | 0.3 | Epoxy resin 9 | 1.2 |
| Epoxy resin 4 | 0.4 | Epoxy resin 10 | 1.5 |
| Epoxy resin 5 | 0.5 |
| Serial Number | Epoxy-Resin Type | ) | Filling Rate (%) |
|---|---|---|---|
| A-1 | Epoxy resin 1 (0.2 ) | 53.8 | |
| A-2 | 59.8 | ||
| A-3 | 66.2 | ||
| B-1 | Epoxy resin 5 (0.5 ) | 53.8 | |
| B-2 | 59.8 | ||
| B-3 | 66.2 | ||
| C-1 | Epoxy resin 8 (1.0 ) | 53.8 | |
| C-2 | 59.8 | ||
| C-3 | 66.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, Q.; Fu, X. Prediction of Thermal Conductivity of Litz Winding by Least Square Method and GA-BP Neural Network Based on Numerical Simulations. Energies 2023, 16, 7295. https://doi.org/10.3390/en16217295
Dong Q, Fu X. Prediction of Thermal Conductivity of Litz Winding by Least Square Method and GA-BP Neural Network Based on Numerical Simulations. Energies. 2023; 16(21):7295. https://doi.org/10.3390/en16217295
Chicago/Turabian StyleDong, Qi, and Xiaoli Fu. 2023. "Prediction of Thermal Conductivity of Litz Winding by Least Square Method and GA-BP Neural Network Based on Numerical Simulations" Energies 16, no. 21: 7295. https://doi.org/10.3390/en16217295
APA StyleDong, Q., & Fu, X. (2023). Prediction of Thermal Conductivity of Litz Winding by Least Square Method and GA-BP Neural Network Based on Numerical Simulations. Energies, 16(21), 7295. https://doi.org/10.3390/en16217295






