Calibrating the Ångström–Prescott Model with Solar Radiation Data Collected over Long and Short Periods of Time over the Tibetan Plateau
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Collected in the Radiation Stations for Exploring the Effect of Calibration Data Length on the Performance of the Ångström–Prescott Model
2.2. Data Measured during the Scientific Expedition for Model Calibration and Testing Different Paramerization Methods in the Central Tibetan Plateau
2.3. Description of the Ångström–Prescott Model
- (1)
- FAO method
- (2)
- Gopinathan method
- (3)
- LiuXY method
- (4)
- LiuJD method
2.4. Model Evaluation
3. Results
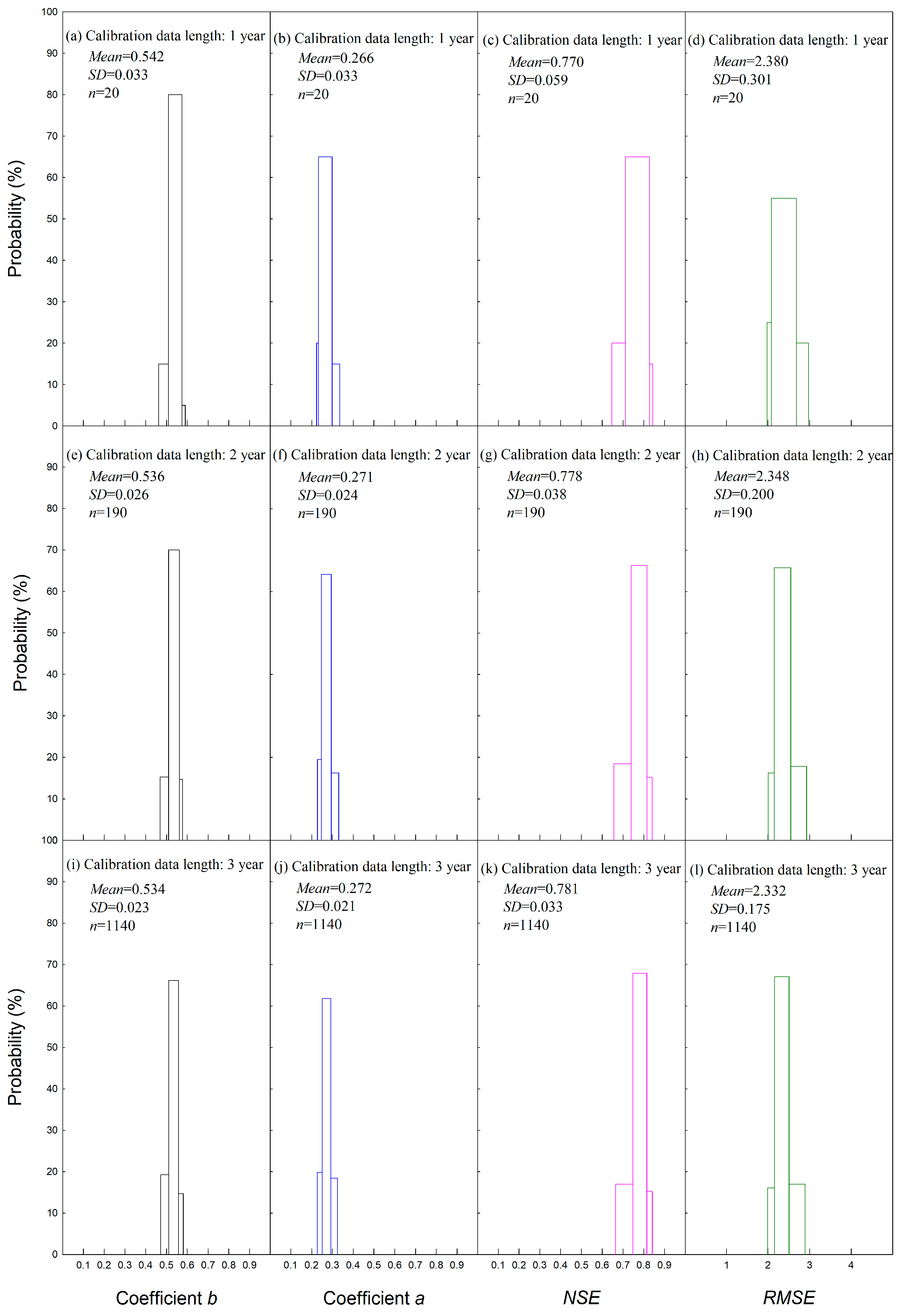
3.1. Exploration of the Effect of Calibration Length on the Performance of the Ångström–Prescott Model over the Tibetan Plateau
3.1.1. Calibration of the Ångström–Prescott Model in Routine Method
3.1.2. Calibration of the Ångström–Prescott Model with Different Data Lengths
3.2. Model Calibration and Evaluation of Different Parametrization Methods with Expedition Observations in Bange
3.2.1. Preliminary Analysis of the Expedition Data in Bange
3.2.2. Calibration of the Ångström–Prescott Model with Observations in Bange
3.2.3. Evaluation of Different Parametrization Methods for Calculating the Coefficients of the Ångström–Prescott Model in Bange
4. Discussion
4.1. Characteristics of the Coefficients of a and b over the Tibetan Plateau
4.2. Unrealistic Global Parameterization Method and Necessary Local Calibration over the Tibetan Plateau
4.3. Uncertainties and Future Research
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gueymard, C.A. The sun’s total and spectral irradiance for solar energy applications and solar radiation models. Sol. Energy 2004, 76, 423–453. [Google Scholar] [CrossRef]
- Ordoñez Palacios, L.E.; Bucheli Guerrero, V.; Ordoñez, H. Machine learning for solar resource assessment using satellite images. Energies 2022, 15, 3985. [Google Scholar] [CrossRef]
- Hunt, L.A.; Kuchar, L.; Swanton, C.J. Estimation of solar radiation for use in crop modeling. Agric. For. Meteorol. 1998, 91, 293–300. [Google Scholar] [CrossRef]
- Miller, D.G.; Rivington, M.; Matthews, K.B.; Bellocchi, G. Testing the spatial applicability of the Johnson-Woodward method for estimating solar radiation from sunshine duration data. Agric. For. Meteorol. 2008, 148, 466–480. [Google Scholar] [CrossRef]
- Liu, X.; Xu, Y.; Zhong, X.; Zhang, W.; Porter, J.R.; Liu, W.L. Assessing models for parameters of the Ångström-Prescott formula in China. Appl. Energy 2012, 96, 327–338. [Google Scholar] [CrossRef]
- Li, H.; Ma, W.; Lian, Y.; Wang, X.; Zhao, L. Global solar radiation estimation with sunshine duration in Tibet, China. Renew. Energy 2011, 36, 3141–3145. [Google Scholar] [CrossRef]
- Liu, J.; Liu, J.; Linderholm, H.W.; Chen, D.; Yu, Q.; Wu, D.; Haginoya, S. Observation and calculation of the solar radiation on the Tibetan Plateau. Energy Convers. Manag. 2012, 57, 23–32. [Google Scholar] [CrossRef]
- Wolf, K.; Ehrlich, A.; Mech, M.; Hogan, R.; Wendisch, M. Evaluation of ECMWF radiation scheme using aircraft observations of spectral irradiance above clouds. J. Atmos. Sci. 2020, 77, 2665–2685. [Google Scholar] [CrossRef]
- Varga, A.J.; Breuer, H. Sensitivity of simulated temperature, precipitation, and global radiation to different WRF configurations over the Carpathian Basin for regional climate applications. Clim. Dyn. 2020, 55, 2849–2866. [Google Scholar] [CrossRef]
- Wong, M.S.; Zhu, R.; Liu, Z.; Lu, L.; Peng, J.; Tang, Z.; Chan, W.K. Estimation of Hong Kong’s solar energy potential using GIS and remote sensing technologies. Renew. Energy 2016, 99, 325–335. [Google Scholar] [CrossRef]
- Song, X.; Huang, Y.; Zhao, C.; Liu, Y.; Lu, Y.; Chang, Y.; Yang, J. An approach for estimating solar photovoltaic potential based on rooftop retrieval from remote sensing images. Energies 2018, 11, 3172. [Google Scholar] [CrossRef]
- Pinker, R.T.; Frouin, R.; Li, Z. A review of satellite methods to derive surface shortwave irradiance. Remote Sens. Environ. 1995, 51, 108–124. [Google Scholar] [CrossRef]
- Voyant, C.; Notton, G.; Kalogirou, S.; Nivet, M.L.; Paoli, C.; Motte, F.; Fouilloy, A. Machine learning methods for solar radiation forecasting: A review. Renew. Energy 2017, 105, 569–582. [Google Scholar] [CrossRef]
- Taki, M.; Rohani, A.; Yildizhan, H. Application of machine learning for solar radiation modeling. Theor. Appl. Climatol. 2021, 143, 1599–1613. [Google Scholar] [CrossRef]
- Zhou, L.; Pan, S.; Wang, J.; Vasilakos, A.V. Machine learning on big data: Opportunities and challenges. Neurocomputing 2017, 237, 350–361. [Google Scholar] [CrossRef]
- Ångström, A. Solar and terrestrial radiation. Q. J. R. Met. Soc. 1924, 50, 121–125. [Google Scholar] [CrossRef]
- Prescott, J.A. Evaporation from a water surface in relation to solar radiation. Trans. R. Soc. S. Aust. 1940, 64, 114–118. [Google Scholar]
- Bristow, K.L.; Campbell, G.S. On the relationship between incoming solar radiation and daily maximum and minimum temperature. Agric. For. Meteorol. 1984, 31, 159–166. [Google Scholar] [CrossRef]
- Hargreaves, G.L.; Hargreaves, G.H.; Riley, J.P. Irrigation water requirements for Senegal River Basin. J. Irrig. Drain. Eng. 1985, 111, 265–275. [Google Scholar] [CrossRef]
- Meza, F.; Varas, E. Estimation of mean monthly solar global radiation as a function of temperature. Agric. For. Meteorol. 2000, 100, 231–241. [Google Scholar] [CrossRef]
- McCaskill, M.R. Prediction of solar radiation from rain day information using regionally stable coefficients. Agric. For. Meteorol. 1990, 51, 247–255. [Google Scholar] [CrossRef]
- Hook, J.E.; McClendon, R.W. Estimation of solar radiation data missing from long-term meteorological records. Agron. J. 1992, 84, 739–742. [Google Scholar] [CrossRef]
- Wu, G.; Liu, Y.; Wang, T. Methods and strategy for modeling daily global solar radiation with measured meteorological data—A case study in Nanchang station, China. Energy Convers. Manag. 2007, 48, 2447–2452. [Google Scholar] [CrossRef]
- Gouda, S.G.; Hussein, Z.; Luo, S.; Yuan, Q. Review of empirical solar radiation models for estimating global solar radiation of various climate zones of China. Prog. Phys. Geogr. Earth Environ. 2020, 44, 168–188. [Google Scholar] [CrossRef]
- Ogolo, E.O. Evaluating the performance of some predictive models for estimating global solar radiation across the varying climatic conditions in Nigeria. Pac. J. Sci. Technol. 2010, 11, 60–72. [Google Scholar]
- Adaramola, M.S. Estimating global solar radiation using common meteorological data in Akure, Nigeria. Renew. Energy 2012, 47, 38–44. [Google Scholar] [CrossRef]
- Thornton, P.E.; Running, S.W. An improved algorithm for estimating incident daily solar radiation from measurements of temperature, humidity, and precipitation. Agric. For. Meteorol. 1999, 93, 211–228. [Google Scholar] [CrossRef]
- Weiss, A.; Hays, C.J. Simulation of daily solar irradiance. Agric. For. Meteorol. 2004, 123, 187–199. [Google Scholar] [CrossRef]
- Liu, D.L.; Scott, B.J. Estimation of solar radiation in Australia from rainfall and temperature observation. Agric. For. Meteorol. 2001, 106, 41–59. [Google Scholar] [CrossRef]
- Chen, R.; Kang, E.; Yang, J.; Lu, S.; Zhao, W. Validation of five global radiation models with measured daily data in China. Energy Convers. Manag. 2004, 45, 1759–1769. [Google Scholar] [CrossRef]
- Chen, R.; Kang, E.; Lu, S.; Yang, J.; Ji, X.; Zhang, Z.; Zhang, J. New methods to estimate global radiation based on meteorological data in China. Energy Convers. Manag. 2006, 47, 2991–2998. [Google Scholar] [CrossRef]
- Liu, X.; Mei, X.; Li, Y.; Wang, Q.; Jensen, J.R.; Zhang, Y.; Porter, J.R. Evaluation of temperature-based global solar radiation models in China. Agric. For. Meteorol. 2009, 149, 1433–1446. [Google Scholar] [CrossRef]
- Liu, J.; Pan, T.; Chen, D.; Zhou, X.; Yu, Q.; Flerchinger, G.N.; Shen, Y. An improved Ångström-type model for estimating solar radiation over the Tibetan Plateau. Energies 2017, 10, 892. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration—Guidelines for Computing Crop Water Requirements; FAO Irrigation and Drainage Paper 56; Food and Agriculture Organization of the United Nations: Rome, Italy, 1998; Volume 300, p. D05109. [Google Scholar]
- Liu, J.; Linderholm, H.; Chen, D.; Zhou, X.; Flerchinger, G.N.; Yu, Q.; Yang, Z. Changes in the relationship between solar radiation and sunshine duration in large cities of China. Energy 2015, 82, 589–600. [Google Scholar] [CrossRef]
- Pelkowski, J. A physical rationale for generalized Ångström–Prescott regression. Sol. Energy 2009, 83, 955–963. [Google Scholar] [CrossRef]
- Streets, D.G.; Yu, C.; Wu, Y.; Chin, M.; Zhao, Z.; Hayasaka, T.; Shi, G. Aerosol trends over China, 1980–2000. Atmos. Res. 2008, 88, 174–182. [Google Scholar] [CrossRef]
- Gopinathan, K.K. A general formula for computing the coefficients of the correlation connecting global solar radiation to sunshine duration. Sol. Energy 1988, 41, 499–502. [Google Scholar] [CrossRef]
- Jiang, Y.; Shi, B.; Su, G.; Lu, Y.; Li, Q.; Meng, J.; Ding, Y.; Song, S.; Dai, L. Spatiotemporal analysis of ecological vulnerability in the Tibet Autonomous Region based on a pressure-state-response-management framework. Ecol. Indic. 2021, 130, 108054. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models. I. A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Von Storch, H.; Zwiers, F.W. Statistical Analysis in Climate Research; Cambridge University Press: Cambridge, UK, 2001; pp. 3–10. [Google Scholar]
- Gouda, S.G.; Hussein, Z.; Luo, S.; Wang, P.; Gao, H.; Yuan, Q. Empirical models for estimating global solar radiation in Wuhan City, China. Eur. Phys. J. Plus 2018, 133, 517. [Google Scholar] [CrossRef]
- Gouda, S.G.; Hussein, Z.; Luo, S.; Yuan, Q. Model selection for accurate daily global solar radiation prediction in China. J. Clean. Prod. 2019, 221, 132–144. [Google Scholar] [CrossRef]
- Almorox, J.; Hontoria, C. Global solar radiation estimation using sunshine duration in Spain. Energy Convers. Manag. 2004, 45, 1529–1535. [Google Scholar] [CrossRef]
- De Souza, J.L.; Lyra, G.B.; Dos Santos, C.M.; Ferreira Junior, R.A.; Tiba, C.; Lyra, G.B.; Lemes, M.A.M. Empirical models of daily and monthly global solar irradiation using sunshine duration for Alagoas State, Northeastern Brazil. Sustain. Energy Technol. Assess. 2016, 14, 35–45. [Google Scholar] [CrossRef]
- Yang, K.; Huang, G.W.; Tamai, N. A hybrid model for estimating global solar radiation. Sol. Energy 2001, 70, 13–22. [Google Scholar] [CrossRef]
- Kattel, D.B.; Yao, T. Temperature-topographic elevation relationship for high mountain terrain: An example from the southeastern Tibetan Plateau. Int. J. Climatol. 2018, 38, 901–920. [Google Scholar] [CrossRef]
- Domros, M.; Peng, G.B. The Climate of China; Springer: Berlin/Heidelberg, Germany, 1988. [Google Scholar]
- Liu, J.; Sun, Z.; Liang, H. Precipitable water vapor on the Tibetan Plateau estimated by GPS, water vapor radiometer, radiosonde, and numerical weather prediction analysis and its impact on the radiation budget. J. Geophys. Res. 2005, 110, D17106. [Google Scholar] [CrossRef]
- Liu, Y.; Tan, Q.; Pan, T. Determining the parameters of the Ångström-Prescott model for estimating solar radiation in different regions of China: Calibration and modeling. Earth Space Sci. 2019, 6, 1976–1986. [Google Scholar] [CrossRef]
- Ertekin, C.; Evrendilek, F. Spatio-temporal modeling of global solar radiation dynamics as a function of sunshine duration for Turkey. Agric. For. Meteorol. 2007, 45, 36–47. [Google Scholar] [CrossRef]
- Liu, X.; Mei, X.; Li, Y.; Wang, Q.; Zhang, Y.; Porter, J.R. Variation in reference crop evapotranspiration caused by the Ångström–Prescott coefficient: Locally calibrated versus the FAO recommended. Agric. Water Manag. 2009, 96, 1137–1145. [Google Scholar] [CrossRef]
- Lutgens, F.K.; Tarbuk, E.J. The Atmosphere: An Introduction to Meteorology; Prentice Hall: Hoboken, NJ, USA, 2001. [Google Scholar]
- Li, C.; Gong, Y.; Duan, T. Observational study of super solar constant of the solar radiation over Qinghai-Tibet Plateau. J. Chengdu Inst. Meteorol. 2000, 53, 107–112. [Google Scholar]
- Chang, K.; Zhang, Q. Improvement of the hourly global solar model and solar radiation for air-conditioning design in China. Renew. Energy 2019, 138, 1232–1238. [Google Scholar] [CrossRef]
- Li, D.H.; Chen, W.; Li, S.; Lou, S. Estimation of hourly global solar radiation using Multivariate Adaptive Regression Spline (MARS)—A case study of Hong Kong. Energy 2019, 186, 115857. [Google Scholar] [CrossRef]
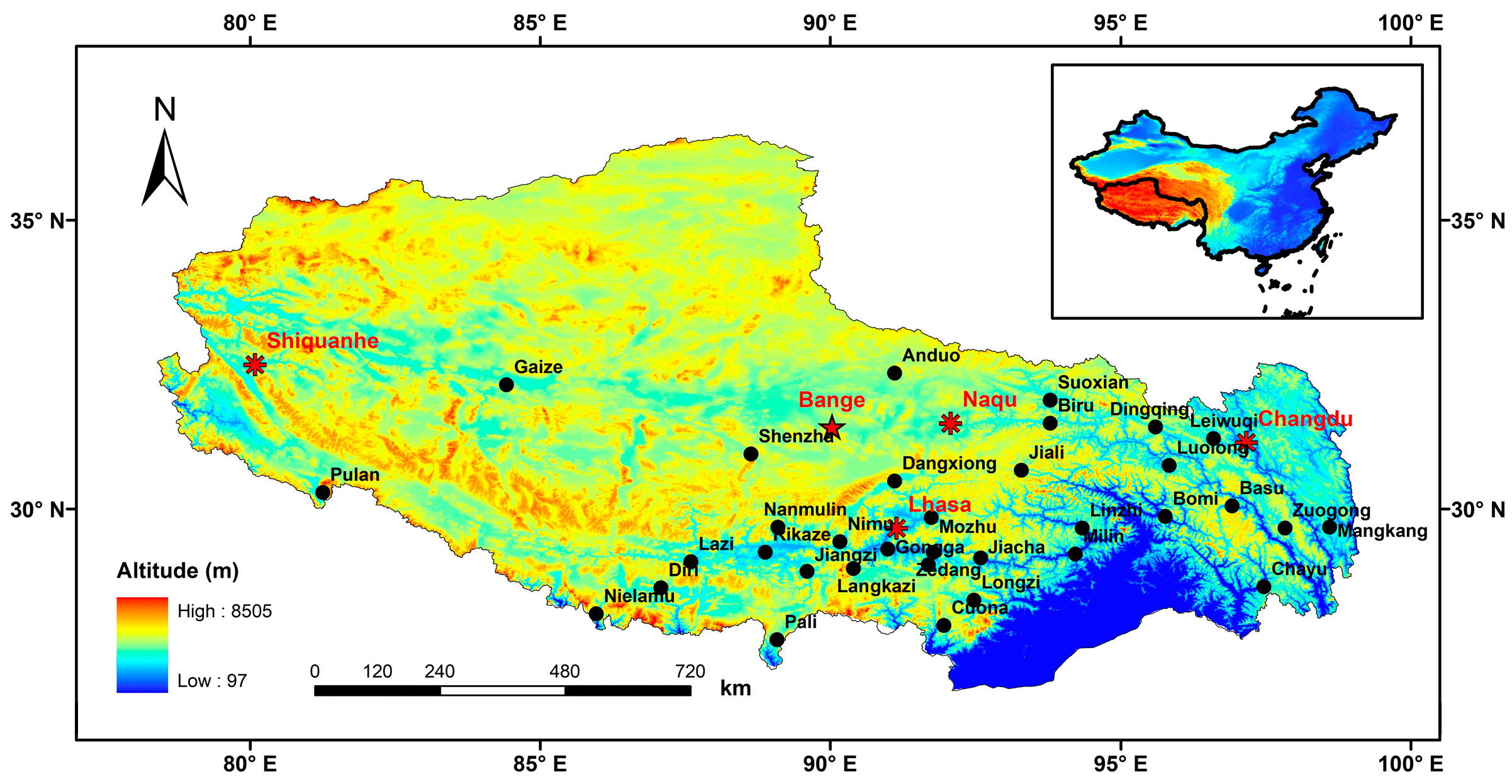




| Station | Latitude/N | Longitude/E | Altitude/m |
|---|---|---|---|
| Lhasa | 29.667 | 91.133 | 3648.9 |
| Naqu | 31.483 | 92.067 | 4507.0 |
| Changdu | 31.150 | 97.167 | 3306.0 |
| Shiquanhe | 32.500 | 80.083 | 4278.6 |
| Station | DL | b | a | NSE | RMSE | MABE | r | DN | n |
|---|---|---|---|---|---|---|---|---|---|
| Lhasa | 1 | 0.542 ± 0.033 | 0.266 ± 0.033 | 0.770 ± 0.059 | 2.380 ± 0.301 | 1.872 ± 0.265 | 0.923 ± 0.002 | 20 | 365–366 |
| 2 | 0.536 ± 0.026 | 0.271 ± 0.024 | 0.778 ± 0.038 | 2.348 ± 0.200 | 1.835 ± 0.175 | 0.924 ± 0.002 | 190 | 730–732 | |
| 3 | 0.534 ± 0.023 | 0.272 ± 0.021 | 0.781 ± 0.033 | 2.332 ± 0.175 | 1.819 ± 0.153 | 0.924 ± 0.002 | 1140 | 1095–1098 | |
| Naqu | 1 | 0.573 ± 0.031 | 0.266 ± 0.022 | 0.718 ± 0.055 | 2.905 ± 0.276 | 2.187 ± 0.248 | 0.882 ± 0.004 | 20 | 365–366 |
| 2 | 0.573 ± 0.020 | 0.266 ± 0.015 | 0.732 ± 0.041 | 2.837 ± 0.210 | 2.119 ± 0.188 | 0.882 ± 0.003 | 190 | 730–732 | |
| 3 | 0.571 ± 0.016 | 0.267 ± 0.012 | 0.737 ± 0.032 | 2.814 ± 0.169 | 2.095 ± 0.151 | 0.882 ± 0.002 | 1140 | 1095–1098 | |
| Changdu | 1 | 0.570 ± 0.053 | 0.221 ± 0.023 | 0.862 ± 0.050 | 1.989 ± 0.318 | 1.544 ± 0.293 | 0.945 ± 0.002 | 20 | 365–366 |
| 2 | 0.571 ± 0.036 | 0.222 ± 0.016 | 0.877 ± 0.021 | 1.893 ± 0.150 | 1.453 ± 0.134 | 0.946 ± 0.001 | 190 | 730–732 | |
| 3 | 0.569 ± 0.029 | 0.222 ± 0.013 | 0.884 ± 0.011 | 1.843 ± 0.088 | 1.411 ± 0.081 | 0.946 ± 0.001 | 1140 | 1095–1098 | |
| Shiquanhe | 1 | 0.587 ± 0.106 | 0.260 ± 0.080 | 0.838 ± 0.125 | 2.499 ± 0.766 | 1.840 ± 0.768 | 0.948 ± 0.011 | 20 | 365–366 |
| 2 | 0.584 ± 0.085 | 0.260 ± 0.066 | 0.868 ± 0.052 | 2.320 ± 0.400 | 1.661 ± 0.399 | 0.950 ± 0.006 | 190 | 730–732 | |
| 3 | 0.572 ± 0.083 | 0.273 ± 0.066 | 0.869 ± 0.044 | 2.320 ± 0.356 | 1.653 ± 0.353 | 0.950 ± 0.004 | 1140 | 1095–1098 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Shen, Y.; Zhou, G.; Liu, D.-L.; Yu, Q.; Du, J. Calibrating the Ångström–Prescott Model with Solar Radiation Data Collected over Long and Short Periods of Time over the Tibetan Plateau. Energies 2023, 16, 7093. https://doi.org/10.3390/en16207093
Liu J, Shen Y, Zhou G, Liu D-L, Yu Q, Du J. Calibrating the Ångström–Prescott Model with Solar Radiation Data Collected over Long and Short Periods of Time over the Tibetan Plateau. Energies. 2023; 16(20):7093. https://doi.org/10.3390/en16207093
Chicago/Turabian StyleLiu, Jiandong, Yanbo Shen, Guangsheng Zhou, De-Li Liu, Qiang Yu, and Jun Du. 2023. "Calibrating the Ångström–Prescott Model with Solar Radiation Data Collected over Long and Short Periods of Time over the Tibetan Plateau" Energies 16, no. 20: 7093. https://doi.org/10.3390/en16207093
APA StyleLiu, J., Shen, Y., Zhou, G., Liu, D.-L., Yu, Q., & Du, J. (2023). Calibrating the Ångström–Prescott Model with Solar Radiation Data Collected over Long and Short Periods of Time over the Tibetan Plateau. Energies, 16(20), 7093. https://doi.org/10.3390/en16207093






