Evaluation of Model Predictions of the Unsteady Tidal Stream Resource and Turbine Fatigue Loads Relative to Multi-Point Flow Measurements at Raz Blanchard
Abstract
:1. Introduction
2. Site Focus
2.1. Modelling the Resource
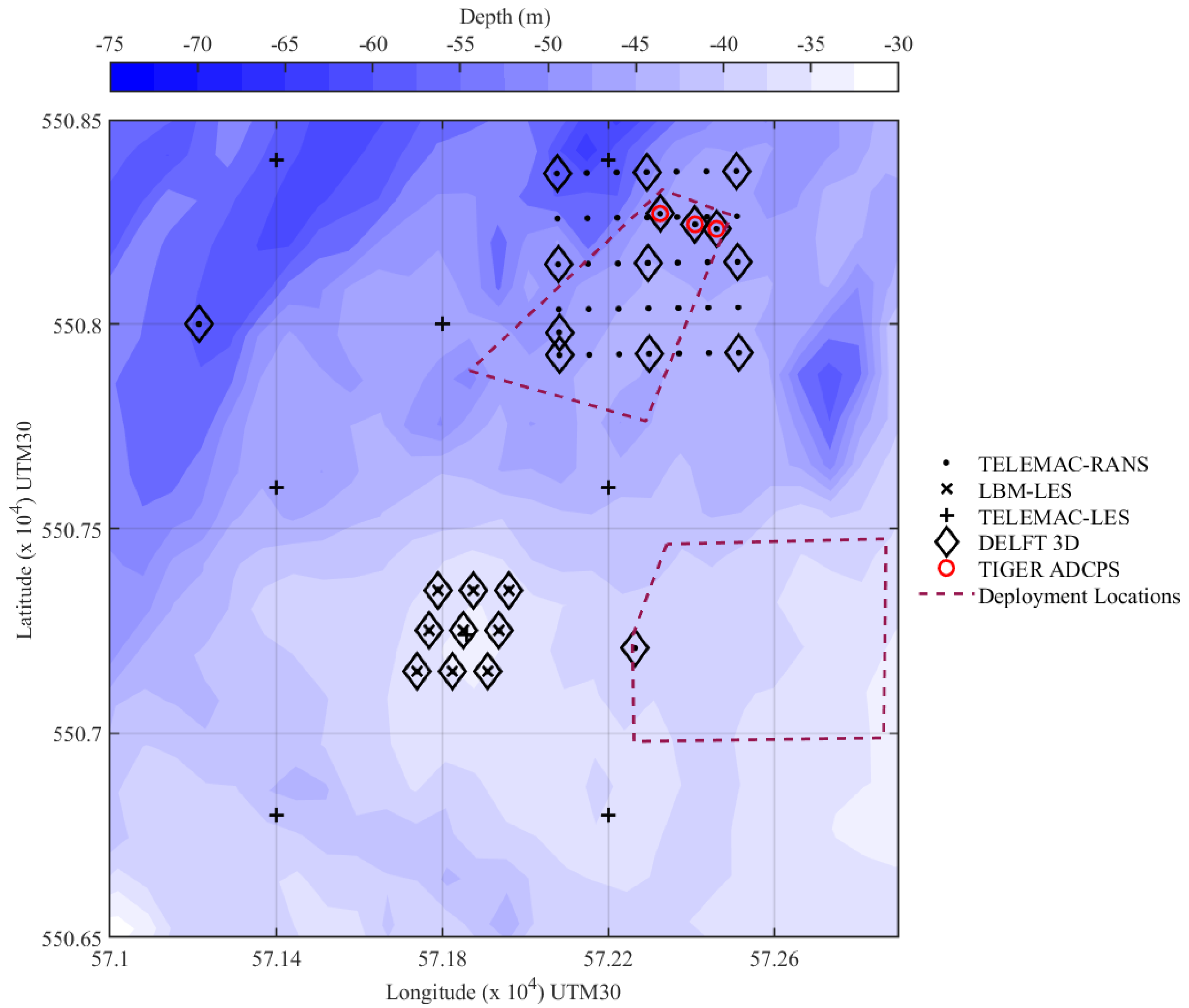
3. Model Set-Up
3.1. Turbine Fatigue Load Prediction
3.2. Turbine Load Prediction in Unsteady Onset Flow
3.3. Onset Flow Field
3.4. Onset Flow Characteristics
4. Onset Flow Conditions
4.1. Occurrence of Conditions
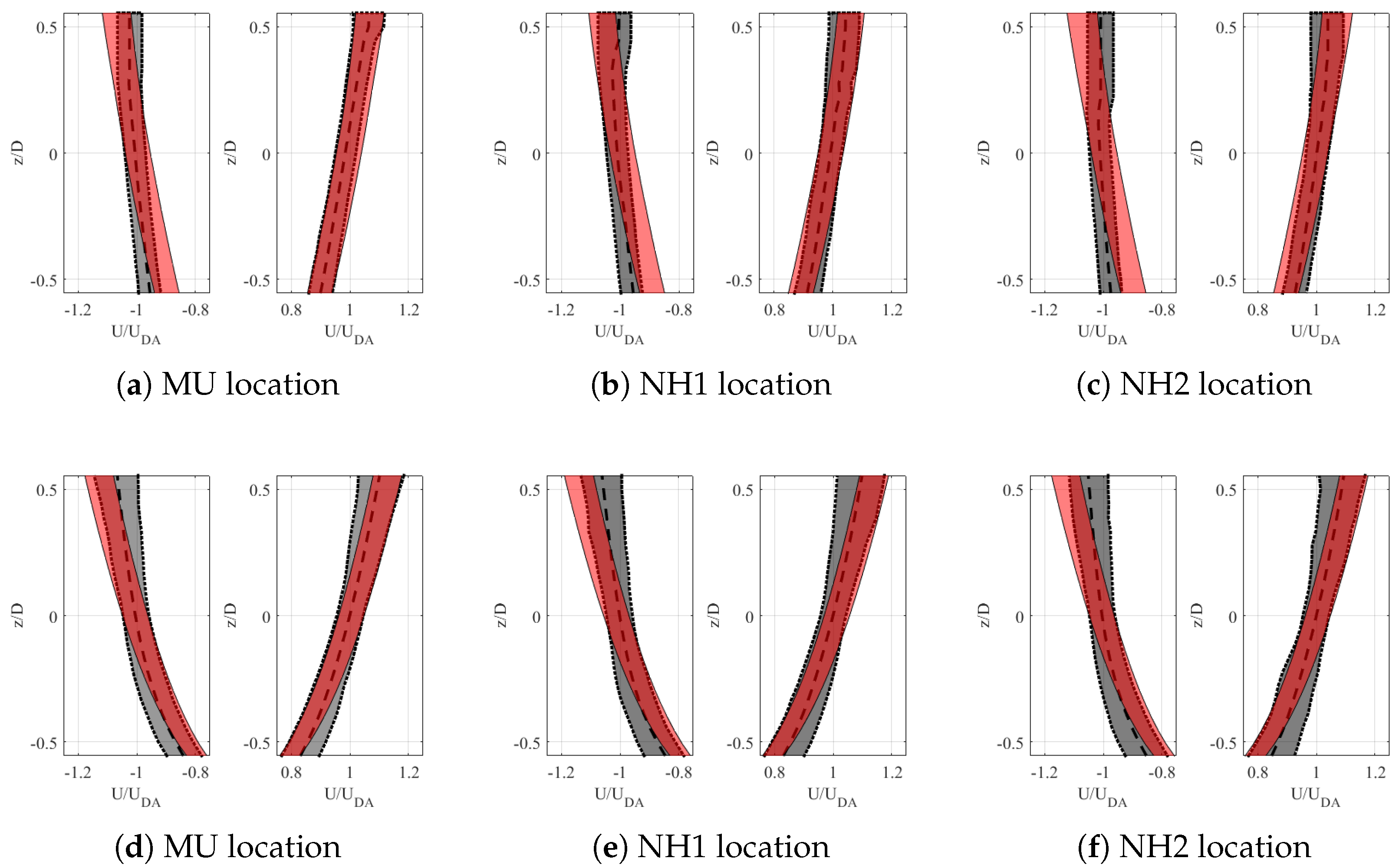
4.2. Shear Profiles
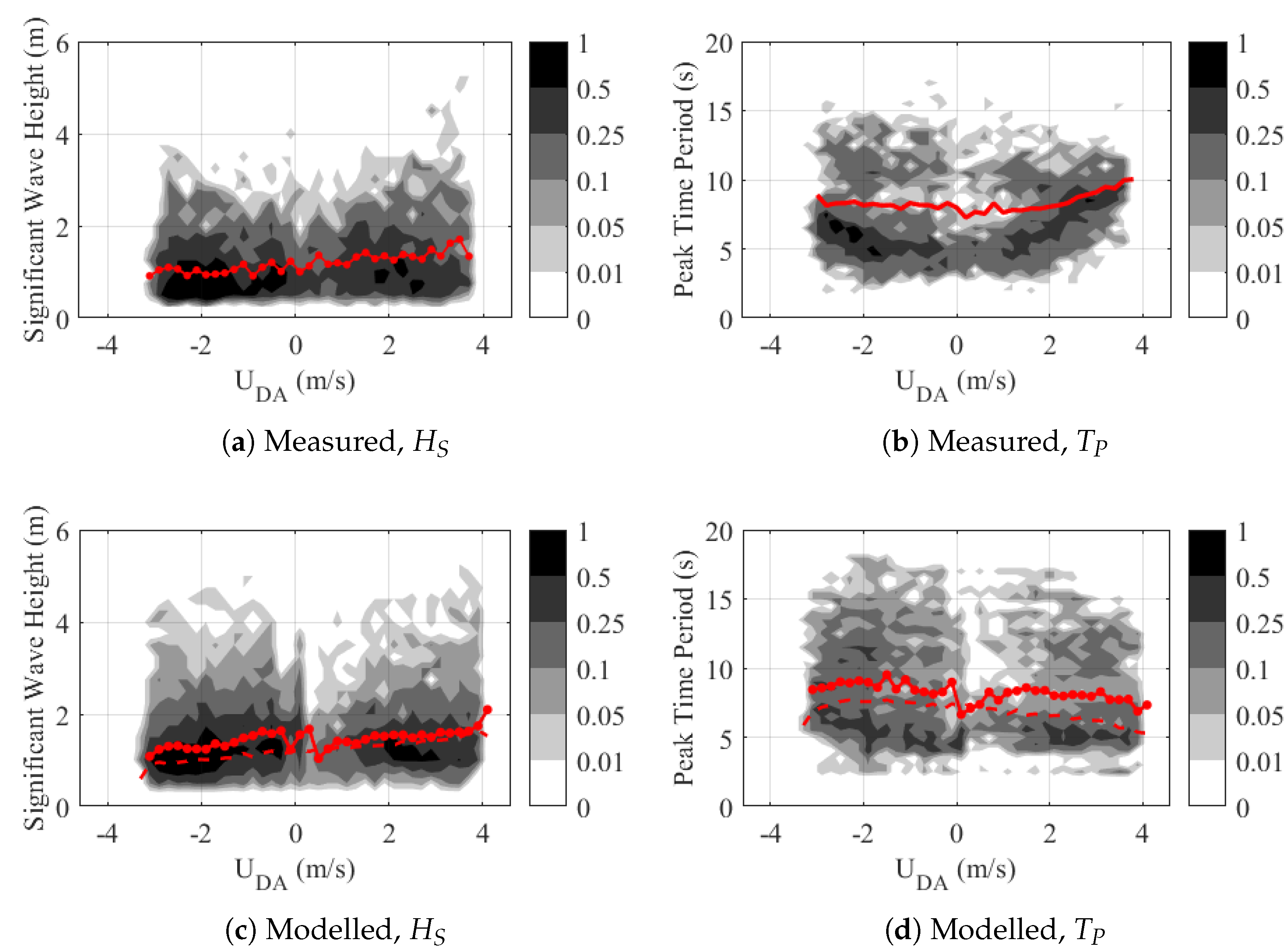
4.3. Waves
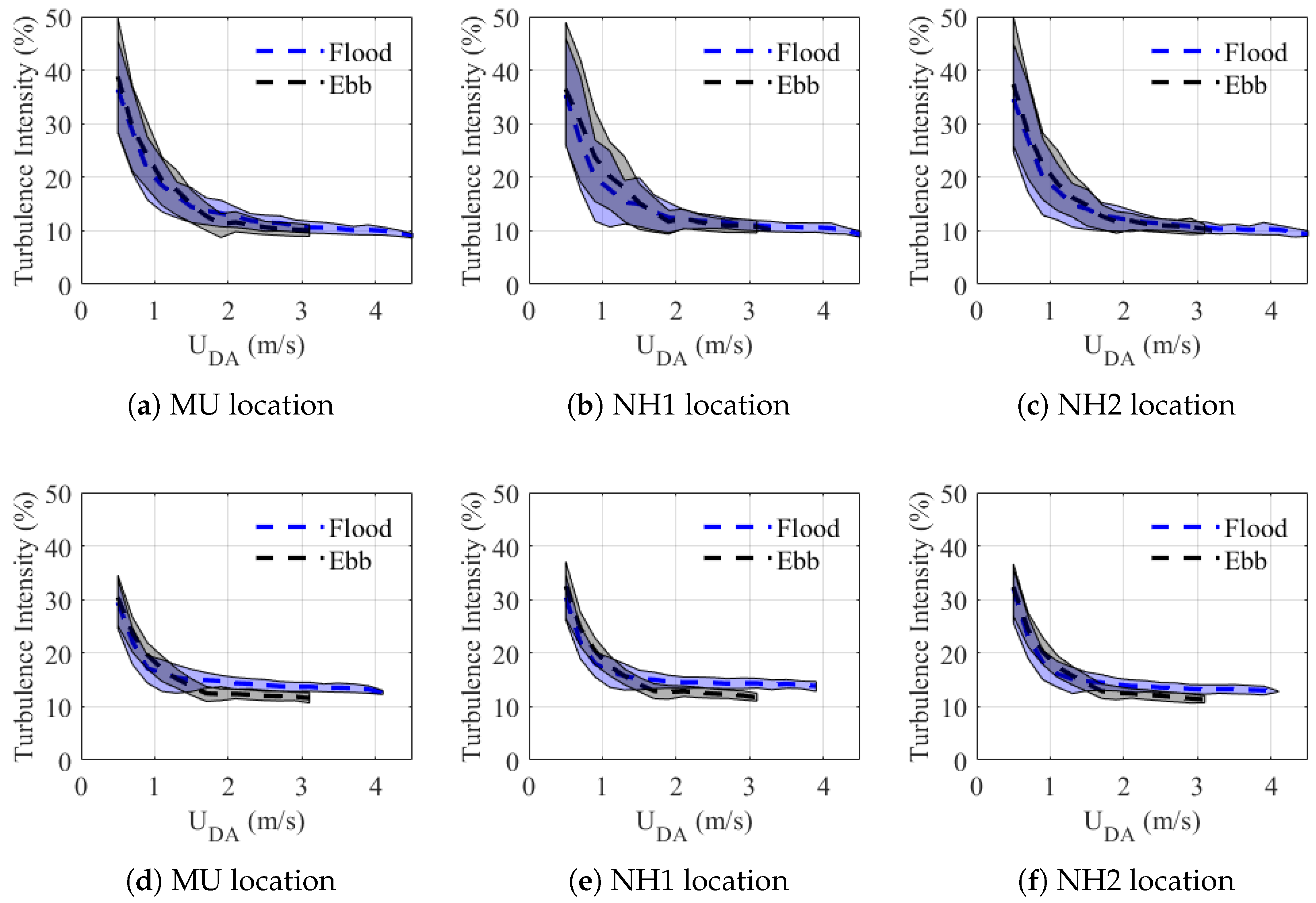
4.4. Turbulence
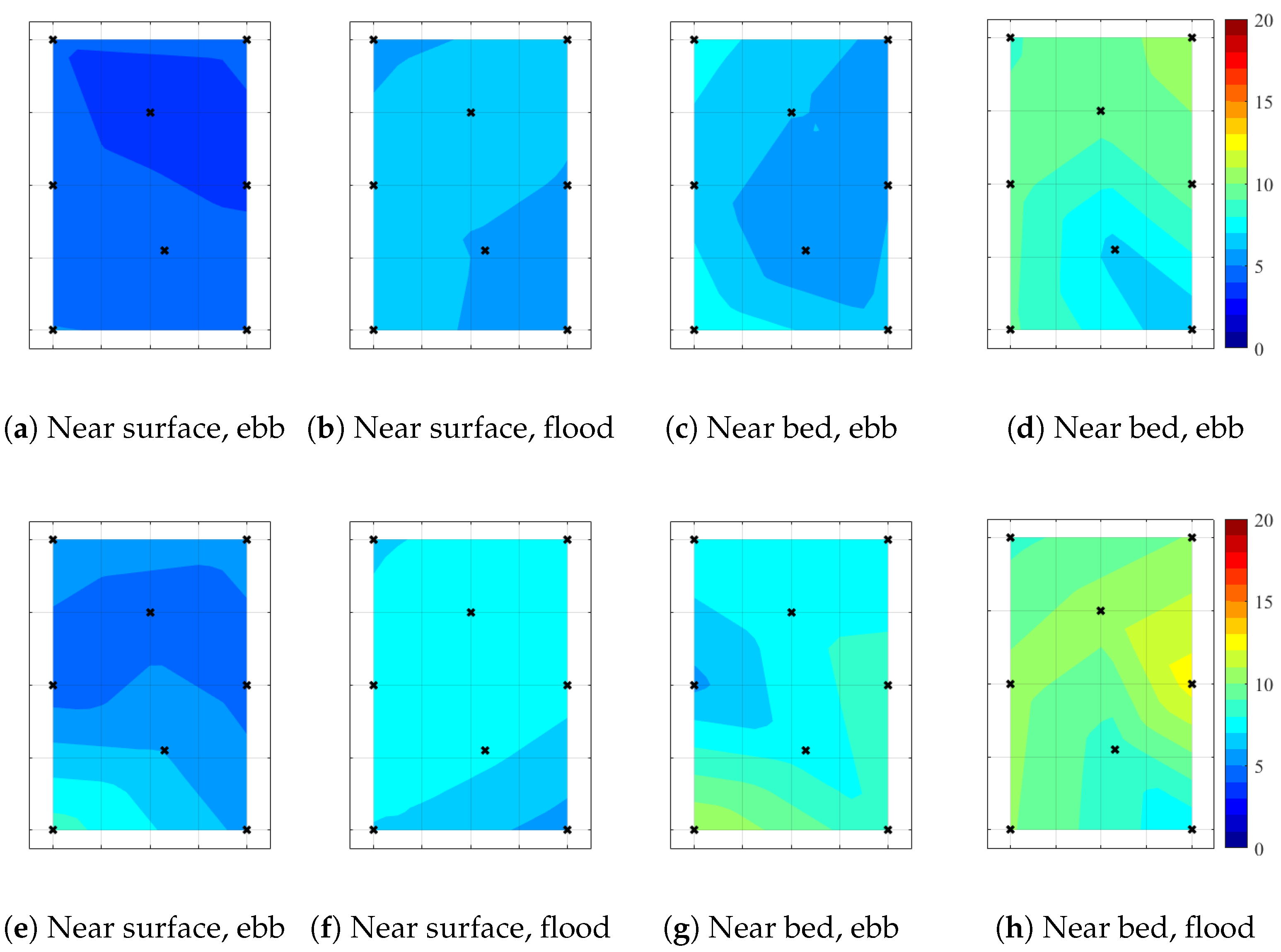
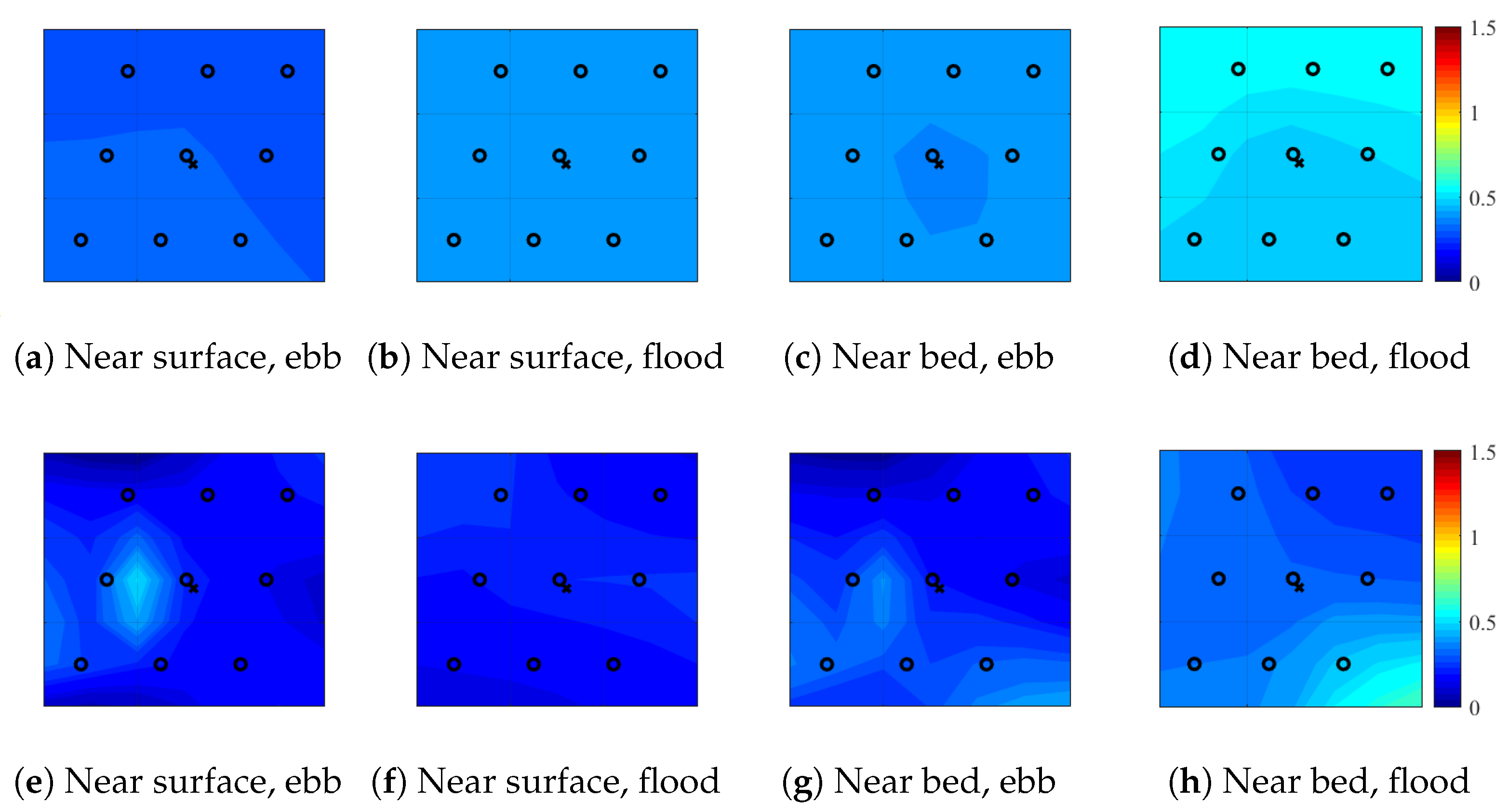
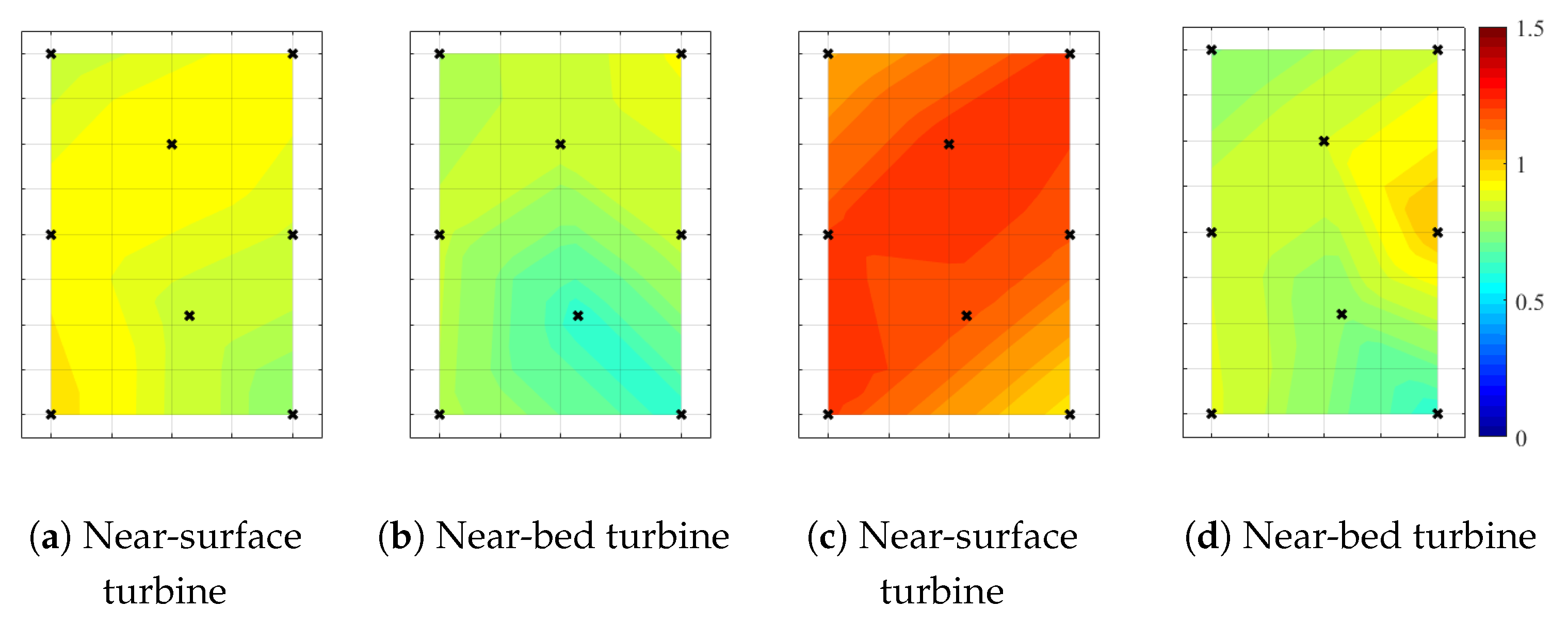
4.5. Spatial Variation of Turbulence
5. Loading on a Device
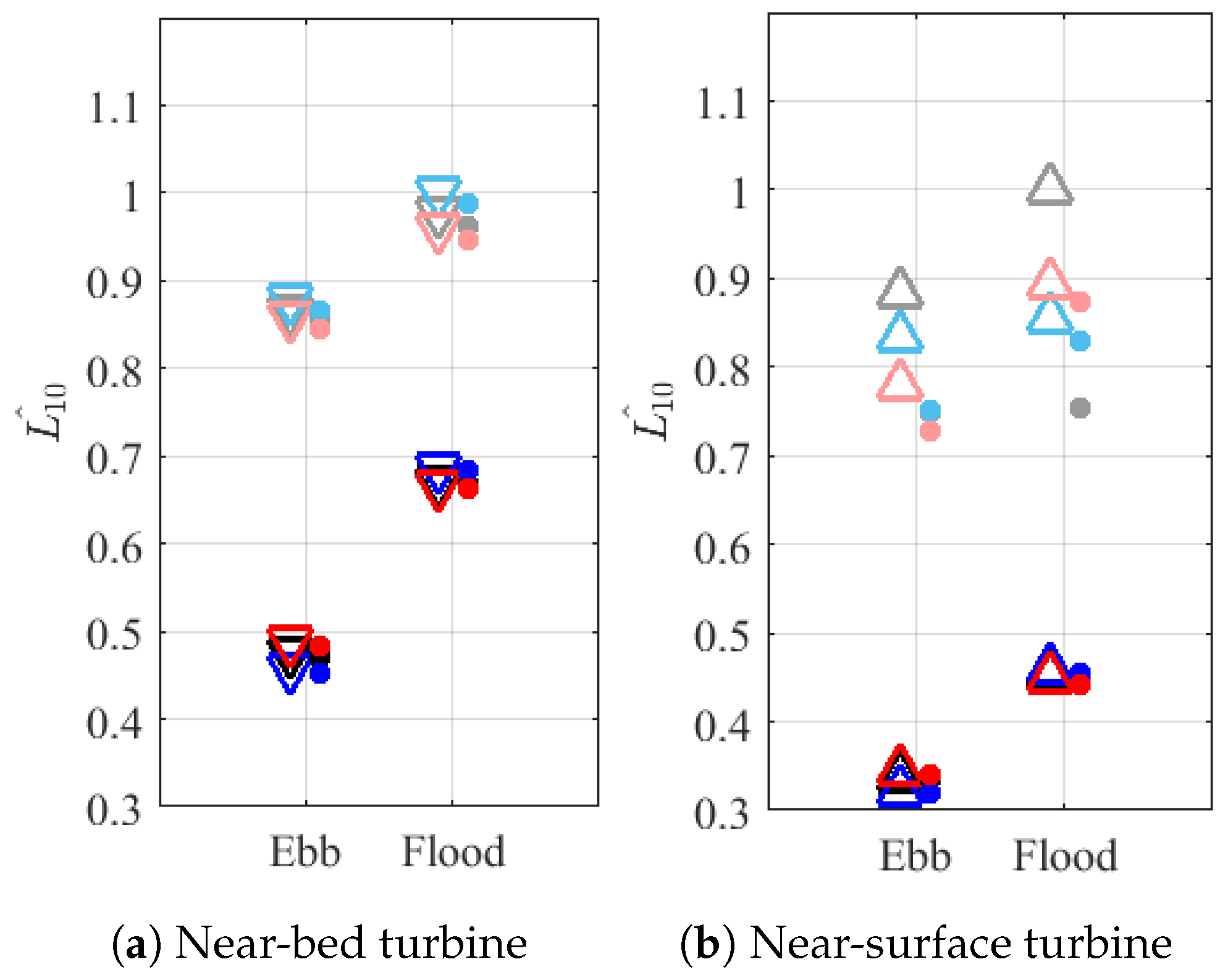
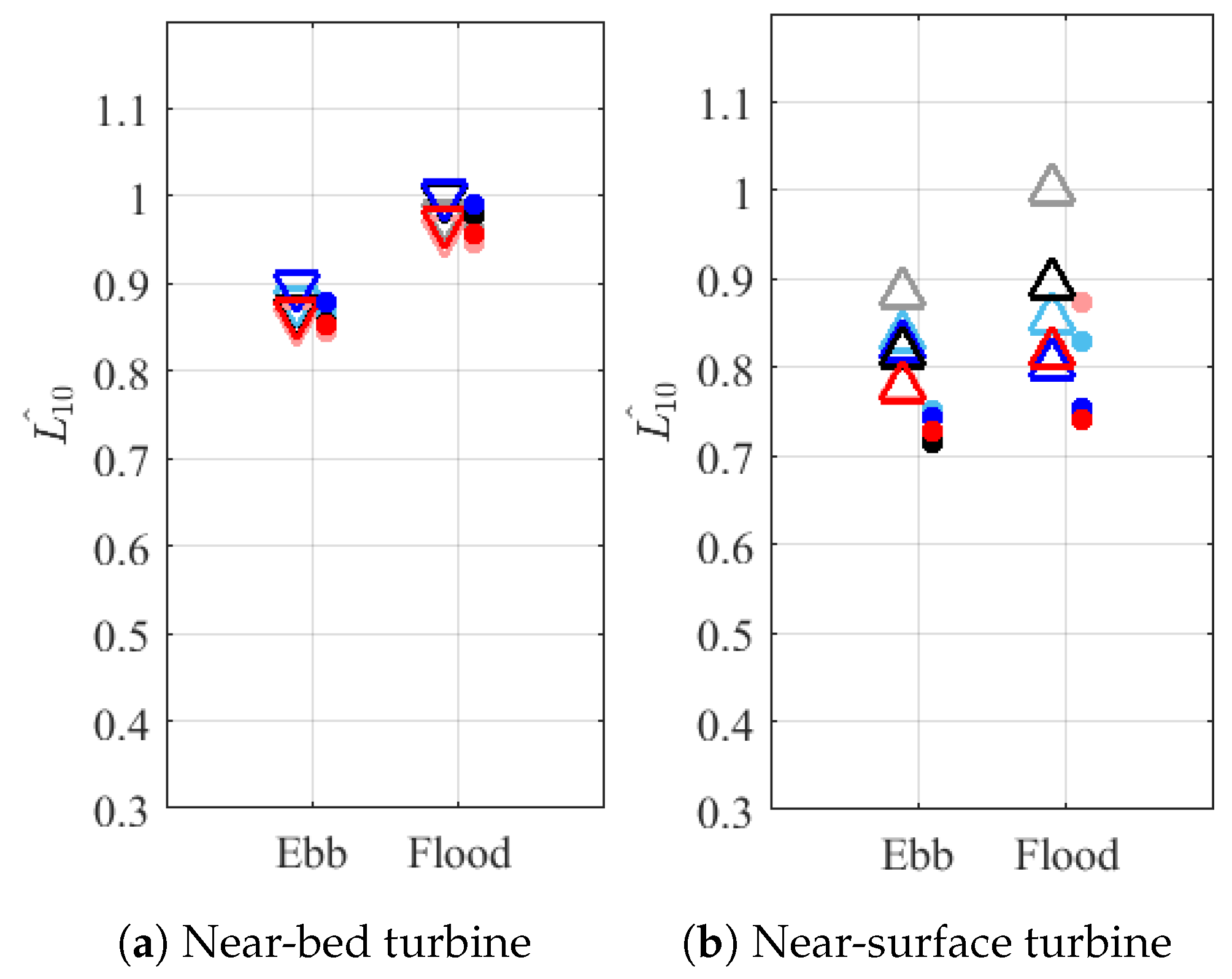
5.1. Influence of Site Location
5.2. Influence of Modelled Conditions
5.3. Influence of High-Fidelity Turbulent Conditions
5.4. Through-Life Loading across Sites
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Coles, D.; Angeloudis, A.; Greaves, D.; Hastie, G.; Lewis, M.; MacKie, L.; McNaughton, J.; Miles, J.; Neill, S.; Piggott, M.; et al. A review of the UK and British Channel Islands practical tidal stream energy resource. Proc. R. Soc. Math. Phys. Eng. Sci. 2021, 477, 20210469. [Google Scholar] [CrossRef]
- Afgan, I.; McNaughton, J.; Rolfo, S.; Apsley, D.; Stallard, T.; Stansby, P. Turbulent flow and loading on a tidal stream turbine by LES and RANS. Int. J. Heat Fluid Flow 2013, 43, 96–108. [Google Scholar] [CrossRef]
- Ahmed, U.; Apsley, D.; Afgan, I.; Stallard, T.; Stansby, P.K. Fluctuating Loads on a Tidal Turbine Due to Velocity Shear and Turbulence: Comparison of CFD with Field Data. Renew. Energy 2017, 112, 235–246. [Google Scholar] [CrossRef]
- Apsley, D.D.; Stallard, T.; Stansby, P.K. Actuator-line CFD modelling of tidal-stream turbines in arrays. J. Ocean. Eng. Mar. Energy 2018, 4, 259–271. [Google Scholar] [CrossRef]
- Ouro, P.; Harrold, M.; Stoesser, T.; Bromley, P. Hydrodynamic loadings on a horizontal axis tidal turbine prototype. J. Fluids Struct. 2017, 71, 78–95. [Google Scholar] [CrossRef]
- Olczak, A.; Stallard, T.; Feng, T.; Stansby, P.K. Comparison of a RANS blade element model for tidal turbine arrays with laboratory scale measurements of wake velocity and rotor thrust. J. Fluids Struct. 2016, 64, 87–106. [Google Scholar] [CrossRef]
- McCann, G.N.; Hitchcock, S.; Lane, S. Implications of Site-Specific Conditions on the Prediction of Loading and Power Performance of a Tidal Stream Device. In Proceedings of the 2nd International Conference of Ocean Energy (ICOE 2008), Brest, France, 15–17 October 2008; pp. 1–9. [Google Scholar]
- Masters, I.; Chapman, J.C.; Willis, M.R.; Orme, J.A.C. A robust Blade Element Momentum Theory model for tidal stream turbines including tip and hub loss corrections. Proc. Inst. Mar. Eng. Sci. Technol. Part J. Mar. Eng. Technol. 2011, 10, 25–35. [Google Scholar] [CrossRef]
- Perez, L.; Cossu, R.; Grinham, A.; Penesis, I. An investigation of tidal turbine performance and loads under various turbulence conditions using Blade Element Momentum theory and high-frequency field data acquired in two prospective tidal energy sites in Australia. Renew. Energy 2022, 201, 928–937. [Google Scholar] [CrossRef]
- Mullings, H.; Stallard, T. Analysis of tidal turbine blade loading due to blade scale flow. J. Fluids Struct. 2022, 114, 103698. [Google Scholar] [CrossRef]
- Mullings, H.; Stallard, T. Assessment of dependency of unsteady onset flow and resultant tidal turbine fatigue loads on measurement position at a tidal site. Energies 2021, 14, 5470. [Google Scholar] [CrossRef]
- Thiébaut, M.; Filipot, J.F.; Maisondieu, C.; Damblans, G.; Duarte, R.; Droniou, E.; Chaplain, N.; Guillou, S. A comprehensive assessment of turbulence at a tidal-stream energy site influenced by wind-generated ocean waves. Energy 2020, 191, 116550. [Google Scholar] [CrossRef]
- Mercier, P.; Guillou, S.S.; Thiébot, J.; Poizot, E. Turbulence characterisation during ebbing and flooding tides in the Raz Blanchard with large eddy simulations. In Proceedings of the 14th European Wave and Tidal Energy Conference, Plymouth, UK, 5–9 September 2021. [Google Scholar]
- Furgerot, L.; Sentchev, A.; Bailly du Bois, P.; Lopez, G.; Morillon, M.; Poizot, E.; Méar, Y.; Bennis, A.C. One year of measurements in Alderney Race: Preliminary results from database analysis. Philos. Trans. Ser. Math. Phys. Eng. Sci. 2020, 378, 20190625. [Google Scholar] [CrossRef] [PubMed]
- Guillou, N.; Neill, S.P.; Thiébot, J. Spatio-temporal variability of tidal-stream energy in north-western Europe. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2020, 378, 20190493. [Google Scholar] [CrossRef] [PubMed]
- Guillou, S.; Bourgoin, A.; Thiébot, J.; Ata, R. On the spatial variability of the flow characteristics at a Tidal energy site: Case of the Raz Blanchard. In Proceedings of the 14th European Wave and Tidal Energy Conference, Plymouth, UK, 5–9 September 2021; pp. 1–8. [Google Scholar]
- Mercier, P.; Grondeau, M.; Guillou, S.; Thiébot, J.; Poizot, E. Numerical study of the turbulent eddies generated by the seabed roughness. Case study at a tidal power site. Appl. Ocean. Res. 2020, 97, 102082. [Google Scholar] [CrossRef]
- Mercier, P.; Guillou, S. The impact of the seabed morphology on turbulence generation in a strong tidal stream. Phys. Fluids 2021, 33, 055125. [Google Scholar] [CrossRef]
- Bennis, A.C.; Furgerot, L.; Bailly Du Bois, P.; Dumas, F.; Odaka, T.; Lathuilière, C.; Filipot, J.F. Numerical modelling of three-dimensional wave-current interactions in complex environment: Application to Alderney Race. Appl. Ocean. Res. 2020, 95, 102021. [Google Scholar] [CrossRef]
- Hardwick, J.; Mackay, E.B.; Ashton, I.G.; Smith, H.C.; Thies, P.R. Quantifying the effects of wave—current interactions on tidal energy resource at sites in the english channel using coupled numerical simulations. Energies 2021, 14, 3625. [Google Scholar] [CrossRef]
- Mackay, E.; Hardwick, J.; Coles, D.; Mercier, P.; Guillou, S.; Pinon, G.; Sedrati, M.; Mullings, H.; Stallard, T.; Ouro, P.; et al. Consolidated Report on Site and Turbine Modelling. Technical Report. 2023. Available online: https://interregtiger.com/download/tiger-report-consolidated-report-on-site-and-turbine-modelling/ (accessed on 20 January 2023).
- Mullings, H.R.; Stallard, T. Assessment of tidal turbine load cycles using synthesised load spectra, including blade-scale fluctuations. In Proceedings of the 13th European Wave and Tidal Energy Conference, Naples, Italy, 1–6 September 2019; pp. 1–9. [Google Scholar]
- Jakovljevi, A.; Paboeuf, S.; Dias, F. Impact of wave-current interactions on tidal current turbine performance in storm conditions. In Proceedings of the 12th European Wave and Tidal Energy Conference, Cork, Ireland, 27 August–2 September 2017; pp. 1–9. [Google Scholar]
- Bourgoin, A.C.; Guillou, S.S.; Thiébot, J.; Ata, R. Turbulence characterization at a tidal energy site using large-eddy simulations: Case of the Alderney Race. Philos. Trans. Ser. Math. Phys. Eng. Sci. 2020, 378, 20190499. [Google Scholar] [CrossRef] [PubMed]
- Thiébaut, M.; Sentchev, A.; Bailly du Bois, P. Monitoring tidal currents with a towed adcp at tidal energy site in alderney race (Raz blanchard). In Advances in Renewable Energies Offshore, Proceedings of the 3rd International Conference on Renewable Energies Offshore, RENEW 2018, Lisbon, Portugal, 8–10 October 2018; CRC Press: Boca Raton, FL, USA, 2018; pp. 49–56. [Google Scholar]
- Sentchev, A.; Nguyen, T.D.; Furgerot, L.; Bailly du Bois, P. Underway velocity measurements in the Alderney Race: Towards a three-dimensional representation of tidal motions. Philos. Trans. Ser. Math. Phys. Eng. Sci. 2020, 378, 20190491. [Google Scholar] [CrossRef] [PubMed]
- ORE Catapult TIGER Site Development Report: The Raz Blanchard T3.2.1. Technical Report. June 2023. Available online: https://interregtiger.com/download/site-development-report-raz-blanchard/ (accessed on 4 July 2023).
- Guion, R.U.G.; Young, A.M. The Frequency Response of Acoustic Doppler Current Profilers Spatiotemporal response and implications for tidal turbine site assessment. In Proceedings of the Oceans 2014, St. John’s, NL, Canada, 14–19 September 2014; pp. 1–10. [Google Scholar]
- Young, A.M.; Atkins, N.R.; Clark, C.J.; Germain, G. An Unsteady Pressure Probe for the Measurement of Flow Unsteadiness in Tidal Channels. IEEE J. Ocean. Eng. 2019, 45, 1411–1426. [Google Scholar] [CrossRef]
- Togneri, M.; Masters, I.; Fairley, I. Wave-turbulence separation at a tidal energy site with empirical orthogonal function analysis. Ocean Eng. 2021, 237, 109523. [Google Scholar] [CrossRef]
- Perez, L.; Cossu, R.; Grinham, A.; Penesis, I. Evaluation of wave-turbulence decomposition methods applied to experimental wave and grid-generated turbulence data. Ocean Eng. 2020, 218, 108186. [Google Scholar] [CrossRef]
- Mullings, H.; Draycott, S.; Stallard, T. Turbine fatigue load prediction from field measurements of waves and turbulence. In Proceedings of the Proceedings of 15th European Wave and Tidal Energy Conference, Bilbao, Spain, 3–7 September 2023; pp. 3–7. [CrossRef]
- Thiébot, J.; Guillou, N.; Guillou, S.; Good, A.; Lewis, M. Wake field study of tidal turbines under realistic flow conditions. Renew. Energy 2020, 151, 1196–1208. [Google Scholar] [CrossRef]
- Thiebot, J.; Bailly du Bois, P.; Guillou, S. Numerical modeling of the effect of tidal stream turbines on the hydrodynamics and the sediment transport-Application to the Alderney Race (Raz Blanchard). Renew. Energy 2015, 75, 356–365. [Google Scholar] [CrossRef]
- Mercier, P.; Grondeau, M.; Guillou, S.; Thiébot, J.; Poizot, E. Towards the modelling of turbulence at tidal stream power sites with the Lattice Boltzmann Method. In Proceedings of the 12th European Wave and Tidal Energy Conference, Cork, Ireland, 27 August–1 September 2017; pp. 1–8.
- Mackay, E.; Hardwick, J.; Thies, P.; Mercier, P.; Grondeau, M.; Guillou, S.; Coles, D.; Pinon, G.; Sedrati, M.; Ouro, P.; et al. Overview of resource and turbine modelling in the Tidal Stream Industry Energiser Project: TIGER. In Proceedings of the 15th European Wave and Tidal Energy Conference, Bilbao, Spain, 3–7 September 2023; pp. 3–7. [CrossRef]
- Milne, I.A.; Sharma, R.N.; Flay, R.G.J.; Bickerton, S. The Role of Waves on Tidal Turbine Unsteady Blade Loading. In Proceedings of the 3rd International Conference on Ocean Energy, Bilbao, Spain, 2–5 September 2010; pp. 1–6. [Google Scholar]
- Parkinson, S.G.; Collier, W.J. Model validation of hydrodynamic loads and performance of a full-scale tidal turbine using Tidal Bladed. Int. J. Mar. Energy 2016, 16, 279–297. [Google Scholar] [CrossRef]
- Downing, S.D.; Socie, D.F. Simple rainflow counting algorithms. Int. J. Fatigue 1982, 4, 31–40. [Google Scholar] [CrossRef]
- Endo, T.; Mitsunaga, K.; Takahashi, K.; Kobayashi, K.; Matsuishi, M. Damage evaluation of metals for random or varying loading—three aspects of rain flow method. Mech. Behav. Mater. 1974, 1–2, 371–380. [Google Scholar]
- Weller, S.D.; Thies, P.R.; Gordelier, T.; Johanning, L. Reducing Reliability Uncertainties for Marine Renewable Energy. J. Mar. Sci. Eng. 2015, 3, 1349–1361. [Google Scholar] [CrossRef]
- Gretton, G.I. PerAWaT—Development of a Computational Fluid Dynamics Model for a Horizontal Axis Tidal Current Turbine WG3 WP5 D1; Technical Report; ETI: Loughborough, UK, 2010. [Google Scholar] [CrossRef]
- Scarlett, G.T.; Sellar, B.; van den Bremer, T.; Viola, I.M. Unsteady hydrodynamics of a full-scale tidal turbine operating in large wave conditions. Renew. Energy 2019, 143, 199–213. [Google Scholar] [CrossRef]
- Ouro, P.; Mullings, H.; Stallard, T. Establishing confidence in predictions of fatigue loading for floating tidal turbines based on large-eddy simulations and unsteady blade element momentum. In Proceedings of the Trends in Renewable Energies Offshore, Lisbon, Portugal, 11 September 2023; pp. 915–924. [Google Scholar] [CrossRef]
- Veers, P. Three-Dimensional Wind Simulation; Technical Report; Sandia National Laboratories: Sandia, CA, USA, 1988. [Google Scholar]
- Milne, I.a.; Day, a.H.; Sharma, R.N.; Flay, R.G. Blade loads on tidal turbines in planar oscillatory flow. Ocean Eng. 2013, 60, 163–174. [Google Scholar] [CrossRef]
- Togneri, M.; Pinon, G.; Carlier, C.; Choma Bex, C.; Masters, I. Comparison of synthetic turbulence approaches for blade element momentum theory prediction of tidal turbine performance and loads. Renew. Energy 2020, 145, 408–418. [Google Scholar] [CrossRef]
- Taylor, G.I. Turbulence in a contracting stream. ZAMM-J. Appl. Math. Mech. Angew. Math. Mech. 1935, 15, 91–96. [Google Scholar] [CrossRef]
- Togneri, M.; Masters, I.; Carlier, C.; Choma Bex, C.; Pinon, G. Comparison of synthetic turbulence approaches for two numerical tidal turbine models. In Proceedings of the 12th European Wave and Tidal Energy Conference, Cork, UK, 27 August–1 September 2017; pp. 1–10. [Google Scholar]
- Jarrin, N.; Benhamadouche, S.; Laurence, D.; Prosser, R. A synthetic-eddy-method for generating inflow conditions for large-eddy simulations. Int. J. Heat Fluid Flow 2006, 27, 585–593. [Google Scholar] [CrossRef]
- DNV-GL. DNV GL STANDARD: Tidal Turbines; Technical Report; DNV GL: Oslo, Norway, 2015. [Google Scholar]
- IEC. Power Performance Assessment of Electricity Producing Tidal Energy Converters, IEC 62600-200; Technical Report; International Electrotechnical Commission: Geneva, Switzerland, 2012. [Google Scholar]
- Mercier, P.; Guillou, S.S. Tracking a large vortex at a tidal power site. In Proceedings of the 15th European Wave and Tidal Energy Conference, Bilbao, Spain, 3–7 September 2023. [CrossRef]
- Choma Bex, C.; Carlier, C.; Fur, A.; Pinon, G.; Germain, G.; Rivoalen, É. A stochastic method to account for the ambient turbulence in Lagrangian Vortex computations. Appl. Math. Model. 2020, 88, 38–54. [Google Scholar] [CrossRef]
- Veers, P. Fatigue Loading of Wind Turbines; Woodhead Publishing Limited: Sawston, UK, 2009; pp. 130–158. [Google Scholar] [CrossRef]
- Mullings, H.R.; Stallard, T.J.; Payne, G.S. Operational Loads on a Tidal Turbine due to Environmental Conditions. In Proceedings of the 27th International Offshore and Polar Engineering Conference, San Francisco, CA, USA, 25–30 June 2017; pp. 1–14. [Google Scholar]


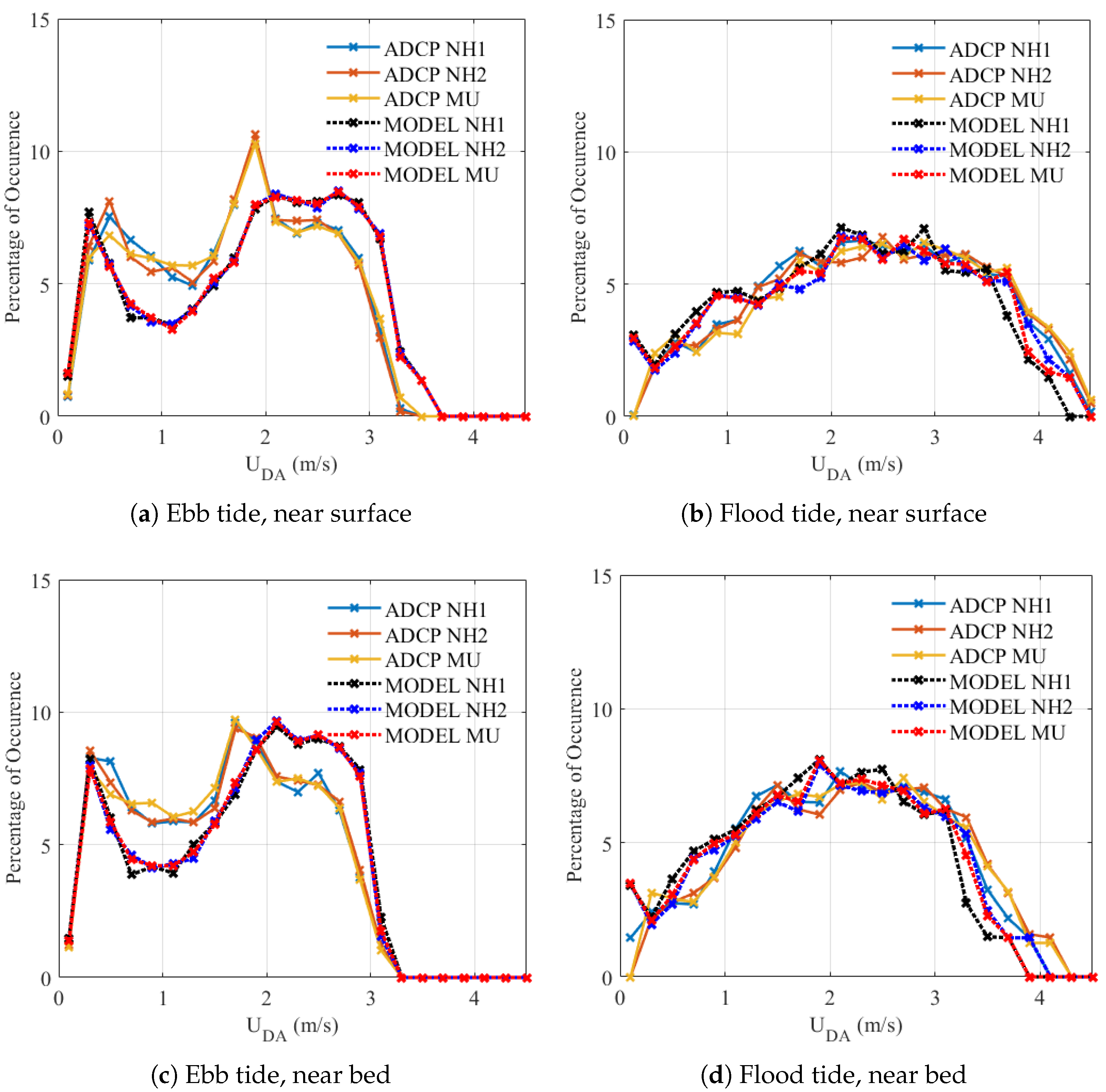
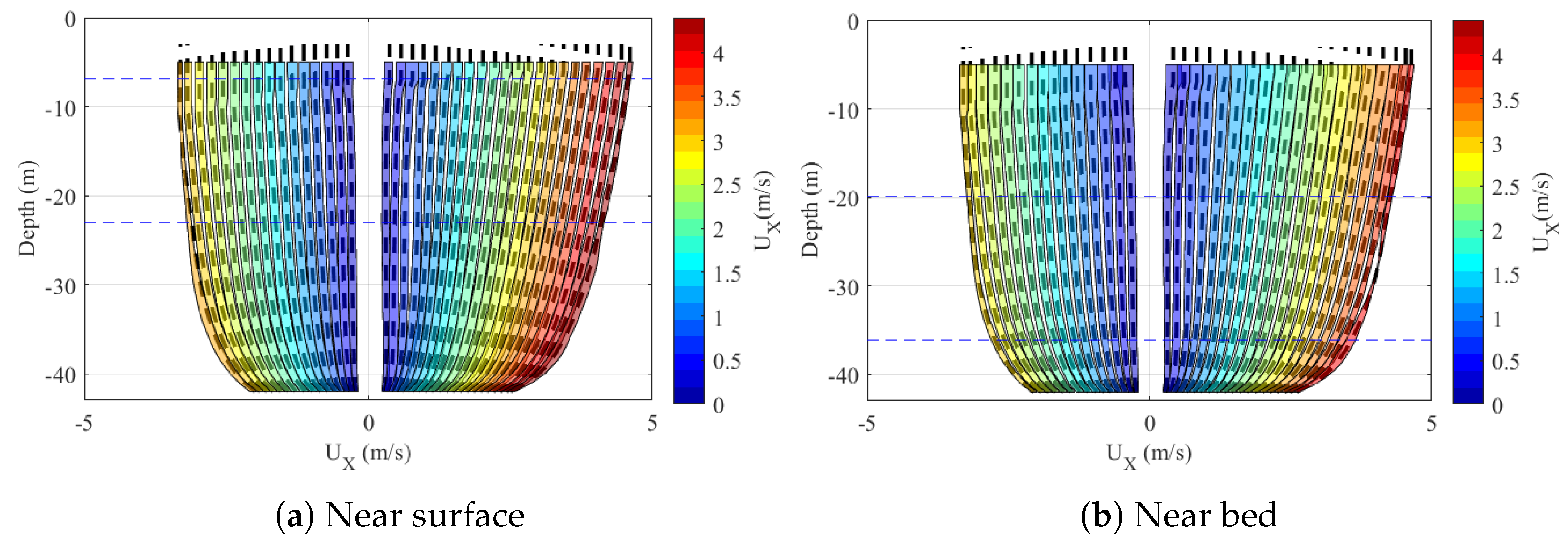
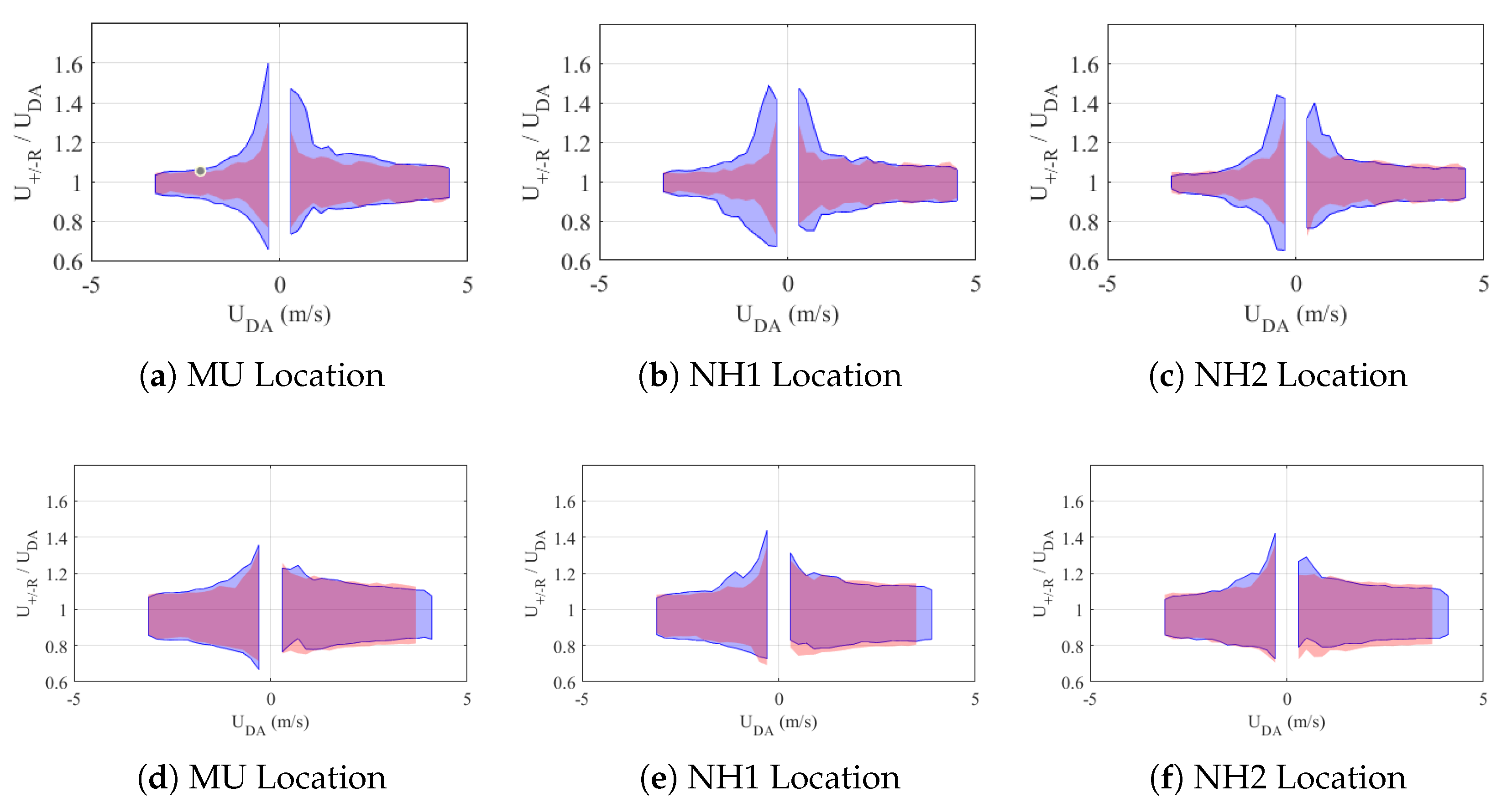





| Device Name | Latitude | Longitude | From | Days |
|---|---|---|---|---|
| NH1 (Teledyne RDI Workhorse Sentinel 600) | 49.72259 | −1.9974 | 15/01/2022 | 63 |
| NH2 (Teledyne RDI Workhorse Sentinel 600) | 49.72225 | −1.9946 | 14/01/2022 | 61 |
| MU (Nortek Signature 500) | 49.72238 | −1.9954 | 15/01/2022 | 78 |
| Model Type | Turbulence Closure | Accounts for Waves | Concurrent with ADCPs | References |
|---|---|---|---|---|
| Telemac RANS | RANS k- | No | Yes | [33,34] |
| Telemac LES | LES | No | No | [16,24] |
| LBM-LES | LES | No | No | [13,17,35] |
| Delft3D | No | Yes | Yes | [20,36] |
| Type of Model | Near Surface | Near Bed |
|---|---|---|
| Telemac RANS (shear and TI) | −30.8% | −32.1% |
| Telemac RANS (shear) with measured TI | −2.7% | −2.9% |
| Telemac LES (shear and TI) | −8.1% | −16.1% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mullings, H.; Draycott, S.; Thiébot, J.; Guillou, S.; Mercier, P.; Hardwick, J.; Mackay, E.; Thies, P.; Stallard, T. Evaluation of Model Predictions of the Unsteady Tidal Stream Resource and Turbine Fatigue Loads Relative to Multi-Point Flow Measurements at Raz Blanchard. Energies 2023, 16, 7057. https://doi.org/10.3390/en16207057
Mullings H, Draycott S, Thiébot J, Guillou S, Mercier P, Hardwick J, Mackay E, Thies P, Stallard T. Evaluation of Model Predictions of the Unsteady Tidal Stream Resource and Turbine Fatigue Loads Relative to Multi-Point Flow Measurements at Raz Blanchard. Energies. 2023; 16(20):7057. https://doi.org/10.3390/en16207057
Chicago/Turabian StyleMullings, Hannah, Samuel Draycott, Jérôme Thiébot, Sylvain Guillou, Philippe Mercier, Jon Hardwick, Ed Mackay, Philipp Thies, and Tim Stallard. 2023. "Evaluation of Model Predictions of the Unsteady Tidal Stream Resource and Turbine Fatigue Loads Relative to Multi-Point Flow Measurements at Raz Blanchard" Energies 16, no. 20: 7057. https://doi.org/10.3390/en16207057
APA StyleMullings, H., Draycott, S., Thiébot, J., Guillou, S., Mercier, P., Hardwick, J., Mackay, E., Thies, P., & Stallard, T. (2023). Evaluation of Model Predictions of the Unsteady Tidal Stream Resource and Turbine Fatigue Loads Relative to Multi-Point Flow Measurements at Raz Blanchard. Energies, 16(20), 7057. https://doi.org/10.3390/en16207057









