MEVO: A Metamodel-Based Evolutionary Optimizer for Building Energy Optimization
Abstract
:1. Introduction
1.1. Literature Review
1.2. Research Gap and Contribution
- The proposed novel method integrates machine learning and optimization via active learning, enhancing the surrogate model within evolutionary optimization by training on limited simulated samples and incorporating additional configurations for a self-updating metamodel, resulting in improved predictive accuracy.
- Utilization of an artificial neural network for prediction and a faster version of particle swarm optimization (MEPSO) for optimization, demonstrating reduced complexity and faster convergence compared to conventional PSO.
- An active learning strategy selects three distinct approaches for simulating offspring at each new generation, involving the optimal MEPSO outcome, crossover, and mutation, aiming to decrease optimization time and enhance convergence of the optimal solution set.
- Application of the developed framework on an actual commercial building with widespread Canadian construction technologies, offering valuable insights for building industry stakeholders in both the public and private sectors.
2. Methodology
- Defining the case building and calibrating the generated model.
- Incorporating the retrofit options and generating a parametric model.
- Formulating the objective function.
- Implementing the optimization strategy (MEVO).
- Evaluating the performance of MEVO optimization by comparing it to MEPSO, PSO, GA, and Bayesian optimizations.
2.1. Optimization Strategy
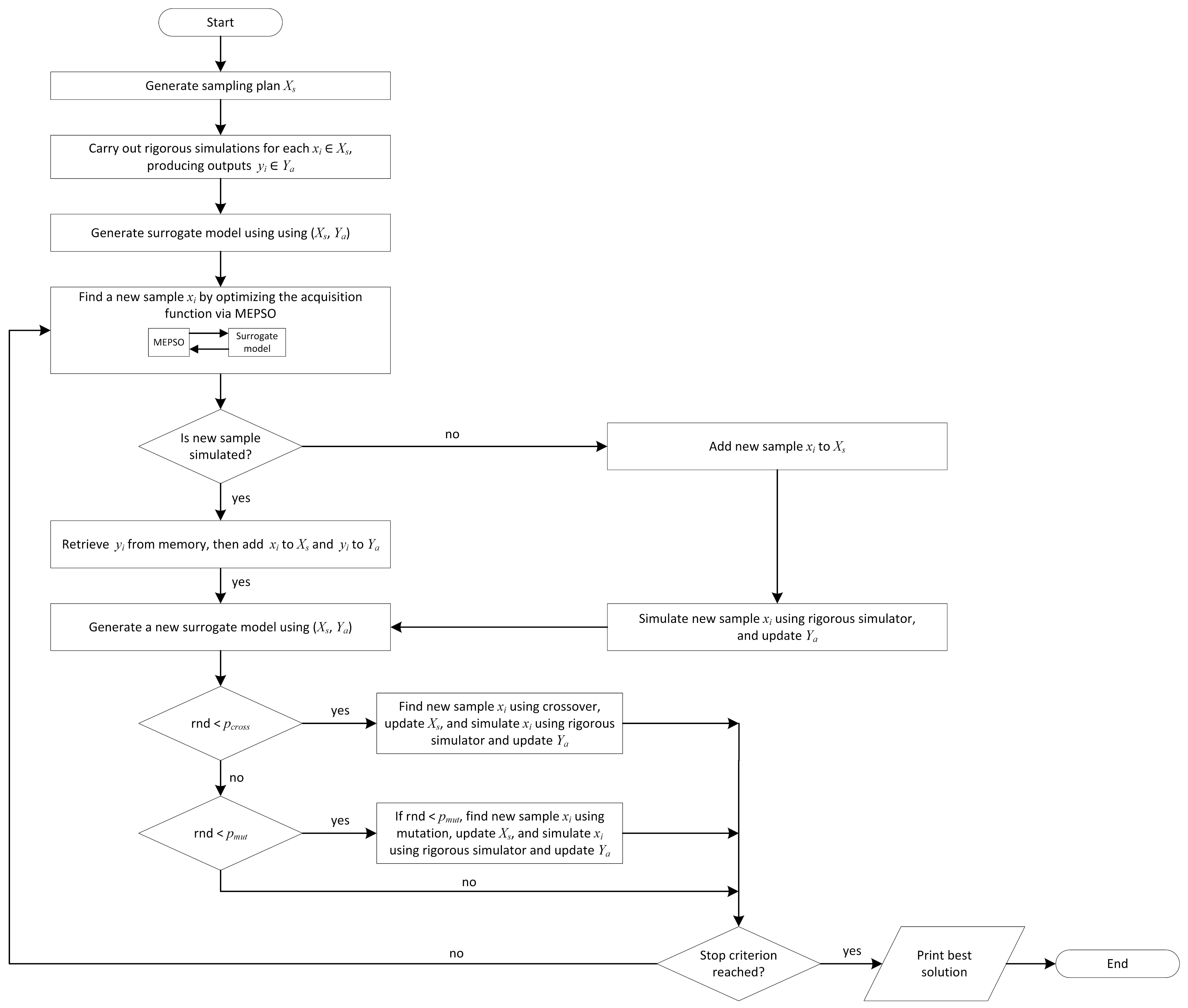
2.1.1. MEVO: Metamodel Evolutionary Optimizer
2.1.2. MEPSO
- The solution of the most dissimilar particle compared to the best global solution of the swarm (in the case of MEPSO-I).
- The best solution that the particle has discovered so far () (in the case of MEPSO-II).
- The best global solution of the swarm (in the case of MEPSO-I).
- A solution of a particle selected with the tournament selection method, as described by the authors of [30] (in the case of MEPSO-II).
2.2. Problem Formulation
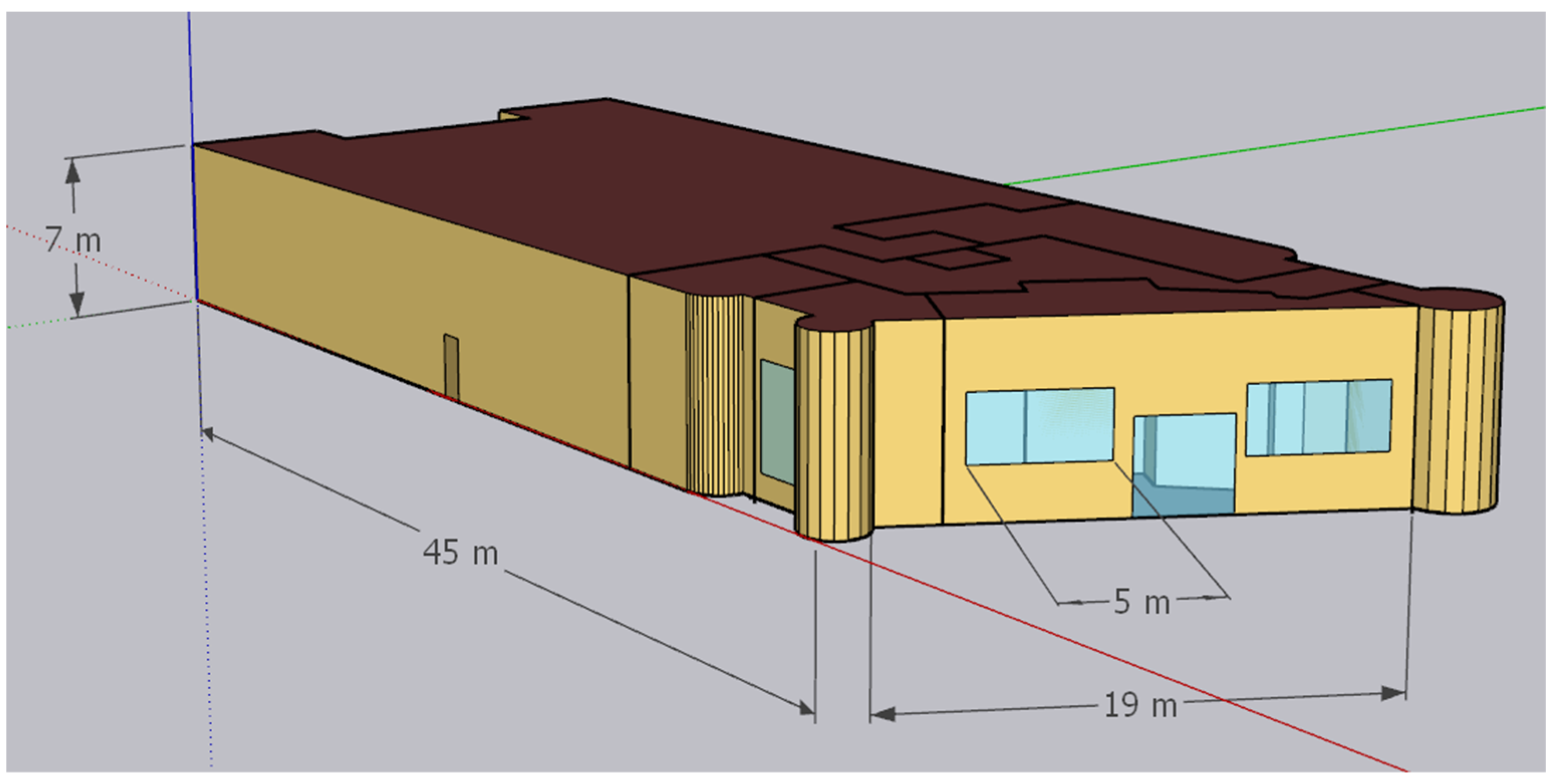
2.3. Case Study Building
2.3.1. Comparison of Simulation Results with Actual Building Energy Consumption
2.3.2. Retrofit Options
2.4. Algorithm Evaluation
- Mean best cost (MBC)—represents the average of the final or best cost observed in the last population across all runs.
- Worst cost (WC)—indicates the highest cost observed among all runs.
- Best cost (BC)—represents the lowest cost observed among all runs.
- Standard deviation (SD)—measures the variability of the final or best cost observed in the last population across all runs.
- Mean computation time (MCT)—denotes the average processing duration in minutes across all runs.
3. Results and Discussion
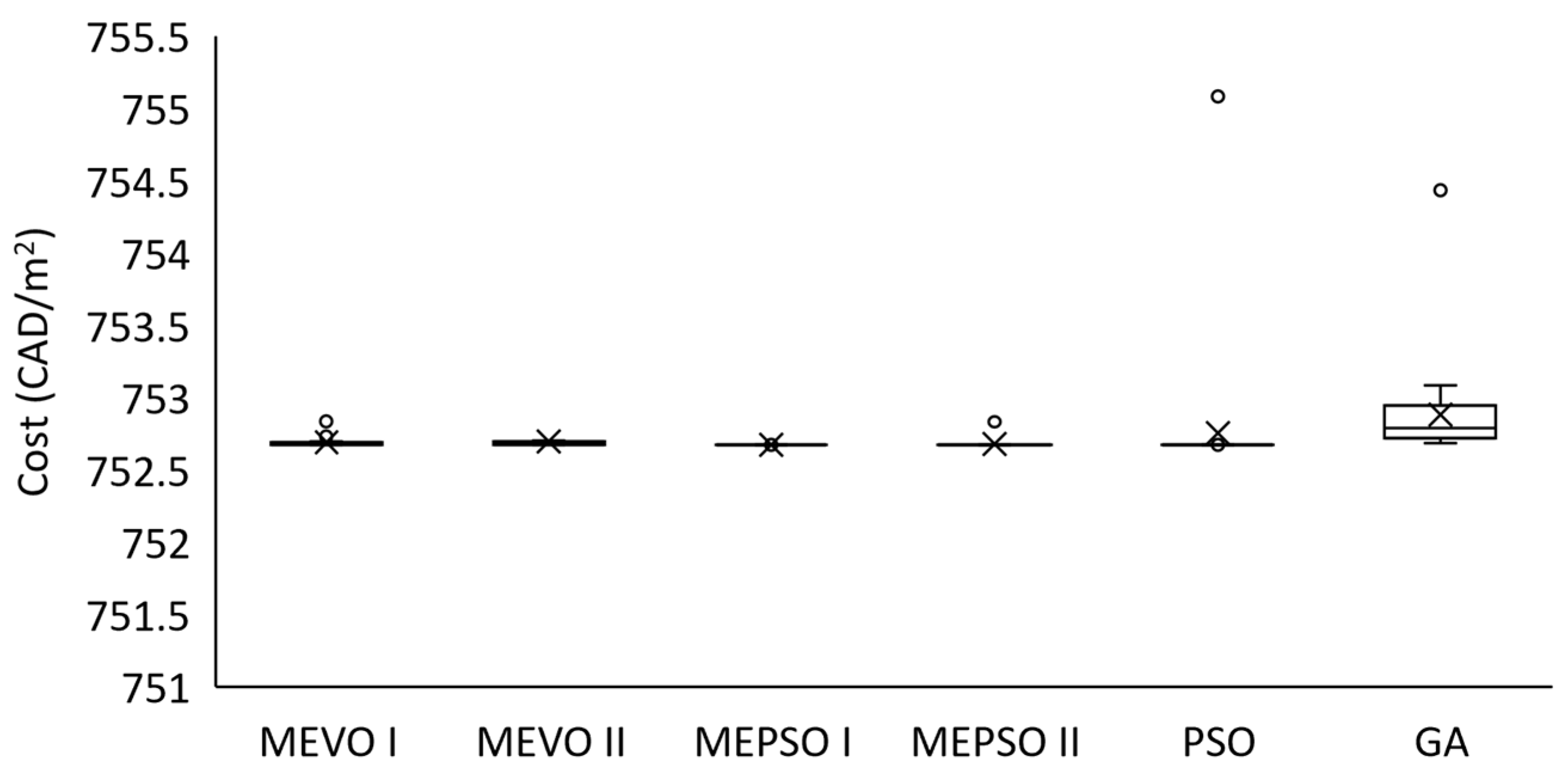
3.1. Comparison between MEVO and Metaheuristic Optimization Algorithms
3.2. Comparison between MEVO and Bayesian Optimization
- Calculation of the convergence index as per Equation (8):where ci,j represents the convergence index for iteration i within a specific run j, yi,j denotes the best objective function value achieved up to iteration i in run j, and signifies the mean of the objective function values obtained within run j.
- Determination of the iteration at which convergence is achieved using Equation (9):
- Subsequently, compute the frequency distribution of tj values for run j = 1 to j = tmax and the corresponding cumulative percentages using bins of size five.
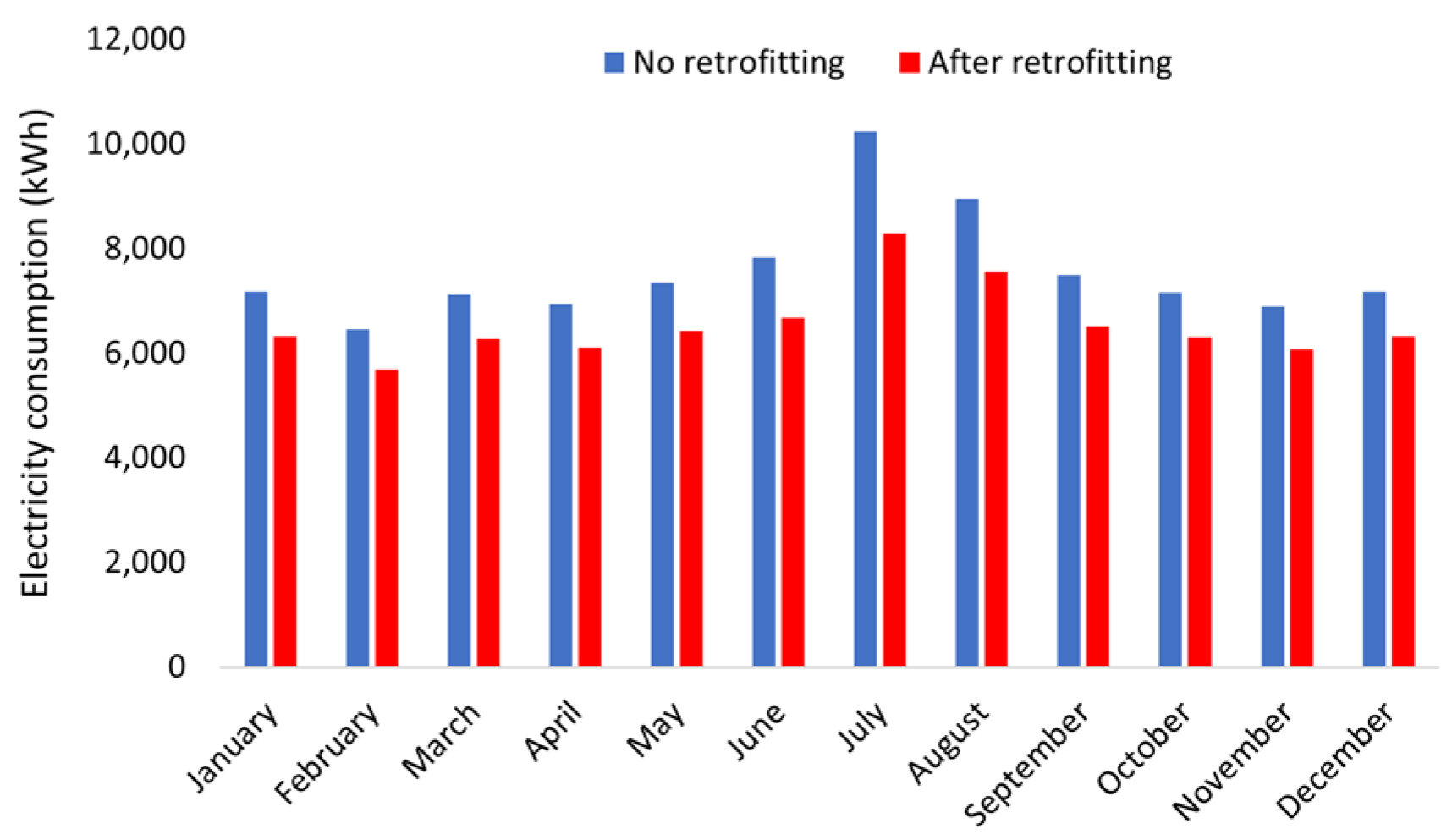
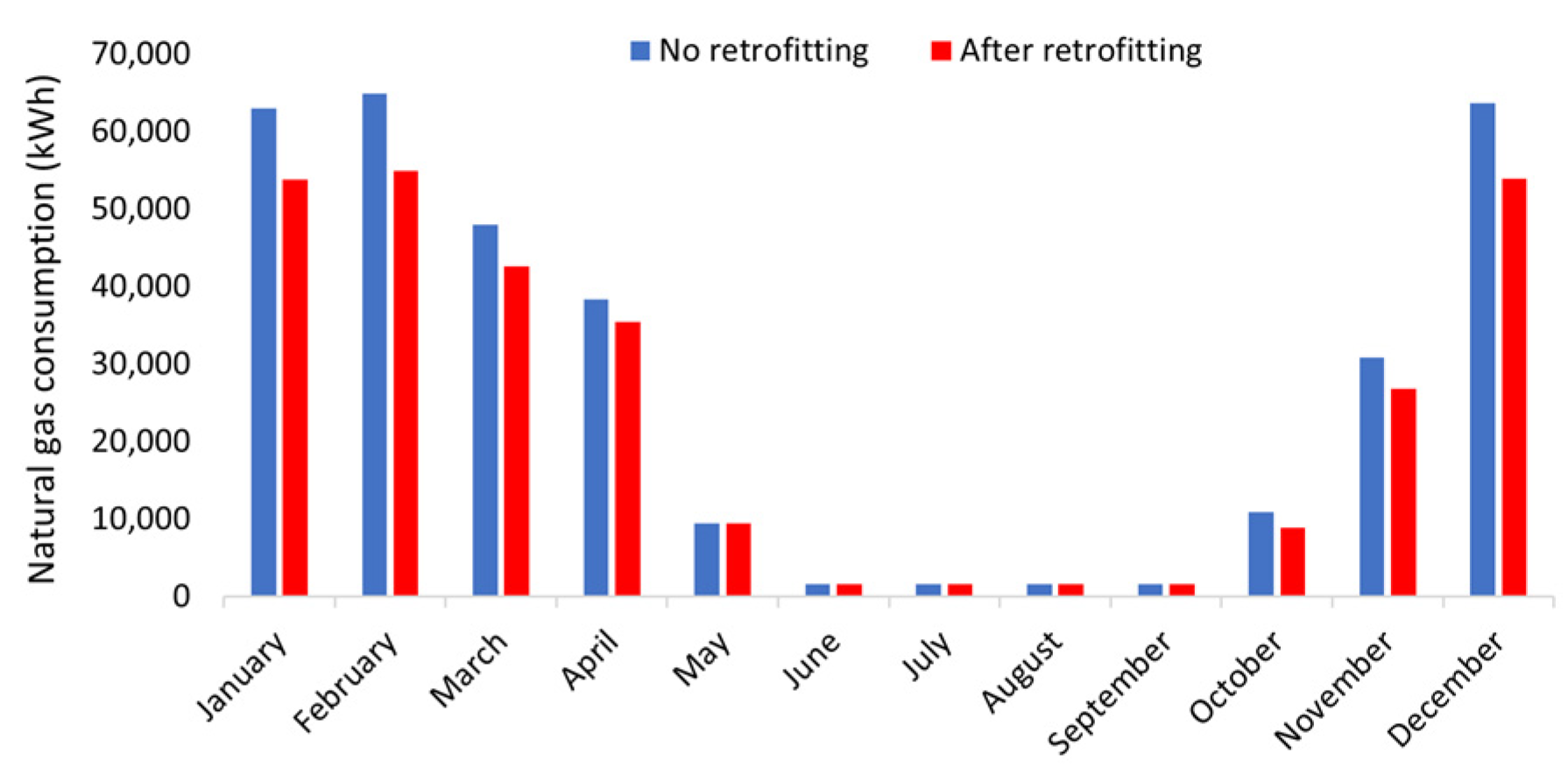
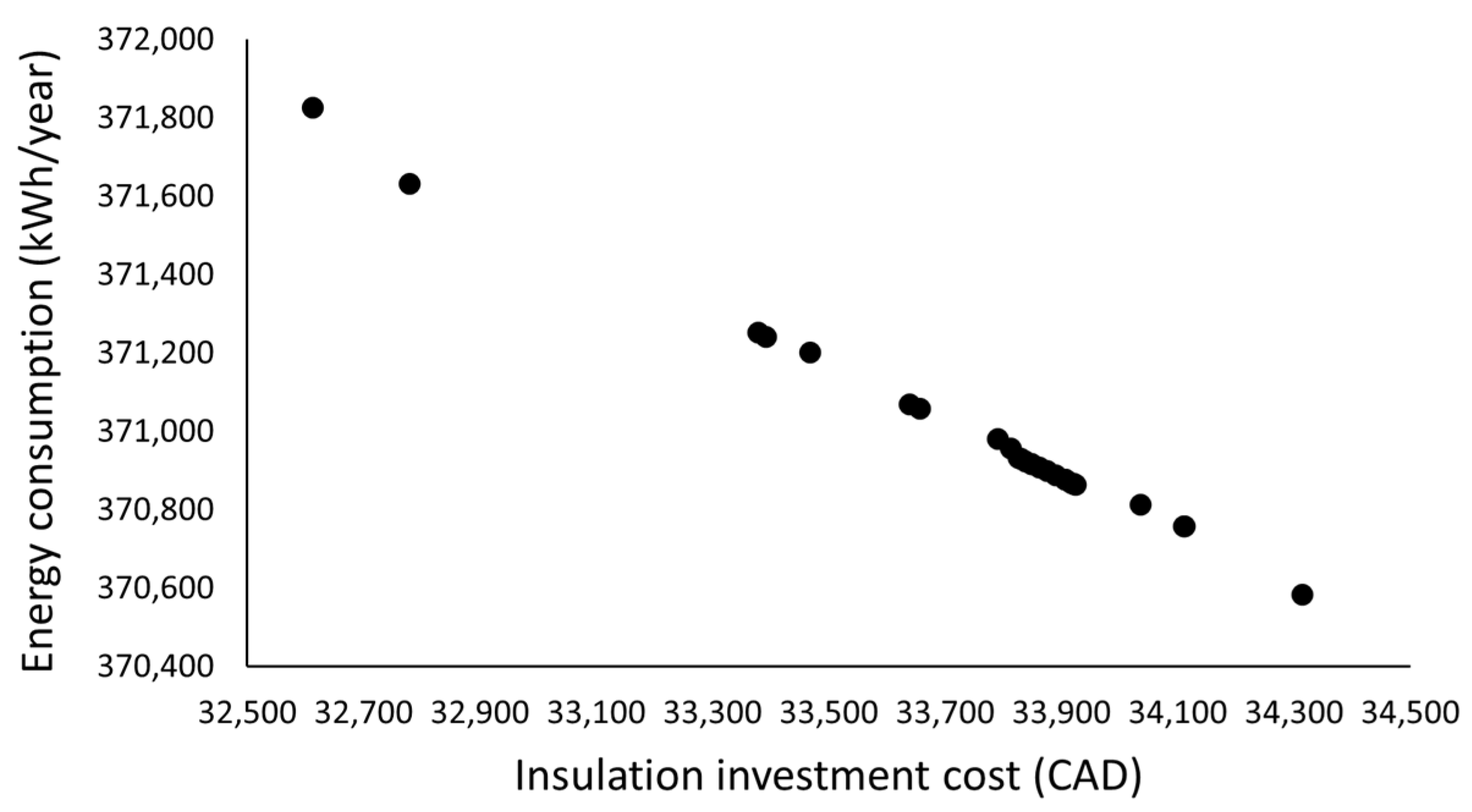
3.3. Scenario Analysis
4. Conclusions and Future Work
- MEVO algorithms are faster than direct optimization using MEPSO-I, MEPSO-II, GA, and PSO. When direct optimization is performed with the metaheuristic optimization algorithms, the computation time ranges from 81.3 min to 110.7 min. In comparison, MEVO ranges from 11.88 min to 13.81 min for the second run and from 20.9 min to 22.5 min for the first run. Shorter computation times allow the decision maker to explore several scenarios in less time, such as the effect of different life spans, discounts, or energy price escalation rates.
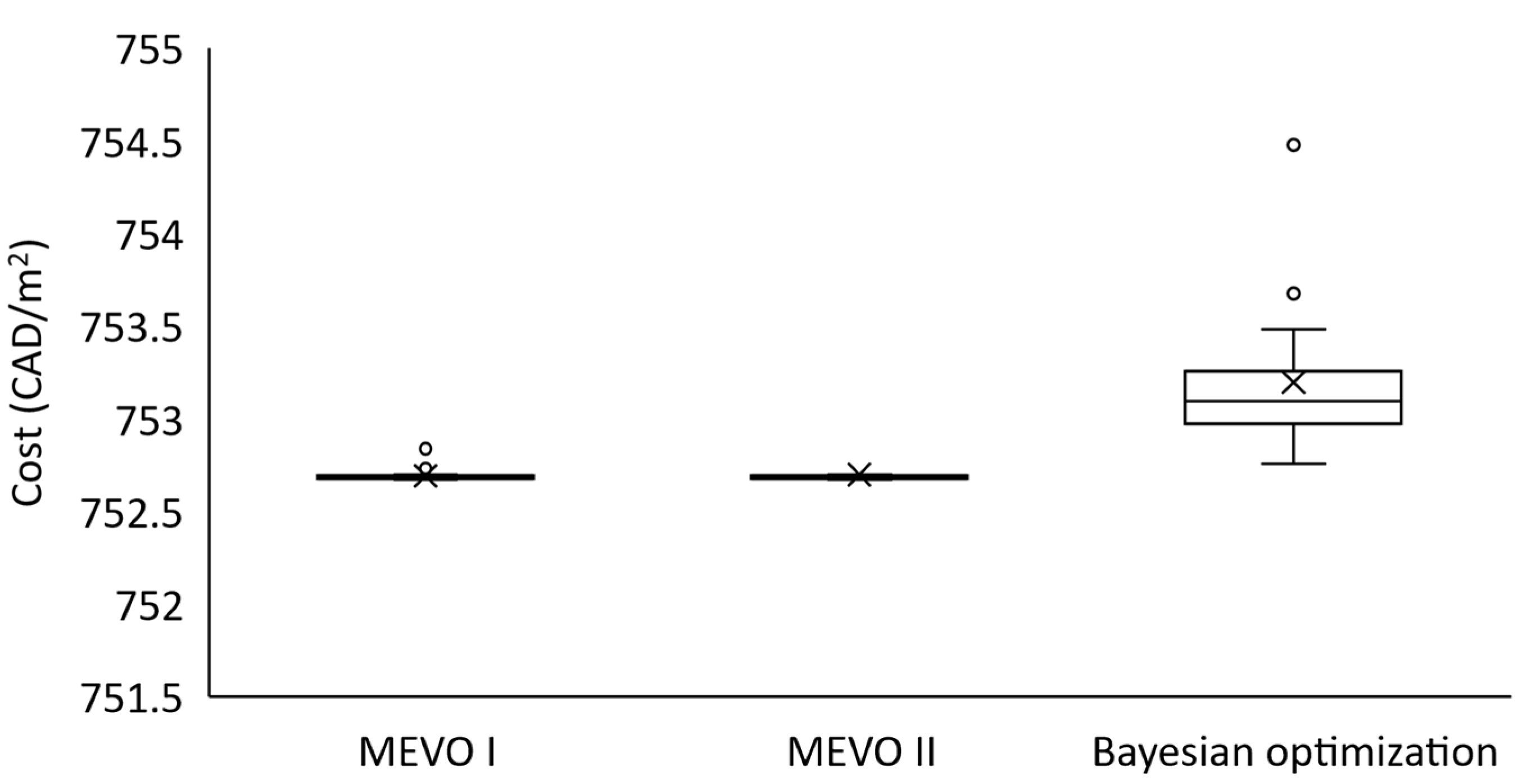
- The solution quality of MEVO is similar to results obtained with direct optimization using the metaheuristic optimization algorithms. The results indicate that MEVO yields similar mean best cost (MBC), best cost (BC), worst cost (WC), and standard deviation (SD) values compared to the metaheuristic optimization algorithms used for direct optimization: GA, PSO, MEPSO-I, and MEPSO-II. In comparison, Bayesian optimization only yields similar mean best cost (MBC), best cost (BC), worst cost (WC), and standard deviation (SD) values compared to the GA and PSO.
- MEVO surpasses Bayesian optimization in terms of solution quality. The Wilcoxon rank-sum test indicates that both MEVO-I and II exhibit significantly better solution qualities, as their p-values are considerably smaller than 0.05 (1.9394 × 10−11 and 3.5170 × 10−11, respectively). The better solution quality of MEVO over Bayesian optimization can be attributed to the crossover and mutation mechanisms in MEVO.
- MEVO presents more repeatability, which reduces the burden of running the algorithm many times. MEVO-I and II display solution variances similar to the metaheuristic algorithms with the lowest variances (MEPSO-I, MEPSO-II, and PSO). Moreover, Bayesian optimization exhibited more scattered results regarding solution distribution than the MEVO algorithms.
- The computational time of MEVO is similar to Bayesian optimization. A possible explanation is that the number of simulations added via the crossover and mutation mechanisms is offset with the filter that checks whether the sample has already been simulated so that its objective function value is retrieved from memory and not from the BPS. However, this must be verified for other case studies where the simulation model takes longer to compute.
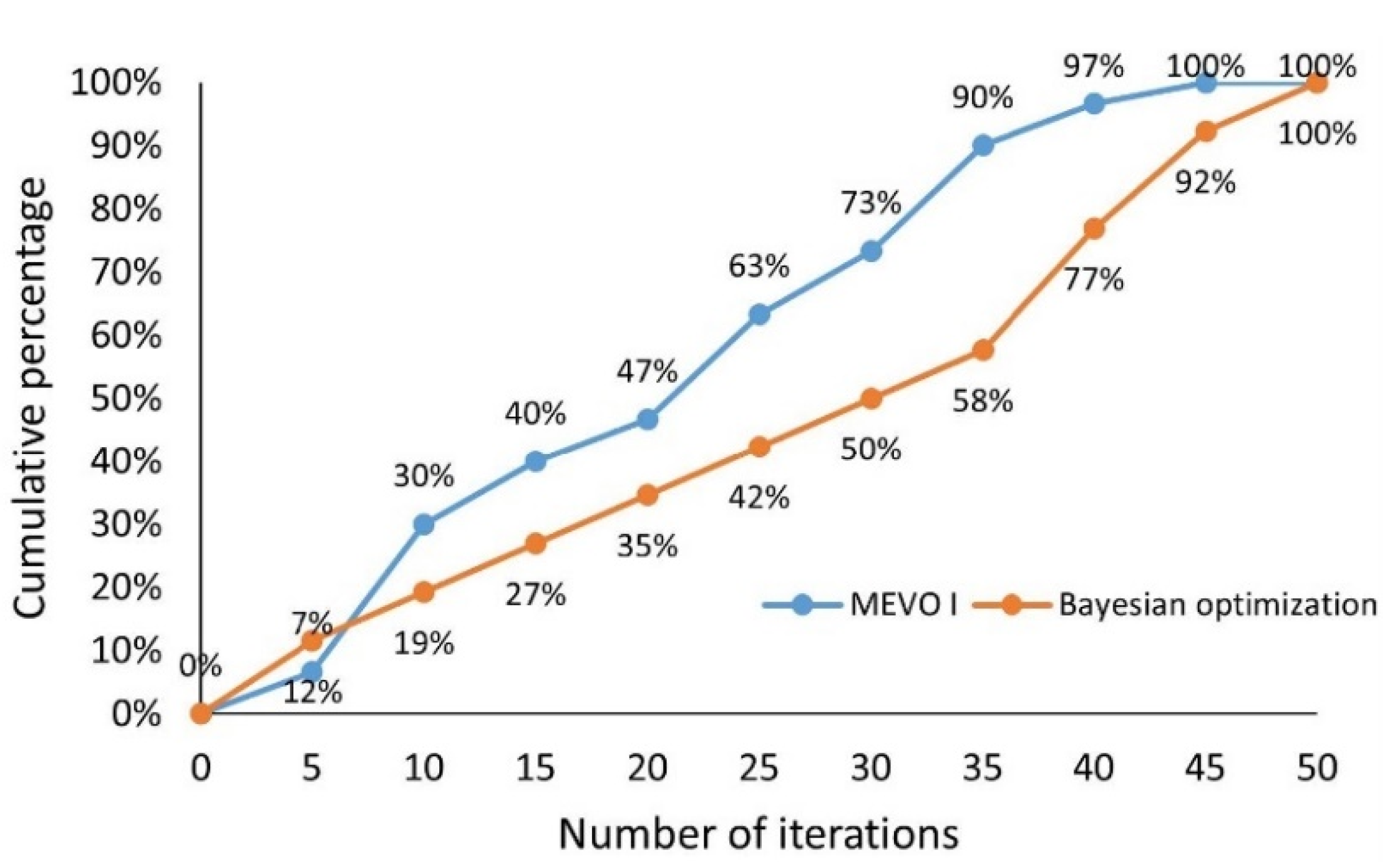
- In comparison to Bayesian optimization, MEVO requires fewer iterations to converge. For example, while 58% of the runs converged with Bayesian optimization, 90% of the runs converged with MEVO. In addition, it was observed that when Bayesian optimization achieved convergence in 77% of the runs, MEVO exhibited convergence in 97% of the runs. Decreasing the number of iterations in the MEVO algorithm had a comparatively lesser impact on the mean solution quality while simultaneously reducing the duration of the optimization process.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- United Nations Environment Programme; Global Alliance for Buildings and Construction. 2021 Global Status Report for Buildings and Construction towards a Zero-Emissions, Efficient and Resilient Buildings and Construction Sector; Technical Report; Global Alliance for Buildings and Construction: Paris, France, 2021; Available online: https://wedocs.unep.org/xmlui/handle/20.500.11822/34572 (accessed on 16 August 2023).
- IEA. Energy Technology Perspectives 2020. Available online: https://www.iea.org/reports/energy-technology-perspectives-2020 (accessed on 16 August 2023).
- IEA. Key World Energy Statistics 2021. Available online: https://www.iea.org/reports/key-world-energy-statistics-2021 (accessed on 16 August 2023).
- Attia, S.; Hamdy, M.; O’Brien, W.; Carlucci, S. Computational optimisation for zero energy buildings design: Interviews results with twenty eight international expert. In Proceedings of the BS2013: 13th Conference of International Building Performance Simulation Association, Chambéry, France, 26–28 August 2013; Available online: https://www.aivc.org/resource/computational-optimisation-zero-energy-buildings-design-interviews-results-twenty-eight (accessed on 16 August 2023).
- Ascione, F.; Bianco, N.; Mauro, G.M.; Vanoli, G.P. A new comprehensive framework for the multi-objective optimization of building energy design: Harlequin. Appl. Energy 2019, 241, 331–361. [Google Scholar] [CrossRef]
- Ciardiello, A.; Rosso, F.; Dell’Olmo, J.; Ciancio, V.; Ferrero, M.; Salata, F. Multi-objective approach to the optimization of shape and envelope in building energy design. Appl. Energy 2020, 280, 115984. [Google Scholar] [CrossRef]
- Mostafazadeh, F.; Eirdmousa, S.J.; Tavakolan, M. Energy, economic and comfort optimization of building retrofits considering climate change: A simulation-based NSGA-III approach. Energy Build. 2023, 280, 112721. [Google Scholar] [CrossRef]
- Tavakolan, M.; Mostafazadeh, F.; Eirdmousa, S.J.; Safari, A.; Mirzaei, K. A parallel computing simulation-based multi-objective optimization framework for economic analysis of building energy retrofit: A case study in Iran. J. Build. Eng. 2022, 45, 103485. [Google Scholar] [CrossRef]
- Melo, A.; Versage, R.; Sawaya, G.; Lamberts, R. A novel surrogate model to support building energy labelling system: A new approach to assess cooling energy demand in commercial buildings. Energy Build. 2016, 131, 233–247. [Google Scholar] [CrossRef]
- Sharif, S.A.; Hammad, A. Developing surrogate ANN for selecting near-optimal building energy renovation methods considering energy consumption, LCC and LCA. J. Build. Eng. 2019, 25, 100790. [Google Scholar] [CrossRef]
- Razmi, A.; Rahbar, M.; Bemanian, M. PCA-ANN integrated NSGA-III framework for dormitory building design optimization: Energy efficiency, daylight, and thermal comfort. Appl. Energy 2022, 305, 117828. [Google Scholar] [CrossRef]
- Chegari, B.; Tabaa, M.; Simeu, E.; Moutaouakkil, F.; Medromi, H. An optimal surrogate-model-based approach to support comfortable and nearly zero energy buildings design. Energy 2022, 248, 123584. [Google Scholar] [CrossRef]
- Kubwimana, B.; Najafi, H. A Novel Approach for Optimizing Building Energy Models Using Machine Learning Algorithms. Energies 2023, 16, 1033. [Google Scholar] [CrossRef]
- Gengembre, E.; Ladevie, B.; Fudym, O.; Thuillier, A. A Kriging constrained efficient global optimization approach applied to low-energy building design problems. Inverse Probl. Sci. Eng. 2012, 20, 1101–1114. [Google Scholar] [CrossRef]
- Tresidder, E.; Zhang, Y.; Forrester, A.I.J. Acceleration of building design optimisation through the use of kriging surrogate models. In Proceedings of the First Building Simulation and Optimization Conference, Loughborough, UK, 10–11 September 2012; Available online: http://apps1.eere.energy.gov/buildings/energyplus/ (accessed on 30 August 2023).
- Gilan, S.S.; Goyal, N.; Dilkina, B. Active learning in multi-objective evolutionary algorithms for sustainable building design. In Proceedings of the Genetic and Evolutionary Computation Conference 2016—GECCO’16, Denver, CO, USA, 20–24 July 2016; Association for Computing Machinery: New York, NY, USA, 2016; pp. 589–596. [Google Scholar] [CrossRef]
- Bamdad, K.; Cholette, M.E.; Bell, J. Building energy optimization using surrogate model and active sampling. J. Build. Perform. Simul. 2020, 13, 760–776. [Google Scholar] [CrossRef]
- Lahmar, S.; Maalmi, M.; Idchabani, R. Multiobjective building design optimization using an efficient adaptive Kriging metamodel. Simulation 2023. [Google Scholar] [CrossRef]
- Mirzaei, K.; Safari, A.; Jalilzadeh, S.; Mostafazadeh, F.; Tavakolan, M.; Safari, M. Environmental, social, and economic benefits of buildings energy retrofit projects: A case study in Iran’s construction industry. In Proceedings of the Construction Research Congress 2020: Infrastructure Systems and Sustainability, Tempe, Arizona, 8–10 March 2020; pp. 693–701. [Google Scholar] [CrossRef]
- Yang, X.; Chen, Z.; Zou, Y.; Wan, F. Improving the Energy Performance and Economic Benefits of Aged Residential Buildings by Retrofitting in Hot–Humid Regions of China. Energies 2023, 16, 4981. [Google Scholar] [CrossRef]
- Li, H.; Gutierrez, L.; Toda, H.; Kuwazuru, O.; Liu, W.; Hangai, Y.; Kobayashi, M.; Batres, R. Identification of material properties using nanoindentation and surrogate modeling. Int. J. Solids Struct. 2016, 81, 151–159. [Google Scholar] [CrossRef]
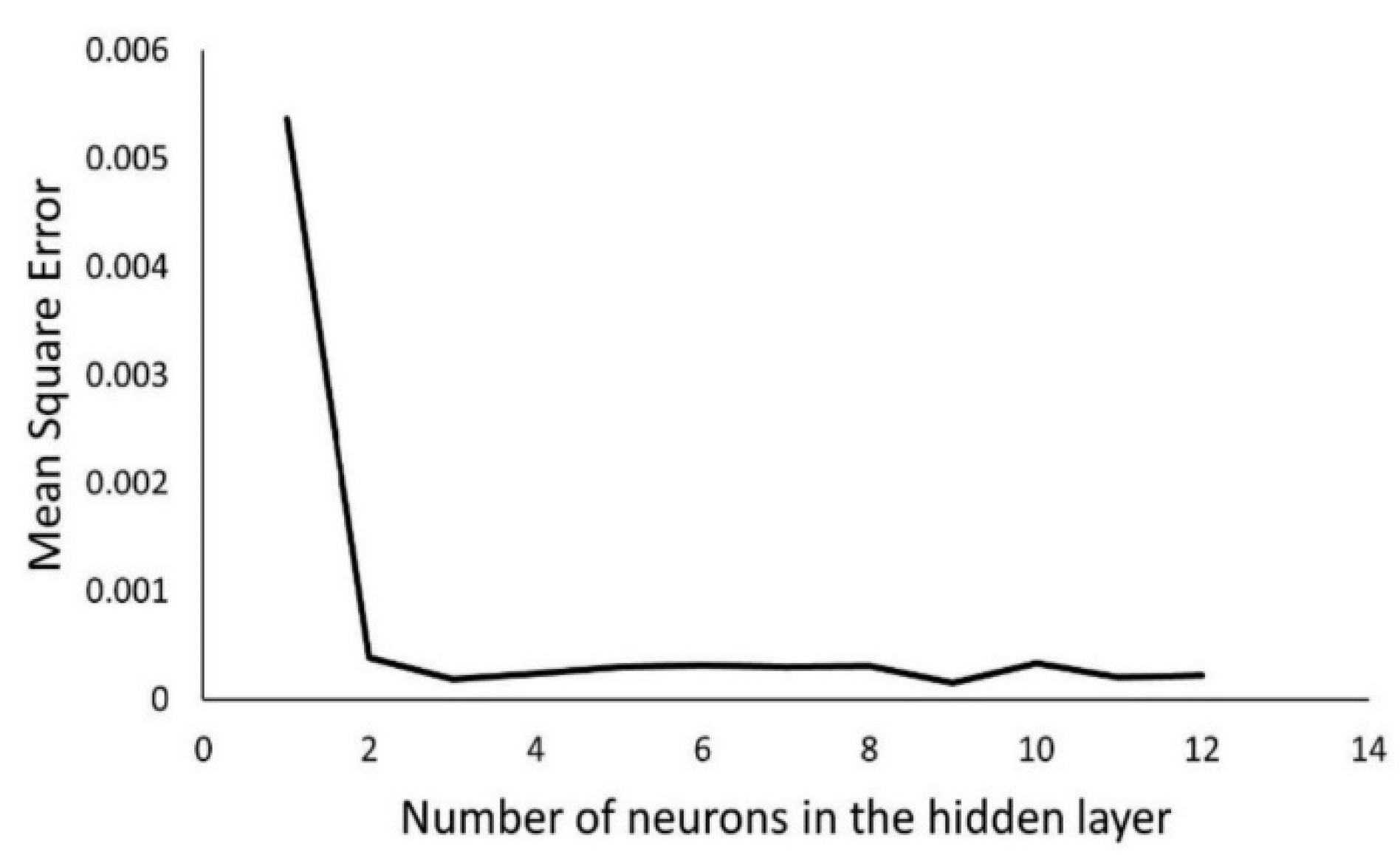
- Roman, N.D.; Bre, F.; Fachinotti, V.D.; Lamberts, R. Application and characterization of metamodels based on artificial neural networks for building performance simulation: A systematic review. Energy Build. 2020, 217, 109972. [Google Scholar] [CrossRef]
- Westermann, P.; Evins, R. Surrogate modelling for sustainable building design—A review. Energy Build. 2019, 198, 170–186. [Google Scholar] [CrossRef]
- Wortmann, T. Genetic evolution vs. function approximation: Benchmarking algorithms for architectural design optimization. J. Comput. Des. Eng. 2019, 6, 414–428. [Google Scholar] [CrossRef]
- Jones, D.R.; Schonlau, M.; Welch, W.J. Efficient Global Optimization of Expensive Black-Box Functions. J. Glob. Optim. 1998, 13, 455–492. [Google Scholar] [CrossRef]
- Solano-Rojas, B.J.; Villalón-Fonseca, R.; Batres, R. Micro Evolutionary Particle Swarm Optimization (MEPSO): A new modified metaheuristic. Syst. Soft Comput. 2023, 5, 200057. [Google Scholar] [CrossRef]
- Garud, S.S.; Karimi, I.A.; Kraft, M. Design of computer experiments: A review. Comput. Chem. Eng. 2017, 106, 71–95. [Google Scholar] [CrossRef]
- Batres, R. Generation of operating procedures for a mixing tank with a micro genetic algorithm. Comput. Chem. Eng. 2013, 57, 112–121. [Google Scholar] [CrossRef]
- Bessaou, M.; Siarry, P. A genetic algorithm with real-value coding to optimize multimodal continuous functions. Struct. Multidiscip. Optim. 2001, 23, 63–74. [Google Scholar] [CrossRef]
- Luke, S. Essentials of Metaheuristics: A Set of Undergraduate Lecture Notes, 2nd ed.; Lulu: Richmond, VA, USA, 2013; Available online: https://cs.gmu.edu/~sean/book/metaheuristics/Essentials.pdf (accessed on 9 October 2023).
- Haupt, R.L.; Haupt, S.E. Practical Genetic Algorithms, 2nd ed.; Wiley Interscience: Hoboken, NJ, USA, 2004. [Google Scholar]
- Dadras, Y.; Kavgic, M.; Alaei, O. Investigation of the thermal transmittances calculated using new infrared technology developed by qea tech. In Proceedings of the 16th Canadian Conference on Building Science and Technology, Vaughan, ON, Canada, 27–28 October 2022; pp. 2014–2023. [Google Scholar]
- Meacham, B.J.; Associates, M.; Mifiree, C. Performance-Based Building Regulatory Systems: Structure, Hierarchy and Linkages. J. Struct. Eng. Soc. New Zealand 2004, 17, 37–51. [Google Scholar]
- Historical Data-Climate-Environment and Climate Change Canada. Available online: https://climate.weather.gc.ca/historical_data/search_historic_data_e.html (accessed on 16 August 2023).
- Sengupta, M.; Xie, Y.; Lopez, A.; Habte, A.; Maclaurin, G.; Shelby, J. The National Solar Radiation Data Base (NSRDB). Renew. Sustain. Energy Rev. 2018, 89, 51–60. [Google Scholar] [CrossRef]
- American Society of Heating, Refrigerating and Air-Conditioning Engineers. In ASHRAE Guideline 14-2014: Measurement of Energy, Demand and Water Savings, ASHRAE Guideline; American Society of Heating, Refrigerating, and Air-Conditioning Engineers, 2014.
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Biggs, M.C. Minimization Algorithms Making Use of Non-quadratic Properties of the Objective Function. IMA J. Appl. Math. 1971, 8, 315–327. [Google Scholar] [CrossRef]
- Sengupta, S.; Basak, S.; Peters, R.A., II. Particle Swarm Optimization: A Survey of Historical and Recent Developments with Hybridization Perspectives. Mach. Learn. Knowl. Extr. 2019, 1, 157–191. [Google Scholar] [CrossRef]



| Parameter | Description | Value |
|---|---|---|
| pe | Electricity price in $/kWh | 0.143 CAN$/kWh |
| pg | The natural gas price in $/kWh | 0.0135 CAN$/kWh |
| t | Life span of the building | 50 years |
| dn | Nominal discount | 5% |
| e | Inflation rate | 3% |
| g | Energy price escalation rate | 2% |
| Decision Variable | Lower Value | Upper Value |
|---|---|---|
| The thickness of the insulation material (m) | 0.0252 | 0.127 |
| Window’s U-factor (W/m2K) | 1.3 | 1.8 |
| Solar heat gain coefficient | 0.1 | 0.3 |
| Algorithm | Parameter | |
|---|---|---|
| MEVO-I | The maximum number of iterations | 50 |
| Probability of crossover | 0.1 | |
| Probability of mutation | 0.1 | |
| MEPSO integrated into MEVO | ||
| Alpha | 0.6 | |
| Beta | 0.9 | |
| Maximum number of epochs | 5 | |
| Maximum number of internal loop iterations | 5 | |
| Individuals in the internal loop | 20 | |
| MEVO-II | The maximum number of iterations | 50 |
| Probability of crossover | 0.1 | |
| Probability of mutation | 0.1 | |
| MEPSO integrated into MEVO | ||
| Alpha | 0.02 | |
| Beta | 0.96 | |
| Maximum number of epochs | 5 | |
| Maximum number of internal loop iterations | 10 | |
| Individuals in the internal loop | 20 | |
| MEPSO-I | The maximum number of epochs | 1 |
| Maximum number of internal loop iterations | 7 | |
| Individuals in the internal loop | 20 | |
| Alpha 1 | 0.6 | |
| Beta 2 | 0.9 | |
| MEPSO-I | The maximum number of epochs | 4 |
| Maximum number of internal loop iterations | 5 | |
| Individuals in the internal loop | 20 | |
| Alpha 2 | 0.02 | |
| Beta 2 | 0.96 | |
| PSO | Inertia weight 2 | 0.8 |
| Cognition coefficient | 2.05 | |
| Social coefficient | 2.05 | |
| The termination criterion | Maximum of 25 iterations with 20 particles | |
| GA | Crossover fraction | 0.5 |
| Mutation fraction | 0.5 | |
| Population size | 50 | |
| Generations | 30 | |
| MEVO-I | MEVO-II | MEPSO-I | MEPSO-II | GA | PSO | |
|---|---|---|---|---|---|---|
| MBC (CAD/m2) | 752.6928 | 752.6986 | 752.6746 | 752.6807 | 752.8825 | 752.7562 |
| Best cost (CAD/m2) | 752.6740 | 752.6741 | 752.6740 | 752.6740 | 752.6873 | 752.6741 |
| Worst cost (CAD/m2) | 752.8377 | 752.8558 | 752.6876 | 752.8335 | 754.4349 | 755.0850 |
| Standard deviation (CAD/m2) | 0.0333 | 0.0506 | 0.0025 | 0.0291 | 0.3176 | 0.4398 |
| Mean computation time (min) | 13.412 +9.078 | 11.8871 +9.078 | 81.3136 | 89.1136 | 110.6959 | 99.2034 |
| MEVO-I | MEVO-II | Bayesian Optimization | |
|---|---|---|---|
| MBC (CAD/m2) | 752.6928 | 752.6986 | 753.1964 |
| Best cost (CAD/m2) | 752.6740 | 752.6741 | 752.7597 |
| Worst cost (CAD/m2) | 752.8377 | 752.8558 | 754.4766 |
| Standard deviation (CAD/m2) | 0.0333 | 0.0506 | 0.4039 |
| Mean computation time (min) | 13.412 +9.078 | 11.8871 +9.078 | 11.8684 +9.078 |
| Life Span (years) | Insulation (m) | Window U-Value (W/m2K) | SHGC | Natural Gas Consumption (kWh) | Electricity Consumption (kWh) | Natural Gas Consumption Reduction | Electricity Consumption Reduction |
|---|---|---|---|---|---|---|---|
| 20 | 0.0254 | 1.3000 | 0.1000 | 306,390.8615 | 80,531.0916 | 8.70% | 11.32% |
| 30 | 0.0317 | 1.3000 | 0.1000 | 301,558.3723 | 79,842.1703 | 10.14% | 12.08% |
| 40 | 0.0391 | 1.3000 | 0.1000 | 297,064.1325 | 79,203.8643 | 11.48% | 12.78% |
| 50 | 0.0493 | 1.3000 | 0.1000 | 292,286.1111 | 78,579.7222 | 12.90% | 13.47% |
| Discount Rate (years) | Insulation (m) | Window U-Value (W/m2K) | SHGC | Natural Gas Consumption (kWh) | Electricity Consumption (kWh) | Natural Gas Consumption Reduction | Electricity Consumption Reduction |
|---|---|---|---|---|---|---|---|
| 3% | 0.0711 | 1.3000 | 0.1000 | 285,227.7778 | 77,651.3889 | 15.00% | 14.49% |
| 5% | 0.0493 | 1.3000 | 0.1000 | 292,286.1111 | 78,579.7222 | 12.90% | 13.47% |
| 7% | 0.0341 | 1.3000 | 0.1000 | 299,961.6717 | 79,616.0683 | 10.61% | 12.33% |
| 10% | 0.0254 | 1.3000 | 0.1000 | 306,390.8615 | 80,531.0916 | 8.70% | 11.32% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Batres, R.; Dadras, Y.; Mostafazadeh, F.; Kavgic, M. MEVO: A Metamodel-Based Evolutionary Optimizer for Building Energy Optimization. Energies 2023, 16, 7026. https://doi.org/10.3390/en16207026
Batres R, Dadras Y, Mostafazadeh F, Kavgic M. MEVO: A Metamodel-Based Evolutionary Optimizer for Building Energy Optimization. Energies. 2023; 16(20):7026. https://doi.org/10.3390/en16207026
Chicago/Turabian StyleBatres, Rafael, Yasaman Dadras, Farzad Mostafazadeh, and Miroslava Kavgic. 2023. "MEVO: A Metamodel-Based Evolutionary Optimizer for Building Energy Optimization" Energies 16, no. 20: 7026. https://doi.org/10.3390/en16207026
APA StyleBatres, R., Dadras, Y., Mostafazadeh, F., & Kavgic, M. (2023). MEVO: A Metamodel-Based Evolutionary Optimizer for Building Energy Optimization. Energies, 16(20), 7026. https://doi.org/10.3390/en16207026








