Abstract
Steel production is one of the biggest emitters of greenhouse gas in the industrial sector with about 8% of total global CO emissions. Although the majority of emissions can be attributed to primary steel production, there is also potential for reducing CO emissions in downstream steel processing. Large industrial furnaces, which are necessary for heating steel, are currently primarily fired with natural gas and by-product gases from primary steel production, offering great potential for heat recovery measures from exhaust gases. However, switching to alternative climate-neutral fuels could change this potential and thus jeopardize the economic viability of heat recovery measures. In the present work, it was therefore examined to what extent a change in energy sources in industrial furnaces affects the potential use of heat recovery in steel processing. For this purpose, an optimization model was used that takes into account heat recovery by means of direct heat transfer, heat pumps and heat distribution systems. Potential future changes in energy supply for industrial furnaces were examined using different storylines. Two different energy price scenarios were also considered to address uncertain developments in energy markets. The results show that heat recovery is a cost-effective and definitely recommendable measure. Switching to alternative fuels has little impact on the use of heat recovery. Electrification and thus the elimination of flue gas, on the other hand, greatly reduces the potential for heat recovery.
1. Introduction
Background and Motivation
Around the world, the industrial sector is undergoing significant changes forced by CO reduction targets to mitigate the impact of current climatic change. The European Union aims for CO neutrality by 2050 and reducing total greenhouse gas emissions by 55% until 2030, as stated in EU Climate Target plan 2030, as part of the European Green Deal [1]. The Iron and Steel sector is responsible for around 8% of global final energy demand and emitted 3.4 Gt CO in the year 2019, accounting for 7% of the energy sector’s CO emissions [2]. As the global steel demand is also projected to increase by more than one-third from 1.82 Gt steel in 2020 to 2.55 Gt steel in 2050 [3], measures targeting the decarbonisation of the energy supply system and the overall efficiency of steelmaking are required. The steel sector is currently the largest industrial consumer of coal, which provides around 75% of the sector’s energy demand followed by electricity and natural gas (NG) [2]. These energy carriers are directly related to the most common production route the blast furnace (BF)–basic oxygen furnace (BOF) steel-making process, which uses a mix of liquid iron and scrap steel and accounts for close to 60% of the crude steel output in the EU [4]. The available decarbonisation measures range in efficiency enhancement such as top gas recycling over carbon capture and storage (CCS) to shifting to hydrogen-based fuels or using electric arc furnaces (EAFs) instead [5]. For the substitution of the BF the production of direct reduction iron (DRI) from the direct reduction of iron ore in the form of lumps, pellets, or fines into iron by a reducing gas, is an option. It is usually combined with an EAF as the produced pellets are advantageous for this technology.
The finishing line of steel works treats the raw steel and turns it into final steel products such as tin plates, wires, rails, etc. Steel is treated in reheating furnaces, often employing mixtures of by-product gases from the steel-making processes and NG, while steam is used for heating purposes such as heating acids baths for pickling, preheating of cooling and cleaning water and heating of lubrication systems [6]. Although the energy demand for steam is relatively low compared to the energy used in the large industrial furnaces for steel making (in Austria 105 GWh/12 MW primary energy consumption for steam at 10.326 GWh of total energy demand in the iron and steel sector in 2020—(1%)), there is still considerable savings potential in the heating system of the steel finishing line. An example given in the BAT document for the iron and steel industry [6] points out that hot rolling and annealing lines bare the potential to supply steam for other facilities from heat recovery of furnace fumes. Currently, steam is mostly generated using fossil fuels or by-product gases from the BF or BOF. However, these by-product gases will not be available if primary steel making is changed to hydrogen-based DRI or is shifted to secondary steel using scrap and EAFs.
Studies highlight the varying potentials of direct heat recovery (DHR) measures and industrial heat pumps (HPs) in the steel industry. For example, Kosmadakis et al. [7] point out that the heat requirement for the iron and steel sector in the European Union between 100 and 200 °C is around 30 TWh/year. McBrien et al. [8] showed the potential of a fully integrated DHR system saving up to 2.5 GJ per tonne of hot rolled steel. However, they do not account for distances and feasibility. The road-map for the Austrian steel and iron industry also mentions the significance of DHR and other heat recovery measures, especially in the finishing lines at lower temperatures [9]. Additionally, feeding excess heat into district heating systems can be a possibility to valorise heat surplus, as shown by Weinberger et al. [10] and Li et al. [11].
For the identification of excess heat potentials, pinch-based total site analysis and mathematical programming approaches such as heat exchanger network synthesis (HENS) are suitable [12] and have been widely used. A review by Schlosser et al. [13] highlights that Pinch Analysis can be used to identify feasible integration points for HPs from a thermodynamic point of view. It also yields important insights for total site integration showing heating requirements and excess heat potentials for inter-facility heat transfer. Depending on the imbalance between heat demands and availability of excess heat inter-facility distribution systems [14] can increase the overall energy efficiency of industrial sites significantly [15]. There are already some additions for the integration of HP [13] and distribution systems [16].
However, it is still unclear how a transition of industrial furnaces to carbon-free energy sources such as biogas (BG), hydrogen or potential electrification will affect the economic viability of measures for excess heat usage. Changing the energy carrier in the future might alter excess heat potentials and thus might jeopardise the economics of heat recovery measures implemented today. Thus, identifying future-proof measures is important to facilitate implementation. However, the identification of the best time for investments and realisation is not clear. Early implementation reduces the cumulative CO emissions of the finishing line, but given the limited life expectancy of equipment, implementation at a later time could make more sense economically.
In the present work, a scenario analysis for the finishing line of an integrated steel works was conducted to identify cost-optimal heat recovery measures depending on potential future boundary conditions. In contrast to most previous works on heat integration in the iron and steel industry, such as McBrien et al. [8] highlighting heat recovery potentials from an energy viewpoint, in this study, cost-efficient heat recovery measures are identified by means of Pinch Analysis and mathematical programming taking into account distances between sinks and sources and the availability of heat exchange technologies for difficult-to-harness heat sources. DHR and heat recovery by means of HPs is restricted to the individual facilities on the production site to prohibit extensive piping and intermediate circuits. This way, technical feasibility for the implementation of heat recovery measures is ensured.
The mathematical programming formulation used in this work comprises the possibilities for DHR by means of heat exchanger (HEX), heat recovery using HPs and the possibility for an inter-facility steam network. A time frame from 2020 to 2050 was considered for optimisation with the objective of minimising total costs. Investment decisions can be made at each trigger point which correlates with changes in the surrounding system such as fuel switching either in the reheating furnaces or for the external steam supply. Limited lifetime for HEX and HPs are considered, meaning that reinvestment is required for prolonged usage of equipment. Two different price scenarios were considered for energy carriers and several storylines were developed for the decarbonisation of furnaces considering BG, hydrogen and electrification. Even though the focus of the present study lies on heat recovery in the finishing line, CO emissions and economics for the different storylines and alternative energy carriers were analysed to observe the results of heat recovery in relation to the surrounding processes. In a post-processing step, CCS was considered to reduce carbon emissions for storylines where fossil fuels were still used in the furnaces.
In the following chapters, the analysed finishing line is described, heat recovery potentials are presented and the optimisation model used to identify the cost-optimal heat recovery system is introduced. Finally, results are presented and discussed.
2. Case Study
The ArcelorMittal Asturias plant is an integrated steel plant that has the steel process divided into two sites, Gijón and Avilés. At first, pig iron is casted into different shapes such as slabs, blooms and billets in the steel shop. These semi-finished products are processed further in the finishing line, which is the focus of this work. The main facilities in the finishing line are the hot strip mill (HSM), galvanizing line (GAL), pickling line (PL) and continuous annealing line (CAL), which are depicted in Figure 1, including their steam supply system. While water is often used for cleaning purposes, steam is used as a heat transfer medium. Furthermore, NG blendings are used as fuel for the reheating furnaces in the HSM, while NG is currently used to produce steam and supply furnaces in the CAL and GAL.

Figure 1.
Schematic layout of the considered parts of the steel plant.
2.1. Heat Recovery Potentials
The stream table for all facilities is introduced in Table 1. Temperature levels are rounded and the power is normalised by the maximum value. Currently, high-pressure steam is used to supply heat for several streams in different facilities. One stream with a relatively low target temperature requirement is supplied in the HSM (stream 6: 45 °C), two streams with moderate target temperatures in the GAL (stream 1: 70 °C; stream 3: 55 °C), three streams in the CAL (stream 1: 80 °C; stream 3: 90 °C; stream 9: 80 °C) and four streams in the PL (stream 1: 90 °C; stream 2: 90°C; stream 4: 85 °C; stream 5: 85 °C). Besides streams that require active cooling, there are also excess heat streams such as flue gas from reheating furnaces and cooling water that can be used for heat recovery (Table 1/availability level 1). Furthermore, there are excess heat sources that can theoretically be used for heat recovery, such as heat from hot steel, but are technically difficult to utilise and might require specialised and prohibitively expensive equipment (Table 1, availability level 2).

Table 1.
Stream table for all facilities.
Internal heat recovery potentials for each facility and for the entire finishing line are shown in Figure 2 in the form of Composite Curves calculated for a minimum approach temperature of 30 °C. These curves show the aggregated heating requirements (blue) and excess heat potentials/cooling requirements (red). An overlap of the curves indicates potential for DHR. The Grand composite Curves are derived directly from the Composite Curves and show the residual heating and cooling demands and the temperature levels at which heat can be supplied to or extracted from the system. In the Composite Curves, excess heat streams usable with common HEX (strong red) and excess heat streams requiring specialised equipment (pale red) are distinguished. The heat load axis is normalised by the maximum heat load at all availability levels. The Composite curves show that the CAL heat demands could only be met if specialised equipment was used. However, since heat recovery from these sources is yet subject to research, only readily available heat recovery technologies were considered for further analysis. In the HSM there is still approximately 9% excess heat available above 200 °C after DHR potentials are fully exploited. All residual heating requirements in the GAL (2%), CAL (3%), and PL (1% ) could be met using excess heat from the HSM.

Figure 2.
Composite Curves (top) and Grand Composite Curves (bottom)—light colors indicate that streams with availability level 2 were considered.
2.2. Storylines
Based on the urgent need for CO reduction many steel-producing companies defined goals similar to the goals mentioned in the Climate Action Report from ArcelorMittal [17], with reduction targets from 25% in 2020, decreasing to zero emissions in 2050. This leads to a variety of possible future scenarios for the energy systems in steel production in general and for the finishing line, in particular, that might influence heat recovery potentials and thus the economics of heat recovery measures. To investigate the impact of different decarbonisation pathways, storylines were created, implying changes in the energy system at a certain point in time. In Figure 3, eight storylines are summarised and depicted. In the current system, a mixture of NG and basic oxygen furnace gas (BOFG) is used as fuel for the furnaces in the HSM while NG is burnt in the furnaces of the GAL and CAL. Steam is supplied from an external steam boiler that also uses NG. For story lines A to E, it is assumed that the external steam is still produced using NG while for storyline F BG, it is used from 2035 onward. In storyline G, from 2035 onward, the steam demand has to be covered internally by means of high temperature HPs, electric boilers (EBs) and/or DHR.

Figure 3.
Energy supply storylines A–G.
For all discussed storylines, it is assumed that the BF–BOF route is replaced by a DRI–eaf route in 2035. Therefore, BOFG will not be available anymore, which directly affects the reheating furnace of the HSM. In storyline A, the furnace in the HSM is powered by 100% NG, whereas in storyline B, BG is used. In storyline C, NG is used until 2045, and then the system is changed to an electrically-powered furnace. Electricity-powered furnaces are also used in storylines D, F and G starting from 2035. For both story lines E1 and E2, the fuel is first switched to NG as an intermediate solution and is finally replaced by H in 2040. Opposed to storyline E1, in E2 it is assumed that the air preheating in the furnace is improved using new recuperative burners resulting in increased furnace efficiency but reduced heat recovery potentials from the flue gas.
2.3. Fuel Switch in the HSM
The impact of different potentially renewable fuels on the resulting flue gas stream in the furnace of the HSM was estimated using the process simulation tool IPSEpro. A steady-state model was used to calculate the resulting flue gas stream under the assumption that the heat transfer inside the furnace is not affected by the flue gas composition. The flue gas temperature at the outlet of the furnace was assumed to be around 800 °C, while air preheating was limited to approximately 50% of the temperature. Increased air recirculation was assumed inside the furnace to keep the flame temperature at a constant level to avoid increased NOx emissions. Thus, the different types of fuels are affecting flue gas heat loads and flue gas temperature after air preheating. The minimum allowable temperature level is set to a value roughly 15% above the dew point of the flue gas to avoid condensation. In the case of hydrogen, the limit is decreased down to 150 °C as the flue gas is to be assumed to be less problematic for the HEX. For hydrogen, the additional storyline E2 was examined with increased air preheating of roughly 60% leading to an increase in the furnace efficiency but the potential for heat recovery of the flue gas is reduced by around 60%. The usable excess heat from the furnace flue gas in the HSM is shown in Figure 4 for the different fuels. Electrification of the furnace is assumed to eliminate flue gas steams altogether.

Figure 4.
Available excess heat in HSM for various fuels relative to the base case.
2.4. Energy Price Scenarios
Figure 5 shows the price forecasts for the different energy carriers considered in the individual storylines but also prices for CCS and for CO certificates. The price forecast for NG is based on [18,19] but was modified especially in the near future to address the current situation in the energy markets due to the Ukraine conflict in 2022. After 2025, a decrease of the NG price is expected, as it is projected that the tension on the world market will resolve. The electricity scenario Electricity ES is based on the Energy Brainpool forecast for 2021 [18] but corrected by the difference between European prices and national prices for Spain. The H price H ES is linked to this scenario, assuming that if H is cheaper, then electricity will be used for power generation and thus is somewhat coupled. The same but vice-versa applies for the Electricity ESF scenario, which is linked to the forecast H ESF. In contrast to the H ES/Electricity ES scenario, this forecast is relatively optimistic and is based on the levelised cost of hydrogen production assumed by Bloomberg [20]. The forecast for BG prices is based on an International Energy Agency (IEA) outlook for bio-methane [21] and also considers assumptions for local availability and infrastructure for BG as these are key factors. The forecast for CO certificate prices is again taken from [18], assuming a significant increase until 2050. Moreover, CCS is considered since recent IEA projections indicate that by 2050 it will lead to cumulative direct emission reductions of 16% of global iron and steel emissions [22]. Based on the data available in the IEA Technology Report [23], a constant price of EUR 112 /t is assumed for the considered time frame between 2020 and 2050 since the costs for CCS technology, especially considering further development in the future are difficult to asses [24].
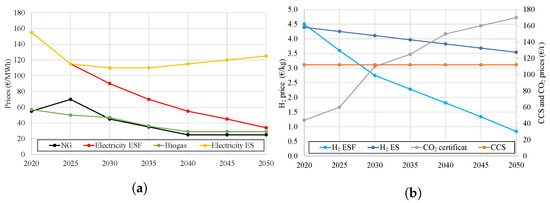
Figure 5.
Price forecasts for (a) NG, electricity and BG and (b) hydrogen, CCS and CO certificates.
3. Optimisation of Heat Recovery System
To identify the cost-optimal heat recovery system for the individual storylines and price forecasts, a mathematical programming formulation, more specifically an mixed - integer linear programming (MILP) model, was used that builds upon previous work by various authors (Figure 6). In the present work, a new formulation is presented that allows us to consider renewal and replacement investments for heat recovery equipment. The basic structure of the optimisation model is shown in Figure 7, including the interfaces between the individual sub-models, which are described in more detail in this chapter.
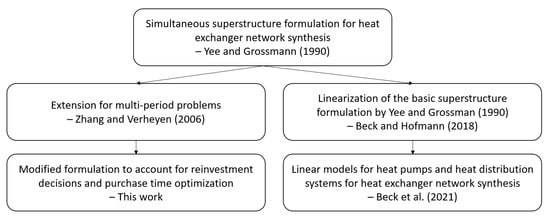
Figure 6.
Previous work contributing to the model used in this work [14,25,26,27].
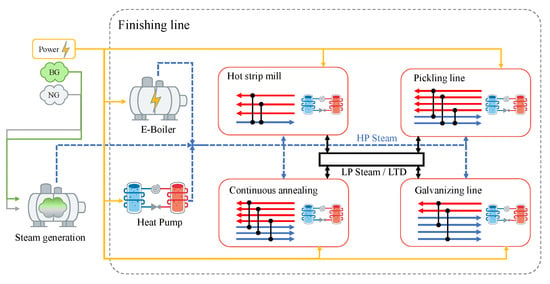
Figure 7.
Schematic representation of the optimisation model for the energy system in the finishing line.
3.1. Heat Exchanger Network Synthesis
The model for HENS is based on a linearised version (Beck and Hofmann [25]) of Yee and Grossman’s stage-wise superstructure mixed - integer nonlinear programming (MINLP) formulation [26]. It is further extended to multiple operating periods similar to the formulation proposed by Zhang and Verheyen [27]. In the present case the process duration is the time frame from 2020 to 2050, and the individual periods thus correspond to multiple years of continuous operation. In the following, an extension is introduced that accounts for limited equipment lifetime and thus limited operating times. This modification is used to examine changes to the heat recovery system throughout the years with respect to changes in both equipment costs and also changing heating and cooling requirements and excess heat sources. Replacements are thought of as costs for new equipment, which can be of differing size or capacity compared to the initial investment.
In the HENS model, costs for equipment are determined for each period t through step-fixed costs , which are realised if the equipment exists (z = 1) and variable costs depending on a continuous variable y.
A logical constraint using a so-called big-M factor M (very large number)
to force the continuous variable y to zero if the equipment does not exist ().
If investments should be made at a time where the life expectancy exceeds the considered time frame, a reduction factor is used to consider only a part of the investment costs in the objective function. This way, investments in heat recovery equipment close to 2050 are not disadvantageous in terms of costs per unit heat recovered.
Since equipment lifetime can exceed a single period and thus can use multiple periods without reinvestment-only realised costs are considered in the objective function. Additional logical constraints are used to only realise equipment costs at the beginning of its usage.
Here, is an auxiliary binary variable used to trigger the cost realisation in the first period of equipment installation and is constrained through
where is the number of discrete time periods starting with period index t until the lifetime of the respective equipment is exceeded or the considered time frame ends. This can be interpreted as finding the maximum of subject to and .
Calculation time is reduced through consideration of a non-equal period duration. This reduces the flexibility regarding investment times, but since major changes to the boundary conditions are considered through the introduction of additional time periods, this restriction is very unlikely to alter the results in a meaningful way.
3.2. Heat Pump Model for Integration in HENS
The HP model used in this study was proposed by Beck et al. [14] as an extension for HENS superstructure formulations (Figure 8). The HP model uses a so-called second law efficiency to describe the deviation of a real HP from the ideal thermodynamic cycle.

Figure 8.
(a) Schematic representation of a two-stage superstructure with two hot and two cold streams, (b) extension for HP integration.
Linearisation allows us to use MILP solvers to solve the optimisation model, which reduces the required computational efforts compared to MINLP formulations. In the basic nonlinear model, the governing equations are
and
which can be modelled as nonlinear constraints in the optimisation model. The evaporator heat load of the HP is equal to all heat transferred from all hot streams (sources).
Similarly, the condenser heat load of the HP is equal to heat transferred to all cold streams (sinks).
Linearised HP models for the integration in HENS formulations have been presented in the past. Prendl and Hofmann [28], for example, proposed a formulation that uses piece-wise linear constraints to address the nonlinearities in the model. One issue for the linearisation is the bounds for the domain of condenser and evaporator heat loads to address all possible integration points. The approach first briefly presented by Beck et al. [14] is also used in the present work and addresses this issue through direct linearisation of the possible heat loads for each HEX separately. The condenser and evaporator capacities for the individual hot and cold process streams are modelled as individual virtual HPs, which significantly tightens the bounds for possible heat loads and thus improves approximations. For each potential condenser and its respective heat loads, a virtual heat load at the evaporator is modelled using the second law efficiency model and vice versa. The sum of the virtual condenser heat loads and the actual loads at the condensers can then be connected through an equality constraint. Ideally, both virtual condenser and evaporator heat loads and actual condenser or evaporator heat loads are equal. However, due to linearisation of the correlation between condenser and evaporator heat loads and temperature levels, a certain error cannot be avoided. In the following, the linearised model by Beck et al. [14] is described in more detail.
The correlation between the evaporator heat loads and the corresponding virtual condenser heat load is modelled depending on the temperature dT using the coefficients
In the same manner, the virtual evaporator heat loads and the actual condenser heat loads are modelled.
In both equations, the slack variables s and s, which are used for activating or deactivating stream connections, are limited by logical constrains so that
and
In the model, the actual and virtual condenser heat loads are equal
but with the electricity consumption
and
A schematic representation of the model can be seen in Figure 9.
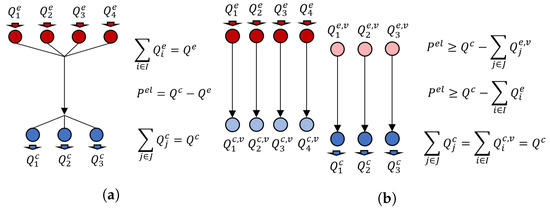
Figure 9.
Schematic representation of (a) nonlinear and (b) new linear HP model, including basic constraints.
Table 2 summarises all important parameters of the HP model. The costs for the HP are divided into costs for the HEX (condenser and evaporator) and the residual HP costs, including a variable and fixed term.

Table 2.
Basic data of the HP.
The error in terms of relative deviation from the actual coefficient of performance (COP) calculated with the nonlinear model is presented in Figure 10. The test runs were conducted with a random number between 1 and 11 of hot and cold streams with random stream parameters. Hot streams were initialised with a starting temperature of 70 to 80 °C, a heat capacity flow rate between 0 and 5 kW/K and a target temperature of 0 to 10 °C below the starting temperature. Similarly, the cold streams were initialised with a starting temperature of 80 to 90 °C, a heat capacity flow rate between 0 and 5 kW/K and a target temperature 0 to 20 °C above the starting temperature.
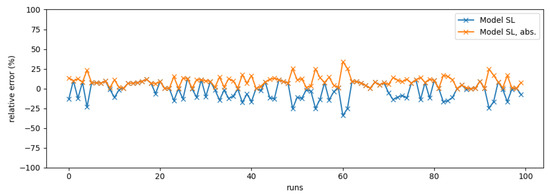
Figure 10.
Relative error and its absolute value for 100 test runs with random stream configurations.
3.3. Low Temperature Distribution System
Direct connection of heat sources and sinks of different facilities is not feasible due to prohibitively long distances, which promotes integration of an intermediate heat transfer cycle. Based on preliminary analysis, a range between 120 °C and 300 °C has been identified as most promising for the implementation of such a network. Common media for heat distribution are hot water and super-heated steam but within the available temperature range, low pressure stream is the most promising option. The low temperature distribution system (LTD) model first used by Beck et al. [14] is presented in detail in the following and can be integrated into the optimisation model to function as both hot and cold utility with the additional constraint, where the infeed and outfeed of the system need to be balanced.
where is the set of faculties that the LTD is potentially connecting. In the present case, the connection between the HSM and the CAL share the same piping as the connection between the HSM and the GAL, thus, if both facilities are connected, fixed investment costs for the pipeline should not be considered twice. Existence of a connection is realised through
where is the binary variable depicting existence of a connection and and represent the existence of a HEX for either hot internal utility or cold internal utility that transfer in the HENS model. Index f represents the facility. Fixed costs for the connections are modelled as
and
where is the cost coefficient for step-fixed costs, whereas variable costs are modelled using
and
where is the heat load to or from the LTD.
The basic cost function used to derive step-fixed and variable costs of the LTD are described through the factorial approach for cost estimation
with the installation factor , the piping based costs , the insulation costs , the Chemical Engineering Plant Cost Index factor and the length of the piping L. This approach for calculation of equipment and installation costs was suggested by Smith [29] considering the equations and coefficients proposed by Ulrich and Vasudevan [30] for complex networks excluding investment costs for fittings. This approach was validated for 5, 10 and 15 cm pipe diameters but yields unrealistic costs for larger diameters. Thus, for heat loads requiring larger diameters, multiple pipes were considered to be able to apply the presented cost function.
The installation factor
depends on the nominal pipe diameter in cm, which can be obtained considering steam velocities.
For the present case, steam velocities were set to 20 m/s. The piping base costs also follow a square-law function of
Costs for insulation
are related to the actual outer bare-pipe diameter and the optimal thickness of the insulation, which is obtained through
both in cm. The optimal thickness of the insulation depends pipe diameter and on the temperature difference between fluid and ambient . Heat losses in the LTD are neglected in the model. In the present case-study, the piping length L is parameterised for each connection between the individual facilities and is thus fixed (see Table 3).

Table 3.
Piping length.
For each connection, the cost coefficients and in Equations (20) to (24) are derived through linear approximation of the costs function Equation (25) evaluated for heat loads from 0 to 6 MW, which is the approximate range that heat recovery can take place in, according to the Composite Curves in Figure 2.
3.4. Local Steam Generation
In story line G, the external steam generator is replaced by local electrified steam production by means of either HPs or EBs. These units are modelled using predefined temperature levels for heat production units and linear efficiencies. Minimum part load constraints have not been considered in this work in order to reduce computational complexity.
The thermal output of an EB is related to its input using a fixed efficiency factor .
Similarly, for HPs, the efficiency is expressed as the coefficient of performance , which is a function of utilisation temperature , source temperature and the second law efficiency .
For HPs, the correlations between heat output , heat input and power are
and
3.5. Objective Function
In the proposed model, investment costs for HEX connecting either hot and cold streams directly , HEX connecting streams to utilities (including LTD and HPs) with , EB and HPs for internal steam production and , HP for heat recovery and costs for LTD are considered. Furthermore, energy costs for external steam supply and electricity purchase are part of the objective function.
Electricity purchase includes electricity for steam generation HPs, EBs and HPs for heat recovery.
Costs for external steam supply are determined by hot utility consumption and the fuel specific energy prices , which depend on the individual storylines.
4. Results
The results for the optimal heat recovery system presented in the following were generated, applying the MILP model described in Section 3, which was solved using CPLEX 12.9 with a stopping criteria of 2 hours of CPU-time. The resulting optimality gap was between 0 and 5% depending on the storyline. Costs and CO emissions for industrial furnaces were calculated separately based on storyline definitions and simulations for fuel switching. Similarly, costs and CO mitigation for the use of CCS were also calculated based on price forecasts and the furnace emissions based on furnace simulations.
Figure 11 shows the resulting annual emissions for the year 2050 for all storylines and for both energy price scenarios. However, the axis is normalised by the maximum value appearing in story line 0 (business-as-usual (BAU)) so that the emission reduction for the other story lines can be highlighted in percent. In the BAU storyline, the finishing line accounts for 220 kt/year. In storyline A, a switch to NG and carbon capture reduces CO-emissions in the HSM of a factor of around 50%. Emissions for the smaller furnaces in the GAL and CAL are mitigated due to electrification and emissions from steam production are eliminated through heat recovery. All other storylines, except for C and D, bring down emissions to zero in 2050. Storylines C and D assume electrification of all furnaces until 2050, which causes a demand for external steam production and thus consumption of natural gas since in these storylines excess heat from the HSM is not available any more. Scenarios F and G are inherently carbon-free since both furnaces and steam supply are limited to carbon-free fuels or electrification. The results show that the annual emissions in 2050 are not sensitive to the different price scenarios even though electricity prices differ by a large amount starting by 2025 at EUR 20 /MWh and increasing until 2050 to EUR 80 /MWh on average (Figure 5).

Figure 11.
Annual CO emission reduction for the finishing line in 2050.
Figure 12 and Figure 13 show the total costs over the considered time frame of 2020 to 2050 for the steam supply and heat recovery system. Both cost axes are normalised by the values of the BAU storyline for ensuring an easier comparison between different storylines. In the BAU case, there were only OPEX for external steam supply. No investments were considered. In all other storylines, a small percentage of total costs can be attributed to costs for DHR. The major cost shares are the LTD, including HEX and piping, OPEX for steam as a hot utility and OPEX for HP electricity consumption. Especially in storyline G, expenses for electricity are significant since steam is produced by means of high temperature HPs. In storylines C, D, F and G, furnaces are electrified at some point, meaning that there is no excess heat available. This means that for story lines C, D and F, external steam supply becomes necessary, resulting in OPEX for hot utility.
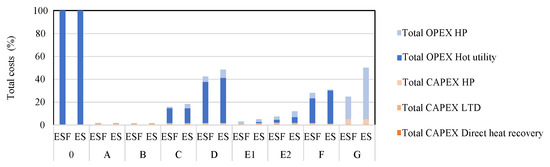
Figure 12.
Total costs for heat recovery measures and steam supply.
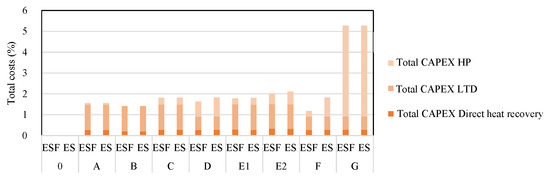
Figure 13.
Total costs for heat recovery measures and steam supply—only CAPEX.
The fact that the optimal heat recovery system is very similar for both energy price scenarios ES and ESF is also shown in Figure 14. This highlights the reduction of CO emissions compared to the BAU case for all storylines and both energy price scenarios. Thereby, CCS is used if it is economically beneficial. Moreover, Figure 14 also shows the trend of always or never using CCS for the ESF scenario. However, the results are similar for the ES scenario with a lesser amount of cost reduction in both cases.
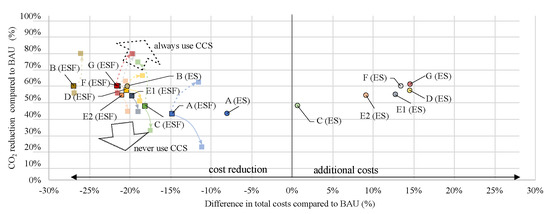
Figure 14.
CO mitigation and impact of CCS with respect to cost difference to BAU scenario.
In both price scenarios, BG is the most cost effective substitution for NG and BOFG. This is also due to the fact that the BG price was regarded independent from electricity and hydrogen prices. Together with story lines F and G, the BG case results in the highers overall CO reduction of approximately 58%. However, even though BG shows to be the most promising way for decarbonisation of the finishing line, its availability is highly uncertain even for the plant operator. Switching to NG plus CCS (storyline A) yields drastically reduced CO mitigation potentials with roughly a 40% reduction compared to the BAU case. The economics for story lines C, D, G, F with electrification of the furnace in the HSM are highly sensitive to the underlying price forecasts. Total costs are in the range of −23% up to +15% compared to the BAU case. Similarly, storylines employing hydrogen as fuel (E1 and E2) show a broad range in total costs for the finishing line (−22% up to +13%). Considering that BG might not be or just partially available, full electrification, including HPs for steam supply (story line G) would be the most cost efficient and also potentially carbon-free solution for the finishing line in the ESF price scenario. For the ES price scenario, a pareto front can be observed. The cheapest storyline—but also the one with the least CO reduction—was storyline A using NG ad CCS. The next best options would be storyline C with increasing electrification (similar costs to BAU case, CO reduction of 45%), storyline E2 with an increase in costs of 8% and a CO reduction of 51% and then scenario F with a switch to BG for steam production and electrified furnaces with a CO reduction of 58% and an increase in total costs of 13%. For price scenario ES, the storylines E1, D and G are not on the pareto front and thus are suboptimal.
4.1. Heat Recovery System
The resulting inter-facility heat recovery system for storyline A and price scenario ESF is presented in Figure 15 as an example. In this scenario, DHR is considered in all facilities highlighted through the black stream connections. A HP is only placed in the CAL for heat recovery and all facilities are connected through the LTD.

Figure 15.
Heat exchanger network (HEN) for storyline A and price scenario ESF.
Investments in DHR were very similar throughout all of the storylines. All cost data presented in the following is normalised with total costs from the base case. In 2020, between 0.15% and 0.18% were invested in HEX for DHR for both price scenarios and in 2035, replacements of 0.05% to 0.15% were purchased. This resulted in average investments of 0.27% in price scenario ESF and 0.28% in price scenario ES for the entire duration.
Table 4 shows which heat recovery measures were part of the optimal solution in the individual storylines and price scenarios. For all storylines and both price scenarios, the LTD system was installed, connecting all facilities in 2020. However, the system was not renewed in 2035 in storylines D, F and G with electrification of all furnaces starting in this period. In all other scenarios, heat loads in the HEX connecting the LTD to the individual facilities were increased and thus replacement costs for HEX were approximately 0.65% compared to the initial costs of around 0.28%.

Table 4.
Usage of heat recovery measures (X: used in both energy price scenarios, -: not used at all) for the HSM, GAL, CAL and PL.
HPs are part of the optimal solution for all storylines except for storyline B. In the other storylines, total investments of 0.07% to 0.91% were realised in scenario ESF with an average of 0.52% and 4.35% in story line G, whereas for ES, investments decrease to an average of 0.36% for storylines A to F. HP costs for storyline G remained the same with 4.35%.
For all storylines, other than the electrification storyline G, total CAPEX are in the range of 1.15% to 2.07%. CAPEX for G was 5.27% for both energy price scenarios.
Total costs can be reduced significantly compared to the base case by 53% to 100% depending on the storyline. All storylines with excess heat available from the HSM in 2035–2050 resulted in a high cost reduction of at least 90%. Cost reduction for storylines with electrified furnaces in the HSM (C, D, F, G) cost reduction was decreased to 55% to 86%. Insensitive of electricity price scenario and fuel type in the HSM, heat recovery measures reduced total costs for the considered period considerably. Average annual savings were 2.13% to 3.33% of the total costs of the base case per year. Average payback periods were 0.4 to 1.6 years depending on price scenario and storyline.
The specific energy consumption for steam generation in the BAU case was 79.4 MJ per tonne of steel. Since the present work aims at a reduction in steam generation, this value represents the potentials for energy savings by means of heat recovery. Depending on the storyline and price scenarios, a reduction of 50.4 to 79.4 MJ/t for steam generation was obtained. Energy consumption for HPs was in the range of 0 to 9.6 MJ/t and has been included. CO emissions for steam production in the base case were 463.6 kt. Using DHR, emissions were drastically reduced in storylines A, B, C, E1, E2, F (BG for steam production) and G (internal electrified steam generation) to 0 kt to 50.9 kt. Only in storyline D, emissions remain relatively high at 153.3 and 168.5 kt depending on price scenarios. In all scenarios and storylines, CO mitigation could be realised and, at the same time, cost savings can be achieved. On average, external steam demand is reduced by 90% (ESF) and 88% (ES). Higher electricity prices reduce the usage of HPs, which in turn, results in a higher utility purchase. Even though it would theoretically still be possible to supply the GAL and CAL facilities with electrified furnaces with heat from the HSM under the assumption of a minimum approach temperature in HEX of 30 °C and a temperature of 120 °C for the LTD system, it does not make sense from an economic viewpoint.
4.2. Fuel Switch in the Hot Strip Mill
Regarding CO mitigation in the finishing line fuel switching in the HSM has a much larger lever compared to heat recovery measures since the primary energy consumption of the large furnace is 10 times higher compared to the energy used for steam production.
4.3. Impact of Carbon Capture and Storage
Using the price forecasts shown in Figure 5, implementation of CCS becomes favourable compared to CO certificates in 2030. For all analyses in this work, it was assumed that CCS is applied as soon as this threshold is passed. Additionally, in Figure 14, cost reduction and CO mitigation is depicted for the cases where CCS is always used, despite the unfavourable economics and where CCS is never used. Clearly, for both cases, costs increase; however, if CCS is always used starting from the beginning, the cumulative emission reduction is significant. For story lines B, D, F and G, cumulative emissions can be reduced by 77%. At this point, it needs to be emphasised that the cost assumption for CCS will be underestimated if the system is used only for a short period of time and thus needs to be treated with caution.
5. Conclusions
The results of the presented study show that the cost-optimised usage of heat recovery measures is relatively independent of the price scenarios for electricity and hydrogen and that with current and future energy prices heat recovery will be a business case with low payback periods with average payback periods below 2 years, where longer payback periods need to be expected for inter-facility heat exchange and relatively short payback periods for DHR. Potential reductions of specific energy consumption for steam production of up to 79 MJ/t steel could be obtained. In a similar study by McBrien et al. [8], they identified theoretical potentials of up to 3 GJ/t reduction, but they considered all heating and cooling requirements in an integrated steel mill, including the steel shop and the coking plant. Moreover, they allowed for stream connections that are difficult due to limited technical feasibility and prohibitive distances. Considering total CO emissions in the steel production, the contribution to CO-mitigation of heat recovery measures is low compared to a switch to carbon-free fuels in the reheating furnaces (HSM, GAL, CAL) in the finishing line. In the use case presented in this work, steam supply that can be reduced through heat recovery accounts for only 7% of the finishing line’s total emissions. However, costs for a fuel switch strongly depend on price scenarios and thus switching fuels can both increase or decrease overall costs whereas heat recovery is always worthwhile and reduces overall costs. The analysis showed that the usage of HPs shows the largest dependency regarding energy prices; however, in both considered price scenarios, HPs were introduced into the system to a very similar extent. The overall range of change in total costs for the energy supply in the finishing line from 2020 to 2050 lies between −28% and + 15% compared to the BAU case. Considering the cost assumptions for this study, employment of BG as a substitution for by-product gases and NG is cost efficient if available. Considering bio energy and carbon capture (BECCS), BG could be even more promising since carbon emissions could be net-negative and at some point, CCS will likely become cheaper than purchasing CO certificates. Without considering BECCS, cumulative CO emissions in the finishing line of the considered steel plant can be reduced by up to 80% if CCS is used right away, whereas in the case where CCS is used from the point where it is competitive in terms of economics cumulative emissions are reduced by 60% through a switch to carbon-neutral fuels in 2035, such as BG, hydrogen or electrified furnaces. In the present study, the time of fuel switches was imposed as a boundary condition; however, in future work, this could also be subject to optimisation. Furthermore, methanation should be considered in future work as it could reduce risks related with retrofitting of existing furnaces and thus facilitate usage of hydrogen as fuel.
Author Contributions
Conceptualisation, A.B., J.U. and F.H.; methodology, A.B. and J.U.; software, A.B. and J.U.; formal analysis, J.U.; validation, A.B.; investigation, A.B., J.U. and I.S.-G.; resources, A.B., J.U. and I.S.-G.; data curation, J.U.; writing—original draft preparation, A.B. and J.U.; writing—review and editing, A.B., J.U. and I.S.-G.; visualisation, A.B. and J.U.; supervision, F.H.; project administration, F.H.; funding acquisition, F.H. All authors have read and agreed to the published version of the manuscript.
Funding
This work was conducted within the BAMBOO project, which received funding from the European Union’s Horizon 2020 research and Innovation programme under grant agreement N°820771.
Data Availability Statement
Data presented in figures and tables are available on request from the corresponding author. Most data used to derive information presented in the paper is not publicly available due to confidentiality reasons.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Acronyms | |
| BAU | business-as-usual |
| BECCS | bio energy and carbon capture and storage |
| BG | biogas |
| BOF | basic oxygen furnace |
| BOFG | basic oxygen furnace gas |
| CAL | continuous annealing line |
| CCS | carbon capture and storage |
| COP | coefficient of performance |
| DHR | direct heat recovery |
| DRI | direct reduction iron |
| EAF | electric arc furnace |
| ES | energy price scenario Spain |
| ESF | energy price scenario Spain - falling prices |
| GAL | galvanising line |
| HEN | heat exchanger network |
| HENS | heat exchanger network synthesis |
| HEX | heat exchanger |
| HP | heat pump |
| HSM | hot strip mill |
| IEA | International Energy Agency |
| LTD | low temperature distribution system |
| MILP | mixed-integer linear programming |
| MINLP | mixed-integer nonlinear programming |
| NG | natural gas |
| PL | pickling line |
| Sets | |
| FAC | facilities |
| I | hot process stream |
| J | hot process stream |
| TYPE | heat exchanger types |
| Parameters | |
| efficiency (-) | |
| big-M coefficient (-) | |
| c | cost coefficient (EUR) |
| capital costs for piping (EUR) | |
| price index (-) | |
| specific insulation costs (EUR/m) | |
| specific piping costs (EUR/m) | |
| cost reduction factor (-) | |
| actual pipe diameter () | |
| nominal pipe diameter () | |
| bare module factor (-) | |
| L | piping length () |
| inlet temperature (°C) | |
| outlet temperature (°C) | |
| source temperature for heat pump () | |
| outlet temperature (°C) | |
| ambient temperature (°C) | |
| flow velocity () | |
| Subscripts | |
| f | index for facility |
| i | index for hot process stream |
| INS | subscript for insulation |
| j | index for cold process stream |
| P.CS | subscript for piping base costs |
| t | index for time interval |
| Superscripts | |
| c | condenser |
| Direct | direct heat exchange |
| e | evaporator |
| el | electric |
| fix | fixed costs |
| fuel | fuel specific |
| HEX | heat exchanger |
| LTD | low temperature distribution system |
| PSC | cold process stream |
| PSH | hot process stream |
| real | realised costs |
| type | heat exchanger type |
| UC | cold utility |
| UH | hot utility |
| UIC | cold intermediate utility |
| UIH | hot intermediate utility |
| unit | unit in the supply system |
| v | virtual heat load |
| var | variable costs |
| Variables | |
| capacity of supply unit | |
| total annual cost (EUR) | |
| C | cost (EUR) |
| coefficient of performance | |
| E | energy flow () |
| l | thermal losses () |
| P | power consumption () |
| Q | thermal power () |
| T | temperature (°C) |
| y | continuous variable |
| z | binary variable (-) |
References
- European Commision. State of the Union 2020: EU Climate Target Plan 2030: Building a Modern, Sustainable and Resilient Europe; Publications Office of the European Union: Luxembourg, 2020.
- IEA—International Energy Agency. Iron and Steel Technology Roadmap; IEA (2020), Iron and Steel Technology Roadmap, IEA: Paris, France, 2020.
- Sun, Y.; Tian, S.; Ciais, P.; Zeng, Z.; Meng, J.; Zhang, Z. Decarbonising the iron and steel sector for a 2 °C target using inherent waste streams. Nat. Commun. 2022, 13, 297. [Google Scholar] [CrossRef] [PubMed]
- The European Steel Association—EUROFER. European Steel in Figures 2021; The European Steel Association: Brussels, Belgium, 2021. [Google Scholar]
- Draxler, M.; Tobias Kempken, T.H.; Jean-Christophe Pierret, J.B.; Antonello Di Donato, M.D.S.; Chuan, W. Technology Assessment and Roadmapping (Deliverable 1.2). 2021. Available online: https://www.estep.eu/assets/Uploads/210308-D1-2-Assessment-and-roadmapping-of-technologies-Publishable-version.pdf (accessed on 13 November 2022).
- Rainer, R.; Miguel, A.M.; Serge, R.; Luis, D.S. Best Available Techniques (BAT) Reference Document: For: Iron and Steel Production: Industrial Emissions Directive 2010/75/EU: (Integrated Pollution Prevention and Control); Publications Office: Luxembourg, 2012. [Google Scholar]
- Kosmadakis, G. Estimating the potential of industrial (high-temperature) heat pumps for exploiting waste heat in EU industries. Appl. Therm. Eng. 2019, 156, 287–298. [Google Scholar] [CrossRef]
- McBrien, M.; Serrenho, A.C.; Allwood, J.M. Potential for energy savings by heat recovery in an integrated steel supply chain. Appl. Therm. Eng. 2016, 103, 592–606. [Google Scholar] [CrossRef]
- Pulm, P.; Raupenstrauch, H. Roadmap Industrie—Energieeffizienz in der Eisen- und Stahlindustrie; Klima- und Energiefonds der Österreichischen Bundesregierung: Vienna, Austria, 2014. [Google Scholar]
- Weinberger, G.; Amiri, S.; Moshfegh, B. On the benefit of integration of a district heating system with industrial excess heat: An economic and environmental analysis. Appl. Energy 2017, 191, 454–468. [Google Scholar] [CrossRef]
- Li, Y.; Xia, J.; Fang, H.; Su, Y.; Jiang, Y. Case study on industrial surplus heat of steel plants for district heating in Northern China. Energy 2016, 102, 397–405. [Google Scholar] [CrossRef]
- Klemeš, J.J.; Kravanja, Z. Forty years of heat integration: Pinch analysis (PA) and mathematical programming (MP). Curr. Opin. Chem. Eng. 2013, 2, 461–474. [Google Scholar] [CrossRef]
- Schlosser, F.; Arpagaus, C.; Walmsley, T. Heat pump integration by Pinch analysis for industrial applications: A review. Chem. Eng. Trans. 2019, 76. [Google Scholar]
- Beck, A.; Unterluggauer, J.; Knöttner, S.; Niño, C.G.; Angel, J.G.; Arias, M.L.; Solis, I. Optimized waste heat utilization in the steel industry with industrial heat pumps and low-temperature distribution system. In Proceedings of the 12. Internationale Energiewirtschaftstagung an der TU Wien (IEWT 2021), Vienna, Austria, 7–10 September 2021. [Google Scholar]
- Tao, R.; Liu, L.; Gu, S.; Zhuang, Y.; Zhang, L.; Du, J. Flexible synthesis of inter-plant heat exchanger networks considering the operation of intermediate circles. Chem. Eng. Trans. 2020, 81, 13–18. [Google Scholar]
- Chang, C.; Chen, X.; Wang, Y.; Feng, X. Simultaneous optimization of multi-plant heat integration using intermediate fluid circles. Energy 2017, 121, 306–317. [Google Scholar] [CrossRef]
- Arcelormittal. Climate Action Report 2; Arcelormittal: Luxemburg, 2021. [Google Scholar]
- Zhou, H. Update: EU Energy Outlook 2050—How will Europe evolve over the next 30 years? 2019. Available online: https://blog.energybrainpool.com/en/update-eu-energy-outlook-2050-how-will-europe-evolve-over-the-next-30-years/ (accessed on 29 March 2022).
- IEA—International Energy Agency. World Energy Outlook 2021; World Energy Outlook 2021, IEA: Paris, France, 2021.
- Bloomberg NEF. Hydrogen Economy Outlook—Key Messages. 2019. Available online: https://data.bloomberglp.com/professional/sites/24/BNEF-Hydrogen-Economy-Outlook-Key-Messages-30-Mar-2020.pdf (accessed on 13 November 2022).
- IEA—International Energy Agency. Outlook for Biogas and Biomethane: Prospects for Organic Growth; IEA: Paris, France, 2020.
- IEA—International Energy Agency. Cumulative Direct Emission Reductions by Mitigation Strategy in the Sustainable Development Scenario between 2020 and 2050; IEA: Paris, France, 2020.
- IEA—International Energy Agency. Energy Technology Perspectives 2020—Special Report on Carbon Capture Utilisation and Storage; OECD Publishing: Paris, France, 2020.
- Birat, J. Global Technology Roadmap for CCS in Industry. 2010. Available online: https://www.globalccsinstitute.com/archive/hub/publications/15671/global-technology-roadmap-ccs-industry-steel-sectoral-report.pdf (accessed on 13 November 2022).
- Beck, A.; Hofmann, R. A Novel Approach for Linearization of a MINLP Stage-Wise Superstructure Formulation. Comput. Chem. Eng. 2018, 112, 17–26. [Google Scholar] [CrossRef]
- Yee, T.F.; Grossmann, I.E. Simultaneous optimization models for heat integration—II. Heat exchanger network synthesis. Comput. Chem. Eng. 1990, 14, 1165–1184. [Google Scholar] [CrossRef]
- W. Verheyen, N.Z. Design of flexible heat exchanger network for multi-period operation. Chem. Eng. Sci. 2006, 61, 7730–7753. [Google Scholar] [CrossRef]
- Prendl, L.; Hofmann, R. An extended approach for the integration of heat pumps into hens multi-period MILP superstructure formulation for industrial applications. In Computer Aided Chemical Engineering; Elsevier: Amsterdam, The Netherlands, 2020; Volume 48, pp. 1351–1356. [Google Scholar]
- Smith, R. Chemical Process: Design and Integration; John Wiley & Sons: Hoboken, NJ, USA, 2005; John Wiley & Sons Ltd, The Atrium, Southern Gate, Chichester, West Sussex PO19 8SQ, England. [Google Scholar]
- Ulrich, G.D.; Vasudevan, P.T. Short-cut piping costs: This method saves precious time in preparing estimates for pre-design and other approximated analyses. Chem. Eng. 2006, 113, 44–50. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).