Design of Variable Pitch Control Method for Floating Wind Turbine
Abstract
1. Introduction
2. Main Parameters of Floating Wind Turbine
3. Floating Wind Turbine Model
3.1. Establishment of Floating Wind Turbine Model
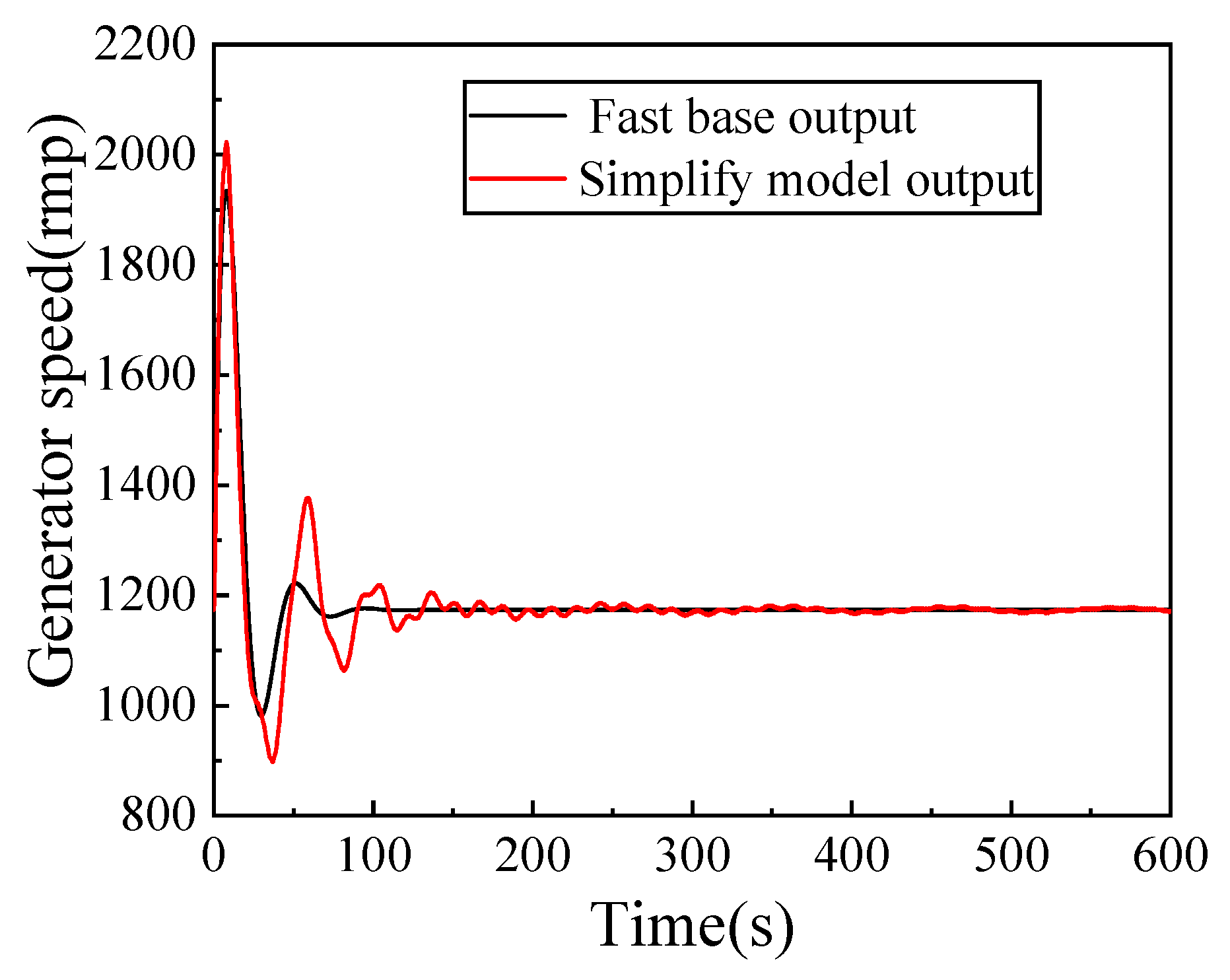
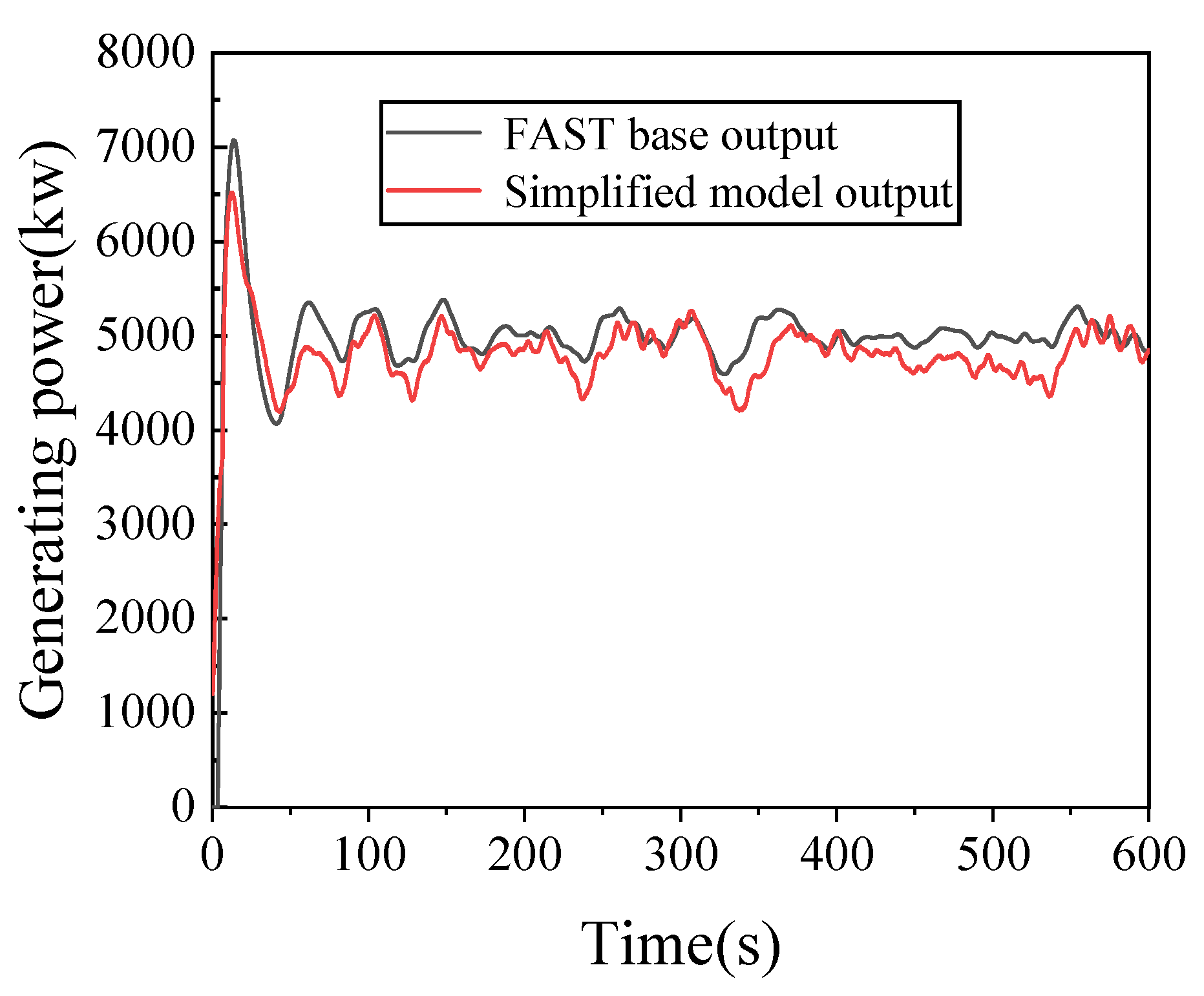
3.2. Verification of Floating Wind Turbine Model
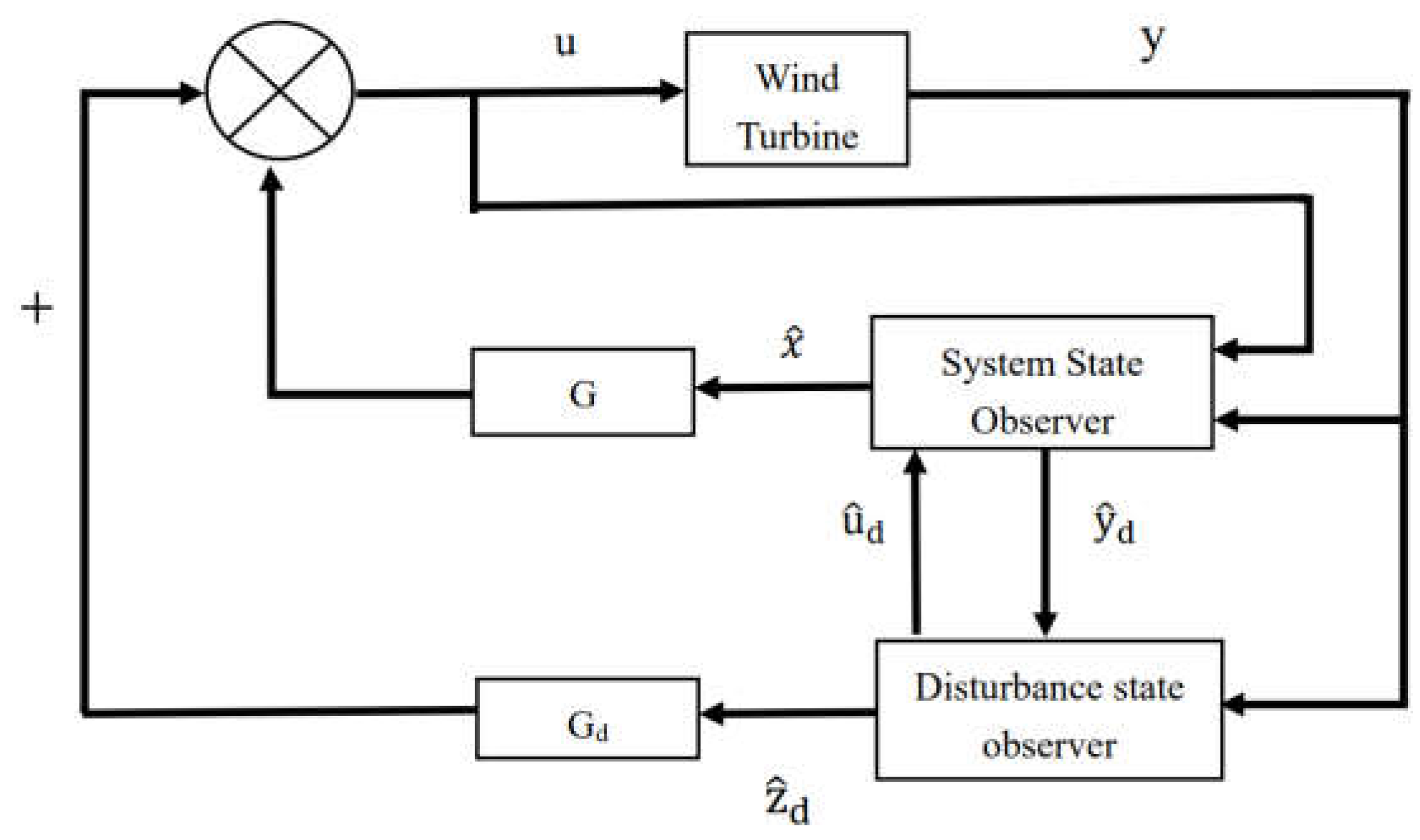
3.3. Design of Disturbance Adaptive Control Based on Genetic Algorithm Fractional PID State Feedback
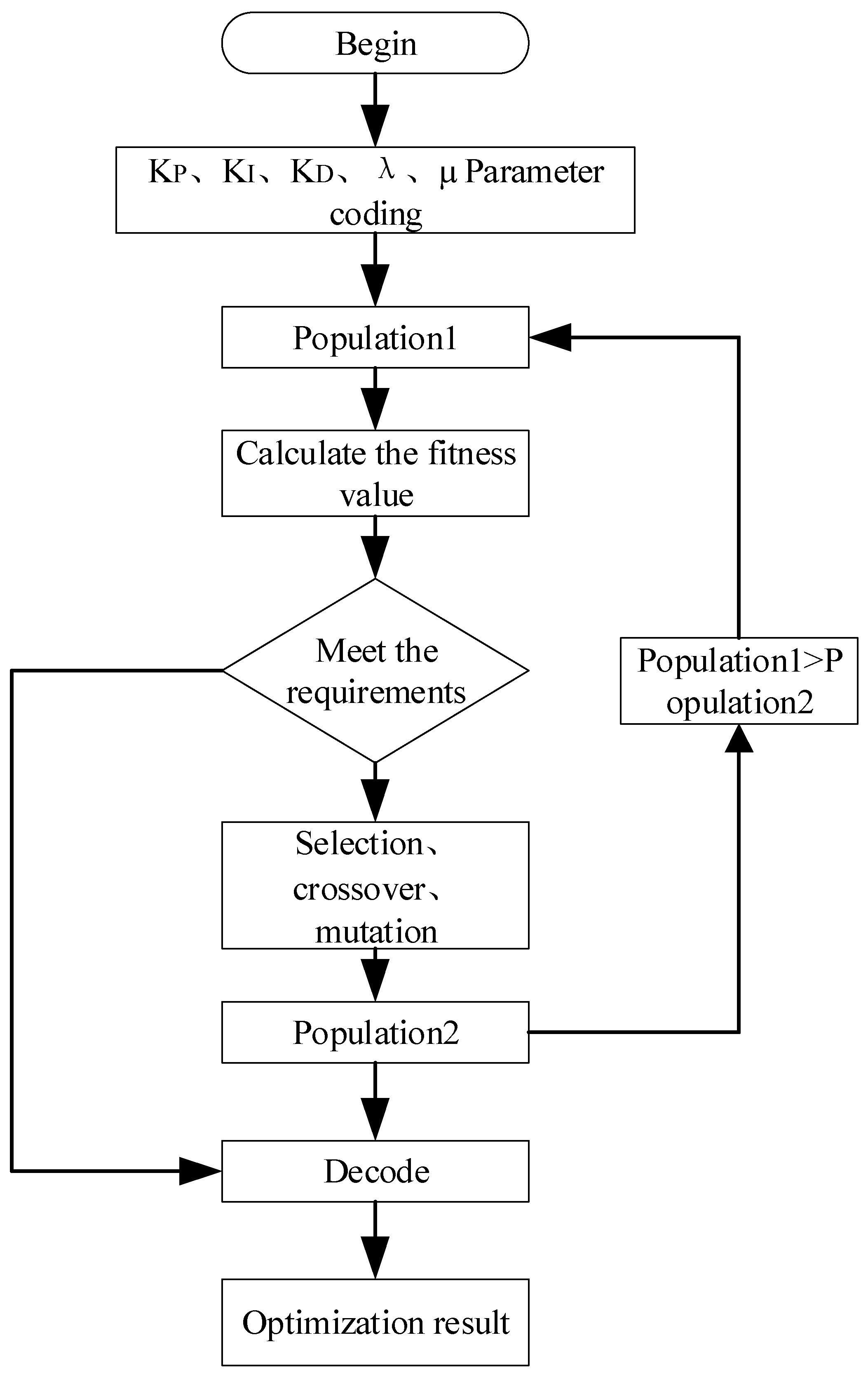
3.4. PID Parameter Optimization Based on Genetic Algorithm
- Initialize the parameter population and set the population size, number of variables, genetic algebra, maximum number of iterations, crossover probability and mutation probability.
- Set the parameter range of to (0.01, 0.2), (0.01, 0.2), (0.01, 1), (0, 1), (0, 1).
- Use a binary encoding method for convenient genetic operation and obtaining the optimal solution after decoding.
- Determine the individual evaluation method, namely the individual fitness function.
- When the parameters are optimized and the fitness of individuals of the population is not equal to the average fitness, use the fitness allocation function to allocate the fitness. Use the selection operator, cross probability operator and mutation probability operator to operate the population and generate the next-generation population.
- When the parameters converge or reach the target value, the optimal parameters of the system are obtained. The flow chart of the genetic algorithm optimization of PID parameters is shown in Figure 4.
3.5. Determination of Fitness Function
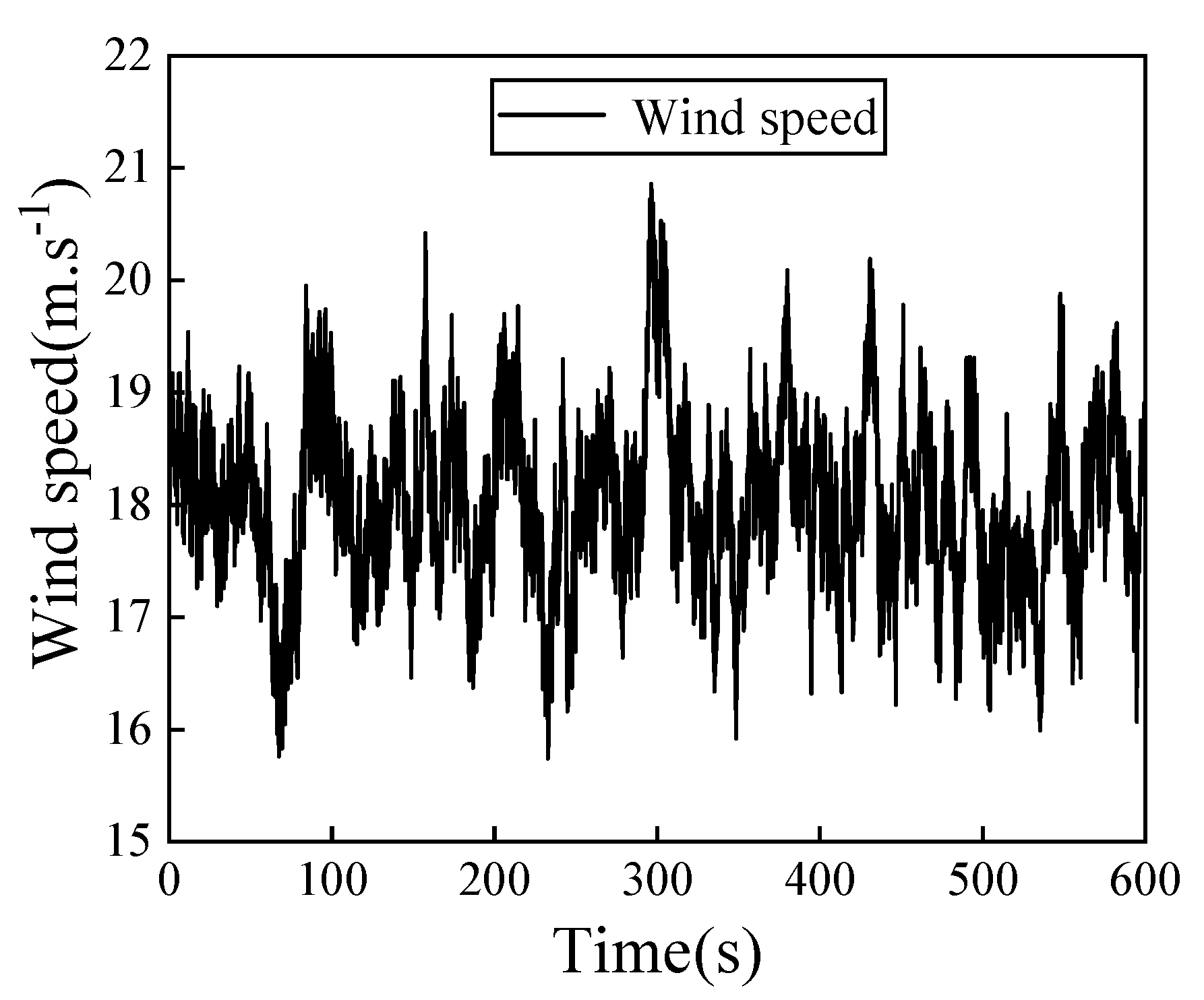
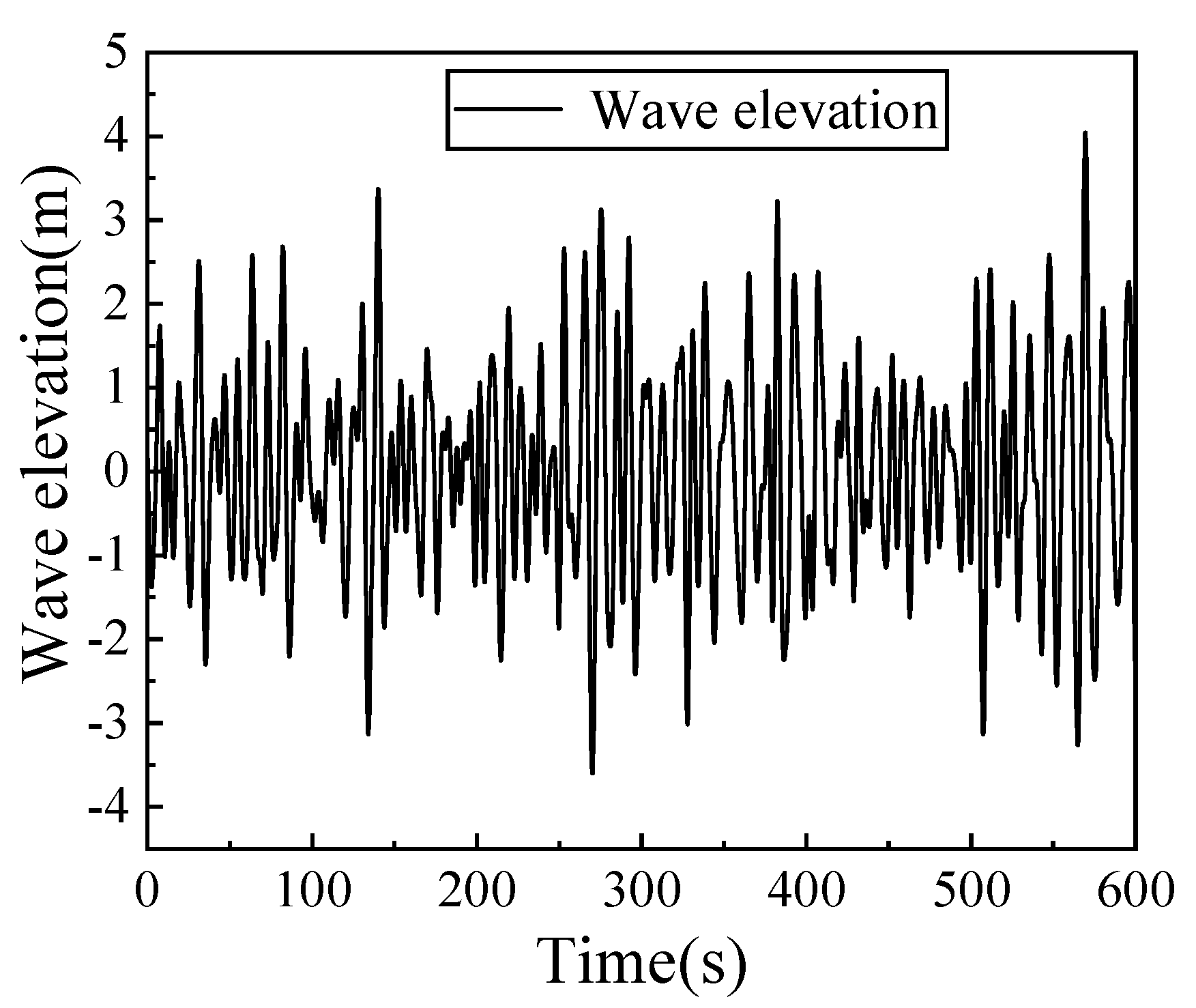
4. Simulation Experiment
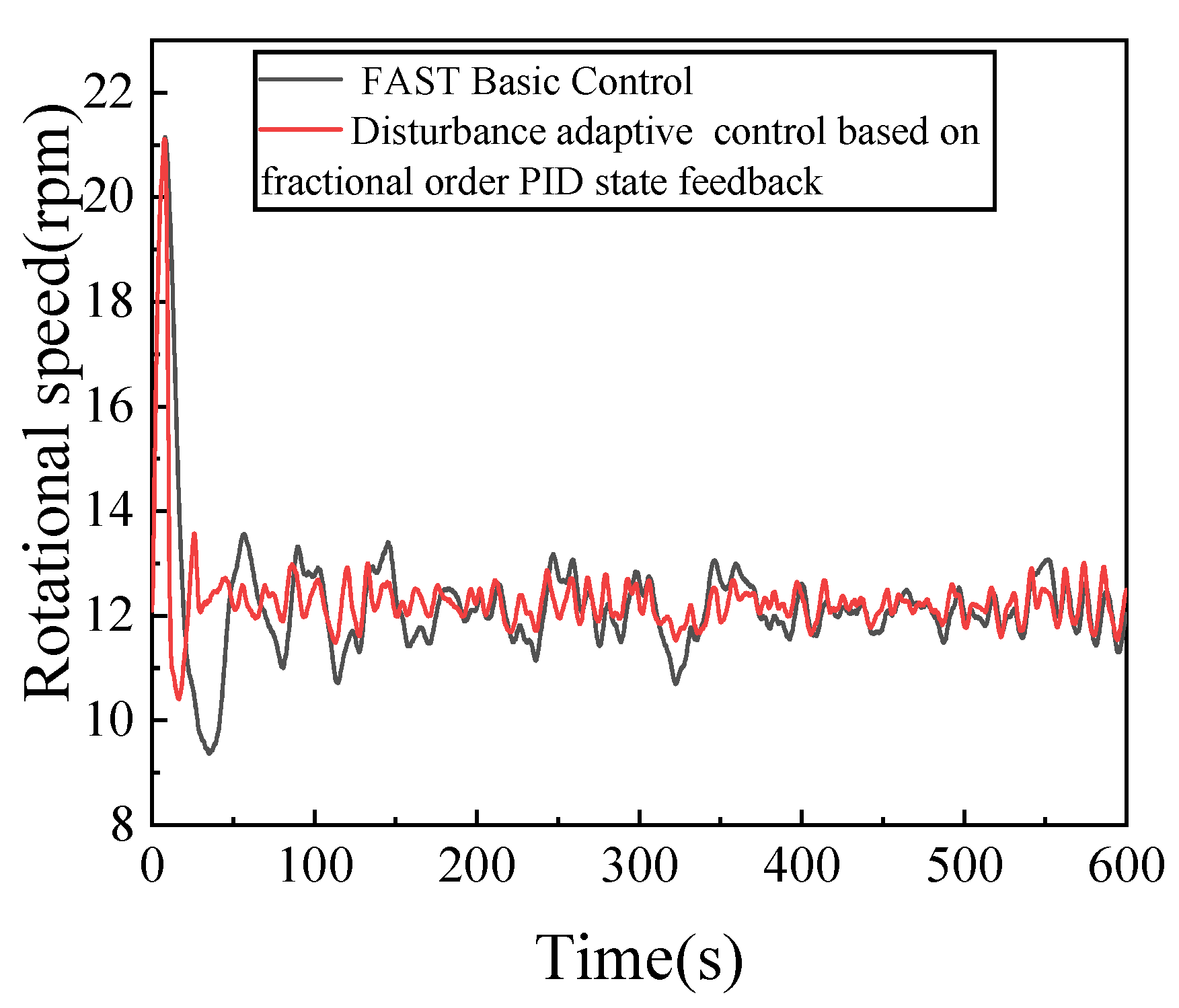
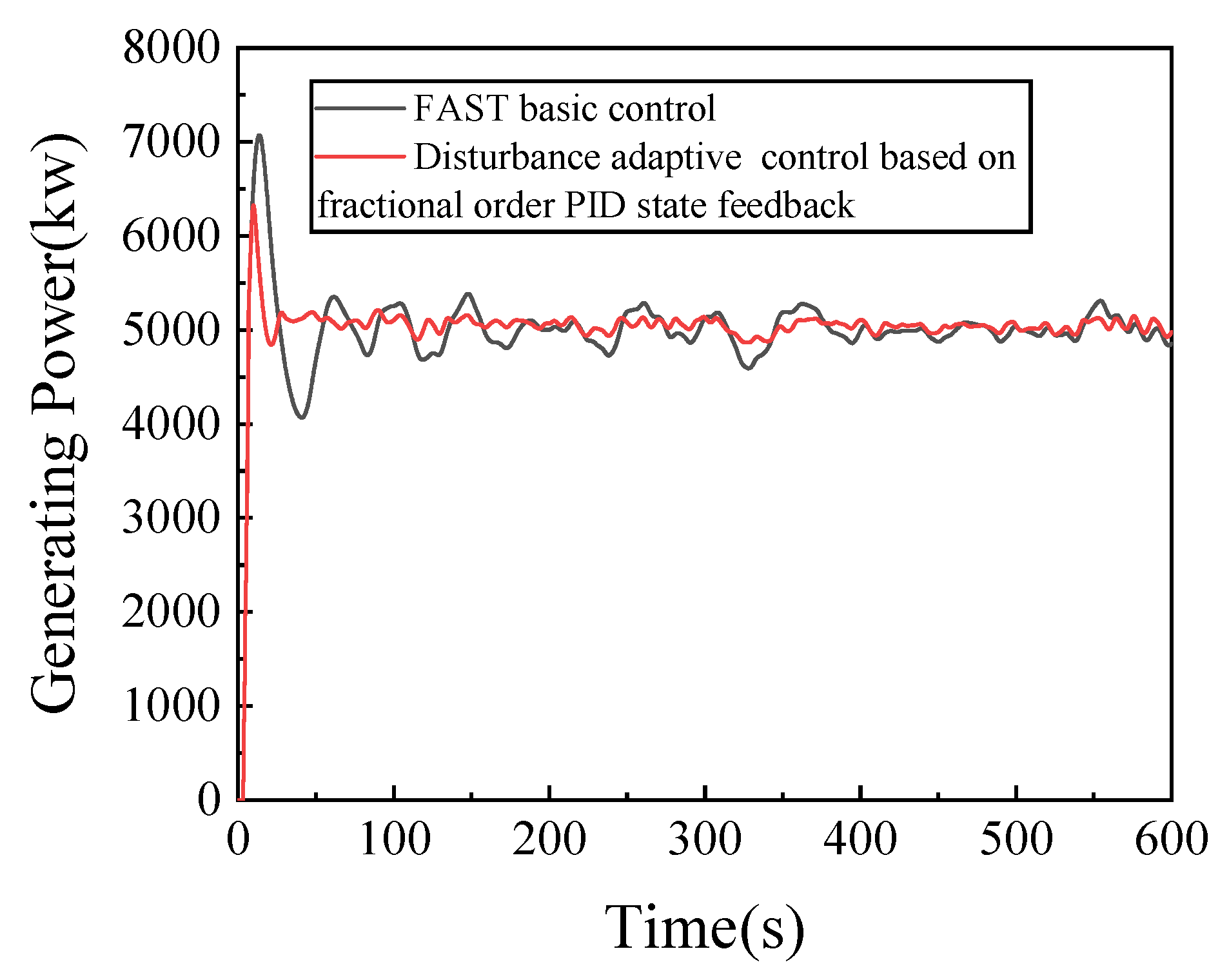
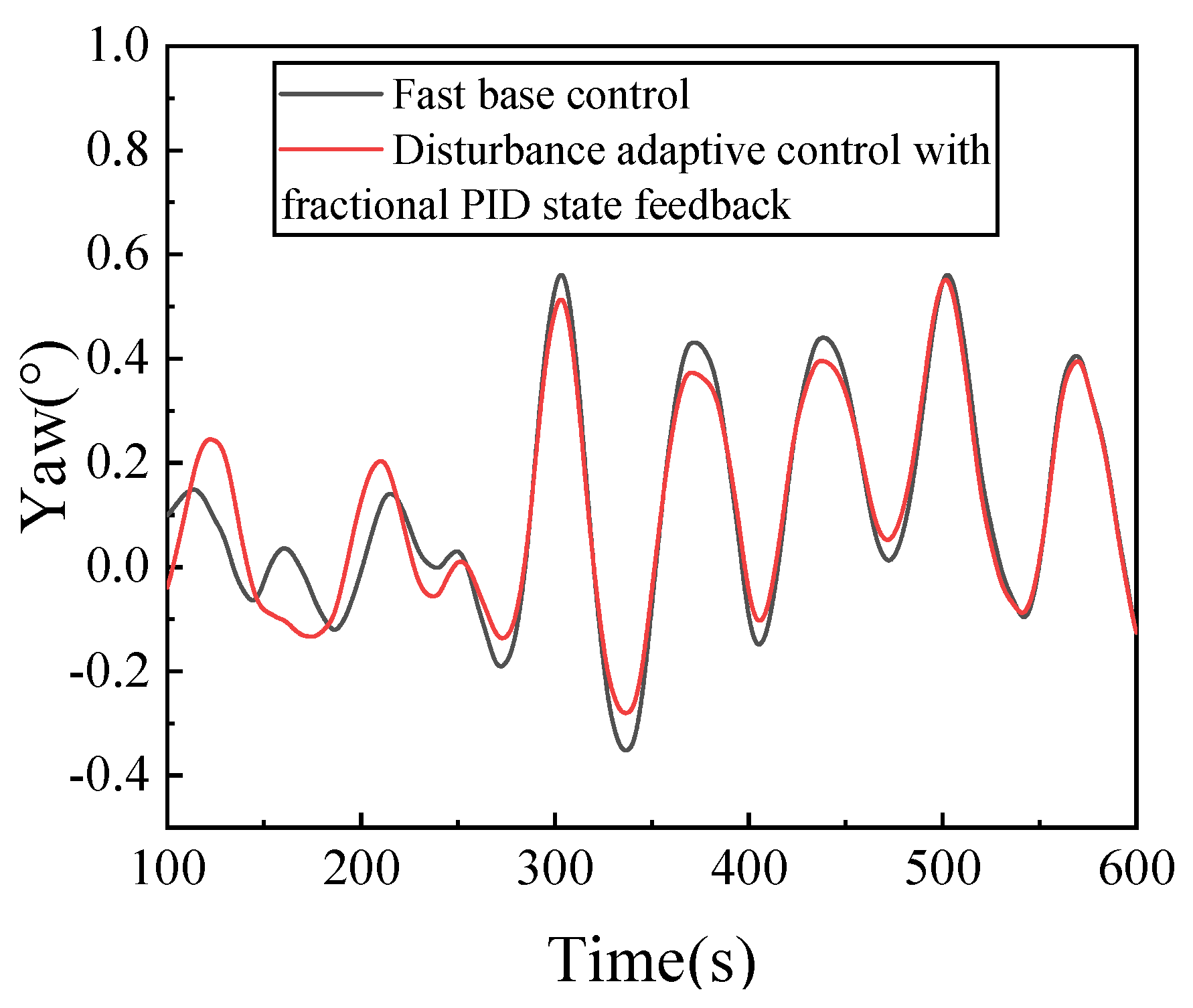
4.1. Study on Control Effect of Floating Wind Turbine
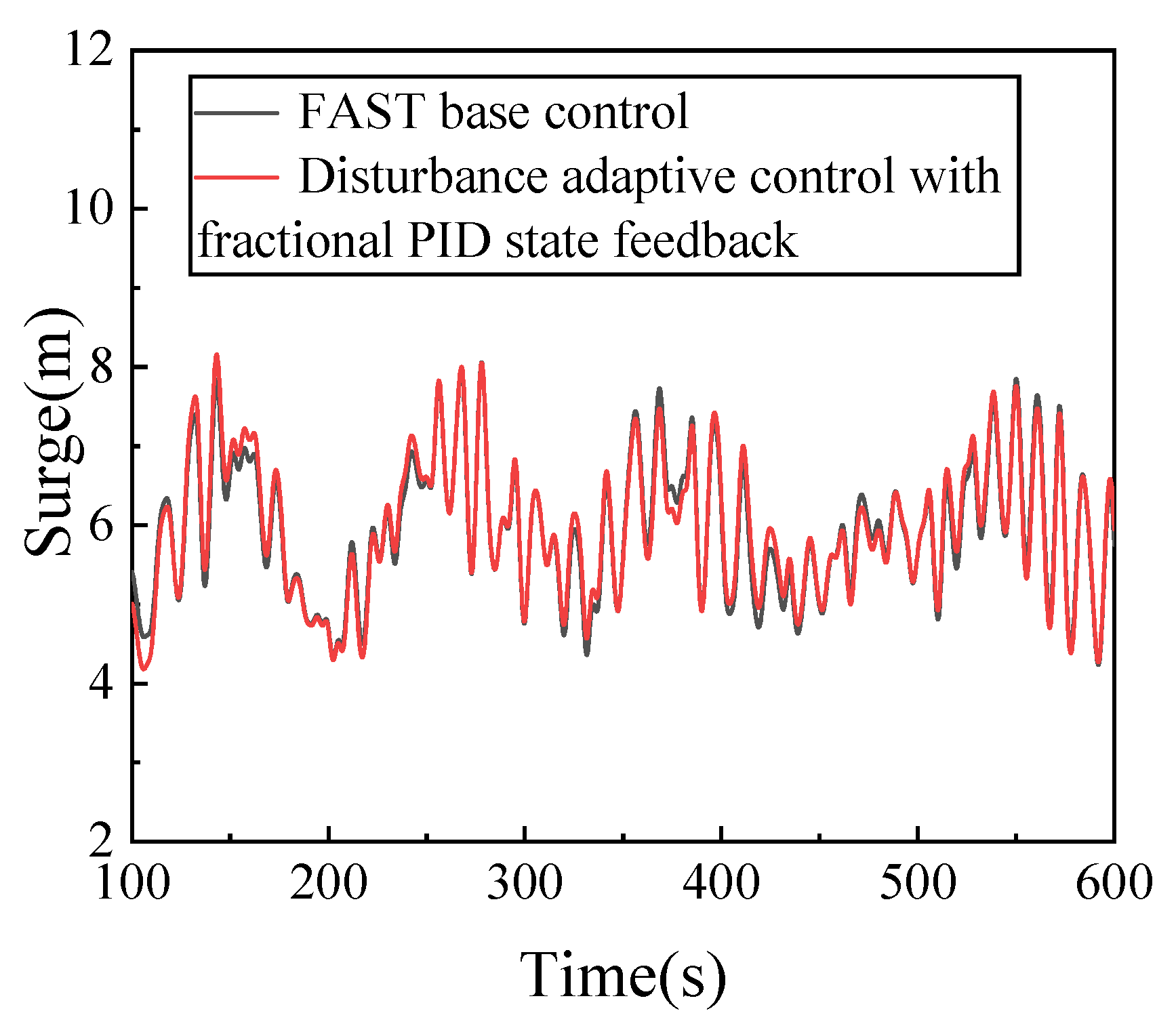
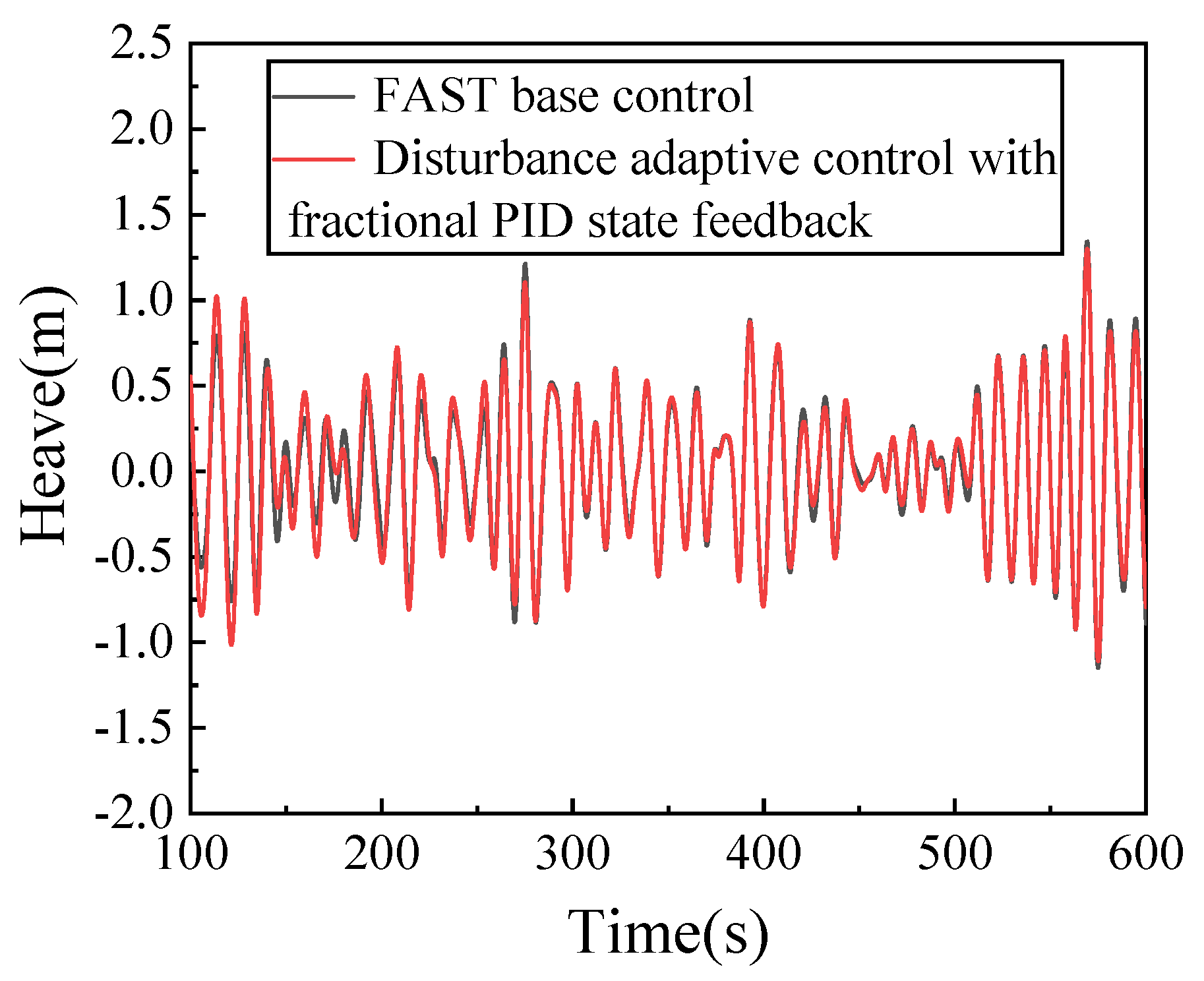
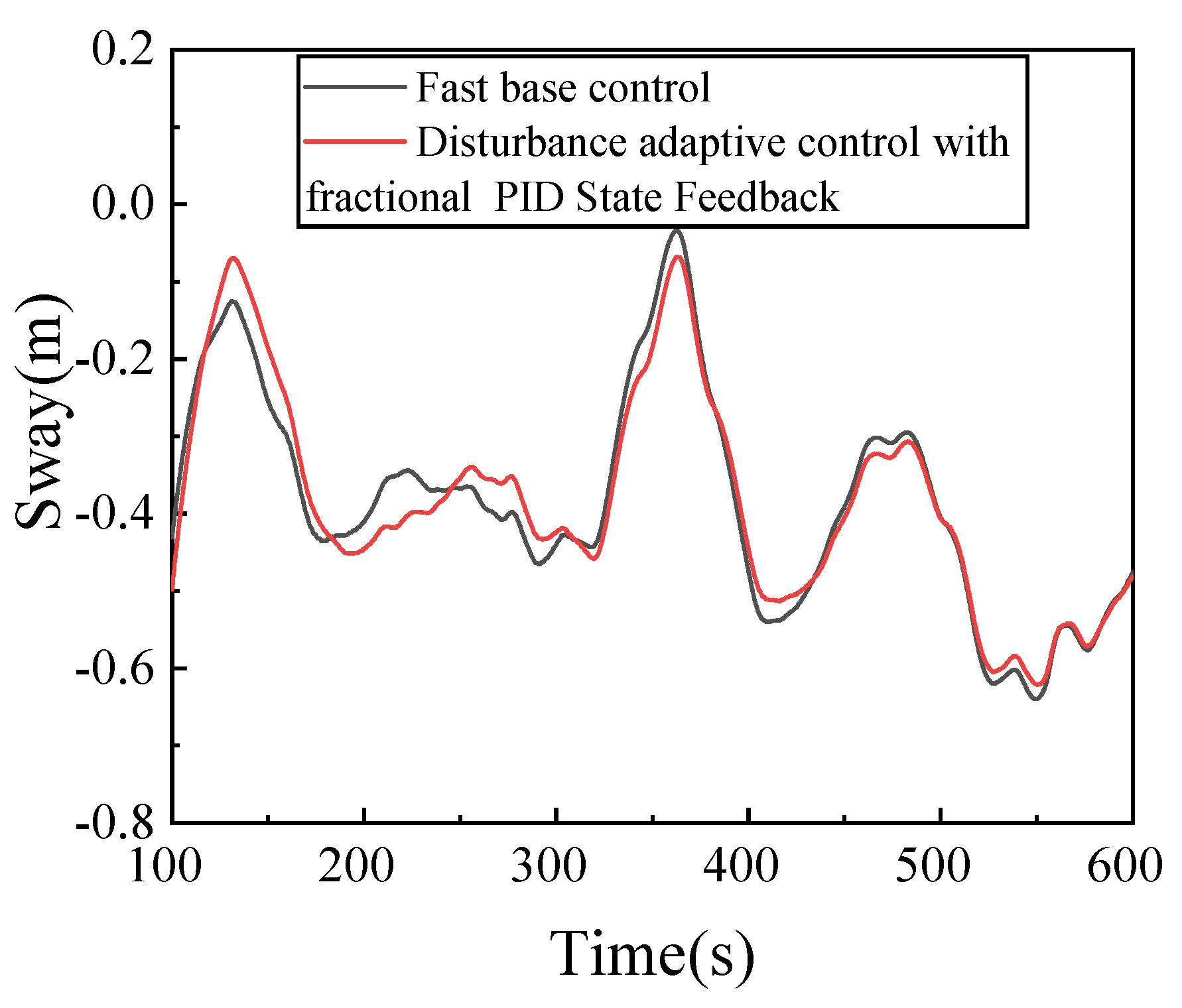
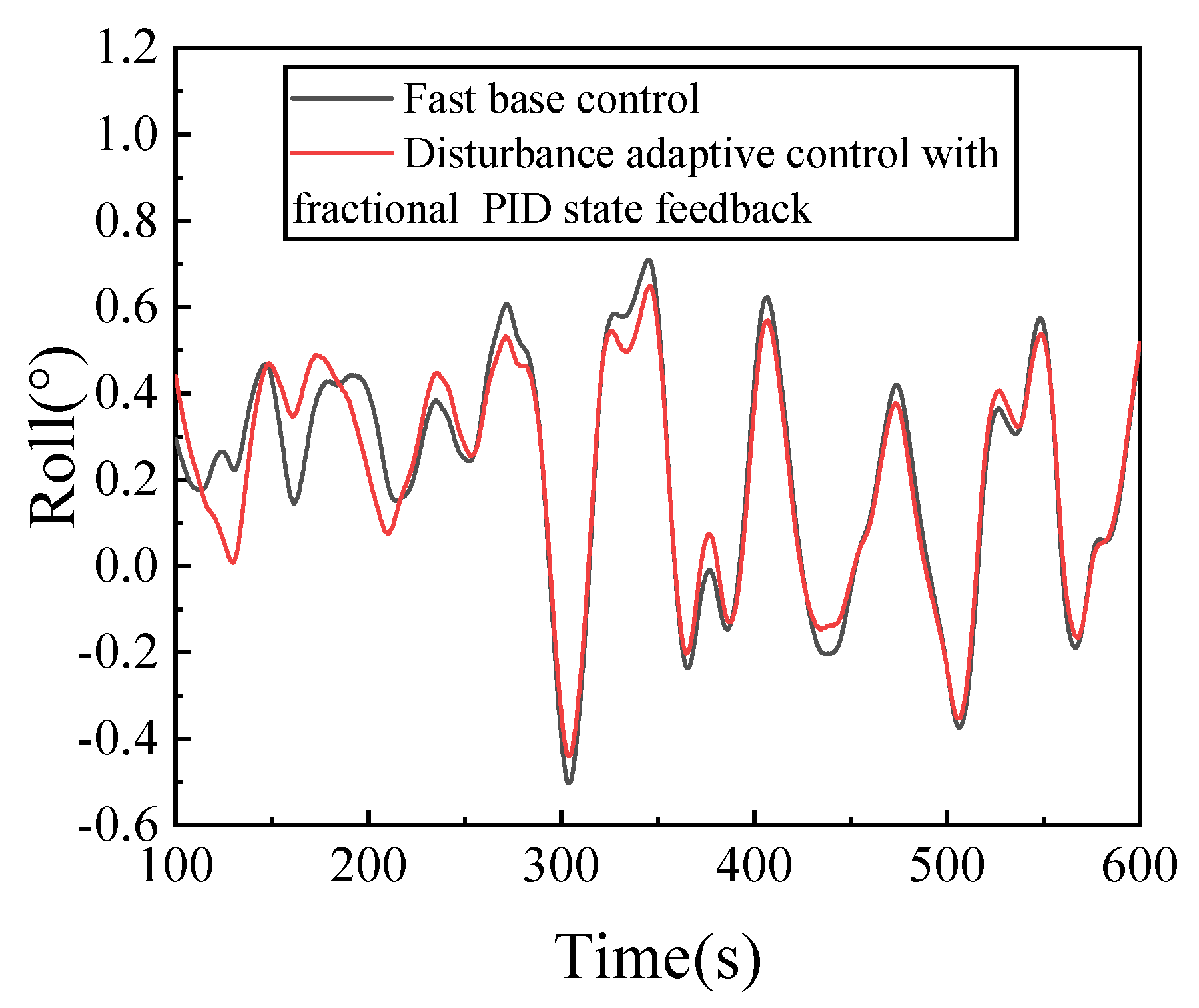
4.2. Stability Analysis of Floating Wind Turbine
5. Conclusions
- (1)
- Compared with the FAST base control, the speed fluctuation of the wind wheel of the floating wind turbine on the sea is lesser; it can be quickly adjusted to changes in wind speed.
- (2)
- Compared with the FAST base control, the power fluctuation of floating wind turbine is smaller, and the overshoot is smaller and more stable.
- (3)
- Compared with the FAST base control, the surge and heave fluctuation increase, while the fluctuation of the other four degrees of freedom decreases. The control algorithm also plays a certain role in maintaining the stability of the floating wind turbine platform.
Author Contributions
Funding
Conflicts of Interest
References
- Mittal, A.; Sreenivas, K.; Taylor, L.K.; Hereth, L.; Hilbert, C.B. Blade-resolved simulations of a model wind turbine: Effect of temporal convergence. Wind Energy 2016, 19, 1761–1783. [Google Scholar] [CrossRef]
- Porté-Agel, F.; Bastankhah, M.; Shamsoddin, S. Wind-Turbine and Wind-Farm Flows: A Review. Bound.-Layer Meteorol. 2020, 174, 1–59. [Google Scholar] [CrossRef] [PubMed]
- Carraro, M.; De Vanna, F.; Zweiri, F.; Benini, E.; Heidari, A.; Hadavinia, H. CFD modeling of wind turbine blades with eroded leading edge. Fluids 2022, 7, 302. [Google Scholar] [CrossRef]
- Niu, Y.-G.; Li, X.-M.; Lin, Z.-W.; Li, M.-Y. Multiple models decentralized coordinated control of doubly fed induction generator. Int. J. Electr. Power Energy Syst. 2015, 64, 921–930. [Google Scholar] [CrossRef]
- Ana, S.; Itsaso, M.M.; Tapia, G.; Vechiu, I. Second-order sliding-mode controller design and tuning for grid synchronization and power control of a wind turbine-driven DFIG. In Proceedings of the IET Conference on Renewable Power Generation (RPG 2011), Edinburgh, UK, 6–8 September 2011; IET: London, UK, 2012. [Google Scholar]
- Evangelista, C.; Puleston, P.; Valenciaga, F.; Fridman, L.M. Lyapunov-Designed Super-Twisting Sliding Mode Control for Wind Energy Conversion Optimization. IEEE Trans. Ind. Electron. 2013, 60, 538–545. [Google Scholar]
- Palejiya, D.; Shaltout, M.; Yan, Z.; Chen, D. Stability of wind turbine switching control. Int. J. Control 2015, 88, 193–203. [Google Scholar] [CrossRef]
- Colombo, L.; Corradini, M.L.; Ippoliti, G.; Orlando, G. Pitch angle control of a wind turbine operating above the rated wind speed: A sliding mode control approach. ISA Trans. 2020, 96, 95–102. [Google Scholar] [CrossRef] [PubMed]
- Yin, X.; Zhang, W.; Jiang, Z.; Pan, L. Adaptive robust integral sliding mode pitch angle control of an electro-hydraulic servo pitch system for wind turbine. Mech. Syst. Signal Process. 2019, 133, 105704. [Google Scholar] [CrossRef]
- Aghaeinezhad, S.M.; Taghizadeh, M.; Mazare, M.; Kazemi, M.G. Individual Pitch Angle Control of a Variable Speed Wind Turbine Using Adaptive Fractional Order Non-Singular Fast Terminal Sliding Mode Control. Int. J. Precis. Eng. Manuf. 2021, 22, 511–522. [Google Scholar] [CrossRef]
- Civelek, Z. Optimization of Fuzzy Logic (Takagi-Sugeno) Blade Pitch Angle Controller in Wind Turbines by Genetic Algorithm. Eng. Sci. Technol. Int. J. 2020, 23, 1–9. [Google Scholar] [CrossRef]
- Ma, R.; Hu, S.J.; Fu, X.B.; Xu, H.H.; Li, N.H. Torque control and pitch control strategy in VSCF wind turbine above rated wind speed. In Advanced Materials Research II. Part 2; Trans Tech Publications: Stafa-Zurich, Switzerland, 2012; pp. 1715–1720. [Google Scholar]
- Aissaoui, A.G.; Tahour, A.; Essounbouli, N.; Nollet, F.; Abid, M.; Chergui, M.I. A Fuzzy-PI control to extract an optimal power from wind turbine. Energy Convers. Manag. 2013, 65, 688–696. [Google Scholar] [CrossRef]
- De Corcuera, A.D.; Pujana-Arrese, A.; Ezquerra, J.M.; Segurola, E.; Landaluze, J. H∞ Based Control for Load Mitigation in Wind Turbines. Energies 2012, 5, 938–967. [Google Scholar] [CrossRef]
- Namik, H.; Stol, K. Performance analysis of individual blade pitch control of offshore wind turbines on two floating platforms. Mechatronics 2011, 21, 691–703. [Google Scholar] [CrossRef]
- Namik, H.; Stol, K. Individual Blade Pitch Control of a Spar-Buoy Floating Wind Turbine. IEEE Trans. Control Syst. Technol. 2014, 22, 214–223. [Google Scholar] [CrossRef]
- Lasheen, A.; Elshafei, A.L. Wind-turbine collective-pitch control via a fuzzy predictive algorithm. Renew. Energy 2016, 87, 298–306. [Google Scholar] [CrossRef]
- Jafarnejadsani, H.; Pieper, J.; Ehlers, J. Adaptive control of a variable-speed variable-pitch wind turbine using radial-basis function neural network. IEEE Trans. Control Syst. Technol. 2013, 21, 2264–2272. [Google Scholar] [CrossRef]
- Lackner, M.A. Controlling Platform Motions and Reducing Blade Loads for Floating Wind Turbines. Wind. Eng. 2009, 33, 541–553. [Google Scholar] [CrossRef]
- Jiao, X.; Yang, Q.; Fan, B.; Chen, Q.; Sun, Y.; Wang, L. EWSE and Uncertainty and Disturbance Estimator Based Pitch Angle Control for Wind Turbine Systems Operating in Above Rated Wind Speed Region. J. Dyn. Syst. Meas. Control 2019, 142, 031006. [Google Scholar] [CrossRef]
- Shivaji, K.; Ritula, T. Comparative Analysis of Fractional-Order PID Controller for Pitch Angle Control of Wind Turbine System. In Computing in Engineering and Technology; Springer: Singapore, 2019; pp. 647–657. [Google Scholar]

| Parameter Name | Numerical Value |
|---|---|
| Number of blades/(m·s−1) | 3 |
| Cut-in velocity/(m·s−1) | 3 |
| Rated wind speed/(m·s) | 11.4 |
| Cut-out wind speed/(m·s−1) | 25 |
| Rated power/MW | 5 |
| Height of hub/m | 126 |
| Diameter of wind turbine/m | 90 |
| Tower height/m | 77.6 |
| Running water depth/m | 200 |
| Tower and top mass/kg | 599,718 |
| Parameter Name | Numerical Value |
|---|---|
| Diameter of main floating column/m | 6.5 |
| Diameter of side floating column/m | 12 |
| Diameter of base floating column/m | 24 |
| Platform quality/kg | 13,473,000 |
| Platform pitch moment of inertia/(kg·m2) | 6.837 × 109 |
| Platform pitch moment of inertia/(kg·m2) | 6.837 × 109 |
| Platform pitch moment of inertia/(kg·m2) | 1.226 × 1010 |
| Parameter | Fast Base Control | Adaptive Disturbance Control Based on Fractional Order PID State Feedback | |
|---|---|---|---|
| Rotational speed/(r·min−1) | Maximum | 13.41 | 13.01 |
| Minimum | 10.69 | 11.55 | |
| Standard deviation | 0.504 | 0.286 | |
| Generating Power/(kw) | Maximum | 5384 | 5168 |
| Minimum | 4593 | 4868 | |
| Standard deviation | 152.38 | 60.42 | |
| Parameter | Fast Base Control | Adaptive Disturbance Control Based on Fractional Order PID State Feedback | |
|---|---|---|---|
| Surge/(m) | Maximum | 8.053 | 8.155 |
| Minimum | 4.234 | 4.181 | |
| Standard deviation | 0.835 | 0.859 | |
| Pitch/(°) | Maximum | 4.855 | 5.107 |
| Minimum | 1.591 | 1.802 | |
| Standard deviation | 0.603 | 0.552 | |
| Parameter | Fast Base Control | Adaptive Disturbance Control Based on Fractional Order PID State Feedback | |
|---|---|---|---|
| Sway/(m) | Maximum | −0.034 | −0.058 |
| Minimum | −0.64 | −0.621 | |
| Standard deviation | 0.138 | 0.137 | |
| Roll/(°) | Maximum | 0.709 | 0.664 |
| Minimum | −0.502 | −0.450 | |
| Standard deviation | 0.267 | 0.253 | |
| Parameter | Fast Base Control | Adaptive Disturbance Control Based on Fractional Order PID State Feedback | |
|---|---|---|---|
| Heave/(m) | Maximum | 1.343 | 1.3 |
| Minimum | −1.149 | −1.109 | |
| Standard deviation | 0.410 | 0.426 | |
| Yaw/(°) | Maximum | 0.561 | 0.547 |
| Minimum | −0.352 | −0.293 | |
| Standard deviation | 0.211 | 0.200 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, J.; Cheng, Z.; Liu, D. Design of Variable Pitch Control Method for Floating Wind Turbine. Energies 2023, 16, 821. https://doi.org/10.3390/en16020821
Yuan J, Cheng Z, Liu D. Design of Variable Pitch Control Method for Floating Wind Turbine. Energies. 2023; 16(2):821. https://doi.org/10.3390/en16020821
Chicago/Turabian StyleYuan, Jiawang, Zhijiang Cheng, and Dengquan Liu. 2023. "Design of Variable Pitch Control Method for Floating Wind Turbine" Energies 16, no. 2: 821. https://doi.org/10.3390/en16020821
APA StyleYuan, J., Cheng, Z., & Liu, D. (2023). Design of Variable Pitch Control Method for Floating Wind Turbine. Energies, 16(2), 821. https://doi.org/10.3390/en16020821






