Energy Potentials of Agricultural Biomass and the Possibility of Modelling Using RFR and SVM Models
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Collection
2.2. Nonlinear Modelling
2.3. Models Verification
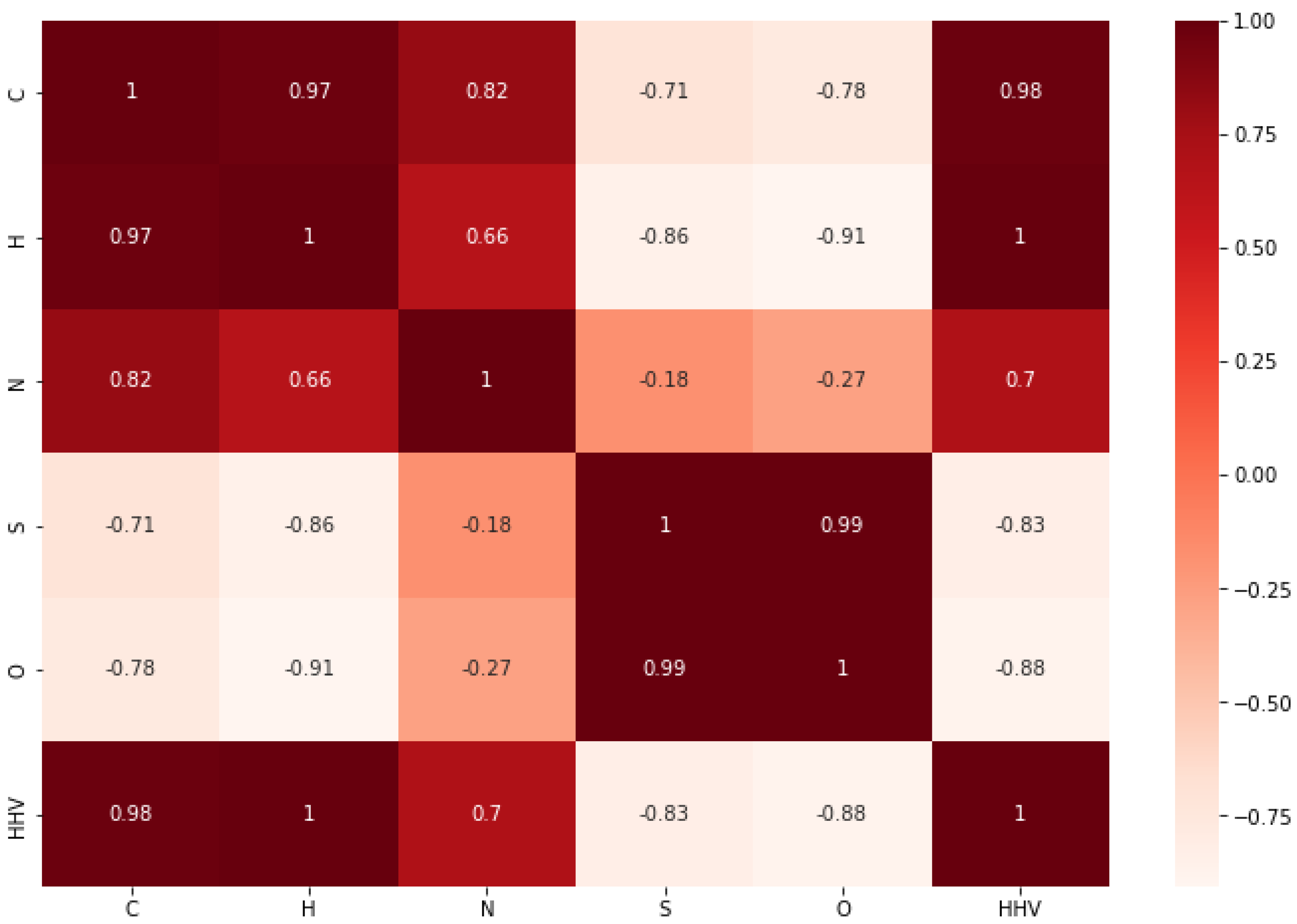
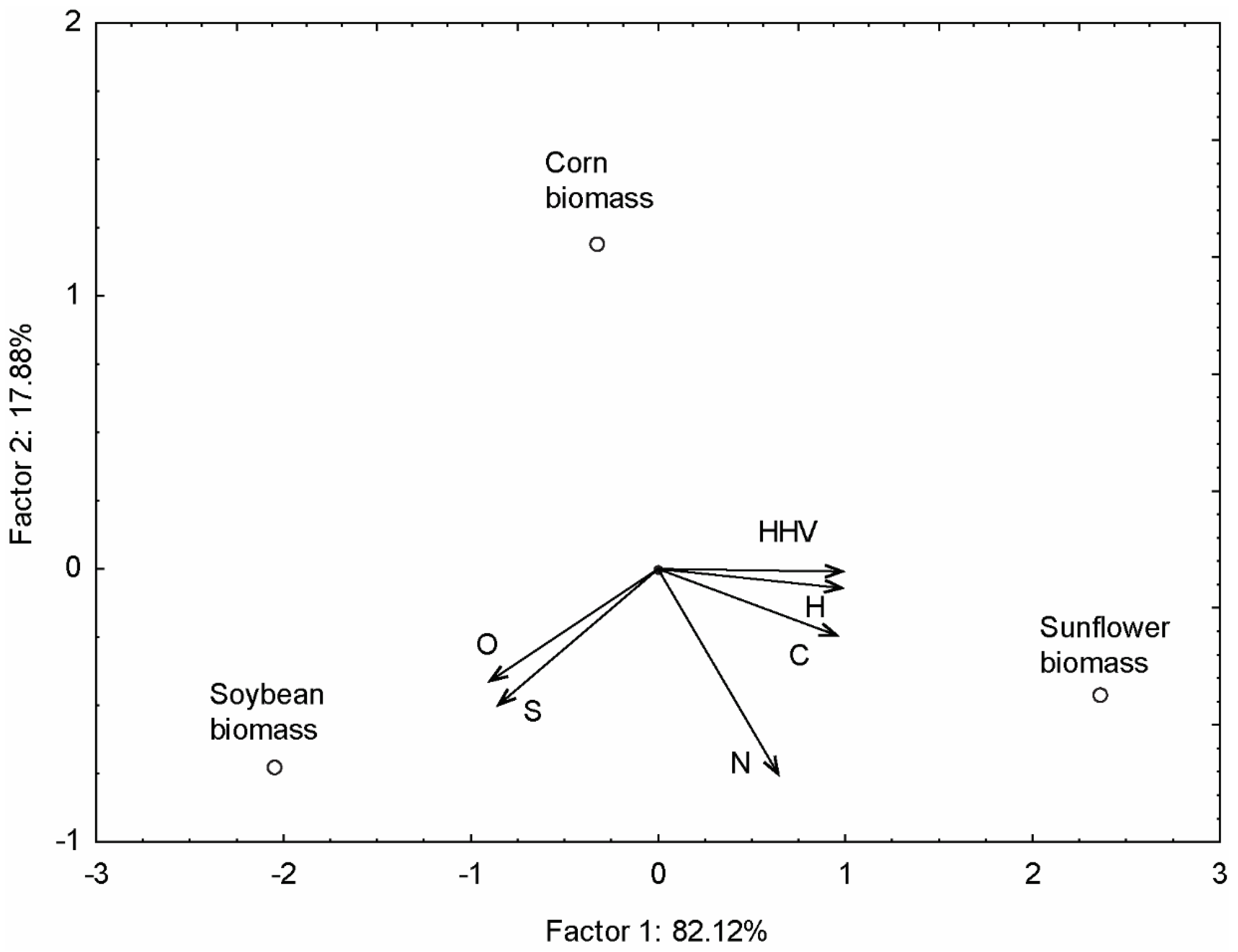
3. Results
4. Discussion
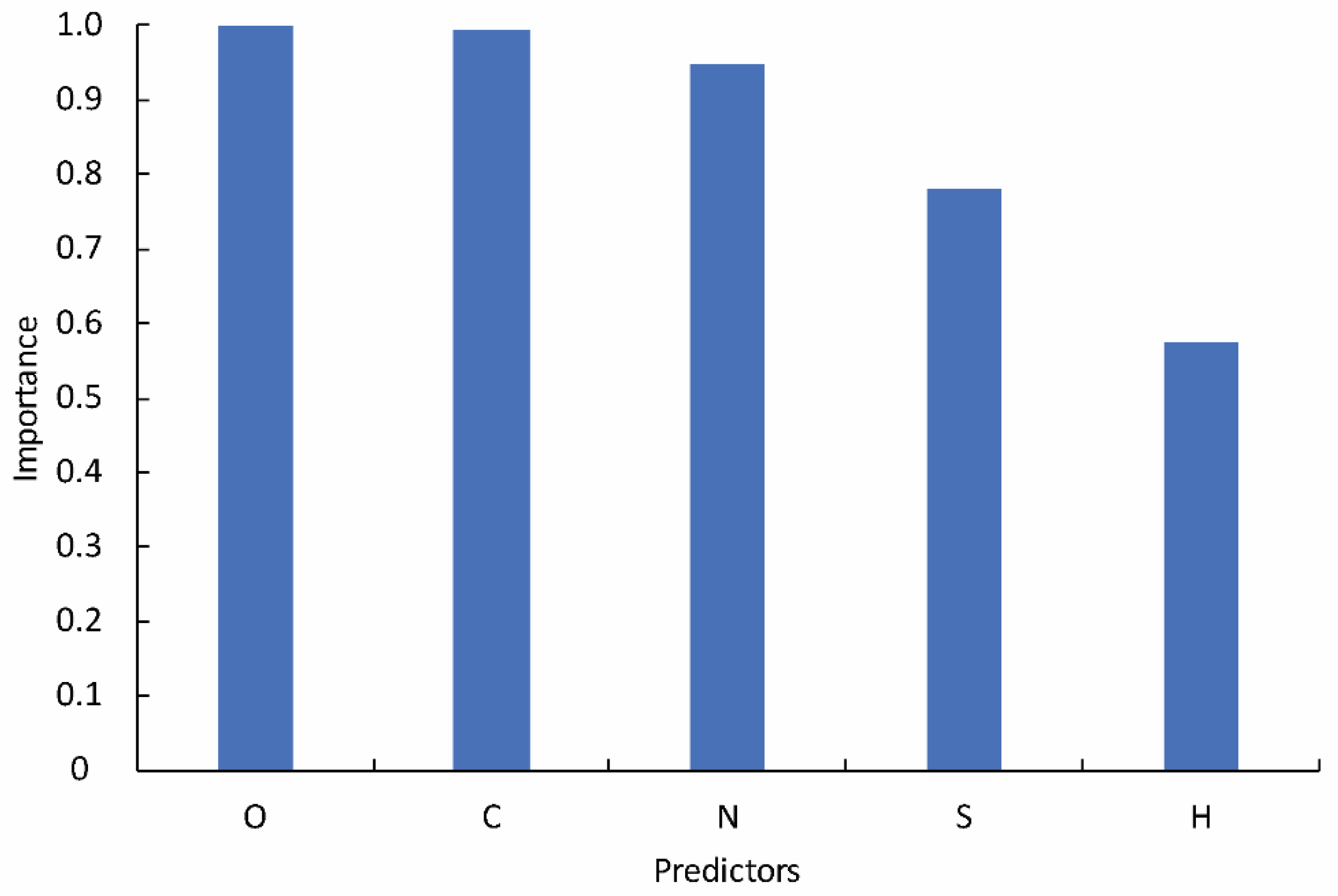
4.1. Support Vector Machine (SVM)
4.2. Random Forest Regression (RFR)
4.3. Goodness of Fit
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Antar, M.; Lyu, D.; Nazari, M.; Shah, A.; Zhou, X.; Smith, D.L. Biomass for a sustainable bioeconomy: An overview of world biomass production and utilization. Renew. Sustain. Energy Rev. 2021, 139, 110691. [Google Scholar] [CrossRef]
- Biswas, B.; Pandey, N.; Bisht, Y.; Singh, R.; Kumar, J.; Bhaskar, T. Pyrolysis of agricultural biomass residues: Comparative study of corn cob, wheat straw, rice straw and rice husk. Bioresour. Technol. 2017, 237, 57–63. [Google Scholar] [CrossRef] [PubMed]
- Cai, J.; Wu, W.; Liu, R. An overview of distributed activation energy model and its application in the pyrolysis of lignocellulosic biomass. Renew. Sustain. Energy Rev. 2014, 36, 236–246. [Google Scholar] [CrossRef]
- Erol, M.; Haykiri-Acma, H.; Küçükbayrak, S. Calorific value estimation of biomass from their proximate analyses data. Renew. Energy 2010, 35, 170–173. [Google Scholar] [CrossRef]
- Khunphakdee, P.; Korkerd, K.; Soanuch, C.; Chalermsinsuwan, B. Data-driven correlations of higher heating value for biomass, waste and their combination based on their elemental compositions. Energy Rep. 2014, 8, 36–42. [Google Scholar] [CrossRef]
- Asonja, A.; Desnica, E.; Radovanović, L.Z. Energy efficiency analysis of corn cob used as a fuel. Energy Sources Part B Econ. Plan. Policy 2017, 12, 1–7. [Google Scholar] [CrossRef]
- Krisnawati, A.; Adie, M.M. Variability of Biomass and Harvest Index from Several Soybean Genotypes as Renewable Energy Source. Energy Procedia 2015, 65, 14–21. [Google Scholar] [CrossRef]
- Muchlish Adie, M.; Krisnawati, A. Soybean Opportunity as Source of New Energy in Indonesia. Int. J. Renew. Energy Dev. 2014, 3, 37–43. [Google Scholar] [CrossRef]
- Antonopoulou, G.; Dimitrellos, G.; Beobide, A.S.; Vayenas, D.; Lyberatos, G. Chemical Pretreatment of Sunflower Straw Biomass: The Effect on Chemical Composition and Structural Changes. Waste Biomass Valorization 2015, 6, 733–746. [Google Scholar] [CrossRef]
- Qian, H.; Zhu, W.; Fan, S.; Liu, C.; Lu, X.; Wang, Z.; Huang, D.; Chen, W. Prediction models for chemical exergy of biomass on dry basis from ultimate analysis using available electron concepts. Energy 2017, 131, 251–258. [Google Scholar] [CrossRef]
- Noushabadi, A.S.; Dashti, A.; Ahmadijokani, F.; Hu, J.; Mohammadi, A.H. Estimation of higher heating values (HHVs) of biomass fuels based on ultimate analysis using machine learning techniques and improved equation. Renew. Energy 2021, 179, 550–562. [Google Scholar] [CrossRef]
- Dai, Z.; Chen, Z.; Selmi, A.; Jermsittiparsert, K.; Denić, N.M.; Nešić, Z. Machine learning prediction of higher heating value of biomass. Biomass-Convers. Biorefinery 2021, 11, 1–9. [Google Scholar] [CrossRef]
- Roman, K.; Barwicki, J.; Rzodkiewicz, W.; Dawidowski, M. Evaluation of Mechanical and Energetic Properties of the Forest Residues Shredded Chips during Briquetting Process. Energies 2021, 14, 3270. [Google Scholar] [CrossRef]
- Ibikunle, R.A.; Lukman, A.F.; Titiladunayo, I.F.; Akeju, E.A.; Dahunsi, S.O. Modeling and robust prediction of high heating values of municipal solid waste based on ultimate analysis. Energy Sources Part A Recover. Util. Environ. Eff. 2020, 1–18. [Google Scholar] [CrossRef]
- Nieto, P.G.; Garcia-Gonzalo, E.; Lasheras, F.S.; Paredes–Sánchez, J.; Fernández, P.R. Forecast of the higher heating value in biomass torrefaction by means of machine learning techniques. J. Comput. Appl. Math. 2019, 357, 284–301. [Google Scholar] [CrossRef]
- Bychkov, A.L.; Denkin, A.I.; Tikhova, V.D.; Lomovsky, O.I. Prediction of higher heating values of plant biomass from ultimate analysis data. J. Therm. Anal. Calorim. 2017, 130, 1399–1405. [Google Scholar] [CrossRef]
- Grubor, M.; Krička, T.; Bilandžija, N.; Jurišić, V.; Voća, N.; Antonović, A.; Matin, A. Maize straw as an energy source for solid fuel production. In 53. Hrvatski i 13. Međunarodni Simpozij Agronoma; Rozman, V., Antunović, Z., Eds.; Sveučilišta Josipa Jurja Strossmayera u Osijeku: Osijek, Croatia, 2018. [Google Scholar]
- Matin, A.; Krička, T.; Bilandžija, N.; Jurišić, V.; Grubor, M.; Antonović, A.; Lakić, J.; Voća, N. Varieties influence on soybean straw biomass combustible and noncombustible properties. In 53. Hrvatski i 13. Međunarodni Simpozij Agronoma; Rozman, V., Antunović, Z., Eds.; Sveučilišta Josipa Jurja Strossmayera u Osijeku: Osijek, Croatia, 2018. [Google Scholar]
- Demirbaş, A. Fuel Characteristics of Olive Husk and Walnut, Hazelnut, Sunflower, and Almond Shells. Energy Sources 2002, 24, 215–221. [Google Scholar] [CrossRef]
- Krička, T.; Matin, A.; Voća, N.; Pospišil, A.; Grubor, M.; Šaronja, I.; Jurišić, V. Changes in nutritional and energy properties of soybean seed and hull after roasting. Res. Agric. Eng. 2018, 64, 96–103. [Google Scholar] [CrossRef]
- Tumuluru, J.S.; Kremer, T.; Wright, C.T.; Boardman, R.D. Proximate and Ultimate Compositional Changes in Corn Stover during Torrrefaction using Thermogravimetric Analyzer and Microwaves. In Proceedings of the 2012 ASABE Annual International Meeting, Dallas, TX, USA, 29 July–1 August 2012; pp. 1348–1365. [Google Scholar] [CrossRef]
- Tahir, M.H.; Irfan, R.M.; Hussain, M.B.; Alhumade, H.; Al-Turki, Y.; Cheng, X.; Karim, A.; Ibrahim, M.; Rathore, H.A. Catalytic Fast Pyrolysis of Soybean Straw Biomass for Glycolaldehyde-Rich Bio-oil Production and Subsequent Extraction. ACS Omega 2021, 6, 33694–33700. [Google Scholar] [CrossRef]
- Ahmad, S.; Zhu, X.; Wei, X.; Zhang, S. Influence of process parameters on hydrothermal modification of soybean residue: Insight into the nutrient, solid biofuel, and thermal properties of hydrochars. J. Environ. Manag. 2021, 283, 111981. [Google Scholar] [CrossRef]
- Riva, G.; Foppa Pedretti, E.; Toscano, G.; Duca, D.; Rossini, G.; Mengarelli, C. Torrefaction of residues and by-products from sunflower chain. J. Agric. Eng. 2013, 44, 601–606. [Google Scholar] [CrossRef]
- Liu, X.; Hua, W.; Wu, S. Characterization of Thermo-Chemical Degradation and Pyrolysis Properties for Three Kinds of Biomass Residues. BioResources 2016, 11, 8806–8819. [Google Scholar] [CrossRef]
- Tortosa Masiá, A.A.; Buhre, B.J.P.; Gupta, R.P.; Wall, T.F. Characterising ash of biomass and waste. Fuel Process. Technol. 2007, 88, 1071–1081. [Google Scholar] [CrossRef]
- Turzyński, T.; Kluska, J.; Ochnio, M.; Kardaś, D. Comparative Analysis of Pelletized and Unpelletized Sunflower Husks Combustion Process in a Batch-Type Reactor. Materials 2021, 14, 2484. [Google Scholar] [CrossRef] [PubMed]
- Özyuğuran, A.; Yaman, S.; Küçükbayrak, S. Prediction of calorific value of biomass based on elemental analysis. Int. Adv. Res. Eng. J. 2018, 2, 254–260. Available online: https://www.dergipark.gov.tr (accessed on 2 September 2022).
- Schonlau, M.; Zou, R.Y. The random forest algorithm for statistical learning. Stata J. 2020, 20, 3–29. [Google Scholar] [CrossRef]
- Ding, S.; Zhu, Z.; Zhang, X. An overview on semi-supervised support vector machine. Neural Comput. Appl. 2017, 28, 969–978. [Google Scholar] [CrossRef]
- Zendehboudi, A.; Baseer, M.; Saidur, R. Application of support vector machine models for forecasting solar and wind energy resources: A review. J. Clean. Prod. 2018, 199, 272–285. [Google Scholar] [CrossRef]
- Arsenović, M.; Pezo, L.; Stanković, S.; Radojević, Z. Factor space differentiation of brick clays according to mineral con-tent:Prediction of final brick product quality. Appl. Clay Sci. 2015, 115, 108–114. [Google Scholar] [CrossRef]
- Bilandžija, N.; Voća, N.; Leto, J.; Jurišić, V.; Grubor, M.; Matin, A.; Krička, T. Yield and Biomass Composition of Miscanthus x Giganteus in the Mountain Area of Croatia. In Transactions of FAMENA; University of Zagreb: Zagreb, Croatia, 2018; Volume 42, pp. 51–60. [Google Scholar]
- Rutledge, D.N. Comparison of Principal Components Analysis, Independent Components Analysis and Common Components Analysis. J. Anal. Test. 2018, 2, 235–248. [Google Scholar] [CrossRef]
- Beattie, J.R.; Esmonde-White, F.W.L. Exploration of Principal Component Analysis: Deriving Principal Component Analysis Visually Using Spectra. Appl. Spectrosc. 2021, 75, 361–375. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Huang, F.; Cheng, Y. Computational performance optimization of support vector machine based on support vectors. Neurocomputing 2016, 211, 66–71. [Google Scholar] [CrossRef]
- Han, S.; Kim, H. Optimal Feature Set Size in Random Forest Regression. Appl. Sci. 2021, 11, 3428. [Google Scholar] [CrossRef]
- Nguyen, Q.V.; Lin Huang, M.; Simoff, S. Enhancing Scatter-plots with Start-plots for Visualising Multi-dimensional Data. In Proceedings of the 2020 24th International Conference Information Visualisation (IV), Melbourne, Australia, 7–11 September 2020; pp. 80–85. [Google Scholar] [CrossRef]
- Xing, J.; Luo, K.; Wang, H.; Gao, Z.; Fan, J. A comprehensive study on estimating higher heating value of biomass from proximate and ultimate analysis with machine learning approaches. Energy 2019, 188, 116077. [Google Scholar] [CrossRef]
- Kramer, K.A.; Hall, L.O.; Goldgof, D.B.; Remsen, A.; Luo, T. Fast Support Vector Machines for Continuous Data. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2009, 39, 989–1001. [Google Scholar] [CrossRef] [PubMed]

| Sample | C (%) | H (%) | N (%) | S (%) | O (%) | HHV (MJ/kg) |
|---|---|---|---|---|---|---|
| Corn biomass | 48.45 ± 7.3 a | 5.29 ± 1.11 b | 0.70 ± 0.50 a | 0.08 ± 0.09 a | 38.11 ± 11.22 a | 19.42 ± 2.72 a |
| Soybean biomass | 47.37 ± 3.48 a | 4.53 ± 0.73 a | 1.38 ± 2.32 b | 0.22 ± 0.3 b | 46.5 ± 6.83 b | 17.93 ± 1.04 a |
| Sunflower biomass | 54.16 ± 8.9 b | 6.51 ± 0.9 c | 2.22 ± 1.64 c | 0.06 ± 0.13 a | 35.62 ± 9.25 a | 22.46 ± 4.41 b |
| Significance | ** | * | * | ** | * | * |
| Minimum | 47.37 | 4.53 | 0.70 | 0.06 | 35.62 | 17.93 |
| Maximum | 54.16 | 6.51 | 2.22 | 0.22 | 46.50 | 22.46 |
| Average | 49.99 | 5.44 | 1.44 | 0.12 | 40.08 | 19.94 |
| Vector No. | Weights | Support Vector | Decision Constant | ||||
|---|---|---|---|---|---|---|---|
| C | H | N | S | O | |||
| 1 | 9.00 | 0.22 | 0.63 | 0.07 | 0.07 | 0.73 | −0.09 |
| 2 | −7.34 | 0.20 | 0.68 | 0.07 | 0.12 | 0.70 | |
| 3 | −0.21 | 0.95 | 0.00 | 0.21 | 0.02 | 0.00 | |
| 4 | −1.01 | 0.35 | 0.49 | 0.00 | 0.32 | 0.96 | |
| 5 | 0.34 | 0.25 | 0.71 | 0.11 | 0.47 | 0.83 | |
| 6 | −9.00 | 0.28 | 0.67 | 0.17 | 0.09 | 0.72 | |
| 7 | 6.14 | 0.51 | 0.70 | 0.16 | 0.00 | 0.64 | |
| 8 | −1.95 | 0.77 | 0.96 | 0.57 | 0.00 | 0.36 | |
| 9 | 4.02 | 1.00 | 0.97 | 0.59 | 0.00 | 0.20 | |
| Residual Analysis | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Model | x2 | RMSE | MBE | MPE | SSE | AARD | R2 | Skewness | Kurtosis | SD | Variance |
| SVM model | 0.82 | 0.90 | −0.03 | 3.07 | 49.28 | 44.12 | 0.93 | −3.04 | 14.32 | 0.91 | 0.82 |
| RFR model | 5.99 | 2.43 | −0.01 | 8.32 | 359.53 | 103.30 | 0.79 | 0.94 | 2.08 | 2.45 | 5.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brandić, I.; Antonović, A.; Pezo, L.; Matin, B.; Krička, T.; Jurišić, V.; Špelić, K.; Kontek, M.; Kukuruzović, J.; Grubor, M.; et al. Energy Potentials of Agricultural Biomass and the Possibility of Modelling Using RFR and SVM Models. Energies 2023, 16, 690. https://doi.org/10.3390/en16020690
Brandić I, Antonović A, Pezo L, Matin B, Krička T, Jurišić V, Špelić K, Kontek M, Kukuruzović J, Grubor M, et al. Energy Potentials of Agricultural Biomass and the Possibility of Modelling Using RFR and SVM Models. Energies. 2023; 16(2):690. https://doi.org/10.3390/en16020690
Chicago/Turabian StyleBrandić, Ivan, Alan Antonović, Lato Pezo, Božidar Matin, Tajana Krička, Vanja Jurišić, Karlo Špelić, Mislav Kontek, Juraj Kukuruzović, Mateja Grubor, and et al. 2023. "Energy Potentials of Agricultural Biomass and the Possibility of Modelling Using RFR and SVM Models" Energies 16, no. 2: 690. https://doi.org/10.3390/en16020690
APA StyleBrandić, I., Antonović, A., Pezo, L., Matin, B., Krička, T., Jurišić, V., Špelić, K., Kontek, M., Kukuruzović, J., Grubor, M., & Matin, A. (2023). Energy Potentials of Agricultural Biomass and the Possibility of Modelling Using RFR and SVM Models. Energies, 16(2), 690. https://doi.org/10.3390/en16020690







