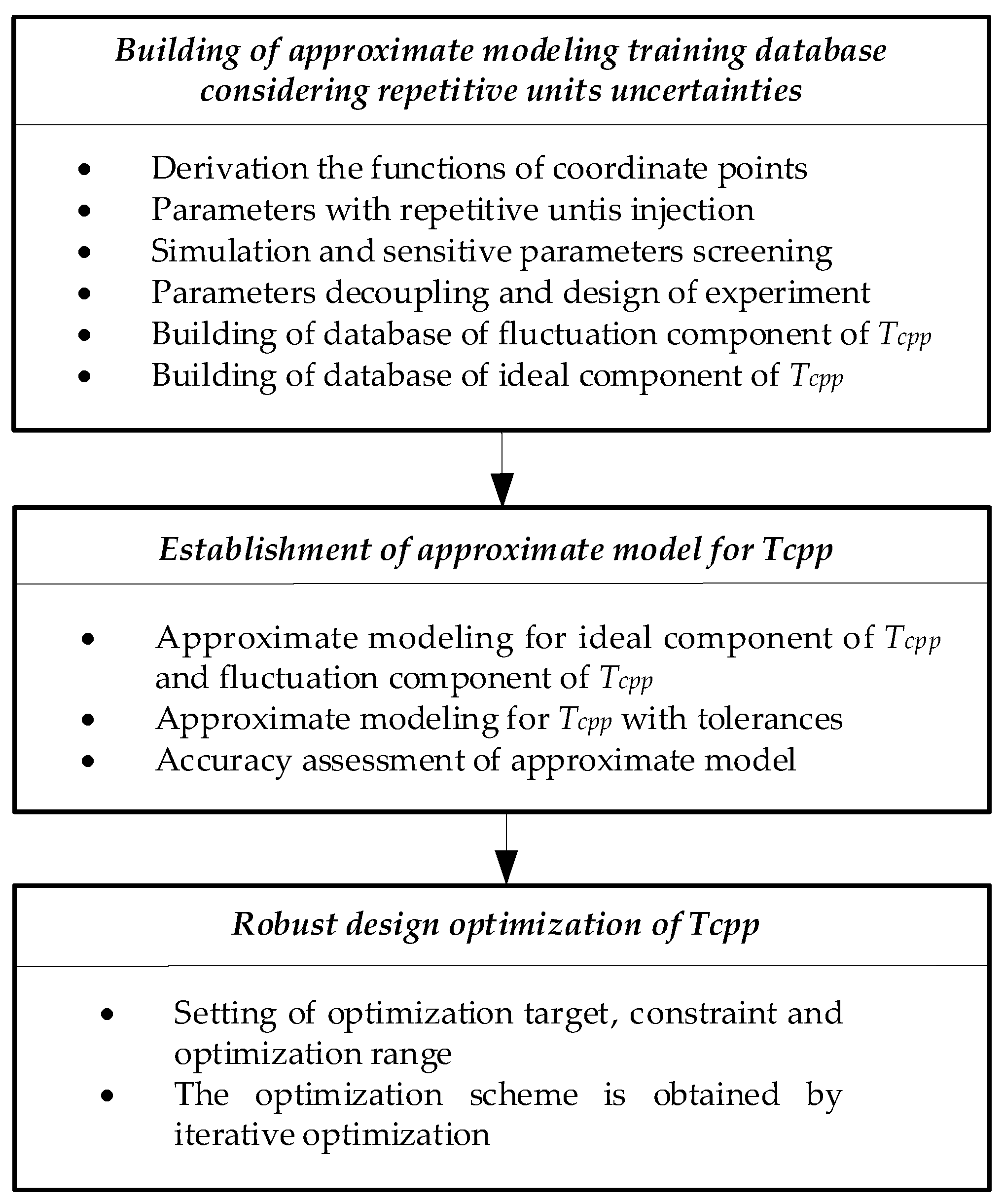
In the actual production process of the PMSM, there are inevitable manufacturing uncertainties because the structure of the PMSM has repetitive units, and the uncertainty of a single design parameter comes from multiple units. The traditional RDO needs to consider this issue, and the optimization scheme obtained is insignificant in actual production. In order to solve this problem, the uncertainties of repetitive units caused by manufacturing uncertainties are fully considered in the RDO process for the PMSM. In order to take into account the calculation accuracy and efficiency of the RDO, an approximate model considering the uncertainties of the actual manufacturing process was established to replace the FEA. Therefore, the actual machining parameters of the PMSM need to be accurately analyzed by FEA first, from which the training data with the actual production conditions were extracted for approximate modeling. In
Section 2.2, the parametric FEA of this paper is different from traditional FEA, which can independently assign repetitive unit values of the motor, and the parametric FEA model by the actual production processing was established. The parameter values of repetitive units and the output characteristic values from parametric FEA were extracted as the training database for approximate modeling. The parametric FEA involved a large number of design parameters. In order to reduce the dimension of the approximate model and improve the efficiency of approximate modeling, the sensitivity analysis method was used to screen out the critical parameters that significantly impacted the model’s output response as design parameters. A design of experiments (DoE) method used to establish the approximate model training database in this paper is proposed. The approximate modeling method considering repetitive unit uncertainties is proposed in
Section 2.3. It was embedded into the RDO as described in
Section 2.4.
2.2. The Building of an Approximate Modeling Training Database Considering Repetitive Unit Uncertainties
The traditional PMSM FEA uses Ansys software to build a symmetrical or quarter-simplified model. The repetitive unit parameters in the same structure are treated equally, which cannot reflect the influence of the manufacturing uncertainties on the output characteristics. In order to consider the manufacturing processing dispersion of repetitive units, the repetitive units of the PMSM model should be assigned independently, so the parametric FEA method was adopted in this study to obtain the FEA model, which is consistent with the actual manufacturing conditions. On this basis, sensitivity analysis was carried out, and the significant design parameters were screened out. Then, the training database of approximate modeling was constructed according to the selected design parameters.
- (a)
According to the relative position of each unit, the coordinate function containing the parameter value variable of repetitive units is established.
- (b)
According to the actual values of input parameters, the coordinate functions are calculated to obtain the model with the actual values, and the Tcpp is extracted by simulation.
- (c)
Single-factor sensitivity analysis selects the most significant factors affecting Tcpp. The formula for sensitivity analysis is shown as follows:
where
Si is the sensitivity of the
ith parameter
xi to the target
f(
x), and Δ
xi is incremental of
xi. The
ith parameter is successively set to plus-minus tolerance of its center value
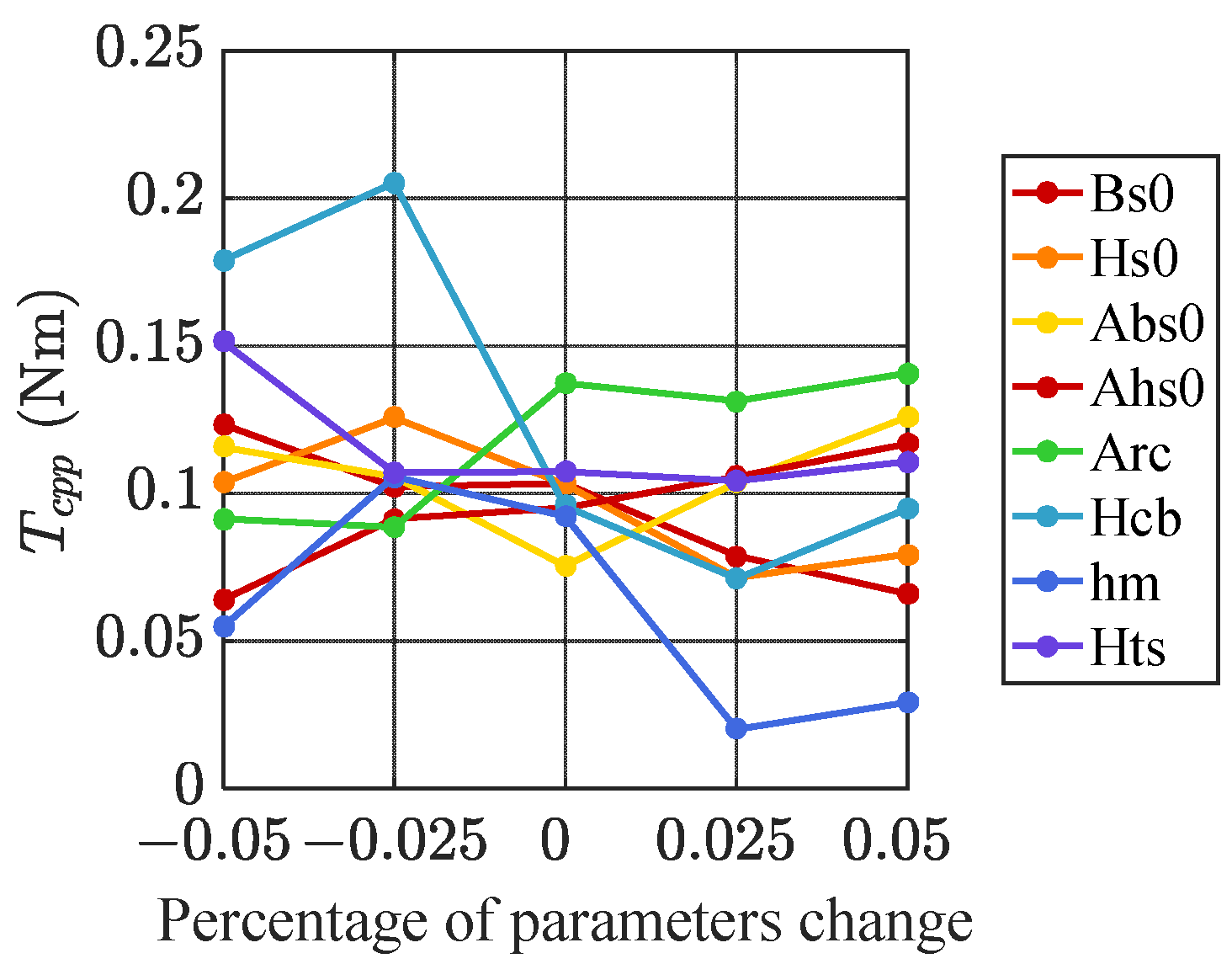
x0, and the other parameters are unchanged. It is worth noting that if the changeable parameters are from the repetitive units, Monte Carlo sampling (MCS) should be carried out within the tolerance range to obtain a set of parameter values with tolerances of the number of repetitive units, which will be injected into the parametric FEA to obtain the model with tolerances.
The parameters sensitive to Tcpp are screened out through sensitivity analysis, which is used as the design parameters for the following RDO research.
- (d)
The training database was constructed.
A parametric FEA describing the actual motor parameters can be obtained based on the above analysis. Through the DoE, the sample data by the actual production dispersion of Tcpp are obtained by parametric FEA, which is used for approximate modeling training.
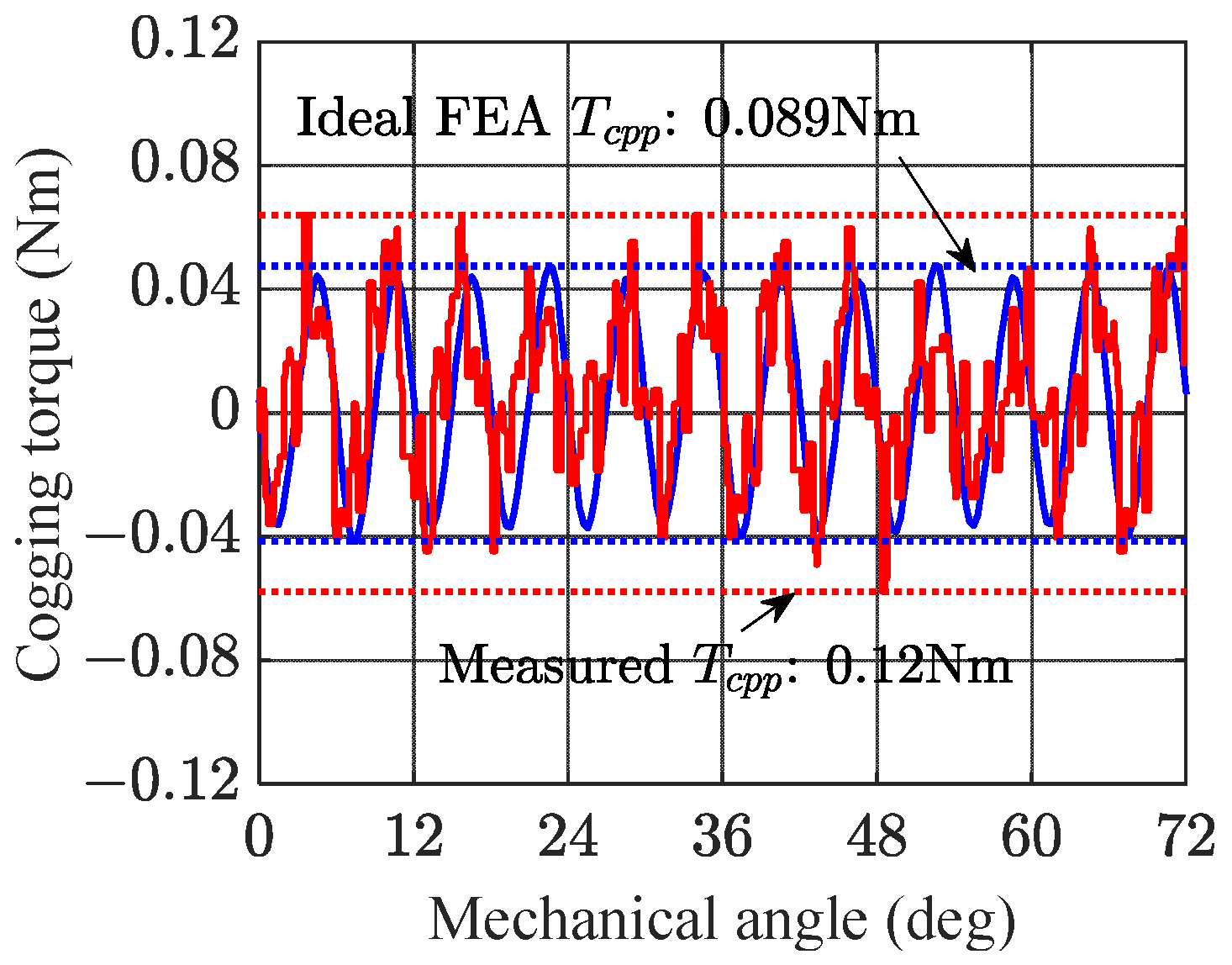
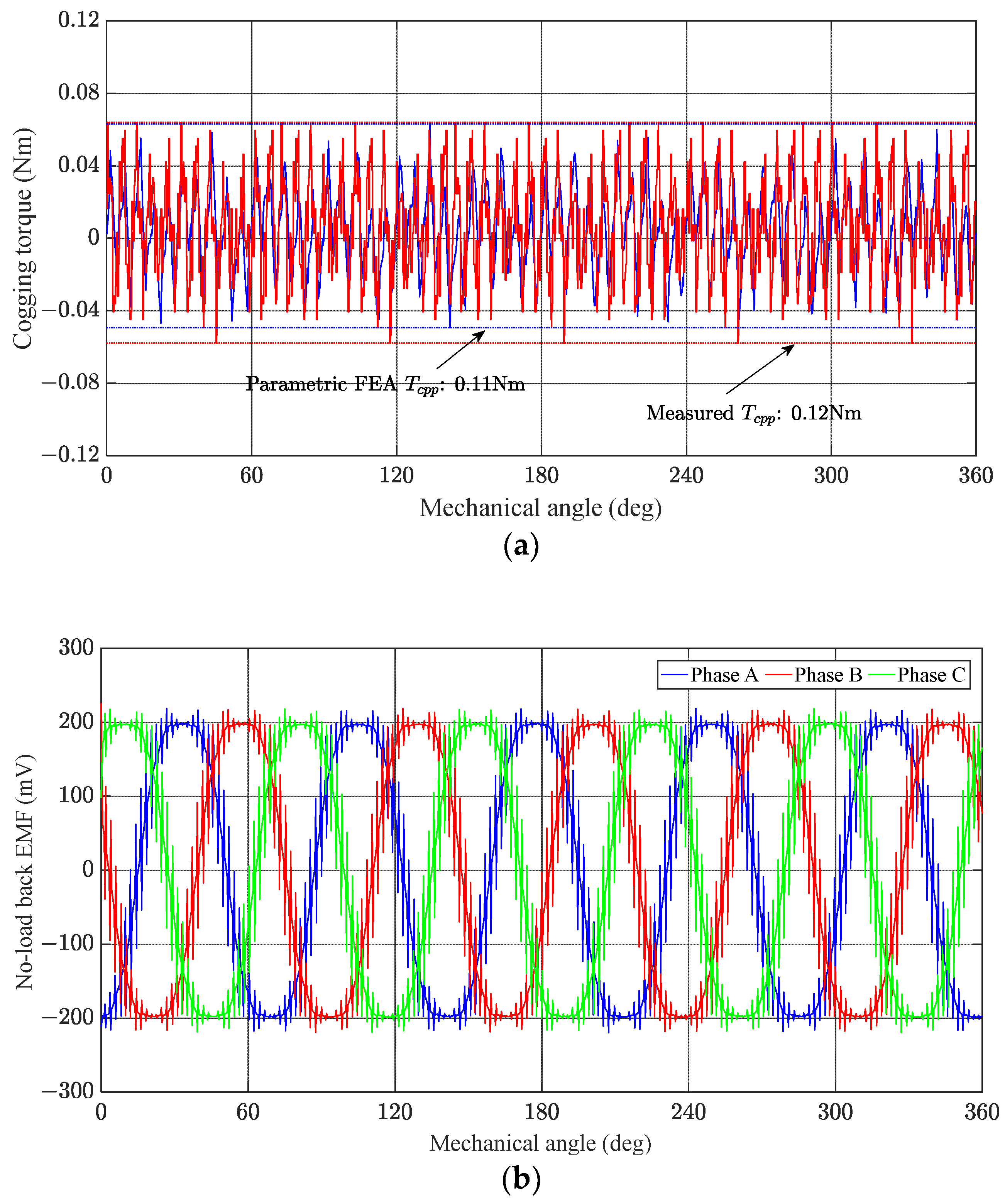
An approximate model was established in this study to fit the cogging torque of the PMSM as an example. Cogging torque can be considered a series of periodic waveforms. The peak-to-peak value of the cogging torque (
Tcpp) is the difference between the maximum and minimum values of cogging torque in one or more cycles. In most existing studies,
Tcpp is used to quantify cogging torque, which is defined as:
where
Tcpp is the peak-to-peak value of cogging torque,
Tcog is the cogging torque, and
φ gives the rotor angle.
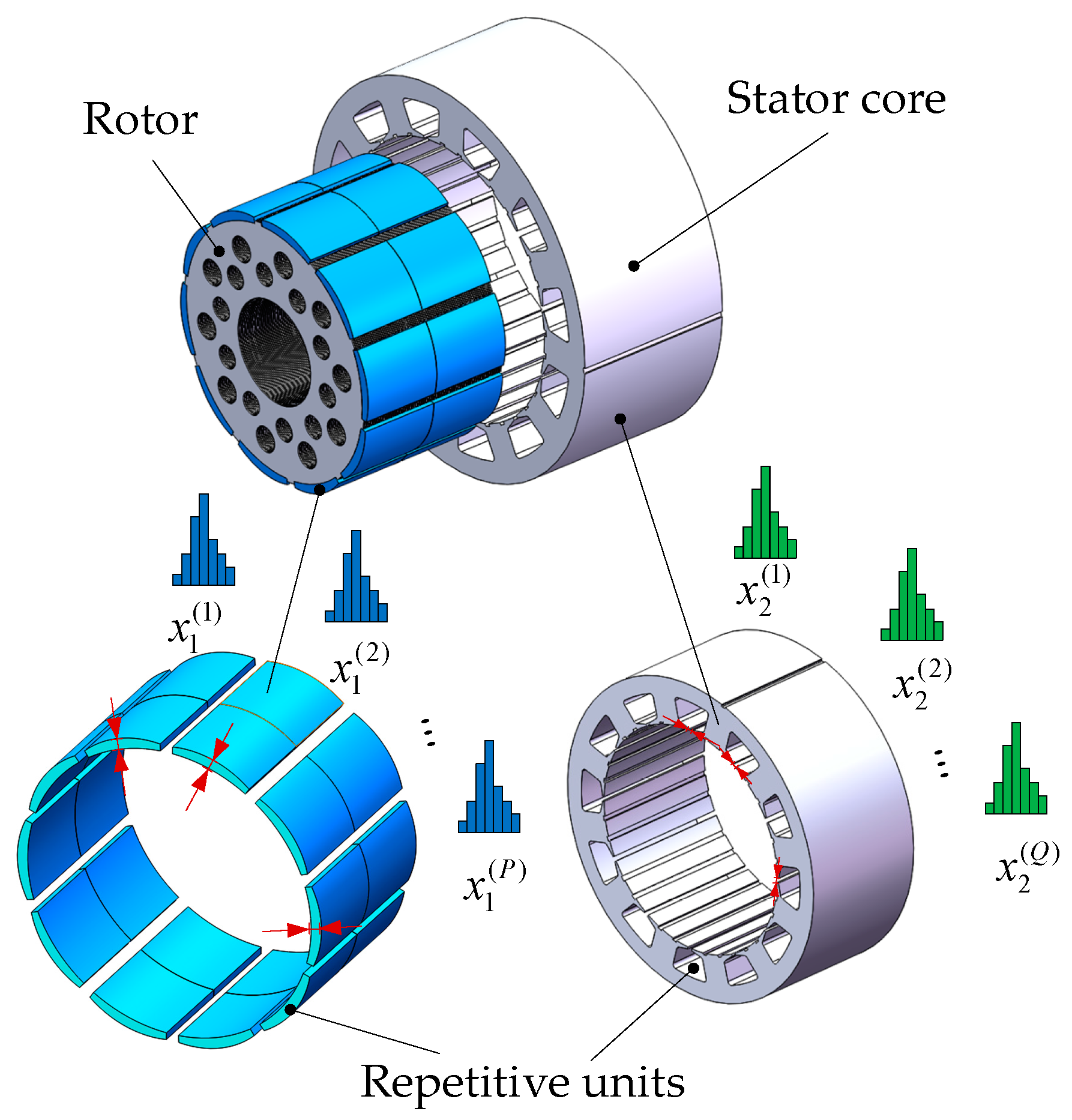
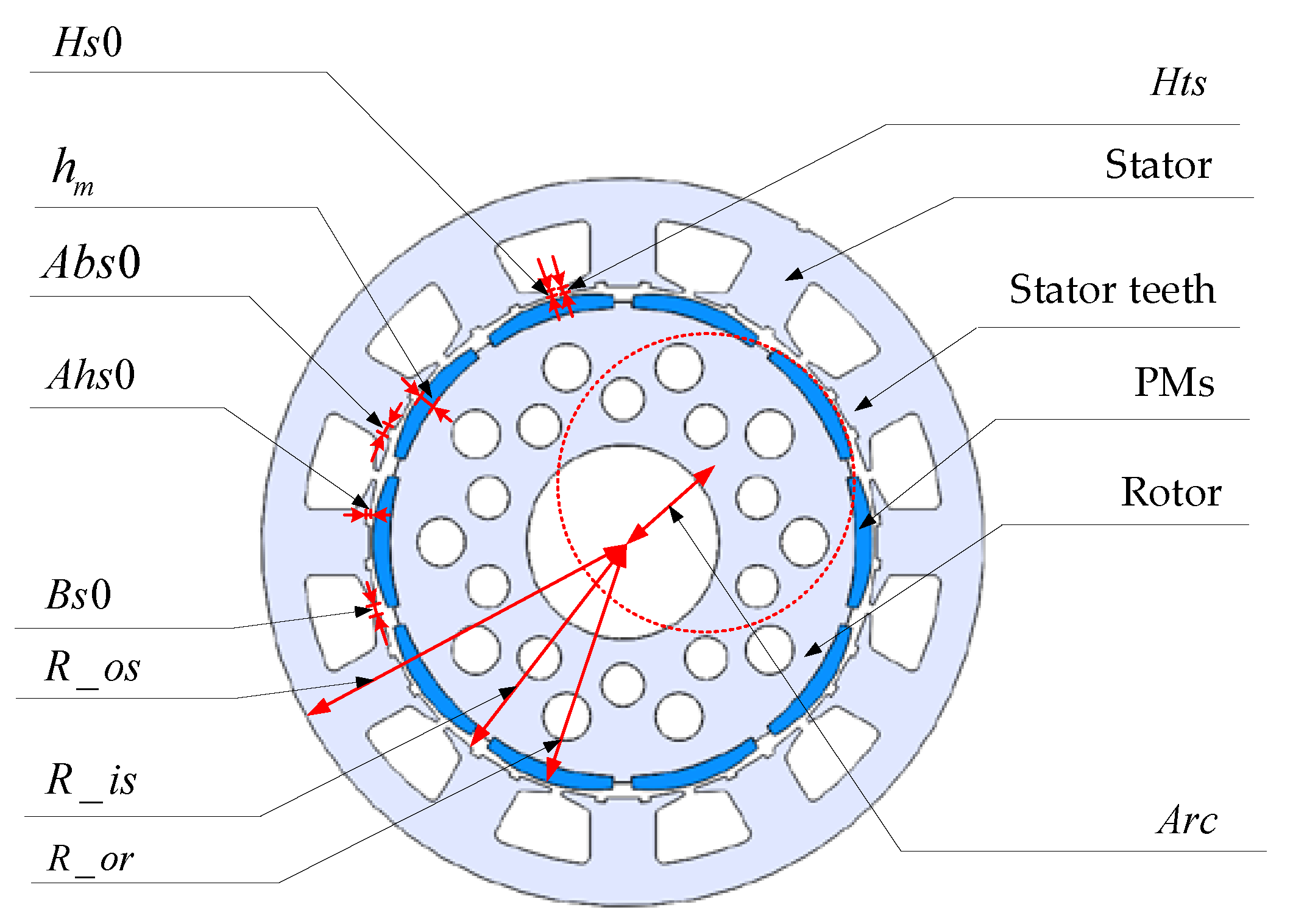
Assume a surface-mounted permanent magnet synchronous motor (PMSM) with
P poles and
Q slots, of which the schematic diagram of repetitive units of the PMSM is shown in
Figure 3. Several uncertainties from a single source can be involved owing to repetitive units in the PMSM. Their variation of structures and material properties can be approximately regarded as random variables following a Gaussian distribution. In this paper, “repetitive units” is used to describe the structural characteristics of the PMSM.
Consider a motor with
K design parameters that has center value
x = {
x1, x2, …, xK}, where the deviations between actual design parameters and ideal center values can be presented as
σ = {
σ1,
σ2,
…,
σK}, and the number of repetitive units of the
kth design parameter is
pk. Then, for convenience of expression, the center value after taking repetitive units into account can be expanded to
X,
where
=
= … =
. In manufacturing, the repetitive units of the PMSM inevitably have manufacturing deviations. Their corresponding deviations are expanded to
Σ,
Thus, the design parameters of a motor make up a random variable
Z,
which is assumed to form multivariate Gaussian distributions. The manufacturing deviation rate of each repetitive unit is defined as the ratio of the random parameter tolerance and its corresponding center value, which means the rate at the parameters changes. It can be represented as
ζ,
Assume that
f(
Z) is the approximate function of the
Tcpp, which can be presented as Equation (7) based on Taylor expansion:
If we omit the higher-order terms, Formula (7) can be expressed by first-order Taylor expansion as:
where
X is the center values vector of design parameters, and
Z is the design parameters vector with manufacturing deviations.
Z −
X is the deviation between the actual value and the center value of each parameter, that is, the manufacturing deviation of each design parameter.
f′(
X) is the gradient near the center value vector of the design parameter. Take the manufacturing deviation rate as
ζ, that is,
ζ =
Σ/
X = (
Z − X)/
X, then Equation (8) can be expressed as:
Equation (9) can be further transformed into:
that is,
If we use f1 to represent the first term in the bracket on the right, shown as ; and g1 to represent the second term in the bracket on the right, shown as .
Then,
f(
Z) can be expressed as:
In the process of approximate modeling, we first performed an approximate calculation of the first component to obtain
. At this point,
X is the input variable of the model, and as a known value, the gradient
at this point is an unknown but constant value, which does not influence the approximate calculation of
. Therefore, in the approximate calculation of the second component
, only the input variable
ζ, the manufacturing deviation rate, needs to be considered as the input variable. Equation (12) can be further written as:
Thus, the approximate model of Tcpp can be composed of two parts: the ideal component of Tcpp caused by the center value of the design parameters and the fluctuation component of Tcpp caused by the manufacturing deviation rate of the design parameters. On this basis, the approximate calculation of Tcpp can be performed on the ideal component and the fluctuation component in turn. Thus, the effects of center value X and manufacturing deviation rate ζ on Tcpp are decoupled to achieve the purpose of modeling separately.
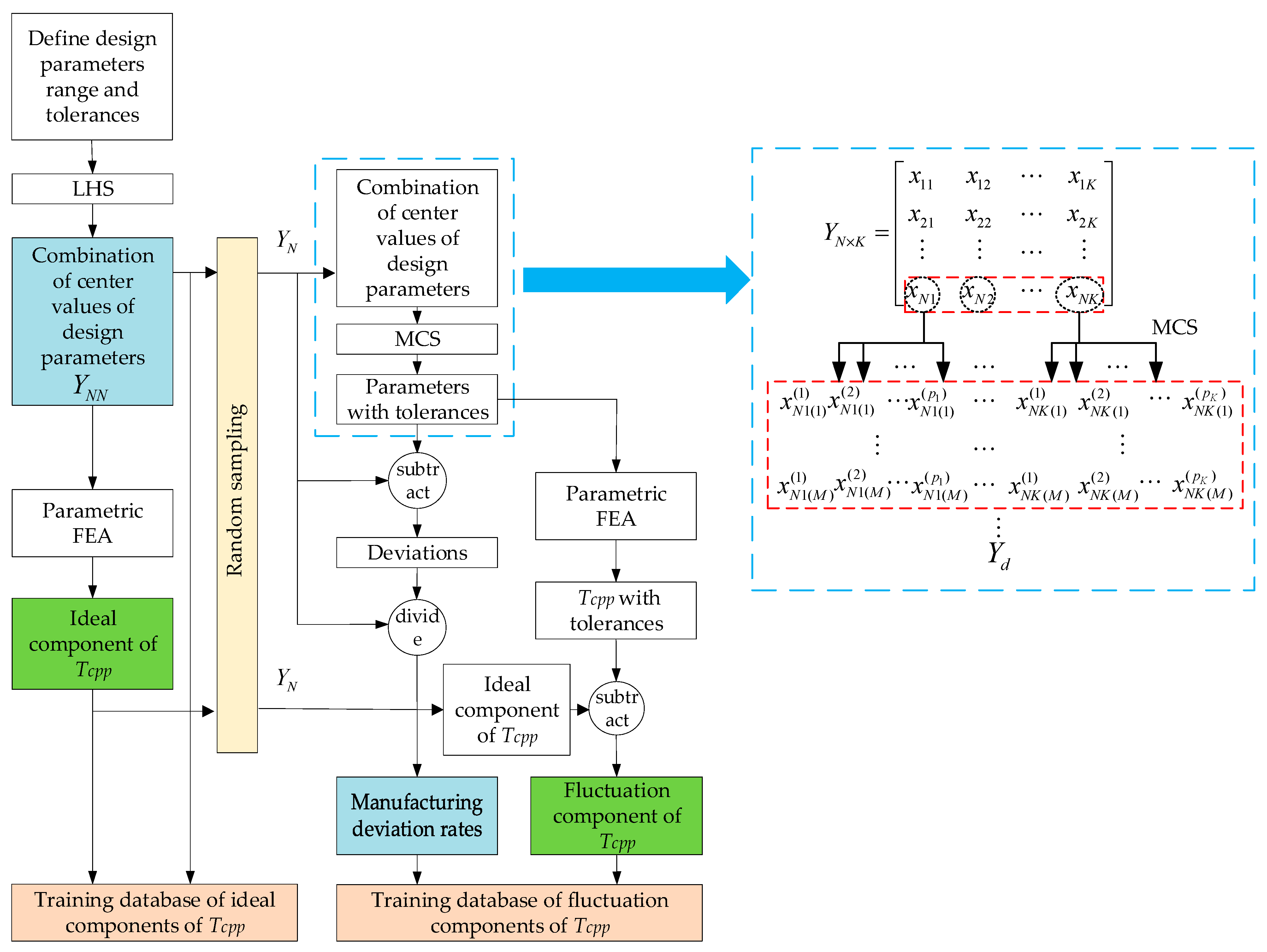
In order to establish approximate modeling of the ideal component and the fluctuation component of
Tcpp, the corresponding input data of the model are the center values and the manufacturing deviation rates of the design parameters. The procedure for establishing the corresponding training database is shown in
Figure 4.
The steps to build the training database are as follows:
- (1)
The design parameters range and tolerances are defined. For the filling of the design space, Latin hypercube sampling (LHS) [
19] is used to sample combinations of center values of the design parameters in the design parameter range. Assuming that there are
K design parameters, LHS obtains
NN groups of center value combinations. Parametric FEA is performed on each group of samples to obtain
Tcpp without tolerance, which, together with the sampling center values of design parameters, is the training database of ideal components of
Tcpp constituted.
- (2)
N samples are randomly selected from the
NN groups of center values samples. Considering the manufacturing deviations of repetitive units, Monte Carlo sampling (MCS) for each group of design parameter center values can obtain the actual parameter values with manufacturing tolerances. As shown in the dashed box on the right of
Figure 4, the numbers of their corresponding repetitive units for
K design parameters can be presented by
p1, p2, …, pK. According to experience, all design parameters are subject to the Gaussian distribution. Thus, MCS with Gaussian distribution performed
M times for each group of center value combinations. The
Nth group is taken as an example; the first design parameter
xN1 contains
p1 repetitive units, which can be expanded into
, , …, , according to its manufacturing deviations in the first sampling. Other
N-1 groups of parameters are sampled as this rule. In the end, a high-dimension matrix
Yd is obtained, of which the dimension is
d =
N ×
M ×
pK. The
Tcpp database with tolerances is obtained by parametric FEA, which subtracted the
Tcpp ideal component with the center value of the corresponding design parameter to obtain the database of the
Tcpp fluctuation component. In addition, the difference between the parameters with tolerances and the corresponding center values of design parameters is divided by the corresponding center values of design parameters to obtain the manufacturing deviation rate. The manufacturing deviation rate data, together with the fluctuation component of
Tcpp, constitute the training database of fluctuation components of
Tcpp.
2.3. The Establishment of the Approximate Model for Tcpp
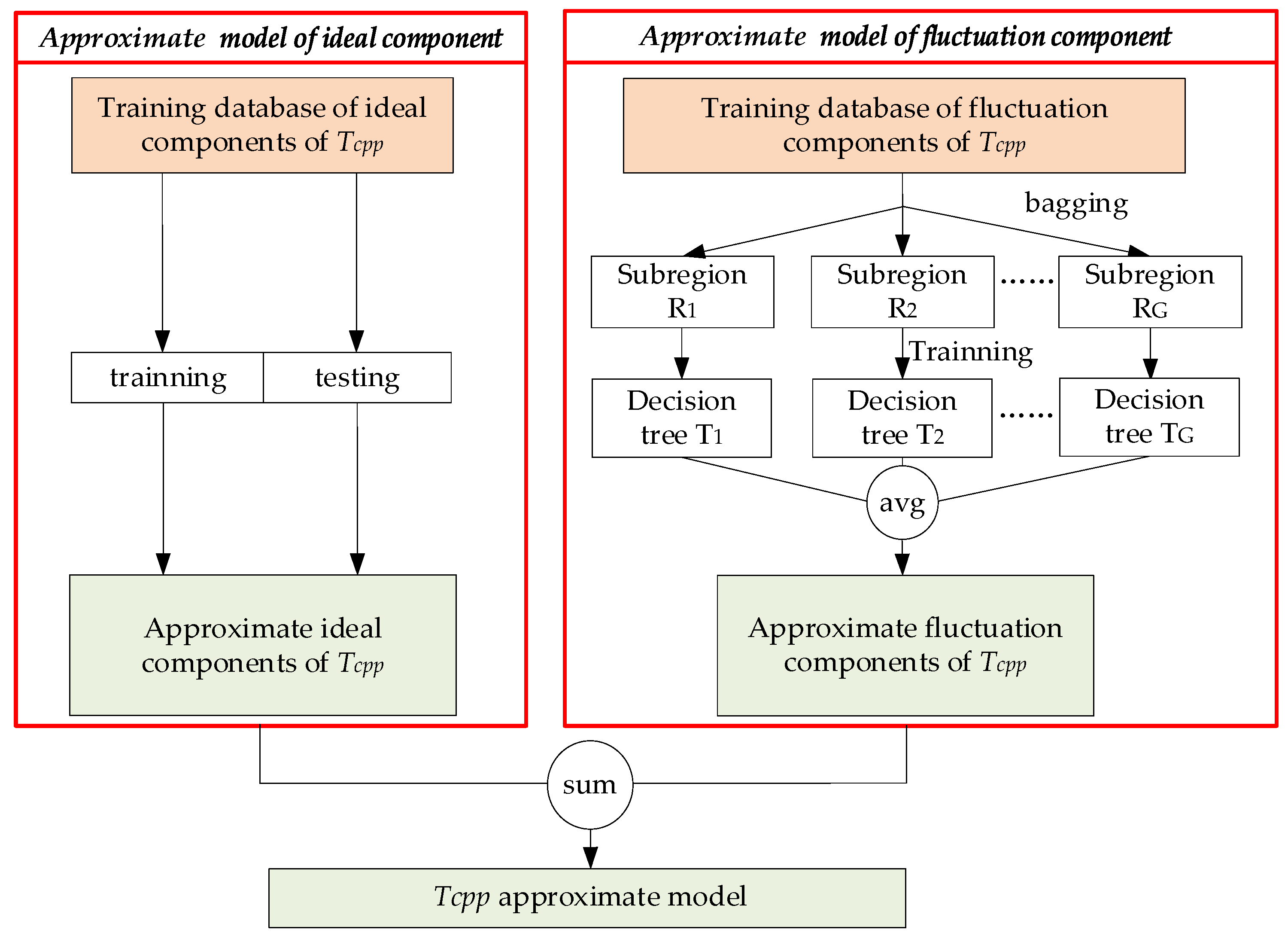
According to the DoE of
Section 2.2, we proposed the compensate fluctuation (CF) approximate modeling method, which established the approximate models for
Tcpp considering manufacturing uncertainties of repetitive units. Based on the approximate modeling of the ideal component of
Tcpp, the fluctuation component is supplemented and added to the ideal component model; that is, the ideal and fluctuation components of
Tcpp are modeled and then added to obtain the
Tcpp approximate model.
The proposed CF approximate modeling method is carried out for the two components. The flow chart of the proposed method is shown in
Figure 5.
Firstly, a conventional approximate modeling method is searched to establish the ideal component of Tcpp. The center values vector of design parameters X is the input data. f1(X) is the ideal component of Tcpp, the output data.
Secondly, for the fluctuation component of
Tcpp,
g1(
ζ), that is
g1((
Z − X)/
X), caused by manufacturing deviation rate (
Z − X)/
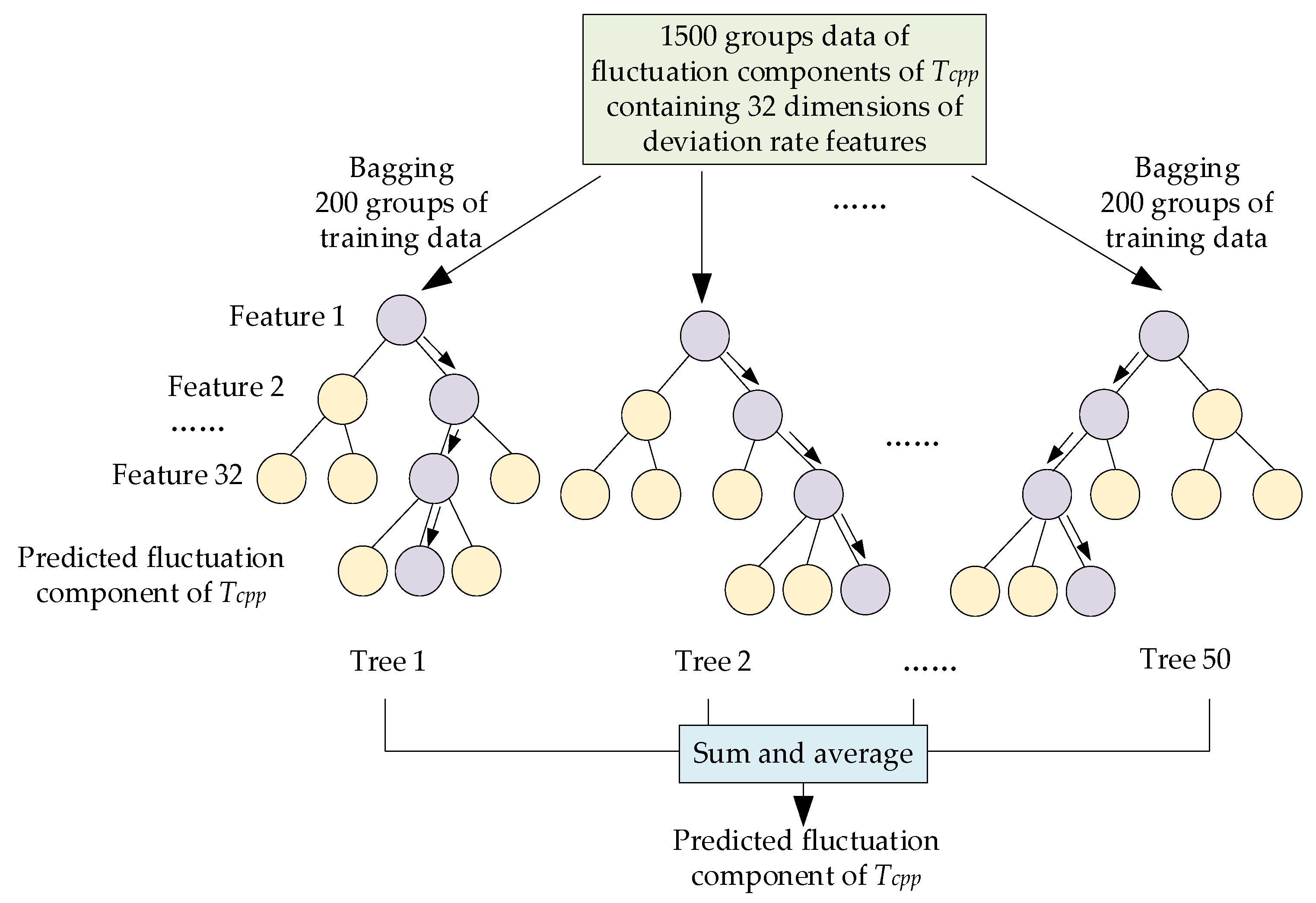
X, the random forest (RF) method [
20] based on bagging [
21,
22] is used for the establishment of the approximate model. First, the subspaces of the fluctuation component training database are constructed. The manufacturing deviation rates and the corresponding
Tcpp fluctuation component database obtained by DoE in
Section 2.2 are sampled with replacement multiple times based on bagging, and various training database subspaces are obtained. The subspaces of the training database
R1,
R2, …,
RG, and corresponding decision trees
T1, T2, …,
TG are obtained. Each subspace contained several pieces of training data from the entire training database, and the number of training data contained in all decision trees far exceeded the total number of the training database. Then, the database of each subspace
Rg is trained to establish a decision tree
Tg to approximate the fluctuation component of
Tcpp. According to the information gained, the order of the input parameter features in the leaf nodes of the decision tree is determined. Then the training data are divided according to the judgment index of the input parameter features at each leaf node until it cannot be divided further. The training objective of each decision tree is to minimize the difference between the predicted fluctuation component from the output of the tree and the actual fluctuation component, which means that the tree’s output is close to the actual value. The training objective is shown as follows:
where
yg is the actual fluctuation component of
Tcpp, i.e., the FEA result;
ζi is the
ith manufacturing deviation rates vector from
N ×
M samples and
Tg(
ζi) is the predicted value of
Tcpp fluctuation component for the
gth tree model.
When the model is used to approximate the fluctuation component of
Tcpp, assuming that the number of the decision tree is
G, the manufacturing deviation rates should be input to the fluctuation component model. Then the outputs of all decision trees are averaged to obtain the predicted value of the final fluctuation component of
Tcpp as Equation (15):
where
Tg(
ζi) is the output of the
gth decision tree;
g1(
ζ) is the predicted value of the fluctuation component of
Tcpp.
Finally, the predicted
Tcpp with tolerances can be calculated as the sum of the above two components, shown as:
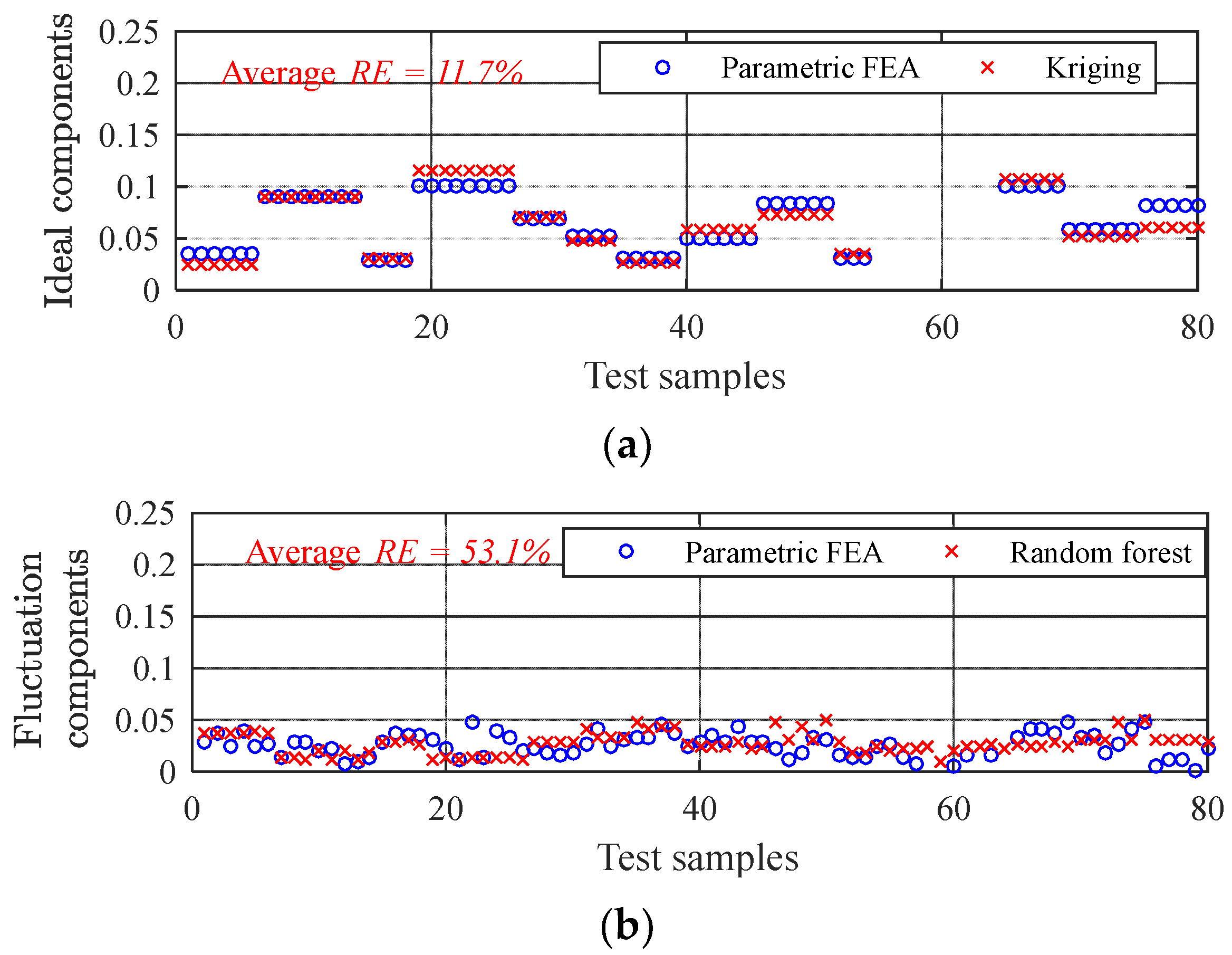
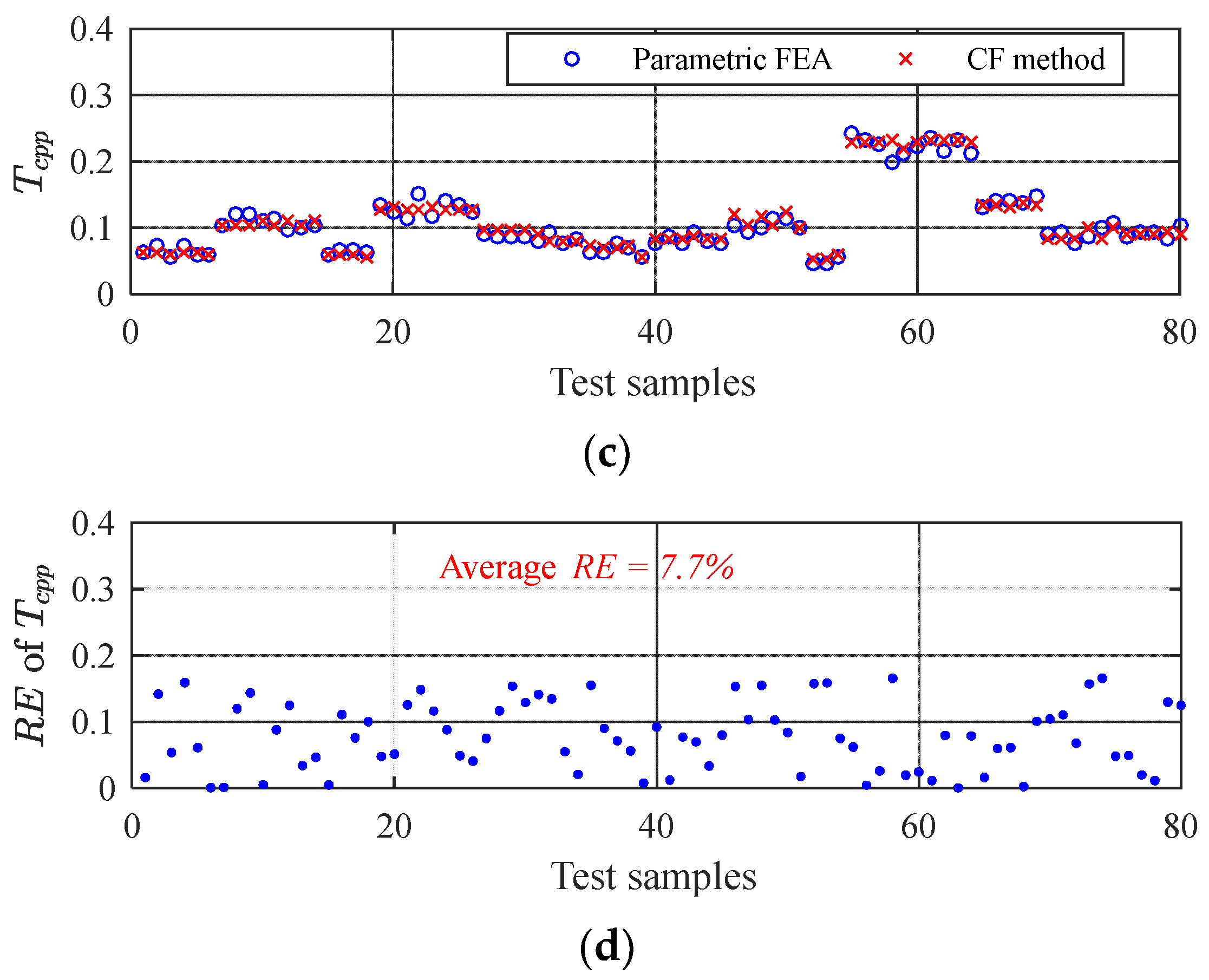
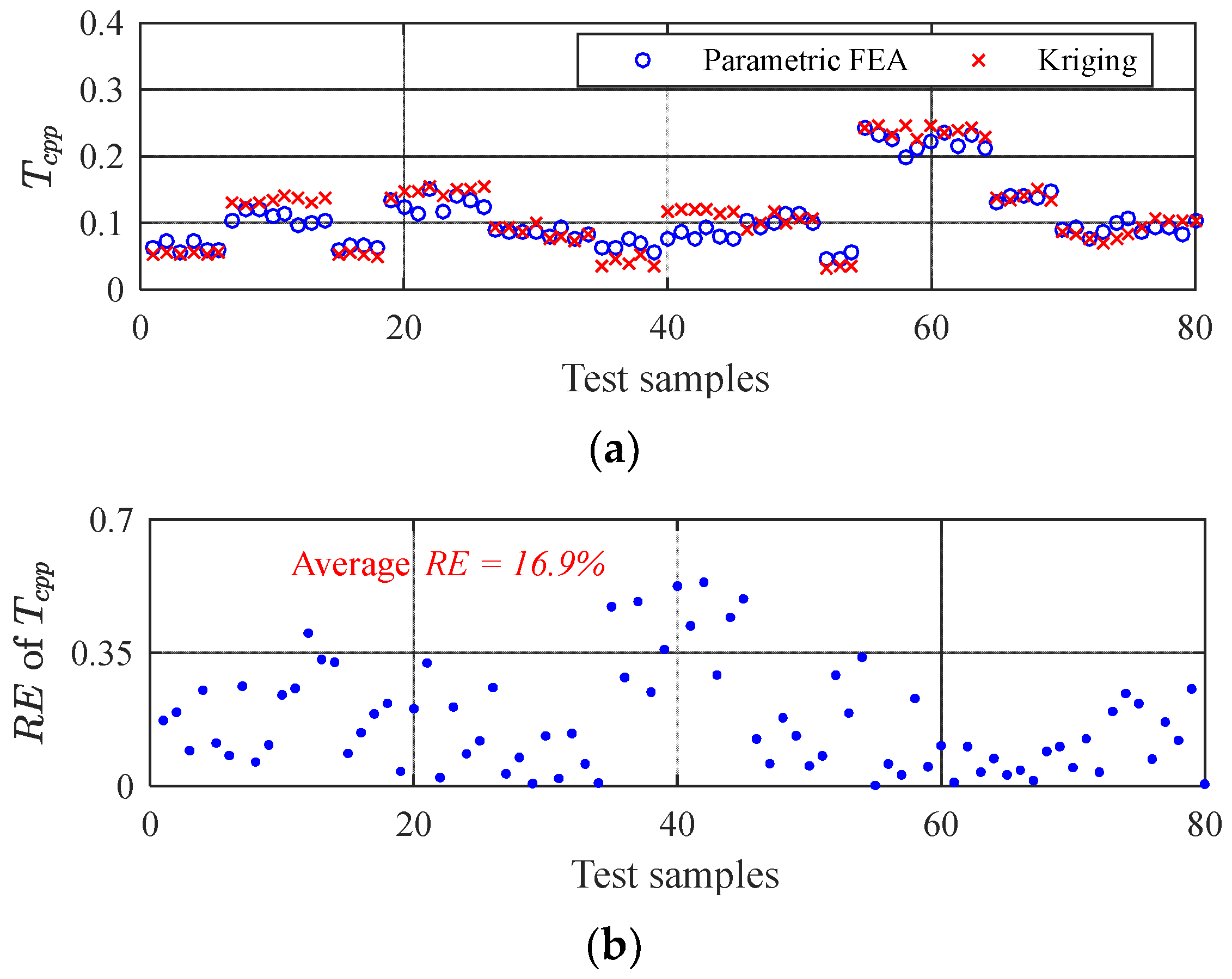
The accuracy of the approximate model is evaluated by relative error (
RE):
where
ns is the number of selected test samples, and
Yj(
Xj,
ζj) is the
jth actual response value of the test sample, i.e., the parametric FEA value.
(
Xj,
ζj,) is the
jth predicted value of the approximate model. A poor
RE reflects high model accuracy.
2.4. RDO of Tcpp Considering Repetitive Unit Parameter Uncertainties
Different combinations of design parameters affect the consistency of output characteristics of the PMSM. In order to improve the consistency of output characteristics of the batch PMSM, it is necessary to find some design schemes to make the mean values of the output characteristics as close as possible to the design object and distributed in a concentrated manner in the presence of manufacturing deviation while ensuring the performance also meets the requirements. In this study, the particle swarm optimization (PSO) method is used to optimize the design parameters and realize the robust design of the PMSM, considering the manufacturing uncertainties of repetitive units. The optimization objective function is shown in Equation (19). The optimization objective is to minimize the mean and standard deviation of the
Tcpp of the PMSM, and the constraint is that the no-load back electromotive force (
BEMF) is not lower than its threshold. The optimization will be stopped when the mean and standard deviation of the
Tcpp are lower than their respective thresholds. The specific implementation is shown in
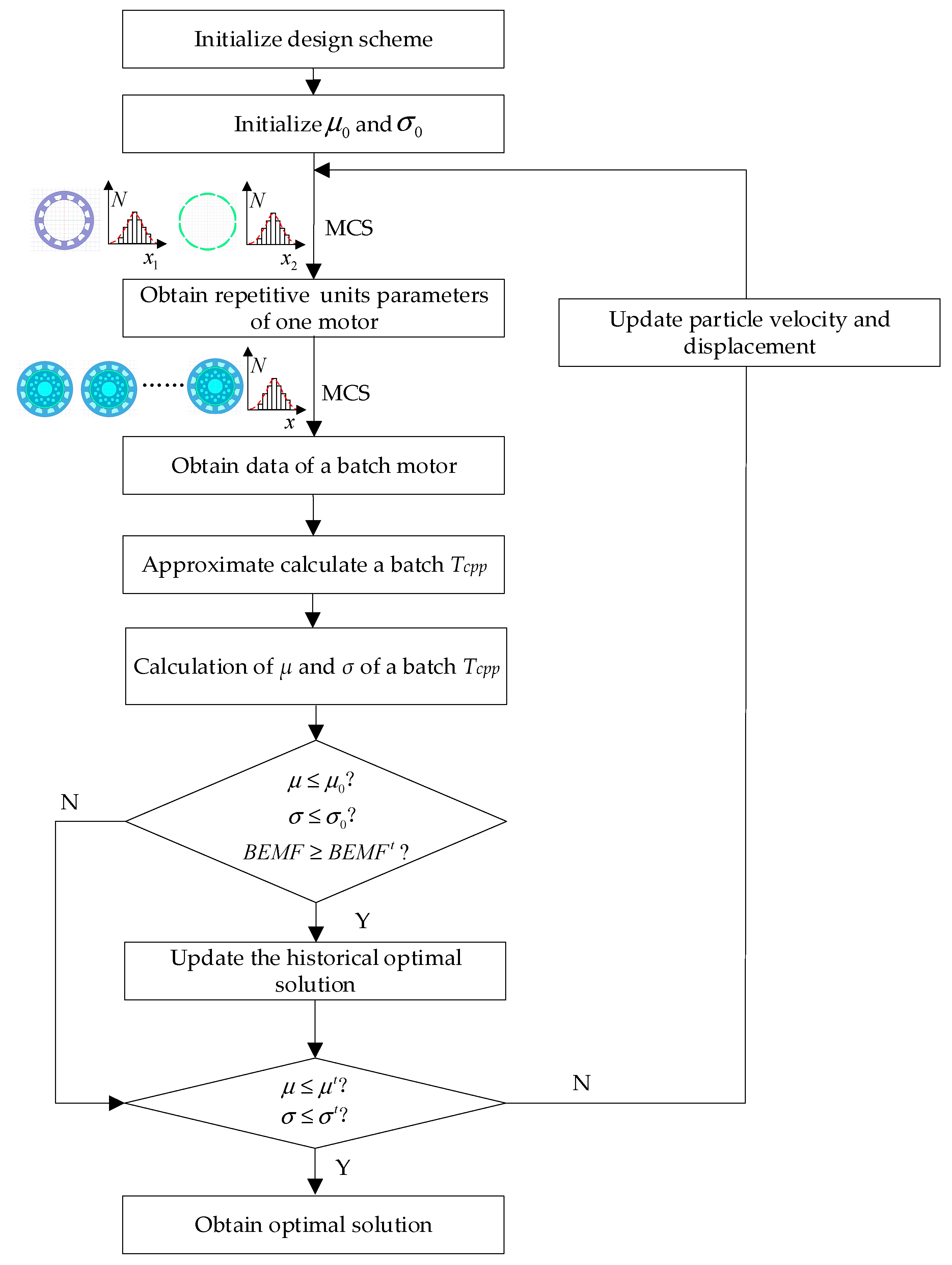
Figure 6.
The steps of robust design optimization (RDO) with repetitive unit uncertainties are as follows:
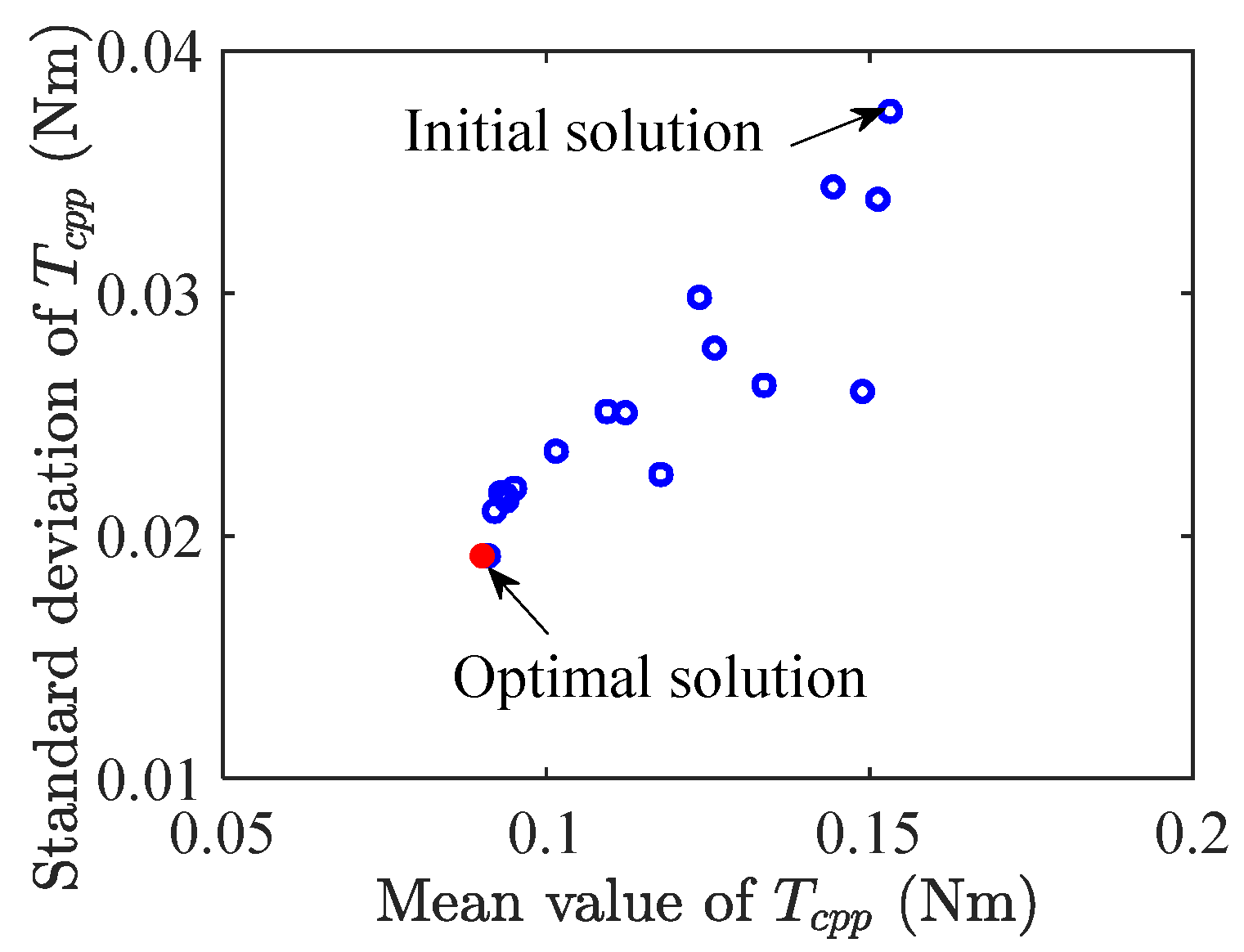
Step 1, the design scheme: the mean value and standard deviation are initialized. The MCS is performed according to the actual manufacturing deviations to sample the parameters of the repetitive units in one motor. Then, MCS is performed according to the deviations of the batch motor to obtain the parameters of the batch motor. The approximate model is used to calculate the batch motor’s Tcpp value to calculate the batch motor’s statistical characteristics, such as the mean and standard deviation.
Step 2, the mean and standard deviation of the current scheme are compared with the historical scheme. If the current scheme is better than the historical scheme, it replaces the optimal one; Otherwise, the historical optimal solution is kept, and it is determined whether the optimization goal is achieved. If the optimization goal is achieved, the optimal solution is output. Otherwise, the particle position and velocity are updated, and steps 1 and 2 are repeated.
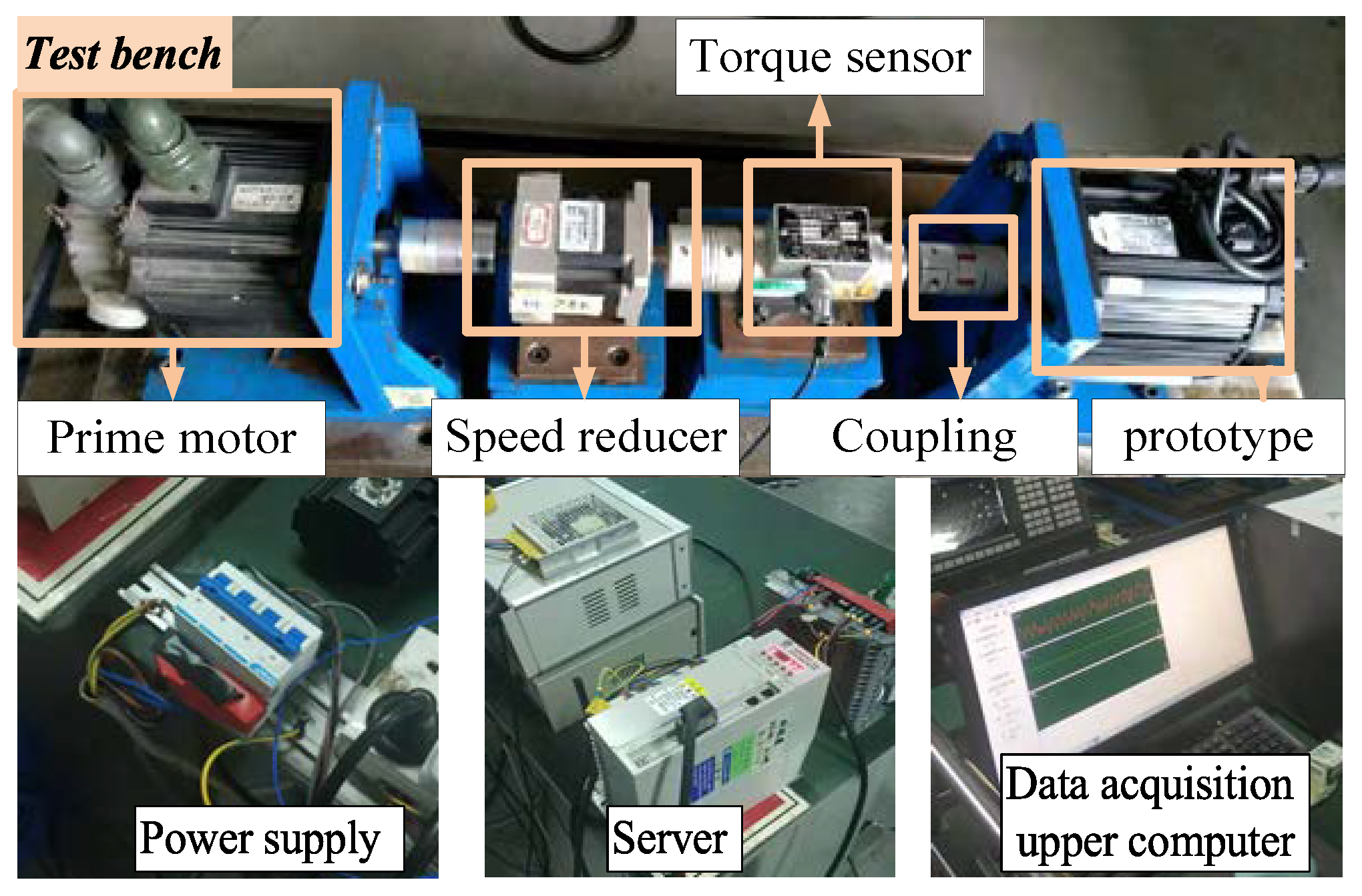
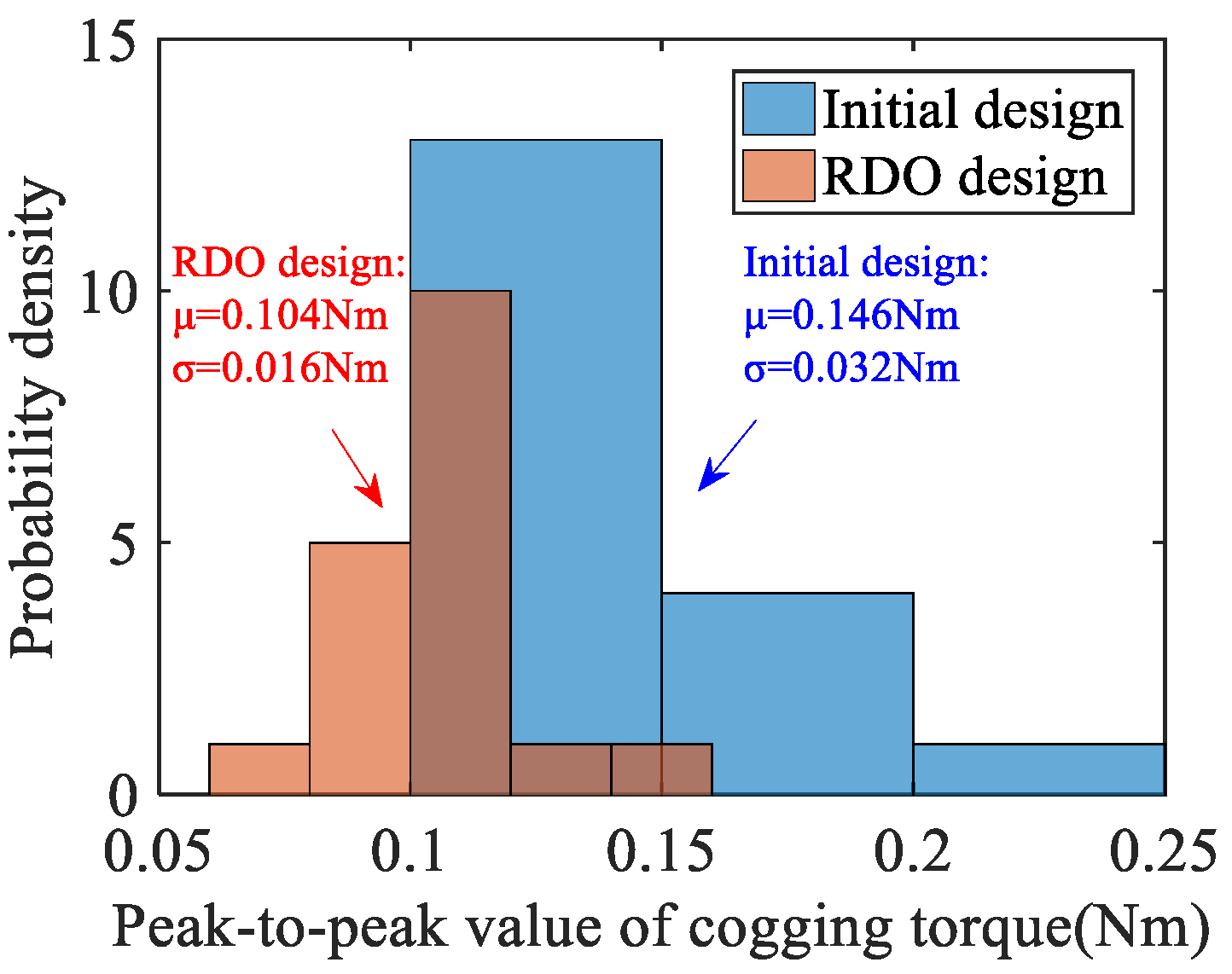
According to the optimal design scheme, MCS is carried out to obtain a batch of the motor according to the design tolerances, the parametric FEA is conducted, and the robustness of the optimized motor is verified. In addition, several prototypes are produced to test and verify the scheme’s effectiveness.