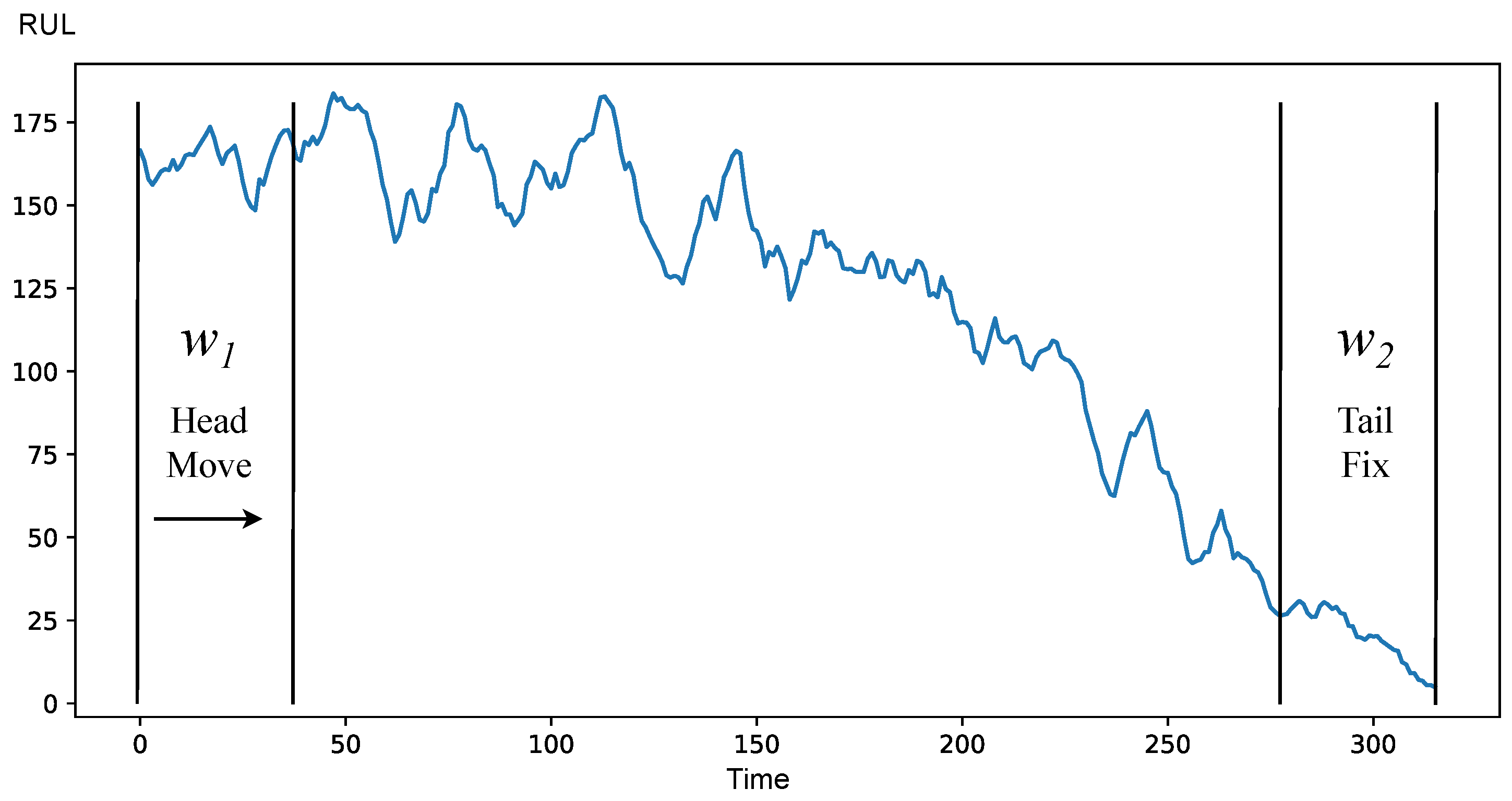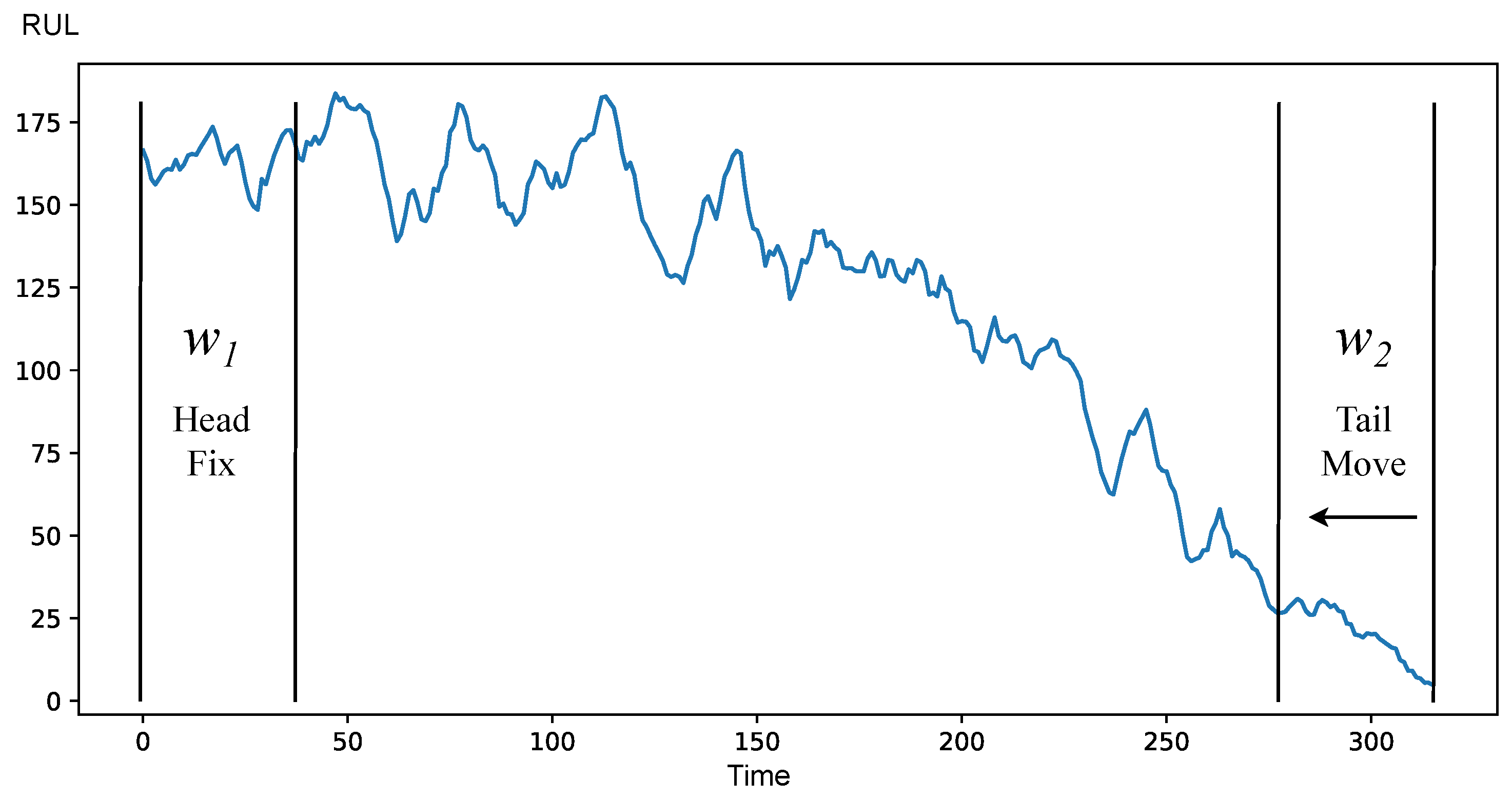1. Introduction
Gas turbines are used for various applications from energy generation to propulsion, gas compression, etc. With the shift towards clean energy production, a new use for gas turbines as a supporting back-up load balancing tool has emerged [
1]. Gas turbines have advantages of small footprint, high power to weight ratio, mobility and quick startups as well as mobility and fast deployment [
2,
3].
This use also brought new challenges which include a variety of operating conditions, frequent and irregular operation cycles [
2,
4]. These make gas turbines more susceptible to failures, which are mostly random [
5]. Likewise, latest technologies which allow making turbines more efficient make them more complex as well, which complicates diagnostics making it more costly as well [
6]. With that, the described case requires high availability and readiness [
7].
The failures cause downtime by making gas turbine unavailable for energy production and require costly repairs and even replacement of a unit altogether [
6]. Failures in total may account for up to a third of the operating cost [
8]. These factors require new improved flexible and robust strategies for the maintenance of energy generating equipment.
There are multiple strategies to conduct maintenance. All of them can be divided into two groups: reactive and proactive strategies [
9]. The reactive or run-to-failure strategy is to perform maintenance in the event of a failure. This is used mostly for inexpensive, expendable or non-serviceable equipment. In general, only proactive strategies are used for the maintenance of complex energy equipment. These include periodic and preventive strategies, which are used either exclusively or in conjunction with each other [
10].
Periodic strategy is the most prevalent form of maintenance nowadays. Periodic maintenance is a regularly scheduled operation based on operating time, generally specified in manufacturer recommendations. While this strategy is easy to implement and follow, it does not prevent random failures, which constitute more than three quarters of all failures [
6] and might lead to an increased probability of failure right after maintenance. It also might not be adequate for harsh and extreme operating conditions, where equipment wear is greater than in average conditions.
Preventive maintenance is based on the inspection of condition of energy equipment using non-destructive monitoring methods. This strategy uses predetermined acceptable ranges for values of parameters [
11]. Repairs may be scheduled if the inspection of parameters or condition of energy equipment shows out-of-range deviation in readings or other flaws in operation, such as excessive noise or vibration.
Industry 4.0 brought new digital technologies, as IoT (internet of things), cloud computing and big data to enable improved failure detection and optimized asset management through the use of computerized analytics and machine learning [
12]. Advancements in IoT (internet of things) allowed better availability of sensors, improvements to data transfer and storage [
13].
More advanced and promising maintenance strategy that originates from concept of Industry 4.0 is a proactive reliability-centered maintenance, which is based on forecasting of health index and remaining useful life of the energy equipment [
10]. This is a data-driven strategy that relies on data collected from the sensors to make forecasts about future condition of energy equipment and possible failures. Having such forecast may allow the decision-maker to adjust maintenance schedule or to perform additional inspections.
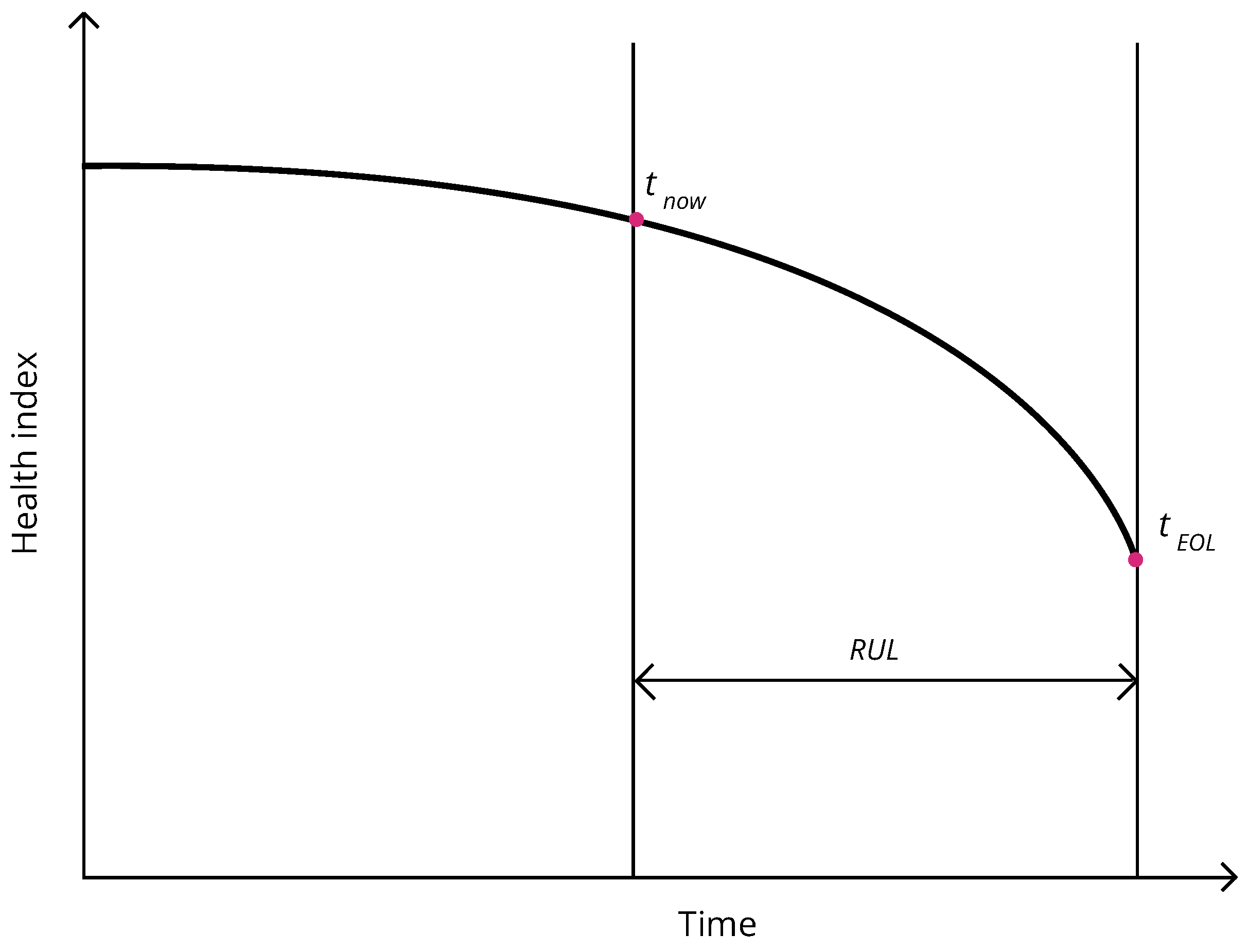
The main parameter for this strategy is the remaining useful life (RUL) [
14]. It is defined as operating time between current or set moment in time
and the time of the end of life of energy equipment
as Formula (
1) shows.
Figure 1 demonstrates RUL, health index and the relation between them. The end of life might be either the next failure of energy equipment or a state when further operation is impossible without a major loss of functionality or is going to lead to a failure.
The hypothesis of this paper is that if the accuracy of defining stages of energy equipment operation and splitting data according to them is improved, forecasting RUL is going to become more accurate. The contribution of the paper is a new proposed method for degradation process identification (DPI) as a part of reliability-centered maintenance methodology. The idea if the method is based on sliding windows and Kruskal-Wallis test to compare data within these windows. A Head Move—Head Move strategy of sliding windows allows to define starting point of energy equipment degradation. A method uses two partially overlapping sliding windows moving from start of operation to the end of life of energy equipment. Based on this data separation, we applied a convolutional neural network-based forecasting model for RUL prediction.
2. A Method of Degradation Process Identification as a Part of Reliability-Centered Maintenance Methodology
2.1. Reliability-Centered Maintenance Methodology
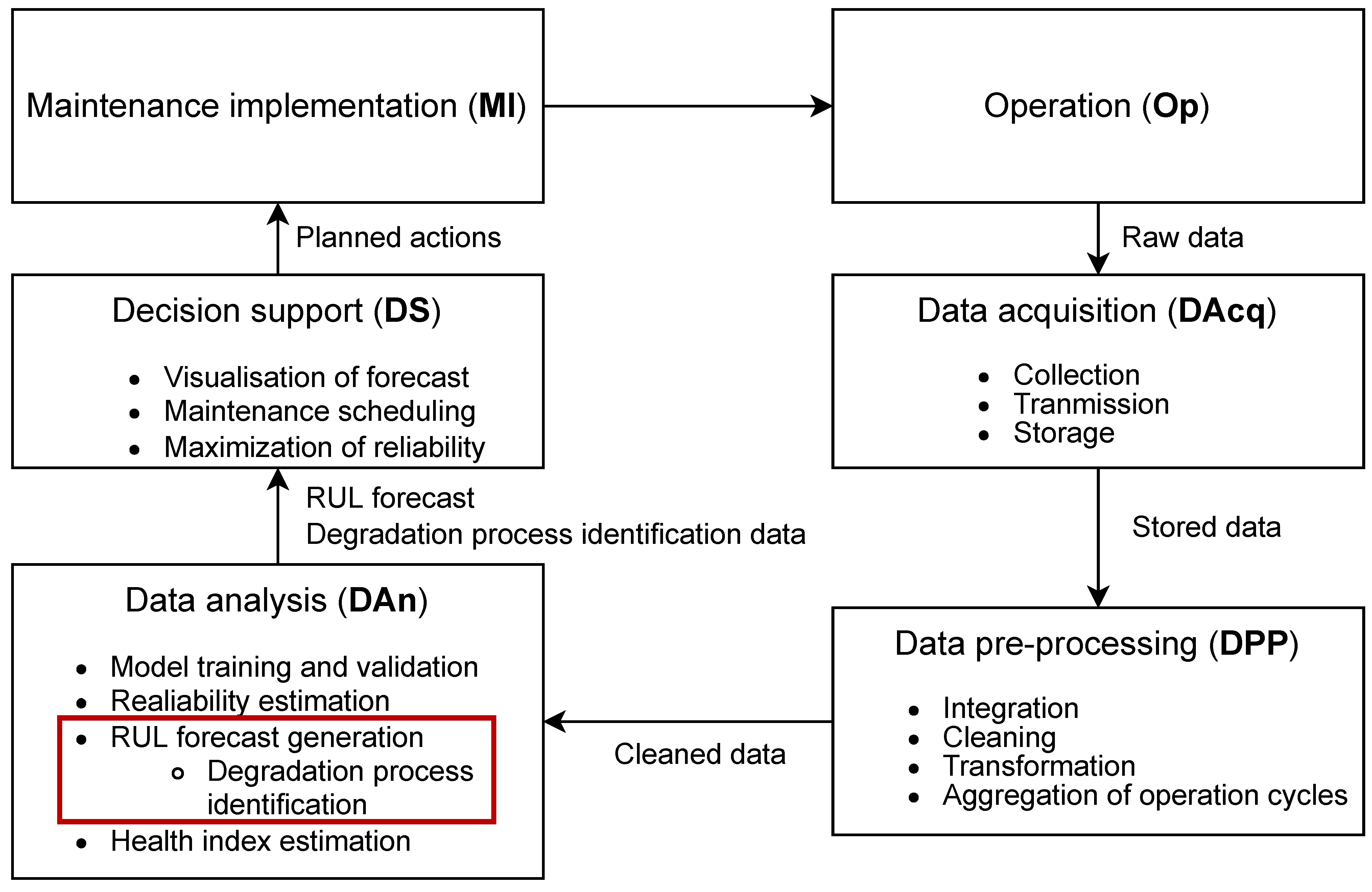
Methodology of a typical reliability-centered maintenance that implements RUL-based predictive maintenance for energy equipment consists of the following steps [
15,
16]: data acquisition (DAcq), data pre-processing (DPP), data analysis (DAn), decision support (DS), maintenance implementation(MI) and operation (Op).
Figure 2 illustrates the aforementioned methodology. Highlighted in red is a focus of this article.
DAcq is the first step of process, where data are collected from equipment through a network of sensors to a centralized storage. At the DPP step, the data are integrated, cleaned, transformed. Data for operation cycles is aggregated to a single value for each parameter of energy equipment [
18]. During DAn, the step data analysis and machine learning are used to generate a RUL forecast.
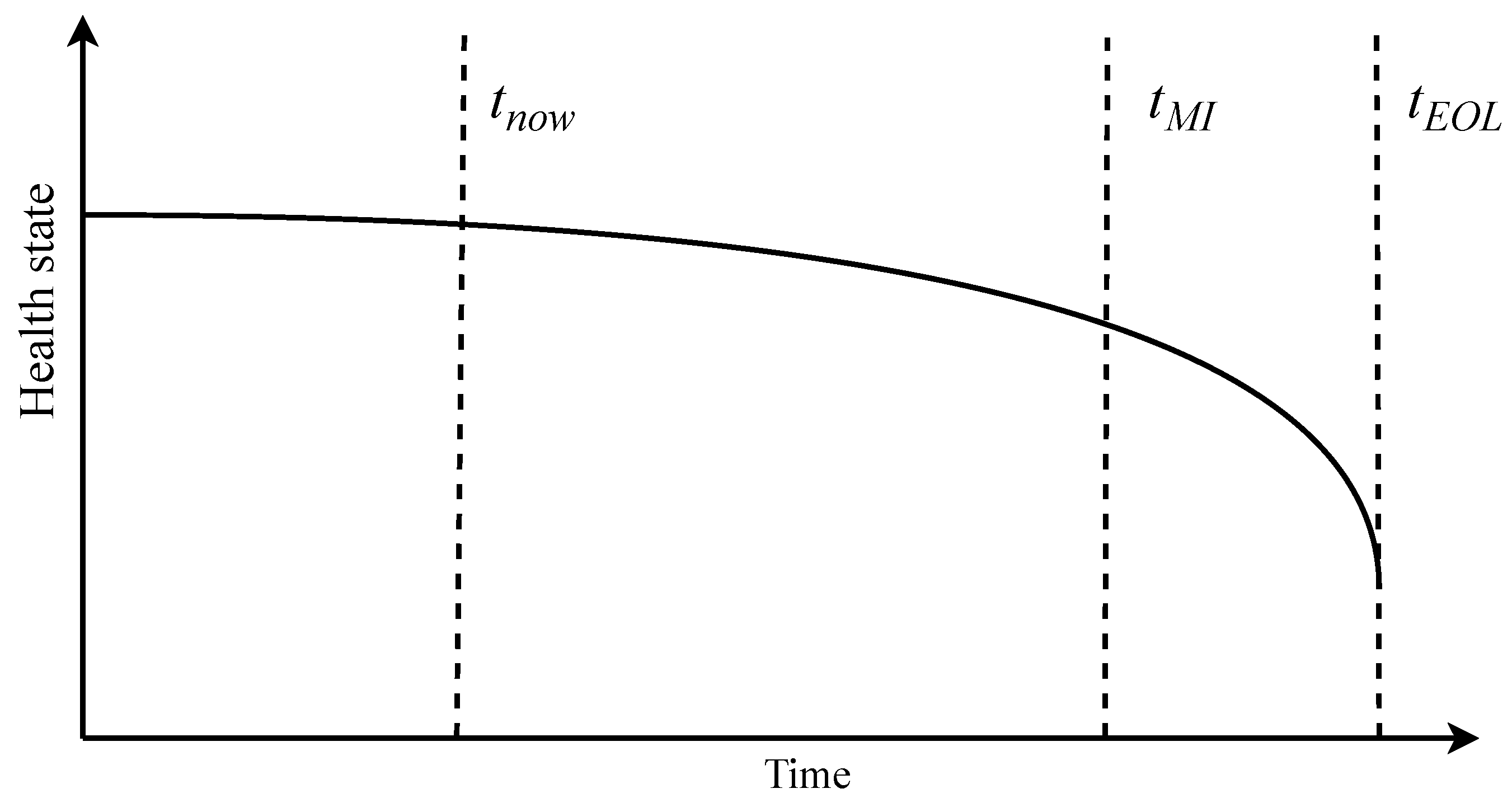
At stage of DS maintenance schedule is adjusted according to the forecast, as displayed at
Figure 3. The maintenance is scheduled for
at a
moment in time when the failure is forecasted to occur at
. This leads to the MI step, at which the schedule from the previous step is implemented in a real world at
for improved energy equipment operation.
Managerial actions that are planned at the DS step are significantly affected by the accuracy of RUL forecast, produced at DAn step—the higher the accuracy of the forecast, the more efficient actions can be planned and carried out at MI step [
14]. Managerial actions might be such as the equipment’s mode optimizing, risk-based inspection, repair, and many others.
Proposed DPI method is a part of DAn step, which is expressed in mitigation of inaccuracies of RUL forecasting through splitting data into two stages—the normal mode of operation and degradation process, which is conducted before model training. For testing purposes, the whole method includes the DPP step as well, consisting of data splitting, transformation, normalization, and other parts of DAn step, including CNN-based model, its training and validation, and the generation of the forecast.
2.2. An Overview of State-of-the-Art Research of RUL Forecasting
The accuracy of RUL forecast is a crucial aspect of the efficient application of the proactive strategy [
14]. The more accurate the forecast is, the more precision is available for maintenance scheduling, which means that it would not be scheduled too early or too late. This, in turn, leads to a more optimal number of stops for maintenance and lower downtime in general.
There are many RUL prediction methods and strategies based on a wide range of forecasting algorithms and models. In the review [
19], L. Zhang et al. looked at RUL forecasting methods, based on SVM-based algorithms and their advantages for multivariate time series analysis. C. Lu et al. investigated [
20] stacked denoising autoencoder (SDA)—a deep learning method, which was shown to be suitable for certain health state identifications for signals containing ambient noise and working condition fluctuations for effective fault diagnostics. H. Z. Huang et al. reviewed [
21] Support vector machine (SVM)-based methods and pointed out the ability to continually improve SVM and obtain a novel idea for RUL prediction using SVM in future works, particularly with tracking of the degradation process. G. A. Susto et al. presented [
9] a multiple classifier machine learning methodology for predictive maintenance. Methodology included training multiple classification modules with different prediction horizons to provide different performance tradeoffs in terms of frequency of unexpected failures and unexploited lifetime, and then employing this information in an operating cost-based maintenance decision system to minimize the expected costs. P. G. Nieto et al. presented [
22] a hybrid PSO–SVM-based model for the prediction of the remaining useful life of aircraft engines. The proposed hybrid model combined the support vector machines with the particle swarm optimization (PSO) technique. M. Yan et al. presented [
23], a method of RUL prediction of bearings, which can evaluate the degradation stage of bearings through dimensionless measurements and exploit the optimal RUL prediction through hybrid degradation tracing model in the degradation stage, which is based on an SVM classificator. T. Praveenkumar et al. investigated [
24], the usage of SVM-based models and time domain statistical features, such as mean, median, etc., to forecast failures in gearboxes. K. Dhalmahapatra et al. developed [
25] a decision support system for failure forecasting, using a multi-step knowledge discovery process involving multiple correspondence analysis (MCA), t-SNE algorithm and K-means clustering. S. S. Ng et al. proposed [
26] a naive Bayes model for RUL prediction of batteries under different operating conditions and showed its competitiveness in accuracy with SVM based models and importance of different operating conditions and their impact on degradation of equipment. S. Patil et al. proposed a new approach for RUL prediction [
27], which includes the use of ensemble regression techniques such as Random Forest and Gradient Boosting for prediction of RUL with time-domain features, which are extracted from the given data.
Artificial neural networks are common in recent years. There are several main directions, focusing on different architectures, such as LSTM and CNN.
J. Deutsch et al. [
28] presented a deep belief network-based approach for RUL prediction of rotating components for big data applications. P. Khumprom et al. [
29] developed a new model, based on recurrent neural networks with amplified dropout to increase number of training runs. R. Zhao et al. [
30] investigated application of Long Short-Term Memory networks (LSTMs) for machine health monitoring in the first study about a empirical evaluation of LSTMs-based machine health monitoring systems and introduced a real life tool wear test. A. Sagheer and M. Kotb proposed [
31] a pre-trained LSTM-based stacked autoencoder (LSTM-SAE) approach in an unsupervised learning fashion to replace the random weight initialization strategy adopted in deep LSTM recurrent networks to improve the performance in modelling multivariate time series (MTS) data, particularly when attempting to process highly non-linear and long-interval MTS datasets. Y. Zhang et al. [
32] proposed an adaptive recurrent neural network (RNN) to predict the remaining life of Li batteries, and a technique for optimizing the weights of the network structure through a cyclic Levenberg–Marquardt method. F. Zhou et al. [
33] proposed an early diagnosis method based on Deep neural networks (DNN). The high-dimensional fault features extracted by deep learning are reduced into one-dimensional, and then the life prediction model is constructed by using the nonlinear fitting method. L. Mao et al. [
34] developed a hybrid LSTM-STW and GS-LM method to decompose the data into high-frequency and low-frequency components, create separate RUL predictions using the LSTM-based model and integrate them to obtain final prediction. B. Long et al. [
35] proposed LSTM-based forecasting method with an improved data construction method for a lower number of data samples available, which is able to increase the accuracy of forecast for lithium-ion batteries.
G. S. Babu et al. [
36] made the first application of deep convolutional neural networks (CNN) to RUL forecasting. K. B. Lee et al. [
37] introduced the FDC-CNN model, based on CNN architecture, in which a receptive field tailored to multivariate sensor signals slides along the time axis, to extract fault features, which enables the association of the output of the first convolutional layer with the structural meaning of the raw data, making it possible to locate the variable and time information that represents process faults. L. Ren et al. [
38] proposed new feature extraction method to obtain the eigenvector that is suitable for deep CNN. In the prediction phase, a smoothing method is proposed to deal with the discontinuity problem found in the prediction results. J. Zhao et al. [
39] reviewed forecasting methods for RUL and outlined the suitability of CNN for monitoring massive data and its ability to realize automatic feature extraction and recognition without manual participation and intervention. C. Sai et al. proposed [
14,
40] a new hybrid approach for RUL forecasting introducing a model, based on combination of CNN and LSTM and showed accuracy improvements of a combined approach compared to only using the CNN or LSTM-based models.
Several articles [
14,
20,
22] cover the forecasting of turbofan engines [
18], which is the main focus of this article. Out of them, methods based on convolutional neural networks (CNN) are looking to be the most promising, being widely accepted and very precise, and reaching an accuracy of 18.90 (RMSE) [
14].
However, as much as we upgrade architecture of forecasting methods, at some point they going to reach a limit of performance. After that, optimizations and improvements for forecasting procedure that can be performed beyond the scope of forecasting model itself are going to play an important role in increasing accuracy.
Research [
23,
41] shows the viability of splitting data into separate parts or modes of operation in accordance to the health index of energy equipment for improving accuracy of forecast. Basically, at least two modes of operation can be distinguished: normal operation and degradation [
41] and a separate forecasting models can be built for each of the parts. For these parts, the task of splitting is essentially a task of finding a point in time series at which the degradation starts.
2.3. An Idea of the DPI Method
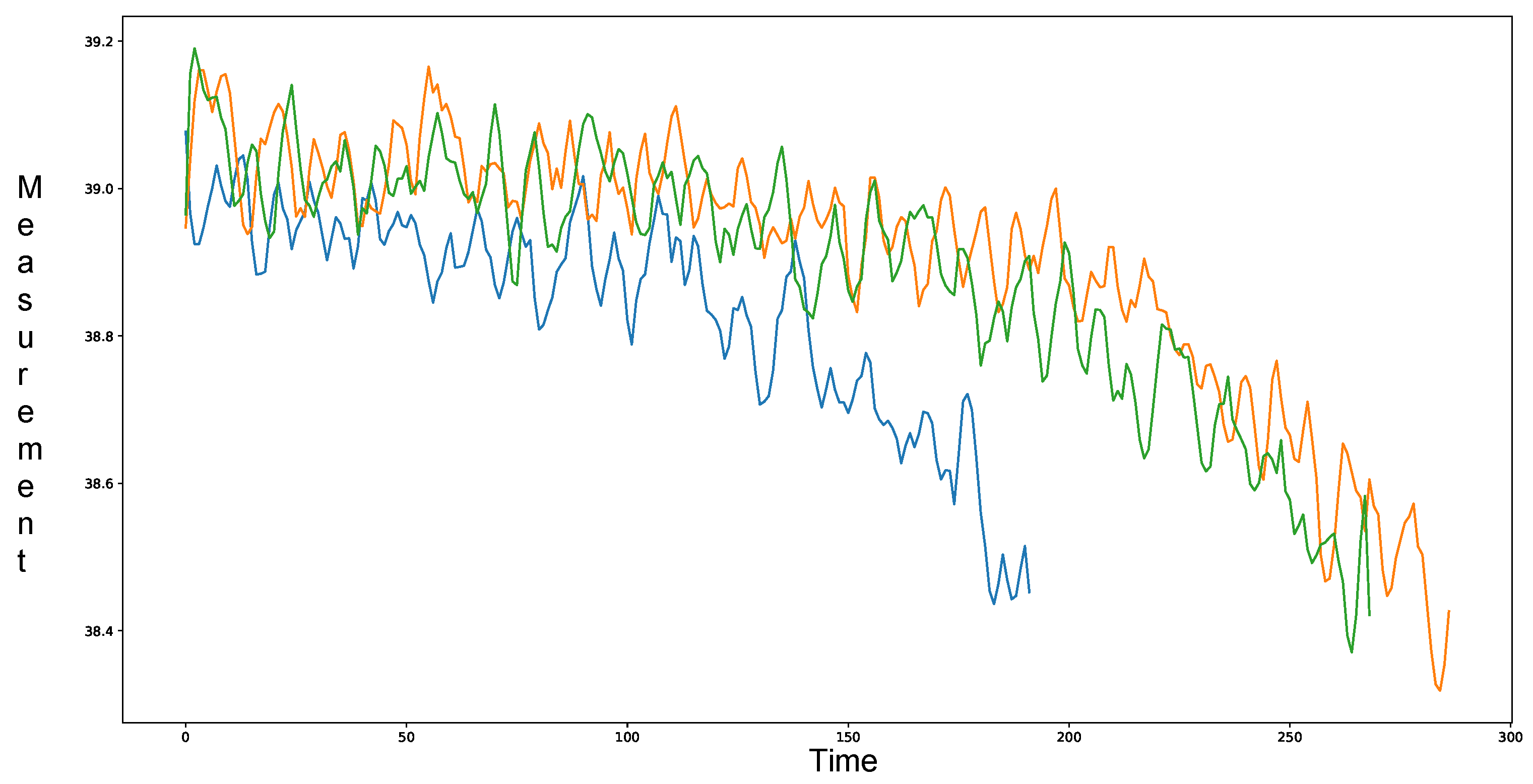
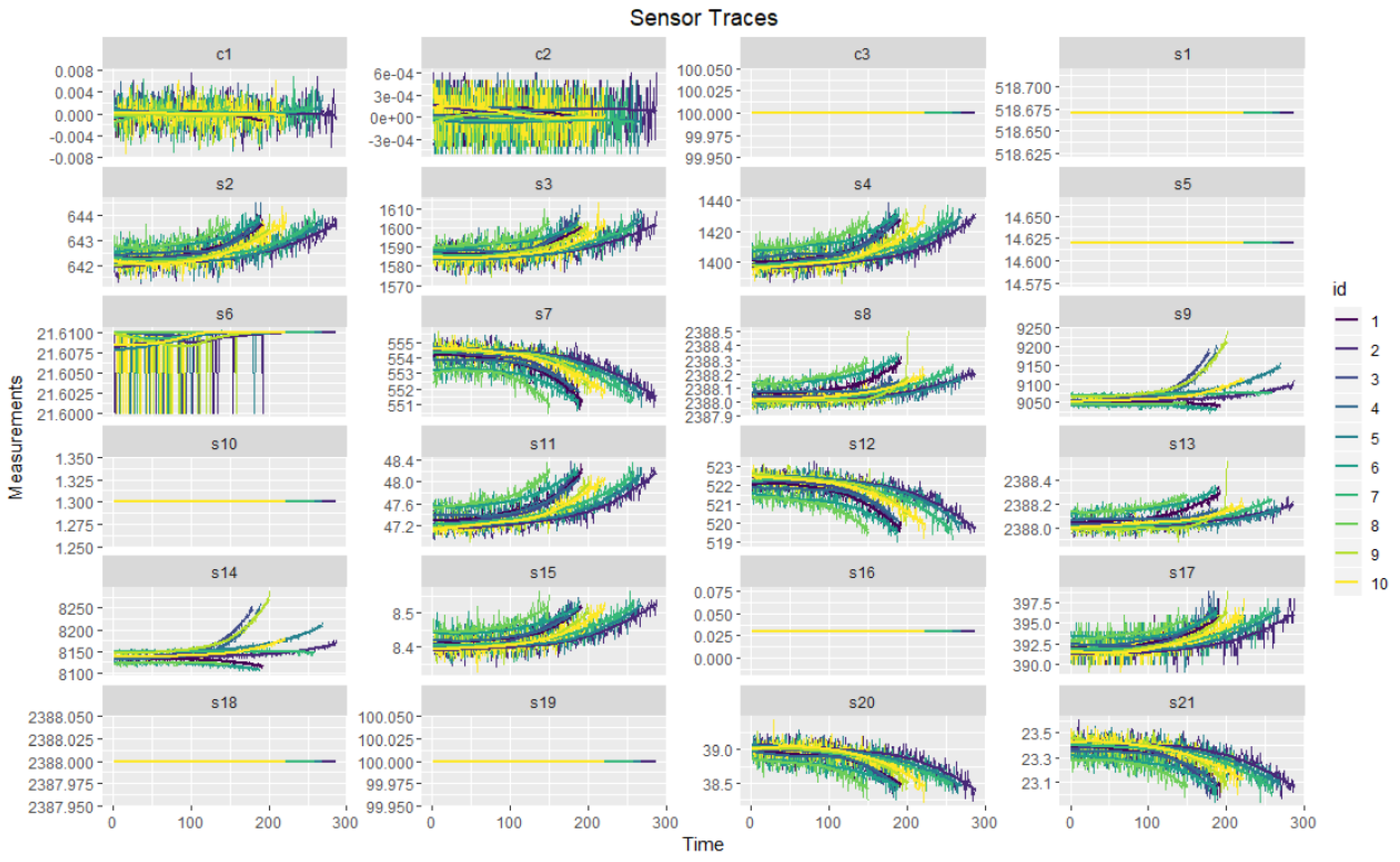
During the operation of energy equipment, after some point in time, the degradation process begins. An example of operation data is provided at
Figure 4.
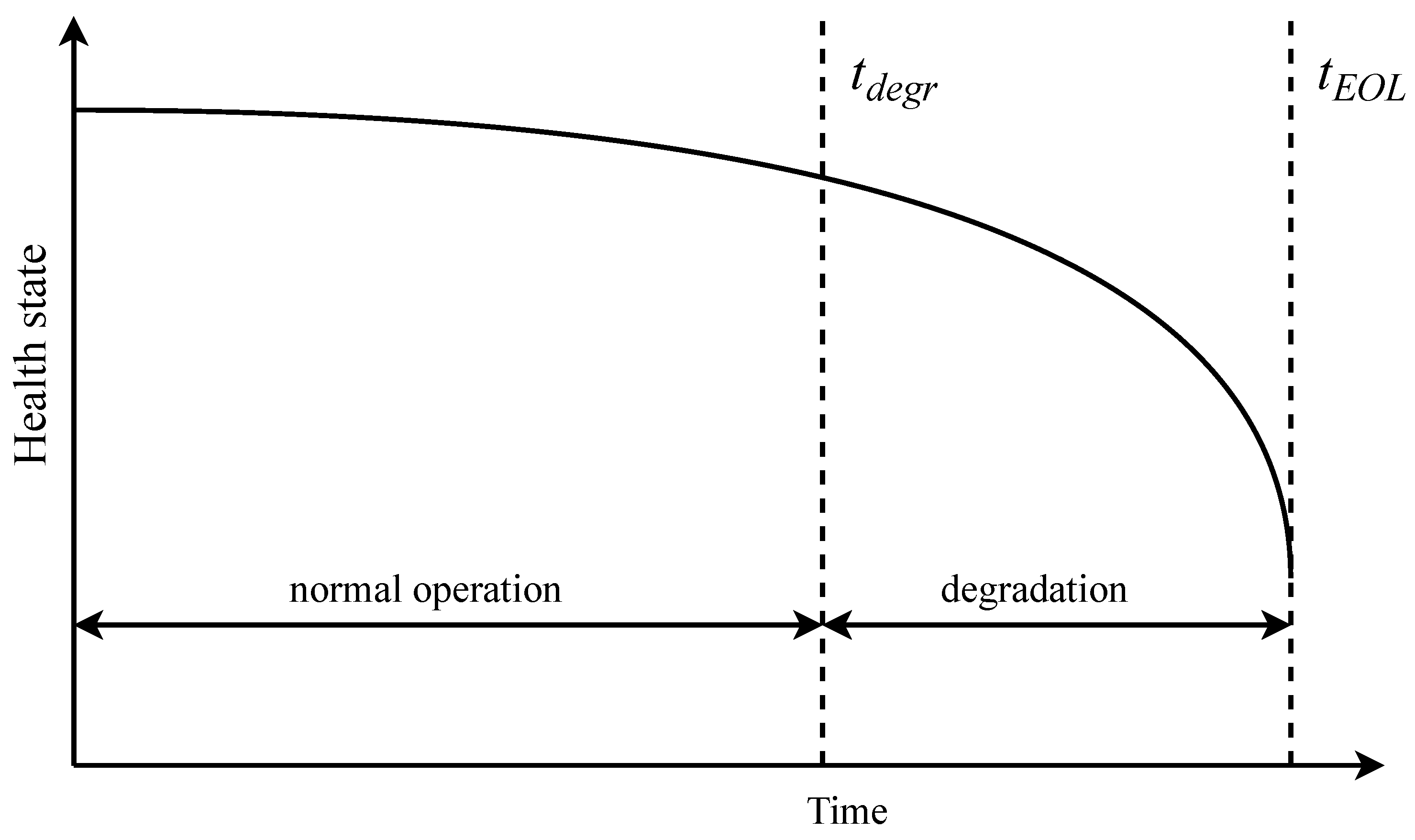
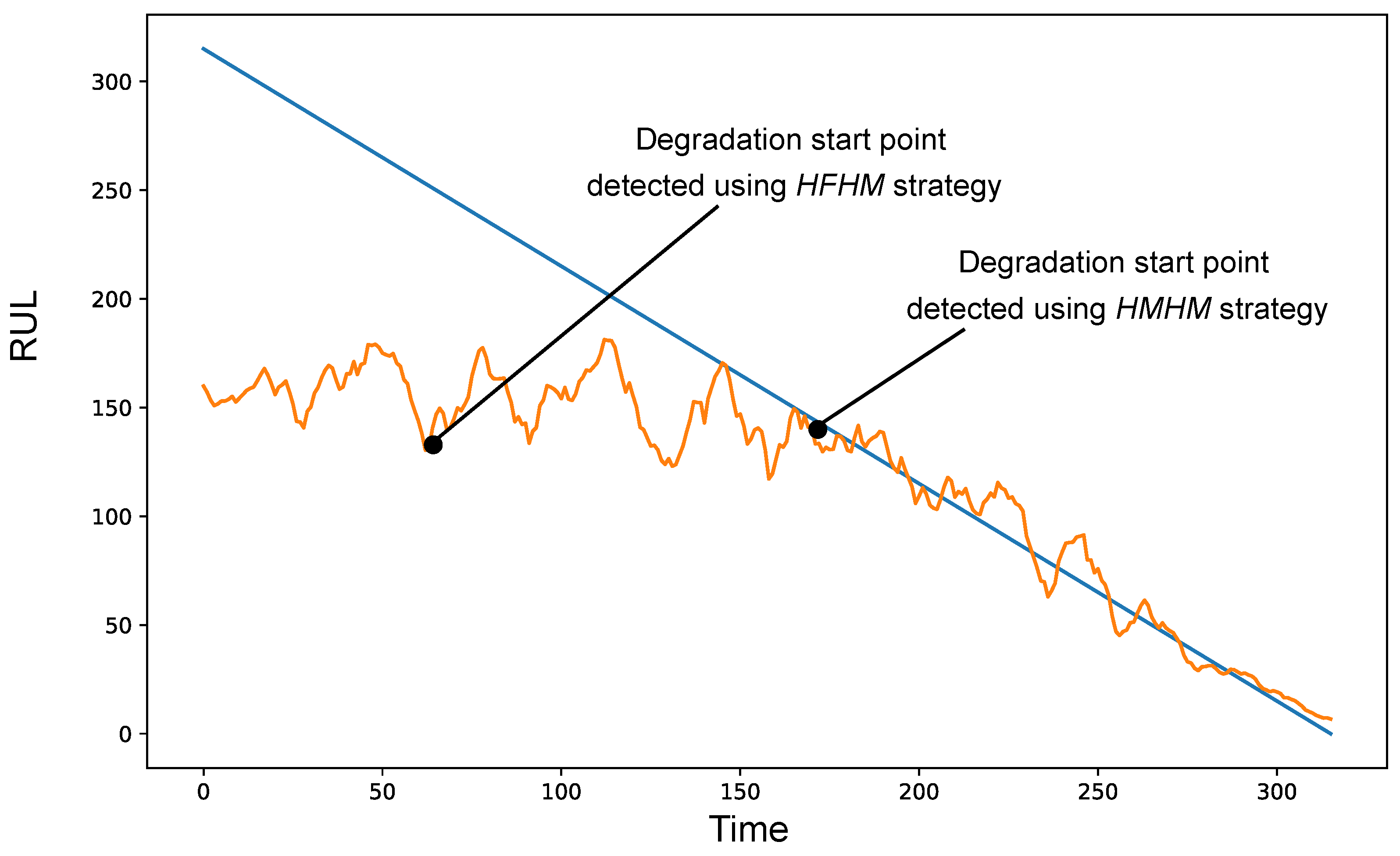
Figure 5 shows an illustration of the degradation process.
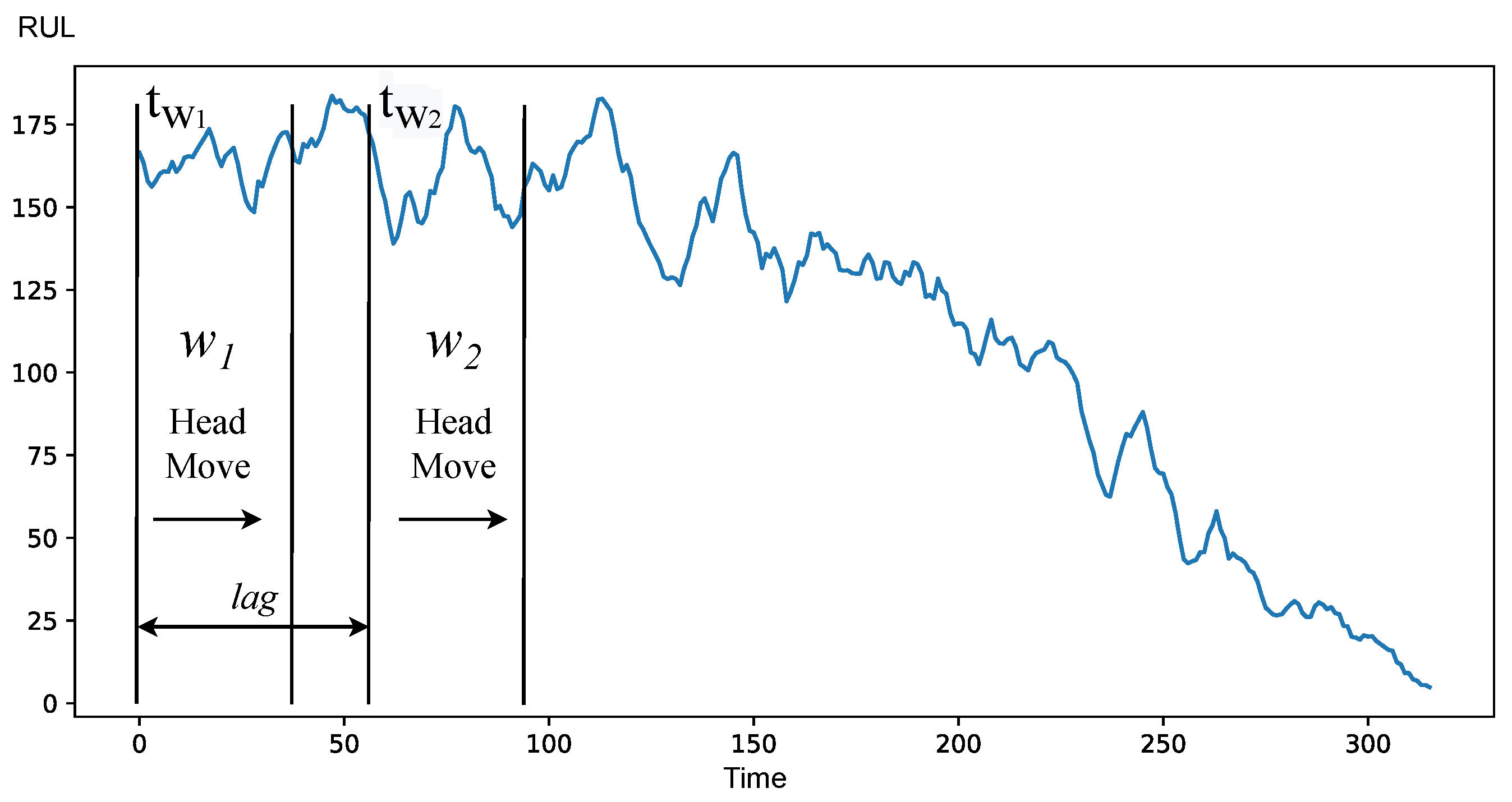
To determine the point at which the degradation process begins (starting point of degradation) we propose a new DPI method based on sliding windows. We apply two windows , of size w to a univariate time series and compare data values in these windows.
There are two types of windows possible in our framework: and . is a window that has its initial position at the beginning of the operation. is a window that originates at the end of useful life.
We consider two possible operations for manipulating the position of windows: and . is an operation which changes the position of window against time series. It has two parameters: distance and direction. Distance is measured in number of consecutive measurements on which position is changing. In the proposed method, the distance is set to 1 for every case.
Which direction the window in is moving is dependent on its type. Direction can be either forward, which means from beginning of operation to end of life, and backwards, which is the opposite. is moved in a forward direction, —in backward direction. is an operation that puts the window at a certain preset position and does not move it over time.
To compare data within windows we use the Kruskal-Wallis test [
42]. We assume that windows are different if the null-hypothesis is failed for two given windows, otherwise they are similar. Windows which belong to the normal operation stage are expected to be similar to each other and windows which belong to degradation stage are different. This is because during normal operation the sensor data stay relatively unchanged, and during the degradation stage we observe significant changes in the data.
Positive check and negative check are the terms used for the description of the comparison results. A positive check is a result of the comparison of two windows with the Kruskal-Wallis test, which returns the value of more than 0.05, which means that windows can be considered similar. A negative check is a result of comparison of two windows with Kruskal-Wallis test, which returns the value of less than 0.05, which means that windows cannot be considered similar.
In this framework, we distinguish five possible strategies of moving windows. They are provided in
Table 1. Other possible strategies are either duplicates of the provided ones or not suitable for time series analysis (e.g., two fixed windows).
HMTF strategy allows for comparing every part of the historical data to the final range just before the end of life by moving window
towards
where
is located. This is beneficial because we can safely assume that the process near the end of life is in the degradation stage. However, this strategy has a disadvantage of being able to be used only on historical data and not on real-time data, because it requires the
value to work. Moreover, it has a requirement for comparison operation, where the check for two windows in the degradation stage needs to be positive. With our selected method of comparison, it is not possible due to the fact that windows in the degradation stage are different.
Figure 6 illustrates the idea of the HMTF strategy.
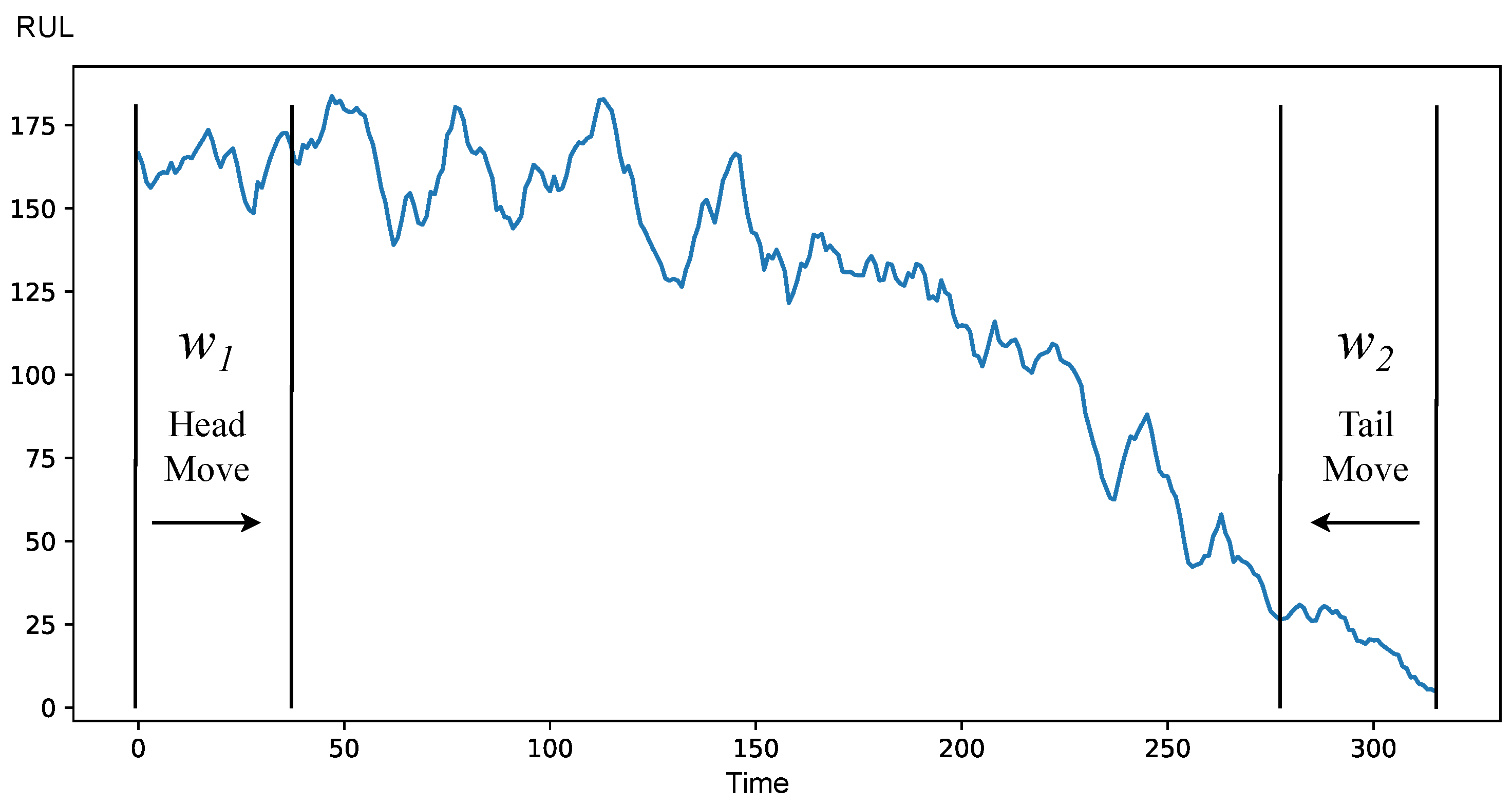
The HMTM strategy consists of the two windows
and
moving towards each other. At the start, two windows are assumed to be different, because they should belong to different processes. The beginning of the degradation stage is determined when the check for data in the windows is positive. This strategy also has a disadvantage of requiring a value of
to function; hence, it can be only used on historical data. Demonstration of HMTM is provided at
Figure 7 and shows how the proposed method works for the HMTM strategy.
The HFTM strategy is based on the following: a window
is fixed at beginning of operation and a window
is moving from the end of life towards the first one. We assume that data at the beginning of the operation belongs to a normal operation stage. At the start, a comparison of data belonging to windows should return a negative check result. The beginning of degradation is at the point where the check result becomes positive. This strategy also has a disadvantage of requiring the position of the end of life point
to function; hence, it can be only used on historical data. The demonstration of HFTM strategy is provided at
Figure 8.
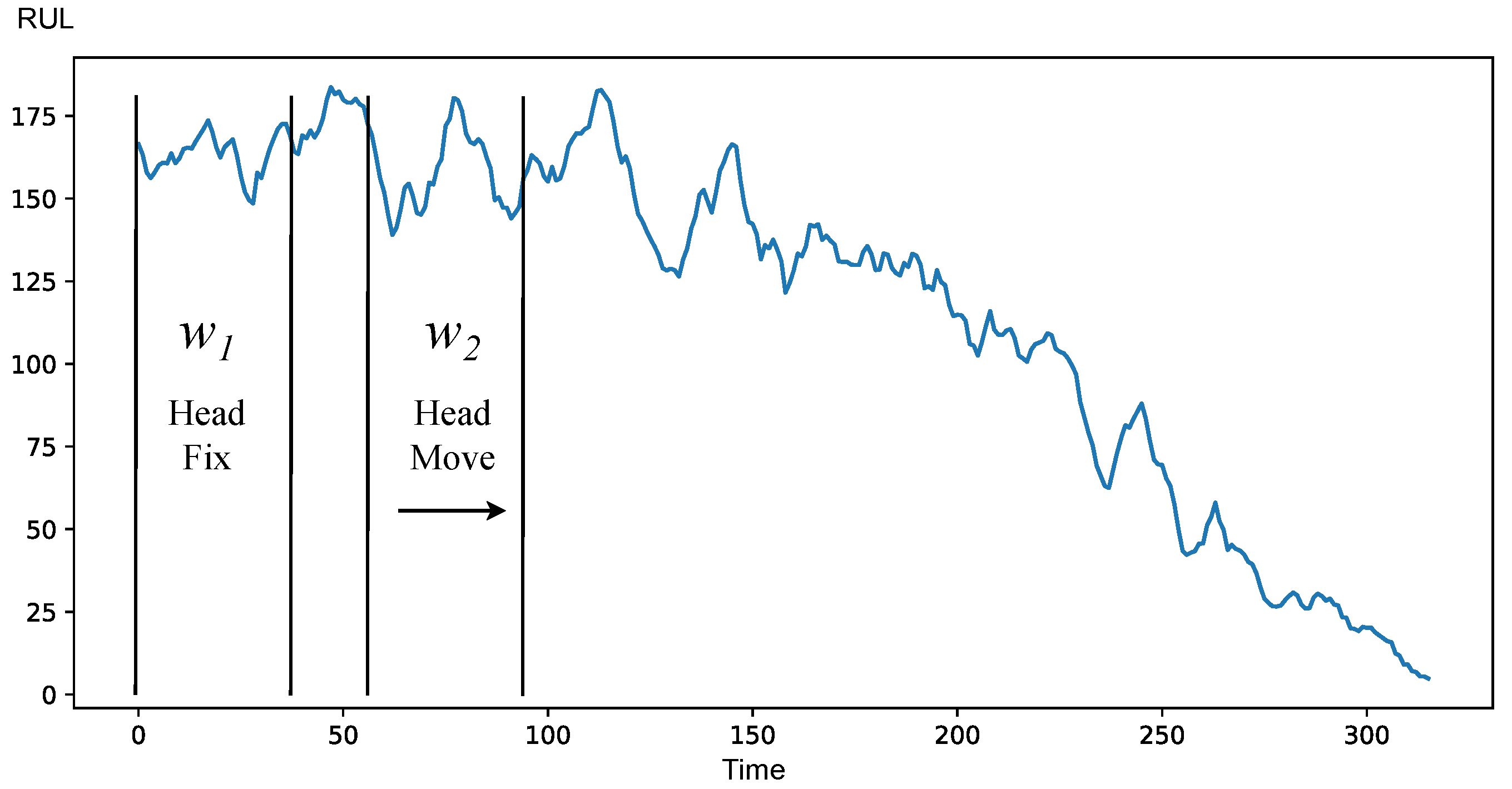
HFHM strategy consists of the
window fixed at the beginning of the operation and other window
moving from the first one towards end of life. At the start, the windows should be similar. The beginning of degradation is at the point where they become different. This strategy is similar to HFTM and is an improvement on it, because it does not require it to know the value of
. An illustration of of HFHM is provided at
Figure 9.
HMHM strategy consists of two windows
,
moving from the beginning of the operation towards the end of life. The distance and amount of overlap of two windows is described by parameter
, which is a difference between the starting points of windows, as shown in Formula (
2).
where
are the positions of the left edges of windows
and
, accordingly.
If then two windows are overlapping.
The beginning of degradation is at the point where
,
cannot be considered similar, i.e., Kruskal-Wallis value of
. Demonstration of HMHM is provided at
Figure 10.
This strategy is more robust than the HFHM, because it accounts for possible drift in values during normal operation, which otherwise might have been considered as a sign of degradation. To achieve this, the strategy utilizes a lag of a second order parameter to adjust the sensitivity of detection. The meaning of this parameter is a number of consequent negative checks. The higher the value of the parameter, the less sensitive this strategy is for data fluctuations, and vice-versa—the lower the value of the parameter, the more sensitive is the strategy.
2.4. A Scheme of the DPI Method
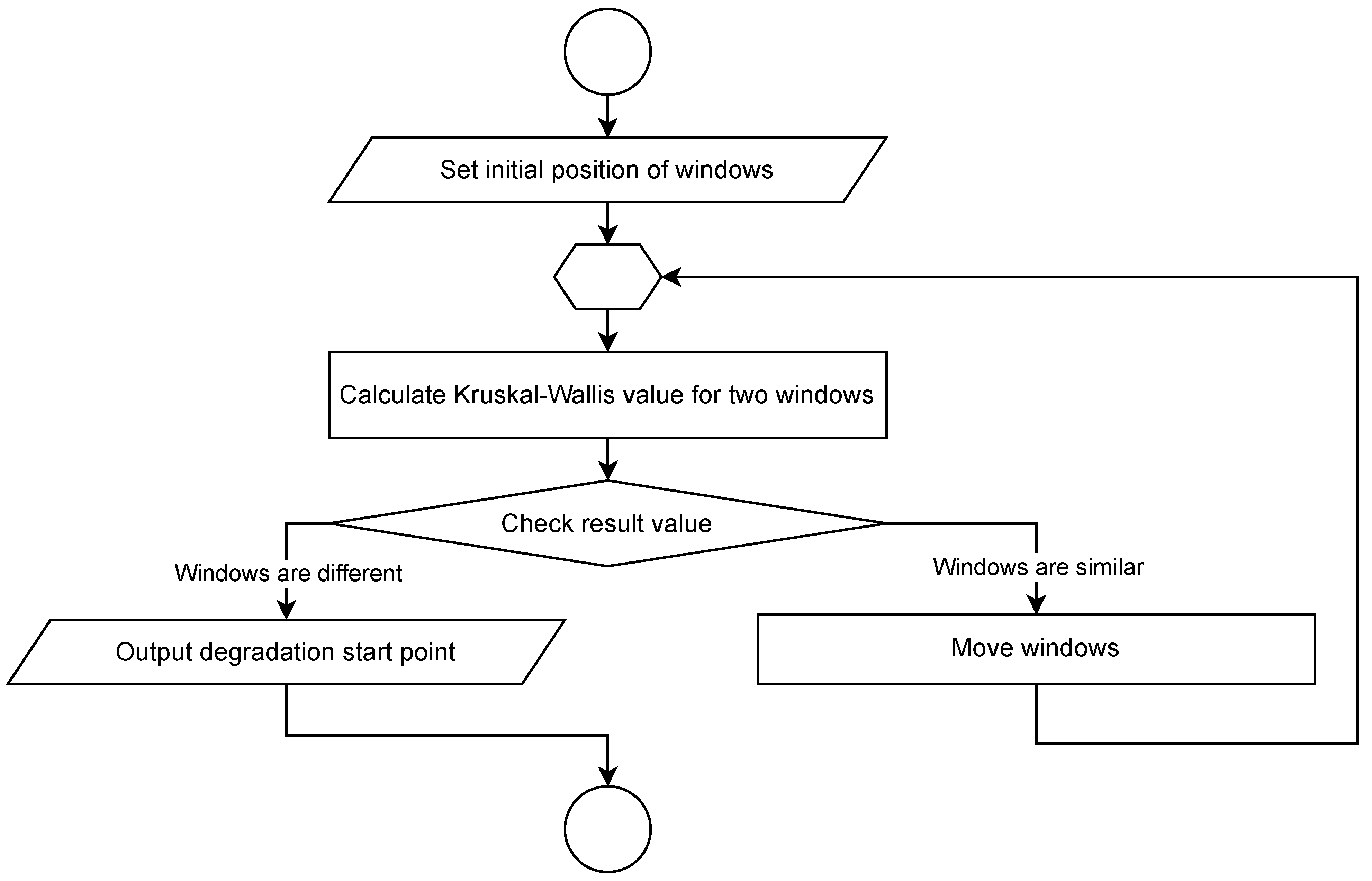
The general description of the DPI method is depicted at the
Figure 11. Algorithm 1 shows operation of the method for HMHM strategy to produce the degradation start point
on data
x using two moving windows
and
with the size
w. HMHM strategy also requires lag
l input parameter, which is the distance between two windows
and
. Another parameter is
, which is a lag of a second order, i.e., the number of iterations for which Kruskal-Wallis condition has to be met in order to consider it a true start of the degradation process and reduce noise.
| Algorithm 1 Determining degradation start point using HMHM strategy. |
Input: Output: ▹ Initial position of the first window ▹ Initial position of the second window ▹ Flag that indicates whether degradation start point was found ▹ Current number of consequent negative checks whiledo if then ▹ Reached end of data without finding point else ▹ Data in the first window ▹ Data in the second window ▹ Calculate using Kruskal-Wallis test if then else end if if then else ▹ Move windows a step forward and repeat end if end if end while
|
2.5. Update RUL Forecasting Using Proposed Method
To mitigate inaccuracies of RUL forecasting in models that use the whole data from the beginning of the operation to the end of life, we split data into two stages—normal mode of operation and the degradation process. To do this, we used a DPI method described in
Section 2.3.
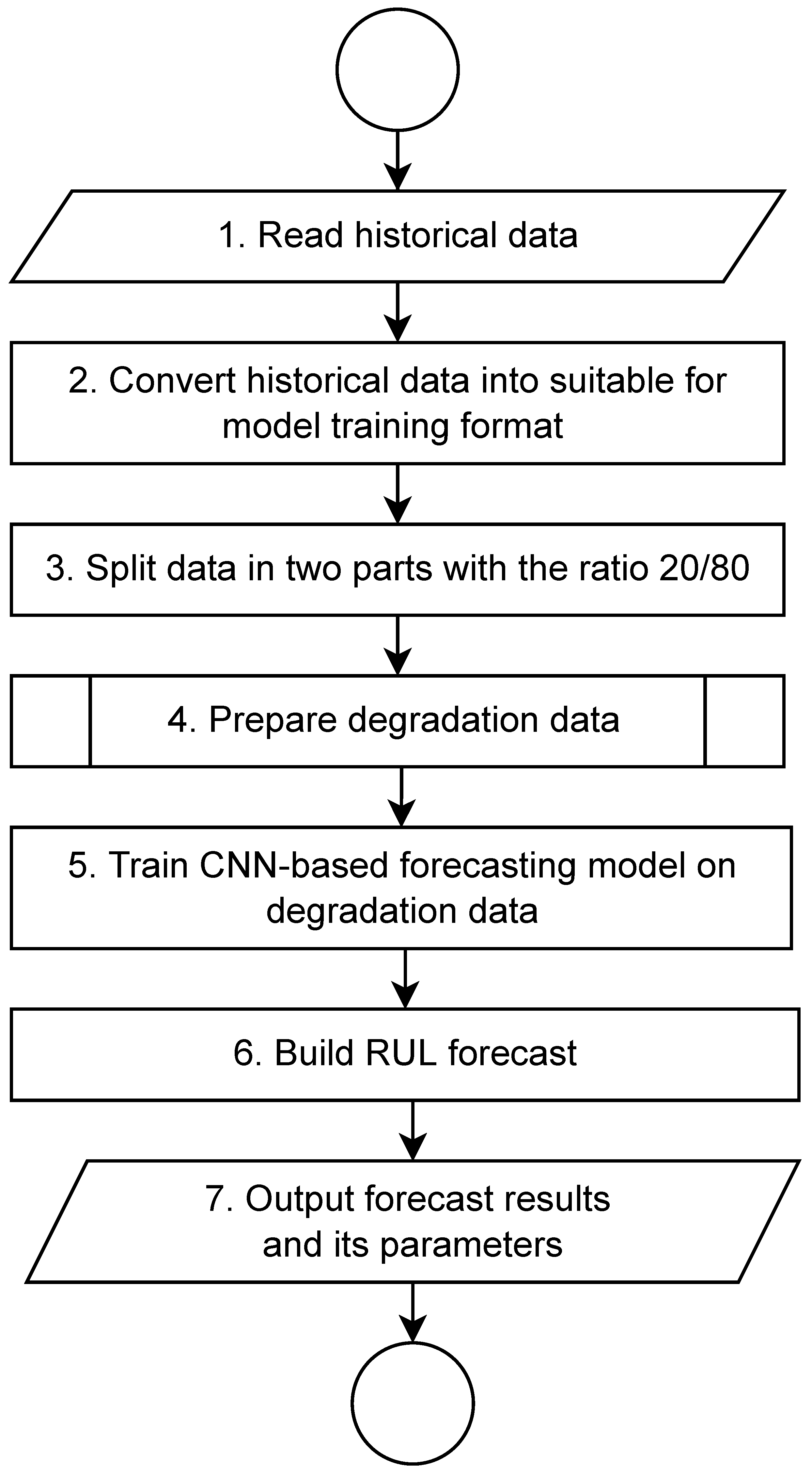
Figure 12 displays the top level diagram of the whole implementation of the method for RUL forecasting.
At step 1 of the method, the raw historical data is loaded from .csv file. The data consists of the following attributes: engine number, cycle number, parameters and values from various sensors.
At step 2, the data are prepared for further use in training forecasting models. First, the remaining useful life (RUL) is calculated for each line. Then, all parameters with zero variation are removed from the data. Then, all input parameters and sensor values are normalized. Finally, inputs and outputs for learning are prepared. The RUL value of measurement is taken as an output. The two-dimensional array of sensor parameters of length w, that represents w consequent measurements before the corresponding RUL value, is formed as input.
At step 3, the data are split into two parts: of size 20 percent and of 80 percent of total data.
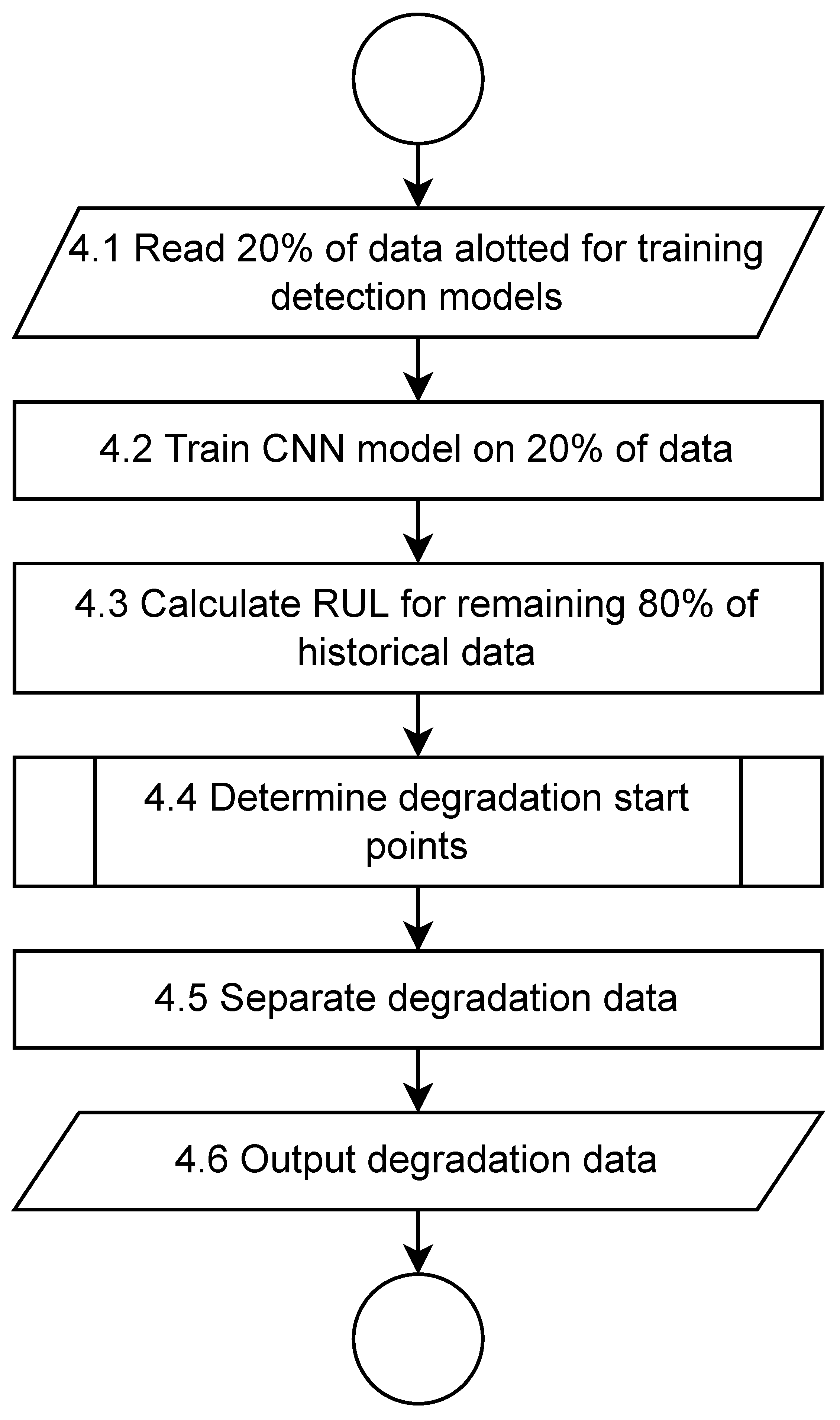
At step 4, data for the degradation process are split.
Figure 13 provides a flowchart with a further breakdown of this step. At step 4.1, part of the data
of size 20 percent is read. At step 4.2, this
data are used for training the first CNN-based forecasting model. At step 4.3, the trained model is used to forecast the RUL for
data.
Then, at step 4.4, points at which the degradation begins are determined.
Figure 11 provides a flowchart of the determination of degradation start point. At step 4.4.1, the initial positions for moving windows are set according to the selected strategy. At step 4.4.2, the statistical test is performed on data that these windows cover. At step 4.4.3, the test result check is performed. At step 4.4.4, if the windows are different, the degradation start point is set at the location of one of the windows. At step 4.4.5, if the windows are the same, their positions are moved and the execution moves to step 4.4.2.
At step 4.5, data are split into normal process and degradation, where the degradation data are located after the degradation start point. At step 4.6, these data are outputted for further use in the following steps.
At step 5, data from step 4 are used for training the CNN-based forecasting model. At step 6, the forecast for RUL is built using model from step 5. At step 7, the forecast result is outputted.
2.6. CNN Architecture
We use the convolutional neural network (CNN) as a benchmark method as well as in conjunction with proposed methods’ strategies. CNN is a Deep Learning algorithm, which can take in an input two-dimensional array, assign importance (learnable weights and biases) to various aspects/objects in the image and be able to differentiate one from the other [
44].
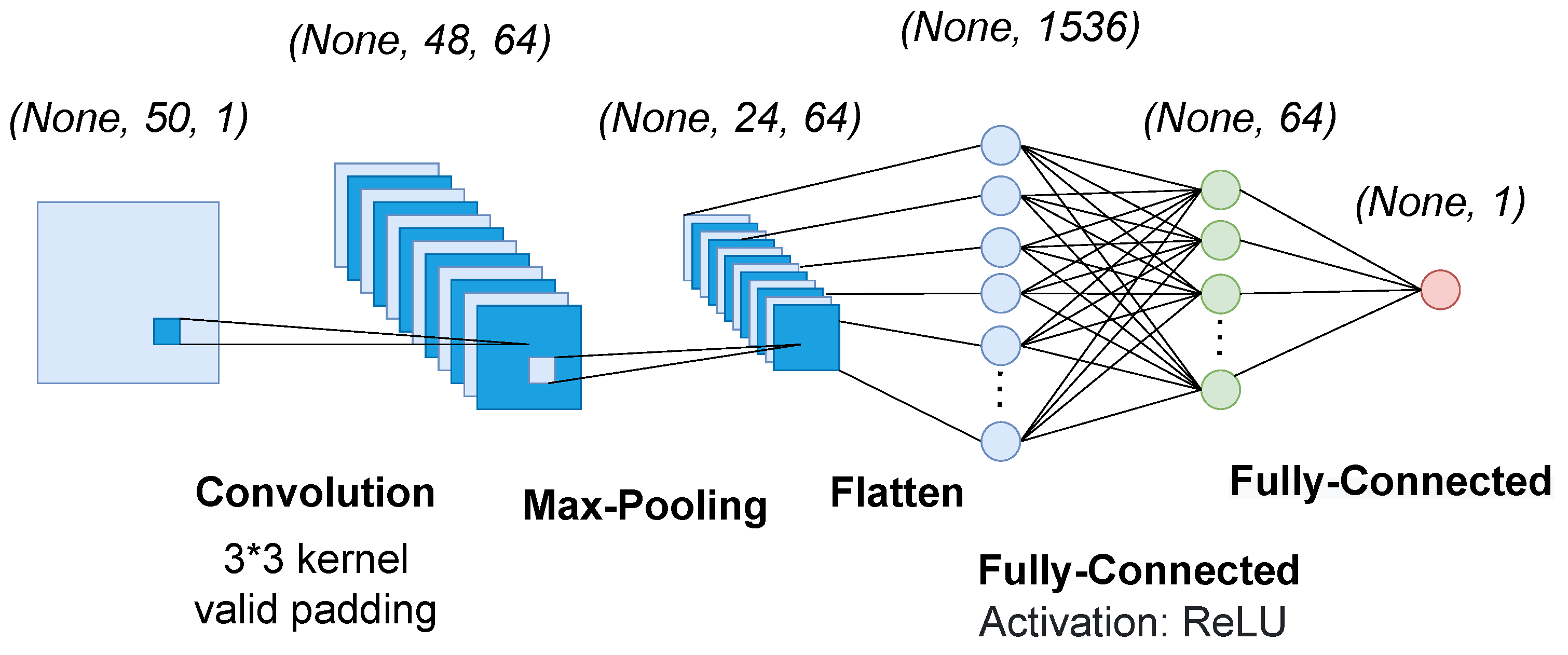
Figure 14 provides a visual scheme of the CNN used in the experiment.
The specific model that we use in this research was developed by Cuong Sai [
14].
Figure 15 provides a scheme of the architecture of that neural network.
Architecture of CNN includes one convolution layer, one pooling layer, flattened and two fully connected (dense) layers. Convolution layer receives input as a two-dimensional array and converts it to 64 filters with kernel size of 3 × 3 and valid padding and stride size of 1. Pooling is performed using max operation and pool size of 2 × 2. Pooling output is then flattened. After that there are two fully connected layers, one of which reduces dimension to 64 using ReLU activation and the other provides reduction to a single continuous output value using sum operation.
4. Discussion
In the experiment proposed, the DPI method in combination with the forecasting model was compared to the same forecasting model without any additional data preparation conducted as a baseline. The CNN model was selected because of its accuracy and prevalence in recent research. All related to CNN model parameters were kept the same across all tests. Baseline CNN model on the given data with given parameters showed an accuracy of 18.35 points MAE.
The Kruskal-Wallis test helps to determine the start of negative changes in the process we call degradation. The criterion is very basic and effective at the same time, showing the applicability of statistical tests to the data during the degradation start point detection. However, future work may be carried out to devise more comprehensive test for improved accuracy.
Some strategies require additional logic for the degradation start point detection, e.g., HMHM and its lag of a second order , but their primary objective is to make the DPI method less susceptible to random changes in data.
The strategy of moving sliding windows across data is the main variable point in the proposed DPI method. Depending on a strategy, the obtained results vary significantly, which can be attributed to the nature of a specific strategy.
HMTF strategy combined with a baseline CNN forecasting method shows an accuracy of 4.07 MAE, which is, basically, the most accurate result of the proposed method. However it is not applicable to real world scenarios because of: (1) it is required to know when failure is going to happen for this strategy to function; hence, its only a synthetic test of possible capabilities of the proposed method, (2) due to how late in the life of energy equipment it sets a degradation start point, indicated by how little data it considers to be a degradation (only about 5 percent), it would have poor performance in earlier stages of the equipment’s life and, thus, late reaction times.
The HMTM strategy shows a result of 13.57 MAE, which is an average result among tested strategies. If we look at the data distribution, we can observe that this strategy finds about 50 percent of data to belong to degradation process. Basically, it means that it puts the degradation start point in the middle of the life of energy equipment most of the times. This can be explained by the nature of the movement of windows in this strategy. They move towards each other with fixed equal speed and meet roughly in the middle. To mitigate this, further improvement to the comparison of data in the windows technique can be conducted. Moreover, it is possible to add a more comprehensive algorithm to adjust the size of a step for each window individually. This strategy is also unusable in the real world scenario because it requires one to know when failure is going to occur.
HFTM shows an accuracy of 15.28 MAE, which is one of the smallest increases in comparison to the benchmark method out of all the strategies. This is because it detects the beginning of the degradation point very early, as can be observed from the fact that part of the data considered that the degradation is over 85 percent. This is contrary to the proposal of splitting the data set into a normal operation and degradation process, as it only takes out small percentage of data. This also is not a very accurate representation of a real world process, as significant degradation would not occur in energy equipment for a majority of its lifespan. Moreover, it means that data that represent a normal operation are going to get mixed with one of the degradation process and decrease the accuracy of the forecasting model. This can be attributed to the first window being fixed, thus giving only a small range of the possible variation of values during the normal operation. The further tuning of sensitivity and the increasing range of the allowed values can be beneficial for the accuracy of this strategy, as it could allow to put the degradation start point further in the lifetime of the energy equipment. This strategy is also not usable in real world scenarios due to the requirement of knowing the end of life.
The HFHM strategy is very similar to a HFTM with 16.12 MAE, but conducted in reverse. it shows that practically the same accuracy and similar percent of data is considered degradation. This strategy, however, can be used in a real world scenario, because it does not require knowledge of the end of life point to function.
Finally, the HMHM strategy that shows the result of 9.38 MAE, which is better than the average but still not as good as HMTF. This strategy considers about 43 percent of data on average to be degradation, which means that it can provide a better reaction time, making the forecast of the remaining useful life when over a third of a lifespan of energy equipment is still left. This strategy is more robust than HFHM because it can account for smaller changes in values from sensors and overall is the most balanced option out of all the considered strategies. A minimum amount of change in the health index, which is required for it to trigger, is higher than in some other strategies, which is going to prevent data from the early stages of operation to mix in with degradation data, while not being too high and having a late reaction time. Moreover, this strategy can be used in a real world scenario because it does not require the coordinate of the end of life to function.
There is an observable correlation between the accuracy of the forecast and position of the degradation start point in the lifespan of the energy equipment. The further the point is, the more accurate the forecast is. This observation supports the trend that the degradation of energy equipment speeds up towards the end of life.
With the use of the proposed degradation start point detection method, it is possible to double the accuracy of the forecasting method in real world scenarios (HMHM strategy) and up to four times increase in the accuracy when performing synthetic tests (HMTF strategy).
Increasing the accuracy of RUL forecast provides higher quality data for the decision support step and allows for increased precision in managerial decisions for maintenance planning. This, in turn, would improve the reaction to possible failures by reducing the chance of failure occurring and reduce operating costs.
We may point to the following limitations of the proposed method:
- (1)
The method is used on aggregated data for each operation cycle, i.e., each equipment parameter has only one value for each given operation cycle. In real life, we have a set of values for every equipment parameter that describes the operation cycle. The length of the set is defined by the duration of the cycle and granularity of data acquisition. Therefore, we need preprocessed aggregated data to use with the proposed method, which necessitates the additional dependency on data aggregation algorithms.
- (2)
Tail-based strategies (HMTF, HMTM and HFTM) could not be used in a real life scenario because they require knowledge of the end of life time of equipment to operate; hence, they can only be used as a benchmark on historical data. That is why all our significant results are obtained based on Head-move strategies.
- (3)
We use aggregated value of RUL forecast based on all parameters to perform DPI, which is a possible limiting factor for achieving the maximum accuracy of the degradation process identification. Thus, a shift to the estimation of the beginning of the degradation process based on individual parameters of equipment and their correlation may give better accuracy and more control over DPI.