Abstract
Using low-temperature (shallow) groundwater as a heat source or heat sink is a common practice to supply space heating or cooling, especially in the United States, Canada, China, and several European countries. The groundwater heat pump (GWHP) system has been extensively studied in recent decades using numerical approaches, which have some limitations in understanding the soil’s thermal behavior. Therefore, a laboratory-scale experimental study involving cooling tests was carried out to investigate the impact of GWHP on system performance and sustainability with varying groundwater flow velocities and injection and abstraction rates. The results demonstrated that groundwater flow velocity, as well as injection and abstraction rates, significantly impact thermal plume development. Higher injection and abstraction rates create a larger thermal plume, thereby decreasing abstraction temperature. However, groundwater flow prevents heat development around the well by dispersing the heat in the groundwater flow direction. Furthermore, the results indicate that the energy gain only increased by 81% and 107%, with a respective increase of 100% and 200% in injection and abstraction rates.
1. Introduction
The ground source heat pump (GSHP) is a technology that can benefit from the constant temperature of the shallow ground as a heat sink for space cooling during summer and as a heat source for space heating during winter [1]. One common application of GSHP systems is a groundwater heat pump (GWHP), which utilizes low-temperature (<32 °C) groundwater to fulfill heating and cooling requirements for buildings [2]. GSHP systems exhibit high efficiency compared to conventional heating and cooling technologies. The efficiency of heat pumps is defined as the coefficient of performance, and it may range between 4 and 6 depending on the source temperature, the technology used, and the operating mode (heating or cooling) [1]. GSHPs can provide heating and cooling solutions at the district level with low greenhouse gas emissions [2].
In GWHP applications, it is generally preferred to reinject the thermally used groundwater back into the same aquifer to maintain aquifer pressure stability [3]. This practice generally creates a thermal plume starting from injection wells. In certain instances, this thermal plume may extend to the abstraction well due to the coupled effect of convection and conduction. This phenomenon is referred to as thermal feedback when the injection temperature is constant and as thermal recycling when the difference between injection and abstraction temperature is constant [4]. If the source temperature changes, the thermal feedback may affect the system’s sustainability and even cause system failure [5]. Thermal feedback may occur, especially in urban areas where the required distance between the injection and abstraction well cannot be guaranteed due to the lack of available land area [6]. Many recent studies have focused on thermal feedback to choose optimal configurations when designing a GWHP system. The occurrence of thermal feedback in a GWHP system mainly depends on factors such as the distance between wells, abstraction and injection rates (heating or cooling loads), groundwater flow velocity (hydraulic gradient), aquifer size, and injection temperature [5]. All the parameters affecting the system’s efficiency and sustainability should be considered and analyzed carefully before installation.
Thermal feedback has been extensively studied in recent decades, with the implementation of analytical solutions to analyze this phenomenon. Banks [5] introduced analytical solutions to address thermal feedback, proposing that analytical solutions could serve as an initial screening tool. Pophillat et al. [7] investigated thermal plume development using three analytical formulations, one without groundwater flow and two with two varying groundwater flow velocities. Their comparison of these analytical solutions indicated their applicability in assessing the thermal effects of GWHP systems, although it was noted that this approach could potentially lead to overestimating the thermal impact of such systems. Milnes and Perrochet [4] presented an analytical solution for assessing the impact of thermal feedback. They conclude that this analytical approach can be used as a screening tool to identify potentially viable conditions for further analysis. They also highlighted that defining steady-state conditions for dynamic systems presents some limitations. Furthermore, Banks [5] pointed out that the limitations of analytical solutions in groundwater systems include challenges related to well placement, seasonal variations in loads and temperatures, multiple well configurations, heterogeneity of the aquifer, and three-dimensional abstraction and re-injection scenarios.
Numerical approaches have also been used to study the phenomenon of thermal feedback and determine optimal system configurations [8,9,10]. Many of these studies have utilized FEFLOW, a finite element subsurface flow and transport simulator, to analyze the effect of thermal feedback [7,10,11,12,13,14,15,16,17,18,19]. Some of these have been conducted based on case studies involving the establishment of GWHP systems [6,10,12,20,21,22,23]. Additionally, there are alternative numerical tools available for simulating heat and mass transport, as well as groundwater flow, including SHEMAT (Simulator for Heat and Mass Transport) and HST3D (Heat and Solute Transport in Three-Dimensional Groundwater Flow Systems). Although numerical tools for investigating the performance of GWHPs are powerful and widely used, they have certain limitations. For instance, they rely on simplifications and assumptions to make the mathematical models tractable and computationally efficient. Furthermore, numerical models are based on input parameters and initial conditions that are subject to uncertainties, thereby making them (numerical tools) unable to capture complex real-world conditions with regard to heat and liquid movement in soil and the changes in ambient air temperature.
Laboratory-scale testing provides an alternative approach for evaluating thermal plume dimensions and the impact of thermal feedback on system performance. The sandbox model is a widely employed experimental method for investigating such systems, although its application to GWHP systems has been relatively limited. For instance, Park et al. [24] have conducted a laboratory-scale experimental study coupled with numerical modeling in which the effect of the thermal dispersion coefficient under forced groundwater flow has been investigated. It was found that groundwater flow influences the thermal dispersion coefficient, leading to an increase in its value even at low velocities. Another experimental study, associated with a numerical computation, was carried out by Jiang et al. [25], where they investigated the effect of different well types on the thermal breakthrough in the aquifer. Their findings demonstrated that increasing the number of injection and abstraction wells or expanding the distance between them can reduce the likelihood of thermal breakthroughs. Another experimental study conducted by Giordano et al. [26] focused on the thermal effects of heat injection in porous media for underground thermal energy storage applications, using electrical apparent resistivity measurements. The outcomes highlighted that the electrical measurement results can be utilized to predict heat transfer in saturated porous media. The results demonstrated an acceptable level of agreement in terms of thermal plume development when compared to various approaches. Zhou et al. [27] investigated the impact of groundwater flow on aquifer temperature by carrying out a simulation-based model coupled with an experimental study to validate the numerical model. The results indicated that a horizontal upstream groundwater flow can delay the timing of thermal breakthrough in heating-only applications. Song et al. [28] conducted an experimental study to investigate the thermal impact of various operation modes on a single-well GWHP system. They discovered that when heating and cooling loads are in close proximity, it increases heat extraction. Li et al. [29] carried out an experimental study to examine the influence of groundwater flow variation on heat transfer characteristics. They compared different layouts of abstraction and injection well groups to enhance the efficiency of GWHP. They observed that higher groundwater flow velocity results in a more significant change in the abstraction temperature, resulting in faster thermal breakthrough. The literature shows that no studies were carried out on the impacts of different injection, abstraction, and groundwater flow rates on the thermal plume development for a well doublet.
Although many numerical studies on thermal feedback due to the operation of the GWHP system have been conducted, laboratory-scale experimental studies on thermal feedback are limited. It has been observed that while real-scale experiments are more reliable, they have some limitations. For instance, conducting a real-scale underground investigation for a GWHP system is expensive and time-consuming as it requires special equipment and drilling. Real-scale experiments are site-specific, with each site having its unique characteristics. Furthermore, the system must be available for testing, and the testing may require permission from the authorities. In contrast, laboratory-scale testing proves to be cost-effective and scalable, allowing for design at various scales. Within laboratory-scale testing, parameters affecting the system configuration, such as groundwater flow, well distance, injection and abstraction rate, and temperature, can be meticulously controlled and adjusted.
The main aim of this paper is to investigate the impact of GWHP operation parameters on system performance and sustainability for space heating operations. In addition, we established a laboratory-scale sandbox model to study the thermal plume development around the injection well and the thermal feedback resulting from cold water injection. The tests were performed under three different groundwater flow velocities to observe their impact on the thermal plume development. Furthermore, we explored the effect of injection and abstraction rates on thermal plume development. The experimental results were compared with the analytical approach, revealing an acceptable level of agreement. The findings can serve as a valuable tool for validating numerical models and provide significant insights to researchers and designers. However, it is important to acknowledge that these results may be context-specific, as they could be influenced by potential variations in the experimental parameters.
2. Materials and Methods
2.1. Overall Design
The experimental setup was designed to study the effects of injection and abstraction rates and groundwater flow rates on the performance of a GWHP system. The experimental setup was designed to permit the system to be run under various groundwater flow rates. The tank, which is made of glass-reinforced plastic, has external dimensions of 1.178 m × 0.721 m × 0.715 m (L × W × H). The thickness of the tank wall is 8 mm. All sides of the tank were covered with an insulation board of 0.05 m thickness. The tank was divided into three sections with steel mesh. A fabric was placed on the mesh to serve as a filter to prevent sand particles from passing through the mesh. The middle chamber, which is 0.825 m long, was filled with Red Hill-110 sand to a height of 0.5 m from the bottom of the tank. The other parts on the left and right were filled with water to control the groundwater flow by keeping the water head stable on the left tank and changing the water level on the right side. These hydraulic head tanks have a length of 0.123 m. These tanks were also filled with gravel to support the separator plate. Gravel does not affect groundwater flow as it has a higher hydraulic conductivity than sand. Excess water purge faucets were placed on both sides (see Figure 1). Faucets were placed at different elevations to give the desired head difference. Three faucets at each level meet the overflow rate created by the hydraulic head difference given.
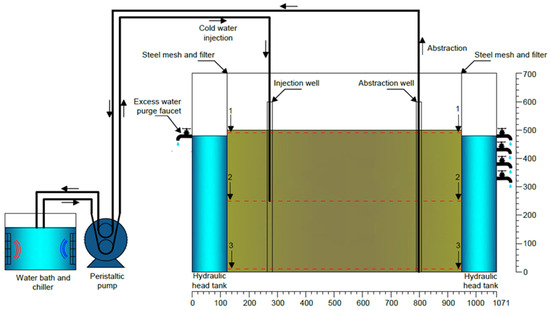
Figure 1.
Schematic diagram of the experimental setup.
Two acrylic tubes with a length of 0.6 m and inner and outer diameters of 14 and 16 mm, respectively, were placed in the tank. The locations of the tubes are shown in Figure 1 and indicated as point A and point E for injection and abstraction well, respectively (see Figure 2). The acrylic tubes acted as injection and abstraction wells. Many holes were drilled along the acrylic tubes to ensure the water flowed inside and outside from the well surface easily. The same fabric material used for the separation was used as a filter for acrylic tubes to prevent the wells from clogging. As shown in Figure 1, the injection and abstraction wells were placed 0.15 m away from the hydraulic head tanks on the center line of the tank in the width direction. They are 0.525 m apart from each other.
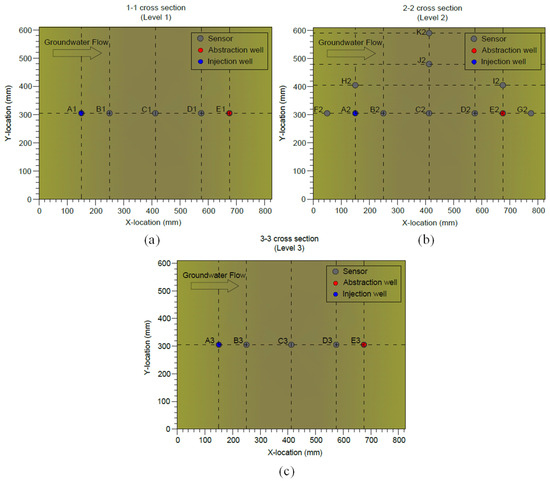
Figure 2.
The locations of the sensors located at (a) level 1, (b) level 2, and (c) level 3.
A chiller attached to a water bath to keep the temperature stable is used as a cold water source for injection. An adjustable peristaltic pump with two heads (channels) transfers water from the water bath tank to the injection well and from the abstraction well to the water bath tank. The pump’s flow rate range is 0.036–108 mL/min per channel, which enables us to run the test at flow rates of 25, 50, and 75 mL/min.
2.2. Location of the Sensors
The locations of the sensors used in the experiment are shown in Figure 2. The temperature sensors used in this experiment are the PT100 resistance temperature detector (RTD) and DS18B20 temperature sensor. The PT100 sensors are relatively more accurate than the DS18B20 sensors. Therefore, PT100 sensors were placed at the locations where accuracy is important, i.e., injection well, abstraction well, and between injection and abstraction wells. Besides their accuracy, the PT100 sensor is smaller than the DS18B20 sensor, which makes it possible to place three sensors in one well.
As shown in Figure 2, the temperature sensors were placed at three different depths, namely level 1, level 2, and level 3, located at the surface, at 0.25 m depth (middle of the sand), and at 0.5 m depth (bottom of the sand). These locations are illustrated in Figure 1 as 1-1, 2-2, and 3-3 cross sections, each marked with an arrow. There are five temperature sensors at level 1 and level 3. However, 11 temperature sensors were located at the middle level (level 2) because it is expected that this level will be the least affected by the external ambient temperature in comparison to the top and bottom levels.
The temperature sensors were connected to the data loggers, which can transfer temperature readings to a computer via a Universal Serial Bus (USB). Two types of data loggers were used for the DS18B20 and PT100 temperature sensors.
2.3. Test Results for the Thermal Properties of the Sand
Some of the thermal properties of the sand and water tank are given in Table 1. Before the preparation was started, a particle size distribution test was performed for Red Hill-110 to characterize the diameter of the sand particles. The average particle size (D50) was determined as 0.235 mm, which is within the range of fine sand. The hydraulic conductivity of the setup was determined by maintaining a constant water head to the left side of the model and allowing the water to flow through the soil and discharge at the right side of the setup. Water was collected from one of the faucets and used to measure the hydraulic conductivity, and was found to be 8.4 × 10−5 m/s. Also, a couple of constant head permeability tests were performed to determine the saturated hydraulic conductivity of the sand, and the saturated hydraulic conductivity from these tests was found to be 2.4 × 10−4 m/s. The average of the results obtained from the two different tests is given in Table 1. This test was followed by other characterization tests such as porosity, density, and specific heat capacity.

Table 1.
Material properties.
2.4. Details of Experimental Cases
In this study, five different cooling tests were performed to understand the effect of injection, abstraction rate, and groundwater flow velocity on thermal plume evolution. For this purpose, three different injection and abstraction rates were chosen. These are 25, 50, and 75 mL/min, named I25, I50, and I75, respectively. We conducted three tests where different head differences were given at a constant injection and abstraction rate of 75 mL/min. These head differences are 0, 50, and 150 mm; they are named I75, G50, and G150. Many trail tests were conducted to determine the groundwater velocities depending on the given head differences. The groundwater flow was measured during the tests. The average groundwater flow rates were 96 mL/min and 288 mL/min for the given head differences of 50 and 150 mm, respectively. The details of the different cases investigated are shown in Table 2.

Table 2.
Injection and abstraction rates given, head differences and measured groundwater flow rates.
2.5. Test Procedure
The injection temperature for five cooling tests (cooling down the ground as a result of space heating) was set to 5 °C in the water bath. However, heat loss occurs between the hoses and the room, which causes an increase in water temperature. This increase is affected by the injection flow rate.
Each test has a continuous cooling period of 96 h. The cooling period was chosen depending on the time it requires sand to reach an almost steady state condition. The recovery period is different for each test. It starts just after the cooling period. The recovery period is 64, 169, 160, 104, and 70 h for tests I25, I50, I75, G50, and G150, respectively. The duration of the recovery period was also chosen depending on the time the steady state condition was reached.
3. Results and Discussion
3.1. Comparison of Laboratory Test with Analytical Models
A comparison of the experimental investigation results with analytical models was carried out using the analytical formula proposed by Milnes and Perrochet [4]. The equation is applicable to well doublets and exclusively accounts for pure advection. Advective return flow may take place between injection and abstraction wells, potentially leading to thermal breakthrough after a certain duration of operation, once the following condition is met:
where q is the Darcy flux [m/day], b is the thickness [m], Q is the injection/abstraction rate [m3/day], and L is the distance between injection and abstraction wells [m].
The proposed method requires computing the α fraction, which represents the portion of the injected flow rate that returns to the abstraction well. It can be calculated as follows:
Determining the α fraction involves performing a simplified heat balance calculation focused solely on advection for the abstraction well under steady-state conditions. In the context of thermal feedback, where the injection temperature Ti is constant, the pumping temperature Tp can be calculated as follows:
where Ta is the ambient temperature [°C], and ΔT is the temperature difference between injection and abstraction temperature [°C].
To illustrate the proposed approach, let us consider test G150, with an injection/abstraction rate (Q) of 6.48 m3/day, aquifer thickness (b) of 0.5 m, Darcy flux (q) at 2.46 m/day, return flow criterion (X) of 6.36 (greater than 1), α fraction of 0.5, ambient temperature (Ta) of approximately 19 °C, and temperature difference (ΔT) of approximately 10.5 °C. The computation results in a steady-state abstraction temperature (Tp) of 13.65 °C. The measured temperature in the experimental test closely aligns with the result of the analytical method. The same approach was applied to test G50, resulting in a steady-state abstraction temperature (Tp) of 11.03 °C. The comparison of the results is shown in Figure 3.
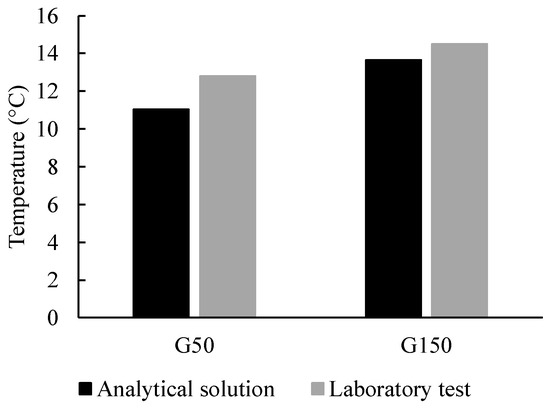
Figure 3.
Comparison of analytical solution and laboratory test results for tests G50 and G150 for a steady-state abstraction temperature.
The root mean square error (RMSE) and the maximum error (Errmax) were calculated using Equations (4) and (5) to analyze the results further.
where Texperiment and Tanalytical represent experimental and analytical results, respectively. The results, given in Table 3, show a close agreement between the experimental test results and the analytical model, especially for test G150. However, the large error encountered in test G50 could be attributed to the inability of the analytical model to capture heat transfer at low groundwater flow velocities.

Table 3.
Error analysis.
3.2. Thermal Energy Calculations for Each Scenario
The thermal energy gained from groundwater abstraction varies during the operation for each case. The thermal energy gain from the groundwater can be calculated by the following equation:
where Q is the heat energy [kJ], m is the mass [kg], Cave is the average specific heat calculated at the average temperature [kJ/kgK], and ∆T is the change in temperature [K].
Q = mCaveΔT
As the thermal energy gain varies with time, it was calculated using the temperature reading recorded at the end of each hour until the end of the cooling period. Figure 4 shows the thermal energy gain during the operation. In each case, the thermal energy gain follows a decreasing trend due to thermal feedback. However, this situation depends on two factors, as given in Equation (6). All tests followed a decreasing trend in the thermal energy gain. However, their magnitude varies depending on the abstraction rate and groundwater flow velocity.
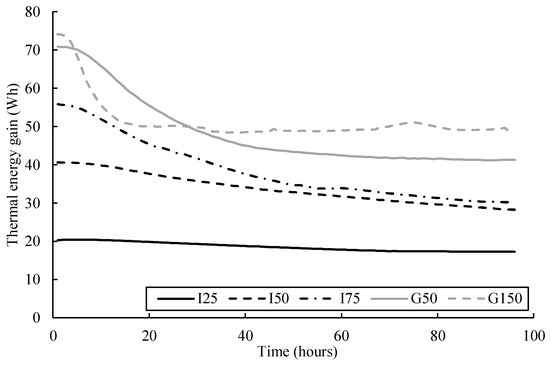
Figure 4.
Thermal energy gain from the groundwater during the cooling operation for five tests.
Varying abstraction and injection rate has a significant impact on the thermal energy gain. The calculated thermal energy gain was about 56, 41, and 20.3 Wh in tests I75, I50, and I25, respectively, an hour after the test began. In these three tests, the thermal energy gain decreased by 46%, 30%, and 15% at the end of the cooling period due to the decrease in the abstraction temperature. It can be seen that the decrease in the abstraction and injection rate decreases the thermal feedback influence on the abstraction temperature. The total thermal energy gain, as shown in Figure 5, is around 3.7 kWh (38.5 W), 3.2 kWh (33.3 W), and 1.8 kWh (18.8 W) for tests I75, I50, and I25, respectively. The total thermal energy gain is 14% and 51% lower in tests I50 and I25 compared to test I75.
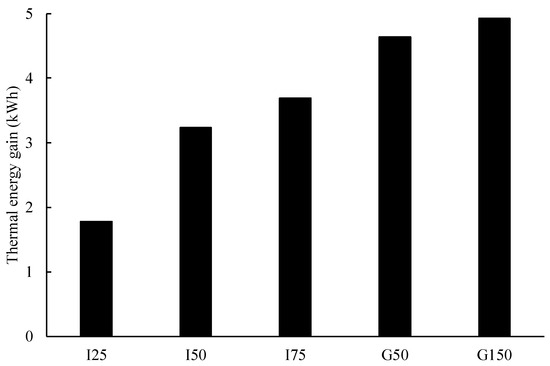
Figure 5.
Total thermal energy gain calculated for 96 h for five tests.
The impact of groundwater flow can be observed in Figure 3 and Figure 4. In tests G50 and G150, the calculated thermal energy gain at the end of the first hour was about 70.9 and 74.1 Wh, respectively. In test G150, the thermal energy decreased in the first 20 h, after which it was almost constant until the end of the cooling period. Similarly, the energy gain in test G50 witnessed a quick decrease in the first 50 h, and then it was almost constant. The thermal energy gain at the end of the cooling period decreased by 42% and 34% in tests G50 and G150, respectively. However, compared to test I75, the decrease in these two tests was relatively lower. This is due to the groundwater flow, which lowers the thermal feedback influence on the abstraction temperature. As shown in Figure 4, the total thermal energy gain is around 4.64 kWh (48.3 W) and 4.92 kWh (51.25 W) in tests G50 and G150, which is about 20% and 25% higher compared to test I75.
3.3. Analyses of Evolution of Thermal Distribution for Case I75
3.3.1. Injection and Abstraction Temperature
Figure 6 presents the results of temperature changes in the injection and abstraction wells at level 1, level 2, and level 3. The initial temperatures observed at the injection and abstraction wells are around 15 °C and 15.5 °C, respectively. At the start of the test, water at a constant temperature of 5 °C was injected continuously into the injection well and reached almost a steady state after 8 h. The water absorbed heat as it was being transferred from the water bath to the injection well. The maximum changes in temperature observed in the injection well were 7.5 °C, 7.1 °C, and 7.3 °C at level 1, level 2, and level 3, respectively, and remained relatively the same throughout the test. Some fluctuations in temperature were observed in the injection well. This may be due to the fluctuation in injection water temperature in the water bath.
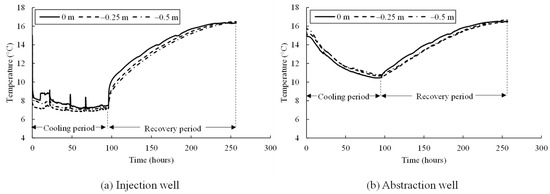
Figure 6.
Temperature measurements at (a) injection well and (b) abstraction well at three levels.
A temperature change was observed at the abstraction well after about an hour due to the thermal plume caused by water injection at 5 °C (see Figure 6b). The temperature at the abstraction well gradually decreased until the end of the cooling period, after which the temperatures observed at the abstraction well were 10.5 °C, 10.7 °C, and 10.8 °C at level 1, level 2, and level 3, respectively, at a decrease rate of about 0.05 °C per hour. The abstraction temperature was not affected by the fluctuation in injection temperature.
The observed temperature at the injection well after 96 h, when pumping was stopped, suddenly increased in the first hour, followed by a gradual increase at a rate of 0.06 °C per hour until it reached a steady state. At this point, the temperature stabilized at around 16.5 °C. The temperature measured at the end of recovery is 1.5 °C higher than the initial temperature. This result can be attributed to heat loss arising due to poor insulation. Furthermore, the temperature at the abstraction well started increasing at a rate of 0.04 °C per hour until the end of recovery. The average temperature at the abstraction well is around 16.6 °C at the end of the recovery period. The observed temperature at the end of recovery is 1.1 °C higher than the initial temperature, which can again be attributed to heat loss.
3.3.2. Vertical Thermal Distribution
Vertical thermal distribution observed at points A, B, C, D, and E at the depths of 0, 0.25, and 0.5 m (Levels 1, 2, and 3) is shown in Figure 7. The figure indicates the temperature readings at three stages: the initial, end of cooling, and recovery period.
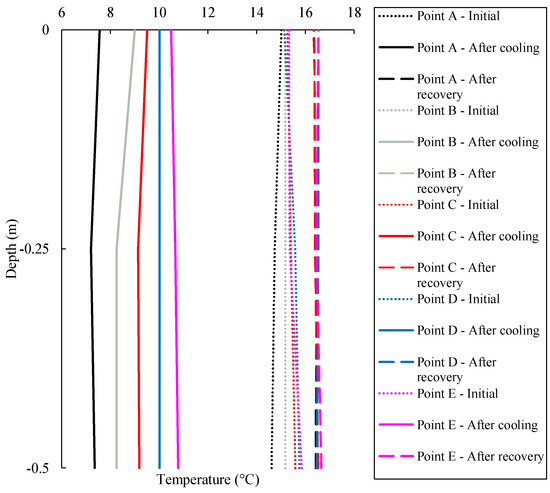
Figure 7.
Vertical thermal distribution at point A, B, C, D, and E.
The variation in the initial temperature of the sand is negligible at different depths. However, it varies through the model domain. The temperature observed at the end of recovery also has a negligible difference at different levels. The initial temperature is around 1.2 °C lower than the temperature observed after recovery at each observation point. This result can be attributed to the heat loss between the sandbox and the room.
The maximum temperature change observed at point A (injection well) is at level 2, as the water injection occurs at this level. The measured temperature at level 2 is 7.2 °C, with a decrease of about 51% after 96 h of cooling. The temperature decrease is 2% lower at level 1 and level 3 than at level 2. Point B witnessed a temperature decrease of 6.9 °C at level 2 and level 3. However, the temperature decrease is slightly lower at level 1 with a value of 6.2 °C. In the middle of the injection and abstraction well (point C), the maximum temperature drop was observed at level 2, where the temperature decreased by 41%, followed by level 3 and level 1, with a decrease of 40% and 38%, respectively. At point D, the temperature decrease is the same at each level, and it is around 5.5 °C with a decrease of 35%. The temperature decrease observed at the abstraction well (point E) followed a different pattern where the maximum drop was observed at level 3. The temperature decrease at the abstraction well is 4.8 °C, 4.7 °C, and 5.1 °C at level 1, level 2, and level 3, respectively.
3.3.3. Temperature Evolution
Figure 8 shows the horizontal distribution versus time at points B, C, D, J, and K. All the observation points followed almost the same trend, where the temperature decreased until the end of the cooling period. After that, it increased gradually during the recovery period until it reached a steady state.
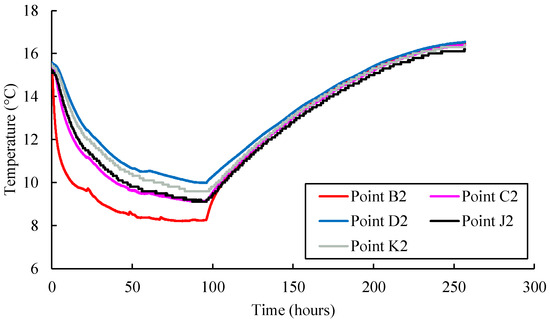
Figure 8.
Temperature evolution at observation points B, C, D, J, and K.
As shown in Figure 8, point B2 almost reached a steady state after 55 h of cooling at 8.3 °C with an average decrease rate of 0.13 °C per hour. During the recovery period, the temperature increased gradually from 8.3 °C to 16.5 °C in 160 h with an average rate of 0.05 °C per hour.
Point D witnessed a continuous decrease in temperature until the end of the cooling period. However, the temperature decrease is higher in the first 40 h at a rate of 0.115 °C per hour, while the decrease rate is 0.02 °C per hour between the 40th hour and 96th hour. During the recovery, point D witnessed an almost gradual increase from 10 °C to 16.5 °C at a rate of 0.04 °C per hour.
Points C, J, and K are located 0.262, 0.315, and 0.387 m away from the injection well, respectively. These observation points witnessed a similar change in temperature as they are located close to each other. The observed temperature decreased until the end of the cooling period and increased during the recovery period. The temperature change observed at the end of the cooling period is 6.1 °C with a decrease rate of 0.064 °C per hour. After the recovery period, the average observed temperature at these points is around 16.4 °C, which is a 7.1 °C increase at a rate of 0.04 °C per hour.
3.3.4. Horizontal Thermal Distribution
The temperature distribution throughout the sandbox model is shown in Figure 9. The temperature readings were obtained at three levels (level 1, level 2, and level 3) along the center line in the width direction for the initial stage, end of cooling, and end of recovery. The distance is presented along the x-axis, starting from 100 mm to the left side of the injection well and ending at 100 mm to the right side of the abstraction well.
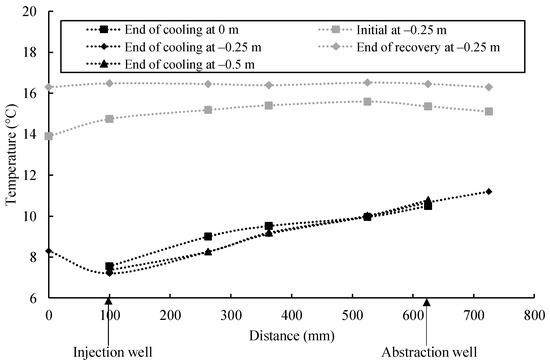
Figure 9.
Temperature change with distance for test I75.
The initial temperature of the soil is 14 °C on the left side, and it is around 15 °C on the other parts. After the cooling period, the maximum reduction was observed at the injection well with an observed temperature of about 7.2 °C. The observed temperature difference between level 2 and level 3 is negligible. However, the temperature measured at the top of the soil (i.e., level 1) is slightly different from the other depths. This can be attributed to the heat loss between the top of the soil and the air between the soil and the insulation board, which was located 0.2 m above the soil top. At the end of the cooling period, the highest temperature was observed as 11.2 °C at the point located the furthest to the injection well. At the end of the recovery period, the soil temperature reached a steady condition with a temperature of around 16.5 °C.
3.4. Impact of Different Injection and Abstraction Rates on Heat Transfer
3.4.1. Injection and Abstraction Temperature
Figure 10 shows the temperature readings at the injection and abstraction wells for the tests (I25, I50, and I75) conducted at injection and abstraction rates of 25, 50, and 75 mL/min. As the highest impact was observed at level 2, the temperature readings from this level were taken to compare the results of different injection and abstraction rates.
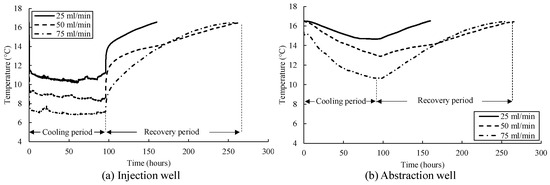
Figure 10.
Temperature measurements at (a) injection well and (b) abstraction well for three tests (I25, I50, and I75).
It can be seen that the temperature change is maximum when the injection rate is 75 mL/min (I75). A temperature of about 7.1 °C was observed just after the cooling period started due to cold water injection at 5 °C. There is a heat loss that occurs due to the water transfer from the water bath to the injection well. The magnitude of the heat loss varies depending on the injection flow rate. The temperature magnitude in the injection well decreases to 7.1 °C, 8.2 °C, and 10.5 °C, with a decrease of 52%, 50%, and 36% for the I75, I50, and I25 tests, respectively. The temperature reduction is higher in test I75 than in I50 and I25. This result can be attributed to the amount of energy injected into the injection well and varied heat loss in different tests.
As shown in Figure 10b, the observed abstraction temperature follows a similar trend as the injection well. The maximum temperature decrease was observed in test I75, with an observed temperature value of around 10.6 °C at the end of the cooling period. The observed abstraction temperature is around 12.9 °C and 14.7 °C in tests I50 and I25, respectively. The abstraction temperature decreased by 31%, 22%, and 10% in tests I75, I50, and I25, respectively. The abstraction water temperature in tests I50 and I25 has 18% and 28% less reduction, respectively, compared to test I75 due to the given injection rates. It is clear that a higher injection rate will cause a more significant thermal plume, undermining the long-term performance of the abstraction well.
The soil temperature reached almost 16.5 °C at the end of the recovery period for the three tests at the injection and abstraction wells. The temperature observed at the injection well increased suddenly in the first couple of hours, after which a gradual increase was observed. The observed temperature in the abstraction well rose gradually during the recovery period. The increasing trend observed in the injection and abstraction wells is significantly different, which can be attributed to the response to temperature changes. As the injection well experienced a higher temperature change relative to the initial soil temperature, a faster recovery was observed compared to the abstraction well.
3.4.2. Temperature Contours
The temperature contours at the cross-sectional view taken from level 2 are shown in Figure 11 for the three tests, I75, I50, and I25. The temperature readings were taken at the end of the cooling period. The water head tanks are on the right and left ends. So, the temperature readings on the right and left are the water temperatures in the water tanks. It can be seen that the lowest temperature is observed at the injection point, whilst the highest temperature is observed at the right end of the model, which is the region farthest from the injection well. The effect of injecting cold water decreases toward the abstraction well in each case.
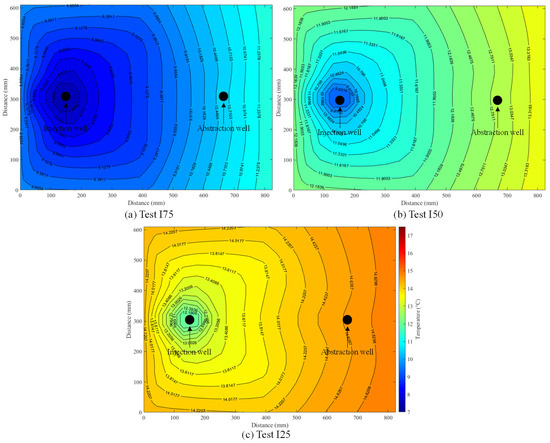
Figure 11.
Temperature contours of tests (a) I75, (b) I50, and (c) I25.
Figure 11a shows the temperature contours of the test conducted at an injection and abstraction rate of 75 mL/min (I75). This is the test where the highest thermal impact was seen. The minimum and maximum temperature readings are 7.1 °C and 11.5 °C, respectively. There is a decrease rate of about 0.6 °C per 100 mm from the injection toward the abstraction well.
The temperature contours of the second test (I50) conducted at 50 mL/min are illustrated in Figure 11b. The minimum and maximum temperatures observed are 8.6 °C and 13.6 °C. The effect of injecting cold water decreases toward the abstraction well at a rate of 1.17 °C per 100 mm from the injection well to the middle point (point C2) and at a rate of 0.47 °C per 100 mm from the middle point to the abstraction well.
The temperature contours of the test conducted at an injection and abstraction rate of 25 mL/min (I25) are shown in Figure 11c. The minimum temperature was observed at the injection well, and it was 11.3 °C, whilst the maximum temperature was observed at the right end of the model, and it was 14.9 °C. The impact of injecting water decreases toward the abstraction well at a rate of 1 °C per 100 mm from the injection well to point C2 and at a rate of about 0.29 °C per 100 mm from C2 to the abstraction well.
As seen in the figures, different injection and abstraction rates create different thermal impacts in the soil. The temperature distribution is the lowest in test I75, where the average temperature is around 9.25 °C, followed by test I50, where the average temperature is about 10.9 °C. The highest temperature, which means the lowest thermal impact, is observed in test I25, where the mean temperature is 13.1 °C.
3.5. Impact of Different Groundwater Velocities on Heat Transfer
3.5.1. Injection and Abstraction Temperature
The observed temperatures at the injection and abstraction well for the tests (I75, G50, and G150) conducted under a head difference of 0, 50, and 150 mm at an injection/abstraction rate of 75 mL/min are shown in Figure 12. The temperature readings were taken from level 2 as the maximum change in temperature was observed at that level. It needs to be stated that the initial soil temperature is different in each test. This can be attributed to the residual heat impact of the previous test and the temperature of incoming freshwater into the system.
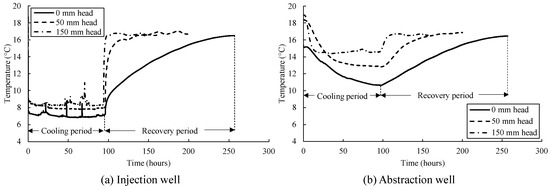
Figure 12.
Temperature measurements at (a) injection and (b) abstraction well for three tests (I75, G50, and G150).
Figure 12a shows the results of temperature evolution at the injection well for three tests (I75, G50, and G150). The results showed that the maximum change in temperature magnitude was recorded in test I75, with an observed temperature value of about 7.1 °C. The recorded temperature magnitude in the well decreases to about 7.82 °C and 8.23 °C for the G50 and G150 tests, respectively. The 10% and 15% reduction in the observed temperature drop is due to the flow of warmer groundwater (at an average measured temperature of 16.6 °C), which slows down the cooling caused by the injection of cold water.
The results of temperature change at the abstraction well for the three tests are shown in Figure 12b. It can be seen that due to warmer groundwater flow, the initial temperature in tests G50 and G150 is higher than in test I75. The maximum temperature drop was observed in test I75. The temperature at the abstraction well decreased to about 10.6 °C. At the end of the cooling period, the observed temperature was about 12.8 °C and 14.6 °C in tests G50 and G150, respectively. During the cooling period, the observed temperature at the abstraction well decreased by 31%, 30%, and 23% in tests I75, G50, and G150, respectively. The abstraction temperature decrease observed in tests G50 and G150 was relatively lower than in test I75 due to the flow of warm groundwater.
During the recovery period, a sudden increase at the injection well was observed at the beginning of tests G50 and G150 due to the flow of warm groundwater. However, the temperature in the injection well witnessed a gradual increase in test I75. The temperature at the abstraction well followed a similar trend, where the observed temperature quickly increased in tests G50 and G150 while it rose gradually in test I75. The average temperature observed at both wells is around 16.6 °C at the end of the recovery period for the three tests.
3.5.2. Temperature Contours
Figure 13 shows the temperature contours at the cross-sectional view taken from level 2 for the tests conducted under a head difference of 0, 50, and 150 mm (I75, G50, and G150). These figures show the temperature readings taken at the end of the cooling period. The lowest temperature was observed at the injection well in each case. The highest temperature was observed on the rightmost side of the tank for test I75. However, it was observed at the leftmost end of the tank for tests G50 and G150 due to warm water inflow from that side of the tank.
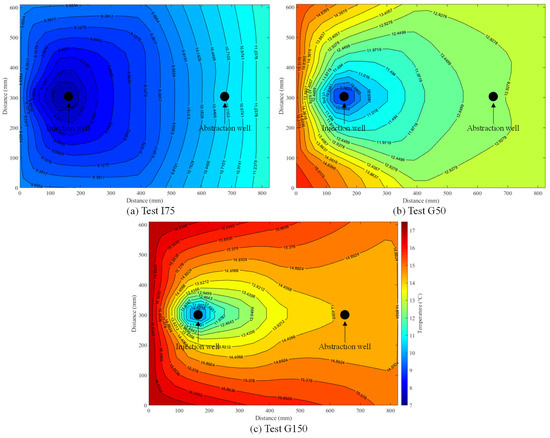
Figure 13.
Temperature contours of the tests (a) I75, (b) G50, and (c) G150.
The I75 test without groundwater flow shows the highest thermal impact caused by injection from Figure 13a (as discussed in Section 3.3). For the test conducted under the head difference of 50 mm (Figure 13b), the lowest temperature was observed at the injection well at 8 °C. The highest temperature was observed at the left side of the tank where the water comes in, at a temperature of about 15.7 °C. The effect of injecting cold water decreases toward the abstraction well as soil temperature increases at a rate of 1.5 °C per 100 mm from the injection well to the middle point (point C2) and at a rate of 0.4 °C per 100 mm from the middle point to the abstraction well.
For test G150 (Figure 13c), the lowest observed temperature is at the injection well at 8.3 °C. The maximum temperature was observed on the left side of the tank at 17.3 °C. The effect of injecting cold water decreases toward the abstraction well as the soil temperature increases at a rate of 2 °C per 100 mm from the injection well to the middle point (point C2) and at a rate of 0.4 °C per 100 mm from the middle point to the abstraction well.
As can be seen in the three figures, groundwater flow has a significant impact on thermal plume characteristics. The effect of the cold water injection is highest in test I75 compared to other tests conducted with a groundwater flow. A faster flow of warm groundwater heats up the ground, reduces the influence of cold water injection, and enhances the long-term performance of the abstraction well. The average temperatures calculated for the measuring points are 9.25 °C for I75, 11.9 °C for G50, and 12.8 °C for G150.
3.5.3. Thermal Photos
For the initial stage, the temperature reading in the middle is 19.3 °C. The minimum observed temperature is around 16.1 °C on the left side, where the water comes in, whilst the temperature observed on the other end of the sand is about 18.5 °C. The maximum temperature shown in the color scale is the temperature of the cables.
At the end of the cooling period, the temperature observed in the middle is 14.6 °C. The thermal plume, starting from the injection well and spreading toward the abstraction well, can be observed in dark color. The minimum temperature was measured at the injection well. However, in Figure 14b, it can be seen that the minimum temperature is observed around the abstraction well, which is around 12.6 °C. This could be because the thermal photo was taken a couple of minutes after the end of the cooling period. In that case, the thermal plume might have moved toward the abstraction well due to the groundwater flow.
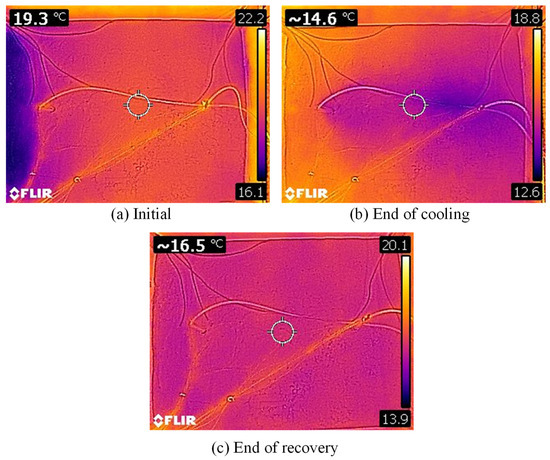
Figure 14.
Temperature distribution at the surface for test G150: (a) initial stage, (b) end of cooling, and (c) end of recovery.
The observed temperature is 16.5 °C in the middle at the end of the recovery period. It is almost the same along the surface of the sand.
4. Conclusions
In this study, a series of laboratory-scale cooling tests were conducted involving three different injection and abstraction rates and three different groundwater flow velocities. The effect of cold water injection on the soil temperature, the thermal plume dimension, and the change in abstraction temperature was observed using temperature sensors placed inside the soil. The experiment provides information about how the variation in flow rate and groundwater flow velocity affects the thermal plume development, the dimension and direction of the thermal plume, and the abstraction water temperature and, hence, the thermal energy gain. The following conclusions can be drawn from this research.
- Cold water injection creates a thermal plume starting from the injection well and reaching the abstraction well in all cases due to a coupled effect of convection and conduction, which reduces the abstraction water temperature and reduces system performance and sustainability. Therefore, a close distance between the injection and abstraction well is not ideal for the GWHP system.
- Increasing the injection and abstraction rates results in larger thermal plume dimensions, thus worsening system performance and sustainability. Despite a 100% and 200% increase in injection and abstraction rates, the energy gain only increased by 81% and 107%.
- Groundwater flow positively impacts the system’s sustainability as it mitigates the effects of the cold water injection. The observed temperatures at the abstraction well at the end of the cooling period are 10.7 °C, 12.9 °C, and 14.6 °C for the test conducted under a head difference of 0 (I75), 50 (G50), and 150 mm (G150), respectively. Therefore, it is significant to consider the groundwater flow direction when designing the locations of the injection and abstraction wells.
- The maximum decrease in thermal energy gain from the abstracted water occurred in test I75, with a decrease of 46%. The maximum energy gain was observed in test G150, followed by G50, I75, and I50. Test I25 had the lowest thermal energy gain due to the low abstraction rate.
In summary, the results emphasize the crucial need to account for groundwater flow velocity, injection and abstraction rates during GWHP system design. Additionally, the distance between injection and abstraction wells emerges as another vital parameter that demands careful consideration. However, it is important to note that altering the distance between injection and abstraction wells was not feasible in this sandbox model setup. Further research should explore these aspects through large-scale field tests or numerical simulations.
Author Contributions
Conceptualization, T.S., A.K.S. and R.M.S.; methodology, T.S.; validation, T.S.; investigation, T.S.; data curation, T.S.; writing—original draft preparation, T.S.; writing—review and editing, A.K.S., R.M.S. and L.C.; supervision, A.K.S., R.M.S. and L.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data is available upon request from the corresponding author.
Acknowledgments
The first author of this paper, Taha Sezer, expresses gratitude for receiving Ph.D. funding from the Ministry of National Education of Türkiye.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Singh, R.M.; Sani, A.K.; Amis, T. An overview of ground-source heat pump technology. In Managing Global Warming: An Interface of Technology and Human Issues; Academic Press: Cambridge, MA, USA, 2019. [Google Scholar] [CrossRef]
- Younis, M.; Bolisetti, T.; Ting, D. Ground source heat pump systems: Current status. Int. J. Environ. Stud. 2010, 67, 405–415. [Google Scholar] [CrossRef]
- Agemar, T.; Weber, J.; Schulz, R. Deep Geothermal Energy Production in Germany. Energies 2014, 7, 4397–4416. [Google Scholar] [CrossRef]
- Milnes, E.; Perrochet, P. Assessing the impact of thermal feedback and recycling in open-loop groundwater heat pump (GWHP) systems: A complementary design tool. Hydrogeol. J. 2013, 21, 505–514. [Google Scholar] [CrossRef]
- Banks, D. Thermogeological assessment of open-loop well-doublet schemes: A review and synthesis of analytical approaches. Hydrogeol. J. 2009, 17, 1149–1155. [Google Scholar] [CrossRef]
- Galgaro, A.; Cultrera, M. Thermal short circuit on groundwater heat pump. Appl. Therm. Eng. 2013, 57, 107–115. [Google Scholar] [CrossRef]
- Pophillat, W.; Attard, G.; Bayer, P.; Hecht-Méndez, J.; Blum, P. Analytical solutions for predicting thermal plumes of groundwater heat pump systems. Renew. Energy 2020, 147, 2696–2707. [Google Scholar] [CrossRef]
- Sciacovelli, A.; Guelpa, E.; Verda, V. Multi-scale modeling of the environmental impact and energy performance of open-loop groundwater heat pumps in urban areas. Appl. Therm. Eng. 2014, 71, 780–789. [Google Scholar] [CrossRef]
- Freedman, V.L.; Waichler, S.R.; Mackley, R.D.; Horner, J.A. Assessing the thermal environmental impacts of an groundwater heat pump in southeastern Washington State. Geothermics 2012, 42, 65–77. [Google Scholar] [CrossRef]
- Russo, S.L.; Gnavi, L.; Roccia, E.; Taddia, G.; Verda, V. Groundwater Heat Pump (GWHP) system modeling and Thermal Affected Zone (TAZ) prediction reliability: Influence of temporal variations in flow discharge and injection temperature. Geothermics 2014, 51, 103–112. [Google Scholar] [CrossRef]
- Russo, S.L.; Civita, M.V. Open-loop groundwater heat pumps development for large buildings: A case study. Geothermics 2009, 38, 335–345. [Google Scholar] [CrossRef]
- Park, D.K.; Kaown, D.; Lee, K.-K. Development of a simulation-optimization model for sustainable operation of groundwater heat pump system. Renew. Energy 2020, 145, 585–595. [Google Scholar] [CrossRef]
- Boon, D.P.; Farr, G.J.; Abesser, C.; Patton, A.M.; James, D.R.; Schofield, D.I.; Tucker, D.G. Groundwater heat pump feasibility in shallow urban aquifers: Experience from Cardiff, UK. Sci. Total Environ. 2019, 697, 133847. [Google Scholar] [CrossRef] [PubMed]
- Russo, S.L.; Taddia, G.; Baccino, G.; Verda, V. Different design scenarios related to an open loop groundwater heat pump in a large building: Impact on subsurface and primary energy consumption. Energy Build. 2011, 43, 347–357. [Google Scholar] [CrossRef]
- Russo, S.L.; Taddia, G.; Verda, V. Development of the thermally affected zone (TAZ) around a groundwater heat pump (GWHP) system: A sensitivity analysis. Geothermics 2012, 43, 66–74. [Google Scholar] [CrossRef]
- Park, B.-H.; Bae, G.-O.; Lee, K.-K. Importance of thermal dispersivity in designing groundwater heat pump (GWHP) system: Field and numerical study. Renew. Energy 2015, 83, 270–279. [Google Scholar] [CrossRef]
- Taddia, G.; Russo, S.L.; Verda, V. Comparison between neural network and finite element models for the prediction of groundwater temperatures in heat pump (GWHP) systems. In Engineering Geology for Society and Territory: Applied Geology for Major Engineering Projects; Springer International Publishing: New York, NY, USA, 2015; Volume 6, pp. 255–258. [Google Scholar] [CrossRef]
- Piga, B.; Casasso, A.; Pace, F.; Godio, A.; Sethi, R. Thermal Impact Assessment of Groundwater Heat Pumps (GWHPs): Rigorous vs. Simplified Models. Energies 2017, 10, 1385. [Google Scholar] [CrossRef]
- Nam, Y.; Ooka, R. Numerical simulation of ground heat and water transfer for groundwater heat pump system based on real-scale experiment. Energy Build. 2010, 42, 69–75. [Google Scholar] [CrossRef]
- Birks, D.; Adamson, C.; Woods, M.G.; Holmes, G. Evaluation of measures to improve the performance of an open loop ground source heat pump system in the chalk aquifer: A case study. Q. J. Eng. Geol. Hydrogeol. 2022, 55, qjegh2021-074. [Google Scholar] [CrossRef]
- Blázquez, C.S.; Verda, V.; Nieto, I.M.; Martín, A.F.; González-Aguilera, D. Analysis and optimization of the design parameters of a district groundwater heat pump system in Turin, Italy. Renew. Energy 2020, 149, 374–383. [Google Scholar] [CrossRef]
- Permanda, R.; Ohtani, T. Thermal Impact by Open-Loop Geothermal Heat Pump Systems in Two Different Local Underground Conditions on the Alluvial Fan of the Nagara River, Gifu City, Central Japan. Energies 2022, 15, 6816. [Google Scholar] [CrossRef]
- Gizzi, M.; Taddia, G.; Abdin, E.C.; Russo, S.L. Thermally Affected Zone (TAZ) Assessment in Open-Loop Low-Enthalpy Groundwater Heat Pump Systems (GWHPs): Potential of Analytical Solutions. Geofluids 2020, 2020, 2640917. [Google Scholar] [CrossRef]
- Park, B.-H.; Lee, B.-H.; Lee, K.-K. Experimental investigation of the thermal dispersion coefficient under forced groundwater flow for designing an optimal groundwater heat pump (GWHP) system. J. Hydrol. 2018, 562, 385–396. [Google Scholar] [CrossRef]
- Jiang, Y.; Wang, X.; Li, M.; Gao, Q. Investigations on heat flow characteristics of the aquifer for groundwater heat pump (GWHP) composed of different well types. Int. J. Green Energy 2019, 16, 857–866. [Google Scholar] [CrossRef]
- Giordano, N.; Comina, C.; Mandrone, G. Laboratory scale geophysical measurements aimed at monitoring the thermal affected zone in Underground Thermal Energy Storage (UTES) applications. Geothermics 2016, 61, 121–134. [Google Scholar] [CrossRef]
- Zhou, X.; Gao, Q.; Chen, X.; Yu, M.; Zhao, X. Numerically simulating the thermal behaviors in groundwater wells of groundwater heat pump. Energy 2013, 61, 240–247. [Google Scholar] [CrossRef]
- Song, W.; Ni, L.; Yao, Y. Analyses of different operation modes of pumping and recharging well using an indoor sandbox test. Energy Build. 2020, 208, 109660. [Google Scholar] [CrossRef]
- Li, Y.; Shu, L.; Xiao, R.; Niu, S.; Tao, Y.; Ling, Z. How groundwater flow field change affects heat transfer in groundwater heat pumps based on physical experiments. Energy Build. 2023, 282, 112804. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).