Predicting the Performance of PEM Fuel Cells by Determining Dehydration or Flooding in the Cell Using Machine Learning Models
Abstract
:1. Introduction
2. Materials and Methods
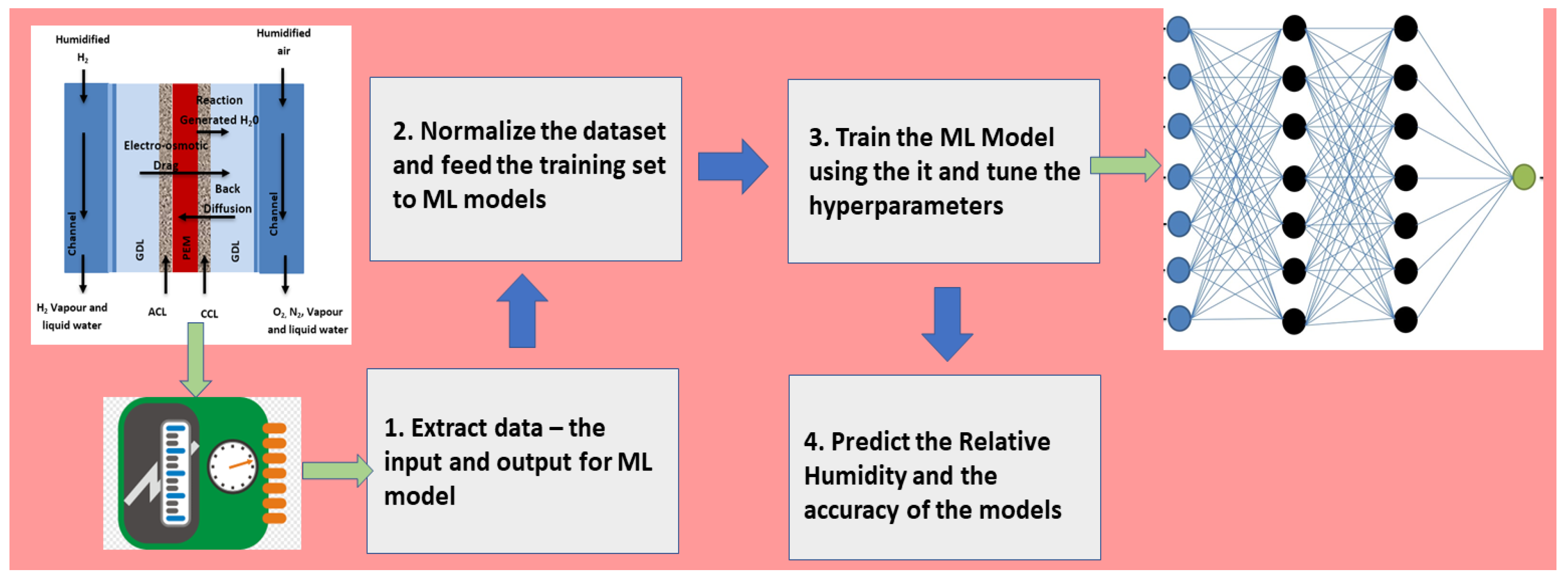
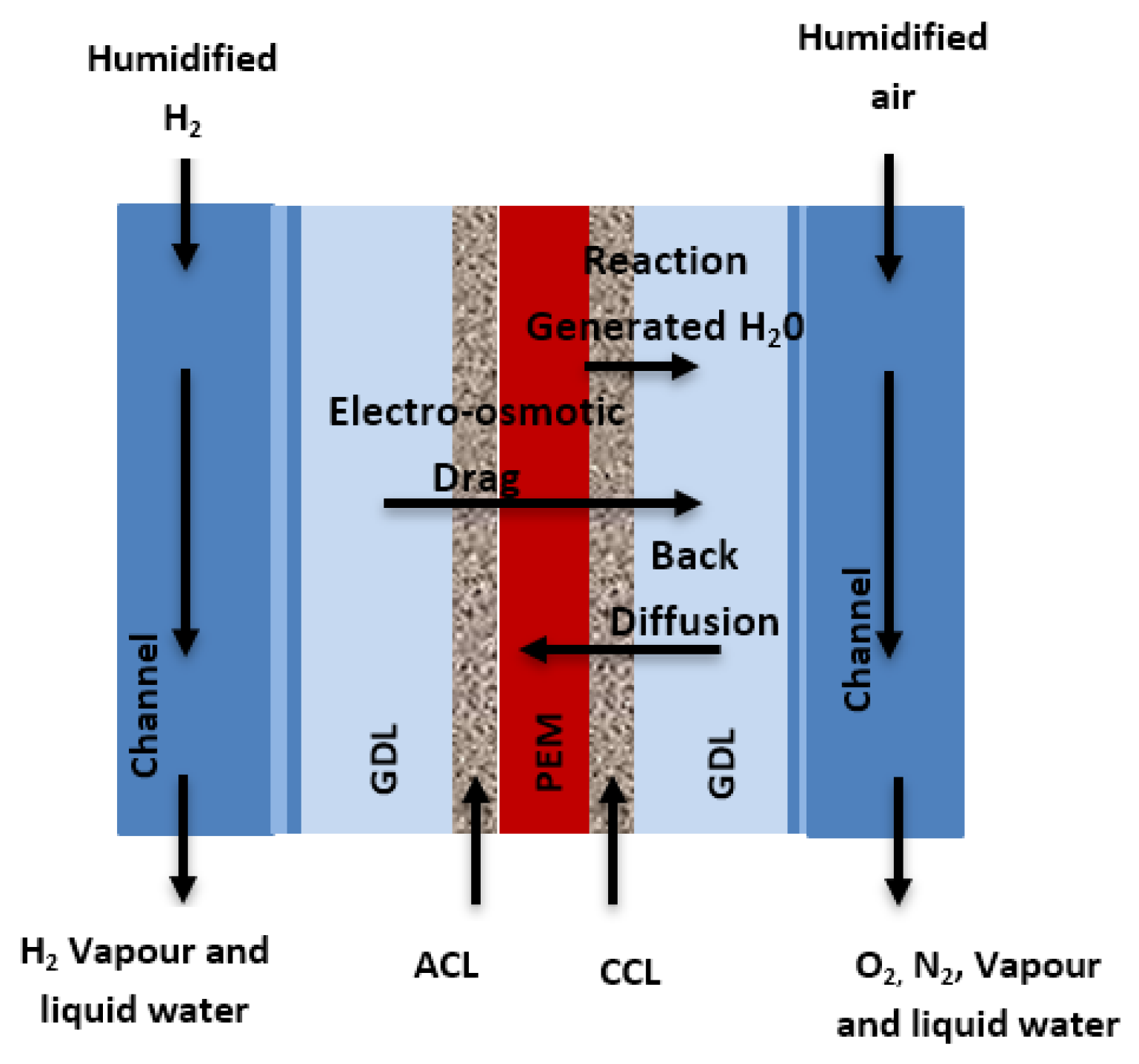
2.1. Data Acquisition
Data Preprocessing and Scaling
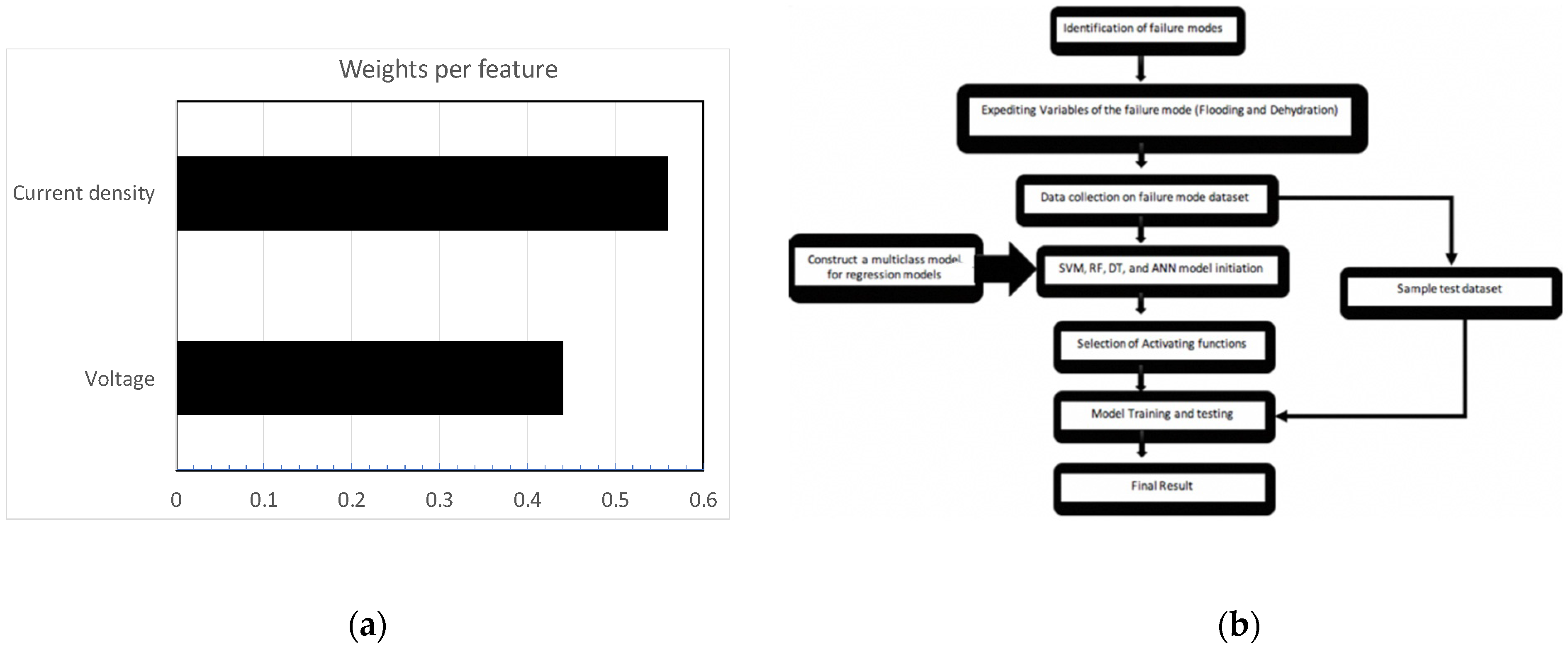
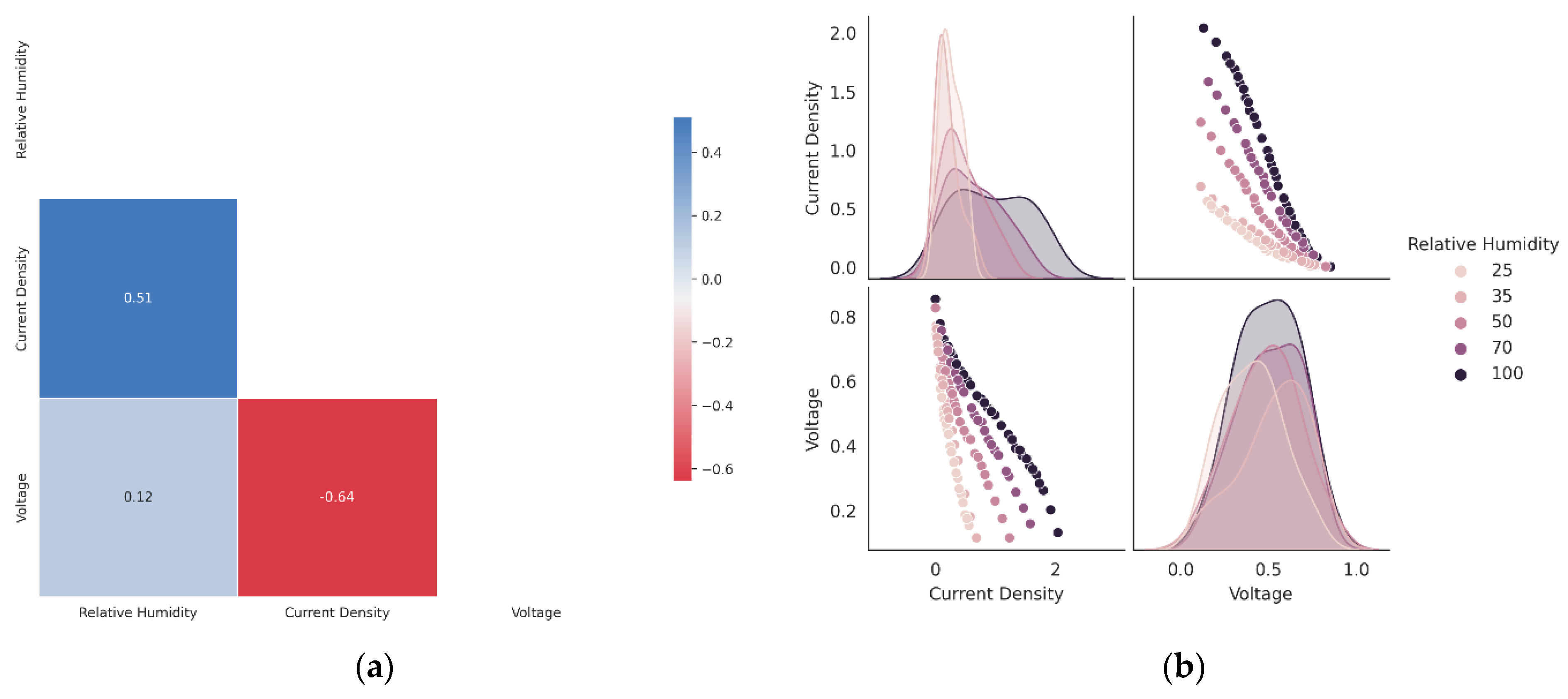
2.2. Feature Selection/Importance
2.3. Machine Learning Models
2.3.1. Support Vector Regression
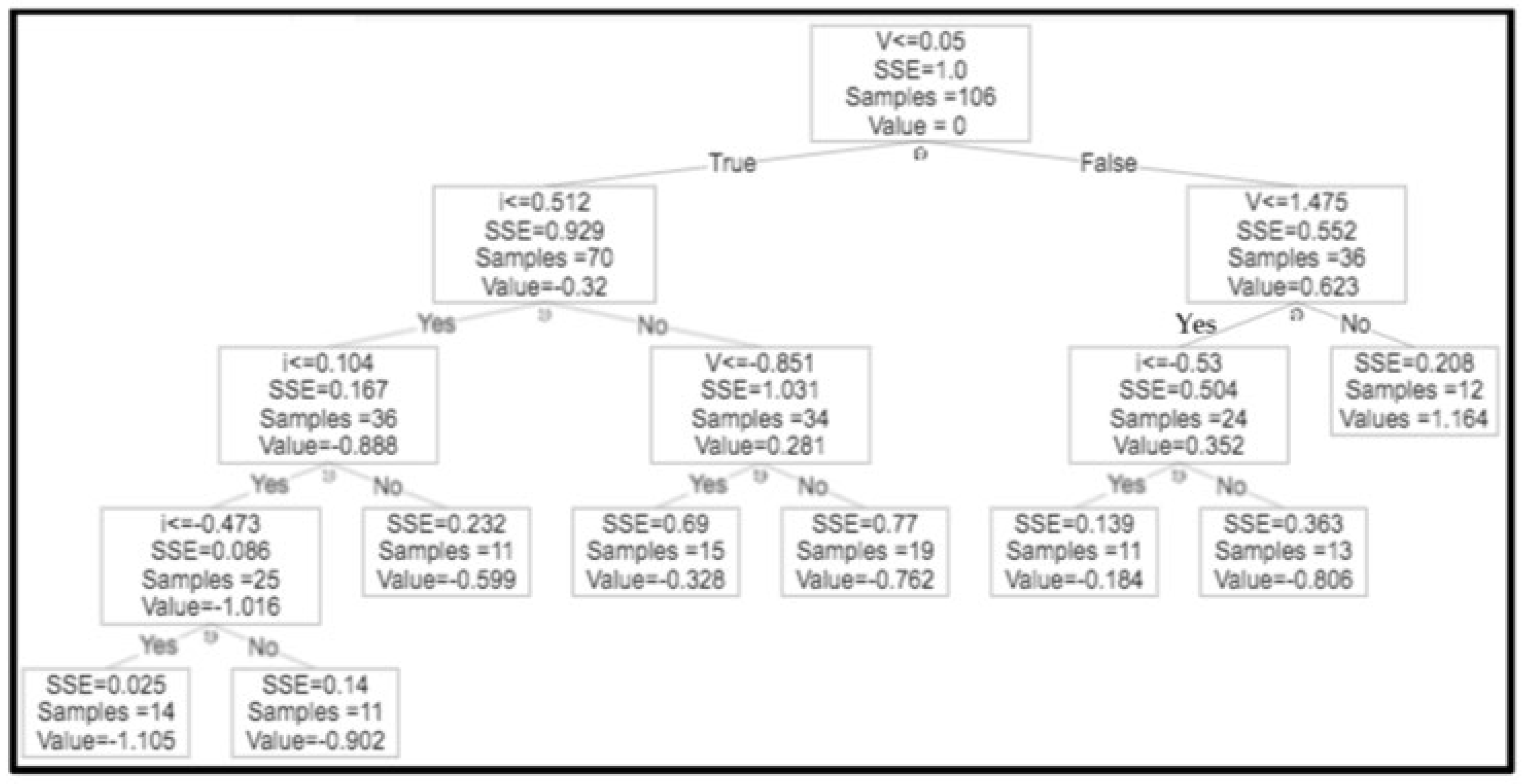
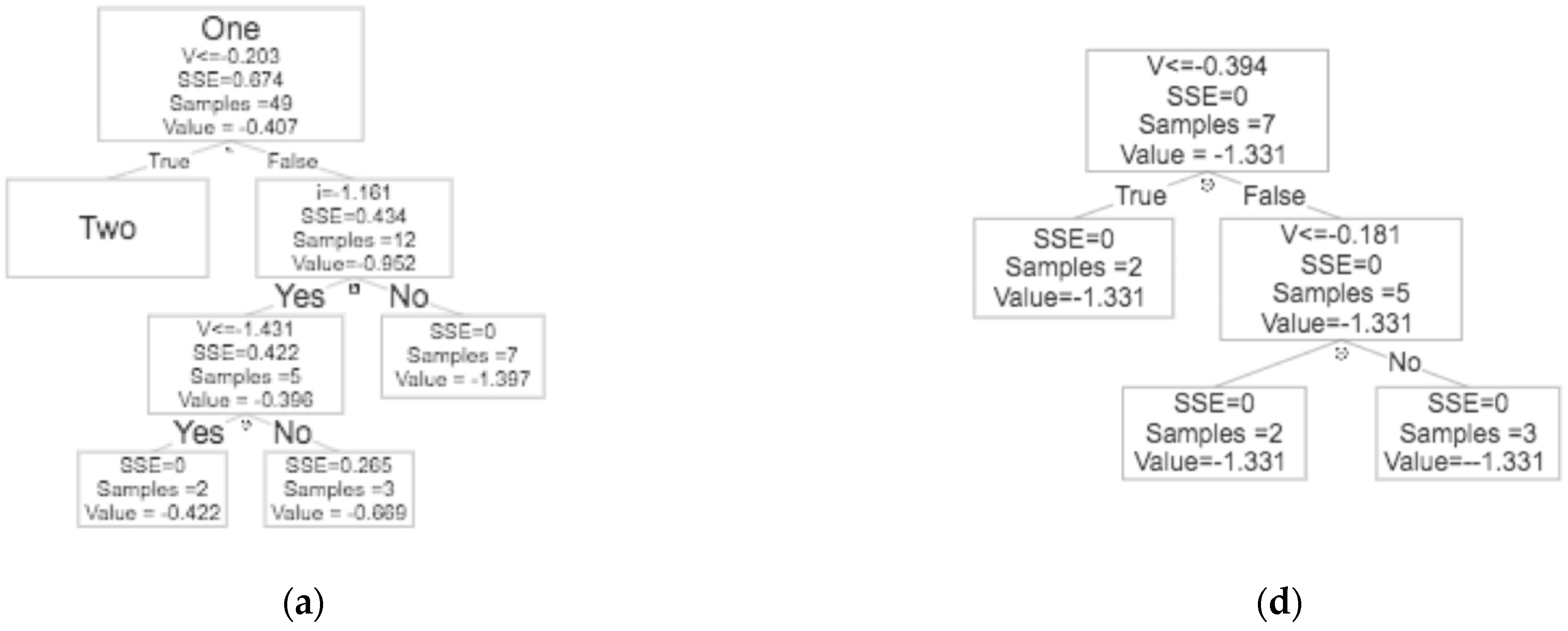
2.3.2. Decision Tree Regression
2.3.3. Random Forest Regression
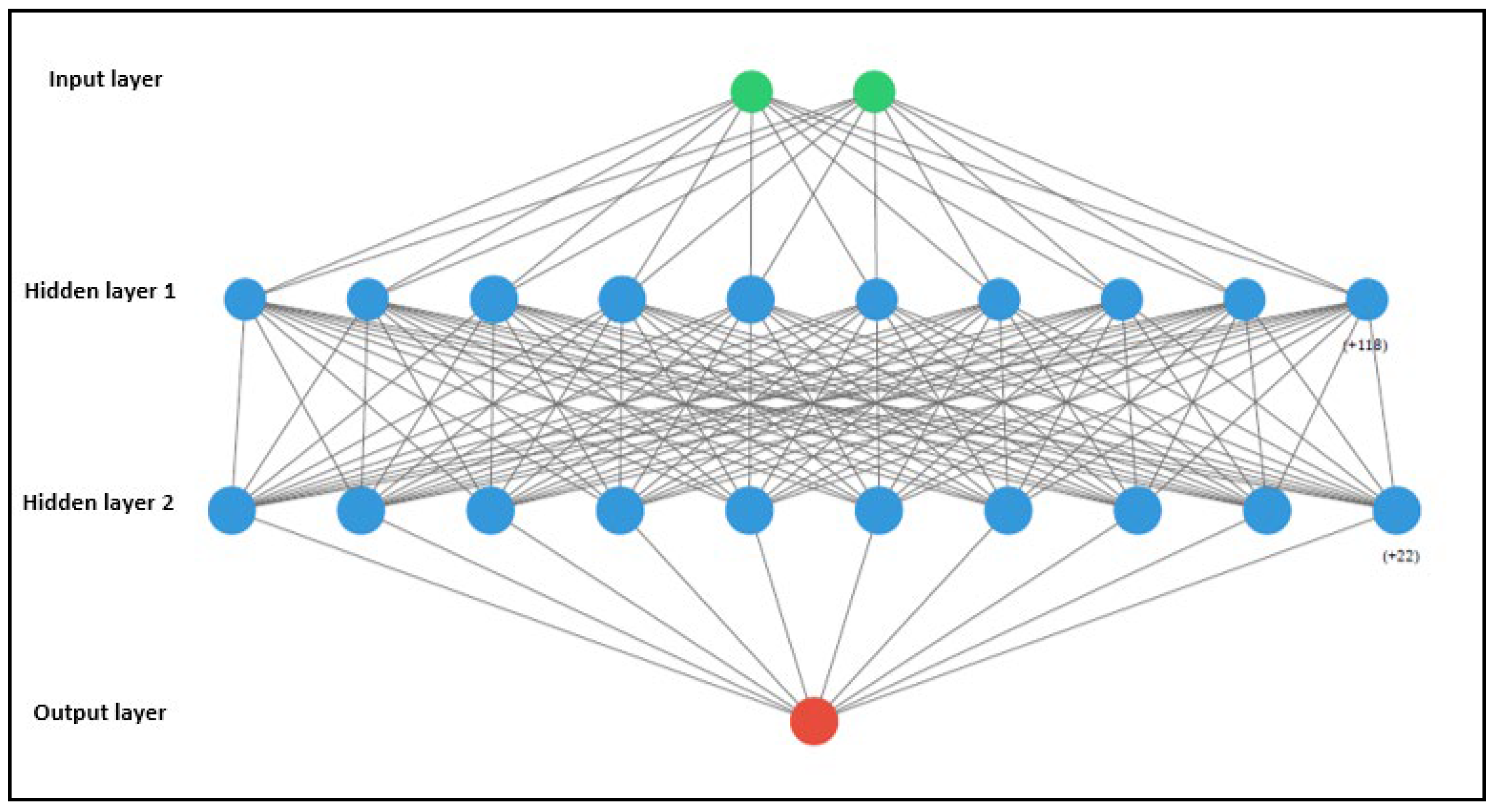
2.3.4. Artificial Neural Network
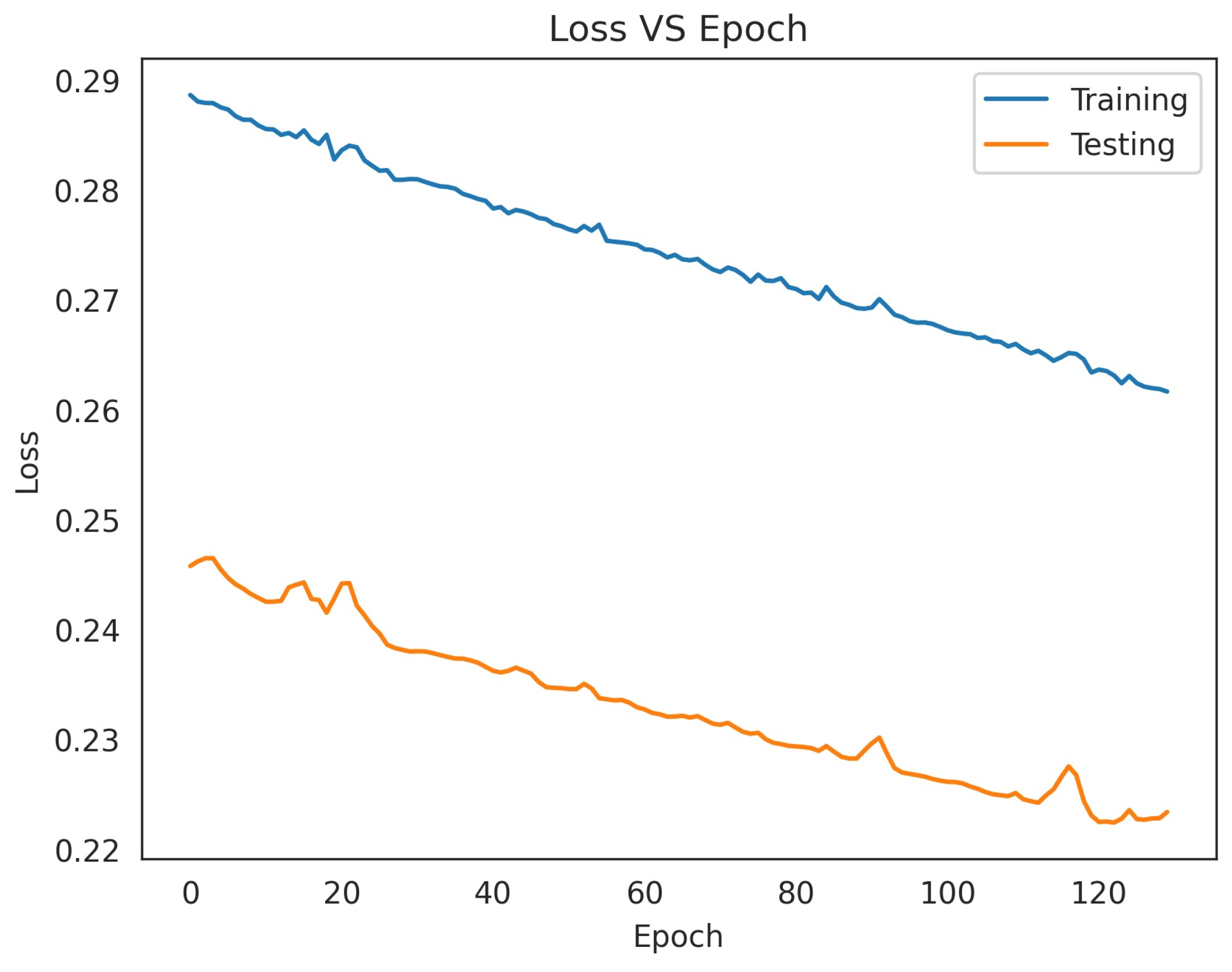
2.3.5. Approach Used to Carry Out ML
3. Results and Discussions
3.1. Analyzing the Dehydration and Flooding in the Cell
3.2. Importance of Relative Humidity in Flooding and Dehydration Predication
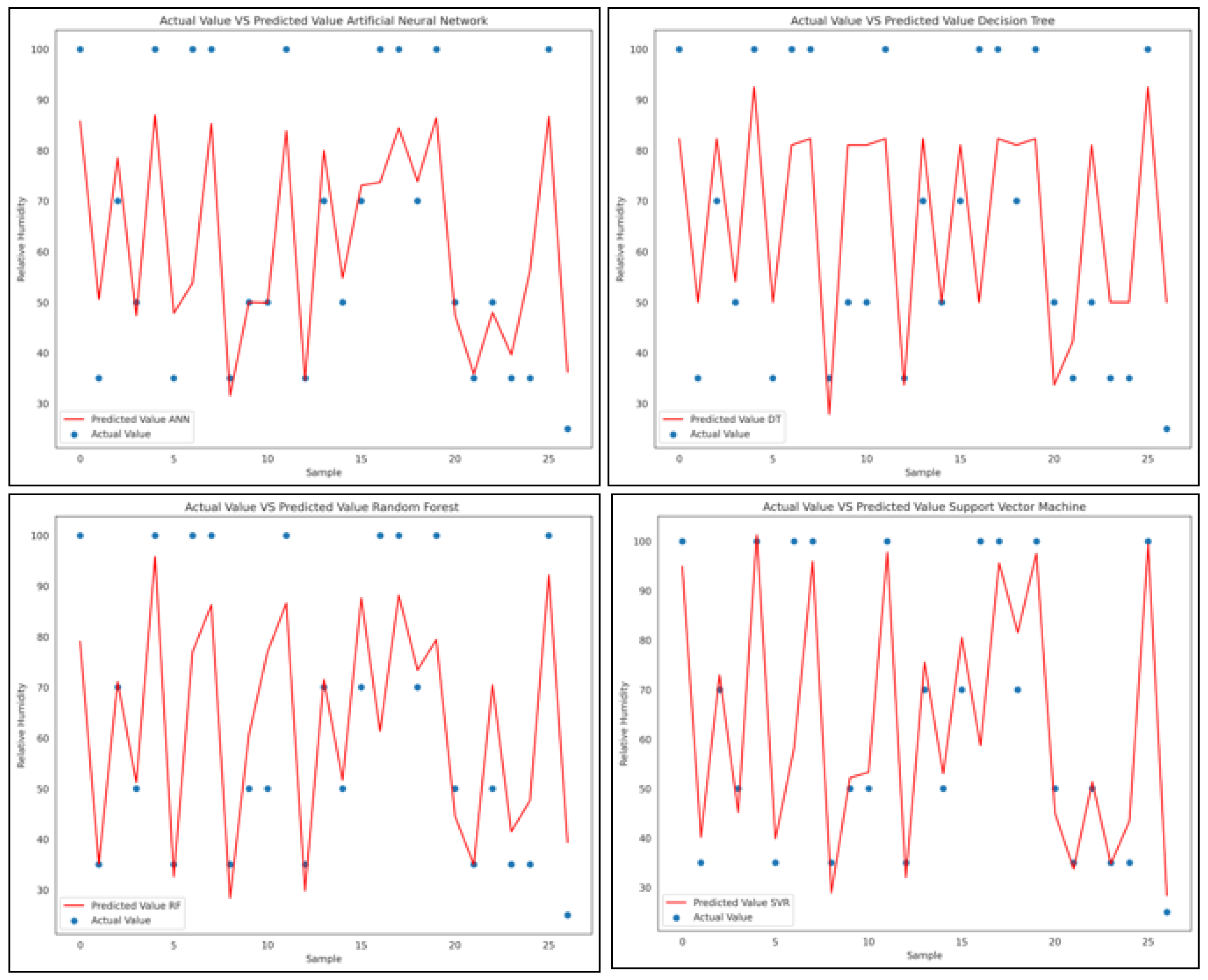
3.3. Comparison of Machine Learning Models
- Since no parameters, except voltage and current, are needed to assess failures in a cell, the proposed model can be applicable to different compositions of the GDL of a PEMFC. It can provide a performance analysis for both the PEMFC and durability of the cell based on the datasets used to train the model;
- The model can predict the cause and effect of failure modes and the performance of a cell. However, the model cannot accurately assess the failure mechanism of the individual components and interfaces of the cell;
- The deep learning model and methods proposed for the dehydration or flooding diagnosis are universal for any GDL materials. It could be applicable for use in testing a cell, as well as stacking and analyzing the proposed failure modes;
- Gathering a larger dataset to compare it with modified FCM and SMOTE algorithms can enhance the fault detection modes for RH cycling in PEMFC tests. However, this approach is beyond the scope of the present study;
- This study involved many features in the diagnosis of dehydration and flooding. Noise in the dataset requires an extra tree classifier to initially identify redundant features. Therefore, feature selection must be performed to reduce the computational cost and time. This is carried out before training the model. The regression approach is adopted to identify and alert for flooding- or dehydration-induced faults in a cell.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| PEMFC | Polymer electrolyte membrane fuel cell |
| ML | Machine learning |
| GDL | Gas diffusion layer |
| ANN | Artificial neural network |
| RF | Random forest |
| DT | Decision tree |
| SVM | Support vector machine |
| RH | Relative humidity |
| ORR | Oxygen reduction reaction |
| FCM | Fuzzy C means algorithm |
| SMOTE | Synthetic minority oversampling technique |
| R2 | R squared (correlation coefficient) |
| MSE | Mean squared |
| RMSE | Root mean square error |
| MAE | Mean absolute error |
| Yi | Observed value |
| Yp | Predicted value |
| CFD | Computational fluid dynamics |
References
- Li, T.; Wang, K.; Wang, J.; Liu, Y.; Han, Y.; Xu, Z.; Lin, G.; Liu, Y. Optimization of GDL to improve water transferability. Renew. Energy 2021, 179, 2086–2093. [Google Scholar] [CrossRef]
- Raman, S.; Iyeswaria, K.B.; Narasimhan, S.; Rengaswamy, R. Effects of water induced pore blockage and mitigation strategies in low temperature PEM fuel cells—A simulation study. Int. J. Hydrogen Energy 2017, 42, 23799–23813. [Google Scholar] [CrossRef]
- Springer, T.E.; Zawodzinski, T.A.; Gottesfeld, S. Polymer Electrolyte Fuel Cell Model. J. Electrochem. Soc. 1991, 138, 2334–2342. [Google Scholar] [CrossRef]
- Bernardi, D.M.; Verbrugge, M.W. A Mathematical Model of the Solid-Polymer-Electrolyte Fuel Cell. J. Electrochem. Soc. 1992, 139, 2477–2491. [Google Scholar] [CrossRef]
- Bednarek, T.; Tsotridis, G. Issues associated with modelling of proton exchange membrane fuel cell by computational fluid dynamics. J. Power Sources 2017, 343, 550–563. [Google Scholar] [CrossRef]
- Williams, M.V.; Kunz, H.R.; Fenton, J.M. Analysis of Polarization Curves to Evaluate Polarization Sources in Hydrogen/Air PEM Fuel Cells. J. Electrochem. Soc. 2005, 152, A635. [Google Scholar] [CrossRef]
- Pourrahmani, H.; van Herle, J. Water management of the proton exchange membrane fuel cells: Optimizing the effect of microstructural properties on the gas diffusion layer liquid removal. Energy 2022, 256, 124712. [Google Scholar] [CrossRef]
- Cawte, T.; Bazylak, A. A 3D convolutional neural network accurately predicts the permeability of gas diffusion layer materials directly from image data. Curr. Opin. Electrochem. 2022, 35, 101101. [Google Scholar] [CrossRef]
- Chauhan, V.; Mortazavi, M.; Benner, J.Z.; Santamaria, A.D. Two-phase flow characterization in PEM fuel cells using machine learning. Energy Rep. 2020, 6, 2713–2719. [Google Scholar] [CrossRef]
- Yu, Y.; Chen, S. Numerical study and prediction of water transfer in gas diffusion layer of proton exchange membrane fuel cells under vibrating conditions. Int. J. Energy Res. 2022, 46, 18781–18795. [Google Scholar] [CrossRef]
- Dhanushkodi, S.R. Experimental Methods and Mathematical Models to Examine Durability of Polymer Electrolyte Membrane Fuel Cell Catalysts. Ph.D. Thesis, University of Waterloo, Waterloo, ON, Canada, 2013. Available online: http://hdl.handle.net/10012/7619 (accessed on 1 May 2023).
- Zhang, J.; Tang, Y.; Song, C.; Xia, Z.; Li, H.; Wang, H.; Zhang, J. PEM fuel cell relative humidity (RH) and its effect on performance at high temperatures. Electrochim. Acta 2008, 53, 5315–5321. [Google Scholar] [CrossRef]
- Saleh, M.M.; Okajima, T.; Hayase, M.; Kitamura, F.; Ohsaka, T. Exploring the effects of symmetrical and asymmetrical relative humidity on the performance of H2/air PEM fuel cell at different temperatures. J. Power Sources 2007, 164, 503–509. [Google Scholar] [CrossRef]
- Sahu, I.P.; Krishna, G.; Biswas, M.; Das, M.K. Performance Study of PEM Fuel Cell under Different Loading Conditions. Energy Procedia 2014, 54, 468–478. [Google Scholar] [CrossRef]
- Kim, K.-H.; Lee, K.-Y.; Lee, S.-Y.; Cho, E.; Lim, T.-H.; Kim, H.-J.; Yoon, S.P.; Kim, S.H.; Lim, T.W.; Jang, J.H. The effects of relative humidity on the performances of PEMFC MEAs with various Nafion® ionomer contents. Int. J. Hydrogen Energy 2010, 35, 13104–13110. [Google Scholar] [CrossRef]
- Gunn, S.R. Support vector machines for classification and regression. ISIS Tech. Rep. 1998, 14, 5–16. [Google Scholar]
- Trafalis, T.B.; Ince, H. Support vector machine for regression and applications to financial forecasting. In Proceedings of the IEEE-INNS-ENNS International Joint Conference on Neural Networks, IJCNN 2000, Neural Computing: New Challenges and Perspectives for the New Millennium, Como, Italy, 27–27 July 2000; IEEE: Piscataway, NJ, USA, 2000; Volume 6. [Google Scholar]
- Pekel, E. Estimation of soil moisture using decision tree regression. Theor. Appl. Climatol. 2020, 139, 1111–1119. [Google Scholar] [CrossRef]
- Xu, M.; Watanachaturaporn, P.; Varshney, P.K.; Arora, M.K. Decision tree regression for soft classification of remote sensing data. Remote Sens. Environ. 2005, 97, 322–336. [Google Scholar] [CrossRef]
- Wang, L.; Zhou, X.; Zhu, X.; Dong, Z.; Guo, W. Estimation of biomass in wheat using random forest regression algorithm and remote sensing data. Crop J. 2016, 4, 212–219. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Y.; Zhang, J. New machine learning algorithm: Random forest. In Information Computing and Applications, Proceedings of the Third International Conference, ICICA 2012, Chengde, China, 14–16 September 2012; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Setiono, R.; Leow, W.K.; Zurada, J.M. Extraction of rules from artificial neural networks for nonlinear regression. IEEE Trans. Neural Netw. 2002, 13, 564–577. [Google Scholar] [CrossRef]
- Asiltürk, I.; Çunkaş, M. Modeling and prediction of surface roughness in turning operations using artificial neural network and multiple regression method. Expert Syst. Appl. 2011, 38, 5826–5832. [Google Scholar] [CrossRef]
- Ambesange, S.; Vijayalaxmi, A.; Sridevi, S.; Venkateswaran; Yashoda, B.S. Multiple heart diseases prediction using logistic regression with ensemble and hyper parameter tuning techniques. In Proceedings of the 2020 Fourth World Conference on Smart Trends in Systems, Security and Sustainability (WorldS4), London, UK, 27–28 July 2020; IEEE: Piscataway, NJ, USA, 2020. [Google Scholar]
- Carton, J.G.; Lawlor, V.; Olabi, A.G.; Hochenauer, C.; Zauner, G. Water droplet accumulation and motion in PEM (Proton Exchange Membrane) fuel cell mini-channels. Energy 2012, 39, 63–73. [Google Scholar] [CrossRef]
- Afra, M.; Nazari, M.; Kayhani, M.H.; Sharifpur, M.; Meyer, J.P. 3D experimental visualization of water flooding in proton exchange membrane fuel cells. Energy 2019, 175, 967–977. [Google Scholar] [CrossRef]
- Zhang, J.; Li, H.; Shi, Z.; Zhang, J. Effects of hardware design and operation conditions on PEM fuel cell water flooding. Int. J. Green Energy 2010, 7, 461–474. [Google Scholar] [CrossRef]
- Laribi, S.; Mammar, K.; Sahli, Y.; Koussa, K. Analysis and diagnosis of PEM fuel cell failure modes (flooding & dehydration) across the physical parameters of electrochemical impedance model: Using neural networks method. Sustain. Energy Technol. Assess. 2019, 34, 35–42. [Google Scholar]
- Debenjak, A.; Gasperin, M.; Pregelj, B.; Atanazijevič-Kunc, M.; Petrovčič, J.; Jovan, V. Detection of Flooding and Dehydration inside a PEM Fuel Cell Stack. Stroj. Vestn./J. Mech. Eng. 2013, 59, 56–64. [Google Scholar] [CrossRef]
- Brèque, F.; Ramousse, J.; Dubé, Y.; Agbossou, K.; Adzakpa, P. Sensibility study of flooding and dehydration issues to the operating conditions in PEM Fuel Cells. Int. J. Energy Environ. IJEE 2010, 1, 1–20. [Google Scholar]
- Xu, H.; Kunz, H.R.; Fenton, J.M. Analysis of proton exchange membrane fuel cell polarization losses at elevated temperature 120 °C and reduced relative humidity. Electrochim. Acta 2007, 52, 3525–3533. [Google Scholar] [CrossRef]
- Jiang, R.; Kunz, H.R.; Fenton, J.M. Influence of temperature and relative humidity on performance and CO tolerance of PEM fuel cells with Nafion®–Teflon®–Zr (HPO4)2 higher temperature composite membranes. Electrochim. Acta 2006, 51, 5596–5605. [Google Scholar] [CrossRef]
- Abe, T.; Shima, H.; Watanabe, K.; Ito, Y. Study of PEFCs by AC impedance, current interrupt, and Dew point measurements: I. Effect of humidity in oxygen gas. J. Electrochem. Soc. 2003, 151, A101. [Google Scholar] [CrossRef]
- Broka, K.; Ekdunge, P. Oxygen and hydrogen permeation properties and water uptake of Nafion® 117 membrane and recast film for PEM fuel cell. J. Appl. Electrochem. 1997, 27, 117–123. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)?–Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1525–1534. [Google Scholar] [CrossRef]
- Allen, D.M. Mean square error of prediction as a criterion for selecting variables. Technometrics 1971, 13, 469–475. [Google Scholar] [CrossRef]
- Cameron, A.C.; Windmeijer, F.A.G. An R-squared measure of goodness of fit for some common nonlinear regression models. J. Econ. 1997, 77, 329–342. [Google Scholar] [CrossRef]
- Lee, K.-Y.; Kim, K.-H.; Kang, J.-J.; Choi, S.-J.; Im, Y.-S.; Lee, Y.-D.; Lim, Y.-S. Comparison and analysis of linear regression & artificial neural network. Int. J. Appl. Eng. Res. 2017, 12, 9820–9825. [Google Scholar]


| Models and Method | Findings and Research Needs | Reference |
|---|---|---|
| Artificial neural network | Maximum liquid removal by the GDL was predicted using permeability and porosity as inputs. | [7] |
| Convolution neural network | The permeability of the gas diffusion layer was predicted. | [8] |
| Logistic regression, artificial Neural network and support vector machine | Two-phase flow pressure drops in the flow channel of the PEM were classified into three categories using ML. | [9] |
| Genetic algorithm–back propagation neural network | Prediction of water saturation in the GDL. | [10] |
| Index | Relative Humidity | Current Density | Voltage |
|---|---|---|---|
| 133 | 133 | 133 | |
| Mean | 60.45112782 | 0.545865791 | 0.495899594 |
| Std. | 28.48084581 | 0.495256446 | 0.186822813 |
| Min. | 0 | 0.00395502 | 0.11413 |
| 25% | 35 | 0.171083 | 0.358696 |
| 50% | 50 | 0.369474 | 0.505435 |
| 75% | 100 | 0.82204 | 0.63587 |
| Max. | 100 | 2.0389 | 0.9491952 |
| Model | Hyperparameter Value | |
|---|---|---|
| Support vector regression | Kernel | RBF |
| C | 14 | |
| Decision tree | Max_depth | 5 |
| Min_sample_leaf | 2 | |
| min_weight_fraction_leaf | 0.1 | |
| Artificial neural network | Optimizer | Adamax |
| loss | Mean-square-error | |
| Activation | ReLU (for Input and hidden layer) Tanh (for output) | |
| Hidden Layer | 2 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zaveri, J.C.; Dhanushkodi, S.R.; Kumar, C.R.; Taler, J.; Majdak, M.; Węglowski, B. Predicting the Performance of PEM Fuel Cells by Determining Dehydration or Flooding in the Cell Using Machine Learning Models. Energies 2023, 16, 6968. https://doi.org/10.3390/en16196968
Zaveri JC, Dhanushkodi SR, Kumar CR, Taler J, Majdak M, Węglowski B. Predicting the Performance of PEM Fuel Cells by Determining Dehydration or Flooding in the Cell Using Machine Learning Models. Energies. 2023; 16(19):6968. https://doi.org/10.3390/en16196968
Chicago/Turabian StyleZaveri, Jaydev Chetan, Shankar Raman Dhanushkodi, C. Ramesh Kumar, Jan Taler, Marek Majdak, and Bohdan Węglowski. 2023. "Predicting the Performance of PEM Fuel Cells by Determining Dehydration or Flooding in the Cell Using Machine Learning Models" Energies 16, no. 19: 6968. https://doi.org/10.3390/en16196968
APA StyleZaveri, J. C., Dhanushkodi, S. R., Kumar, C. R., Taler, J., Majdak, M., & Węglowski, B. (2023). Predicting the Performance of PEM Fuel Cells by Determining Dehydration or Flooding in the Cell Using Machine Learning Models. Energies, 16(19), 6968. https://doi.org/10.3390/en16196968











