Possibility of Energy Recovery from Airflow around an SUV-Class Car Based on Wind Tunnel Testing
Abstract
:1. Introduction
1.1. Energy Harvesting: Concept and Principles
1.2. Energy Harvesting in Road Transport
1.3. Objectives
2. Materials and Methods
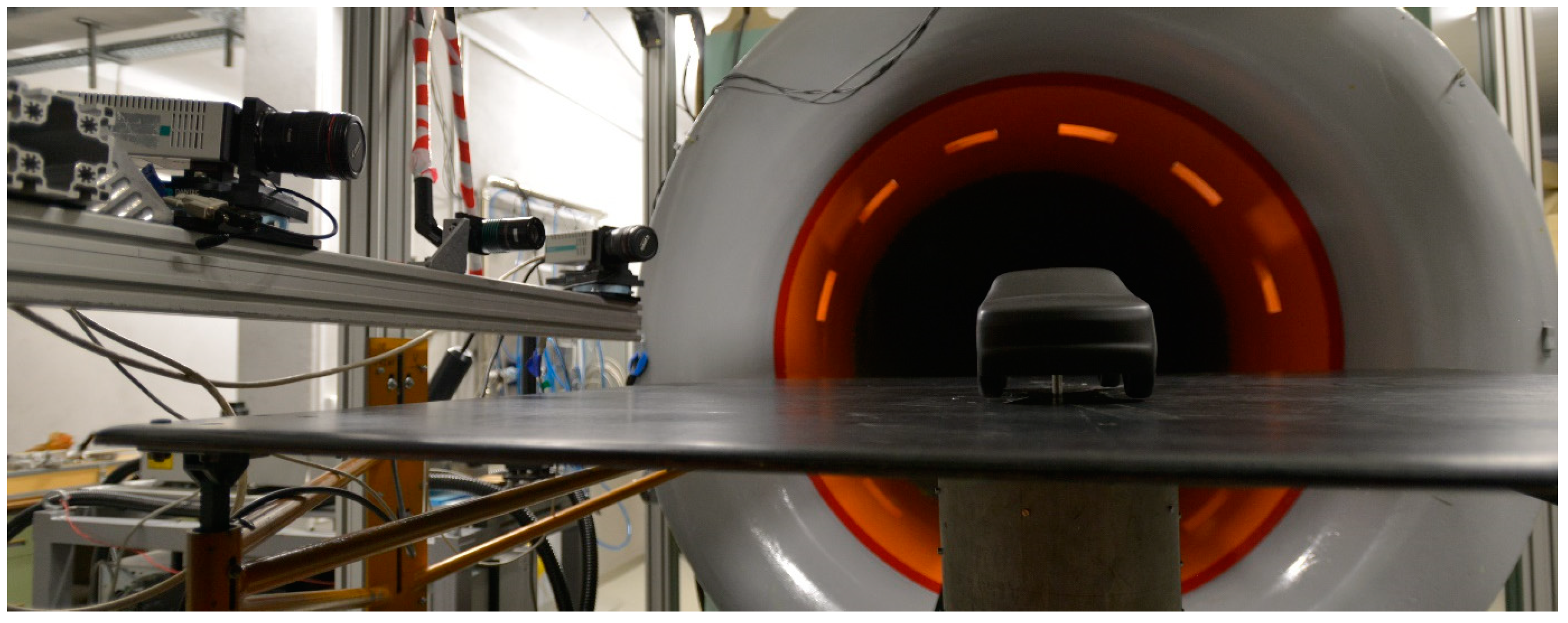
2.1. Experimental Setup
- Length (L) = 422 mm.
- Width (W) = 186 mm.
- Height (H) = 161 mm.
- Wheelbase (WB) = 277 mm.
2.2. Methods Applied in the Experiment
- Stokes force—a viscous drift force, acting on the particle’s boundary with the fluid.
- Force caused by the pressure gradient.
- Resistance of adjoint mass.
- Basset force—the force related with the unsteady movement of a spherical particle.
- Other external forces (magnetic, thermal, etc.).
- Longitudinal position from x = −0.4 L to x = 0.1 L (point of x = 0 lies on the aft point of the car, i.e., rear bumper).
- Transversal position from y = 0 to y = 0.8 W (point of y = 0 lies in the plane of symmetry of the car; due to expected symmetry of the flow, only a half of the object was observed).
- Vertical position from z = 0 to z = 2 H (point of z = 0 lies on the ground).
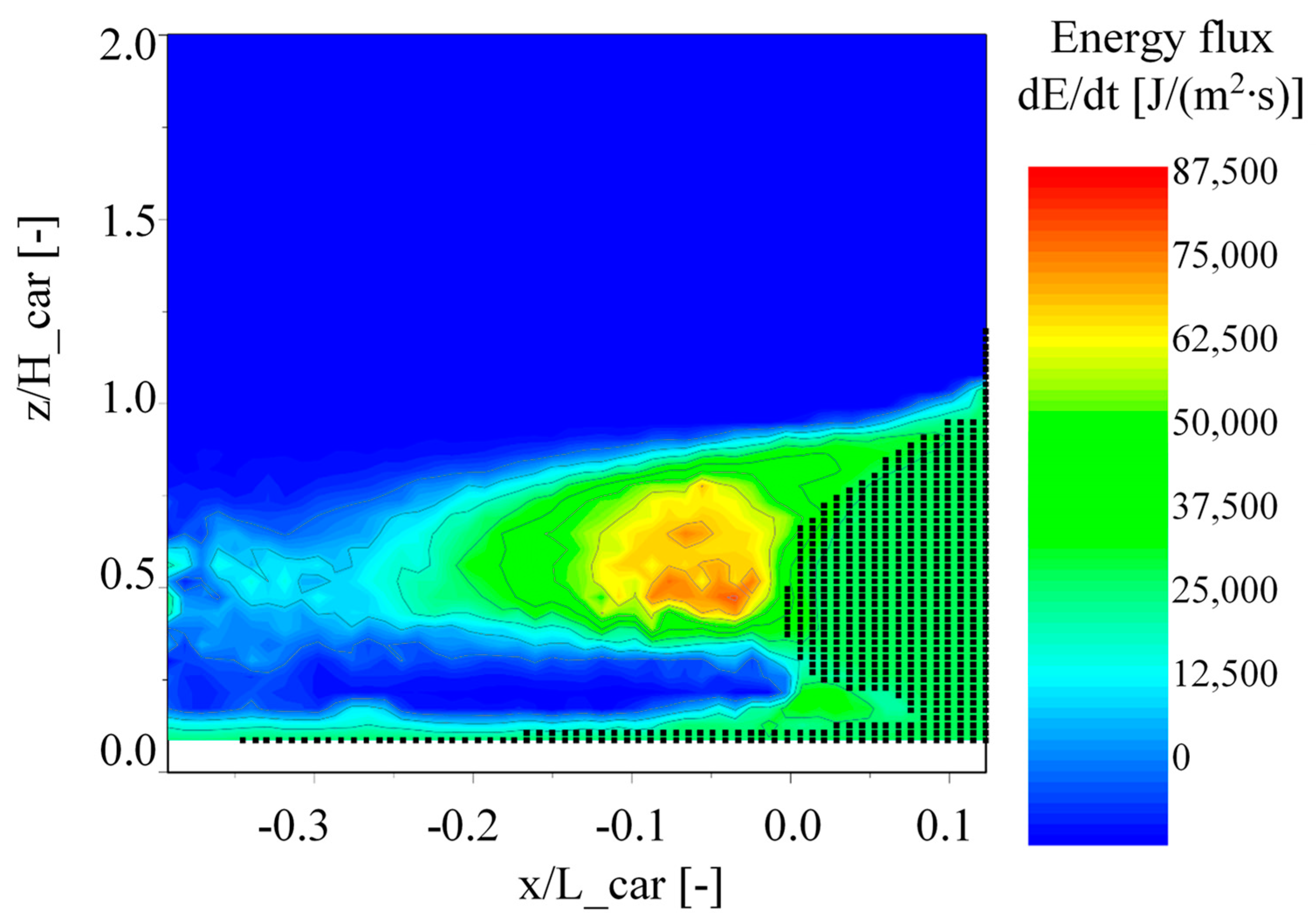
- As we obtained the spatial distribution of the velocity in the inertial coordinate system, it was possible to calculate the kinetic energy of the flow that passed through a selected control section with an elementary area during a unitary time—which means an energy flux, . According to [21], this parameter may be then calculated using the basic equation as follows:
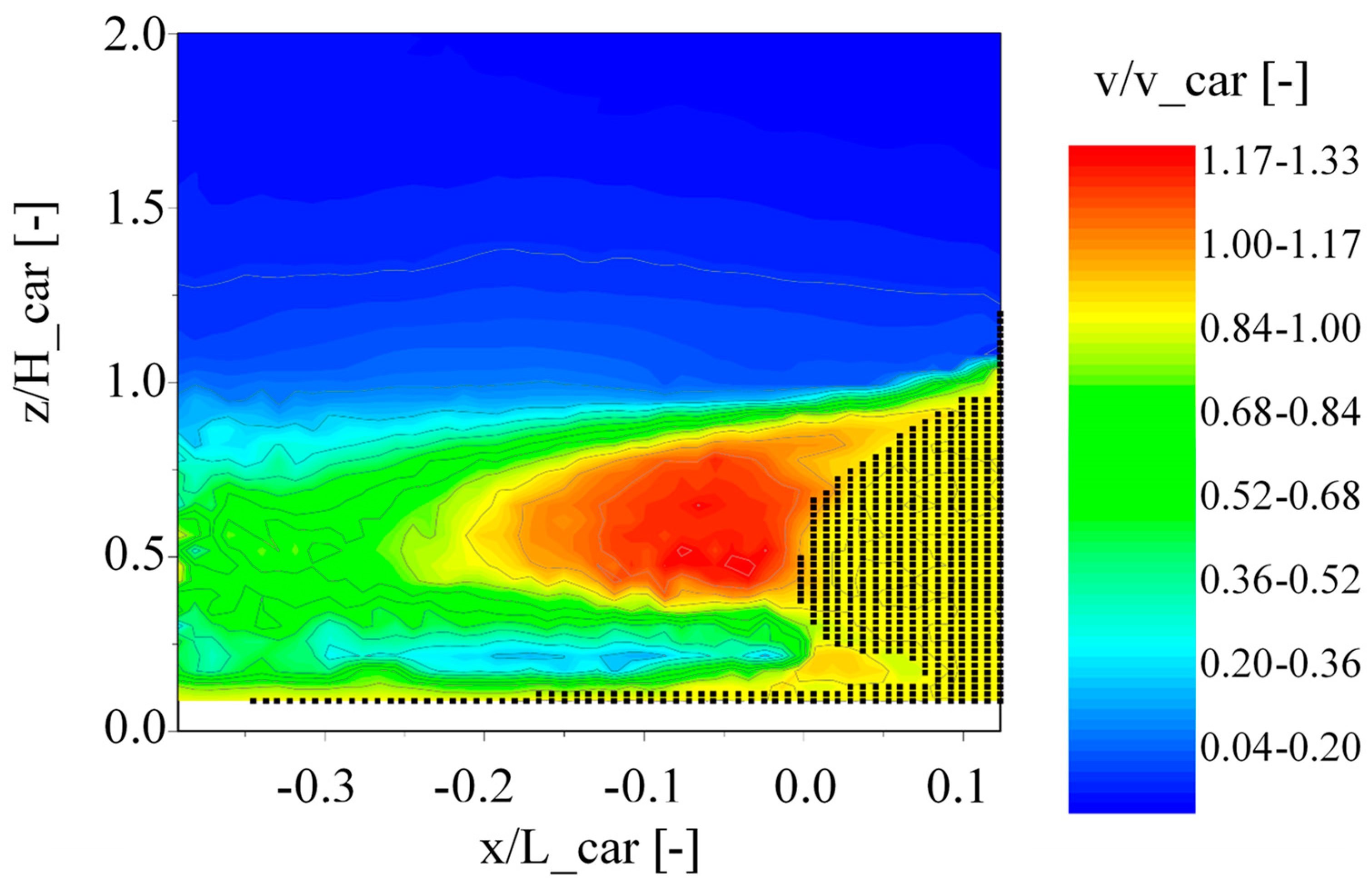
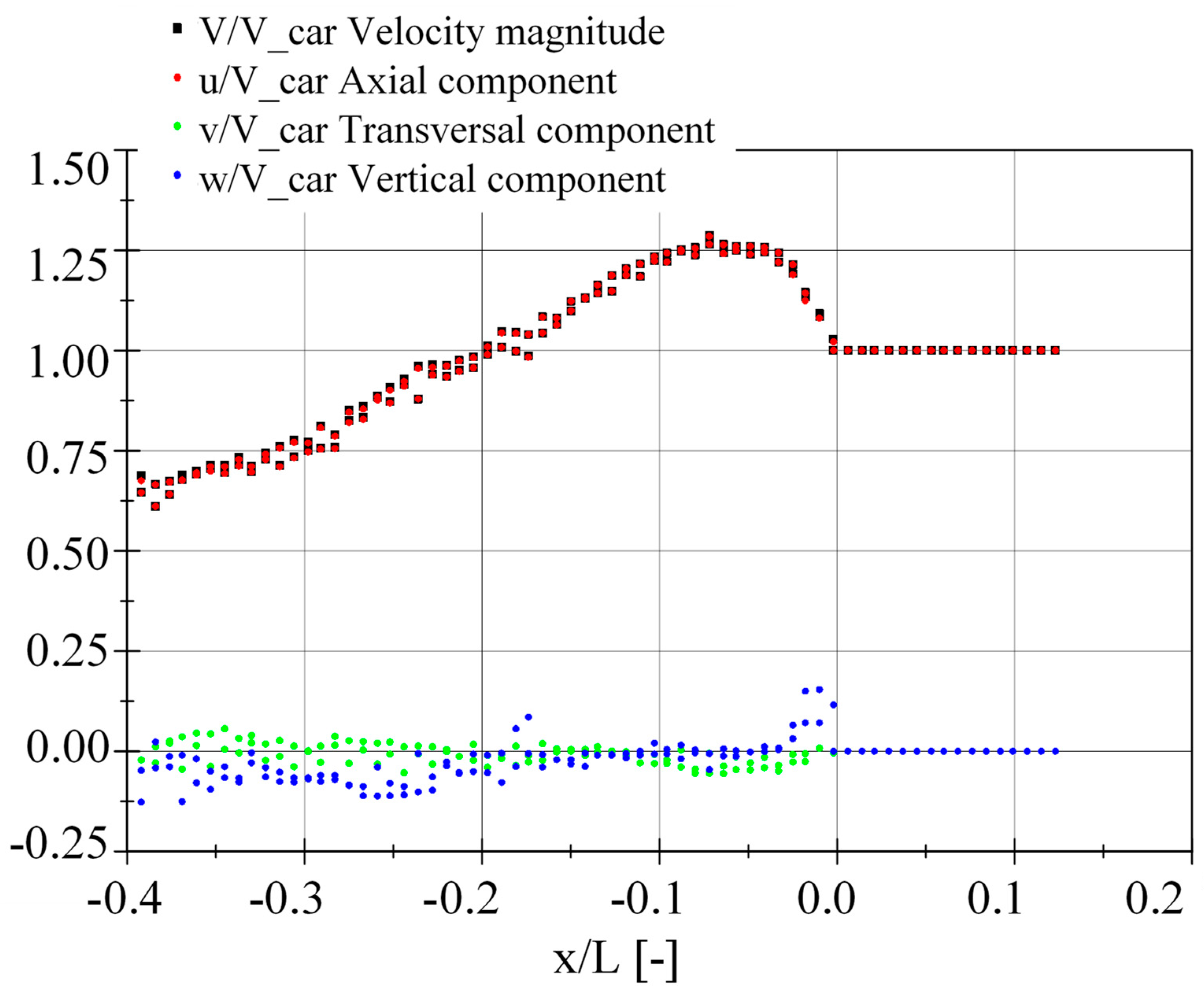
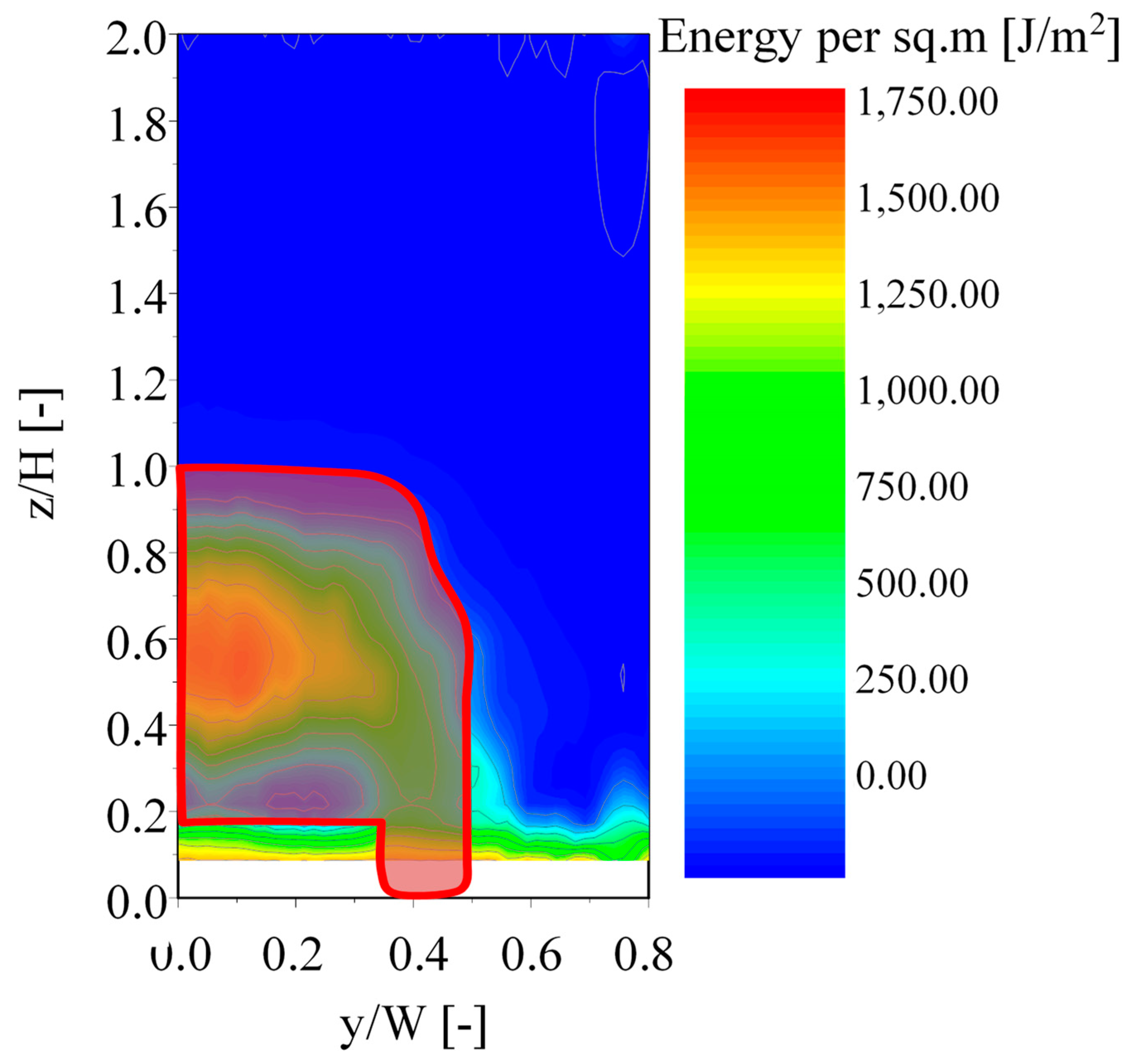
3. Results
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tutak, M.; Brodny, J. Renewable energy consumption in economic sectors in the EU-27. The impact on economics, environment and conventional energy sources. A 20-year perspective. J. Clean. Prod. 2022, 345, 131076. [Google Scholar] [CrossRef]
- Shirazi, M.; Fuinhas, J.A. Portfolio decisions of primary energy sources and economic complexity: The world’s large energy user evidence. Renew. Energy 2023, 202, 347–361. [Google Scholar] [CrossRef]
- Boldyryev, S.; Kuznetsov, M.; Ryabova, I.; Krajačić, G.; Kaldybaeva, B. Assessment of renewable energy use in natural gas liquid processing by improved process integration with heat pumps. e-Prime—Adv. Electr. Eng. Electron. Energy 2023, 5, 100246. [Google Scholar] [CrossRef]
- Usman, M.; Radulescu, M. Examining the role of nuclear and renewable energy in reducing carbon footprint: Does the role of technological innovation really create some difference? Sci. Total Environ. 2022, 841, 156662. [Google Scholar] [CrossRef] [PubMed]
- Jiang, L.; Jiang, H. Analysis of predictions considering mineral prices, residential energy, and environmental risk: Evidence from the USA in COP 26 perspective. Resour. Policy 2023, 82, 103431. [Google Scholar] [CrossRef]
- Krzywonos, M.; Skudlarski, J.; Kupczyk, A.; Wojdalski, J.; Tucki, K. Forecast for transport biofuels in Poland in 2020–2030. Przem. Chem. 2015, 94, 2218–2222. [Google Scholar] [CrossRef]
- Vujanović, M.; Besagni, G.; Duić, N.; Markides, C.N. Innovation and advancement of thermal processes for the production, storage, utilization and conservation of energy in sustainable engineering applications. Appl. Therm. Eng. 2023, 221, 119814. [Google Scholar] [CrossRef]
- Sharmin, T.; Khan, N.R.; Akram, M.S.; Ehsan, M.M. A State-of-the-Art Review on Geothermal Energy Extraction, Utilization, and Improvement Strategies: Conventional, Hybridized, and Enhanced Geothermal Systems. Int. J. Thermofluids 2023, 18, 100323. [Google Scholar] [CrossRef]
- Sagdic, K.; Eş, I.; Sitti, M.; Inci, F. Smart materials: Rational design in biosystems via artificial intelligence. Trends Biotechnol. 2022, 40, 987–1003. [Google Scholar] [CrossRef]
- Mishra, A.; Gangele, A. Smart Materials For Clean And Sustainable Technology For Smart Cities. Mater. Today Proc. 2020, 29, 338–342. [Google Scholar] [CrossRef]
- Maurya, K.K.; Rawat, A.; Jha, G. Smart materials and electro-mechanical impedance technique: A review. Mater. Today Proc. 2020, 33, 4993–5000. [Google Scholar] [CrossRef]
- Sossou, G.; Demoly, F.; Belkebir, H.; Qi, H.J.; Gomes, S.; Montavon, G. Design for 4D printing: A voxel-based modeling and simulation of smart materials. Mater. Des. 2019, 175, 107798. [Google Scholar] [CrossRef]
- Jiao, P.; Chen, T.; Xie, Y. Self-adaptive mechanical metamaterials (SMM) using shape memory polymers for programmable postbuckling under thermal excitations. Compos. Struct. 2021, 256, 113053. [Google Scholar] [CrossRef]
- Wang, Y.; Qiu, Y.; Kong, F.; Zhang, H. Research on nonlinear correction of giant magnetostrictive material optical current transformer. Energy Rep. 2022, 8, 983–988. [Google Scholar] [CrossRef]
- Xu, H.; Pei, Y.; Fang, D.; Ai, S. An energy-based dynamic loss hysteresis model for giant magnetostrictive materials. Int. J. Solids Struct. 2013, 50, 672–679. [Google Scholar] [CrossRef]
- Singh, P.K.; Pareta, A.S.; Panda, S.K. Influence of the bi-nonlinearity on the characterization of mode I fracture parameter JIc for a cracked giant magnetostrictive material in the coupled magneto-elastic field: An experimental and numerical study. Eng. Fract. Mech. 2023, 279, 109046. [Google Scholar] [CrossRef]
- Kaleta, J.; Wiewiórski, P. Magnetovisual method for monitoring thermal demagnetization of permanent magnets used in magnetostrictive actuators. J. Rare Earths 2014, 32, 236–241. [Google Scholar] [CrossRef]
- Nandy, M.; Lahiri, B.B.; Philip, J. Visual detection of defects in carbon steel using magnetic nanoemulsions: Effect of stabilizing moieties on the defect detection sensitivity. Sens. Actuators A Phys. 2020, 314, 112220. [Google Scholar] [CrossRef]
- Boumaiz, M.; Ghazi, M.; Mazer, S.; Fattah, M.; Bouayad, A.; Bekkali, M.; Balboul, Y. Energy harvesting based WBANs: EH optimization methods. Procedia Comput. Sci. 2019, 151, 1040–1045. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, X.; Rasim, Y.; Wang, C.; Du, B.; Yuan, Y. Design, modelling and practical tests on a high-voltage kinetic energy harvesting (EH) system for a renewable road tunnel based on linear alternators. Appl. Energy 2016, 164, 152–161. [Google Scholar] [CrossRef]
- Pan, H.; Qi, L.; Zhang, A.; Yan, J. Kinetic energy harvesting technologies for applications in land transportation: A comprehensive review. Appl. Energy 2021, 286, 116518. [Google Scholar] [CrossRef]
- Zuo, J.; Dong, L.; Yang, F.; Guo, Z.; Wang, T.; Zuo, L. Energy harvesting solutions for railway transportation: A comprehensive review. Renew. Energy 2023, 202, 56–87. [Google Scholar] [CrossRef]
- Bai, S.; Liu, C. Overview of energy harvesting and emission reduction technologies in hybrid electric vehicles. Renew. Sustain. Energy Rev. 2021, 147, 111188. [Google Scholar] [CrossRef]
- Vu, N.H.; Pham, T.T.; Shin, S. Flat concentrator photovoltaic system for automotive applications. Sol. Energy 2019, 190, 246–254. [Google Scholar] [CrossRef]
- Rakov, V. Determination of optimal characteristics of braking energy recovery system in vehicles operating in urban conditions. Transp. Res. Procedia 2020, 50, 566–573. [Google Scholar] [CrossRef]
- Buenaventura, A.B.; Azzopardi, B. Energy recovery systems for retrofitting in internal combustion engine vehicles: A review of techniques. Renew. Sustain. Energy Rev. 2015, 41, 955–964. [Google Scholar] [CrossRef]
- Shen, Z.G.; Tian, L.L.; Liu, X. Automotive exhaust thermoelectric generators: Current status, challenges and future prospects. Energy Convers. Manag. 2019, 195, 1138–1173. [Google Scholar] [CrossRef]
- Carvalho, R.; Martins, J.; Pacheco, N.; Puga, H.; Costa, J.; Vieira, R.; Goncalves, L.M.; Brito, F.P. Experimental validation and numerical assessment of a temperature-controlled thermoelectric generator concept aimed at maximizing performance under highly variable thermal load driving cycles. Energy 2023, 280, 127979. [Google Scholar] [CrossRef]
- Howell, J.; Gaylard, A. Improving SUV Aerodynamics. In Proceedings of the 6th MIRA International Vehicle Aerodynamics Conference, Gaydon, Warwickshire, UK, 25–26 October 2006; Volume 1, pp. 1–17. [Google Scholar]
- Chaligné, S.; Turner, R.; Gaylard, A. The Aerodynamics Development of the New Land Rover Discovery. Prog. Veh. Aerodyn. Therm. Manag. 2018, 1, 145–159. [Google Scholar] [CrossRef]
- Scurtu, I.L.; Balcau, M.; Jurco, A.; Craciun, I.; Kiraly, A.; Szabo, I. Evaluation and improving the aerodynamics of the commercial van. J. Ind. Des. Eng. Graph. 2023, 18, 17–22. [Google Scholar]
- Jazar, R.M. Vehicle Dynamics Theory and Applications, 1st ed.; Springer: New York, NY, USA, 2008; pp. 37–888. [Google Scholar] [CrossRef]
- Fago, B.; Lindner, H.; Mahrenholtz, O. The effect of ground simulation on the flow around vehicles in wind tunnel testing. J. Wind Eng. Ind. Aerodyn. 1991, 38, 47–57. [Google Scholar] [CrossRef]
- An Experimental Study of the Ground Transportation System(GTS) Model in the NASA Ames 7- by 10-Ft Wind Tunnel. Available online: https://ntrs.nasa.gov/citations/20010038028 (accessed on 4 September 2023).
- Rejniak, A.A.; Gatto, A. Upstream wind tunnel model mounting: The forgotten method for road vehicle aerodynamics. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2021, 235, 1992–2012. [Google Scholar] [CrossRef]
- Stryczniewicz, W. Anemometria Obrazowa PIV w Praktyce Badań Aerodynamicznych, 1st ed.; Wydawnictwa Naukowe Sieć Badawcza Łukasiewicz—Instytutu Lotnictwa: Warsaw, Poland, 2020; pp. 1–105. [Google Scholar]
- Raffel, M.; Willert, C.E.; Wereley, S.T.; Kompenhans, J. Particle Image Velocimetry—A Practical Guide, 3rd ed.; Springer: Cham, Switzerland, 2007; pp. 33–641. Available online: https://link.springer.com/content/pdf/10.1007/978-3-319-68852-7.pdf (accessed on 4 September 2023).
- Adrian, R.J. Twenty Years Of Particle Image Velocimetry. Exp. Fluids 2005, 39, 159–169. [Google Scholar] [CrossRef]
- Corradini, M.L.; Zhu, C.; Fan, L.S.; Jean, R.H. Multiphase Flow. In Handbook of Fluid Dynamics, 2nd ed.; Johnson, R.W., Ed.; CRC Press: UK, London, 2016; pp. 20.1–20.104. ISBN 978-143984957-6/978-143984955-2. Available online: https://www.routledge.com/Handbook-of-Fluid-Dynamics-Second-Edition/Johnson/p/book/9781439849552 (accessed on 4 September 2023).
- Kompenhans, J.; Schröder, A.; Raffel, M.; Kähler, C.; Arnott, A.; Bao, F.; Sammler, B.; Schneider, G.; Stasicki, B.; Frahnert, H.; et al. Application of Particle Image Velocimetry, Theory and Practice. In Application of Particle Image Velocimetry, Theory and Practice, Ordner-. PIV-Course. Available online: https://elib.dlr.de/12616/ (accessed on 4 September 2023).
- Kosowski, K.; Tucki, K.; Kosowski, A. Application of Artificial Neural Networks in Investigations of Steam Turbine Cascades. J. Turbomach.-Trans. ASME 2010, 132, 014501–014505. [Google Scholar] [CrossRef]
- Kosowski, K.; Tucki, K.; Kosowski, A. Turbine stage design aided by artificial intelligence methods. Expert Syst. Appl. 2009, 36, 11536–11542. [Google Scholar] [CrossRef]
- Şahin, M.E.; Blaabjerg, F.; Sangwongwanich, A. A comprehensive review on supercapacitor applications and developments. Energies 2022, 15, 674. [Google Scholar] [CrossRef]
- Laadjal, K.; Cardoso, A.J.M. A review of supercapacitors modeling, SoH, and SoE estimation methods: Issues and challenges. Int. J. Energy Res. 2021, 45, 18424–18440. [Google Scholar] [CrossRef]
- Gao, D.; Luo, Z.; Liu, C.; Fan, S. A survey of hybrid energy devices based on supercapacitors. Green Energy Environ. 2023, 8, 972–988. [Google Scholar] [CrossRef]
- Adekoya, G.J.; Adekoya, O.C.; Ugo, U.K.; Sadiku, E.R.; Hamam, Y.; Ray, S.S. A mini-review of artificial intelligence techniques for predicting the performance of supercapacitors. Mater. Today Proc. 2022, 62, S184–S188. [Google Scholar] [CrossRef]
- Ma, N.; Yin, H.; Wang, K. Prediction of the Remaining Useful Life of Supercapacitors at Different Temperatures Based on Improved Long Short-Term Memory. Energies 2023, 16, 5240. [Google Scholar] [CrossRef]
- Sun, X.; Zhang, Y.; Zhang, Y.; Wang, L.; Wang, K. Summary of Health-State Estimation of Lithium-Ion Batteries Based on Electrochemical Impedance Spectroscopy. Energies 2023, 16, 5682. [Google Scholar] [CrossRef]
- Tawfik, W.Z.; Mohammad, S.N.; Rahouma, K.H.; Tammam, E.; Salama, M.G. An artificial neural network model for capacitance prediction of porous carbon-based supercapacitor electrodes. J. Energy Storage 2023, 73, 108830. [Google Scholar] [CrossRef]
- Mian, S.H.; Nazir, M.S.; Ahmad, I.; Khan, S.A. Optimized nonlinear controller for fuel cell, supercapacitor, battery, hybrid photoelectrochemical and photovoltaic cells based hybrid electric vehicles. Energy 2023, 283, 129121. [Google Scholar] [CrossRef]
- Wu, Y.; Huang, Z.; Zheng, Y.; Liu, Y.; Li, H.; Che, Y.; Peng, J.; Teodorescu, R. Spatial–temporal data-driven full driving cycle prediction for optimal energy management of battery/supercapacitor electric vehicles. Energy Convers. Manag. 2023, 277, 116619. [Google Scholar] [CrossRef]
- Nanda, S.; Ghosh, S.; Thomas, T. Machine learning aided cyclic stability prediction for supercapacitors. J. Power Sources 2022, 546, 231975. [Google Scholar] [CrossRef]
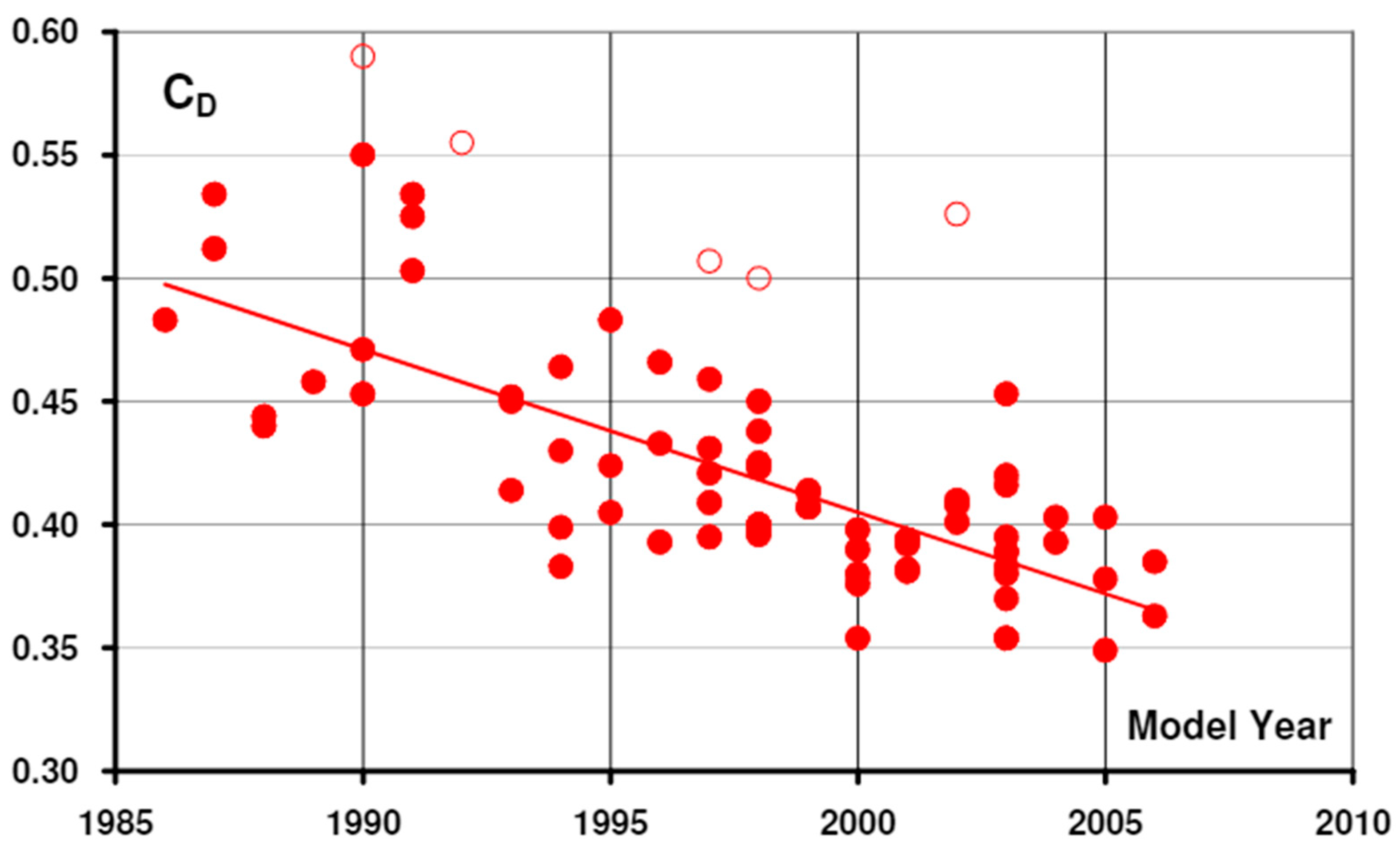
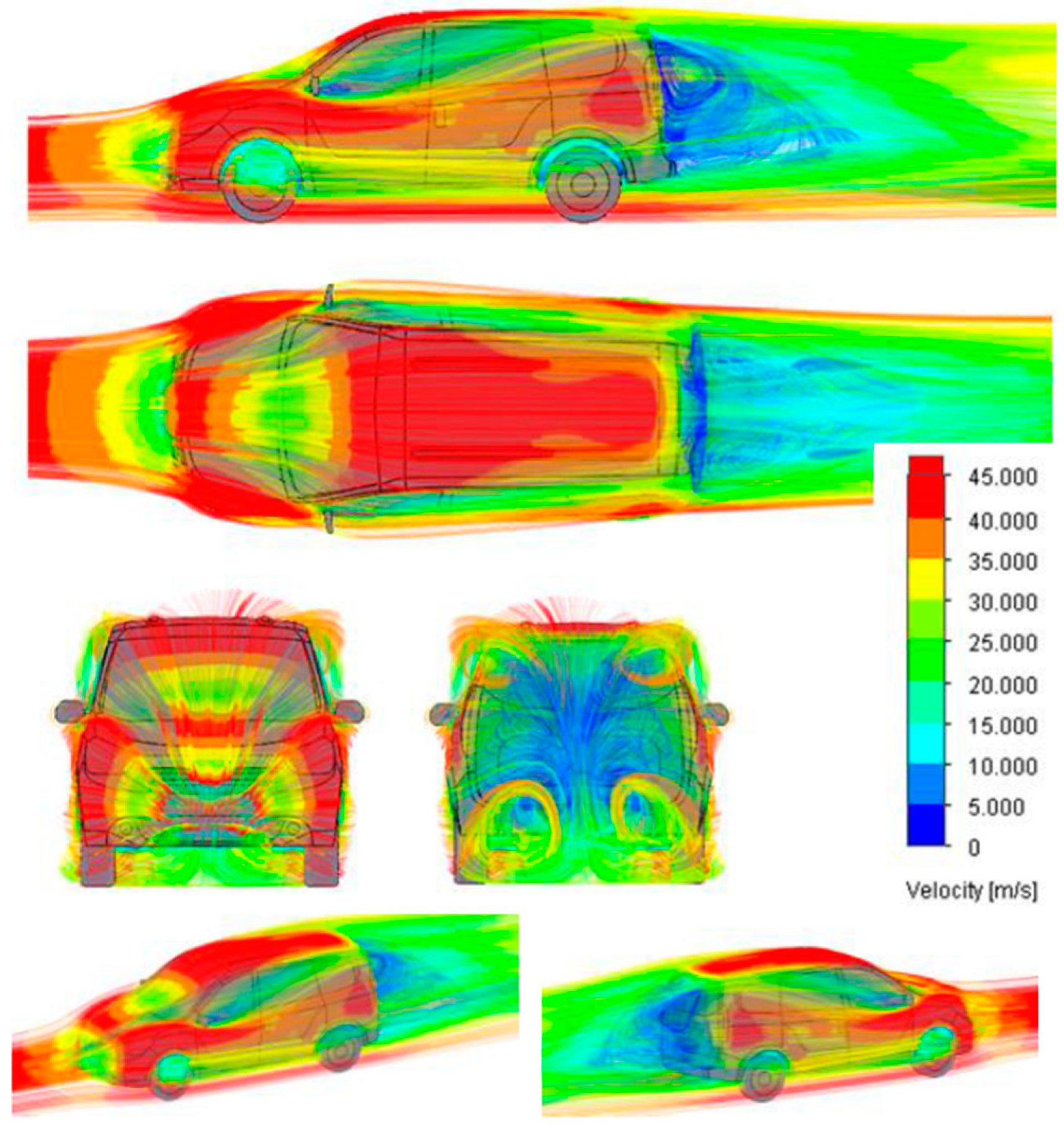
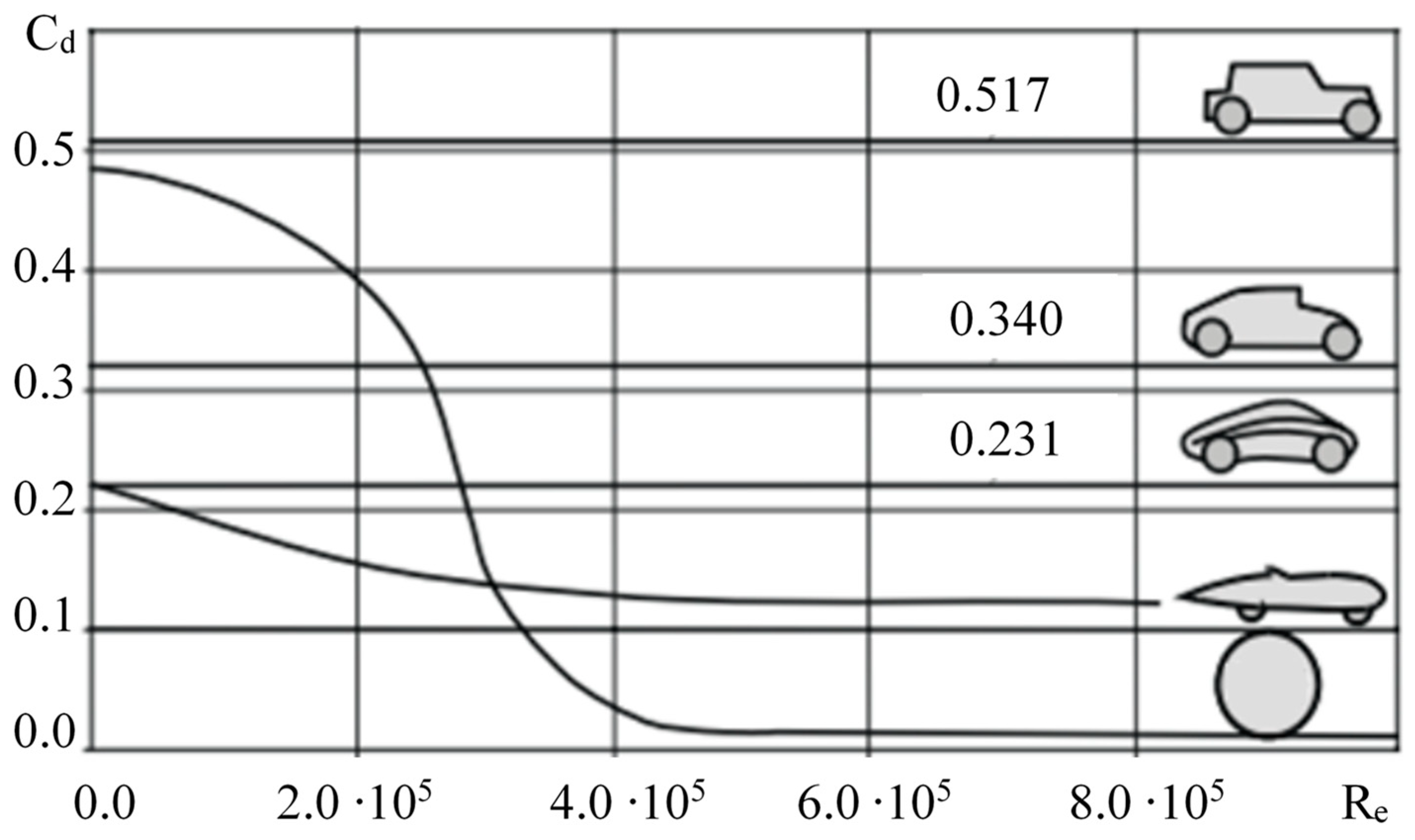

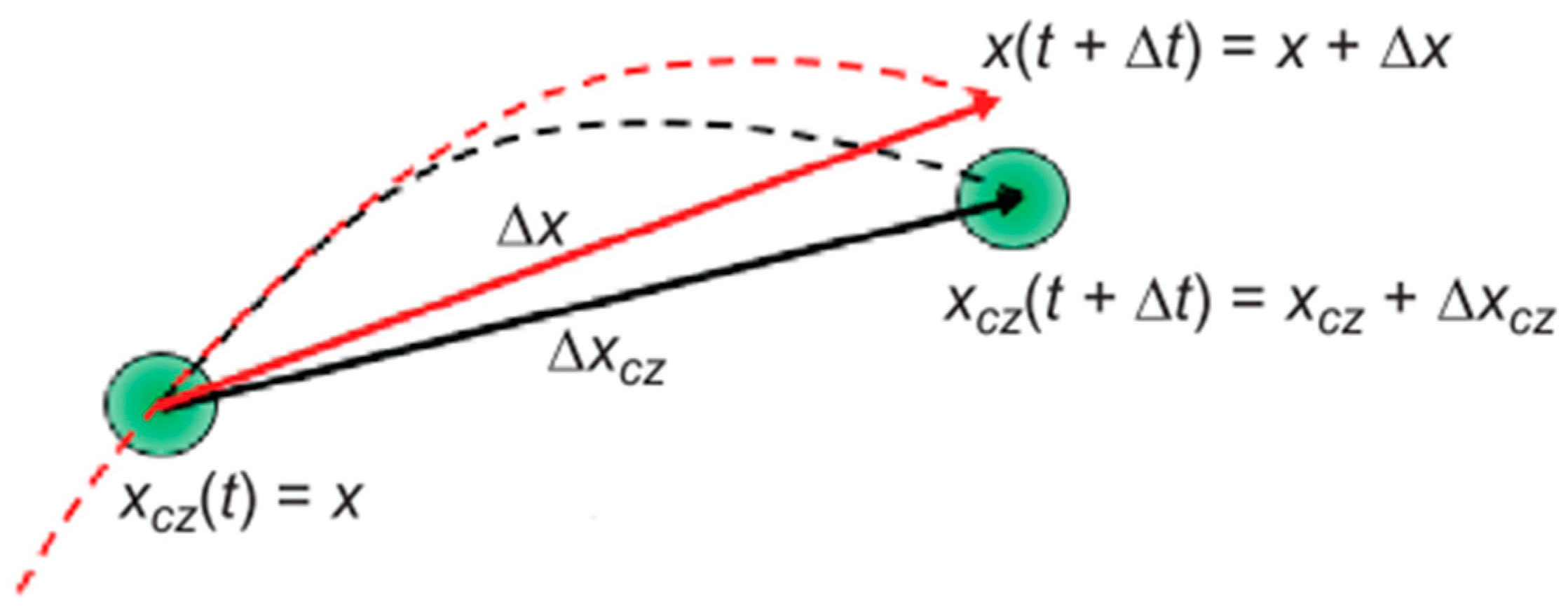

| Parameter | SUV | Saloon Car |
|---|---|---|
| Drag coefficient | 0.4 | 0.3 |
| Frontal area | 3.0 m2 | 2.0 m2 |
| Weight | 2500 kg | 1700 kg |
| Total resistance at 150 km/h | 1720 N | 943 N |
| Rolling resistance at 150 km/h | 423 N | 300 N |
| Aerodynamic drag force at 150 km/h | 1276 N | 646 N |
| Material | State of Matter | ||
|---|---|---|---|
| Di-ethil-hexil-sebacate (DEHS) oil | Liquid | 1 | 2 |
| Olive oil | Liquid | 2 | 5 |
| Titanium dioxide TiO2 | Solid | 0.5 | 0.5 |
| Helium filled soap bubbles (HFSB) | Liquid | 300 | 25 |
| Y | Z | y | z | y/W | z/H | Energy Per sq.m |
|---|---|---|---|---|---|---|
| 6 | 0 | −243.999 | 0 | 0 | 0.20948 | 238.044 |
| 15 | 0 | −214.233 | 0 | 0 | 0.394363 | 1191.37 |
| 25 | 0 | −181.159 | 0 | 0 | 0.599788 | 1665.08 |
| 35 | 0 | −148.086 | 0 | 0 | 0.805214 | 1019.41 |
| 44 | 0 | −118.32 | 0 | 0 | 0.990096 | 52.8572 |
| 54 | 0 | −85.2459 | 0 | 0 | 1.19552 | 25.1932 |
| 6 | 8 | −243.999 | 40 | 0.215054 | 0.20948 | 186.518 |
| 15 | 8 | −214.233 | 40 | 0.215054 | 0.394363 | 881.242 |
| 25 | 8 | −181.159 | 40 | 0.215054 | 0.599788 | 1384.61 |
| 35 | 8 | −148.086 | 40 | 0.215054 | 0.805214 | 596.567 |
| 44 | 8 | −118.32 | 40 | 0.215054 | 0.990096 | 52.3818 |
| 54 | 8 | −85.2459 | 40 | 0.215054 | 1.19552 | 22.2057 |
| 6 | 15 | −243.999 | 75 | 0.403226 | 0.20948 | 799.63 |
| 15 | 15 | −214.233 | 75 | 0.403226 | 0.394363 | 870.287 |
| 25 | 15 | −181.159 | 75 | 0.403226 | 0.599788 | 578.935 |
| 35 | 15 | −148.086 | 75 | 0.403226 | 0.805214 | 285.509 |
| 44 | 15 | −118.32 | 75 | 0.403226 | 0.990096 | 36.0309 |
| 54 | 15 | −85.2459 | 75 | 0.403226 | 1.19552 | 17.4157 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruchała, P.; Orynycz, O.; Stryczniewicz, W.; Tucki, K. Possibility of Energy Recovery from Airflow around an SUV-Class Car Based on Wind Tunnel Testing. Energies 2023, 16, 6965. https://doi.org/10.3390/en16196965
Ruchała P, Orynycz O, Stryczniewicz W, Tucki K. Possibility of Energy Recovery from Airflow around an SUV-Class Car Based on Wind Tunnel Testing. Energies. 2023; 16(19):6965. https://doi.org/10.3390/en16196965
Chicago/Turabian StyleRuchała, Paweł, Olga Orynycz, Wit Stryczniewicz, and Karol Tucki. 2023. "Possibility of Energy Recovery from Airflow around an SUV-Class Car Based on Wind Tunnel Testing" Energies 16, no. 19: 6965. https://doi.org/10.3390/en16196965
APA StyleRuchała, P., Orynycz, O., Stryczniewicz, W., & Tucki, K. (2023). Possibility of Energy Recovery from Airflow around an SUV-Class Car Based on Wind Tunnel Testing. Energies, 16(19), 6965. https://doi.org/10.3390/en16196965








