Abstract
A permanent magnet synchronous motor (PMSM) is a nonlinear, strongly coupled, controlled object with time-varying, fractional-order characteristics. It is difficult to achieve the ideal control effect by using the traditional control method when motor parameter changes and load perturbations occur during the operation of the PMSM, so a fractional-order adaptive fuzzy backstepping control method is proposed to improve the system’s fast response and anti-jamming ability in the case of sudden changes in rotational speed, load perturbations and other conditions. Initially, the fractional order theory is introduced, backstepping control is utilized to decompose the system into multiple subsystems, and a fractional order-based Lyapunov function is designed for each subsystem to ensure the system’s stability. Suitable control laws, as well as parameter adaptive laws, are derived through rigorous mathematical derivation. Finally, a fractional order adaptive fuzzy backstepping controller (FOAB-FPID) is designed by combining the advantages of fuzzy control. Then a mechanical simulation model of the PMSM is established to verify the validity of the designed controller, followed by three sets of comparative experiments: PID, fuzzy PID (F-PID), and integer-order adaptive fuzzy backstepping (IOAB-FPID), which are selected to simulate the PMSM under the control of the four controllers. Finally, it is validated on the constructed PMSM experimental platform. Simulation and experimental results show that FOAB-FPID can adaptively adjust system parameters during sudden speed changes, achieve real-time speed tracking, and maintain speed stability under load perturbations and internal parameter uptake. Compared with the three control strategies, reached PMSM system has better acceleration, fast response performance, and better anti-disturbance ability, which proves the rationality and effectiveness of the FOAB-FPID control method.
1. Introduction
Permanent Magnet Synchronous Motor (PMSM) is a high-performance motor type widely used because of its high efficiency, low noise, long life, etc. [1,2,3]. Conventional PMSM speed controllers usually use a cascaded PID control strategy, where an outer-loop speed controller and an inner-loop current controller act together to stabilize the desired dynamic error [4,5]. However, the PMSM is a nonlinear and strongly coupled controlled object [6,7]. It makes the design of the speed controller have some limitations and challenges.
Benefiting from the rapid development of the mathematics of differential geometry, the related theories and applications of nonlinear control systems are becoming increasingly mature. Many nonlinear control strategies have been proposed by domestic and foreign researchers, such as sliding mode control [8], fuzzy control [9], model predictive control [10], feedback linearization control [11], and backstepping control [12,13]. The literature [14] proposes an iterative learning control strategy for both performance improvement and simple controller structure. In the literature [15], an observer-based adaptive neural network finite-time dynamic surface control method is proposed to improve the robustness of the system; the literature [16] presents a novel sensor-less speed tracking control scheme to improve the robustness of the system. However, the above papers need to consider more internal parameter variations and load perturbations in the system. More seriously, they all focus on integer order, ignoring the fractional order characteristics of the PMSM system [17,18].
The fractional order theory has been developed and enriched recently and has begun to be widely applied to nonlinear systems [19,20]. During their early exploration, scholars found that fractional algorithms were usually more accurate than integer algorithms when modelling some complex nonlinear systems [21]. Some scholars have proposed some analytical and numerical methods for fractional differential equations [22] and discussed the stability and performance analysis of fractional order systems [23,24]. Then, fractional-order control strategies are more widely used in nonlinear system control [25]. Some new control algorithms and strategies are proposed [26,27,28,29], such as fractional order PID control, fractional order sliding mode control, fractional order differential equation-based control, adaptive fractional order control, etc. Some scholars and experts demonstrated that inductance and capacitance are essentially fractional orders [30], so existing PMSM systems suffer from non-integer orders in kinetic processes with memory and hereditary mass diffusion or heat conduction [31], and fractional order theory has been increasingly applied to PMSM control with good results in recent years. In the literature [32], a fractional-order sliding mode control method was proposed to solve the shortcomings of the traditional control method, such as weak immunity and significant jitter. The literature [33] improved a fractional-order controller to improve speed tracking and immunity performance. This paper explores how to ensure the system’s rapid response and excellent robustness in the case of sudden speed change, external disturbance, fractional influence, etc. Firstly, the mathematical model and structure of PMSM are studied. Then, the system is decomposed into several subsystems by using the advantage of fractional-order calculus theory combined with the mathematical derivation of the backstepping control method of multivariate adaptive change. The Lyapunov function is designed for each subsystem based on fractional-order calculus to ensure stability. A FOAB-FPID controller is designed by combining the advantages of fuzzy control with strong adaptability to parameter variation, nonlinearity, and model inaccuracy of the controlled object. The simulation and experimental results show that the method has a better control effect.
This paper is organized as follows: in Section 2, the PMSM mathematical model is derived, followed by the derivation of the control law, and the adaptive law, and the design of the FOAB-FPID controller. In Section 3, the simulation model is built and simulated. Section 4 is experimental platform validation. Section 5 compares the simulation and experimental results. Section 6 concludes.
2. Controller Design
2.1. PMSM Mathematical Model
The PMSM can be broadly classified into two forms: surface-mounted and built-in, as the permanent magnets mounted on the motor’s rotor are in different structural positions. The surface-mounted type is relatively cheaper and has a simpler structure than the built-in type. Since this paper is not a high-performance study of the motor, the surface-mounted permanent magnet synchronous motor, id = 0 control, is chosen. Assuming smooth rotor and stator surfaces, neglecting core saturation, ignoring eddy currents and hysteresis losses, and current triple symmetry, the voltage equation of the PMSM in the d-q axis rotating coordinate system is as follows [34].
where ud and uq are the corresponding voltage components, id, and iq are the current components, wr is the rotor mechanical angular velocity, and RS is the stator resistance, nP is the number of motor pole pairs, and are the magnetic chain components in the d-q axis rotational coordinate system. The mechanical equation of motion and the electromagnetic torque equation are as follows [35]:
where the rotor magnetic chain. Neglecting the inhomogeneity of the air gap of the surface-mounted PMSM, where . is the electromagnetic torque, is the load torque, B is the damping factor, and J is the rotational inertia. Equation (3) can be deduced from Equations (1) and (2).
2.2. FOAB-FPID Controller Design
The fractional order calculus is a non-integer order calculus with three common forms of definition, and this paper selects the Caputo form [36], defined as:
where is the gamma function, is the order, , and is the integer order calculus of the function.
Lemma 1.
Let be a continuous differentiable function, then:
Converting Equation (3) to fractional order form:
Define the speed following error , q-axis current following error , d-axis current following error , stator resistance error , load torque error . As shown in Equation (7).
where is the desired motor speed, is the desired q-axis current, is the desired d-axis current, is the estimated stator resistance, and is the estimated load torque. In this paper, we study the case where the speed varies occasionally, ignoring the effect of magnetic circuit saturation. According to the above parameter settings, the mathematical design of the PMSM system is carried out using the backstepping method. Based on the fractional order differential definitions and Formulas (6) and (7), get the fractional order derivative speed to follow the error.
Select the Lyapunov function: . Where is the speed error feedback gain and is greater than 0, the fractional order derivative of the Lyapunov function is obtained from Equations (4), (5) and (8).
From Equation (9) above, the desired q-axis current can be set as follows:
When the q-axis current satisfies the above equation, we obtain the fractional derivative of the d-q-axis current following the error. Introduce the Lyapunov function, and then obtain the fractional order derivation. Where, and are the adaptive rates of change of and ,and are greater than 0.
After a series of derivations, in order to satisfy the PMSM system stabilization, the control law and adaptive law are selected as follows:
By substituting Equation (12) into the equation, the fractional order derivative of Y2 is less than or equal to 0. Through the above mathematical derivation, it can be seen that the system is asymptotically stable as the time ‘t’ increases., , converges to zero exponentially when ‘t’ tends to infinity, the speed of the PMSM and the d-q-axis current converge exponentially to its desired value. To differ from the traditional control with fixed parameters, this paper sets the adaptive adjustment feedback gain in the dynamic regulation process, sets the adaptive feedback gain for the speed error of fractional order derivatives, and sets the adaptive feedback gain for the load torque error and the adaptive feedback gain for the stator resistance error. It adaptively adjusts the parameters according to the real-time operation of PMSM to ensure the dynamic response performance of PMSM speed regulation.
The fuzzy system consists of four parts: fuzzification, knowledge base, fuzzy rule inference, and defuzzification [37]. A two-dimensional fuzzy controller is selected, and the fractional order derivatives of the speed error and the rate of change of speed error are used as the fuzzy controller inputs, and , , and are used as the fuzzy controller outputs. theoretical domain setting needs to take into account the control accuracy, and it must be able to decay to 0 in the range of this domain, introducing the scaling factor and continuously simulating the experiment; the normalized field of , was determined as [–3, 3]. The variation of random variables is approximately normally distributed, and the normalized theoretical field of can be found as [0, 1/3, 2/3, 1, 4/3, 5/3, 2], the normalized field of as [−0.06, 0.06], and the normalization field of as [−0.06, 0.06], corresponding to the fuzzy language representation as [NB, NM, NS, ZO, PS, PM, PB], in combination with the control variable method. , , and three can be approximated as three of the traditional PID controller. From Equations (5), (14) and (18), it can be seen that with constant output electromagnetic torque and constant viscous friction coefficient, the fractional order speed error rate of change is related to the load torque . During the motor acceleration phase, decreases, and it is necessary to increase the value of , it decreases the value of thus increasing the influence of feedback on the control law and let converge to 0 asymptotically. Similarly, in the motor acceleration phase, adding cannot speed up the system response, and it is necessary to reduce to reduce the impact on . Similarly, the fuzzy rules of , , can be obtained by debugging. The fuzzy rules are shown in Table 1 and Table 2.

Table 1.
kω fuzzy control rules table.

Table 2.
Fuzzy control rules table.
3. Analysis of Simulation Results
To verify the effectiveness of the design scheme in this paper, the control system of PMSM is built in MATLAB/Simulink, and the parameters of the PMSM system are set in the simulation: stator inductance , motor rotational inertia , magnetic chain , and the number of pole pairs is 4. Considering the influence of the gain on the control accuracy and convergence of the system, the feedback gains , were finally taken as 550 and 950 through repeated tests. The simulation sampling rate is 10 kHz, the simulation period is 0.1 s, and the initial reference speed of the motor is set to 900 rpm. The simulation results are compared for the PMSM system with four controllers: PID, FPID, IOAB-FPID, and FOAB-FPID. The speed is adjusted to 600 rpm at 0.05 s and 930 rpm at 0.07 s. The speed tracking of the system under the four control strategies is shown in Figure 1. When the speed rises in the start-up phase, the PID control responds the slowest, the FPID control responds fast but with a significant overshoot, and the FOAB-FPID control curve is smooth with fast response and no overshoot. The reaction of PID and IOAB-FPID control is slow when the command speed decreases, and the reaction by FPID control and FOAB-FPID control is fast. The adjustment time is short, but the FPID overshoot is still significant, and the result is the same as above when the command speed increases. It can be concluded that the FOAB-FPID control performs best and has the best control performance in the three-time states of the start-up phase, commanded speed decrease, and oversaw speed increase.
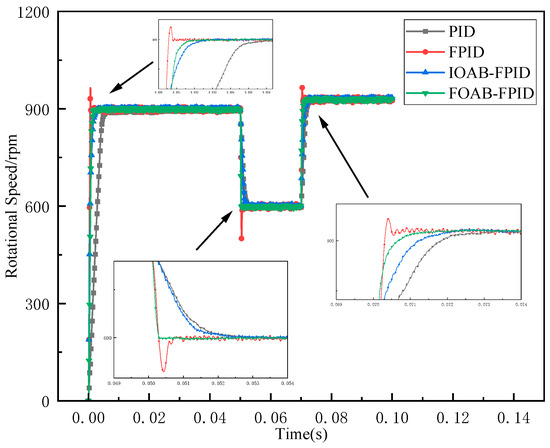
Figure 1.
Comparison when the command speed is changed.
The load torque TL is changed when the speed is constant, and then the speed immunity of the PMSM system is analyzed. The load torque varies: 3.2 N-m is added at 0.05 s, and 2.4 N-m is subtracted at 0.07 s. Figure 2 shows the speed comparison after adding the load torque. The figure shows that the FOAB-FPID control speed is the least affected than the other three controls when the load torque is added.
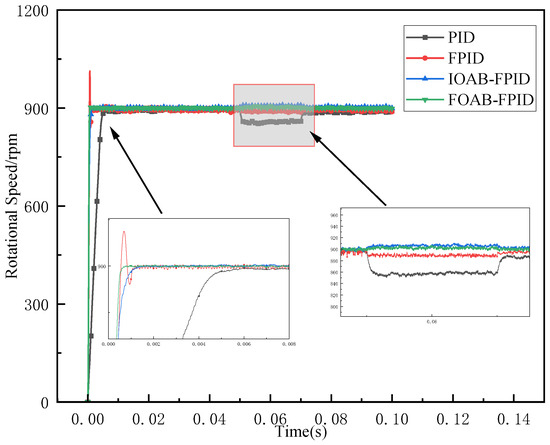
Figure 2.
Speed comparison when adding load torque.
When the PMSM runs at no load, the stator resistance is changed for simulation analysis, and the initial stator resistance value is set to 2.875 . When the PMSM runs at no load, the stator resistance Rs changes as follows: at 0.05 s, add 5 , and at 0.07 s, subtract 3 . A comparison of speed change when stator resistance changes is shown in Figure 3. The figure shows that the FOAB-FPID control has a shorter speed rise time and faster response.
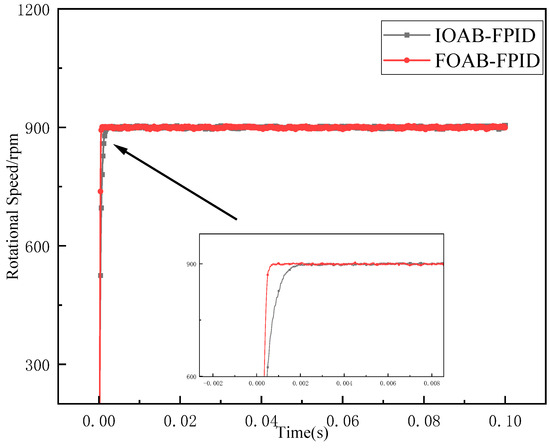
Figure 3.
Stator resistance change speed comparison.
4. Experimental Verification
The algorithm implementation of four controllers, PID, FPID, IOAB-FPID, and FOAB-FPID, is completed on the experimental platform to verify the speed regulation performance of PMSM under the four controllers. To ensure consistency, the experimental motor parameters are selected in the same way as in the simulation. The experimental platform and the principle of PMSM vector control are shown in Figure 4. The control core is chosen as TI’s DSP28335 chip with a carrier frequency of 10 KHz; the speed measurement module is used to collect the motor speed display (the feedback speed of the speed loop is calculated from the encoder data collected by EQEP); the magnetic powder brake module is used to adjust the external load torque input.
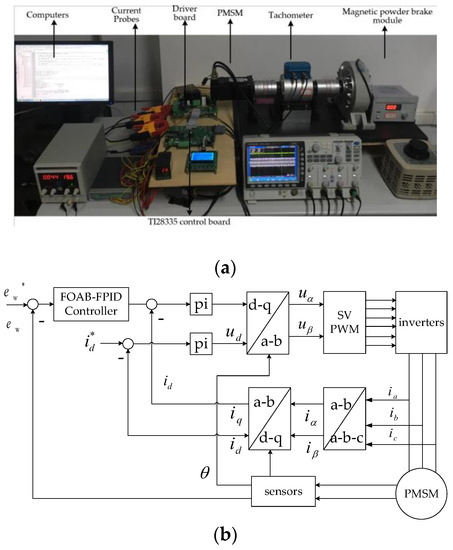
Figure 4.
PMSM experimental platform. (a) Experimental platforms. (b) PMSM vector control schematic; ew* is the trajectory of a given position, ew is the actual location, id* is the given current components on d-axis respectively.
When the speed changes abruptly, the tracking and response ability of the system speed under different control schemes are tested. Firstly, the instruction speed is changed and compared, with speed changes from 900 rpm to 840 rpm and 900 rpm to 960 rpm, to verify the speed tracking response of the PMSM under different controls during speed drop and rise.
The three-phase currents and rotational speeds of the speed reduction experimental results are shown in Figure 5, which can be seen: With the PID controller, the motor rotational speed showed an overshoot of about 20% when the speed reduction command was received, and the adjustment time was about 904.6 ms, whereas the FPID control rotational speed was overshooting by approximately 35.5%, and the adjustment time was about 787.7 ms. The IOAB-FPID control of the three-phase current shows apparent fluctuation, and the adjustment time is about 585.7 ms. At the same time, the FOAB-FPID still responds smoothly and quickly when the speed command changes in the same way, and the current does not fluctuate obviously, which shortens the adjustment period to about 488.9 ms. The comprehensive analysis shows that when the rotational speed of the PMSM decreases, the FOAB-FPID control of the rotational speed response is the fastest, and the tracking performance is the best. It is the quickest and has the best tracking performance.
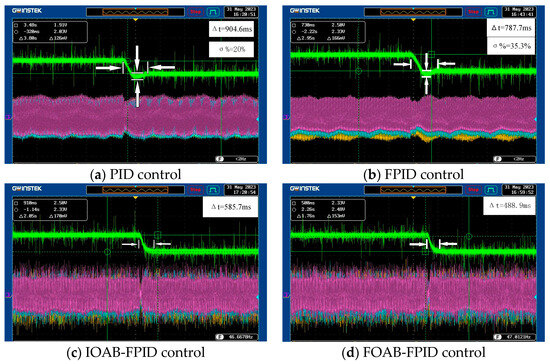
Figure 5.
Experimental results of different control speed reduction.
The results of the speed-up experiment are shown in Figure 6. The speed overshoot of the PID control is about 27.5%, and the adjustment time is about 987 ms. The speed overshoot of the FPID control is about 30%, and the adjustment time is about 786.7 ms. The IOAB-FPID control has a slight jitter when the speed rises, no noticeable overshoot, and the adjustment time is about 701.9 ms. While the FOAB-FPID control can still respond smoothly and quickly when the speed command changes, no evident overshoot occurs, and the adjustment time is about 368.8 ms. It can be seen that the FOAB-FPID control performance is better than the other three when the motor speed rises. The controller is better than the other three.
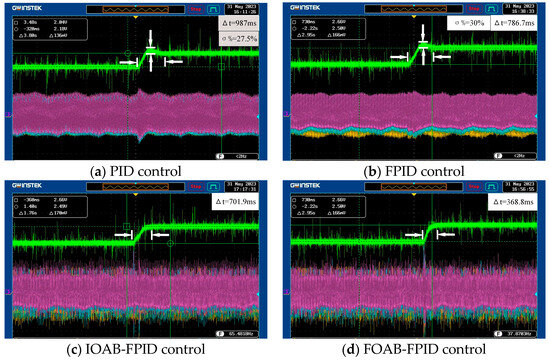
Figure 6.
Experimental results of different control lift speeds.
The speed is kept constant, and the load torque is added to test the anti-interference capability of the PMSM system. A load torque of 3.2 N-m is added at 900 rpm. The magnetic powder braking module provides the load torque to analyze the variation of PMSM speed and three-phase current under different control conditions. The experimental results are shown in Figure 7.
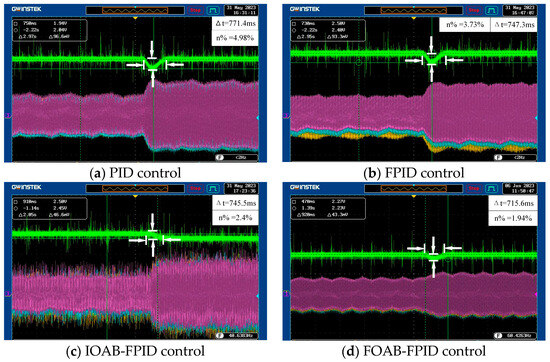
Figure 7.
Experimental results of different controls when 3.2 N.m load torque is added.
As shown in Figure 7, the motor speed fluctuated under all four controls when the load torque was added, and the percentage speed drop and the specific value could be calculated based on the marker in the upper left corner of the oscilloscope. The speed fluctuated more under PID and FPID control, and overshoot occurred when the rate picked up. The speed fluctuation of IOAB-FPID control is slight, and the response time is fast but fails to return to the command speed. The speed fluctuation of FOAB-FPID control is slight, and the adjustment is fast and returns to the command speed after a particular adjustment time. The performance of the system parameters under the four control schemes is shown in Table 3.

Table 3.
Performance indicators under different controls.
5. Discussion
In simulations and experiments, we conducted several sets of experiments with sudden changes in speed and the addition of load to analyze the controller performance regarding response speed, regulation time, and overshoot. Comparative analysis of the simulation and experimental results shows that there is almost no overshooting in the PID control in simulation, but the response is slow with the longest regulation time; overshooting occurs in the experiment with the longest regulation time. The FPID control was more quickly regulated in simulation, but the overshoot was very large; in the experiment, the overshoot was large, and the regulation time was long. The IOAB-FPID control at simulation did not almost overshoot, and the regulation time was shorter; at the experiment, there was almost no overshoot, and the regulation time was shorter, but the speed did not return to the original value. The FOAB-FPID control has no overshoot and rapid regulation during simulation; it has no overshoot and the fastest response and shortest regulation time during the experiment. Through comparative analysis, we found that the experimental results and simulation results are the same, but there are subtle differences in the reasons that are manifold, such as debugging too many parameters that failed to adjust to the optimal matching parameters of the system, the experimental data acquisition by the time of the impact of the larger cannot be continuously collected, the software program algorithm failed to capture the speed change, and so on. By analyzing the results of several experiments on the command speed down, up, and adding load torque, both in the simulation and experimental FOAB-FPID controller is the best; in the speed of the sudden change and input load torque after the speed fluctuation is smaller and can return to the command faster; the responsiveness and tracking performance are the best; to a certain extent, it has a better ability to resist interference; and the parameter adjustment after matching the experimental The effect will be better after parameter adjustment and matching. Both simulation and experiment show that it has some practical significance for engineering applications.
6. Conclusions
The problem of speed regulation performance for a PMSM based on a fractional-order adaptive fuzzy backstepping control method has been studied. First, the fractional order theory is introduced in the mathematical modelling of PMSM to overcome the influence of non-integer order on the system speed regulation, and the backstepping method is used to derive the system’s adaptive and control laws. Second, a FOAB-FPID controller is designed in conjunction with fuzzy logic, which ensures that the system is able to adaptively regulate the parameters to overcome the load disturbance problem better. Third, the control group was designed under the same conditions. For the proposed method, this paper draws the following conclusions through simulation and experiments: The FOAB-FPID control has the fastest response and the best following adaptation to reach the commanded rotational speed at the earliest, with the smallest fluctuation in rotational speed, the fastest dynamic response, and the best resistance to the load disturbance. It is proved by analysis that, compared with PID control, FPID control, and IOAB-FPID control, this control strategy not only improves the response speed and reduces the overshooting amount of speed but also ensures the speed control accuracy and dynamic performance under perturbation and enhances the robustness of the system. It verified the rationality and effectiveness of our proposed control method, which can be applied to practical engineering.
Author Contributions
Conceptualization, L.Z. and J.M.; methodology, L.Z.; software, L.Z.; validation, L.Z. and Z.H.; formal analysis, J.M., Q.W. and T.Q.; investigation, Z.H. and C.C.; resources, J.M.; data curation, L.Z. and T.Q.; writing—original draft preparation, L.Z.; writing—review and editing, J.M., Q.W. and L.Z.; visualization, J.M., Q.W. and Z.H.; supervision, J.M. and C.C.; project administration, J.M.; All authors have read and agreed to the published version of the manuscript.
Funding
National Natural Science Foundation of China (62163006); Guizhou provincial science and technology department (PGTS [2021]G442;[2022]G244;[2023]G096;[2023]G179).
Data Availability Statement
Data is unavailable due to ethical restrictions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Xu, Y.; Yao, M.; Sun, X. Overview of Position-Sensorless Technology for Permanent Magnet Synchronous Motor Systems. World Electr. Veh. J. 2023, 14, 212. [Google Scholar] [CrossRef]
- Mercorelli, P. Control of Permanent Magnet Synchronous Motors for Track Applications. Electronics 2023, 12, 3285. [Google Scholar] [CrossRef]
- Sheela, A.; Suresh, M.; Shankar, V.G.; Panchal, H.; Priya, V.; Atshaya, M.; Sadasivuni, K.K.; Dharaskar, S. FEA based analysis and design of PMSM for electric vehicle applications using magnet software. Int. J. Ambient. Energy 2022, 43, 2742–2747. [Google Scholar] [CrossRef]
- Kim, S.-K.; Lee, J.-S.; Lee, K.-B. Self-tuning adaptive speed controller for permanent magnet synchronous motor. IEEE Trans. Power Electron. 2016, 32, 1493–1506. [Google Scholar] [CrossRef]
- Huang, X.; Pan, H.; Yuan, K. Speed and Current Control of PMSM based on Double MPC. In Proceedings of the 2020 7th International Forum on Electrical Engineering and Automation (IFEEA), Hefei, China, 25–27 September 2020; pp. 300–304. [Google Scholar]
- Meng, Y.; Liu, B.; Wang, L. Speed control of PMSM based on an optimized ADRC controller. Math. Probl. Eng. 2019, 2019, 1074702. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, Y.; Zhang, X.; Liang, J. A new reaching law for antidisturbance sliding-mode control of PMSM speed regulation system. IEEE Trans. Power Electron. 2019, 35, 4117–4126. [Google Scholar] [CrossRef]
- Ren, H.; Liu, D. Nonlinear feedback control of chaos in permanent magnet synchronous motor. IEEE Trans. Circuits Syst. II Express Briefs 2006, 53, 45–50. [Google Scholar]
- Zhang, X.; Sun, L.; Zhao, K.; Sun, L. Nonlinear speed control for PMSM system using sliding-mode control and disturbance compensation techniques. IEEE Trans. Power Electron. 2012, 28, 1358–1365. [Google Scholar] [CrossRef]
- Wang, L.; Tian, M.; Gao, Y. Fuzzy self-adapting PID control of PMSM servo system. In Proceedings of the 2007 IEEE International Electric Machines & Drives Conference, Antalya, Turkey, 3–5 May 2007; pp. 860–863. [Google Scholar]
- Zhang, X.; Zhang, L.; Zhang, Y. Model predictive current control for PMSM drives with parameter robustness improvement. IEEE Trans. Power Electron. 2018, 34, 1645–1657. [Google Scholar] [CrossRef]
- Apte, A.; Joshi, V.A.; Mehta, H.; Walambe, R. Disturbance-observer-based sensorless control of PMSM using integral state feedback controller. IEEE Trans. Power Electron. 2019, 35, 6082–6090. [Google Scholar] [CrossRef]
- Sun, X.; Yu, H.; Yu, J.; Liu, X. Design and implementation of a novel adaptive backstepping control scheme for a PMSM with unknown load torque. IET Electr. Power Appl. 2019, 13, 445–455. [Google Scholar] [CrossRef]
- Zheng, S.; Tang, X.; Song, B. Adaptive pseudo-derivative feedback with a feed-forward gain controller for permanent magnet synchronous motor servo system based on integrated iterative learning control. Proc. Inst. Mech. Eng. Part I J. Syst. Control. Eng. 2015, 229, 250–265. [Google Scholar] [CrossRef]
- Cheng, S.; Yu, J.; Lin, C.; Zhao, L.; Ma, Y. Neuroadaptive finite-time output feedback control for PMSM stochastic nonlinear systems with iron losses via dynamic surface technique. Neurocomputing 2020, 402, 162–170. [Google Scholar] [CrossRef]
- Ke, S.-S.; Lin, J.-S. Sensorless speed tracking control with backstepping design scheme for permanent magnet synchronous motors. In Proceedings of the 2005 IEEE Conference on Control Applications, Toronto, ON, Canada, 28–31 August 2005; CCA: Montreal, QC, Canada, 2005; pp. 487–492. [Google Scholar]
- Nicola, M.; Nicola, C.-I.; Marian, D. Sensorless Control of PMSM Based on FOC Strategy and Fractional Order PI Controller. In Proceedings of the 2020 International Conference and Exposition on Electrical and Power Engineering (EPE), Iasi, Romania, 22–23 October 2020; pp. 302–307. [Google Scholar]
- Ma’Bdeh, A.; Tawalbeh, N.; El-Khazali, R. Sensorless Speed Control of a PMSM Using Fractional-Order Extended State Observer. In Proceedings of the 2023 International Conference on Fractional Differentiation and Its Applications (ICFDA), Ajman, United Arab Emirates, 14–16 March 2023; pp. 1–5. [Google Scholar]
- Ma, Z.; Ma, H. Adaptive Fuzzy DSC Design of Strict-Feedback Fractional-Order Nonlinear Systems. In Proceedings of the 2019 Chinese Control and Decision Conference (CCDC), Nanchang, China, 3–5 June 2019; pp. 1386–1391. [Google Scholar]
- Ma, Z.; Ma, H. Reduced-order observer-based adaptive backstepping control for fractional-order uncertain nonlinear systems. IEEE Trans. Fuzzy Syst. 2019, 28, 3287–3301. [Google Scholar] [CrossRef]
- Caponetto, R.; Murgano, E. Model Order Reduction: A comparison between Fractional and Integer Order Approximation. In Proceedings of the 2019 IEEE International Conference on Systems, Man and Cybernetics (SMC), Bari, Italy, 6–9 October 2019; pp. 2037–2041. [Google Scholar]
- Shah, R.; Khan, H.; Farooq, U.; Baleanu, D.; Kumam, P.; Arif, M. A new analytical technique to solve system of fractional-order partial differential equations. IEEE Access 2019, 7, 150037–150050. [Google Scholar] [CrossRef]
- Wen, X.-J.; Wu, Z.-M.; Lu, J.-G. Stability analysis of a class of nonlinear fractional-order systems. IEEE Trans. Circuits Syst. II Express Briefs 2008, 55, 1178–1182. [Google Scholar] [CrossRef]
- Tavazoei, M.S. Comments on “Stability analysis of a class of nonlinear fractional-order systems”. IEEE Trans. Circuits Syst. II Express Briefs 2009, 56, 519–520. [Google Scholar] [CrossRef]
- Verma, A.; Guha, D. Fractional-Order Robust Controller Applied to Nonlinear Dynamical System. In Proceedings of the 2022 Second International Conference on Power, Control and Computing Technologies (ICPC2T), Raipur, India, 1–3 March 2022; pp. 1–5. [Google Scholar]
- Singhal, R.; Padhee, S.; Kaur, G. Design of fractional order PID controller for speed control of DC motor. Int. J. Sci. Res. Publ. 2012, 2, 1–8. [Google Scholar]
- Chen, X.; Li, S.; Cui, Y.; Xu, Y.; Xu, M. Research on permanent magnet synchronous motor based on fractional order fuzzy sliding mode control. In Proceedings of the 2017 Chinese Automation Congress (CAC), Jinan, China, 20–22 October 2017; pp. 4123–4127. [Google Scholar]
- Dorcák, E.; Valsa, J.; Terpák, J.; Gonzalez, E. Comparison of the methods for the calculation of fractional-order differential equations. In Proceedings of the 2011 12th International Carpathian Control Conference (ICCC), Velke Karlovice, Czech Republic, 25–28 May 2011; pp. 80–84. [Google Scholar]
- Li, L.; Sun, Y. Adaptive fuzzy control for nonlinear fractional-order uncertain systems with unknown uncertainties and external disturbance. Entropy 2015, 17, 5580–5592. [Google Scholar] [CrossRef]
- Zhang, B.; Pi, Y.; Luo, Y. Fractional order sliding-mode control based on parameters auto-tuning for velocity control of permanent magnet synchronous motor. ISA Trans. 2012, 51, 649–656. [Google Scholar] [CrossRef]
- Zhong, C.-Q.; Wang, L.; Xu, C.-F. Path tracking of permanent magnet synchronous motor using fractional order fuzzy PID controller. Symmetry 2021, 13, 1118. [Google Scholar] [CrossRef]
- Xiao, Q.; Liu, Z.; Zhang, Y.; Li, Z.; Luo, B.; Wang, T. Improved Higher-Order Sliding Mode Controller for Model Predictive Current Control of PMSM. Prog. Electromagn. Res. C 2022, 123, 117–133. [Google Scholar] [CrossRef]
- Mehmood, C.A.; Kavasseri, R.G. On the use of fractional-order controllers for performance improvements in ac drives. Electr. Power Compon. Syst. 2015, 43, 485–490. [Google Scholar] [CrossRef]
- Thike, R.; Pillay, P. Mathematical model of an interior PMSM with aligned magnet and reluctance torques. IEEE Trans. Transp. Electrif. 2020, 6, 647–658. [Google Scholar] [CrossRef]
- Liu, G.; Xu, C.; Wang, L. Modified ADRC Design of Permanent Magnet Synchronous Motor Based on Improved Memetic Algorithm. Sensors 2023, 23, 3621. [Google Scholar] [CrossRef]
- Molderez, T.R.; Rabaey, K.; Verhelst, M. Experimental study of fractional-order RC circuit model using the Caputo and Caputo-Fabrizio derivatives. Ieee Trans. Circuits Syst. I-Regul. Pap. 2021, 68, 1068–1079. [Google Scholar] [CrossRef]
- Hoai, H.-K.; Chen, S.-C.; Chang, C.-F. Realization of the neural fuzzy controller for the sensorless PMSM drive control system. Electronics 2020, 9, 1371. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).