Prediction of Battery Return Volumes for 3R: Remanufacturing, Reuse, and Recycling
Abstract
:1. Introduction
2. Weibull Distribution-Based Failure Rate for LIBs in Commercial Vehicles
2.1. Failure Rate
- Early failures are characterized by errors in the design and production process owing to the manufacturer or errors in the process of assembly and manual settings. These failures tend to be high at the lifetime beginning but then decrease over time.
- Random failures are known for their sudden shutdown and error due to causes that are subjective (organizational problems, operator error, faulty maintenance), stress-related (temporary variation in stress exceeding component strength), and stochastic. This is not related to the aging of the component and is largely unpredictable.
- Aging failures are present when the failure during this period is caused by the deteriorating condition of the component in proportion to its age.
2.2. Faults of Lithium-Ion Battery Systems
2.3. Overview of Aging Mechanisms for Battery Cells and Systems
2.4. Weibull Function and Its Relation to Battery Failure Prediction
2.5. Weibull Parameter Selection
| Research | Cathode/Anode | Testing Method | Parameters for Weibull |
|---|---|---|---|
| [39] | LCO, graphite | 1C charge/ 10C discharge, 24 pouch cells | |
| [41] | Unknown | 0.5A charge/ 0.5A discharge, 12x pouch cells | |
| [34] | NMC, graphite | Voltage-limited cycling w/4A 48x 18650-type | |
| [47] | 1P96S, ternary LIB (module) | From BMS after 6 years of usage | |
| [40] | LFP, graphite | 1A charge/ 0.5A discharge, 96x 18650-type | |
| [48,49] | LMO, graphite | 0.33C charge/1.5C discharge | |
| [48,49] | LFO, graphite | 0.33C charge/1.5C discharge |
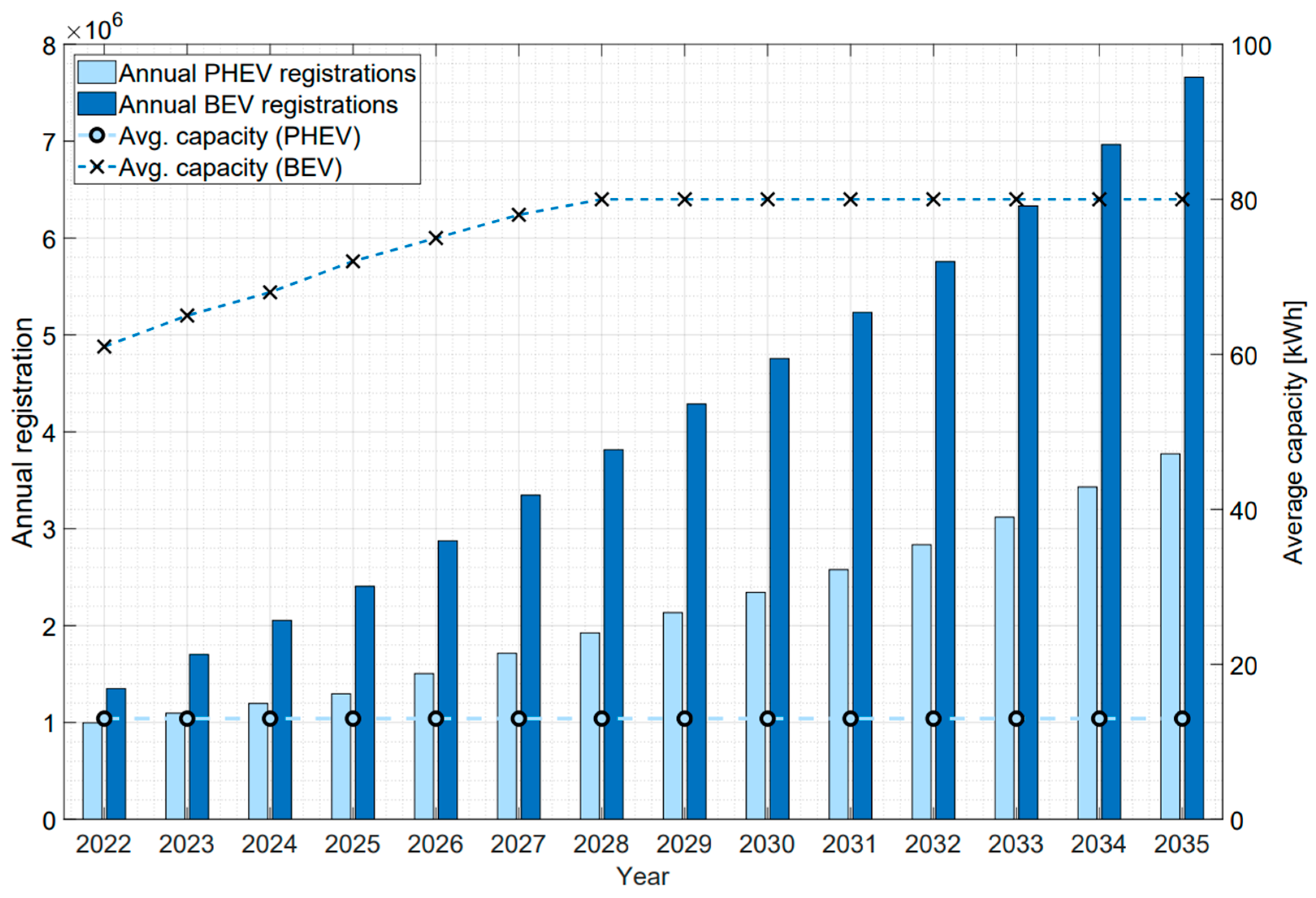
3. Results: Forecast of Battery Return Volumes
3.1. Battery Data Analytics
3.2. Implementation of Battery Data in Weibull Prognose Tool for Battery Return Volumes
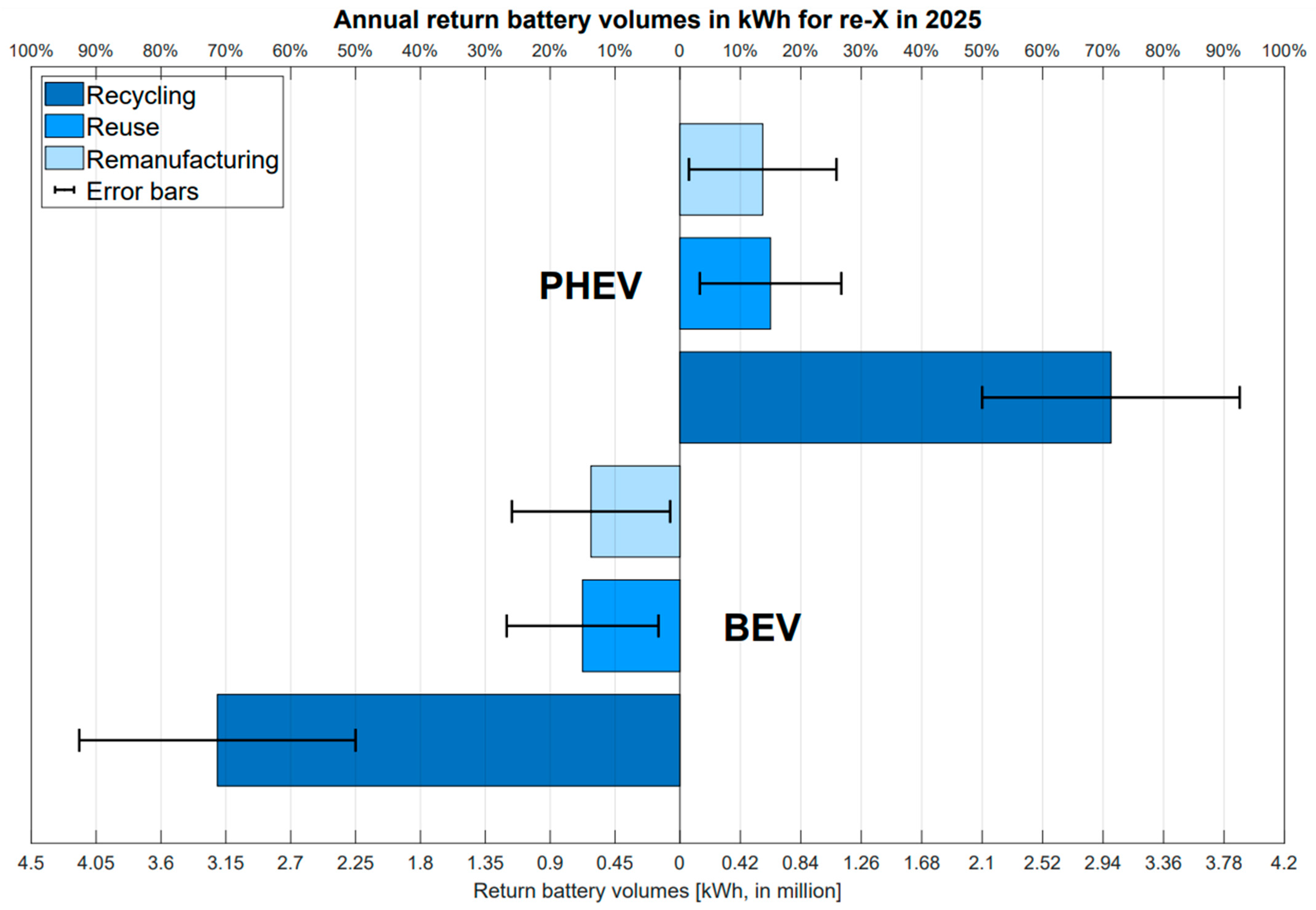
4. Battery Circular Economy and 3R Strategies
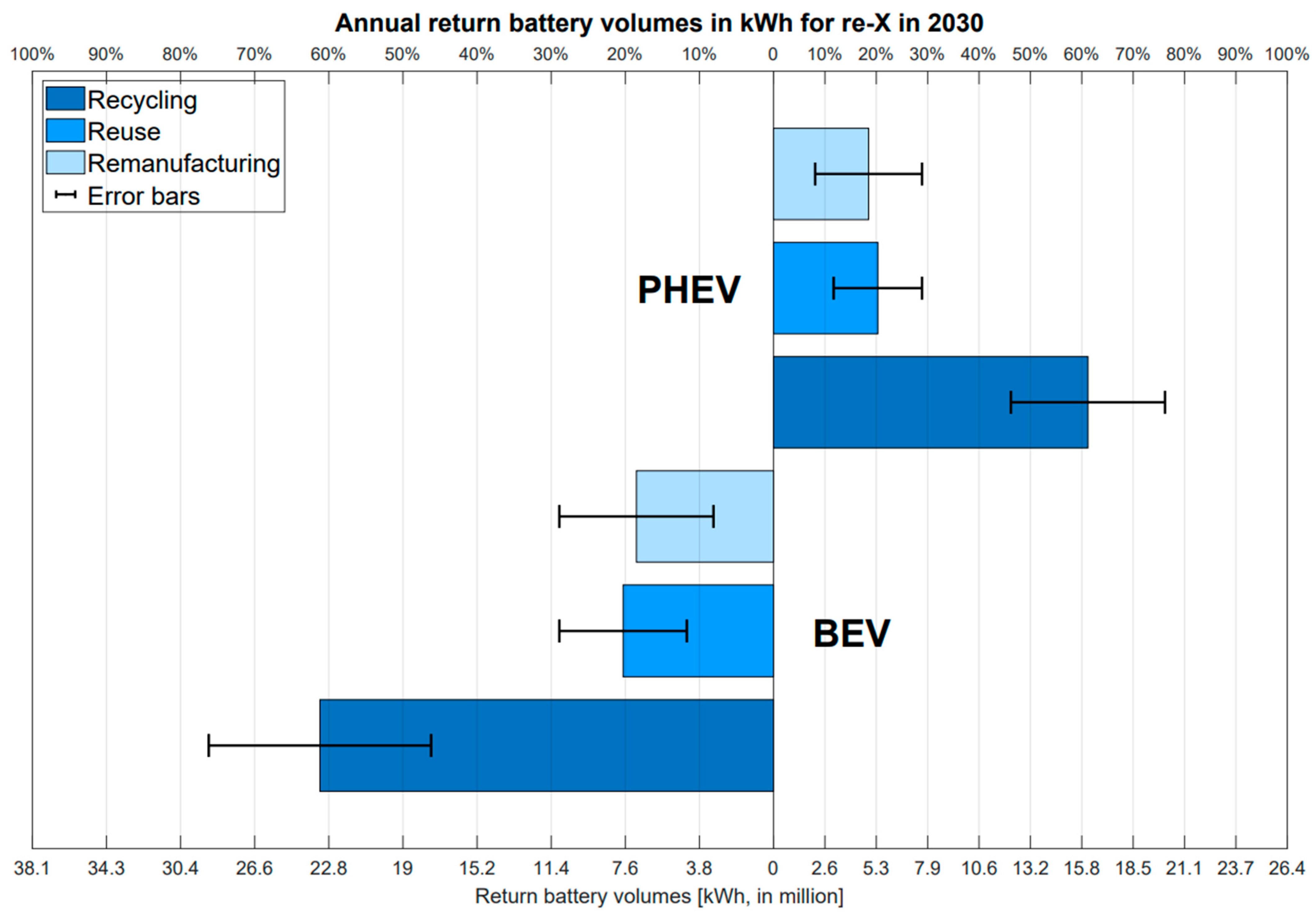
Quantification of Return Volumes for 3R Strategies
5. Discussion
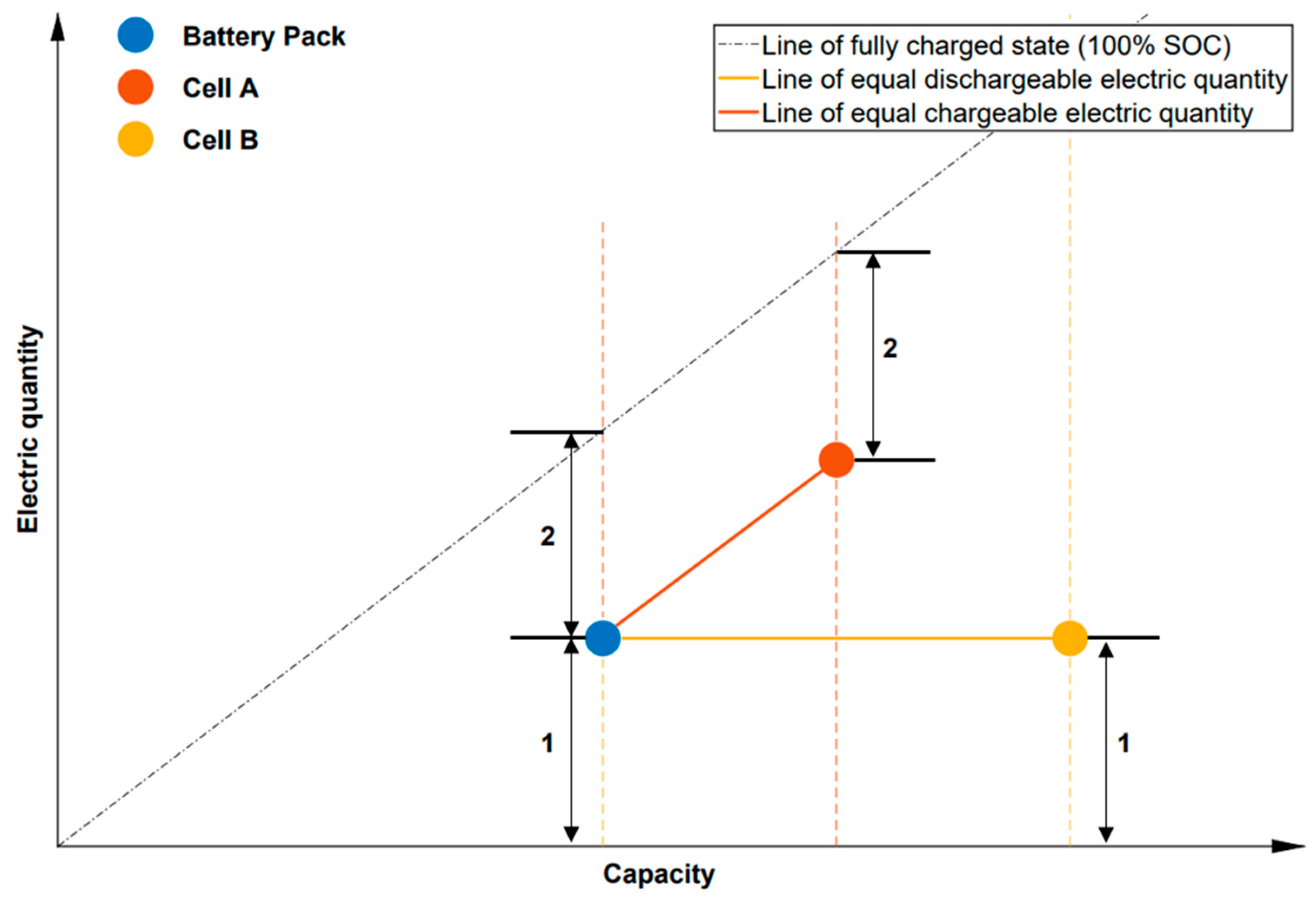
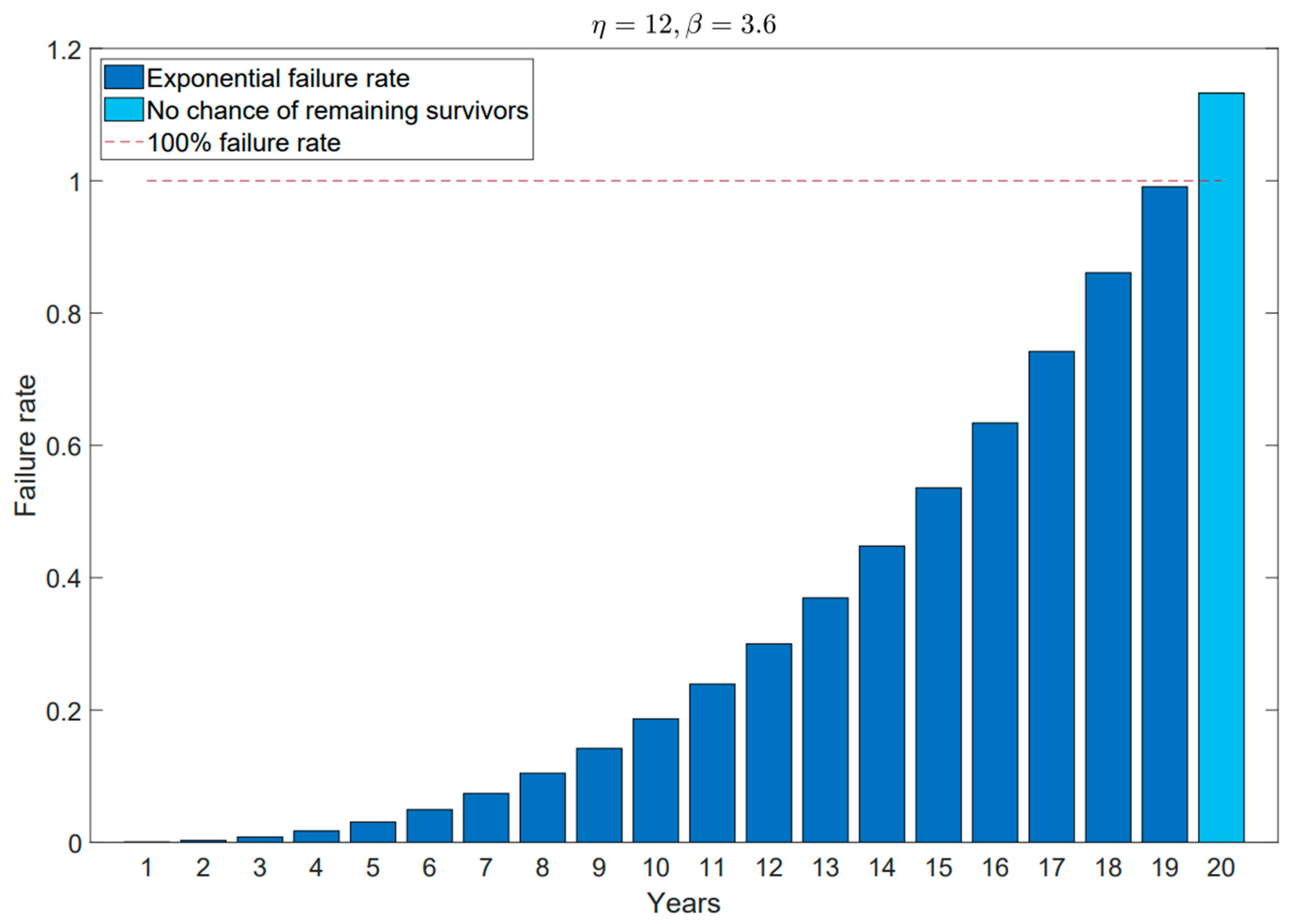
- Upon reviewing the available literature on fitting LIB degradation data to the Weibull distribution, the paper concludes this by referencing the parameter found in [47]. When looking at the Weibull parameter in the cited research, the result reflects a suitable Weibull distribution that matches the failure data distribution of a series-connected battery module, which is known to be more vulnerable to the barrel effect when compared with a parallel-connected configuration. Along with assumption 3, we came to a scale parameter of twelve years, which reflects a normalized expectation that around 65% of vehicle batteries will need to be serviced or replaced after twelve years of usage for vehicles from 2013 to 2030. In order to obtain a better fitting parameter for a distribution of choice (in this paper, the Weibull distribution), data from battery management systems from multiple BEV and PHEV models have to be assessed.
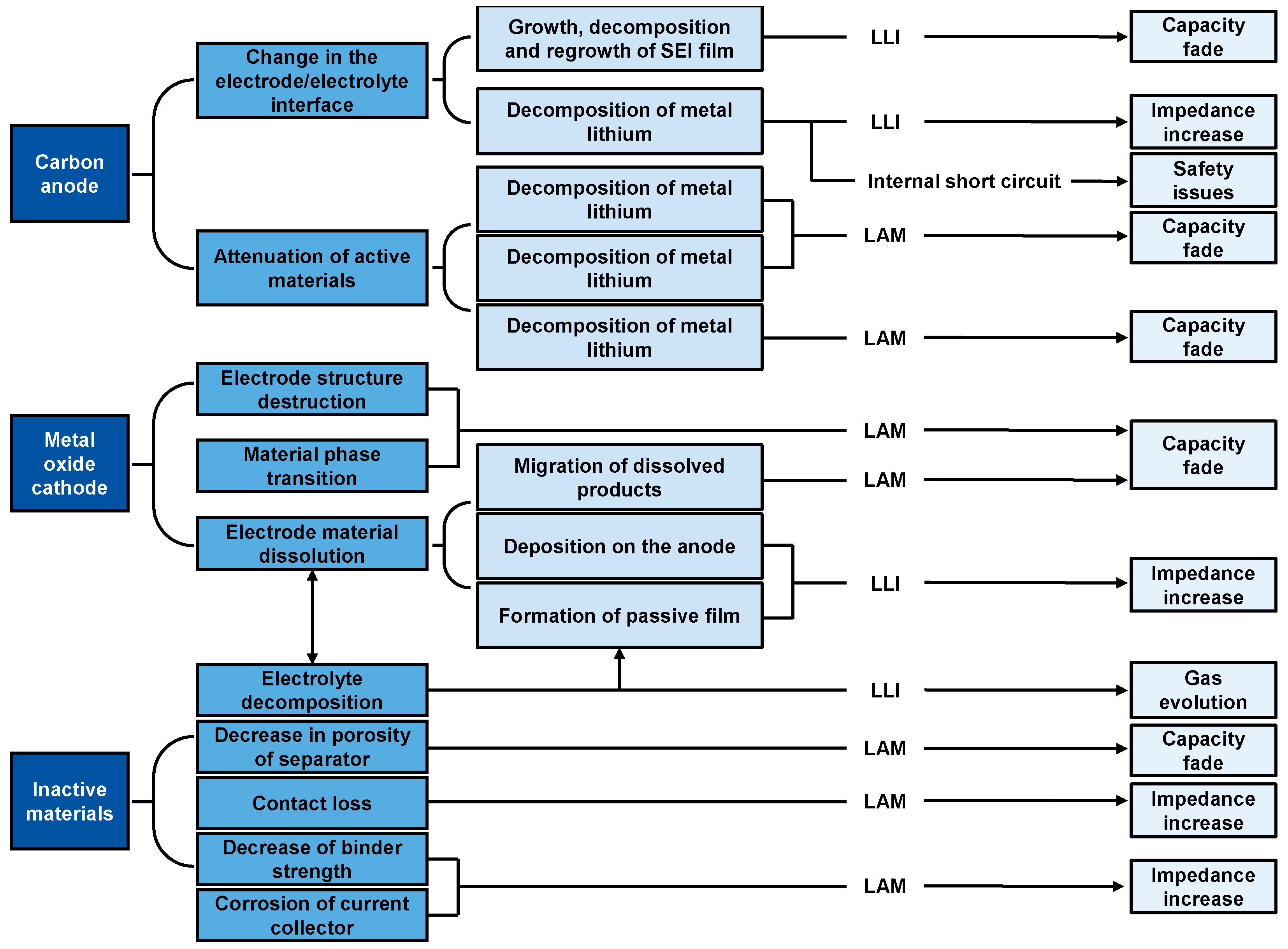
- Only one out of many degradation and aging modes is considered; for a better judgment of the actual return battery flow, we need to calculate what is known as the “system failure rate”. As seen in Figure 2, there are different failure modes for a battery system that can lead to different types of degradation, thus causing earlier aging or failure. The scale of complexity can be exponential, and therefore, if this approach is taken, an optimal methodology should include an effort vs. result accuracy analysis. System failure rate can be calculated through simple series or parallel system models and/or by using more advanced methods for the total consideration of many components within the system.
- The usage trend (user profile) has not been given a separate examination, where we only took the normalized assumption of around one EFC every two days for all vehicles.
- The threshold of 80% was chosen for the calculation of returning battery volumes in kWh. This is common practice for BEVs. However, for EVs, especially for PHEVs, there could be discrepancies.
- Technology advancement, LIB technology will get better, and the aging trend might no longer be similar. Other technologies related to BEVs, such as swapping stations and other charging profiles from different charging stations, also affect the aging aspect of battery systems.
- Methods of replacement of faulty battery packs when a vehicle is being serviced can also differ.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kurmayer, N.J. German Transport Minister Backs Electric Cars in E-Fuel Debate. 14 January 2022. Available online: https://www.euractiv.com/section/electric-cars/news/german-transport-minister-backs-electric-cars-in-e-fuel-debate/ (accessed on 14 April 2023).
- Road|European Alternative Fuels Observatory. Available online: https://alternative-fuels-observatory.ec.europa.eu/transport-mode/road (accessed on 14 April 2023).
- Kabir, M.M.; Demirocak, D.E. Degradation mechanisms in Li-ion batteries: A state-of-the-art review. Int. J. Energy Res. 2017, 41, 1963–1986. [Google Scholar] [CrossRef]
- BGB I. I S. 1582, Batteriegesetz vom 25.06.2009: Gesetz über das Inverkehrbringen, die Rücknahme und die Umweltverträgliche Entsorgung von Batterien und Akkumulatoren (BattG). Available online: https://www.gesetze-im-internet.de/battg/BJNR158210009.html (accessed on 15 August 2023).
- European Comission. Proposal for a REGULATION OF THE EUROPEAN PARLIAMENT AND OF THE COUNCIL Concerning Batteries and Waste Batteries, Repealing Directive 2006/66/EC and Amending Regulation (EU) No 2019/1020; European Comission: Brussels, Belgium, 2020. [Google Scholar]
- Gaines, L.; Richa, K.; Spangenberger, J. Key issues for Li-ion battery recycling. MRS Energy Sustain. 2018, 5, 12. [Google Scholar] [CrossRef]
- Mossali, E.; Picone, N.; Gentilini, L.; Rodrìguez, O.; Pérez, J.M.; Colledani, M. Lithium-ion batteries towards circular economy: A literature review of opportunities and issues of recycling treatments. J. Environ. Manag. 2020, 264, 110500. [Google Scholar] [CrossRef]
- Gillespie, T. Rising Battery Costs Hit Carmakers, Threaten Climate-Change Push. Bloomberg [Online]. 30 November 2021. Available online: https://www.bloomberg.com/news/articles/2021-11-30/even-the-battery-boom-can-t-escape-world-s-supply-chain-woes?leadSource=uverify%20wall (accessed on 14 April 2023).
- Liu, Z.; Song, J.; Kubal, J.; Susarla, N.; Knehr, K.W.; Islam, E.; Nelson, P.; Ahmed, S. Comparing total cost of ownership of battery electric vehicles and internal combustion engine vehicles. Energy Policy 2021, 158, 112564. [Google Scholar] [CrossRef]
- DIN EN 13306:2018-02; Instandhaltung—Begriffe der Instandhaltung; Dreisprachige Fassung EN_13306:2017. Beuth Verlag GmbH: Berlin, Germany, 2018.
- Moubray, J. Reliability-Centered Maintenance, 2nd ed.; [3.rev.]; Industrial Press: New York, NY, USA, 2000; ISBN 9780831131463. [Google Scholar]
- Steck-Winter, H.; Stölting, C. Ersatzteilbedarfsplanung für Thermoprozessanlagen: Zeitschrift für gasbeheizte Thermoprozesse. GWI 2016, 65, 55–65. [Google Scholar]
- Xiong, R.; Sun, W.; Yu, Q.; Sun, F. Research progress, challenges and prospects of fault diagnosis on battery system of electric vehicles. Appl. Energy 2020, 279, 115855. [Google Scholar] [CrossRef]
- Jiang, J.; Zhang, C. Fundamentals and Applications of Lithium-Ion Batteries in Electric Drive Vehicles; Wiley: Singapore, 2015; ISBN 9781118414798. [Google Scholar]
- Zheng, Y.; Ouyang, M.; Lu, L.; Li, J. Understanding aging mechanisms in lithium-ion battery packs: From cell capacity loss to pack capacity evolution. J. Power Sources 2015, 278, 287–295. [Google Scholar] [CrossRef]
- Birkl, C.R.; Roberts, M.R.; McTurk, E.; Bruce, P.G.; Howey, D.A. Degradation diagnostics for lithium ion cells. J. Power Sources 2017, 341, 373–386. [Google Scholar] [CrossRef]
- Xiong, R.; Pan, Y.; Shen, W.; Li, H.; Sun, F. Lithium-ion battery aging mechanisms and diagnosis method for automotive applications: Recent advances and perspectives. Renew. Sustain. Energy Rev. 2020, 131, 110048. [Google Scholar] [CrossRef]
- Dubarry, M.; Pastor-Fernández, C.; Baure, G.; Yu, T.F.; Widanage, W.D.; Marco, J. Battery energy storage system modeling: Investigation of intrinsic cell-to-cell variations. J. Energy Storage 2019, 23, 19–28. [Google Scholar] [CrossRef]
- Ma, C.; Chang, L.; Cui, N.; Duan, B.; Zhang, Y.; Yu, Z. Statistical relationships between numerous retired lithium-ion cells and packs with random sampling for echelon utilization. Energy 2022, 257, 124692. [Google Scholar] [CrossRef]
- Han, X.; Lu, L.; Zheng, Y.; Feng, X.; Li, Z.; Li, J.; Ouyang, M. A review on the key issues of the lithium ion battery degradation among the whole life cycle. eTransportation 2019, 1, 100005. [Google Scholar] [CrossRef]
- Wang, X.; Fang, Q.; Dai, H.; Chen, Q.; Wei, X. Investigation on Cell Performance and Inconsistency Evolution of Series and Parallel Lithium-Ion Battery Modules. Energy Technol. 2021, 9, 2170071. [Google Scholar] [CrossRef]
- Rumpf, K.; Naumann, M.; Jossen, A. Experimental investigation of parametric cell-to-cell variation and correlation based on 1100 commercial lithium-ion cells. J. Energy Storage 2017, 14, 224–243. [Google Scholar] [CrossRef]
- Hua, Y.; Zhou, S.; Cui, H.; Liu, X.; Zhang, C.; Xu, X.; Ling, H.; Yang, S. A comprehensive review on inconsistency and equalization technology of lithium-ion battery for electric vehicles. Int. J. Energy Res. 2020, 44, 11059–11087. [Google Scholar] [CrossRef]
- Zhou, Z.; Duan, B.; Kang, Y.; Cui, N.; Shang, Y.; Zhang, C. A low-complexity state of charge estimation method for series-connected lithium-ion battery pack used in electric vehicles. J. Power Sources 2019, 441, 226972. [Google Scholar] [CrossRef]
- Lv, J.; Song, W.; Feng, Z.; Li, Y.; Ding, Y. Performance and comparison of equalization methods for lithium ion batteries in series. Int. J. Energy Res. 2021, 45, 4669–4680. [Google Scholar] [CrossRef]
- Rausand, M.; Barros, A.; Høyland, A. System Reliability Theory: Models, Statistical Methods, and Applications, 3rd ed.; John Wiley & Sons Inc: Hoboken, NJ, USA, 2020; ISBN 9781119373520. [Google Scholar]
- Weibull, W. A Statistical Theory of the Strength of Materials; Generalstabens Litografiska Anstalts Förlag: Stockholm, Sweden, 1939. [Google Scholar]
- Zok, F.W. On weakest link theory and Weibull statistics. J. Am. Ceram. Soc. 2017, 100, 1265–1268. [Google Scholar] [CrossRef]
- Lai, C.D.; Murthy, D.N.P.; Xie, M. Weibull distributions. WIREs Comp. Stat. 2011, 3, 282–287. [Google Scholar] [CrossRef]
- Almalki, S.J.; Nadarajah, S. Modifications of the Weibull distribution: A review. Reliab. Eng. Syst. Saf. 2014, 124, 32–55. [Google Scholar] [CrossRef]
- Tan, J.; Yao, Z.; Ye, M.; Shen, J. An optimized combination inspired by the wooden-barrel effect for Li-S pouch cells. Cell Rep. Phys. Sci. 2021, 2, 100659. [Google Scholar] [CrossRef]
- Barré, A.; Deguilhem, B.; Grolleau, S.; Gérard, M.; Suard, F.; Riu, D. A review on lithium-ion battery ageing mechanisms and estimations for automotive applications. J. Power Sources 2013, 241, 680–689. [Google Scholar] [CrossRef]
- O’Connor, P.D.T.; Kleyner, A. Practical Reliability Engineering, 5th ed.; Wiley: Chicester, UK, 2012; ISBN 9780470979822. [Google Scholar]
- Johnen, M.; Schmitz, C.; Kateri, M.; Kamps, U. Fitting lifetime distributions to interval censored cyclic-aging data of lithium-ion batteries. Comput. Ind. Eng. 2020, 143, 106418. [Google Scholar] [CrossRef]
- Mouais, T.; Kittaneh, O.A.; Majid, M.A. Choosing the Best Lifetime Model for Commercial Lithium-Ion Batteries. J. Energy Storage 2021, 41, 102827. [Google Scholar] [CrossRef]
- Wu, J.; Cui, X.; Zhang, H.; Lin, M. Health Prognosis With Optimized Feature Selection for Lithium-Ion Battery in Electric Vehicle Applications. IEEE Trans. Power Electron. 2021, 36, 12646–12655. [Google Scholar] [CrossRef]
- Prabhakar Murthy, D.N.; Bulmer, M.; Eccleston, J.A. Weibull model selection for reliability modelling. Reliab. Eng. Syst. Saf. 2004, 86, 257–267. [Google Scholar] [CrossRef]
- Blischke, W.R.; Murthy, D.N.P. Reliability: Modeling, Prediction, and Optimization; Wiley: New York, NY, USA, 2000; ISBN 9780471184508. [Google Scholar]
- Harris, S.J.; Harris, D.J.; Li, C. Failure statistics for commercial lithium ion batteries: A study of 24 pouch cells. J. Power Sources 2017, 342, 589–597. [Google Scholar] [CrossRef]
- Li, R.; Wu, J.; Wang, H.; Guo, J.; Li, G. Reliability assessment and failure analysis of lithium iron phosphate batteries. Inf. Sci. 2014, 259, 359–368. [Google Scholar] [CrossRef]
- Eom, S.-W.; Kim, M.-K.; Kim, I.-J.; Moon, S.-I.; Sun, Y.-K.; Kim, H.-S. Life prediction and reliability assessment of lithium secondary batteries. J. Power Sources 2007, 174, 954–958. [Google Scholar] [CrossRef]
- Lehner, S.; Baumhöfer, T.; Sauer, D.U. Disparity in initial and lifetime parameters of lithium-ion cells. IET Electr. Syst. Transp. 2016, 6, 34–40. [Google Scholar] [CrossRef]
- Lehner, S.; Baumhöfer, T.; Sauer, D.U. Necessity and methods to improve battery lifetime on system level. In Proceedings of the 28th International Electric Vehicle Symposium and Exhibition 2015, EVS 2015, Goyang, Republic of Korea, 3–6 May 2015. [Google Scholar]
- Jiang, Y.; Jiang, J.; Zhang, C.; Zhang, W.; Gao, Y.; Guo, Q. Recognition of battery aging variations for LiFePO4 batteries in 2nd use applications combining incremental capacity analysis and statistical approaches. J. Power Sources 2017, 360, 180–188. [Google Scholar] [CrossRef]
- Chiodo, E.; Lauria, D.; Andrenacci, N.; Pede, G. Accelerated life tests of complete lithium-ion battery systems for battery life statistics assessment. In Proceedings of the 2016 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Capri, Italy, 22–24 June 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1073–1078. [Google Scholar]
- Carnovale, A.; Li, X. A modeling and experimental study of capacity fade for lithium-ion batteries. Energy AI 2020, 2, 100032. [Google Scholar] [CrossRef]
- Zhao, Q.; Jiang, H.; Chen, B.; Wang, C.; Xu, S.; Zhu, J.; Chang, L. Research on State of Health for the Series Battery Module Based on the Weibull Distribution. J. Electrochem. Soc. 2022, 169, 20523. [Google Scholar] [CrossRef]
- Ganjeizadeh, F.; Tapananon, T.; Lei, H. Predicting Reliability of Lithium Ion Batteries. Int. J. Eng. Res. Technol. (IJERT) 2014, 3. [Google Scholar]
- Han, X.; Ouyang, M.; Lu, L.; Li, J.; Zheng, Y.; Li, Z. A comparative study of commercial lithium ion battery cycle life in electrical vehicle: Aging mechanism identification. J. Power Sources 2014, 251, 38–54. [Google Scholar] [CrossRef]
- Zhu, J.; Mathews, I.; Ren, D.; Li, W.; Cogswell, D.; Xing, B.; Sedlatschek, T.; Kantareddy, S.N.R.; Yi, M.; Gao, T.; et al. End-of-life or second-life options for retired electric vehicle batteries. Cell Rep. Phys. Sci. 2021, 2, 100537. [Google Scholar] [CrossRef]
- Thompson, D.L.; Hartley, J.M.; Lambert, S.M.; Shiref, M.; Harper, G.D.J.; Kendrick, E.; Anderson, P.; Ryder, K.S.; Gaines, L.; Abbott, A.P. The importance of design in lithium ion battery recycling—A critical review. Green. Chem. 2020, 22, 7585–7603. [Google Scholar] [CrossRef]
- IEA. Global EV Sales by Scenario, 2020–2030. Available online: https://www.iea.org/data-and-statistics/charts/global-ev-sales-by-scenario-2020-2030 (accessed on 28 May 2023).
- Köllner, C. Verbrenner-Ausstieg: Die Pläne der Autohersteller. springerprofessional.de. 9 September 2023. Available online: https://www.springerprofessional.de/antriebsstrang/verkehrswende/verbrenner-ausstieg--die-plaene-der-autohersteller/18906344 (accessed on 28 May 2023).
- Kampker, A.; Heimes, H.H.; Offermanns, C.; Vienenkötter, J.; Frank, M.; Holz, D. Identification of Challenges for Second-Life Battery Systems—A Literature Review. WEVJ 2023, 14, 80. [Google Scholar] [CrossRef]
- PEM Institute. Batteriemonitor 2021: Die Wertschöpfungskette im Spannungsfeld von Ökonomie und Ökologie. Available online: https://www.pem.rwth-aachen.de/global/show_document.asp?id=aaaaaaaabgmfusq (accessed on 28 May 2023).
- Kachate, N.; Sharma, D.; Baidya, K. Material recovery in Li-ion battery recycling: Case study. Mater. Today: Proc. 2023, 72, 1498–1502. [Google Scholar] [CrossRef]




| Actuator | Battery Pack | Sensor |
|---|---|---|
|
|
|
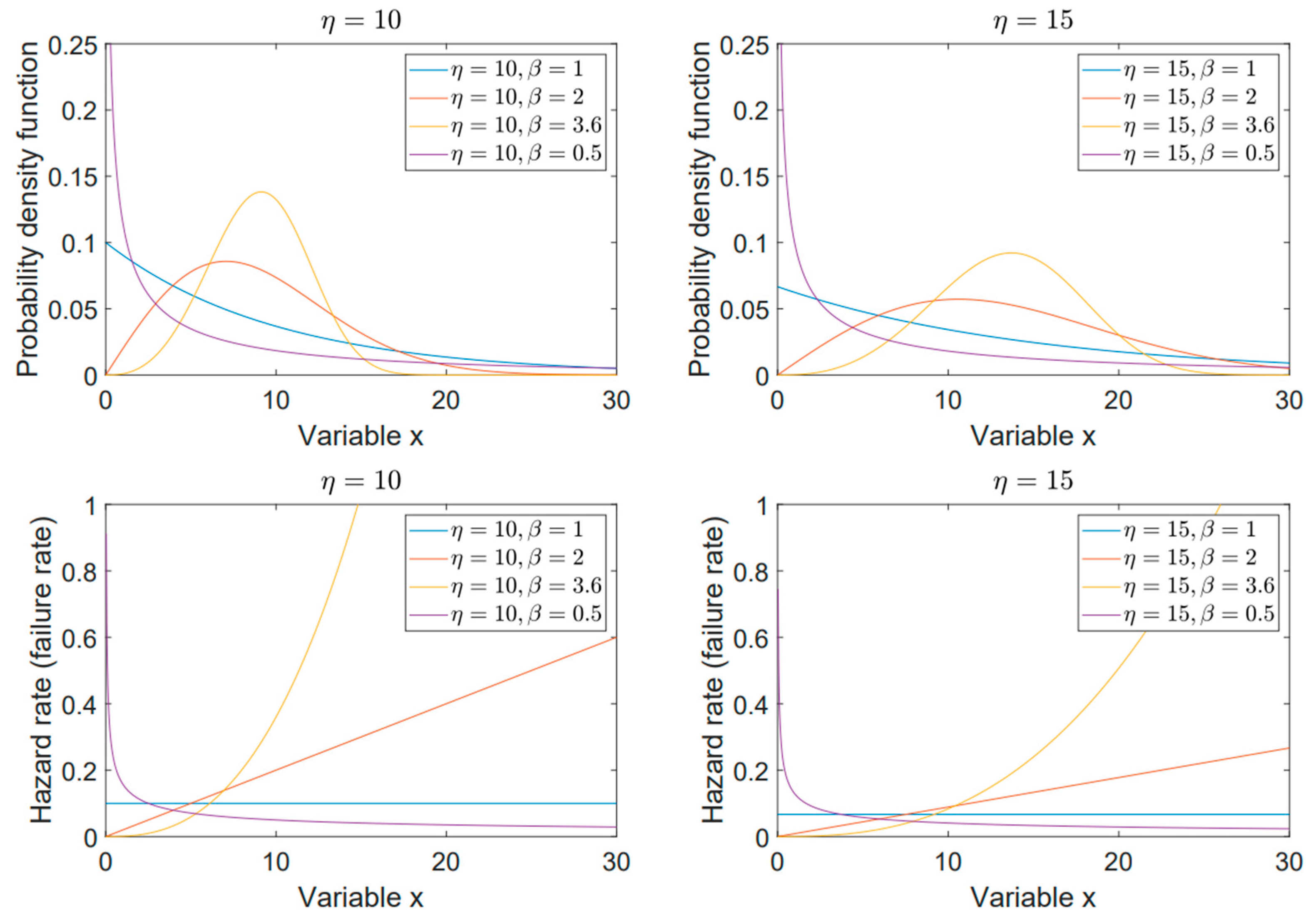
| Shape Parameter | Behavior |
|---|---|
| The exponential reliability function (constant hazard rate) results, with , which corresponds with random failures. | |
| We obtain a decreasing hazard rate reliability function, which corresponds with early failures. | |
| We obtain an increasing hazard rate reliability function, which corresponds with aging failures. | |
| The distribution approximates a normal distribution (PDF), showing that the Weibull distribution can approximate other distributions as well, making it very versatile. |
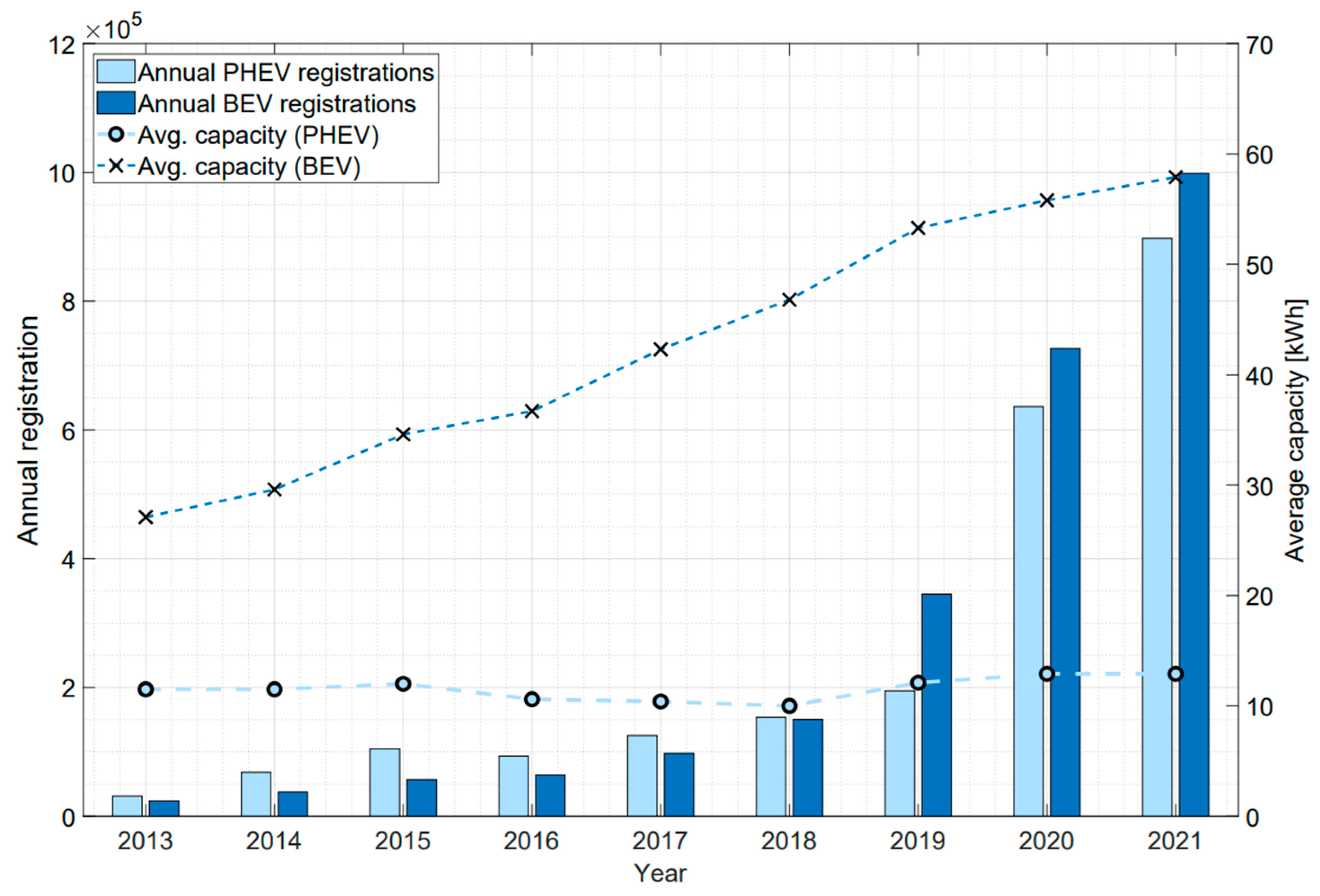
| Year | Avg. Capacity (BEV) | Share of Best-Selling Cars | Avg. Capacity (PHEV) | Share of Total |
|---|---|---|---|---|
| 2013 | 27.1 kWh | 91% | 11.5 kWh * | 80% * |
| 2014 | 29.6 kWh | 97% | 11.5 kWh | 99% |
| 2015 | 34.6 kWh | 94% | 12.0 kWh | 96% |
| 2016 | 36.7 kWh | 94% | 10.6 kWh | 92% |
| 2017 | 42.3 kWh | 90% | 10.4 kWh | 68% |
| 2018 | 46.8 kWh | 88% | 10.0 kWh | 64% |
| 2019 | 53.3 kWh | 83% | 12.1 kWh | 67% |
| 2020 | 55.8 kWh | 62% | 12.9 kWh | 38% |
| 2021 | 57.9 kWh | 51% | 12.9 kWh * | 26% * |
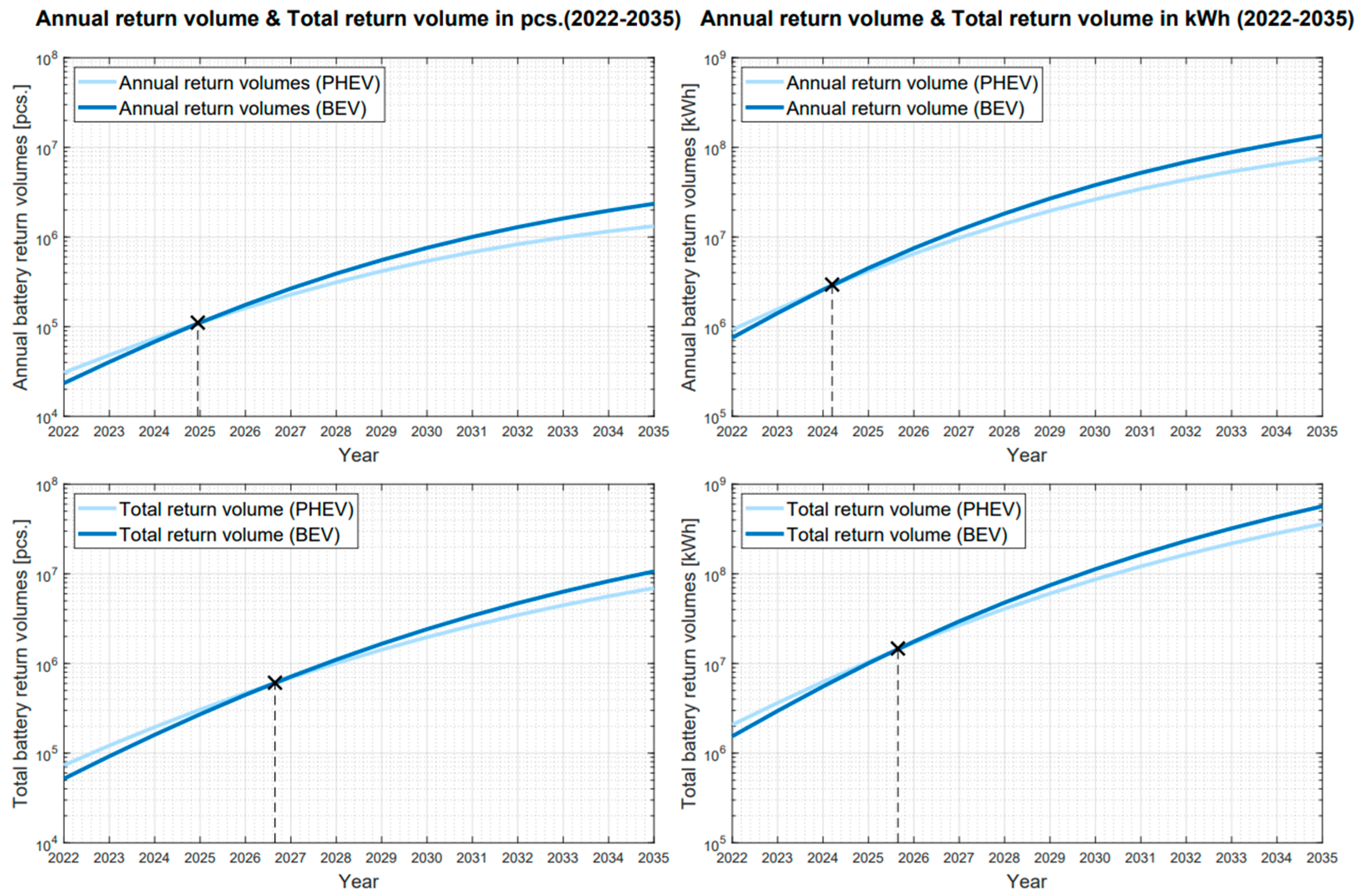
| Year | Battery Return Volumes | ||
|---|---|---|---|
| BEV | PHEV | ||
| 2025 | Annual | 111,146 pcs. 4,504,121 kWh | 110,721 pcs. 4,197,944 kWh |
| Total | 271,454 pcs. 10,046,714 kWh | 306,036 pcs. 10,442,706 kWh | |
| 2030 | Annual | 757,619 pcs. 38,056,955 kWh | 539,636 pcs. 26,377,840 kWh |
| Total | 2,415,738 pcs. 112,795,785 kWh | 1,964,189 pcs. 86,754,640 kWh | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kampker, A.; Heimes, H.H.; Offermanns, C.; Frank, M.; Klohs, D.; Nguyen, K. Prediction of Battery Return Volumes for 3R: Remanufacturing, Reuse, and Recycling. Energies 2023, 16, 6873. https://doi.org/10.3390/en16196873
Kampker A, Heimes HH, Offermanns C, Frank M, Klohs D, Nguyen K. Prediction of Battery Return Volumes for 3R: Remanufacturing, Reuse, and Recycling. Energies. 2023; 16(19):6873. https://doi.org/10.3390/en16196873
Chicago/Turabian StyleKampker, Achim, Heiner Hans Heimes, Christian Offermanns, Merlin Frank, Domenic Klohs, and Khanh Nguyen. 2023. "Prediction of Battery Return Volumes for 3R: Remanufacturing, Reuse, and Recycling" Energies 16, no. 19: 6873. https://doi.org/10.3390/en16196873
APA StyleKampker, A., Heimes, H. H., Offermanns, C., Frank, M., Klohs, D., & Nguyen, K. (2023). Prediction of Battery Return Volumes for 3R: Remanufacturing, Reuse, and Recycling. Energies, 16(19), 6873. https://doi.org/10.3390/en16196873









