Abstract
One of the most famous methods for minimizing power loss is distribution network reconfiguration (DNR). Accordingly, many researchers have focused their work on finding a network’s optimal configuration in planning mode. However, few address the switching sequence process during operation mode. This paper introduces an innovative approach to minimize power loss in distribution networks. It addresses the often-overlooked real-time switching sequence order (SSO) during network operation, ensuring a smooth transition to the optimal configuration within operational constraints. Simultaneously, it optimizes distribution network reconfiguration (DNR) and distributed generation location and sizing (DG-LS) to maximize load capacity. The primary goal is to reduce power losses, improve voltage profiles, and enhance network efficiency. Utilizing multi-objective decision methods based on AHP, particle swarm optimization (PSO), and firefly algorithm (FA), this study achieves efficient results for SSO, DNR, and DG-LS optimization.
1. Introduction
The minimization of power loss is important for power quality and system efficiency [1]. Network reconfiguration is the most common method for minimizing loss, improving voltage quality, and load balancing in planning mode [2]. Reconfiguration is performed by changing the network topography based on opening and closing the tie and sectionalizing switches while maintaining the distribution radial configuration, feed-connected loads, and bus voltage limitations [3]. The distribution network reconfiguration (DNR) process is essential yet challenging, since it is a nonlinear and large-scale optimization problem. In addition, DNR is subject to some limitations and constraints [4]. Therefore, many researchers have devoted their work to dealing with this issue to develop effective methods for DNR [5]. Different meta-heuristic methods were studied to achieve practical solutions for DNR in load balancing for minimizing power loss [6]. In [7], DNR for improving the power quality and system reliability using genetic algorithms (GAs) was presented. The study in [8] solved the power loss problem using ant colony optimization (ACO). The conventional ACO was modified to avoid mesh checks and reduce computational time. In [9], a fuzzy adaptive particle swarm optimization (PSO) for power loss minimization was presented using optimal load response for distribution network (DN). The optimal load was combined with the price signal to control demand management. The authors in [10] provided a wide-scope review of swarm intelligence algorithms by highlighting their strengths and functions. Additionally, they provided different applications of engineering fields in optimization problems. In [11,12], a power-flow-minimum heuristic algorithm was proposed for the loss minimization of radial distribution. This algorithm used the optimum flow pattern concept by solving Kirchhoff’s current and voltage law formulas. The authors of [13,14] combined both system reliability and power loss minimization. DNR with multi-stage and multi-load scenarios for DN in planning mode was proposed in [15]. The presented method combined DG with DNR, including a microgrid in operation mode. The effect of renewable energy sources and electrical energy storage on the DN voltage stability index was studied in [16]. In [17], DNR was used for minimizing power loss and improving the voltage profile based on the model-free reinforcement learning (RL) approach, which improves optimization performance by accelerating the training process. The authors in [18] proposed statistical machine learning theories to quickly solve the optimal planning of distribution networks. Different technologies were used: Copula functions and Markov chains were used to capture the variability in the weather; consumption behavior probability was used for the model of weather-sensitive load; probabilistic power flow was evaluated using stochastic response surface; and the probabilistic inequality theory was used to estimate the function of the stochastic programming model. The proposed methodology showed its effectiveness when compared with other methods.
Furthermore, applying an integrated distributed generator (DG) to the distribution network resulted in a great impact on the distribution system operation. However, integrated DG in a non-optimal location and sizing may cause voltage volatility and power loss to increase. Therefore, the DNR problem had to be handled simultaneously with DG integration [19]. Optimal DG location is defined as the best site of the DG in the distribution network, while optimal DG sizing is defined as the optimal DG output generation that minimizes power loss and improves voltage profile [20]. While, in [21], the authors considered the discretized DNR via a dataset method to find the local optimal solution and reduce the search complexity using the water cycle algorithm (WCA), the authors in [22] used a grey wolf optimizer (GWO) to minimize the search complexity and solve the optimistic combinatorial problems. In [23], the authors presented multi-objective management operations to reduce power loss, emissions of pollution gas, and operation costs by integrating DG into the DNR process. In [24], the authors minimized power loss and improved the voltage profile using a mixed particle swarm optimization (MPSO) method. This method combined the conventional PSO with binary particle swarm optimization (BPSO) methods to improve the performance effectiveness of the proposed method in finding the optimal solution. The authors in [25] used a hybrid PSO with a GWO optimizer to solve the DNR problem that integrated renewable and conventional DGs. The hybrid approach obtained results better than the individual approach. In [26], the research proposed a new method using evolutionary programming (EP) and firefly algorithm (FA) that combined DNR with DG sizing and protection devices. The aim was to minimize power loss and keep protection devices working in both fault and normal system operation. In [27,28,29], the authors proposed an optimal DNR simultaneously with optimal sitting for wind turbines (WTs) and photovoltaic panels (PVs) to minimize the cost of the power loss and improve reliability. In [30], the authors proposed a cooperative multiple-task reallocation under constraints problem for heterogeneous UAVs based on combining an ant colony optimization algorithm with fuzzy C-means clustering. In [31], a skeleton-network reconfiguration methodology for restoring loads quickly after a complete blackout was presented based on discrete particle swarm optimization and network topology. The proposed methodology provided effective decisions under the uncertain system situation. In [32], the authors provided detailed data and characteristics for agricultural electrification loads. This information will be important for power plant technology, agricultural energy internet (AEI), and digital twin technology. In the AEI, the new energy transmission negative impact will be reduced while the park efficiency and energy utilization rate will be increased. In [33], the authors presented a novel methodology for optimizing the combination between rural energy systems and photovoltaic greenhouse load control. The obtained results showed that by using the presented methodology, the energy costs will be minimized. In [34], the authors proposed a new methodology for DNR based on the minimum branch current in the network with fast computational times.
Moreover, another important issue that has been investigated is the maximum load that can be added to a network without violating the constraints, which is called loadability or maximum load capacity (MLC) [35]. DNR and DG sizing and location were used to achieve maximum loadability with minimum power loss using an efficient two-stage algorithm. The first stage minimized power loss using DNR and the second one improved the loadability [36]. In [37], the authors presented a new method for DNR to maximize the network loadability using the continuation power flow (CPF) theorem and discrete artificial bee colony (DABC) algorithms. In [38], DG placement integrated with the DNR method using hybrid particle swarm optimization (PSO) was proposed. System constraints were considered, such as voltage and line limitations besides the level of the DG penetration. The vortex searching algorithm (VS) was added to the previous work in [39]. It is faster and more accurate than HPSO in finding the optimal solution. In [40], the authors addressed different scenarios to minimize power loss and enhancement loadability without violating the constraints. In [41], the study presented a multi-objective approach that maximizes the system loadability through DNR integrated with distributed energy resources based on a comprehensive teaching–learning-based optimization method. In [42], the authors presented a new efficient method that minimizes power loss using DNR and improves system loadability based on limit-induced and saddle-node systems. In [43], a new methodology integrated the capacitor sizing into the DNR and DG sizing methods using Jaya optimization, which minimizes power loss and enhancement loadability. In this paper, a simultaneous DNR and DG location and sizing system incorporated with MLC is proposed for minimizing active power loss (Ploss) and reactive power loss (Qloss) and enhancing voltage profile index (IVD) using FA and PSO on IEEE 33-bus and IEEE 69-bus systems.
It is noteworthy that few works have focused on minimizing power loss through switching sequence processes during operation mode. In [44], the authors presented a new methodology that reconfigured the network in real time while incorporating renewable DGs. An analytic hierarchy process (AHP) was used to determine the best switching sequence for a real network. The results show that the real-time reconfiguration modified the system performance. In [45], the authors proposed an online fast reconfiguration method for a real system. This aimed to minimize voltage rise issues, reduce DG contribution, and alleviate line congestion. In [46], the authors provided a real-time reconfiguration data-driven method in a short time that aimed to minimize power loss, improve voltage bus, and enhance reliability. In [47], the authors focused on minimizing power loss and improving the bus voltage during the real-time reconfiguration process within DGs. In this paper, a real-time methodology is proposed to find the optimal real-time switching sequence order (SSO) which transfers the network from the initial configuration to the optimal configuration without violating the constraints on the operation mode.
Different from the published works mentioned above, this paper adopts two synchronized contributions in sequential order:
- The first contribution is to find the optimal distribution network reconfiguration (DNR) simultaneously with optimal distributed generation location and sizing (DG-LS), which achieves the maximum active and reactive load capacities of the distribution network (DN) in planning mode. Most of the existing literature has focused on finding the minimum power loss.
- The unique contribution of this paper is to present an efficient methodology to find the optimal real-time switching sequence order (SSO), which allows the network to change its topography from the initial configuration to the optimal configuration without violating the constraints on operation mode. This is achieved based on the optimal solution obtained from the first contribution. Most of the existing literature has focused on finding the optimal configuration of the network in planning mode.
The main aim of this methodology is to minimize active and reactive power losses, improve the voltage profile index (IVD), and maximize the active and reactive load capacity of the network. Moreover, part of the results are compared with other published works. The remainder of this paper is organized as follows. In Section 2, the mathematical formulation and constraints are presented. In Section 3, the proposed approach is presented. Results and discussion are provided in Section 4. Conclusions are provided in Section 5.
2. Mathematical Formulation and Constraints
The first problem is determining the opening and closing switches, the DG bus location, and the output generation that achieve the minimum Ploss and Qloss and the best IVD in addition to the maximum PL and QL capacity. The second problem is to find the real-time switching sequence order (SSO) which changes the network from the initial configuration to the final configuration under the minimum Ploss and Qloss and best IVD through maximum the PL and QL capacity. This is conducted under technical constraints and limitations concerning bus voltage limits and power flow and is based on a multi-objective decision approach (MODA). The problems can be formulated using (1) to (10).
where , , , and are the fitness F weight factors. For the same unit, the fitness terms are modified as follows:
Power loss is given as follows:
where is the net active power loss, is the active power loss after reconfiguration, is the active power loss before reconfiguration, is the resistance in the branch N, is the branch current, N is the branch number, and M is the other branch number.
where is the net reactive power loss, is the reactive power loss after reconfiguration, is the reactive power before reconfiguration, and is the reactance in branch N.
where is the maximum PL and QL capacity factor at bus i.
where is the bus nominal voltage, is the bus i voltage, and i numbers from bus 2 to bus n.
where is the receiving bus voltage and is the same as , and is the sending bus voltage.
DNR and SSO must meet the operating constraints, as follows:
- Power Constraints
There are two types of power constraints [26]:
- The power injection constraint.
This constraint is to ensure that there is no power flowing from the DG units to the grid, which may cause protection issues, as shown by Equations (9) and (10).
- The power balance constraint.
This constraint is to guarantee the principle of equilibrium. Thus, the supply of power must be equal to its demand, i.e., the summation of the power loss and power load must equal the summation of the power generated by the substation and DG units, as shown by Equations (11) and (12).
where and are the active and reactive DG size, respectively; k is the DG number; and are the load active and reactive power, respectively; and are the main substation active and reactive power, respectively; and nbus is the bus number.
- 2.
- DG Constraintswhere and are the DG the acceptable upper and lower limits, respectively.
- 3.
- Voltage Constraintswhere Vbus is the voltage bus, and VMin and VMax are the voltage minimum (Min) and maximum (Max) values, respectively. Any bus voltage must be between 0.95 p.u and 1.05 p.u (±5% of rated value) [48].VMin ≤ Vbus ≤ Vmax
- 4.
- Distribution Topology Form Constraints
The distribution network should be in a radial form, which is the most essential constraint. The DNR works in a radial structure since it is simple to construct, design, and maintain. This minimizes the cost of construction and operational costs [49,50].
- 5.
- Load Constraint
All buses must be connected and receive power from the sources.
- 6.
- Maximum Load Capacity Factor Constraints
This constraint means that the active and reactive power load could add to the original network without violating any of the constraints, achieving the minimum active and reactive power losses, which can be formed as follows:
where λ is the MLC factor for each bus, which must be between 1 and 1.4, and it is multiplied by the active and reactive power load of each bus. Each bus must meet PL and QL values equal to or larger than the original load values.
1≤ λ ≤ 1.4
3. Proposed Approach
In this section, the new methodology is proposed in two stages. The first stage proposes an optimal DNR simultaneously with optimal DG-LS under planning mode. The second stage proposes an optimal real-time switching sequence order (SSO) which changes the network from the initial configuration to the optimal configuration under operation mode. The AHP approach was used for determining the fitness weight factors for the multi-objective decision fitness. PSO and FA algorithms were used to find the optimal solution for the DNR, DG-LS, and SSO processes. The methodology aims to minimize Ploss and Qloss, enhance IVD, and maximize the active and reactive load capacity that could be added to the original network load.
3.1. Simultaneous Optimal DNR with DG Location and Sizing for MLC
In this section, AHP is used as a MODA for determining the weight factors of fitness. FA and PSO were the optimization methods used to find the optimal DNR simultaneously with DG-LS for MLC.
3.1.1. Analytic Hierarchy Process (AHP)
AHP was presented as an instrument for the fulfillment of a performance planner with various criteria [51]. AHP was addressed in [52] as an easy, practical, and efficient approach to decision making to deal with complicated, unstructured, and myriad problems. AHP was utilized to determine the weight factors based on the system power index for different function indices. The method of AHP is established on a comparison between multi-criteria. The valuation of the weight factors uses scale numbers from 1 to 7 based on comparing objective functions [53]. The AHP relative importance scale matrix is presented in Table 1 for different indices.

Table 1.
Matrix of relative importance.
Table 2 presents the evaluation of the weight factors based on the arrangement of the matrix scale. Furthermore, Figure 1 illustrates the AHP construction steps by initially determining the alternatives participating in the decision making. Then, they are constructed in the hierarchical mode. After that, based on relative importance, the comparison matrix is constructed. Finally, the weight factors are determined.

Table 2.
Weight factors in the AHP approach.

Figure 1.
AHP flowchart.
3.1.2. Firefly (FA)
FA is one of the meta-heuristic optimizations which is a nature-inspired method [54] addressed by Yang in [55]. FA is strongly robust for complex problems that could find the optimal global solution without being trapped in local solutions. The authors of [56,57] present more details about the FA working principle. The functions of FA and AHP are illustrated in a simple flowchart in Figure 2 for solving the proposed strategy. The detailed steps for this strategy are presented as follows:
- Determine the FA parameters, iteration number, and initial population size.
- Set the network parameters like PL and QL load of the buses, resistance, reactance values of the lines, and initial values of the bus’s voltages.
- Mark the fitness weight factors based on the AHP approach.
- Generate simultaneous random network initial populations (X) which fulfill all constraints and limitations. X indicates the network tie switches number (S) for the new configuration, DG location (DGL), DG sizing (DGS), and MLC factors (λ).where n is the tie switch number; q is the DG number; and m is the initial population size.
- Run the load flow code which is based on the Newton–Raphson method. Then, evaluate the Ploss and Qloss values, maximum PL and QL values of each bus, and Max and Min values of the bus’s voltages for the entire network. Then, calculate the fitness.
- Sort the populations from low to high fitness. Save the best light intensity which represents the fitness minimum value.
- Start the mutation iteration loop by evaluating the fitness value for each population generated on matrix X related to Equation (1).
- Sort the populations from low to high fitness based on their light intensity. Save the best light intensity which represents the fitness minimum value.
- Update the elements of matrix X based on the FA optimization considering all limitations and constraints based on the following equations:where is the attractiveness when ; is the two FAs’ space; and is the coefficient of the light absorption.where is the cartesian space between the and FAs, which represents the matrix rows; is the parameter’s optimized number; and and represent a component of the cartesian coordinates and of the FAs and , respectively.where the initial term is the movement of FAs, where is attracted to the brighter ; the next term is affected by the attraction; the final term represents the random parameter related to .
- Rank the updated movement from low to high fitness.
- Repeat the above steps from 5 to 9 until reaching the maximum iteration.
- Stop the approach and output the final optimum solution, which represents the network’s new configuration, the DG’s locations, the DG’s sizing, the MLC factors, the fitness value, IVD, the maximum PL and QL load for all buses, and the minimum Ploss and Qloss of the network.
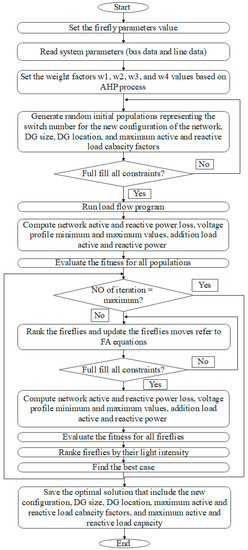
Figure 2.
FA flowchart of the presented strategy for determining optimal DNR with DG-LS for MLC.
3.1.3. Particle Swarm Optimization (PSO)
PSO is also a meta-heuristic optimization technique. It was proposed in 1995 [58]. PSO is easy, fast, and simple to code and understand. For more detail about PSO’s working principle, see [59,60]. The functions of PSO and AHP are illustrated in a simple flowchart in Figure 3 for solving the proposed strategy. The detailed steps for this strategy are presented as follows:
- Determine the PSO parameters, iteration number, and initialization population size.
- The population stage is the same as in the FA approach (step 2 to step 6).
- Start the mutation iteration loop by evaluating the fitness value for each population generated on matrix X related to Equation (1).
- Sort the populations from low to high fitness based on their light intensity. Save the best light intensity, which represents the fitness minimum value.
- Update the particle position and velocity of matrix X related to its own searching experience and other particle experience , considering all limitations and constraints. The update of the particles’ velocity and position is conducted based on the following equations:where and are the particle current position at iteration and , respectively; and are particle ’s current velocity at iteration and , respectively; and are the PSO weighting factors; and are a random number; and are the initial Max and Min weight, respectively; and and are the current and maximum iteration number, respectively.
- Rank the updated movement from low to high fitness.
- Repeat the above steps, from 4 to 6, until reaching the maximum iteration.
- Stop the approach and output the final optimum solution, which represents the network’s new configuration, DG-LS, the MLC factors, the fitness value, IVD, the maximum PL and QL load for all buses, and the minimum Ploss and Qloss of the network.
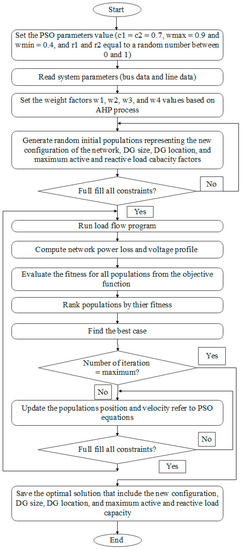
Figure 3.
PSO flowchart of the presented strategy for determining optimal DNR with DG-LS for MLC.
3.2. Optimal Switching Sequence Order (SSO)
In this section, FA and PSO are the optimization methods used to find the optimal switching sequence order (SSO). In the SSO process, the tie switch which is normally open will be changed to closed, and some of the sectionalizing switches which are normally closed will change to open to change the form of the network from its initial form to its final form. For more explanation about the SSO process, an IEEE 16-bus network is used as illustrated in Figure 4. In this network, there are 3 tie switches and 14 sectionalizing switches. The tie switch will change from open to closed and the same number of sectionalizing switches (3) will change from closed to open during a specific sequence. In this case, there are different probabilities for changing the switches’ states. In this case, it is critical to use an optimization technique to find the optimal SSO.
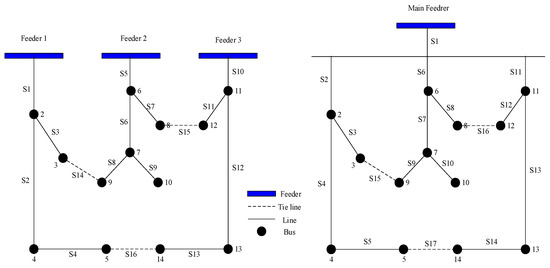
Figure 4.
IEEE 16-bus distribution network.
3.2.1. Firefly
The main steps of this SSO process using FA are as follows:
- Determine the FA parameters, iteration number, and initial population size.
- Set the network parameters like active and reactive power load of the buses, resistance, reactance values of the lines, and initial values of the bus’s voltages.
- Mark the fitness weight factors based on the AHP approach.
- Set the initial (original) configuration of the distribution network.
- Identify the final (optimal) configuration of the distribution network, the location and size of the DGs, and the MLC factors obtained from the reconfiguration process (presented in Section 3.1 (B)).
- Generate random network initial populations (x). x indicates the switching sequence order (SSO) which transfers the network from the initial configuration to the optimal configuration without violating the constraints of the voltage.where and are the switches to be closed and open during the SSO process, respectively, and z is the number of steps needed to change the form of the network from initial to optimal.
- Evaluate the Ploss and Qloss and the IVD for each step during the SSO process for each population.
- Calculate the fitness value for each step during the SSO process for each population.
- Sum the total fitness for all steps for each population in matrix x.
- Sort the populations from low to high fitness. Save the best light intensity, which represents the total fitness minimum value.
- Start the mutation iteration loop by evaluating the total fitness value for each population in matrix x.
- Update the elements of matrix x based on the FA optimization, considering all limitations and constraints based on Equations (17)–(19).
- Rank the updated movement from low to high total fitness.
- Repeat the above steps, from 12 to 14, until reaching the maximum iteration.
- Stop the approach and output the final optimum solution that represents the optimal switching sequence order (SSO), which transfers the network from the initial configuration to the optimal configuration, minimum Ploss and Qloss of the network, and best IVD. The function of FA is illustrated in Figure 5 in a simple flowchart for solving the proposed strategy of the SSO process.
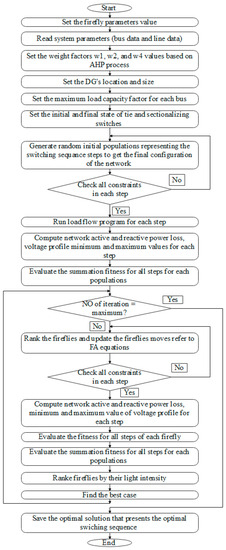 Figure 5. FA flowchart of the presented strategy to determine the optimal SSO process.
Figure 5. FA flowchart of the presented strategy to determine the optimal SSO process.
3.2.2. PSO
The main steps of this SSO process using PSO are as follows:
- Determine the PSO parameters, iteration number, and initial population size.
- Repeat steps 2 to 4 as in FA.
- Identify the final (optimal) configuration of the distribution network, the location and size of the DGs, and the MLC factors obtained from the reconfiguration process (presented in Section 3.1 (C)).
- The population stage is the same as that in the FA approach (steps 6 to 10).
- Start the mutation iteration loop by evaluating the total fitness value for each population in matrix x.
- Update the elements of matrix x based on the PSO optimization considering all limitations and constraints based on Equations (20)–(22).
- Rank the updated movement from low to high total fitness.
- Repeat the above steps, from 5 to 7, until reaching the maximum iteration.
- Stop the approach and output the final optimum solution that represents the optimal switching sequence order (SSO), which transfers the network from the initial configuration to the optimal configuration, minimum Ploss and Qloss of the network, and best IVD. The function of PSO is illustrated in Figure 6 in a simple flowchart for solving the proposed strategy of the SSO process.
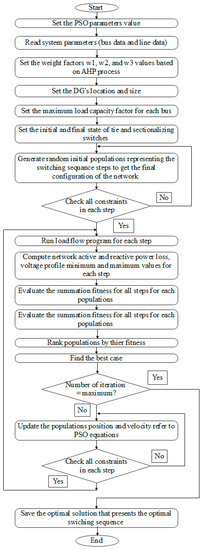 Figure 6. PSO flowchart of the presented strategy to determine the optimal SSO process.
Figure 6. PSO flowchart of the presented strategy to determine the optimal SSO process.
4. Results and Discussion
The validity of the proposed strategy was tested on two test systems. The first test system was the IEEE 33-bus. The one-line diagram of the IEEE 33-bus is shown in Figure 7. The nominal voltage of the system was 12.66 kV and the base apparent power was 100 MVA. The initial data of the system are presented in Table 3. Other data like active and reactive power load of the buses and resistance and reactance values of the lines are reported in [6,61]. The second test system was the 69-bus test system. The one-line diagram of the IEEE 69-bus is shown in Figure 8. The nominal voltage of the system was 12.66 kV and the base apparent power was 100 MVA. The initial data of the system are presented in Table 4. Other data like active and reactive power load of the buses and resistance and reactance values of the lines are reported in [6,61,62].
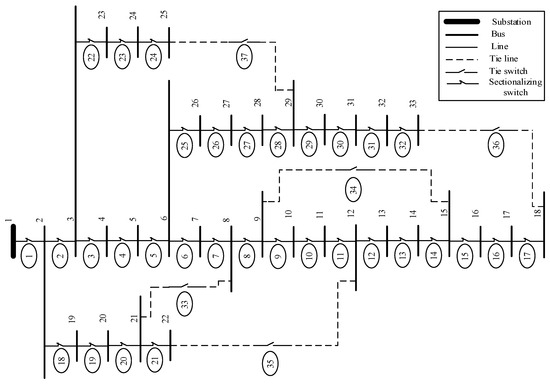
Figure 7.
IEEE 33-bus distribution network.

Table 3.
Comparison of simulation optimal DNR with DG-LS results for IEEE 33-bus network.
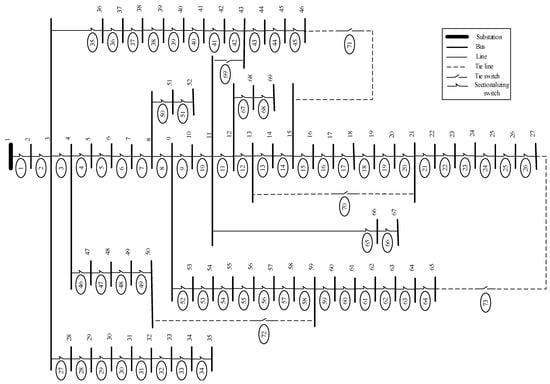
Figure 8.
IEEE 69-bus distribution network.

Table 4.
Comparison of simulation optimal DNR with DG-LS results for IEEE 69-bus network.
4.1. Influence of DNR and DG-LS on Network Performance
The first contribution of this work is to propose a new methodology that reduces active and reactive power loss, improves voltage profile, and increases the bus PL and QL through a simultaneous DNR and DG-LS approach.
4.1.1. Impact of DNR and DG-LS on Power Loss
Power loss is the first issue to be addressed. Table 3 presents details of the initial (original) and final (optimal) network cases for the IEEE 33-bus. For the initial case, switches numbered 33 to 37 are opened, while other switches are closed. PL and QL loads are 3715 kW and 2300 kVAR, respectively. Ploss and Qloss are 202.4 kW and 135 kVAR, respectively. Min and Max bus voltages are 0.913 p.u and 1 p.u, respectively. While the optimal configuration using PSO is when switches numbered 27, 17, 6, 11, and 13 are opened, the optimal DGs’ locations and sizing are on bus 15, with size 0.47608 MW; bus 8, with size 0.72063 MW; and bus 29, with size 1.86442 MW. The minimum fitness is 0.3043. The total active and reactive network power loads are maximized to 4264.2 kW and 2553.5 kVAR, respectively, compared to the initial case. The PL and QL loads added are 14.78% and 11.02% above the initial case, respectively. The Ploss and Qloss are minimized to 73.3 kW and 55 kVAR, respectively, compared to the initial case. The Ploss and Qloss reduction is 63.78% and 59.26%, respectively. Min and Max bus voltages are improved to 0.9663 p.u and 1 p.u, respectively, compared to the initial case. In addition, the optimal configuration using FA is when switches numbered 27, 17, 6, 11, and 13 are opened. The optimal DGs’ locations and sizing are on bus 15, with size 0.44495 MW; bus 7, with size 0.66420 MW; and bus 29, with size 1.73274 MW. The minimum fitness is 0.27798. The total PL and QL loads are maximized to 3984.8 kW and 2424.3 kVAR, respectively, compared to the initial case. The PL and QL loads added are 7.26% and 5.4% above the initial case, respectively. The Ploss and Qloss are minimized to 67.02 kW and 49.78 kVAR, respectively, compared to the initial case. The Ploss and Qloss reduction is 66.89% and 63.13%, respectively. Min and Max bus voltages are improved to 0.9675 p.u and 1 p.u, respectively, compared to the initial case. It is clear that FA is better at minimizing both fitness power losses and enhancement voltage profile, while PSO can maximize the added power load better than FA.
Table 4 presents details of the initial (original) and final (optimal) network cases for the IEEE 69-bus. For the initial case, switches numbered 69 to 73 are opened, while other switches are closed. PL and QL loads are 3801.89 kW and 2694.1 kVAR, respectively. Ploss and Qloss are 224.557 kW and 102 kVAR, respectively. Min and Max bus voltages are 0.9093 p.u and 1 p.u, respectively. While the optimal configuration using PSO is when switches numbered 58, 39, 25, 18, and 43 are opened, the optimal DGs’ locations and sizing are on bus 63, with size 1.806623 MW; bus 68, with size 1.049059 MW; and bus 37, with size 0.576134 MW. The minimum fitness is 0.26666. The total active and reactive network power loads are maximized to 3866.91 kW and 2739.77 kVAR, respectively, compared to the initial case. The PL and QL loads added are 1.71% and 1.695% above the initial case. The Ploss and Qloss are minimized to 57.88 kW and 47.348 kVAR, respectively, compared to the initial case. The Ploss and Qloss reduction is 74.22% and 53.58%, respectively. Min and Max bus voltages are improved to 0.976022 p.u and 1.0026 p.u, respectively, compared to the initial case. In addition, the optimal configuration using FA is when switches numbered 17, 42, 62, 56, and 13 are opened. The optimal DGs’ locations and sizing are on bus 3, with size 1.43198 MW; bus 61, with size 1.64518 MW; and bus 21, with size 1.00133 MW. The minimum fitness is 0.20972. The total active and reactive network power loads are maximized to 3849.42 kW and 2727.53 kVAR, respectively, compared to the initial case. The PL and QL loads added are 1.25% and 1.24% above the initial case, respectively. The Ploss and Qloss are minimized to 46.093 kW and 36.553 kVAR, respectively, compared to the initial case. The Ploss and Qloss reduction is 79.47% and 64.16%, respectively. Min and Max bus voltages are improved to 0.984597 p.u and 1 p.u, respectively, compared to the initial case. FA is better at minimizing both fitness and power losses and enhancement voltage profile, while PSO can maximize the added power load better than FA.
4.1.2. Impact of DNR and DG-LS on Power Load
Power load is the second issue to be handled. This presents the added PL and QL to the network without violating the constraints or increasing the power loss. Table 5 illustrates the maximum power load capacity factor (λ) for each bus of the IEEE 33-bus using PSO and FA methods. This factor multiplies with the bus’s active and reactive loads, i.e., how much the active and reactive loads could increase. Table 6 presents the new active power load for each bus of the IEEE 33-bus using PSO and FA methods. Table 7 presents the new reactive power load for each bus of the IEEE 33-bus using PSO and FA methods. The new load after optimization is larger than the initial network load, i.e., the network load could increase without violating the limitations. This serves the continuous population increase.

Table 5.
Maximum power load capacity factor for the IEEE 33-bus network.

Table 6.
New active power load (kW) for the IEEE 33-bus network.

Table 7.
New reactive power load (kVAR) for the IEEE 33-bus network.
Table 8 illustrates the maximum power load capacity factor (λ) for each bus of the IEEE 69-bus using PSO and FA methods. Table 9 presents the new active power load for each bus of the IEEE 69-bus using PSO and FA methods. Table 10 presents the new reactive power load for each bus of the IEEE 69-bus using PSO and FA methods. Additionally, for 69 buses, the network could accommodate a larger load capacity than the initial load.

Table 8.
Maximum power load capacity factor for the IEEE 69-bus network.

Table 9.
New active power load (kW) for the IEEE 69-bus network.

Table 10.
New reactive power load (kVAR) for the IEEE 69-bus network.
4.1.3. Impact of DNR and DG-LS on Voltage Profile
Voltage profile is the third issue to be discussed. Figure 9 illustrates the voltage profile for the initial IEEE 33-bus network and the voltage profile after optimization using PSO and FA. Figure 10 illustrates the voltage profile for the initial IEEE 69-bus network and the voltage profile after optimization using PSO and FA. As can be seen in the two figures, after optimization, the minimum voltage bus increases to an allowable value, where all bus voltages become close to one. In addition, FA achieved a voltage profile better than that of PSO.
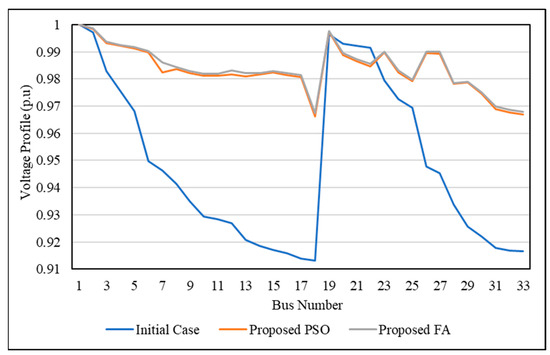
Figure 9.
Voltage profile of the DNR and DG-LS method for the IEEE 33-bus network.
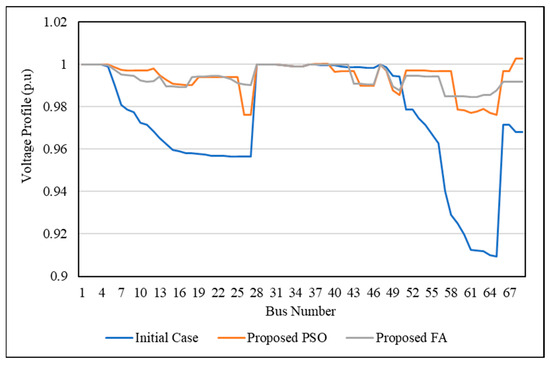
Figure 10.
Voltage profile of the DNR and DG-LS method for the IEEE 69-bus network.
4.1.4. Impact of DNR and DG-LS on Optimization Performance
Optimization technique performance is the fourth issue to be examined. The conversion curve is best examined between optimizations, since it shows the performance clearly. Figure 11 shows the convergence curves of the PSO and FA optimization methods for the IEEE 33-bus network. Figure 12 shows the convergence curves of the PSO and FA optimization methods for the IEEE 69-bus network. FA obtained an optimal value (minimum fitness value) better than PSO. In addition, FA could find the optimal solution faster than PSO.
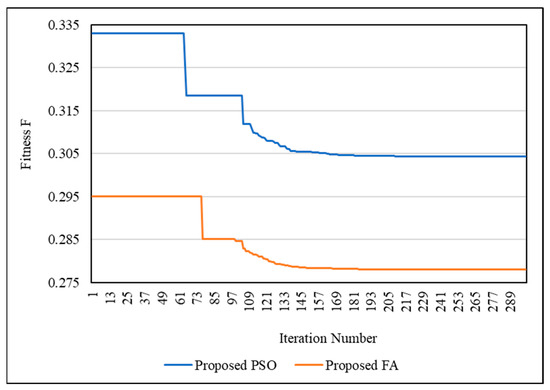
Figure 11.
Convergence curves of DNR and DG-LS for IEEE 33-bus network.
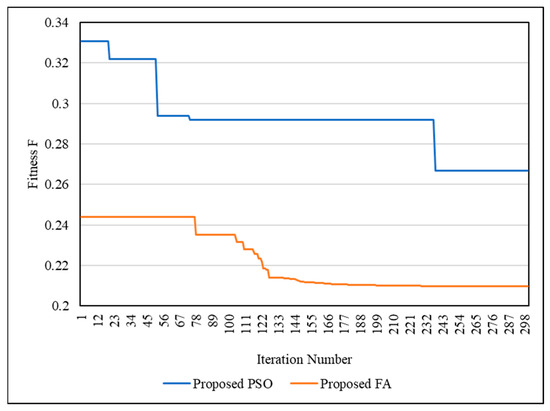
Figure 12.
Convergence curves of DNR and DG-LS for IEEE 69-bus network.
Moreover, the power of the presented methodology was compared with other published works. Table 11 shows the comparison results of the 33-bus network. The power loss based on the proposed methodology using the FA method is 54.997 kW, which is smaller than other methods in the table. Thus, the reduction loss for the proposed method is the highest one (72.83%). Table 12 shows the comparison results of the 69-bus network. The power loss based on the proposed methodology using the FA method is 39.16 kW, which is smaller than other methods in the table. Thus, the reduction loss for the proposed method is the highest one (82.56%). This makes the proposed methodology using FA better than the published methods since it simultaneously optimizes the network reconfiguration and DG location and sizing. This means that FA could find the optimal solution for network reconfiguration with optimal DG-LS, which achieved the minimum power loss and best voltage profile because FA was not trapped in a local optimal solution like other methods.

Table 11.
Comparison of different optimization results of the 33-bus network.

Table 12.
Comparison of different optimization results of the 69-bus network.
4.2. Influence of SSO on Network Performance
Once the optimal configuration was found, as in the previous section, it was time to transfer the network from the initial configuration to the optimal configuration. This conversion method is called switching sequence order (SSO). To change the topology of the network from the initial form to the optimal form, some of the network switches are changed from open to closed or from closed to open. In this work, the SSO is achieved without violating the voltage constraints, and with a minimum Ploss and Qloss, the network will run (in operation mode).
4.2.1. Impact of SSO on Power Loss
The initial configuration of the IEEE 33-bus is when switches numbered 33, 34, 35, 36, and 37 are opened. The optimal configuration obtained using PSO and FA from the previous section of the reconfiguration process is when switches numbered 27, 17, 6, 11, and 13 are opened. Furthermore, the DGs’ location, sizing, and MLC factors are set as they are in the previous section of the reconfiguration process. Table 13 illustrates the results from the SSO process for the IEEE 33-bus. The order of changing the switches’ status via the PSO and FA methods is as follows:

Table 13.
Simulation results of optimal SSO methodology for IEEE 33-bus network.
Step 1: closed switch number 37 → Step 2: opened switch number 27 → Step 3: closed switch number 35 → Step 4: opened switch number 11 → Step 5: closed switch number 36 → Step 6: opened switch number 17 → Step 7: closed switch number 33 → Step 8: opened switch number 6 → Step 9: closed switch number 34 → Step 10: opened switch number 13. During these steps, the Min and Max bus voltages and Ploss and Qloss are determined to calculate the total Ploss and Qloss through the overall SSO process. It is clear from the results that FA obtained a lower fitness value and total Ploss and Qloss than those obtained by PSO. However, both optimizations have the same SSO; the difference in fitness and power is caused by the different DG location and sizing and MLC factors for both PSO and FA caused by the reconfiguration process. Moreover, the proposed method could change the network from the initial form to the optimal form without violating the voltage constraints. In other words, all buses during the change process keep their voltage between 0.95 p.u and 1.05 p.u.
The initial configuration of the IEEE 69-bus is when switches numbered 69, 70, 71, 72, and 73 are opened. The optimal configuration obtained using PSO from the previous section is when switches numbered 58, 39, 25, 18, and 43 are opened. The optimal configuration obtained using FA from the previous section is when switches numbered 17, 42, 62, 56, and 13 are opened. Furthermore, the DGs’ location, sizing, and MLC factors are set as they are in the previous section of the reconfiguration process. Table 14 illustrates the results from the SSO process for the IEEE 69-bus. For example, the order of changing the switches’ status using the FA method is as follows:

Table 14.
Simulation results of optimal SSO methodology for IEEE 69-bus network.
Step 1: closed switch number 72 → Step 2: opened switch number 56 → Step 3: closed switch number 73 → Step 4: opened switch number 62 → Step 5: closed switch number 71 → Step 6: opened switch number 13 → Step 7: closed switch number 70 → Step 8: opened switch number 17 → Step 9: closed switch number 69 → Step 10: opened switch number 42. The fitness value using FA is lower than that using PSO, 2.296 and 2.727, respectively. The Ploss and Qloss through the SSO process using FA are lower than those from PSO. This makes the total Ploss and Qloss for the overall SSO process using FA better than using PSO. Moreover, the proposed method can change the network from the initial form to the optimal form without violating the voltage constraints. This means that any random SSO will violate the voltage constraints and increase the power loss, or sometimes disconnect some loads. This makes the proposed methodology vital for network performance.
4.2.2. Impact of SSO on Voltage Profile
For more explanation, the voltage profile during the SSO process (through each step) was compared with the initial case of the IEEE 33-bus, shown in Figure 13 using PSO and in Figure 14 using FA. It is clear that all bus voltages have a value within the allowable limitation and are better than the initial case. This means that the proposed method provides an SSO method to change the network from the initial form to the optimal form in operation mode without violating any constraints or any limitations, and without disconnecting any load from the electricity feeding.
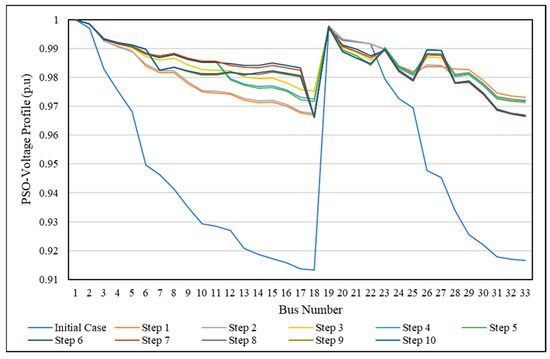
Figure 13.
Voltage profile of the SSO method for the IEEE 33-bus network using PSO.
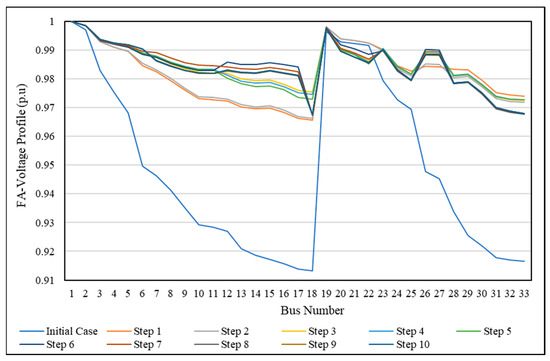
Figure 14.
Voltage profile of the SSO method for the IEEE 33-bus network using FA.
Figure 15 and Figure 16 show the voltage profile of the SSO method for the IEEE 69-bus network using PSO and FA, respectively. From the curves, all bus voltages have a value within the allowable limitation and are better than the initial case.
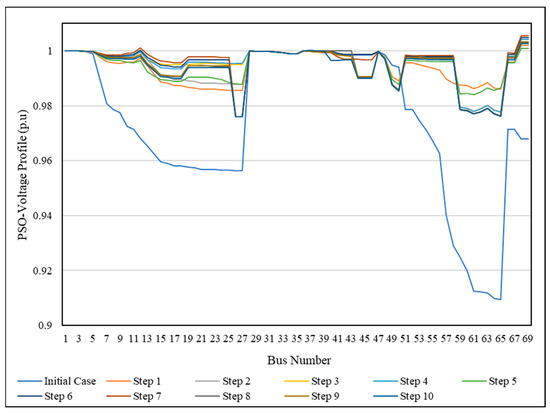
Figure 15.
Voltage profile of the SSO method for the IEEE 69-bus network using PSO.
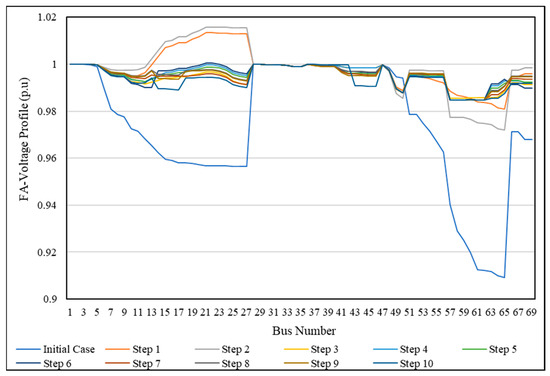
Figure 16.
Voltage profile of the SSO method for the IEEE 69-bus network using FA.
4.2.3. Impact of SSO on Optimization Performance
The optimization techniques’ performance was also examined using the SSO process. Figure 17 shows the convergence curves of SSO for the IEEE 33-bus network using PSO and FA. Figure 18 shows the convergence curves of SSO for the IEEE 69-bus network using PSO and FA. It is clear that FA is better than PSO in finding the optimal solution. Additionally, FA is faster than PSO. This means that FA can obtain the optimal solution through a number of iterations lower than PSO.
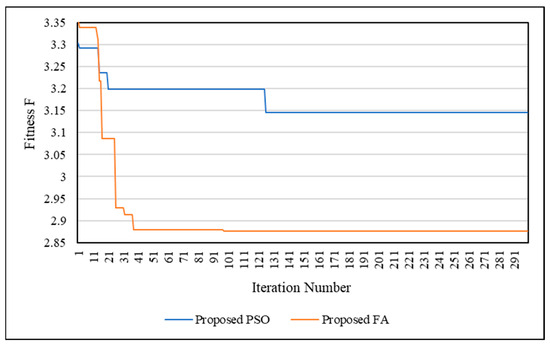
Figure 17.
Convergence curves of SSO for IEEE 33-bus network.
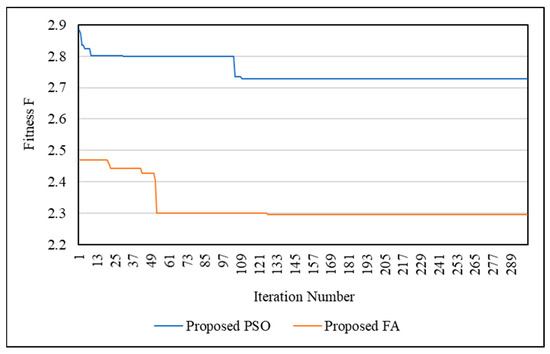
Figure 18.
Convergence curves of SSO for IEEE 69-bus network.
5. Conclusions
In this paper, two contributions are presented: the first contribution proposed a new methodology for simultaneous optimal DNR and DG location and sizing for maximum load capacity based on an analytic hierarchy process as a multi-objective decision approach integrated with PSO and FA optimization techniques in planning mode. The second contribution proposed a new strategy for real-time optimal switching sequence order (SSO) in operation mode that allows the network to transfer from the initial configuration form to the optimal configuration form obtained from the DNR process. The SSO process uses AHP integrated with PSO and FA as a tool for finding the optimal solution without violating the network constraints. Both contributions aim to minimize active and reactive power loss and voltage profile enhancement while maximizing the active and reactive power loads. The proposed methods used the AHP approach for solving the fitness weight factors problem. PSO and FA optimization techniques were used to solve the reconfiguration, DG location, sizing, and SSO problems. Two test systems were used to prove the power of the proposed methodology. The obtained results show the high efficiency and effectiveness of the presented methodology in finding the optimal SSO that safely transfers the network configuration with Ploss and Qloss and the best IVD through the overall SSO process. In addition, the proposed methodology shows high ability in finding the optimal DNR and optimal DGs locations and sizing that achieved minimum Ploss and Qloss values and the best voltage profile while maximizing the PL and QL load. Moreover, this study tested the effectiveness of PSO and FA optimizations. The obtained results prove that FA is faster and stronger in finding the optimal solution for complicated problems such as the DNR and SSO problems. Additionally, FA proved its capability in finding the optimal solution compared with other published optimization techniques.
Author Contributions
Conceptualization, O.B.; data curation, O.B. and J.J.; formal analysis, O.B.; investigation, O.B.; methodology, O.B.; validation, O.B. and J.J.; formal analysis, O.B.; writing—original draft, O.B. and J.J.; writing—review and editing, O.B. and J.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank Palestine Technical University—Kadoorie (PTUK) for supporting this research.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shayeghi, H.; Mahdavi, M. Studying the effect of losses coefficient on transmission expansion planning using decimal codification based GA. Planning 2009, 5, 6. [Google Scholar]
- Macedo, L.H.; Franco, J.F.; Mahdavi, M.; Romero, R. A contribution to the optimization of the reconfiguration problem in radial distribution systems. J. Control Autom. Electr. Syst. 2018, 29, 756–768. [Google Scholar] [CrossRef]
- Hosseini, H.; Jalilzadeh, S.; Nabaei, V.; Govar, G.Z.; Mahdavi, M. Enhancing deregulated distribution network reliability for minimizing penalty cost based on reconfiguration using BPSO. In Proceedings of the 2008 IEEE 2nd International Power and Energy Conference, Johor Bahru, Malaysia, 1–3 December 2008; IEEE: New York, NY, USA, 2008; pp. 983–987. [Google Scholar]
- Zheng, W.; Huang, W.; Hill, D.J.; Hou, Y. An adaptive distributionally robust model for three-phase distribution network reconfiguration. IEEE Trans. Smart Grid 2020, 12, 1224–1237. [Google Scholar] [CrossRef]
- Mahdavi, M.; Alhelou, H.H.; Hatziargyriou, N.D.; Al-Hinai, A. An efficient mathematical model for distribution system reconfiguration using AMPL. IEEE Access 2021, 9, 79961–79993. [Google Scholar] [CrossRef]
- Baran, M.E.; Wu, F.F. Network reconfiguration in distribution systems for loss reduction and load balancing. IEEE Trans. Power Deliv. 1989, 4, 1401–1407. [Google Scholar] [CrossRef]
- Gupta, N.; Swarnkar, A.; Niazi, K. Distribution network reconfiguration for power quality and reliability improvement using Genetic Algorithms. Int. J. Electr. Power Energy Syst. 2014, 54, 664–671. [Google Scholar] [CrossRef]
- Swarnkar, A.; Gupta, N.; Niazi, K.R. Adapted ant colony optimization for efficient reconfiguration of balanced and unbalanced distribution systems for loss minimization. Swarm Evol. Comput. 2011, 1, 129–137. [Google Scholar] [CrossRef]
- Hu, W.; Chen, Z.; Bak-Jensen, B.; Hu, Y. Fuzzy adaptive particle swarm optimisation for power loss minimisation in distribution systems using optimal load response. IET Gener. Transm. Distrib. 2014, 8, 1–10. [Google Scholar] [CrossRef]
- Tang, J.; Liu, G.; Pan, Q. A review on representative swarm intelligence algorithms for solving optimization problems: Applications and trends. IEEE/CAA J. Autom. Sin. 2021, 8, 1627–1643. [Google Scholar] [CrossRef]
- Goswami, S.K.; Basu, S.K. A new algorithm for the reconfiguration of distribution feeders for loss minimization. IEEE Trans. Power Deliv. 1992, 7, 1484–1491. [Google Scholar] [CrossRef]
- Gomes, F.V.; Carneiro, S.; Pereira, J.L.R.; Vinagre, M.P.; Garcia, P.A.N.; De Araujo, L.R. A new distribution system reconfiguration approach using optimum power flow and sensitivity analysis for loss reduction. IEEE Trans. Power Syst. 2006, 21, 1616–1623. [Google Scholar] [CrossRef]
- Duan, D.-L.; Ling, X.-D.; Wu, X.-Y.; Zhong, B. Reconfiguration of distribution network for loss reduction and reliability improvement based on an enhanced genetic algorithm. Int. J. Electr. Power Energy Syst. 2015, 64, 88–95. [Google Scholar] [CrossRef]
- Narimani, M.R.; Azizi Vahed, A.; Azizipanah-Abarghooee, R.; Javidsharifi, M. Enhanced gravitational search algorithm for multi-objective distribution feeder reconfiguration considering reliability, loss and operational cost. IET Gener. Transm. Distrib. 2014, 8, 55–69. [Google Scholar] [CrossRef]
- Shen, X.; Shahidehpour, M.; Zhu, S.; Han, Y.; Zheng, J. Multi-stage planning of active distribution networks considering the co-optimization of operation strategies. IEEE Trans. Smart Grid 2016, 9, 1425–1433. [Google Scholar] [CrossRef]
- Azizivahed, A.; Arefi, A.; Ghavidel, S.; Shafie-Khah, M.; Li, L.; Zhang, J.; Catalão, J.P. Energy management strategy in dynamic distribution network reconfiguration considering renewable energy resources and storage. IEEE Trans. Sustain. Energy 2019, 11, 662–673. [Google Scholar] [CrossRef]
- Wang, B.; Zhu, H.; Xu, H.; Bao, Y.; Di, H. Distribution network reconfiguration based on NoisyNet deep Q-learning network. IEEE Access 2021, 9, 90358–90365. [Google Scholar] [CrossRef]
- Fu, X.; Guo, Q.; Sun, H. Statistical machine learning model for stochastic optimal planning of distribution networks considering a dynamic correlation and dimension reduction. IEEE Trans. Smart Grid 2020, 11, 2904–2917. [Google Scholar] [CrossRef]
- Islam, M.R.; Lu, H.; Hossain, M.; Li, L. Mitigating unbalance using distributed network reconfiguration techniques in distributed power generation grids with services for electric vehicles: A review. J. Clean. Prod. 2019, 239, 117932. [Google Scholar] [CrossRef]
- Sultana, B.; Mustafa, M.; Sultana, U.; Bhatti, A.R. Review on reliability improvement and power loss reduction in distribution system via network reconfiguration. Renew. Sustain. Energy Rev. 2016, 66, 297–310. [Google Scholar] [CrossRef]
- Muhammad, M.A.; Mokhlis, H.; Naidu, K.; Amin, A.; Franco, J.F.; Othman, M. Distribution network planning enhancement via network reconfiguration and DG integration using dataset approach and water cycle algorithm. J. Mod. Power Syst. Clean Energy 2019, 8, 86–93. [Google Scholar] [CrossRef]
- Pujari, H.K.; Rudramoorthy, M. Grey wolf optimisation algorithm for solving distribution network reconfiguration considering distributed generators simultaneously. Int. J. Sustain. Energy 2022, 41, 2121–2149. [Google Scholar] [CrossRef]
- Hamida, I.B.; Salah, S.B.; Msahli, F.; Mimouni, M.F. Optimal network reconfiguration and renewable DG integration considering time sequence variation in load and DGs. Renew. Energy 2018, 121, 66–80. [Google Scholar] [CrossRef]
- Essallah, S.; Khedher, A. Optimization of distribution system operation by network reconfiguration and DG integration using MPSO algorithm. Renew. Energy Focus 2020, 34, 37–46. [Google Scholar] [CrossRef]
- Abd El-salam, M.F.; Beshr, E.; Eteiba, M.B. A new hybrid technique for minimizing power losses in a distribution system by optimal sizing and siting of distributed generators with network reconfiguration. Energies 2018, 11, 3351. [Google Scholar] [CrossRef]
- Rahim, M.N.A.; Mokhlis, H.; Bakar, A.H.A.; Rahman, M.T.; Badran, O.; Mansor, N.N. Protection coordination toward optimal network reconfiguration and DG sizing. IEEE Access 2019, 7, 163700–163718. [Google Scholar] [CrossRef]
- Fathi, R.; Tousi, B.; Galvani, S. Allocation of renewable resources with radial distribution network reconfiguration using improved salp swarm algorithm. Appl. Soft Comput. 2023, 132, 109828. [Google Scholar] [CrossRef]
- Swaminathan, D.; Rajagopalan, A. Optimized Network Reconfiguration with Integrated Generation Using Tangent Golden Flower Algorithm. Energies 2022, 15, 8158. [Google Scholar] [CrossRef]
- Sayed, M.M.; Mahdy, M.Y.; Abdel Aleem, S.H.; Youssef, H.K.; Boghdady, T.A. Simultaneous Distribution Network Reconfiguration and Optimal Allocation of Renewable-Based Distributed Generators and Shunt Capacitors under Uncertain Conditions. Energies 2022, 15, 2299. [Google Scholar] [CrossRef]
- Tang, J.; Chen, X.; Zhu, X.; Zhu, F. Dynamic reallocation model of multiple unmanned aerial vehicle tasks in emergent adjustment scenarios. IEEE Trans. Aerosp. Electron. Syst. 2022, 59, 1139–1155. [Google Scholar] [CrossRef]
- Liu, Y.; Gu, X. Skeleton-network reconfiguration based on topological characteristics of scale-free networks and discrete particle swarm optimization. IEEE Trans. Power Syst. 2007, 22, 1267–1274. [Google Scholar] [CrossRef]
- Zhang, X.; Fu, X.; Xue, Y.; Chang, X.; Bai, X. A review on basic theory and technology of agricultural energy internet. IET Renew. Power Gener. 2023. [Google Scholar] [CrossRef]
- Fu, X.; Zhou, Y. Collaborative optimization of PV greenhouses and clean energy systems in rural areas. IEEE Trans. Sustain. Energy 2022, 14, 642–656. [Google Scholar] [CrossRef]
- Zin, A.A.M.; Ferdavani, A.K.; Khairuddin, A.B.; Naeini, M.M. Reconfiguration of radial electrical distribution network through minimum-current circular-updating-mechanism method. IEEE Trans. Power Syst. 2011, 27, 968–974. [Google Scholar]
- Venkatesh, B.; Ranjan, R.; Gooi, H. Optimal reconfiguration of radial distribution systems to maximize loadability. IEEE Trans. Power Syst. 2004, 19, 260–266. [Google Scholar] [CrossRef]
- Tyagi, A.; Verma, A.; Bijwe, P. Reconfiguration for loadability limit enhancement of distribution systems. IET Gener. Transm. Distrib. 2018, 12, 88–93. [Google Scholar] [CrossRef]
- Aman, M.M.; Jasmon, G.B.; Bakar, A.H.A.; Mokhlis, H. Optimum network reconfiguration based on maximization of system loadability using continuation power flow theorem. Int. J. Electr. Power Energy Syst. 2014, 54, 123–133. [Google Scholar] [CrossRef]
- Aman, M.M.; Jasmon, G.B.; Bakar, A.H.A.; Mokhlis, H. A new approach for optimum simultaneous multi-DG distributed generation Units placement and sizing based on maximization of system loadability using HPSO (hybrid particle swarm optimization) algorithm. Energy 2014, 66, 202–215. [Google Scholar] [CrossRef]
- Latreche, Y.; Bouchekara, H.; Javaid, M.; Aman, M.; Mokhlis, H.; Kerrour, F. Optimal incorporation of multiple distributed generation units based on a new system maximum loadability computation approach and vortex searching algorithm. Int. J. Appl. Power Eng. (IJAPE) 2019, 8, 186–208. [Google Scholar] [CrossRef][Green Version]
- Raut, U.; Mishra, S. An improved Elitist–Jaya algorithm for simultaneous network reconfiguration and DG allocation in power distribution systems. Renew. Energy Focus 2019, 30, 92–106. [Google Scholar] [CrossRef]
- Quadri, I.A.; Bhowmick, S.; Joshi, D. Multi-objective approach to maximise loadability of distribution networks by simultaneous reconfiguration and allocation of distributed energy resources. IET Gener. Transm. Distrib. 2018, 12, 5700–5712. [Google Scholar] [CrossRef]
- Hemmatpour, M.H.; Mohammadian, M.; Gharaveisi, A.A. Optimum islanded microgrid reconfiguration based on maximization of system loadability and minimization of power losses. Int. J. Electr. Power Energy Syst. 2016, 78, 343–355. [Google Scholar] [CrossRef]
- Abbasi, M. Simultaneous Power Network Reconfiguration and DG Allocation Using Improved Jaya Algorithm for Maximum Loadability Improvement and Power Loss Reduction. Comput. Res. Prog. Appl. Sci. Eng. 2021, 7, 2310. [Google Scholar]
- Bernardon, D.; Mello, A.; Pfitscher, L.; Canha, L.; Abaide, A.; Ferreira, A. Real-time reconfiguration of distribution network with distributed generation. Electr. Power Syst. Res. 2014, 107, 59–67. [Google Scholar] [CrossRef]
- Koutsoukis, N.C.; Siagkas, D.O.; Georgilakis, P.S.; Hatziargyriou, N.D. Online reconfiguration of active distribution networks for maximum integration of distributed generation. IEEE Trans. Autom. Sci. Eng. 2016, 14, 437–448. [Google Scholar] [CrossRef]
- Yin, Z.; Ji, X.; Zhang, Y.; Liu, Q.; Bai, X. Data-driven approach for real-time distribution network reconfiguration. IET Gener. Transm. Distrib. 2020, 14, 2450–2463. [Google Scholar] [CrossRef]
- Masteri, K.; Venkatesh, B. Real-time smart distribution system reconfiguration using complementarity. Electr. Power Syst. Res. 2016, 134, 97–104. [Google Scholar] [CrossRef]
- Shukla, J.; Das, B.; Pant, V. Consideration of small signal stability in multi-objective DS reconfiguration in the presence of distributed generation. IET Gener. Transm. Distrib. 2017, 11, 236–245. [Google Scholar] [CrossRef]
- Fetouh, T.; Elsayed, A.M. Optimal control and operation of fully automated distribution networks using improved tunicate swarm intelligent algorithm. IEEE Access 2020, 8, 129689–129708. [Google Scholar] [CrossRef]
- Xing, H.; Hong, S. Ordinal optimisation approach for complex distribution network reconfiguration. J. Eng. 2019, 2019, 5055–5058. [Google Scholar] [CrossRef]
- Venkaiah, C.; Jain, R.V. Multi-objective JAYA algorithm based optimal location and sizing of distributed generation in a radial distribution system. In Proceedings of the 2017 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Bangalore, India, 8–10 November 2017; IEEE: New York, NY, USA, 2017; pp. 1–6. [Google Scholar]
- Saaty, R.W. The analytic hierarchy process—What it is and how it is used. Math. Model. 1987, 9, 161–176. [Google Scholar] [CrossRef]
- Wilson, B.M.R.; Khazaei, B.; Hirsch, L. Cloud adoption decision support for SMEs using Analytical Hierarchy Process (AHP). In Proceedings of the 2016 IEEE 4th Workshop on Advances in Information, Electronic and Electrical Engineering (AIEEE), Vilnius, Lithuania, 10–12 November 2016; IEEE: New York, NY, USA, 2016; pp. 1–4. [Google Scholar]
- Gandomi, A.H.; Yang, X.-S.; Alavi, A.H. Mixed variable structural optimization using firefly algorithm. Comput. Struct. 2011, 89, 2325–2336. [Google Scholar] [CrossRef]
- Yang, X. Nature-Inspired Metaheuristic Algorithms. 2010. Firefly Algorithm; Luniver Press: Bristol, UK, 2011; pp. 79–90. [Google Scholar]
- Liang, R.-H.; Wang, J.-C.; Chen, Y.-T.; Tseng, W.-T. An enhanced firefly algorithm to multi-objective optimal active/reactive power dispatch with uncertainties consideration. Int. J. Electr. Power Energy Syst. 2015, 64, 1088–1097. [Google Scholar] [CrossRef]
- Yang, X.-S. Firefly Algorithms for Multimodal Optimization, International Symposium on Stochastic Algorithms, 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 169–178. [Google Scholar]
- Eberhart, R.; Kennedy, J. In A new optimizer using particle swarm theory, MHS’95. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; IEEE: New York, NY, USA, 1995; pp. 39–43. [Google Scholar]
- Balakrishna, G.; Babu, C.S. Particle swarm optimization based network reconfiguration in distribution system with distributed generation and capacitor placement. Int. J. Eng. Sci. 2014, 3, 55–60. [Google Scholar]
- Badran, O.; Mekhilef, S.; Mokhlis, H.; Dahalan, W. Optimal reconfiguration of distribution system connected with distributed generations: A review of different methodologies. Renew. Sustain. Energy Rev. 2017, 73, 854–867. [Google Scholar] [CrossRef]
- Bouchekara, H. Comprehensive Review of Radial Distribution Test Systems; Authorea: Hoboken, NJ, USA, 2020. [Google Scholar]
- Savier, J.; Das, D. Impact of network reconfiguration on loss allocation of radial distribution systems. IEEE Trans. Power Deliv. 2007, 22, 2473–2480. [Google Scholar] [CrossRef]
- Rao, R.S.; Ravindra, K.; Satish, K.; Narasimham, S. Power loss minimization in distribution system using network reconfiguration in the presence of distributed generation. IEEE Trans. Power Syst. 2012, 28, 317–325. [Google Scholar] [CrossRef]
- Imran, A.M.; Kowsalya, M.; Kothari, D. A novel integration technique for optimal network reconfiguration and distributed generation placement in power distribution networks. Int. J. Electr. Power Energy Syst. 2014, 63, 461–472. [Google Scholar] [CrossRef]
- Badran, O.; Mokhlis, H.; Mekhilef, S.; Dahalan, W. Multi-Objective network reconfiguration with optimal DG output using meta-heuristic search algorithms. Arab. J. Sci. Eng. 2018, 43, 2673–2686. [Google Scholar] [CrossRef]
- Haider, W.; Hassan, S.J.U.; Mehdi, A.; Hussain, A.; Adjayeng, G.O.M.; Kim, C.-H. Voltage profile enhancement and loss minimization using optimal placement and sizing of distributed generation in reconfigured network. Machines 2021, 9, 20. [Google Scholar] [CrossRef]
- Raut, U.; Mishra, S. An improved sine–cosine algorithm for simultaneous network reconfiguration and DG allocation in power distribution systems. Appl. Soft Comput. 2020, 92, 106293. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).