Enhancing the Power Performance of Latent Heat Thermal Energy Storage Systems: The Adoption of Passive, Fractal Supports
Abstract
:1. Introduction
- Realization of optimized blends of PCMs: blends can be formulated in the attempt to get the desired PCM thermal properties to better suit the designed application [10];
- Adoption of highly conductive thermal supports: realized in the forms of fins, blades, heat pipes, and foams [11]. Their exploitation strongly enhances thermal conductivity (>200×, when embedding the PCM in porous graphite [12,13]), but can lead to detachment phenomena between the PCM and the thermal support. This phenomenon is due to the volumetric variation during melting/solidification and causes poor performance in repeated cycles [14];
- Addition of micro-/nano-particles: the adoption of micro/nano-particles, nano-fibers, nano-tubes, and other nano-scale fillers can actually provide remarkable enhancements in specific heat, thermal conductivity, and thermal diffusivity (pristine graphene allows an increase in thermal conductivity up to [15,16]);
2. Materials and Methods
- is a relaxation parameter, chosen to be on the order of 0.5 to ensure that the relaxation of is faster than the other dynamics;
- is the non-dimensional Stefan number, given by , with the specific heat and the latent heat;
- is the characteristic temperature difference: we fix , as in [7].
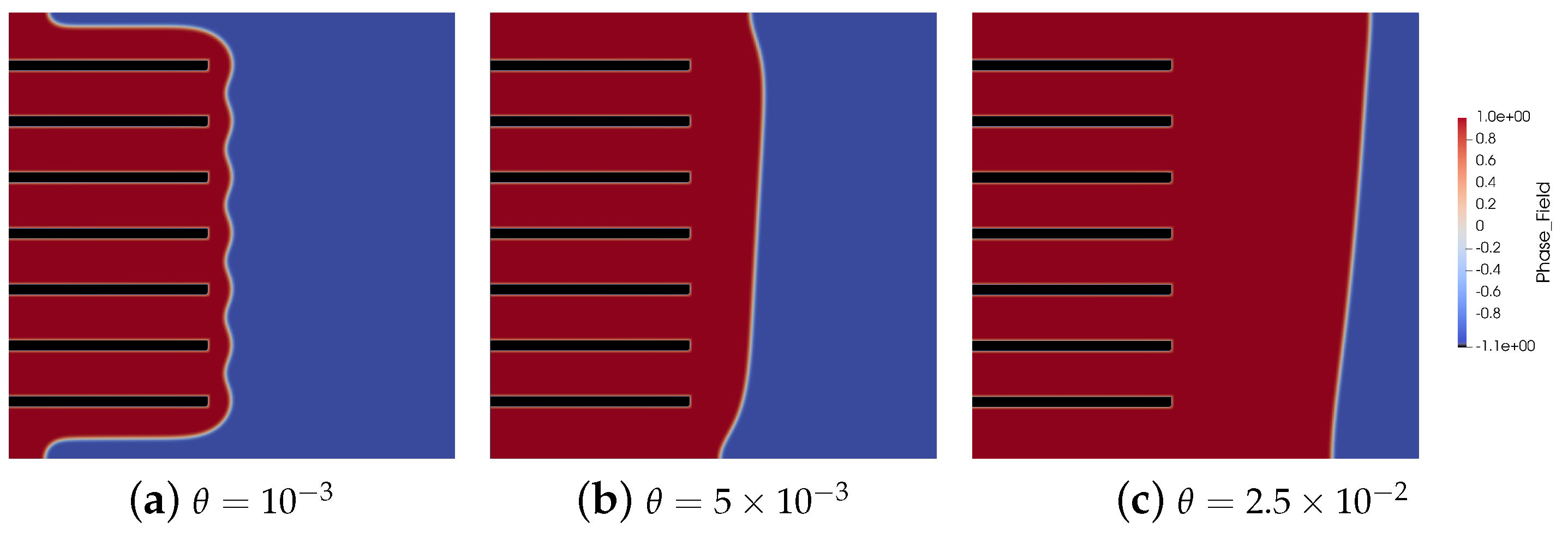
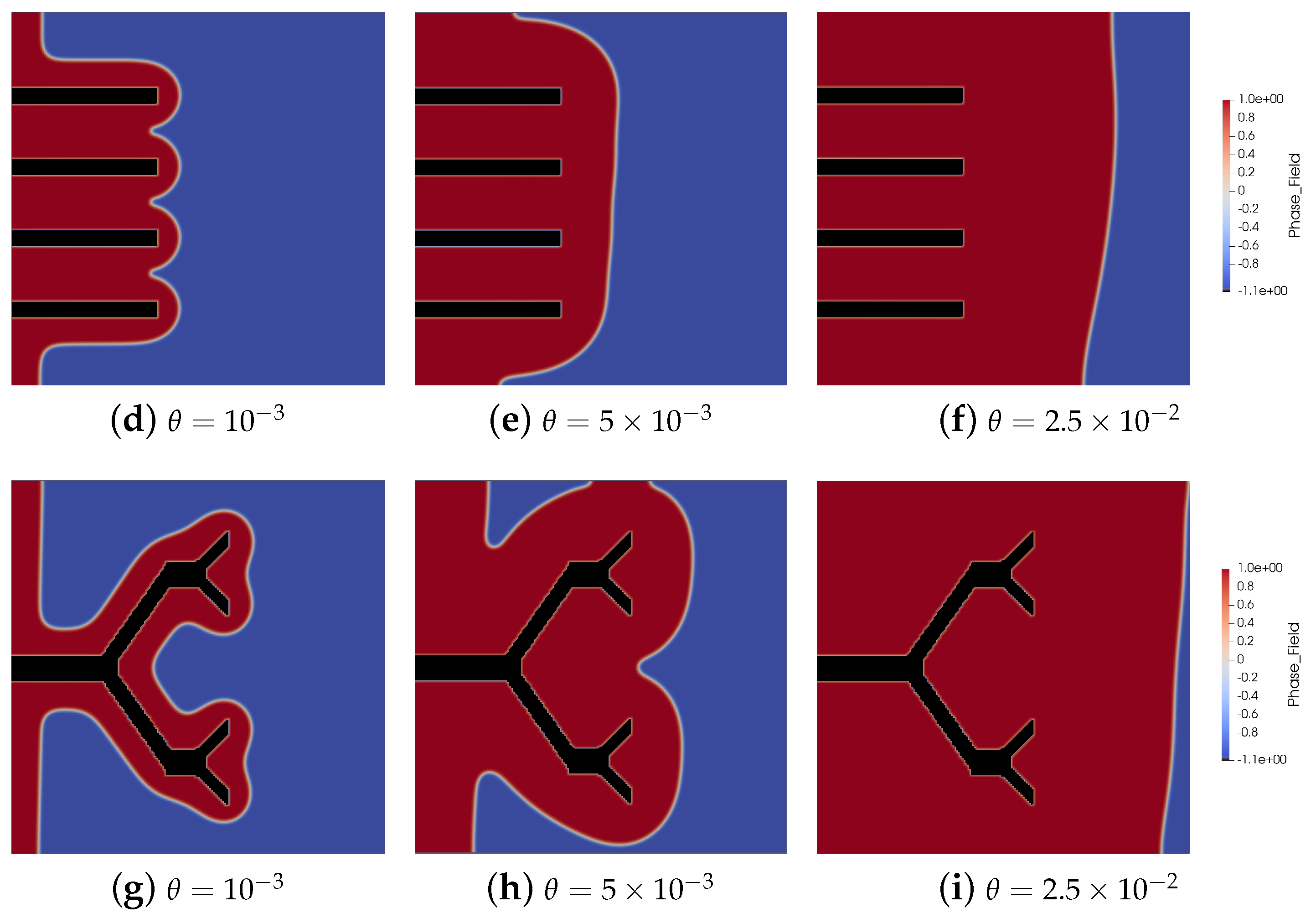
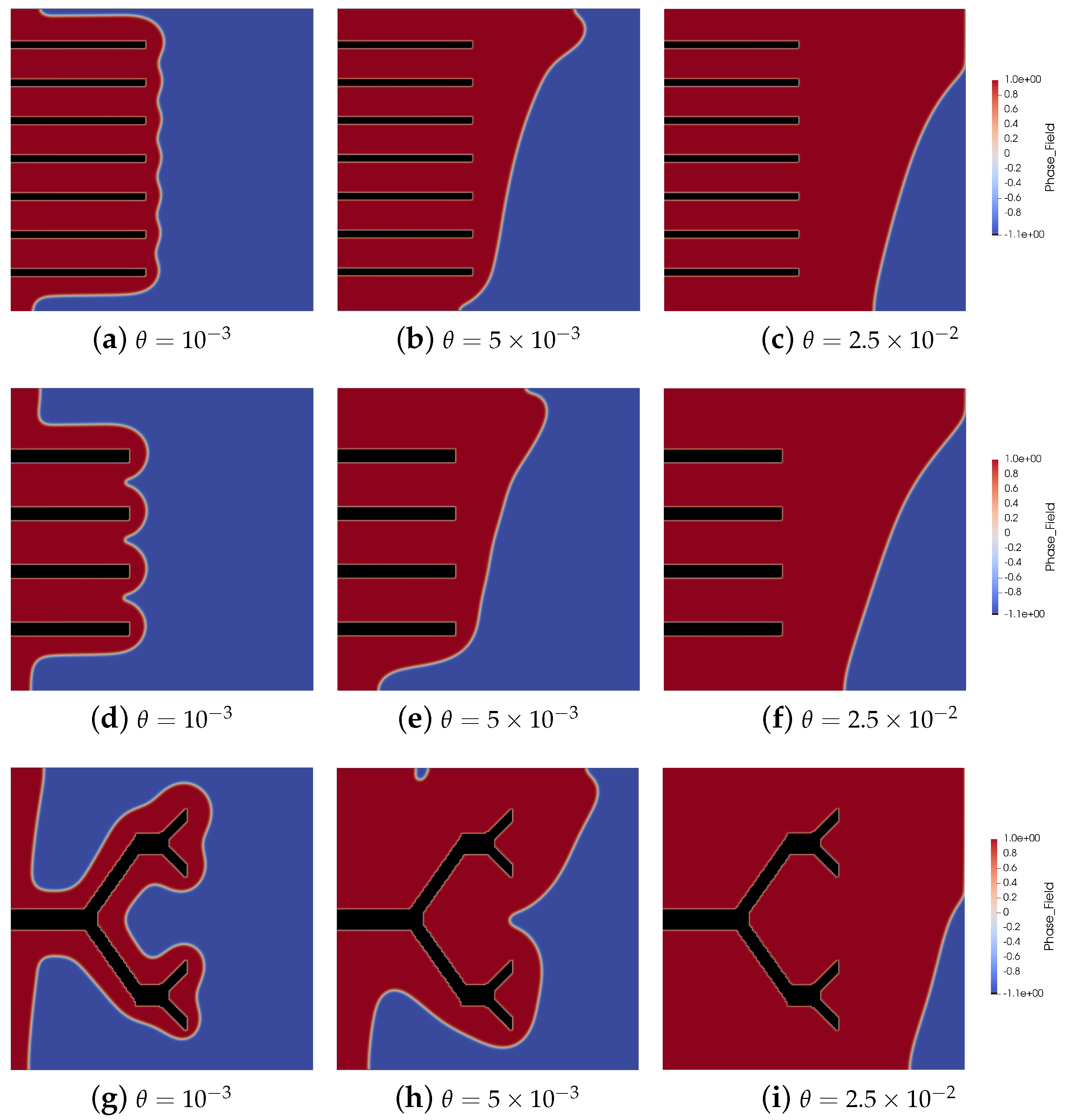
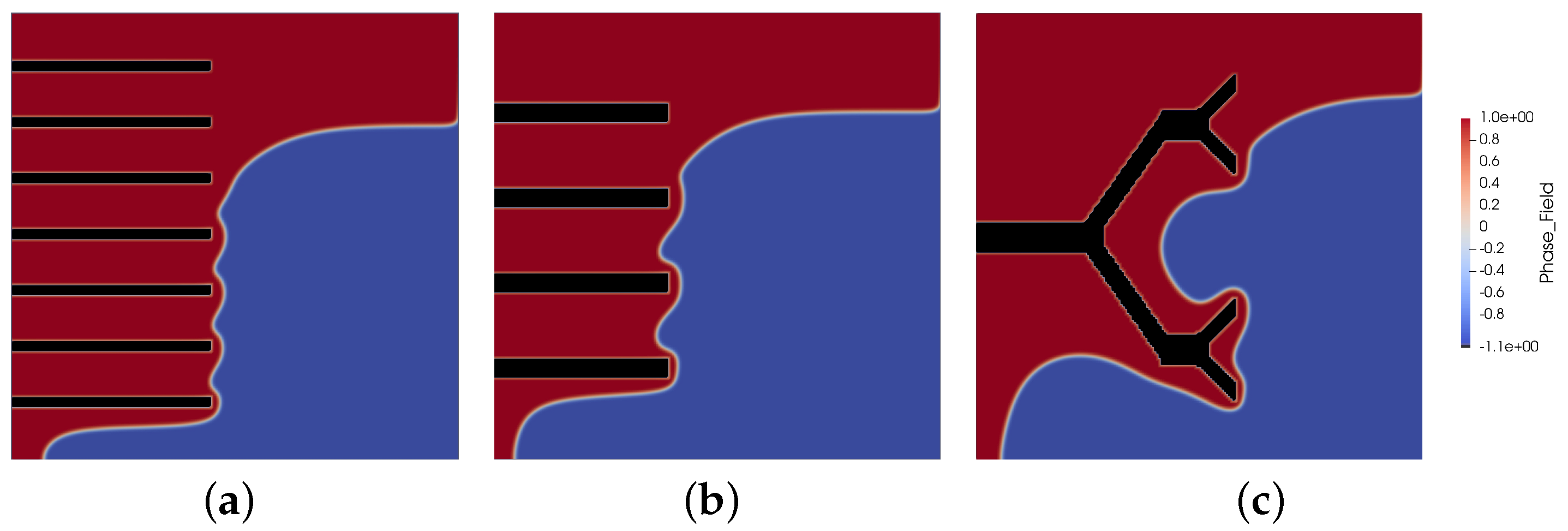
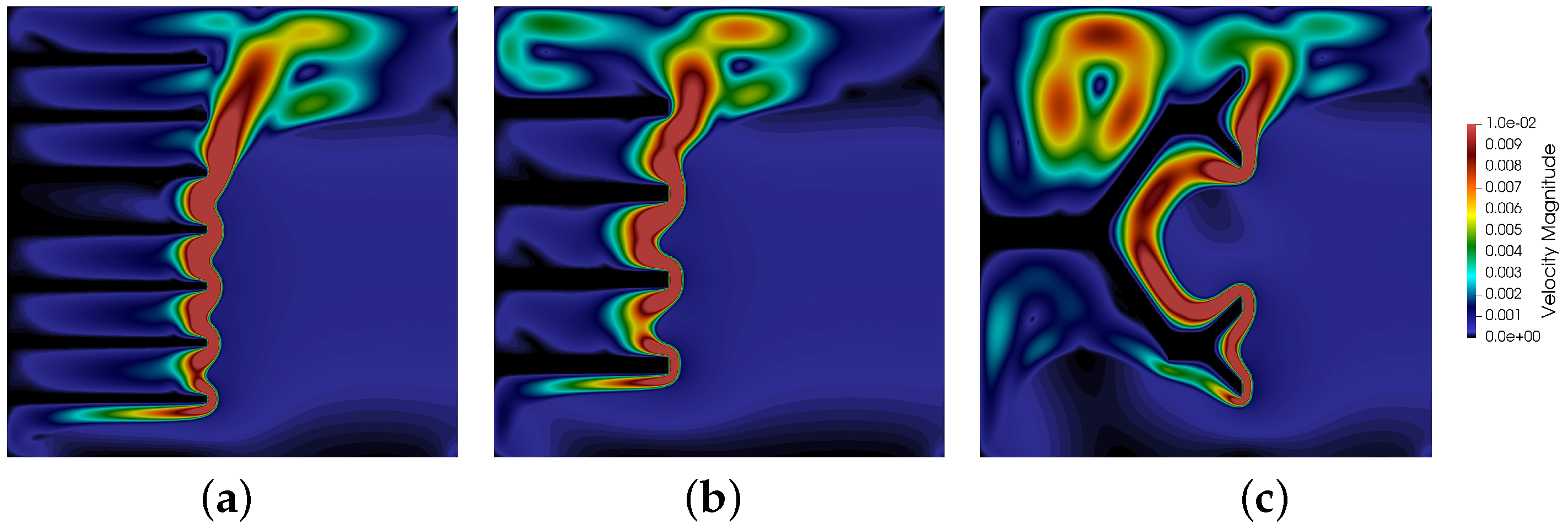
3. Validation, Results, and Discussion
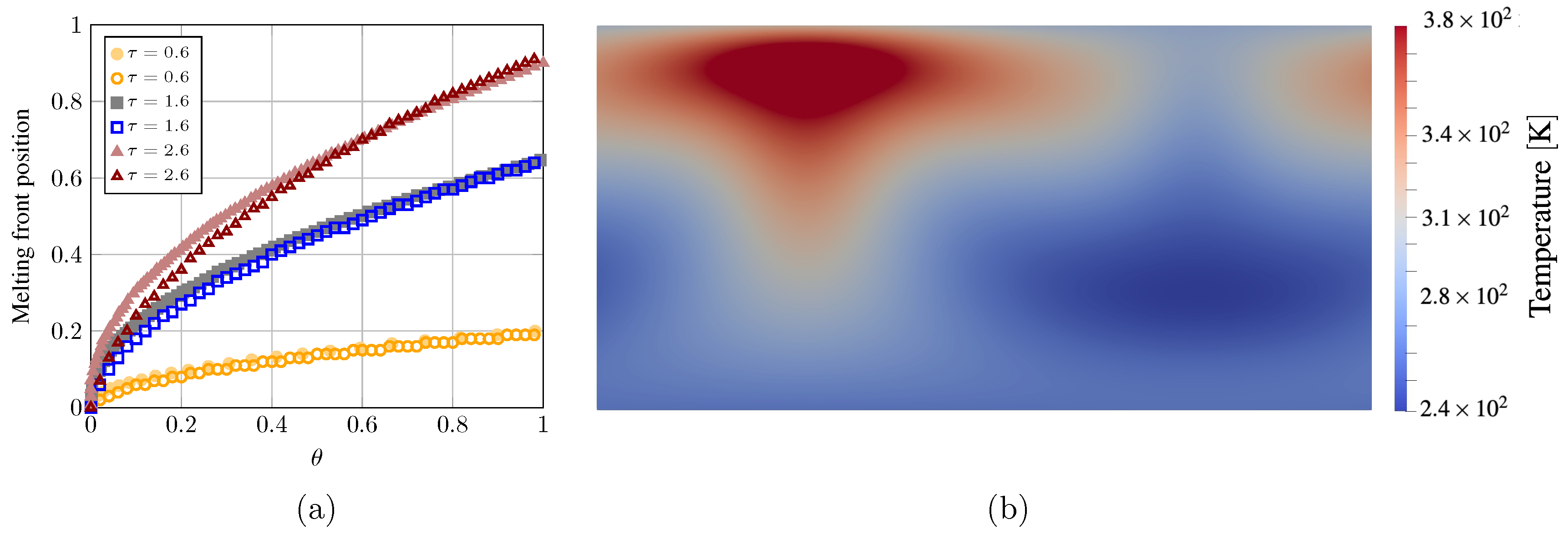
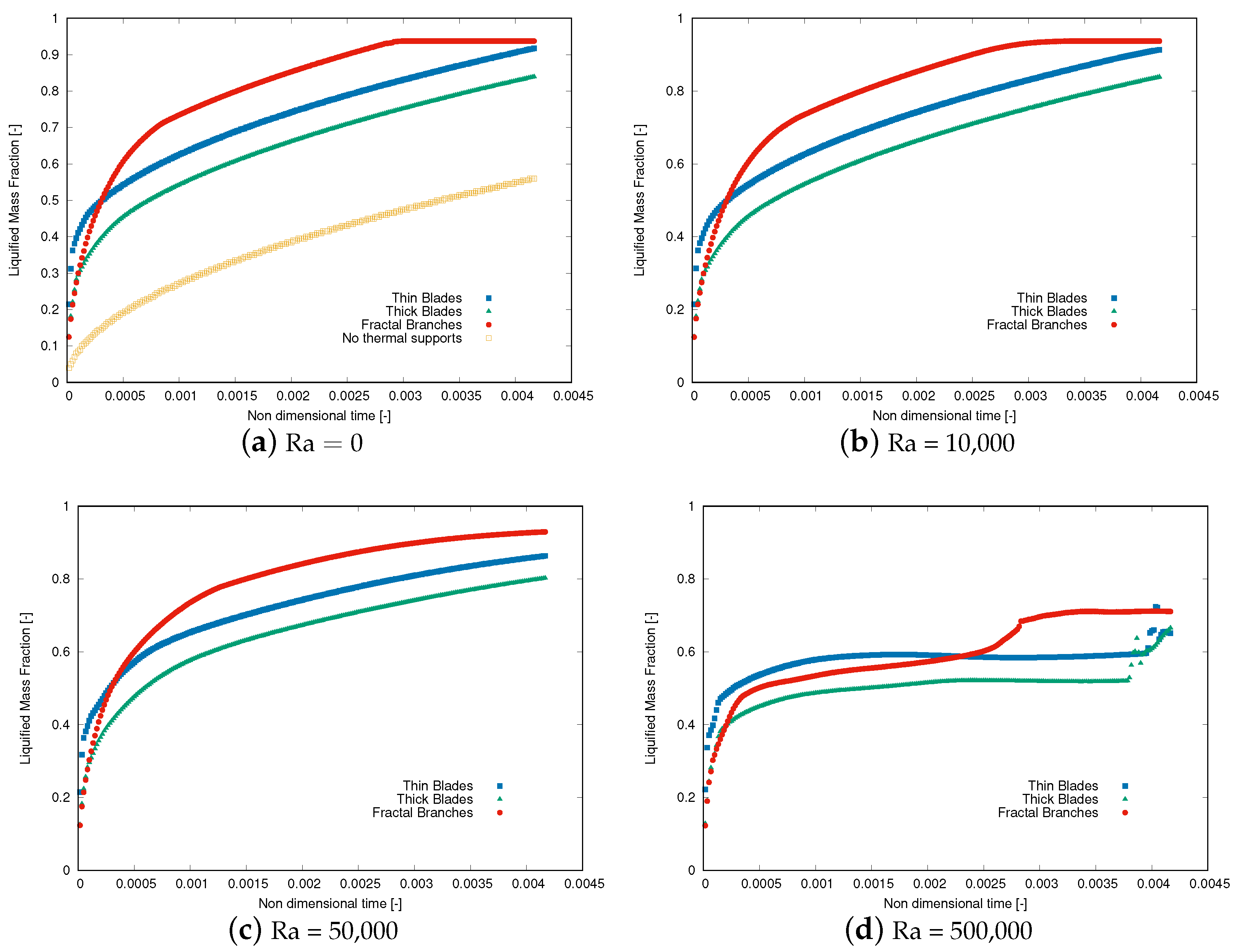
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mahon, H.; O’Connor, D.; Friedrich, D.; Hughes, B. A review of thermal energy storage technologies for seasonal loops. Energy 2022, 239, 122207. [Google Scholar] [CrossRef]
- IEA. Renewables. 2019. Available online: https://www.iea.org/reports/renewables-2019 (accessed on 22 February 2023).
- Gutierrez, A.; Miró, L.; Gil, A.; Rodríguez-Aseguinolaza, J.; Barreneche, C.; Calvet, N.; Py, X.; Fernández, A.I.; Grágeda, M.; Ushak, S.; et al. Advances in the valorization of waste and by-product materials as thermal energy storage (TES) materials. Renew. Sustain. Energy Rev. 2016, 59, 763–783. [Google Scholar] [CrossRef]
- Sadeghi, G. Energy storage on demand: Thermal energy storage development, materials, design, and integration challenges. Energy Storage Mater. 2022, 46, 192–222. [Google Scholar] [CrossRef]
- Gunasekara, S.N.; Barreneche, C.; Inés Fernández, A.; Calderón, A.; Ravotti, R.; Ristić, A.; Weinberger, P.; Ömur Paksoy, H.; Koçak, B.; Rathgeber, C.; et al. Thermal energy storage materials (TESMs)—What does it take to make them fly? Crystals 2021, 11, 1276. [Google Scholar] [CrossRef]
- Guo, S.; Liu, Q.; Zhao, J.; Jin, G.; Wu, W.; Yan, J.; Li, H.; Jin, H. Mobilized thermal energy storage: Materials, containers and economic evaluation. Energy Convers. Manag. 2018, 177, 315–329. [Google Scholar] [CrossRef]
- Facci, A.L.; Lauricella, M.; Succi, S.; Villani, V.; Falcucci, G. Optimized modeling and design of a PCM-enhanced H2 storage. Energies 2021, 14, 1554. [Google Scholar] [CrossRef]
- Cabeza, L.F.; Castell, A.; Barreneche, C.d.; De Gracia, A.; Fernández, A. Materials used as PCM in thermal energy storage in buildings: A review. Renew. Sustain. Energy Rev. 2011, 15, 1675–1695. [Google Scholar] [CrossRef]
- Cabeza, L.F. Advances in thermal energy storage systems: Methods and applications. In Advances in Thermal Energy Storage Systems; Elsevier: Amsterdam, The Netherlands, 2021; pp. 37–54. [Google Scholar]
- Nazir, H.; Batool, M.; Osorio, F.J.B.; Isaza-Ruiz, M.; Xu, X.; Vignarooban, K.; Phelan, P.; Kannan, A.M. Recent developments in phase change materials for energy storage applications: A review. Int. J. Heat Mass Transf. 2019, 129, 491–523. [Google Scholar] [CrossRef]
- Mahdi, J.M.; Lohrasbi, S.; Nsofor, E.C. Hybrid heat transfer enhancement for latent-heat thermal energy storage systems: A review. Int. J. Heat Mass Transf. 2019, 137, 630–649. [Google Scholar] [CrossRef]
- Sedeh, M.M.; Khodadadi, J. Thermal conductivity improvement of phase change materials/graphite foam composites. Carbon 2013, 60, 117–128. [Google Scholar] [CrossRef]
- Wei, G.; Wang, G.; Xu, C.; Ju, X.; Xing, L.; Du, X.; Yang, Y. Selection principles and thermophysical properties of high temperature phase change materials for thermal energy storage: A review. Renew. Sustain. Energy Rev. 2018, 81, 1771–1786. [Google Scholar] [CrossRef]
- Almonti, D.; Mingione, E.; Tagliaferri, V.; Ucciardello, N. Design and analysis of compound structures integrated with bio-based phase change materials and lattices obtained through additive manufacturing. Int. J. Adv. Manuf. Technol. 2021, 119, 149–161. [Google Scholar] [CrossRef]
- Warzoha, R.J.; Fleischer, A.S. Effect of graphene layer thickness and mechanical compliance on interfacial heat flow and thermal conduction in solid–liquid phase change materials. ACS Appl. Mater. Interfaces 2014, 6, 12868–12876. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Mu, B. Effect of different dimensional carbon materials on the properties and application of phase change materials: A review. Appl. Energy 2019, 242, 695–715. [Google Scholar] [CrossRef]
- Sarbu, I.; Dorca, A. Review on heat transfer analysis in thermal energy storage using latent heat storage systems and phase change materials. Int. J. Energy Res. 2019, 43, 29–64. [Google Scholar] [CrossRef]
- Succi, S. The Lattice Boltzmann Equation for Fluid Dynamics and Beyond; Clarendon: Oxford, UK, 2001. [Google Scholar]
- Krüger, T.; Kusumaatmaja, H.; Kuzmin, A.; Shardt, O.; Silva, G.; Viggen, E.M. The Lattice Boltzmann Method; Springer: Berlin/Heidelberg, Germany, 2017; Volume 10, pp. 978–983. [Google Scholar]
- Miller, W.; Succi, S.; Mansutti, D. Lattice Boltzmann model for anisotropic liquid-solid phase transition. Phys. Rev. Lett. 2001, 86, 3578. [Google Scholar] [CrossRef]
- Falcucci, G.; Amati, G.; Fanelli, P.; Krastev, V.K.; Polverino, G.; Porfiri, M.; Succi, S. Extreme flow simulations reveal skeletal adaptations of deep-sea sponges. Nature 2021, 595, 537–541. [Google Scholar] [CrossRef]
- Falcucci, G.; Polverino, G.; Porfiri, M.; Amati, G.; Fanelli, P.; Krastev, V.K.; Succi, S. Reply to: Models of flow through sponges must consider the sponge tissue. Nature 2022, 603, E26–E28. [Google Scholar] [CrossRef]
- Krastev, V.; Falcucci, G. Simulating engineering flows through complex porous media via the lattice Boltzmann method. Energies 2018, 11, 715. [Google Scholar] [CrossRef]
- Falcucci, G.; Chiatti, G.; Succi, S.; Mohamad, A.A.; Kuzmin, A. Rupture of a ferrofluid droplet in external magnetic fields using a single-component lattice Boltzmann model for nonideal fluids. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2009, 79, 056706. [Google Scholar] [CrossRef]
- Sbragaglia, M.; Benzi, R.; Biferale, L.; Succi, S.; Sugiyama, K.; Toschi, F. Generalized lattice Boltzmann method with multirange pseudopotential. Phys. Rev. E 2007, 75, 026702. [Google Scholar] [CrossRef] [PubMed]
- Falcucci, G.; Bella, G.; Chiatti, G.; Chibbaro, S.; Sbragaglia, M.; Succi, S. Lattice Boltzmann Models with Mid-Range Interactions. Comm. Comput. Phys. 2007, 2, 1071–1084. [Google Scholar]
- Colosqui, C.E.; Falcucci, G.; Ubertini, S.; Succi, S. Mesoscopic simulation of non-ideal fluids with self-tuning of the equation of state. Soft Matter 2012, 8, 3798–3809. [Google Scholar] [CrossRef]
- Huber, C.; Parmigiani, A.; Chopard, B.; Manga, M.; Bachmann, O. Lattice Boltzmann model for melting with natural convection. Int. J. Heat Fluid Flow 2008, 29, 1469–1480. [Google Scholar] [CrossRef]
- Pareschi, G.; Frapolli, N.; Chikatamarla, S.S.; Karlin, I.V. Conjugate heat transfer with the entropic lattice Boltzmann method. Phys. Rev. E 2016, 94, 013305. [Google Scholar] [CrossRef]
- Chiappini, D.; Donno, A. A comparison between different fractal grid generation methods coupled with lattice Boltzmann approach. AIP Conf. Proc. 2016, 1738, 270003. [Google Scholar]
- Chiappini, D. A coupled lattice Boltzmann-finite volume method for phase change material analysis. Int. J. Therm. Sci. 2021, 164, 106893. [Google Scholar] [CrossRef]
- Wu, S.; Yan, T.; Kuai, Z.; Pan, W. Thermal conductivity enhancement on phase change materials for thermal energy storage: A review. Energy Storage Mater. 2020, 25, 251–295. [Google Scholar] [CrossRef]
- Joshi, V.; Rathod, M.K. Experimental and numerical assessments of thermal transport in fins and metal foam infused latent heat thermal energy storage systems: A comparative evaluation. Appl. Therm. Eng. 2020, 178, 115518. [Google Scholar] [CrossRef]
- Li, J.; Zheng, Y.; Liu, X. Enhancing discharging performance of a phase change thermal storage unit with a fractal space-filling matrix. J. Renew. Sustain. Energy 2021, 13, 014102. [Google Scholar] [CrossRef]
- Yu, C.; Wu, S.; Huang, Y.; Yao, F.; Liu, X. Charging performance optimization of a latent heat storage unit with fractal tree-like fins. J. Energy Storage 2020, 30, 101498. [Google Scholar] [CrossRef]
- Succi, S. The Lattice Boltzmann Equation: For Complex States of Flowing Matter; Oxford University Press: Oxford, UK, 2018. [Google Scholar]
- Ben Ltaifa, K.; D’Orazio, A.; Dhahri, H. Numerical analysis of mixed convection heat transfer and laminar flow in a rectangular inclined micro-channel totally filled with Water/Al2O3 Nano fluid. J. Therm. Anal. Calorim. 2021, 144, 2465–2482. [Google Scholar] [CrossRef]
- Miller, W.; Succi, S. A lattice Boltzmann model for anisotropic crystal growth from melt. J. Stat. Phys. 2002, 107, 173–186. [Google Scholar] [CrossRef]
- D’Orazio, A.; Karimipour, A.; Mosavi, A. Develop lattice Boltzmann method and its related boundary conditions models for the benchmark oscillating walls by modifying hydrodynamic and thermal distribution functions. Eur. Phys. J. Plus 2020, 135, 915. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Hydrodynamic and Hydromagnetic Stability; Courier Corporation: Chelmsford, MA, USA, 2013. [Google Scholar]
- Chaabane, R.; Kolsi, L.; Jemni, A.; Alshammari, N.K.; D’Orazio, A. Numerical study of the Rayleigh–Bénard convection in two-dimensional cavities heated by elliptical heat sources using the lattice Boltzmann method. Phys. Fluids 2021, 33, 123605. [Google Scholar] [CrossRef]
- Pelusi, F.; Lulli, M.; Sbragaglia, M.; Bernaschi, M. TLBfind: A Thermal Lattice Boltzmann code for concentrated emulsions with FINite-size Droplets. Comput. Phys. Commun. 2022, 273, 108259. [Google Scholar] [CrossRef]
- Jany, P.; Bejan, A. Scaling theory of melting with natural convection in an enclosure. Int. J. Heat Mass Transf. 1988, 31, 1221–1235. [Google Scholar] [CrossRef]
- Bertrand, O.; Binet, B.; Combeau, H.; Couturier, S.; Delannoy, Y.; Gobin, D.; Lacroix, M.; Le Quéré, P.; Médale, M.; Mencinger, J.; et al. Melting driven by natural convection A comparison exercise: First results. Int. J. Therm. Sci. 1999, 38, 5–26. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amati, G.; Succi, S.; Falcucci, G. Enhancing the Power Performance of Latent Heat Thermal Energy Storage Systems: The Adoption of Passive, Fractal Supports. Energies 2023, 16, 6764. https://doi.org/10.3390/en16196764
Amati G, Succi S, Falcucci G. Enhancing the Power Performance of Latent Heat Thermal Energy Storage Systems: The Adoption of Passive, Fractal Supports. Energies. 2023; 16(19):6764. https://doi.org/10.3390/en16196764
Chicago/Turabian StyleAmati, Giorgio, Sauro Succi, and Giacomo Falcucci. 2023. "Enhancing the Power Performance of Latent Heat Thermal Energy Storage Systems: The Adoption of Passive, Fractal Supports" Energies 16, no. 19: 6764. https://doi.org/10.3390/en16196764
APA StyleAmati, G., Succi, S., & Falcucci, G. (2023). Enhancing the Power Performance of Latent Heat Thermal Energy Storage Systems: The Adoption of Passive, Fractal Supports. Energies, 16(19), 6764. https://doi.org/10.3390/en16196764






