Mathematical Modeling of Alkaline Direct Glycerol Fuel Cells
Abstract
:1. Introduction
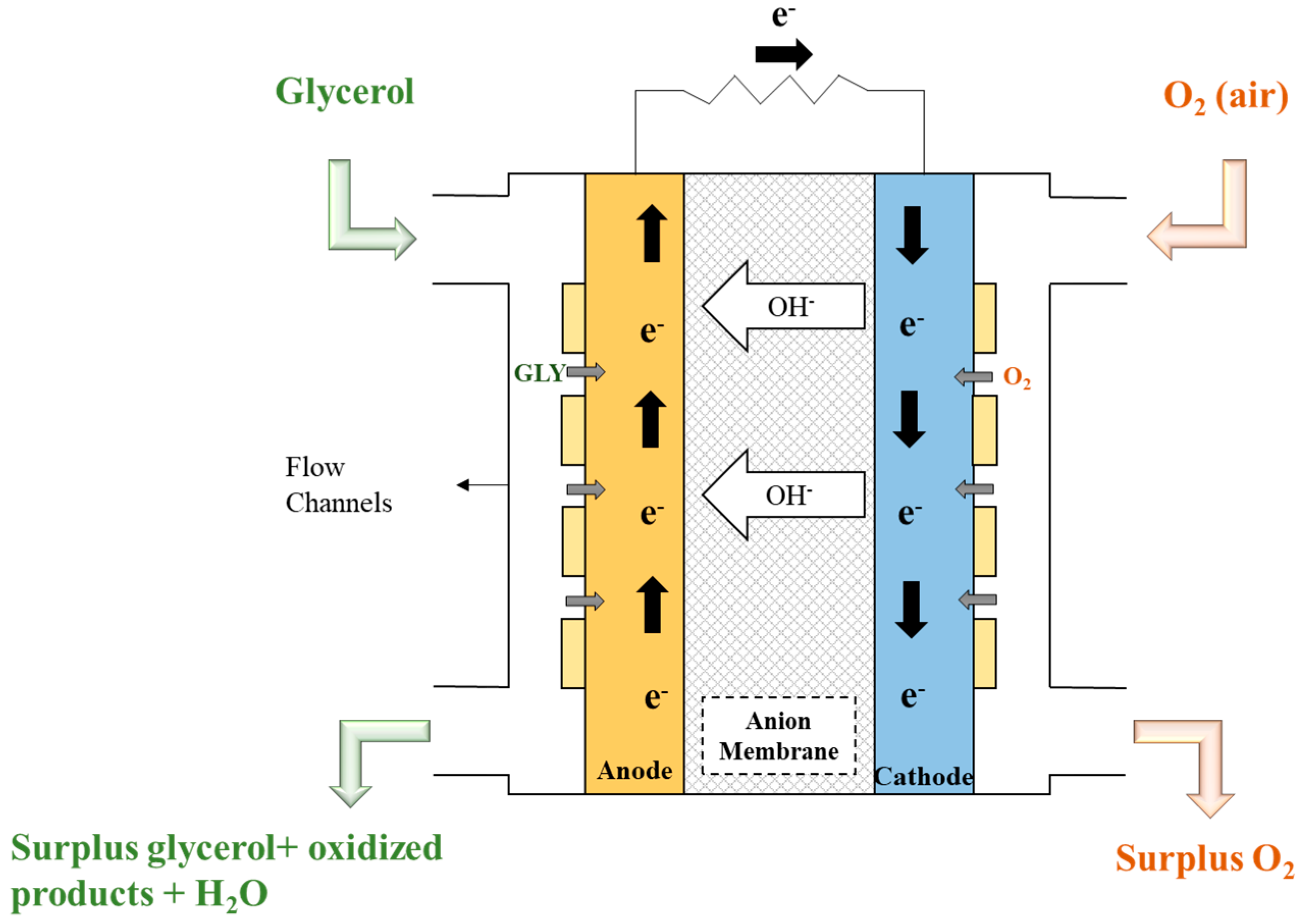
2. Materials and Methods
2.1. Realistic Phenomenological Model
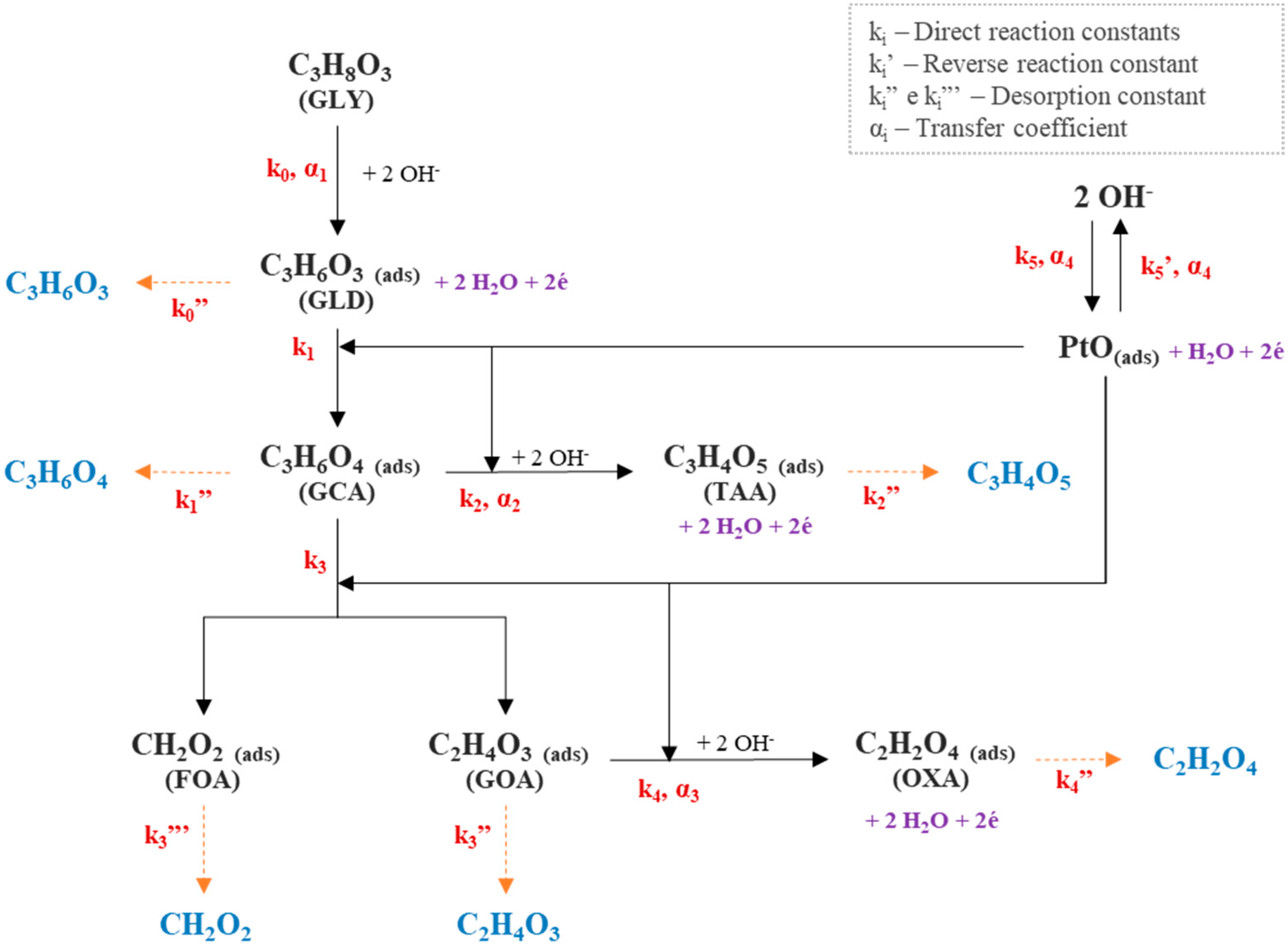
2.1.1. Complete Phenomenological Model at 60 °C
Calculation of Anodic Overpotential
Constraint Equations and Current Density Calculation
Nonlinear Regression with Constraints
Statistical Study of the Parameters
Determination of the Model Parameters with Greatest Influence
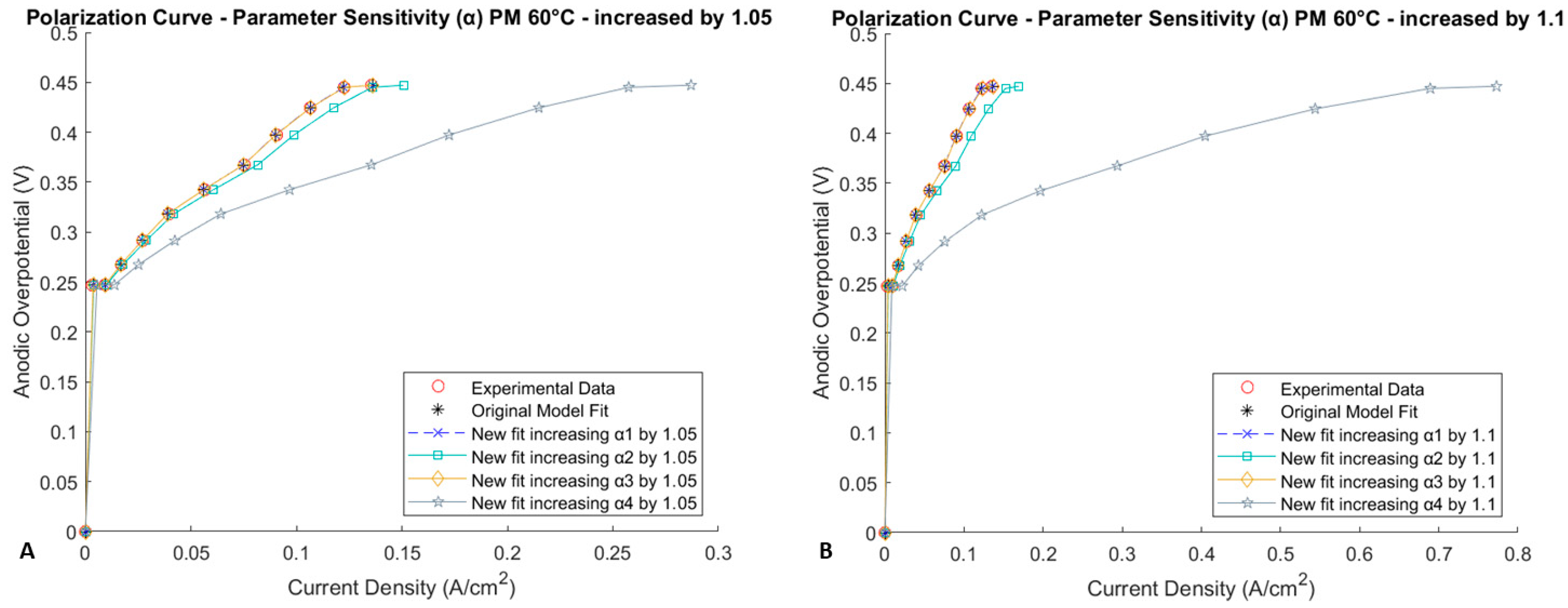
Parameter Sensitivity (Graphical Method)
Influence of the Most Significant Parameters on the Adsorbed Intermediates Distribution
- (a)
- The kinetic parameter values were fixed, with the most sensitive kinetic constants being multiplied by factors of 1.5, 5, and 10, while the other parameters, including the transfer coefficients, were fixed at their original values.
- (b)
- A new fitting of the polarization curve to the experimental data was performed (with changes from the original values by multiplying the most sensitive constants), only altering the values of the lower and upper limits and the initial estimates of the coverage fractions, in each operation of the algorithm, in order to minimize the SSE value.
- (c)
- This procedure was performed for each multiplication factor, finally comparing the coverage fraction distributions obtained.
2.1.2. Additional Mechanistic Models Developed
Simplified Phenomenological Models 1 and 2
Phenomenological Model at 90 °C
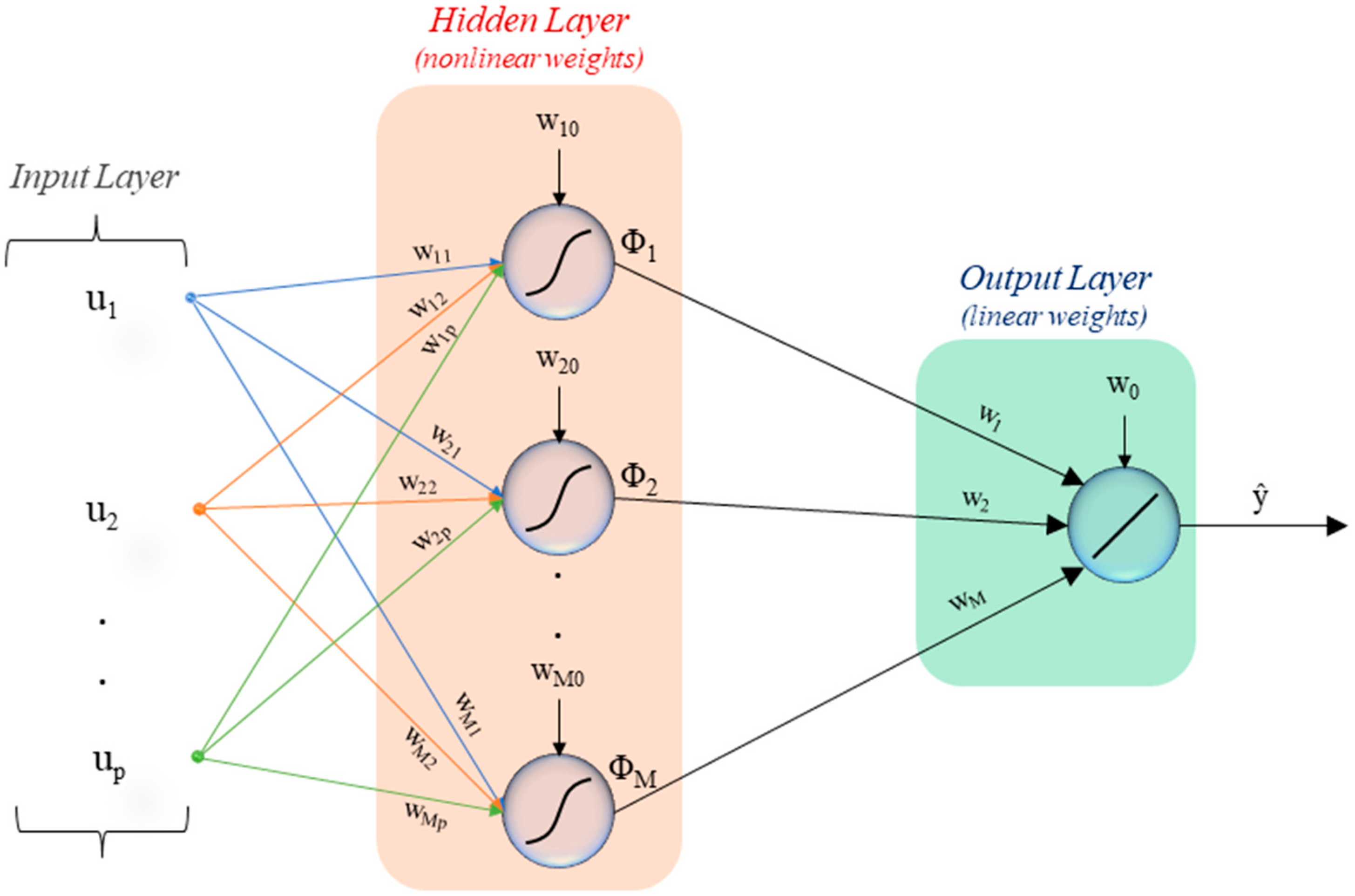
2.2. Artificial Neural Networks
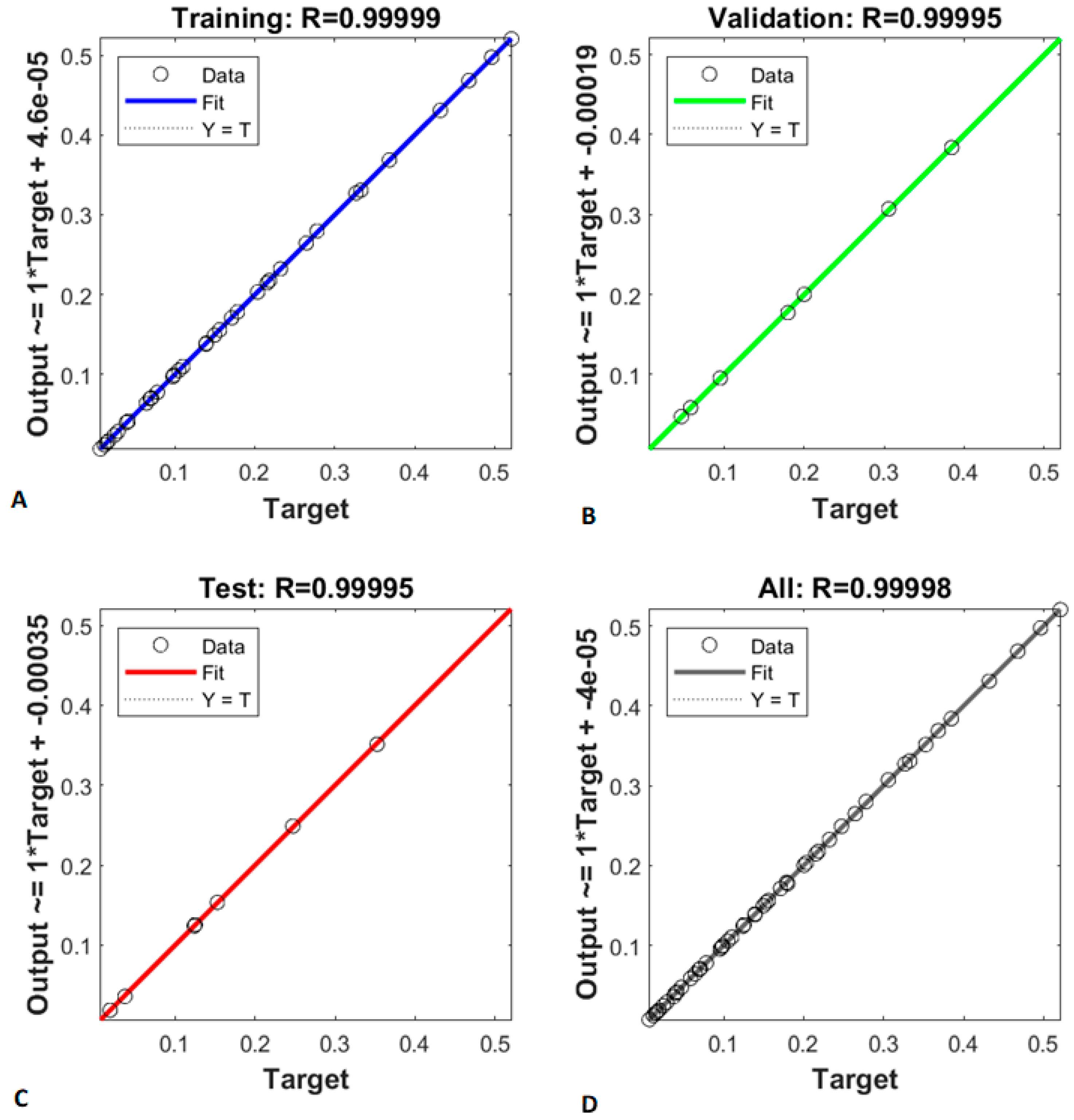
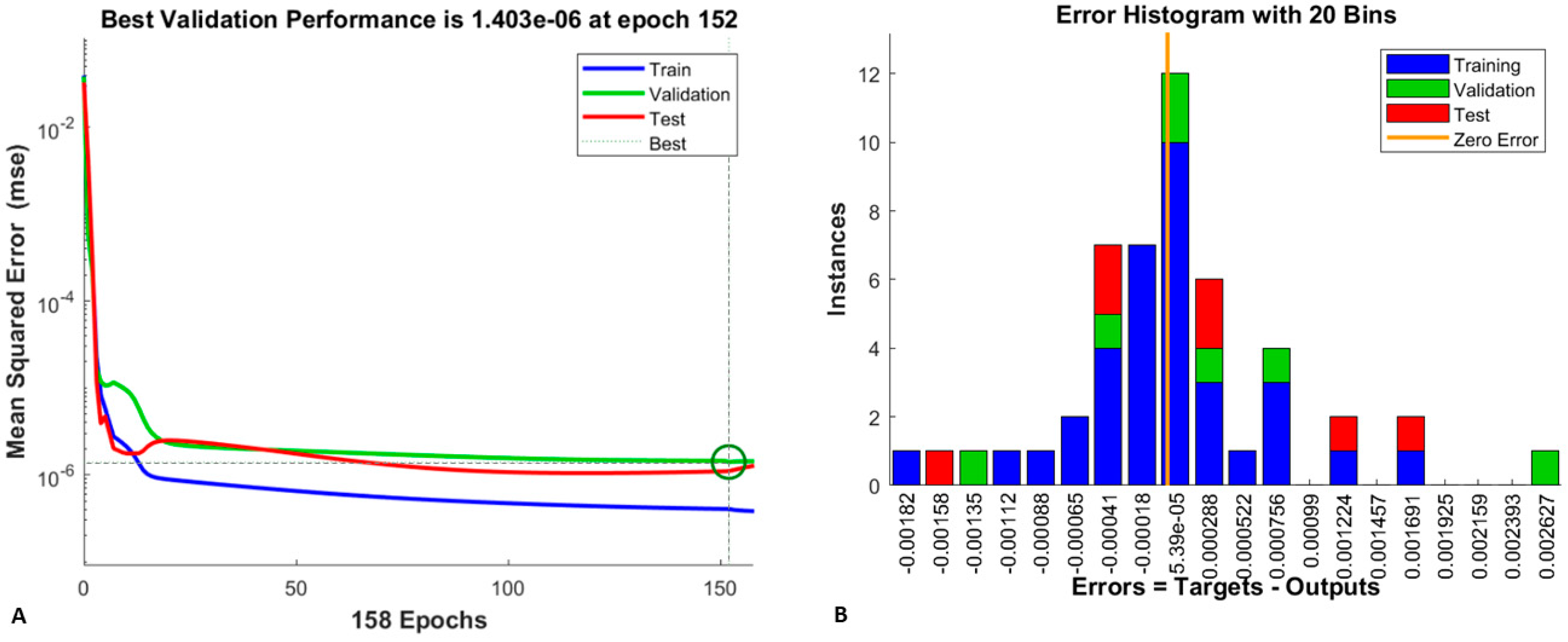
2.2.1. Training, Validation, and Testing of the Neural Network
2.2.2. Neural Network Performance Assessment
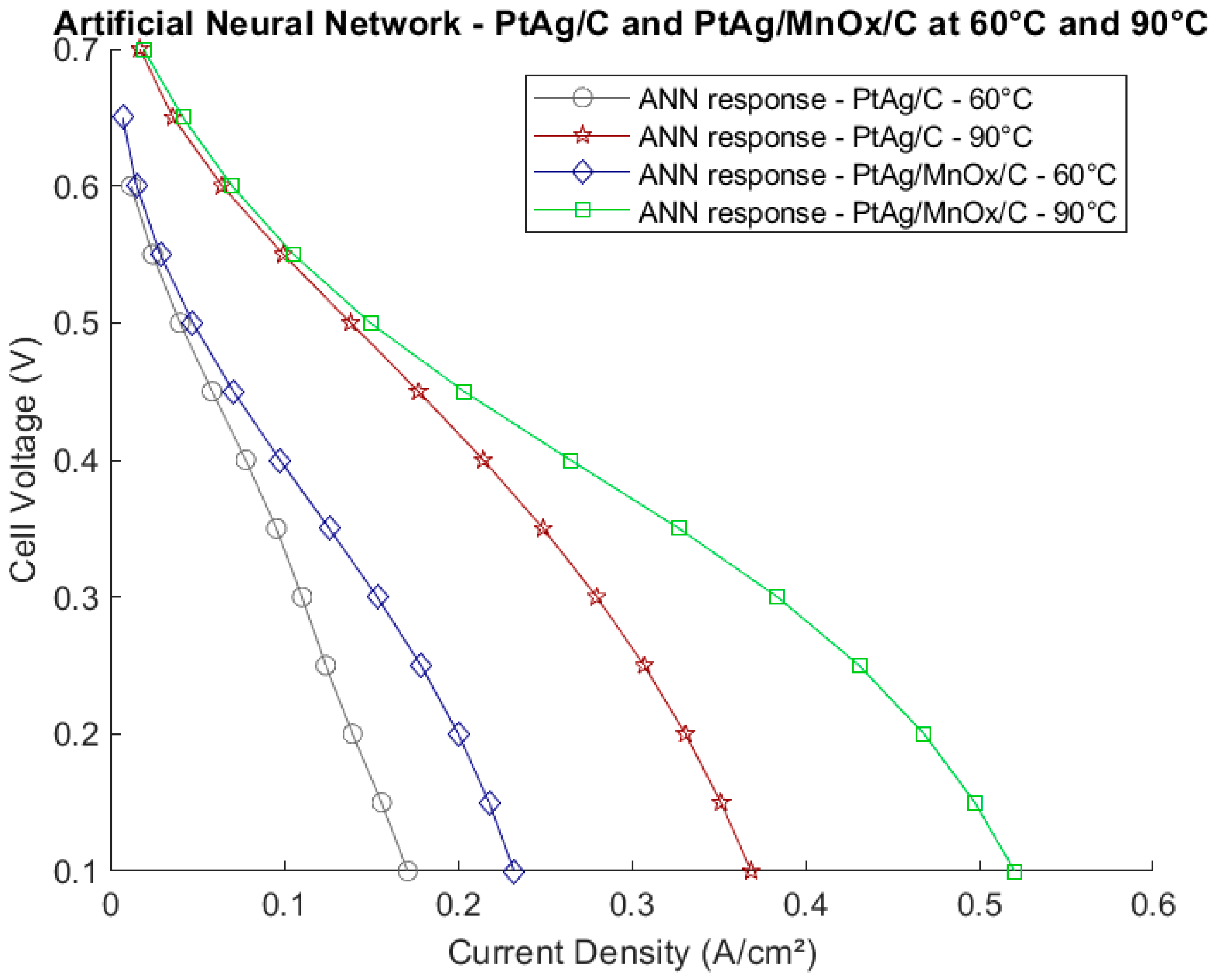
2.2.3. Neural Network for Polarization Curves of PtAg/C and PtAg/MnOx/C Electrodes at 60 °C and 90 °C
3. Results and Discussion
3.1. Phenomenological Models
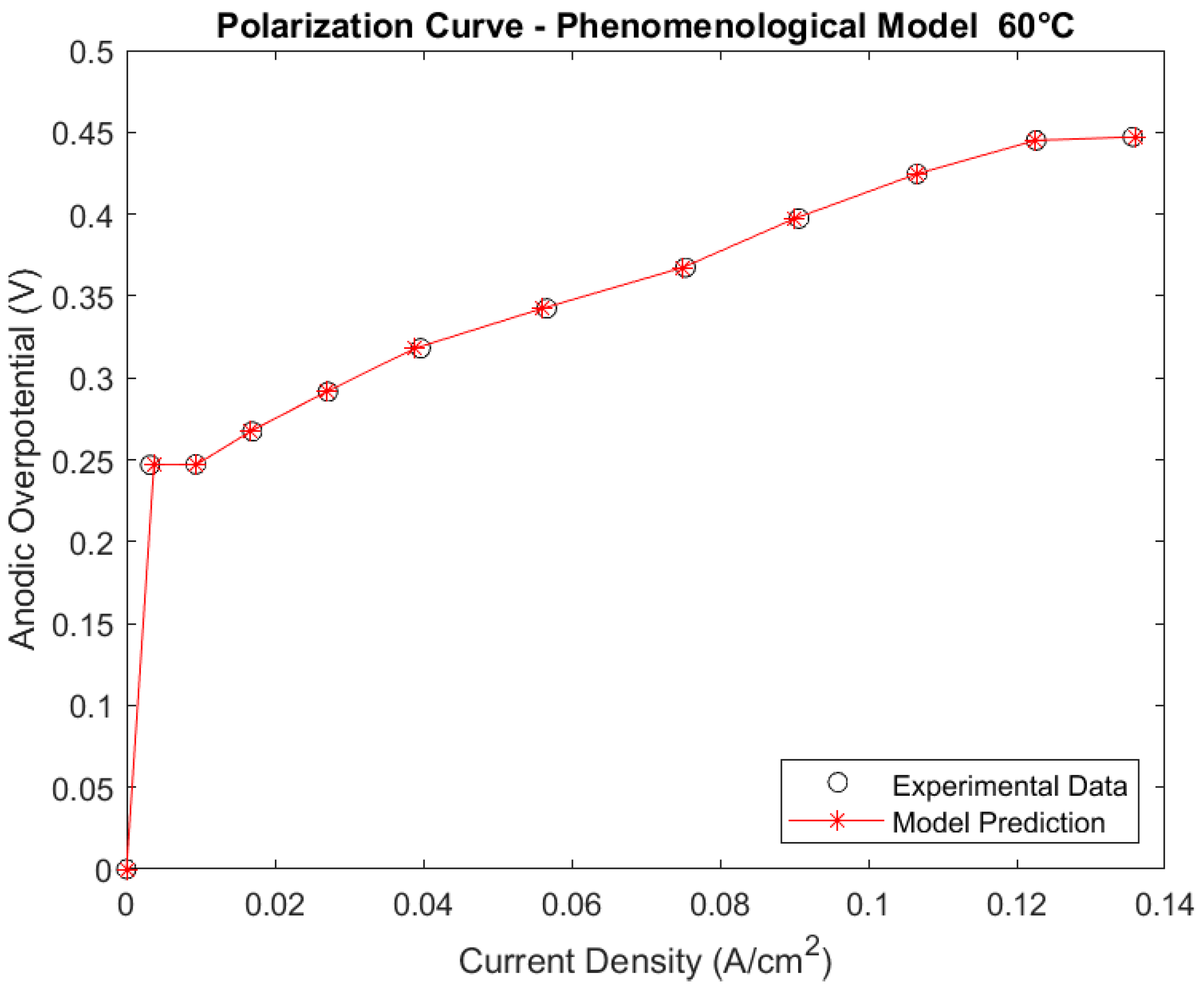
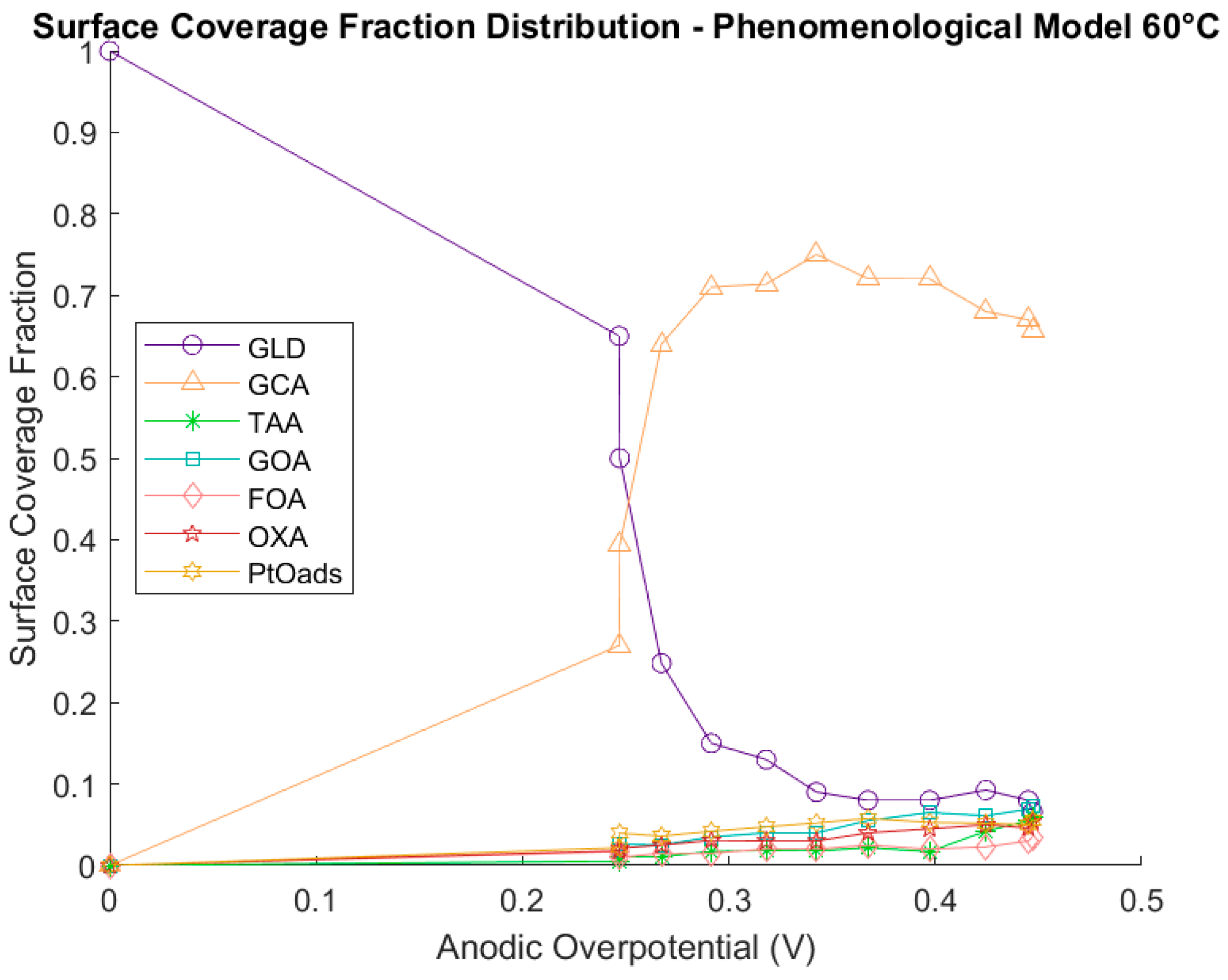
3.1.1. Phenomenological Model at 60 °C
Polarization Curve
Catalyst Coverage Distribution
Statistical Study of the Parameters
Parameter Sensitivity
Impact of the Most Sensitive Parameters on the Coverage Fraction Distribution
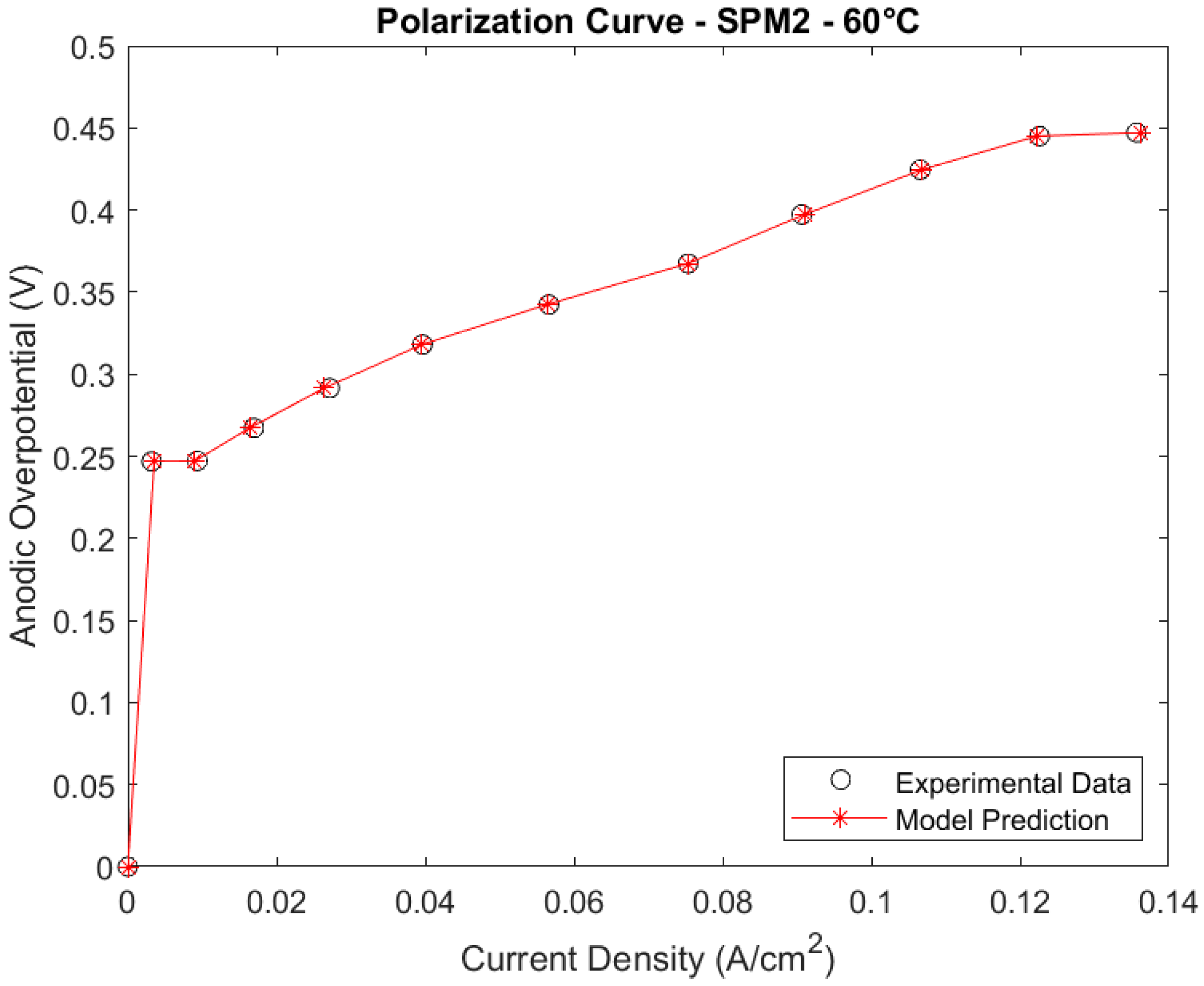
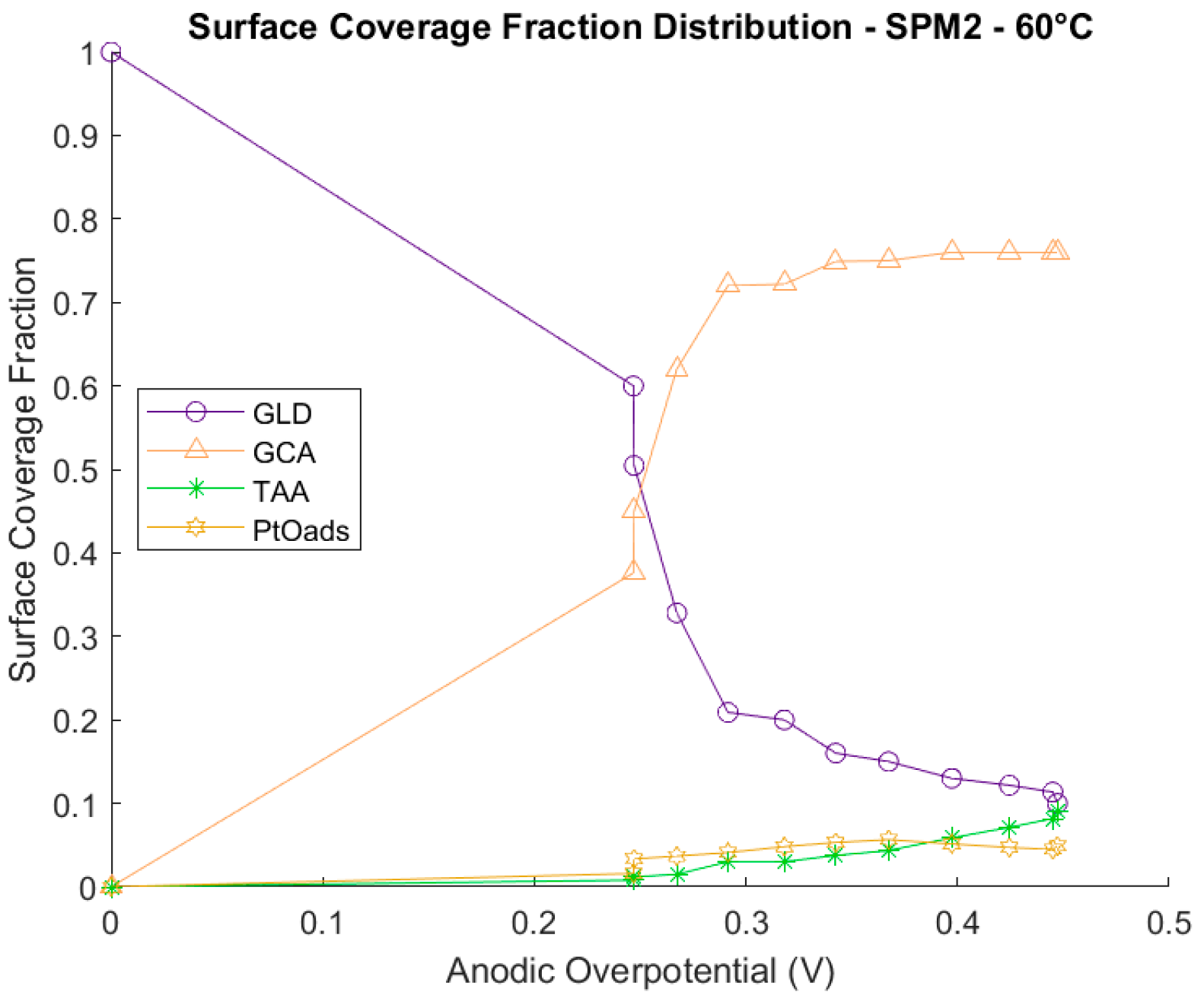
3.1.2. Simplified Models 1 and 2
Polarization Curves
Catalyst Coverage Distributions
Statistical Study of the Parameters
3.1.3. Comparison between the Full Model at 60 °C and Simplified Models 1 and 2
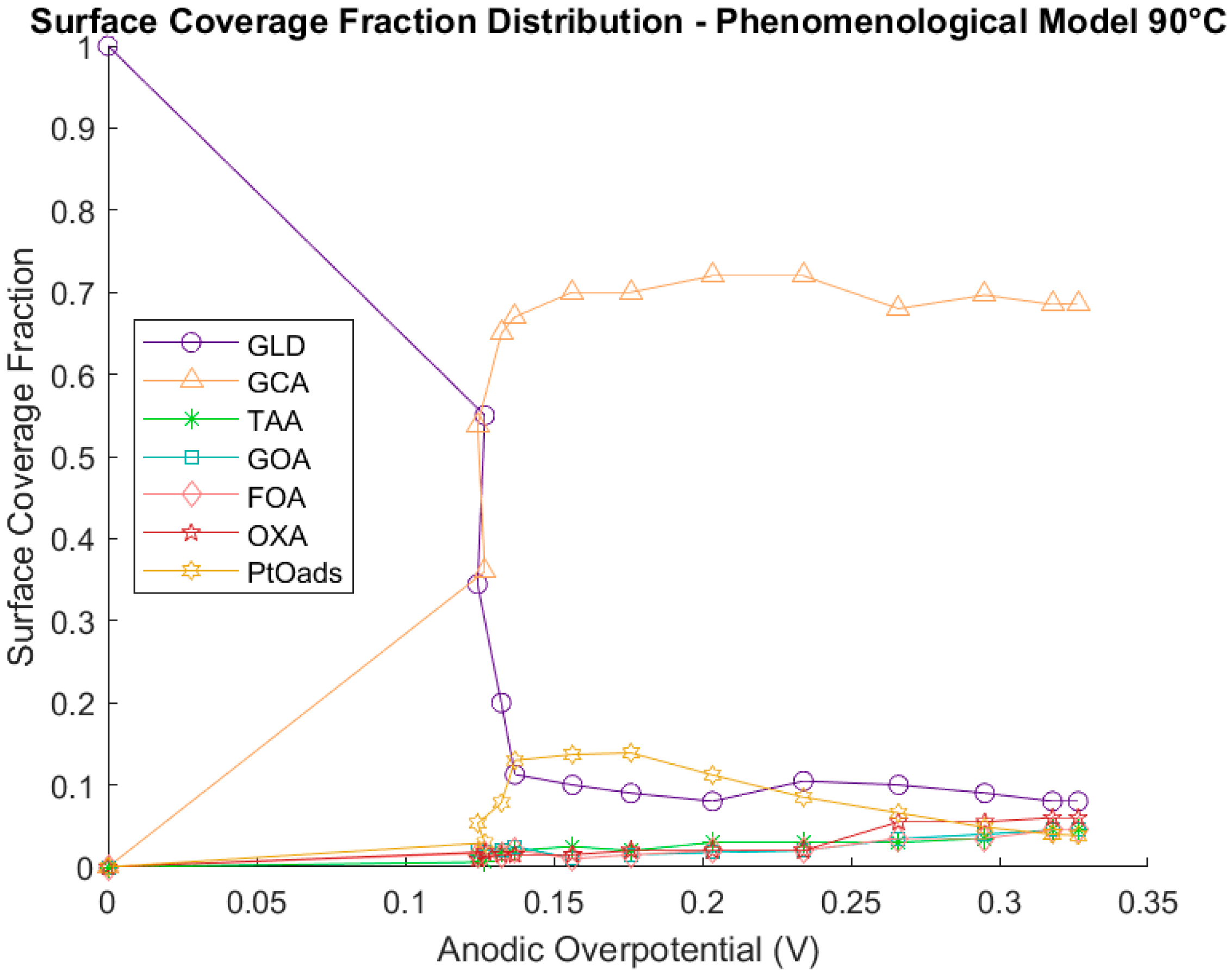
3.1.4. Phenomenological Model at 90 °C
Polarization Curves
Catalyst Coverage Distribution
Statistical Study of the Parameters
3.1.5. Additional Validation of PMs at 60 °C and 90 °C
3.2. Neural Network for the PtAg/C and PtAg/MnOx/C Electrodes at 60 °C and 90 °C
3.3. Pros and Cons of the Developed Models
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| List of Symbols | |
| E0 | open circuit potential (V or mV) |
| Vcel | cell potential (V or mV) |
| η | overpotential (V or mV); subscripts indicate anodic (A) and cathodic (C); conc: concentration |
| F | Faraday constant (96,845 C/mol e−) |
| R | ideal gas constant (8.3145 V·C/(mol·K)) |
| T | absolute temperature (K) |
| Cgly | glycerol concentration (mol/m3) |
| i | current density (A/m2 or A/cm2) |
| i0 | exchange current density (A/m2 or A/cm2) |
| iL | limiting current density (A/m2 or A/cm2) |
| Rmem | membrane ohmic resistance (Ω·m2) |
| k | reaction kinetic constants |
| α | charge transfer coefficient |
| θi | coverage fraction for adsorbed species i |
| n | number of electrons |
| N | number of sample data |
| H | Hessian matrix |
| σ2 | noise variance |
| wi | output layer weights |
| wij | hidden layer weights |
| ϕi | hidden layer perceptrons output |
| y | process output |
| ŷ | model output |
| List of Abbreviations | |
| AFC | alkaline fuel cell |
| ANN | artificial neural network |
| DEFC | direct ethanol fuel cell |
| DGFC | direct glycerol fuel cell |
| FOA | formic acid |
| GCA | glyceric acid |
| GLD | glyceraldehyde |
| GLY | glycerol |
| GOA | glycolic acid |
| MLP | multilayer perceptron |
| MSE | mean squared error |
| OXA | oxalic acid |
| PBI | polybenzimidazole |
| PM | phenomenological model |
| RMSE | root mean squared error |
| SAMFC | solid alkaline membrane fuel cell |
| SD | standard deviation |
| SE | standard error |
| SPEFC | solid polymer electrolyte fuel cell |
| SPM1 | simplified phenomenological model 1 |
| SPM2 | simplified phenomenological model 2 |
| SSE | sum of squared errors |
| TAA | tartronic acid |
Appendix A
References
- Gomes, J.F.; Tremiliosi-Filho, G. Spectroscopic Studies of the Glycerol Electro-Oxidation on Polycrystalline Au and Pt Surfaces in Acidic and Alkaline Media. Electrocatalysis 2011, 2, 96–105. [Google Scholar] [CrossRef]
- Gomes, J.F.; Paula, F.B.C.; Gasparotto, L.H.S.; Tremiliosi-Filho, G. The influence of the Pt crystalline surface orientation on the glycerol electro-oxidation in acidic media. Electrochim. Acta 2012, 76, 88–93. [Google Scholar] [CrossRef]
- Kwon, Y.; Schouten, K.J.P.; Koper, M.T.M. Mechanism of the Catalytic Oxidation of Glycerol on Polycrystalline Gold and Platinum Electrodes. ChemCatChem 2011, 3, 1176–1185. [Google Scholar] [CrossRef]
- Roquet, L.; Belgsir, E.M.; Léger, J.-M.; Lamy, C. Kinetics and mechanisms of the electrocatalytic oxidation of glycerol as investigated by chromatographic analysis of the reaction products: Potential and pH effects. Electrochim. Acta 1994, 39, 2387–2394. [Google Scholar] [CrossRef]
- Wang, Y.; Li, L.; Hu, L.; Zhuang, L.; Lu, J.; Xu, B. A feasibility analysis for alkaline membrane direct methanol fuel cell: Thermodynamic disadvantages versus kinetic advantages. Electrochem. Commun. 2003, 5, 662–666. [Google Scholar] [CrossRef]
- Coutanceau, C.; Demarconnay, L.; Lamy, C.; Léger, J.-M. Development of electrocatalysts for solid alkaline fuel cell (SAFC). J. Power Sources 2006, 156, 14–19. [Google Scholar] [CrossRef]
- Behr, A.; Eilting, J.; Irawadi, K.; Leschinski, J.; Lindner, F. Improved utilisation of renewable resources: New important derivatives of glycerol. Green Chem. 2008, 10, 13–30. [Google Scholar] [CrossRef]
- Bianchi, C.L.; Canton, P.; Dimitratos, N.; Porta, F.; Prati, L. Selective oxidation of glycerol with oxygen using mono and bimetallic catalysts based on Au, Pd and Pt metals. Catal. Today 2005, 102–103, 203–212. [Google Scholar] [CrossRef]
- Zhang, Z.; Xin, L.; Li, W. Electrocatalytic oxidation of glycerol on Pt/C in anion-exchange membrane fuel cell: Cogeneration of electricity and valuable chemicals. Appl. Catal. B Environ. 2012, 119–120, 40–48. [Google Scholar] [CrossRef]
- Zhou, Y.; Shen, Y.; Piao, J. Sustainable Conversion of Glycerol into Value-Added Chemicals by Selective Electro-Oxidation on Pt-Based Catalysts. ChemElectroChem 2018, 5, 1636–1643. [Google Scholar] [CrossRef]
- Houache, M.S.E.; Hughes, K.; Baranova, E.A. Study on catalyst selection for electrochemical valorization of glycerol. Sustain. Energy Fuels 2019, 3, 1892–1915. [Google Scholar] [CrossRef]
- Garcia, R.; Besson, M.; Gallezot, P. Chemoselective catalytic oxidation of glycerol with air on platinum metals. Appl. Catal. A Gen. 1995, 127, 165–176. [Google Scholar] [CrossRef]
- Kimura, H. Selective oxidation of glycerol on a platinum-bismuth catalyst by using a fixed bed reactor. Appl. Catal. A Gen. 1993, 105, 147–158. [Google Scholar] [CrossRef]
- Kimura, H.; Tsuto, K.; Wakisaka, T.; Kazumi, Y.; Inaya, Y. Selective oxidation of glycerol on a platinum-bismuth catalyst. Appl. Catal. A Gen. 1993, 96, 217–228. [Google Scholar] [CrossRef]
- Gallezot, P. Selective oxidation with air on metal catalysts. Catal. Today 1997, 37, 405–418. [Google Scholar] [CrossRef]
- Worz, N.; Brandner, A.; Claus, P. Platinum−bismuth-catalyzed oxidation of glycerol: Kinetics and the origin of selective deactivation. J. Phys. Chem. C 2009, 114, 1164–1172. [Google Scholar] [CrossRef]
- Kwon, Y.; Birdja, Y.; Spanos, I.; Rodriguez, P.; Koper, M.T.M. Highly Selective Electro-Oxidation of Glycerol to Dihydroxyacetone on Platinum in the Presence of Bismuth. ACS Catal. 2012, 2, 759–764. [Google Scholar] [CrossRef]
- Ilie, A.; Simoes, M.; Baranton, S.; Coutanceau, C.; Martemianov, S. Influence of operational parameters and of catalytic materials on electrical performance of direct glycerol solid alkaline membrane fuel cells. J. Power Sources 2011, 196, 4965–4971. [Google Scholar] [CrossRef]
- Lobato, J.; Cañizares, P.; Rodrigo, M.A.; Piuleac, C.-G.; Curteanu, S.; Linares, J.J. Direct and inverse neural networks modelling applied to study the influence of the gas diffusion layer properties on PBI-based PEM fuel cells. Int. J. Hydrogen Energy 2010, 35, 7889–7897. [Google Scholar] [CrossRef]
- Sousa, R., Jr.; Gonzalez, E.R. Mathematical modeling of polymer electrolyte fuel cells. J. Power Sources 2005, 147, 32–45. [Google Scholar] [CrossRef]
- Simões, M.; Baranton, S.; Coutanceau, C. Electro-oxidation of glycerol at Pd based nano-catalysts for an application in alkaline fuel cells for chemicals and energy cogeneration. Appl. Catal. B Environ. 2010, 93, 354–362. [Google Scholar] [CrossRef]
- Milewski, J.; Szczęśniak, A.; Szabłowski, Ł.; Dybiński, O.; Miller, A. Artificial neural network model of molten carbonate fuel cells: Validation on experimental data. Int. J. Energy Res. 2019, 43, 6740–6761. [Google Scholar] [CrossRef]
- Sousa, R., Jr.; Anjos, D.M.; Tremiliosi-Filho, G.; Gonzalez, E.R.; Coutanceau, C.; Sibert, E.; Léger, J.-M.; Kokoh, K.B. Modeling and simulation of the anode in direct ethanol fuels cells. J. Power Sources 2008, 180, 283–293. [Google Scholar] [CrossRef]
- Maia, L.K.K.; Sousa, R., Jr. Three-dimensional CFD modeling of direct ethanol fuel cells: Evaluation of anodic flow field structures. J. Appl. Electrochem. 2016, 47, 25–37. [Google Scholar] [CrossRef]
- de Oliveira, D.S.B.L.; Colmati, F.; de Sousa, R., Jr. Reaction Kinetics-Based Modeling and Parameter Sensitivity Analysis of Direct Ethanol Fuel Cells. Energies 2022, 15, 9143. [Google Scholar] [CrossRef]
- Oliveira, D.S.B.L.; Colmati, F.; Gonzalez, E.R.; Sousa, R., Jr. Neurofuzzy modelling on the influence of Pt–Sn catalyst properties in direct ethanol fuel cells performance: Fuzzy inference system generation and cell power density optimization. Int. J. Hydrogen Energy 2023, 48, 24481–24491. [Google Scholar] [CrossRef]
- Han, X.; Chadderdon, D.J.; Qi, J.; Xin, L.; Li, W.; Zhou, W. Numerical analysis of anion-exchange membrane direct glycerol fuel cells under steady state and dynamic operations. Int. J. Hydrogen Energy 2014, 39, 19767–19779. [Google Scholar] [CrossRef]
- Garcia, A.C.; Ferreira, E.B.; Barros, V.V.S.; Linares, J.J.; Tremiliosi-Filho, G. PtAg/MnOx/C as a promising electrocatalyst for glycerol electro-oxidation in alkaline medium. J. Electroanal. Chem. 2017, 793, 188–196. [Google Scholar] [CrossRef]
- Nelles, O. Nonlinear System Identification—From Classical Approaches to Neural Networks and Fuzzy Models, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Boekel, M.A.J.S. Statistical Aspects of Kinetic Modeling for Food Science Problems. J. Food Sci. 1996, 61, 477–486. [Google Scholar] [CrossRef]
- MathWorks Inc. Constrained Nonlinear Algorithms. Help Center. 2022. Available online: https://www.mathworks.com/help/optim/ug/constrained-nonlinear-optimization-algorithms.html#brnox01 (accessed on 5 August 2022).
- Pinto, G.A. Biorefinaria de Soro de Queijo: Engenharia de Bioprocessos e Sistemas Aplicada à Transformação de um Resíduo Poluente em Produtos com Valor Agregado [Cheese Whey Biorefinery: Bioprocess and Systems Engineering Applied to the Transformation of a Pollutant Waste into Value-Added Products]. Ph.D. Thesis, Universidade Federal de São Carlos, São Paulo, Brazil, 2008. (In Portuguese). [Google Scholar]
- Beale, M.H.; Hagan, M.T.; Demuth, H.B. Neural Network Toolbox™: User’s Guide, 7th ed.; Mathworks: Natick, MA, USA, 2010. [Google Scholar]
- Sousa, R., Jr.; Colmati, F.; Gonzalez, E.R. Modeling techniques applied to the study of gas diffusion electrodes and proton exchange membrane biochemical fuel cells. J. Power Sources 2006, 161, 183–190. [Google Scholar] [CrossRef]
- Demirel, S.; Lucas, M.; Wärnå, J.; Salmi, T.; Murzin, D.; Claus, P. Reaction kinetics and modelling of the gold catalysed glycerol oxidation. Top. Catal. 2007, 44, 299–305. [Google Scholar] [CrossRef]




| Constant | Value | Reference |
|---|---|---|
| R (V·C/(mol·K)) | 8.314 | - |
| F (C/mol) | 96,485.3 | - |
| CGLY (mol/m3) | 1000 | [27] |
| CO2/CO2,ref | 1 | [27] |
| i0_c (A/m2) | 0.31 | [27] |
| Rmem (Ω·m2) | 2.85 × 10−5 | [23] |
| αC | 0.66 | Assumed |
| ilim 60 °C (A/m2) | 1400 | Assumed |
| ilim 90 °C (A/m2) | 3100 | Assumed |
| E0 (V) | 1.05 | Fitted to the ideal model |
| Parameter | Units | Value | SE | SD | Deviation Magnitude |
|---|---|---|---|---|---|
| k2 | mol/(m2·s) | 1.65 × 10−3 | 7.47 × 10−6 | 1.53 × 10−5 | 9.24 × 10−3 |
| k5 | mol/(m2·s) | 2.00 × 10−4 | 7.64 × 10−9 | 1.56 × 10−8 | 7.80 × 10−5 |
| k5′ | mol/(m2·s) | 1.00 | 1.05 × 10−2 | 2.14 × 10−2 | 2.14 × 10−2 |
| α2 | - | 0.26 | 7.84 × 10−4 | 1.60 × 10−3 | 6.16 × 10−3 |
| α4 | - | 1.50 | 3.05 × 10−6 | 6.23 × 10−6 | 4.16 × 10−6 |
| Parameter | Units | Value | SE | SD | Deviation Magnitude |
|---|---|---|---|---|---|
| k2 | mol/(m2·s) | 1.65 × 10−3 | 1.52 × 10−10 | 3.10 × 10−10 | 1.88 × 10−7 |
| k5 | mol/(m2·s) | 2.00 × 10−4 | 1.05 × 10−11 | 2.14 × 10−11 | 1.07 × 10−7 |
| k5′ | mol/(m2·s) | 1.00 | 1.40 × 10−7 | 2.86 × 10−7 | 2.86 × 10−7 |
| α2 | - | 0.26 | 3.53 × 10−9 | 7.20 × 10−9 | 2.77 × 10−8 |
| α4 | - | 1.49 | 4.17 × 10−9 | 8.52 × 10−9 | 5.72 × 10−9 |
| Parameter | Units | Value | SE | SD | Deviation Magnitude |
|---|---|---|---|---|---|
| k2 | mol/(m2·s) | 1.65 × 10−3 | 1.46 × 10−8 | 2.97 × 10−8 | 1.80 × 10−5 |
| k2″ | mol/(m2·s) | 3.88 × 10−2 | 3.56 × 10−7 | 7.27 × 10−7 | 1.87 × 10−5 |
| k5 | mol/(m2·s) | 2.00 × 10−4 | 4.89 × 10−12 | 1.00 × 10−12 | 5.00 × 10−8 |
| k5′ | mol/(m2·s) | 0.25 | 6.14 × 10−4 | 1.25 × 10−4 | 5.03 × 10−3 |
| α2 | - | 0.26 | 1.76 × 10−8 | 3.59 × 10−8 | 1.38 × 10−7 |
| α4 | - | 1.54 | 2.35 × 10−9 | 4.79 × 10−9 | 3.11 × 10−9 |
| Full PM | SPM1 | SPM2 | ||||
|---|---|---|---|---|---|---|
| Parameter | Value | Deviation Magnitude | Value | Deviation Magnitude | Value | Deviation Magnitude |
| k2 | 1.65 × 10−3 | 9.24 × 10−3 | 1.65 × 10−3 | 1.88 × 10−7 | 1.65 × 10−3 | 1.80 × 10−5 |
| k5 | 2.00 × 10−4 | 7.80 × 10−5 | 2.00 × 10−4 | 1.07 × 10−7 | 2.00 × 10−4 | 5.00 × 10−8 |
| k5′ | 1.00 | 2.14 × 10−2 | 1.00 | 2.86 × 10−7 | 0.25 | 5.03 × 10−3 |
| α2 | 0.26 | 6.16 × 10−3 | 0.26 | 2.77 × 10−8 | 0.26 | 1.38 × 10−7 |
| α4 | 1.50 | 4.16 × 10−6 | 1.49 | 5.72 × 10−9 | 1.54 | 3.11 × 10−9 |
| Parameter | Units | Value | SE | SD | Deviation Magnitude |
|---|---|---|---|---|---|
| k2 | mol/(m2·s) | 4.50 × 10−3 | 1.15 × 10−6 | 2.35 × 10−6 | 5.23 × 10−4 |
| k5 | mol/(m2·s) | 2.00 × 10−4 | 1.53 × 10−10 | 3.12 × 10−10 | 1.56 × 10−6 |
| k5′ | mol/(m2·s) | 1.00 × 10−2 | 3.56 × 10−6 | 7.27 × 10−6 | 7.25 × 10−4 |
| α2 | - | 0.40 | 1.89 × 10−5 | 3.85 × 10−5 | 9.64 × 10−5 |
| α4 | - | 1.75 | 1.65 × 10−7 | 3.38 × 10−7 | 1.93 × 10−7 |
| Phenomenological Models | |
|---|---|
| Literature |
|
| This Work: Pros |
|
| This Work: Cons |
|
| Artificial Neural Networks | |
|---|---|
| Literature | There is no literature concerning ANNs applied to alkaline DGFCs. |
| This Work: Pros |
|
| This Work: Cons |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pezzini, A.; de Castro, U.J.; de Oliveira, D.S.B.L.; Tremiliosi-Filho, G.; de Sousa Júnior, R. Mathematical Modeling of Alkaline Direct Glycerol Fuel Cells. Energies 2023, 16, 6762. https://doi.org/10.3390/en16196762
Pezzini A, de Castro UJ, de Oliveira DSBL, Tremiliosi-Filho G, de Sousa Júnior R. Mathematical Modeling of Alkaline Direct Glycerol Fuel Cells. Energies. 2023; 16(19):6762. https://doi.org/10.3390/en16196762
Chicago/Turabian StylePezzini, Alessandra, Ubiranilson João de Castro, Deborah S. B. L. de Oliveira, Germano Tremiliosi-Filho, and Ruy de Sousa Júnior. 2023. "Mathematical Modeling of Alkaline Direct Glycerol Fuel Cells" Energies 16, no. 19: 6762. https://doi.org/10.3390/en16196762
APA StylePezzini, A., de Castro, U. J., de Oliveira, D. S. B. L., Tremiliosi-Filho, G., & de Sousa Júnior, R. (2023). Mathematical Modeling of Alkaline Direct Glycerol Fuel Cells. Energies, 16(19), 6762. https://doi.org/10.3390/en16196762







