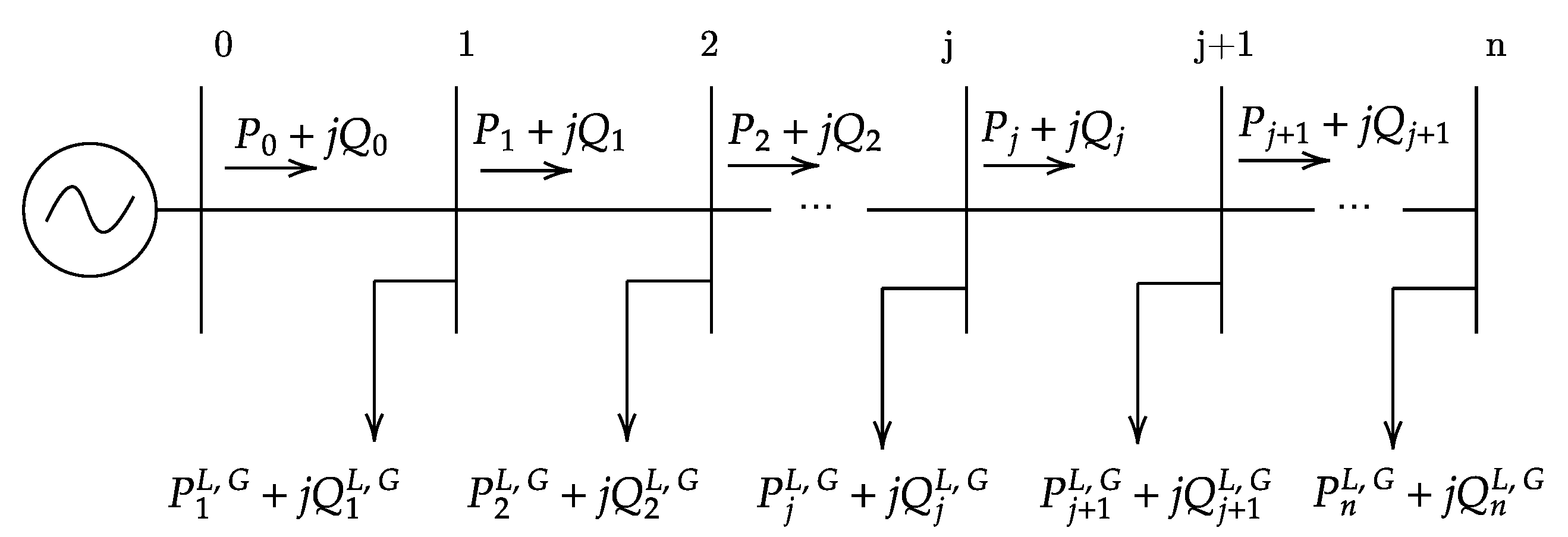Distributed Reactive Power Injection-Based Approach for Minimization of Losses in Electrical Networks Considering Heuristic Algorithms and Voltage Deviation

Abstract

This paper deals with the reduction in electrical losses and the minimization of voltage deviation in electrical power grids. To this end, a novel heuristic-based approach is proposed for controlling reactive power injections along an electrical grid with distributed generation using distributed photovoltaic (PV) generation. The proposed approach consists of applying a heuristic, namely a genetic or firefly algorithm, to solve the loss and voltage deviation optimization problem by controlling PV reactive power injections. The proposed method was tested on a radial 100-bus network with an intense penetration of PV generation. The obtained results indicate that the proposed method consistently yields superior grid performance when compared to algorithms previously proposed in the literature. In fact, it led to a reduction in the active power supplied by the reference bus to the grid, thereby alleviating the burden imposed on the most upstream parts of the distribution network. As a consequence, the proposed method contributes to a power-efficient network, enhancing its loss performance and voltage stability.

1. Introduction

Distribution grids were initially designed as passive systems providing unidirectional power flow from the distribution substation to end consumers. With the widespread adoption of distributed generation (DG), this scenario has changed due to power generation near to the demand. This way, electrical networks may experience bi-directional power flow, especially in systems with high DG penetration. This has created many challenges in the operation of distribution networks, which now behave as active systems and require real-time control and the optimization of multiple distributed power sources.

In the last 10 years, photovoltaic (PV) distributed generation has rapidly advanced. The integration of small-scale DG into the grid does not significantly alter the voltage profile of the network or the directionality of power flow, thereby having a minimal impact on grid performance. However, recent studies have shown that a high penetration rate of DG in the electrical network may increase the occurrence of overvoltages along the network.

Traditionally, distribution grid operation has followed an approach known as fit-and-forget: the distribution grid feeders are designed with a capacity to handle long-term changes in demand for a set period of time, such as one or two decades. On the other hand, when DG penetration is significant, the utility must continually analyze requests for DG installation and approve them only if the new PV connection is not likely to the violate operational limits of the electrical grid [1].

In this sense, DG penetration becomes significant, and the fit-and-forget approach ceases to be valid as the grid becomes unable to handle the load and DG power output variations. This has led to the development of the connect-and-manage approach for distribution network operation, as demonstrated in [2]. In this context, network operators manage the PV power injected into the distribution system based on the load, network capacity, and time of day. These decisions are made based on network parameters, such as instantaneous value and the direction of active and reactive power, as well as voltage and current values at the PV connection point. Some studies have attempted to estimate the grid DG installation capacity. For instance, in [3], the authors demonstrated that the DG capacity should be limited to a maximum of 15% of peak demand so as to avoid issues in the distribution system, such as reverse power flow and transients voltages surges.

Aside from estimating the grid DG capacity, it is of great importance to devise PV reactive power control methods to regulate voltage and power in DG systems. These control methods play a crucial role in maintaining grid stability, managing voltage fluctuations, and ensuring optimal power flow, as discussed in [4,5]. However, while existing methods have proven effective to some extent, there is a need for further advancements in this field. In this context, the present article proposes a novel method for controlling both voltage and power in DG systems, aiming to enhance system performance and address the challenges posed by increasing DG integration. This work proposes the use of PV inverters for reactive power control, utilizing distributed reactive power injection across multiple grid buses. The major innovation of this work is proposing a new method that can reduce electrical losses, while minimizing voltage deviation and alleviating the burden on the distribution network.

This work is structured as follows: Section 2 consists of a comprehensive review of related works. In Section 3, the distribution grid modeling is described in detail. Section 4 provides a comprehensive description of the proposed method, elucidating how the heuristic algorithms interact with the power flow and effectively optimize the proposed objective function. Section 5 provides a detailed comparison of the performance of the proposed method with other works. Finally, Section 6 concludes that the proposed method could achieve better results in terms of the power losses and voltage profile than other works.

2. Previous Works

Reactive power injection in power systems is essential for voltage control, preventing overvoltage, and reducing losses. By strategically injecting or absorbing reactive power, voltage levels can be regulated, ensuring system stability. This control mechanism improves equipment performance, minimizes inefficiencies, and enhances the overall system reliability. The efficient use of reactive power injection helps maintain optimal voltage profiles and mitigates operational challenges in power systems. The grid-tied PV inverters can inject not only generated active power, but also reactive power into the grid. This capability has been shown to be more efficient and prone to fine-tuning than the classical methods of reactive power injection, such as capacitor banks, as discussed in [6].

Some studies proposed hybrid control schemes, combining inverters with capacitors, as discussed in [7]. In [8], a proposal for reactive power dispatch control is presented for voltage regulation and power factor improvement. Ref. [9] proposed a method for reactive power control in PV systems for voltage regulation based on the sensitivity of the feeder impedance. In [10], the authors proposed a method for reactive power dispatch using inverters connected to PV systems and an energy storage system. The approach uses an estimation of electrical power losses in the distribution network to calculate the value of reactive power to be injected to minimize losses. Through the energy storage system, it is possible to have a larger margin for dispatching reactive power, rather than solely relying on environmental conditions such as temperature and irradiance.

A critical issue regarding PV inverter reactive power injection is the optimal sizing of inverter apparent power, as it must be ensured that both active and reactive power are supplied to the grid. Typically, in a PV inverter that only outputs active power, the apparent power can be set to approximately 85% of the rated DC power, as discussed in [11]. This is further discussed in [12], where the author proposes an analytical methodology to determine the power rating of a PV inverter that does not output reactive power. On the other hand, it is shown in [13] that, to achieve higher efficiency in PV systems that also output reactive power, the inverter should have apparent power that is greater than the rated DC power.

In [14], an algorithm is proposed that injects reactive power into the grid to reduce losses and improve its voltage profile. However, this method requires PV inverters with high apparent power values, with an oversizing of up to 60%. In [15], a voltage sensitivity matrix-based reactive power control scheme is presented. Through the examination of the impact of changes in node injection power on node voltage, a sensitivity matrix is constructed to determine the relationship between active and reactive power and the voltage of each key node. However, the method was only validated for a six-bus grid. The work of [16] introduces a multi-area and multi-period optimal reactive power dispatch model. This model can minimize voltage deviation, reactive power deviation, and the total reactive power generated while considering operational constraints. In [17], a control strategy for PV inverters is presented to mitigate voltage disturbances due to high PV energy penetration in low-voltage distribution grids. This approach addresses the PV active power transmission, load balance, and reactive power compensation, ultimately reducing losses.

Recent works in the field have predominantly relied on analytical approaches, as demonstrated by studies such as [14,15]. These approaches have contributed valuable insights into voltage control for distribution networks with distributed generation. However, an alternative avenue for potential improvement lies in the utilization of heuristic algorithms. These algorithms offer a complementary approach to address the complexity and nonlinearities inherent in voltage control problems.

In this sense, this work proposes the application of the genetic and firefly algorithms for controlling PV reactive power injections in grids with high DG penetration. The considered goal is to minimize power losses and improve the network voltage profile.

Genetic algorithm (GA) is a stochastic optimization algorithm inspired by the process of natural selection and genetics in biological evolution. It is a type of evolutionary algorithm that uses the principles of selection, crossover, and mutation to generate new populations of candidate solutions, as demonstrated in [18]. The GA is an effective method for solving complex optimization problems and it has been widely applied to solve problems that involve optimization, as presented in [19]. Firefly algorithm (FA) is a bio-inspired optimization algorithm that mimics the flashing behavior of fireflies to search for optimal solutions. FA is based on the principle of social attraction, and the flashing behavior of fireflies is used to represent the search process [20]. The algorithm has been shown to be effective in solving complex optimization problems with multiple objectives and constraints [21]. GA and FA were chosen as optimization techniques due to their ability to find optimal solutions in large search spaces. The key parameters of these heuristic algorithms are: population size (P) and maximum iterations/generations (G); randomness ($\alpha$), attractiveness between fireflies ($\beta$), and the coefficient of luminous absorption by the environment ($\gamma$) for FA; mutation probability ($p_m$) and crossover probability ($p_c$) for GA.

3. Modeling and Problem Statement

In what follows, the power grid modeling approach adopted in this work is described. Subsequently, the considered grid optimization problems are formally stated. Consider an ($n+1$)-bus distribution network, which is assumed as radial because the power flow is unidirectional, from the first to the last bus [14]. As shown in Figure 1, let the nodes be numbered from 0 to n, where index $j=0$ denotes the slack bus. The power flowing from the reference bus j to bus $j+1$ is given by $P_j+j{Q}_j$. At each bus, there is a load that consumes active and reactive power, and a PV generator may exist. The power consumed by bus j is $P_j^{L,G}+j{Q}_j^{L,G}$, which is equal to the difference between the load and PV powers at the bus. Therefore, powers flowing out of adjacent buses are related as $P_{j+1}+j{Q}_{j+1}=(P_j+j{Q}_j)-(P_{j+1}^{L,G}+j{Q}_{j+1}^{L,G})$. The active and reactive power values of the loads, as well as the active power generated at the nodes with generation, are randomly generated.

The reactive power at each bus is defined as the difference between the load reactive power and the generated reactive power, such that $Q^{L,G}=Q^L-Q^G$. In this study, only the generated power is controlled since load shedding is not considered. With the exception of bus 0 (which is the slack bus), all other buses are taken as PQ load buses since there are no synchronous compensators in the distribution. Such buses may or may not have PV generation. The distance between the buses is given by L; the resistance of the distribution line between the buses is R and X is the reactance; $S_{inv}$ is the apparent power of the PV inverter in each bus. Regarding the load characteristics, the active power consumed at each bus is randomly defined between two values: [$P_{min}^L,P_{max}^L$]. Similarly, the reactive power of the load is also randomly generated. The voltage and current waveforms are considered ideal, with no consideration given to the harmonic distortions generated by the inverter. Consequently, both voltage and current waveforms are treated as ideal. Given all PQ bus powers, a power flow algorithm can be executed to calculate the remaining quantities of the system, such as voltage magnitudes, phase angles, and losses. In this article, power flow computations are carried out with the Newton–Raphson method. The Newton–Raphson method is widely used in power system analysis due to its ability to handle complex and highly nonlinear systems accurately and efficiently [22].

3.1. Problem Statement

Three reactive power injection optimization scenarios are considered in this work. The first scenario solely aims to minimize power losses in the network, with no restriction on bus voltages. This problem can be stated as follows:

$$\left\{\begin{array}{cccccc}& \underset{Q_j^G}{\mathrm{minimize}}& & P_{losses}\left(Q^G\right)=\sum _{j=1}^{n-1}R·I_j^2& & \mathrm{for}\mathrm{all}j=1,2,\dots ,n,\end{array}\right.$$

(1)

where $I_j$ is the current flowing from bus $j-1$ to bus j.

In the second scenario, the objective is to adjust the voltage profile by reducing deviation from the nominal value of 1 pu at all buses, without concern for electrical losses. The voltage deviation $\delta V_j$ is defined as the absolute value of the difference between the voltage at the bus and the nominal voltage of each bus, and it must be smaller than a preset value defined as $\mathsf{\Delta }V$ such that $\delta V_j\le \mathsf{\Delta }V$. The voltage values in each bus must remain between two values: $V_{nominal}-\mathsf{\Delta }V\le V_j\le V_{nominal}+\mathsf{\Delta }V$. Hence, in this scenario, the following optimization problem is taken into account:

$$\left\{\begin{array}{cccccc}& \underset{Q_j^G}{\mathrm{minimize}}& & \delta V_j\left(Q^G\right)=|V_j-V_{nominal}|& & \mathrm{for}\mathrm{all}j=1,2,\dots ,n,\end{array}\right.$$

(2)

The third scenario aims to minimize losses while maintaining appropriate voltage levels at the buses, thereby introducing a constraint into the optimization process, given that the minimization of power losses and the minimization of voltage deviation are two conflicting objectives. In this scenario, the constrained optimization is a way to reconcile these objectives (power losses and voltage deviation). The associated optimization problem can be described as follows:

$$\left\{\begin{array}{ccccccc}& \underset{Q_j^G}{\mathrm{minimize}}& & P_{losses}\left(Q^G\right)& \mathrm{subject}\mathrm{to}& & \delta V_j\left(Q_j^G\right)\le \mathsf{\Delta }V,j=1,2,\dots ,n,\end{array}\right.$$

(3)

where $Q^G=[Q_1^G,Q_2^G,\dots ,Q_n^G]$ is the vector of the generated reactive power (decision variables), $P_{losses}\left(Q_j^G\right)$ represents the losses in the cables between the buses which is the objective function to be minimized, and $\delta V_j\left(Q_j^G\right)\le \mathsf{\Delta }V$ are the inequality constraints.

4. Proposed Method

One of the main advantages of heuristics algorithms is their ability to effectively explore the search space. The GA and FA are not limited to finding local optima but can also find global optima in complex, multi-dimensional search spaces. Moreover, such algorithms can handle problems with multiple objectives and constraints, which makes them versatile optimization tools. Furthermore, heuristic algorithms also have the ability to handle noisy data and constraints, making them suitable for real-world problems where data are often noisy or incomplete [19].

The GA operates on a population of candidate solutions; each solution is represented by a chromosome, which is a string of genes. The fitness function evaluates the quality of each solution and the fittest individuals are selected for reproduction. Crossover and mutation operators are then applied to generate new offspring, which replace the weaker individuals in the population. This process is repeated for a number of generations until a satisfactory solution is found [23]. On the other hand, the FA represents each candidate solution in the population as a firefly. The attractiveness of each firefly is given by its brightness, which is computed in terms of its fitness value. The fireflies move towards brighter ones, and the distance between them is determined by their relative brightness and their distance. The algorithm updates the position of each firefly based on its brightness and the attractiveness of its neighbors [24].

In this study, the aforementioned algorithms are employed to compute the reactive power injections that optimize the objective functions described in Section 3.1; the general procedure is as follows. At first, the fixed grid parameters are specified, such as L, R, and X. In the first iteration, an initial solution is randomly generated. It is described by a $P\times n$ matrix ${\mathbf{Q}}_{\mathbf{M}}^{\mathbf{G}}$, whose rows span the heuristic algorithm population size P and whose columns correspond to each component of a candidate solution vector $Q^G$. At each iteration, the heuristic algorithm generates a new P-member population by applying its operators over the previous one and outputs the $Q^G$ that best minimizes the considered objective function. The objective function value associated to each candidate $Q^G$ is obtained by computing a power flow analysis with the Newton–Raphson algorithm (see Section 3.1). The entire process is outlined in Algorithm 1.

Algorithm 1 Heuristic (GA or FA)-based reactive power control for loss and voltage deviation minimization.

Require:  Set the electrical system parameters: n, R, X, PF, $P_j^L$, $Q_j^L$, $P_j^G$ Require:  Set the heuristic algorithm parameters: P, G; $\alpha$, $\beta$ and $\gamma$ for FA; $p_m$ and $p_c$ for GA. Require:  Set the cost function to be minimized (Equation (1), (2), or (3)). Ensure:  $Q^G$. Optimized solution for reactive power generation according to the cost function 1: Generate the initial population randomly 2: Run power flow and calculate the voltage, phase angle and currents in the line for initial solution 3: for $g=1$ to G do 4:     Run heuristic algorithm (GA or FA) to generate $Q^G$ 5:     Run power flow for each $Q^G$ 6:     Calculate the cost function for each solution of the $Q^G\in$ columns ${\mathbf{Q}}_{\mathbf{M}}^{\mathbf{G}}$ 7: end for 8: return  $Q^G$

5. Validation

In what follows, a simulation-based validation of the proposed PV reactive power control approach is carried out. All simulations have been carried out in MATLAB 2019a. The performance of the heuristic algorithms is compared with the algorithms described in the works of [14,15]. In the following results, the nomenclatures GA/FA ($\delta V$), GA/FA ($P_{losses}$), and GA/FA (optimized) refer to the results applying Algorithm 1 considering optimization scenarios 1, 2, and 3, respectively. The first scenario solely focuses on minimizing losses, the second scenario aims to minimize voltage deviations, and the third scenario combines loss minimization with a voltage deviation constraint.

5.1. Simulation Parameters

Table 1. Parameters for the system.

Parameter	Value
Real power load ($P^L$)	10–40 kW
Reactive power load ($Q^L$)	80–90% of real power
Distance between buses (L)	100 m
Number of buses (n)	100
Generated real power ($P_j^G$)	10 kW to 40 kW
Maximum voltage deviation ($\mathsf{\Delta }V$)	$\delta V\le 3\%$
Penetration factor (PF)	90%
Apparent power of PV inverter ($S_{inv}$)	$1.6·P_j^G$

provides a summary of the grid parameters considered in this study, which were based on [14]. The distance between the buses is $L=100$ m; the resistance of the distribution line between the buses is $R=0.5\mathsf{\Omega }/$km, and the reactance is $X=0.33\mathsf{\Omega }$/km. The electrical grid considered in this work is a rural single-phase network with 7.2 kV, a radial characteristic, and 100 buses in addition to the reference bus. It is known that this particular grid configuration is able to supply $n=100$ buses without DG under normal operating conditions [14]. The maximum apparent power of each PV inverter is taken as 1.6 times greater than the rated active power of its associated PV module. Such apparent power oversizing is similar that adopted in the simulation studies of [14] and takes into account the additional apparent power required to ensure the accommodation of reactive power support by the inverters. This modeling approach agrees with recent distribution practices; in fact, the European standard for grid-tied PV systems stipulates mandatory reactive power reserves via inverter oversizing [25].

The real power of the load $P_j^L$ is randomly generated between 10 kW and 40 kW, using a uniform probability distribution. The reactive power of the load is randomly generated at between 80% and 90% of the real power. As a result, a low power factor is obtained, ranging between 0.74 and 0.78. The simulations are designed for static scenarios. The distance between the buses is fixed at 100 m, and the generated power at each bus $P_j^G$ is randomly generated between 10 kW and 40 kW, similarly to the load power. In our simulations, we introduced random values to mimic the unpredictability of load and generation, yet our approach consistently minimized losses and maintained acceptable voltage levels across buses. This approach aims to assess how the network behaves concerning electrical losses and voltage levels when given fixed values of generation and load. The voltage deviation limit adopted in this study was 3%. The penetration factor, defined as the percentage of buses capable of generating power, was set to 0.9. In many cases, the electrical grid infrastructure cannot accommodate the connection of a large number of PV systems. Nevertheless, in this study, we deliberately chose to work within this challenging scenario to emphasize the advantages of using heuristic algorithms to minimize voltage deviations and reduce electrical losses. Thus, the aim of this study was to evaluate the performance of the proposed approaches in a grid with a significant PV impact.

The adopted GA and FA parameters are presented in

Table 2. Parameters for the genetic algorithm.

Parameter	Value
Population size (P)	10
Generations (G)	100
Crossover rate ($p_c$)	Varying linearly from 0.8 to 0.2
Mutation rate ($p_m$)	Varying from 0.01 to 0.1
Mutation step size ($m_{ss}$)	0.05 of the value
Selection method	Tournament
Elitism	The best individual

and

Table 3. Parameters for the firefly algorithm.

Parameter	Value
Population size (P)	10
Iterations (G)	100
Randomness parameter ($\alpha$)	0.5
Attractiveness between fireflies ($\beta$)	0.2
Coefficient of luminous absorption ($\gamma$)	1

, respectively. Such parameters were initially defined arbitrarily and subsequently tuned via trial-and-error testing. In the case of the genetic algorithm, the population size consists of 10 individuals, and the number of generations is defined as 100. The crossover rate decreases linearly from 80% to 20% because initially, it is preferred to have a high mutation rate to achieve greater genetic variability. However, this becomes less advantageous in later generations. The mutation rate starts at 1% and linearly increases up to 10% since, in the final generations, it is desirable to introduce more mutations to explore the solution space and avoid a potential local minimum. The mutation step size is set to 0.05, which means that, if mutation occurs, an individual’s genes can be altered by up to 5% of their original value. The tournament method was used as an elitism technique for selecting the individual [23] to be retained in the next generation. In the case of the firefly algorithm, a population of 10 fireflies and 100 iterations were defined. The randomness parameter was set to 50%. This parameter determines the movement of the fireflies, where very high values result in completely random movement, and very low values limit the movement solely based on the brightness of the fireflies. The attractiveness among the fireflies was set to 20%, and the coefficient of light absorption by the medium was defined as 1. These values affect the convergence behavior of the FA, as described by the equations presented in [21].

5.2. Obtained Results

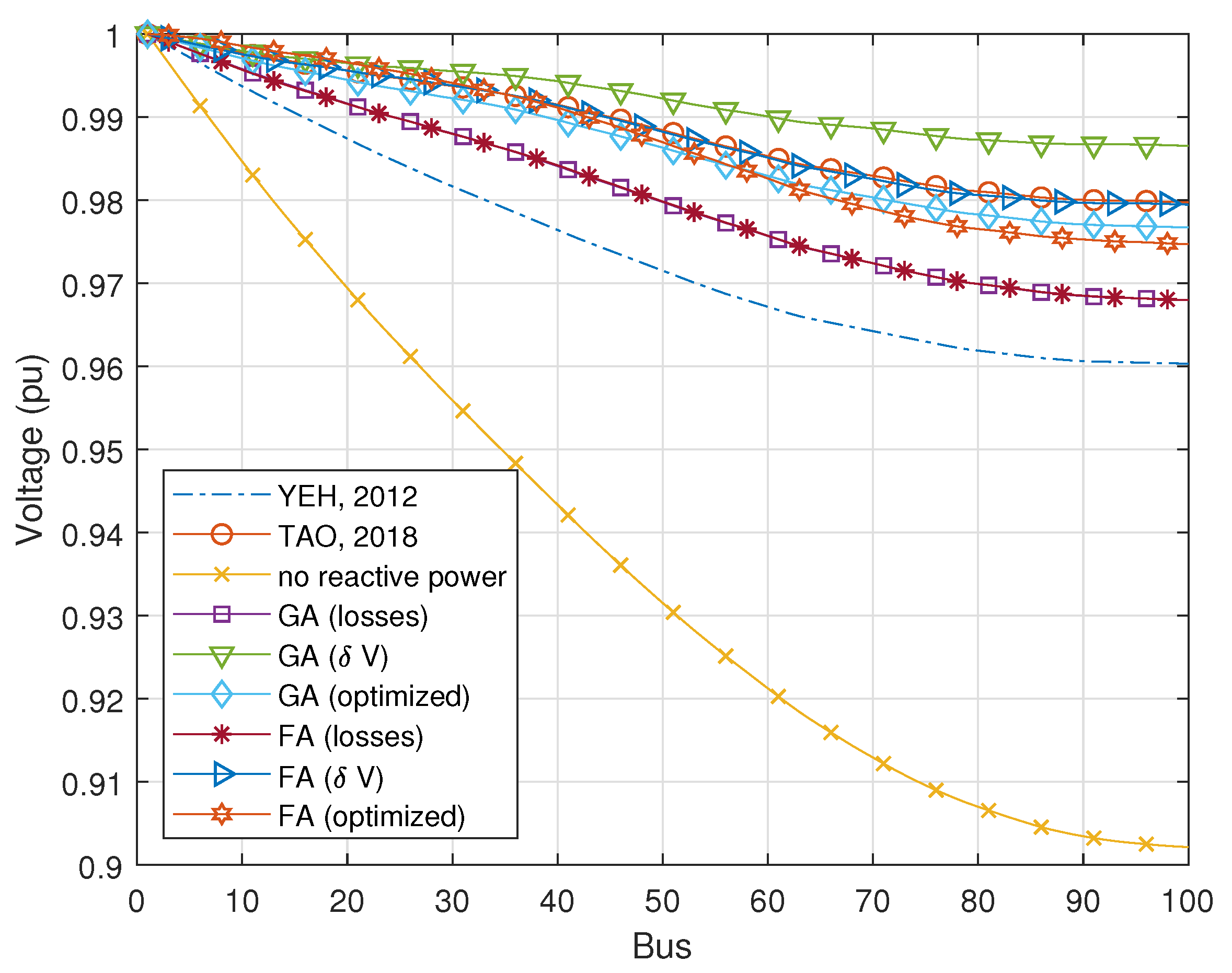
5.2.1. Voltage Profiles

The voltage profiles in the electrical network are presented in Figure 2. It can be observed that, without reactive support, the grid voltage profile decreases rapidly along the grid, reaching levels close 0.9 pu towards the most downstream buses. It occurs because it is a radial network with primary generation only at the initial bus. Five algorithms achieved voltage deviations below 3%: GA ($\delta V$), FA ($\delta V$), GA (optimized), FA (optimized), and the algorithm from [15]. Among these algorithms, the GA (voltage) algorithm obtained the lowest voltage deviations, providing values closer to 1 pu throughout the entire network. In the optimized case, scenario 3, both the GA and FA algorithms adhered to constraints and did not violate the lower voltage limits. However, the other algorithms, at some point in the network, provided voltages below 0.97 pu, violating the established voltage deviation limit. The key distinction between curves lies in the method of injecting reactive power into the network. In other words, by adjusting the reactive power values at the buses, it becomes possible to alter the entire voltage profile of the electrical network.

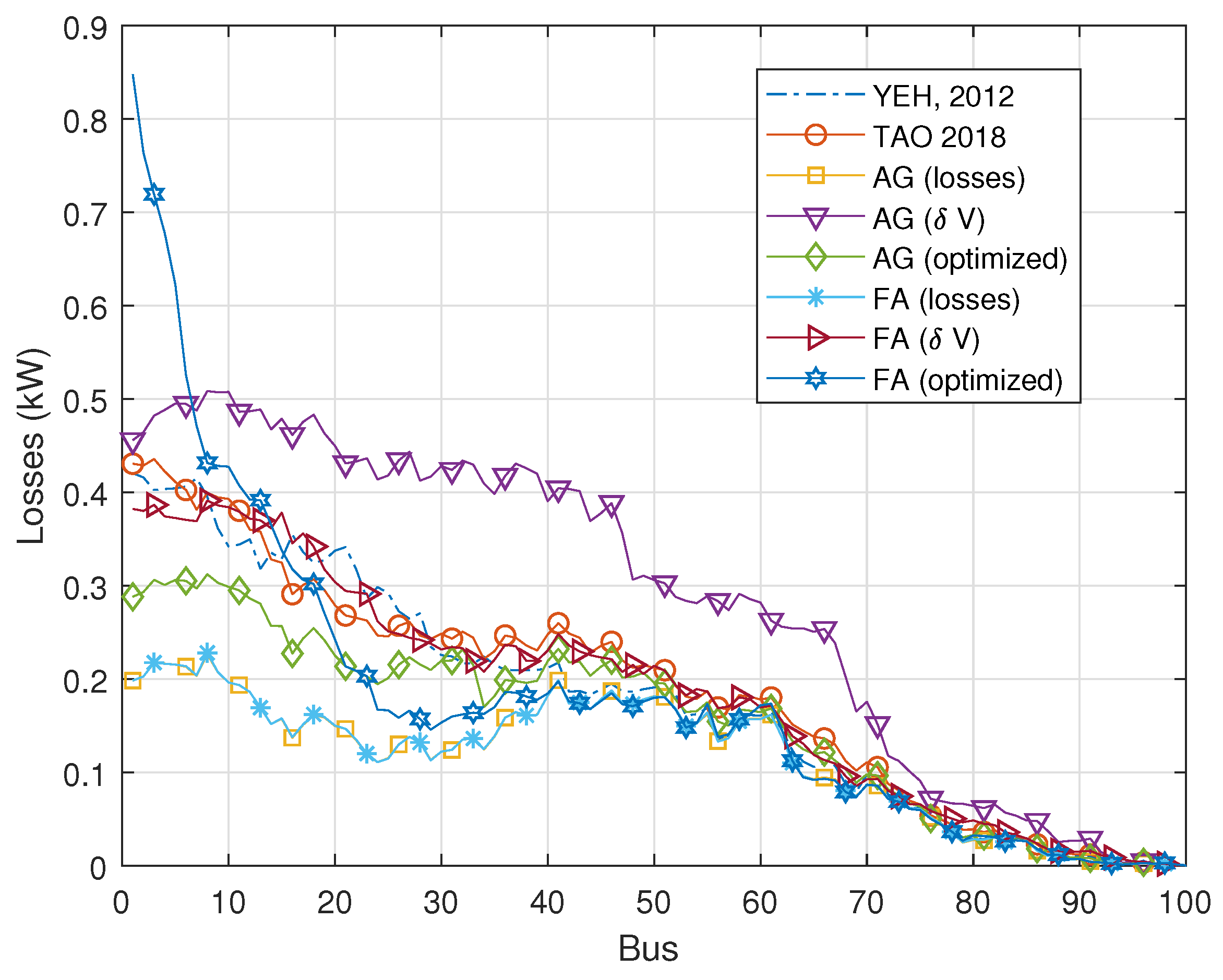
5.2.2. Real Power Losses

Electrical losses in the network mainly occur in the cables connecting one bus to another. These losses are primarily caused by the Joule effect due to the electrical resistance of the cables. The values of losses between buses primarily depend on the magnitude of the electrical current flowing between them. Figure 3 presents a comparison of electrical losses per bus for each algorithm. Since there is distributed reactive compensation throughout the electrical network, in addition to the active power generated by the PV systems, the loss curves vary from bus to bus and from method to method. In general, it can be observed that algorithms that solely minimize voltage deviation tend to have higher losses, such as GA ($\delta V$). On the other hand, algorithms that solely minimize losses without considering the voltage profile achieve the lowest loss results. The algorithms in scenario 3, which minimize losses while adhering to the voltage deviation constraint, yield intermediate loss values between scenario 1 (loss minimization) and scenario 2 (voltage deviation minimization). The total electrical losses, obtained by summing all the electrical losses between the buses shown in Figure 3, can be calculated as $P_{losses}\left(Q^G\right)={\sum }_{j=1}^{n-1}R·I_j^2$. These values are presented in

Table 4. Power losses (kW).

Method	Value (kW)
No reactive power	190.367
YEH, 2012 [14]	17.747
TAO, 2018 [15]	18.690
GA ($P_{losses}$)	11.578
GA ($\delta V$)	28.305
GA (optimized)	15.631
FA ($P_{losses}$)	11.581
FA ($\delta V$)	18.406
FA (optimized)	15.540

. The case with no reactive power exhibits the highest observed losses and is presented for comparison purposes only. The total losses for the best cases are close to 11 kW, achieved by FA and GA in scenario 1. However, in this scenario, there are voltage violations. Hence, the algorithms that provide the lowest losses without violating the voltage limits are FA and GA in scenario 3, that is, FA (optimized) and GA (optimized), with losses close to 15 kW.

In

Table 5. Active power supplied by the slack bus (kW).

Method	Value (kW)
No reactive power	613.299
YEH, 2012 [14]	440.679
TAO, 2018 [15]	441.625
GA ($P_{losses}$)	434.509
GA ($\delta V$)	551.237
GA (optimized)	438.563
FA ($P_{losses}$)	434.513
FA ($\delta V$)	441.338
FA (optimized)	438.472

, the generated active power values at the slack bus are presented. These values were obtained through power flow analysis. It is important for this value to be minimized so that the power consumed by the load is generated as closely as possible to the respective buses. The optimized GA and FA algorithms (scenario 3) achieve the lowest values without violating the voltage limits, approximately 438 kW.

5.2.3. Reactive Power Utilization

Table 6. Ratio between $Q^g$ and $S_{inv}$.

Method	Value
YEH, 2012 [14]	0.5038
TAO, 2018 [15]	0.7841
GA ($P_{losses}$)	0.6424
GA ($\delta V$)	0.7906
GA (optimized)	0.7295
FA ($P_{losses}$)	0.6443
FA ($\delta V$)	0.7681
FA (optimized)	0.7570

provides a comparison of the proposals in this article with other studies regarding the relative utilization of the reactive power capacity. The table shows the ratio between the total reactive power injected by PV and the maximum total reactive power of PV, which is limited by the apparent power of the inverter, i.e., $\frac{{\sum }_{j=1}^n{Q}_j^G}{{\sum }_{j=1}^n{S}_{inv,j}}$. This allows for a comparison of the voltage performance and losses with the overall reactive power utilization. It can be observed that the highest values occur in the methods that aim to minimize voltage deviation, as [15] and GA ($\delta V$). This is due to the fact that voltage is more sensitive to variations in reactive power compared to losses, which have a stronger relationship with electric current. Therefore, a greater amount of reactive power is required to correct the voltage profile of the power grid compared to minimizing electrical losses. The proposed methods, GA (optimized) and FA (optimized), achieve the lowest possible values while respecting the voltage deviation constraint of 3%. Although methods like [14] may yield lower values, the voltage values in those methods exceed the limits defined in this study.

While our proposed method involves establishing communication between the control center and nodes, resembling centralized scheduling, the advances in communication technologies, such as 5G, edge computing, and IoT, are reducing the drawbacks of centralized control and offering solutions for more robust network management. Based on the obtained results, it is evident that the following methodology is the most suitable concerning the injection of reactive power into the grid through PV generation.

6. Conclusions

This paper outlines a novel approach for injecting distributed reactive power along an electrical grid with distributed generation, utilizing PV inverters. The proposed method, described by Algorithm 2, consists in choosing GA ($\delta V$) in the Algorithm 1 if voltage violations are the main concern. To achieve the lowest losses without considering voltage limits, GA ($P_{losses}$) is the best option in the Algorithm 1. For minimizing reactive power utilization while adhering to a 3% voltage deviation constraint, the optimal choice is the FA (optimized), as pointed out by Algorithm 2. This approach was evaluated in a radial network and demonstrated a superior performance compared to existing methods. It effectively achieves the specified objectives and offers an enhanced solution for optimizing power systems. The controlled injection of reactive power had a positive impact on minimizing losses and enhancing the voltage profile of the electrical network. Overall, this work provides a promising solution for improving the efficiency and stability of power systems through the integration of PV technology.

Algorithm 2 Reactive power injection method.

Ensure:  $Q^G$. Optimized solution for reactive power generation according to the cost function 1: if (scenario 1) then 2:     Choose GA ($P_{losses}$) 3: end if 4: if (scenario 2) then 5:     Choose GA ($\delta V$) 6: end if 7: if (scenario 3) then 8:     Choose FA (optimized) 9: end if 10: return  $Q^G$

From the simulation results, a superior performance of our approach in a radial network is verified, which underscores its potential to enhance the operation and reliability of power systems, especially in scenarios with a high penetration of distributed generation. In summary, our work not only contributes valuable insights into the integration of PV technology but also offers a tangible and effective solution for power system operators and planners. By controlling the injection of reactive power, our approach not only reduces losses but also improves the overall voltage profile, ultimately contributing to more stable and efficient electrical networks.