Experimental Validation of Iterative Learning Control for DC/DC Power Converters
Abstract
:1. Introduction
- To switch the buck DC/DC converter into a switching system consisting of two different states of on and off and to use the switching-period average operator and the state-space average method to create the equivalent of a linear time-varying continuous circuit. Its conversion rule is determined by the duty cycle of the switch tube control signal.
- The system is controlled by an open-loop PD-type ILC. In addition to using ILC to control the buck DC/DC converter, the results are compared with traditional PI control.
- This paper also uses the traditional PI-type buck converter control method and compares and analyzes the control effects of both control techniques. One can see from the simulation and experimental results that the ILC has obvious advantages compared with the traditional PI control.
2. Modeling of the Buck Converter and Problem Statement
2.1. Modeling of Buck Converter Based on Traditional Control
2.1.1. Formation of Model in Broader Perspective
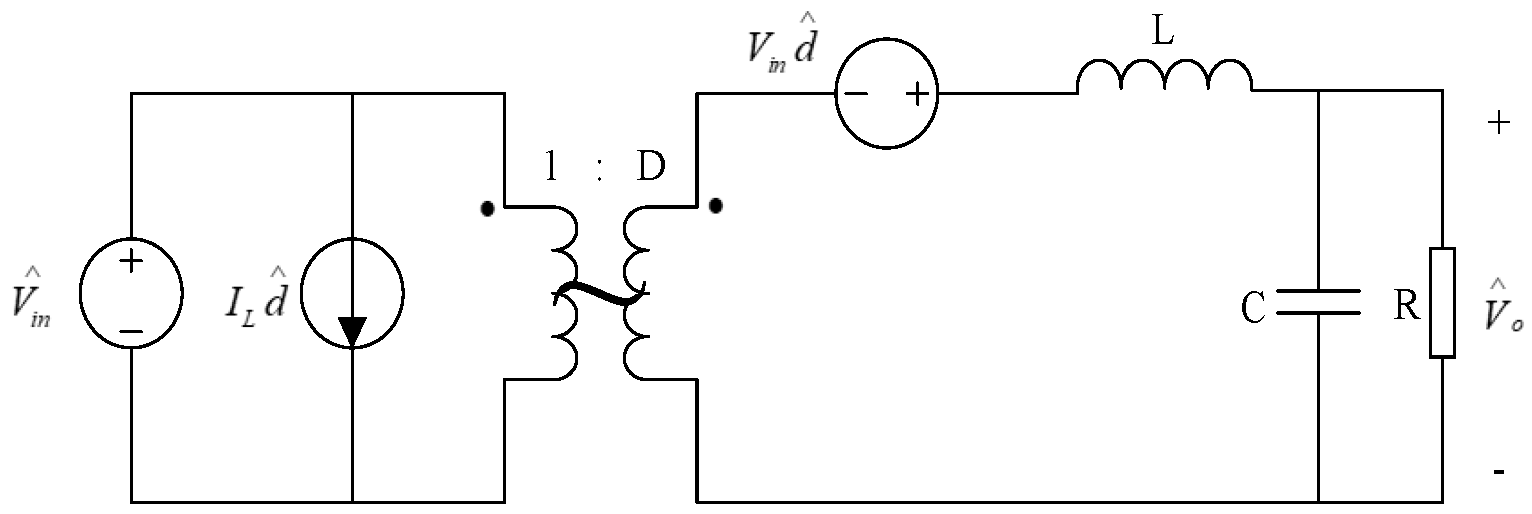
2.1.2. Formation of Small Signal Model
2.2. Design of Traditional PI Controller
2.3. Modeling of Buck Converter Based on Iterative Learning Control
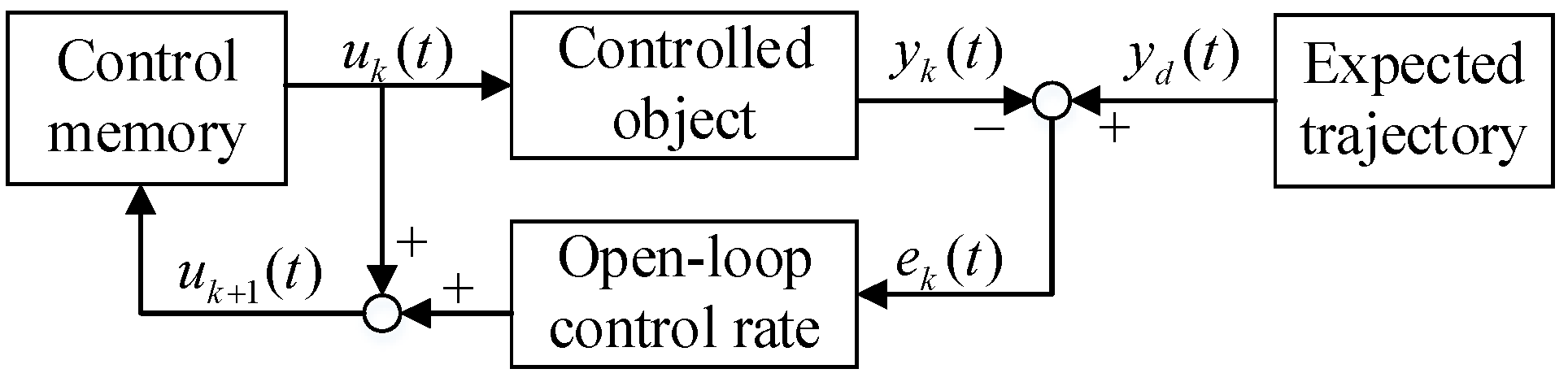
3. Iterative Learning Control Scheme
3.1. Fundamentals of ILC Control
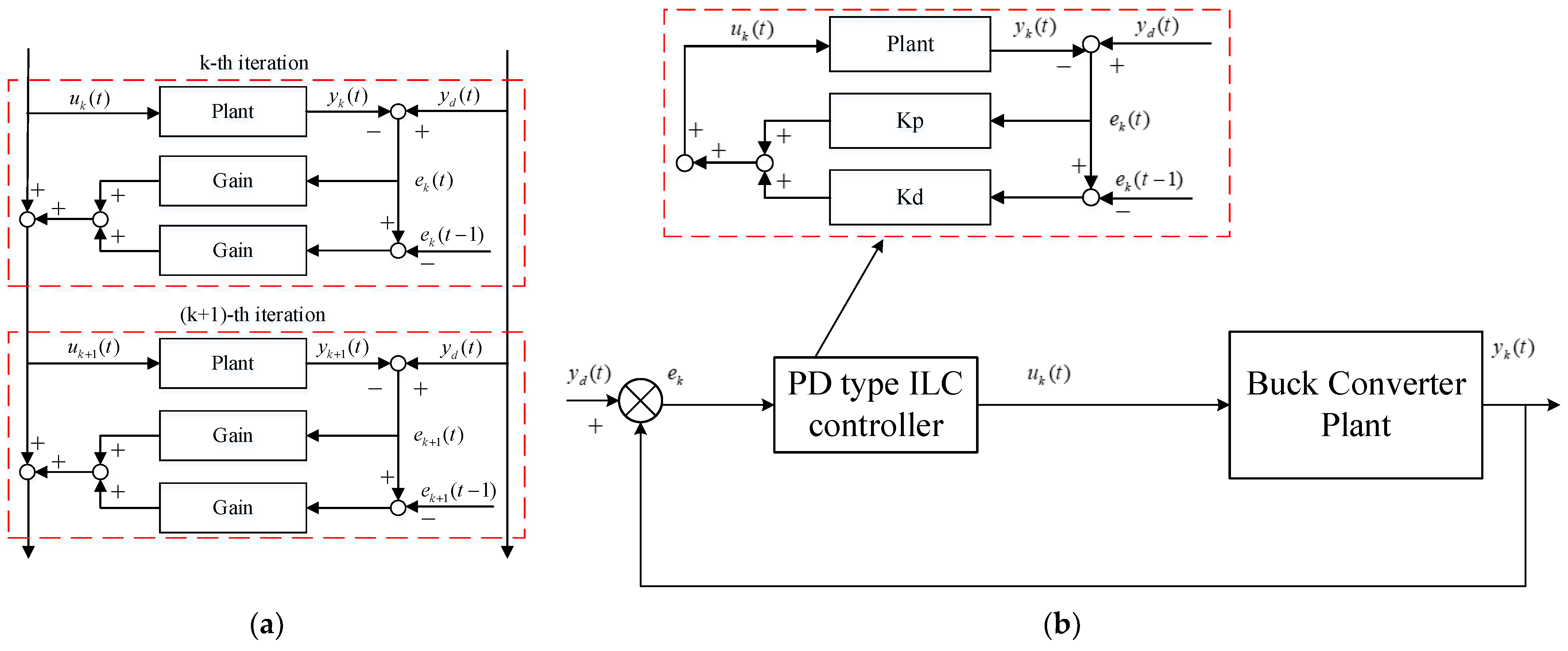
3.2. Learning Law of Proposed ILC
4. Implementation of Iterative Learning Control for Buck Converter
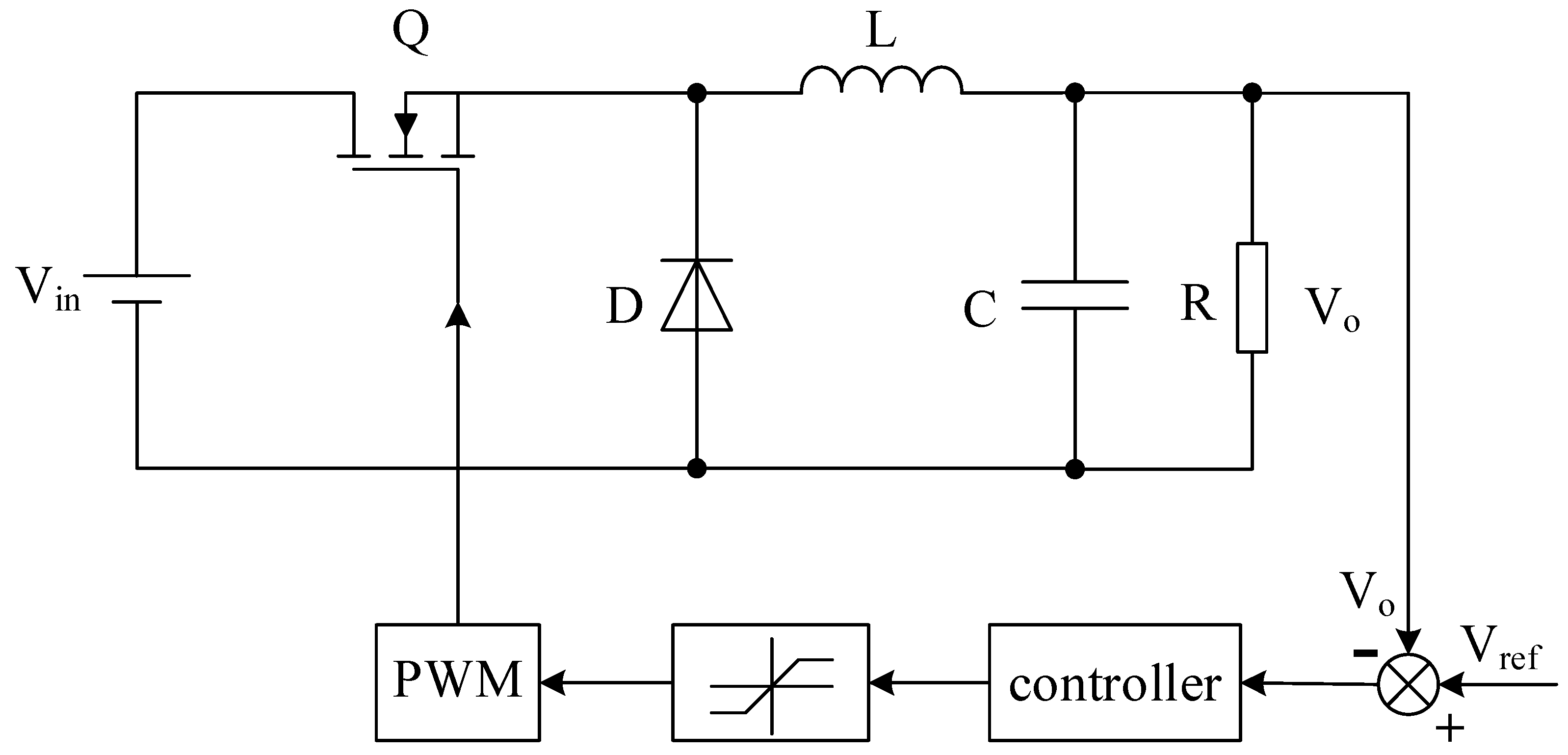
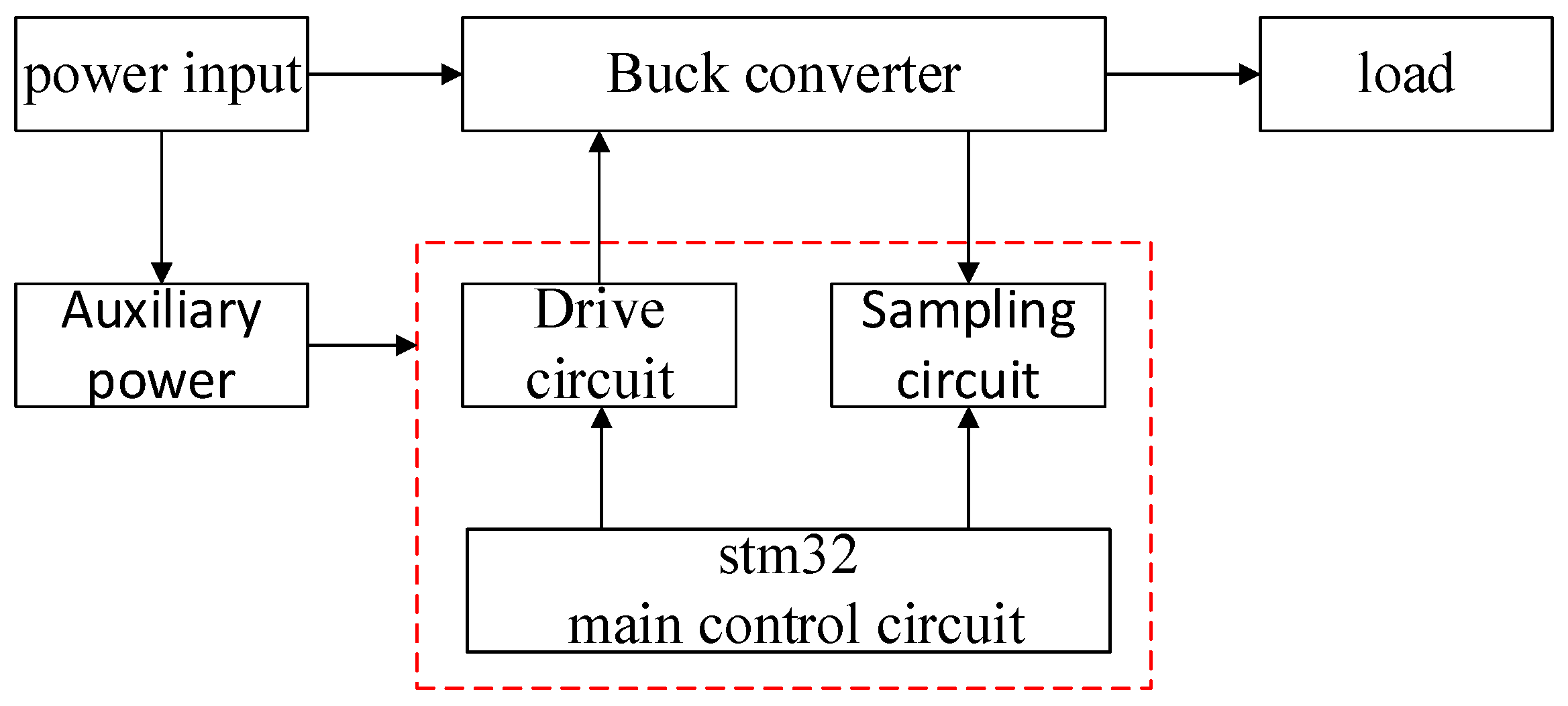
4.1. System Schematic Structure
4.2. Sampling Filtering Method
4.3. Implementation of Iterative Control Learning
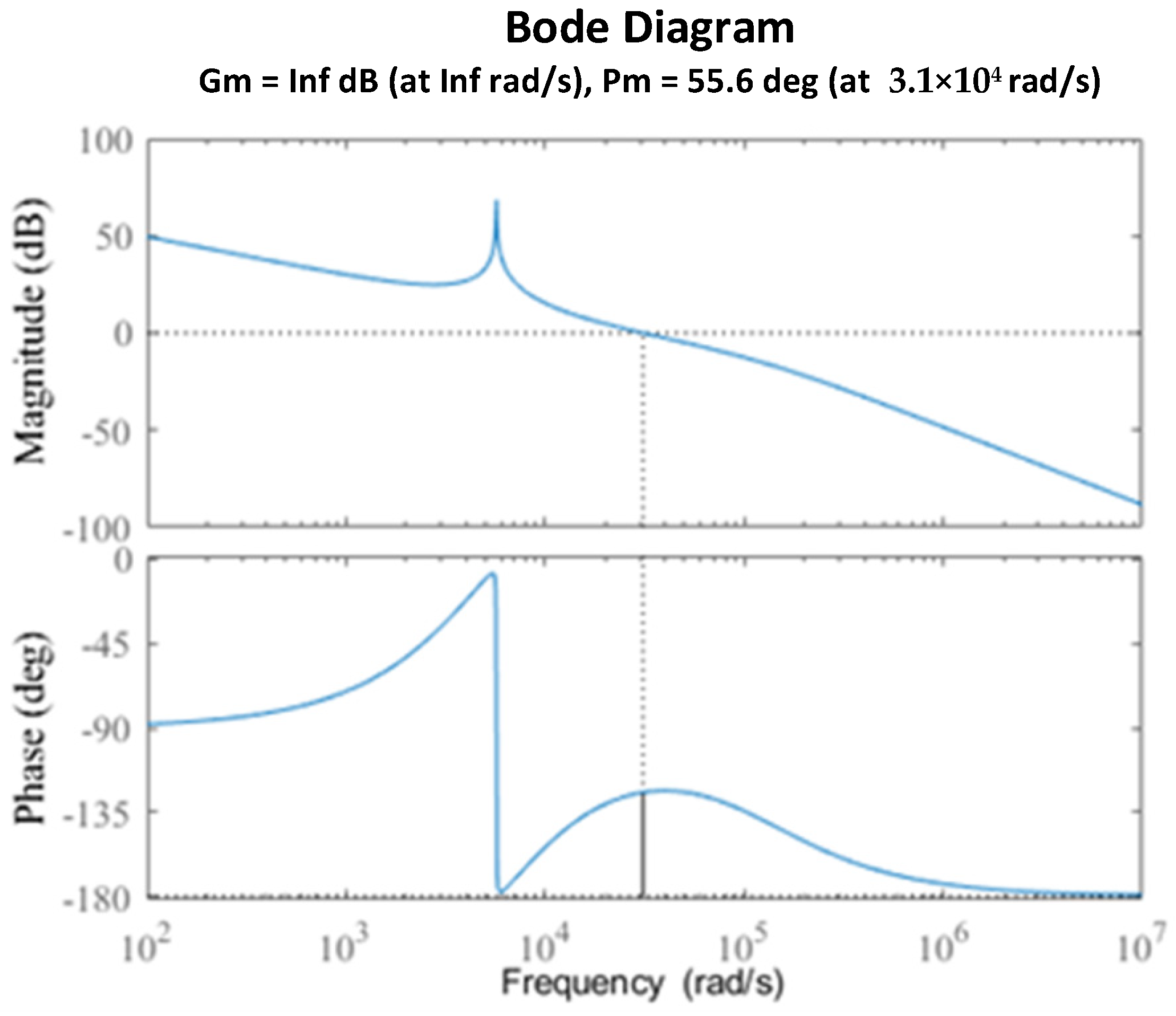
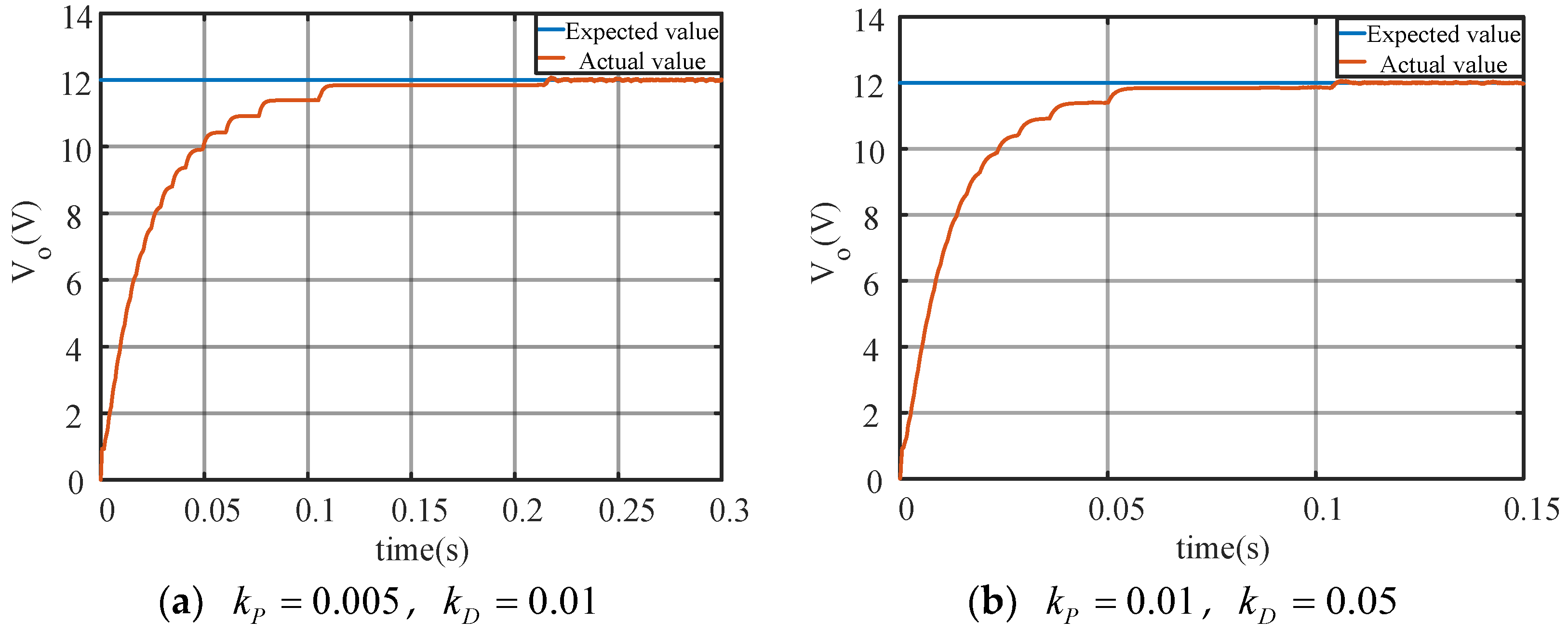
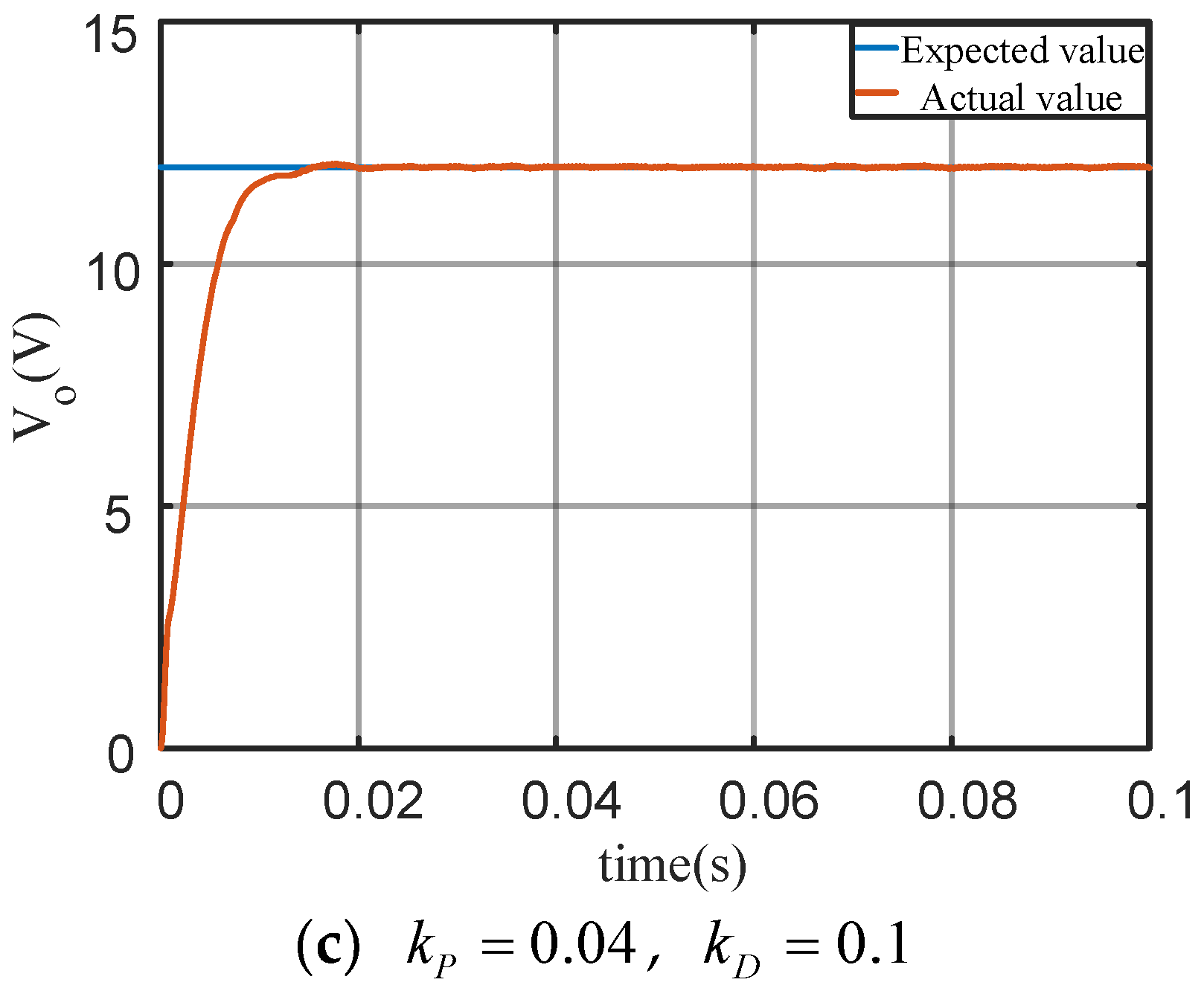
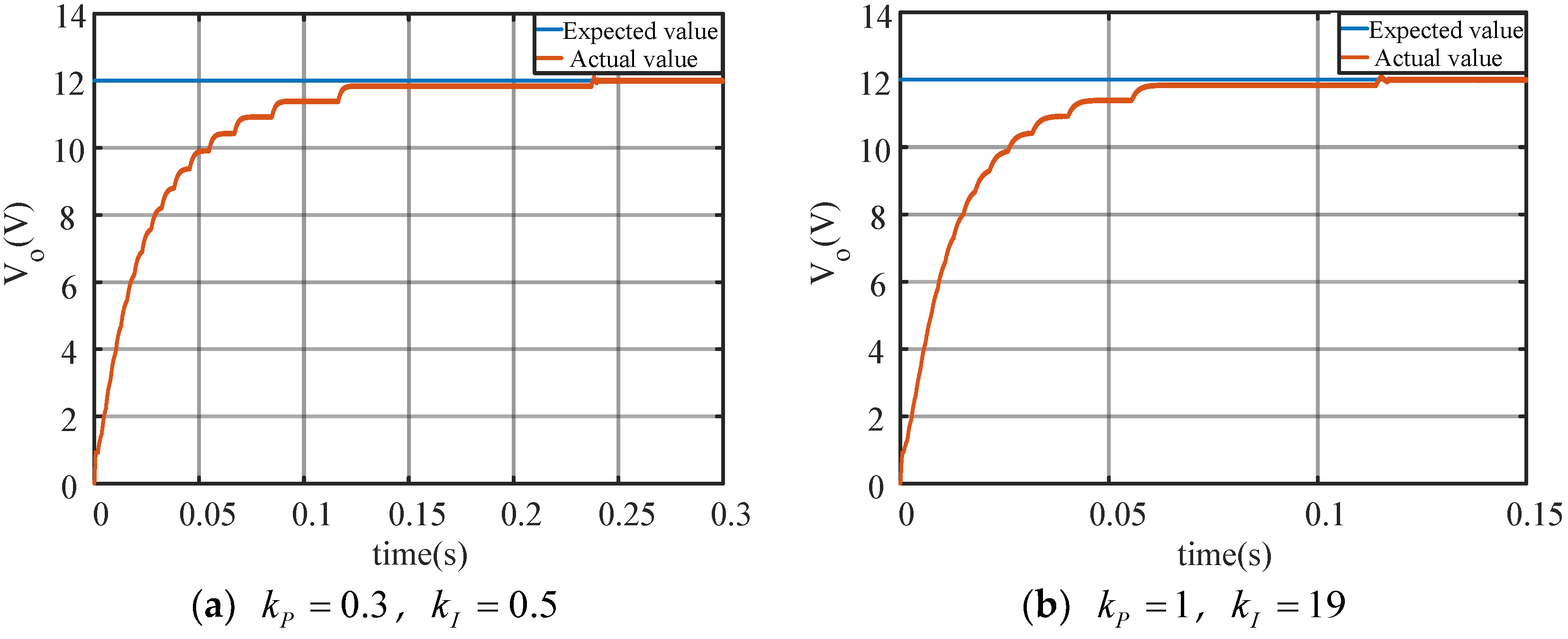
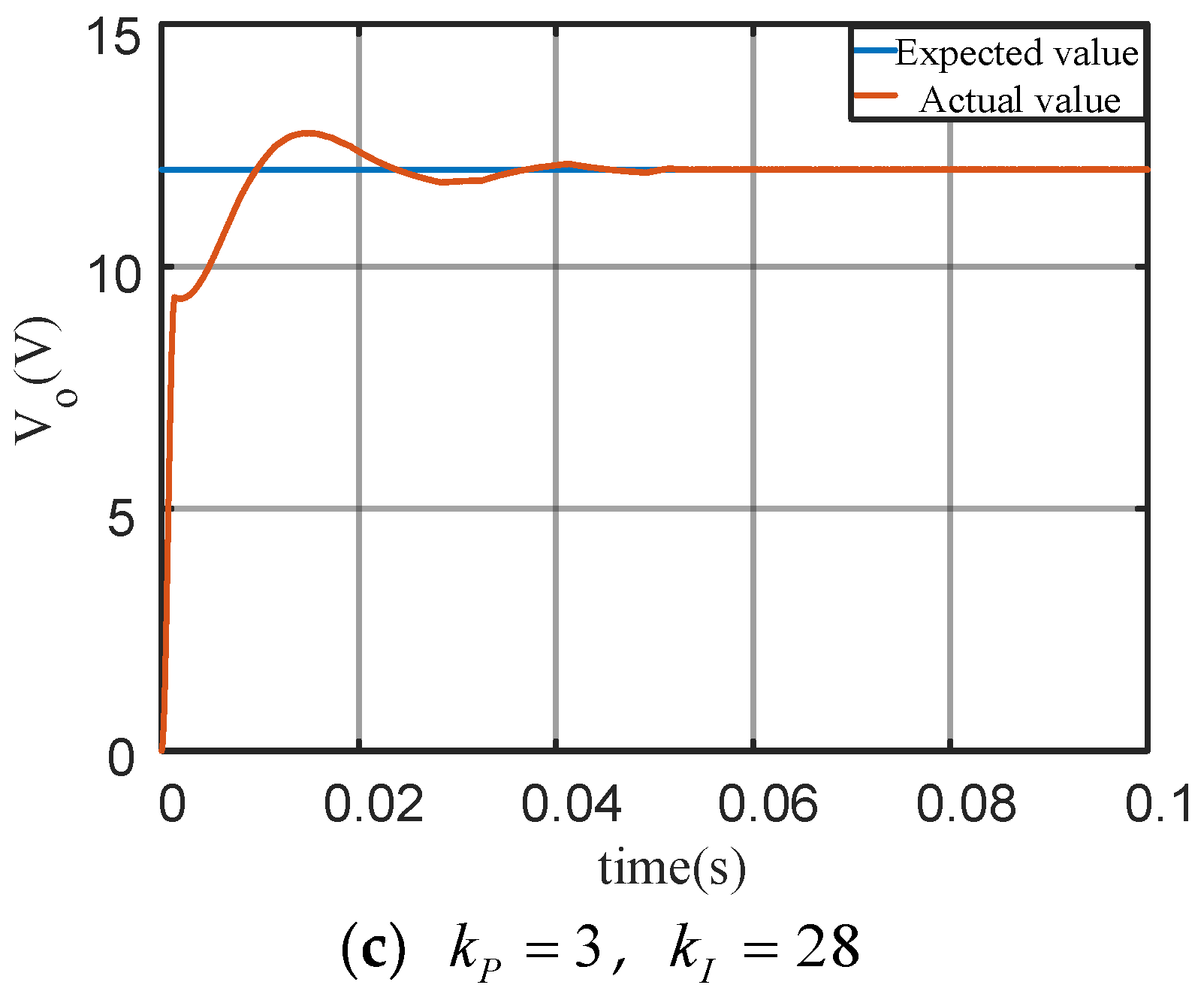
5. Main Simulation Results and Analysis
5.1. Simulation Verfication
5.2. Experimental Results
6. Conclusions
- We have proposed a new scheme that switches the buck DC/DC converter into a switching system that further consists of two different states of on and off, and we used the switching period average operator and the state space average method to equivalent a linear time-varying continuous circuit. This law is determined by the duty cycle of the switch tube control signal.
- We have successfully controlled the system with an open-loop PD-type ILC. Additionally, we have used the ILC to control the buck DC/DC converter, and our results have been compared to typical PI control.
- We have proven that the traditional PI-type buck converter control method is effective and compared the both control effects. We have evaluated, in simulation and experimental results, that the ILC has obvious advantages compared with typical PI control.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wei, F.; Bojin, Q.; Yipeng, W.; Haolin, L. High power DC-DC converter for renewable energy power system. In Proceedings of the 2014 IEEE Conference and Expo Transportation Electrification Asia-Pacific (ITEC Asia-Pacific), Beijing, China, 31 August–3 September 2014; pp. 1–4. [Google Scholar] [CrossRef]
- Rasin, Z.; Rahman, M.F. Control of bidirectional DC-DC converter for battery storage system in grid-connected quasi-Z-source pv inverter. In Proceedings of the 2015 IEEE Conference on Energy Conversion (CENCON), Johor Bahru, Malaysia, 19–20 October 2015; pp. 205–210. [Google Scholar] [CrossRef]
- Matsumori, H.; Kosaka, T.; Sekido, K.; Kim, K.; Egawa, T.; Matsui, N. Isolated DC-DC Converter utilizing GaN power device for Automotive Application. In Proceedings of the 2019 IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 17–21 March 2019; pp. 1704–1709. [Google Scholar] [CrossRef]
- Ning, J.; Zeng, J.; Du, X. A Four-port Bidirectional DC-DC Converter for Renewable Energy-Battery-DC Microgrid System. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; pp. 6722–6727. [Google Scholar] [CrossRef]
- Liu, H.; Liu, K.; Sun, B. Analysis of energy management strategy for energy-storage type elevator based on supercapacitor. In Proceedings of the 2017 11th IEEE International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG), Cadiz, Spain, 4–6 April 2017; pp. 175–180. [Google Scholar] [CrossRef]
- Yi, Z.; Chen, Z.; Yin, K.; Wang, L.; Wang, K. Sensing as the key to the safety and sustainability of new energy storage devices. Prot. Control Mod. Power Syst. 2023, 8, 27. [Google Scholar] [CrossRef]
- Zhang, M.; Yang, D.; Du, J.; Sun, H.; Li, L.; Wang, L.; Wang, K. A review of SOH prediction of Li-ion batteries based on data-driven algorithms. Energies 2023, 16, 3167. [Google Scholar] [CrossRef]
- Wang, X.; Wu, M.; Ouyang, L.; Tang, Q. The application of GA-PID control algorithm to DC-DC converter. In Proceedings of the 29th Chinese Control Conference, Beijing, China, 29–31 July 2010; pp. 3492–3496. [Google Scholar]
- Hongmei, L.; Xiao, Y. Sliding-mode PID control of DC-DC converter. In Proceedings of the 2010 5th IEEE Conference on Industrial Electronics and Applications, Taichung, Taiwan, 15–17 June 2010; pp. 730–734. [Google Scholar] [CrossRef]
- Guo, Y.; Zhang, C.; Wang, Z.; Huang, L. Study on the method of fuzzy PID control for DC/DC converter. In Proceedings of the 2010 International Conference on Information, Networking and Automation (ICINA), Kunming, China, 18–19 October 2010; pp. V1–329–V1–332. [Google Scholar] [CrossRef]
- Puchta, E.D.P.; Lucas, R.; Ferreira, F.R.V.; Siqueira, H.V.; Kaster, M.S. Gaussian adaptive PID control optimized via genetic algorithm applied to a step-down DC-DC converter. In Proceedings of the 2016 12th IEEE International Conference on Industry Applications (INDUSCON), Curitiba, Brazil, 20–23 November 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Malik, P.S.; Gawas, S.S.; Patel, I.A.; Parsekar, N.P.; Parab, A.A.; Parkar, S.S. Transient Response Improvement of DC to DC Converter by Using Auto-tuned PID Controller. In Proceedings of the 2018 Second International Conference on Inventive Communication and Computational Technologies (ICICCT), Coimbatore, India, 20–21 April 2018; pp. 546–549. [Google Scholar] [CrossRef]
- Zayed, M.E.; Zhao, J.; Li, W.; Elsheikh, A.H.; Abd Elaziz, M.; Yousri, D.; Zhong, S.; Mingxi, Z. Predicting the performance of solar dish Stirling power plant using a hybrid random vector functional link/chimp optimization model. Sol. Energy 2021, 222, 1–17. [Google Scholar] [CrossRef]
- Zayed, M.E.; Zhao, J.; Elsheikh, A.H.; Li, W.; Sadek, S.; Aboelmaaref, M.M. A comprehensive review on Dish/Stirling concentrated solar power systems: Design, optical and geometrical analyses, thermal performance assessment, and applications. J. Clean. Prod. 2021, 283, 124664. [Google Scholar] [CrossRef]
- Rezk, H.; Mazen, A.-O.; Gomaa, M.R.; Tolba, M.A.; Fathy, A.; Abdelkareem, M.A.; Olabi, A.; Abou Hashema, M. A novel statistical performance evaluation of most modern optimization-based global MPPT techniques for partially shaded PV system. Renew. Sustain. Energy Rev. 2019, 115, 109372. [Google Scholar] [CrossRef]
- Rezk, H.; Arfaoui, J.; Gomaa, M.R. Optimal parameter estimation of solar PV panel based on hybrid particle swarm and grey wolf optimization algorithms. Int. J. Interact. Multimed. Artif. Intell. 2021, 6, 145–155. [Google Scholar] [CrossRef]
- Bao, H.; Shu, P.; Wang, Q. Accurate visual representation learning for single object tracking. Multimed. Tools Appl. 2022, 81, 24059–24079. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Y.; Tang, L.; Zhang, Q. Multi-Objective Ensemble Learning with Multi-Scale Data for Product Quality Prediction in Iron and Steel Industry. IEEE Trans. Evol. Comput. 2023. [Google Scholar] [CrossRef]
- Storey, E.E.; Helmy, A.S. Optimized preprocessing and machine learning for quantitative Raman spectroscopy in biology. J. Raman Spectrosc. 2019, 50, 958–968. [Google Scholar] [CrossRef]
- Ma, N.; Yin, H.; Wang, K. Prediction of the Remaining Useful Life of Supercapacitors at Different Temperatures Based on Improved Long Short-Term Memory. Energies 2023, 16, 5240. [Google Scholar] [CrossRef]
- Sun, X.; Zhang, Y.; Zhang, Y.; Wang, L.; Wang, K. Summary of Health-State Estimation of Lithium-Ion Batteries Based on Electrochemical Impedance Spectroscopy. Energies 2023, 16, 5682. [Google Scholar] [CrossRef]
- Hoehler, D.; Haag, J.; Kozlov, A.M.; Stamatakis, A. A representative performance assessment of maximum likelihood based phylogenetic inference tools. bioRxiv 2022. [Google Scholar] [CrossRef]
- Tsypkin, Y.Z. Robust Control Systems with Internal Nominal Models. In Control of Uncertain Dynamic Systems; CRC Press: Boca Raton, FL, USA, 2020; pp. 501–509. [Google Scholar]
- Tsypkin, Y.Z.; Polyak, B. Frequency domain criterion for robust stability of polytope of polynomials. In Control of Uncertain Dynamic Systems; CRC Press: Boca Raton, FL, USA, 2020; pp. 491–499. [Google Scholar]
- Arimoto, S.; Kawamura, S.; Miyazaki, F. Bettering operation of Robots by learning. J. Robot. Syst. 2007, 1, 123–140. [Google Scholar] [CrossRef]
- Li, G. High-order iterative learning control for nonlinear systems. In Proceedings of the 2017 6th Data Driven Control and Learning Systems (DDCLS), Chongqing, China, 26–27 May 2017; pp. 191–196. [Google Scholar] [CrossRef]
- Zhang, R.; Hou, Z.; Chi, R.; Li, Z. Data-driven iterative learning control for I/O constrained LTI systems. In Proceedings of the 2016 35th Chinese Control Conference (CCC), Chengdu, China, 27–29 July 2016; pp. 3166–3171. [Google Scholar] [CrossRef]
- Jingli, K. Iterative learning control algorithm based on Chebyshev orthonormal basis for nonlinear systems. In Proceedings of the 2015 34th Chinese Control Conference (CCC), Hangzhou, China, 28–30 July 2015; pp. 3017–3021. [Google Scholar] [CrossRef]
- Shan-hai, X.; Zhong, Z.; Xin, Z. PD-type open-closed-loop iterative learning control in the networked control system. In Proceedings of the 2016 Chinese Control and Decision Conference (CCDC), Yinchuan, China, 28–30 May 2016; pp. 5738–5744. [Google Scholar] [CrossRef]
- Ruikun, Z.; Ronghu, C. Iterative learning control for a class of MIMO nonlinear system with input saturation constraint. In Proceedings of the 2017 36th Chinese Control Conference (CCC), Dalian, China, 26–28 July 2017; pp. 3543–3547. [Google Scholar] [CrossRef]
- Riaz, S.; Lin, H.; Waqas, M.; Afzal, F.; Wang, K.; Saeed, N. An accelerated error convergence design criterion and implementation of lebesgue-p norm ILC control topology for linear position control systems. Math. Probl. Eng. 2021, 2021, 5975158. [Google Scholar] [CrossRef]
- Xining, Z.; Chenglin, L.; Fei, L. A class of P-type fuzzy iterative learning control design. In Proceedings of the 31st Chinese Control Conference, Hefei, China, 25–27 July 2012; pp. 3052–3056. [Google Scholar]
- Riaz, S.; Lin, H.; Akhter, M.P. Design and implementation of an accelerated error convergence criterion for norm optimal iterative learning controller. Electronics 2020, 9, 1766. [Google Scholar] [CrossRef]
- Yan, Q.; Cai, J.; Wu, L.; Zhou, Q. Error-Tracking Iterative Learning Control for Nonlinearly Parametric Time-Delay Systems with Initial State Errors. IEEE Access 2018, 6, 12167–12174. [Google Scholar] [CrossRef]
- Dai, X.; Tian, S.; Peng, Y.; Luo, W. Closed-loop P-type iterative learning control of uncertain linear distributed parameter systems. IEEE/CAA J. Autom. Sin. 2014, 1, 267–273. [Google Scholar] [CrossRef]
- Yan, Q.; Cai, J.; Yu, Y. Suboptimal learning control for nonlinear dynamic systems. In Proceedings of the 2017 Chinese Automation Congress (CAC), Jinan, China, 20–22 October 2017. [Google Scholar]
- Wang, J.; Wang, Y.; Wang, W.; Cao, L.; Jin, Q. Adaptive iterative learning control based on unfalsified strategy applied in batch process. J. Cent. South Univ. 2015, 46, 1318–1325. [Google Scholar]
- Zhang, X.; Wang, B.; Gamage, D.; Ukil, A. Model predictive and iterative learning control based hybrid control method for hybrid energy storage system. IEEE Trans. Sustain. Energy 2021, 12, 2146–2158. [Google Scholar] [CrossRef]
- Wang, X.; Luo, Y.; Qin, B.; Guo, L. Power dynamic allocation strategy for urban rail hybrid energy storage system based on iterative learning control. Energy 2022, 245, 123263. [Google Scholar] [CrossRef]
- Angalaeswari, S.; Jamuna, K. Design and implementation of a robust iterative learning controller for voltage and frequency stabilization of hybrid microgrids. Comput. Electr. Eng. 2020, 84, 106631. [Google Scholar] [CrossRef]
- Özbek, N.S.; Çelik, Ö. Design and analysis of a novel adaptive learning control scheme for performance promotion of grid-connected PV systems. Sustain. Energy Technol. Assess. 2022, 52, 102045. [Google Scholar] [CrossRef]
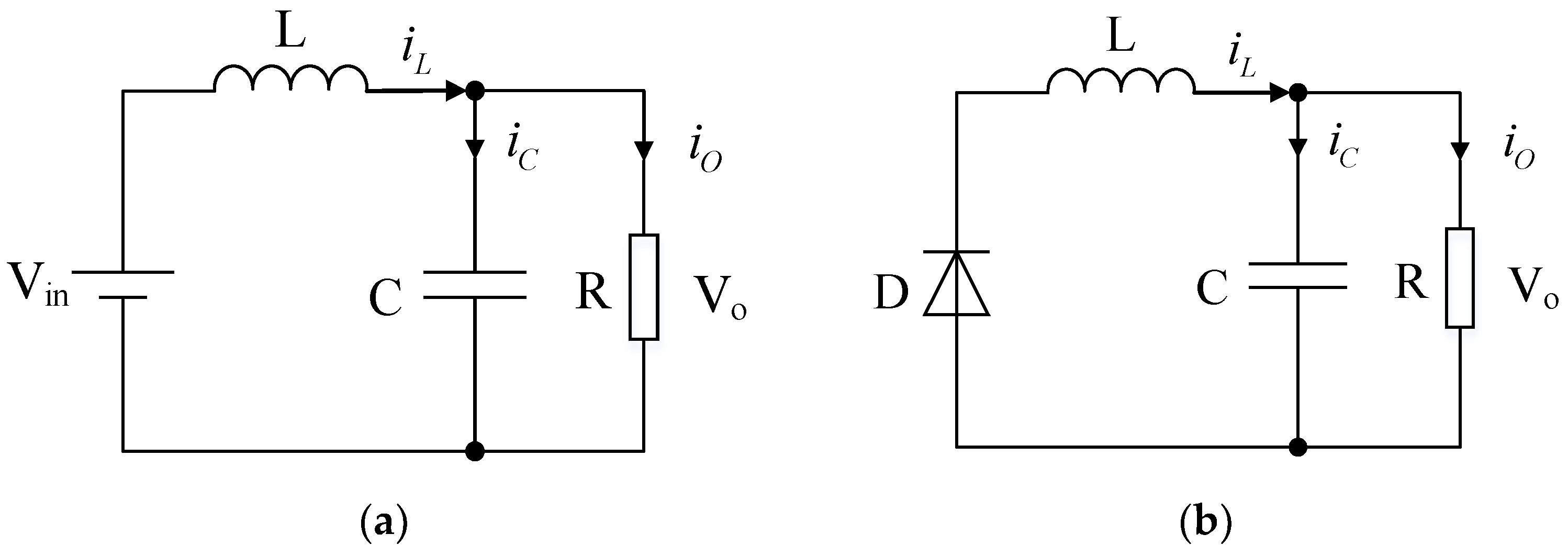



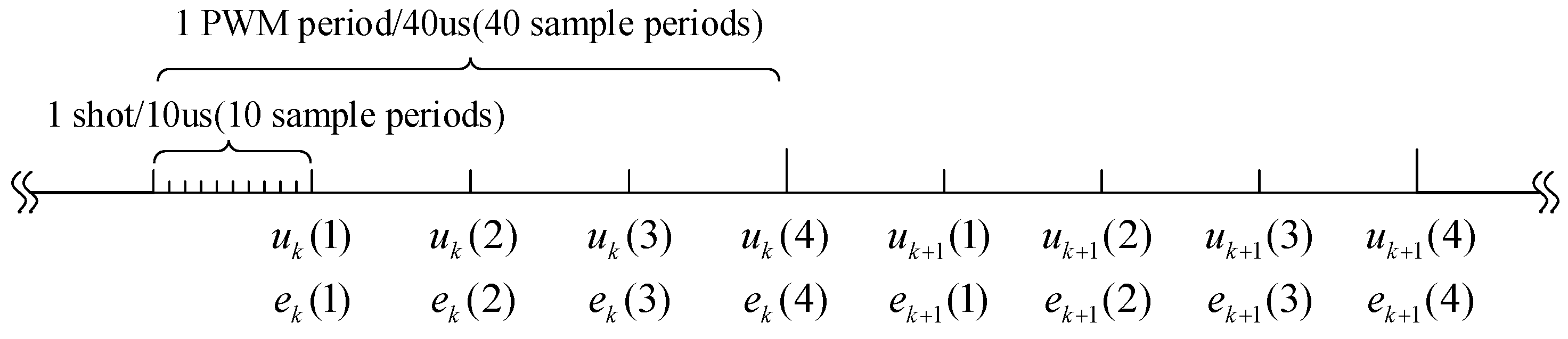


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, B.; Riaz, S.; Zhao, Y. Experimental Validation of Iterative Learning Control for DC/DC Power Converters. Energies 2023, 16, 6555. https://doi.org/10.3390/en16186555
Li B, Riaz S, Zhao Y. Experimental Validation of Iterative Learning Control for DC/DC Power Converters. Energies. 2023; 16(18):6555. https://doi.org/10.3390/en16186555
Chicago/Turabian StyleLi, Bingqiang, Saleem Riaz, and Yiyun Zhao. 2023. "Experimental Validation of Iterative Learning Control for DC/DC Power Converters" Energies 16, no. 18: 6555. https://doi.org/10.3390/en16186555
APA StyleLi, B., Riaz, S., & Zhao, Y. (2023). Experimental Validation of Iterative Learning Control for DC/DC Power Converters. Energies, 16(18), 6555. https://doi.org/10.3390/en16186555







