Influence of the Skin and Proximity Effects on the Thermal Field in a System of Two Parallel Round Conductors
Abstract
:1. Introduction
2. Methods
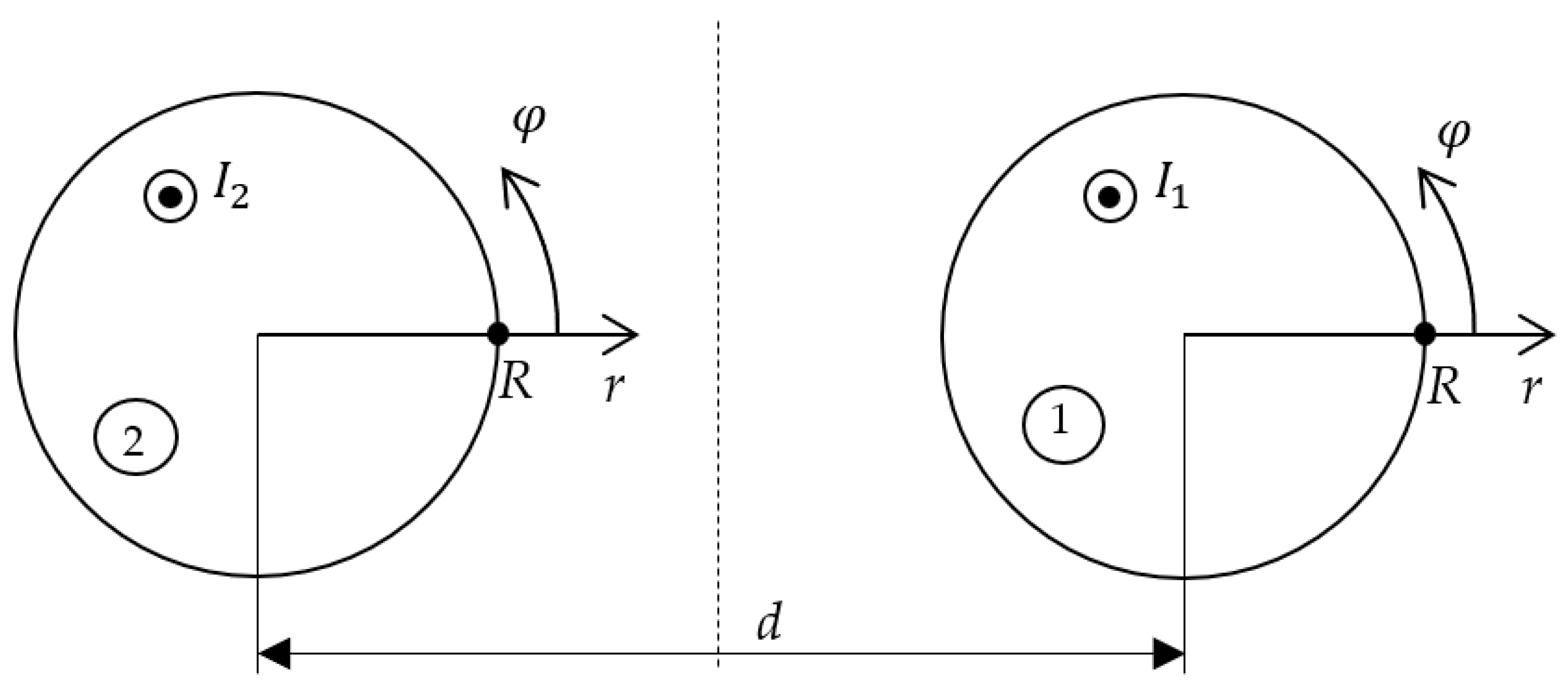
2.1. Assumptions
2.2. Governing Equations
2.3. The Method of Green’s Function
2.4. The Algorithm
- Begin from the shape of the conductor (here, two cylindrical conductors of radius separated by distance ), material parameters and , heat transfer coefficient and the current density in the conductors (here given by Equation (1)).
- Determine the Green’s function corresponding to the shape and equations describing heat exchange—here given by Equations (3)–(6). Note that Green’s function does not depend on the current density or electrical parameters and is calculated only once—see Equations (8)–(9).
- Use Equation (7) to determine the temperature at any point in the conductor.
- Calculate such quantities as the steady-state current rating.
3. Results
3.1. Green’s Function
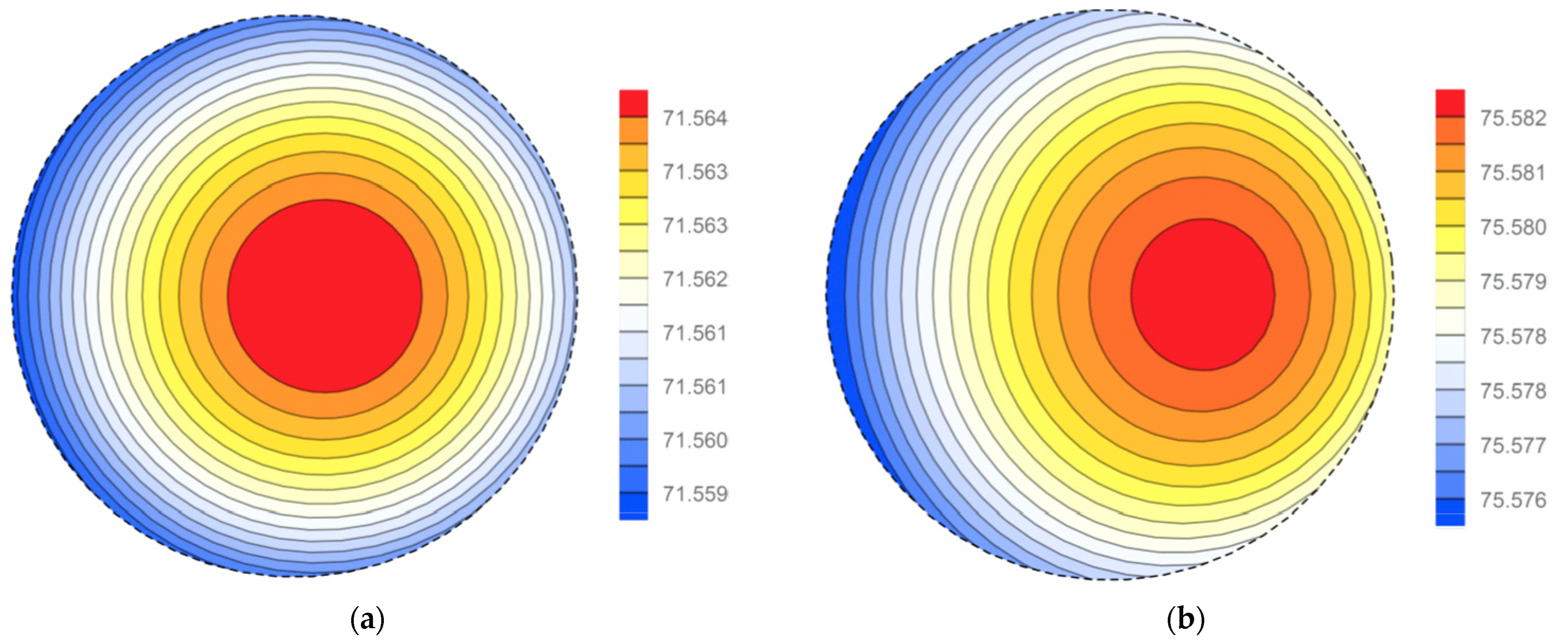
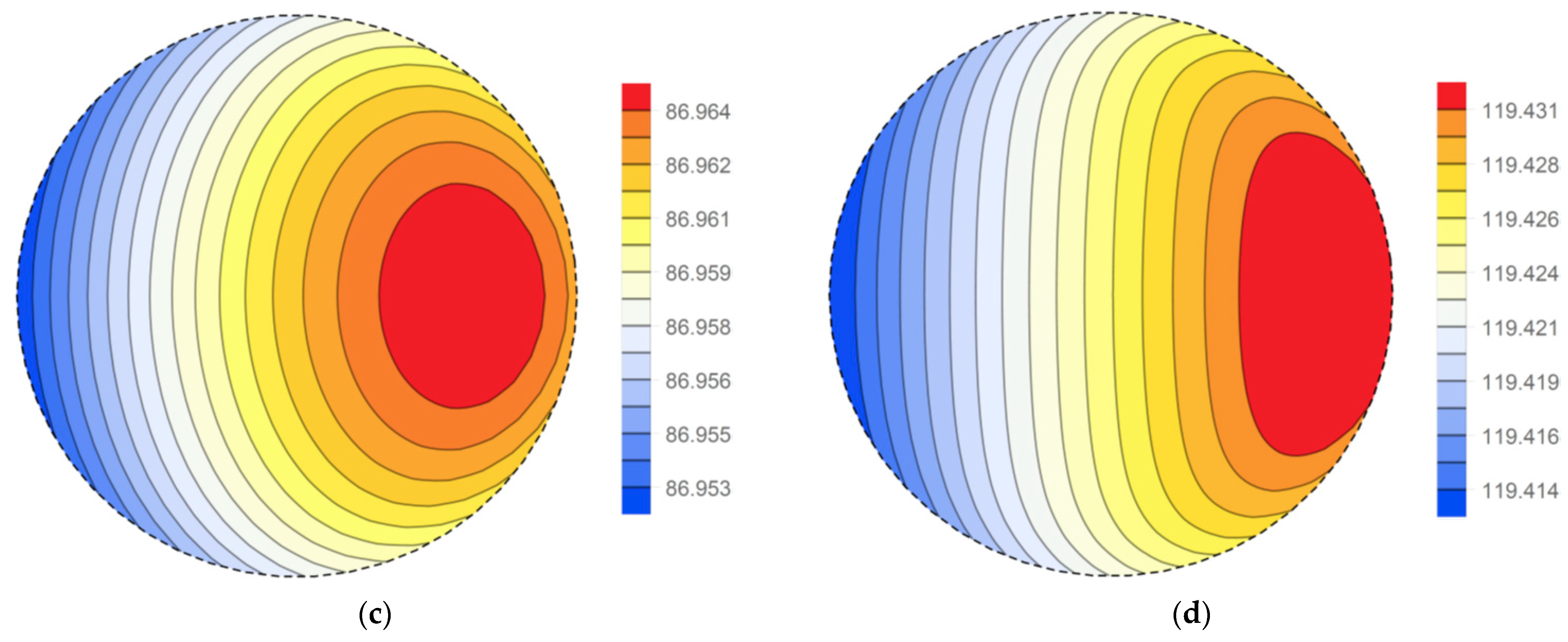
3.2. Temperature Distribution
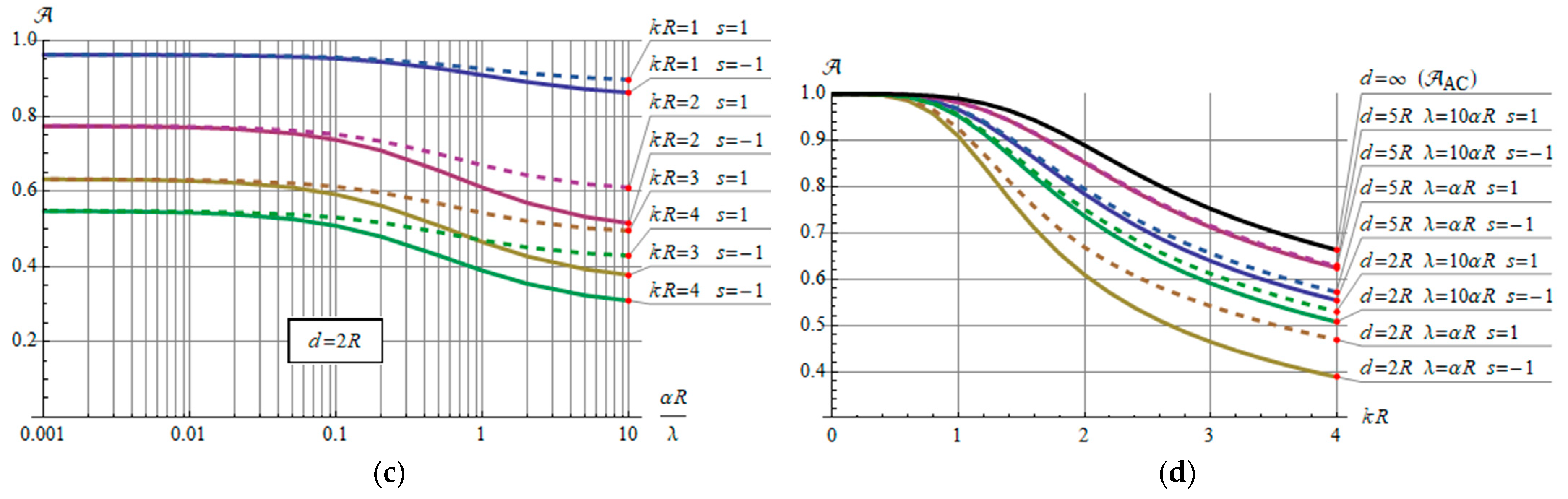
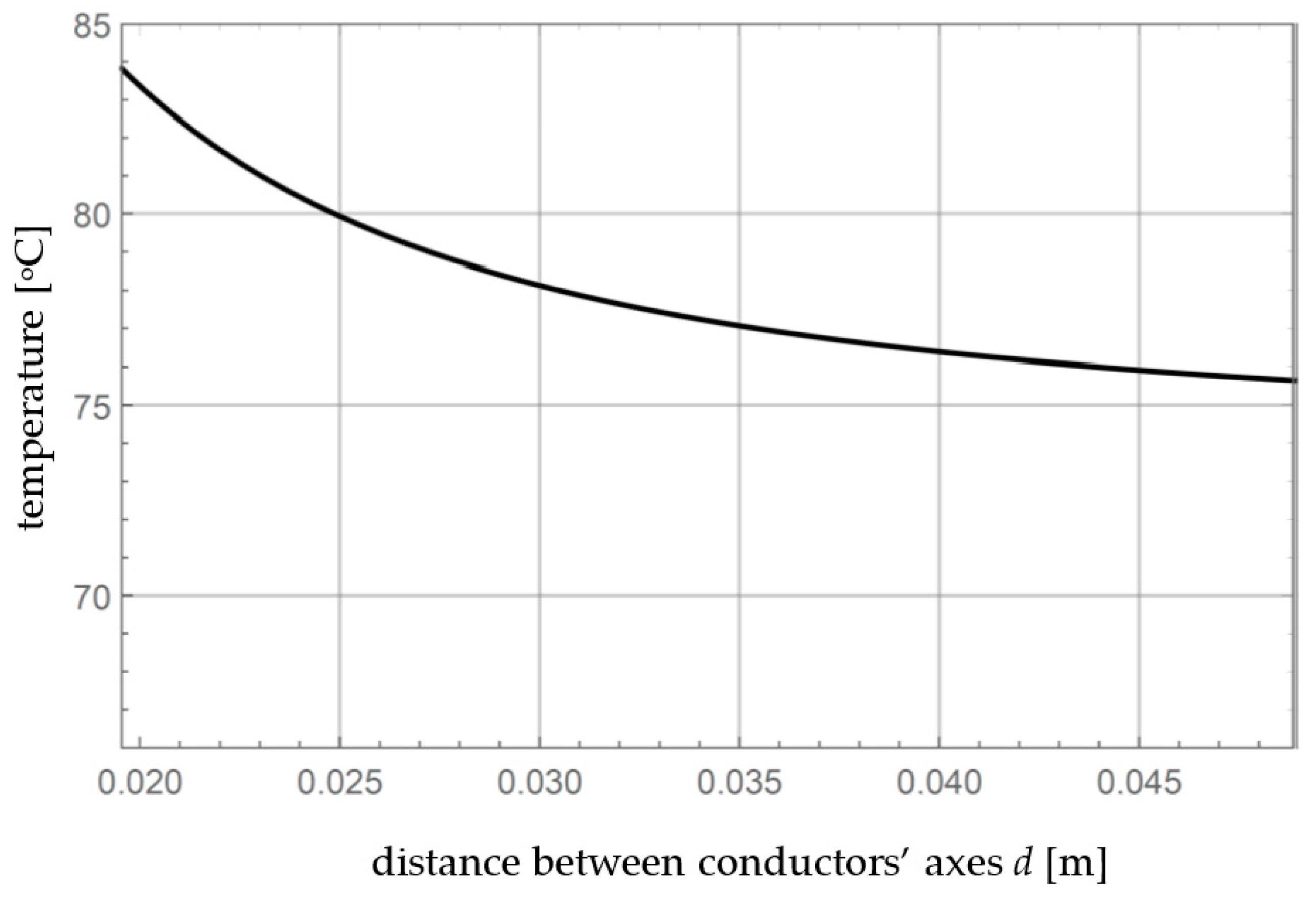
3.3. Temperature on the Conductor’s Surface
- the skin effect strength, ;
- the relative distance between the conductors, ;
- the heat transport ratio, ;
- the direction and modulus of current in the neighboring wire, (complex number);
- the observation point on the wire surface (angle ).
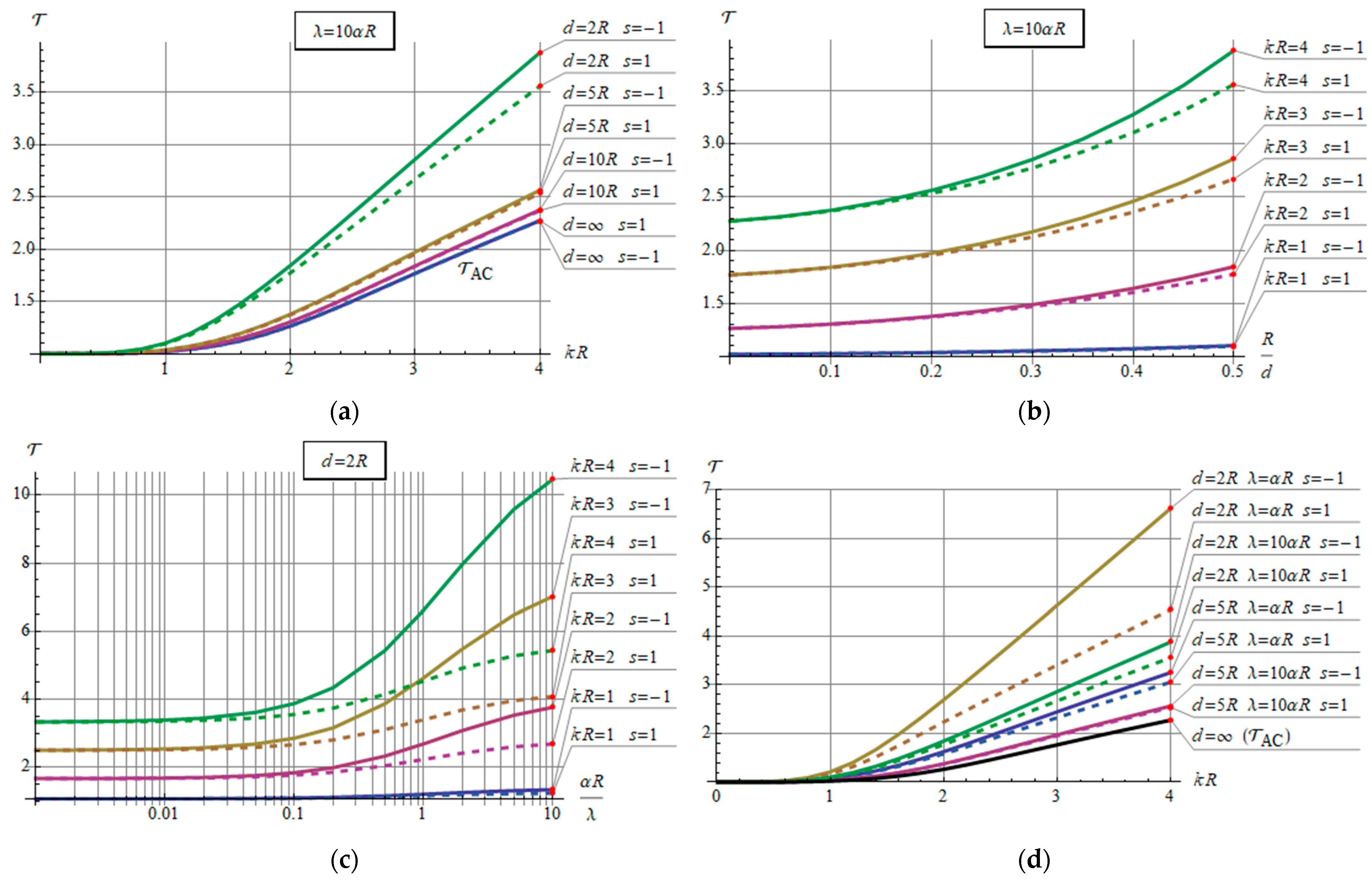
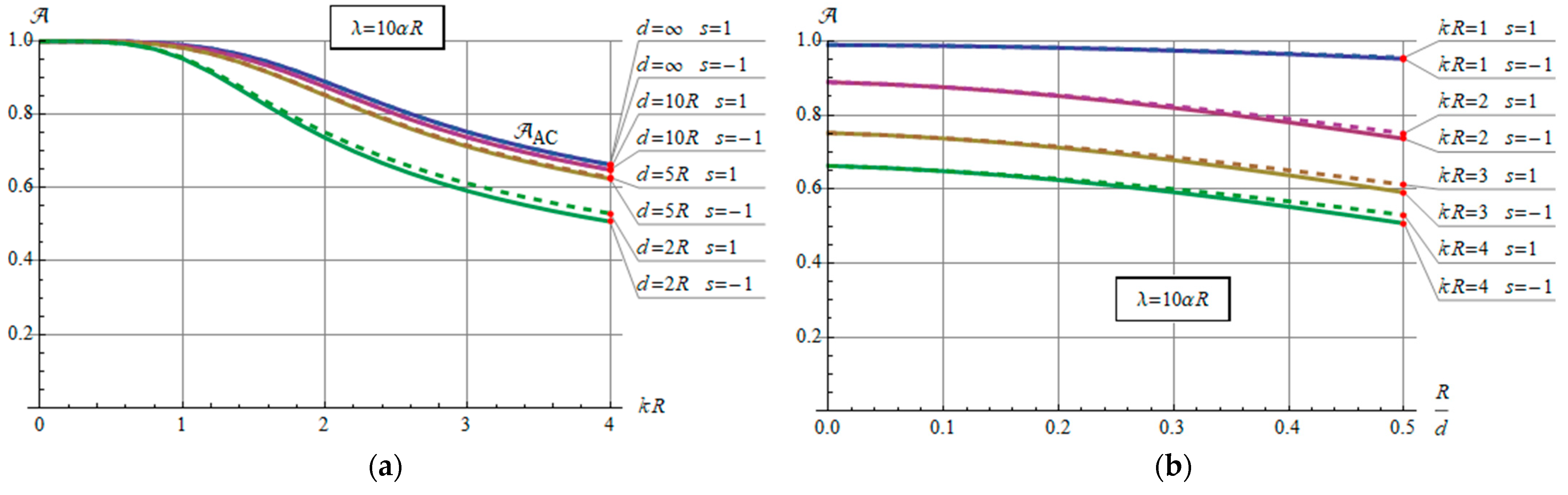
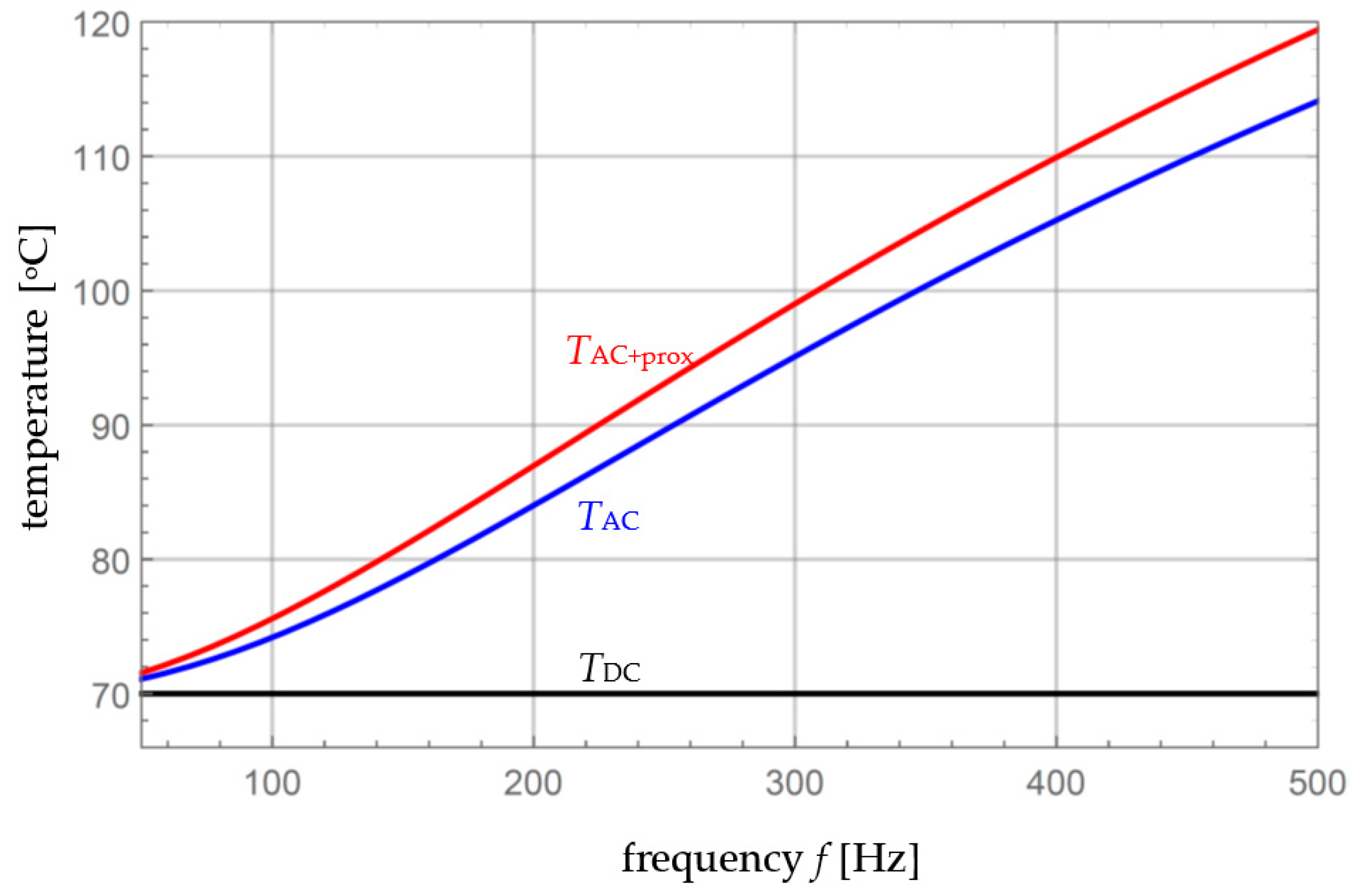
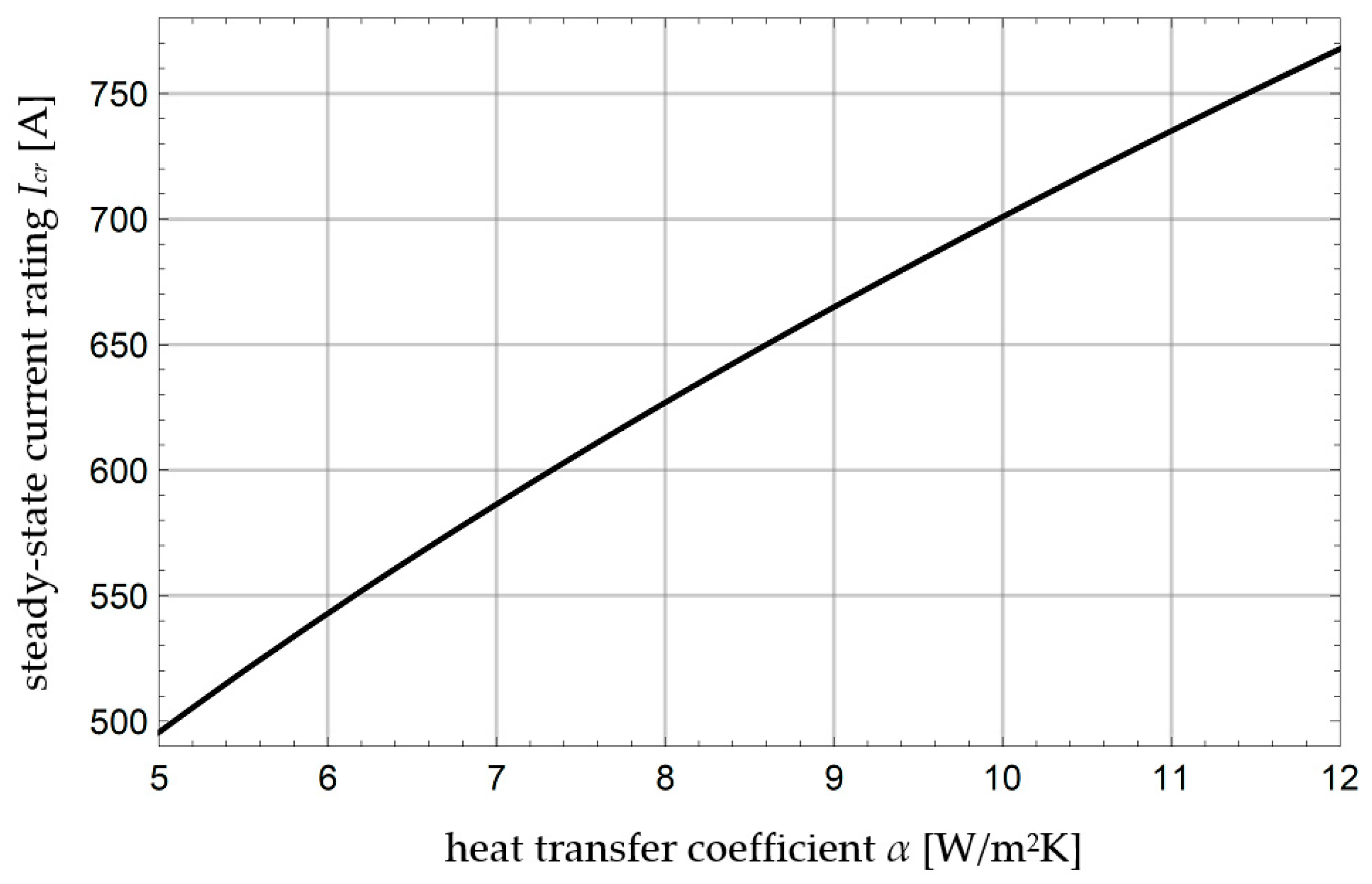
3.4. Steady-State Current Rating of the Conductor
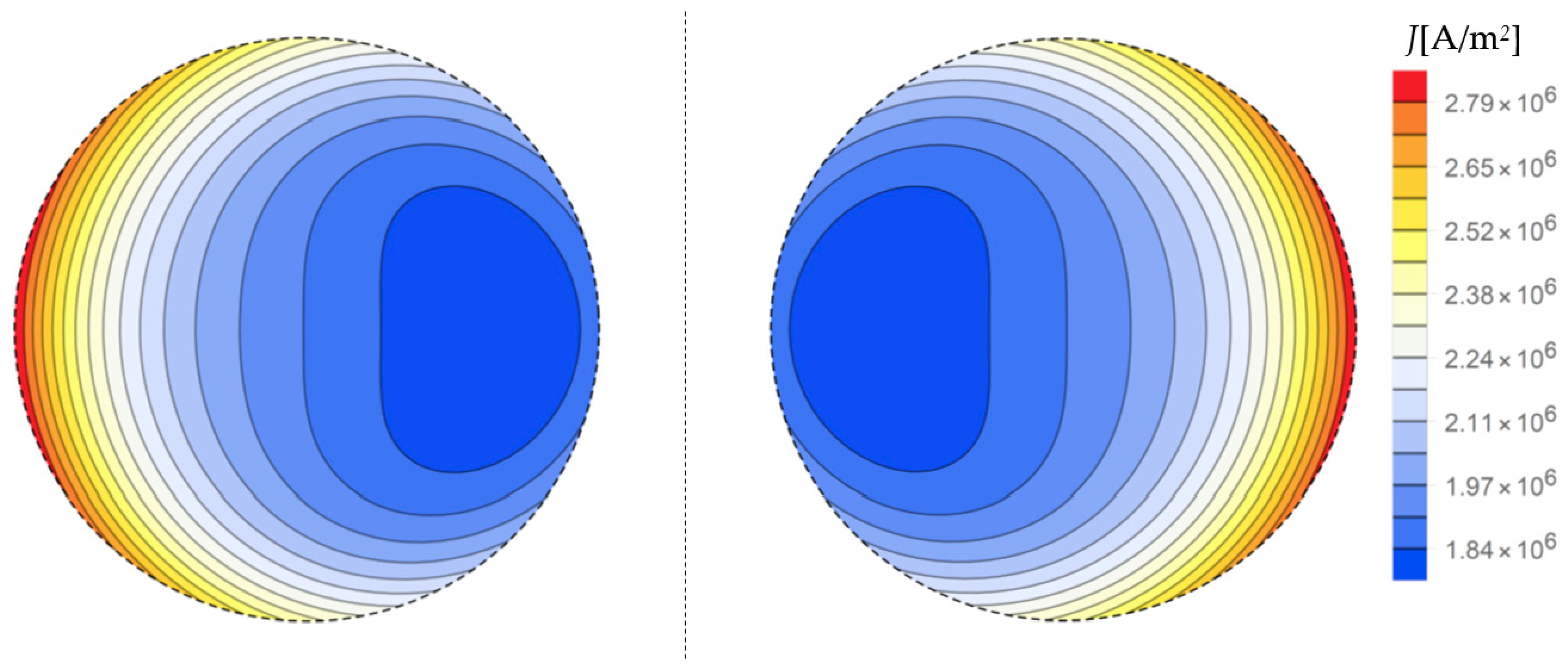
4. Numerical Examples
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Derivation of Equation (35)
- if , then ;
- if , then ;
- if two numbers of are equal and greater than zero and the third one equals zero, then ;
- if two numbers of are greater than zero and the third one equals their sum, then ;
- otherwise, .
References
- Anders, G.J. Rating of Electric Power Cables: Ampacity Computations for Transmission, Distribution and Industrial Application; McGraw-Hill Professional: Columbus, OH, USA, 1997. [Google Scholar]
- Morgan, V.T. The current distribution, resistance and internal inductance of linear power system conductors—A review of explicit equations. IEEE Trans. Power Deliv. 2013, 38, 1252–1262. [Google Scholar] [CrossRef]
- Popović, Z.; Popović, B.D. Introductory Electromagnetics; Prentice Hall: Hoboken, NJ, USA, 1998. [Google Scholar]
- Shazly, J.H.; Mostafa, A.M.; Ibrahim, D.K.; Abo El Zahab, E.E. Thermal analysis of high-voltage cables with several types of insulation for different configuration in the presence of harmonics. IET Gener. Transm. Distrib. 2017, 11, 3439–3448. [Google Scholar] [CrossRef]
- Wang, Z.; Zhong, J.; Jiang, J.; Hr, Y.; Wang, Z.; Zhang, H. Development of temperature rise simulation APP for three-phase common enclosure GIS/GIL. In Proceedings of the 5th IEEE Conference on Energy Internet and Energy System Integration, Taiyuan, China, 22–25 October 2021. [Google Scholar]
- Szczegielniak, T.; Kusiak, D.; Jabłoński, P. Thermal analysis of the medium voltage cable. Energies 2021, 14, 4164. [Google Scholar] [CrossRef]
- Smirnova, L.; Juntunen, R.; Murashko, K.; Musikka, T.; Pyrhönen, J. Thermal analysis of the laminated busbar system of a multilevel converter. IEEE Trans. Power Electron. 2016, 31, 1479–1488. [Google Scholar] [CrossRef]
- Li, S.; Han, Y.; Liu, C. Coupled multiphysics field analysis of high-current irregular-shaped busbar. IEEE Trans. Compon. Packag. Manuf. Technol. 2019, 9, 1805–1814. [Google Scholar] [CrossRef]
- Chávez, O.; Godínez, F.; Méndez, F.; Aguilar, A. Prediction of temperature profiles and ampacity for a monometallic conductor considering the skin effect and temperature-dependent resistivity. Appl. Therm. Eng. 2016, 109, 401–412. [Google Scholar] [CrossRef]
- Levèvre, A.; Miègeville, L.; Fouladgar, J.; Olivier, G. 3-D Computation of transformers overheating under nonlinear loads. IEEE Trans. Magn. 2005, 41, 1564–1567. [Google Scholar] [CrossRef]
- Shimotsu, T.; Koike, K.; Kondo, K. Temperature rise estimation of high power transformers of contactless power transfer system considering the influence of skin effect and proximity effect. In Proceedings of the 19th International Conference on Electrical Machines and Systems, ICEMS, Chiba, Japan, 13–16 November 2016. [Google Scholar]
- Szczegielniak, T.; Jabłoński, P.; Kusiak, D. Analytical approach to current rating of three-phase power cable with round conductors. Energies 2023, 16, 1821. [Google Scholar] [CrossRef]
- Kocot, H.; Kubek, P. The analysis of radial temperature gradient in bare stranded conductors. Przegląd Elektrotechniczny 2017, 10, 132–135. [Google Scholar] [CrossRef]
- Zaręba, M.; Gołębiowski, J. The thermal characteristics of ACCR lines as a function of wind speed—An analytical approach. Bull. Pol. Acad. Sci. Tech. Sci. 2022, 70, e141006. [Google Scholar] [CrossRef]
- Gołębiowski, J.; Zaręba, M. Analytical modelling of the transient thermal field of a tubular bus in nominal rating. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2019, 38, 642–656. [Google Scholar] [CrossRef]
- Henke, A.; Frei, S. Fast analytical approaches for the transient axial temperature distribution in single wire cables. IEEE Trans. Ind. Electron. 2022, 69, 4158–4166. [Google Scholar] [CrossRef]
- Wang, P.Y.; Ma, H.; Liu, G.; Han, Z.Z.; Guo, D.M.; Xu, T.; Kang, L.Y. Dynamic thermal analysis of high-voltage power cable insulation for cable dynamic thermal rating. IEEE Access 2019, 7, 56095–56106. [Google Scholar] [CrossRef]
- Shen, P.; Guo, X.; Fu, M.; Ma, H.; Wang, Y.; Chu, Q. Study on temperature field modeling and operation optimization of soil buried double-circuit cables. In Proceedings of the 20th International Conference on Electrical Machines and Systems (ICEMS), Sydney, Australia, 11–14 August 2017. [Google Scholar] [CrossRef]
- Jabłoński, P.; Szczegielniak, T.; Kusiak, D.; Piątek, Z. Analytical-numerical solution for the skin and proximity effect in two parallel round conductors. Energies 2019, 12, 3584. [Google Scholar] [CrossRef]
- Lehner, G. Electromagnetic Field Theory; Springer: Heidelberg, Germany, 2010. [Google Scholar]
- Riley, K.F.; Hobson, M.P.; Bence, S.J. Mathematical Methods for Physics and Engineering; Cambridge University Press: New York, NY, USA, 2002. [Google Scholar]
- Manneback, C. An integral equation for skin effect in parallel conductors. J. Math. Phys. 1922, 1, 123–146. [Google Scholar] [CrossRef]
- Dlabač, T.; Filipović, D. Integral equation approach for proximity effect in a two-wire line with round conductors. Tech. Vjesn. 2015, 22, 1065–1068. [Google Scholar] [CrossRef]
- Latif, M.J. Heat Conduction; Springer: Haidelberg, Germany, 2009. [Google Scholar]
- Hahn, D.W.; Ozisik, M.N. Heat Conduction; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Bergman, T.L.; Lavine, A.S.; Incropera, F.P.; Dewitt, D.P. Fundamentals of Heat and Mass Transfer; John Wiley and Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Cole, K.D.; Beck, J.V.; Haji-Sheikh, A.; Litkouhi, B. Heat Conduction Using Green’s Functions; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Greenberg, M.D. Applications of Green’s Functions in Science and Engineering; Dover Publications: Mineola, NY, USA, 2015. [Google Scholar]
- Duffy, D.G. Green’s Functions with Applications; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Greenberg, M.D. Advanced Engineering Mathematics; Prentice Hall: Hoboken, NJ, USA, 1988. [Google Scholar]
- Wolfram Research Inc. Mathematica; Wolfram Research Inc.: Champaign, IL, USA, 2020. [Google Scholar]
- Nithiarasu, P.; Lewis, R.W.; Seetharamu, K.N. Fundamentals of the Finite Element Method for Heat and Mass Transfer; John Wiley and Sons: Chichester, UK, 2016. [Google Scholar]
- Brener, S.; Scott, R.L. The Mathematical Theory of Finite Element Method; Springer: Berlin, Germany, 2008. [Google Scholar]
- COMSOL Multiphysics, Version 4.3. Documentation for COMSOL Release 4.3. COMSOL: Burlington, MA, USA, 2013.



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zaręba, M.; Szczegielniak, T.; Jabłoński, P. Influence of the Skin and Proximity Effects on the Thermal Field in a System of Two Parallel Round Conductors. Energies 2023, 16, 6341. https://doi.org/10.3390/en16176341
Zaręba M, Szczegielniak T, Jabłoński P. Influence of the Skin and Proximity Effects on the Thermal Field in a System of Two Parallel Round Conductors. Energies. 2023; 16(17):6341. https://doi.org/10.3390/en16176341
Chicago/Turabian StyleZaręba, Marek, Tomasz Szczegielniak, and Paweł Jabłoński. 2023. "Influence of the Skin and Proximity Effects on the Thermal Field in a System of Two Parallel Round Conductors" Energies 16, no. 17: 6341. https://doi.org/10.3390/en16176341
APA StyleZaręba, M., Szczegielniak, T., & Jabłoński, P. (2023). Influence of the Skin and Proximity Effects on the Thermal Field in a System of Two Parallel Round Conductors. Energies, 16(17), 6341. https://doi.org/10.3390/en16176341





