Modelling Methodologies to Design and Control Renewables and Hydrogen-Based Telecom Towers Power Supply Systems
Abstract
1. Introduction
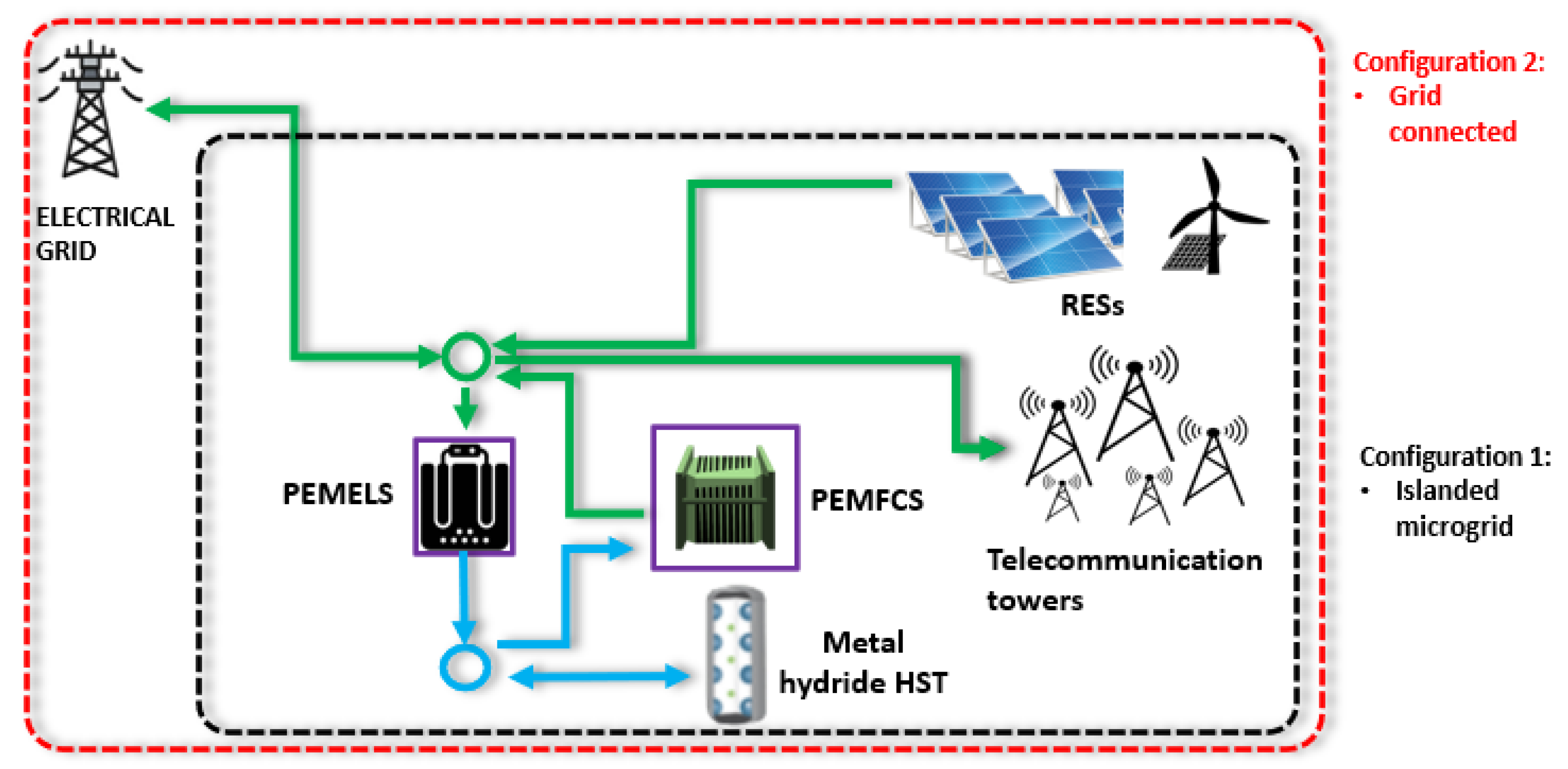
2. Plant Description
3. Model Description
3.1. PV and Wind Turbine Calculation Procedure
3.2. PEMFC and PEMEL Systems
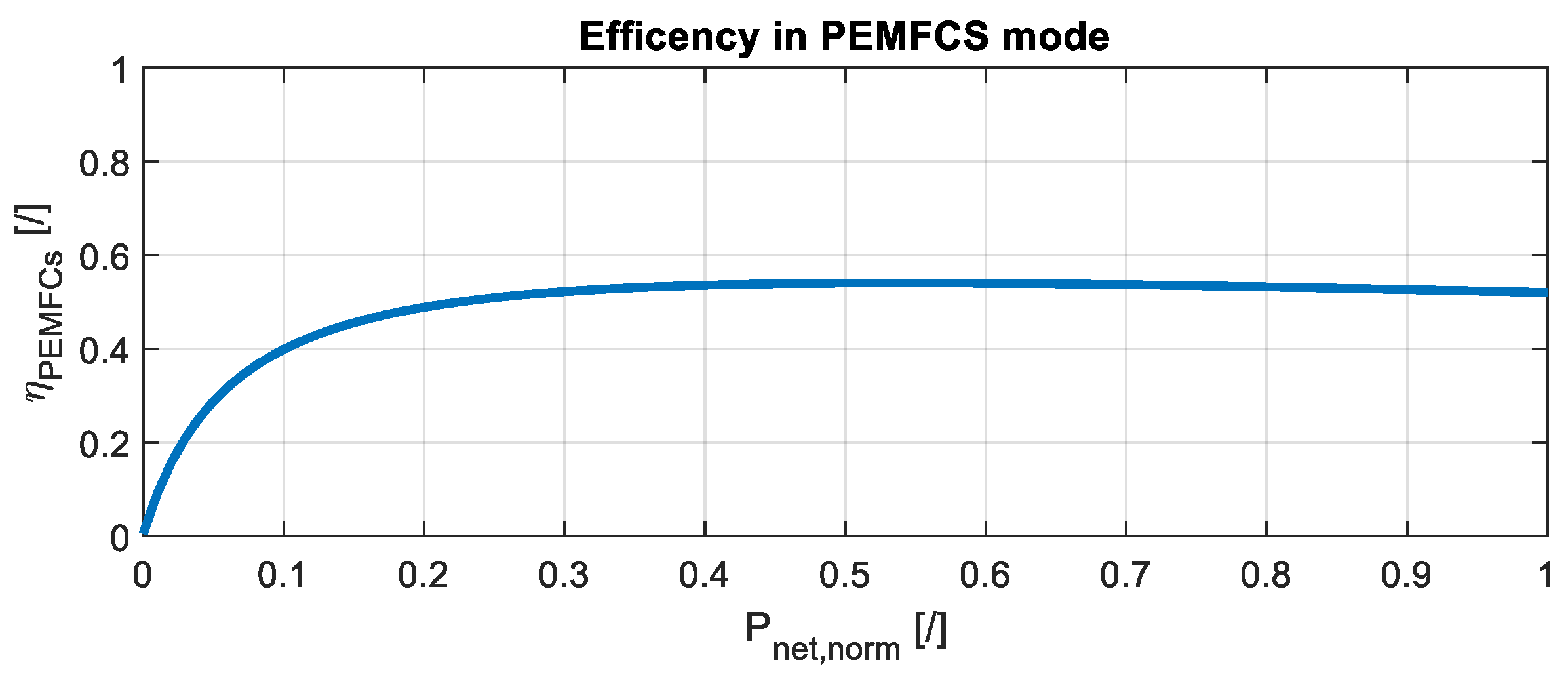
3.3. PEMFCS Mode
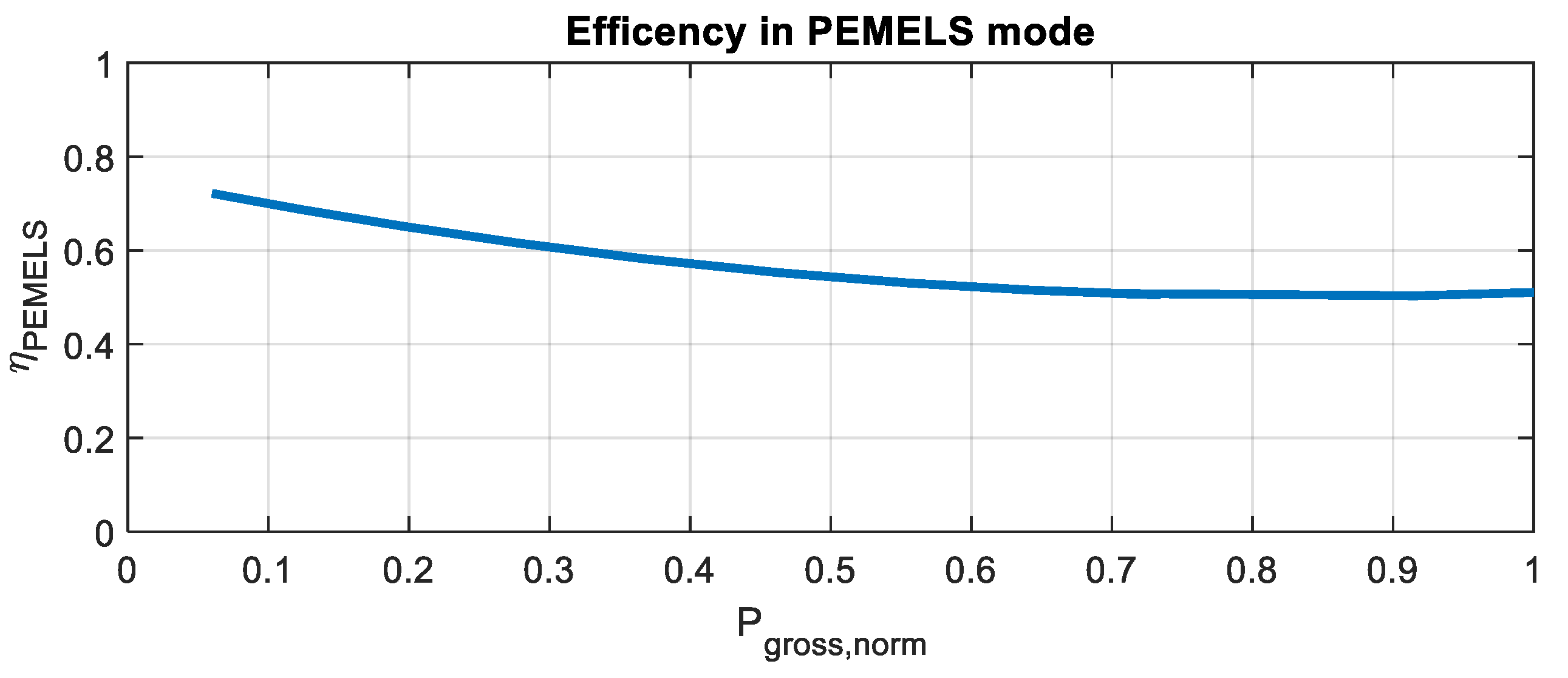
3.4. PEMELS Mode
3.5. Hydrogen Storage Hourly State Calculation
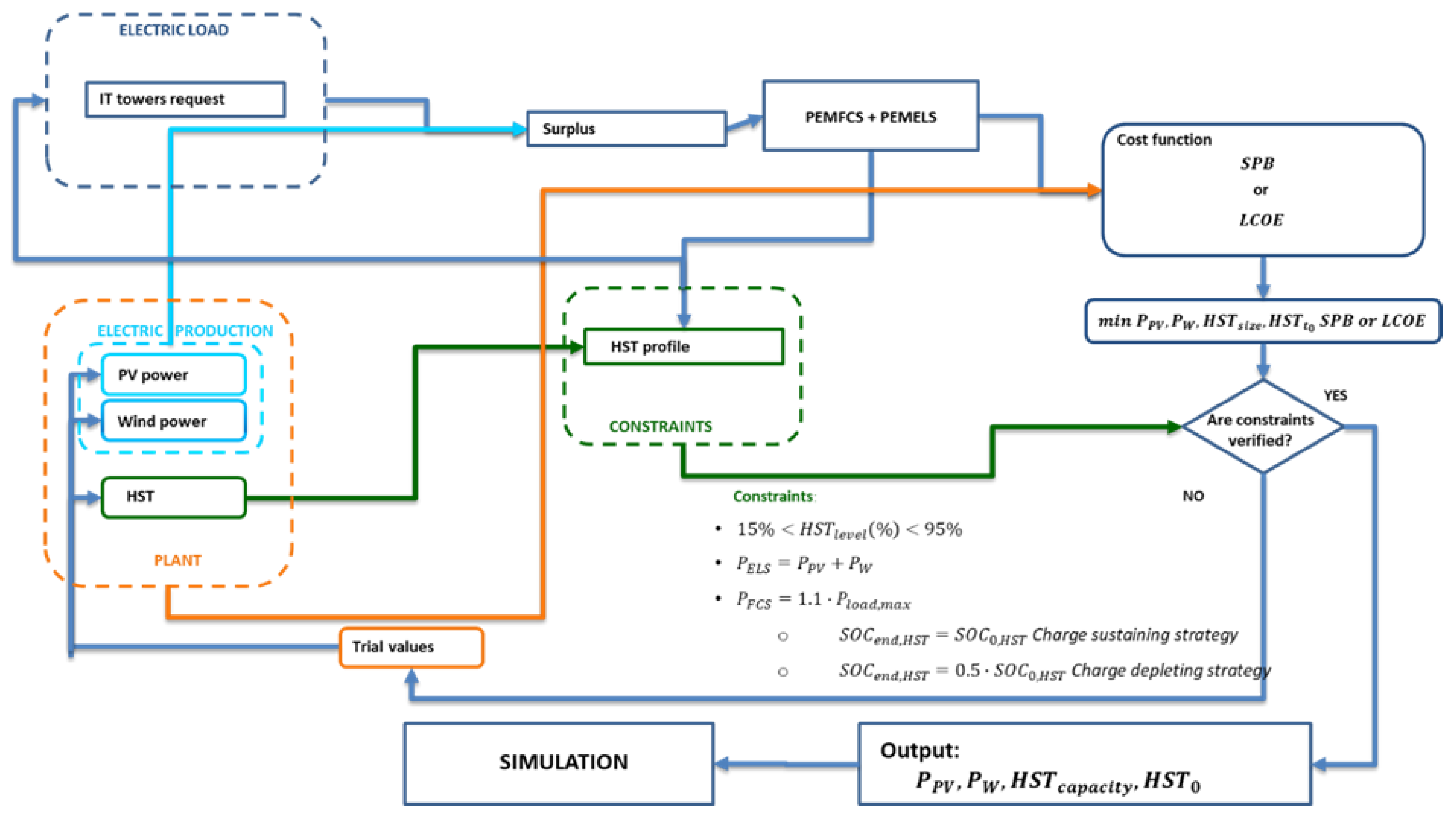
4. Optimisation Procedure
- (1)
- the state of charge of the hydrogen tank has to lay between 15% and 95%;
- (2)
- the nominal power of the PEMELS must be equal to the summation of installed PV and wind turbine nominal power, so as to avoid having renewable energy wasted;
- (3)
- the nominal power of the PEMFCS must be equal to the maximum value of the load oversized by 10% to cover intermittency of renewable sources;
- (4)
- the final level of the tank must be equal to the initial level in case of charge sustaining strategy. This implies that, considering SPB and LCOE formulas, the term representing the hydrogen bought ( is always negligible. Meanwhile, if the charge depleting strategy is used, the final level of the tank must be equal to half of its initial level.
5. DP Routine
- (1)
- ;
- (2)
- ;
- (3)
- , considering charge sustaining strategy;
- (4)
- , considering charge depleting strategy.
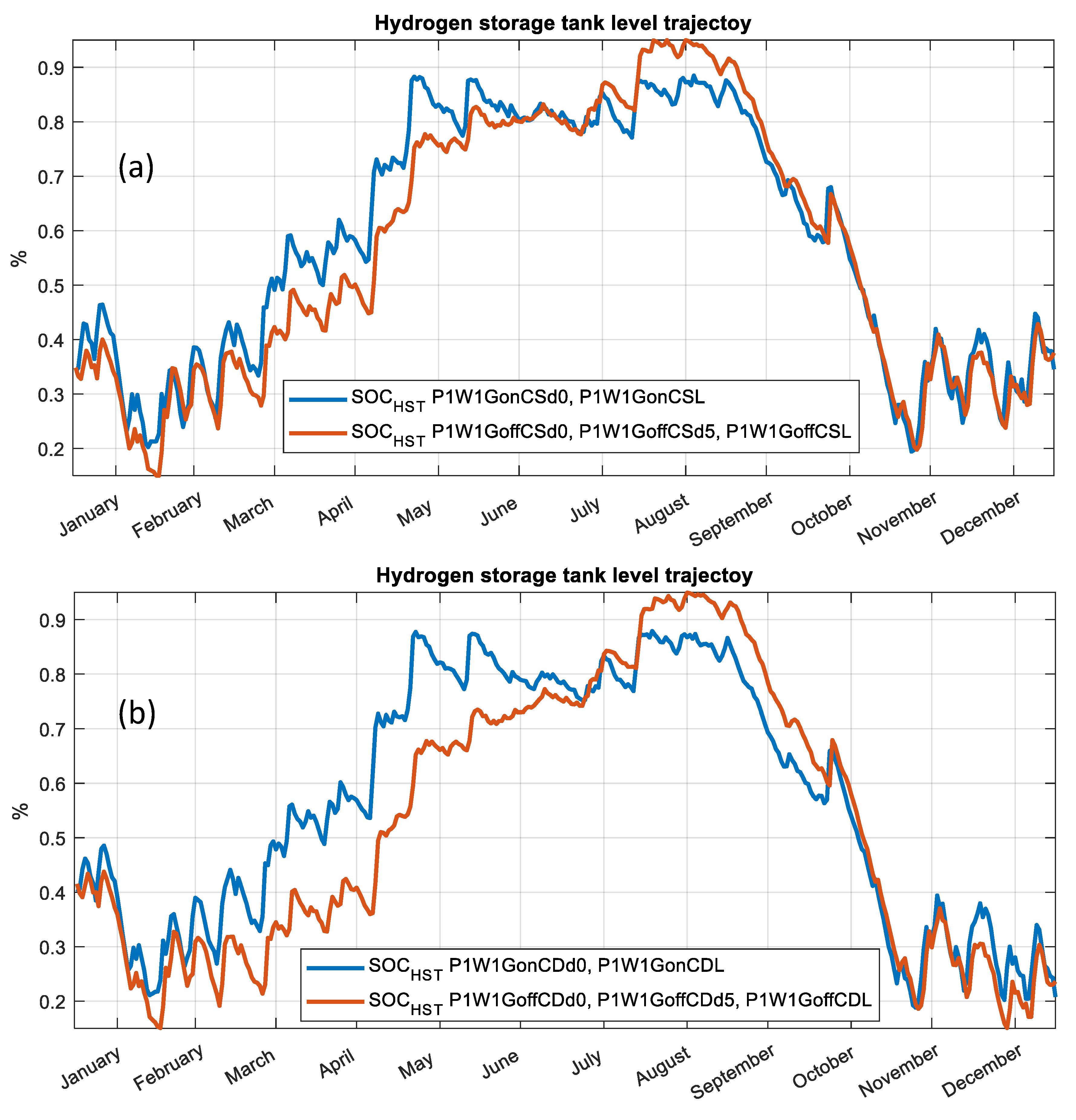
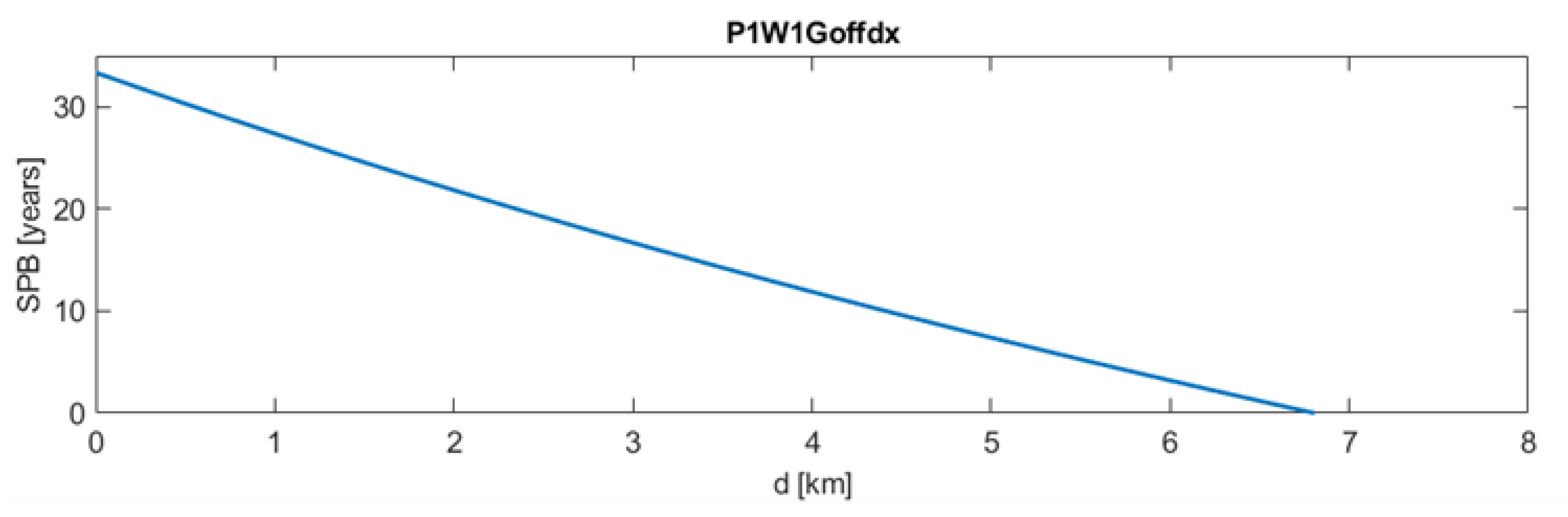
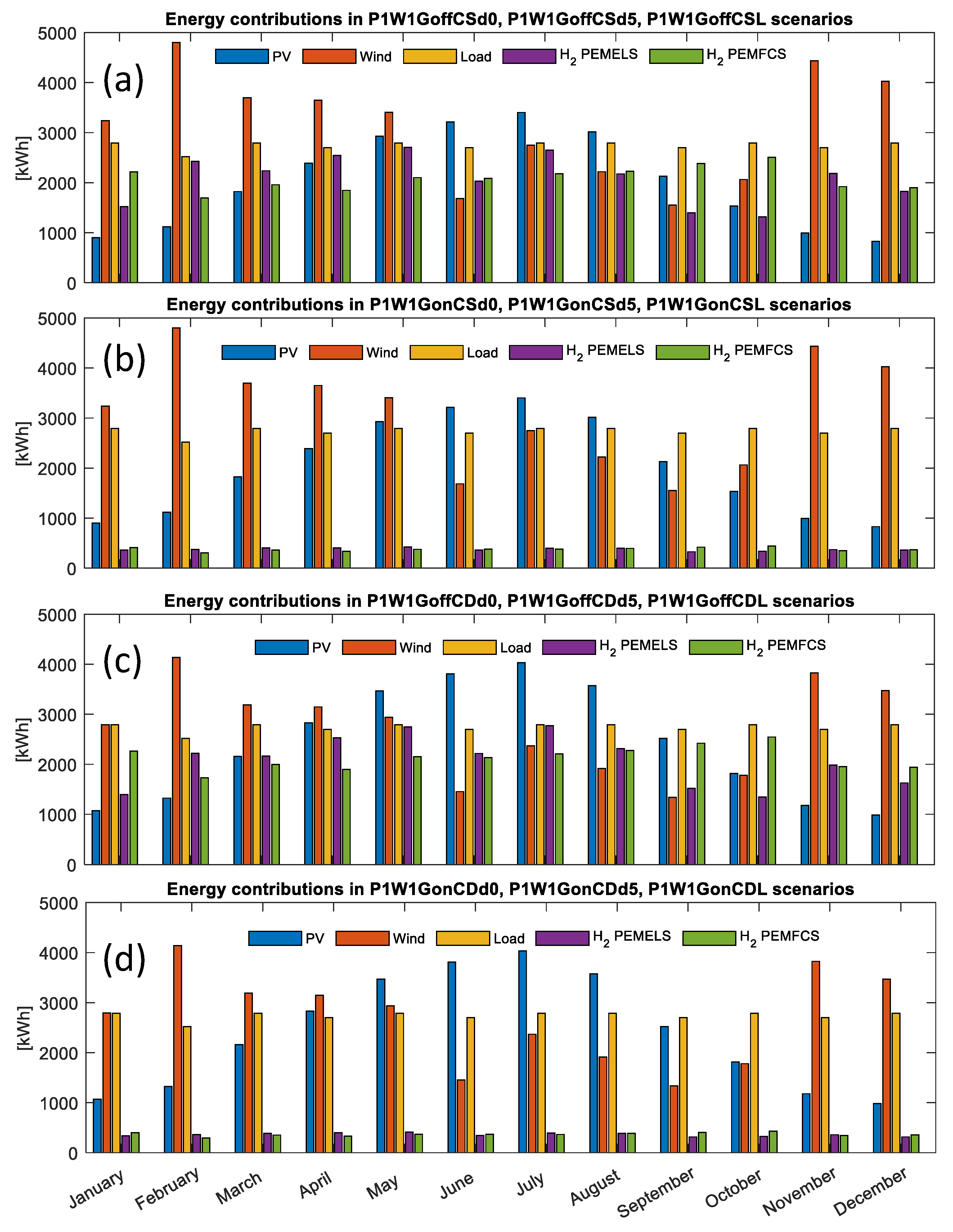
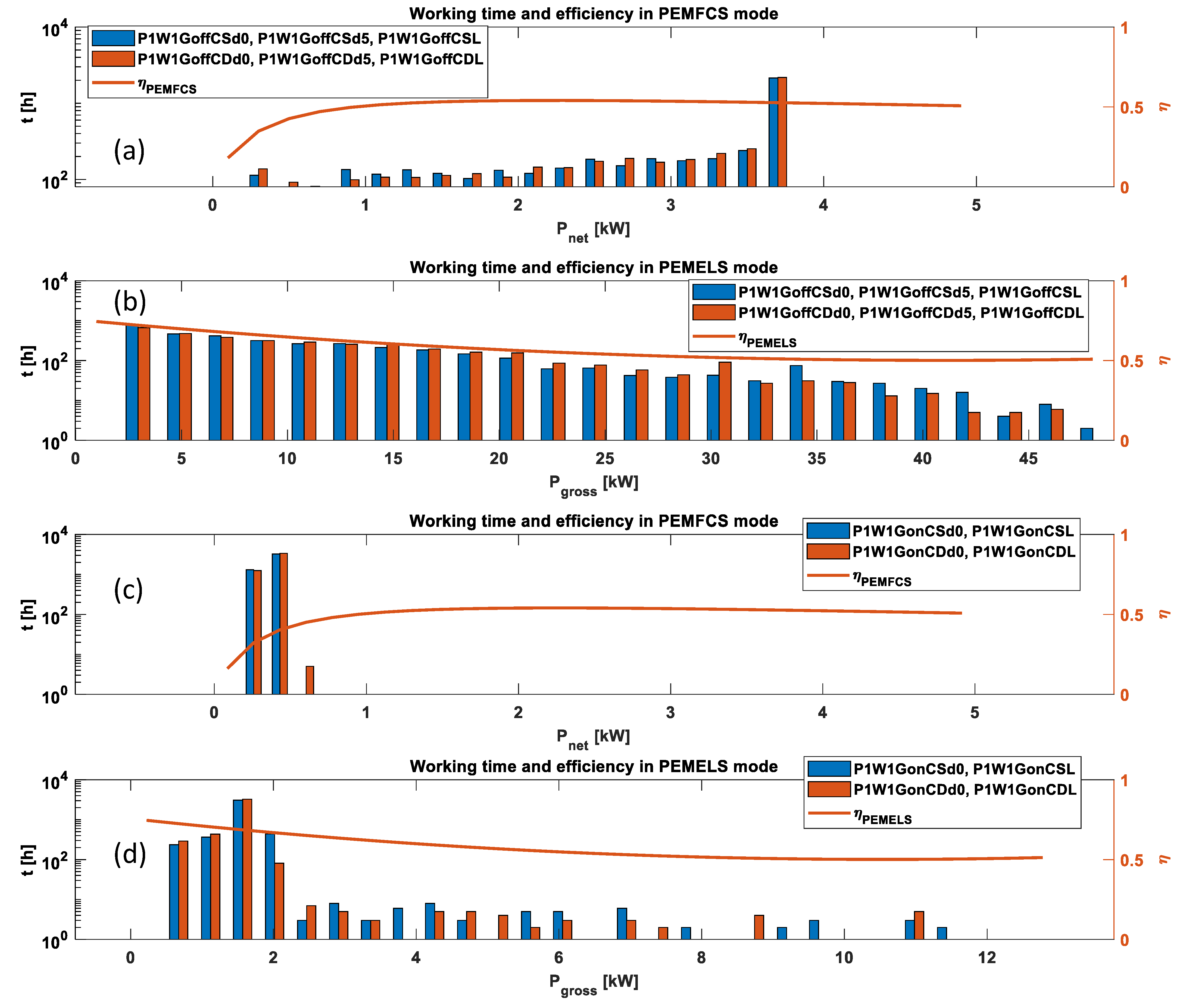
6. Results
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| CAPEX | Capital expenditure |
| DP | Dynamic programming |
| HST | Hydrogen storage tank |
| LHV | Lower heating value |
| MH | Metal hydride |
| OPEX | Operational expenditure |
| PEMELS | Proton exchange membrane electrolyser system |
| PEMFCS | Proton exchange membrane fuel cell system |
| RESs | Renewable energy sources |
| rSOC | Reversible oxide cell |
| Symbols | |
| ABC | Annual bill cost [€] |
| Cge | Capex for grid extension [€/km] |
| D | Grid extension distance |
| d | Discount rate |
| Ey,i | Energy required from the microgrid at the ith year [kWh] |
| IC | Installation cost of the microgrid [€] |
| J | Performance index of DP routine |
| LCOE | Levelised cost of energy [€/kWh] |
| MC | Annual maintenance cost for the microgrid [€] |
| MCge | Annual maintenance cost for grid extension [€] |
| mH2, PEMELS, j | Mass of hydrogen generated in PEMELS mode at the jth hour [kg] |
| mH2, PEMFCS, j | Mass of hydrogen consumed in PEMFCS mode at the jth hour [kg] |
| mH2, tank, j | Mass of hydrogen entering/leaving the HST at the jth hour [kg] |
| n | Longest investment period |
| PPEMELS,nominal | PEMELS nominal electric power [kW] |
| PPEMFCS,nominal | PEMFCS nominal electric power [kW] |
| Pgrid,j | Electric power from the electric grid at the jth hour [kW] |
| pH2 | Hydrogen price [€/kg] |
| Pmin | PEMFCS or PEMELS minimum working power [kW] |
| PPEM,j | PEMFCS and PEMELS power split at the jth hour [kW] |
| PPV,j | Photovoltaics electric power production at the jth hour [kW] |
| PW,j | Wind power production at the jth hour [kW] |
| R | Replacement cost [€] |
| S | Renewable (i.e., generated by PV and/or wind turbine) power surplus or shortage [kW] |
| SOC | State of charge |
| SPB | Simple payback period [years] |
| t | Fuel cell system or electrolyser working time [h] |
| TC | Total microgrid cost (excluding installation cost) [€] |
| TD | Tax deduction |
| TL | Total electric load [kW] |
| Case Scenarios Nomenclature | |
| |
| |
| |
| |
| Example | |
| Plant with no wind turbines, grid connected not grid extended in a charge depleting strategy: | |
| Plant with wind turbines, off-grid in a charge sustaining strategy optimised with LCOE: | |
References
- Tazay, A.F.; Hazza GA, W.; Zerkaoui, S.; Alghamdi, S.A. Optimal Design and Techno-economic Analysis of a Hybrid Solar-wind Power Resource: A Case Study at Al baha University, KSA. Int. J. Energy Prod. Manag. 2022, 7, 13–34. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, J.; Yang, L.; Ma, B.; Sun, G.; Youssefi, N. Optimal designing of a hybrid renewable energy system connected to an unreliable grid based on enhanced African vulture optimizer. ISA Trans. 2022, 129, 424–435. [Google Scholar] [CrossRef] [PubMed]
- Usman, M. HOMER Analysis for Integrating Solar Energy in Off-Grid and On-Grid SCO Telecommunication Sites. In Proceedings of the 2019 1st Global Power, Energy and Communication Conference (GPECOM), Cappadocia, Turkey, 12–15 June 2019; pp. 270–275. [Google Scholar]
- Haddad, A.; Ramadan, M.; Khaled, M. Triple hybrid system coupling fuel cell with wind turbine thermal solar system. Int. J. Hydrogen Energy 2019, 45, 11484–11491. [Google Scholar] [CrossRef]
- Amutha, W.M.; Rajini, V. Techno-economic evaluation of various hybrid power systems for rural telecom. Renew. Sustain. Energy Rev. 2015, 43, 553–561. [Google Scholar] [CrossRef]
- Li, Z.; Zheng, Z.; Xu, L.; Lu, X. A review of the applications of fuel cells in microgrids: Opportunities and challenges. BMC Energy 2019, 1, 8. [Google Scholar] [CrossRef]
- Maoulida, F.; Rabah, D.; El Ganaoui, M.; Aboudou, K.M. PV-Wind-Diesel System for Energy Supply on Remote Area Applied for Telecommunication Towers in Comoros. Open J. Energy Effic. 2021, 10, 50–72. [Google Scholar] [CrossRef]
- Schmidt, O.; Gambhir, A.; Staffell, I.; Hawkes, A.; Nelson, J.; Few, S. Future cost and performance of water electrolysis: An expert elicitation study. Int. J. Hydrogen Energy 2017, 42, 30470–30492. [Google Scholar] [CrossRef]
- Rispoli, N.; Vitale, F.; Califano, F.; Califano, M.; Polverino, P.; Rosen, M.A.; Sorrentino, M. Constrained optimal design of a reversible solid oxide cell-based multiple load renewable microgrid. J. Energy Storage 2020, 31, 101570. [Google Scholar] [CrossRef]
- Jansen, G.; Dehouche, Z.; Corrigan, H. Cost-effective sizing of a hybrid Regenerative Hydrogen Fuel Cell energy storage system for remote & off-grid telecom towers. Int. J. Hydrogen Energy 2021, 46, 18153–18166. [Google Scholar] [CrossRef]
- Ayodele, T.R.; Mosetlhe, T.C.; Yusuff, A.A.; Ogunjuyigbe, A.S.O. Off-grid hybrid renewable energy system with hydrogen storage for South African rural community health clinic. Int. J. Hydrogen Energy 2021, 46, 19871–19885. [Google Scholar] [CrossRef]
- Luta, D.N.; Raji, A.K. Decision-making between a grid extension and a rural renewable off-grid system with hydrogen generation. Int. J. Hydrogen Energy 2018, 43, 9535–9548. [Google Scholar] [CrossRef]
- Pellegrini, M.; Guzzini, A.; Saccani, C. Experimental measurements of the performance of a micro-wind turbine located in an urban area. Energy Rep. 2021, 7, 3922–3934. [Google Scholar] [CrossRef]
- Lai, C.S.; McCulloch, M.D. simple cost of electricity for solar photovoltaic and electrical energy storage. Appl. Energy 2017, 190, 191–203. [Google Scholar] [CrossRef]
- Califano, M.; Sorrentino, M.; Rosen, M.A.; Pianese, C. Optimal heat and power management of a reversible solid oxide cell based microgrid for effective technoeconomic hydrogen consumption and storage. Appl. Energy 2022, 319, 11926. [Google Scholar] [CrossRef]
- Taghavifar, H.; Zomorodian, Z.S. Techno-economic viability of on grid micro-hybrid PV/Wind/Gen System for an educational building in Iran. Renew. Sustain. Energy Rev. 2021, 143, 110877. [Google Scholar] [CrossRef]
- Vitale, F.; Rispoli, N.; Sorrentino, M.; Rosen, M.A.; Pianese, C. On the use of dynamic programming for optimal energy management of grid-connected reversible solid oxide cell-based renewable microgrids. Energy 2021, 225, 120304. [Google Scholar] [CrossRef]
- Parida, B.; Iniyan, S.; Goic, R. A review of solar photovoltaic technologies. Renew. Sustain. Energy Rev. 2011, 15, 1625–1636. [Google Scholar] [CrossRef]
- Alma Solar. Panneau Solaire I’M SOLAR 280p. Available online: https://www.alma-solarshop.fr/panneau-i-m-solar/1335-panneau-solaire-i-m-solar-370w-mono-noir.html (accessed on 4 February 2023).
- Aeolos. Wind Turbine. Available online: http://www.windturbinestar.com/3kwv-v-aeolos-wind-turbine.html (accessed on 4 February 2023).
- ENEA. Solar Database. Available online: http://www.solaritaly.enea.it/%0ACalcRggmmOrizz/Calcola.php.%0A (accessed on 4 February 2023).
- Marocco, P.; Ferrero, D.; Lanzini, A.; Santarelli, M. The role of hydrogen in the optimal design of off-grid hybrid renewable energy systems. J. Energy Storage 2022, 46, 103893. [Google Scholar] [CrossRef]
- Sorrentino, M.; Pianese, C.; Maiorino, M. An integrated mathematical tool aimed at developing highly performing and cost-effective fuel cell hybrid vehicles. J. Power Sources 2013, 221, 308–317. [Google Scholar] [CrossRef]
- Kotowicz, J.; Jurczyk, M.; Węcel, D. Equipment Exploitation in Power to Gas Installation. New Trends Prod. Eng. 2018, 1, 409–418. [Google Scholar] [CrossRef][Green Version]
- Hancke, R.; Holm, T.; Ulleberg, Ø. The case for high-pressure PEM water electrolysis. Energy Convers. Manag. 2022, 261, 115642. [Google Scholar] [CrossRef]
- Roy, A.; Watson, S.; Infield, D. Comparison of electrical energy efficiency of atmospheric and high-pressure electrolysers. Int. J. Hydrogen Energy 2006, 31, 1964–1979. [Google Scholar] [CrossRef]
- Scheepers, F.; Stähler, M.; Stähler, A.; Rauls, E.; Müller, M.; Carmo, M.; Lehnert, W. Improving the efficiency of PEM electrolyzers through membrane-specific pressure optimization. Energies 2020, 13, 612. [Google Scholar] [CrossRef]
- Orioli, A.; Franzitta, V.; Di Gangi, A.; Foresta, F. The recent change in the italian policies for photovoltaics: Effects on the energy demand coverage of grid-connected pv systems installed in urban contexts. Energies 2016, 9, 944. [Google Scholar] [CrossRef]
- Hydrogen Council. Path to Hydrogen Competitiveness: A Cost Perspective. 88. 2020. Available online: www.hydrogencouncil.com (accessed on 4 February 2023).
- Sparber, W.; Weiss, W.; Sanner, B.; Angelino, L.; De Gregorio, M.; Février, N.; Haslinger, W.; Kujbus, A.; Landolina, S.; Stryi-Hipp, G.; et al. Strategic Research and Innovation Agenda for RHC; Publications Office of the European Union: Luxembourg, 2022. [Google Scholar] [CrossRef]
- MathWorks. Find Minimum of Constrained Nonlinear Multivariable Function—MATLAB Fmincon. Available online: https://it.mathworks.com/help/optim/ug/fmincon.html#busog7r-options (accessed on 4 February 2023).
- Sundström, O.; Guzzella, L. A generic dynamic programming Matlab function. In Proceedings of the 2009 IEEE Control Applications, (CCA) & Intelligent Control, (ISIC), St. Petersburg, Russia, 8–10 July 2009; pp. 1625–1630. [Google Scholar] [CrossRef]
- Anderson, E.; Ayers, K.; Capuano, C. R&D Focus Areas Based on 60,000 hr Life PEM Water Electrolysis Stack Experience. In Proceedings of the 1st International Workshop on Durability and Degradation Issues in PEM Electrolysis Cells and Its Components, Freiburg, Germany, 12 March 2013. [Google Scholar]
- ARERA. 2023. Available online: https://www.arera.it/it/dati/eep35.htm# (accessed on 4 February 2023).
| Parameter | Unit | Value |
|---|---|---|
| Maximum power | [W] | 270 |
| Efficiency | - | 0.16 |
| Dimensions (length × width × height) | [mm] | 992 × 40 × 1640 |
| Parameter | Unit | Value |
|---|---|---|
| Maximum power | [kW] | 3.6 |
| Cut-in wind speed | [m/s] | 1.5 |
| Nominal wind speed | [m/s] | 10 |
| Cut-out wind speed | [m/s] | 25 |
| Components | Unit | Unit Cost |
|---|---|---|
| PV plant: panel, inverter | [€/kW] | 817 (600, 217) |
| Wind turbine: tower, rotor, inverter, grid-on controller | [€/kW] | 2513 (504, 1108, 635, 266) |
| HST [30] | [€/kg] | 1200 |
| PEMFCS [30] | [€/kW] | 1200 |
| PEMELS [30] | [€/kW] | 500 |
| Parameter | Unit | P1W1GoffCSd0 | P1W1GonCSd0 | P1W1GoffCSd5 | P1W1GoffCSL | P1W1GonCSL |
|---|---|---|---|---|---|---|
| PV power | [kW] | 16.71 | 16.71 | 16.71 | 16.71 | 16.71 |
| Wind power | [kW] | 31.45 | 31.45 | 31.45 | 31.45 | 31.45 |
| HSTsize | [kg] | 104.57 | 10.457 | 104.57 | 104.57 | 10.457 |
| SOC0,HST | [%] | 34.81 | 34.81 | 34.81 | 34.81 | 34.81 |
| PEMFCS power | [kW] | 4.12 | 4.12 | 4.12 | 4.12 | 4.12 |
| PEMELS power | [kW] | 48.16 | 12.36 | 48.16 | 48.16 | 12.36 |
| SPB | [years] | 33.348 | 6.997 | 7.397 | / | / |
| LCOE | [€/kWh] | / | / | / | 0.520 | 0.209 |
| Capital invest. | [€] | 247,200 | 116,520 | 247,200 | 247,200 | 116,520 |
| Parameter | Unit | P1W1GoffCDd0 | P1W1GonCDd0 | P1W1GoffCDd5 | P1W1GoffCDL | P1W1GonCDL |
|---|---|---|---|---|---|---|
| PV power | [kW] | 19.80 | 19.80 | 19.79 | 19.79 | 19.79 |
| Wind power | [kW] | 27.11 | 27.11 | 27.12 | 27.13 | 27.13 |
| HSTsize | [kg] | 99.03 | 9.903 | 98.96 | 98.92 | 9.892 |
| SOC0,HST | [%] | 41.51 | 41.51 | 41.49 | 41.47 | 41.47 |
| PEMFCS power | [kW] | 4.12 | 4.12 | 4.12 | 4.12 | 4.12 |
| PEMELS power | [kW] | 46.91 | 12.36 | 46.91 | 46.91 | 12.36 |
| SPB | [years] | 28.533 | 6.361 | 5.213 | / | / |
| LCOE | [€/kWh] | / | / | / | 0.489 | 0.195 |
| Capital invest. | [€] | 231,540 | 107,470 | 231,480 | 231,450 | 107,490 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aliberti, P.; Sorrentino, M.; Califano, M.; Pianese, C.; Capozucca, L.; Cristiani, L.; Lops, G.; Mancini, R. Modelling Methodologies to Design and Control Renewables and Hydrogen-Based Telecom Towers Power Supply Systems. Energies 2023, 16, 6316. https://doi.org/10.3390/en16176316
Aliberti P, Sorrentino M, Califano M, Pianese C, Capozucca L, Cristiani L, Lops G, Mancini R. Modelling Methodologies to Design and Control Renewables and Hydrogen-Based Telecom Towers Power Supply Systems. Energies. 2023; 16(17):6316. https://doi.org/10.3390/en16176316
Chicago/Turabian StyleAliberti, Paolo, Marco Sorrentino, Marco Califano, Cesare Pianese, Luca Capozucca, Laura Cristiani, Gianpiero Lops, and Roberto Mancini. 2023. "Modelling Methodologies to Design and Control Renewables and Hydrogen-Based Telecom Towers Power Supply Systems" Energies 16, no. 17: 6316. https://doi.org/10.3390/en16176316
APA StyleAliberti, P., Sorrentino, M., Califano, M., Pianese, C., Capozucca, L., Cristiani, L., Lops, G., & Mancini, R. (2023). Modelling Methodologies to Design and Control Renewables and Hydrogen-Based Telecom Towers Power Supply Systems. Energies, 16(17), 6316. https://doi.org/10.3390/en16176316








