Medium-Term Hydrothermal Scheduling of the Infiernillo Reservoir Using Stochastic Dual Dynamic Programming (SDDP): A Case Study in Mexico
Abstract
1. Introduction
Objective and Motivation
- The MTHS problem is intrinsically stochastic because the variables involved cannot be accurately forecasted (see [14]).
- Given that system reservoirs can transfer energy from one time period to another (it may be from hours to even years ahead, depending on the physical characteristics of the reservoir), the problem is coupled in time. Because of this characteristic, before making decisions regarding the quantity of water to use to produce electric energy, we need to estimate the economic consequences of those decisions. Figure 1 displays a representation of the decision process in hydrothermal systems; it shows that operating decisions influence future operating costs. For example, if reservoirs are depleted in the present and low inflows occur in the future, more thermal generation will be needed to supply energy demand, which will increase the system’s operating cost (or even imply an energy shortage if thermal installed capacity is not sufficient to supply demand). On the other hand, if reservoir levels are kept high in the present through a more intensive use of thermal resources and high inflows occur in the future, the reservoirs’ storage capacities may be exceeded and there will be spillages in the system, increasing the risk of flooding for riparian communities settled downstream the reservoirs. Additionally, the spilled water represents wasted energy (see [28,29]).
- It is a nonlinear optimization problem because of the thermal cost functions and the hydroelectric production functions [30]. However, since the hydrothermal scheduling problem is too complex to be solved by a single optimization model, it is usually decomposed into a chain of subproblems with different planning horizons and degrees of detail in the system representation. Given that this work is focused on a medium-term planning horizon (up to 3 years for the Mexican power system), these functions are approximated by a linear model in order to put greater emphasis on modeling the uncertain nature of the MTHS problem.
- It is a large-scale problem because the number of scenarios grows exponentially with the number of stages [13].
2. Deterministic HTS versus Stochastic HTS
Stochastic HTS
3. Mathematical Modeling
3.1. Scenario Tree Generation
3.2. Stochastic Dual Dynamic Programming Algorithm
3.3. Solution Quality Evaluation
3.3.1. Upper-Bound Estimation on the Expected Policy Cost
3.3.2. Lower-Bound Estimation on the Optimal Solution of the Original Stochastic Program
4. Case Studies Analysis
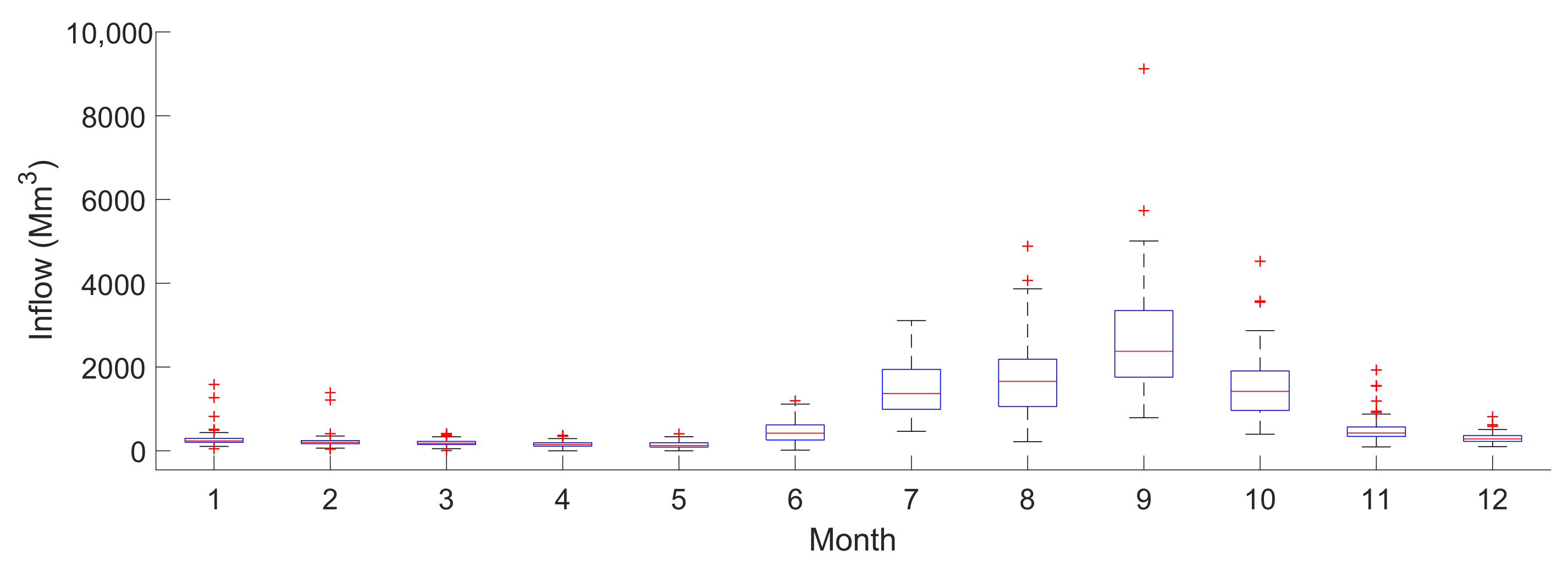
4.1. Data Analysis
Probability Distributions Fitting
4.2. Results Analysis
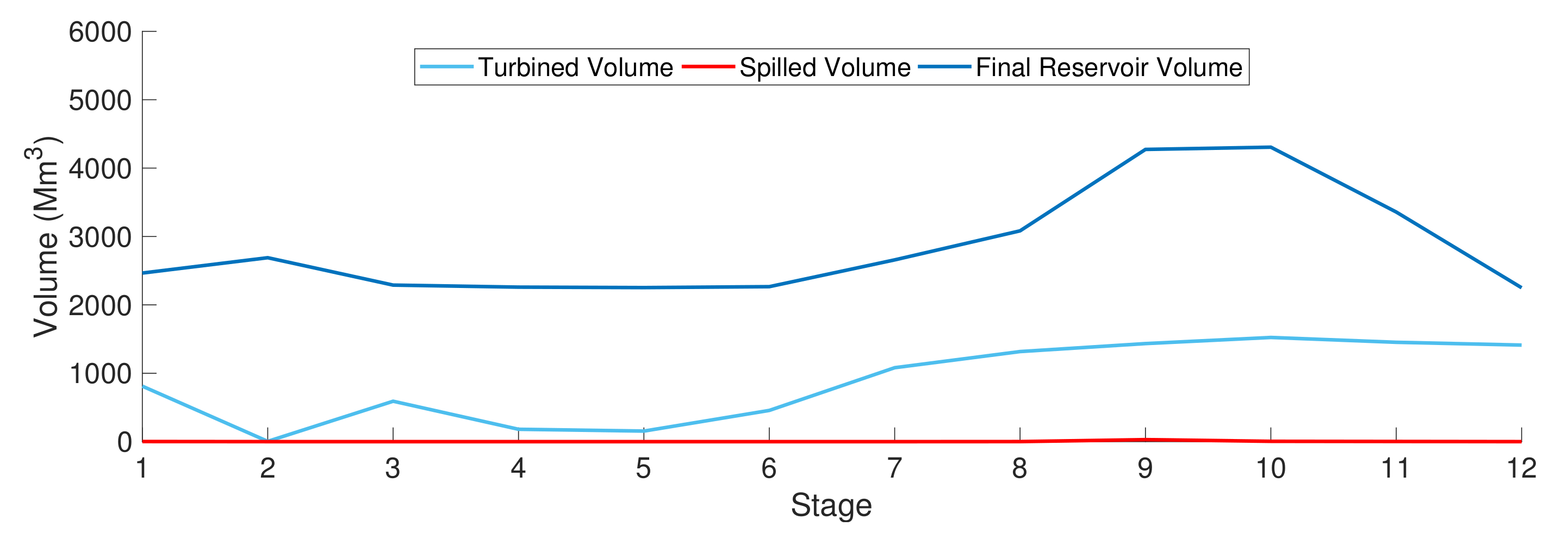
4.2.1. Operating Policies Computation
4.2.2. Solution Quality Evaluation
4.2.3. Operating Policy Simulation
4.2.4. Computational Complexity
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| n: | Number of inflow realizations for each stage. |
| : | Number of scenarios sampled to estimate the upper bound on the expected policy cost. |
| : | Number of scenario trees sampled to estimate the lower bound on the optimal solution of the original stochastic program. |
| : | Incremental cost of thermal plant (USD/MWh). |
| : | Hydro plant productivity factor (MWh/(m/s)). |
| : | Energy demand in stage (MWh). |
| : | Reservoir initial volume in the first stage (Mm). |
| : | Generation in stage t of thermal plant j and scenario (MWh). |
| : | Inflow to the reservoir during stage t and scenario (Mm). |
| : | Hydro plant turbined outflow during stage t and scenario (m/s). |
| : | Hydro plant spilled outflow during stage t and scenario (m/s). |
| : | Reservoir volume at the end of stage t and scenario (Mm). |
| : | Dual variable of the power balance equation of stage t and scenario (USD/MWh). |
| : | Dual variable of the stream-flow balance equation of stage t and scenario (USD/Mm). |
| : | Sample space associated with the original stochastic process. |
| : | Sample space associated with the finite sampled scenario tree. |
| : | Optimal objective value of the stochastic program defined on . |
| : | Optimal objective value of the stochastic program defined on . |
| : | Stage ancestor of scenario . |
| : | Set of stage descendants of scenario . |
| : | Sample mean estimator of the expected policy cost. |
| : | Sample variance estimator of the expected policy cost. |
| : | Sample mean of the total operating cost of scenario trees. |
| : | Sample variance of the total operating cost of scenario trees. |
| : | Factor to convert a given flow rate (m/s) to an equivalent monthly volume (Mm),equal to for a 30-day month (see [27]). |
| : | Tolerance . |
Appendix A. Selected Probability Distribution Functions
| Distribution | Probability Density Function | |
|---|---|---|
| 3-P Burr | ||
| 4-P Burr | ||
| 2-P Gamma | ||
| 3-P Gamma | ||
| Gumbel Max | ||
| Johnson SB | ||
| Log-Logistic | ||
| Wakeby | Not explicitly defined | |
References
- International Renewable Energy Agency (IRENA). Remap 2030 A Renewable Energy Roadmap; International Renewable Energy Agency: Masdar City, United Arab Emirates, 2014; Available online: https://www.irena.org/publications/2014/Jan/REmap-2030-Summary-of-findings-January-2014 (accessed on 1 January 2022).
- United Nations Environment Programme and Centre, Frankfurt School-UNEP and Finance, Bloomberg New Energy. Global Trends in Renewable Energy Investment 2015; United Nations: New York, NY, USA, 2015. [Google Scholar]
- International Renewable Energy Agency (IRENA). Renewable Energy Market Analysis: Latin America; International Renewable Energy Agency: Masdar City, United Arab Emirates, 2016; Available online: https://www.irena.org/publications/2016/Nov/Renewable-Energy-Market-Analysis-Latin-America (accessed on 1 March 2021).
- United Nations Environment Programme and Frankfurt School-UNEP Centre and Bloomberg New Energy Finance. Global Trends in Renewable Energy Investment 2016; United Nations: New York, NY, USA, 2016. [Google Scholar]
- Kelman, R.; Harrison, D. Integrating Renewables with Pumped Hydro Storage in Brazil: A Case Study; HAL: Lyon, France, 2019; pp. 1–23. [Google Scholar]
- Electric Power Research Center (EPRI). Flexible Operation of Hydropower Plants; Electric Power Research Center: Palo Alto, CA, USA, 2017; pp. 1–76. [Google Scholar]
- Siemonsmeier, M.; Baumanns, P.; van Bracht, N.; Schönefeld, M.; Schönbauer, A.; Moser, A.; Dahlhaug, O.; Heidenreich, S. Hydropower Providing Flexibility for a Renewable Energy System: Three European Energy Scenarios; The European Union: Brussels, Belgium, 2018; pp. 1–79. [Google Scholar]
- Wolfgang, O.; Henden, A.L.; Belsnes, M.M.; Baumann, C.; Maaz, A.; Schäfer, A.; Moser, A.; Harasta, M.; Døble, T. Scheduling when Reservoirs are Batteries for Wind- and Solar-power. Energy Procedia 2016, 87, 173–180. [Google Scholar] [CrossRef][Green Version]
- International Energy Agency (IEA). Energy Policies Beyond IEA Countries: Mexico 2017; International Energy Agency: Paris, France, 2017. [Google Scholar]
- Araripe Neto, T.A.; Cotia, C.B.; Pereira, M.V.F.; Kelman, J. Comparison of Stochastic and Deterministic Approaches in Hydrothermal Generation Scheduling. In Proceedings of the IFAC Symposium on Planning and Operation of Electric Energy Systems, Rio de Janeiro, Brazil, 22–25 July 1985. [Google Scholar]
- Ceciliano, J.L.; Álvarez, J.; De-la-Torre, A.; Nieva, R.; Guillén, I.; Navarro, R.; Perales, F.; Torres, C.; Sánchez, A.; Yildirim, M.B. Power System Operator in Mexico Reveals Millions in Savings by Updating its Short-Term Thermal Unit Commitment Model. Interfaces 2016, 46, 493–502. [Google Scholar] [CrossRef]
- Treistman, F.; Maceira, M.E.; Penna, D.D.; Machado, J.; Rotunno, O. Synthetic Scenario Generation of Monthly Streamflows Conditioned to the El Niño-Southern Oscillation: Application to Operation Planning of Hydrothermal Systems. Stoch. Environ. Res. Risk Assess. 2020, 34, 331–353. [Google Scholar] [CrossRef]
- Gonçalves, R.E.C.; Finardi, E.C.; Da Silva, E.L.; Dos Santos, M.L.L. Comparing Stochastic Optimization Methods to Solve the Medium-Term Operation Planning Problem. Comput. Appl. Math. 2011, 30, 289–313. [Google Scholar] [CrossRef]
- Larroyd, P.V.; De Matos, V.L.; Finardi, E.C. Assessment of Risk-Averse Policies for the Long-Term Hydrothermal Scheduling Problem. Energy Syst. 2017, 8, 103–125. [Google Scholar] [CrossRef]
- Terry, L.A.; Pereira, M.V.F.; Araripe Neto, T.A.; Silva, L.F.C.A.; Sales, P.R.H. Coordinating the Energy Generation of the Brazilian National Hydrothermal Electrical Generating System. Interfaces 1986, 16, 16–38. [Google Scholar] [CrossRef]
- Pereira, M.V.F.; Pinto, L.M.V.G. Stochastic Optimization of a Multireservoir Hydroelectric System: A Decomposition Approach. Water Resour. Res. 1985, 21, 779–792. [Google Scholar] [CrossRef]
- Souza, R.C.; Marcato, A.L.M.; Dias, B.H.; Oliveira, F.L.C. Optimal Operation of Hydrothermal Systems with Hydrological Scenario Generation through Bootstrap and Periodic Autoregressive Models. Eur. J. Oper. Res. 2012, 222, 606–615. [Google Scholar] [CrossRef]
- Oliveira, F.L.C.; Souza, R.C.; Marcato, A.L.M. A Time Series Model for Building Scenarios Trees Applied to Stochastic Optimisation. Int. J. Electr. Power Energy Syst. 2015, 67, 315–323. [Google Scholar] [CrossRef]
- Calili, R.F.; Souza, R.C.; Galli, A.; Armstrong, M.; Marcato, A.L.M. Estimating the Cost Savings and Avoided CO2 Emissions in Brazil by Implementing Energy Efficient Policies. Energy Policy 2013, 67, 4–15. [Google Scholar] [CrossRef]
- Brigatto, A.; Street, A.; Valladão, D.M. Assessing the Cost of Time-Inconsistent Operation Policies in Hydrothermal Power Systems. IEEE Trans. Power Syst. 2017, 6, 4541–4550. [Google Scholar] [CrossRef]
- Rosemberg, A.; Street, A.; Dias, J.; Silva, T.; Valladao, D.; Dowson, O. HydroPowerModels.jl: A Julia/JuMP Package for Hydrothermal Economic Dispatch Optimization. Proc. JuliaCon Conf. 2020, 1, 35. [Google Scholar]
- Andrieu, L.; Henrion, R.; Römisch, W. A Model for Dynamic Chance Constraints in Hydro Power Reservoir Management. Eur. J. Oper. Res. 2010, 207, 579–589. [Google Scholar] [CrossRef][Green Version]
- Van Ackooij, W.; Henrion, R.; Möller, A.; Zorgati, R. Joint Chance Constrained Programming for Hydro Reservoir Management. Optim. Eng. 2014, 15, 509–531. [Google Scholar] [CrossRef]
- Philpott, A.; De Matos, V.L.; Finardi, E.C. On Solving Multistage Stochastic Programs with Coherent Risk Measures. Oper. Res. 2013, 61, 957–970. [Google Scholar] [CrossRef]
- De Queiroz, A.R. A Sampling-Based Decomposition Algorithm with Application to Hydrothermal Scheduling: Cut Formation and Solution Quality. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, 2011. [Google Scholar]
- De Matos, V.L.; Morton, D.P.; Finardi, E.C. Assessing Policy Quality in a Multistage Stochastic Program for Long-Term Hydrothermal Scheduling. Ann. Oper. Res. 2016, 253, 713–731. [Google Scholar] [CrossRef]
- Finardi, E.C.; Decker, B.U.; De Matos, V.L. An Introductory Tutorial on Stochastic Programming Using a Long-Term Hydrothermal Scheduling Problem. J. Control. Autom. Electr. Syst. 2013, 3, 361–376. [Google Scholar] [CrossRef]
- Pereira, M.V.F.; Pinto, L.M.V.G. Multi-Stage Stochastic Optimization Applied to Energy Planning. Math. Program. 1991, 52, 359–375. [Google Scholar] [CrossRef]
- Pineiro, M.E. Stochastic Dual Dynamic Programming Applied to the Energetic Operation Planning of Hydrothermal Systems with Inflows Stochastic Process Representation by Periodic Auto-Regressive Models; Electrical Energy Research Center (Cepel): Rio De Janeiro, Brazil, 1993. (In Portuguese) [Google Scholar]
- De Matos, V.L.; Finardi, E.C. A Computational Study of a Stochastic Optimization Model for Long Term Hydrothermal Scheduling. Int. J. Electr. Power Energy Syst. 2012, 43, 1443–1452. [Google Scholar] [CrossRef]
- Kelman, J.; Kelman, R.; Pereira, M.V.F. Firm Energy of Hydroelectric Systems and Multiple uses of Water Resources. Braz. J. Water Resour. 2010, 9, 189–198. (In Portuguese) [Google Scholar]
- Da Costa, J.P.; De Oliveira, G.C.; Legey, L.F.L. Reduced Scenario Tree Generation for Mid-term Hydrothermal Operation Planning. In Proceedings of the 2006 9th International Conference on Probabilistic Methods Applied to Power Systems, PMAPS, Stockholm, Sweden, 11–15 June 2006. [Google Scholar]
- Sen, S.; Higle, J.L. An Introductory Tutorial on Stochastic Linear Programming Models. Interfaces 1999, 22, 33–61. [Google Scholar] [CrossRef]
- Birge, J.R.; Louveaux, F. Introduction to Stochastic Programming; Springer: New York, NY, USA, 2011. [Google Scholar]
- Infanger, G.; Morton, D.P. Cut Sharing for Multistage Stochastic Linear Programs with Interstage Dependency. Math. Program. Ser. A B 1996, 75, 241–256. [Google Scholar] [CrossRef]
- Homem-De-Mello, T.; De Matos, V.L.; Finardi, E.C. Sampling Strategies and Stopping Criteria for Stochastic Dual Dynamic Programming: A Case Study in Long-Term Hydrothermal Scheduling. Energy Syst. 2011, 2, 1–31. [Google Scholar] [CrossRef]
- Shapiro, A. Analysis of Stochastic Dual Dynamic Programming Method. Eur. J. Oper. Res. 2010, 209, 63–72. [Google Scholar] [CrossRef]
- De Matos, V.L. A Model for the Annual Energetic Operation Planning Considering Advanced Stochastic Programming Techniques. Ph.D. Thesis, Federal University of Santa Catarina, Florianopolis, Brazil, 2012. (In Portuguese). [Google Scholar]
- Da Silva, E.L.; Finardi, E.C. Parallel Processing Applied to the Planning of Hydrothermal Systems. IEEE Trans. Parallel Distrib. Syst. 2003, 14, 721–729. [Google Scholar] [CrossRef]
- Shapiro, A.; Tekaya, W.; Da-Costa, J.P.; Soares, M.P. Report for Technical Cooperation between Georgia Institute of Technology and ONS; Georgia Institute of Technology and National System Operator: Atlanta, GA, USA, 2011. [Google Scholar]
- Philpott, A.; Pritchard, G. EMI-DOASA; Electric Power Optimization Centre: Cambridge, MA, USA, 2013. [Google Scholar]
- Fredo, G.L.M.; Finardi, E.C.; De Matos, V.L. Assessing Solution Quality and Computational Performance in the Long-Term Generation Scheduling Problem Considering Different Hydro Production Function Approaches. Renew. Energy 2018, 131, 45–54. [Google Scholar] [CrossRef]
- Chiralaksanakul, A.; Morton, D.P. Assessing Policy Quality in Multi-Stage Stochastic Programming; Humboldt-Universität zu Berlin, Mathematisch-Naturwissenschaftliche Fakultät II, Institut für Mathematik: Berlin, Germany, 2004. [Google Scholar]
- Shapiro, A.; Philpott, A. A Tutorial on Stochastic Programming. Tutorial 2007, 131, 45–54. [Google Scholar]
- International Hydropower Association (IHA). 2018 Hydropower Status Report: Sector Trends and Insights; International Hydropower Association: London, UK, 2018; Available online: https://www.hydropower.org/publications/2018-hydropower-status-report (accessed on 1 June 2022).
- Arganis, M.L.; Mendoza, R.; Domínguez, R.; Carrizosa, E. Operating Policies of El Infiernillo Dam for Hydropower Electricity Generation with Stochastic Dynamic Programming. Ribagua 2015, 2, 97–104. (In Spanish) [Google Scholar]
- Ministry of Energy (SENER). Renewable Energies Outlook 2016–2030. Available online: https://www.gob.mx/sener/documentos/energy-sector-outlooks-2016-2030 (accessed on 1 February 2021).
- Federal Electricity Commission (CFE)—Sub Direction of Non-Regulated Businesses. Meteorological Synopsis and Preliminar Forecasting, January 4th, 2021; Federal Electricity Commission: Mexico City, Mexico, 2021. (In Spanish) [Google Scholar]
- Arganis, M.L.; Mendoza, R.; Domínguez, R. Operation of Three Hydroelectric Dams using Guide Curves and Stochastic Dynamic Programming. Water Technol. Sci. 2012, 3, 97–114. (In Spanish) [Google Scholar]
- Feldman, R.M.; Valdez-Flores, C. Applied Probability and Stochastic Processes; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]



















| Thermal Power Plants | Hydropower Plant | ||||||
|---|---|---|---|---|---|---|---|
| Plant | Incr. Cost USD/(MWh) | Inst. Cap. (MW) | Ini. Vol. (Mm) | Min. Vol. (Mm) | Max. Vol. (Mm) | Max. Turb. Outflow (m/s) | Productivity Factor (MWh/(m/s)) |
| 1 | 10 | 100 | |||||
| 2 | 20 | 150 | |||||
| 3 | 40 | 200 | 3000 | 2250 | 6053.75 | 1300 | 0.96 |
| 4 | 80 | 250 | |||||
| 5 | 500 | 1000 | |||||
| Parameter | Stage 1 | Stage 2 |
|---|---|---|
| Operating Cost (USD) | 29,954.96 | 11,410.52 |
| TP (MWh) | 100 | 100 |
| TP (MWh) | 150 | 150 |
| TP (MWh) | 200 | 185.26 |
| TP (MWh) | 224.44 | 0 |
| TP (MWh) | 0 | 0 |
| HP (MWh) | 325.56 | 564.74 |
| Initial Volume (Mm) | 3000 | 2250 |
| Inflow (Mm) | 129.02 | 1524.79 |
| Turbined Outflow (m/s) | 339.13 | 588.27 |
| Spilled Outflow (m/s) | 0 | 0 |
| Final Volume (Mm) | 2250 | 2250 |
| Parameter | Stage 1 | Stage 2 |
|---|---|---|
| Operating Cost (USD) | 32,000 | 128,874.07 |
| TP (MWh) | 100 | 100 |
| TP (MWh) | 150 | 150 |
| TP (MWh) | 200 | 200 |
| TP (MWh) | 250 | 250 |
| TP (MWh) | 0 | 193.75 |
| HP (MWh) | 300 | 106.25 |
| Initial Volume (Mm) | 3000 | 2319.02 |
| Inflow (Mm) | 129.02 | 217.86 |
| Turbined Outflow (m/s) | 312.50 | 110.68 |
| Spilled Outflow (m/s) | 0 | 0 |
| Final Volume (Mm) | 2319.02 | 2250 |
| Parameter | Stage 1 | Stage 2 |
|---|---|---|
| Operating Cost (USD) | 32,000 | 162,231.48 |
| TP (MWh) | 100 | 100 |
| TP (MWh) | 150 | 150 |
| TP (MWh) | 200 | 200 |
| TP (MWh) | 250 | 250 |
| TP (MWh) | 0 | 260.46 |
| HP (MWh) | 300 | 39.54 |
| Initial Volume (Mm) | 3000 | 2319.02 |
| Inflow (Mm) | 129.02 | 37.73 |
| Turbined Outflow (m/s) | 312.50 | 41.18 |
| Spilled Outflow (m/s) | 0 | 0 |
| Final Volume (Mm) | 2319.02 | 2250 |
| Case | Total Operating Cost (USD) |
|---|---|
| Optimistic scenario | 41,365.48 |
| Expected scenario | 160,874.07 |
| Pessimistic scenario | 194,231.48 |
| Variable | Stage 1 | Stage 2 | ||
|---|---|---|---|---|
| Optimistic | Expected | Pessimistic | ||
| Scenario | Scenario | Scenario | ||
| Operating Cost (USD) | 32,000 | 10,388 | 128,874.07 | 162,231.48 |
| TP (MWh) | 100 | 100 | 100 | 100 |
| TP (MWh) | 150 | 150 | 150 | 150 |
| TP (MWh) | 200 | 159.70 | 200 | 200 |
| TP (MWh) | 250 | 0 | 250 | 250 |
| TP (MWh) | 0 | 0 | 193.75 | 260.46 |
| HP (MWh) | 300 | 590.30 | 106.25 | 39.54 |
| Initial Volume (Mm) | 3000 | 2319.02 | 2319.02 | 2319.02 |
| Inflow (Mm) | 129.02 | 1524.79 | 217.86 | 37.73 |
| Turbined Outflow (m/s) | 312.50 | 614.90 | 110.68 | 41.18 |
| Spilled Outflow (m/s) | 0 | 0 | 0 | 0 |
| Final Volume (Mm) | 2319.02 | 2250 | 2250 | 2250 |
| Reservoir | Hydropower Plant | Installed Capacity (MW) | Maximum Volume (Mm) |
|---|---|---|---|
| Caracol | Carlos Ramírez Ulloa | 3 × 200 MW | 697.46 |
| Adolfo López Mateos | Infiernillo | 6 × 200 MW | 6053.75 |
| José María Morelos y Pavón | La Villita | 4 × 80 MW | 221.29 |
| Month | Distribution | Statistic | Month | Distribution | Statistic |
|---|---|---|---|---|---|
| January | Wakeby | July | Johnson SB | ||
| February | Wakeby | August | Two-Parameter Gamma | ||
| March | Four-Parameter Burr | September | Three-Parameter Gamma | ||
| April | Wakeby | October | Gumbel Max | ||
| May | Wakeby | November | Wakeby | ||
| June | Three-Parameter Burr | December | Log-Logistic |
| Month | Distribution | Fitting Parameters | Domain | ||||
|---|---|---|---|---|---|---|---|
| January | Wakeby | ||||||
| February | Wakeby | ||||||
| March | 4-P Burr | - | |||||
| April | Wakeby | ||||||
| May | Wakeby | ||||||
| June | 3-P Burr | - | - | ||||
| July | Johnson SB | - | |||||
| August | 2-P Gamma | - | - | - | |||
| September | 3-P Gamma | - | - | ||||
| October | Gumbel Max | - | - | - | |||
| November | Wakeby | ||||||
| December | Log-Logistic | - | - | ||||
| Distribution | Inverse Cumulative Distribution Function |
|---|---|
| 3-P Burr | |
| 4-P Burr | |
| 2-P Gamma | |
| 3-P Gamma | |
| Gumbel Max | |
| Johnson SB | |
| Log-Logistic | |
| Wakeby |
| Case | Branch Size | Total Number of Scenarios | Case | Branch Size | Total Number of Scenarios | Case | Branch Size | Total Number of Scenarios |
|---|---|---|---|---|---|---|---|---|
| 1 | 5 | 4.9 × 10 | 11 | 2800 | 8.3 × 10 | 21 | 11,000 | 2.9 × 10 |
| 2 | 10 | 1.0 × 10 | 12 | 3600 | 1.3 × 10 | 22 | 12,000 | 7.4 × 10 |
| 3 | 20 | 2.0 × 10 | 13 | 4400 | 1.2 × 10 | 23 | 13,000 | 1.8 × 10 |
| 4 | 50 | 4.9 × 10 | 14 | 5200 | 7.5 × 10 | 24 | 14,000 | 4.0 × 10 |
| 5 | 100 | 1.0 × 10 | 15 | 6000 | 3.6 × 10 | 25 | 15,000 | 8.6 × 10 |
| 6 | 400 | 4.2 × 10 | 16 | 6800 | 1.4 × 10 | 26 | 16,000 | 1.8 × 10 |
| 7 | 800 | 8.6 × 10 | 17 | 7600 | 4.9 × 10 | 27 | 17,000 | 3.4 × 10 |
| 8 | 1200 | 7.4 × 10 | 18 | 8400 | 1.5 × 10 | 28 | 18,000 | 6.4 × 10 |
| 9 | 1600 | 1.8 × 10 | 19 | 9200 | 4.0 × 10 | 29 | 19,000 | 1.2 × 10 |
| 10 | 2000 | 2.0 × 10 | 20 | 10,000 | 1.0 × 10 | 30 | 20,000 | 2.0 × 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marín Cruz, I.; Badaoui, M.; Mota Palomino, R. Medium-Term Hydrothermal Scheduling of the Infiernillo Reservoir Using Stochastic Dual Dynamic Programming (SDDP): A Case Study in Mexico. Energies 2023, 16, 6288. https://doi.org/10.3390/en16176288
Marín Cruz I, Badaoui M, Mota Palomino R. Medium-Term Hydrothermal Scheduling of the Infiernillo Reservoir Using Stochastic Dual Dynamic Programming (SDDP): A Case Study in Mexico. Energies. 2023; 16(17):6288. https://doi.org/10.3390/en16176288
Chicago/Turabian StyleMarín Cruz, Ignacio, Mohamed Badaoui, and Ricardo Mota Palomino. 2023. "Medium-Term Hydrothermal Scheduling of the Infiernillo Reservoir Using Stochastic Dual Dynamic Programming (SDDP): A Case Study in Mexico" Energies 16, no. 17: 6288. https://doi.org/10.3390/en16176288
APA StyleMarín Cruz, I., Badaoui, M., & Mota Palomino, R. (2023). Medium-Term Hydrothermal Scheduling of the Infiernillo Reservoir Using Stochastic Dual Dynamic Programming (SDDP): A Case Study in Mexico. Energies, 16(17), 6288. https://doi.org/10.3390/en16176288






