Next Article in Journal
Proposing a Hybrid BTMS Using a Novel Structure of a Microchannel Cold Plate and PCM
Next Article in Special Issue
A Model-Aware Comprehensive Tool for Battery Energy Storage System Sizing
Previous Article in Journal
Resilience of Natural Gas Pipeline System: A Review and Outlook
Previous Article in Special Issue
Degradation Prediction and Cost Optimization of Second-Life Battery Used for Energy Arbitrage and Peak-Shaving in an Electric Grid
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Energies
Volume 16
Issue 17
10.3390/en16176239
energies-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

HPPC Test Methodology Using LFP Battery Cell Identification Tests as an Example

by
Tadeusz Białoń
1,2,
Roman Niestrój
1,2,
Wojciech Skarka
3,4,* and
Wojciech Korski
2
1
Department of Electrical Engineering and Computer Science, Faculty of Electrical Engineering, Silesian University of Technology, 44-100 Gliwice, Poland
2
Łukasiewicz Research Network—Institute of Innovative Technologies EMAG, 40-189 Katowice, Poland
3
Department of Fundamentals of Machinery Design, Faculty of Mechanical Engineering, Silesian University of Technology, 44-100 Gliwice, Poland
4
Bumech S.A., 40-389 Katowice, Poland
*
Author to whom correspondence should be addressed.
Energies 2023, 16(17), 6239; https://doi.org/10.3390/en16176239
Submission received: 30 June 2023 / Revised: 20 August 2023 / Accepted: 24 August 2023 / Published: 28 August 2023
(This article belongs to the Special Issue Battery Modelling, Applications, and Technology)
Browse Figures
Versions Notes

Abstract

:
The aim of this research was to create an accurate simulation model of a lithium-ion battery cell, which will be used in the design process of the traction battery of a fully electric load-hull-dump vehicle. Discharge characteristics tests were used to estimate the actual cell capacity, and hybrid pulse power characterization (HPPC) tests were used to identify the Thevenin equivalent circuit parameters. A detailed description is provided of the methods used to develop the HPPC test results. Particular emphasis was placed on the applied filtration and optimization techniques as well as the assessment of the quality and the applicability of the acquired measurement data. As a result, a simulation model of the battery cell was created. The article gives the full set of parameter values needed to build a fully functional simulation model. Finally, a charge-depleting cycle test was performed to verify the created simulation model.

1. Introduction

The research described here aims to create an accurate simulation model of a battery cell, which will be used in the design process of the traction battery of a fully electric load-hull-dump (LHD) vehicle. The model-based design (MBD) method [1,2] was used to create numerical models of vehicle subassemblies in order to test them by means of simulation. The MBD method is frequently used to design vehicles and mobile robots [3], as well as to design manned and unmanned aerial vehicles [4,5]. The practical importance of model-based techniques in energy storage analysis and design is also underlined in [6,7,8,9,10].
The most basic element of a traction battery is a single cell. Its equivalent circuit, describing the static and dynamic properties, is the starting point for creating a simulation model. In practice, many different forms of battery cell equivalent circuits are used [11,12,13,14,15,16,17,18,19,20,21], taking into account various physical and chemical phenomena. The appropriate choice of model depends on its intended use and the method by which its parameters will be identified.
Battery cell models are often used in the form of an equivalent circuit [11,12,13,16,22,23,24,25], and many authors emphasize the advantages of this method. The first advantage is the simplicity of the model, most often composed of resistors and capacitors, and a voltage source to represent the battery’s OCV [15,16,17,26]. The battery’s electrical properties are described by their characteristics dependent on the state of charge (SOC) of the cell. Another advantage is the flexibility. The complexity of the equivalent circuit (i.e., number of RC pairs in the Thevenin model) can be adjusted according to the desired model accuracy and applied parameter identification method. To represent battery cell properties over a wide frequency range, an additional inductance may be introduced [27,28]. In this work it is omitted, because the inductance value cannot be identified with the HPPC tests. The third important advantage is the composability. Introducing additional elements to the model, phenomena such as self-discharge can be taken into consideration [18]. The equivalent circuit element characteristics can also be extended with the thermal and aging model, creating a multi-physical model [29].
The equivalent circuit model approach also shows high fidelity in simulating battery performance characteristics [30,31,32,33]. Model fidelity, which measures how closely a model or simulation mimics the state and behavior of a real-world item, is crucial in MBD.
For the purposes of battery design using the MBD method, models describing the dependence of the open-circuit voltage (OCV) characteristics on SOC [11,18,34,35] and the dynamic properties of the cell with one or two time constants are most often used. The Thevenin circuit [17,20,25,36,37,38] is such model and was used in the research described here.
In general, it is difficult to estimate battery parameters quickly and accurately from input–output cycling data [23,24,39]; therefore, special identification tests must be used. The pulse charge or discharge test [14,40,41,42] or hybrid pulse power characterization (HPPC) tests [43,44,45,46,47], combined with charge and discharge characteristics [44,48,49], are the most commonly used. These tests (performed once) can reflect the properties of the cell for the current state of health (SOH), so they cannot identify the effects of cell aging [21] or changes in its parameters during long-term operation. They are also unable to identify self-discharge effects [50]. These effects, however, have little impact on the basic operational properties of the battery and are usually neglected in the design process with the MBD method.
Identification of resistor–capacitor (RC) parameters of the Thevenin equivalent circuit depends on the HPPC impulse voltage approximation quality with an exponential function [40,48,49,51] or multi-exponential function [35,47,48]. However, usually two exponential terms are used. Approximation may be performed by optimization. Deterministic optimization methods may be used [21,44,52]. However, in this case, the optimization result depends on the starting point of the algorithm, which is not always easy to choose. However, this problem does not occur in population-based metaheuristic algorithms [53]. Such algorithms, i.e., genetic algorithms [17,54,55], particle swarm optimization (PSO) [21,52,56], and others [57], are also used for HPPC results processing. PSO was also applied in the research described here.
This article details the step-by-step process of preparing HPPC tests and processing their results. Typical technical problems, including those resulting from the physical properties of lithium-ion iron phosphate (LFP) cells, are discussed and methods of solving them are proposed. LFP battery cells have a lower energy density than the most popular electromobility applications of nickel manganese cobalt (NMC) cells [58,59], but they ensure greater safety of use due to much lower susceptibility to thermal runaway [59,60]. LFP battery cells also perform more favorably in terms of product sustainability [61,62].
The article describes the issues that are a continuation of the research described in the article [63].
The novelties are as follows:
  • An optimization-based battery cell time constant identification algorithm is implemented in software written by the authors.
  • An HPPC-based method for OCV vs. SOC characteristic determination is established.
  • Other contributions of the article are as follows:
  • This paper gives the values of all parameters necessary to build a fully parameterized mathematical model of the cell.
  • The paper explains the HPPC test development methodology step by step. In the literature, usually only the results of HPPC are given, but the process of obtaining them is not described. This paper fills that gap.
  • The paper discusses potential flaws in the HPPC test results. Not every HPPC pulse recorded during measurements is suitable for further analysis and must be omitted. In the literature, this problem is hardly commented on. This paper fills that gap.
  • The paper applies edge detection techniques in the analysis of the HPPC test results.
  • The paper remarks on battery cell true capacity experimental estimation.

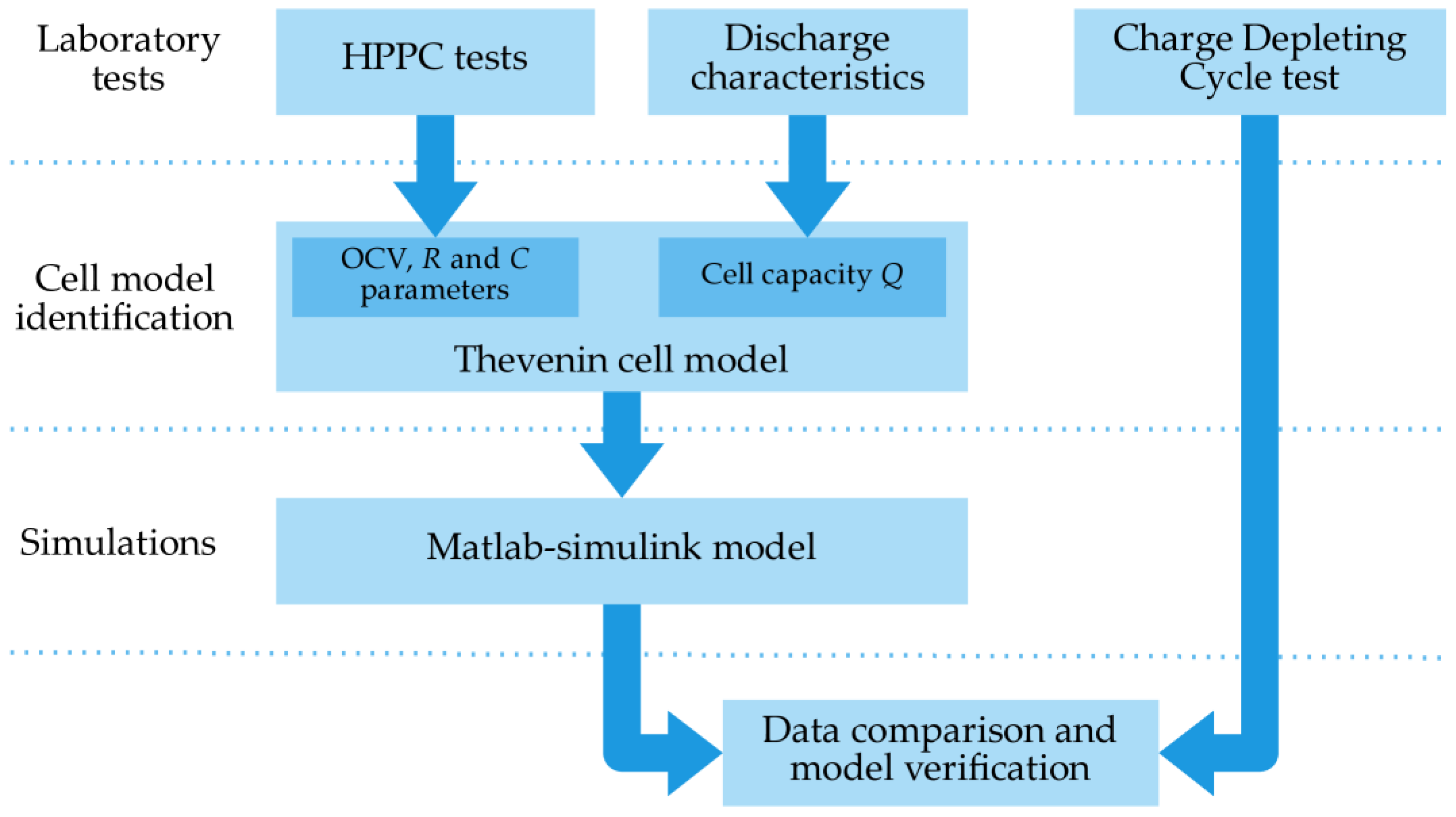
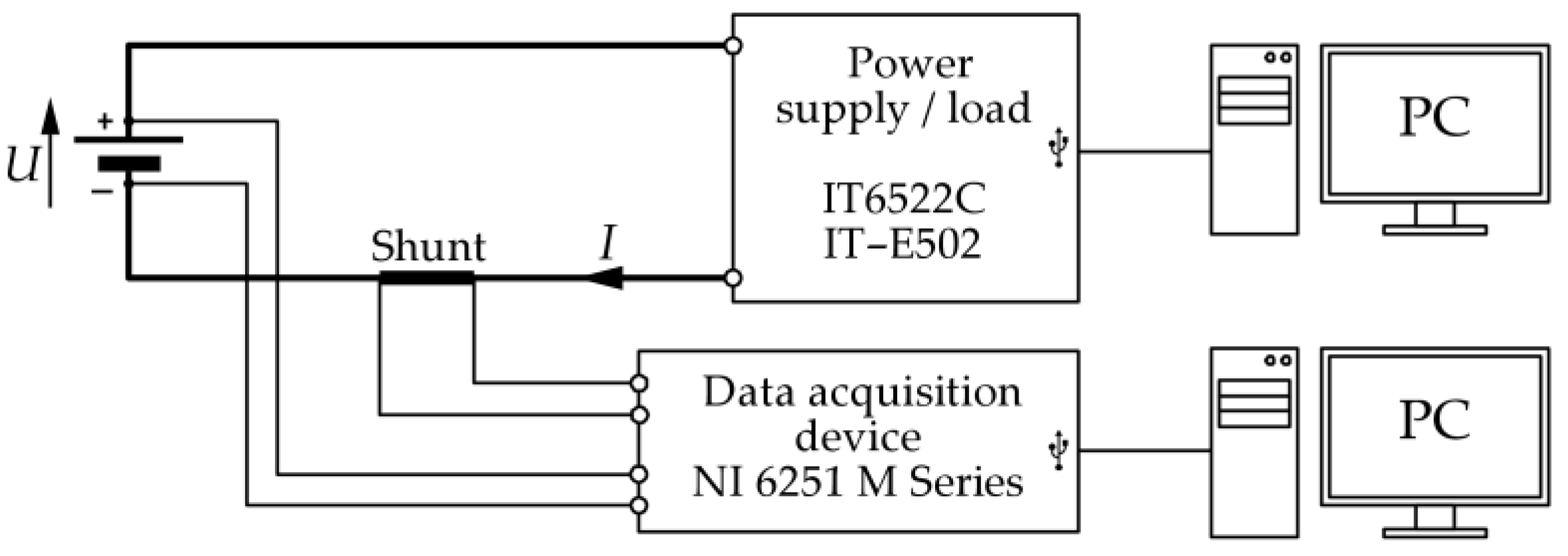
2. Materials and Methods

The general research methodology is schematically presented in Figure 1.
The research was divided into three main stages: laboratory tests, identification of cell parameters based on test results, and creation of a simulation model and simulations (Figure 1). In the laboratory phase, tests were performed that were the basis for model identification and its subsequent verification. Identification of the parameters of the cell model was carried out using software written by the authors, using innovative optimization algorithms based on particle swarm optimization (PSO) and the Levenberg–Marquardt method. Known signal processing techniques, such as edge detection and filtering of measurement data, were also used in an original way. As a result, a simulation model was created in the MATLAB/Simulink environment, using the Simscape Electrical library.
The tests were carried out for the LFP (LiFePO4) battery cell with the rated parameters given in Table 1. The following laboratory tests were carried out: discharge characteristics to estimate the actual cell capacity, HPPC tests to identify the equivalent circuit parameters, and a charge-depleting cycle (CDC) test [64] to verify the identified mathematical model.
The tests were carried out in the laboratory setup shown in Figure 2. The voltage at the cell terminals and at the shunt was recorded using a National Instruments NI 6251 M A series data acquisition device was equipped with a 16-bit analog-to-digital converter. The sampling rate was 135 Hz during HPPC tests and 100 Hz during the CDC test. The main element of the setup was a programmable power supply with a load function ITECH IT6522C, additionally equipped with a dedicated power dissipater module IT-E502. This set enables both power supply and active load up to 3000 W and 120 A DC. The power supply may operate in constant current (CC) and constant voltage (CV) modes. The battery cell was operated in CC mode, in accordance with the given reference current test profile, only if the cell voltage value was within the tolerable limits given in Table 1. When the cell voltage reached the minimum or maximum value, the power supply was switched into CV mode, in which the current was limited to keep the voltage within specified limits. Measurements were carried out at an ambient temperature of about 22 °C, with deviations up to 1 °C.
The simulation model created during the research directly reflects the structure of the laboratory setup. Not only a battery cell model based on Thevenin’s equivalent circuit (Section 3.1) was created, but also an active power supply model was created, including the implementation of CC/CV mechanisms. This makes it possible to compare the simulation results with the laboratory CDC test results. In both cases, i.e., in the real power supply and its simulation model, the same profile of the reference current was implemented.

3. Results

The aim of the research was to create an accurate simulation model of an LFP battery cell. The basis of the model was the equivalent circuit described in Section 3.1, the parameters of which were determined on the basis of HPPC test results as described in Section 3.3. The cell capacity set in the simulation model was determined by the methods described in Section 3.2. The method of verifying the identified model is described in Section 3.4.

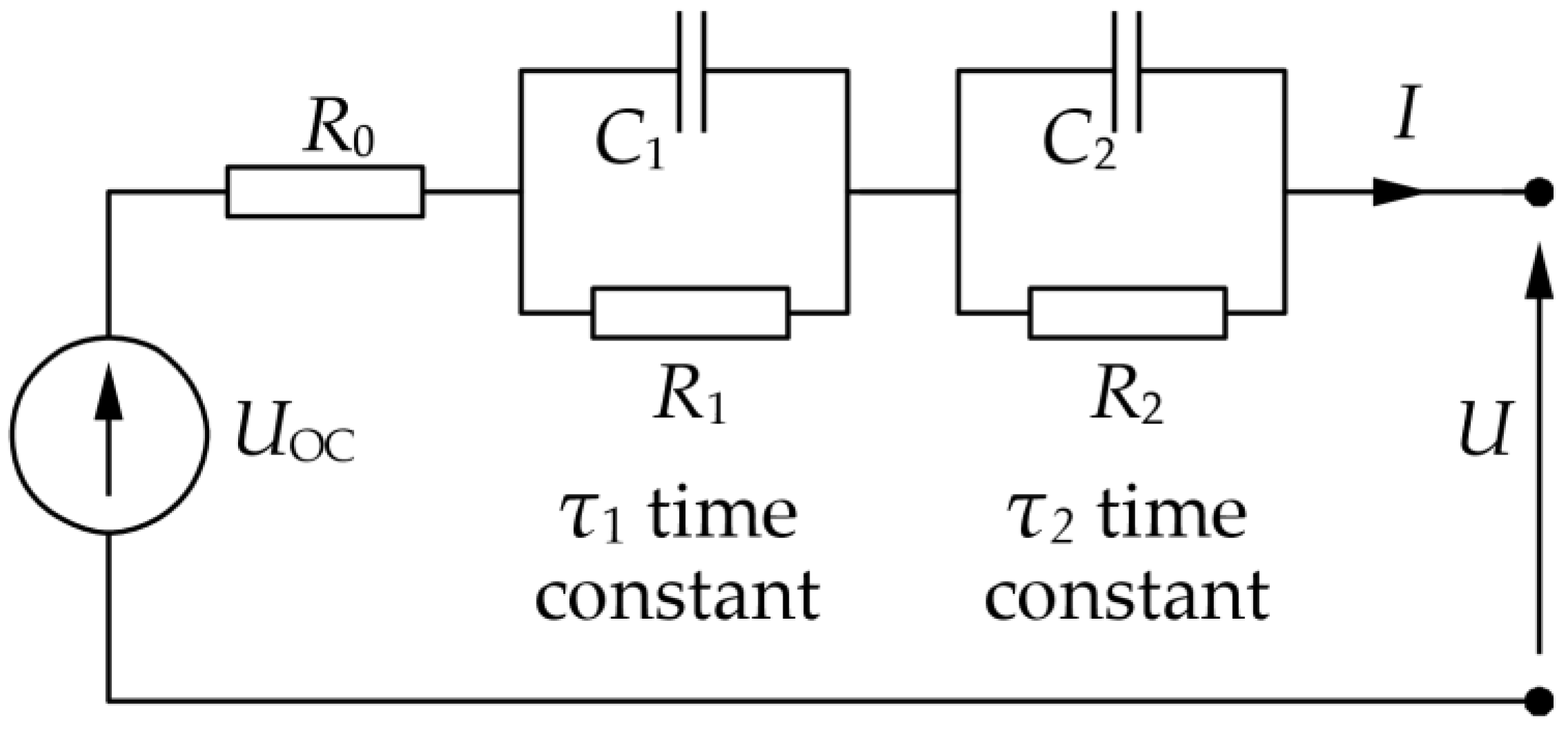
3.1. Battery Cell Equivalent Circuit

A mathematical model of the battery cell in the form of a Thevenin equivalent circuit [21,37,38,46,65,66,67] was used (Figure 3). The circuit contains two RC pairs, thus simulating two time constants of the dynamic model [65,66,68,69]:
τ1 = R1C1, τ2 = R2C2,
Thevenin models are usually used with one to five RC pairs and their corresponding time constants. In the case of LFP cells, the first (smallest) time constant has values of a few seconds, whereas the second has values of tens of seconds. The third time constant is measured in tens of minutes, etc. HPPC tests can only identify the first two RC pairs (see Section 3.3), so the others are omitted [22].
All the resistances, capacities as well as the OCV (UOC in Figure 3) depend on the SOC of the cell [31], which is estimated on the basis of the cell current [22,37,51,57,67,68,70]:
S O C = S O C 0 − 1 Q ∫ 0 t I d τ ,
where SOC0 is the initial SOC of the cell, and Q is the cell capacity. Note that the actual cell capacity depends on many factors, such as temperature and SOH of the cell, and is usually different from the rated one, Qn. Here, it was estimated based on the measurement results as described in Section 3.2.
Determination of the OCV vs. SOC characteristic is described in Section 3.3.2. The determination of the dependence of RC parameters on SOC is described in Section 3.3.4 and Section 3.3.5.

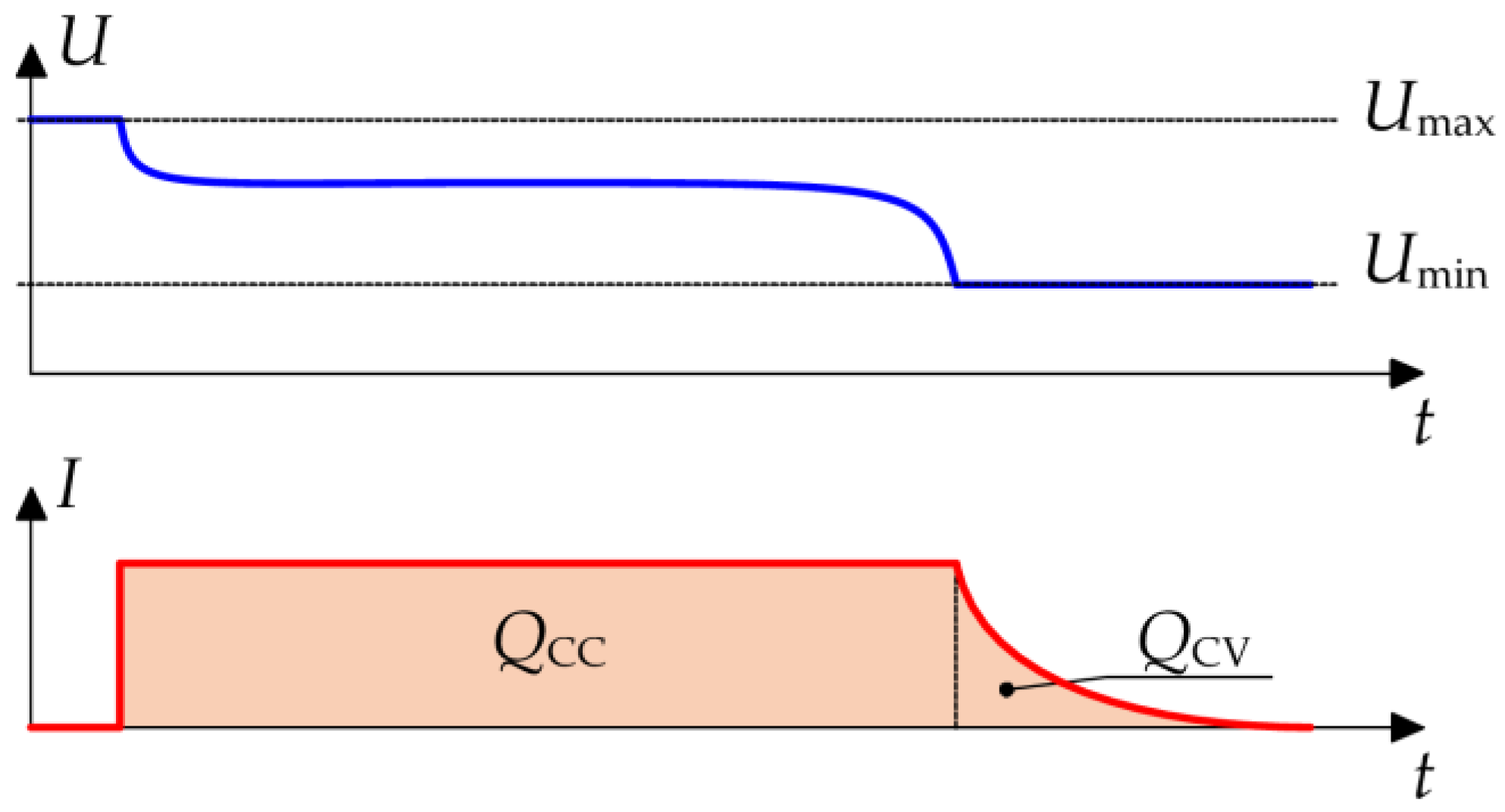
3.2. Capacity and State of Charge Estimation

The actual capacity of the cell is usually different from the nominal one and is crucial from the point of view of correct parameterization of the created mathematical model. The correctness of determining the SOC depends on this, and more precisely, it is necessary to determine the value of Q in Formula (2), corresponding to SOC = 1.
By definition, the charge drawn from the battery is equal to the integral of the current over time [71]:
Q = ∫ 0 t I d τ .
In geometric interpretation, Q is the area under the current waveform. However, recording of the battery discharge current can be made at different values of I, and different assumptions as to the operating conditions. Two different methods were used here. The first was a measurement based on the discharge characteristics [44,48,49]. The second, proposed by the authors, was the use of current waveforms recorded during HPPC tests [63].
Discharge tests were performed at four different current values (0.5 C, 1 C, 2 C, and 3 C) by recording the current and voltage. The tests were started with the cell charged to the maximum voltage (Table 1) and after several hours of relaxation. The current was recorded while the laboratory setup was operating in the CC mode, and the charge taken under these conditions was called QCC (Figure 4).
When the cell voltage reached the minimum value, and the system went into CV mode, the recording continued until the current completely dropped to 0. The charge determined under these conditions was called QCV. The results obtained during the tests are summarized in Table 2, and the recorded transients are shown in Figure 5.
Table 2 shows that the total charge taken from the cell during the discharge tests was slightly dependent on the current. However, the proportion between the QCC and QCV values changes. The higher the discharge current, the lower the QCC and the higher the QCV.
Then, the total charge taken from the cell during the HPPC tests (described in Section 3.3) was determined by integrating the currents recorded in each of the 18 tests and summing the results. The value of Q = 50.71 Ah was obtained (see Table 3 in Section 3.3).
It should be noted that all measured charge values (in discharge and HPPC tests) were greater than the nominal cell capacitance Qn, but the differences between them were significant. Therefore, the question as to which of them should be treated as the final one (the total capacity of the cell) should be asked, which will be used in the created mathematical model. In order to find the answer, a number of simulations were carried out for all the values obtained and the results of the selected values are presented in Section 3.4. The best result was obtained for the value of Q = 45.7 Ah, calculated as the average of the QCC values for all four current values (average of the values from the third column of Table 2).

3.3. HPPC Tests

The basic idea of an HPPC test is to analyze the cell voltage response to a rectangular current pulse. This response is a multi-exponential waveform, the time constants of which should be determined in the identification process [17,44,46,48,69]:
U = U OC − I R 0 − I R 1 1 − e − t τ 1 − I R 2 1 − e − t τ 2 .
In order for the determination of the time constant to be possible and precise, the recorded voltage response should last several times longer than the expected length of the time constant [43]. So, the longer the recorded transient, the better. On the other hand, a single HPPC pulse should be as short as possible so as not to change the SOC of the battery, which results directly from (2). The HPPC pulse length used in practice is therefore a compromise between these two requirements. In the case of nickel manganese cobalt (NMC) cells, the first two time constants are relatively short [63] and do not exceed a dozen or so seconds, so pulses from 9 s to 18 s are sufficient. Usually 10 s pulses are used [16,43,44,45]. In the case of the considered LFP cell, the time constants are longer, so the duration time of the HPPC pulses was extended to 60 s.
In practice, HPPC profiles containing different numbers of pulses are used, but it is always an even number [16,44,55]. This is because the pulses always occur in pairs (a charging pulse with a discharging pulse), so that the series of pulses does not change the SOC of the cell. The number of pairs of pulses may be different, sometimes only one is used [69]. When there is more than one pair, then individual pairs differ in current values. Here, four pairs of pulses were used, successively with current values of 0.5 C, 1 C, 2 C, and 3 C (Figure 6). The greater the current value, the greater the voltage change in response to the impulse, so the easier it is to record (see Section 3.3.1). On the other hand, the greater the current value, the greater the SOC change during the pulse duration, which may cause the problems described in Section 3.3.3. The order of the pulses in the pair also matters. For high SOC values, the discharge pulse was used first. Starting with a charging pulse would risk increasing the cell voltage during the pulse duration, which for a high SOC value (close to 1) could cause the measurement system to switch from CC to CV mode and cut the pulse (see Section 3.3.3). For small SOC values (close to 0), for the same reason, the order was reversed with the charging pulse used first. The sequence change is seen in Table 3 after test number 7.
Another important consideration is the relaxation time between pulses. In principle, it should be much longer than the expected values of the time constants of the cell, so that before the next pulse occurs, the cell voltage has time to stabilize after the preceding pulse. However, due to the very large time constants of the examined LFP cell, it was difficult to meet this assumption. In the conducted tests, a relaxation time between pulses of 20 min was used (Figure 6).
The last element of the HPPC profile shown in Figure 6 is the discharge of the cell before the next HPPC test. The values of the cell equivalent circuit parameters change most rapidly for very small and very large SOC values, but for intermediate values (SOC ≈ 0.5), they are almost constant. To capture the shape of the characteristics, a discharge of 0.05 Qn was used for large SOC values, and then the interval was increased to 0.1 Qn to return to 0.05 Qn for small SOC values.
Successive HPPC tests were carried out until the total charge taken from the battery during the test dropped significantly below the set discharge value (0.05 Qn), which resulted from the fact that the discharge pulses in the profile were cut off by the CC/CV mechanism due to reaching the minimum voltage. All the performed tests are summarized in Table 3, where ΔQ is the charge taken from the cell during the whole HPPC test (including final discharge by 0.05/0.1 Qn). For the last two tests (17 and 18), this value drops significantly, which means that the cell is already discharged. 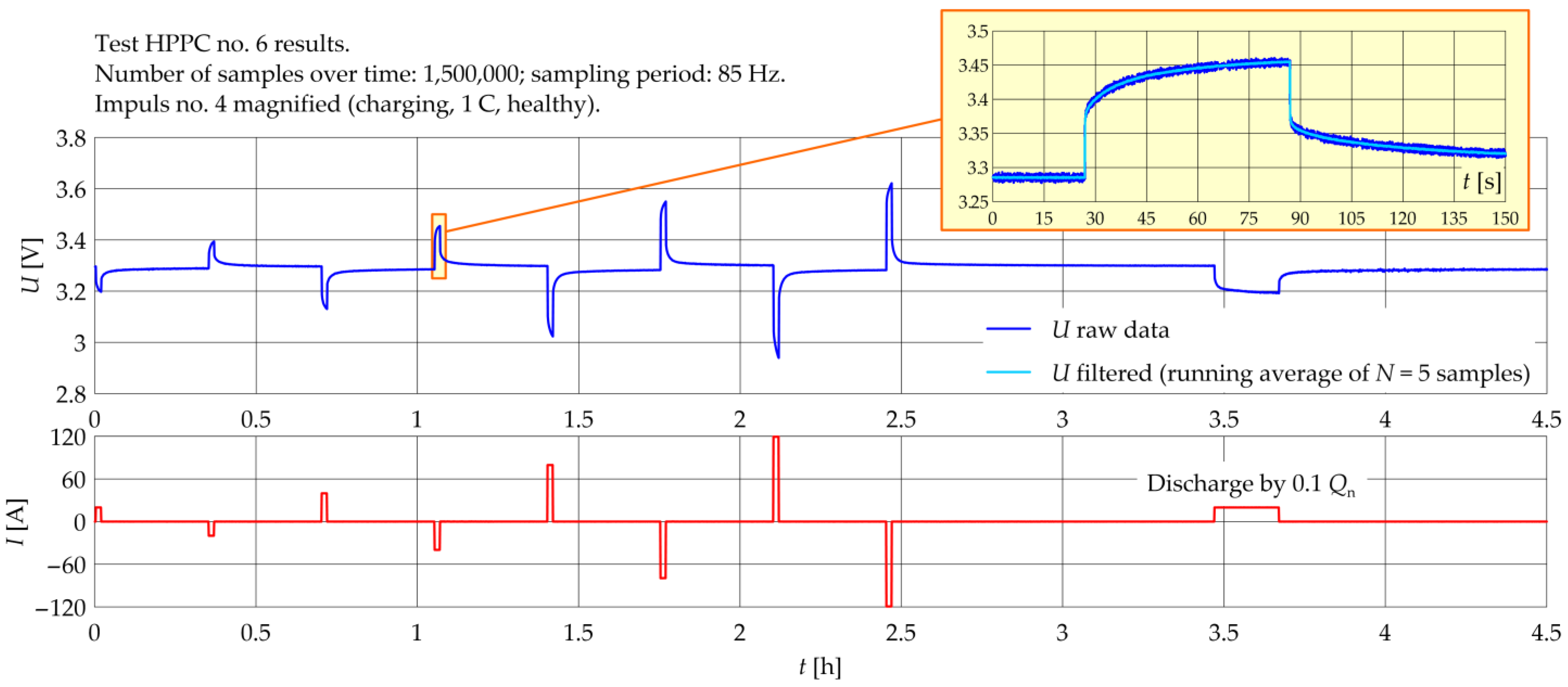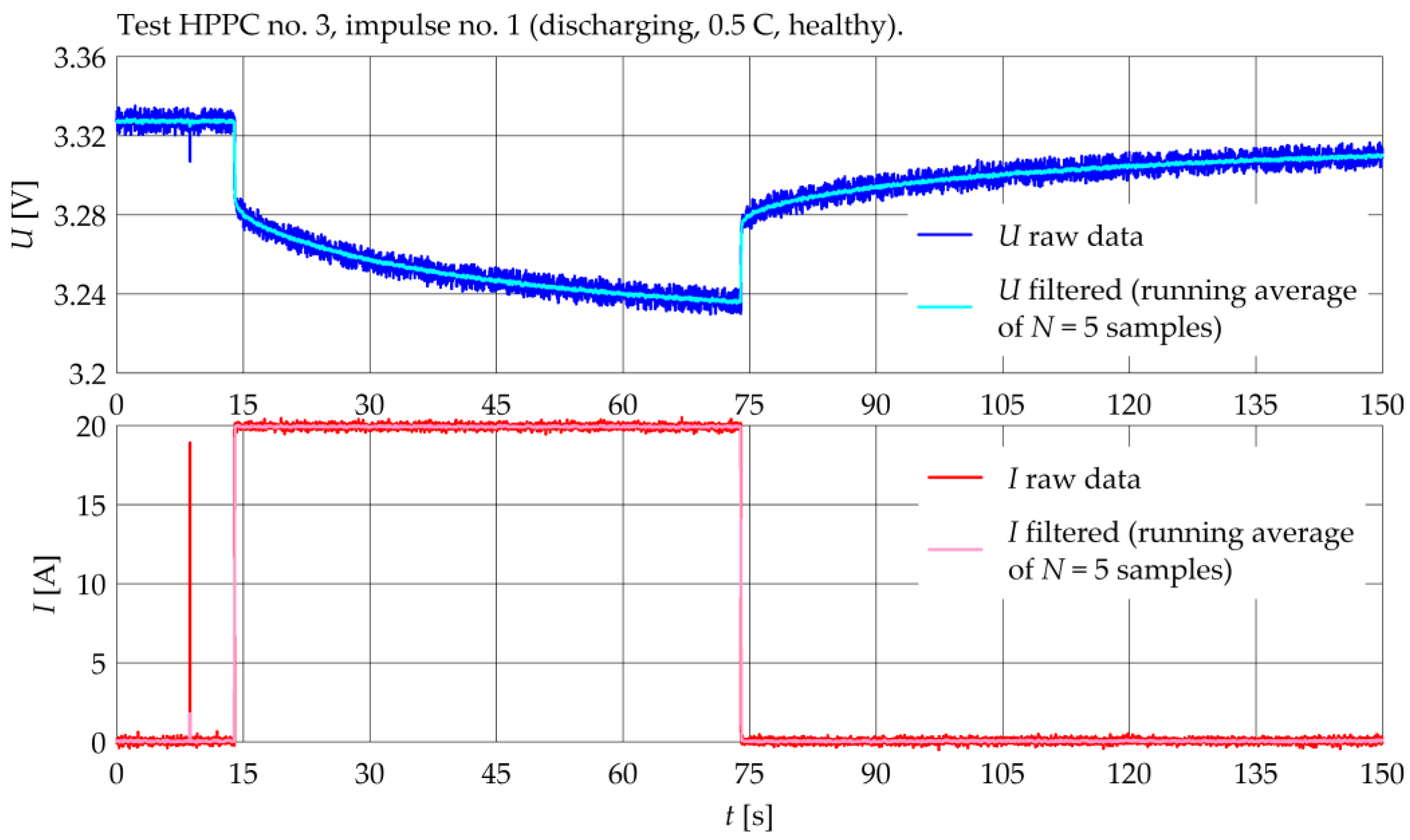In Table 3, Q is the total value of the charge taken from the cell at the end of the given test, taking into account the charge taken in the preceding tests.

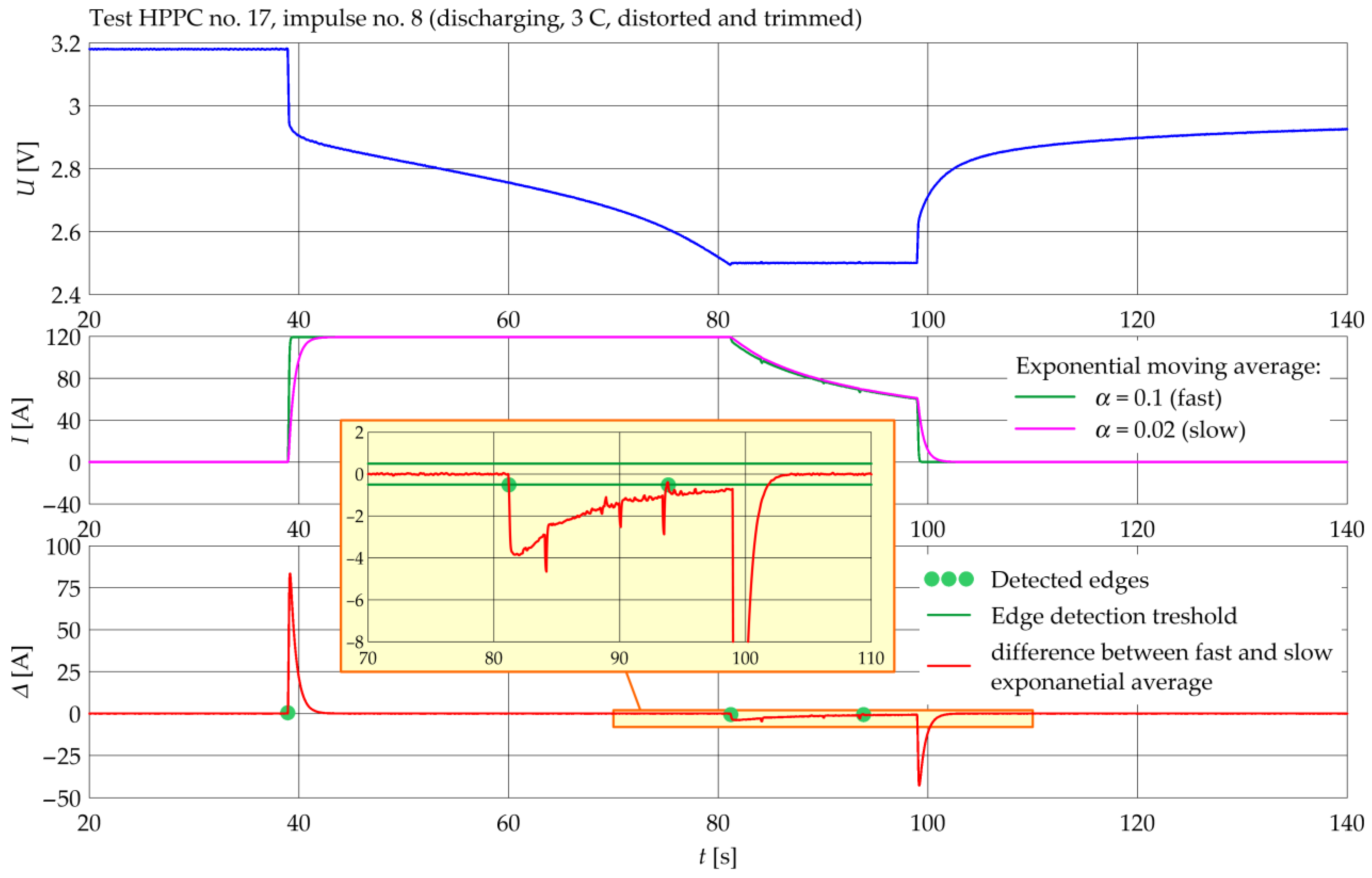
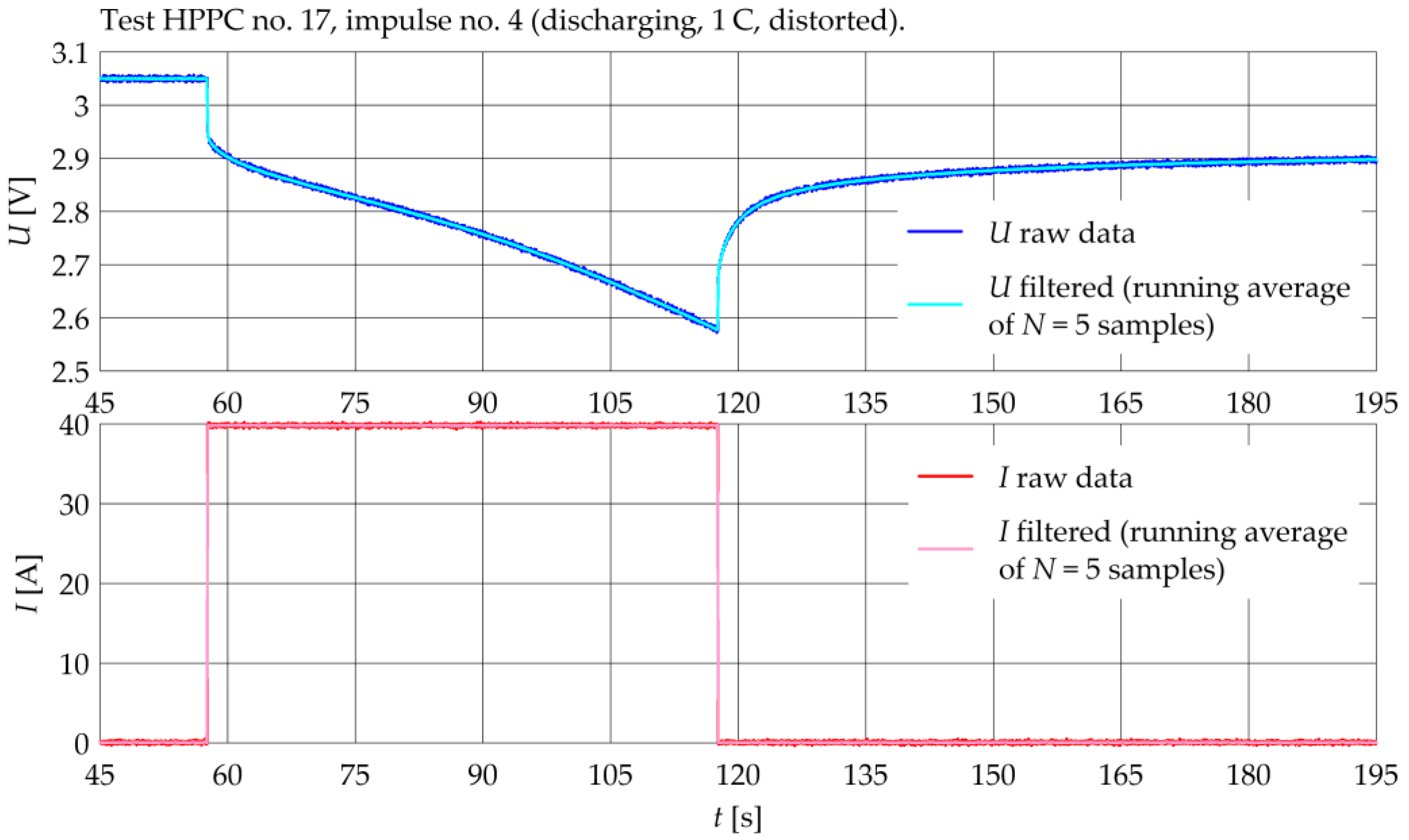
3.3.1. Filtering and Slope Detection

The recorded HPPC test transients shown in Figure 6 contain 1,500,000 samples over time. For this reason, precise localization of the beginnings and ends of HPPC pulses is a challenge. In addition, the recorded waveforms, in particular the voltages, contain a lot of noise that hinders further analysis. The high noise content results from the unfavorable proportion of the analyzed voltage changes to the measuring range of the data acquisition device. The voltage changes caused by an HPPC pulse range from ten to several tens of mV, whereas the measured voltage values reach up to 4 V. Therefore, a measuring transducer with a range of 10 V was used. Consequently, the analyzed changes constitute only a few percent of the measurement range, which, even with good quality converters and 16-bit sampling, results in a relatively large amount of noise.
Both problems, noise removal in the voltage transient and detection of the beginnings and ends of pulses based on the current transient, can be solved by using appropriate data-filtering techniques.
To detect the edges marking the beginnings and ends of the pulses, a method based on the analysis of the transient of the difference of two exponential averages was used:
r i α = I i i = 1 α I i + 1 − α r i − 1 i > 1 ,
Δ i = r i α fast − r i α slow .
In (5) and (6), Ii is the i-th sample of the current waveform, ri is the i-th sample of the exponential moving average, α is the weight coefficient, and Δi is the i-th sample of the waveform difference. The principle of operation of the method is shown in Figure 7. The difference Δ between two waveforms averaged with different weight values α (αslow = 0.02, αfast = 0.1) contains peaks at moments when there is a rapid change in the trend of the source waveform.
An edge is detected when the value of Δ exceeds the set threshold, which was 0.5 here. It should be noted that the values of the weight coefficient α are selected according to the sampling frequency of the source waveform, and the threshold value should be selected according to the noise content and disturbances in the source waveform.
A running average of order N = 5 was used to filter out the noise from the voltage waveform:
U filtered   i = 1 2 N + 1 ∑ k = i − N i + N U k .
In (7), i is the sample number of the measured voltage U that corresponds to the Ufiltered i filtered voltage sample. The filtration consists of calculating the average for N samples preceding and following the sample with the number i.
This simple method gave good results due to the high sampling frequency of the recorded voltage waveform and the random character of the filtered noise. Order N = 5 was sufficient, and its low value introduced negligible distortion of the voltage waveform, having no significant impact on the subsequent identification of time constants. The filtration results for an exemplary HPPC pulse recorded at the smallest of the applied currents of 0.5 C (i.e., in conditions where the relative noise content is the highest) are shown in Figure 8.

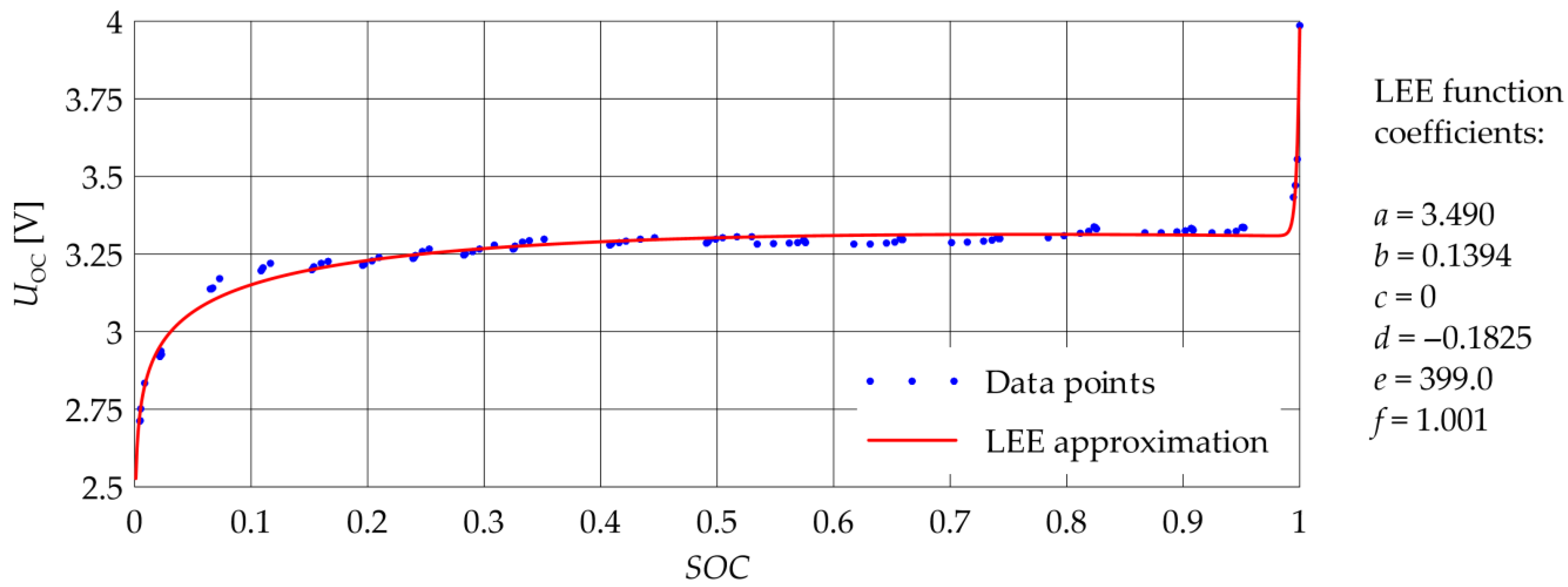
3.3.2. OCV vs. SOC Characteristic

The OCV characteristic, represented by UOC (i.e., the voltage source in the Thevenin equivalent circuit), is identified by measurement. The averaged charging and discharging characteristics may be used here [44,48,49]. However, this method has some disadvantages. The measured cell voltage contains not only the OCV but also the voltage drop at the impedance, which also depends on the SOC. Moreover, the measured charge and discharge capacities differ due to power losses. This makes it difficult to correlate them before the averaging.
To avoid these problems, the authors proposed a method for determining the OCV characteristics based on the results of HPPC tests, consisting of averaging (over a 10 s time period) the voltage recorded in the no-current state before each pulse. The SOC value corresponding to the voltage obtained this way is calculated in reference to the total charge of all HPPC tests, that is, the Q value from the last row of Table 3.
A measurement-based OCV characteristic is too irregular to be directly applied in the cell mathematical model and must be approximated [11,70,72,73,74,75,76]. Choice of the appropriate approximating function is a further problem. Several types of functions were tested, but a log-linear exponential (LLE) function [11,75] gave the best result [63]. The LEE function has the following form:
U OC S O C = a + b   ln S O C + c + d   S O C + e e S O C − f .
Its coefficients a to f were obtained by optimization with the particle swarm method (PSO) described in [63]. The resulting function plot and its coefficient values are given in Figure 9.

3.3.3. Impulse Evaluation and Selection

Once identified and filtered (Section 3.3.1), the HPPC impulses need to be selected for further time constant identification. The problem is that not all recorded impulses are suitable for further analysis. They may contain defects resulting from the measurement method (CC/CV mechanism) or from the physical properties of the cell.
Figure 10 schematically shows the shape and interpretation of a healthy (suitable for further analysis) pulse [11,14] and two cases of faulty pulses. Examples of recorded healthy impulses are shown in Figure 6 and Figure 8.
Pulse trimming (Figure 10) is easy to detect by analyzing the sequence of previously detected edges and the distances between them. A healthy pulse has two edges, falling and rising (which one is the first depends on whether the impulse is charging or discharging), separated in time by the assumed pulse length. Deviation from this pattern suggests that the pulse has been trimmed (Figure 7). Trimming occurs when the cell voltage reaches the limit during the duration of the pulse, and therefore, the measurement system switches from CC to CV mode.
In the performed tests, trimming always occurred together with the second defect, distortion by the OCV characteristic (Figure 10). Pulse distortion occurs for small SOC values, close to 0, and large ones, close to 1. This is because in these areas the OCV characteristic is the steepest (Figure 9). Therefore, even a slight change in SOC during the pulse duration causes a significant change in the voltage UOC of the cell, which translates into the shape of the recorded waveform U (Figure 10). The shape of the waveform ceases to depend only on the time constants τ1 and τ2, which is a necessary assumption to make the identification of these constants possible. In the extreme case, the recorded waveform bends in a direction opposite (Figure 11) so that it results from (4), assuming that the time constants τ1 and τ2 are positive.
In Table 3, summarizing the HPPC tests, trimmed pulses are marked in red and distorted pulses in yellow. Only healthy pulses marked in green were used in further analysis.

3.3.4. Impulse Waveform Approximation

The filtered and selected HPPC pulses were approximated by Function (4) to identify the time constants τ1 and τ2 and the resistances R0, R1, and R2. Then, on the basis of Formula (1), capacities C1 and C2 were calculated. The approximation was carried out using the PSO optimization method. At this stage of the research, a configuration of the PSO algorithm was found that guaranteed high repeatability of the obtained results. The fully informed particle swarm cognition method and the 8th order ring lattice swarm topology were used. The cognition factor was 4.1, the swarm consisted of 64 particles, and the number of iterations of the algorithm was set to 180.
The optimization method used and the experiments performed with it were described in a separate article [63].

3.3.5. R and C vs. SOC Characteristics Approximation

The results of the approximation described in Section 3.3.4 are the values of the cell equivalent circuit parameters and the corresponding SOC values. These values are presented in the form of points on the graphs in Figure 12. These points are arranged in more or less regular bands, which should be approximated with continuous functions in order to create a mathematical model of the cell. A polynomial approximation was used, and several experiments were performed with polynomials of various orders. The best results were obtained for 3rd order polynomials:
f S O C = a + b   S O C + c   S O C 2 + d   S O C 3 .
The approximation was carried out using the Levenberg–Marquardt method. The resistance and capacitance characteristics were approximated and the polynomial coefficients obtained are summarized in Table 4. In Figure 12, in the graphs of R and C values, the blue lines are the waveforms of Function (9) with the parameters from Table 4. The blue lines in the graphs τ1 and τ2 are the product of the approximating functions, respectively R1 and C1 for τ1, R2 and C2 for τ2, according to (1).

3.4. Model Verification

The approximated OCV (Section 3.3.2), R0, R1, R2, C1, and C2 (Section 3.3.5) characteristics fully describe the Thevenin equivalent circuit shown in Figure 3. This circuit, together with functions describing its parameters, was implemented in the MATLAB/Simulink environment by creating a simulation model of the cell, in a similar way as in [31]. The last parameter describing the model is the charge value Q corresponding to SOC = 1. Due to the problems with determining the actual capacity of the cell described in Section 3.2, this value was found by performing a series of simulations of the cell operating in model conditions and comparing their results with the transients recorded in the laboratory.
As model operating conditions, a current load profile based on the CDC [64], used to test batteries of hybrid vehicles, was used. The application of cycle-based tests is a typical strategy for battery cell mathematical model verification. Other popular cycle-based tests are the dynamic stress test (DST) [46,51,65,68], ARTEMIS [57,77], and others [17,28,54,66,69,75,78,79]. The applied CDC cycle consists of a set of discharge pulses of different value (acceleration and driving at a constant speed) as well as charging ones (regenerative braking). A single cycle was about 7 min long and discharged the cell by 3.3% of Qn, so it was repeated over 30 times until the cell was fully discharged.
Figure 13 shows the selected simulation results compared with the waveform recorded in the laboratory. The values of capacitance Q used in the simulation model are summarized in Table 5. The simulation accuracy has been evaluated with root-mean-square (RMS) error [49,65,68,69,74] given by the formula:
e rms = 1 K ∑ k = 1 K U m e a s u r e m e n t t k − U s i m u l a t i o n t k 2 .
The data in Table 5 are ordered from the lowest erms value (best result) to the highest. In Figure 13, the voltage relative error transients are shown, calculated as follows:
δ U = U m e a s u r e m e n t − U s i m u l a t i o n U m e a s u r e m e n t 100 % .
The δU error statistics for transients presented in Figure 13 are presented in Table 6. The order of the data in Table 6 is the same as in Table 5 and Figure 13.

4. Discussion

When identifying the parameters of the mathematical model of the cell, a major problem was determining its actual capacity, which comes from a comparison of the transients obtained for various Q values shown in Figure 13. The values obtained by the different methods (Section 3.2) varied considerably. They also differed from the nominal capacity Qn. It should be noted that according to the discharge characteristics provided in the cell data sheet by the cell manufacturer, the cell capacity at normal temperature (i.e., the temperature at which the tests described herein were performed) varied with the discharge current from about 1.04 Qn (3 C) to 1.15 Qn (0.5 C).
These values correspond to QCC values in Table 2. Particularly significant here was the value of the discharge current. This is why the capacity determined from the HPPC tests was the largest. This was because, during these tests, the charge was taken from the cell in small increments separated by long relaxation times. Thus, the cell had a lot of time to regenerate and rebuild the voltage lowered by the discharge.
For these reasons, we decided to treat the result of the CDC test (Section 3.4) as an indication, because the working conditions during this test were close to the real working conditions of the battery in the vehicle. Cell capacitance identified using the method giving a result consistent with the CDC test will, therefore, have the highest value in use.
The applied edge detection algorithm was an effective method of extracting individual pulses from the entire recorded HPPC test transient (Section 3.3.1). It was also helpful in identifying trimmed pulses (Section 3.3.3). Nevertheless, the detection of slopes sometimes encountered problems resulting from the properties of the equipment used in the laboratory setup. For example, in Figure 7, the enlarged fragment of the Δ waveform shows disturbances in the form of short peaks. These disturbances often occurred just after the power supply switched from CC to CV mode. They probably resulted from the way the operation of the control system was implemented in the applied active power supply. In Figure 7, this disturbance caused the detection of an additional, non-existent edge. The result of the operation of the power supply control system is also visible in the current waveform in Figure 8, this being the cause of the “false impulse”. This pulse, despite the high peak value, was very short, so it had no significant effect on the SOC of the cell. These types of pulses appeared in the no-current state when the change took place in the set value of the cut-off voltage (voltage at which the power supply switched from CC to CV mode). Such a change was performed before each change in the direction of the current flow: before charging, the value was set to 4 V, and before discharging, the value was set to 2.5 V. These pulses also sometimes resulted in the detection of a non-existent edge, which had to be taken into account in the analysis.
After identifying the time constants, the applied HPPC pulses, extended to 60 s, were too short to correctly identify the second time constant of Thevenin’s model. The graphs in Figure 12 show that the points corresponding to the identified R0 values are arranged in a narrow, regular band, which proves good quality of identification. In the case of the time constant τ1, the obtained band is much wider and the dispersion of values is greater, but some regularity is still visible. In the case of the time constant τ2, the dispersion of the results is very large, and their arrangement on the graph does not show any regularity. Note that the values of the time constant τ2 in Figure 12 changed in the interval from 30 s to 120 s, i.e., by 400%. Probably, in individual cases, values greater than 120 s would have been obtained, if not for the fact that such a value was set as a limitation of the search space in the applied PSO algorithm. It should be noted that, as stated in Section 3.3, to ensure good quality identification of the exponential waveform time constants, the length of its recorded fragment should be several times greater than the length of its time constants. However, with the applied HPPC pulse length equal to 60 s, more than half of the identified τ2 values were greater, even up to two times. Increasing the duration of the HPPC pulses would be undesirable, because it would cause changes too large in the SOC during the pulse duration. In the case of the tested LFP type cell, resignation from determining two time constants in favor of only one should be considered, as well as shortening the duration of the HPPC pulse. Let us also pay attention to the obtained resistance and capacitance values, given in Figure 12. The resistances are of the order of mΩ, which results in high short-circuit currents of lithium-ion cells. Capacitances are of the order of kF. Similar values were obtained, for example, in [32].
Reducing the HPPC pulse duration would reduce problems with distortion of their voltage response by the OCV characteristics (Section 3.3.3). It should be noted that the distortion effect in the form of a voltage waveform bent in the opposite direction shown in Figure 10 and Figure 11 is an extreme case. When the distortion was small, the distorted impulse did not differ in shape from the healthy one, but the time constants identified on its basis had overestimated values. It is possible that this effect (at least partially) is responsible for the lack of regularity of the results presented in the τ2 graph in Figure 12. This problem, however, requires confirmation and further analysis.
Among the functions known in the literature, the LEE function was selected to approximate the OCV characteristic. It has three SOC-dependent terms that are the most suitable for the specific shape of the LFP cell OCV characteristic. The logarithmic term describes the shape of the characteristic for SOC close to 0, linear describes the slope of the middle part of the characteristic, and exponential describes its shape for SOC close to 1. As the comparison of the measurement and simulation results showed, the OCV characteristic had the greatest impact on the accuracy of the simulation model. The enlarged fragment of the graph in Figure 13 shows that the simulated and measured voltage waveforms had a very similar shape, but there was a slowly varying offset between them. The Thevenin equivalent circuit (Figure 3) shows that the cell impedance, composed of the R and C elements, was responsible for the shape of the waveform, this being the response to current changes. The offset, on the other hand, is the result of differences in UOC (OCV) voltages.
Table 6 summarizes the voltage RMS error statistics, corresponding to the waveforms in Figure 13. Error values averaged over time and peak values are presented. The data are presented for entire transients and for a limited time range, from 5 min to 180 min. In this range, the cell operates on the almost linear part of the OCV characteristic, i.e., in the most typical conditions from a practical point of view.
The data show that for the optimal cell capacity (Q = 45.7 Ah) the average voltage errors were less than 1%, which proves the very good fidelity of the obtained simulation model. Error peaks under typical operating conditions (5–180 min) are at an acceptable level of about 10%. The peak values correspond to the dynamic states (with rapid changes in the load current), and their values are influenced primarily by the quality of identifying the parameters of the RC pairs related to the time constants. Note, that for the reasons described in Section 3.3, only two time constants have been identified, which affects the precision of the model in dynamic states. It should also be noted that in the literature, models with only one time constant [24,25,30,31,39] are sufficiently considered to be accurate.
In conclusion, despite the previously described problems, the identification of time constants and R and C elements had a satisfactory effect, and the accuracy of the obtained simulation model can be improved by better methods of identification and approximation of the OCV characteristics.

5. Conclusions

The research showed the following:
  • Among the various cell capacity values obtained as measurements, the best performance of the mathematical model was obtained for the averaged charge taken from the cell during discharge in the CC mode for different current values. Therefore, this method is recommended for determining the actual capacity of the cell.
  • The OCV characteristics of the LFP cell are best approximated by the LEE function.
  • Identification of the second time constant of the LFP cell is difficult, because of its large value, greater than a typical HPPC impulse duration.
  • Suggestions for further research:
  • It would be advisable to develop methods for automatic quality evaluation of HPPC impulses, based on the criteria given in Section 3.3.3, which would enable full automation of the HPPC test results processing.
  • A method should be developed to detect the occurrence of distortion of HPPC pulses in cases where the distortion is small and does not significantly change the shape of the voltage waveform yet, but already overestimates the obtained values of time constants.
  • Simulation model accuracy may be improved by better OCV characteristic approximation.

Author Contributions

Conceptualization, T.B. and R.N.; methodology, T.B. and R.N.; software, T.B.; validation, T.B., R.N., W.S. and W.K.; formal analysis, T.B.; investigation, T.B., R.N. and W.K.; resources, T.B., R.N., W.S. and W.K.; data curation, T.B.; writing—original draft preparation, T.B.; writing—review and editing, T.B., R.N., W.S. and W.K.; visualization, T.B.; supervision, W.S. and W.K.; project administration, W.K.; funding acquisition, W.S. and W.K. All authors have read and agreed to the published version of the manuscript.

Funding

This project was co-financed by the European Regional Development Fund in accordance with the contract POIR.01.01.01-00-1427/20-00.

Data Availability Statement

Not applicable.

Acknowledgments

The authors would like to acknowledge the help of Katarzyna Lota and Kamil Frączek (Łukasiewicz Research Network—Institute of Non-Ferrous Metals) in supplying cells for the research.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Diampovesa, S.; Hubert, A.; Yvars, P.A. Designing physical systems through a model-based synthesis approach. Example of a Li-ion battery for electrical vehicles. Comput. Ind. 2021, 129, 103440. [Google Scholar] [CrossRef]
  2. Skarka, W. Model-Based Design and Optimization of Electric Vehicles. In Proceedings of the 25th ISPE International Conference on Transdisciplinary Engineering, Modena, Italy, 3–6 July 2018; Volume 7, pp. 566–575. [Google Scholar]
  3. Niestrój, R.; Rogala, T.; Skarka, W. An Energy Consumption Model for Designing an AGV Energy Storage System with a PEMFC Stack. Energies 2020, 13, 3435. [Google Scholar] [CrossRef]
  4. Mateja, K.; Skarka, W.; Peciak, M.; Niestrój, R.; Gude, M. Energy Autonomy Simulation Model of Solar Powered UAV. Energies 2023, 16, 479. [Google Scholar] [CrossRef]
  5. Peciak, M.; Skarka, W.; Mateja, K.; Gude, M. Impact Analysis of Solar Cells on Vertical Take-Off and Landing (VTOL) Fixed-Wing UAV. Aerospace 2023, 10, 247. [Google Scholar] [CrossRef]
  6. Giannelos, S.; Borozan, S.; Aunedi, M.; Zhang, X.; Ameli, H.; Pudjianto, D.; Konstantelos, I.; Strbac, G. Modelling Smart Grid Technologies in Optimisation Problems for Electricity Grids. Energies 2023, 16, 5088. [Google Scholar] [CrossRef]
  7. Giannelos, S.; Djapic, P.; Pudjianto, D.; Strbac, G. Quantification of the Energy Storage Contribution to Security of Supply through the F-Factor Methodology. Energies 2020, 13, 826. [Google Scholar] [CrossRef]
  8. Raventós, O.; Bartels, J. Evaluation of Temporal Complexity Reduction Techniques Applied to Storage Expansion Planning in Power System Models. Energies 2020, 13, 988. [Google Scholar] [CrossRef]
  9. Tang, Z.; Song, A.; Wang, S.; Cheng, J.; Tao, C. Numerical Analysis of Heat Transfer Mechanism of Thermal Runaway Propagation for Cylindrical Lithium-ion Cells in Battery Module. Energies 2020, 13, 1010. [Google Scholar] [CrossRef]
  10. Li, N.; Zhang, H.; Zhang, X.; Ma, X.; Guo, S. How to Select the Optimal Electrochemical Energy Storage Planning Program? A Hybrid MCDM Method. Energies 2020, 13, 931. [Google Scholar] [CrossRef]
  11. Davis, K.; Hayes, J.G. Comparison of Lithium-Ion Battery Pack Models Based on Test Data from Idaho and Argonne National Laboratories. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020; pp. 5626–5632. [Google Scholar] [CrossRef]
  12. Rahmoun, A.; Biechl, H. Modelling of li-ion batteries using equivalent circuit diagrams. Electr. Rev. 2012, 2, 152–156. [Google Scholar]
  13. Tremblay, O.; Dessaint, L.; Dekkiche, A. A Generic Battery Model for the Dynamic Simulation of Hybrid Electric Vehicles. In Proceedings of the IEEE Vehicle Power and Propulsion Conference, Arlington, TX, USA, 9–12 September 2007; pp. 274–279. [Google Scholar] [CrossRef]
  14. Cipin, R.; Toman, M.; Prochazka, P.; Pazdera, I. Identification of Li-ion Battery Model Parameters. In Proceedings of the International Conference on Electrical Drives & Power Electronics (EDPE), The High Tatras, Slovakia, 24–26 September 2019; pp. 225–229. [Google Scholar] [CrossRef]
  15. Chen, S.X.; Tseng, K.J.; Choi, S.S. Modeling of Lithium-Ion Battery for Energy Storage System Simulation. In Proceedings of the Asia-Pacific Power and Energy Engineering Conference, Wuhan, China, 28–30 March 2009; pp. 1–4. [Google Scholar] [CrossRef]
  16. Huang, K.; Wang, Y.; Feng, J. Research on equivalent circuit Model of Lithium-ion battery for electric vehicles. In Proceedings of the 3rd World Conference on Mechanical Engineering and Intelligent Manufacturing (WCMEIM), Shanghai, China, 4–6 December 2020; pp. 492–496. [Google Scholar] [CrossRef]
  17. He, H.; Xiong, R.; Fan, J. Evaluation of Lithium-Ion Battery Equivalent Circuit Models for State of Charge Estimation by an Experimental Approach. Energies 2011, 4, 582–598. [Google Scholar] [CrossRef]
  18. Sibi Krishnan, K.; Pathiyil, P.; Sunitha, R. Generic Battery model covering self-discharge and internal resistance variation. In Proceedings of the IEEE 6th International Conference on Power Systems (ICPS), New Delhi, India, 4–6 March 2016; pp. 1–5. [Google Scholar] [CrossRef]
  19. Wu, W.; Qin, L.; Wu, G. State of power estimation of power lithium-ion battery based on an equivalent circuit model. J. Energy Storage 2022, 51, 104538. [Google Scholar] [CrossRef]
  20. Khattak, A.A.; Khan, A.N.; Safdar, M.; Basit, A.; Zaffar, N.A. A Hybrid Electric Circuit Battery Model Capturing Dynamic Battery Characteristics. In Proceedings of the IEEE Kansas Power and Energy Conference (KPEC), Manhattan, KS, USA, 13–14 July 2020; pp. 1–6. [Google Scholar] [CrossRef]
  21. Mueller, K.; Schwiederik, E.; Tittel, D. Analysis of parameter identification methods for electrical Li-Ion battery modelling. In Proceedings of the World Electric Vehicle Symposium and Exhibition (EVS27), Barcelona, Spain, 17–20 November 2013; pp. 1–9. [Google Scholar] [CrossRef]
  22. Meng, J.; Yue, M.; Diallo, D. Nonlinear extension of battery constrained predictive charging control with transmission of Jacobian matrix. Int. J. Electr. Power Energy Syst. 2023, 146, 108762. [Google Scholar] [CrossRef]
  23. Komal, S.; Kamyar, M.; Zunaib, A. Online reduced complexity parameter estimation technique for equivalent circuit model of lithium-ion battery. Electr. Power Syst. Res. 2020, 185, 106356. [Google Scholar] [CrossRef]
  24. Maletić, F.; Deur, J. Analysis of ECM-based Li-Ion Battery State and Parameter Estimation Accuracy in the Presence of OCV and Polarization Dynamics Modeling Errors. In Proceedings of the IEEE 29th International Symposium on Industrial Electronics (ISIE), Delft, The Netherlands, 17–19 June 2020; pp. 1318–1324. [Google Scholar] [CrossRef]
  25. Simin, P.; Gang, S.; Yunfeng, C.; Xu, C. Control of different-rating battery energy storage system interface to a microgrid. Przegląd Elektrotechniczny (Electr. Rev.) 2011, 87, 256–262. [Google Scholar]
  26. Meng., J.; Boukhnifer, M.; Diallo, D. Lihtium-ion battery monitoring and observability analysis with extended equivalent circuit model. In Proceedings of the IEEE Mediterranean Conference on Control and Automation (MED), Saint-Raphaël, France, 15–18 September 2020; pp. 764–769. [Google Scholar]
  27. Westerhoff, U.; Kurbach, K.; Lienesch, F.; Kurrat, M. Analysis of lithium-ion battery models based on electrochemical impedance spectroscopy. Energy Technol. 2016, 4, 1620–1630. [Google Scholar] [CrossRef]
  28. Stroe, D.I.; Swierczynski, M.; Stroe, A.I.; Knudsen Kær, S. Generalized Characterization Methodology for Performance Modelling of Lithium-Ion Batteries. Batteries 2016, 2, 37. [Google Scholar] [CrossRef]
  29. Cordoba-Arenas, A.; Onori, S.; Rizzoni, G.A. Control-oriented lithium-ion battery pack model for plug-in hybrid electric vehicle cycle-life studies and systems design with consideration of health management. J. Power Sources 2015, 279, 791–808. [Google Scholar] [CrossRef]
  30. Liaw, B.Y.; Nagasubramanian, G.; Jungst, R.G.; Doughty, D.H. Modeling of lithium ion cells—A simple equivalent-circuit model approach. Solid State Ion. 2004, 175, 835–839. [Google Scholar] [CrossRef]
  31. Huria, T.; Ceraolo, M.; Gazzarri, J.; Jackey, R. High fidelity electrical model with thermal dependence for characterization and simulation of high power lithium battery cells. In Proceedings of the IEEE International Electric Vehicle Conference, Greenville, SC, USA, 4–8 March 2012; pp. 1–8. [Google Scholar] [CrossRef]
  32. Sockeel, N.; Shahverdi, M.; Mazzola, M.; Meadows, W. High-Fidelity Battery Model for Model Predictive Control Implemented into a Plug-In Hybrid Electric Vehicle. Batteries 2017, 3, 13. [Google Scholar] [CrossRef]
  33. Li, K.; Soong, B.H.; Tseng, K.J. A high-fidelity hybrid lithium-ion battery model for SOE and runtime prediction. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition (APEC), Tampa, FL, USA, 26–30 March 2017; pp. 2374–2381. [Google Scholar] [CrossRef]
  34. Hemi, H.; M’Sirdi, N.K.; Naamane, A.; Ikken, B. Open Circuit Voltage of a Lithium ion Battery Model Adjusted by Data Fitting. In Proceedings of the 6th International Renewable and Sustainable Energy Conference (IRSEC), Rabat, Morocco, 5–8 December 2018; pp. 1–5. [Google Scholar]
  35. Zhang, Q.; Shang, Y.; Li, Y.; Cui, N.; Duan, B.; Zhang, C. A novel fractional variable-order equivalent circuit model and parameter identification of electric vehicle Li-ion batteries. ISA Trans. 2020, 97, 448–457. [Google Scholar] [CrossRef]
  36. Baczyńska, A.; Niewiadomski, W.; Gonçalves, A.; Almeida, P.; Luís, R. Li-NMC Batteries Model Evaluation with Experimental Data for Electric Vehicle Application. Batteries 2018, 4, 11. [Google Scholar] [CrossRef]
  37. Somakettarin, N.; Funaki, T. Study on Factors for Accurate Open Circuit Voltage Characterizations in Mn-Type Li-Ion Batteries. Batteries 2017, 3, 8. [Google Scholar] [CrossRef]
  38. Gao, Y.; Ji, W.; Zhao, X. SOC Estimation of E-Cell Combining BP Neural Network and EKF Algorithm. Processes 2022, 10, 1721. [Google Scholar] [CrossRef]
  39. Rothenberger, M.J.; Docimo, D.J.; Ghanaatpishe, M.; Fathy, H.K. Genetic optimization and experimental validation of a test cycle that maximizes parameter identifiability for a Li-ion equivalent-circuit battery model. J. Energy Storage 2015, 4, 156–166. [Google Scholar] [CrossRef]
  40. Nemes, R.; Ciornei, S.; Ruba, M.; Hedesiu, H.; Martis, C. Modeling and simulation of first-order Li-Ion battery cell with experimental validation. In Proceedings of the 8th International Conference on Modern Power Systems (MPS), Cluj-Napoca, Romania, 21–23 May 2019; pp. 1–6. [Google Scholar] [CrossRef]
  41. Nemes, R.O.; Ciornei, S.M.; Ruba, M.; Martis, C. Parameters identification using experimental measurements for equivalent circuit Lithium-Ion cell models. In Proceedings of the 11th International Symposium on Advanced Topics in Electrical Engineering (ATEE), Bucharest, Romania, 28–30 March 2019; pp. 1–6. [Google Scholar] [CrossRef]
  42. Hua, X.; Zhang, C.; Offer, G. Finding a better fit for lithium ion batteries: A simple, novel, load dependent, modified equivalent circuit model and parameterization method. J. Power Sources 2021, 484, 229117. [Google Scholar] [CrossRef]
  43. Li, Z.; Shi, X.; Shi, M.; Wei, C.; Di, F.; Sun, H. Investigation on the Impact of the HPPC Profile on the Battery ECM Parameters’ Offline Identification. In Proceedings of the Asia Energy and Electrical Engineering Symposium (AEEES), Chengdu, China, 28–31 May 2020; pp. 753–757. [Google Scholar] [CrossRef]
  44. Haghjoo, Y.; Khaburi, D.A. Modeling, simulation, and parameters identification of a lithium-ion battery used in electric vehicles. In Proceedings of the 9th Iranian Conference on Renewable Energy & Distributed Generation (ICREDG), Mashhad, Iran, 23–24 February 2022; pp. 1–7. [Google Scholar] [CrossRef]
  45. Tran, M.K.; Mathew, M.; Janhunen, S.; Panchal, S.; Raahemifar, K.; Fraser, R.; Fowler, M. A comprehensive equivalent circuit model for lithium-ion batteries, incorporating the effects of state of health, state of charge, and temperature on model parameters. J. Energy Storage 2021, 43, 103252. [Google Scholar] [CrossRef]
  46. Deng, S.D.; Liu, S.Y.; Wang, L.; Xia, L.L.; Chen, L. An improved second-order electrical equivalent modeling method for the online high power Li-ion battery state of charge estimation. In Proceedings of the IEEE 12th Energy Conversion Congress & Exposition—Asia (ECCE-Asia), Singapore, 24–27 May 2021; pp. 1725–1729. [Google Scholar] [CrossRef]
  47. Parthasarathy, C.; Laaksonen, H.; Halagi, P. Characterisation and Modelling Lithium Titanate Oxide Battery Cell by Equivalent Circuit Modelling Technique. In Proceedings of the IEEE PES Innovative Smart Grid Technologies—Asia (ISGT Asia), Brisbane, Australia, 5–8 December 2021; pp. 1–5. [Google Scholar] [CrossRef]
  48. Navas, S.J.; Cabello González, G.M.; Pino, F.J.; Guerra, J.J. Modelling Li-ion batteries using equivalent circuits for renewable energy applications. Energy Rep. 2023, 9, 4456–4465. [Google Scholar] [CrossRef]
  49. Wang, J.; Jia, Y.; Yang, N.; Lu, Y.; Shi, M.; Ren, X.; Lu, D. Precise equivalent circuit model for Li-ion battery by experimental improvement and parameter optimization. J. Energy Storage 2022, 52, 104980. [Google Scholar] [CrossRef]
  50. Sörés, M.A.; Hartmann, B. Overview of possible methods of determining self-discharge. In Proceedings of the IEEE International Conference on Environment and Electrical Engineering and IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Madrid, Spain, 9–12 June 2020; pp. 1–5. [Google Scholar] [CrossRef]
  51. Tang, A.; Gong, P.; Li, J.; Zhang, K.; Zhou, Y.; Zhang, Z. A State-of-Charge Estimation Method Based on Multi-Algorithm Fusion. World Electr. Veh. J. 2022, 13, 70. [Google Scholar] [CrossRef]
  52. Jarrraya, I.; Degaa, L.; Rizoug, N.; Chabchoub, M.H.; Trabelsi, H. Comparison study between hybrid Nelder-Mead particle swarm optimization and open circuit voltage—Recursive least square for the battery parameters estimation. J. Energy Storage 2022, 50, 104424. [Google Scholar] [CrossRef]
  53. Castanho, D.; Guerreiro, M.; Silva, L.; Eckert, J.; Antonini Alves, T.; Tadano, Y.d.S.; Stevan, S.L., Jr.; Siqueira, H.V.; Corrêa, F.C. Method for SoC Estimation in Lithium-Ion Batteries Based on Multiple Linear Regression and Particle Swarm Optimization. Energies 2022, 15, 6881. [Google Scholar] [CrossRef]
  54. Pizarro-Carmona, V.; Castano-Solís, S.; Cortés-Carmona, M.; Fraile-Ardanuy, J.; Jimenez-Bermejo, G. GA-based approach to optimize an equivalent electric circuit model of a Li-ion battery-pack. Expert Syst. Appl. 2021, 172, 114647. [Google Scholar] [CrossRef]
  55. Huang, Y.; Li, Y.; Jiang, L.; Qiao, X.; Cao, Y.; Yu, J. Research on Fitting Strategy in HPPC Test for Li-ion battery. In Proceedings of the IEEE Sustainable Power and Energy Conference (iSPEC), Beijing, China, 21–23 November 2019; pp. 1776–1780. [Google Scholar] [CrossRef]
  56. Wang, C.; Xu, M.; Zhang, Q.; Feng, J.; Jiang, R.; Wei, Y.; Liu, Y. Parameters identification of Thevenin model for lithium-ion batteries using self-adaptive Particle Swarm Optimization Differential Evolution algorithm to estimate state of charge. J. Energy Storage 2021, 44, 103244. [Google Scholar] [CrossRef]
  57. Hamida, M.A.; El-Sehiemy, R.A.; Ginidi, A.R.; Elattar, E.; Shaheen, A.M. Parameter identification and state of charge estimation of Li-Ion batteries used in electric vehicles using artificial hummingbird optimizer. J. Energy Storage 2022, 51, 104535. [Google Scholar] [CrossRef]
  58. Szewczyk, P.; Łebkowski, A. Comparative Studies on Batteries for the Electrochemical Energy Storage in the Delivery Vehicle. Energies 2022, 15, 9613. [Google Scholar] [CrossRef]
  59. Łebkowski, Ł. Temperature, Overcharge and Short-Circuit Studies of Batteries used in Electric Vehicles. Prz. Elektrotechniczny 2017, 93, 67–73. [Google Scholar] [CrossRef]
  60. Ohneseit, S.; Finster, P.; Floras, C.; Lubenau, N.; Uhlmann, N.; Seifert, H.J.; Ziebert, C. Thermal and Mechanical Safety Assessment of Type 21700 Lithium-Ion Batteries with NMC, NCA and LFP Cathodes–Investigation of Cell Abuse by Means of Accelerating Rate Calorimetry (ARC). Batteries 2023, 9, 237. [Google Scholar] [CrossRef]
  61. Kiemel, S.; Glöser-Chahoud, S.; Waltersmann, L.; Schutzbach, M.; Sauer, A.; Miehe, R. Assessing the Application-Specific Substitutability of Lithium-Ion Battery Cathode Chemistries Based on Material Criticality, Performance, and Price. Resources 2021, 10, 87. [Google Scholar] [CrossRef]
  62. Forte, F.; Pietrantonio, M.; Pucciarmati, S.; Puzone, M.; Fontana, D. Lithium Iron Phosphate Batteries Recycling: An Assessment of Current Status. Crit. Rev. Environ. Sci. Technol. 2021, 51, 2232–2259. [Google Scholar]
  63. Białoń, T.; Niestrój, R.; Korski, W. PSO-Based Identification of the Li-Ion Battery Cell Parameters. Energies 2023, 16, 3995. [Google Scholar] [CrossRef]
  64. Belt, J.R. Battery Test Manual for Plug-In Hybrid Electric Vehicles, 2nd ed.; U.S. Department of Energy Vehicle Technologies Program: Idaho Falls, ID, USA, 2010. [Google Scholar] [CrossRef]
  65. Yang, Z.; Wang, X. An improved parameter identification method considering multi-timescale characteristics of lithium-ion batteries. J. Energy Storage 2023, 59, 106462. [Google Scholar] [CrossRef]
  66. Karimi, D.; Behi, H.; Van Mierlo, J.; Berecibar, M. Equivalent Circuit Model for High-Power Lithium-Ion Batteries under High Current Rates, Wide Temperature Range, and Various State of Charges. Batteries 2023, 9, 101. [Google Scholar] [CrossRef]
  67. Guenther, C.; Barillas, J.K.; Stumpp, S.; Danzer, M.A. A dynamic battery model for simulation of battery-to-grid applications. In Proceedings of the 3rd IEEE PES Innovative Smart Grid Technologies Europe (ISGT Europe), Berlin, Germany, 14–17 October 2012; pp. 1–7. [Google Scholar] [CrossRef]
  68. Shi, J.; Guo, H.; Chen, D. Parameter identification method for lithium-ion batteries based on recursive least square with sliding window difference forgetting factor. J. Energy Storage 2021, 44, 103485. [Google Scholar] [CrossRef]
  69. Tran, M.-K.; DaCosta, A.; Mevawalla, A.; Panchal, S.; Fowler, M. Comparative Study of Equivalent Circuit Models Performance in Four Common Lithium-Ion Batteries: LFP, NMC, LMO, NCA. Batteries 2021, 7, 51. [Google Scholar] [CrossRef]
  70. Feng, D.; Huang, J.; Jin, P.; Chen, H.; Wang, A.; Zheng, M. Parameter Identification and Dynamic Simulation of Lithium-Ion Power Battery Based on DP Model. In Proceedings of the 14th IEEE Conference on Industrial Electronics and Applications (ICIEA), Xi’an, China, 19–21 June 2019; pp. 1275–1279. [Google Scholar] [CrossRef]
  71. Einhorn, M.; Conte, V.F.; Kral, C.; Fleig, J.; Permann, R. Parameterization of an electrical battery model for dynamic system simulation in electric vehicles. In Proceedings of the IEEE Vehicle Power and Propulsion Conference, Lille, France, 1–3 September 2010; pp. 1–7. [Google Scholar] [CrossRef]
  72. Yu, Q.; Wan, C.; Li, J.; E, L.; Zhang, X.; Huang, Y.; Liu, T. An Open Circuit Voltage Model Fusion Method for State of Charge Estimation of Lithium-Ion Batteries. Energies 2021, 14, 1797. [Google Scholar] [CrossRef]
  73. Gao, L.; Liu, S.; Dougal, R.A. Dynamic lithium-ion battery model for system simulation. IEEE Trans. Compon. Packag. Technol. 2002, 25, 495–505. [Google Scholar] [CrossRef]
  74. Wen, F.; Duan, B.; Zhang, C.; Zhu, R.; Shang, Y.; Zhang, J. High-Accuracy Parameter Identification Method for Equivalent-Circuit Models of Lithium-Ion Batteries Based on the Stochastic Theory Response Reconstruction. Electronics 2019, 8, 834. [Google Scholar] [CrossRef]
  75. Baccouche, I.; Jemmali, S.; Manai, B.; Omar, N.; Amara, N.E.B. Improved OCV Model of a Li-Ion NMC Battery for Online SOC Estimation Using the Extended Kalman Filter. Energies 2017, 10, 764. [Google Scholar] [CrossRef]
  76. Pillai, P.; Sundaresan, S.; Kumar, P.; Pattipati, K.R.; Balasingam, B. Open-Circuit Voltage Models for Battery Management Systems: A Review. Energies 2022, 15, 6803. [Google Scholar] [CrossRef]
  77. Shaheen, A.M.; Hamida, M.A.; El-Sehiemy, R.A.; Elattar, E.E. Optimal parameter identification of linear and non-linear models for Li-Ion Battery Cells. Energy Rep. 2021, 7, 7170–7185. [Google Scholar] [CrossRef]
  78. Plett, G.L. High-performance battery-pack power estimation using a dynamic cell model. IEEE Trans. Veh. Technol. 2004, 53, 1586–1593. [Google Scholar] [CrossRef]
  79. Marušić, D.; Vašak, M. Efficient Method of Identifying a Li-Ion Battery Model for an Electric Vehicle. In Proceedings of the IEEE 20th International Power Electronics and Motion Control Conference (PEMC), Brasov, Romania, 25–28 September 2022; pp. 421–426. [Google Scholar] [CrossRef]
Energies 16 06239 g001
Figure 1. Research methodology overview.
Figure 1. Research methodology overview.
Energies 16 06239 g001
Energies 16 06239 g002
Figure 2. Laboratory setup overview.
Figure 2. Laboratory setup overview.
Energies 16 06239 g002
Energies 16 06239 g003
Figure 3. Thevenin equivalent circuit of the battery cell.
Figure 3. Thevenin equivalent circuit of the battery cell.
Energies 16 06239 g003
Energies 16 06239 g004
Figure 4. Cell capacity estimation based on discharge characteristic.
Figure 4. Cell capacity estimation based on discharge characteristic.
Energies 16 06239 g004
Energies 16 06239 g005
Figure 5. Discharge characteristics for cell capacity estimation.
Figure 5. Discharge characteristics for cell capacity estimation.
Energies 16 06239 g005
Energies 16 06239 g006
Figure 6. Exemplary HPPC test result.
Figure 6. Exemplary HPPC test result.
Energies 16 06239 g006
Energies 16 06239 g007
Figure 7. Edge detection method on the example of trimmed HPPC impulse.
Figure 7. Edge detection method on the example of trimmed HPPC impulse.
Energies 16 06239 g007
Energies 16 06239 g008
Figure 8. Exemplary HPPC impulse before and after data filtering. Near t = 10 s, a false peak generated by the control system of the active power supply is visible.
Figure 8. Exemplary HPPC impulse before and after data filtering. Near t = 10 s, a false peak generated by the control system of the active power supply is visible.
Energies 16 06239 g008
Energies 16 06239 g009
Figure 9. OCV characteristic approximated with LEE function.
Figure 9. OCV characteristic approximated with LEE function.
Energies 16 06239 g009
Energies 16 06239 g010
Figure 10. Shape of a single (charging) HPPC impulse and its potential flaws.
Figure 10. Shape of a single (charging) HPPC impulse and its potential flaws.
Energies 16 06239 g010
Energies 16 06239 g011
Figure 11. Exemplary HPPC impulse distorted by OCV characteristic.
Figure 11. Exemplary HPPC impulse distorted by OCV characteristic.
Energies 16 06239 g011
Energies 16 06239 g012
Figure 12. Thevenin equivalent circuit R and C parameter characteristics approximated with 3rd order polynomial.
Figure 12. Thevenin equivalent circuit R and C parameter characteristics approximated with 3rd order polynomial.
Energies 16 06239 g012
Energies 16 06239 g013
Figure 13. Comparison of simulation and measurement CDC test results. Simulations performed for various values of cell capacity.
Figure 13. Comparison of simulation and measurement CDC test results. Simulations performed for various values of cell capacity.
Energies 16 06239 g013
Table 1. ThunderSky Winston LFP040AHA cell nominal parameters.
Table 1. ThunderSky Winston LFP040AHA cell nominal parameters.
ParameterValue
Capacity Qn40 Ah
Energy density82.5 Wh/kg
Voltage (min./nominal/max.)2.5/3.3/4.0
Current (typical/max. discharge)20 A (0.5C 1)/400 A (10C 1)
1 Battery cell C-rating, based on nominal capacity: 1C = 40 A.
Table 2. Cell capacity measurement results based on discharge characteristics.
Table 2. Cell capacity measurement results based on discharge characteristics.
Relative Discharge
Current		Total Discharge
Q [Ah]		Discharge in CC Mode
QCC [Ah]		Discharge in CV Mode
QCV [Ah]
0.5C47.7146.301.407
1C47.7145.781.934
2C47.7045.212.495
3C47.6245.412.212
Table 3. HPPC tests and impulses summary.
Table 3. HPPC tests and impulses summary.
HPPC
Test
No.		Impulse No., Type and Relative Current ValueΔQ
[Ah]		ΔQ/Qn
[%]		Q
[Ah]
1
0.5 C		2
0.5 C		3
1 C		4
1 C		5
2 C		6
2 C		7
3 C		8
3 C
1(−)(+)(−)(+)(−)(+)(−)(+)2.416.032.41
2(−)(+)(−)(+)(−)(+)(−)(+)2.215.534.63
3(−)(+)(−)(+)(−)(+)(−)(+)4.2110.538.84
4(−)(+)(−)(+)(−)(+)(−)(+)4.2110.5313.05
5(−)(+)(−)(+)(−)(+)(−)(+)4.2210.5417.27
6(−)(+)(−)(+)(−)(+)(−)(+)4.2310.5721.50
7(−)(+)(−)(+)(−)(+)(−)(+)4.2210.5625.72
8(+)(−)(+)(−)(+)(−)(+)(−)4.2110.5429.93
9(+)(−)(+)(−)(+)(−)(+)(−)4.2210.5534.16
10(+)(−)(+)(−)(+)(−)(+)(−)2.165.4036.31
11(+)(−)(+)(−)(+)(−)(+)(−)2.185.4538.49
12(+)(−)(+)(−)(+)(−)(+)(−)2.205.5140.70
13(+)(−)(+)(−)(+)(−)(+)(−)2.215.5242.90
14(+)(−)(+)(−)(+)(−)(+)(−)2.225.5445.12
15(+)(−)(+)(−)(+)(−)(+)(−)2.205.4947.32
16(+)(−)(+)(−)(+)(−)(+)(−)2.225.5549.54
17(+)(−)(+)(−)(+)(−)(+)(−)0.922.3150.46
18(+)(−)(+)(−)(+)(−)(+)(−)0.250.6250.71
Impulses: ●—healthy, ●—trimmed, ●—distorted, (+)—charging, (−)—discharging.
Table 4. R and C parameters 3rd order polynomial approximation coefficients values.
Table 4. R and C parameters 3rd order polynomial approximation coefficients values.
abcd
R03.551 × 10−3−6.172 × 10−38.993 × 10−3−4.267 × 10−3
R19.601 × 10−4−1.154 × 10−31.611 × 10−3−5.716 × 10−4
R26.169 × 10−3−2.678 × 10−24.690 × 10−2−2.485 × 10−2
C15549−1.359 × 1045.058 × 104−3.397 × 104
C21.712 × 1048.510 × 104−2.850 × 104−4.243 × 104
Table 5. Cell capacities used in simulations and resulting voltage error value.
Table 5. Cell capacities used in simulations and resulting voltage error value.
Voltage
RMS Error		Cell Capacity
Q [Ah]		Comment
0.043245.7Average for discharge characteristics, CC mode only
0.048747.7Average for discharge characteristics, CC + CV
0.12050.7HPPC tests total discharge
0.16740.0Qn—nominal cell capacity
Table 6. Simulation results—voltage relative error statistics.
Table 6. Simulation results—voltage relative error statistics.
Cell Capacity
Q [Ah]		Average Error
|δU| [%]		Average Error for t from 5 min to 180 min |δU| [%]Peak Error
|δU| [%]		Peak Error for t from 5 min to 180 min |δU| [%]
45.70.9770.75114.99.62
47.71.070.80514.69.83
50.72.440.87322.910.1
402.730.57920.49.04
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Białoń, T.; Niestrój, R.; Skarka, W.; Korski, W. HPPC Test Methodology Using LFP Battery Cell Identification Tests as an Example. Energies 2023, 16, 6239. https://doi.org/10.3390/en16176239

AMA Style

Białoń T, Niestrój R, Skarka W, Korski W. HPPC Test Methodology Using LFP Battery Cell Identification Tests as an Example. Energies. 2023; 16(17):6239. https://doi.org/10.3390/en16176239

Chicago/Turabian Style

Białoń, Tadeusz, Roman Niestrój, Wojciech Skarka, and Wojciech Korski. 2023. "HPPC Test Methodology Using LFP Battery Cell Identification Tests as an Example" Energies 16, no. 17: 6239. https://doi.org/10.3390/en16176239

APA Style

Białoń, T., Niestrój, R., Skarka, W., & Korski, W. (2023). HPPC Test Methodology Using LFP Battery Cell Identification Tests as an Example. Energies, 16(17), 6239. https://doi.org/10.3390/en16176239

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop