Next Article in Journal
Survey of Novel Architectures for Energy Efficient High-Performance Mobile Computing Platforms
Previous Article in Journal
Lithofacies Characteristics and Methodology to Identify Lacustrine Carbonate Rocks via Log Data: A Case Study in the Yingxi Area, Qaidam Basin
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Energies
Volume 16
Issue 16
10.3390/en16166042
energies-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

Review of Low Inertia in Power Systems Caused by High Proportion of Renewable Energy Grid Integration

by
Jiyu Song
†,
Xinhang Zhou
†,
Zhiquan Zhou
*,
Yang Wang
,
Yifan Wang
and
Xutao Wang
School of Electrical and Information Engineering, Jiangsu University, Zhenjiang 212013, China
*
Author to whom correspondence should be addressed.
†
These authors contributed equally to this work.
Energies 2023, 16(16), 6042; https://doi.org/10.3390/en16166042
Submission received: 26 July 2023 / Revised: 9 August 2023 / Accepted: 10 August 2023 / Published: 18 August 2023
(This article belongs to the Section A: Sustainable Energy)
Browse Figures
Versions Notes

Abstract

:
With the power industry moving toward a green and low-carbon direction, renewable energy is occupying an increasingly larger share in the power system. However, compared with traditional thermal power generation, the instability of new energy generation is very prominent, which also leads to a decrease in the inertia of the power system after the grid integration of a high proportion of renewable energy. If no measures are taken, this may lead to frequency collapse accidents. Therefore, this paper first introduces two international major power outage accidents that have occurred in recent years, analyzing the causes, and then summarizes the inspiration obtained from the accidents. Subsequently, some research results on low inertia-related issues in the power system caused by the high proportion of new energy grid integration in recent years were summarized and analyzed from three aspects: inertia evaluation methods, optimal operation measures for the power system, and under frequency load-shedding (the abbreviation “ULFS” in the following text stands for it) schemes. Finally, suggestions were made for future research directions.

1. Introduction

As global environmental problems become increasingly serious, the environmental pollution caused by conventional power generation is receiving increasing attention. However, most countries around the world still mainly rely on traditional thermal power generation, and the proportion of thermal power generation in total power generation has been constantly increasing over the last few decades. In China, for example, the proportion of thermal power generation in the whole power generation had continued to grow since 1949, reaching a high level of 81.17% in 2001. However, in 2019, the proportion of thermal power generation in China fell below 70% for the first time and even further to 68% in 2021. In addition, China has set a grand target to reduce the share of thermal power generation to less than 50% by 2050, reflecting the high importance attached to renewable power generation in the future [1]. It can be seen that increasing the proportion of renewable energy power generation will be the trend of development for countries around the world in the future. Although the energy industry in many countries has been affected by COVID-19 to varying degrees in recent years, the newly added installed capacity of global renewable energy reached 315 GW by 2021, which is a record high; the new installed capacity of solar and wind energy accounts for 90% of all new renewable energy installations, and the proportion of solar and wind power generation exceeds 10% of global power generation for the first time [2].
In view of the advantages of renewable energy power generation, such as environmental sustainability (the process of generating electricity releases less carbon dioxide or other harmful substances), increasing economic benefits (renewable energy resources are abundant, not depleted, and do not require additional costs to reduce pollution), and flexible distribution (renewable energy can be laid out and utilized in various geographical environments and different conditions), countries around the world have begun to improve the level of new energy power generation and increase the proportion of new energy power generation [3,4,5]. However, even though the advantages of renewable energy power generation are huge, with the increase in the proportion of renewable energy power generation in power system, the “low inertia” problem is becoming more and more prominent.
The inertia of a power system comes mainly from rotating components, including generators, motors, and other equipment. When the load in the power system changes, the inertia of these rotating components can provide additional energy reserves so that the system can maintain a stable operating state and reduce the impact of disturbances. The large-scale integration of renewable energy will replace synchronous generators with large mechanical rotating inertia and strong disturbance resilience, resulting in a significant reduction in system equivalent inertia, as shown in Figure 1: when the proportion of traditional thermal power generation in the power system is high, the power system is stable and has sufficient inertia; when renewable energy sources such as photovoltaic and wind power dominate the power system, the inertia of the power system will decrease. The inertia has a very important impact on the stability and reliability of the power system. The larger the inertia of the power system, the better its stability. On the contrary, if the inertia is insufficient, the stability of the system will be affected and even lead to the collapse of the system [6].
There are two main reasons for the reduction in the inertia of a high proportion of renewable energy power systems. Firstly, renewable energy generation differs from traditional energy sources. Traditional energy sources such as coal and oil have the characteristic of adjustable supplies, while new energy sources such as wind and light intensity have unadjustable supplies due to the limitations of natural conditions. As the proportion of new energy generation, as an unstable part in the grid, increases, it leads to a decrease in the overall inertia level of the power system.
Secondly, the power generation equipment for new energy sources is also different from that of traditional thermal power generation. Thermal power units are generally synchronous generators, which are huge rotary machines that can store a large amount of mechanical inertia to provide inertia support for the power system. However, new energy power generation equipment, such as photovoltaic power generation, does not have mechanical rotating components, and therefore cannot provide inertia support for the power system. Although wind turbines appear to have a moment of inertia, it is actually decoupled from the power grid due to the fact that the wind turbine needs to be connected to the grid through the inverter, so it cannot provide inertia support effectively. However, it is worth noting that with the gradual maturity of virtual inertia control technology, new energy is considered to have “virtual inertia” and can also provide certain inertia support for the system, which will be detailed in the following [7,8].
Although researchers have designed numerous solutions to address the problem of low inertia, accidents related to low inertia continue to emerge, such as the “9.28” blackout in South Australia in 2016 (the detailed process and cause analysis of this blackout can be obtained from these three references [9,10]) and the accidents in London, the UK and Texas, USA, which will be introduced below. Therefore, it is necessary to systematically sort out the issues related to the inertia of the power system. Reference [11] classified and discussed methods for evaluating inertia; reference [12] compares and analyzes different existing strategies from the perspectives of inertia control and inertia demand assessment. This type of review starts from one aspect of the low-inertia problem. Although the analysis is in depth, it does not allow beginners to quickly understand and comprehensively recognize the impact of low inertia in power systems; reference [13] comprehensively analyzed such problems, but it did not describe how to quickly and effectively solve such problems under large-scale power deficiency, and power systems are on the brink of collapse. Therefore, this paper introduces the relevant methods of low-frequency load shedding to make up for this lack.
In order to further solve the above problems, this paper also summarizes the corresponding measures in the planning and operation of the power system to ensure that the stable power supply and operation safety of the power system can still be guaranteed after the proportion of new energy is significantly increased. At present, the main international methods are as follows:
(1)
Online evaluation of equivalent inertia: accurate and real-time assessment of system equivalent inertia based on large disturbance events, small disturbance events or quasi-steady-state operating conditions is essential to measure the resilience of power system with high proportion of renewable energy. This assessment helps detect the system’s supporting capacity, predict inertia level trends, provide guidance for optimizing system scheduling, and ensure the stability and safety of system operations (in Section 3).
(2)
Optimal scheduling: with the goal of improving the economic efficiency of system operation, with frequency security taken as the constraint, after considering various factors such as safety margin, the scheduling strategy of the power system is optimized to maximize the benefits brought by the grid integration of new energy (in Section 4.1).
(3)
Adopting virtual inertia control technology: regarding solar energy, wind energy and other new energy power generation, either because there is no mechanical rotary inertia or because it is decoupled from the grid, it is intuitively unable to provide inertia support for the power system. But in fact, through special means and control methods, new energy power generation can also play a certain role in frequency and voltage regulation, having inertia like thermal power units, which is called virtual inertia (in Section 4.2).
(4)
UFLS: in case of emergency due to accidents, load shedding shall be carried out to avoid further frequency drop and system collapse. When taking UFLS, factors such as the scale of system power deficiency and the importance of load should be considered comprehensively to determine which loads and the amount of loads to be shed (in Section 5).
On this basis, the content of this paper is organized as follows: in Section 2, two real cases that have occurred in recent years are reviewed. By introducing the whole process of the events, readers can understand the damage caused by low inertia to the power system and real life. Moreover, the negligence and the lessons learned from the accident are summarized. In Section 3, this paper mainly summarizes the different online evaluation methods of equivalent inertia based on large disturbance, small disturbance and quasi-steady state in recent years. In Section 4, the optimal operation methods for low-inertia power systems with a high proportion of renewable energy in recent years are introduced from two aspects: scheduling optimization and virtual inertia control. In Section 5, compared with traditional strategies, the research results in UFLS in recent years are sorted out, which have a smaller impact and better effect. Finally, in Section 6, the full text is summarized, and the suggestions for future research on the low-inertia problem of the power system are proposed.
In addition, for the convenience of readers’ understanding, the abbreviations in this article can be found in the Abbreviations.

2. Cases of Major Electrical Accidents Related to Low Inertia in Recent Years

2.1. The “8.9” Blackout in Britain

On 9 August 2019, around 17:00 London time, a large-scale power outage occurred in the United Kingdom. During the incident, certain regions in England and Wales experienced power cuts, affecting one million people.
The incident was caused by a failure at the Little Barford gas-fired power station in Bedfordshire, Eastern England. At this time, a loss of 730 MW in power generation occurred, and the system frequency began to decline. However, due to limited low-frequency tolerance of the turbines at the Hornsea offshore wind farm in Northeast England, a significant number of units went offline after experiencing faults, resulting in a loss of approximately 900 MW in wind power generation. This exacerbated the power deficit in the system, leading to a further drop in the power system frequency beyond the allowable range of fluctuations. Ultimately, this triggered the operation of the UFLS mechanism, resulting in widespread power outages in certain regions of the UK. To prevent any further decline in system frequency, pumped-storage hydroelectric power plants quickly increased their output by approximately 1000 MW to compensate for the power shortfall, protecting the unaffected parts of the main grid and ultimately avoiding a catastrophic system-wide collapse [14].
During the outage, a total of 1878 MW of power generation was lost within the grid, accounting for 6.5% of the total load. The system frequency also dropped from 50 Hz to 48.8 Hz [15].
According to the analysis from references [14,15], the incident exposed several issues within the United Kingdom’s national grid, including the high proportion of renewable energy sources with insufficient regulation capabilities from traditional power generation units, lack of unified dispatching capabilities, and inadequate awareness of the safety of the renewable energy power system. This resulted in negative impacts such as economic losses and social panic, so it is necessary to implement inertia online assessment and ensure sufficient energy storage backup for power compensation. Other countries with a high proportion of renewable energy in their grids should take this incident as a cautionary lesson.

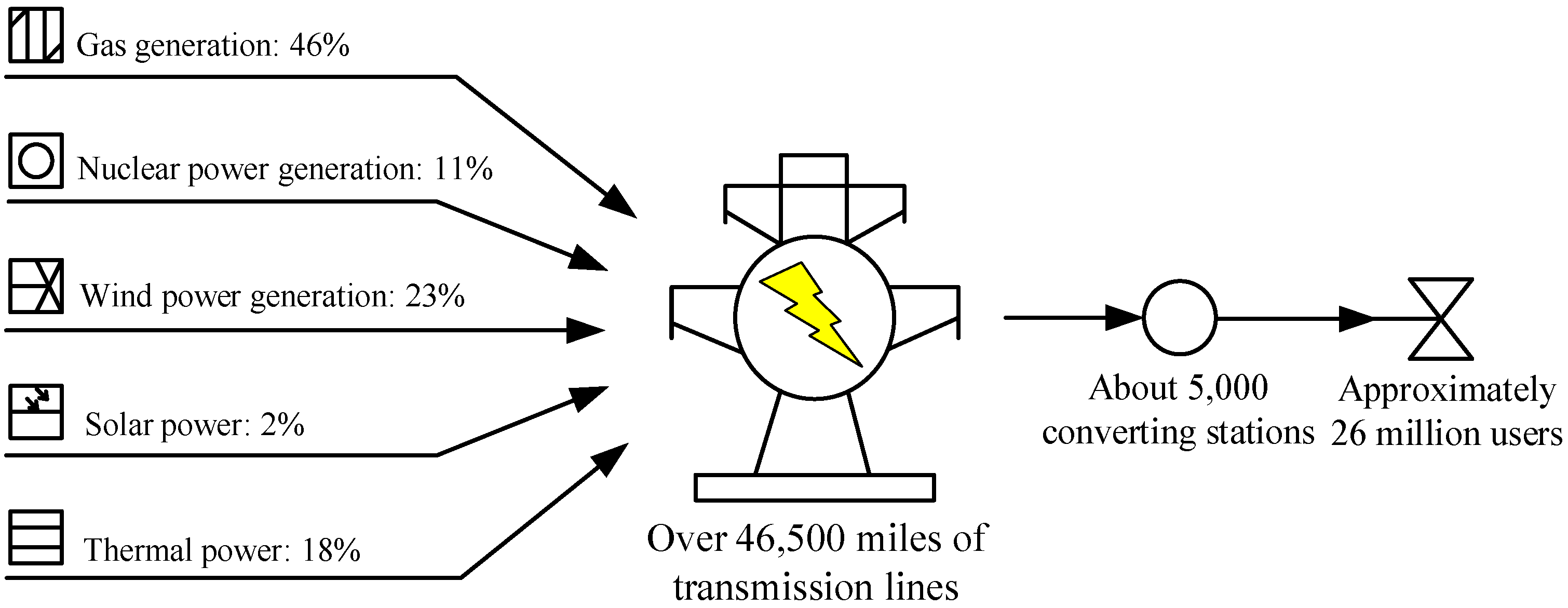
2.2. The “2.15” Blackout in Texas, USA

A severe power outage occurred in Texas, United States on 15 February 2021. Due to extreme weather conditions, power plants were unable to provide approximately 24,000 MW of net power generation, resulting in a maximum power loss of 52,277 MW and a peak load shedding of 20,000 MW. The supply of natural gas to gas-thermal power plants was limited, and several high-voltage direct current lines were constrained due to emergencies in neighboring areas. On 16 February, some generating units were restored, but others went offline, resulting in no net increase in power generation. Planned outages were reduced during the daytime and increased during the nighttime peak period. As temperatures began to rise on 17 February, the pressure on power outages eased, leading to an increase in power generation. On 18 February, power generation continued to increase, and the final planned outage order was canceled at 12:42; grid integration for large industrial facilities were restored. However, due to the damage caused by the blizzard, some power deficiency remained and required manual repairs. On 19 February, the emergency status was downgraded to Level 2 at 9:00, Level 1 at 10:00, and normal operation was restored at 10:35 [16].
Although the specific causes of the accident involve complex factors, the low inertia of the power system is still regarded as one of the key factors.
In the Texas power outage event, the main electricity supply issue was caused by extremely cold weather and widespread winter storms. This resulted in a sudden and significant increase in electricity demand that the power system was unable to meet, leading to a reduction in system inertia and a sharp decline in system stability.
The low system inertia, in turn, restricted the system’s ability to respond. Low inertia means that the system has lower resistance to sudden changes in load, resulting in an inability to quickly respond to these fluctuations. In the Texas power outage event, the extremely cold temperatures led to a sudden increase in demand, but the power system was unable to rapidly adjust its generation capacity to meet the requirements. Equipment with low inertia was unable to provide sufficient power, resulting in grid saturation and localized power deficiency.
Meanwhile, in this event, there was relatively limited energy diversification in Texas. The energy composition of the Texas power system is illustrated in Figure 2. The proportion of new energy generation in Texas has reached 82%, with wind power accounting for 23% and natural gas accounting for 46% (as of the year prior to the occurrence of the accident in 2020). The cold weather caused wind turbines to freeze and solar panels to be covered in snow, reducing the supply of renewable energy. The lack of diversified energy sources and reserves makes the power system more susceptible to failures caused by extreme weather conditions.
In addition, the power system in Texas exhibited a lack of resilience when facing a large-scale load impact. The system’s inability to adapt quickly to the changes in load resulted in equipment damage, line failures, and generator failures. Additionally, the lack of backup generators and suitable emergency measures prevented the system from recovering quickly in the face of sudden loads.
It is worth mentioning that the characteristics of the Texas power system also had an impact on the event. The Texas power system operates independently of the national interconnected power grid and places a greater emphasis on market and competition mechanisms. During this winter storm event, the market mechanism led to drastic fluctuations in electricity prices, causing some generators to be uneconomical to operate or unable to provide power in the short term [17,18].
Based on the analysis and summary of this incident in conjunction with the reference [15], the following recommendations are given:
(1)
Establish a real-time communication system between the electricity and gas systems to quickly identify and address faults, thereby enhancing system resilience.
(2)
Accelerate the development of backup resources such as energy storage and gas storage facilities to alleviate the burden of dispatching and compensating for renewable energy systems. Additionally, establish emergency mechanisms for extreme energy supply events to minimize the losses and negative social impacts caused by accidents.
(3)
Fully leverage the response level of multi-energy resources on the demand side and enhance the flexible load regulation capacity based on external factors and supply–demand relationships, ensuring the optimal allocation of resources in a wider range and a greater variety of energy sources. Especially in emergency scenarios, the flexible regulation capabilities of end-users’ multi-energy loads can be fully utilized to ensure the secure operation of the power system on a larger scale.
From the analysis of the two recent typical cases mentioned above, it can be observed that a power system with a high proportion of renewable energy can be greatly disturbed when influenced by external factors (primarily environmental factors such as lightning strikes, snowstorms, etc.). Insufficient resilience to disturbances can further result in grid failures, disconnections of renewable energy units, exacerbating grid instability, and even collapse. To avoid this series of adverse consequences, it is crucial to optimize the operation of the power grid and introduce fast and highly accurate inertia evaluation strategies.

3. Inertia Evaluation Methods for Power Systems

Insufficient inertia support capability in the power grid is the major cause of power outages in high-penetration renewable energy power systems. Therefore, a real-time and accurate evaluation of inertia in the power grid has become an important measure to ensure stable grid operation and serves as a guideline for optimizing the operation of the power system. Currently, high-penetration renewable energy power systems utilize three types of inertia evaluation methods based on perturbation types: inertia evaluation based on large disturbance events, inertia evaluation based on small disturbance events, and quasi-steady-state inertia evaluation. With the help of PMU (Phasor Measurement Unit) in a wide-area measurement system, real-time changes in the operating state of the power system are obtained, and the overall process of evaluating inertia in high-penetration renewable energy power systems is shown in Figure 3.
In Figure 3, representative research achievements are listed for the three categories of inertia online evaluation methods, such as the autoregressive sliding model and Markov-switching model. Furthermore, cutting-edge research results are also included, such as the concept of central frequency squared deviation. The research findings in the figure will be mentioned in the following sections, and a critical analysis of the advantages and limitations of these three evaluation methods will be provided.

3.1. Inertia Evaluation Based on Large Disturbance Events

Nowadays, measurement data in power systems have become easily accessible with the widespread adoption of PMU and WAMS (Wide Area Measurement System). By relying on time-series measurement data during significant disturbances in the power grid, it is possible to achieve the assessment of system-equivalent inertia.
Through the Newton–Raphson model and modal confidence criterion, the system inertia is accurately evaluated based on wide-area data by parameter identification [19]. In reference [20], a multi-dimensional evaluation method of power grid inertia level considering the characteristics of inertia space-time distribution is selected based on the following three quantitative indicators: inertia distribution index, rate of change inertia and rotational kinetic energy of the operating unit. The overall size, time dimension and space dimension of the power grid system are evaluated and analyzed, and the validity of the evaluation method is verified based on the test results of power grid operation data in Yunnan, China. Since the existing inertia evaluation methods based on frequency events focus on the whole system and ignore the property of regional distribution, the inertia distribution between regions will be unbalanced. In reference [21], the evaluation method of system partition inertia is improved. Based on the selection of the partition and the main unit, the difference is calculated, and the frequency of the main unit and the power on the regional liaison line were measured after the occurrence of frequency events, so as to complete the inertia evaluation of each region. A drawback is that the selection of the calculation time period will affect the assessment results of inertia levels in each region. A drawback is that the selection of the calculation time period will affect the assessment results of inertia levels in each region.
Professor F. Milano, a Fellow of the IEEE, proposed the concept of a frequency divider to linearly represent the frequencies at various nodes in a system, using the actual operating speeds of synchronous units in the system as boundary conditions, as shown in Equation (1):
ω B = 1 + D B ω G + 1 D B = − B BB + B B 0 − 1
In the equation, ω B represents the frequencies at various bus nodes in the system; ω G represents the frequencies of various generator units in the system; B BB represents the admittance matrix of the system network; D B represents the generator admittance matrix; and B B 0 represents the self-admittance matrix of the bus nodes.
Combined with the equivalent oscillation equation of the system, the online inertia evaluation of each node of the system is completed through the active power and frequency data of the generator node [22]. However, this method does not consider the estimation of inertia for asynchronous power sources. Based on the symbolic function, reference [23] solves the problem of numerical instability caused by the existence of singularity in the estimation model. In order to solve the impact of imprecision of disturbance occurrence time and communication error on inertia evaluation, the concept of central frequency squared deviation is introduced, and the frequency acquisition point is located based on the inertia graph center to calculate the minimum system output and critical minimum inertia in primary frequency modulation [24].

3.2. Inertia Evaluation Based on Small Disturbance Events

In highly automated and complex scenarios, the actual operation of the power grid system may be inconsistent with the preset power, and the impact of large disturbance events needs to be evaluated in advance to avoid system instability. In order to solve the defects of this method, the inertia evaluation method of the power system based on small disturbance events is proposed.
Reference [25] estimates the inertia based on the dynamic system mode parameters (frequency and damping) measured by the Wide Area Measurement System. The principle of the parameter estimation method is the weighted least squares method, which is calculated by using the measured modal frequency and the sensitivity of damping. Moreover, the results show that the damping measurement does not affect the estimation of generator inertia. This method overcomes the problem of the observability of the system’s inertia when the measurement data are small, and it includes the assumed values of the parameters as pseudo-measured values to complete the inertia estimation. Based on the frequency dynamic response of power systems under small perturbations, a new closed-loop recognition algorithm is proposed in reference [26] to evaluate the equivalent inertia of the system. Reference [27] takes the power grid with a high proportion of new energy as the research object, and it identifies the system oscillation modes under small disturbance events through coordinate transformation so as to calculate the equivalent inertia of the system. References [27,28] give the concept of the nodal inertia of a power system in view of the shortcomings of traditional inertia research, which mainly focuses on the system aspect and neglects the research of each node inertia. Based on the dynamic characteristics of node frequency under small disturbance, the visualization index of inertia space-time characteristics is proposed to make up for the ability to master the space-time characteristics of the power system. In reference [29], the critical minimum inertia is calculated by the two constraints of the frequency change rate after disturbance and the lowest frequency. Based on the theory of a power wave, reference [30] calculates the relationship between electromechanical propagation speed and equivalent inertia, and it completes the inertia evaluation according to the measurement of electromechanical wave speed.

3.3. Inertia Evaluation Based on Quasi-Steady-State Operation

The evaluation methods of equivalent inertia based on large disturbance events and small disturbance events need to apply external disturbance to the system, so they cannot complete the real-time detection of the inertia of the unit under normal operation. However, including the change of the power of the unit, the continuous action of the load switch, etc., will cause frequency disturbance. Therefore, the on-line evaluation of power grid inertia under steady-state operation needs to be further developed and studied. Reference [31] takes the ratio of inertia as a metric of the system’s frequency support capability, calculates the ratio of inertia of the maximum power disturbance that the system can bear through the response of real-time online data, and completes the evaluation and detection of the system’s frequency support capability. Reference [32] uses dynamic regressor extension and the mixing method to identify solution parameters based on the equivalent aggregation model of renewable energy and frequency regulation units. The switching Markov–Gaussian model is constructed to carry out a correlation analysis of equivalent inertia based on historical data, so as to complete PMU measurement under a quasi-steady state and realize the real-time online evaluation of power grid equivalent inertia [33]; however, this evaluation method requires abundant historical measurement data to ensure accuracy. Reference [34] explains the different sources of power grid inertia from two perspectives: theoretical inertia and computational inertia, and proposes a new inertia evaluation method for photovoltaic power generation according to the response process of inertia. In reference [35], the frequency deviation and load power deviation measured by PMU are taken as inputs in a stable state, and an autoregressive moving average model of equivalent inertia is constructed to transform the discrete model into a continuous model for order reduction. The equivalent inertia of the system is obtained by calculating the zero-pole model gain of the reduced order transfer function. Due to the problems of poor adaptability and low accuracy in current grid inertia assessment, reference [36] uses a regionalized grid equivalent frequency model to verify the adaptability of the output data to the identification process under different disturbances so as to use the system error model to complete the continuous estimation of the grid regional inertia under quasi-steady-state operation. Aiming at the inertia trend prediction, the inertia probability model of hybrid Copula and other methods is proposed to create a multi-scale equivalent inertia trend prediction method [11].

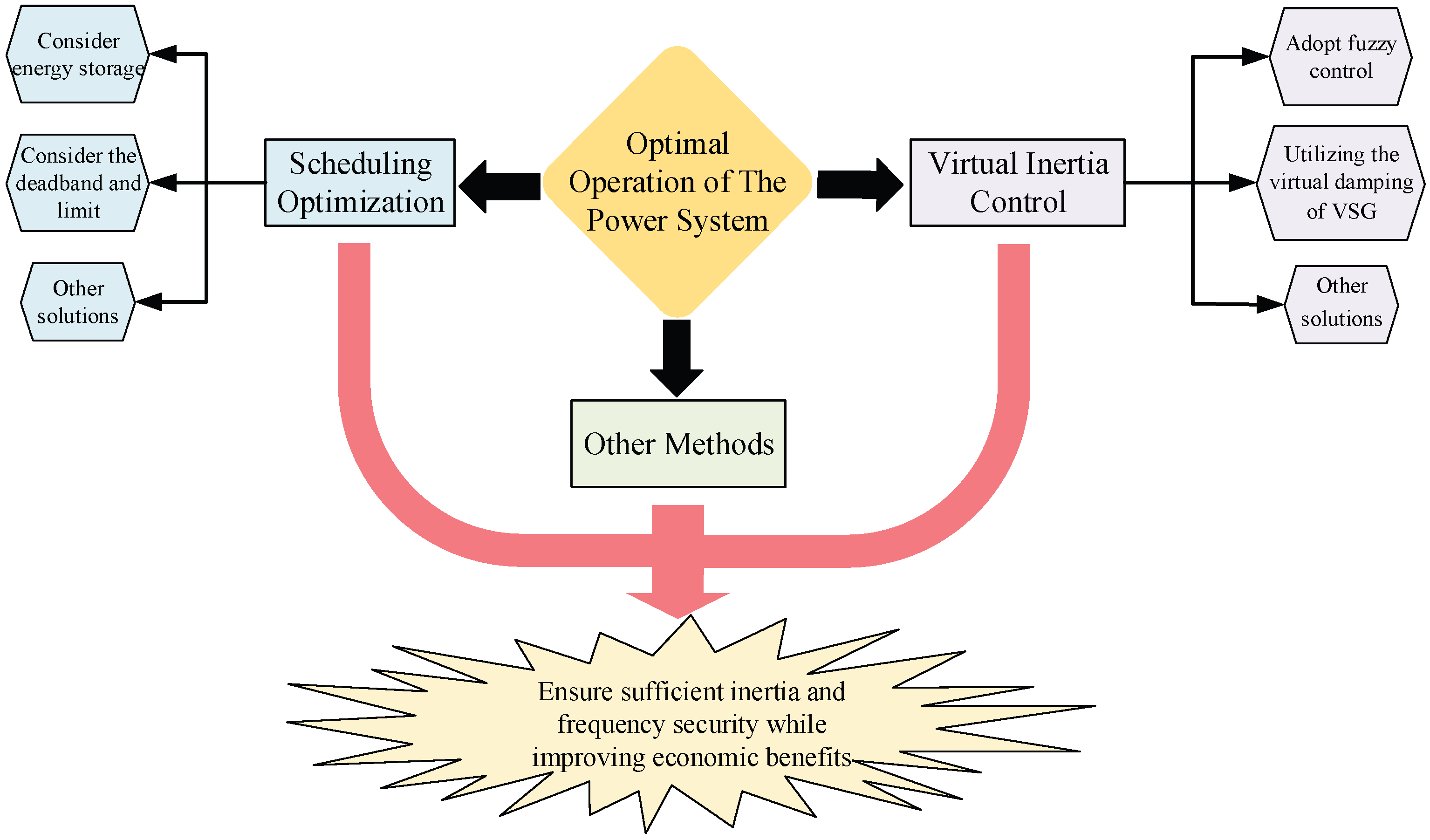
4. Optimal Operation Measures for Power Systems

As has been introduced in the beginning of this paper, increasing the proportion of renewable energy generation can reduce environmental pollution, but the problem of low inertia will become increasingly serious in power systems. In order to solve this contradiction, many researchers have proposed their solutions. As can be seen in Figure 4, with the same intention of ensuring frequency security while improving economic benefits, the solutions are roughly classified into three categories: scheduling optimization, virtual inertia control and other methods.

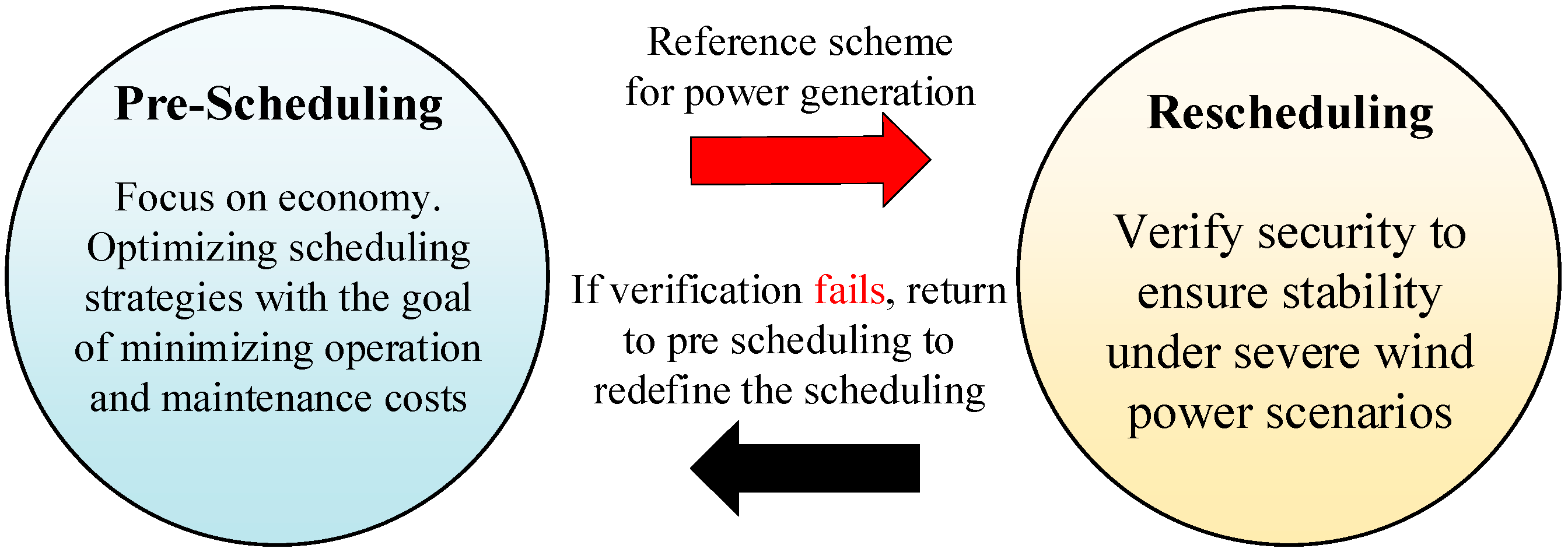
4.1. Scheduling Optimization

Optimizing power system scheduling can reduce the operation and maintenance costs, and it can improve the economic benefits of system operation, so it has always been a research field of great concern. In large-scale new energy grid integration systems, due to the reduction in system inertia, economic benefits cannot be pursued blindly. Therefore, researchers in related fields have proposed many scheduling strategies that take the need of both sides into account. The main achievements in recent years are summarized as follows:
The participation of the energy storage part in the frequency regulation of the power grid can inhibit the frequency fluctuations caused by the grid integration of new energy. Consequently, reference [37] takes the energy storage model into account, and the uncertainty of wind power is processed in a scenario-based manner. After linearizing the frequency constraint, model prediction control is adopted to add the constraint to the traditional model to optimize the unit commitment and economic scheduling of the power grid. Reference [38] proposes a compensation mechanism of frequency regulation ancillary services based on demand tightness, which can reflect the frequency regulation demand in real time, thus being helpful to promote frequency modulation facilities to participate in the frequency regulation of a power grid in a timely manner. With the intention of reducing the cost of frequency regulation as much as possible, the joint scheduling strategy of thermal power and energy storage is optimized under this market mechanism.
Aiming at the impact of multiple uncertainties on the RIES (Regional-Integrated Energy System), an RIES optimization model containing IDR (Integrated Demand Response), multiple uncertainties and multi-energy coupling is proposed in reference [39] to effectively ensure the cooperative operation of the RIES and improve the reliability and economy of it. A new control strategy for a photovoltaic–storage combined system is proposed in the reference [40] to solve the problem of light abandonment and inaccurate control in a photovoltaic-storage system. The strategy aims to minimize the RMSE (Root Mean Square Error) between the active output and the planned active output of the photovoltaic-storage combined power generation system, and it improves the response speed of the energy storage system and the schedulability of the combined system.
Most researchers ignore the cost of carbon trading when optimizing the scheduling, while reference [41] takes it into consideration. A low-carbon economic scheduling model, which covers the cost of system operation and carbon trading, is established in this research for IESs (Integrated Energy Systems) to achieve the purpose of minimizing the total cost. Aside from reducing the operation cost, environmental and economic benefits are increased under such scheduling. Reference [42] proposes a two-stage risk scheduling model, as has been shown in Figure 5. In the first stage, the safe capacity boundary of wind power that can be integrated to the grid is obtained, and the costs of operation and risk are taken into account to optimize the scheduling strategy of the power system, focusing on economy. In the second stage, safety verification is carried out to ensure that frequency security can be guaranteed even under severe wind power scenarios.
Reference [43] takes the influence of a primary frequency regulation dead zone and amplitude limit into consideration; then, it establishes frequency security constraints on this basis. Subsequently, an optimization method is proposed to solve the problem of the high nonlinearity of the established constraints. The unit commitment scheme based on this constraint can minimize the operation costs while solving the frequency stability problem of large-scale wind power grid integration power systems. Reference [44] proposes a scheduling optimization strategy based on an inertia evaluation model by establishing a multi-timescale optimal operation model that includes day-ahead, intraday and real-time. The strategy continuously obtains the output state of each unit and adjusts it in a timely manner in the next stage to meet the inertia requirement of the power system and obtain the most economical and reliable scheduling strategy.
In addition to inertia constraints, reference [45] also takes other aspects into constraints while designing scheduling optimization strategies, such as reserve capacity and climbing ability. Moreover, the influence of weighting factors on the multi-objective optimization results is taken into consideration to propose a scheduling optimization strategy, which dynamically selects the weighting factors of multi-objective optimization according to the condition of load and achieves better results. Reference [46] constructs a two-stage dual-level scheduling optimization model of a distributed energy system in an active distribution network. Moreover, after introducing the DE (Differential Evolution factor), the ICA (Imperialist Competitive Algorithm) is improved and incorporated into DE-ICA, and it is adopted to solve the dispatch optimization model of an energy system. By using this method, the optimal scheduling strategy can be obtained, and the problem whereby the current scheduling optimization model of energy system has low hierarchical scheduling capability can be solved.

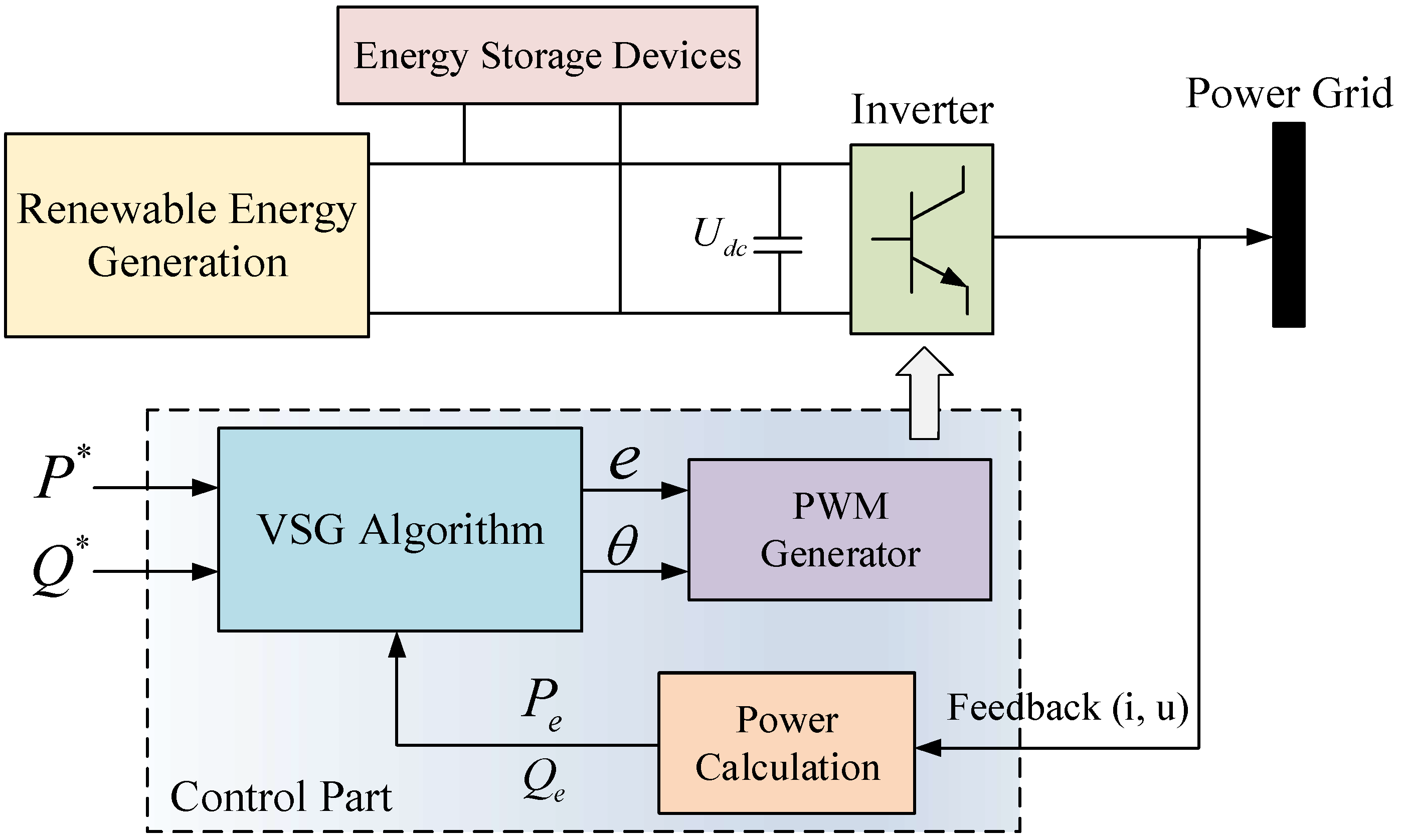
4.2. Virtual Inertia Control

Compared with traditional inertia, virtual inertia is no longer an inherent attribute of the object but more like a concept. Since wind power, photovoltaic power and other new energy power generation are weakly coupled with the power system or even completely decoupled, they seemingly cannot provide inertia support. But in fact, by adopting the virtual inertia control algorithm, new energy generation also has the capacity to supplement the inertia of thermal power units, working like synchronous generators to achieve the function of frequency and voltage regulation. Therefore, virtual inertia control technology has broad application prospects, and there are many studies focusing on it. As an important part of virtual inertia control technology, virtual synchronous generator technology introduces the rotor motion equation into the control algorithm of the inverter, controlling the energy storage devices to absorb or release energy to resist disturbance. Although having no mechanical energy and inertia, new energy generation can still improve the inertia and damping level of the power systems effectively after adopting the VSG algorithm. The structure of the virtual synchronous generator is shown in Figure 6.
The measuring module will obtain the information about the current and voltage in the grid; then, the active power P e and reactive power Q e can be calculated. The reference values P * and Q * provided by the scheduling information are combined with the obtained values P e and Q e to obtain the output voltage amplitude e and power angle θ through the VSG control algorithm. According to these parameters, the PWM generator will generate control signals to control the conduction and turn off of the switch tubes in the inverter, enabling the new energy generation to resist disturbance, providing virtual inertia.
Aiming at solving the problem where the parameters of virtual inertia control cannot be set reasonably, reference [47] proposes a virtual inertia cooperative control strategy, which is suitable for the wind power and energy storage system. The parameters of the virtual inertia controller are designed by reasonably distributing the required inertia to wind power and energy storage. Finally, by locking the controller at the right time, the problem of frequency overshoot and even secondary drop existing in the traditional control method is solved.
In order to solve the problem of coordinated distribution of virtual inertia among wind turbines, reference [48] proposes an evaluation index to quantify the inertia response ability of wind turbines. Based on this index, an inertia coordination distribution method is proposed, which considers the inertia demand of the power system and the inertia response ability of the wind turbine itself. While releasing the inertia response capability of the wind turbine, the same problem as reference [47] also is solved through this method. Reference [49] proposes a distributed adaptive virtual inertia control method to suppress the oscillation of multiple VSG (Virtual Synchronous Generator) grids and improve the dynamic frequency response.
In view of the obvious effect of SOC (Storage state of Charge) on regulating virtual inertia, reference [50] proposes a fuzzy adaptive virtual inertia control strategy of an energy storage system considering SOC, which can effectively extend the working life of energy storage by avoiding the deep over-charging and over-discharging of energy storage units. Reference [51] proposes a virtual inertia control strategy for variable speed wind turbines based on the extreme time of frequency change, which not only reliably meets the frequency regulation requirements of the system but also greatly improves the active support performance for the power grid.
In reference [52], fuzzy control is introduced into virtual inertia control for a wind–thermal system. According to the operating conditions of a DFIG (Doubly Fed Induction Generator) and the wind power penetration ratio in the power system, the coefficient of frequency regulation proportion of wind power is dynamically determined by fuzzy control. On this basis, the variation range of the parameters in virtual inertia control is finally determined after considering the relationship between the differential coefficient of inertial frequency regulation control and the equivalent inertia constant of DFIG in the wind–thermal incremental system model. Reference [53] proposes an adaptive virtual inertia control method based on LQR (Line Quadratic Regulator), which improves the inertia support ability of new energy grid integration convertors based on DC capacitor energy virtual inertia control.
Through training a BP (Back Propagation) neural network with EMD (Empirical Mode Decomposition), a time-series wind speed model can be established to predict the short-term wind speed. Based on such a prediction, reference [54] proposes a coordinated-control strategy for the wind farm virtual inertia response. Although the traditional strategy completes the field-level inertia response, it does not consider the differences in the inertia response capacity of each different unit when implementing the frequency regulation power control of wind turbines, and the newly proposed strategy solves this problem. Reference [55] proposes a coordinated control strategy of VSG controller parameters combining the online identification of a dominant oscillation mode and particle swarm optimization algorithm. Through making use of the virtual damping of VSGs more effectively, the frequency stability of the power system with a high proportion of wind power can be improved in this strategy.

4.3. Other Optimization Methods

In addition to the above two mainstream optimization methods that can improve the economic benefits of the power system while maintaining the sufficient inertia of the system effectively, in recent years, some researchers have also proposed solutions from a new perspective, which is an effective supplement to the traditional scheme, and it also broadens the research ideas of future studying.
In reference [56], slice sampling is introduced into MCMC (Markov Chain Monte Carlo) method to propose a new equivalent inertia probability evaluation method for the power system, which is significant for the operation optimization of a power system. Traditional evaluation ways could not effectively reflect the time-series change trend of the inertia in a power system with a high proportion of renewable energy. Reference [57] defines the concept of an ISR (Inertia Security Region) and proposes the index of the ratio of area to the perimeter of the ISR, inertia security margin, and inertia reserve coefficient. By paying attention to these characteristic indexes of ISR, schedulers can monitor the situation of inertia in a power system and ensure the stability of frequency. Reference [58] extended the traditional concept of inertia in a power system, proposing the concept of generalized inertia. After classifying different forms of inertia, a generalized inertia response system and analyzing method are proposed to provide a new way to optimize the operation of a power system.
There have been many methods proposed to optimize the operation of power systems in recent years, and this paper only summarizes some of them. For the research productions summarized in this paper, Table 1 displays some representative methods and their advantages and disadvantages to facilitate readers’ overview.

5. UFLS Schemes under Large-Scale Power Deficiency

The large-scale grid integration of new energy power generation will reduce the proportion of thermal power, and the instability problem of new energy generation is very significant compared with traditional thermal power. As is widely known, voltage in the power grid is related to reactive power while frequency is related to active power, so when the power generation equipment cannot provide enough active power, the reduction in grid frequency will occur. Once the frequency goes below a certain limit, great attention must be paid to it, and even some emergency measures should be taken to prevent the occurrence of frequency collapse. UFLS is one of the most common means. When a disturbance occurs, the figure of whether the frequency is in a safe state according to the system inertia is shown in Figure 7.
In its report on the operation and challenges of low-inertia power systems, the EPRI (Electric Power Research Institute) compares the minimum inertia limits of the Texas, South Australia, and Ireland systems. Based on the findings of this study and references [12,13], relevant data and various evaluation metrics for the three regions are summarized, as shown in Table 2.
When selecting metrics, Ireland and North America determine the penetration rate of asynchronous power sources and system inertia requirements based on the minimum frequency and RoCoF (Rate of Change of Frequency) values in frequency security indicators. Australia determines the inertia safety threshold using the supply–demand curve of frequency response and inertia. In terms of inertia monitoring requirements, North America requires hourly monitoring, which has a high level of method complexity but possesses inertia prediction capability. Ireland only needs to calculate the system inertia level once, making the metric relatively simple and easy to use. Australia’s method for assessing inertia requirements has a moderate level of complexity, with the key being the determination of the inertia demand curve.
UFLS is a protective measure that sheds part of the load when the frequency of the power system decreases below the preset protection value to reduce the power imbalance of the system and prevent the frequency collapse. The UFLS thresholds and related information in some regions of the world are listed in Table 1. However, load shedding means that some areas will suffer power cuts, and the economic benefits of many parties will be hurt. Therefore, how to set up suitable load-shedding schemes to reduce the negative impact as much as possible has always been the focus of attention. From today’s perspective, there are many shortcomings in traditional strategies [59,60,61,62,63]. For example, reference [62] proposes a base-set setting approach based on the set of chosen parameter values and a global optimal UFLS scheme algorithm after obtaining the base set. But the load is not classified according to importance. Although the difference in importance of the loads and the effect of load shedding on the sensitivity of frequency recovery in the power system are considered in reference [63], the proposed scheme has high cost and poor engineering practicability.
With further research, relatively better load-shedding schemes have been proposed in recent years. By establishing the relationship between the power deficit of the power system and the frequency deviation area of the bus, reference [64] proposes a method to calculate the power deficit of the system more accurately. Based on the calculation, a new UFLS strategy is proposed, which accelerates the system’s frequency recovery.
Different from reference [64], reference [65] studies the quantified relationship between the active power deficiency of the power system and the voltage deviation instead of the frequency deviation area of the bus. The traditional algorithm for calculating the power deficiency of the power system may result in inaccuracy due to the inability to accurately determine the change in system inertia and the assumption that the voltage remains constant. By exploring the characteristics of load variation with the system voltage and frequency, a real-time measurement method for system inertia and system power deficiency based on load-side response information is proposed to overcome the shortcoming of the traditional algorithm, obtaining the most suitable adaptive load-shedding scheme.
Reference [66] applies the monotone control system theory to analyze the UFLS problem. Combined with the sensitivity analysis, the full-state model is adopted to synthesize the coupling relationship between frequency and power angle, voltage and related parameters, which obtains a good scalability while analyzing the dynamic process of the system under disturbance as realistically as possible. The analysis also has a guiding significance for the parameters setting when the power grid fails.
In view of the fact that many existing researchers rely on high-speed communication infrastructures and a large number of PMUs to ensure the effect of the proposed strategy, reference [67] proposes a new load-shedding strategy to improve the frequency stability of the power system by retaining the voltage stability, which overcomes this shortcoming. In this strategy, the reactive power margin is adopted as an indicator to define the bus strength, and a higher percentage of load shedding is applied to relatively weaker buses to ensure the stability of voltage and frequency after a contingency.

6. Conclusions and Prospect

In the context of the increase in the proportion of renewable energy connected to the grid, this paper introduces the significance of inertia in power systems and the reasons for its reduction, and it took real cases as the starting point, from three aspects of inertia evaluation, low-inertia system optimal operation, and UFLS schemes. We also combined the research status of low inertia problems in power systems. However, given the complex and diverse realities, any research results are bound to have application limitations, and other inadequacies may gradually reveal themselves over time. Therefore, this paper puts forward the following suggestions for the future research on the grid integration of a high proportion of renewable energy:
(1)
In terms of theoretical improvement: at present, the relevant theoretical analysis of the frequency response of the power system has been relatively complete, but the electromechanical dynamic process of the power system is very complicated because it is affected by the distribution of inertia. Future research can focus on exploring the coupling mechanism between the system’s electromechanical dynamic process and the space distribution of inertia, and it can provide a new vision for the stable operation of a high-proportion new energy power system.
(2)
In terms of inertia evaluation, research is conducted on comprehensive inertia detection and evaluation based on technologies such as big data and artificial intelligence. With the widespread application of high-performance devices such as PMUs, the accurate processing of large amounts of system data has become easier. In the future, an online high-precision detection model can be constructed based on real-time data such as grid node frequency, switch operating status, and the spatiotemporal distribution characteristics of inertia. Furthermore, starting from application scenarios, research is conducted on inertia evaluation and warning systems that meet the requirements of various levels, issuing warning messages regarding the insufficient inertia in both real-time and predictive operational modes.
(3)
In terms of grid integration and decoupling: in low-inertia power systems, the integration of a large number of distributed energy resources and energy storage devices has made the system structure more complex. Grid integration and decoupling issues have become a challenge in low inertia research, requiring research efforts to enhance the effective integration of distributed energy resources and energy storage devices while maintaining system stability and controllability.
(4)
In terms of simulation construction, due to the uniqueness of low-inertia power systems, the complexity of real situations and the diversity of unverified power system optimization methods, researchers need to continuously optimize and upgrade existing simulation platforms and algorithms in order to simulate real scenarios better and obtain accurate data.
(5)
In terms of emergency measures under large-scale power deficiency: researchers can explore the feasibility of taking additional measures before implementing UFLS rather than focusing all their efforts on mitigating the negative impacts and optimizing load-shedding strategies. For instance, in hydroelectric power plants, a reasonable generation scheduling can be designed by considering multiple sources of data and past experiences. This involves storing varying volumes of water based on different circumstances and releasing it during emergency situations to temporarily generate additional power for emergency use.

Author Contributions

Conceptualization, Y.W. (Yang Wang) and Z.Z.; validation, J.S., X.Z. and Z.Z.; formal analysis, J.S. and X.Z.; investigation, X.W.; resources, Y.W. (Yifan Wang); data curation, J.S.; writing—original draft preparation, J.S., X.Z. and Z.Z.; writing—review and editing, Z.Z. and Y.W. (Yifan Wang); visualization, X.W.; supervision, Y.W. (Yang Wang) and Y.W. (Yifan Wang). All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

UFLSUnder Frequency Load Shedding
PVPhotovoltaic
PMUPhasor Measurement Unit
WAMSWide Area Measurement System
RIESRegional Integrated Energy System
IDRIntegrated Demand Response
RMSERoot Mean Square Error
IESIntegrated Energy Systems
DEDifferential Evolution factor
ICAImperialist Competitive Algorithm
PWMPulse Width Modulation
VSGVirtual Synchronous Generator
SOCStorage state of Charge
DFIGDoubly Fed Induction Generator
LQRLine Quadratic Regulator
BPBack Propagation
DCDirect Current
EMDEmpirical Mode Decomposition
MCMCMarkov Chain Monte Carlo
ISRInertia Security Region
RoCoFRate of Change of Frequency

References

  1. Zhang, Q.; Zhou, Q. Research on the Development Path of China’s Thermal Power Generation Technology Based on the Goal of “Carbon Peak and Carbon Neutralization”. Power Gener. Technol. 2023, 44, 143–154. [Google Scholar]
  2. Ren 21. Renewables 2022 Global Status Report [EB/OL]. Available online: https://www.ren21.net/gsr-2022/ (accessed on 20 April 2022).
  3. Tang, J.; Li, S. Analysis of the Influence of Grid-connected High Permeability New Energy on the Frequency Characteristics of Power Grid. Electr. Eng. 2023, 4, 58–62+133. [Google Scholar]
  4. Li, X.; Wu, G.; Yuan, X.; Wu, L. Research on Economic Evaluation of Renewable Energy Generation Side Energy Storage Projects. Electr. Power Sci. Eng. 2023, 1–12. [Google Scholar]
  5. Su, G.; Yi, H.; Kurban, A.; Guo, T.; Hao, W.; Huan, J. Multi-Objective capacity optimization of renewable energypower system considering techno-economic comparisons of various energy storage technologies. Acta Energiae Solaris Sin. 2022, 43, 424–431. [Google Scholar]
  6. Wang, Y.; Wang, X.; Lu, M. Research on Inertia Related Problems of High Proportion of New Energy. Northeast. Electr. Power Technol. 2023, 44, 20–27+46. [Google Scholar]
  7. Zhang, H.; Gao, Z.; Cao, Y.; Qin, H.; Yang, D.; Ma, H. Review and prospect of research on power system inertia with high-penetration of renewable energy source. J. Shandong Univ. (Eng. Sci.) 2022, 52, 1–13. [Google Scholar]
  8. Mehigan, L.; Al Kez, D.; Collins, S.; Foley, A.; Ó’Gallachóir, B.; Deane, P. Renewables in the European power system and the impact on system rotational inertia. Energy 2020, 203, 117776. [Google Scholar] [CrossRef]
  9. Zeng, H.; Sun, F.; Li, T.; Zhang, Q.; Tang, J.; Zhang, T. Analysis of “9.28” in South Australia and its enlightenment to China. Autom. Electr. Power Syst. 2017, 41, 1–6. [Google Scholar]
  10. Yan, R. The anatomy of the 2016 South Australia blackout: A catastrophic event in a high renewable network. IEEE Trans. Power Syst. 2018, 33, 5374–5388. [Google Scholar] [CrossRef]
  11. Zhang, W.; Wen, Y.; Chi, F.; Wang, K.; Li, L. Research Framework and Prospect on Power System Inertia Estimation. Proc. CSEE 2021, 41, 6842–6856. [Google Scholar]
  12. Liu, Z.; Zhou, M.; Li, Z. Fault recovery strategy of active distribution network based on mutation particle swarm opti-mization algorithm. Electr. Power Autom. Equip. 2021, 41, 1–11+53. [Google Scholar]
  13. Wang, B.; Yang, D.; Cai, G. Review of Research on Power System Inertia Related Issues in the Context of High Penetration of Renewable Power Generation. Power Syst. Technol. 2020, 44, 2998–3007. [Google Scholar]
  14. Teng, S.; Gong, Y.; Zhang, P.; Li, X. Analysis of Great Blackout Accident in Britain on August 9, 2019 and Enlightenment to Beijing Power Network. Electr. Power Surv. Des. 2020, 2, 5–8. [Google Scholar]
  15. Sun, H.; Xu, T.; Guo, Q.; Xi, G.; Zhang, J.Y.; Tu, J.Z. Analysis on Blackout in Great Britain Power Grid on August 9th, 2019 and Its Enlightenment to Power Grid in China. Proc. CSEE 2019, 39, 6183–6192. [Google Scholar]
  16. Hou, Y.; Ding, Y.; Bao, M.; Liang, Z.; Song, Y.; Guo, C. Analysis of Texas Blackout from the Perspective of Electricity-gas Coupling and Its Enlightenment to the Development of China’s New Power System. Proc. CSEE 2022, 42, 7764–7775. [Google Scholar]
  17. Zhang, G.; Zhong, H.; Tan, Z.; Cheng, T.; Xia, Q.; Kang, C. Texas electric power crisis of 2021 warns of a new blackout mechanism. CSEE J. Power Energy Syst. 2022, 8, 1–9. [Google Scholar]
  18. Menati, A.; Xie, L. A Preliminary Study on the Role of Energy Storage and Load Rationing in Mitigating the Impact of the 2021 Texas Power Outage. In Proceedings of the 2021 North American Power Symposium (NAPS), College Station, TX, USA, 14–16 November 2021; pp. 1–5. [Google Scholar]
  19. Song, G.; Bialek, J. Synchronous machine inertia constants updating using Wide Area Measurements. In Proceedings of the IEEE Pes International Conference & Exhibition on Innovative Smart Grid Technologies, Berlin, Germany, 14–17 October 2012. [Google Scholar]
  20. Xiao, Y.; Lin, X.; Wen, Y. Multi-Dimensional Assessment of the Inertia Level of Power Systems with High Penetration of HVDCs and Renewables. Electr. Power Constr. 2020, 41, 19–27. [Google Scholar]
  21. Liu, F.; Xun, G.; Wang, F. Assessment Method of System Partition Inertia Based on Differential Calculation Method. Autom. Electr. Power Syst. 2020, 44, 46–53. [Google Scholar]
  22. Zeng, F.; Zhang, J.; Zhou, Y. Online identification of inertia distribution in normal operating power system. IEEE Trans. Power Syst. 2020, 35, 3301–3304. [Google Scholar] [CrossRef]
  23. Liu, M.; Chen, J.; Milano, F. On-line inertia estimation for synchronous and non-synchronous devices. IEEE Trans. Power Syst. 2021, 36, 2693–2701. [Google Scholar] [CrossRef]
  24. Li, D.; Zhang, J.; Xu, B. Equivalent Inertia Assessment in Renewable Power System Considering Frequency Distribution Properties. Power Syst. Technol. 2020, 44, 2913–2921. [Google Scholar]
  25. Guo, S.; Norris, S.; Bialek, J. Adaptive parameter estimation of power system dynamic model using modal information. IEEE Trans. Power Syst. 2014, 29, 2854–2861. [Google Scholar] [CrossRef]
  26. Zhang, J.; Han, C. Online identification of power system equivalent inertia constant. IEEE Trans. Ind. Electron. 2017, 64, 8098–8107. [Google Scholar] [CrossRef]
  27. Panda, R.K.; Mohapatra, A.; Srivastava, S.C. Online estimation of system inertia in a power network utilizing synchrophasor measurements. IEEE Trans. Power Syst. 2019, 35, 3122–3132. [Google Scholar] [CrossRef]
  28. Cai, G.; Wang, B.; Yang, D. Inertia estimation based on observed electromechanical oscillation response for power systems. IEEE Trans. Power Syst. 2019, 34, 4291–4299. [Google Scholar] [CrossRef]
  29. Guo, X.; Bi, T.; Liu, F. Estimating maximum penetration level of renewable energy based on frequency stability constrains in networks with high-penetration wind and photovoltaic energy. Renew. Energy Resour. 2020, 38, 84–90. [Google Scholar]
  30. You, S.; Liu, Y.; Kou, G. Non-invasive identification of inertia distribution change in high renewable systems using distribution level PMU. IEEE Trans. Power Syst. 2017, 33, 1110–1112. [Google Scholar] [CrossRef]
  31. Zeng, F.; Zhang, J. Temporal and Spatial Characteristics of Power System Inertia and Its Analysis Method. Proc. CSEE 2020, 40, 50–58+373. [Google Scholar]
  32. Liu, Q.; Yu, Z.; Zhang, L. Online Frequency Support Capacity Assessment of Power Grid Based on Inertia Ratio. Power Syst. Technol. 2023, 47, 493–502. [Google Scholar]
  33. Cao, X.; Stephen, B.; Abdulhadi, I.F.; Booth, C.D.; Burt, G.M. Switching Markov Gaussian models for dynamic power system inertia estimation. IEEE Trans. Power Syst. 2015, 31, 3394–3403. [Google Scholar] [CrossRef]
  34. Li, D.; Guo, T.; Liu, Q. Inertia estimation of renewable power system considering photovoltaics. Acta Energiae Solaris Sin. 2021, 42, 174–179. [Google Scholar]
  35. Tuttelberg, K.; Kilter, J.; Wilson, D.; Uhlen, K. Estimation of power system inertia from ambient wide area measurements. IEEE Trans. Power Syst. 2018, 33, 7249–7257. [Google Scholar] [CrossRef]
  36. Li, S.; Xia, Z.; Cheng, X. Continuous Estimation Method of Power System Inertia Based on Ambient Disturbance. Proc. CSEE 2020, 40, 4430–4439+4723. [Google Scholar]
  37. Xu, Z.; Wang, C.; Zheng, H. Frequency constrained unit commitment and economic dispatch with storage in low-inertia power system. Adv. Technol. Electr. Eng. Energy 2020, 39, 25–32. [Google Scholar]
  38. Liu, J.; Jia, Y.; Chen, H. Market Mechanism and Scheduling Strategy of Ancillary Services Considering Real-time Frequency Regulation Requirements. Power Syst. Technol. 2022, 46, 1269–1278. [Google Scholar]
  39. Yang, H.; Li, M.; Jiang, Z.; Zhang, P. Multi-time scale optimal scheduling of regional integrated energy systems considering integrated demand response. IEEE Access 2020, 8, 5080–5090. [Google Scholar] [CrossRef]
  40. Cao, S.; Wu, X.; Liu, J. Scheduling Optimization Control Strategy of PV-and-Storage Combined Power Generation System. Electr. Mach. Control Appl. 2023, 50, 89–94. [Google Scholar]
  41. Xu, T.; Cheng, C.; Ren, F. Optimal Scheduling of Integrated Energy Systems Considering Carbon Trading. J. Phys. Conf. Ser. 2022, 2395, 012053. [Google Scholar] [CrossRef]
  42. Xin, X.; Wang, T.; Gu, X. Unit Commitment and Risk Dispatch Considering Multi-Regional Frequency Dynamic Security Under Large-scale Wind Power Access. Proc. CSEE 2023, 1–16. [Google Scholar]
  43. Shen, J.; Li, W.; Li, Z. Unit Commitment of Power System with High Proportion of Wind Power Considering the Deadband and Limiter of Primary Frequency Response. Power Syst. Technol. 2022, 46, 1326–1337. [Google Scholar]
  44. Wang, Y.; Wang, Y.; Zhao, Z.; Zhou, Z.; Hou, Z. Multi-Timescale Optimal Operation Strategy for Renewable Energy Power Systems Based on Inertia Evaluation. Energies 2023, 16, 3577. [Google Scholar] [CrossRef]
  45. Wu, X.; Cao, S.; An, T. Multi-Objective Scheduling Optimization Strategy of Regional Power Grid Considering the Influence of Weighting Factors. Electr. Mach. Control Appl. 2023, 50, 81–88. [Google Scholar]
  46. Zeng, M.; Peng, L.; Wang, L. Two-stage dual-level dispatch optimization model of distributed energy system in active distribution network. Electr. Power Autom. Equip. 2016, 36, 108–115. [Google Scholar]
  47. Zhang, X.; Hu, J.; Fu, Y. Virtual Inertia Demand and Collaborative Support Technology of Wind Power and Energy Storage System. Trans. China Electrotech. Soc. 2023, 1–14. [Google Scholar]
  48. Xu, B.; Zhang, L.; Yao, Y.; Yu, X.; Yang, Y.; Li, D. Virtual Inertia Coordinated Allocation Method Considering Inertia Demand and Wind Turbine Inertia Response Capability. Energies 2021, 14, 5002. [Google Scholar] [CrossRef]
  49. Fu, S.; Sun, Y.; Liu, Z. Power oscillation suppression in multi-VSG grid with adaptive virtual inertia. Int. J. Electr. Power Energy Syst. 2021, 135, 107472. [Google Scholar] [CrossRef]
  50. Zhang, X.; Li, D.; Yang, Z. Fuzzy adaptive virtual inertia control of energy storage systems considering SOC constraints. Energy Rep. 2023, 9, 2431–2439. [Google Scholar] [CrossRef]
  51. Zhang, X.; Jin, Z.; Fu, Y. Virtual Inertia Constrain and Support Control of Wind Turbines Based on Variable Frequency Limit Time. High Volt. Eng. 2023, 49, 2491–2505. [Google Scholar]
  52. Ke, X.; Zhang, W.; Li, P. Fuzzy Adaptive Virtual Inertia Control for High Wind Power Penetration System. Power Syst. Technol. 2020, 44, 2127–2136. [Google Scholar]
  53. Li, H.; Lu, G.; Zhou, L. Adaptive Virtual Inertia Control of New Energy Based on LQR. Electr. Drive 2023, 1–7. [Google Scholar]
  54. Wang, Z.; Gao, J.; Zhao, B. Wind farm virtual inertia coordinated control technology based on wind speed prediction. Acta Energiae Solaris Sin. 2020, 44, 2127–2136. [Google Scholar]
  55. Yang, T.; Liao, Y. Coordinated control method of virtual inertia and virtual damping for interconnected power system with doubly-fed wind farm. Electr. Power Autom. Equip. 2020, 40, 92–100. [Google Scholar]
  56. Wang, Q.; Yao, L.; Xu, J. S-MCMC Based Equivalent Inertia Probability Evaluation for Power Systems with High Proportional Renewable Energy. Power Syst. Technol. 2023, 1–13. [Google Scholar]
  57. Lin, X.; Wen, Y.; Yang, W. Inertia Security Region: Concept, Characteristics, and Assessment Method. Proc. CSEE 2021, 41, 3065–3079. [Google Scholar]
  58. Sun, D.; Wang, B.; Li, W. Research on Inertia System of Frequency Response for Power System with High Penetration Electronics. Proc. CSEE 2020, 40, 5179–5192. [Google Scholar]
  59. Song, Z.; Liu, J.; Liu, Y. Response model of DFIG for real-time simulation of large-scale wind farms. Electr. Power Autom. Equip. 2014, 34, 95–100+119. [Google Scholar]
  60. Bo, D.; He, J.; Wang, X. Adaptive UFLS scheme based on grey correlation analysis. Power Syst. Prot. Control 2014, 42, 20–25. [Google Scholar]
  61. Tan, W.; Yi, Y.; Lin, J. A New Low-frequency Load Shedding Scheme Based on Ordered Binary Decision Diagram. Guangdong Electr. Power 2014, 27, 79–83. [Google Scholar]
  62. Xie, D.; He, H.; Chang, X. An Approach to Design Power System under Frequency Load Shedding Scheme Taking Coherent Area and Global Optimization into Account. Power Syst. Technol. 2010, 34, 106–112. [Google Scholar]
  63. Gao, X.; Yao, L.; Zhang, H. Under Frequency Load Shedding Scheme Optimization Based on Load Frequency Characteristics. Proc. CSU-EPSA 2015, 27, 82–88. [Google Scholar]
  64. Liu, K.; Zhang, J.; Li, J. Power Deficit Calculation and under Frequency Load Shedding Strategy Based on the Frequency Deviation Area. Trans. China Electrotech. Soc. 2021, 36, 1040–1051. [Google Scholar]
  65. Wang, H.; He, P.; Jiang, Y. Under-frequency load shedding scheme based on estimated inertia. Electr. Power Autom. Equip. 2019, 39, 51–56+63. [Google Scholar]
  66. Liu, Y.; Chen, M.; Li, J. Monotonic control characteristics of under-frequency load shedding in power system. Electr. Power Autom. Equip. 2023, 43, 182–189. [Google Scholar]
  67. Shazon, M.N.H.; Deeba, S.R.; Modak, S.R. A Frequency and Voltage Stability-Based Load Shedding Technique for Low Inertia Power Systems. IEEE Access 2021, 9, 78947–78961. [Google Scholar]
Energies 16 06042 g001
Figure 1. The low-inertia characteristic of a high-penetration renewable energy power system.
Figure 1. The low-inertia characteristic of a high-penetration renewable energy power system.
Energies 16 06042 g001
Energies 16 06042 g002
Figure 2. Energy composition of Texas power system in 2020.
Figure 2. Energy composition of Texas power system in 2020.
Energies 16 06042 g002
Energies 16 06042 g003
Figure 3. Process for assessing equivalent inertia in high-penetration renewable energy systems.
Figure 3. Process for assessing equivalent inertia in high-penetration renewable energy systems.
Energies 16 06042 g003
Energies 16 06042 g004
Figure 4. Classification of the optimal operation measures for power systems.
Figure 4. Classification of the optimal operation measures for power systems.
Energies 16 06042 g004
Energies 16 06042 g005
Figure 5. Two-stage risk-scheduling model.
Figure 5. Two-stage risk-scheduling model.
Energies 16 06042 g005
Energies 16 06042 g006
Figure 6. Schematic diagram of the structure of the virtual synchronous generator.
Figure 6. Schematic diagram of the structure of the virtual synchronous generator.
Energies 16 06042 g006
Energies 16 06042 g007
Figure 7. Schematic diagram of frequency security in power system.
Figure 7. Schematic diagram of frequency security in power system.
Energies 16 06042 g007
Table 1. Summary of some research productions.
Table 1. Summary of some research productions.
Reference NumberCategoryAdvantagesDisadvantages
[35]Scheduling optimizationConsiders energy storage, adopts model prediction controlIgnores that the frequency of bus in the power systems is not completely the same
[36]Scheduling optimizationProposes a compensation mechanism of frequency regulation ancillary services based on demand tightness to reduce the costThe proposed mechanism may lead to a decrease in the economic benefits of energy storage
frequency regulation when the frequency
regulation demand is small
[39]Scheduling optimizationProposes a two-stage risk scheduling model, which balances economy and
security		Only suitable for multi-regional systems with a high proportion of wind power and a large gap in the wind power resources distribution
[40]Scheduling optimizationTakes the influence of primary frequency regulation dead zone and amplitude limit into considerationDue to the highly nonlinearity of the constructed frequency security constraints, although the proposed algorithm can improve the quality of the optimized solution, it cannot guarantee that it is the optimal one
[48]Virtual inertia controlImproves the credibility of wind turbine inertia evaluation, proposes a virtual
inertia control strategy to meet the
frequency regulation requirements		Improves the credibility but does not propose an accurate method for evaluating the virtual inertia of wind turbines
[49]Virtual inertia controlIntroduces fuzzy control into virtual
inertia control for wind–thermal systems, enables wind turbines to supply inertia
under various operating conditions		As the proportion of wind power generation
increases in power systems, the secondary drop in frequency becomes increasingly severe
[53]Other methodsProposes a new equivalent inertia
probability evaluation method for power systems to effectively reflect the time-series change trend of the inertia		Ignores the impact of energy storage in power systems on the equivalent inertia evaluation
Table 2. UFLS and related information of some regions in the world.
Table 2. UFLS and related information of some regions in the world.
RegionSystem ScaleUFLS Threshold/HzMaximum Load/GWSecurity IndexTime Precision
TexasLarge interconnected system59.373RoCoFHour
South AustraliaLarge island47.63.4—Daily/Monthly
IrelandSmall island48.96.5 f nadir —
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Song, J.; Zhou, X.; Zhou, Z.; Wang, Y.; Wang, Y.; Wang, X. Review of Low Inertia in Power Systems Caused by High Proportion of Renewable Energy Grid Integration. Energies 2023, 16, 6042. https://doi.org/10.3390/en16166042

AMA Style

Song J, Zhou X, Zhou Z, Wang Y, Wang Y, Wang X. Review of Low Inertia in Power Systems Caused by High Proportion of Renewable Energy Grid Integration. Energies. 2023; 16(16):6042. https://doi.org/10.3390/en16166042

Chicago/Turabian Style

Song, Jiyu, Xinhang Zhou, Zhiquan Zhou, Yang Wang, Yifan Wang, and Xutao Wang. 2023. "Review of Low Inertia in Power Systems Caused by High Proportion of Renewable Energy Grid Integration" Energies 16, no. 16: 6042. https://doi.org/10.3390/en16166042

APA Style

Song, J., Zhou, X., Zhou, Z., Wang, Y., Wang, Y., & Wang, X. (2023). Review of Low Inertia in Power Systems Caused by High Proportion of Renewable Energy Grid Integration. Energies, 16(16), 6042. https://doi.org/10.3390/en16166042

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop