Next Article in Journal
Irradiation Analysis of Tensile Membrane Structures for Building-Integrated Photovoltaics
Next Article in Special Issue
Experimental Study on Macroscopic Spray and Fuel Film Characteristics of E40 in a Constant Volume Chamber
Previous Article in Journal
Effect of Microporous Layer Ink Homogenisation on the Through-Plane Gas Permeability of PEFC Porous Media
Previous Article in Special Issue
An Ab Initio RRKM-Based Master Equation Study for Kinetics of OH-Initiated Oxidation of 2-Methyltetrahydrofuran and Its Implications in Kinetic Modeling
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Energies
Volume 16
Issue 16
10.3390/en16165943
energies-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

A Theoretical Study of NH2 Radical Reactions with Propane and Its Kinetic Implications in NH3-Propane Blends’ Oxidation

by
Binod Raj Giri
1,*,
Krishna Prasad Shrestha
2,*,
Tam V.-T. Mai
3,4,
Sushant Giri
1,
Mohammad Adil
1,
R. Thirumaleswara Naik
1,5,
Fabian Mauss
6 and
Lam Kim Huynh
7,8,*
1
Clean Combustion Research Center, Physical Science and Engineering Division, King Abdullah University of Science and Technology (KAUST), Thuwal 23955-6900, Saudi Arabia
2
Physics and Chemistry of Materials, Theoretical Division, Los Alamos National Laboratory, Los Alamos, NM 87545, USA
3
Institute of Fundamental and Applied Sciences, Duy Tan University, 06 Tran Nhat Duat, Tan Dinh Ward, District 1, Ho Chi Minh City 70000, Vietnam
4
Faculty of Natural Sciences, Duy Tan University, Da Nang City 550000, Vietnam
5
Department of Mechanical Engineering, Indian Institute of Science, Bangalore 560001, India
6
Thermodynamics and Thermal Process Engineering, Brandenburg University of Technology, Siemens-Halske-Ring 8, 03046 Cottbus, Germany
7
School of Chemical and Environmental Engineering, International University, Quarter 6, Linh Trung Ward, Thu Duc City, Ho Chi Minh City 70000, Vietnam
8
Vietnam National University, Ho Chi Minh City 70000, Vietnam
*
Authors to whom correspondence should be addressed.
Energies 2023, 16(16), 5943; https://doi.org/10.3390/en16165943
Submission received: 9 June 2023 / Revised: 31 July 2023 / Accepted: 6 August 2023 / Published: 11 August 2023
(This article belongs to the Special Issue Low-Carbon Fuel Combustion from Fundamentals to Applications)
Browse Figures
Versions Notes

Abstract

:
The reaction of NH2 radicals with C3H8 is crucial for understanding the combustion behavior of NH3/C3H8 blends. In this study, we investigated the temperature dependence of the rate coefficients for the hydrogen abstraction reactions of C3H8 by NH2 radicals using high-level theoretical approaches. The potential energy surface was constructed at the CCSD(T)/cc-pV(T, Q)//M06-2X/aug-cc-pVTZ level of theory, and the rate coefficients were computed using conventional transition state theory, incorporating the corrections for quantum tunneling and hindered internal rotors (HIR). The computed rate coefficients showed a strong curvature in the Arrhenius behavior, capturing the experimental literature data well at low temperatures. However, at T > 1500 K, the theory severely overpredicted the experimental data. The available theoretical studies did not align with the experiment at high temperatures, and the possible reasons for this discrepancy are discussed. At 300 K, the reaction of NH2 with C3H8 predominantly occurs at the secondary C-H site, which accounts for approximately 95% of the total reaction flux. However, the hydrogen abstraction reaction at the primary C-H site becomes the dominant reaction above 1700 K. A composite kinetic model was built, which incorporated the computed rate coefficients for NH2 + C3H8 reactions. The importance of NH2 + C3H8 reactions in predicting the combustion behavior of NH3/C3H8 blends was demonstrated by kinetic modeling.

1. Introduction

Ammonia has recently gained worldwide attention as a future energy carrier, with the potential to combat global warming by decarbonizing the energy sectors. However, the direct use of ammonia as an energy source has several limitations, such as low laminar flame speed, high auto-ignition temperature, high heat of vaporization, narrow flammability limits (16–25% by volume in air), and high NOx emissions [1]. Some researchers have explored the direct application of neat ammonia in internal combustion engines [2,3]. However, due to its poor combustion characteristics, a dual-fuel approach has been widely suggested to achieve the desired physical and chemical properties of ammonia for its use in combustion devices [4,5,6,7,8,9,10,11,12,13].
Over the past few years, we have been exploring the combustion behavior of ammonia blended with reactive oxygenated fuels like dimethyl ether (DME) [10], diethyl ether (DEE) [8,12], dimethoxymethane (DMM) [7], methanol (CH3OH), and ethanol (C2H5OH) [14]. It is well-known that co-firing NH3 with these reactive fuels increases the system’s complexity. The fundamental understanding of the interaction chemistry between the carbon and nitrogen families is still in its infancy. It makes the accurate modeling of the combustion behavior of NH3 dual-fuel combustion far more complex. Recently, we studied the combustion behavior of the NH3/DEE blend over a wide range of experimental conditions [8,12]. Our findings revealed that the kinetic model can only accurately capture the low-temperature oxidation data by including cross-reactions between the carbon and nitrogen families. Our recent work on NH3/CH3OH/C2H5OH [14] led us to a similar conclusion. Therefore, the cross-chemistry between carbon and nitrogen chemistry is of utmost importance for accurately modeling NH3 dual-fuel combustion. Unfortunately, there is limited availability of experimental and theoretical studies targeting the cross-reactions between nitrogen and carbon species.
Only a limited number of studies exploring the combustion behavior of NH3 blended with higher hydrocarbons beyond methane exist in the literature. Liquefied petroleum gas (LPG) can also be a good candidate for enhancing the combustion behavior of ammonia. LPG is a mixture of hydrocarbon gases, specifically propane and butane, with a small quantity of olefins. Since propane (C3H8) is a major component of LPG [15], it can serve as a suitable surrogate fuel for LPG. In a recent study, Wang et al. [16] measured the laminar flame speed characteristics of various NH3/C3H8/air blends at an equivalence ratio (ϕ) of 0.6–1.4, a pressure of 1–5 bar and a temperature of 298 K. They used NH3/C3H8 blends with mole ratios of 20%, 50%, and 80% of C3H8. The authors observed a significant enhancement of the laminar flame speed of NH3 by adding C3H8. Further, they also tested five different kinetic models from the literature to predict the laminar flame speeds of NH3/C3H8 blends. They found significant differences in the performance of these kinetic models. In another study, Wang et al. [17] reached a similar conclusion after investigating the blending effects of C1-C4 n-alkanes in promoting the combustion characteristics of ammonia.
Similarly, Chen et al. [18] performed an experimental and kinetic modeling study on various NH3/C1-C3 alkanes/air flames. They investigated the effect of ozone addition on enhancing the laminar burning velocity of NH3 and NH3/C1-C3 alkane blends. They observed a significant increase in the laminar flame speed of NH3 by the addition of the hydrocarbons flames; however, 5000 ppm of ozone addition in the oxidizer stream did not significantly enhance the flame speed compared to the NH3/C1-C3 alkane blends. The kinetic models used by Wang et al. [16] and Chen et al. [18] to predict the laminar flame speed experimental trends omitted the cross-chemistry of the species derived from NH3 and C3H8. These models are not tested at low temperatures due to a lack of experimental data; however, one expects these models to fail as they do not contain the nitrogen and carbon cross-chemistry. Such cross-chemistry can be crucial for accurately predicting the combustion behavior of NH3/hydrocarbon blends. Therefore, having accurate knowledge of NH2 radicals reactions with C3H8 is critical to understand the oxidation behavior of NH3/C3H8 blends.
Several studies have been conducted in characterizing hydrogen abstraction reactions of C3H8 by NH2 radicals, experimentally [19,20,21,22] and theoretically [23,24,25]. The experimentally measured rate coefficients showed a strong curvature in the Arrhenius behavior. Such Arrhenius behavior is nicely captured by the theoretical predictions of Mebel and Lin [23] and Siddique et al. [25]. The theoretical predictions are within a factor of ~2 of the experimental data below 1080 K. An earlier report of the theoretical rate coefficients work from Siddique et al. [24] showed more significant deviations from the experimental data. Lowering the G2M barrier heights of NH2 + C3H8 reactions by 0.5 kcal, Mebel and Lin [23] obtained a better match with the experimental data in the 300–520 K temperature range [k(theory) = (0.94 − 1.25) k (experiment)]. Their G2M barrier heights were significantly higher than those of Siddique et al. [25] at the CBS-QB3 level of theory (8.4 vs. 7.1 and 11.1 vs. 9.2 kcal/mol for secondary and primary C-H sites of C3H8, respectively). This clearly indicates that the energetics of the reaction of NH2 with C3H8 show quantum method dependence. Interestingly, the theoretical predictions of the rate coefficients by Mebel and Lin [23] and Siddique et al. [25] severely overpredict the only available high-temperature shock tube data by Hennig and Wagner [19]. In the worst-case scenario, the mismatch is as high as a factor of 4.2. This warrants high-level theoretical work to resolve the existing discrepancy of the NH2 + C3H8 reaction.
The objective of this work is several-fold: (i) map out the potential surface energy using a high-level quantum method, e.g., CCSD(T)/cc-pV(T, Q)//M06-2X/aug-cc-pVTZ level of theory; (ii) handle the kinetics of NH2 radicals reactions with C3H8 appropriately, ensuring accurate rate coefficients and aiming to resolve the existing discrepancy in the literature; (iii) build a composite kinetic model incorporating the crucial cross-reactions between the nitrogen and carbon families; (iv) validate the kinetic model using available experimental literature data for neat C3H8, neat NH3, and various blends of NH3/C3H8 across a wide range of conditions; (v) as mentioned earlier, no literature data is available for the low-T oxidation kinetics of NH3/C3H8 blends. Therefore, we will employ our kinetic model to predict the low-T combustion behavior of NH3/C3H8 blends, such as ignition delay times. This will provide deeper insights into the role of cross-reactions between the nitrogen and carbon families, particularly their significance at low temperatures in influencing the fundamental combustion characteristics of NH3/hydrocarbon blends.

2. Computational Methods

Similar to our earlier work on NH2 + CH3OH/C2H5OH reactions [14], we optimized the geometry of all the stationary points for the NH2 + C3H8 reaction at the M06-2X//aug-cc-pVTZ level of theory. Our choice of the M06-2X level of theory is based on several earlier studies that reported the best suitability of the M06-2X//aug-cc-pVTZ level of theory for geometry optimizations, frequency calculations, and accurate energetics of many chemical systems [14,26,27,28,29,30,31,32]. We characterized the identity of each stationary point in the potential energy surface (PES) of the NH2 + C3H8 reaction through normal model analysis. We used a scaling factor of 0.971 to correct the harmonic vibrational frequencies obtained at the M06-2X//aug-cc-pVTZ level of theory [33]. The correction factor compensates for the deviation between the experimental and theoretical values of the vibrational frequencies. Scaled vibrational frequencies yielded zero-point corrected vibrational energies (ZPVE), eventually leading to zero-point corrected electronic energies. Additionally, at the same level of theory, we performed the IRC calculations [34,35] to map out the transition state, connecting the reactants and products appropriately. We used the lowest-lying conformers for the species involved to construct the potential energy surface and the subsequent kinetic analysis. We listed the optimized geometry and molecular parameters of all the stationary points in Tables S1 and S2 of the Supplementary Information (SI). For all the electronic structure calculations, we employed Gaussian09 Software [36].
For accurate energetic description, we utilized the computationally expensive coupled-cluster method with single and double excitations, including the perturbative treatment of triple excitations, CCSD(T) [37,38,39]. Notably, the CCSD(T) method represents the gold standard in quantum chemistry. We performed CCSD(T) calculations using Dunning’s correlation-consistent triple-ζ(cc-pVTZ) and quadruple-ζ(cc-pVQZ) basis sets and then extrapolated these energies to achieve CCSD(T) energies at the complete basis set (CBS) limit. We employed Halkier’s scheme [40] of two-point extrapolation. Thus, we can refer to the extrapolated CCSD(T) energies as CCSD(T)/cc-pV(T, Q)//M06-2X/aug-cc-pVTZ level of theory. All the values of our T1 diagnostics are less than 0.02, indicating that the single reference electronic structure method employed here is adequate for an accurate energetic description of the reaction of NH2 radicals with propane.
As we will demonstrate later, the reactions of NH2 radicals with C3H8 involve simple hydrogen abstractions occurring through distinct transition states (TS). Therefore, with reasonable accuracy, one can calculate the rate coefficients for the hydrogen abstraction reaction of C3H8 by NH2 using conventional transition state theory (TST). We employed multi-species multi-channel (MSMC) code [41,42] to compute the high-pressure limiting rate coefficients (k∞ (T)). We used one-dimensional (1D) asymmetrical potential for Eckart’s tunneling treatment. For accurate partition functions, we treated the low vibrational modes of C3H8, and the transition states as hindered internal rotors (HIR). Table S1 of Supplementary Information identifies these low vibrational modes as internal rotors in bold. Our previous work [43,44] describes the procedure of the HIR correction of the partition function. For HIR correction, we scanned the hindered rotor potential V(θ) as a function of the torsional angle (θ) along the single bonds (C-C bonds for C3H8 and C-C and C-N bonds of the TSs) using the M06-2X/cc-pVDZ level of theory via a relaxed potential energy scan with a step size of 10° in θ. We have compiled the hindered rotor potential V(θ) scans in Figure S1 of Supplementary Information.

3. Kinetic Modeling

Recently, we have developed a detailed kinetic model to accurately predict the oxidation kinetics of diethyl ether (DEE) and ammonia (NH3) blends and their interaction with NOx chemistry [12]. Over the past five years, we have progressively built and validated this hierarchical kinetic model for C1-C4 fuels, incorporating various experimental data across a wide range of conditions. Our kinetic model demonstrated satisfactory performance in capturing the oxidation behavior of C1-C2 hydrocarbon/oxygenated fuels and their interaction with NOx. Note that our kinetic model embodied the detailed NOx chemistry from our previous works [45,46], which showed remarkable performance for NOx modeling during the oxidation of hydrocarbons/oxygenates and their blends with NH3. However, our previous model [12] did not contain C3 hydrocarbons; particularly, propene (C3H6) and propane (C3H8) chemistry need to be included.
In this work, we have added the subset of C3 hydrocarbon chemistry (i.e., C3H6 and C3H8), aiming to characterize the combustion behavior of NH3/C3H8 blends reasonably. We adopted the subset of C3 hydrocarbon chemistry from the experimental and modeling work of Burke et al. [47,48], who validated C3H6 oxidation chemistry over a wide range of conditions. However, the authors did not test the predictive capabilities of their model for C3H8 oxidation. In this study, we first validated the kinetic model for neat NH3 and C3H8 experimental data before validating against the NH3/C3H8 blend. Our past experiences in modeling NH3-hydrocarbons/oxygenates duel-fuel combustion [7,8,9,12] indicated the importance of cross-reactions between the carbon and nitrogen families. Such interaction chemistry is critical to accurately model the combustion behavior of NH3 and hydrocarbons or oxygenated fuel blends. Therefore, our current model incorporates the reactions of NH2 radical with C3H8, which is one of the most critical reactions between the carbon and nitrogen families during the oxidation of NH3/C3H8 blends. As discussed earlier, we employed CCSD(T)/cc-pV(T, Q)//M06-2X/aug-cc-pVTZ level of theory combined with the transition state theory to compute the temperature dependence of the reaction rate coefficients of reaction (1) and reaction (2).
The NH2 radical can react with C3H8 to form n-propyl (NC3H7) or iso-propyl (IC3H7) radicals, Reaction (1) or reaction (2), respectively:
C3H8 + NH2 = NC3H7 + NH3
C3H8 + NH2 = IC3H7 + NH3
The hydrogen abstraction reactions of C3H8 by NO2 can also yield NC3H7 and IC3H7 radicals (Reactions (3)–(6)). The rate constants for these reactions are adopted from the theoretical work of Chai and Goldsmith [49].
C3H8 + NO2 = NC3H7 + HONO
C3H8 + NO2 = NC3H7 + HNO2
C3H8 + NO2 = IC3H7 + HONO
C3H8 + NO2 = IC3H7 + HNO2
NO is abundant under the combustion environment of NH3 and its blend with other fuels, verified by our previous study [12]. The reaction of NO with the peroxyl radicals (RO2) can significantly alter the low-temperature combustion behavior of the fuel [46]. Therefore, the reactions of NO with the peroxy radicals pertinent to NC3H7O2 and IC3H7O play a critical role in accurately predicting the low-T oxidation kinetics of NH3/C3H8 blends. Unfortunately, no experimental and/or theoretical data for these reactions are available in the literature. Consequently, we took CH3O2 + NO [50] as a reaction analogy to estimate the rate coefficients for Reactions (7) and (8).
NC3H7O2 + NO = NC3H7O + NO2
IC3H7O2 + NO = IC3H7O + NO2

4. Results and Discussion

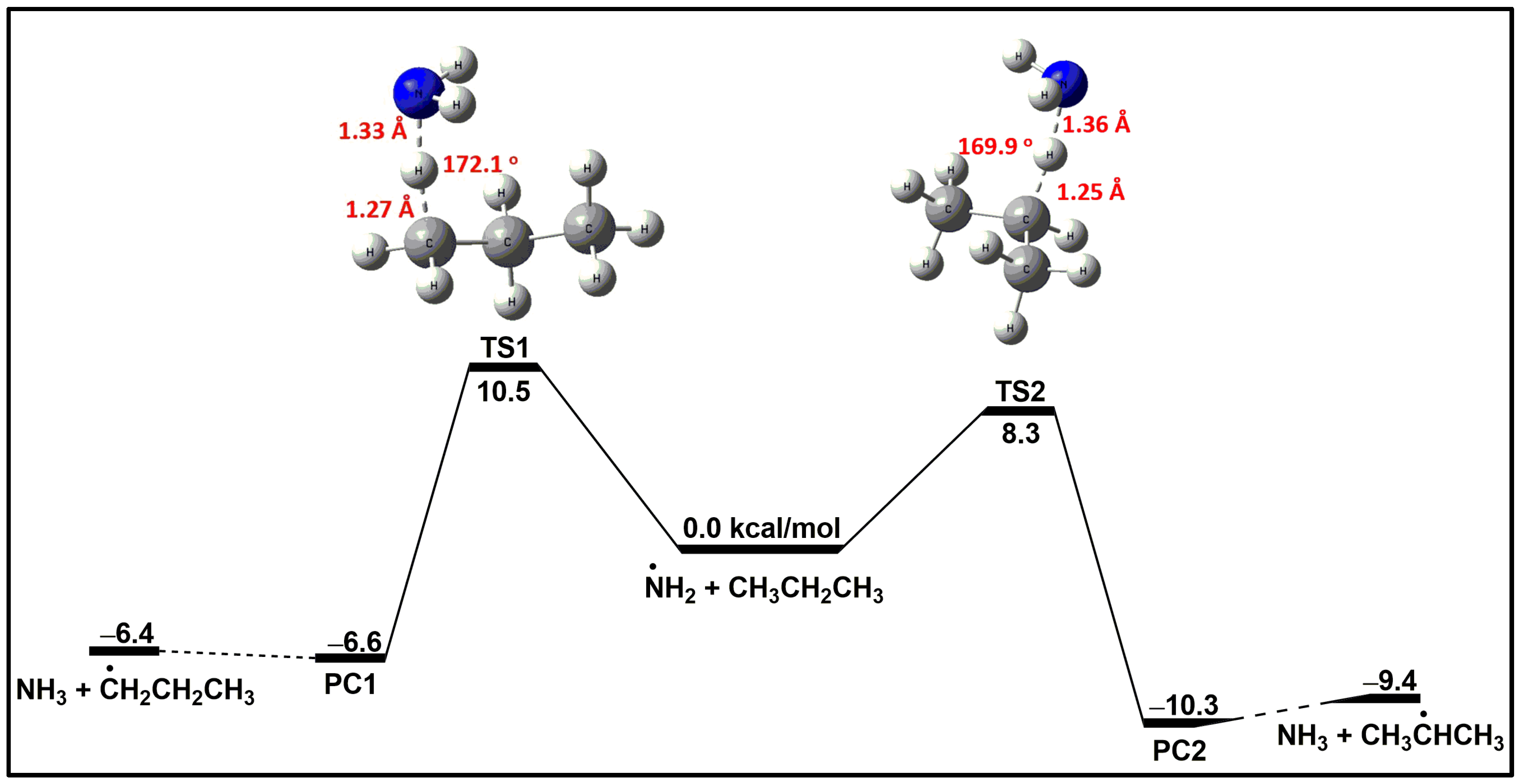
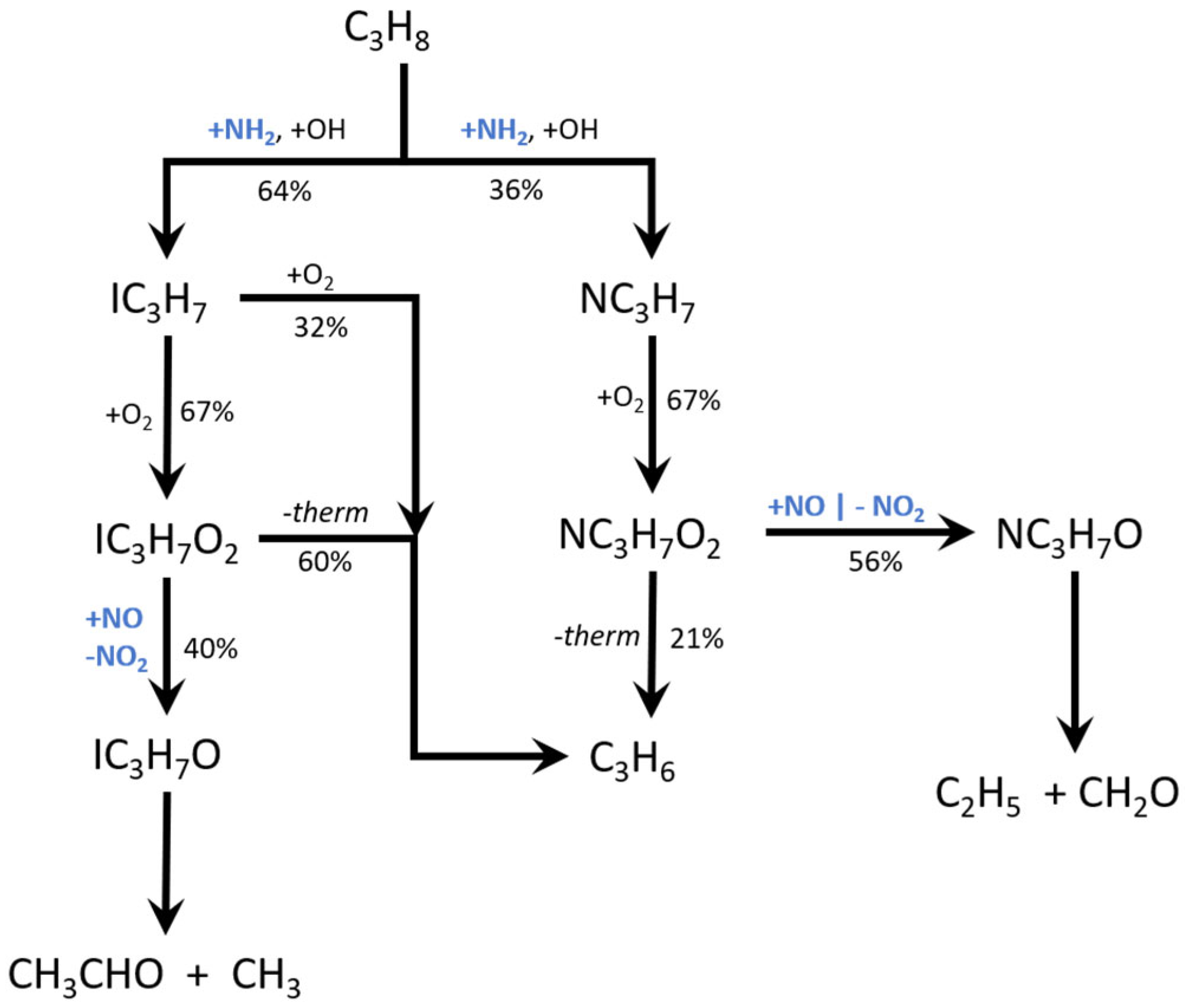
4.1. Potential Energy Surface (PES)

Figure 1 illustrates the potential energy surface (PES) of the reaction of NH2 radicals with C3H8. The reaction energetics were obtained using the CCSD(T)/cc-pV(T, Q)//M06-2X/aug-cc-pVTZ level of theory. As shown, the energy barrier (ΔE0≠) for the hydrogen abstraction reaction at the primary carbon site (-CH3), reaction (1), was 10.5 kcal/mol, which was 2.2 kcal/mol higher than that at the secondary carbon site (-CH2), i.e., reaction (2). The barrier heights for the reactions of NH2 radicals at the primary and secondary carbon sites of C3H8 nicely correlate with the reaction enthalpies (Δrxn, 0KH°) and bond dissociation energies according to the Evans–Polanyi principle. It is evident that reaction (1) was less exothermic than reaction (2) and occurred via a tighter transition state (ΔE0≠ of TS1 = 10.5 kcal/mol and imaginary frequency (νi) = 1701 cm−1 vs. ΔE0≠ = 8.3 kcal/mol and νi = 1603 cm−1 for TS2). Because both reactions were exothermic, TS1 and TS2 possessed reactant-like characters, revealing early transition states. The ratios of the breaking C….H bond (rC….H) to the forming H….N bond (rH….N), L = rC….H/rH….N, of TS1 and TS2 were 0.95 and 0.92, respectively. Again, these less than one L values indicate the early transition state. TS2 appeared to be closer to the reactants’ geometry; therefore, Reaction (2) traversing via TS2 was more exothermic (Δrxn, 0KH° = −9.4 kcal/mol vs. −6.4 kcal/mol). For both the transition states, the bond angle (δC…H….N) was almost collinear (see Figure 1).
Interestingly, we located the product complexes PC1 and PC2 for reaction (1) and reaction (2), respectively. However, these reaction complexes exhibited little binding energy (<1 kcal/mol), indicating their energy proximity to the corresponding products. Previous theoretical studies by Siddique et al. [24] and Mebel and Lin [23] did not indicate the existence of such complexes for the NH2 + n-alkanes/branched alkanes reactions. The reported values of the barrier heights in these works depict a significant discrepancy for both reactions, indicating the energetics of NH2 + C3H8 reactions exhibit strong dependence on the ab initio methods. For example, Mebel and Lin [23] reported barrier heights ranging from 11.1–11.6 kcal/mol and 13.3–15.5 kcal/mol for reaction (1) at the G2M and CCSD(T) based approaches, respectively. For reaction (2), the barrier heights ranged from 8.4–8.6 kcal/mol (G2M-based approaches) and 9.7–12.9 kcal/mol (CCSD(T) method). Based on the G2M energetics, their computed values of the rate coefficients showed a reasonable agreement with the experimental values below 1100 K. However, at high temperatures (T > 1500 K), the theoretical rate coefficients significantly overestimated (by a factor of 2.6–4.1) the experimental rate coefficients. By adjusting the G2M barrier height by 0.5 kcal/mol, the authors found a better agreement at low temperatures while worsening the scenarios at high temperatures. Siddique et al. [24] reported significantly lower barrier heights, e.g., 9.2 and 7.1 kcal/mol, for Reactions (1) and (2) in the CBS-QB3 composite method, respectively. One can observe a similar trend for higher alkanes + NH2 reactions. Siddique et al. [24] reported an overall mean unsigned deviation (MUD) of 2.3 kcal/mol for the barrier heights of NH2 + selected alkanes (C1-C4) reactions. Our values of the barrier heights at the CCSD(T)/cc-pV(T, Q)Z//M06-2X/aug-cc-pVTZ compare very well with those reported by Mebel and Lin [23] for the G2M methods within chemical accuracy (~1 kcal/mol). However, a larger deviation (~2 kcal/mol) was observed for the heat of reactions.

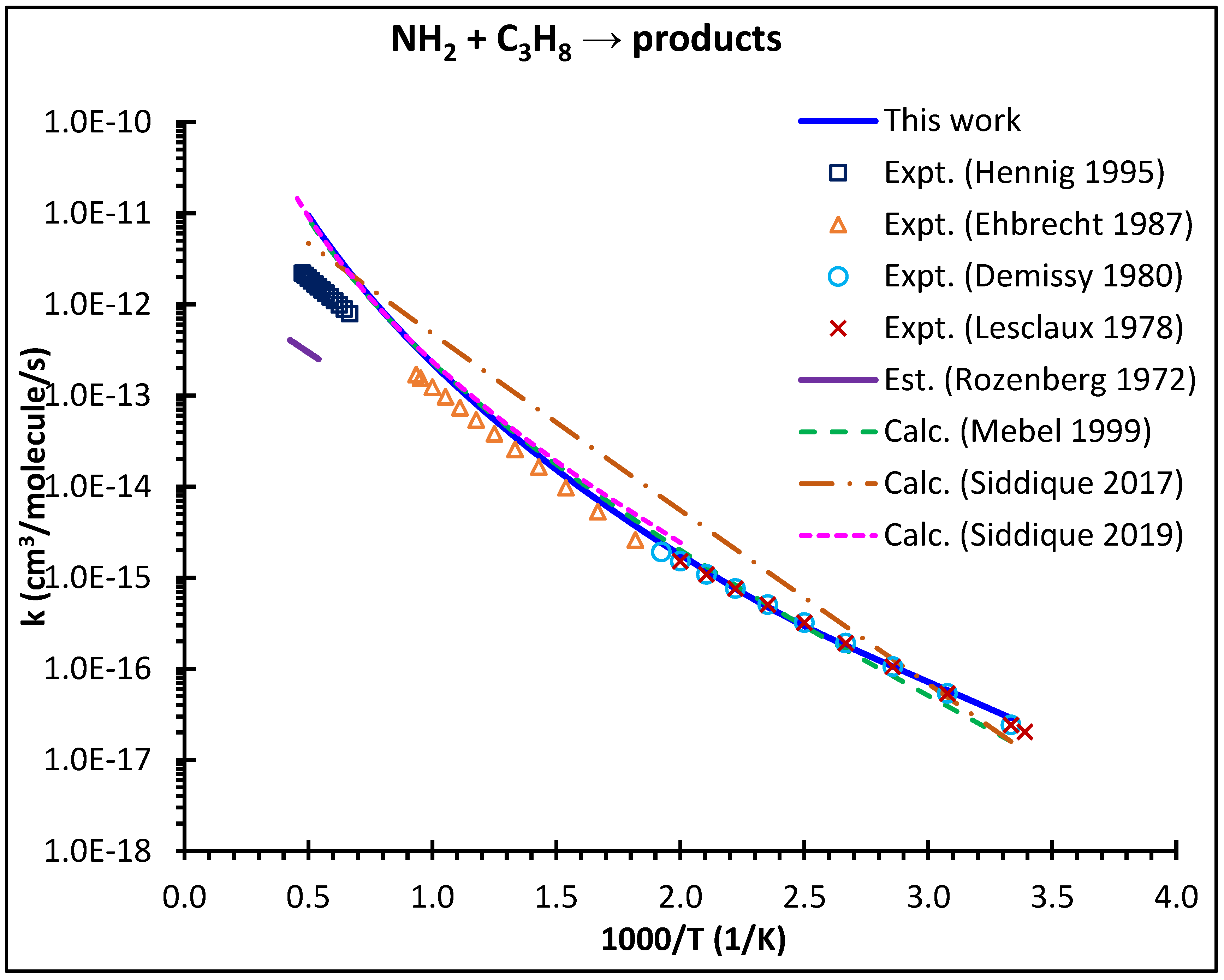
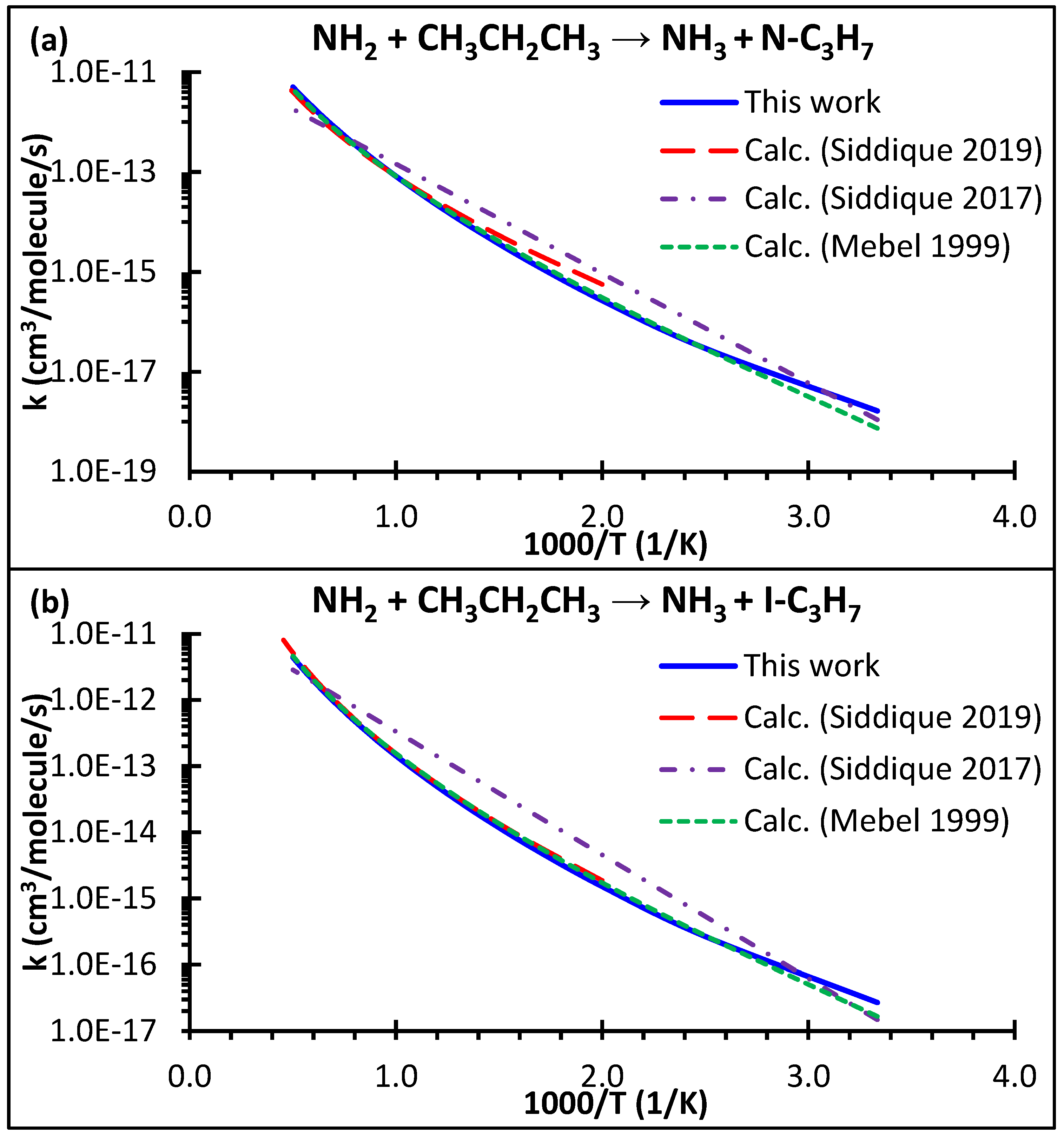
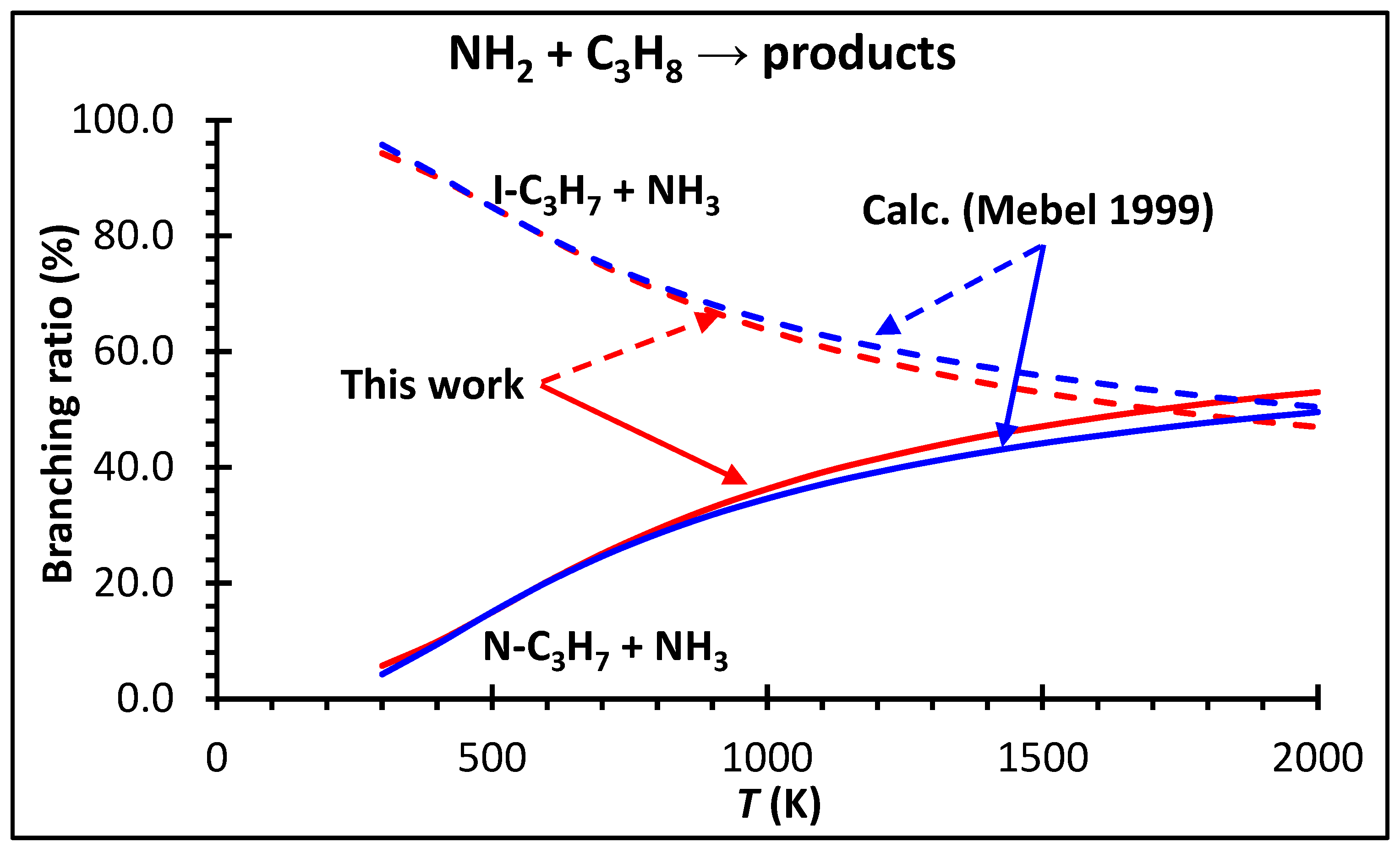
4.2. High-Pressure Limiting Rate Coefficients k∞ (T)

The computed PES revealed that the reaction of NH2 radicals with C3H8 is a simple type of hydrogen abstraction reaction (see Figure 1). The post-reaction complexes (PCs) had no kinetic relevance due to the shallow nature of the well. Their energies were very close to those of the dissociated fragments, i.e., final products. One can expect that their pressure stabilization was extremely difficult, even at very high pressures. Therefore, we handled the kinetics of the NH2 + C3H8 reaction using the conventional transition state rate theory (TST) with explicit corrections of quantum tunneling and hindered internal rotors. Figure 2 displays our computed values for the temperature dependence of the high-pressure limiting rate coefficients (k∞ (T)), whereas Figure 3a,b provide the individual rate coefficients for reactions (1) and (2), respectively. Table 1 further compiles the three-Arrhenius parameters obtained by fitting the computed rate coefficients over the 300–2000 K temperature range (see Table S3 for k∞ (T)).
Figure 2 compares our computed rate coefficients with the available literature data. Our theory excellently captures the experimental trends of the temperature dependence of the rate coefficients, with the exception of the high-temperature experimental data reported by Hennig and Wagner [19]. At high temperatures, our theoretical predictions of the rate coefficients are ~2.6–4.5 higher than the measurements of Hennig and Wagner [19]. Mebel and Lin [23] made a similar observation. As stated earlier, their theoretical predictions were 2.6–4.1 higher than the experimental values over the temperature range of 1500–1900 K. Along the same line, the theoretical rate coefficients reported by Siddique et al. [24,25] are significantly higher than the experimental data (see Figure 2). Noteworthy, our theoretical predictions of k∞ (T) excellently agree with the recent theoretical works of Mebel and Lin [23] and Siddique et al. [25]. However, Siddique et al. [24] earlier reports of the rate coefficients (derived using the CBS-QB3 and TST methods) showed a more significant deviation from the experimental literature data (see Figure 2). For example, their reported values lie within a factor of 0.17–0.69 of the experimental value over the temperature range of 300–500 K, whereas their values are higher by a factor of 3.8–4.4 in the intermediate temperatures (T = 500 − 1000 K). In their subsequent work, Siddique et al. [25] recalculated the rate coefficients based on the CBS-QB3 energies from their earlier work, which showed an excellent agreement with our work, including the one from Mebel and Lin [23] (see Figure 2). Not only for the total rate coefficients but also the individual rate coefficients for Reactions (1) and (2), we observed an excellent agreement with the earlier theoretical reports from Mebel and Lin [23] and Siddique et al. [25] (see illustration in Figure 3a,b). Note that the green lines in Figure 2 and Figure 3 represent the rate coefficients calculated by Mebel and Lin [23] with the adjustment of G2M barrier heights by 0.5 kcal/mole lower for both reactions, including Eckart tunneling correction.
As shown in Figure 2, our theory remarkably predicts the experimental values of the rate coefficients reported by Demissy et al. [22] and Lesclaux et al. [21] at low temperatures (T = 300–520 K). For example, at 300 K, our value of the theoretical rate coefficient of 2.89 × 10−17 cm3/molecule/s excellently matches the experimental value of 2.7 × 10−17 cm3/molecule/s reported by Demissy et al. [22] and Lesclaux et al. [21]. This shows that quantum tunneling is important for predicting reliable rate coefficients at low temperatures. This is particularly true for the type of reactions being dealt with here. For such reactions, the light hydrogen atom between the two heavy moieties can easily penetrate the classically forbidden potential energy barrier, increasing the rate coefficients significantly at low temperatures. Therefore, tunneling is a quantum mechanical effect, and its correction depends upon several factors, e.g., potential barrier height, shape of the barrier, reduced mass of the system, and imaginary frequency of the transition state. Vandeputte et al. [52] theoretically studied the effect of hindered internal rotation and quantum tunneling on the rate coefficients of 21 hydrogen abstraction reactions by methyl radicals. The authors have nicely demonstrated the effect of quantum tunneling on the activation energy (Ea and pre-exponential factor (A). Quantum tunneling has a pronounced effect on Ea; its effect on Ea decreases with increasing temperature. At low temperatures, the tunneling correction has a significant impact on logA. As temperature increases, the effect of quantum tunneling on logA diminishes rapidly. At 300 K, we find that quantum tunneling increased the rate coefficients by 36.8 and 18.5 fold for Reactions (1) and (2), respectively. At 500 K, the quantum tunneling factor is ca. 3 for both reactions. Our calculations show large imaginary frequencies υ‡ (TS1) = 1700.9 cm−1 and υ‡ (TS2) = 1603 cm−1 corresponding to Reactions (1) and (2), respectively. The large imaginary frequency hints to a small barrier width of a reaction, resulting in pronounced quantum tunneling. Our observation of the large quantum tunneling correction is not surprising. Above 1500 K, the contribution of quantum tunneling to the predicted rate coefficients was insignificant (see Table S4). Quantum tunneling has a more pronounced effect on the rate coefficients than the hindered internal rotor (HIR) corrections at low temperatures. We find that HIR corrections had a subtle effect on the rate coefficients at low temperatures (see Figure S2 and Table S5 of Supplementary Information). For example, HIR correction increased the rate coefficients by a factor of ~1.6 at 300 K. Above 1000 K, the rate coefficients could be reliably obtained with rigid rotor–harmonic oscillator (RRHO) approximation; i.e., RRHO and HIR treatment yields no difference in the calculated values of rate coefficient at high temperatures. Vandeputte et al. [52] illustrated how HIR treatment influences both Ea and A factors. They showed that the change in A due to HIR treatment is more significant than that of Ea. At low temperatures, our values of rate coefficients compare with the experimental data better than those of Mebel and Lin [23] (see Figure 2). Here, differences in the theoretical rate coefficients appeared to be originated from RRHO and HIR treatment of the low-frequency modes. Noteworthily, we appropriately treated some low-frequency modes as HIRs to calculate the partition functions accurately.
There are a few important points to consider. First, the reaction of NH2 radicals with C3H8 shows a strong curvature in the Arrhenius behavior. Several factors cause such Arrhenius behavior: (i) strong quantum tunneling and HIR effects at low temperatures, as discussed above; (ii) the temperature dependence of the pre-exponential factor; (iii) the channel switching of the competing reactions, (1) and (2). The reaction of NH2 radicals with C3H8 goes exclusively via reaction (2) below ambient temperature (branching ratio of ~95% at 300 K). In contrast, both reactions contributed equally at 1700 K. Beyond 1700 K, Reaction (1) took over (see Figure 4). Our predictions of the branching ratios nicely resonate with the theoretical predictions from Mebel and Lin [23] (see Figure 4) and Siddique et al. [25] (not shown in Figure 4). Second, our theoretical predictions of the rate coefficients, are like those of Mebel and Lin [23] (see Figure 4) and Siddique et al. [25], which nicely follow the experimental trends of the rate coefficients reported by Ehbrecht et al. [20] in the intermediate T-range (550 ≤ T/K ≤ 1073). The theory overpredicts the experimental kinetic data of Ehbrecht et al. [20] by a factor of ~2 only at the high-temperature end. Third, as seen in Figure 2, all theories severely overpredict the only available high-T experimental data of Hennig and Wagner [19]. The rate coefficient estimates from Rozenberg and Voronkov [51] are far too low. The observed differences between the theoretical and Hennig and Wagner’s experimental rate coefficients [19] at high temperatures urge a closer look.
Surprisingly, and not only in the NH2 + C3H8 reaction, the theoretical and high-T shock tube data from Henning and Wagner [19] also show a large difference to NH2 + CH4/C2H6 reactions (see Mebel and Lin [23]). The theory significantly overpredicts experimentally measured rate coefficients by Henning and Wagner [19] for high temperatures of NH2 + C1-C3 alkane reactions. However, the theoretical predictions agree quite nicely with the experimental data of Wagner and co-workers in the intermediate T-range (T = 400–1080 K). This warrants a closer look into the high-T kinetic measurements of Hennig and Wagner [19]. The authors investigated the reactions of NH2 radicals with C1-C3 alkanes in the temperature range of 1500 K to 2100 K. Using a narrow line laser-absorption technique, and the authors monitored NH2 radicals at 597.375 nm behind incident shock waves. In their experiments, the authors observed an overwhelmingly large concentration of hydrocarbons (0.2–2.1%) compared to 15–80 ppm of N2H4 (NH2 radical precursor) so that the decay of NH2 radicals follows the first-order kinetics. They extracted the rate coefficients of the reactions of NH2 with alkanes from the pseudo-first-order approximation of NH2(t) decay profiles, assuming that the secondary chemistry is unimportant. We believe the secondary chemistry severely compromised their extracted rate coefficients. One can expect a significant loss of the hydrocarbon reactant in their experimental time scale of a few tens of microseconds. For example, we obtained a 1/e decay period (τ1/e) of ≈ 3 μs for the unimolecular decomposition of C3H8 at 1600 K (k(C3H8 → CH3 + C2H5) = 3.2 × 105 s−1 [53]). In such cases, one should obtain the rate coefficients through detailed kinetic modeling of the measured NH2(t) profiles. In addition, one can also argue that the measured NH2(t) profiles at 597.375 nm may have been obscured spectroscopically by interfering intermediate/product species resulting in the slowdown of NH2(t) decay profiles. However, we cannot confirm this claim of any other species interfering with the absorption of NH2 radicals at 597.37 nm. We believe additional experimental studies targeting the reactions of NH2 radicals with alkanes at high-T will help resolve the existing discrepancy.

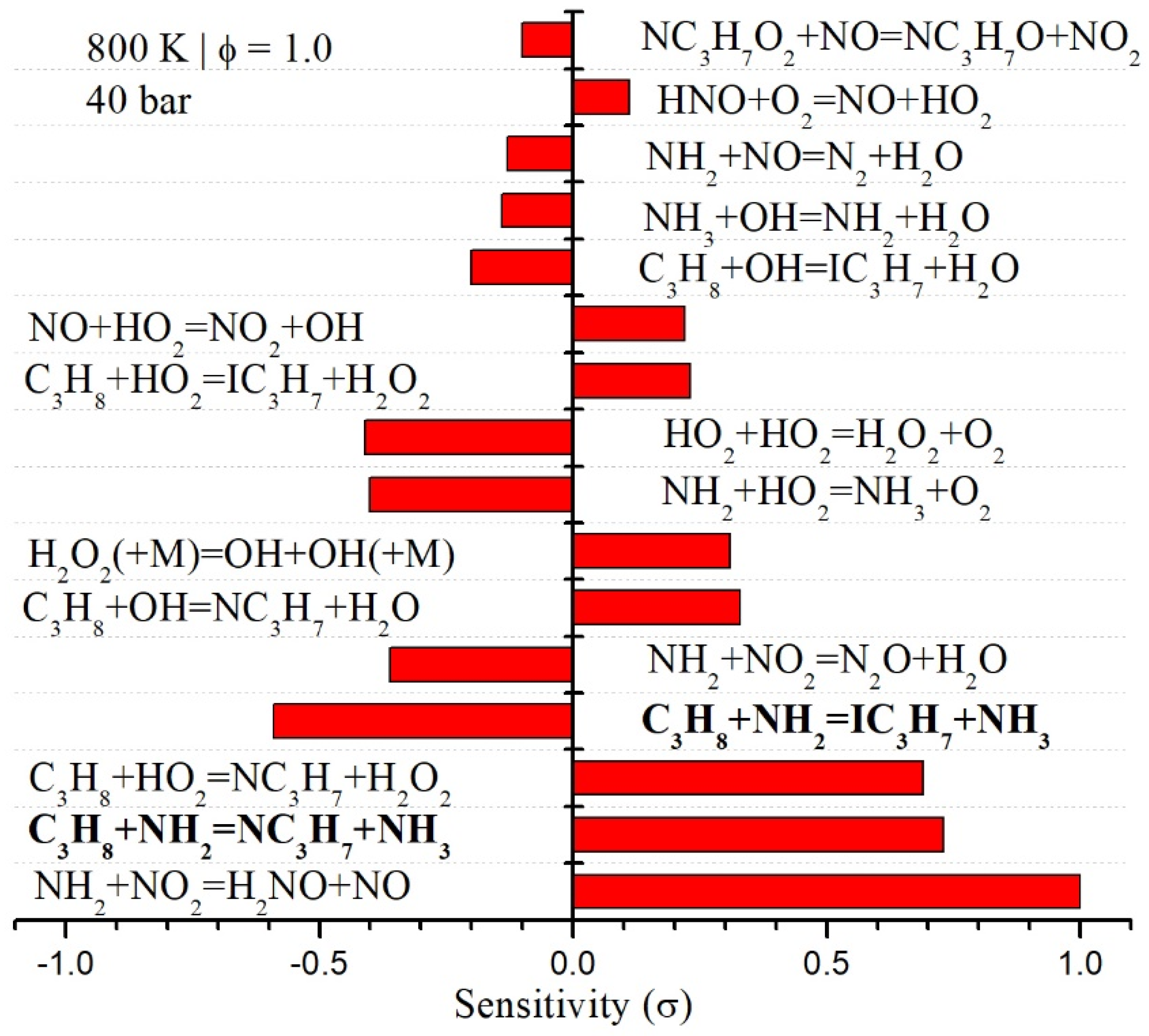
4.3. Kinetic Modeling Implications

As discussed in Section 3, we have developed a composite kinetic model comprising C3 hydrocarbons and NH3 subset chemistry. The developed model has also accommodated essential cross-chemistry between nitrogen and carbon families. In particular, our model has incorporated new rate data for the critical cross-reactions between NH2 radicals and C3H8 obtained in this work using a high level of theory (see discussion above). By incorporating these critical updates of the reaction rate parameters, we will demonstrate the performance of our kinetic model against various experimental targets below.

4.3.1. Laminar Flame Speed

Figure 5 illustrates the predictive capability of our kinetic model against the available literature laminar flame speed (LFS) data for various NH3/C3H8/air blends at 1 bar and 298 K. In Figure 5, the symbols represent the experimental literature data from the recent works of Wang et al. [16] and Chen et al. [18]. The solid and dashed lines correspond to the model predictions from this work. The solid lines depict the modeling results of the complete kinetic mechanism, which includes the cross-reactions between C3H8, and nitrogen chemistry discussed in Section 3. The dashed lines represent the modeling results without considering the cross-reactions between the nitrogen and carbon families. The solid and dashed lines overlap, revealing that the cross-chemistry between the nitrogen and carbon families has minimal influence on accurately predicting the LFS. These results indicate that cross-reactions do not govern the oxidation kinetics of NH3/hydrocarbon blends at high temperatures.
In Figure 5a, we demonstrate a remarkable performance of our kinetic model capturing the ϕ-dependence of the experimental LFS data for different NH3/C3H8 blends. However, for neat C3H8, we observed a little discrepancy. Our model slightly underpredicts the Chen et al. [18] LFS data for the equivalent ratios (ϕ) between 0.9 and 1. We further compared our model predictions against a large pool of the experimental literature data (see Figure S3 of Supplementary Information). The experimental data showed a large scatter around the stoichiometric C3H8/air mixtures. Overall, our model performed well, capturing the observed trends of the ϕ-dependence of most LFS experimental literature data for C3H8/air mixtures. Similarly, Figure 5b plots the LFS data as a function of C3H8 content from 0–100% in the NH3/C3H8 blend. We can observe that with an increase in the C3H8 in a blend, LFS increases. For instance, LFS increased by a factor of 2 and 3, respectively, for 10% and 20% of C3H8 compared to neat NH3 at ϕ = 1.0 and 298 K. For 30% and 40% of C3H8, in the blends, the LFS increased only by a factor of 3.46 and 3.87, respectively. The blend had a steeper gradient of up to 20% of C3H8. The trend was somewhat linear beyond 20% of C3H8 in the mixture. Such a trend indicates that the LFS shows high sensitivity at a low C3H8 mole fraction compared to high C3H8 content in the NH3/C3H8 blends. The model-predicted adiabatic flame temperature and the maximum mole fraction of the key radicals (OH, H, and O) further justify the observed trends of the LFS data (see Figure S4 in Supplementary Information). With an increase in C3H8 content, one can observe a more significant discrepancy between the experimental data of Chen et al. [18] and Wang et al. [16]. Our model shows a better agreement with the measurements of Wang et al. [16] for all NH3/C3H8 blends ( χ C 3 H 8 = 0–100%, χ C 3 H 8 = C 3 H 8 N H 3 + C 3 H 8   ×   100 % ). Further model validations are shown in Figures S5 and S6 for different conditions.

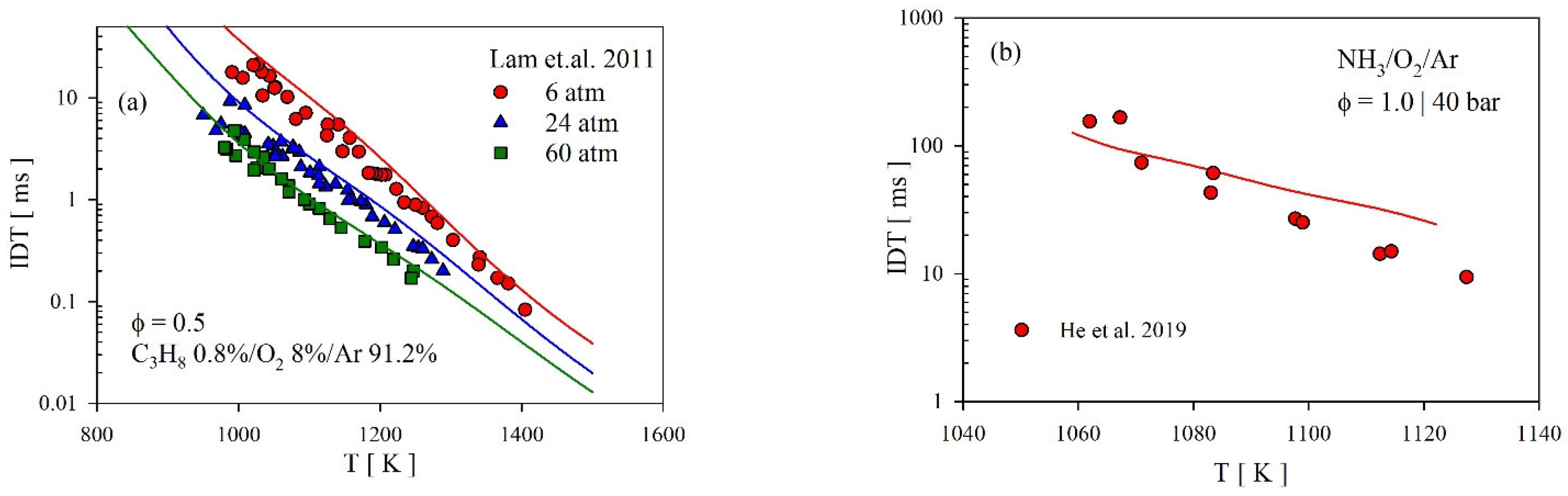
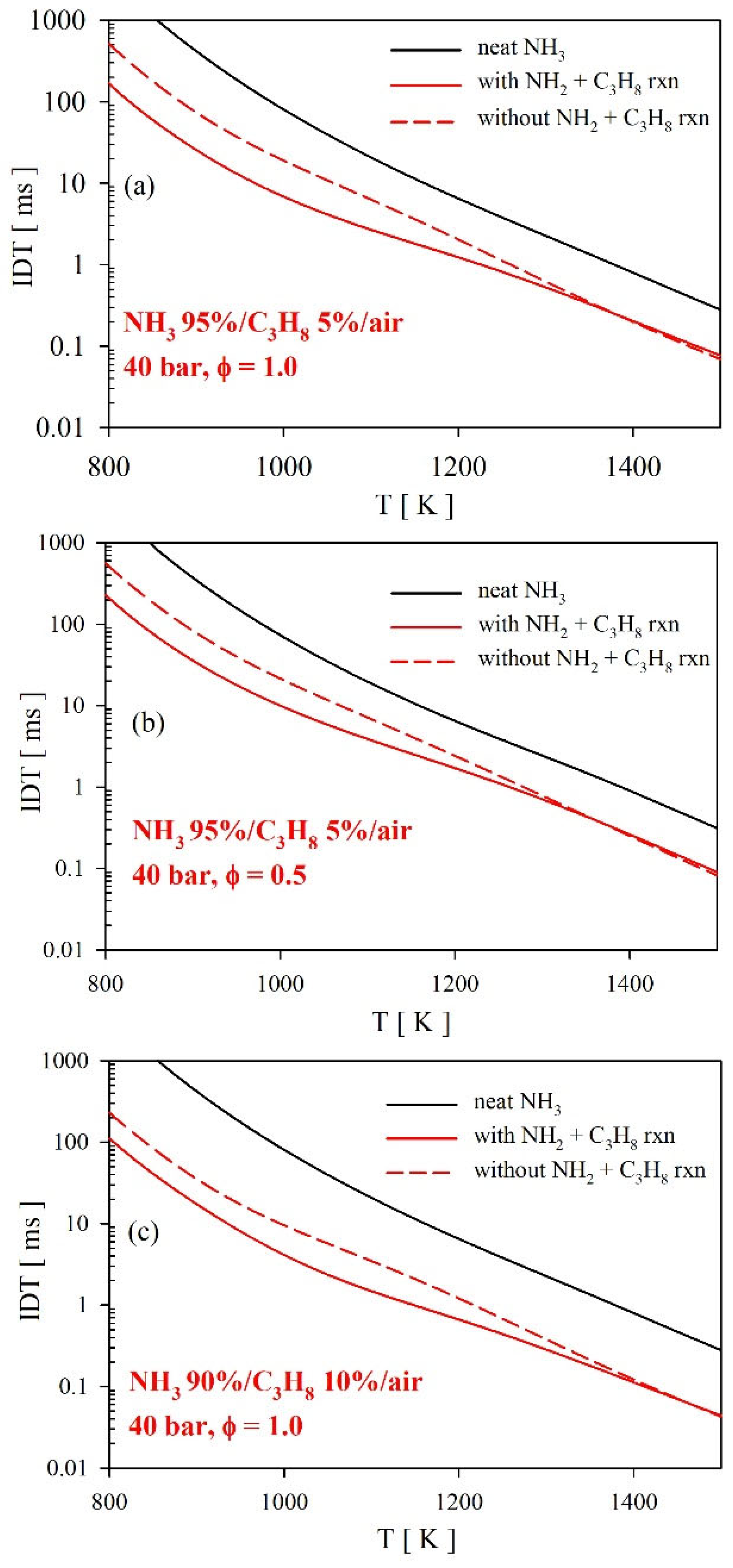
4.3.2. Ignition Delay Time (IDT)

To the best of our knowledge, there are no existing reports in the literature regarding the experimental data for ignition delay times (IDTs) of NH3/C3H8 blends. Therefore, our initial validation process involved confirming the accuracy of our kinetic model by comparing it with IDTs obtained for neat C3H8 and NH3. Validation of the kinetic model against the neat fuels is the only reliable approach in the absence of experimental data for the NH3/C3H8 fuel blend. Subsequently, we conducted a numerical investigation to explore the IDT behavior of NH3/C3H8 blends. Figure 6 displays the predictive capabilities of our kinetic model. The symbols represent experimental IDT data from Lam et al. [54] for C3H8/O2/Ar at ϕ = 0.5 and 6–60 atm (Figure 6a) and NH3/O2/Ar at ϕ = 0.5 and 40 bar from He et al. [55] (Figure 6b). The lines are the model predictions from this work. As seen in Figure 6a, our model remarkably captured IDT’s pressure and temperature dependence for neat C3H8. Likewise, our model effectively predicted the experimental IDT trend of pure NH3 (see Figure 6b). We refer readers to our earlier works [10,12] for further model validations of neat ammonia at other conditions. Overall, our model performed remarkably well in capturing the IDT behavior of neat ammonia. However, it tended to overpredict the IDT of pure NH3 at temperatures higher than 1100 K. At present, we do not want to optimize the kinetic model further to improve its predictive capabilities at high temperatures. However, our model remarkably captured the experimental literature data for the laminar flame speed (Figures S5 and S6 in Supplementary Materials and Figure 5) of various NH3/C3H8 blends. Note that laminar flame speed is driven by high-temperature chemistry.
Figure 7 illustrates the effect of NH2 + C3H8 reactions in predicting the IDT behavior of NH3/C3H8/air blends. It shows a case example for 95%NH3/5%C3H8 (Figure 7a,b) and 90%NH3/10%C3H8 (Figure 7c) blends at 40 bar, ϕ = 1.0 and 0.5. In Figure 7a–c, solid black lines represent the model-predicted IDT for neat NH3. In contrast, the red solid and dashed lines show the IDT predictions, including and excluding NH2 + C3H8 reactions, respectively, in our kinetic model. Unlike the case in the laminar flame speed (see Figure 5), the low-temperature oxidation kinetics of NH3/C3H8 blends were significantly affected by the cross-reaction of NH2 with C3H8. This reaction largely influenced the model prediction by yielding shorter IDTs below 1250 K. Above 1250 K, the NH2 + C3H8 reactions had no significant influence on the model prediction. This observation aligns very well with the model predictions for the laminar flame speed (see Figure 5). The cross-reaction between the nitrogen and carbon families is critical in accurately predicting the combustion behavior of NH3/C3H8 blends at low temperatures.
The IDT predictions for 95%NH3/5%C3H8 were three times shorter (~516 ms vs. 167 ms) with the inclusion of the NH2 + C3H8 reaction at ϕ = 1.0 and 800 K (see Figure 7a). At ϕ = 1.0 and around 1000 K, the IDTs were ~2.8 times shorter, which was about the same as that of the 95%NH3/5%C3H8 blend at ϕ = 0.5 and 800 K (see Figure 7b; the IDTs were shorter by a factor of 2.5 with the inclusion of the NH2 + C3H8 reaction). However, for the 90% NH3/10% C3H8 blend at ϕ = 1.0 and 800 K (see Figure 7c), including the NH2 + C3H8 reaction shortened the IDTs by only a factor of ~2. This indicates that the NH2 + C3H8 reaction significantly impacted the model predictions at low concentrations of C3H8 in the blend, and the sensitivity decreased with the increase of C3H8. This can be partly explained by the fact that with increasing C3H8 concentration, NH2 radicals become less available for reaction. Furthermore, the impact was less pronounced for lean conditions than stoichiometric conditions.
Figure 8 displays the 16 top most sensitive reactions towards IDT at ϕ = 1.0, 800 K, and 40 bar. Positive sensitivity indicates that the reaction enhanced the system reactivity, while negative sensitivity implies the opposite. It is evident that the NH2 + C3H8 reactions were the second and fourth most sensitive reactions influencing the IDTs of model predictions. Interestingly, reaction (1) (NH2 + C3H8 = NC3H7 + NH3) enhanced the system reactivity by shortening the IDTs, whereas reaction (2) (NH2 + C3H8 = IC3H7 + NH3) inhibited it by prolonging the IDT behavior of NH3/C3H8 blends. The reactions of OH radicals with C3H8 exhibited similar behavior.
To obtain further insight into the kinetics, we performed the reaction flux analysis at 800 K, 40 bar and ϕ = 1.0 for 95% NH3/5%C3H8/air blend. Figure 9 shows the results for the major paths only. The reaction pathways indicated by the blue color highlight the interaction between nitrogen and carbon chemistry. As seen, C3H8 was mainly consumed by NH2 and OH radicals yielding IC3H7 and NC3H7. The formed IC3H7 and NC3H7 reacted with O2, forming IC3H7O2 and NC3H7O2, respectively. IC3H7 also reacted with O2 to yield C3H6 + HO2, while NC3H7 underwent unimolecular decomposition to produce C2H4 + CH3 (not shown here). The formed peroxide IC3H7O2 and NC3H7O2 reacted with NO to give IC3H7O and NC3H7O, respectively. Both of these reactions yielded NO2, which reacted with the H-atom, producing NO + OH. This recycled NO and produced OH, which is a highly reactive radical. This NO2↔NO looping promotes the system reactivity. However, the NO + HO2 = NO2 + OH reaction is the main initiation pathway. Within the NH3 chemistry, NO is mainly formed via NH2 → H2NO → HNO route. The formed NO reacts with less reactive HO2 to yield a highly reactive OH radical (NO + HO2 = NO2 + OH). HO2 is known as a very important chain carrier at low and intermediate temperatures. Therefore, IC3H7O2/NC3H7O2 + NO = IC3H7O/NC3H7O + NO2, NO + HO2 = NO2 + OH and NO2 + H = NO + OH reactions manifest into an auto-catalytic system, giving rise to NO↔NO2 looping.
Figure 10 plots the mole fraction time histories of some important species. These plots further reinforce the importance of cross-reactions influencing the reactivity of NH3–propane blend. As seen, the fuels (NH3 (Figure 10a) and C3H8 (Figure 10e)) were consumed earlier with the inclusion of cross-reactions. Both the OH (Figure 10b) and HO2 (Figure 10f) radicals appeared early in the reaction system when cross-reactions were included. Interesting to note here is the evolution of NO (Figure 10d) and NO2 (Figure 10h) species. NO2 started to evolve at early reaction time, while NO did not appear until ~160 ms. At ~160 ms, NO2 was readily consumed, forming NO. The NO↔NO2 looping was mainly governed by the reactions indicated above.
At high temperatures, our model suggests that C3H8 mainly reacted with NH2 to yield IC3H7 and NC3H7 with a minor contribution from the abstraction reactions by OH and H species (not shown here). In contrast to reactions at low temperatures, the reactions of IC3H7 and NC3H7 with O2 were unimportant at high temperatures. Needless to say, the reactions of NO with peroxy radicals (IC3H7O2/NC3H7O2) did not occur at high temperatures. Therefore, NO↔NO2 looping reactions were suppressed (see species profile shown in the Figure S7 of the Supplementary Materials). As seen, NH3 consumption occurred at the same time for both cases (with and without nitrogen and carbon cross-chemistry). Figure S8 displays the heat release rate at 800 K and 1400 K. These results again demonstrate the importance of cross-reactions for blends, which is particularly true at low temperature. Therefore, we conclude that the reactions of NH2 radicals with C3H8 are inevitable in accurately modeling the low-temperature oxidation of NH3/C3H8 fuel blends. Our previous studies also observed similar effects with other fuel blends [10,12,14]. Considering these facts, the observations made here for NH3–propane blends are not too surprising. Again, we note that the importance of cross-reactions between carbon and nitrogen families has not been reported in earlier studies for NH3/C3H8 blends. This is the first study to recognize the importance of the title reactions for modeling NH3/C3H8 blends.

5. Conclusions

We conducted a theoretical investigation of the reactions between NH2 radicals and C3H8 using a high-level ab initio method (CCSD(T)/cc-pV(T, Q)Z//M06-2X/aug-cc-pVTZ level of theory) as well as conventional transition state theory (TST) methods. We demonstrated the kinetic implications of the NH2 + C3H8 reaction in the combustion of NH3-C3H8 dual-fuel blends. Some of the key points are summarized below.
  • The energetics of the NH2 + C3H8 reaction show strong quantum method dependence. Our quantum approach at the CCSD(T)/cc-pV(T, Q)Z//M06-2X/aug-cc-pVTZ level of theory yielded barrier heights of 10.5 and 8.3 kcal/mol for Reactions (1) and (2), respectively. These barrier height values closely match those of the G2M approaches reported by Mebel and Lin [23].
  • Our theory nicely captured the severely curved Arrhenius behavior shown by the experimental literature data. Quantum tunneling and hindered internal rotors corrections are crucial in capturing the experimental rate coefficients at low temperatures.
  • Our theoretical predictions of the rate coefficients excellently matched with those of earlier theoretical studies from Mebel and Lin [23] and Siddique et al. [25]. However, all theories severely overpredict the experimental data of Hennig and Wagner [19] at high temperatures. It appears that the reported high-T kinetic data by Hennig and Wagner [19] are affected by the significant loss of the hydrocarbon reactants such that a simple first-order analysis to extract the rate coefficient is not applicable in their case.
  • Over the temperature range of 300–2000 K, our theoretical rate coefficients can be given by the following Arrhenius expressions in units of cm3/molecule/s:
k1(T) = 2.19 × 10−26 × T4.52 × exp(−2346.7 K/T)
k2 (T) = 1.35 × 10−24 × T3.91 × exp(−1684.0 K/T)
ktotal(T) = 4.00 × 10−26 × T4.47 × exp(−1566.5 K/T)
5.
We developed a composite kinetic model consisting of NH3 and C3H8 subset chemistries. We incorporated the cross-reactions between the nitrogen and carbon families. Additionally, we updated the rate parameters for the reactions of NH2 radicals with C3H8, as determined in this study. To validate our kinetic model, we compared it against available literature data for the oxidation kinetics of neat C3H8, NH3, and NH3/C3H8 blends across various conditions. Our kinetics model remarkably captured the observed trends of the low- and high-temperature experimental literature data.
6.
The reactions of NH2 radicals with C3H8 significantly affected the low-temperature oxidation behavior of NH3/C3H8 blends. We found that the predicted ignition delay times were shortened considerably by including the NH2 + C3H8 reaction. For instance, at ϕ = 1.0 and 800 K for the 95%NH3/5%C3H8 blend, the model predicted ignition delay time was ~ three times shorter with NH2 + C3H8 reactions compared to when these reactions were excluded. Furthermore, we found that the NH2 + C3H8 reactions did not impact the high-temperature chemistry, as observed for the laminar flame speed of NH3/C3H8 blends.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/en16165943/s1.

Author Contributions

Validation, B.R.G. and K.P.S.; Formal analysis, S.G., B.R.G., T.V.-T.M., M.A. and R.T.N.; Investigation, B.R.G. and K.P.S.; Resources, L.K.H. and F.M.; Writing—original draft, B.R.G.; Writing—review & editing, B.R.G., L.K.H. and K.P.S.; Supervision, B.R.G. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no other funding then mentioned in acknowledgments.

Acknowledgments

The authors are thankful to the Office of Sponsored Research at King Abdullah University of Science and Technology (KAUST) for funding the research reported in this publication. We are also thankful to Vietnam National University HoChiMinh City (VNU-HCM) under grant number 562-2023-28-01.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Zamfirescu, C.; Dincer, I. Ammonia as a green fuel and hydrogen source for vehicular applications. Fuel Process. Technol. 2009, 90, 729–737. [Google Scholar] [CrossRef]
  2. Mercier, A.; Mounaïm-Rousselle, C.; Brequigny, P.; Bouriot, J.; Dumand, C. Improvement of SI engine combustion with ammonia as fuel: Effect of ammonia dissociation prior to combustion. Fuel Commun. 2022, 11, 100058. [Google Scholar] [CrossRef]
  3. Mounaïm-Rousselle, C.; Mercier, A.; Brequigny, P.; Dumand, C.; Bouriot, J.; Houillé, S. Performance of ammonia fuel in a spark assisted compression Ignition engine. Int. J. Engine Res. 2022, 23, 781–792. [Google Scholar] [CrossRef]
  4. Mørch, C.S.; Bjerre, A.; Gøttrup, M.P.; Sorenson, S.C.; Schramm, J. Ammonia/hydrogen mixtures in an SI-engine: Engine performance and analysis of a proposed fuel system. Fuel 2011, 90, 854–864. [Google Scholar] [CrossRef]
  5. Reiter, A.J.; Kong, S.C. Combustion and emissions characteristics of compression-ignition engine using dual ammonia-diesel system. Fuel 2011, 90, 854–864. [Google Scholar] [CrossRef] [Green Version]
  6. Dai, L.; Gersen, S.; Glarborg, P.; Mokhov, A.; Levinsky, H. Autoignition studies of NH3/CH4 mixtures at high pressure. Combust. Flame 2020, 218, 19–26. [Google Scholar] [CrossRef]
  7. Elbaz, A.M.; Giri, B.R.; Issayev, G.; Shrestha, K.P.; Mauss, F.; Farooq, A.; Roberts, W.L. Experimental and Kinetic Modeling Study of Laminar Flame Speed of Dimethoxymethane and Ammonia Blends. Energy Fuels 2020, 34, 14726–14740. [Google Scholar] [CrossRef]
  8. Issayev, G.; Giri, B.R.; Elbaz, A.M.; Shrestha, K.P.; Mauss, F.; Roberts, W.L.; Farooq, A. Combustion behavior of ammonia blended with diethyl ether. Proc. Combust. Inst. 2021, 38, 499–506. [Google Scholar] [CrossRef]
  9. Shrestha, K.P.; Lhuillier, C.; Barbosa, A.A.; Brequigny, P.; Contino, F.; Mounaïm-Rousselle, C.; Seidel, L.; Mauss, F. An experimental and modeling study of ammonia with enriched oxygen content and ammonia/hydrogen laminar flame speed at elevated pressure and temperature. Proc. Combust. Inst. 2021, 38, 2163–2174. [Google Scholar] [CrossRef]
  10. Issayev, G.; Giri, B.R.; Elbaz, A.M.; Shrestha, K.P.; Mauss, F.; Roberts, W.L.; Farooq, A. Ignition delay time and laminar flame speed measurements of ammonia blended with dimethyl ether: A promising low carbon fuel blend. Renew. Energy 2022, 181, 1353–1370. [Google Scholar] [CrossRef]
  11. Ronan, P.; Pierre, B.; Christine, M.-R.; Guillaume, D.; Fabien, H. Laminar flame speed of ethanol/ammonia blends–An experimental and kinetic study. Fuel Commun. 2022, 10, 100052. [Google Scholar] [CrossRef]
  12. Shrestha, K.P.; Giri, B.R.; Elbaz, A.M.; Issayev, G.; Roberts, W.L.; Seidel, L.; Mauss, F.; Farooq, A. A detailed chemical insights into the kinetics of diethyl ether enhancing ammonia combustion and the importance of NOx recycling mechanism. Fuel Commun. 2022, 10, 100051. [Google Scholar] [CrossRef]
  13. Thomas, D.E.; Shrestha, K.P.; Mauss, F.; Northrop, W.F. Extinction and NO formation of ammonia-hydrogen and air non-premixed counterflow flames. Proc. Combust. Inst. 2023, 39, 1803–1812. [Google Scholar] [CrossRef]
  14. Giri, B.R.; Shrestha, K.P.; Mai, T.V.T.; Mauss, F.; Huynh, L.K. A theoretical kinetic study of the reactions of NH2 radicals with methanol and ethanol and their implications in kinetic modeling. Int. J. Chem. Kinet. 2023, 55, 3–14. [Google Scholar] [CrossRef]
  15. Synák, F.; Čulík, K.; Rievaj, V.; Gaňa, J. Liquefied petroleum gas as an alternative fuel. Transp. Res. Procedia 2019, 40, 527–534. [Google Scholar] [CrossRef]
  16. Wang, Z.; Ji, C.; Wang, D.; Zhang, T.; Zhai, Y.; Wang, S. Experimental and numerical study on laminar burning velocity and premixed combustion characteristics of NH3/C3H8/air mixtures. Fuel 2023, 331, 125936. [Google Scholar] [CrossRef]
  17. Wang, D.; Wang, Z.; Zhang, T.; Zhai, Y.; Hou, R.; Tian, Z.Y.; Ji, C. A comparative study on the laminar C1–C4 n-alkane/NH3 premixed flame. Fuel 2022, 324, 124732. [Google Scholar] [CrossRef]
  18. Chen, C.; Wang, Z.; Yu, Z.; Han, X.; He, Y.; Zhu, Y.; Konnov, A.A. Experimental and kinetic modeling study of laminar burning velocity enhancement by ozone additive in NH3+O2+N2 and NH3+CH4/C2H6/C3H8+air flames. Proc. Combust. Inst. 2023, 39, 4237–4246. [Google Scholar] [CrossRef]
  19. Hennig, G.; Wagner, H.G.G. A Kinetic Study About the Reactions of NH2( X _ 2B1) Radicals with Saturated Hydrocarbons in the Gas Phase. Berichte Bunsenges. Phys. Chem. 1995, 99, 863–869. [Google Scholar] [CrossRef]
  20. Ehbrecht, J.; Hack, W.; Rouveirolles, P.; Wagner, H.G. Hydrogen Abstraction Reactions By NH2(X2B1)-Radicals From Hydrocarbons in the Gas Phase. Berichte Bunsenges. Phys. Chem. 1987, 91, 700–708. [Google Scholar] [CrossRef]
  21. Lesclaux, R.; Demissy, M. The kinetics of the gas phase reactions of NH2 radicals with alkane and alkyl radicals. J. Photochem. 1978, 9, 110–112. [Google Scholar] [CrossRef]
  22. Demissy, M.; Lesclaux, R. Kinetics of hydrogen abstraction by amino radicals from alkanes in the gas phase. A flash photolysis-laser resonance absorption study. J. Am. Chem. Soc. 1980, 102, 2897–2902. [Google Scholar] [CrossRef]
  23. Mebel, A.M. Prediction of absolute rate constants for the reactions of NH2 with alkanes from ab initio G2M/TST calculations. J. Phys. Chem. A 1999, 103, 2088–2096. [Google Scholar] [CrossRef]
  24. Siddique, K.; Altarawneh, M.; Gore, J.; Westmoreland, P.R.; Dlugogorski, B.Z. Hydrogen Abstraction from Hydrocarbons by NH2. J. Phys. Chem. A 2017, 121, 2221–2231. [Google Scholar] [CrossRef] [PubMed]
  25. Siddique, K.; Altarawneh, M.; Saeed, A.; Zeng, Z.; Gore, J.; Dlugogorski, B.Z. Interaction of NH2 radical with alkylbenzenes. Combust. Flame 2019, 200, 85–96. [Google Scholar] [CrossRef]
  26. Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar] [CrossRef] [Green Version]
  27. Robinson, R.K.; Lindstedt, R.P. A comparative ab initio study of hydrogen abstraction from n-propyl benzene. Combust. Flame 2013, 160, 2642–2653. [Google Scholar] [CrossRef]
  28. Yin, G.; Hu, E.; Zhou, M.; Zhan, H.; Huang, Z. Kinetic Study on the Isomerization and Decomposition of the Alkenyl Radicals of 2,4,4-Trimethyl-1-pentene. Energy Fuels 2020, 34, 14757–14767. [Google Scholar] [CrossRef]
  29. Giri, B.R.; Mai, T.V.T.; Nguyen, T.T.D.; Szőri, M.; Huynh, L.K.; Farooq, A. Kinetic insights into the reaction of hydroxyl radicals with 1,4-pentadiene: A combined experimental and theoretical study. Combust. Flame 2022, 241, 112153. [Google Scholar] [CrossRef]
  30. Giri, B.R.; Mai, T.V.T.; Assali, M.; Nguyen, T.T.D.; Nguyen, H.T.; Szori, M.; Huynh, L.K.; Fittschen, C.; Farooq, A. Reaction kinetics of 1,4-cyclohexadienes with OH radicals: An experimental and theoretical study. Phys. Chem. Chem. Phys. 2022, 24, 7836–7847. [Google Scholar] [CrossRef]
  31. Huynh, L.K.; Mai, T.V.T.; Nguyen, T.T.D.; Nguyen, H.T.; Nguyen, T.T. New mechanistic insights into atmospheric oxidation of aniline initiated by oh radicals. Environ. Sci. Technol. 2021, 55, 7858–7868. [Google Scholar] [CrossRef]
  32. Safaei, Z.; Shiroudi, A.; Zahedi, E.; Sillanpää, M. Atmospheric oxidation reactions of imidazole initiated by hydroxyl radicals: Kinetics and mechanism of reactions and atmospheric implications. Phys. Chem. Chem. Phys. 2019, 21, 8445–8456. [Google Scholar] [CrossRef] [Green Version]
  33. Alecu, I.M.; Zheng, J.; Zhao, Y.; Truhlar, D.G. Computational thermochemistry: Scale factor databases and scale factors for vibrational frequencies obtained from electronic model chemistries. J. Chem. Theory Comput. 2010, 6, 2872–2887. [Google Scholar] [CrossRef]
  34. Hratchian, H.P.; Schlegel, H.B. Accurate reaction paths using a Hessian based predictor-corrector integrator. J. Chem. Phys. 2004, 120, 9918–9924. [Google Scholar] [CrossRef] [PubMed]
  35. Hratchian, H.P.; Schlegel, H.B. Using Hessian updating to increase the efficiency of a Hessian based predictor-corrector reaction path following method. J. Chem. Theory Comput. 2005, 1, 61–69. [Google Scholar] [CrossRef] [PubMed]
  36. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09 Revision D.01. 2009. [Google Scholar]
  37. Purvis, G.D.; Bartlett, R.J. A full coupled-cluster singles and doubles model: The inclusion of disconnected triples. J. Chem. Phys. 1982, 76, 1910–1918. [Google Scholar] [CrossRef]
  38. Scuseria, G.E.; Janssen, C.L.; Schaefer, H.F. An efficient reformulation of the closed-shell coupled cluster single and double excitation (CCSD) equations. J. Chem. Phys. 1988, 89, 7382–7387. [Google Scholar] [CrossRef]
  39. Scuseria, G.E.; Schaefer, H.F. Is coupled cluster singles and doubles (CCSD) more computationally intensive than quadratic configuration interaction (QCISD)? J. Chem. Phys. 1989, 90, 3700–3703. [Google Scholar] [CrossRef]
  40. Halkier, A.; Helgaker, T.; Jørgensen, P.; Klopper, W.; Koch, H.; Olsen, J.; Wilson, A.K. Basis-set convergence in correlated calculations on Ne, N2, and H2O. Chem. Phys. Lett. 1998, 286, 243–252. [Google Scholar] [CrossRef]
  41. Duong, M.V.; Nguyen, H.T.; Truong, N.; Le, T.N.M.; Huynh, L.K. Multi-Species Multi-Channel (MSMC): An Ab Initio-based Parallel Thermodynamic and Kinetic Code for Complex Chemical Systems. Int. J. Chem. Kinet. 2015, 47, 564–575. [Google Scholar] [CrossRef]
  42. Duong, M.V.; Nguyen, H.T.; Mai, T.V.T.; Huynh, L.K. Global minimum profile error (GMPE)-a least-squares-based approach for extracting macroscopic rate coefficients for complex gas-phase chemical reactions. Phys. Chem. Chem. Phys. 2018, 20, 1231–1239. [Google Scholar] [CrossRef] [PubMed]
  43. Le, T.H.M.; Do, S.T.; Huynh, L.K. Algorithm for auto-generation of hindered internal rotation parameters for complex chemical systems. Comput. Theor. Chem. 2017, 1100, 61–69. [Google Scholar] [CrossRef]
  44. Le, T.H.M.; Tran, T.T.; Huynh, L.K. Identification of hindered internal rotational mode for complex chemical species: A data mining approach with multivariate logistic regression model. Chemom. Intell. Lab. Syst. 2018, 172, 10–16. [Google Scholar] [CrossRef]
  45. Shrestha, K.P.; Eckart, S.; Elbaz, A.M.; Giri, B.R.; Fritsche, C.; Seidel, L.; Roberts, W.L.; Krause, H.; Mauss, F. A comprehensive kinetic model for dimethyl ether and dimethoxymethane oxidation and NOx interaction utilizing experimental laminar flame speed measurements at elevated pressure and temperature. Combust. Flame 2020, 218, 57–74. [Google Scholar] [CrossRef]
  46. Shrestha, K.P.; Seidel, L.; Zeuch, T.; Moréac, G.; Dagaut, P.; Mauss, F. On the implications of nitromethane–NOx chemistry interactions for combustion processes. Fuel 2021, 289, 119861. [Google Scholar] [CrossRef]
  47. Burke, S.M.; Metcalfe, W.; Herbinet, O.; Battin-Leclerc, F.; Haas, F.M.; Santner, J.; Dryer, F.L.; Curran, H.J. An experimental and modeling study of propene oxidation. Part 1: Speciation measurements in jet-stirred and flow reactors. Combust. Flame 2014, 161, 2765–2784. [Google Scholar] [CrossRef] [Green Version]
  48. Burke, S.M.; Burke, U.; Donagh, R.M.; Mathieu, O.; Osorio, I.; Keesee, C.; Morones, A.; Petersen, E.L.; Wang, W.; DeVerter, T.A.; et al. An experimental and modeling study of propene oxidation. Part 2: Ignition delay time and flame speed measurements. Combust. Flame 2015, 162, 296–314. [Google Scholar] [CrossRef] [Green Version]
  49. Chai, J.; Goldsmith, C.F. Rate coefficients for fuel + NO2: Predictive kinetics for HONO and HNO2 formation. Proc. Combust. Inst. 2017, 36, 617–626. [Google Scholar] [CrossRef]
  50. Atkinson, R.; Baulch, D.L.; Cox, R.A.; Crowley, J.N.; Hampson, R.F.; Hynes, R.G.; Jenkin, M.E.; Rossi, M.J.; Troe, J. Evaluated kinetic and photochemical data for atmospheric chemistry: Volume II-Gas phase reactions of organic species. Atmos. Meas. Tech. 2006, 6, 3625–4055. [Google Scholar] [CrossRef] [Green Version]
  51. Rozenberg, A.S.; Voronkov, V.G. Rate constants for the interaction of the NH biradical and the aminoradical with alkane molecules. Russ. J. Phys. Chem. 1972, 46, 425. [Google Scholar]
  52. Vandeputte, A.G.; Sabbe, M.K.; Reyniers, M.F.; Van Speybroeck, V.; Waroquier, M.; Marin, G.B. Theoretical study of the thermodynamics and kinetics of hydrogen abstractions from hydrocarbons. J. Phys. Chem. A 2007, 111, 11771–11786. [Google Scholar] [CrossRef]
  53. Baulch, D.L.; Cobos, C.J.; Cox, R.A.; Frank, P.; Hayman, G.; Just, T.; Kerr, J.A.; Murrells, T.; Pilling, M.J.; Troe, J.; et al. Evaluated Kinetic Data for Combustion Modeling. Supplement I. J. Phys. Chem. Ref. Data 1994, 23, 847–848. [Google Scholar] [CrossRef] [Green Version]
  54. Lam, K.Y.; Hong, Z.; Davidson, D.F.; Hanson, R.K. Shock tube ignition delay time measurements in propane/O2/argon mixtures at near-constant-volume conditions. Proc. Combust. Inst. 2011, 33, 251–258. [Google Scholar] [CrossRef]
  55. He, X.; Shu, B.; Nascimento, D.; Moshammer, K.; Costa, M.; Fernandes, R.X. Auto-ignition kinetics of ammonia and ammonia/hydrogen mixtures at intermediate temperatures and high pressures. Combust. Flame 2019, 206, 189–200. [Google Scholar] [CrossRef]
Energies 16 05943 g001
Figure 1. ZPE-corrected energy profile (0 K) for the reaction between NH2 and CH3CH2CH3 calculated at CCSD(T)/cc-pV(T, Q)Z//M06-2X/aug-cc-pVTZ. Units are in kcal/mol.
Figure 1. ZPE-corrected energy profile (0 K) for the reaction between NH2 and CH3CH2CH3 calculated at CCSD(T)/cc-pV(T, Q)Z//M06-2X/aug-cc-pVTZ. Units are in kcal/mol.
Energies 16 05943 g001
Energies 16 05943 g002
Figure 2. Comparison of the total rate constant for the reaction of NH2 + CH3CH2CH3 → products. Literature data are taken from the works of Hennig and Wagner [19] (Expt. (Hennig 1995)), Ehbrecht et al. [20] (Expt. (Ehbrecht 1987)), Demissy et al. [22] (Expt. (Demissy 1980)), Lesclaux et al. [21] (Expt. (Lesclaux 1978)), Mebel et al. [23] (Calc. (Mebel 1999)), Rozenberg et al. [51] (Est. (Rozenberg 1972)) and Siddique et al. (Calc. (Siddique 2017 [24]) and Calc. (Siddique 2019 [25])). (“Expt.”, “Est.” and “Calc.” stand for “experimental”, “estimated” and “calculated” studies, respectively).
Figure 2. Comparison of the total rate constant for the reaction of NH2 + CH3CH2CH3 → products. Literature data are taken from the works of Hennig and Wagner [19] (Expt. (Hennig 1995)), Ehbrecht et al. [20] (Expt. (Ehbrecht 1987)), Demissy et al. [22] (Expt. (Demissy 1980)), Lesclaux et al. [21] (Expt. (Lesclaux 1978)), Mebel et al. [23] (Calc. (Mebel 1999)), Rozenberg et al. [51] (Est. (Rozenberg 1972)) and Siddique et al. (Calc. (Siddique 2017 [24]) and Calc. (Siddique 2019 [25])). (“Expt.”, “Est.” and “Calc.” stand for “experimental”, “estimated” and “calculated” studies, respectively).
Energies 16 05943 g002
Energies 16 05943 g003
Figure 3. Comparison of the individual rate constant for the reaction of NH2 + CH3CH2CH3 → NH3 + N-C3H7 (via TS1) (a) and NH2 + CH3CH2CH3 → NH3 + I-C3H7 (via TS2) (b). Literature data are taken from the works of Mebel et al. [23] (Calc. (Mebel 1999)) and Siddique et al. (Calc. (Siddique 2017 [24]) and Calc. (Siddique 2019 [25])).
Figure 3. Comparison of the individual rate constant for the reaction of NH2 + CH3CH2CH3 → NH3 + N-C3H7 (via TS1) (a) and NH2 + CH3CH2CH3 → NH3 + I-C3H7 (via TS2) (b). Literature data are taken from the works of Mebel et al. [23] (Calc. (Mebel 1999)) and Siddique et al. (Calc. (Siddique 2017 [24]) and Calc. (Siddique 2019 [25])).
Energies 16 05943 g003
Energies 16 05943 g004
Figure 4. Predicted branching ratio for the reaction of NH2 + CH3CH2CH3 → products from this work (red lines) and Mebel and Lin [23] (blue lines).
Figure 4. Predicted branching ratio for the reaction of NH2 + CH3CH2CH3 → products from this work (red lines) and Mebel and Lin [23] (blue lines).
Energies 16 05943 g004
Energies 16 05943 g005
Figure 5. Comparison of the model-predicted laminar flame speed (LFS) with the experimental data for various blends of NH3/C3H8/air at 1 bar and 298 K. (a) LFS variation with the equivalence ratio for various NH3/C3H8/air blends. (b) LFS dependence on the mole fraction variation of C3H8 variation of stochiometric NH3/C3H8/air blends. Symbols represent the experimental data from Chen et al. [18] and Wang et al. [16], whereas the lines are the model predictions from this work, χ C 3 H 8 = C 3 H 8 N H 3 + C 3 H 8   ×   100 % .
Figure 5. Comparison of the model-predicted laminar flame speed (LFS) with the experimental data for various blends of NH3/C3H8/air at 1 bar and 298 K. (a) LFS variation with the equivalence ratio for various NH3/C3H8/air blends. (b) LFS dependence on the mole fraction variation of C3H8 variation of stochiometric NH3/C3H8/air blends. Symbols represent the experimental data from Chen et al. [18] and Wang et al. [16], whereas the lines are the model predictions from this work, χ C 3 H 8 = C 3 H 8 N H 3 + C 3 H 8   ×   100 % .
Energies 16 05943 g005
Energies 16 05943 g006
Figure 6. Ignition delay times of (a) C3H8/O2/Ar at ϕ = 0.5 and 6 (red), 24 (blue) and 60 atm (green), (b) NH3/O2/Ar at ϕ = 1.0 and 40 bar. Symbols: experimental data from [54,55]; lines: model predictions from this work.
Figure 6. Ignition delay times of (a) C3H8/O2/Ar at ϕ = 0.5 and 6 (red), 24 (blue) and 60 atm (green), (b) NH3/O2/Ar at ϕ = 1.0 and 40 bar. Symbols: experimental data from [54,55]; lines: model predictions from this work.
Energies 16 05943 g006
Energies 16 05943 g007
Figure 7. Temperature dependence of the ignition delay times behavior of NH3/C3H8/air blends (a) 95% NH3/5%C3H8 at ϕ = 1.0 and 40 bar, (b) 95% NH3/5%C3H8 at ϕ = 0.5 and 40 bar, and (c) 90% NH3/10%C3H8 at ϕ = 1.0 and 40 bar. Dashed and solid red lines represent the model predictions without and with the inclusion of the NH2 + C3H8 reactions, respectively. Black lines: model predictions for neat NH3.
Figure 7. Temperature dependence of the ignition delay times behavior of NH3/C3H8/air blends (a) 95% NH3/5%C3H8 at ϕ = 1.0 and 40 bar, (b) 95% NH3/5%C3H8 at ϕ = 0.5 and 40 bar, and (c) 90% NH3/10%C3H8 at ϕ = 1.0 and 40 bar. Dashed and solid red lines represent the model predictions without and with the inclusion of the NH2 + C3H8 reactions, respectively. Black lines: model predictions for neat NH3.
Energies 16 05943 g007
Energies 16 05943 g008
Figure 8. Reaction sensitivity analysis towards ignition delay time at 800 K, 40 bar, and ϕ = 1.0 for 95% NH3/5%C3H8/air blend.
Figure 8. Reaction sensitivity analysis towards ignition delay time at 800 K, 40 bar, and ϕ = 1.0 for 95% NH3/5%C3H8/air blend.
Energies 16 05943 g008
Energies 16 05943 g009
Figure 9. Integrated mass flux analysis based on C-atom at 800 K, 40 bar and ϕ = 1.0 for 95% NH3/5%C3H8/air blend. therm: thermal decomposition.
Figure 9. Integrated mass flux analysis based on C-atom at 800 K, 40 bar and ϕ = 1.0 for 95% NH3/5%C3H8/air blend. therm: thermal decomposition.
Energies 16 05943 g009
Energies 16 05943 g010
Figure 10. Concentration time profiles of some important species with and without the cross-reaction between nitrogen and carbon families added in this study. The simulations were carried out at 800 K, 40 bar, and ϕ = 1.0 for 95% NH3/5%C3H8/air blend. Solid lines: with cross-reactions, dashed lines: without cross-reactions. NH3 (a), OH (b), NH2 (c), NO (d), C3H8 (e), HO2 (f), HNO (g) and NO2 (h).
Figure 10. Concentration time profiles of some important species with and without the cross-reaction between nitrogen and carbon families added in this study. The simulations were carried out at 800 K, 40 bar, and ϕ = 1.0 for 95% NH3/5%C3H8/air blend. Solid lines: with cross-reactions, dashed lines: without cross-reactions. NH3 (a), OH (b), NH2 (c), NO (d), C3H8 (e), HO2 (f), HNO (g) and NO2 (h).
Energies 16 05943 g010
Table 1. Fitted Arrhenius parameters, as given by k(T) = ATnexp(−E/T) over T = 300–2000 K. Arrhenius parameters (A and E) are in units of cm3 molecule−1 s−1 and K, respectively. The fitting error is less than 2%.
Table 1. Fitted Arrhenius parameters, as given by k(T) = ATnexp(−E/T) over T = 300–2000 K. Arrhenius parameters (A and E) are in units of cm3 molecule−1 s−1 and K, respectively. The fitting error is less than 2%.
ReactionTSAnE
1. NH2 + C3H8 → NH3 + N-●CH2CH2CH3TS12.19 × 10−264.522346.7
2. NH2 + C3H8 → NH3 + I-CH3CH●CH3TS21.35 × 10−243.911684.0
3. NH2 + C3H8 → products TS1 + TS24.00 × 10−264.471566.5
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Giri, B.R.; Shrestha, K.P.; Mai, T.V.-T.; Giri, S.; Adil, M.; Naik, R.T.; Mauss, F.; Huynh, L.K. A Theoretical Study of NH2 Radical Reactions with Propane and Its Kinetic Implications in NH3-Propane Blends’ Oxidation. Energies 2023, 16, 5943. https://doi.org/10.3390/en16165943

AMA Style

Giri BR, Shrestha KP, Mai TV-T, Giri S, Adil M, Naik RT, Mauss F, Huynh LK. A Theoretical Study of NH2 Radical Reactions with Propane and Its Kinetic Implications in NH3-Propane Blends’ Oxidation. Energies. 2023; 16(16):5943. https://doi.org/10.3390/en16165943

Chicago/Turabian Style

Giri, Binod Raj, Krishna Prasad Shrestha, Tam V.-T. Mai, Sushant Giri, Mohammad Adil, R. Thirumaleswara Naik, Fabian Mauss, and Lam Kim Huynh. 2023. "A Theoretical Study of NH2 Radical Reactions with Propane and Its Kinetic Implications in NH3-Propane Blends’ Oxidation" Energies 16, no. 16: 5943. https://doi.org/10.3390/en16165943

APA Style

Giri, B. R., Shrestha, K. P., Mai, T. V.-T., Giri, S., Adil, M., Naik, R. T., Mauss, F., & Huynh, L. K. (2023). A Theoretical Study of NH2 Radical Reactions with Propane and Its Kinetic Implications in NH3-Propane Blends’ Oxidation. Energies, 16(16), 5943. https://doi.org/10.3390/en16165943

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop