A Mass-In-Mass Metamaterial Design for Harvesting Energy at a Broadband Frequency Range
Abstract
:1. Introduction
2. Model Configurations and Computational Approach
3. Determination of Dispersion Curves
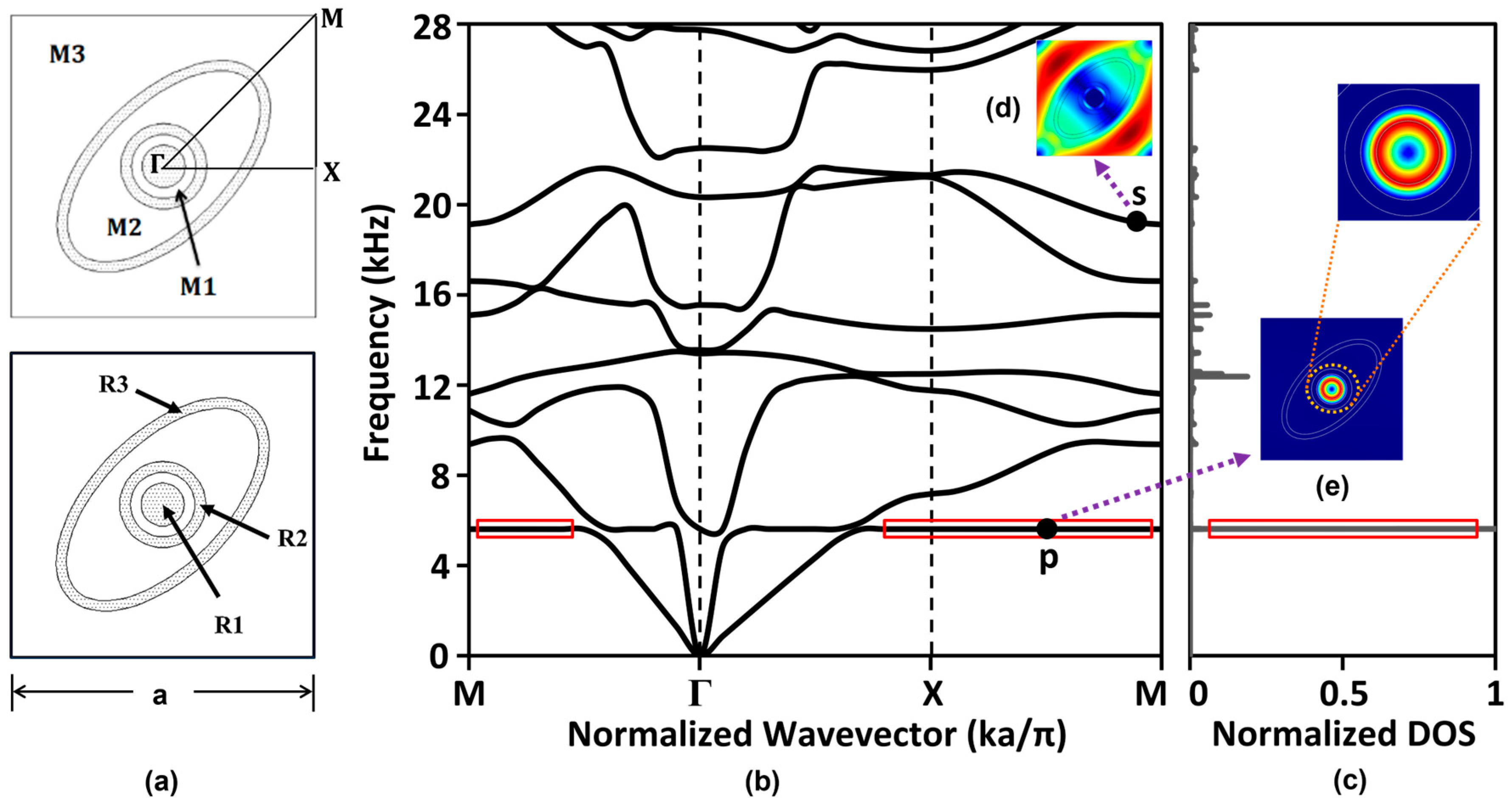
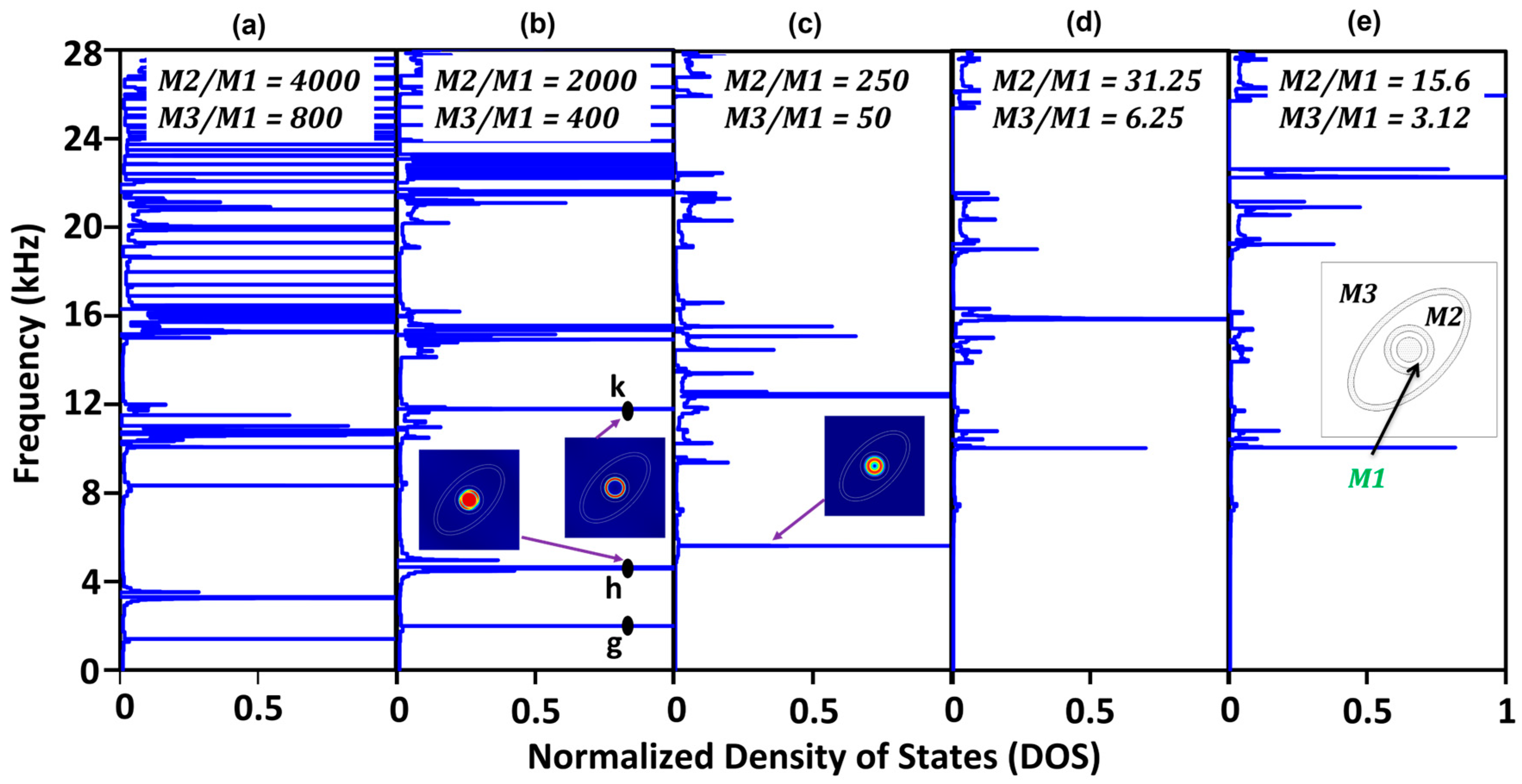
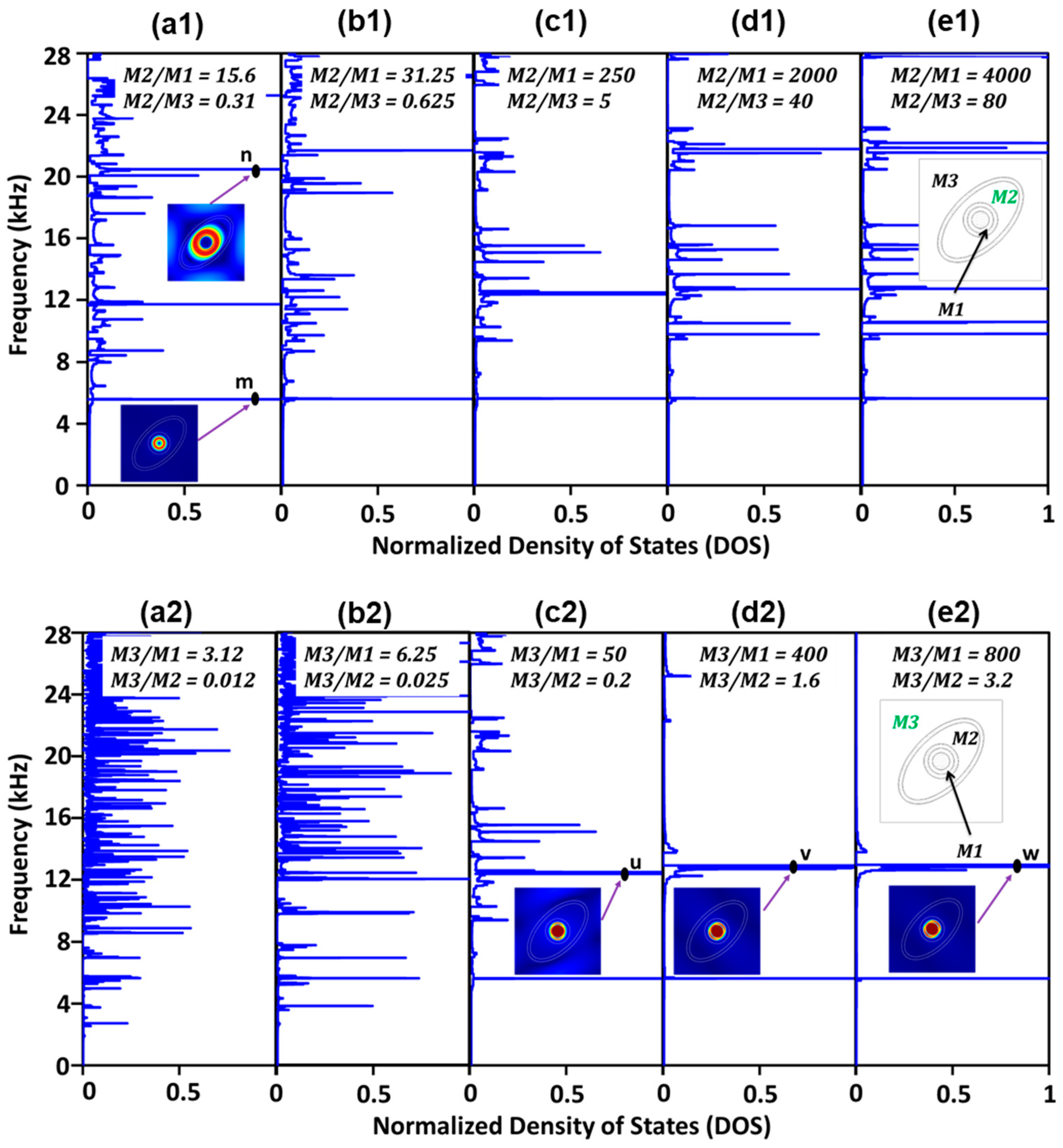
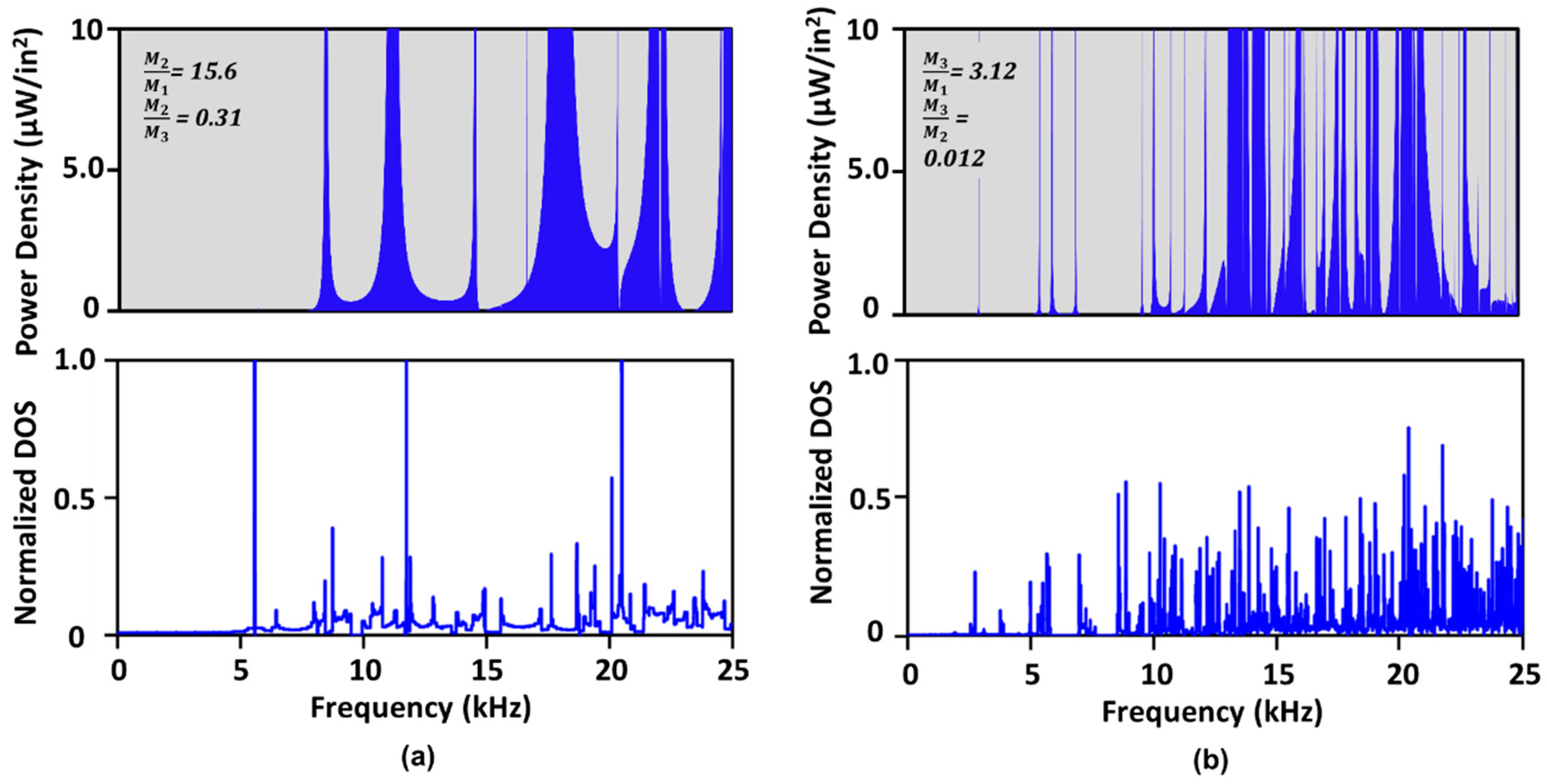
4. Density of States
5. Influence of Matrix Stiffness on Local Resonance Bands
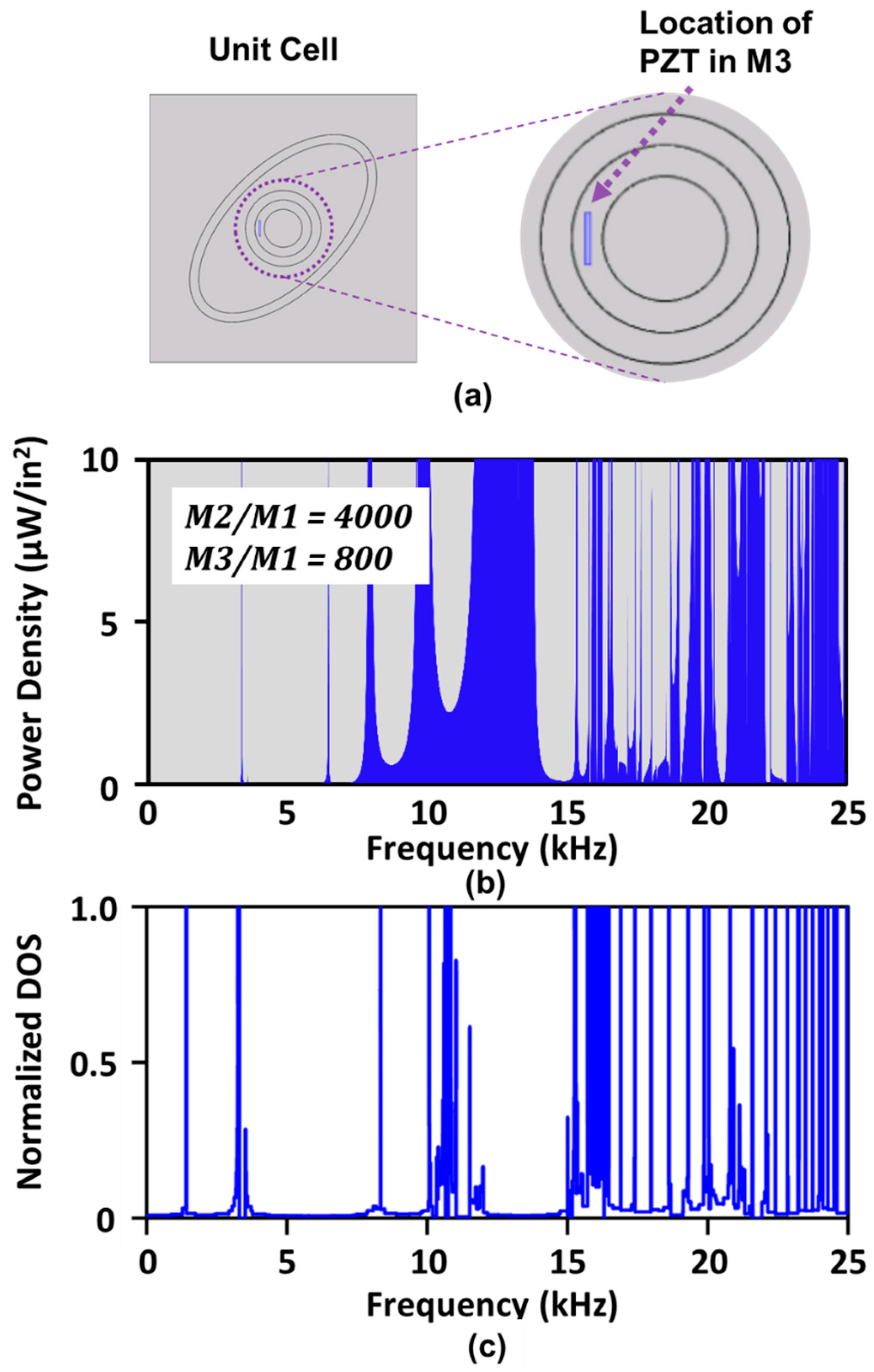
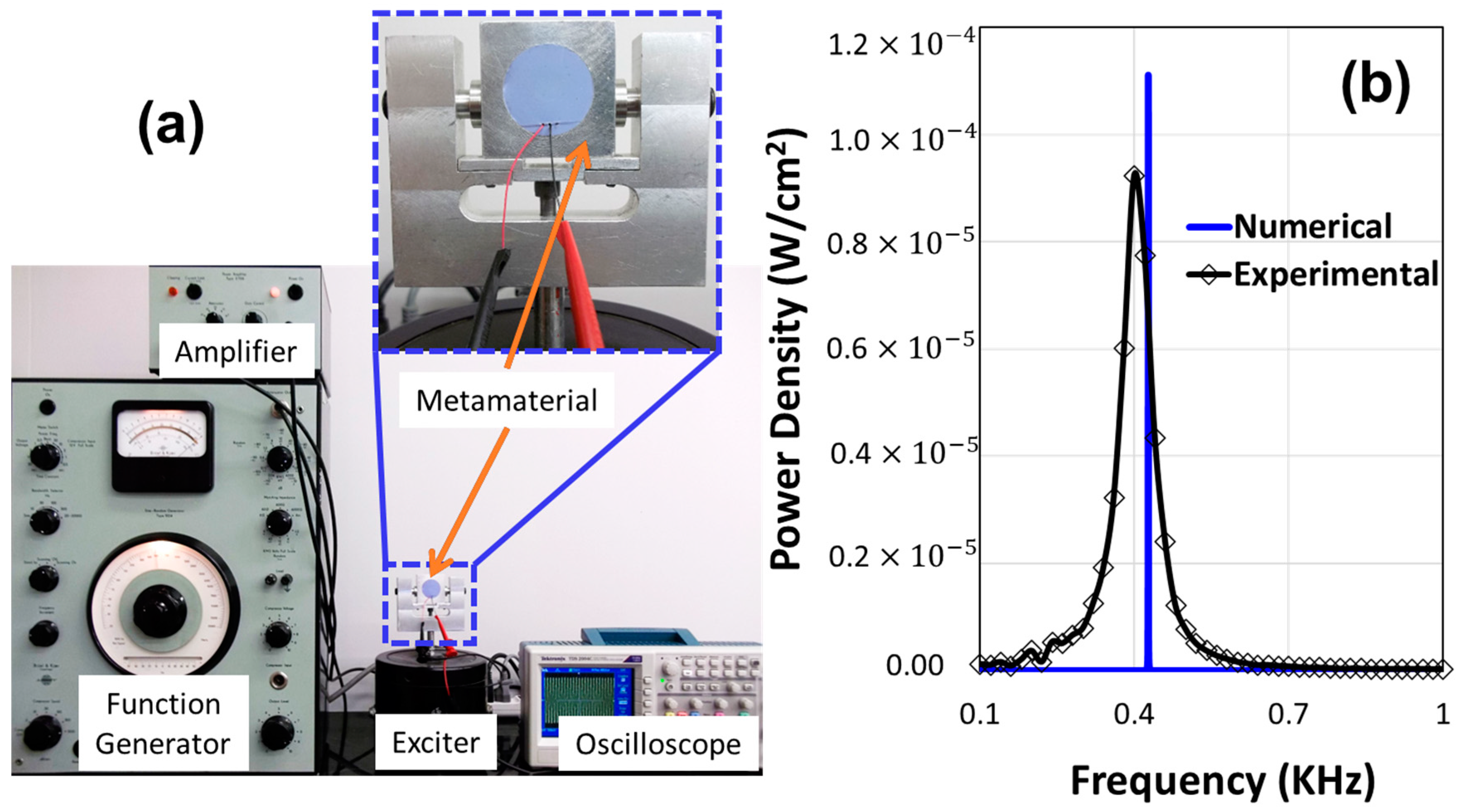
6. Broad Band Energy Harvesting
7. Experimental Investigation
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ahmed, R.U.; Banerjee, S. Low frequency energy scavenging using sub-wave length scale acousto-elastic metamaterial. AIP Adv. 2014, 4, 117114. [Google Scholar] [CrossRef]
- Ahmed, R.; Adiba, A.; Banerjee, S. Energy scavenging from acousto-elastic metamaterial using local resonance phenomenon. In SPIE Smart Structures and Materials + Nondestructive Evaluation and Health Monitoring; SPIE: San Diego, CA, USA, 2015; Volume 9431. [Google Scholar]
- Anton, S.R.; Sodano, H.A. A review of power harvesting using piezoelectric materials (2003–2006). Smart Mater. Struct. 2007, 16, R1–R21. [Google Scholar] [CrossRef]
- Beeby, S.P.; Tudor, M.J.; White, N.M. Energy harvesting vibration sources for microsystems applications. Meas. Sci. Technol. 2006, 17, R175–R195. [Google Scholar] [CrossRef] [Green Version]
- Cook-Chennault, K.A.; Thambi, N.; Sastry, A.M. Powering MEMS portable devices—A review of non-regenerative and regenerative power supply systems with special emphasis on piezoelectric energy harvesting systems. Smart Mater. Struct. 2008, 17, 043001. [Google Scholar] [CrossRef] [Green Version]
- Du, C.; Zhou, D.; Guo, H.-H.; Pang, Y.-Q.; Shi, H.-Y.; Liu, W.-F.; Su, J.-Z.; Singh, C.; Trukhanov, S.; Trukhanov, A.; et al. An ultra-broadband terahertz metamaterial coherent absorber using multilayer electric ring resonator structures based on anti-reflection coating. Nanoscale 2020, 12, 9769–9775. [Google Scholar] [CrossRef]
- Kozlovskiy, A.L.; Shlimas, D.I.; Zdorovets, M.V. Synthesis, structural properties and shielding efficiency of glasses based on TeO2-(1-x)ZnO-xSm2O3. J. Mater. Sci. Mater. Electron. 2021, 32, 12111–12120. [Google Scholar] [CrossRef]
- Firoozy, P.; Khadem, S.E.; Pourkiaee, S.M. Broadband energy harvesting using nonlinear vibrations of a magnetopiezoelastic cantilever beam. Int. J. Eng. Sci. 2017, 111, 113–133. [Google Scholar] [CrossRef]
- Fang, S.; Miao, G.; Chen, K.; Xing, J.; Zhou, S.; Yang, Z.; Liao, W.-H. Broadband energy harvester for low-frequency rotations utilizing centrifugal softening piezoelectric beam array. Energy 2022, 241, 122833. [Google Scholar] [CrossRef]
- Veselago, V.G. The electrodynamics of substances with simultaneously negative values of ε and μ. Phys.-Uspekhi 1968, 10, 509–514. [Google Scholar] [CrossRef]
- Smith, D.R.; Pendry, J.B.; Wiltshire, M.C.K. Metamaterials and Negative Refractive Index. Science 2004, 305, 788–792. [Google Scholar] [CrossRef] [Green Version]
- Pendry, J.B.; Holden, A.J.; Robbins, D.J.; Stewart, W.J. Magnetism from conductors and enhanced nonlinear phenomena. IEEE Trans. Microw. Theory Tech. 1999, 47, 2075–2084. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Ma, Q.; Luo, S.S.; Ye, F.J.; Cui, H.Y.; Cui, T.J. Touch-Programmable Metasurface for Various Electromagnetic Manipulations and Encryptions. Nano-Micro Small 2022, 18, 2203871. [Google Scholar] [CrossRef] [PubMed]
- Ma, Q.; Gao, W.; Xiao, Q.; Ding, L.; Gao, T.; Zhou, Y.; Gao, X.; Yan, T.; Liu, C.; Gu, Z.; et al. Directly wireless communication of human minds via non-invasive brain-computer-metasurface platform. eLight 2022, 2, 11. [Google Scholar] [CrossRef]
- Gao, X.; Ma, Q.; Gu, Z.; Cui, W.Y.; Liu, C.; Zhang, J.; Cui, T.J. Programmable surface plasmonic neural networks for microwave detection and processing. Nat. Electron. 2023, 6, 319–328. [Google Scholar] [CrossRef]
- Du, C.; Zhou, D.; Guo, H.-H.; Pang, Y.-Q.; Shi, H.-Y.; Liu, W.-F.; Singh, C.; Trukhanov, S.; Trukhanov, A.; Xu, Z. Active control scattering manipulation for realization of switchable EIT-like response metamaterial. Opt. Commun. 2021, 483, 126664. [Google Scholar] [CrossRef]
- Khan, S.A.; Ali, I.; Hussain, A.; Javed, H.M.; Turchenko, V.A.; Trukhanov, A.V.; Trukhanov, S.V. Synthesis and Characterization of Composites with Y-Hexaferrites for Electromagnetic Interference Shielding Applications. Magnetochemistry 2022, 8, 186. [Google Scholar] [CrossRef]
- Smirnova, E.I.; Mastovsky, I.; Shapiro, M.A.; Temkin, R.J.; Earley, L.M.; Edwards, R.L. Fabrication and cold test of photonic band gap resonators and accelerator structures. Phys. Rev. Spec. Top.-Accel. Beams 2005, 8, 091302. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Chan, C.T.; Sheng, P. Analytic model of phononic crystals with local resonances. Phys. Rev. B 2005, 71, 014103. [Google Scholar] [CrossRef] [Green Version]
- Mei, J.; Liu, Z.; Wen, W.; Sheng, P. Effective Mass Density of Fluid-Solid Composites. Phys. Rev. Lett. 2006, 96, 024301. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.; Lai, Y.; Zhang, Z.-Q. Effective medium theory for elastic metamaterials in two dimensions. Phys. Rev. B 2007, 76, 205313. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, H.; Ghosh, S.; Sain, T.; Banerjee, S. Hybrid Bessel beam and metamaterial lenses for deep laparoscopic nondestructive evaluation. J. Appl. Phys. 2021, 129, 165107. [Google Scholar] [CrossRef]
- Indaleeb, M.M.; Ahmed, H.; Beard, S.; Banerjee, S. Nondestructive evaluation (NDE) of multilayered attenuative structures using ultrasonic Bessel beams. Mech. Syst. Signal Process. 2023, 187, 109960. [Google Scholar] [CrossRef]
- Ahmed, H.; Ahmed, R.; Indaleeb, M.M.; Banerjee, S. Multifunction acoustic modulation by a multi-mode acoustic metamaterial architecture. J. Phys. Commun. 2018, 2, 115001. [Google Scholar] [CrossRef]
- Hossain, A.; Mustahseen Mobashwer, I.; Mohammadsadegh, S.; Trisha, S.; Susanta, G.; Sourav, B. Investigation of wave trapping and attenuation phenomenon for a high symmetry interlocking micro-structure composite metamaterial. In Smart Structures and NDE for Energy Systems and Industry; SPIE: Denver, CO, USA, 2019; p. 109730W. [Google Scholar]
- Hsu, J.-C. Local resonances-induced low-frequency band gaps in two-dimensional phononic crystal slabs with periodic stepped resonators. J. Phys. D Appl. Phys. 2011, 44, 55401–55409. [Google Scholar] [CrossRef]
- Fan, L.; Zhang, S.-y.; Zhang, H. Transmission characteristics of double negativity acoustic metamaterials studied with fluid impedance theory. J. Acoust. Soc. Am. 2011, 129, 2483. [Google Scholar] [CrossRef]
- Norris, A. Periodic metal structures for acoustic wave control. J. Acoust. Soc. Am. 2011, 130, 2359. [Google Scholar] [CrossRef]
- Krynkin, A.; Umnova, O.; Chong, A.Y.B.; Taherzadeh, S.; Attenborough, K. Predictions and measurements of sound transmission through a periodic array of elastic shells in air. J. Acoust. Soc. Am. 2010, 128, 3496–3506. [Google Scholar] [CrossRef]
- Phani, A.S.; Woodhouse, J.; Fleck, N.A. Wave propagation in two-dimensional periodic lattices. J. Acoust. Soc. Am. 2006, 119, 1995–2005. [Google Scholar] [CrossRef]
- Riaz, A.; Banerjee, S. Wave Propagation in Metamaterial Using Multiscale Resonators by Creating Local Anisotropy. Int. J. Mod. Eng. 2013, 13, 9. [Google Scholar]
- Hirsekorn, M.; Delsanto, P.P.; Batra, N.K.; Matic, P. Modelling and simulation of acoustic wave propagation in locally resonant sonic materials. Ultrasonics 2004, 42, 231–235. [Google Scholar] [CrossRef]
- Oudich, M.; Li, Y.; Assouar, B.M.; Hou, Z. A sonic band gap based on the locally resonant phononic plates with stubs. New J. Phys. 2010, 12, 083049. [Google Scholar] [CrossRef]
- Caballero, D.; Sánchez-Dehesa, J.; Rubio, C.; Mártinez-Sala, R.; Sánchez-Pérez, J.V.; Meseguer, F.; Llinares, J. Large two-dimensional sonic band gaps. Phys. Rev. E 1999, 60, R6316–R6319. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chesnais, C.; Boutin, C.; Hans, S. Effects of the local resonance on the wave propagation in periodic frame structures: Generalized Newtonian mechanics. J. Acoust. Soc. Am. 2012, 132, 2873–2886. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Zhang, X.; Mao, Y.; Zhu, Y.Y.; Yang, Z.; Chan, C.T.; Sheng, P. Locally Resonant Sonic Materials. Science 2000, 289, 1734–1736. [Google Scholar] [CrossRef]
- Krushynska, A.O.; Kouznetsova, V.G.; Geers, M.G.D. Towards optimal design of locally resonant acoustic metamaterials. J. Mech. Phys. Solids 2014, 71, 179–196. [Google Scholar] [CrossRef]
- Krushynska, A.O.; Miniaci, M.; Kouznetsova, V.G.; Geers, M.G.D. Multilayered Inclusions in Locally Resonant Metamaterials: Two-Dimensional Versus Three-Dimensional Modeling. J. Vib. Acoust. 2017, 139, 024501. [Google Scholar] [CrossRef] [Green Version]
- Moscatelli, M.; Ardito, R.; Driemeier, L.; Comi, C. Band-gap structure in two- and three-dimensional cellular locally resonant materials. J. Sound Vib. 2019, 454, 73–84. [Google Scholar] [CrossRef]
- Comi, C.; Marigo, J.-J. Homogenization Approach and Bloch-Floquet Theory for Band-Gap Prediction in 2D Locally Resonant Metamaterials. J. Elast. 2020, 139, 61–90. [Google Scholar] [CrossRef] [Green Version]
- Sugino, C.; Erturk, A. Analysis of multifunctional piezoelectric metastructures for low-frequency bandgap formation and energy harvesting. J. Phys. D Appl. Phys. 2018, 51, 215103. [Google Scholar] [CrossRef]
- Huang, H.H.; Sun, C.T. Wave attenuation mechanism in an acoustic metamaterial with negative effective mass density. New J. Phys. 2009, 11, 013003. [Google Scholar] [CrossRef]
- Huang, H.H.; Sun, C.T.; Huang, G.L. On the negative effective mass density in acoustic metamaterials. Int. J. Eng. Sci. 2009, 47, 610–617. [Google Scholar] [CrossRef]
- Ahmed, R.; Ahmed, H. Understanding the Influence of Resonators on Frequency Band Gaps in Sonic Crystal Metamaterials. In Proceedings of the ASME 2021 Conference on Smart Materials, Adaptive Structures and Intelligent Systems, Online, 14–15 September 2021. [Google Scholar]
- Elabbasi, N. Modeling Phononic Band Gap Materials and Structures. Available online: https://www.comsol.com/blogs/modeling-phononic-band-gap-materials-and-structures/ (accessed on 22 April 2022).
- Brillouin, L. Wave Propagation in Periodic Structures; Dover Publications, Inc.: New York, NY, USA, 1953; p. 255. [Google Scholar]
- Hussein, M. Band Structure Calculations by Modal Analysis. In IUTAM Symposium on Recent Advances of Acoustic Waves in Solids; Wu, T.-T., Ma, C.-C., Eds.; Springer: Dordrecht, The Netherlands, 2010; Volume 26, pp. 319–324. [Google Scholar]
- Zhang, S.; Wu, J.H. Low-Frequency Broadband Energy Harvesting Based on Locally Resonant Phononic Crystals. In Proceedings of the ASME 2013 International Mechanical Engineering Congress and Exposition, San Diego, CA, USA, 15–21 November 2013. [Google Scholar]
- Ahmed, R.; Madisetti, D.; Banerjee, S. A sub-wavelength scale acoustoelastic sonic crystal for harvesting energies at very low frequencies (<~1 kHz) using controlled geometric configurations. J. Intell. Mater. Syst. Struct. 2017, 28, 381–391. [Google Scholar] [CrossRef]
- Turchenko, V.A.; Trukhanov, S.V.; Kostishin, V.G.; Damay, F.; Porcher, F.; Klygach, D.S.; Vakhitov, M.G.; Lyakhov, D.; Michels, D.; Bozzo, B.; et al. Features of structure, magnetic state and electrodynamic performance of SrFe12−xInxO19. Sci. Rep. 2021, 11, 18342. [Google Scholar] [CrossRef] [PubMed]
- Kozlovskiy, A.L.; Alina, A.; Zdorovets, M.V. Study of the effect of ion irradiation on increasing the photocatalytic activity of WO3 microparticles. J. Mater. Sci. Mater. Electron. 2021, 32, 3863–3877. [Google Scholar] [CrossRef]

| Component Name | Outer Dimensions (Inch) | Stiffness (Pa) | Density (kg/m3) | Poisson’s Ratio |
|---|---|---|---|---|
| M1 | Diameter—0.2121 | 10 × 106 | 980 | 0.49 |
| M2 | Major Radius—0.4 Minor Radius—0.2 | 2.5 × 109 | 1250 | 0.38 |
| M3 | 1 × 1 Square | 0.5 × 109 | 1050 | 0.49 |
| R1 | Diameter—0.1414 | 13 × 109 | 11,310 | 0.435 |
| R2 | Diameter—0.2828 | 100 × 109 | 2950 | 0.31 |
| R3 | Major Radius—0.435 Minor Radius—0.235 | 100 × 109 | 2950 | 0.31 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, H.; Ahmed, R. A Mass-In-Mass Metamaterial Design for Harvesting Energy at a Broadband Frequency Range. Energies 2023, 16, 5883. https://doi.org/10.3390/en16165883
Ahmed H, Ahmed R. A Mass-In-Mass Metamaterial Design for Harvesting Energy at a Broadband Frequency Range. Energies. 2023; 16(16):5883. https://doi.org/10.3390/en16165883
Chicago/Turabian StyleAhmed, Hossain, and Riaz Ahmed. 2023. "A Mass-In-Mass Metamaterial Design for Harvesting Energy at a Broadband Frequency Range" Energies 16, no. 16: 5883. https://doi.org/10.3390/en16165883
APA StyleAhmed, H., & Ahmed, R. (2023). A Mass-In-Mass Metamaterial Design for Harvesting Energy at a Broadband Frequency Range. Energies, 16(16), 5883. https://doi.org/10.3390/en16165883







