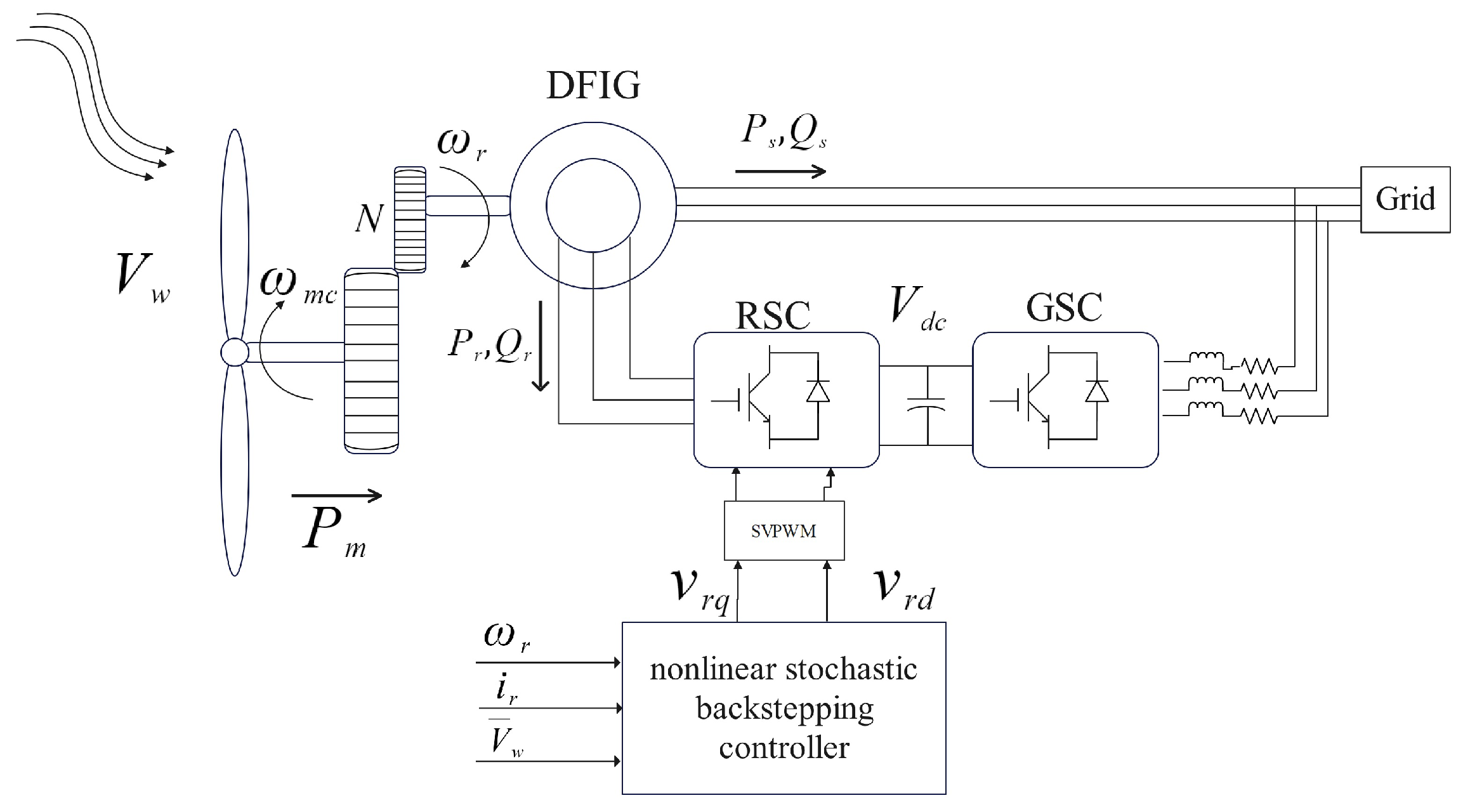
1. Introduction
Energy is a critical factor in industrial growth; however, its development has led to increased greenhouse gas emissions and the production of hazardous and radioactive waste. As a result, the reserve of petroleum, a major energy source, is continuously decreasing, and energy demand will soon exceed supply. Nuclear energy, another significant source for industrial development, is not available to all countries due to expensive installation and political reasons, and it poses ecological risks. Therefore, the industrial sector must shift towards renewable energy sources for several reasons. One of the main advantages of renewable energy sources is that they do not emit greenhouse gases and do not produce toxic or radioactive waste.
Among these energy sources, wind energy is one of the fastest growing ones for electricity production worldwide, and DFIG-WT has become a popular wind power generation system due to its high energy conversion efficiency from variable speed operation and relatively low cost of power electronic converter. The performance of the DFIG-WT depends on the control systems applied on both the turbine and generator sides, which are typically designed using a cascade structure that includes a fast inner loop for power control of the doubly fed induction generator (DFIG) and a slow outer loop for speed control of the drivetrain. Below the rated wind speed, the critical control task is to maximize the captured wind energy through variable speed operation. This requires the DFIG-WT to be fully controllable and operated at an optimal rotor speed according to the stochastic wind speed.
Over the past decade, there has been extensive research on the modeling and control of DFIG-WT. This system has strong nonlinearities due to the aerodynamics of wind turbines, the coupled dynamics of the DFIG and wide operation in the stochastic wind speed. Direct power control (DPC) of DFIG-WT systems has been proposed in [
1,
2] and developed in [
3,
4]. An adaptive compensation control with quasi-synchronous rectification algorithm is first proposed to track maximum power in [
5]. Furthermore, in [
6], Xiong, LY proposes a novel sliding mode control technique for DFIGs based on the fast exponential reaching law to track active/reactive power. Model predictive control is developed for the rotor-side converter (RSC) in [
7]. Predictive rotor current control is developed under unbalanced and distorted grid conditions in [
8] to control the output active/reactive power robustly. Fariba Fateh [
9] utilizes feedback linearization to assume that the power capture coefficient and the desired rotor speed are instantaneously identified for tracking maximum power. However, all the above articles study deterministic systems. Several researchers study stochastic systems in which DFIG-WT is affected by the stochastic wind, such as in reference [
10], who combine the conventional optimal torque control algorithm with the Fokker–Planck–Kolmogorov equation solved by the linear least square method to make the PDF shape of the rotor speed track the desired PDF shape as accurately as possible. Additionally, the work in [
11] presents a new stochastic predictive control approach for variable-speed wind turbines to capture maximum power under the rated wind speed.
In the literature, several works have focused on the wind control problem using backstepping control. For example, backstepping-based direct power control is used to regulate output power under harmonic grid voltage in [
12]. In addition, reference [
13] proposes enhanced low-voltage ride through nonlinear backstepping control of DFIG-based wind turbines in stiff grid conditions. Moreover, Mechter [
14] designs a backstepping controller in the presence of uncertainty based on fuzzy logic theory to extract optimal power for low wind speed. Furthermore, reference [
15] develops an adaptive backstepping approach in DFIG-WT for nonlinear robust control of active and reactive power and utilizes FPGA to implement the effectiveness and the benefit of the proposed controller. However, the backstepping method in stochastic systems for asymptotic control is not investigated in DFIG-WT. On one hand, it is difficult to implement backstepping from deterministic systems to stochastic systems for their second-order differential term in the Itô formula, and the inequality technique is indispensable to avoid the control singularity. On the other hand, nonzero constants are definitively introduced into the Lyapunov analysis, while most of the literature can only achieve the boundness of state in probability. Reference [
16] develops a novel gain suppressing inequality technique to realize the boundness in probability of involved signals and utilizes fuzzy logic to assure asymptotically stability in probability.
All the papers mentioned above and many others in the literature have not discussed the tracking of the maximum output power by tip slip ratio method in nonlinear stochastic backstepping control with the impact of parameter variations of DFIG-WT. This paper proposes adaptive nonlinear stochastic backstepping control based on the gain suppressing theorem of wind turbines for maximum power point tracking (MPPT).
The remainder of this paper is organized as follows. In
Section 2, the Itô stochastic differential equation model of DFIG-WT is constructed; meanwhile, the problem formulation is stated. The preliminaries needed in this paper are stated in
Section 3. The equivalent model and nonlinear stochastic backstepping control of DFIG are designed in
Section 4 to asymptotically track the maximum output power, and stability proof is presented. A simulation study is carried out in
Section 5 to validate the robustness of the proposed controller. Finally, the conclusion is provided in
Section 6.
4. Controller Design for DFIG-WT
To command the nonlinear systems (
1), (
2) and (
14) and employ the Lyapunov stable method, the transformation around the operating point must be used to conceive the controller. The objective of RSC is to maintain the
of the DFIG and the rotor speed
of the wind turbine at the desired references. From the nonlinear system of DFIG-WT, to control
and
, we can adjust
and
by
and
, respectively. To achieve this task, in previous research, backstepping control is used. In this research, a new backstepping controller applied in a nonlinear stochastic system for rotor speed is proposed. We decompose the whole nonlinear control problem into some smaller ones. The conception of stochastic backstepping control law is divided into various design steps. In each step, we calculate a virtual command from the tracking error, which will be used in the next step as a reference. We repeat the operation until obtaining the controller that will be applied to the system. It must be ensured, in each step, that the derivate of the Lyapunov function (definite positive) is always negative.
Firstly, we need a lot of variable substitution and to transform the DFIG-WT system around reference values of system state
,
,
. Let the right of (
1), (
2) and (
14) equal zero; them,
,
,
can be calculated. Define the error variables between the state, input and their reference value as
,
,
,
,
, and denote
,
,
,
,
,
,
,
,
,
,
.
Thus, (
1), (
2) and (
14) can be represented by the equivalent form:
To facilitate the analysis, the changes in coordinates are proposed as , , and . The designed function is virtual control unit.
Step 1: For the first subsystem of system (
23), choose the stochastic Lyapunov function
. The differential operator of
according to (
16) is
In the stochastic system,
is a stochastic process for the external wiener process
, and
is considered as the function of the stochastic process. Utilizing the property of Lemma 2, four terms in (
24) can be further changed into
where the designed constants
,
,
are positive.
On the basis of (
25), one can transform (
24) into the following inequality
where
is represented as
The virtual control unit
in (
26) is developed as
where the adaptive law for
is given in (
30), and
is the designed equivalent virtual unit that is constructed as
where
is the positive designed controller gain and
,
,
, respectively, stand for the estimate of
,
,
. The adaptive law for (
28) is constructed as
where
is a positive designed constant.
Consider the results in (
26)–(
30) and define the estimation error
,
,
. Inequality (
26) is thus rewritten as follows:
Step 2: Augment the stochastic Lyapunov function of Step 2 as
. The error dynamical equation of the second subsystem of the system (
23) can be described as
where we design the new control
to replace actual control
.
The differential operator of
can be calculated using (
16) as follows:
Recalling (
16), (
32) and (
33),
is presented as
Employing Young’s inequality (
19), one obtains that the term in (
34) can be further changed into
where the designed constant
is positive. Combining the results (
31), (
33)–(
35), one can obtain inequality
as follows:
where
is defined as
Then, we zoom
to its upper bound as follows:
According to Lemma 1, we design control signal
u, and adaptive law
, equivalent virtual unit
as
where
,
,
,
are estimates of
,
,
. Define the estimation error
,
,
. The sign function in (
41) is defined as
In succession, the actual controller
in (
2) is presented as
Considering the results in (
37)–(
41), (
36) is thus presented as follows:
Step 3: Augment the stochastic Lyapunov function of Step 2 as
. Notice that
Considering the result of (
44), the differential operator of
is
where
; then, one can obtain that
The control signal
, equivalent virtual control
and adaptive law
are chosen as
Subsequently, the actual controller
is designed as
Thus, inequality (
46) is transformed as
Step 4: For the whole system (
23), choose stochastic Lyapunov function
.
are positive constants.
The parameter updating laws are designed for
,
,
,
,
,
as follows:
Based on (
52) and (
53), the differential operator of V is presented as
Employing Young’s inequality to
, one can obtain
Substituting (
55) into (
54) yields
Asymptotic Stability Analysis
The nonlinear stochastic adaptive control for DFIG-WT is designed completely. Given that the stochastic system (
23), the adaptive laws (
30), (
40), (
50) and (
53), the virtual control
(
28) in step 1, the designed controllers
of DFIG-WT, respectively, in (
43) and (
51) are constructed, one draws the following conclusions:
State error variables , parameter error variables and the adaptive laws , , are kept bounded in probability.
asymptotically converges to in probability.
One can deduce the above-mentioned conclusions by Lemmas 1 and 3 as follows:
Step 1: From the observation of (
56), the stochastic Lyapunov function of system (
23) can be rewritten as
where
, and
. The result of boundness in Lemma 1 can be directly utilized for (
57). By the analysis in [
26],
t can be further extended to
. Immediately, one obtains that state error variables
, parameter error variables
and the adaptive laws
,
,
are bounded in probability.
Step 2: We set
for
. See Lemma 1 in [
16]. One thus obtains that
in (
53) are non-negative. Hence, from (
29), (
41) and (
49), the following constraints must hold:
Hence, the right of the adaptive laws (
30), (
40) and (
50) is non-negative. According to (
58), we have
where
are set as a bounded variable and the boundness of
is derived from (
57). It is noted that
in (
59) are designed as bounded constants. In succession, taking the integration and seeking expectation of (
59) yields
Subsequently, utilizing Lemma 3, one can obtain
From (
61) and the definition of
, one concludes that the rotor speed
asymptotically converges to its desired value
in probability.
5. Simulation Results
The simulation was established in a Python program for a 660 kW machine. In all simulations, we used the parameters of the wind turbine [
14] and generator [
18], as shown in
Table 1. The following operating point is chosen as:
,
,
by letting the right of (
1), (
2) and (
14) equal zero. The function
in (
12) in this paper is chosen as
[
27] by means of modeling wind speed based on stochastic processes. And note that
are the coefficients of the quadratic polynomial fit for
at a stochastic wind speed whose mean value is 15 m/s.
In this section, a new stochastic asymptotic control is designed for the wind turbine with stochastic wind speed.
The initial conditions for the DFIG-WT system are designed as
, and initial conditions for adaptive laws
are all set to be zero. The controller parameters
,
,
,
,
of the stochastic backstepping control are chosen as follows: To avoid instability,
must be satisfied, and to guarantee the adaptive rate of
, we choose
,
,
,
,
and
. Furthermore, the adaptive rate of
can be controlled by increasing
,
,
. Hence, we select
,
and
in this simulation. Similarly,
,
and
are chosen. The parameters
are chosen according to the work in [
16] showing that smaller gain will improve convergence performance. In addition, large positive gain
,
,
,
can be obtained to satisfy young’s inequality of (
19).
The following two cases are considered to validate the effectiveness of the proposed controller.
Case 1: All physical parameters are known and kept constant;
Case 2: Values a, b, c, , , , are unknown and subject to slow variation due to the complex operating conditions compared with the conventional backstepping method.
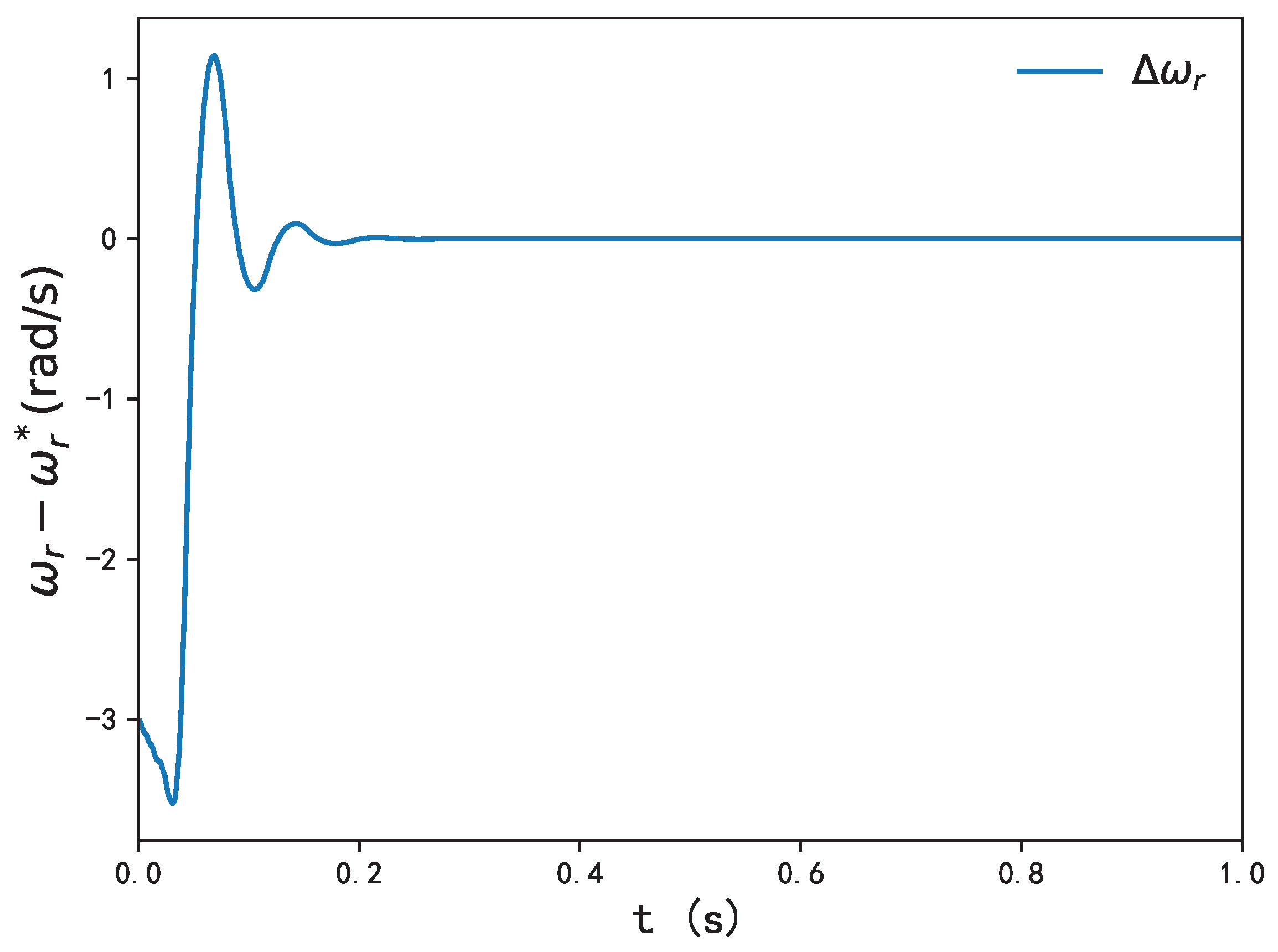
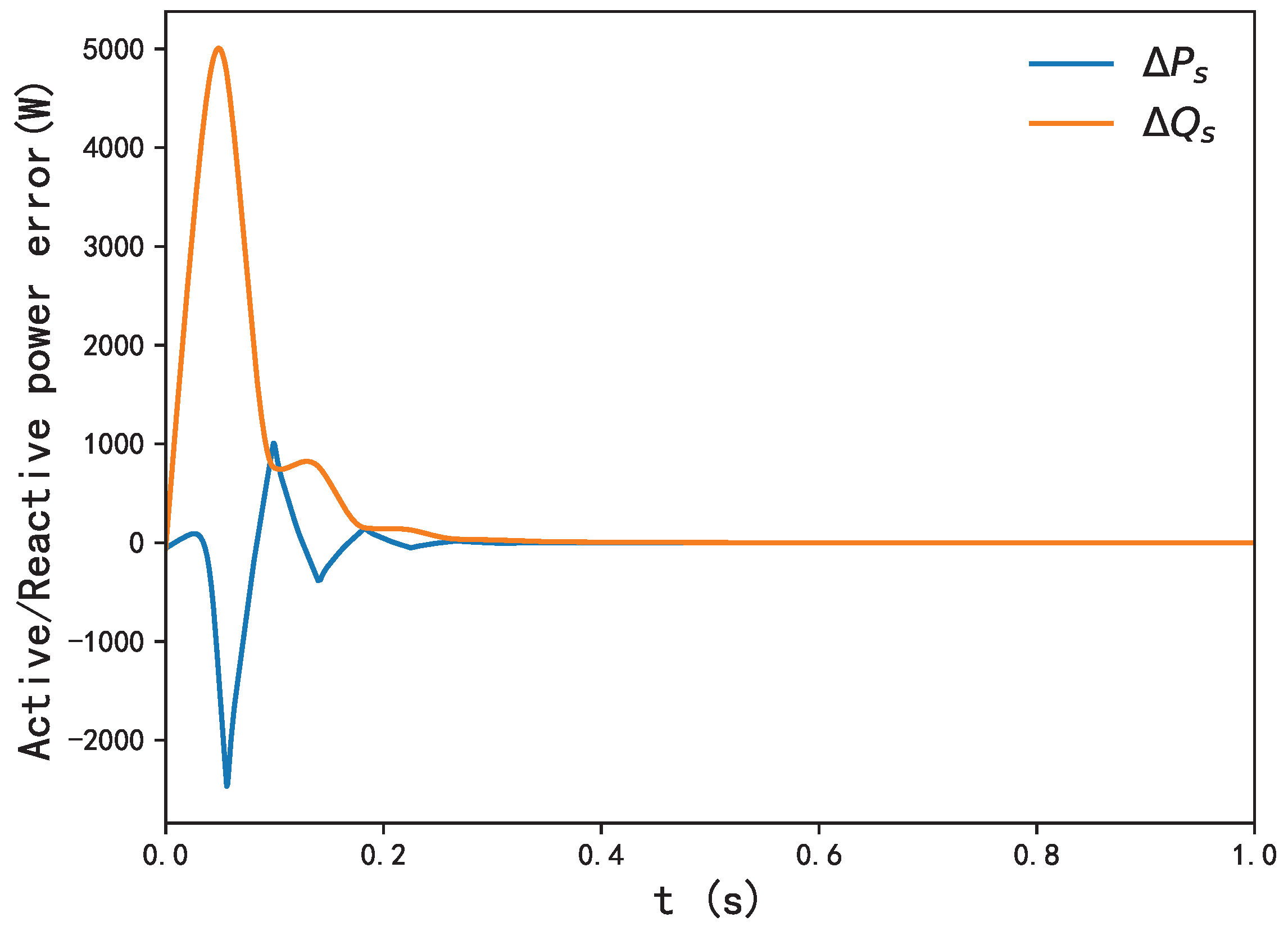
(1) Concerning the output active/reactive power of DFIG-WT,
Figure 6 depicts the error between power reference
and
. The figures show that when the wind velocity fluctuates the mean value with white noise up and down, the errors between
and
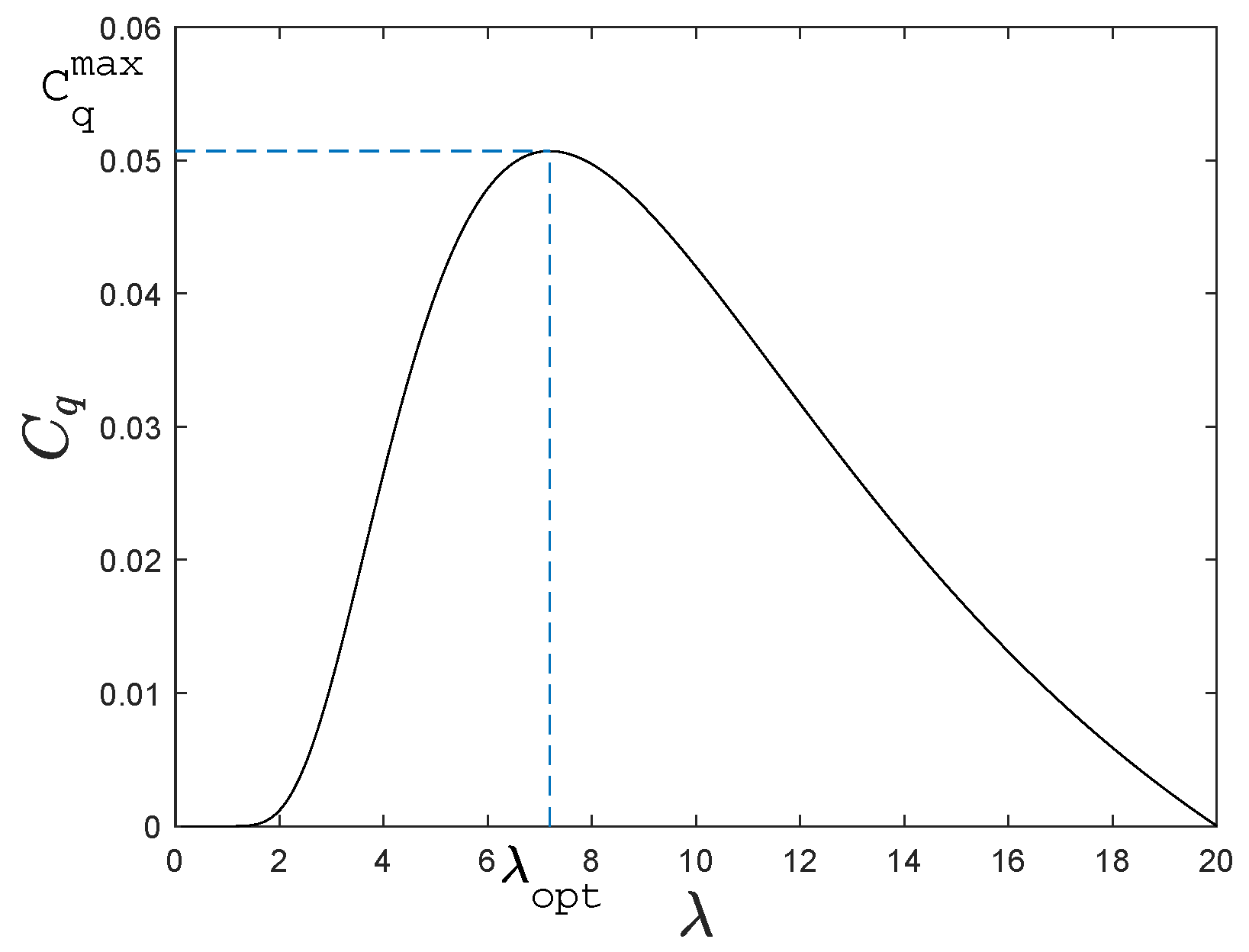
are approximately zero with the proposed method. This is mainly because the torque coefficient
remains around
, as shown in
Figure 2. In other words, with the proposed method, the main objective, which is to have
to
, is completely achieved. Rotor speed
converges swiftly to its optimal speed (
9) at 2.2 s, as shown in
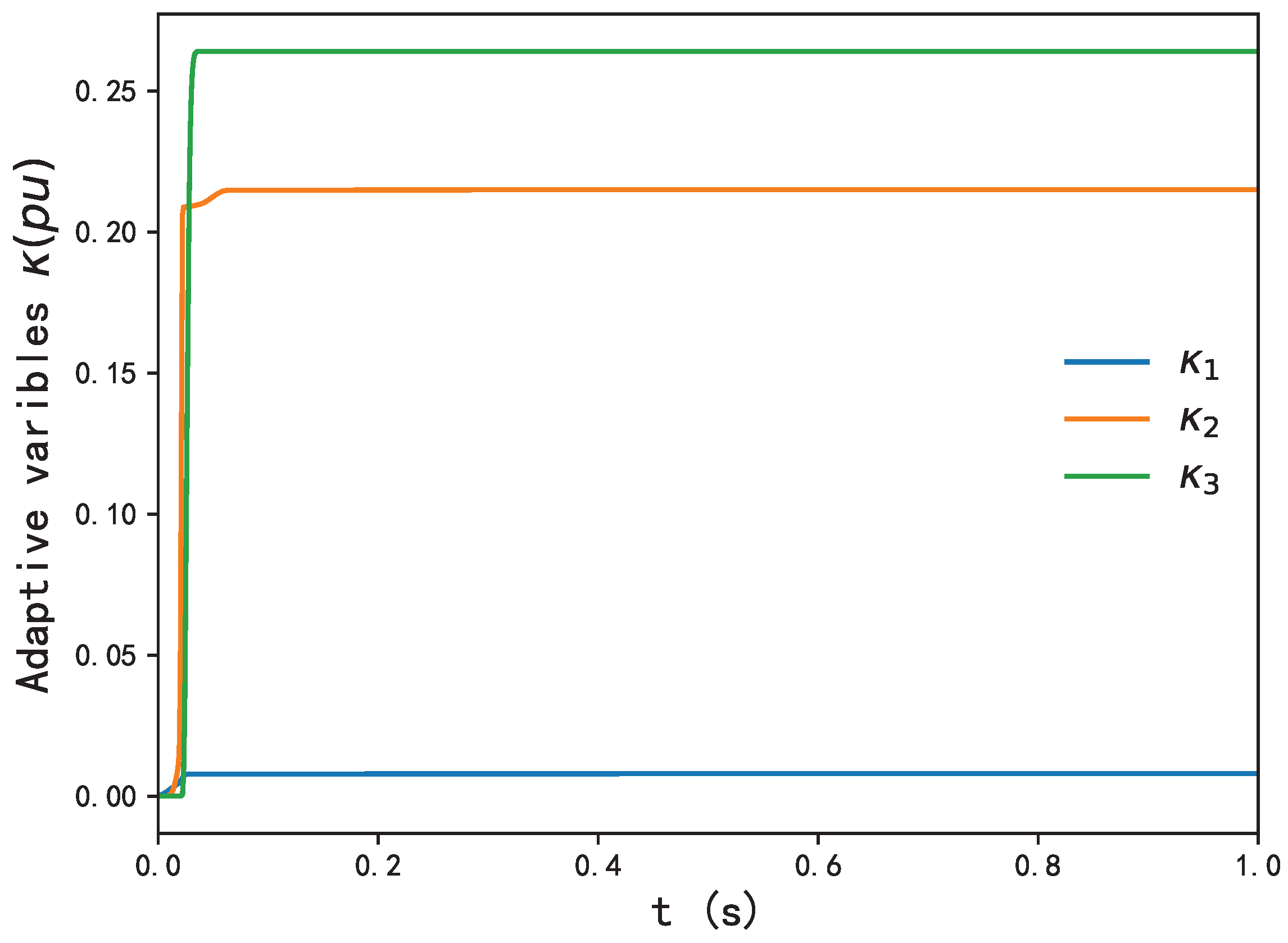
Figure 5. In the meantime, adaptive laws
,
and
for updating the virtual controller are presented in
Figure 7. As depicted in
Figure 7, adaptive laws containing
,
and
quickly converge to stable values with the proposed controller. Therefore, it is shown that the proposed controller has the capacity of achieving the asymptotic control for stochastic nonlinear systems of DFIG-WT.
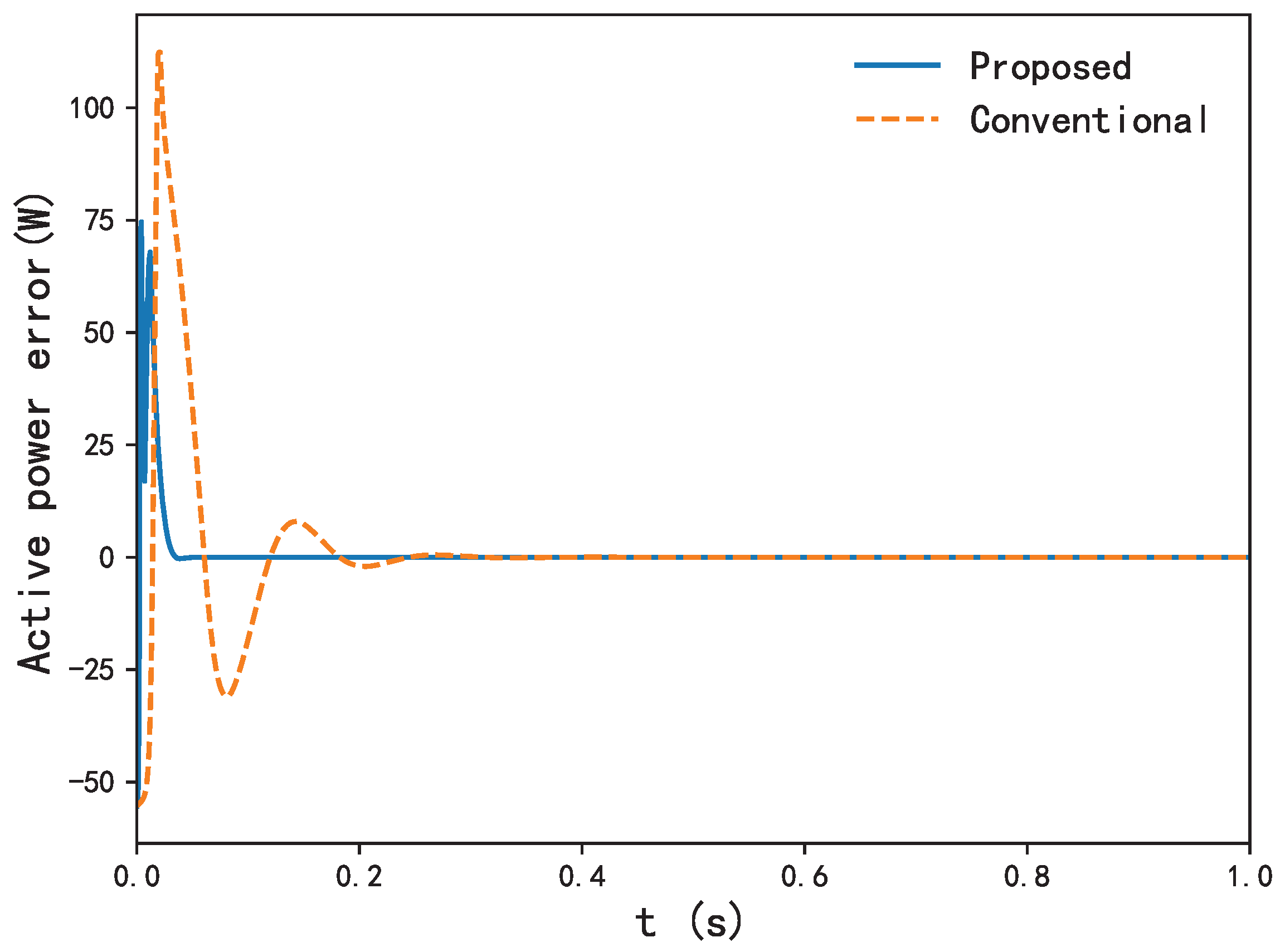
(2) In Case 2, the parameters of the system are subject to changes due to various physical phenomena; so, our controller should provide effective control when the variation of the generator parameters is bounded in comparison with the conventional backstepping controller. In order to test the robustness of the controller, we varied the rotor resistance to , the inductance value of the rotor and stator from its nominal value and the parameters of mechanical torque from their current value.
Similarly,
Figure 8,
Figure 9 and
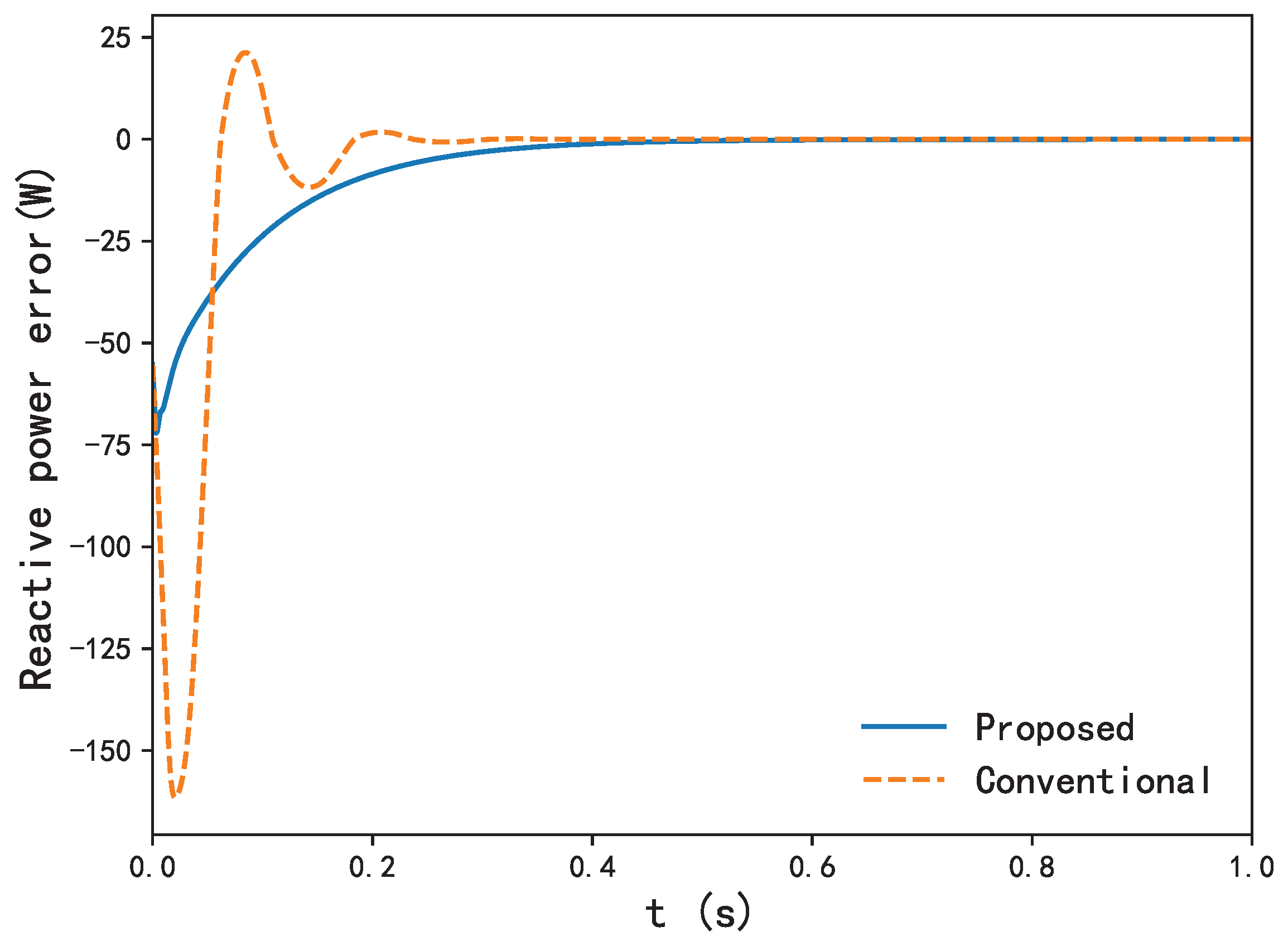
Figure 10 demonstrate that in Case 2,
,
and
converge to zero, while
,
and
converge to their desired references. With the conventional method, however, the convergence rate is much slower compared with proposed controller.
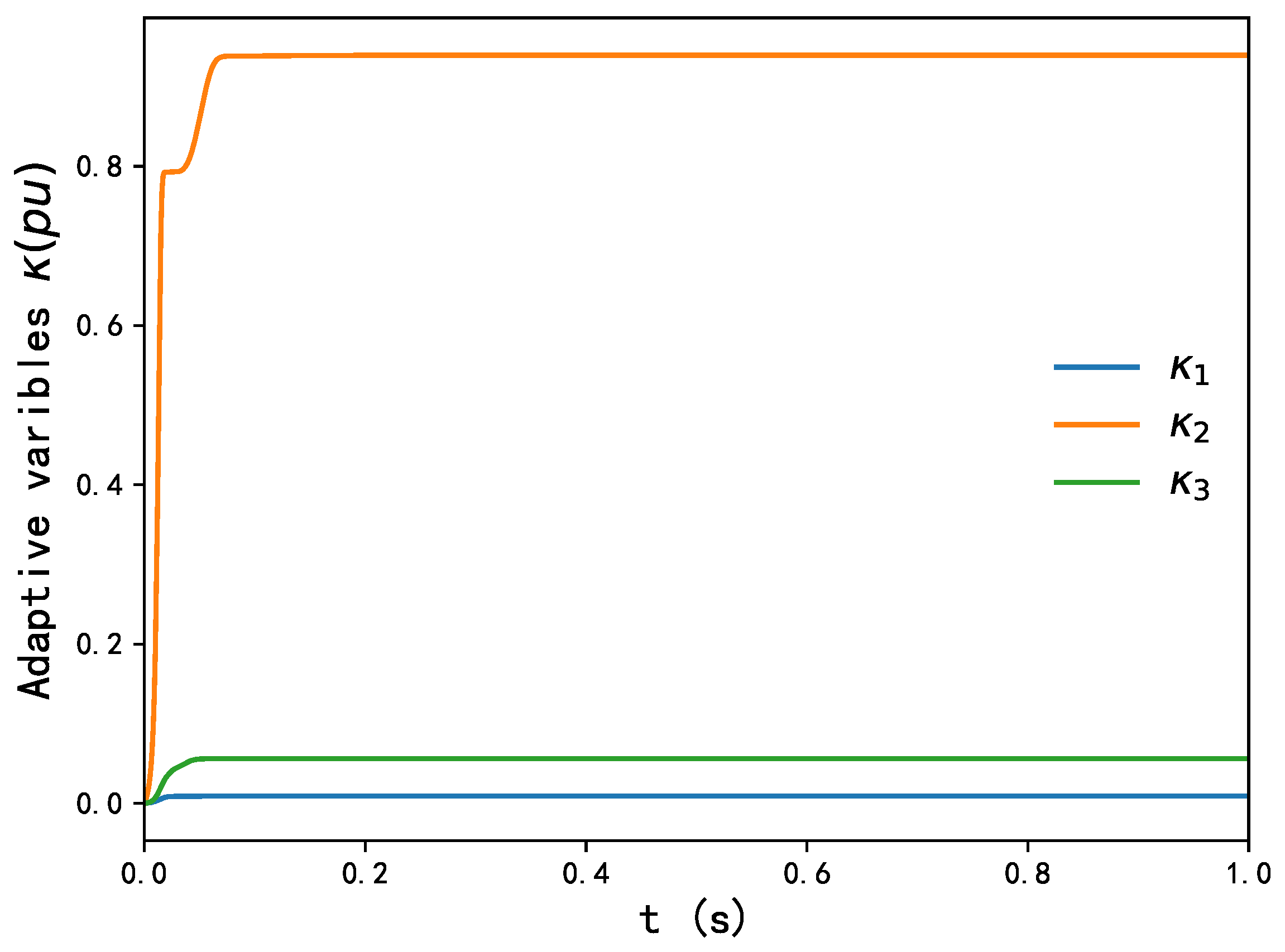
Figure 12 shows
are always positive if its initial values are non-negative. Again, adaptive laws containing
,
and
converge to stability with the proposed controller in
Figure 11.
Figure 8,
Figure 9,
Figure 10,
Figure 11 and
Figure 12 show the effectiveness of varying the parameters of the generator
,
and
on the response of
,
and
, which is directly related to the output active power and reactive power of DFIG-WT, and the performance with variation of parameters is effective for its swift convergence to the desired trajectory compared with the conventional backstepping controller.