An Intermodular Active Balancing Topology for Efficient Operation of High Voltage Battery Packs in Li-Ion Based Energy Storage Systems: Switched (Flying) DC/DC Converter
Abstract
1. Introduction
- (i)
- To present a robust, relatively low-cost, and flexible bidirectional AB topology that eliminates the requirement for multiple power converters, power diodes, transformers, power inductors, and/or auxiliary accumulators that require two additional steps of conversion, thus achieving reduced complexity, a lower failure rate, and lower costs by minimizing the number of components;
- (ii)
- To implement a hardware prototype, including a commercial BMS circuit, DC/DC converter, and switch matrix, to prove that the presented method can be implemented in a real-world application with readily available off-the-shelf components;
- (iii)
- To verify the AB operation by equalizing cells not only within a module but also among the modules as a proof of intermodular balancing concept and achieving pack-level homogeneity for both series-connected and parallel-connected configurations of realistically sized 24-V modules, including a large high voltage (HV) battery pack scenario; and
- (iv)
- To demonstrate the increased runtime and energy delivery of the proposed AB topology when the LIB is under load.
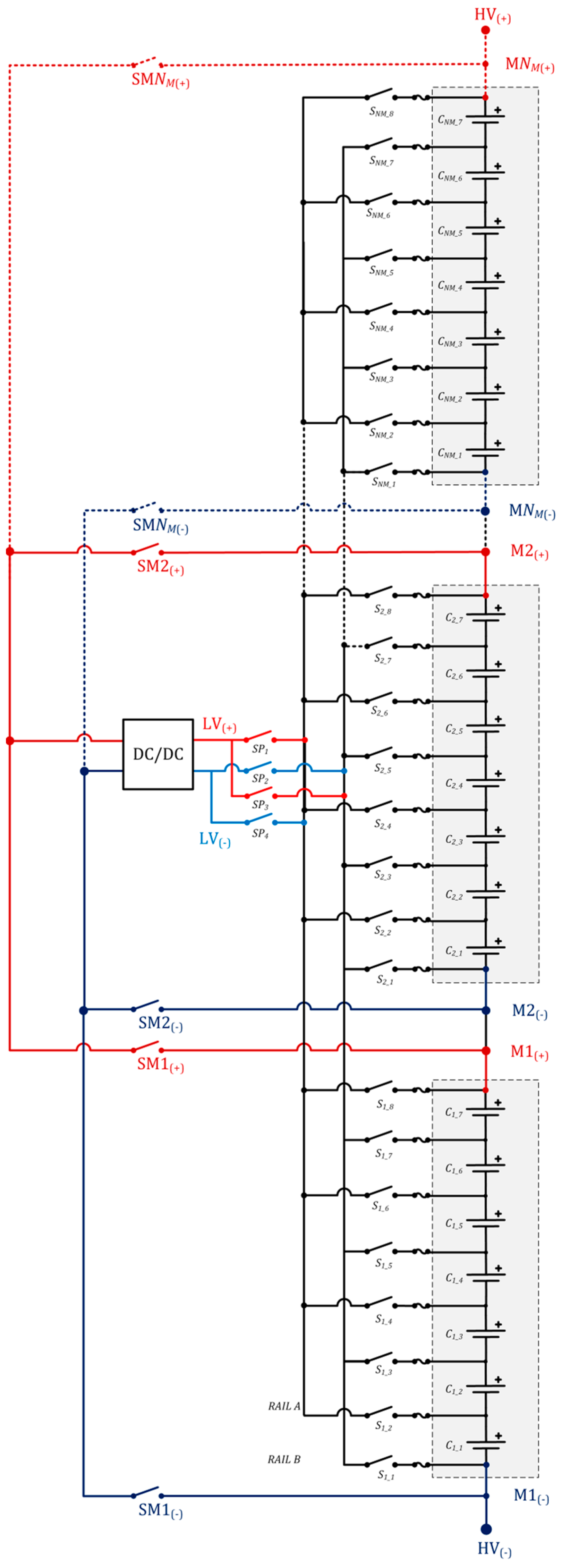
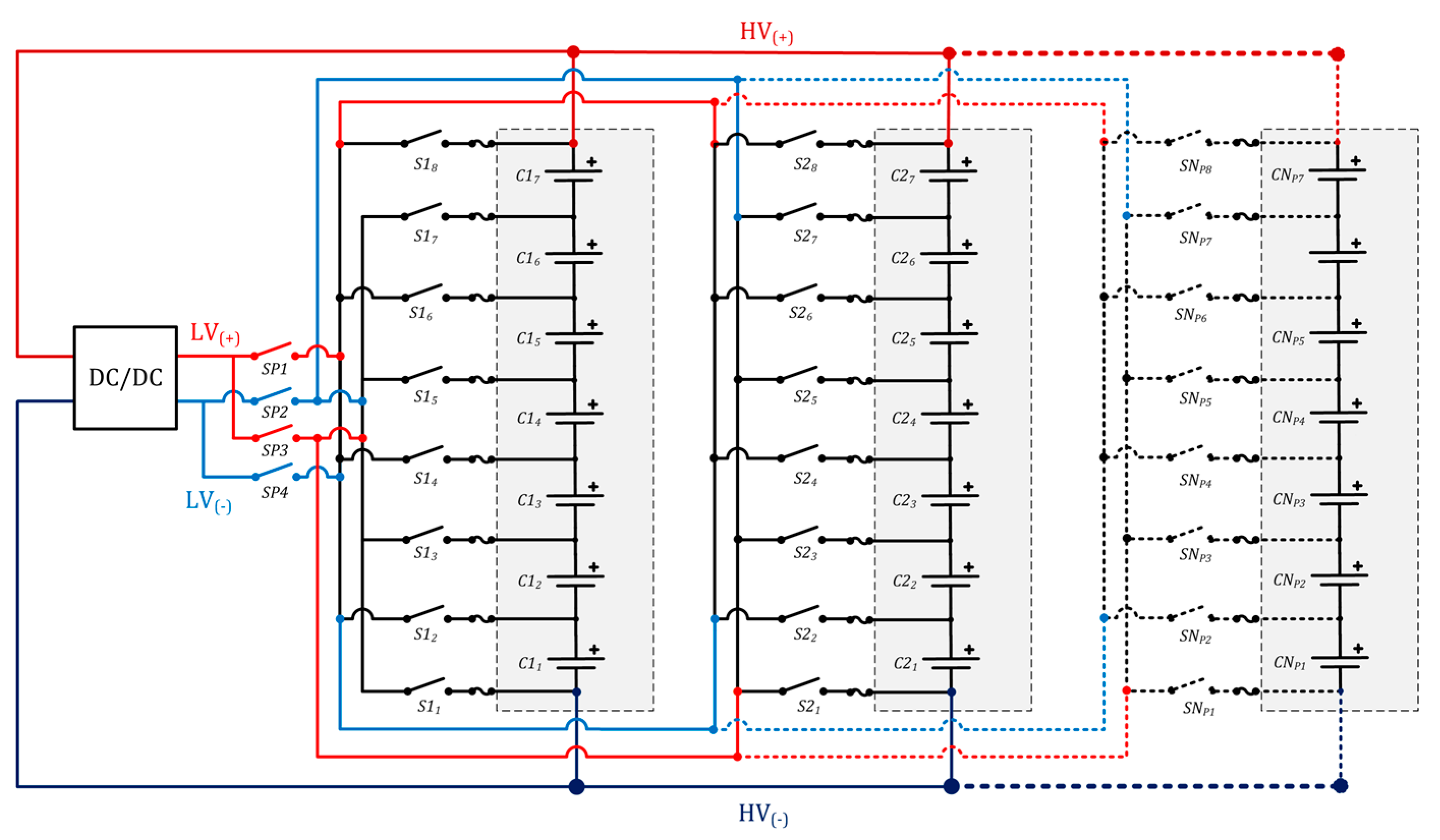
2. The Switched Converter Topology
2.1. S–P (Series of Parallel) Configuration
2.2. P–S (Parallel of Series) Configuration
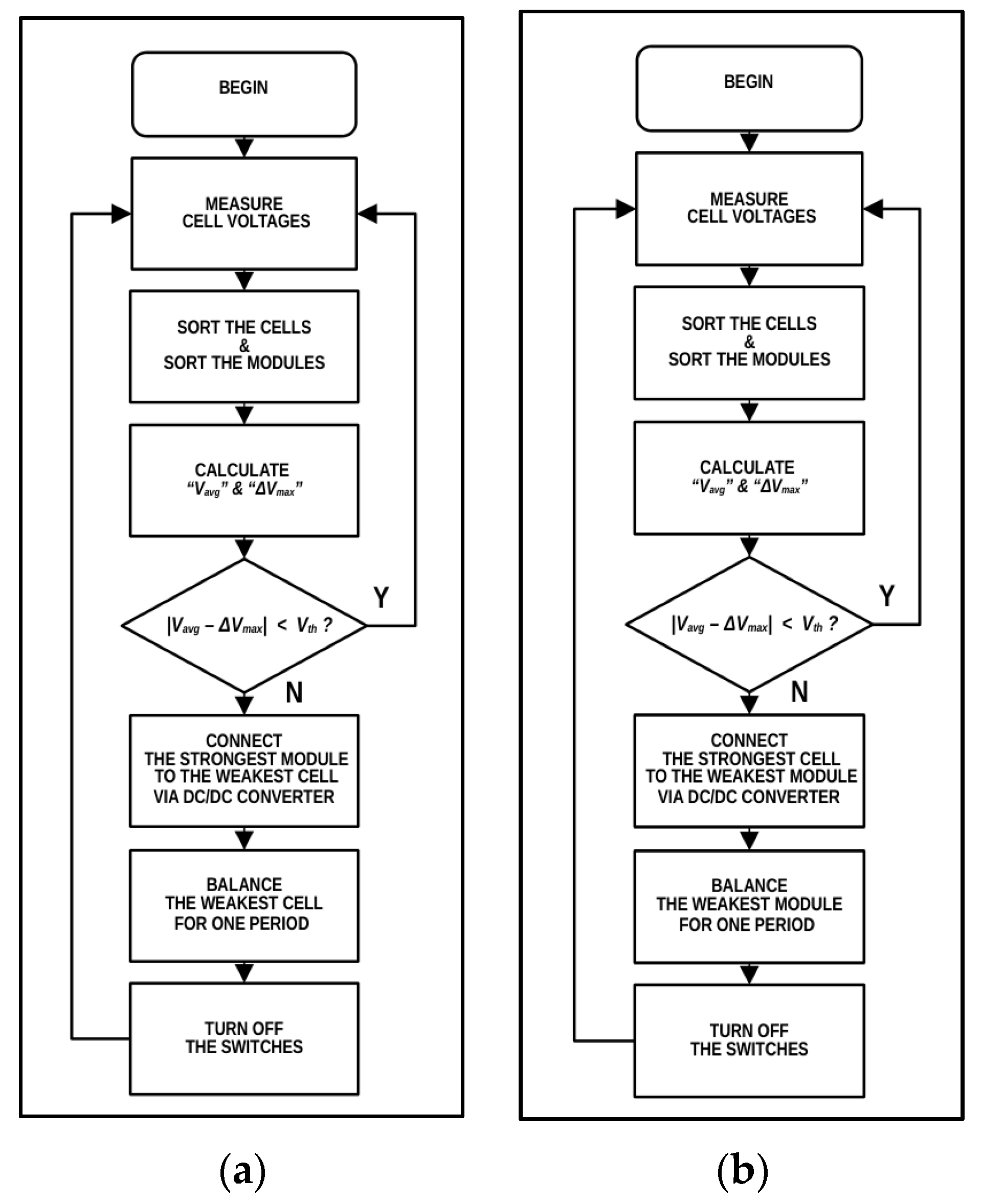
2.3. Balancing Algorithm
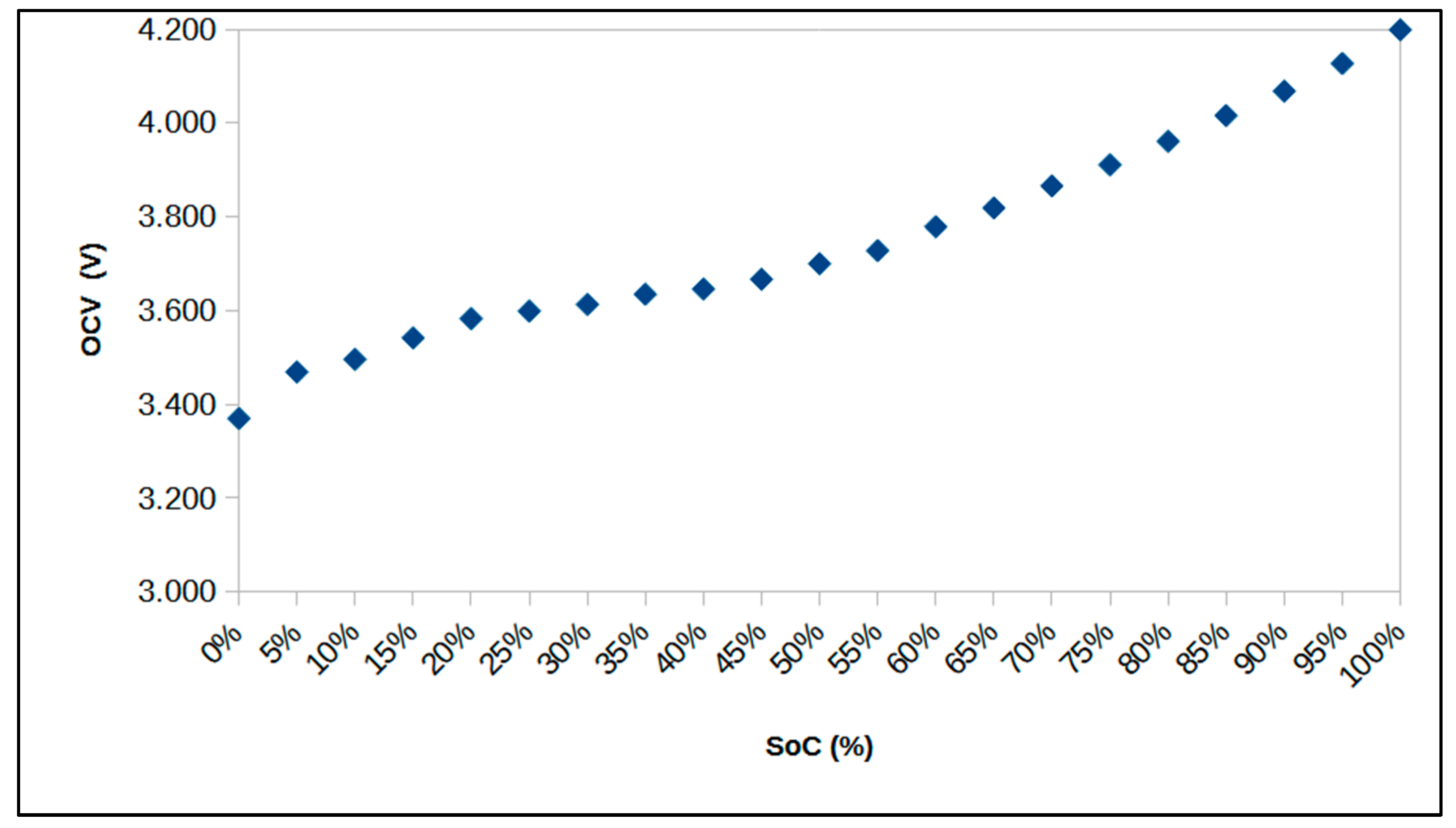
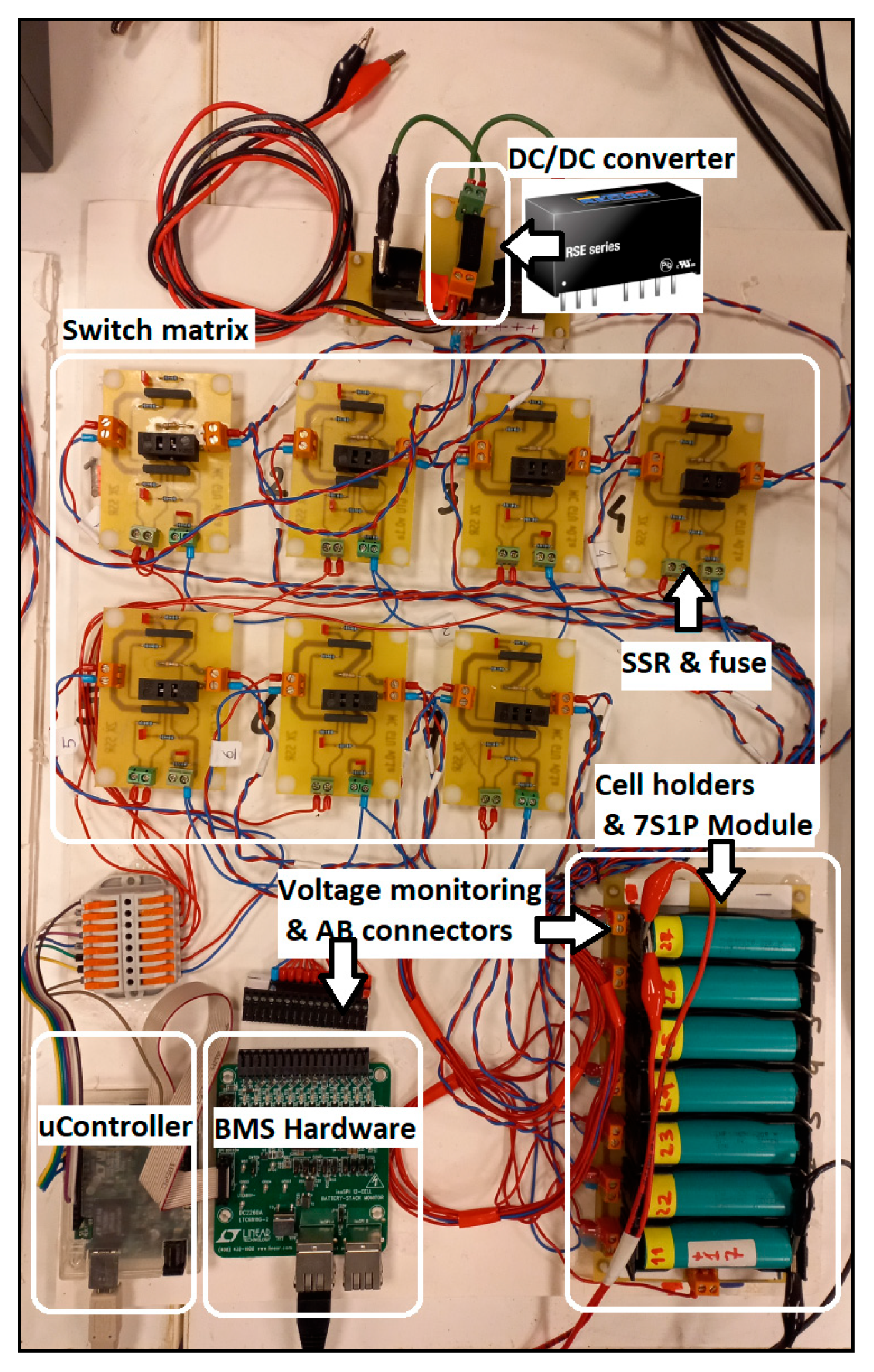
3. Experimental Setup, Materials, and Component Selection
4. Results and Discussion
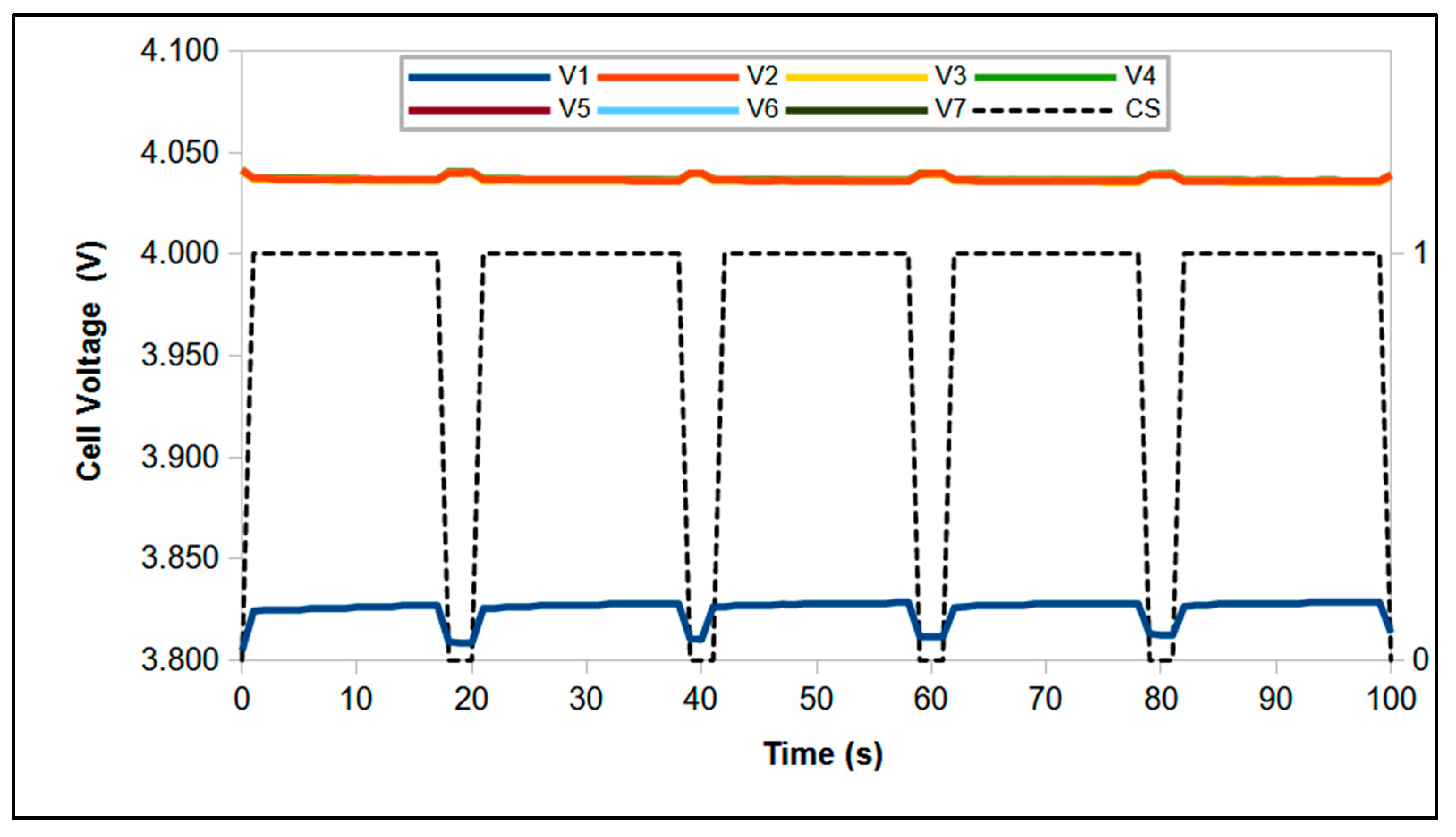
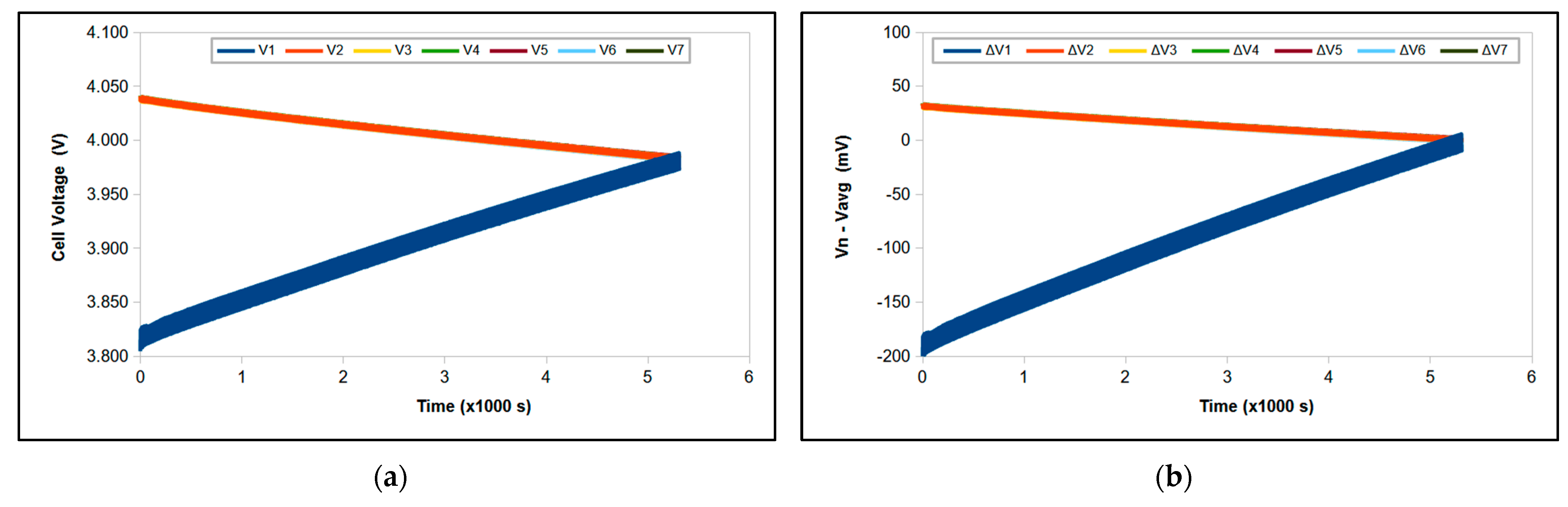
4.1. S–P Single Module (Intramodular) Balancing
4.2. P–S Multimodule (Intermodular) Balancing
4.3. S–P Multimodule (Intermodular) High Voltage Balancing
4.4. AB Verification under Load
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AB | Active Balancing |
| ADC | Analog to Digital Converter |
| AFE | Analog Front End |
| BESS | Battery Energy Storage System |
| BMS | Battery Management System |
| C | C-rate |
| CTC | Cell-to-Chassis Construction |
| CTP | Cell-to-Pack Construction |
| DC | Direct Current |
| DG | Distributed Generation |
| DMM | Digital Multimeter |
| DPDT | Double-Pole Double-Throw |
| ΔSOCmax | Maximum State of Charge Deviation |
| ΔVmax | Maximum Voltage Deviation |
| ESR | Equivalent Series Resistance |
| ESS | Energy Storage System |
| EV | Electric Vehicle |
| H/EV | Hybrid/Electric Vehicle |
| HV | High Voltage |
| IC | Integrated Circuit |
| LFP | Lithium–Iron–Phosphate |
| LIB | Lithium–Ion Battery |
| MOSFET | Metal–Oxide Semiconductor Field Effect Transistor |
| NMC | Nickel–Manganese–Cobalt |
| OCV | Open Circuit Voltage |
| OV | Over-Voltage |
| PB | Passive Balancing |
| PC | Personal Computer |
| PCB | Printed Circuit Board |
| P–S | Parallel Connection of Series Cells |
| Qnom | Nominal Capacity |
| REP | Renewable Energy Plant |
| SC | Super Capacitor |
| SoC | State of Charge |
| SoCavg | Average State of Charge Value |
| SoCmin | Minimum State of Charge Value (Module SoC) |
| SoCth | State of Charge Threshold for Balancing |
| S–P | Series Connection of Parallel Cells |
| SPI | Serial Peripheral Interface |
| UPS | Uninterrupted Power Supply |
| UV | Under-Voltage |
| USB | Universal Serial Bus |
| Vth | Voltage Threshold for Balancing |
| Vavg | Average Voltage Value |
References
- Ackermann, T.; Andersson, G.; Söder, L. Distributed generation: A definition. Electr. Power Syst. Res. 2001, 57, 195–204. [Google Scholar] [CrossRef]
- Gozel, T.; Hocaoglu, M.H.; Eminoglu, U.; Balikci, A. Optimal placement and sizing of distributed generation on radial feeder with different static load models. In Proceedings of the 2005 International Conference on Future Power Systems, Amsterdam, The Netherlands, 18 November 2005; pp. 2–6. [Google Scholar] [CrossRef]
- Chen, H.; Cong, T.N.; Yang, W.; Tan, C.; Li, Y.; Ding, Y. Progress in electrical energy storage system: A critical review. Prog. Nat. Sci. 2009, 19, 291–312. [Google Scholar] [CrossRef]
- Oskouei, M.Z.; Seker, A.A.; Tuncel, S.; Demirbas, E.; Gozel, T.; Hocaoglu, M.H.; Abapour, M.; Mohammadi-Ivatloo, B. A Critical Review on the Impacts of Energy Storage Systems and Demand-Side Management Strategies in the Economic Operation of Renewable-Based Distribution Network. Sustainability 2022, 14, 2110. [Google Scholar] [CrossRef]
- Di Piazza, M.C.; Luna, M.; La Tona, G.; Di Piazza, A. Energy Management of Hybrid PV-Storage Systems for Improved Grid Integration. In Proceedings of the IEEE International Conference on Environment and Electrical Engineering and IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Milan, Italy, 6–9 June 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Hesse, H.C.; Kumtepeli, V.; Schimpe, M.; Reniers, J.; Howey, D.A.; Tripathi, A.; Wang, Y.; Jossen, A. Ageing and Efficiency Aware Battery Dispatch for Arbitrage Markets Using Mixed Integer Linear Programming. Energies 2019, 12, 999. [Google Scholar] [CrossRef]
- Di Piazza, M.C.; Luna, M.; La Tona, G. A Survey of Energy Management Systems Considering Battery State of Health Preservation in Microgrid Applications. In Lecture Notes in Electrical Engineering; Springer: Berlin/Heidelberg, Germany, 2023; p. 993. [Google Scholar] [CrossRef]
- Sepulveda, N.A.; Jenkins, J.D.; Edington, A.; Mallapragada, D.S.; Lester, R.K. The design space for long-duration energy storage in decarbonized power systems. Nat. Energy 2021, 6, 506–516. [Google Scholar] [CrossRef]
- Luna, M.; La Tona, G.; Accetta, A.; Pucci, M.; Pietra, A.; Di Piazza, M.C. Optimal Management of Battery and Fuel Cell-Based Decentralized Generation in DC Shipboard Microgrids. Energies 2023, 16, 1682. [Google Scholar] [CrossRef]
- Widyantara, R.D.; Zulaikah, S.; Juangsa, F.B.; Budiman, B.A.; Aziz, M. Review on Battery Packing Design Strategies for Superior Thermal Management in Electric Vehicles. Batteries 2022, 8, 287. [Google Scholar] [CrossRef]
- Pampel, F.; Pischinger, S.; Teuber, M. A systematic comparison of the packing density of battery cell-to-pack concepts at different degrees of implementation. Results Eng. 2021, 13, 100310. [Google Scholar] [CrossRef]
- Kampker, A.; Heimes, H.H.; Offermanns, C.; Vienenkötter, J.; Robben, T. Framework and Classification of Battery System Architectures. World Electr. Veh. J. 2023, 14, 88. [Google Scholar] [CrossRef]
- Belingardi, G.; Scattina, A. Battery Pack and Underbody: Integration in the Structure Design for Battery Electric Vehicles—Challenges and Solutions. Vehicles 2023, 5, 498–514. [Google Scholar] [CrossRef]
- Waag, W.; Fleischer, C.; Sauer, D.U. Critical review of the methods for monitoring of lithium-ion batteries in electric and hybrid vehicles. J. Power Sources 2014, 258, 321–339. [Google Scholar] [CrossRef]
- Liu, W.; Placke, T.; Chau, K.T. Overview of batteries and battery management for electric vehicles. Energy Rep. 2022, 8, 4058–4084. [Google Scholar] [CrossRef]
- Baumhöfer, T.; Brühl, M.; Rothgang, S.; Sauer, D.U. Production caused variation in capacity aging trend and correlation to initial cell performance. J. Power Sources 2014, 247, 332–338. [Google Scholar] [CrossRef]
- Zilberman, I.; Schmitt, J.; Ludwig, S.; Naumann, M.; Jossen, A. Simulation of voltage imbalance in large lithium-ion battery packs influenced by cell-to-cell variations and balancing systems. J. Energy Storage 2020, 32, 101828. [Google Scholar] [CrossRef]
- Schindler, M.; Sturm, J.; Ludwig, S.; Schmitt, J.; Jossen, A. Evolution of initial cell-to-cell variations during a three-year production cycle. eTransportation 2021, 8, 100102. [Google Scholar] [CrossRef]
- Beck, D.; Dechent, P.; Junker, M.; Sauer, D.U.; Dubarry, M. Inhomogeneities and cell-to-cell variations in lithium-ion batteries, a review. Energies 2021, 14, 3276. [Google Scholar] [CrossRef]
- Hopkins, D.C.; Mosling, C.R.; Hung, S.T. The Use of Equalizing Converters for Serial Charging of Long Battery Strings. In Proceedings of the Applied Power Electronics Conference APEC, Dallas, TX, USA, 10–15 March 1991; pp. 493–498. [Google Scholar]
- Pascual, C.; Krein, P.T. Switched capacitor system for automatic series battery equalization. In Proceedings of the Applied Power Electronics Conference, Atlanta, GA, USA, 27 February 1997; pp. 848–854. [Google Scholar]
- Moore, S.W.; Schneider, P.J. A Review of Cell Equalization Methods for Lithium Ion and Lithium Polymer Battery Systems; SAE Technical Paper 2001-01-0959; Society of Automotive Engineers (SAE): London, UK, 2001. [Google Scholar]
- Cao, J.; Schofield, N.; Emadi, A. Battery Balancing Methods: A Comprehensive Review. In Proceedings of the IEEE Vehicle Power and Propulsion Conference VPPC, Harbin, China, 3–5 September 2008. [Google Scholar]
- Carter, J.; Fan, Z.; Cao, J. Cell equalisation circuits: A review. J. Power Sources 2020, 448, 227489. [Google Scholar] [CrossRef]
- Cassani, P.A.; Williamson, S.S. Significance of battery cell equalization and monitoring for practical commercialization of plug-in hybrid electric vehicles. In Proceedings of the Applied Power Electronics Conference APEC, Washington, DC, USA, 15–19 February 2009; pp. 465–471. [Google Scholar]
- Yuanmao, Y.; Cheng, K.W.E.; Yeung, Y.P.B. Zero-current switching switched-capacitor zero-voltage-gap automatic equalization system for series battery string. IEEE Trans. Power Electron. 2012, 27, 3234–3242. [Google Scholar] [CrossRef]
- Einhorn, M.; Guertlschmid, W.; Blochberger, T.; Kumpusch, R.; Permann, R.; Conte, F.V.; Kral, C.; Fleig, J. A current equalization method for serially connected battery cells using a single power converter for each cell. IEEE Trans. Veh. Technol. 2011, 60, 4227–4237. [Google Scholar] [CrossRef]
- Olalla, C.; Clement, D.; Rodriguez, M.; Maksimovic, D. Architectures and control of submodule integrated DC–DC converters for photovoltaic applications. IEEE Trans. Power Electron. 2013, 28, 2980–2997. [Google Scholar] [CrossRef]
- Costinett, D.; Hathaway, K.; Rehman, M.U.; Evzelman, M.; Zane, R.; Levron, Y.; Maksimovic, D. Active balancing system for electric vehicles with incorporated low voltage bus. In Proceedings of the Applied Power Electronics Conference and Exposition APEC, Fort Worth, TX, USA, 16–20 March 2014; pp. 3230–3236. [Google Scholar]
- Gallardo-Lozano, J.; Romero-Cadaval, E.; Milanes-Montero, M.I.; Guerrero-Martinez, M.A. Battery equalization active methods. J. Power Sources 2014, 246, 934–949. [Google Scholar] [CrossRef]
- Baronti, F.; Roncella, R.; Saletti, R. Performance comparison of active balancing techniques for lithium-ion batteries. J. Power Sources 2014, 267, 603–609. [Google Scholar] [CrossRef]
- Guo, X.; Kang, L.; Huang, Z.; Yao, Y.; Yang, H. Research on a novel power inductor-based bidirectional lossless equalization circuit for series-connected battery packs. Energies 2015, 8, 5555–5576. [Google Scholar] [CrossRef]
- Pinto, C.; de Castro, R.; Barreras, J.V.; Araújo, R.E.; Howey, D.A. Smart Balancing Control of a Hybrid Energy Storage System Based on a Cell-to-Cell Shared Energy Transfer Configuration. In Proceedings of the IEEE Vehicle Power and Propulsion Conference (VPPC), IEEE Transactions on Vehicular Technology VPPC, Chicago, IL, USA, 27–30 August 2018; pp. 1–6. [Google Scholar]
- Pozzi, A.; Zambelli, M.; Ferrara, A.; Raimondo, D.M. Balancing-aware charging strategy for series-connected lithium-ion cells: A nonlinear model predictive control approach. IEEE Trans. Control Syst. Technol. 2020, 28, 1862–1877. [Google Scholar] [CrossRef]
- Farhangi, B.; Toliyat, H.A. Modeling and Analyzing Multiport Isolation Transformer Capacitive Components for Onboard Vehicular Power Conditioners. IEEE Trans. Ind. Electron. 2014, 62, 3134–3142. [Google Scholar] [CrossRef]
- Pereira, T.; Hoffmann, F.; Zhu, R.; Liserre, M. A Comprehensive Assessment of Multiwinding Transformer-Based DC–DC Converters. IEEE Trans. Power Electron. 2021, 36, 10020–10036. [Google Scholar] [CrossRef]
- Zhang, Z.; Ouyang, Z.; Thomsen, O.C.; Andersen, M.A.E. Analysis and Design of a Bidirectional Isolated DC–DC Converter for Fuel Cells and Supercapacitors Hybrid System. IEEE Trans. Power Electron. 2012, 27, 848–859. [Google Scholar] [CrossRef]
- Raghavendra, K.V.G.; Zeb, K.; Muthusamy, A.; Krishna, T.N.V.; Kumar, S.V.S.V.P.; Kim, D.-H.; Kim, M.-S.; Cho, H.-G.; Kim, H.-J. A Comprehensive Review of DC–DC Converter Topologies and Modulation Strategies with Recent Advances in Solar Photovoltaic Systems. Electronics 2020, 9, 31. [Google Scholar] [CrossRef]
- Chen, Z.; Zhou, J.; Zhou, F.; Xu, S. State-of-charge estimation of lithium-ion batteries based on improved H infinity filter algorithm and its novel equalization method. J. Clean. Prod. 2020, 290, 125180. [Google Scholar] [CrossRef]
- Han, W.; Zhang, L.; Han, Y. Computationally efficient methods for state of charge approximation and performance measure calculation in series-connected battery equalization systems. J. Power Sources 2015, 286, 145–158. [Google Scholar] [CrossRef]
- Piller, S.; Perrin, M.; Jossen, A. Methods for state-of-charge determination and their applications. J. Power Sources 2001, 96, 113–120. [Google Scholar] [CrossRef]
- Peng, J.; Meng, J.; Chen, D.; Liu, H.; Hao, S.; Sui, X.; Du, X. A Review of Lithium-Ion Battery Capacity Estimation Methods for Onboard Battery Management Systems: Recent Progress and Perspectives. Batteries 2022, 8, 229. [Google Scholar] [CrossRef]
- Chen, M.; Rincon-Mora, G.A. Accurate Electrical Battery Model Capable of Predicting Runtime and I–V Performance. IEEE Trans. Energy Convers. 2006, 21, 504–511. [Google Scholar] [CrossRef]
- Ceylan, M.; Cengiz, E.; Demir-Cakan, R.; Balikci, A. A Novel Lithium-Sulphur Battery Model for Automotive and Renewable Energy Applications. In Proceedings of the Advanced Battery Power Conference/Kraftwerk Batterie, Aachen, Germany, 27–29 April 2015. [Google Scholar] [CrossRef]
- Ceylan, M.; Balikci, A. A Temperature Dependent Model for LTO/NMC Batteries. ECS Trans. 2019, 95, 113. [Google Scholar] [CrossRef]
- INR18650-20R Cell Specification of Product; V1.2; Samsung SDI: Yongin, Republic of Korea, 2011.
- CPC1218 Datasheet; Rev. 6; IXYS: Milpitas, CA, USA, 2012.
- RSE Series Datasheet; Rev. 4; RECOM Power: Gmunden, Austria, 2020.
- LTC6804-1/LTC6804-2 Multicell Battery Monitors Datasheet; Rev. C; Analog Devices Incorporated: Wilmington, MA, USA, 2016.
- Linduino Datasheet; Rev. C; Analog Devices Incorporated: Wilmington, MA, USA, 2016.
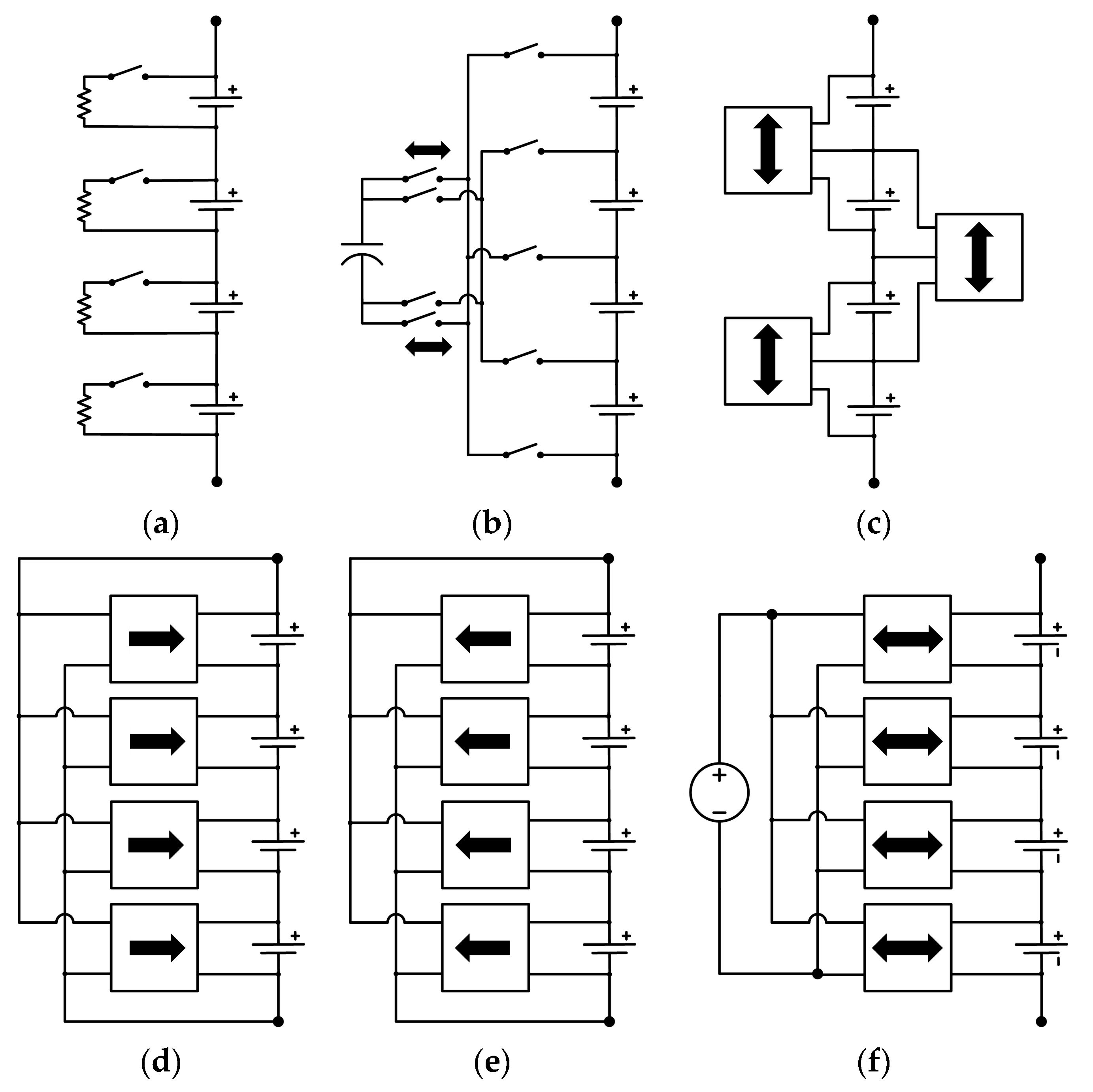





| AB Method | SW | C | L | D | T | CNV | AUX |
|---|---|---|---|---|---|---|---|
| Capacitor (single) | N + 5 | 1 | 0 | 0 | 0 | 0 | 0 |
| Capacitor (multi) | 2N | N-1 | 0 | 0 | 0 | 0 | 0 |
| Inductor (single) | 2N | 0 | 1 | 2N-2 | 0 | 0 | 0 |
| Inductor (multi) | 2N-2 | 0 | N-1 | 0 | 0 | 0 | 0 |
| Single-winding Transformer | N + 6 | 1 * | 0 | 1 | 1 | 0 | 0 |
| Multi-winding Transformer | 1 | N * | 0 | N | 1 | 0 | 0 |
| Multiple Transformer | 1 | N * | 0 | N | N | 0 | 0 |
| Multiple Converter | 0 | 0 | 0 | 0 | 0 | N | 1 ** |
| Switched Converter (Proposed) | N + 5 | 0 | 0 | 0 | 0 | 1 | 0 |
| Cell Form Factor/Capacity (Ah) | Cathode Material | Anode Material | Nominal Voltage (V) | Maximum Charge/Discharge Voltage (V) | Maximum Charge/Discharge Current (A) |
|---|---|---|---|---|---|
| 18,650/2 | Li-NMC | Graphite | 3.7 | 4.2/2.5 | 4/22 |
| Input Voltage Range [V] | Output Voltage [V] | Maximum Output Current [mA] | Typical Efficiency [%] | Isolation Voltage Rating [V] | Isolation Resistance [Ω] |
|---|---|---|---|---|---|
| 18–36 | 5 | 400 | 80 | 2000 (DC) | 109 |
| Cell Number | Initial Voltage (mV) | Initial ΔV (mV) | Final Voltage (mV) | Final ΔV (mV) |
|---|---|---|---|---|
| 1 * | 3804.7 | −202.5 | 3974.4 | −9.7 |
| 2 | 4041.4 | 34.2 | 3984.7 | 1.2 |
| 3 | 4040.6 | 33.4 | 3984.6 | 1.6 |
| 4 | 4041.5 | 34.3 | 3985.1 | 2.0 |
| 5 | 4041.3 | 34.1 | 3984.9 | 1.8 |
| 6 | 4040.6 | 33.4 | 3983 | 0.1 |
| 7 | 4040.5 | 33.3 | 3984.3 | 1.2 |
| Cell Number | Initial SoC (%) | Initial ΔSoC (%) | Final SoC (%) | Final ΔSoC (%) |
|---|---|---|---|---|
| 1 * | 63.2 | −20.7 | 81.2 | −0.8 |
| 2 | 87.4 | 3.4 | 82.1 | 0.1 |
| 3 | 87.4 | 3.4 | 82.1 | 0.1 |
| 4 | 87.4 | 3.4 | 82.1 | 0.1 |
| 5 | 87.4 | 3.4 | 82.1 | 0.1 |
| 6 | 87.4 | 3.4 | 82.1 | 0.1 |
| 7 | 87.4 | 3.4 | 82.1 | 0.1 |
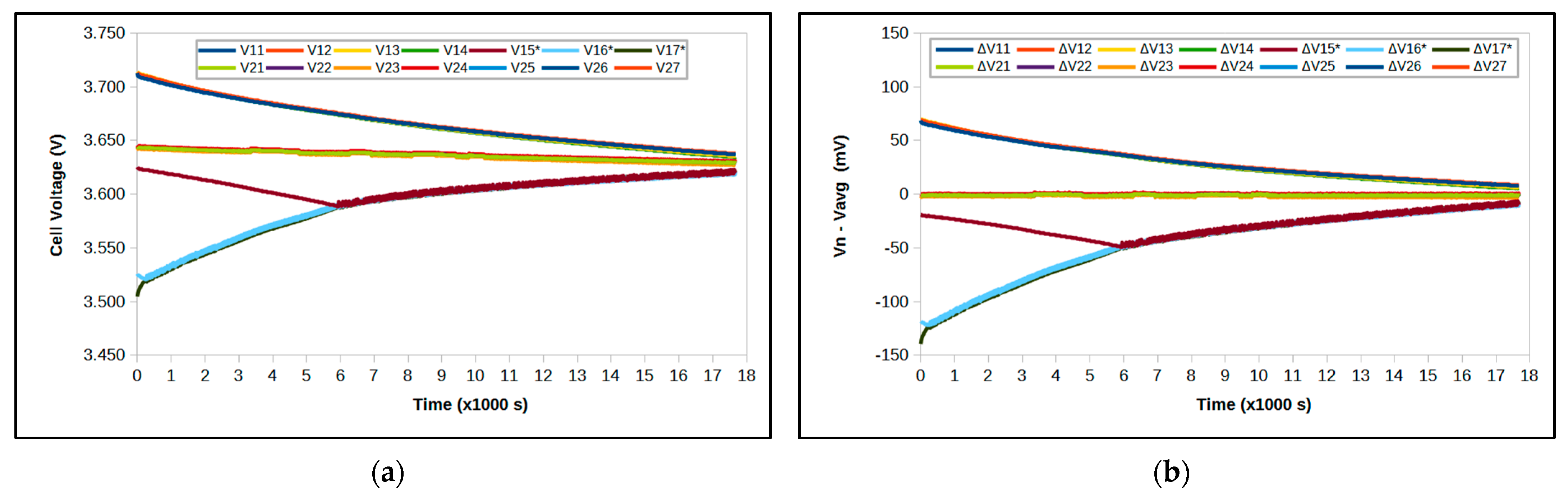
| Cell Number | Initial Voltage (mV) | Initial ΔV (mV) | Final Voltage (mV) | Final ΔV (mV) |
| 11 | 3712.8 | 68.6 | 3636.8 | 7.6 |
| 12 | 3713.3 | 69.1 | 3637.7 | 8.5 |
| 13 | 3714.2 | 70.0 | 3635.7 | 6.5 |
| 14 | 3713.3 | 69.1 | 3634.6 | 5.4 |
| 15 * | 3625.2 | −19.0 | 3619.4 | −9.8 |
| 16 * | 3525.8 | −118.4 | 3621.0 | −8.2 |
| 17 * | 3504.6 | −139.6 | 3619.5 | −9.7 |
| 21 | 3645.6 | −0.2 | 3628.8 | −0.2 |
| 22 | 3645.6 | −0.2 | 3629.1 | 0.1 |
| 23 | 3644.7 | −1.1 | 3627.4 | −1.6 |
| 24 | 3646.9 | 1.1 | 3630.2 | 1.2 |
| 25 | 3645.5 | −0.3 | 3628.6 | −0.4 |
| 26 | 3645.6 | −0.2 | 3628.9 | −0.1 |
| 27 | 3646.4 | 0.6 | 3630.2 | 1.2 |
| Module Number | Initial Voltage (V) | Initial ΔV (mV) | Final Voltage (V) | Final ΔV (mV) |
| M1 | 25.509 | −5.5 | 25.405 | 1 |
| M2 | 25.520 | 5.5 | 25.403 | −1 |
| Cell Number | Initial SoC (%) | Initial ΔSoC (%) | Final SoC (%) | Final ΔSoC (%) |
| 11 | 52.3 | 14.2 | 35.8 | 2.0 |
| 12 | 52.4 | 14.3 | 36.2 | 2.4 |
| 13 | 52.5 | 14.5 | 35.3 | 1.5 |
| 14 | 52.4 | 14.3 | 34.9 | 1.0 |
| 15 * | 32.8 | −5.3 | 31.5 | −2.4 |
| 16 * | 13.2 | −24.8 | 31.8 | −2.0 |
| 17 * | 10.9 | −27.1 | 31.5 | −2.4 |
| 21 | 39.8 | 0.2 | 33.6 | −0.1 |
| 22 | 39.8 | 0.2 | 33.7 | 0.0 |
| 23 | 39.4 | −0.2 | 33.3 | −0.4 |
| 24 | 39.4 | −0.2 | 33.9 | 0.3 |
| 25 | 39.4 | −0.2 | 33.5 | −0.1 |
| 26 | 39.4 | −0.2 | 33.6 | 0.0 |
| 27 | 40.1 | 0.5 | 33.9 | 0.3 |
| Module Number | Initial SoC (SoCmin) (%) | Initial ΔSoC (%) | Final SoC (SoCmin) (%) | Final ΔSoC (%) |
| M1 | 10.9 | −14.25 | 31.5 | −0.9 |
| M2 | 39.4 | 14.25 | 33.3 | 0.9 |
| Cell Number | Initial Voltage (mV) | Initial ΔV (mV) | Final Voltage (mV) | Final ΔV (mV) |
| 11 * | 3892.8 | −92.2 | 3809.0 | −0.1 |
| 12 | 4000.8 | 15.8 | 3807.9 | −1.2 |
| 13 | 4000.3 | 15.3 | 3808.7 | −0.4 |
| 14 | 4000.3 | 15.3 | 3808.4 | −0.7 |
| 15 | 4000.1 | 15.1 | 3809.3 | 0.2 |
| 16 | 4000.4 | 15.4 | 3811.0 | 1.9 |
| 17 | 4000.4 | 15.4 | 3809.5 | 0.4 |
| 21 * | 3562.4 | −87.7 | 3808.2 | −2.3 |
| 22 | 3754.7 | 14.6 | 3815.8 | 5.3 |
| 23 | 3754.9 | 14.8 | 3811.5 | 1.0 |
| 24 | 3754.7 | 14.6 | 3812.2 | 1.7 |
| 25 | 3754.8 | 14.7 | 3814.6 | 4.1 |
| 26 | 3754.6 | 14.5 | 3805.3 | −5.2 |
| 27 | 3754.8 | 14.7 | 3805.9 | −4.6 |
| Module Number | Initial Voltage (V) | Initial ΔV (mV) | Final Voltage (V) | Final ΔV (mV) |
| M1 | 27.895 | 857 | 26.664 | 5 |
| M2 | 26.181 | −857 | 26.674 | 5 |
| Cell Number | Initial SoC (%) | Initial ΔSoC (%) | Final SoC (%) | Final ΔSoC (%) |
| 11 * | 73.0 | −9.1 | 64.1 | 0.0 |
| 12 | 83.6 | 1.5 | 63.9 | −0.2 |
| 13 | 83.6 | 1.5 | 64.0 | −0.1 |
| 14 | 83.6 | 1.5 | 64.0 | −0.1 |
| 15 | 83.6 | 1.5 | 64.1 | 0.0 |
| 16 | 83.6 | 1.5 | 64.3 | 0.2 |
| 17 | 83.6 | 1.5 | 64.1 | 0.0 |
| 21 * | 41.5 | −13.8 | 63.6 | −0.3 |
| 22 | 57.6 | 2.3 | 64.6 | 0.7 |
| 23 | 57.6 | 2.3 | 64.1 | 0.1 |
| 24 | 57.6 | 2.3 | 64.1 | 0.2 |
| 25 | 57.6 | 2.3 | 64.5 | 0.5 |
| 26 | 57.6 | 2.3 | 63.3 | −0.6 |
| 27 | 57.6 | 2.3 | 63.4 | −0.6 |
| Module Number | Initial SoC (SoCmin) (%) | Initial ΔSoC (%) | Final SoC (SoCmin) (%) | Final ΔSoC (%) |
| M1 | 73.0 | 15.75 | 63.9 | 0.3 |
| M2 | 41.5 | −15.75 | 63.3 | −0.3 |
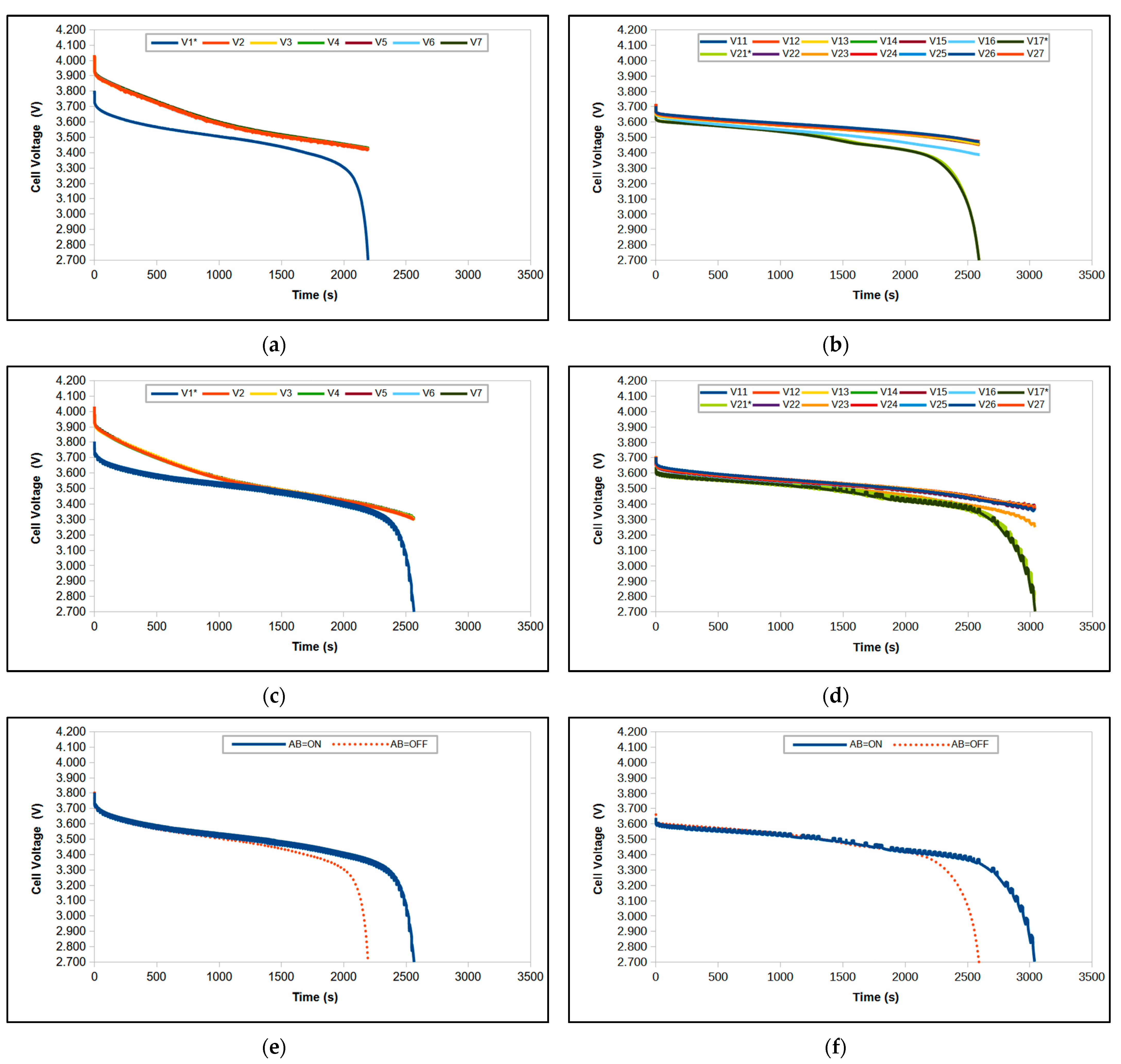
| Pack Type/Load (A) | Min. Initial Voltage (mV) | Min. Initial SoC (%) | Runtime AB = OFF (s) | Energy AB = OFF (Wh) | Runtime AB = ON (s) | Energy AB = ON (Wh) |
|---|---|---|---|---|---|---|
| 7S1P/2 | 3804.1 | 63 | 2195 | 30.562 | 2564 | 35.279 |
| 2P7S/2 | 3639.3 | 37 | 2592 | 35.748 | 3037 | 41.414 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ceylan, M.; Balikci, A. An Intermodular Active Balancing Topology for Efficient Operation of High Voltage Battery Packs in Li-Ion Based Energy Storage Systems: Switched (Flying) DC/DC Converter. Energies 2023, 16, 5608. https://doi.org/10.3390/en16155608
Ceylan M, Balikci A. An Intermodular Active Balancing Topology for Efficient Operation of High Voltage Battery Packs in Li-Ion Based Energy Storage Systems: Switched (Flying) DC/DC Converter. Energies. 2023; 16(15):5608. https://doi.org/10.3390/en16155608
Chicago/Turabian StyleCeylan, Murat, and Abdulkadir Balikci. 2023. "An Intermodular Active Balancing Topology for Efficient Operation of High Voltage Battery Packs in Li-Ion Based Energy Storage Systems: Switched (Flying) DC/DC Converter" Energies 16, no. 15: 5608. https://doi.org/10.3390/en16155608
APA StyleCeylan, M., & Balikci, A. (2023). An Intermodular Active Balancing Topology for Efficient Operation of High Voltage Battery Packs in Li-Ion Based Energy Storage Systems: Switched (Flying) DC/DC Converter. Energies, 16(15), 5608. https://doi.org/10.3390/en16155608







