Comparative Study of Passivity, Model Predictive, and Passivity-Based Model Predictive Controllers in Uninterruptible Power Supply Applications
Abstract
1. Introduction
2. Design of Controllers
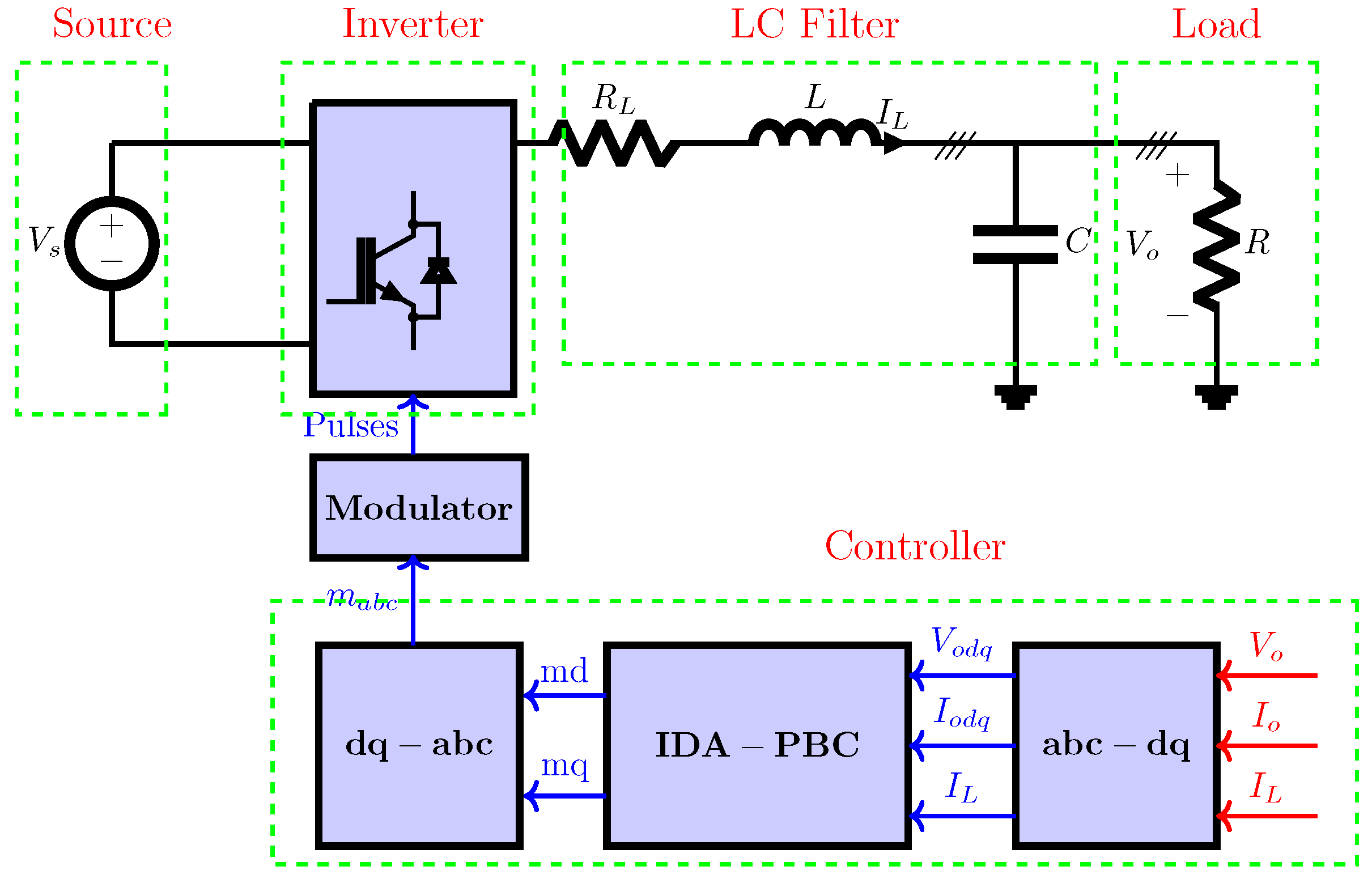
2.1. IDA-PBC Controller Design
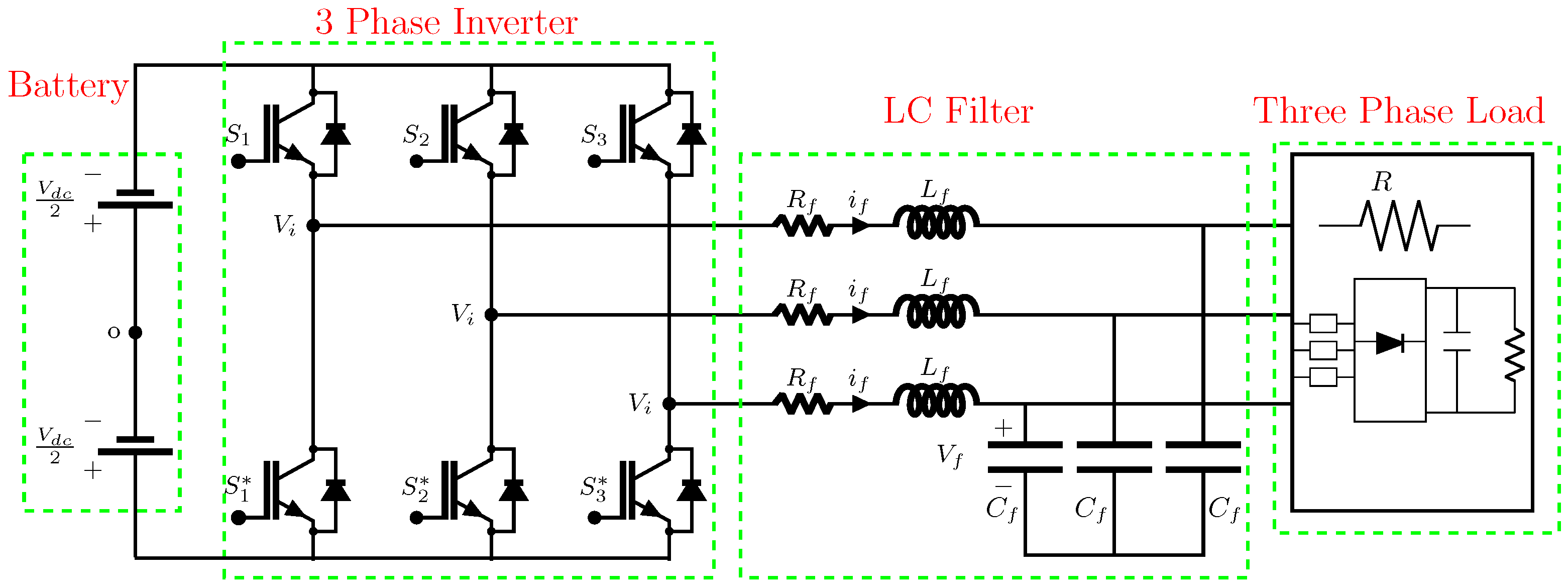
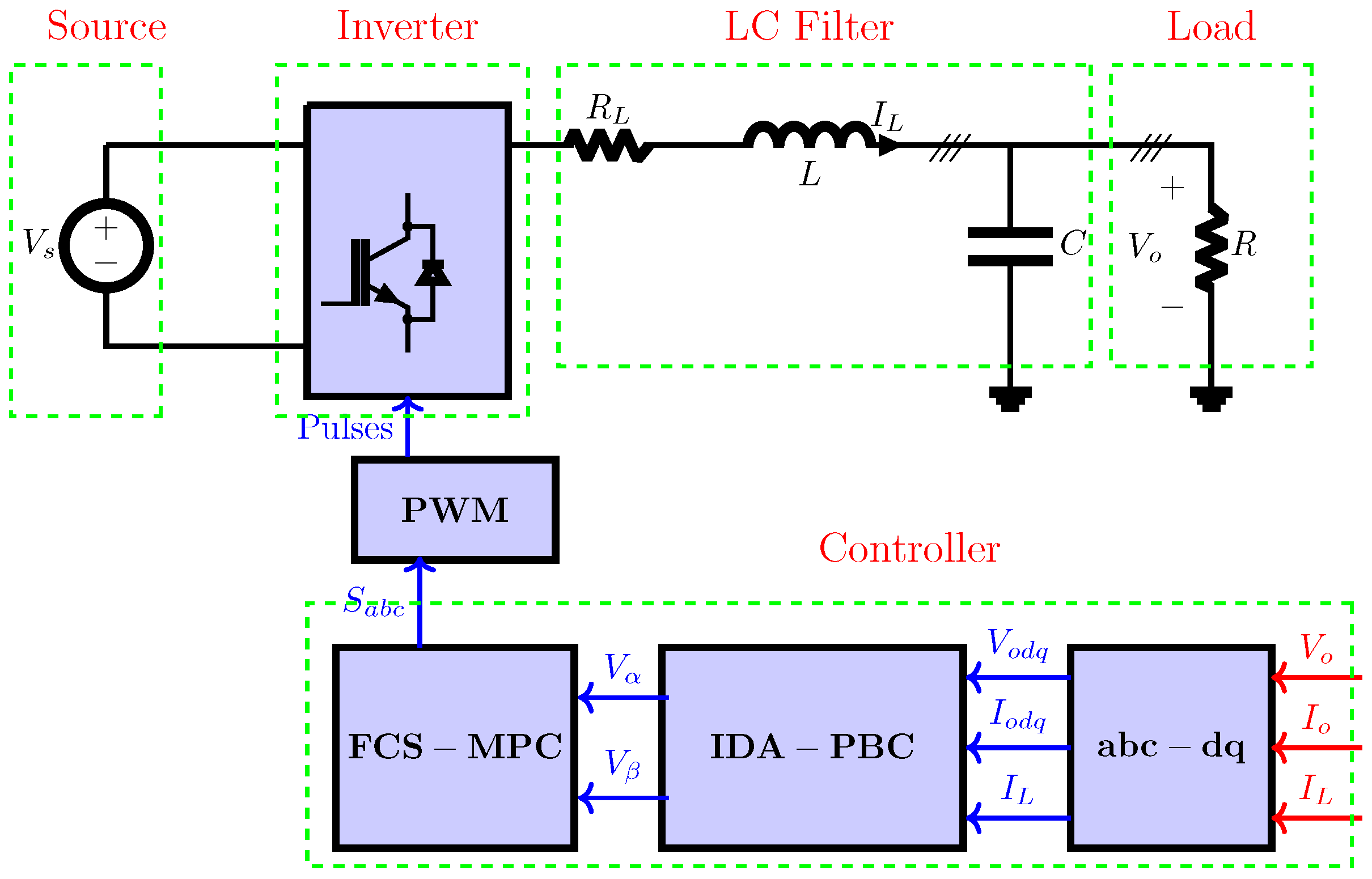
2.2. FCS-MPC Design for Three-Phase VSI
2.3. Passivity-Based-Model Predictive Control
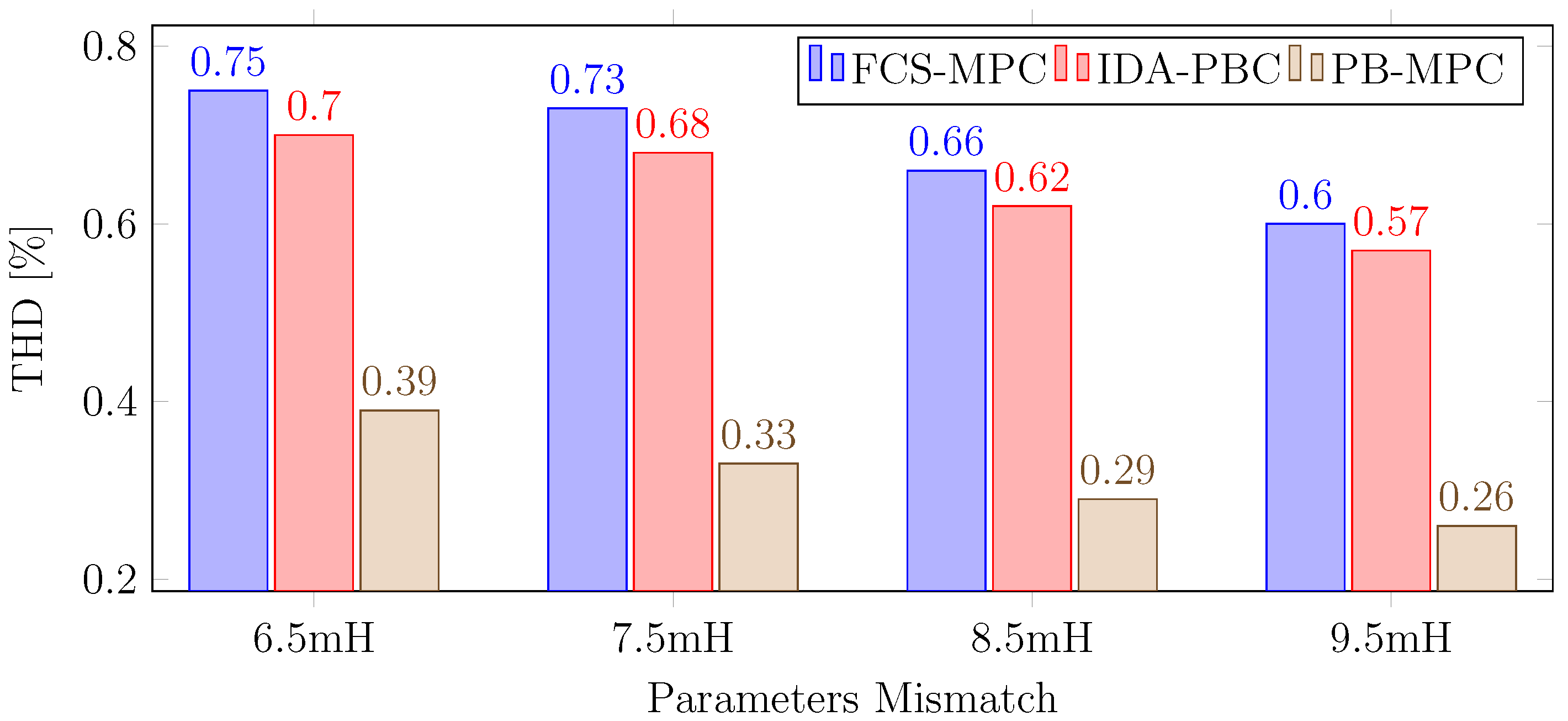
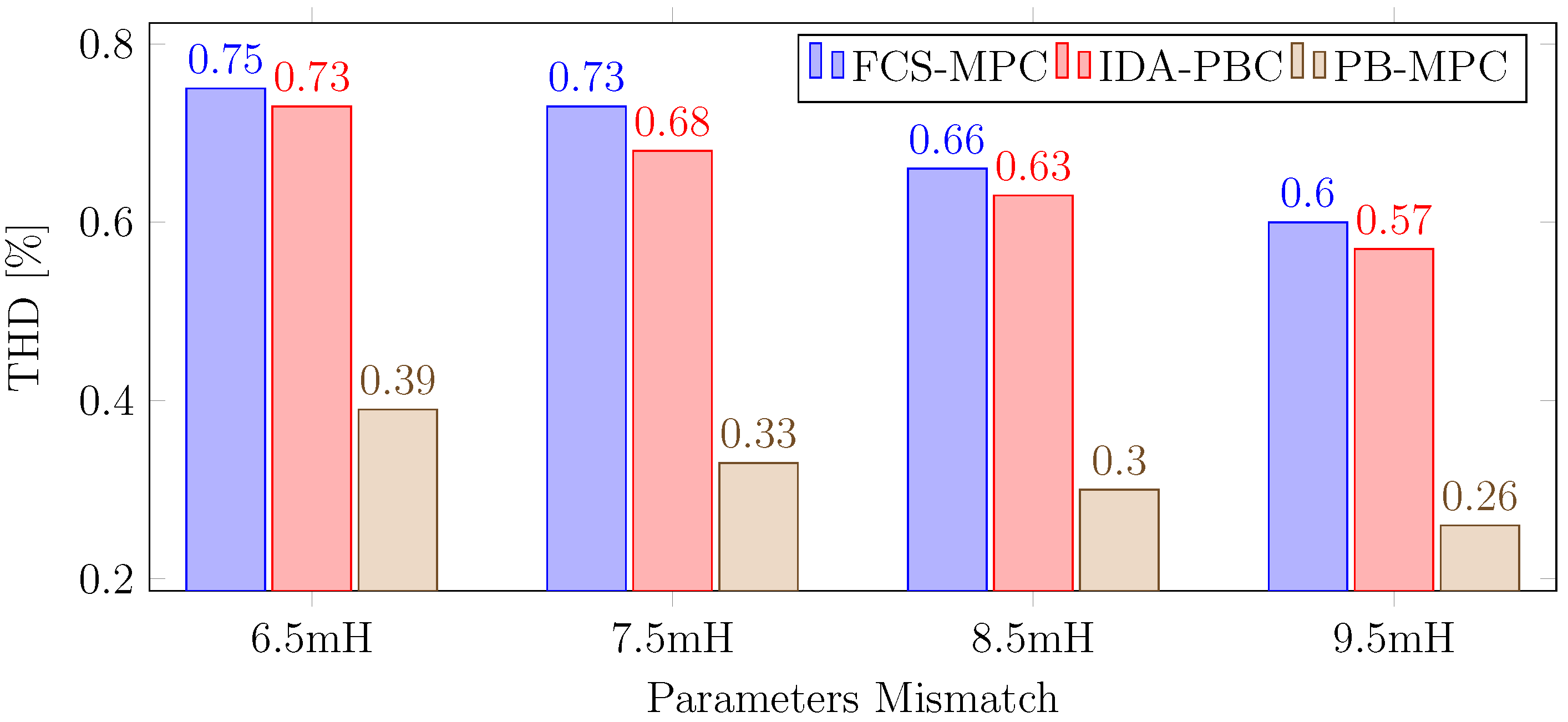
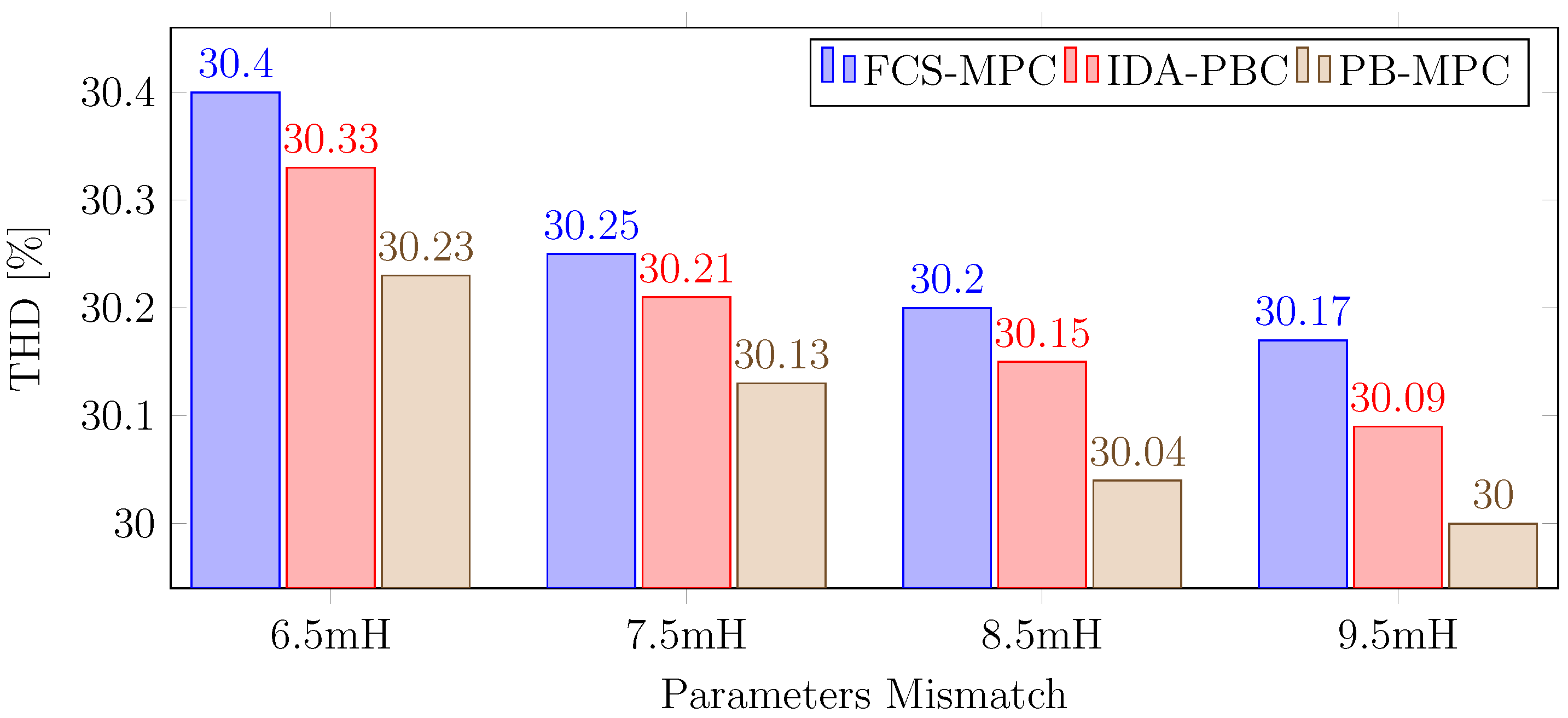
3. Simulation Results
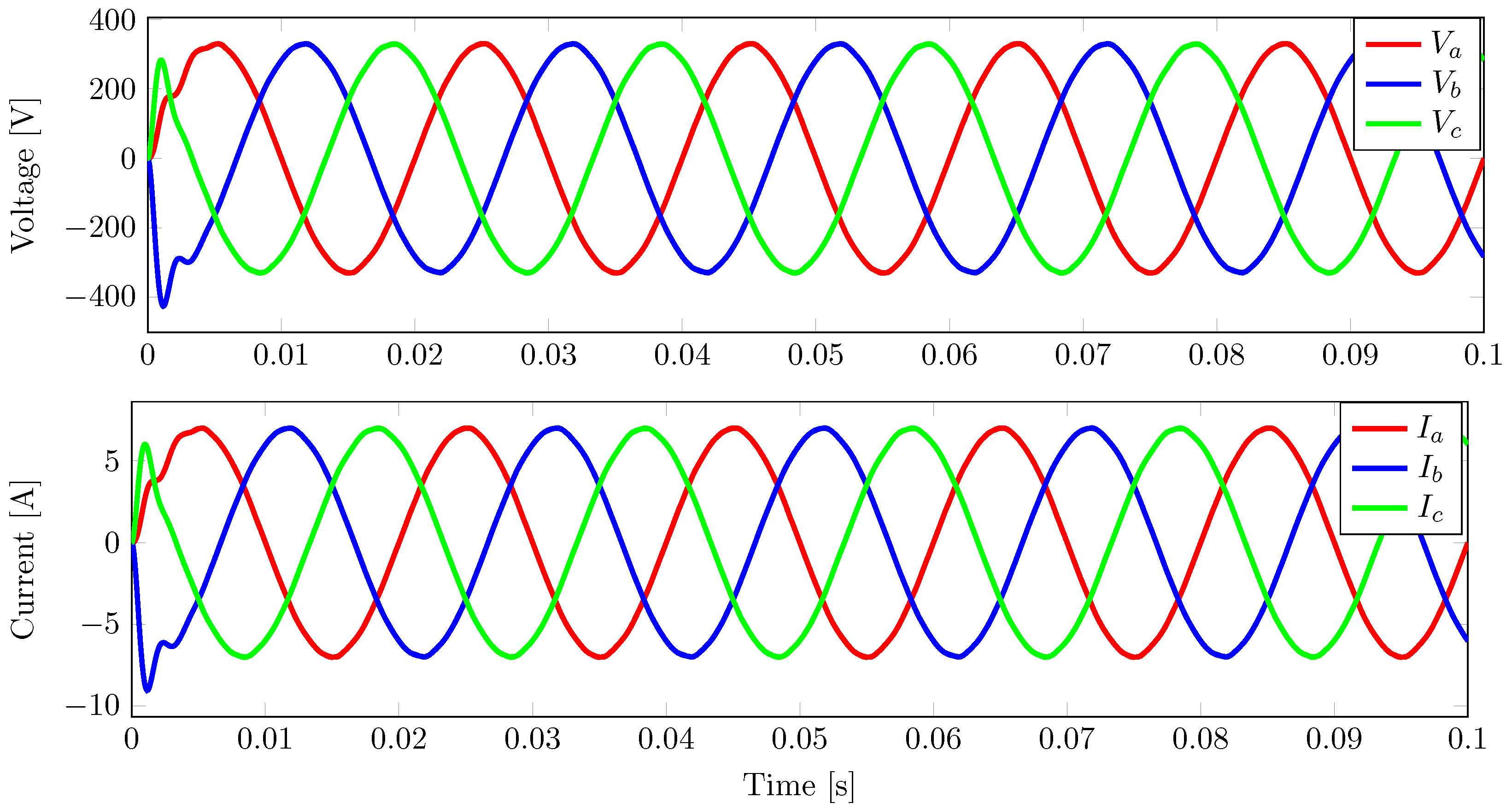
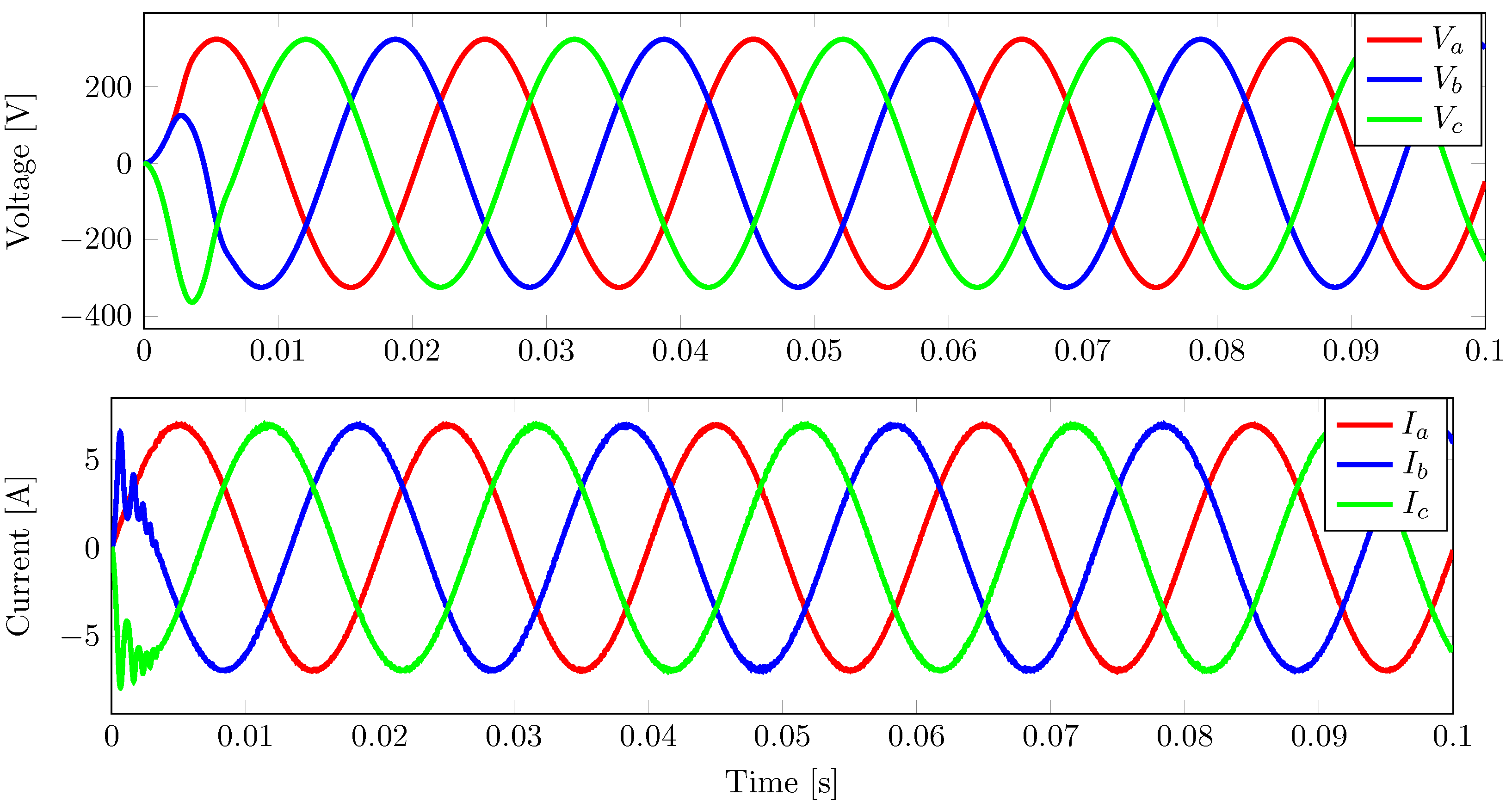
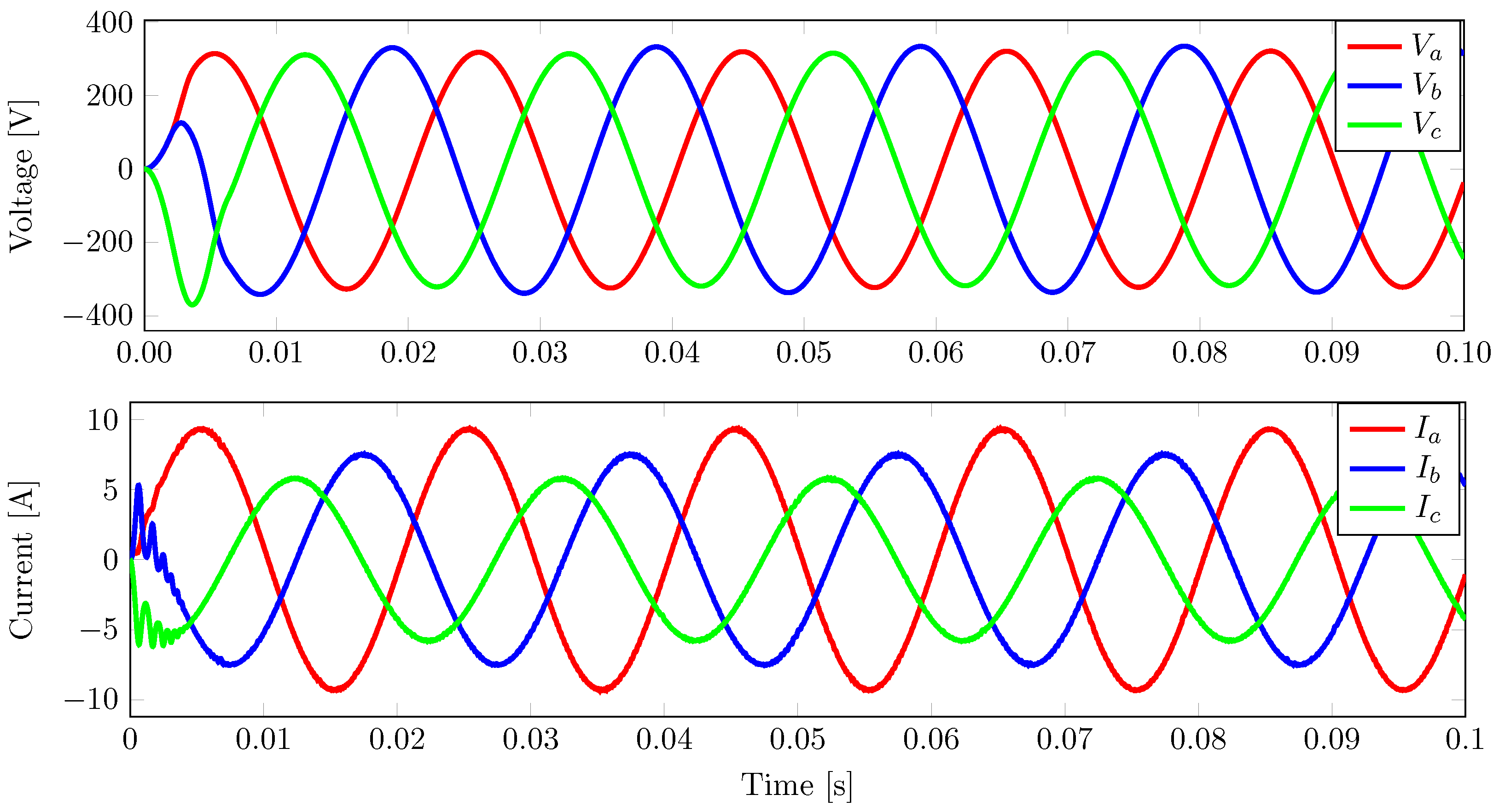
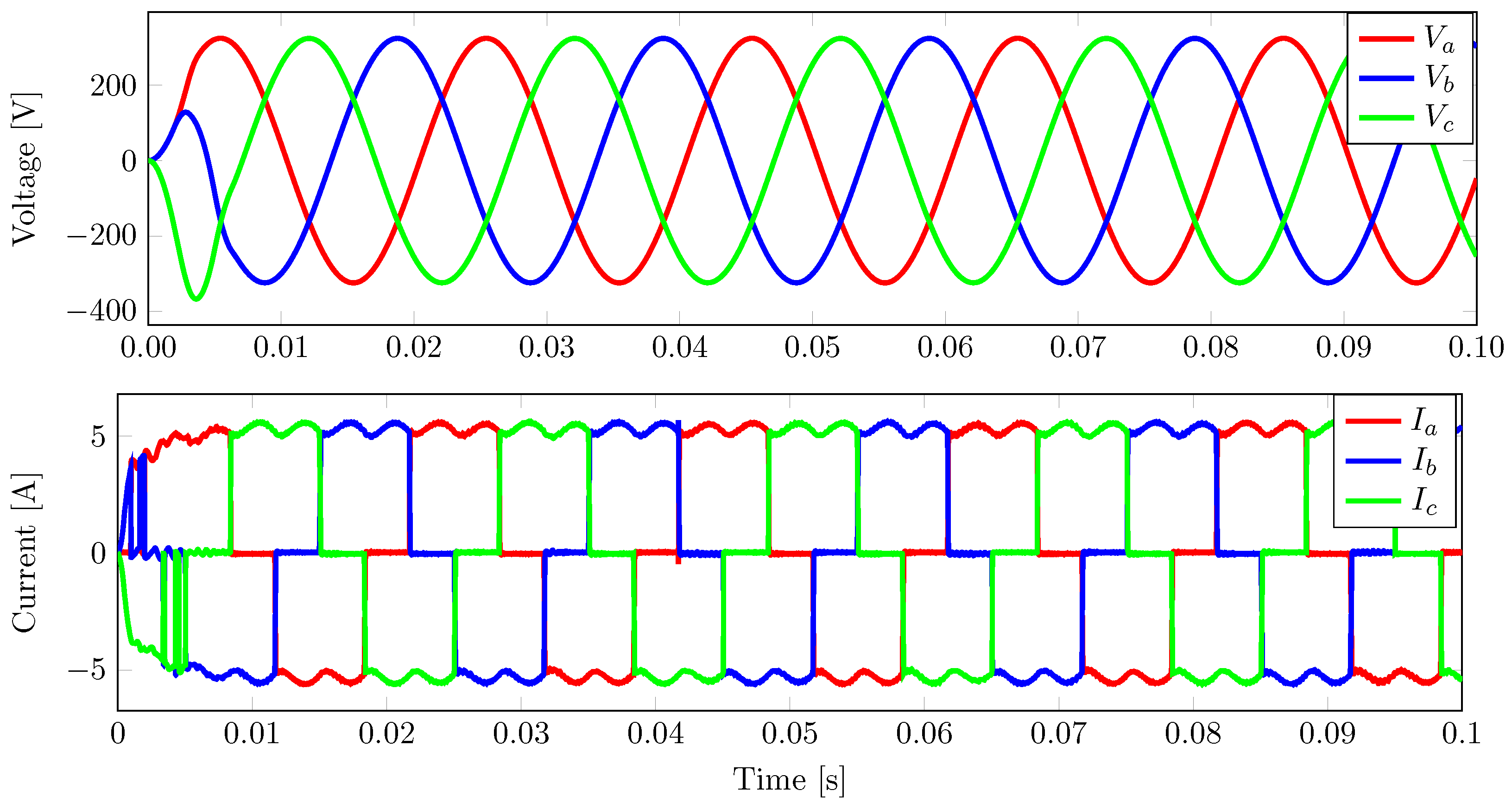
3.1. Performance of Controllers under a Balanced Load
3.1.1. Performance of the IDA-PBC Controller under a Balanced Load
3.1.2. Performance of the FCS-MPC Controller under a Balanced Load
3.1.3. Performance of PB-MPC Controller under a Balanced Load
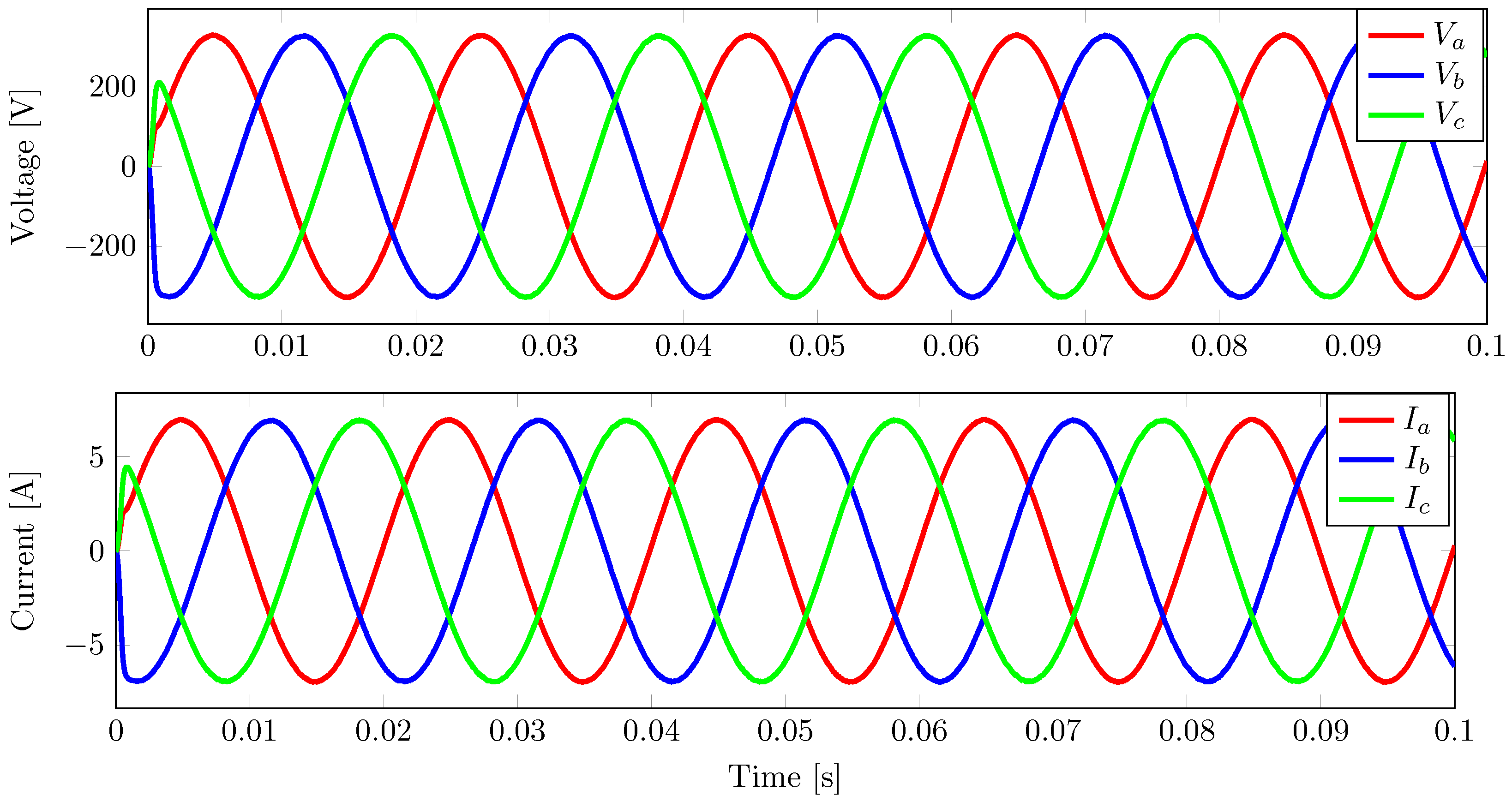
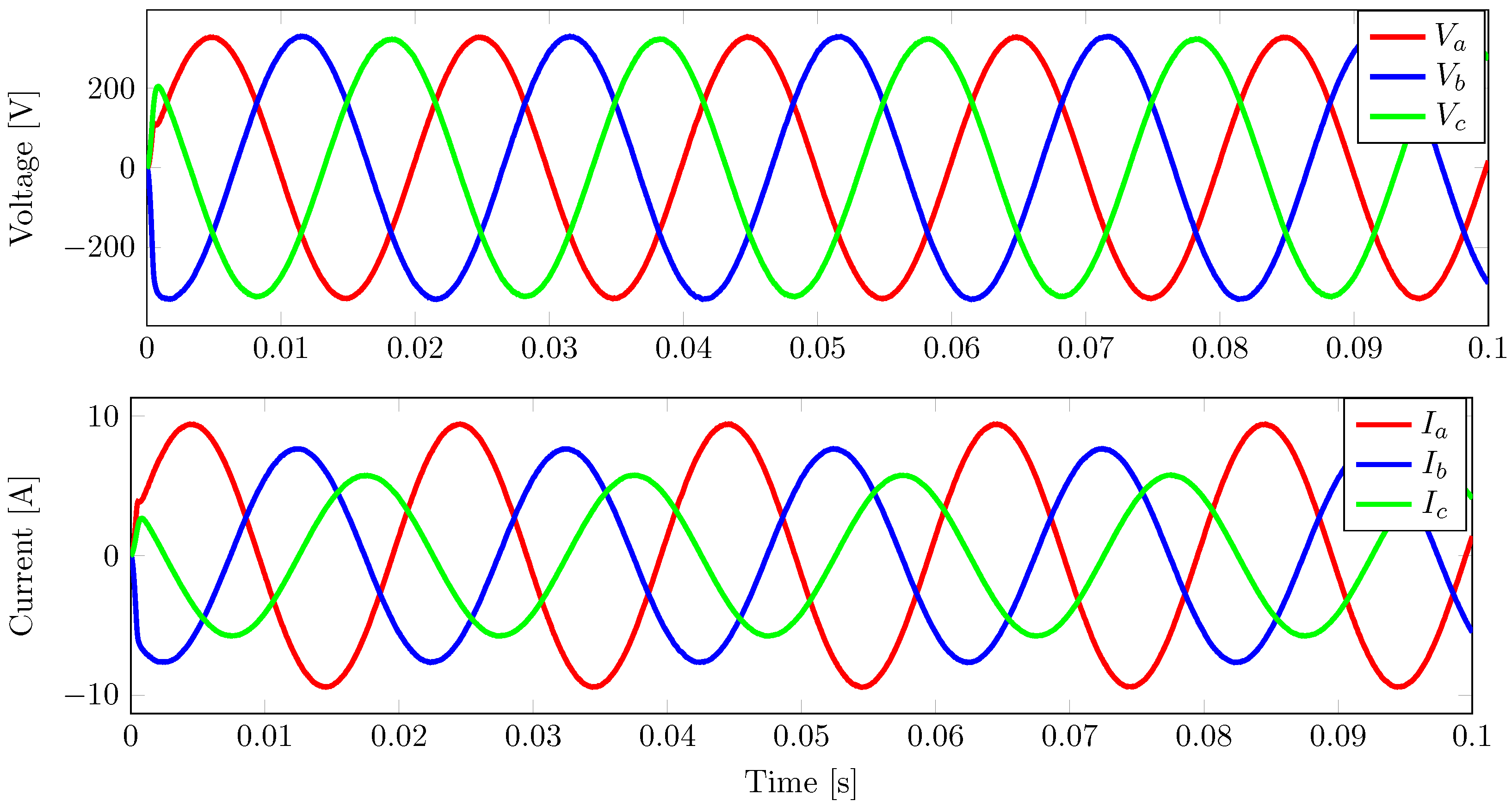
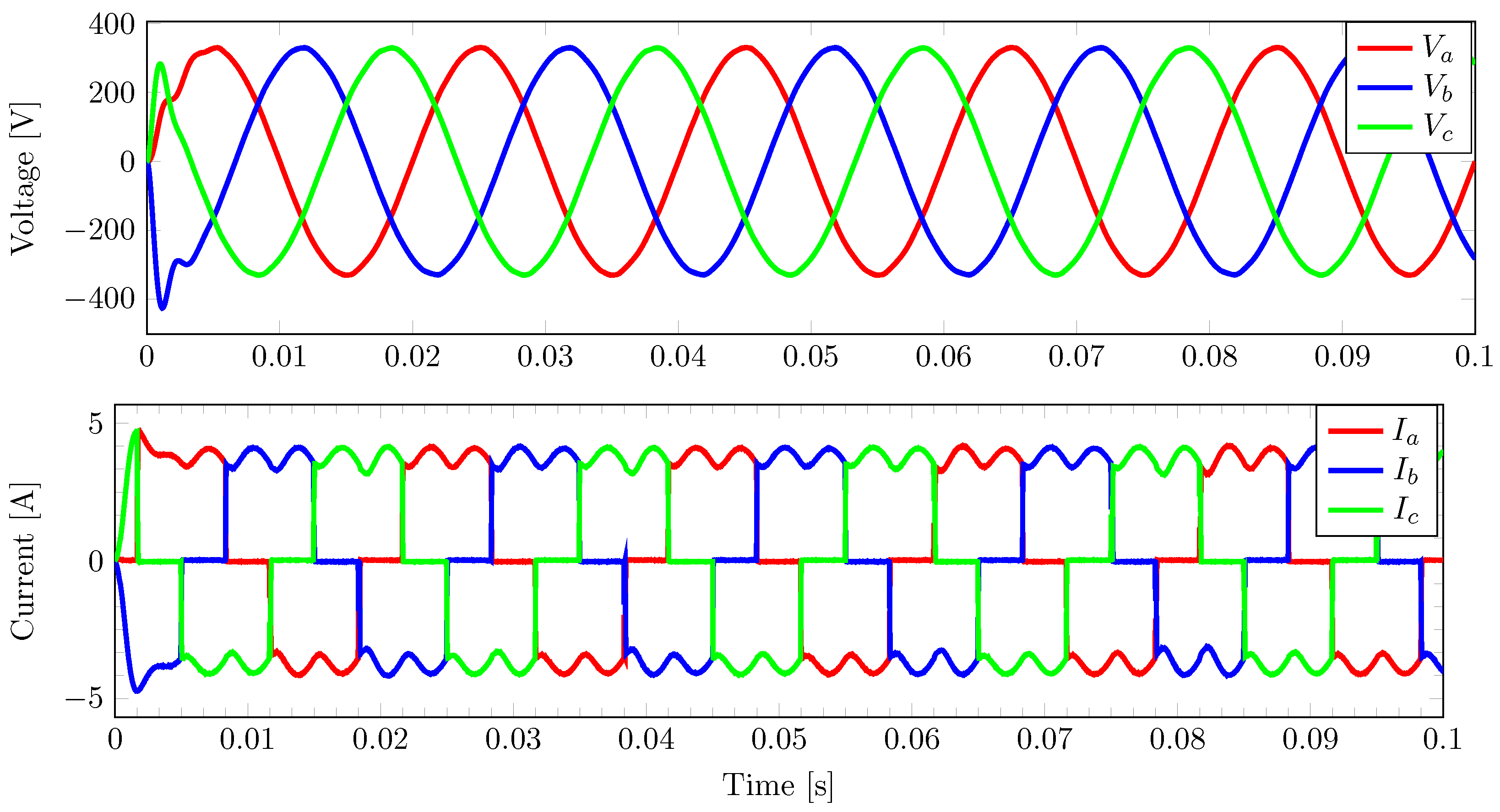
3.2. Performances of Controllers under an Unbalanced Load
3.2.1. Performance of the IDA-PBC Controller under an Unbalanced Load
3.2.2. Performance of the FCS-MPC Controller under an Unbalanced Load
3.2.3. Performance of the PB-MPC Controller under an Unbalanced Load
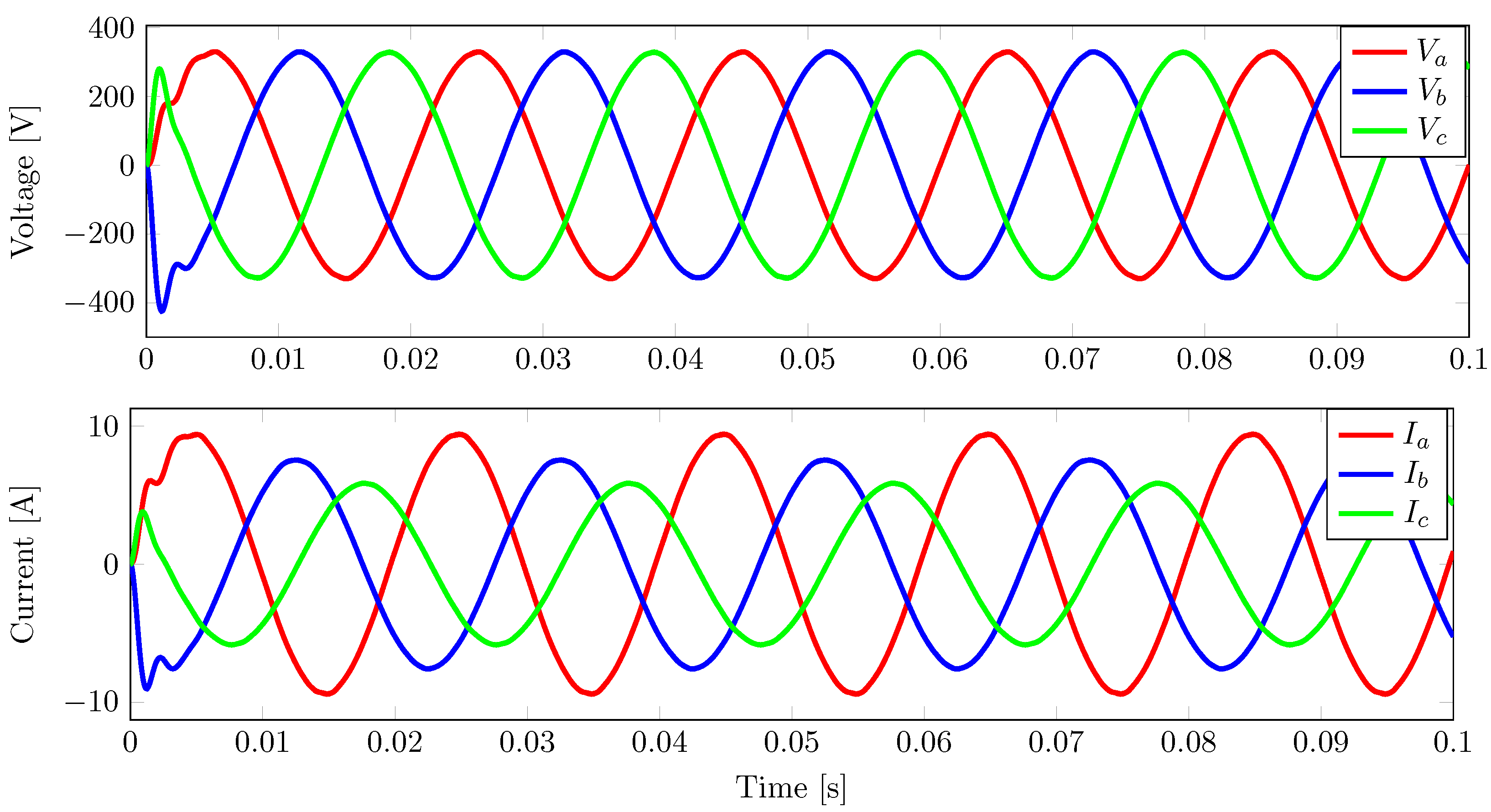
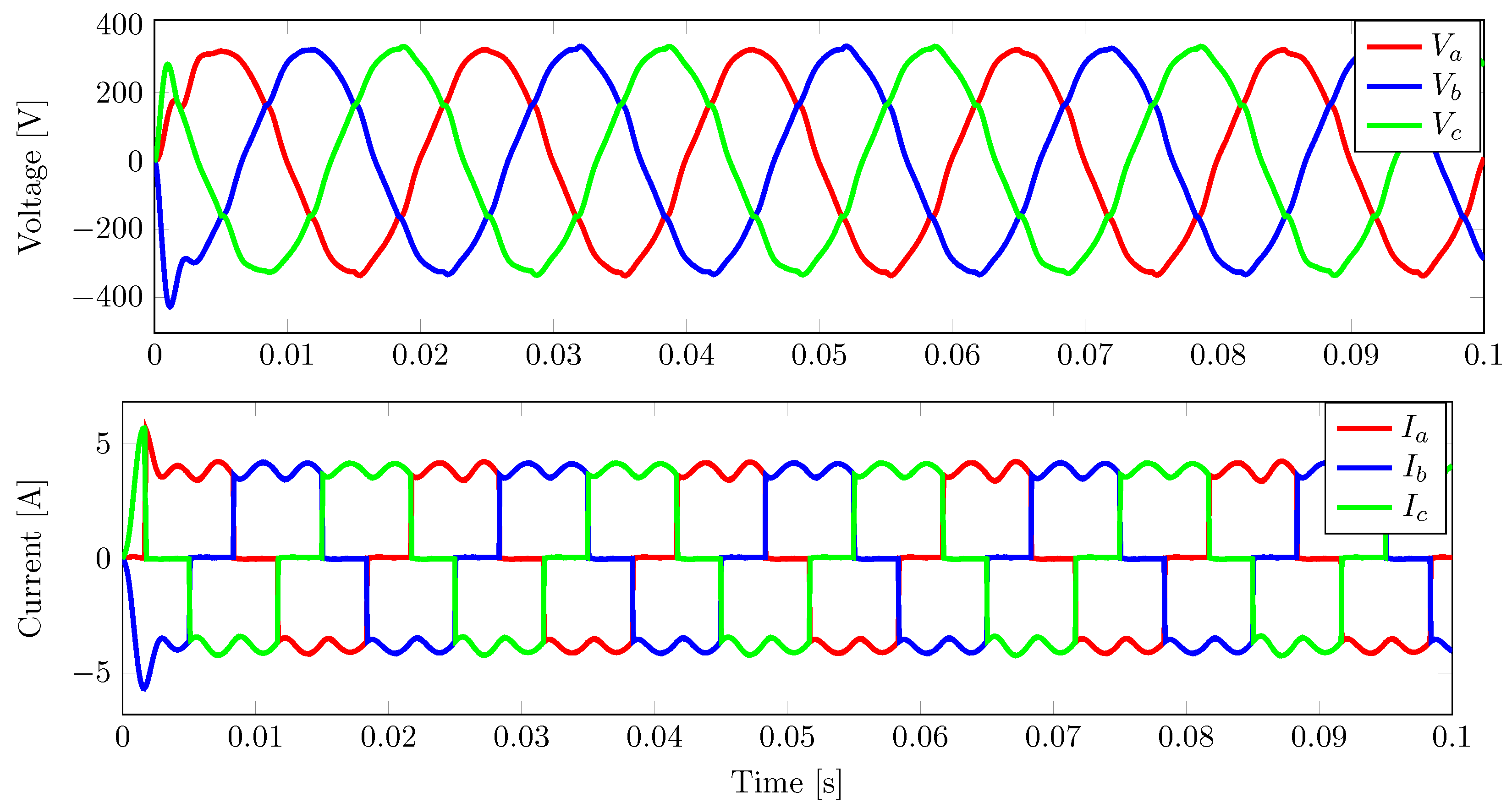
3.3. Performances of Controllers under a Non-Linear Load
3.3.1. Performance of the IDA-PBC Controller under a Non-Linear Load
3.3.2. Performance of the FCS-MPC Controller under a Non-Linear Load
3.3.3. Performance of the PB-MPC Controller under a Non-Linear Load
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| VSI | voltage source inverter |
| IDA-PBC | interconnection and damping assignment passivity-based control |
| FCS-MPC | finite control set model predictive controller |
| PB-MPC | passivity-based model predictive controller |
| THD | total harmonic distortion |
| PWM | pulse width modulation |
| LC | inductor–capacitor |
| switching frequency | |
| UPS | uninterrupted power supply |
References
- Sonawane, V.R.; Patil, S.B. Track and hunt metaheuristic based deep neural network based fault diagnosis model for the voltage source inverter under varying load conditions. Adv. Eng. Softw. 2023, 177, 103414. [Google Scholar] [CrossRef]
- Rafaq, M.S.; Mohammed, S.A.Q.; Choi, H.H.; Jung, J.W. An improved sliding mode control technique to mitigate mismatched parameter uncertainties of three-phase voltage source inverters. IEEE Access 2020, 8, 81932–81942. [Google Scholar] [CrossRef]
- Lin, B.; Peng, L.; Liu, X. Selective pole placement and cancellation for proportional–resonant control design used in voltage source inverter. IEEE Trans. Power Electron. 2022, 37, 8921–8934. [Google Scholar] [CrossRef]
- Ramezani, M.; Li, S.; Golestan, S. Analysis and controller design for stand-alone VSIs in synchronous reference frame. IET Power Electron. 2017, 10, 1003–1012. [Google Scholar] [CrossRef]
- Hans, F.; Schumacher, W.; Chou, S.F.; Wang, X. Design of multifrequency proportional–resonant current controllers for voltage-source converters. IEEE Trans. Power Electron. 2020, 35, 13573–13589. [Google Scholar] [CrossRef]
- Komurcugil, H.; Altin, N.; Ozdemir, S.; Sefa, I. Lyapunov-function and proportional-resonant-based control strategy for single-phase grid-connected VSI with LCL filter. IEEE Trans. Ind. Electron. 2015, 63, 2838–2849. [Google Scholar] [CrossRef]
- Bao, X.; Zhuo, F.; Tian, Y.; Tan, P. Simplified feedback linearization control of three-phase photovoltaic inverter with an LCL filter. IEEE Trans. Power Electron. 2012, 28, 2739–2752. [Google Scholar] [CrossRef]
- Gupta, R.; Ghosh, A.; Joshi, A. Multiband hysteresis modulation and switching characterization for sliding-mode-controlled cascaded multilevel inverter. IEEE Trans. Ind. Electron. 2009, 57, 2344–2353. [Google Scholar] [CrossRef]
- Zhang, K.; Kang, Y.; Xiong, J.; Chen, J. Direct repetitive control of SPWM inverter for UPS purpose. IEEE Trans. Power Electron. 2003, 18, 784–792. [Google Scholar] [CrossRef]
- Gupta, Y.; Parganiha, N.; Doolla, S. Lyapunov Based Controller for 3ϕ VSI Stage of a UPS and a Distributed Generation Units. In Proceedings of the 2019 10th International Conference on Power Electronics and ECCE Asia (ICPE 2019-ECCE Asia), Busan, Republic of Korea, 27–30 May 2019; pp. 1359–1364. [Google Scholar]
- Mohamed, I.S.; Rovetta, S.; Do, T.D.; Dragicević, T.; Diab, A.A.Z. A neural-network-based model predictive control of three-phase inverter with an output LC filter. IEEE Access 2019, 7, 124737–124749. [Google Scholar] [CrossRef]
- Mohamed, I.S.; Zaid, S.A.; Abu-Elyazeed, M.; Elsayed, H.M. Classical methods and model predictive control of three-phase inverter with output LC filter for UPS applications. In Proceedings of the 2013 International Conference on Control, Decision and Information Technologies (CoDIT), Hammamet, Tunisia, 6–8 May 2013; pp. 483–488. [Google Scholar]
- Riar, B.S.; Scoltock, J.; Madawala, U.K. Model predictive direct slope control for power converters. IEEE Trans. Power Electron. 2016, 32, 2278–2289. [Google Scholar] [CrossRef]
- Dekka, A.; Wu, B.; Yaramasu, V.; Zargari, N.R. Model predictive control with common-mode voltage injection for modular multilevel converter. IEEE Trans. Power Electron. 2016, 32, 1767–1778. [Google Scholar] [CrossRef]
- Shchurov, N.; Myatezh, S.; Malozyomov, B.; Shtang, A.; Martyushev, N.; Klyuev, R.; Dedov, S. Determination of Inactive Powers in a Single-Phase AC Network. Energies 2021, 14, 4814. [Google Scholar] [CrossRef]
- Serra, F.M.; De Angelo, C.H.; Forchetti, D.G. IDA-PBC control of a DC–AC converter for sinusoidal three-phase voltage generation. Int. J. Electron. 2017, 104, 93–110. [Google Scholar] [CrossRef]
- Komurcugil, H. Improved passivity-based control method and its robustness analysis for single-phase uninterruptible power supply inverters. IET Power Electron. 2015, 8, 1558–1570. [Google Scholar] [CrossRef]
- Qiu, L.; Liu, X.; Liu, J.; Ma, J.; Zhang, J.; Li, Y.; Fang, Y. Passivity-Based Cascade-Free Finite-Set Model Predictive Control for Nested Neutral Point-Clamped Converters. IEEE Access 2020, 8, 200209–200218. [Google Scholar] [CrossRef]
- Ojaghi, P.; Rahmani, M. LMI-based robust predictive load frequency control for power systems with communication delays. IEEE Trans. Power Syst. 2017, 32, 4091–4100. [Google Scholar] [CrossRef]
- Ahumada, C.; Cárdenas, R.; Saez, D.; Guerrero, J.M. Secondary control strategies for frequency restoration in islanded microgrids with consideration of communication delays. IEEE Trans. Smart Grid 2015, 7, 1430–1441. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, G.; Wang, R.; Schnelle, S.C.; Wang, J. A gain-scheduling driver assistance trajectory-following algorithm considering different driver steering characteristics. IEEE Trans. Intell. Transp. Syst. 2016, 18, 1097–1108. [Google Scholar] [CrossRef]
- Elbarbary, Z.M.; Hamed, H.A.; El-Kholy, E.E. Comments on “A Performance Investigation of a Four-Switch Three-Phase Inverter-Fed IM Drives at Low Speeds Using Fuzzy Logic and PI Controllers”. IEEE Trans. Power Electron. 2022, 33, 8187–8188. [Google Scholar] [CrossRef]
- Ortega, R.; Van Der Schaft, A.; Maschke, B.; Escobar, G. Interconnection and damping assignment passivity-based control of port-controlled Hamiltonian systems. Automatica 2002, 38, 585–596. [Google Scholar] [CrossRef]
- Ortega, R.; Van Der Schaft, A.J.; Mareels, I.; Maschke, B. Putting energy back in control. IEEE Control. Syst. Mag. 2001, 21, 18–33. [Google Scholar]
- Gupta, Y.; Chatterjee, K.; Doolla, S. Controller design, analysis and testing of a three-phase VSI using IDA–PBC approach. IET Power Electron. 2020, 13, 346–355. [Google Scholar] [CrossRef]
- Cortés, P.; Ortiz, G.; Yuz, J.I.; Rodríguez, J.; Vazquez, S.; Franquelo, L.G. Model predictive control of an inverter with output LC filter for UPS applications. IEEE Trans. Ind. Electron. 2009, 56, 1875–1883. [Google Scholar] [CrossRef]
- Albalawi, H.; Bakeer, A.; Zaid, S.A.; Aggoune, E.H.; Ayaz, M.; Bensenouci, A.; Eisa, A. Fractional-Order Model-Free Predictive Control for Voltage Source Inverters. Fractal Fract. 2023, 7, 433. [Google Scholar] [CrossRef]
- Bakeer, A.; Mohamed, I.S.; Malidarreh, P.B.; Hattabi, I.; Liu, L. An Artificial Neural Network-Based Model Predictive Control for Three-Phase Flying Capacitor Multilevel Inverter. IEEE Access 2022, 10, 70305–70316. [Google Scholar] [CrossRef]

| Control Technique | Advantages | Disadvantages |
|---|---|---|
| Model’s predictive control [19,20] | 1. Free of mathematical modeling. | 1. Large computational burden |
| 2. Maximum robustness | 2. Much complexity in the algorithm | |
| 3. Rapid dynamic response and a settling time of 2.71 ms | ||
| Gain Scheduling Method [21] | 1. Contains a general model approach | 1. Parameters are difficult to select |
| 2. Reduced cost | ||
| 3. High robustness | ||
| Sliding Model Control [2] | 1. Simple implementation | 1. Chattering effect problem |
| 2. Fast dynamic response | ||
| 3. Robust to parameter variation and disturbance; settling time of 2.85 ms | ||
| PI Control [22] | 1. Easy to implement | 1. High starting overshoot |
| 2. Sensitive to controller gains | ||
| 3. Sluggish response | ||
| IDA-PBC Control [23] | 1. Stability ensures | |
| PB-MPC Controller [18] | 1. Stability ensures | Complex to design |
| 2. No weighting factors | ||
| 3. Low computational complexity |
| Parameter | Value | Unit |
|---|---|---|
| DC link capacitor voltage | 800 | V |
| Fundamental frequency | 50 | Hz |
| Switching frequency | 10,000 | Hz |
| Filter inductance L | 6.5 | mH |
| Resistance of filter inductor R | 0.2 | |
| Capacitance of filter C | 20 | F |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hussain, S.; Bakeer, A.; Mohamed, I.S.; Marchesoni, M.; Vaccaro, L. Comparative Study of Passivity, Model Predictive, and Passivity-Based Model Predictive Controllers in Uninterruptible Power Supply Applications. Energies 2023, 16, 5594. https://doi.org/10.3390/en16155594
Hussain S, Bakeer A, Mohamed IS, Marchesoni M, Vaccaro L. Comparative Study of Passivity, Model Predictive, and Passivity-Based Model Predictive Controllers in Uninterruptible Power Supply Applications. Energies. 2023; 16(15):5594. https://doi.org/10.3390/en16155594
Chicago/Turabian StyleHussain, Shafquat, Abualkasim Bakeer, Ihab S. Mohamed, Mario Marchesoni, and Luis Vaccaro. 2023. "Comparative Study of Passivity, Model Predictive, and Passivity-Based Model Predictive Controllers in Uninterruptible Power Supply Applications" Energies 16, no. 15: 5594. https://doi.org/10.3390/en16155594
APA StyleHussain, S., Bakeer, A., Mohamed, I. S., Marchesoni, M., & Vaccaro, L. (2023). Comparative Study of Passivity, Model Predictive, and Passivity-Based Model Predictive Controllers in Uninterruptible Power Supply Applications. Energies, 16(15), 5594. https://doi.org/10.3390/en16155594








