Optimal Coordination of Directional Overcurrent Relays Using Hybrid Firefly–Genetic Algorithm
Abstract
1. Introduction
- A modified version of the firefly algorithm is developed to solve the relay coordination problem.
- The standard genetic algorithm is used to solve the relay coordination problem.
- The relay coordination problem is solved by combining two metaheuristic algorithms, the firefly algorithm and genetic algorithm, to obtain a better solution.
- The performance of the modified firefly algorithm, genetic algorithm, and hybrid firefly–genetic algorithm are assessed by implementing them to the standard IEEE 3-bus, 6-bus, 9-bus, and 15-bus test networks.
- The proposed optimization techniques are verified by comparing them to up-to-date optimization algorithms that have been utilized to address the coordination problem.
2. Coordination Problem Formulation
2.1. Objective Function Formulation
2.2. Constraint Formulation
2.2.1. Relay Characteristic Constraints
2.2.2. Relay Coordination Constraints
2.3. Constraint Handling Technique
3. Firefly Algorithm
4. Genetic Algorithm
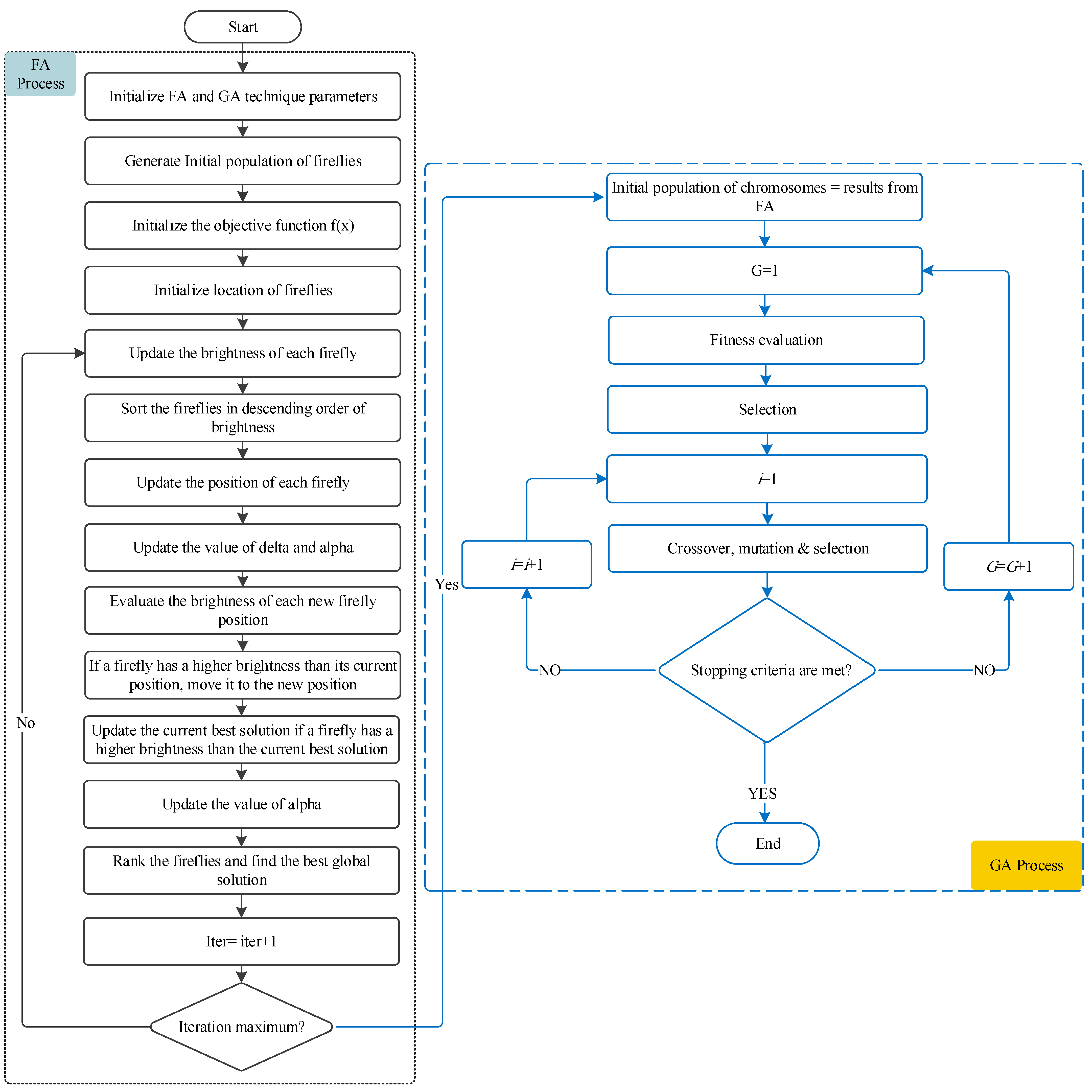
5. Proposed FA-GA Approach for Coordination Problem
| Algorithm 1. Pseudo-code for the proposed hybrid firefly–genetic algorithm |
| FA Starting |
| 1: Initialize FA and GA parameters (number of fireflies (n), generation number of FA (nGerFA), absorption coefficient (γ), attractiveness (βmin and βmax) the randomness strength (α), number of population (nPop), generation number of GA (nGerGA), Crossover probability (Pc) and Mutation probability (Pm)) 2: Objective function f(x), x = (x1, …, xd)T 3: Initialize the population of fireflies randomly within the search space xi (i = 1, 2, … , n). 4: Evaluate the brightness of each firefly using the objective function. 5: While (t < nGerFA) for i = 1:n for j = 1:n Update the brightness of each firefly using Equation (18). Sort the fireflies in descending order of brightness. Update the position of each firefly using Equation (17). Update the value of delta using Equation (20) Update the value of alpha using Equation (19) Evaluate the brightness of each new firefly position. If a firefly has a higher brightness than its current position, move it to the new position. Update the current best solution if a firefly has a higher brightness than the current best solution. Update the value of α using Equation (17). End for j End for i 6: Rank the fireflies and find the best global solution 7: End while 8: Results from FA 9: End FA |
| GA Starting |
| 10: i = 0 11: initial population of chromosomes P(0) = results from FA 12: Evaluate the fitness of each chromosome in the population. 13: While stopping criteria are not met i = i + 1 Select parents from population Apply crossover mechanism with probability Pc Apply mutation mechanism with probability Pm Fitness calculation 14: Rank individuals and find the best global solution 15: End while (if any of the stopping criteria is met) 16: Post-process results and visualization |
6. Simulation Results on Various IEEE Bus Systems
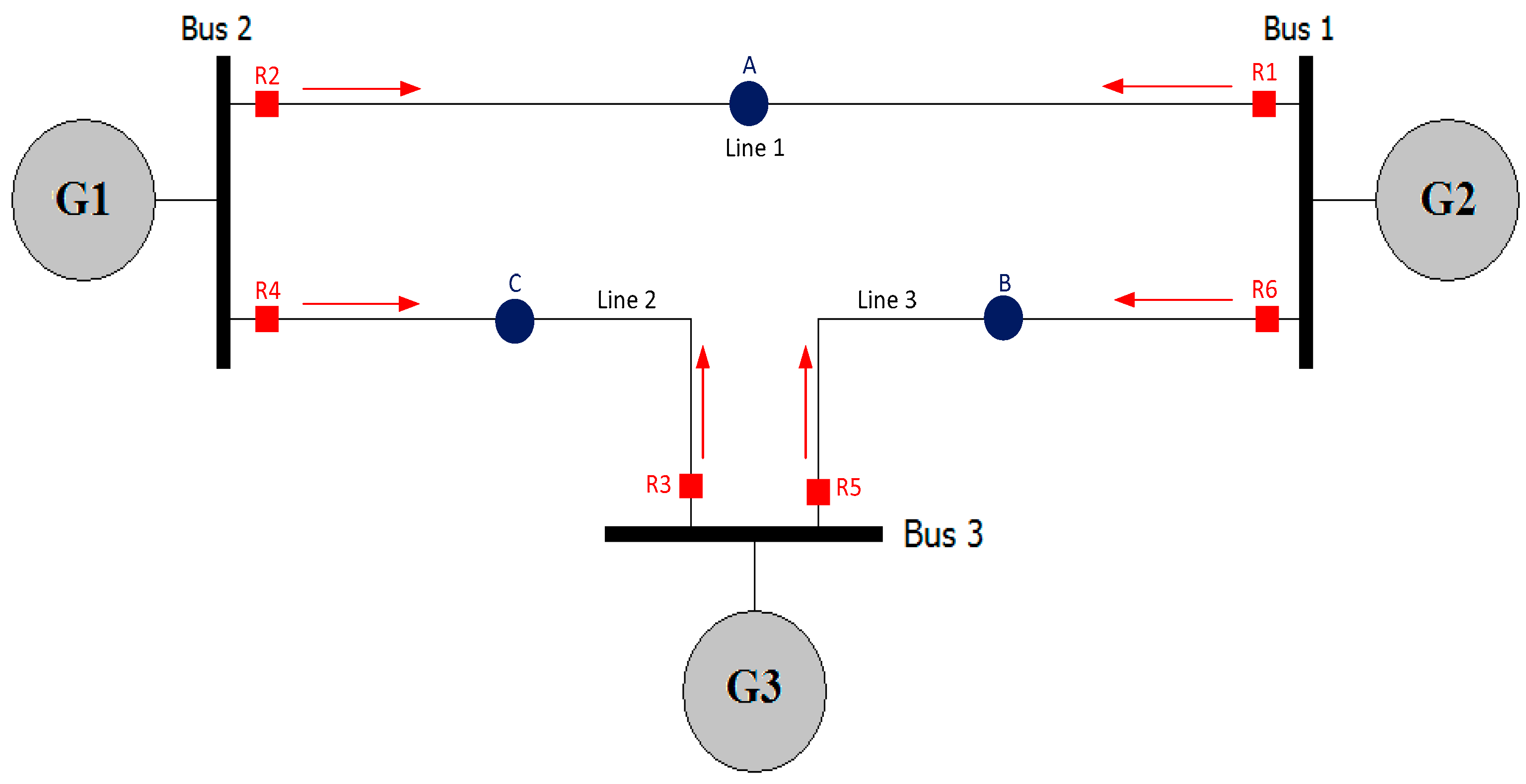
6.1. IEEE 3-Bus Network
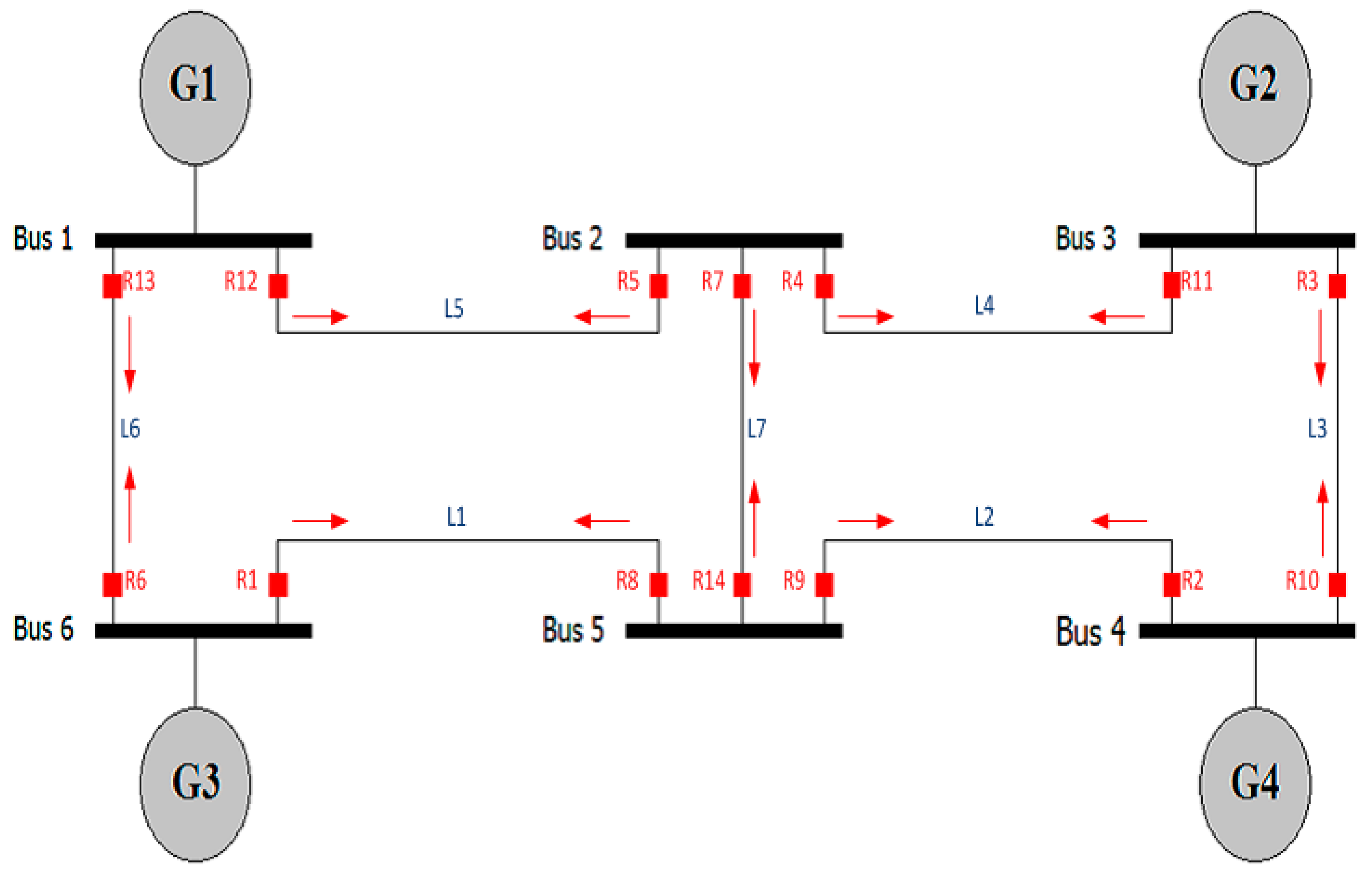
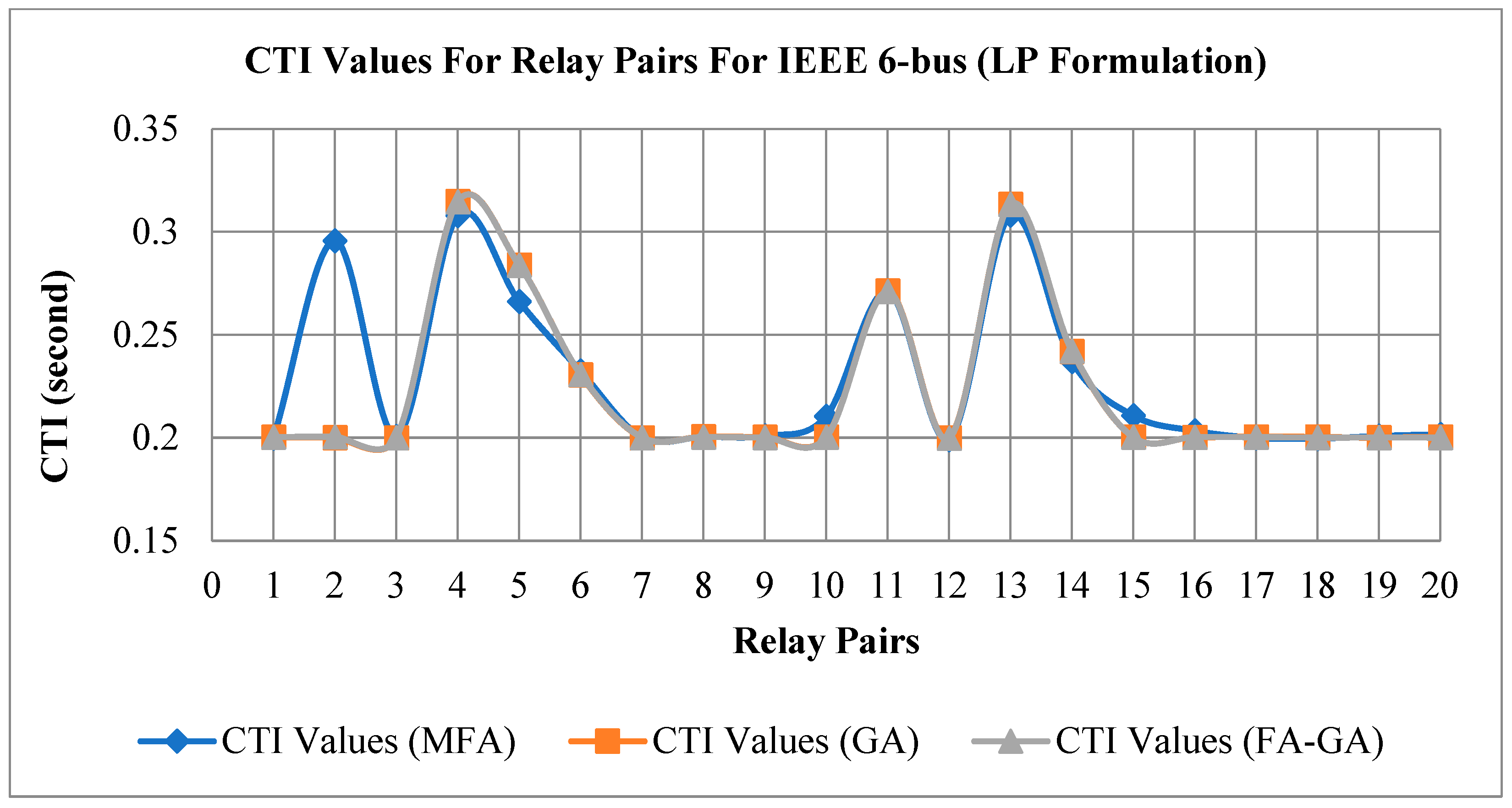
6.2. IEEE 6-Bus Network
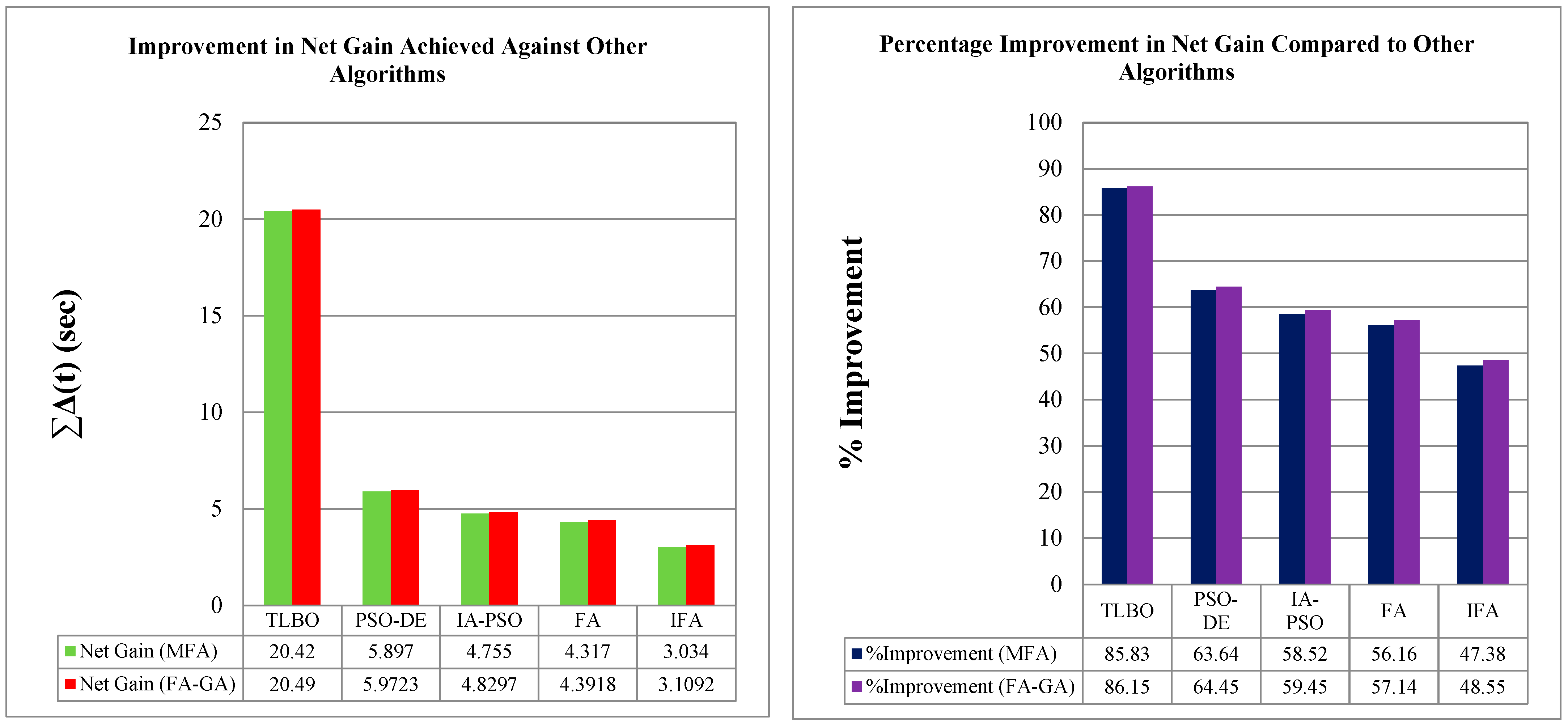
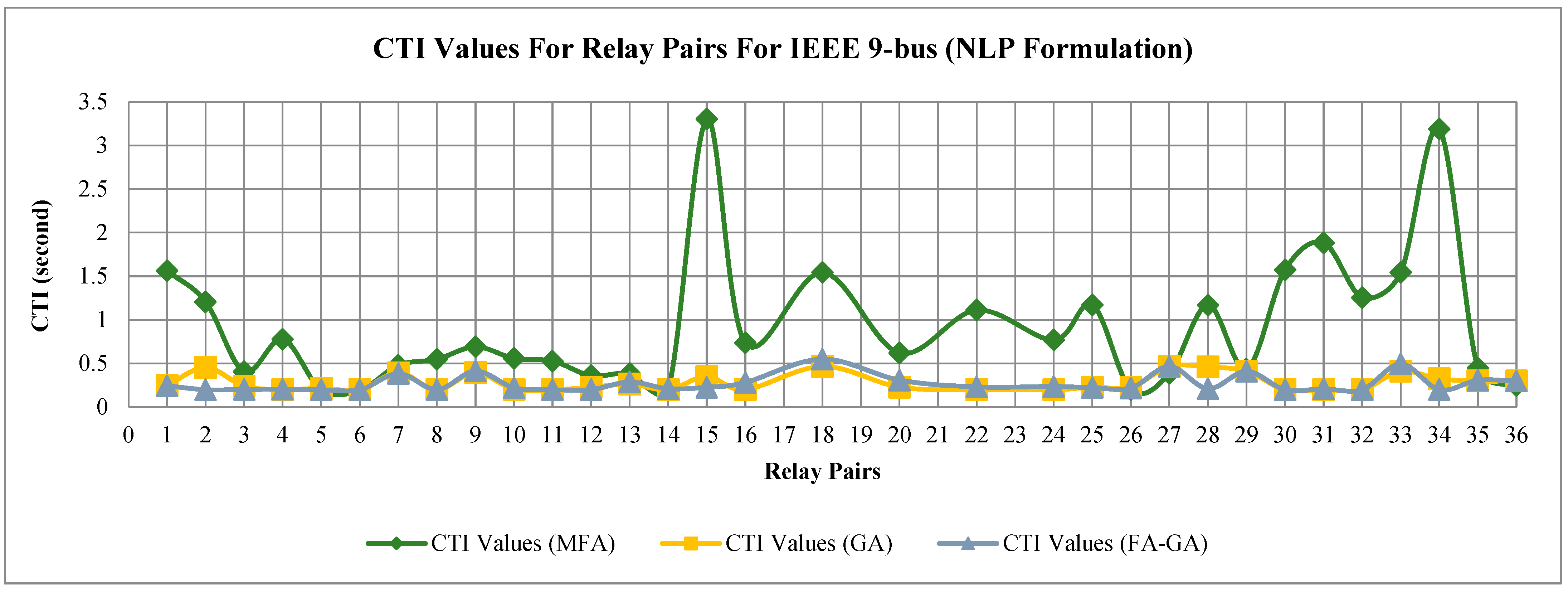
6.3. IEEE 9-Bus Network
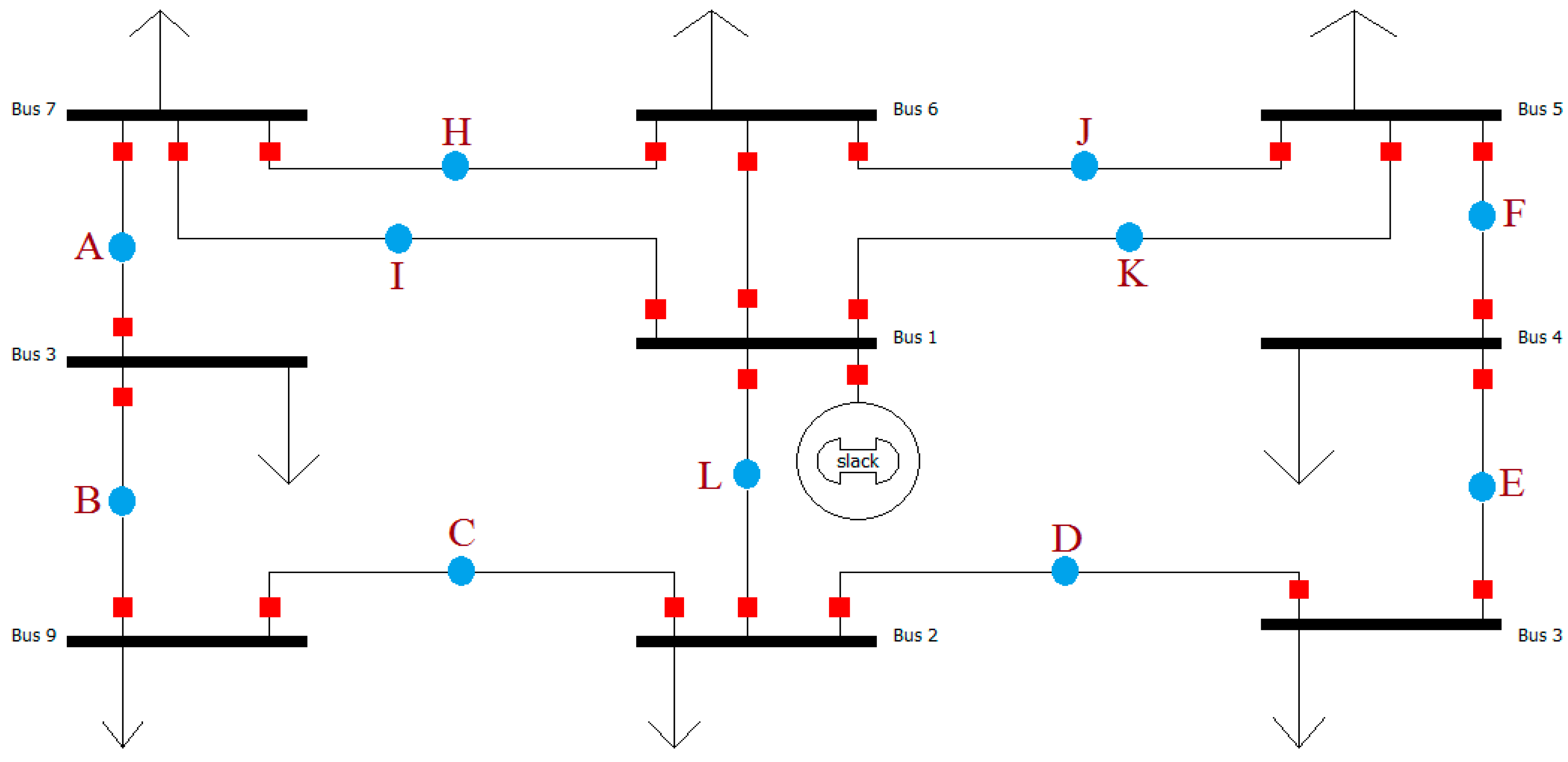
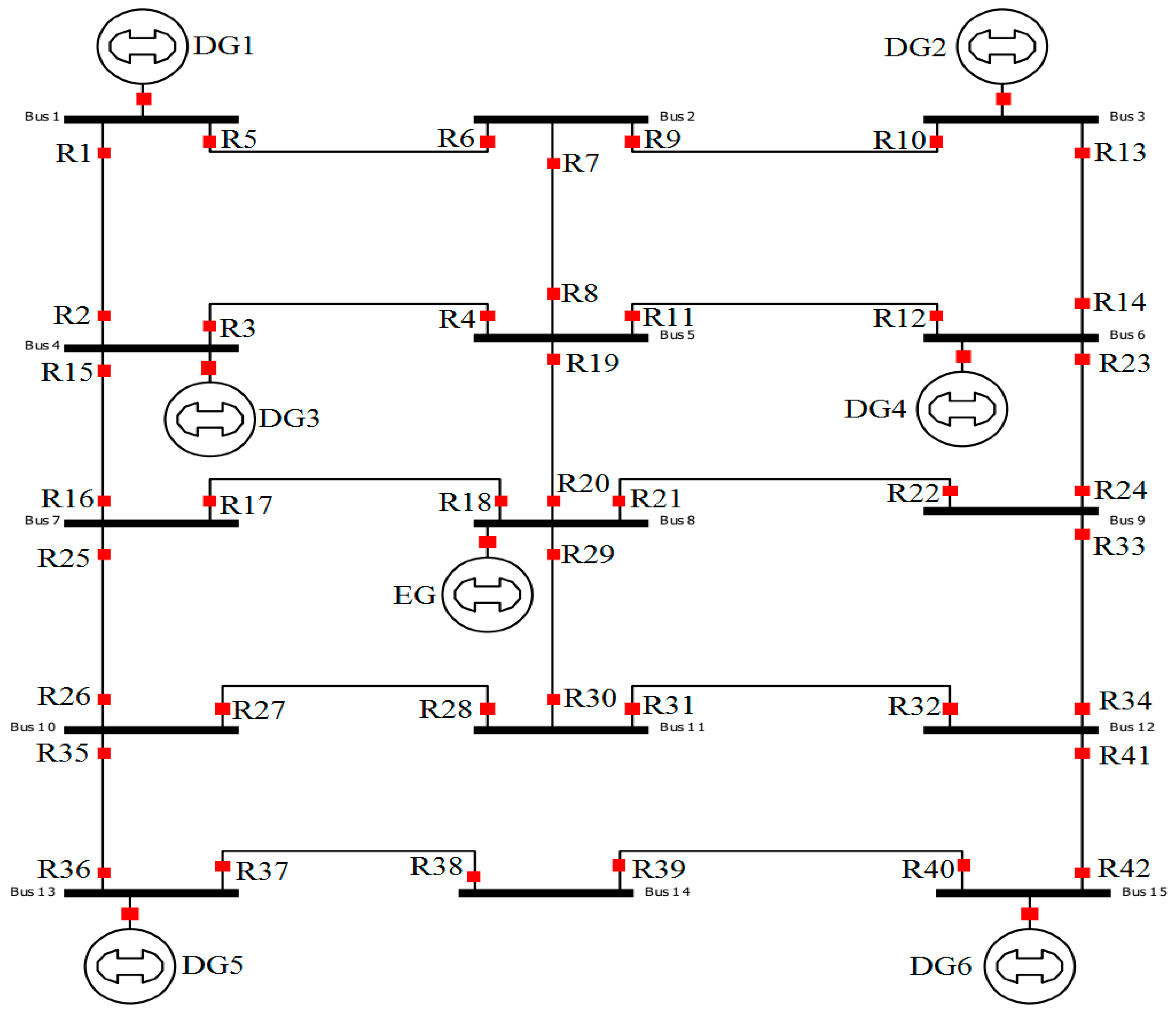
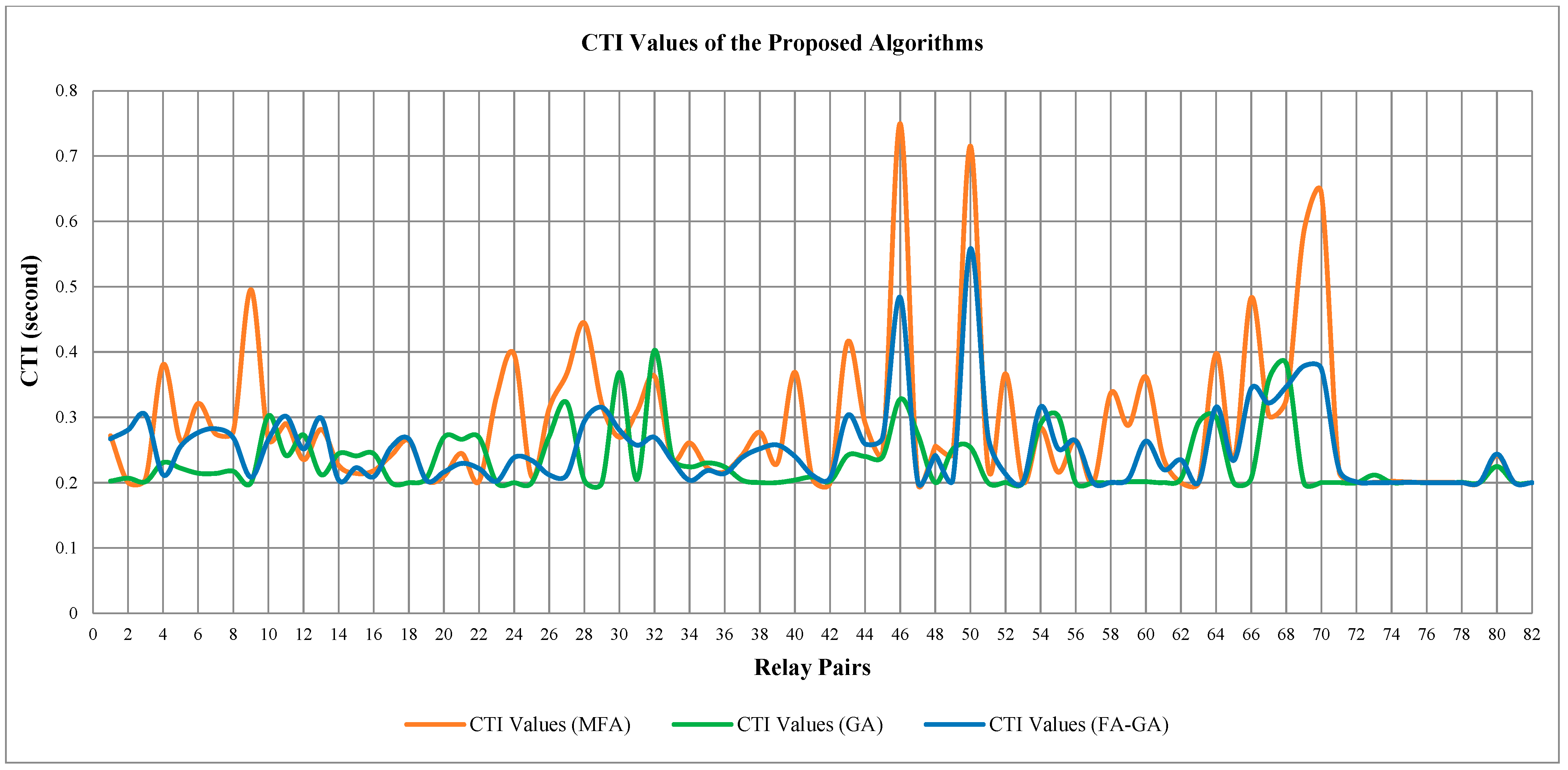
6.4. IEEE 15-Bus Network
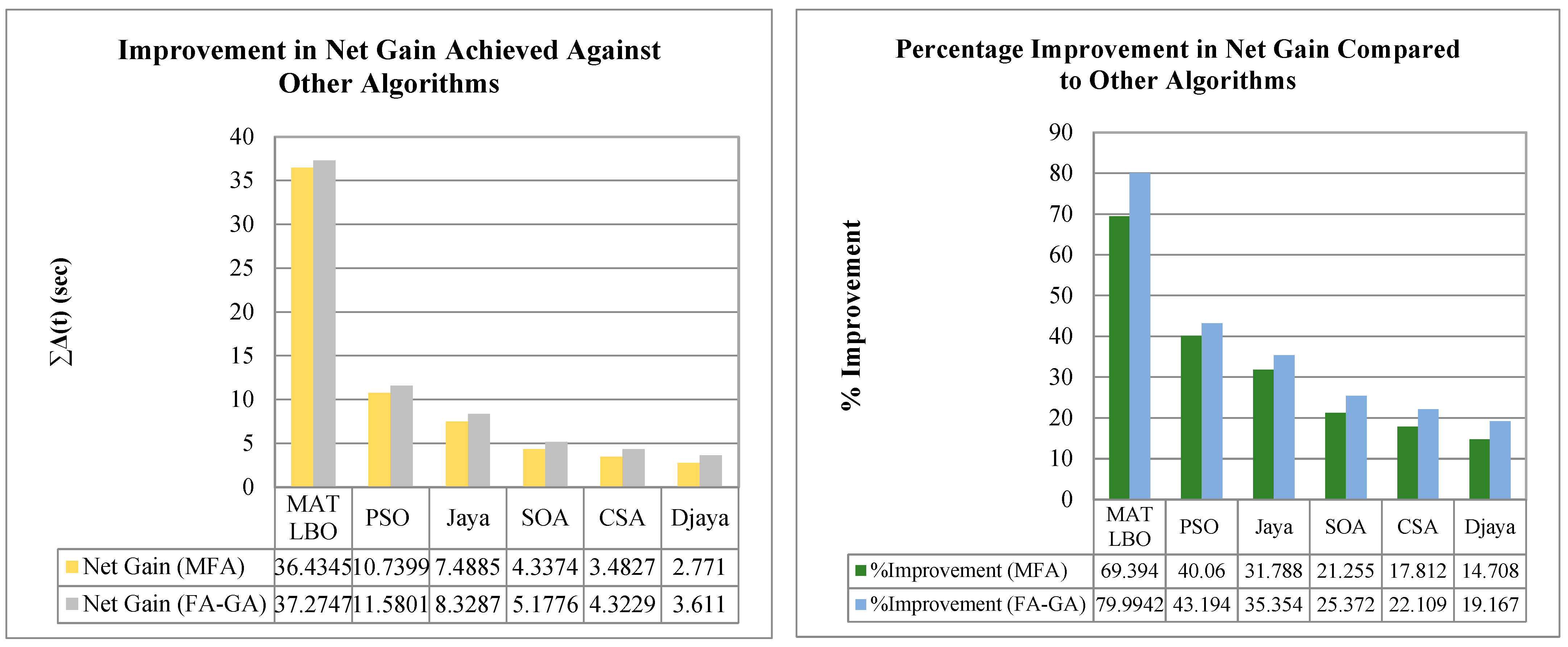
6.5. Number of Objective Function Evaluation
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DOCR | Directional overcurrent relays |
| TMS | Time multiplier setting |
| PS | Plug setting |
| CTI | Coordination time interval |
| LP | Linear programming |
| NLP | Nonlinear programming |
| GAMS | General algebraic modeling system |
| SQP | Sequential quadratic programming |
| AA | Analytical method |
| GA | Genetic algorithm |
| PSO | Particle swarm optimization |
| MINLP | Mixed integer nonlinear programming |
| DE | Differential evolution algorithm |
| IDE | Informative differential evolution |
| SOA | Seeker optimization algorithm |
| ABC | Ant bee colony algorithm |
| OJaya | Oppositional Jaya algorithm |
| DAC | Distance-adaptive coefficient |
| CSA | Cuckoo search algorithm |
| HCSA | Hierarchical clustering mechanism with cuckoo search algorithm |
| GWO | Grey wolf optimizer |
| TLBO | Teaching–learning-based optimization |
| IA-PSO | Immune algorithm and particle swarm optimization |
| FA | Firefly algorithm |
| AFA | Adaptive firefly algorithm |
| IFA | Improved firefly algorithm |
| MFA | Modified firefly algorithm |
| FA-GA | Hybrid firefly–genetic algorithm |
| OF | Objective function |
References
- Rojnić, M.; Prenc, R.; Bulat, H.; Franković, D. A Comprehensive Assessment of Fundamental Overcurrent Relay Operation Optimization Function and Its Constraints. Energies 2022, 15, 1271. [Google Scholar] [CrossRef]
- Usama, M.; Mokhlis, H.; Moghavvemi, M.; Mansor, N.N.; Alotaibi, M.A.; Muhammad, M.A.; Bajwa, A.A. A Comprehensive Review on Protection Strategies to Mitigate the Impact of Renewable Energy Sources on Interconnected Distribution Networks. IEEE Access 2021, 9, 35740–35765. [Google Scholar] [CrossRef]
- Ramli, S.P.; Mokhlis, H.; Wong, W.R.; Muhammad, M.A.; Mansor, N.N. Optimal Coordination of Directional Overcurrent Relay Based on Combination of Firefly Algorithm and Linear Programming. Ain Shams Eng. J. 2022, 13, 101777. [Google Scholar] [CrossRef]
- Yu, J.; Kim, C.-H.; Rhee, S.-B. Oppositional Jaya Algorithm with Distance-Adaptive Coefficient in Solving Directional over Current Relays Coordination Problem. IEEE Access 2019, 7, 150729–150742. [Google Scholar] [CrossRef]
- Albasri, F.A.; Alroomi, A.R.; Talaq, J.H. Optimal Coordination of Directional Overcurrent Relays Using Biogeography-Based Optimization Algorithms. IEEE Trans. Power Deliv. 2015, 30, 1810–1820. [Google Scholar] [CrossRef]
- Mishra, P.; Pradhan, A.K.; Bajpai, P. Adaptive Relay Setting for Protection of Distribution System with Solar PV. In Proceedings of the 2018 20th National Power Systems Conference (NPSC), Tiruchirappalli, India, 14–16 December 2018; pp. 1–5. [Google Scholar]
- Draz, A.; Elkholy, M.M.; El-Fergany, A.A. Slime Mould Algorithm Constrained by the Relay Operating Time for Optimal Coordination of Directional Overcurrent Relays Using Multiple Standardized Tripping Curves. Neural Comput. Appl. 2021, 33, 11875–11887. [Google Scholar] [CrossRef]
- ElFergany, A. Optimal Directional Digital Overcurrent Relays Coordination and Arc Flash Hazard Assessments in Meshed Networks. Int. Trans. Electr. Energy Syst. 2016, 26, 134–154. [Google Scholar] [CrossRef]
- Bedekar, P.P.; Korde, P.N. Determining Optimum Time Multiplier Setting of Overcurrent Relays Using Modified Jaya Algorithm. In Proceedings of the 2017 Innovations in Power and Advanced Computing Technologies (i-PACT), Vellore, India, 21–22 April 2017; pp. 1–6. [Google Scholar]
- Ghanbari, M.; Gandomkar, M.; Nikoukar, J. Protection Coordination of Bidirectional Overcurrent Relays Using Developed Particle Swarm Optimization Approach Considering Distribution Generation Penetration and Fault Current Limiter Placement. IEEE Can. J. Electr. Comput. Eng. 2021, 44, 143–155. [Google Scholar] [CrossRef]
- Trivedi, I.N.; Purani, S.V.; Jangir, P.K. Optimized Over-Current Relay Coordination Using Flower Pollination Algorithm. In Proceedings of the 2015 IEEE International Advance Computing Conference (IACC), Bangalore, India, 12–13 June 2015; pp. 72–77. [Google Scholar]
- ElSayed, S.K.; Elattar, E.E. Hybrid Harris Hawks Optimization with Sequential Quadratic Programming for Optimal Coordination of Directional Overcurrent Relays Incorporating Distributed Generation. Alex. Eng. J. 2021, 60, 2421–2433. [Google Scholar] [CrossRef]
- Damchi, Y.; Dolatabadi, M.; Mashhadi, H.R.; Sadeh, J. MILP Approach for Optimal Coordination of Directional Overcurrent Relays in Interconnected Power Systems. Electr. Power Syst. Res. 2018, 158, 267–274. [Google Scholar] [CrossRef]
- Tiwari, R.; Singh, R.K.; Choudhary, N.K. Coordination of Dual Setting Overcurrent Relays in Microgrid with Optimally Determined Relay Characteristics for Dual Operating Modes. Prot. Control Mod. Power Syst. 2022, 7, 6. [Google Scholar] [CrossRef]
- Sarwagya, K.; Nayak, P.K.; Ranjan, S. Optimal Coordination of Directional Overcurrent Relays in Complex Distribution Networks Using Sine Cosine Algorithm. Electr. Power Syst. Res. 2020, 187, 106435. [Google Scholar] [CrossRef]
- Irfan, M.; Wadood, A.; Khurshaid, T.; Khan, B.M.; Kim, K.-C.; Oh, S.-R.; Rhee, S.-B. An Optimized Adaptive Protection Scheme for Numerical and Directional Overcurrent Relay Coordination Using Harris Hawk Optimization. Energies 2021, 14, 5603. [Google Scholar] [CrossRef]
- Ramli, S.P.I.L.; Mokhlis, H.; Wong, W.R.; Muhammad, M.A.; Mansor, N.N.; Hussain, M.H. Optimal Coordination of Directional Overcurrent Relay Based on Combination Ofimproved Particle Swarm Optimization and Linear Programming Consideringmultiple Characteristics Curve. Turk. J. Electr. Eng. Comput. Sci. 2021, 29, 1765–1780. [Google Scholar] [CrossRef]
- Mansour, M.M.; Mekhamer, S.F.; El-Kharbawe, N. A Modified Particle Swarm Optimizer for the Coordination of Directional Overcurrent Relays. IEEE Trans. Power Deliv. 2007, 22, 1400–1410. [Google Scholar] [CrossRef]
- Bedekar, P.P.; Bhide, S.R.; Kale, V.S. Coordination of Overcurrent Relays in Distribution System Using Linear Programming Technique. In Proceedings of the 2009 International Conference on Control, Automation, Communication and Energy Conservation, Perund, India, 4–6 June 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 1–4. [Google Scholar]
- Bedekar, P.P.; Bhide, S.R.; Kale, V.S. Optimum Time Coordination of Overcurrent Relays Using Two Phase Simplex Method. World Acad. Sci. Eng. Technol. 2009, 28, 1110–1114. [Google Scholar]
- Bedekar, P.P.; Bhide, S.R.; Kale, V.S. Optimum Coordination of Overcurrent Relays in Distribution System Using Dual Simplex Method. In Proceedings of the 2009 Second International Conference on Emerging Trends in Engineering & Technology, Nagpur, India, 16–18 December 2009; pp. 555–559. [Google Scholar]
- Birla, D.; Maheshwari, R.P.; Gupta, H.O. A New Nonlinear Directional Overcurrent Relay Coordination Technique, and Banes and Boons of near-End Faults Based Approach. IEEE Trans. Power Deliv. 2006, 21, 1176–1182. [Google Scholar] [CrossRef]
- Mahari, A.; Seyedi, H. An Analytic Approach for Optimal Coordination of Overcurrent Relays. IET Gener. Transm. Distrib. 2013, 7, 674–680. [Google Scholar] [CrossRef]
- So, C.W.; Li, K.K.; Lai, K.T.; Fung, K.Y. Application of Genetic Algorithm for Overcurrent Relay Coordination. In Proceedings of the Sixth International Conference on Developments in Power System Protection (Conf. Publ. No. 434), Nottingham, UK, 25–27 March 1997; pp. 66–69. [Google Scholar] [CrossRef]
- Uthitsunthorn, D.; Kulworawanichpong, T. Optimal Overcurrent Relay Coordination Using Genetic Algorithms. In Proceedings of the 2010 International Conference on Advances in Energy Engineering, Beijing, China, 19–20 June 2010; pp. 162–165. [Google Scholar]
- Bedekar, P.P.; Bhide, S.R.; Kale, V.S. Optimum Coordination of Overcurrent Relays in Distribution System Using Genetic Algorithm. In Proceedings of the 2009 International Conference on Power Systems, Kharagpur, India, 27–29 December 2009; pp. 1–6. [Google Scholar]
- Adelnia, F.; Moravej, Z.; Farzinfar, M. A New Formulation for Coordination of Directional Overcurrent Relays in Interconnected Networks. Int. Trans. Electr. Energy Syst. 2015, 25, 120–137. [Google Scholar] [CrossRef]
- Al Talaq, M.; Al-Muhaini, M. Optimal Coordination of Time Delay Overcurrent Relays for Power Systems with Integrated Renewable Energy Sources. Energies 2022, 15, 6749. [Google Scholar] [CrossRef]
- Alam, M.N.; Das, B.; Pant, V. A Comparative Study of Metaheuristic Optimization Approaches for Directional Overcurrent Relays Coordination. Electr. Power Syst. Res. 2015, 128, 39–52. [Google Scholar] [CrossRef]
- Hussain, M.H.; Musirin, I.; Rahim, S.R.A.; Abidin, A.F.; Azmi, A. Optimal Overcurrent Relay Coordination Using Particle Swarm Optimization. In Proceedings of the 2013 International Conference on Electrical, Control and Computer Engineering, (InECCE 2013), Kuantan, Pahang, 27–28 August 2013; Volume 2013, pp. 42–47. [Google Scholar]
- Zeineldin, H.H.; El-Saadany, E.F.; Salama, M.M.A. Optimal Coordination of Overcurrent Relays Using a Modified Particle Swarm Optimization. Electr. Power Syst. Res. 2006, 76, 988–995. [Google Scholar] [CrossRef]
- Vijayakumar, D.; Nema, R.K. A Novel Optimal Setting for Directional over Current Relay Coordination Using Particle Swarm Optimization. Int. J. Energy Power Eng. 2008, 2, 928–933. [Google Scholar]
- Vyas, D.; Bhatt, P.; Shukla, V. Coordination of Directional Overcurrent Relays for Distribution System Using Particle Swarm Optimization. Int. J. Smart Grid Clean Energy 2020, 9, 290–297. [Google Scholar] [CrossRef]
- Rashtchi, V.; Gholinezhad, J.; Farhang, P. Optimal Coordination of Overcurrent Relays Using Honey Bee Algorithm. In Proceedings of the International Congress on Ultra Modern Telecommunications and Control Systems, Moscow, Russia, 18–20 October 2010; pp. 401–405. [Google Scholar]
- Yang, H.; Wen, F.; Ledwich, G. Optimal Coordination of Overcurrent Relays in Distribution Systems with Distributed Generators Based on Differential Evolution Algorithm. Int. Trans. Electr. Energy Syst. 2013, 23, 1–12. [Google Scholar] [CrossRef]
- Thangaraj, R.; Pant, M.; Deep, K. Optimal Coordination of Over-Current Relays Using Modified Differential Evolution Algorithms. Eng. Appl. Artif. Intell. 2010, 23, 820–829. [Google Scholar] [CrossRef]
- Singh, M.; Panigrahi, B.K.; Abhyankar, A.R.; Das, S. Optimal Coordination of Directional Over-Current Relays Using Informative Differential Evolution Algorithm. J. Comput. Sci. 2014, 5, 269–276. [Google Scholar] [CrossRef]
- Amraee, T. Coordination of Directional Overcurrent Relays Using Seeker Algorithm. IEEE Trans. Power Deliv. 2012, 27, 1415–1422. [Google Scholar] [CrossRef]
- El-Mesallamy, M.; El-Khattam, W.; Hassan, A.; Talaat, H. Coordination of Directional Overcurrent Relays Using Artificial Bee Colony. In Proceedings of the 22nd International Conference and Exhibition on Electricity Distribution (CIRED 2013), Stockholm, Sweden, 10 June 2013. [Google Scholar]
- Darji, G.U.; Patel, M.J.; Rajput, V.N.; Pandya, K.S. A Tuned Cuckoo Search Algorithm for Optimal Coordination of Directional Overcurrent Relays. In Proceedings of the 2015 International Conference on Power and Advanced Control Engineering (ICPACE), Bengaluru, India, 12–14 August 2015; pp. 162–167. [Google Scholar]
- Ma, L.; Yu, J. Hierarchical Clustering Cuckoo Search Optimization Implemented in Optimal Setting of Directional Overcurrent Relays. Math. Probl. Eng. 2022, 2022, 8966149. [Google Scholar] [CrossRef]
- Korashy, A.; Kamel, S.; Youssef, A.-R.; Jurado, F. Solving Optimal Coordination of Direction Overcurrent Relays Problem Using Grey Wolf Optimization (GWO) Algorithm. In Proceedings of the 2018 Twentieth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 18–20 December 2018; pp. 621–625. [Google Scholar]
- Jamal, N.Z.; Sulaiman, M.H.; Aliman, O.; Mustaffa, Z. Optimal Overcurrent Relays Coordination Using an Improved Grey Wolf Optimizer. Int. J. Adv. Comput. Sci. Appl. 2018, 9. [Google Scholar] [CrossRef]
- Singh, M.; Panigrahi, B.K.; Abhyankar, A.R. Optimal Coordination of Directional Over-Current Relays Using Teaching Learning-Based Optimization (TLBO) Algorithm. Int. J. Electr. Power Energy Syst. 2013, 50, 33–41. [Google Scholar] [CrossRef]
- Kalage, A.A.; Ghawghawe, N.D. Optimum Coordination of Directional Overcurrent Relays Using Modified Adaptive Teaching Learning Based Optimization Algorithm. Intell. Ind. Syst. 2016, 2, 55–71. [Google Scholar] [CrossRef]
- Noghabi, A.S.; Sadeh, J.; Mashhadi, H.R. Considering Different Network Topologies in Optimal Overcurrent Relay Coordination Using a Hybrid GA. IEEE Trans. Power Deliv. 2009, 24, 1857–1863. [Google Scholar] [CrossRef]
- Zellagui, M.; Abdelaziz, A.Y. Optimal Coordination of Directional Overcurrent Relays Using Hybrid PSO-DE Algorithm. Int. Electr. Eng. J. 2015, 6, 1841–1849. [Google Scholar]
- Dehaghani, M.A.; Soltani, M.; Ahmadi, S.M.; Panah, P.G. Application of Artificial Bee Colony Algorithm for Optimal Overcurrent Relay Coordination for Power System Including DGs. Life Sci. J. 2012, 9, 5135–5142. [Google Scholar]
- Zellagui, M.; Hassan, H.A. A Hybrid Optimization Algorithm (IA-PSO) for Optimal Coordination of Directional Overcurrent Relays in Meshed Power Systems. WSEAS Trans. Power Syst. 2015, 10, 240–250. [Google Scholar]
- Tjahjono, A.; Anggriawan, D.O.; Faizin, A.K.; Priyadi, A.; Pujiantara, M.; Taufik, T.; Purnomo, M.H. Adaptive Modified Firefly Algorithm for Optimal Coordination of Overcurrent Relays. IET Gener. Transm. Distrib. 2017, 11, 2575–2585. [Google Scholar] [CrossRef]
- Khurshaid, T.; Wadood, A.; Farkoush, S.G.; Kim, C.-H.; Yu, J.; Rhee, S.-B. Improved Firefly Algorithm for the Optimal Coordination of Directional Overcurrent Relays. IEEE Access 2019, 7, 78503–78514. [Google Scholar] [CrossRef]
- Irfan, M.; Oh, S.-R.; Rhee, S.-B. An Effective Coordination Setting for Directional Overcurrent Relays Using Modified Harris Hawk Optimization. Electronics 2021, 10, 3007. [Google Scholar] [CrossRef]
- Habib, K.; Lai, X.; Wadood, A.; Khan, S.; Wang, Y.; Xu, S. An Improved Technique of Hybridization of PSO for the Optimal Coordination of Directional Overcurrent Protection Relays of IEEE Bus System. Energies 2022, 15, 3076. [Google Scholar] [CrossRef]
- Urdaneta, A.J.; Nadira, R.; Jimenez, L.G.P. Optimal Coordination of Directional Overcurrent Relays in Interconnected Power Systems. IEEE Trans. Power Deliv. 1988, 3, 903–911. [Google Scholar] [CrossRef]
- Al-Roomi, A.R.; El-Hawary, M.E. Is It Enough to Just Rely on Near-End, Middle, and Far-End Points to Get Feasible Relay Coordination? In Proceedings of the 2019 IEEE Canadian Conference of Electrical and Computer Engineering (CCECE), Edmonton, AB, Canada, 5–8 May 2019; pp. 1–5. [Google Scholar]
- Radosavljević, J.; Jevtić, M. Hybrid GSA-SQP Algorithm for Optimal Coordination of Directional Overcurrent Relays. IET Gener. Transm. Distrib. 2016, 10, 1928–1937. [Google Scholar] [CrossRef]
- Yang, X.-S. Cuckoo Search and Firefly Algorithm: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2013; Volume 516, ISBN 3319021419. [Google Scholar]
- Sulaiman, M.; Muhammad, S.; Khan, A. Improved Solutions for the Optimal Coordination of Docrs Using Firefly Algorithm. Complexity 2018, 2018, 7039790. [Google Scholar] [CrossRef]
- Hussain, M.H.; Musirin, I.; Abidin, A.F.; Rahim, S.R.A. Multi-Objective Approach for Solving Directional Overcurrent Relay Problem Using Modified Firefly Algorithm. Delta 2001, 3, 21–26. [Google Scholar]
- Tjahjono, A.; Anggriawan, D.O.; Faizin, A.K.; Priyadi, A.; Pujiantara, M.; Purnomo, M.H. Optimal Coordination of Overcurrent Relays in Radial System with Distributed Generation Using Modified Firefly Algorithm. Int. J. Electr. Eng. Inform. 2015, 7, 691. [Google Scholar] [CrossRef]
- Khan, W.A.; Hamadneh, N.N.; Tilahun, S.L.; Ngnotchouye, J.M. A Review and Comparative Study of Firefly Algorithm and Its Modified Versions. Optim. Algorithms-Methods Appl. 2016, 45, 281–313. [Google Scholar]
- Meena, S.; Chitra, K. Modified Approach of Firefly Algorithm for Non-Minimum Phase Systems. Indian J. Sci. Technol. 2015, 8, 1. [Google Scholar] [CrossRef]
- El-Shorbagy, M.A.; El-Refaey, A.M. A Hybrid Genetic–Firefly Algorithm for Engineering Design Problems. J. Comput. Des. Eng. 2022, 9, 706–730. [Google Scholar] [CrossRef]
- Singh, M.; Panigrahi, B.K.; Abhyankar, A.R. Optimal Overcurrent Relay Coordination in Distribution System. In Proceedings of the 2011 International Conference on Energy, Automation and Signal, Bhubaneswar, India, 28–30 December 2011; pp. 1–6. [Google Scholar]
- Bedekar, P.P.; Bhide, S.R. Optimum Coordination of Directional Overcurrent Relays Using the Hybrid GA-NLP Approach. IEEE Trans. Power Deliv. 2010, 26, 109–119. [Google Scholar] [CrossRef]
- Bedekar, P.P.; Bhide, S.R. Optimum Coordination of Overcurrent Relay Timing Using Continuous Genetic Algorithm. Expert Syst. Appl. 2011, 38, 11286–11292. [Google Scholar] [CrossRef]


| P/B Paris | Primary Relay | Short-Circuit Current (A) | Backup Relay | Short-Circuit Current (A) |
|---|---|---|---|---|
| 1 | 1 | 1978.90 | 5 | 175.00 |
| 2 | 2 | 1525.70 | 4 | 545.00 |
| 3 | 3 | 1683.90 | 1 | 617.22 |
| 4 | 4 | 1815.40 | 6 | 466.17 |
| 5 | 5 | 1499.66 | 3 | 384.00 |
| 6 | 6 | 1766.30 | 2 | 145.34 |
| Relay Number | CTR |
|---|---|
| 1, 4 | 300/5 |
| 2, 3, 5 | 200/5 |
| 6 | 400/5 |
| Relay Number | PS Value | Relay Number | PS Value |
|---|---|---|---|
| 1 | 5.0 | 4 | 4.0 |
| 2 | 1.5 | 5 | 2.0 |
| 3 | 5.0 | 6 | 2.5 |
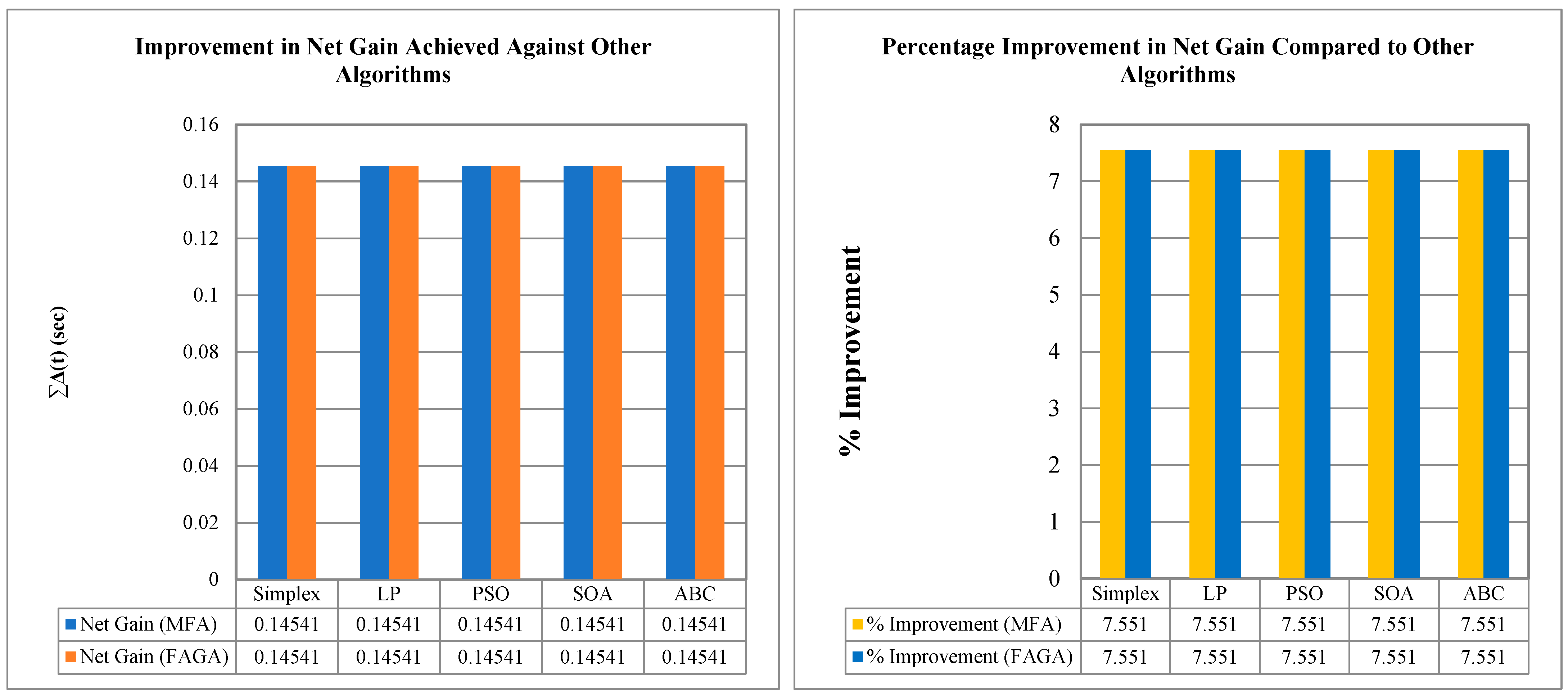
| Method | Time Multiplier Settings (TMS) | OF Value | |||||
|---|---|---|---|---|---|---|---|
| R1 | R2 | R3 | R4 | R5 | R6 | ||
| Simplex [54] | 0.100000 | 0.136400 | 0.10000 | 0.10000 | 0.129800 | 0.10000 | 1.92580 |
| LP [18] | 0.100000 | 0.136400 | 0.10000 | 0.10000 | 0.129800 | 0.10000 | 1.92580 |
| PSO [18] | 0.100000 | 0.136400 | 0.10000 | 0.10000 | 0.129800 | 0.10000 | 1.92580 |
| SOA [38] | 0.100000 | 0.136400 | 0.10000 | 0.10000 | 0.129800 | 0.10000 | 1.92580 |
| ABC [39] | 0.100000 | 0.136400 | 0.10000 | 0.10000 | 0.129800 | 0.10000 | 1.92580 |
| MFA | 0.100000 | 0.100000 | 0.10000 | 0.10000 | 0.100000 | 0.10000 | 1.78039 |
| GA | 0.100016 | 0.100004 | 0.10000 | 0.10000 | 0.100002 | 0.10000 | 1.78047 |
| FAGA | 0.100000 | 0.100000 | 0.10000 | 0.10000 | 0.100000 | 0.10000 | 1.78039 |
| Relay Pairs | CTI | Relay Pairs | CTI | ||||
|---|---|---|---|---|---|---|---|
| MFA | GA | FAGA | MFA | GA | FAGA | ||
| 1 | 0.52319 | 0.52375 | 0.52308 | 4 | 0.48122 | 0.48166 | 0.48140 |
| 2 | 0.63712 | 0.63806 | 0.63705 | 5 | 0.83420 | 0.83452 | 0.83414 |
| 3 | 0.64169 | 0.64170 | 0.64286 | 6 | 0.46982 | 0.46985 | 0.47003 |
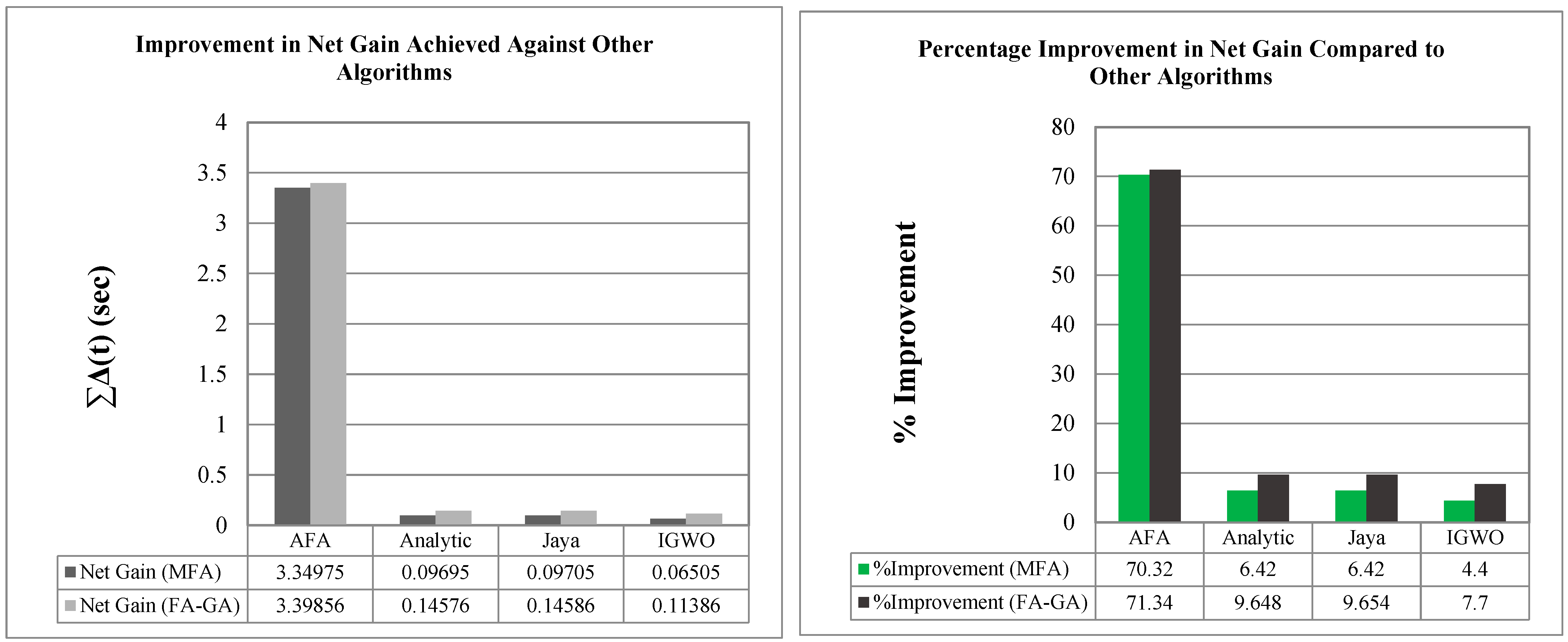
| Variables | AFA [50] | Analytic [23] | Jaya [4] | IGWO [43] | MFA | GA | FAGA |
|---|---|---|---|---|---|---|---|
| TMS1 | 0.1143 | 0.1000 | 0.1000 | 0.1000 | 0.10000 | 0.118970 | 0.100069 |
| TMS2 | 0.1000 | 0.1000 | 0.1000 | 0.1000 | 0.10000 | 0.100001 | 0.100000 |
| TMS3 | 0.1074 | 0.1000 | 0.1453 | 0.1001 | 0.10000 | 0.109758 | 0.100022 |
| TMS4 | 0.1000 | 0.1000 | 0.1000 | 0.1000 | 0.10000 | 0.107297 | 0.100033 |
| TMS5 | 0.1000 | 0.1000 | 0.1000 | 0.1000 | 0.10000 | 0.100004 | 0.100000 |
| TMS6 | 0.1125 | 0.1000 | 0.1000 | 0.1000 | 0.10000 | 0.100011 | 0.100000 |
| PS1 | 1.2500 | 2.7000 | 1.5000 | 1.5000 | 2.22655 | 1.500000 | 1.945890 |
| PS2 | 1.3400 | 2.1250 | 2.9780 | 2.6166 | 1.50351 | 1.500000 | 1.500000 |
| PS3 | 1.2500 | 2.8750 | 1.5000 | 2.9770 | 2.51202 | 1.528990 | 1.787530 |
| PS4 | 1.4300 | 2.3333 | 1.7841 | 1.5850 | 1.69269 | 1.500040 | 1.683100 |
| PS5 | 1.3900 | 2.2750 | 1.8601 | 2.8169 | 1.73700 | 1.500000 | 1.500000 |
| PS6 | 1.2500 | 1.2695 | 1.5000 | 1.5009 | 1.50000 | 1.500070 | 1.500050 |
| OF value | 4.7636 | 1.5108 | 1.5109 | 1.4789 | 1.41385 | 1.401310 | 1.365040 |
| Relay Pairs | CTI | Relay Pairs | CTI | ||||
|---|---|---|---|---|---|---|---|
| MFA | GA | FAGA | MFA | GA | FAGA | ||
| 1 | 0.49924 | 0.38590 | 0.40601 | 4 | 0.27414 | 0.26659 | 0.27309 |
| 2 | 0.20029 | 0.20003 | 0.20000 | 5 | 0.29434 | 0.20005 | 0.20000 |
| 3 | 0.20885 | 0.20019 | 0.20000 | 6 | 0.53264 | 0.53164 | 0.53086 |
| P/B Paris | Primary Relay | Short-Circuit Current (kA) | Backup Relay | Short-Circuit Current (kA) |
|---|---|---|---|---|
| 1 | 1 | 18.172 | 13 | 0.6010 |
| 2 | 2 | 4.8030 | 3 | 1.3650 |
| 3 | 3 | 30.547 | 4 | 0.5528 |
| 4 | 4 | 5.1860 | 12 | 3.4220 |
| 5 | 4 | 5.1860 | 14 | 1.7640 |
| 6 | 5 | 2.8380 | 11 | 1.0740 |
| 7 | 5 | 2.8380 | 14 | 1.7640 |
| 8 | 6 | 18.338 | 8 | 0.7670 |
| 9 | 7 | 4.4960 | 11 | 1.0740 |
| 10 | 7 | 4.4960 | 12 | 3.4220 |
| 11 | 8 | 2.3510 | 2 | 0.8690 |
| 12 | 8 | 2.3510 | 7 | 1.4830 |
| 13 | 9 | 6.0720 | 1 | 4.5890 |
| 14 | 9 | 6.0720 | 7 | 1.4830 |
| 15 | 10 | 4.0770 | 9 | 0.6390 |
| 16 | 11 | 30.939 | 10 | 0.9455 |
| 17 | 12 | 17.705 | 6 | 0.8610 |
| 18 | 13 | 17.821 | 5 | 0.9770 |
| 19 | 14 | 5.4570 | 1 | 4.5890 |
| 20 | 14 | 5.4570 | 2 | 0.8680 |
| Relay Number | CTR |
|---|---|
| 1, 6, 13 | 1200/5 |
| 2, 3, 4, 5, 7, 8, 9, 11, 12, 14 | 800/5 |
| 10 | 600/5 |
| Relay Number | PS Value | Relay Number | PS Value |
|---|---|---|---|
| 1 | 0.8 | 8 | 0.8 |
| 2 | 0.8 | 9 | 0.5 |
| 3 | 1.0 | 10 | 1.0 |
| 4 | 0.5 | 11 | 1.0 |
| 5 | 0.5 | 12 | 1.5 |
| 6 | 0.5 | 13 | 0.5 |
| 7 | 1.0 | 14 | 1.0 |
| TMS | TLBO [44] | PSO-DE [47] | IA-PSO [49] | FA [51] | IFA [51] | MFA | GA | FAGA |
|---|---|---|---|---|---|---|---|---|
| R1 | 0.3780 | 0.4064 | 0.2602 | 0.1002 | 0.1000 | 0.237644 | 0.237645 | 0.237660 |
| R2 | 0.3443 | 0.7506 | 0.4739 | 0.1002 | 0.1000 | 0.141769 | 0.141543 | 0.141515 |
| R3 | 0.2553 | 0.3872 | 0.2406 | 0.1006 | 0.1296 | 0.175244 | 0.145152 | 0.145036 |
| R4 | 0.3346 | 0.4031 | 0.2711 | 0.1102 | 0.1050 | 0.175244 | 0.107978 | 0.108029 |
| R5 | 0.1005 | 0.2005 | 0.1268 | 0.1000 | 0.1007 | 0.136037 | 0.136076 | 0.136054 |
| R6 | 0.2376 | 0.2011 | 0.1264 | 0.4070 | 0.3880 | 0.144476 | 0.142682 | 0.142615 |
| R7 | 0.3000 | 0.2003 | 0.1265 | 0.1092 | 0.1016 | 0.142491 | 0.142060 | 0.141982 |
| R8 | 0.4720 | 0.2133 | 0.1265 | 0.1000 | 0.1000 | 0.101873 | 0.101296 | 0.101237 |
| R9 | 0.0414 | 0.2006 | 0.1268 | 0.1175 | 0.1128 | 0.129268 | 0.125504 | 0.125525 |
| R10 | 0.3323 | 0.2265 | 0.1424 | 0.2860 | 0.1001 | 0.112415 | 0.111617 | 0.111619 |
| R11 | 0.2518 | 0.2610 | 0.1647 | 0.1439 | 0.1143 | 0.135796 | 0.135385 | 0.135377 |
| R12 | 0.2704 | 0.2039 | 0.1401 | 0.3404 | 0.2138 | 0.194383 | 0.190452 | 0.190353 |
| R13 | 0.1735 | 0.2002 | 0.1265 | 0.1063 | 0.1899 | 0.128468 | 0.128572 | 0.128488 |
| R14 | 0.2817 | 0.2837 | 0.1170 | 0.4070 | 0.2881 | 0.160717 | 0.160715 | 0.160723 |
| OF value | 23.787 | 9.2671 | 8.1245 | 7.6866 | 6.4040 | 3.36985 | 3.29554 | 3.29480 |
| Relay Number | MFA | GA | FA-GA | |||
|---|---|---|---|---|---|---|
| PS | TMS | PS | TMS | PS | TMS | |
| 1 | 0.803523 | 0.231888 | 0.501935 | 0.287456 | 0.796199 | 0.224686 |
| 2 | 2.069310 | 0.100000 | 0.500968 | 0.185867 | 1.292700 | 0.100000 |
| 3 | 1.954470 | 0.100238 | 0.793011 | 0.175585 | 1.630010 | 0.100116 |
| 4 | 1.252720 | 0.100000 | 0.501100 | 0.146315 | 0.692906 | 0.100000 |
| 5 | 1.222350 | 0.100000 | 0.500247 | 0.139980 | 0.824645 | 0.100000 |
| 6 | 1.462490 | 0.100004 | 1.015010 | 0.100125 | 0.800335 | 0.100004 |
| 7 | 1.915640 | 0.110990 | 0.727959 | 0.193363 | 1.872390 | 0.106718 |
| 8 | 1.337670 | 0.100000 | 0.500476 | 0.158478 | 1.050680 | 0.100000 |
| 9 | 1.668270 | 0.100003 | 0.500027 | 0.149016 | 0.793758 | 0.100003 |
| 10 | 1.479700 | 0.112366 | 0.500830 | 0.200589 | 1.420370 | 0.110291 |
| 11 | 1.898430 | 0.100002 | 1.428750 | 0.125244 | 1.541010 | 0.100002 |
| 12 | 1.380220 | 0.193785 | 0.502007 | 0.311442 | 1.297330 | 0.192931 |
| 13 | 1.552050 | 0.100000 | 0.500759 | 0.136331 | 0.680346 | 0.100000 |
| 14 | 1.243570 | 0.144867 | 0.592759 | 0.200200 | 1.108790 | 0.141449 |
| OF value | 3.31325 | 3.84454 | 3.01503 | |||
| Primary Relay | Short-Circuit Current | Backup Relay | Short-Circuit Current | Primary Relay | Short-Circuit Current | Backup Relay | Short-Circuit Current |
|---|---|---|---|---|---|---|---|
| 1 | 4863.6 | 15 | 1168.3 | 14 | 4172.5 | 16 | 1031.7 |
| 1 | 4863.6 | 17 | 1293.9 | 14 | 4172.5 | 19 | 1264.1 |
| 2 | 1634.4 | 4 | 1044.2 | 15 | 4172.5 | 13 | 1031.7 |
| 3 | 2811.4 | 1 | 1361.6 | 15 | 4172.5 | 19 | 1264.1 |
| 4 | 2610.5 | 6 | 1226.0 | 16 | 3684.5 | 2 | 653.60 |
| 5 | 1778.0 | 3 | 1124.4 | 16 | 3684.5 | 17 | 1293.9 |
| 6 | 4378.5 | 8 | 711.20 | 17 | 7611.2 | - | 0 |
| 6 | 4378.5 | 23 | 1345.5 | 18 | 2271.7 | 2 | 653.60 |
| 7 | 4378.5 | 5 | 711.20 | 18 | 2271.7 | 15 | 1168.3 |
| 7 | 4378.5 | 23 | 1345.5 | 19 | 7435.8 | - | 0 |
| 8 | 1778.0 | 10 | 1124.4 | 20 | 2624.2 | 13 | 1031.7 |
| 9 | 2610.5 | 7 | 1226.0 | 20 | 2624.2 | 16 | 1031.7 |
| 10 | 2811.4 | 12 | 787.20 | 21 | 7611.2 | - | 0 |
| 11 | 1634.4 | 9 | 1044.2 | 22 | 2271.7 | 11 | 653.60 |
| 12 | 2811.4 | 14 | 1168.2 | 22 | 2271.7 | 14 | 1168.3 |
| 12 | 2811.4 | 21 | 1293.9 | 23 | 7914.7 | - | 0 |
| 13 | 3684.5 | 11 | 653.60 | 24 | 1665.5 | 5 | 711.20 |
| 13 | 3684.5 | 21 | 1293.9 | 24 | 1665.5 | 8 | 711.20 |
| Relay # | MFA | GA | FA-GA | |||
|---|---|---|---|---|---|---|
| PS | TMS | PS | TMS | PS | TMS | |
| 1 | 1.480550 | 0.100000 | 0.713501 | 0.100045 | 0.749105 | 0.10000 |
| 2 | 0.542203 | 0.100000 | 0.500025 | 0.100024 | 0.500089 | 0.10000 |
| 3 | 0.582759 | 0.121327 | 0.639849 | 0.100000 | 0.556856 | 0.11168 |
| 4 | 0.865640 | 0.100006 | 0.667917 | 0.100072 | 0.619558 | 0.10000 |
| 5 | 0.703050 | 0.100000 | 0.500011 | 0.100015 | 0.506492 | 0.10000 |
| 6 | 0.567292 | 0.123330 | 0.696574 | 0.100000 | 0.555085 | 0.11235 |
| 7 | 0.874826 | 0.100022 | 0.668990 | 0.100000 | 0.615549 | 0.10002 |
| 8 | 0.588203 | 0.100000 | 0.500019 | 0.100083 | 0.500068 | 0.10000 |
| 9 | 0.831344 | 0.100000 | 0.500061 | 0.117236 | 0.657638 | 0.10000 |
| 10 | 1.048110 | 0.100000 | 0.502563 | 0.119556 | 0.640949 | 0.10000 |
| 11 | 0.918434 | 0.100035 | 0.500000 | 0.100000 | 0.553641 | 0.10004 |
| 12 | 0.656150 | 0.100100 | 0.500018 | 0.100024 | 0.500022 | 0.10010 |
| 13 | 1.503570 | 0.100000 | 0.503662 | 0.100282 | 0.519555 | 0.10000 |
| 14 | 1.925840 | 0.100026 | 0.785659 | 0.100103 | 0.603911 | 0.10003 |
| 15 | 0.504272 | 0.428972 | 0.594298 | 0.101203 | 0.500122 | 0.11416 |
| 16 | 1.327960 | 0.100138 | 0.507543 | 0.100041 | 0.508474 | 0.10001 |
| 17 | 0.500938 | 0.375384 | 0.982412 | 0.100000 | 0.500328 | 0.11138 |
| 18 | 0.657034 | 0.100000 | 0.500000 | 0.100024 | 0.500284 | 0.10000 |
| 19 | 1.219770 | 0.130127 | 0.500000 | 0.115283 | 0.628484 | 0.10009 |
| 20 | 0.650834 | 0.100114 | 0.500000 | 0.100000 | 0.500077 | 0.10011 |
| 21 | 1.204720 | 0.116052 | 0.622735 | 0.100090 | 0.763314 | 0.10006 |
| 22 | 0.930322 | 0.100000 | 0.500000 | 0.100000 | 0.500055 | 0.10000 |
| 23 | 1.197070 | 0.100036 | 0.512695 | 0.113113 | 0.635455 | 0.10004 |
| 24 | 0.927182 | 0.100000 | 0.500022 | 0.100046 | 0.500281 | 0.10000 |
| OF value | 10.23700 | 7.08666 | 7.03106 | |||
| Primary Relay | Short-Circuit Current | Backup Relay | Short-Circuit Current | Primary Relay | Short-Circuit Current | Backup Relay | Short-Circuit Current | Primary Relay | Short-Circuit Current | Backup Relay | Short-Circuit Current |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 3621 | 6 | 1233 | 15 | 4712 | 1 | 853 | 26 | 2300 | 36 | 1109 |
| 2 | 4597 | 4 | 1477 | 15 | 4712 | 4 | 1477 | 27 | 2011 | 25 | 903 |
| 2 | 4597 | 16 | 743 | 16 | 2225 | 18 | 1320 | 27 | 2011 | 36 | 1109 |
| 3 | 3984 | 1 | 853 | 16 | 2225 | 26 | 905 | 28 | 2525 | 29 | 1828 |
| 3 | 3984 | 16 | 743 | 17 | 1875 | 15 | 969 | 28 | 2525 | 32 | 697 |
| 4 | 4382 | 7 | 1111 | 17 | 1875 | 26 | 905 | 29 | 8346 | 17 | 599 |
| 4 | 4382 | 12 | 1463 | 18 | 8426 | 19 | 1372 | 29 | 8346 | 19 | 1372 |
| 4 | 4382 | 20 | 1808 | 18 | 8426 | 22 | 642 | 29 | 8346 | 22 | 642 |
| 5 | 3319 | 2 | 922 | 18 | 8426 | 30 | 681 | 30 | 1736 | 27 | 1039 |
| 6 | 2647 | 8 | 1548 | 19 | 3998 | 3 | 1424 | 30 | 1736 | 32 | 697 |
| 6 | 2647 | 10 | 1100 | 19 | 3998 | 7 | 1111 | 31 | 2867 | 27 | 697 |
| 7 | 2497 | 5 | 1397 | 19 | 3998 | 12 | 1463 | 31 | 2867 | 29 | 1828 |
| 7 | 2497 | 10 | 1100 | 20 | 7662 | 17 | 599 | 32 | 2069 | 33 | 1162 |
| 8 | 4695 | 3 | 1424 | 20 | 7662 | 22 | 642 | 32 | 2069 | 42 | 907 |
| 8 | 4695 | 12 | 1463 | 20 | 7662 | 30 | 681 | 33 | 2305 | 21 | 1326 |
| 8 | 4695 | 20 | 1808 | 21 | 8384 | 17 | 599 | 33 | 2305 | 23 | 979 |
| 9 | 2943 | 5 | 1397 | 21 | 8384 | 19 | 1372 | 34 | 1715 | 31 | 809 |
| 9 | 2943 | 8 | 1548 | 21 | 8384 | 30 | 681 | 34 | 1715 | 42 | 907 |
| 10 | 3568 | 14 | 1175 | 22 | 1950 | 23 | 979 | 35 | 2095 | 25 | 903 |
| 11 | 4342 | 3 | 1424 | 22 | 1950 | 34 | 970 | 35 | 2095 | 28 | 1192 |
| 11 | 4342 | 7 | 1111 | 23 | 4910 | 11 | 1475 | 36 | 3283 | 38 | 882 |
| 11 | 4342 | 20 | 1808 | 23 | 4910 | 13 | 1053 | 37 | 3301 | 35 | 910 |
| 12 | 4195 | 13 | 1503 | 24 | 2296 | 21 | 175 | 38 | 1403 | 40 | 1403 |
| 12 | 4195 | 24 | 753 | 24 | 2296 | 34 | 970 | 39 | 1434 | 37 | 1434 |
| 13 | 3402 | 9 | 1009 | 25 | 2289 | 15 | 969 | 40 | 3140 | 41 | 1434 |
| 14 | 4606 | 11 | 1475 | 25 | 2289 | 18 | 1320 | 41 | 1971 | 31 | 809 |
| 14 | 4606 | 24 | 753 | 26 | 2300 | 28 | 1192 | 41 | 1971 | 33 | 1162 |
| 42 | 3295 | 39 | 896 |
| Relay Number | CTR |
|---|---|
| 18, 20, 21, 29 | 1600/5 |
| 2, 4, 8, 11, 12, 14, 15, 23 | 1200/5 |
| 1, 3, 5, 10, 13, 19, 36, 37, 40, 42 | 800/5 |
| 6, 7, 9, 16, 24, 25, 26, 27, 28, 31, 32, 33, 35 | 600/5 |
| 17, 22, 30, 34, 38, 39, 41 | 400/5 |
| Relay # | MFA | GA | FA-GA | Relay # | MFA | GA | FA-GA | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PS | TMS | PS | TMS | PS | TMS | PS | TMS | PS | TMS | PS | TMS | ||
| 1 | 2.112490 | 0.100272 | 0.500055 | 0.206152 | 1.57929 | 0.10015 | 22 | 0.604595 | 0.205113 | 1.799800 | 0.129066 | 0.600682 | 0.203577 |
| 2 | 0.818450 | 0.199528 | 0.500000 | 0.208066 | 0.619231 | 0.156986 | 23 | 1.655810 | 0.145834 | 0.506614 | 0.202590 | 1.63823 | 0.112387 |
| 3 | 1.631750 | 0.148360 | 2.047870 | 0.133555 | 1.4755 | 0.14836 | 24 | 2.033670 | 0.114539 | 0.649283 | 0.205760 | 1.53367 | 0.111121 |
| 4 | 1.985600 | 0.102725 | 0.500111 | 0.217709 | 1.8899 | 0.100772 | 25 | 1.328160 | 0.166519 | 0.657970 | 0.248675 | 1.32818 | 0.166667 |
| 5 | 2.051690 | 0.132894 | 0.678760 | 0.252685 | 2.03948 | 0.129964 | 26 | 2.151390 | 0.120819 | 0.501492 | 0.213332 | 2.1177 | 0.110809 |
| 6 | 1.769940 | 0.143683 | 2.298000 | 0.123010 | 1.76994 | 0.133917 | 27 | 1.242180 | 0.151402 | 0.738998 | 0.228699 | 1.24218 | 0.151448 |
| 7 | 2.362570 | 0.126064 | 2.056640 | 0.135935 | 2.28399 | 0.117763 | 28 | 2.048490 | 0.151529 | 2.485720 | 0.137597 | 2.04849 | 0.151529 |
| 8 | 1.370410 | 0.147295 | 1.463750 | 0.145139 | 1.35454 | 0.142412 | 29 | 1.715440 | 0.136204 | 0.500117 | 0.228716 | 1.46182 | 0.127394 |
| 9 | 1.586560 | 0.157093 | 0.643388 | 0.256192 | 1.52382 | 0.147694 | 30 | 1.665180 | 0.126348 | 2.245970 | 0.113577 | 1.65736 | 0.126251 |
| 10 | 0.774944 | 0.216869 | 0.500244 | 0.236010 | 0.751506 | 0.214672 | 31 | 2.437110 | 0.100447 | 0.780606 | 0.219824 | 2.43711 | 0.100447 |
| 11 | 1.132450 | 0.160230 | 0.958190 | 0.154077 | 0.81995 | 0.160108 | 32 | 2.253360 | 0.100045 | 1.977600 | 0.100000 | 2.00336 | 0.100045 |
| 12 | 1.885810 | 0.100060 | 0.633033 | 0.206159 | 1.87019 | 0.10006 | 33 | 1.171590 | 0.197349 | 2.022740 | 0.153101 | 1.17159 | 0.197386 |
| 13 | 1.510500 | 0.170058 | 0.522666 | 0.263739 | 1.21167 | 0.151992 | 34 | 0.976432 | 0.211959 | 0.913722 | 0.231846 | 0.968617 | 0.211885 |
| 14 | 1.019050 | 0.145922 | 1.368390 | 0.115466 | 1.01856 | 0.143969 | 35 | 0.811549 | 0.208108 | 1.036120 | 0.201486 | 0.811591 | 0.208441 |
| 15 | 1.437680 | 0.118373 | 0.500702 | 0.213140 | 1.18377 | 0.11349 | 36 | 1.518780 | 0.131359 | 0.805507 | 0.219030 | 1.51879 | 0.131442 |
| 16 | 1.450150 | 0.133919 | 1.439820 | 0.124083 | 1.4344 | 0.130013 | 37 | 1.471440 | 0.169650 | 0.510730 | 0.271151 | 1.47146 | 0.169834 |
| 17 | 1.171030 | 0.190055 | 2.292620 | 0.101080 | 0.79071 | 0.185416 | 38 | 2.100210 | 0.130993 | 2.497920 | 0.141771 | 2.10021 | 0.131092 |
| 18 | 0.575983 | 0.179936 | 0.504973 | 0.214490 | 0.575983 | 0.179936 | 39 | 1.647920 | 0.155660 | 1.290270 | 0.171159 | 1.64781 | 0.155815 |
| 19 | 1.367610 | 0.154495 | 0.511433 | 0.244176 | 1.3012 | 0.142776 | 40 | 0.765282 | 0.222847 | 1.103120 | 0.211496 | 0.765282 | 0.222603 |
| 20 | 0.841027 | 0.165046 | 0.501041 | 0.222023 | 0.804894 | 0.162605 | 41 | 1.305190 | 0.190438 | 1.139900 | 0.214445 | 1.30519 | 0.190411 |
| 21 | 2.059560 | 0.107406 | 0.500000 | 0.205402 | 1.80958 | 0.102523 | 42 | 1.205710 | 0.149375 | 1.586970 | 0.128640 | 1.20573 | 0.149455 |
| OF value | MFA | 16.0694 | GA | 17.2657 | FA-GA | 15.2292 | |||||||
| Case Study | Method | Number of Objective Function Evaluations | % Improvement |
|---|---|---|---|
| IEEE 3-bus LP | GA | 165,432 | 48.345 |
| FA-GA | 85,454 | ||
| IEEE 3-bus NLP | GA | 173,656 | 53.316 |
| FA-GA | 81,070 | ||
| IEEE 6-bus LP | GA | 266,000 | 54.343 |
| FA-GA | 121,448 | ||
| IEEE 6-bus NLP | GA | 281,200 | 42.674 |
| FA-GA | 161,200 | ||
| IEEE 9-bus NLP | GA | 604,800 | 33.639 |
| FA-GA | 401,350 | ||
| IEEE 15-bus NLP | GA | 602,432 | 47.059 |
| FA-GA | 156,274 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Foqha, T.; Khammash, M.; Alsadi, S.; Omari, O.; Refaat, S.S.; Al-Qawasmi, K.; Elrashidi, A. Optimal Coordination of Directional Overcurrent Relays Using Hybrid Firefly–Genetic Algorithm. Energies 2023, 16, 5328. https://doi.org/10.3390/en16145328
Foqha T, Khammash M, Alsadi S, Omari O, Refaat SS, Al-Qawasmi K, Elrashidi A. Optimal Coordination of Directional Overcurrent Relays Using Hybrid Firefly–Genetic Algorithm. Energies. 2023; 16(14):5328. https://doi.org/10.3390/en16145328
Chicago/Turabian StyleFoqha, Tareq, Maher Khammash, Samer Alsadi, Osama Omari, Shady S. Refaat, Khaled Al-Qawasmi, and Ali Elrashidi. 2023. "Optimal Coordination of Directional Overcurrent Relays Using Hybrid Firefly–Genetic Algorithm" Energies 16, no. 14: 5328. https://doi.org/10.3390/en16145328
APA StyleFoqha, T., Khammash, M., Alsadi, S., Omari, O., Refaat, S. S., Al-Qawasmi, K., & Elrashidi, A. (2023). Optimal Coordination of Directional Overcurrent Relays Using Hybrid Firefly–Genetic Algorithm. Energies, 16(14), 5328. https://doi.org/10.3390/en16145328










