Numerical Study of the Impact of Transverse Ribs on the Energy Potential of Air-Based BIPV/T Envelope Systems
Abstract
1. Introduction
2. Methodology
3. Validation of the Numerical Model
3.1. Numerical Simulation Setup
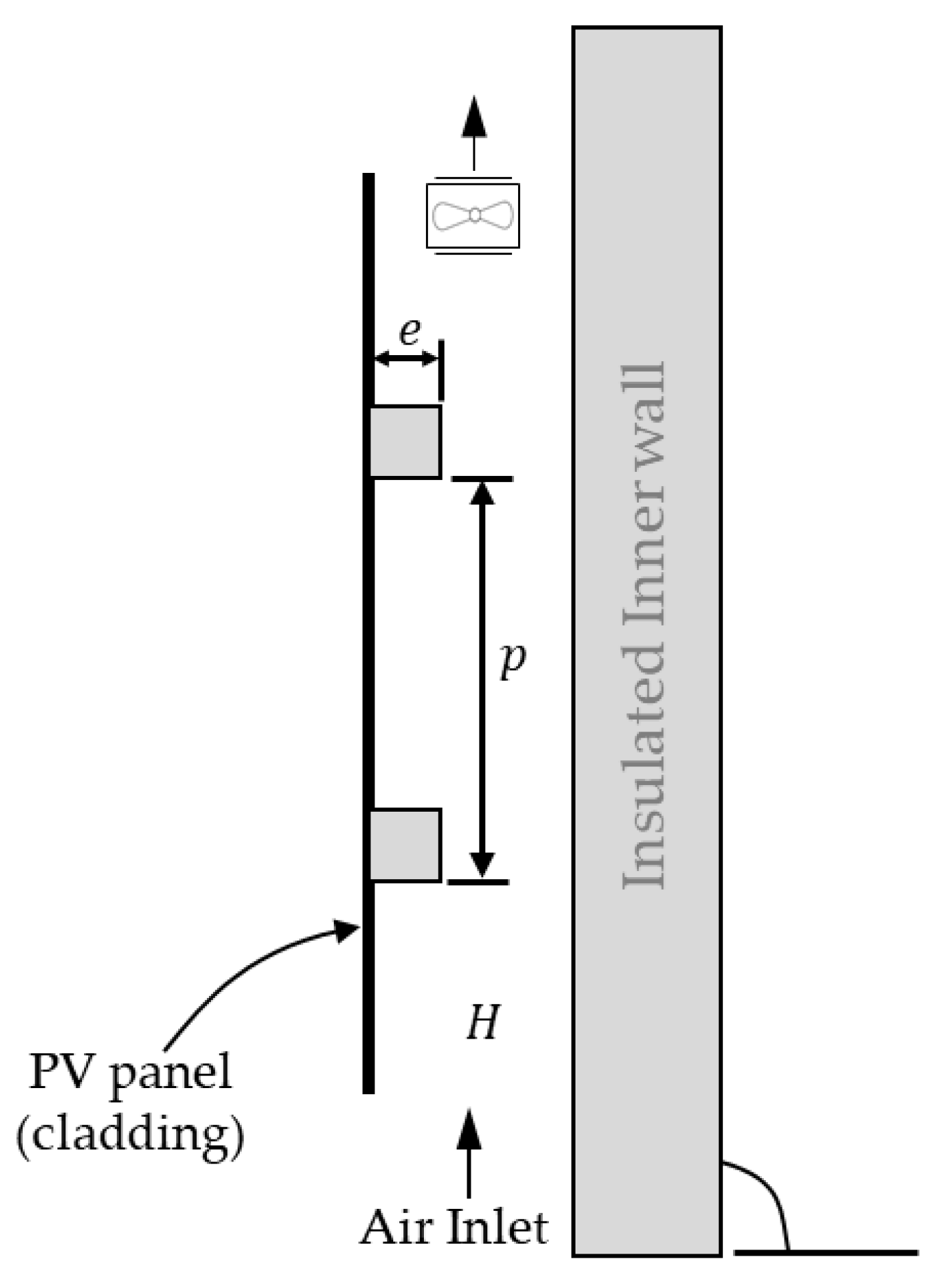
3.1.1. Computational Domain
3.1.2. Boundary Conditions and Solution Strategy
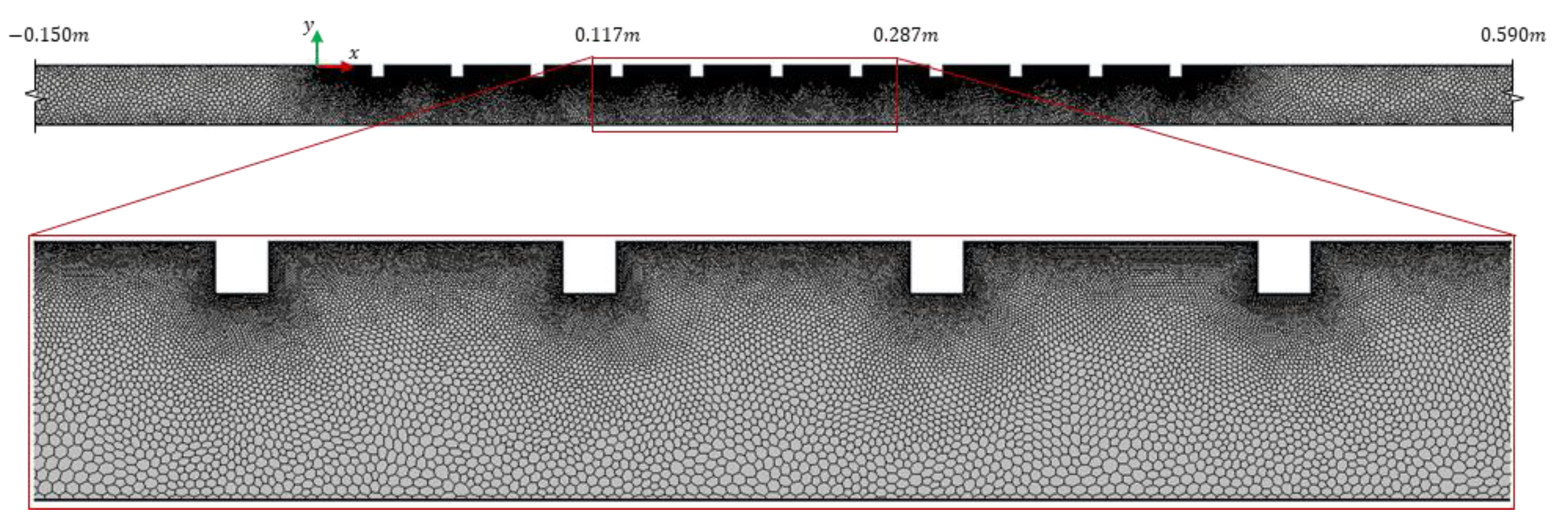
3.1.3. Mesh Generation
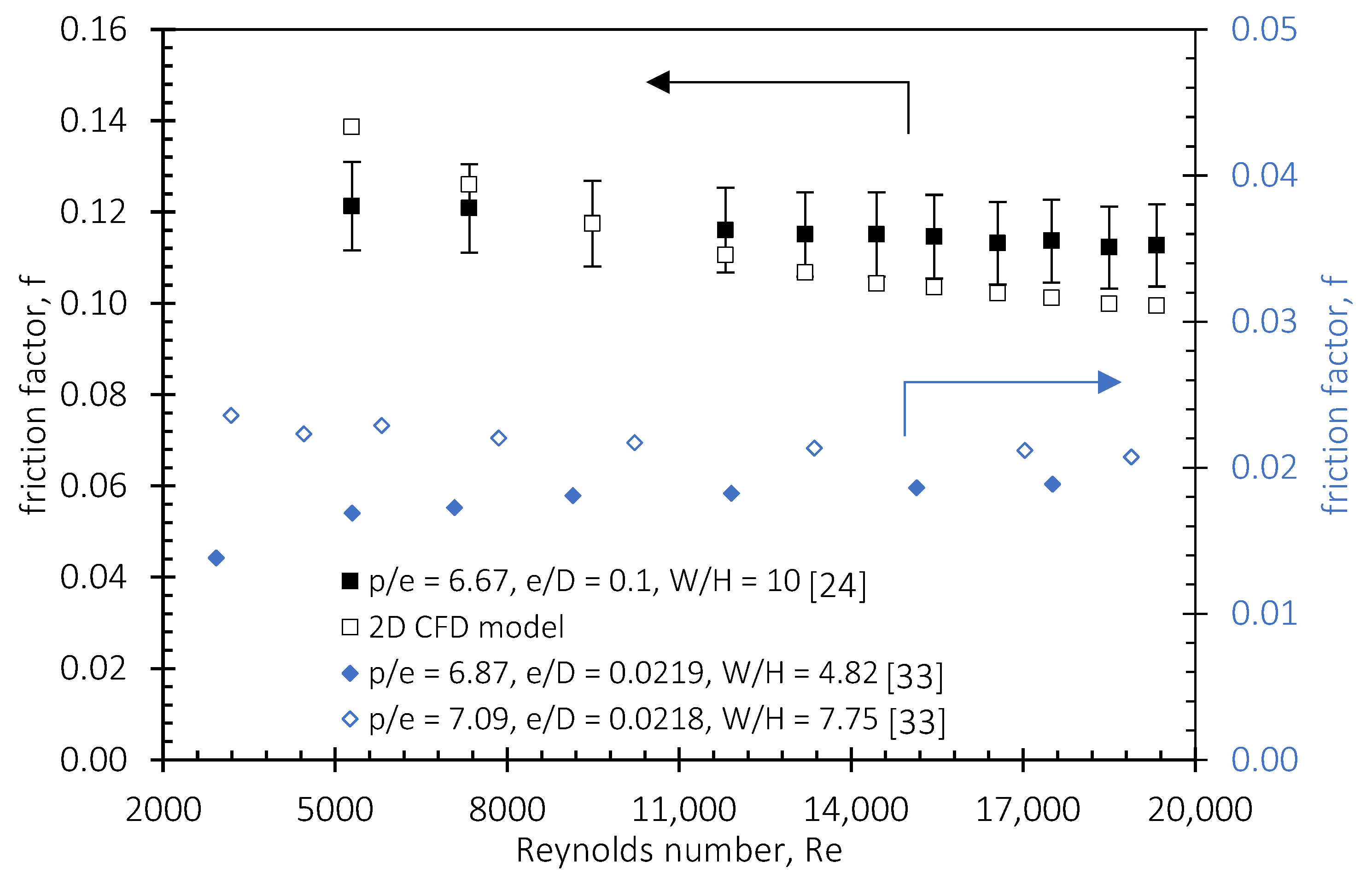
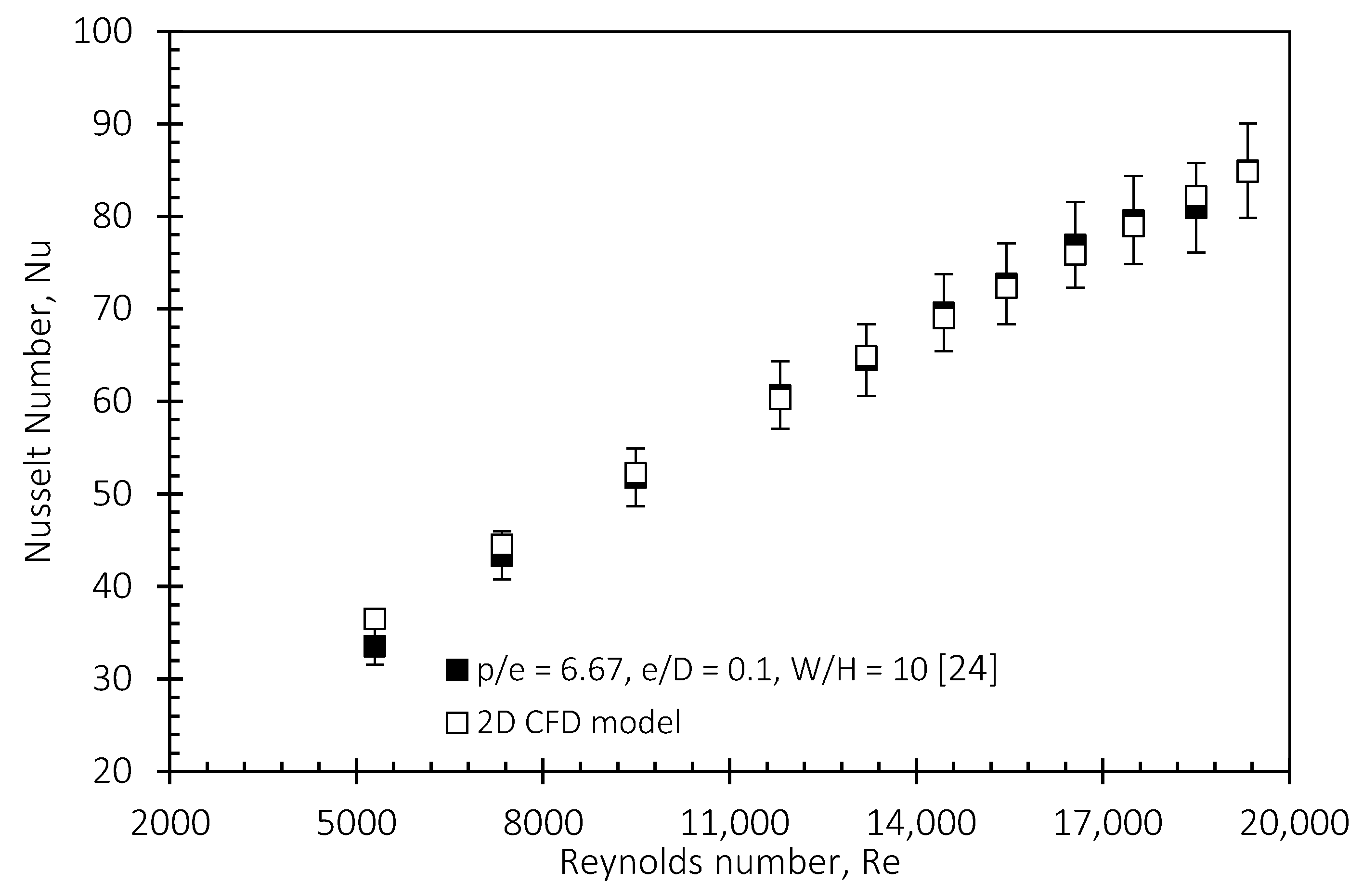
3.2. CFD Validation Results
4. Parametric Analysis Results and Discussion
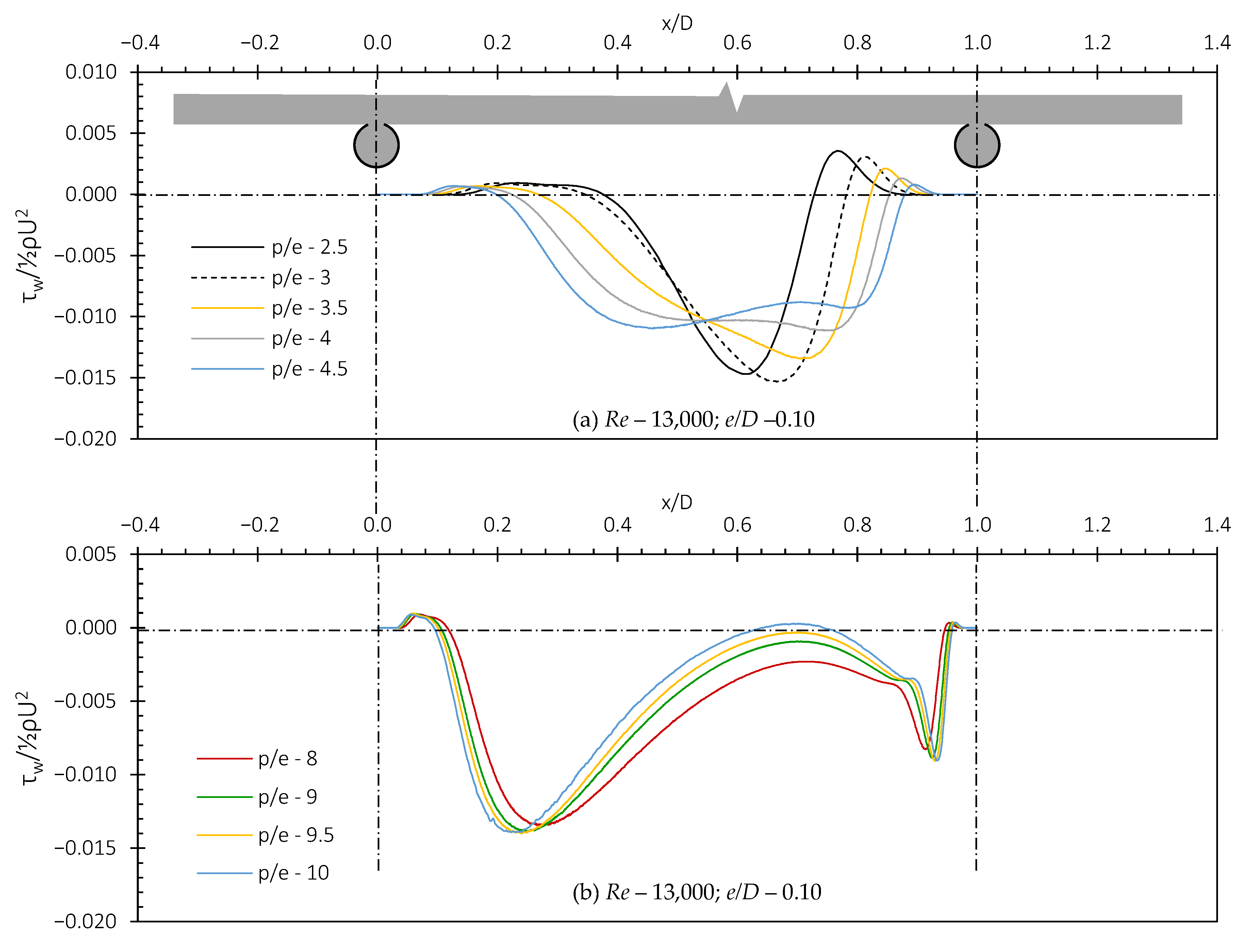
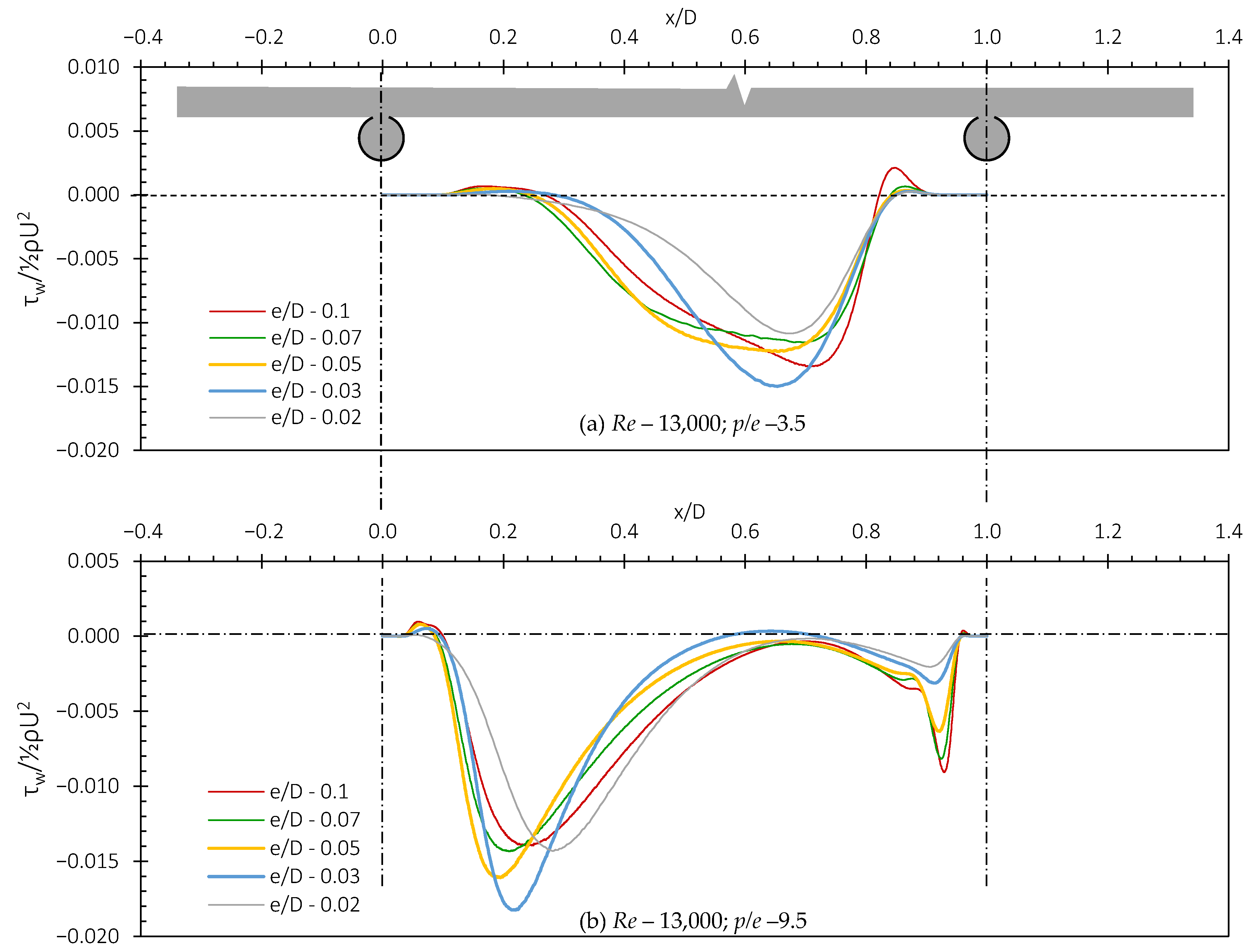
4.1. Flow Structure Characterization: Near-Wall Flow
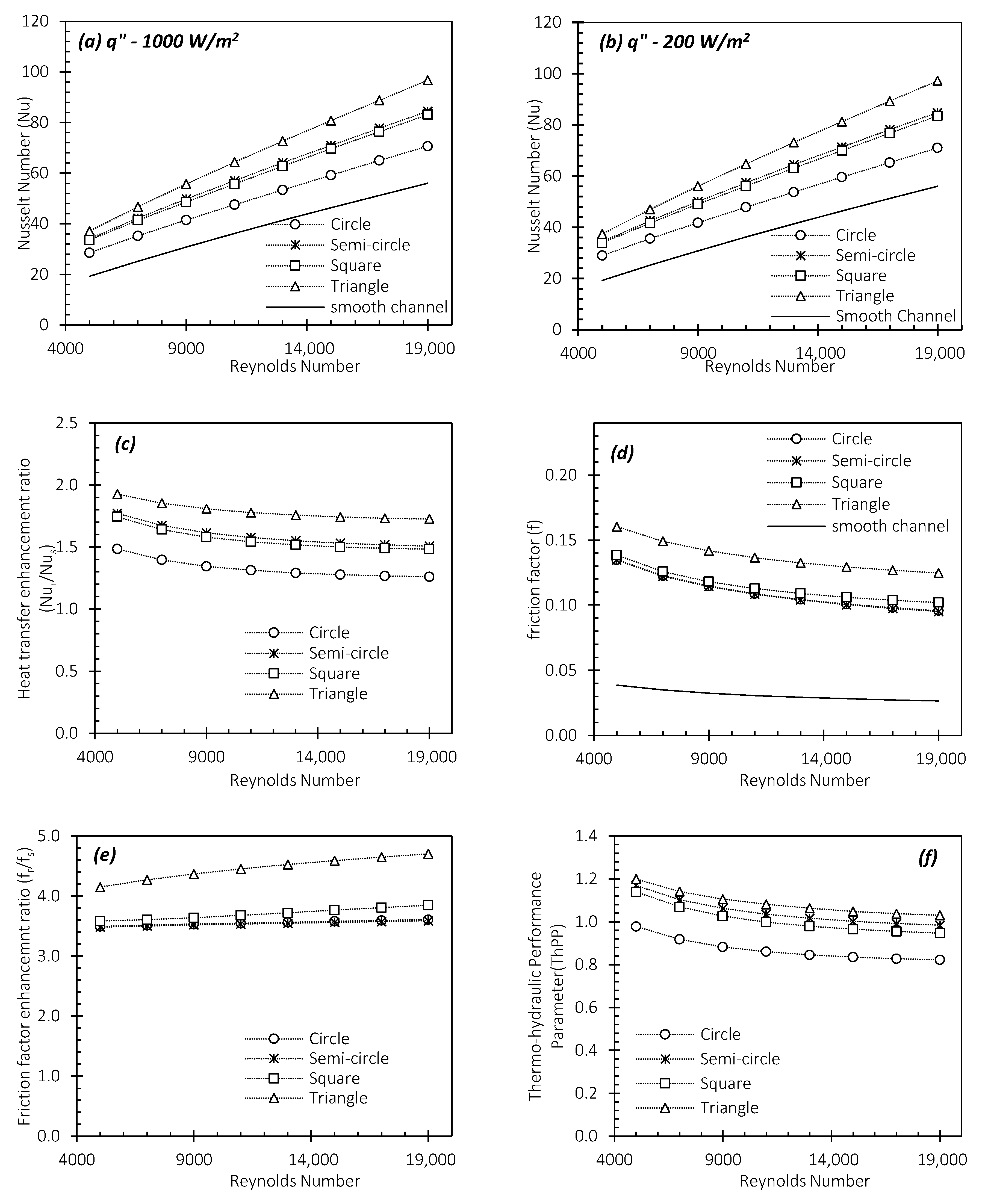
4.2. Effect of Shape of the Transverse Rib Profile
4.2.1. Effect of Shape of the Transverse Rib Profile on Nusselt Number, Friction Factor and Thermohydraulic Performance Parameter
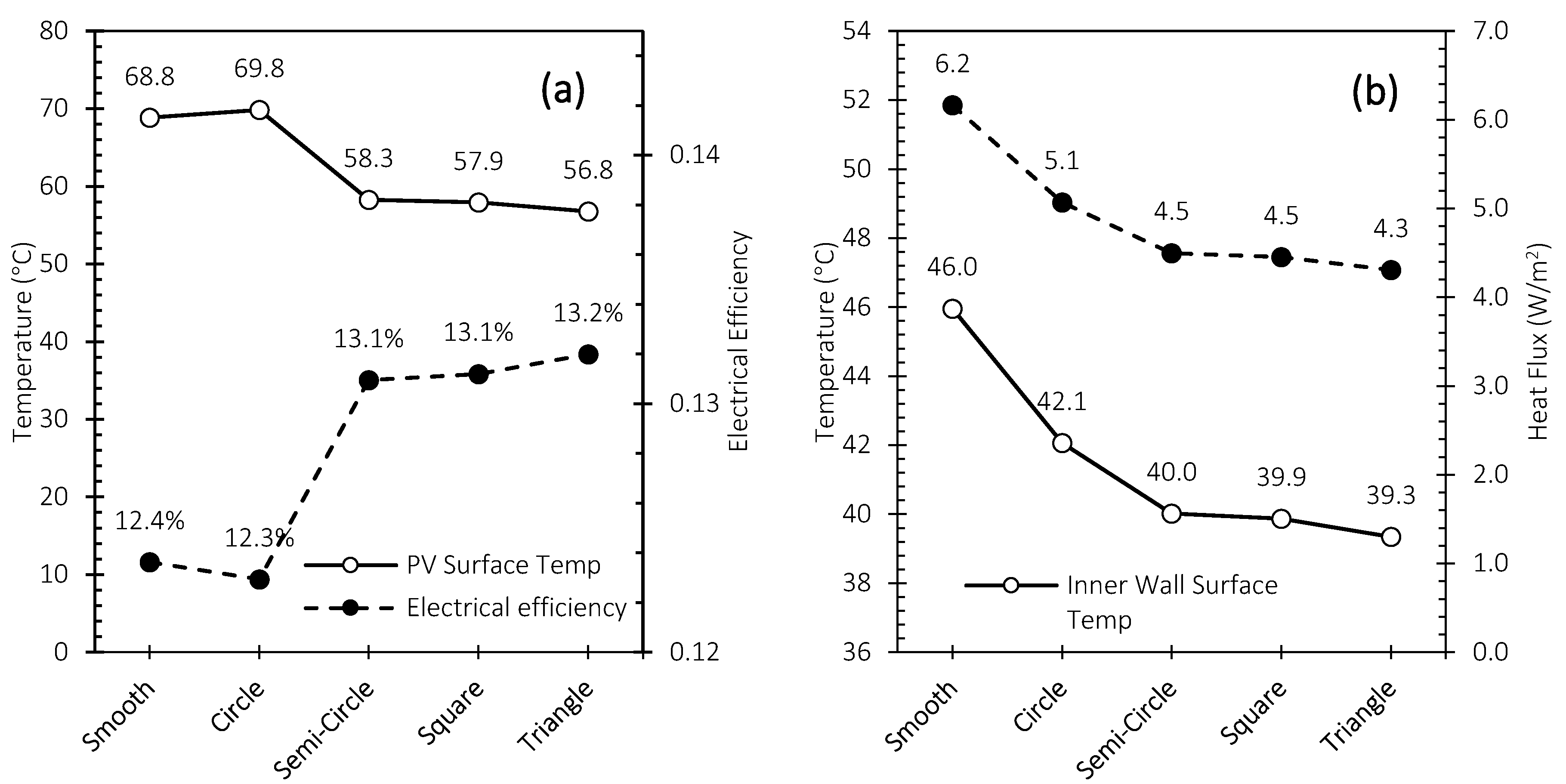
4.2.2. Effect of Shape of the Transverse Rib Profile on Building Heat Gain and Electrical Efficiency
4.3. Effect of Relative Pitch Ratio (p/e)
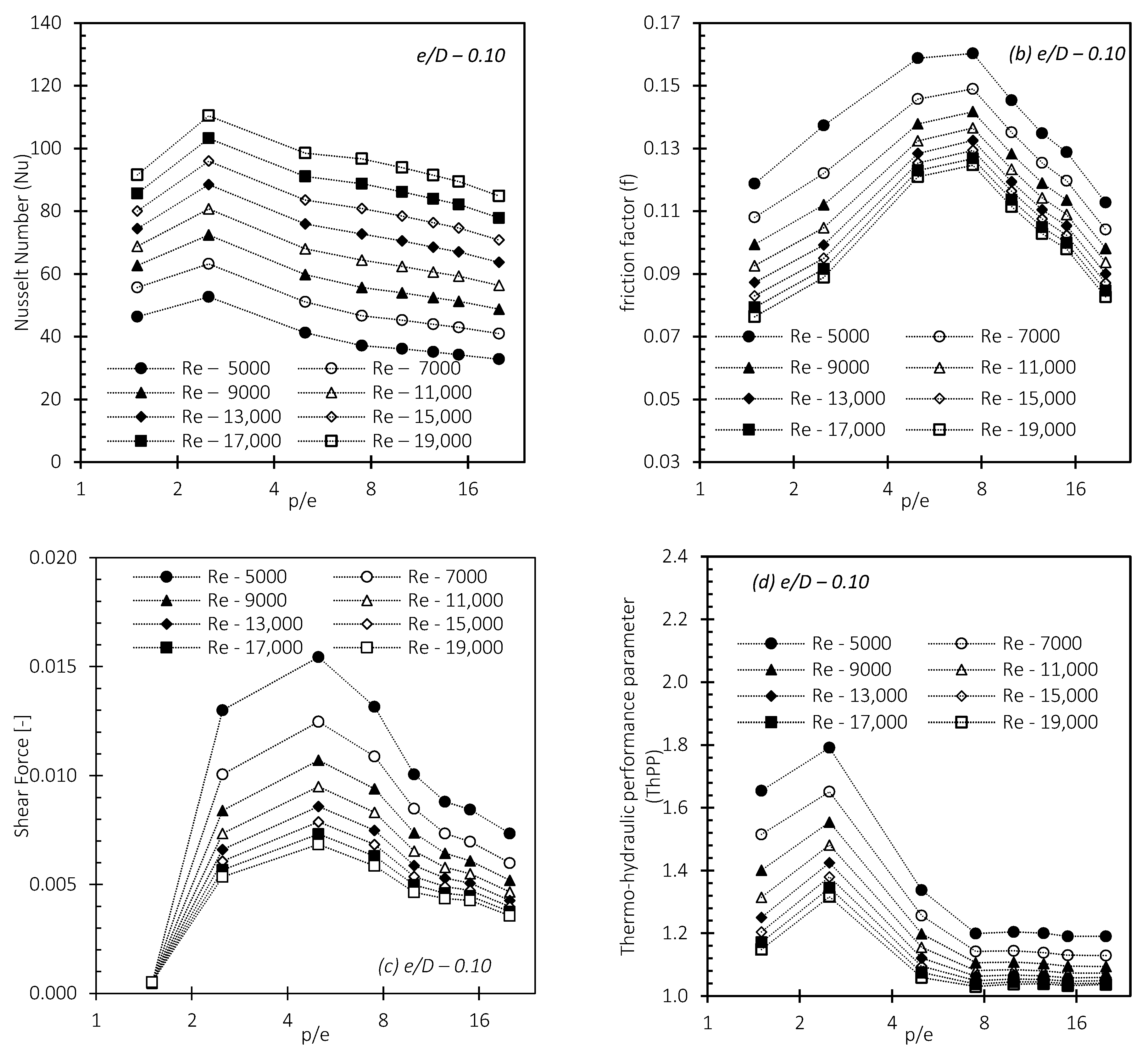
4.3.1. Effect of Relative Pitch Ratio on Nusselt Number, Friction Factor and Thermohydraulic Performance Parameter
4.3.2. Effect of Relative Pitch Ratio on Building Heat Gain and Electrical Efficiency
4.4. Effect of Relative Roughness Height (e/D)
4.4.1. Effect of Relative Roughness Height on Nusselt Number, Friction Factor and Thermohydraulic Performance Parameter
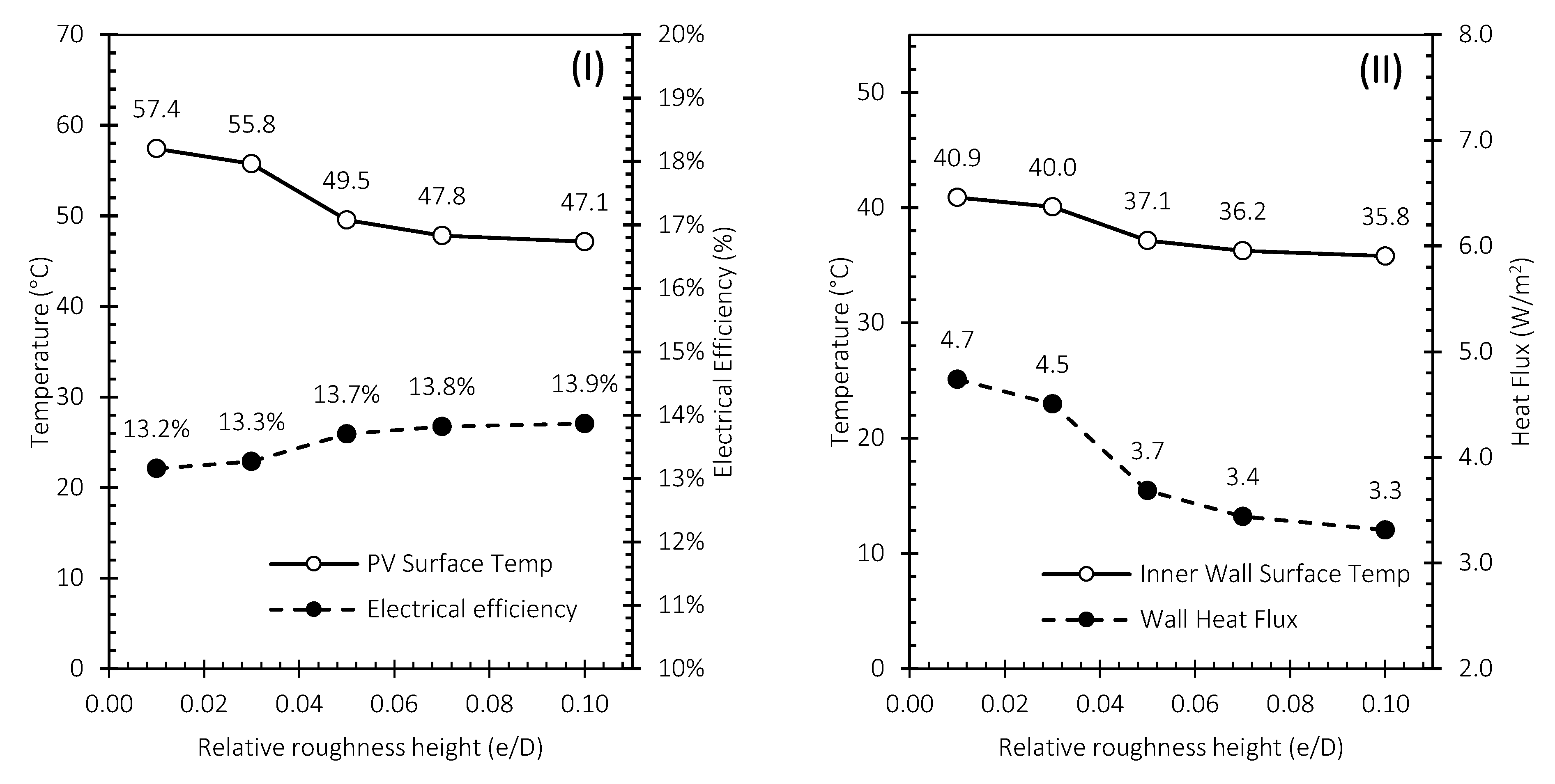
4.4.2. Effect of Relative Roughness Height on Building Heat Gain and Electrical Efficiency
4.5. Development of Correlation for Nusselt Number and Friction Factor
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lai, C.M.; Hokoi, S. Solar façades: A review. Build. Environ. 2015, 91, 152–165. [Google Scholar] [CrossRef]
- Agathokleous, R.A.; Kalogirou, S.A. Double skin facades (DSF) and building integrated photovoltaics (BIPV): A review of configurations and heat transfer characteristics. Renew. Energy 2016, 89, 743–756. [Google Scholar] [CrossRef]
- Peng, C.; Huang, Y.; Wu, Z. Building-integrated photovoltaics (BIPV) in architectural design in China. Energy Build. 2011, 43, 3592–3598. [Google Scholar] [CrossRef]
- Jelle, B.P.; Breivik, C.; Røkenes, H.D. Building integrated photovoltaic products: A state-of-the-art review and future research opportunities. Sol. Energy Mater. Sol. Cells 2012, 100, 69–96. [Google Scholar] [CrossRef]
- Fossa, M.; Ménézo, C.; Leonardi, E. Experimental natural convection on vertical surfaces for building integrated photovoltaic (BIPV) applications. Exp. Therm. Fluid Sci. 2008, 32, 980–990. [Google Scholar] [CrossRef]
- Athienitis, A.K.; Bambara, J.; O’Neill, B.; Faille, J. A prototype photovoltaic/thermal system integrated with transpired collector. Sol. Energy 2011, 85, 139–153. [Google Scholar] [CrossRef]
- Chen, Y.; Athienitis, A.K.; Galal, K. Modeling, design and thermal performance of a BIPV/T system thermally coupled with a ventilated concrete slab in a low energy solar house: Part 1, BIPV/T system and house energy concept. Sol. Energy 2010, 84, 1892–1907. [Google Scholar] [CrossRef]
- Corbin, C.D.; Zhai, Z.J. Experimental and numerical investigation on thermal and electrical performance of a building integrated photovoltaic–thermal collector system. Energy Build. 2010, 42, 76–82. [Google Scholar] [CrossRef]
- Dubey, S.; Sandhu, G.S.; Tiwari, G.N. Analytical expression for electrical efficiency of PV/T hybrid air collector. Appl. Energy 2009, 86, 697–705. [Google Scholar] [CrossRef]
- Kamel, R.S.; Fung, A.S. Modeling, simulation and feasibility analysis of residential BIPV/T+ ASHP system in cold climate—Canada. Energy Build. 2014, 82, 758–770. [Google Scholar] [CrossRef]
- Pantic, S.; Candanedo, L.; Athienitis, A.K. Modeling of energy performance of a house with three configurations of building-integrated photovoltaic/thermal systems. Energy Build. 2010, 42, 1779–1789. [Google Scholar] [CrossRef]
- Peng, J.; Lu, L.; Yang, H.; Han, J. Investigation on the annual thermal performance of a photovoltaic wall mounted on a multi-layer façade. Appl. Energy 2013, 112, 646–656. [Google Scholar] [CrossRef]
- Zogou, O.; Stapountzis, H. Energy analysis of an improved concept of integrated PV panels in an office building in central Greece. Appl. Energy 2011, 88, 853–866. [Google Scholar] [CrossRef]
- Patil, A.K.; Saini, J.S.; Kumar, K. Experimental Investigation of Enhanced Heat Transfer and Pressure Drop in a Solar Air Heater Duct with Discretized Broken V-Rib Roughness. J. Sol. Energy Eng. 2015, 137, 021013. [Google Scholar] [CrossRef]
- Kumar, A.; Kim, M.H. Effect of roughness width ratios in discrete multi V-rib with staggered rib roughness on overall thermal performance of solar air channel. Sol. Energy 2015, 119, 399–414. [Google Scholar] [CrossRef]
- Pandey, N.K.; Bajpai, V.K. Experimental investigation of heat transfer augmentation using multiple arcs with gap on absorber plate of solar air heater. Sol. Energy 2016, 134, 314–326. [Google Scholar] [CrossRef]
- Yang, T.; Athienitis, A.K. A study of design options for a building integrated photovoltaic/thermal (BIPV/T) system with glazed air collector and multiple inlets. Sol. Energy 2014, 104, 82–92. [Google Scholar] [CrossRef]
- Yang, T.; Athienitis, A.K. Experimental investigation of a two-inlet air-based building integrated photovoltaic/thermal (BIPV/T) system. Appl. Energy 2015, 159, 70–79. [Google Scholar] [CrossRef]
- Rounis, E.D.; Athienitis, A.K.; Stathopoulos, T. Multiple-inlet Building Integrated Photovoltaic/Thermal system modelling under varying wind and temperature conditions. Sol. Energy 2016, 139, 157–170. [Google Scholar] [CrossRef]
- Gawande, V.B.; Dhoble, A.S.; Zodpe, D.B.; Chamoli, S. Experimental and CFD investigation of convection heat transfer in solar air heater with reverse L-shaped ribs. Sol. Energy 2016, 131, 275–295. [Google Scholar] [CrossRef]
- Poongavanam, G.K.; Panchabikesan, K.; Leo AJ, D.; Ramalingam, V. Experimental investigation on heat transfer augmentation of solar air heater using shot blasted V-corrugated absorber plate. Renew. Energy 2018, 127, 213–229. [Google Scholar] [CrossRef]
- Gawande, V.B.; Dhoble, A.S.; Zodpe, D.B. Effect of roughness geometries on heat transfer enhancement in solar thermal systems—A review. Renew. Sustain. Energy Rev. 2014, 32, 347–378. [Google Scholar] [CrossRef]
- Agathokleous, R.A.; Kalogirou, S.A. Part I: Thermal analysis of naturally ventilated BIPV system: Experimental investigation and convective heat transfer coefficients estimation. Sol. Energy 2018, 169, 673–681. [Google Scholar] [CrossRef]
- Skullong, S.; Thianpong, C.; Promvonge, P. Effects of rib size and arrangement on forced convective heat transfer in a solar air heater channel. Heat Mass Transf. 2015, 51, 1475–1485. [Google Scholar] [CrossRef]
- Nghana, B.; Tariku, F.; Bitsuamlak, G. Numerical assessment of the impact of transverse roughness ribs on the turbulent natural convection in a BIPV air channel. Build. Environ. 2022, 217, 109093. [Google Scholar] [CrossRef]
- Yadav, A.S.; Bhagoria, J.L. A CFD based thermo-hydraulic performance analysis of an artificially roughened solar air heater having equilateral triangular sectioned rib roughness on the absorber plate. Int. J. Heat Mass Transf. 2014, 70, 1016–1039. [Google Scholar] [CrossRef]
- Incropera, F.P.; Lavine, A.S.; Bergman, T.L.; DeWitt, D.P. Fundamentals of Heat and Mass Transfer; Wiley and Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Ji, J.; He, H.; Chow, T.; Pei, G.; He, W.; Liu, K. Distributed dynamic modeling and experimental study of PV evaporator in a PV/T solar-assisted heat pump. Int. J. Heat Mass Transf. 2009, 52, 1365–1373. [Google Scholar] [CrossRef]
- Nghana, B.; Tariku, F.; Bitsuamlak, G. Assessing ventilation cavity design impact on the energy performance of rainscreen wall assemblies: A CFD study. Build. Environ. 2021, 196, 107789. [Google Scholar] [CrossRef]
- ASHRAE. 2017 ASHRAE Handbook: Fundamentals; ASHRAE: Peachtree Corners, GA, USA, 2017. [Google Scholar]
- STAR CCM + Users Manual. Available online: http://www.cd-adapco.com/products/star-ccm/documentation (accessed on 14 June 2019).
- Kumar, R.; Kumar, A.; Goel, V. Performance improvement and development of correlation for friction factor and heat transfer using computational fluid dynamics for ribbed triangular duct solar air heater. Renew. Energy 2019, 131, 788–799. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)?—Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Karwa, R.; Solanki, S.C.; Saini, J.S. Heat transfer coefficient and friction factor correlations for the transitional flow regime in rib-roughened rectangular ducts. Int. J. Heat Mass Transf. 1999, 42, 1597–1615. [Google Scholar] [CrossRef]
- Awol, A.; Bitsuamlak, G.T.; Tariku, F. Numerical estimation of the external convective heat transfer coefficient for buildings in an urban-like setting. Build. Environ. 2020, 169, 106557. [Google Scholar] [CrossRef]




| Parameter | Values |
|---|---|
| Geometrical parameters | |
| Rib shape | Circle, semi-circle, square and triangle |
| Rib height (e), mm | 1–10 |
| Rib axial pitch (p), mm | 5–100 |
| Relative rib height (e/D) | 0.01–0.10 |
| Relative rib pitch (p/e) | 1.5–20 |
| Heat transfer and flow parameters | |
| Reynolds number (Re) | 5000–19,000 |
| Heat flux, W/m2 | 200, 400, 1000 |
| No. | Grid Count | Nu | % Increase in Nu | f | % Increase in f |
|---|---|---|---|---|---|
| 1 | 97,553 | 44.443 | - | 0.1225 | - |
| 2 | 172,916 | 44.277 | −0.37% | 0.1259 | 2.74% |
| 3 | 377,007 | 44.202 | −0.17% | 0.1250 | −0.66% |
| Flow Regime | Velocity Contour a,b |
|---|---|
| p/e < 3.5 Skimming c | 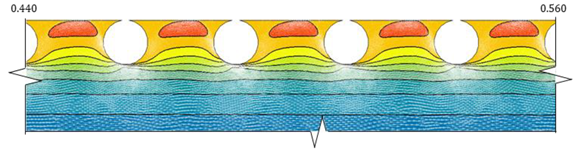 |
 | |
| 3.5 < p/e < 9.5 Wake interference d | 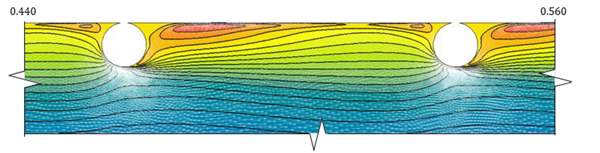 |
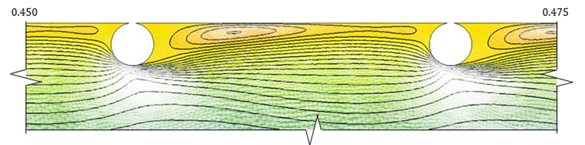 | |
| p/e > 9.5 Isolated roughness e |  |
 |
| Triangular rib: | ||
| R2: 0.93 | (10) | |
| R2: 0.94 | (11) | |
| Circular rib: | ||
| R2: 0.99 | (12) | |
| R2: 0.96 | (13) | |
| Square rib: | ||
| R2: 0.93 | (14) | |
| R2: 0.91 | (15) | |
| Semi-circular rib: | ||
| R2: 0.96 | (16) | |
| R2: 0.96 | (17) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nghana, B.; Tariku, F.; Bitsuamlak, G. Numerical Study of the Impact of Transverse Ribs on the Energy Potential of Air-Based BIPV/T Envelope Systems. Energies 2023, 16, 5266. https://doi.org/10.3390/en16145266
Nghana B, Tariku F, Bitsuamlak G. Numerical Study of the Impact of Transverse Ribs on the Energy Potential of Air-Based BIPV/T Envelope Systems. Energies. 2023; 16(14):5266. https://doi.org/10.3390/en16145266
Chicago/Turabian StyleNghana, Barilelo, Fitsum Tariku, and Girma Bitsuamlak. 2023. "Numerical Study of the Impact of Transverse Ribs on the Energy Potential of Air-Based BIPV/T Envelope Systems" Energies 16, no. 14: 5266. https://doi.org/10.3390/en16145266
APA StyleNghana, B., Tariku, F., & Bitsuamlak, G. (2023). Numerical Study of the Impact of Transverse Ribs on the Energy Potential of Air-Based BIPV/T Envelope Systems. Energies, 16(14), 5266. https://doi.org/10.3390/en16145266