Abstract
A nanofluidic energy absorption system (NEAS) is composed of nanoporous material and functional liquid with high energy absorption density. Applying an electric field to adjust the energy absorption characteristics of a nanofluidic system will open broader prospects for its application. In the current work, ZSM-5 zeolite was adopted as the nanoporous material and water, a 25% KCl solution, and a saturated KCl solution were adopted as functional liquids to configure NEASs. Pressure-induced infiltration experiments were carried out to study the infiltration and defiltration characteristics of the NEASs under the action of an applied electric field. The results show that the introduction of an applied electric field can weaken the hydrogen bonds between molecules, thus reducing the equivalent surface tension and contact angle, changing the infiltrability of liquid molecules into the nanopores, and reducing the infiltration pressure of the system. In an electrolyte solution/zeolite system, the anions and cations move close to the two plate electrodes under the action of an external electric field, and the fluid properties in the central zone of the pressure chamber are close to the water/zeolite system. For both an ultra-low conductivity liquid and an electrolyte solution/zeolite system, applying an electric field can effectively improve the relative outflow rate of liquid, thus improving the reusability of the system.
1. Introduction
Energy absorption/dissipation systems (EAS) are typically used to mitigate or eliminate the influence of external impact energy for protecting humans or certain core components from impact loads. However, its application is limited by its low energy absorption density, and the complex manufacturing process required to enhance its performance is not cost effective. In recent years, nanofluidic energy absorption systems (NEASs), which consist of nanoporous material and functional fluid, have provided vast application prospects, from energy storage [1,2,3] to novel desalination materials [4,5], and have been the research focus of many scholars.
In NEASs, the hydrophobic properties of the nanoporous solid surface make it necessary for the non-wetting liquid to pass through an energy barrier before entering the nanopore. The liquid enters the nanopore only when the external loading force applied to the system is large enough and is compelled to travel along the nanopore channel. In this process, each nanopore with liquid transfer can become an independent buffer, so as to make the NEAS a super buffer. In each loading cycle, part of the external mechanical energy is dissipated in the form of joule heat, and the other part is stored in the form of interfacial energy, which increases the internal energy of the system.
Since the mid-1990s, certain researchers have experimentally explored the thermodynamic system composed of hydrophobic porous materials and water [6,7]. In the subsequent work, scholars have studied the pressure and volume change of NEAS composed of different hydrophobic nanoporous solids, including silica gel [8,9,10], zeolite [11,12,13,14], MCM-41 [15,16], etc., and revealed the relationship between the infiltration volume and pressure.
In the energy absorption/conversion system, for an encapsulated NEAS, the porous material and liquid are fixed. The external force field is a convenient and effective way to control the system parameters, which has attracted many researchers in recent years. Research has been carried out on the thermal effect, stress field, and electromagnetic field in the liquid molecule infiltration process into nanoporous material. For the effect of the temperature field, Zhang et al. experimentally studied the invasion mechanism of hydrophobic nanopores of ZSM-5 zeolite by glycerol with temperature variation. The results show that increasing the system temperature can reduce the critical infiltration pressure barrier and change the wettability of the system [17]. Kong et al. found that increasing the system temperature not only reduced the critical infiltration pressure of the nanopore but also promoted the outflow of infiltrated liquid from the nanopore after unloading [18]. Salman et al. investigated the impact of temperature on the coupled transport of water and ions through a carbon nanotube via molecular dynamics simulations, revealing that an increase in the field strength results in a reversal of ion flux order from cation > anion to anion > cation, consequently leading to a direction change for water flux [19]. Xu et al. discussed the functional relationship between the thermal response transport resistance of the liquid and the nanopore size, transport rate, and liquid properties separately in a carbon nanotube model through non-equilibrium molecular dynamics simulation [20].
To explore the effect of stress field action, scholars conducted molecular dynamics simulation on the process of fluid penetration into nanoporous material under the conditions of a mechanical wave, pressure drive, and high-speed impact [21,22]. Zhang et al. proposed a three-dimensional finite element simulation model of split Hopkinson pressure bar experimental devices to analyze the energy-absorption capabilities of tubes filled with nanofluidic systems, providing valuable insights for engineering applications and helping to reduce the cost of experimentation [23]. Li et al. employed fluid-like liquid nanofoam (LN) in a thin-walled tube and explored the crushing behavior and working mechanism of the LN-filled tube subjected to quasi-static compression and dynamic impact [24].
Electric fields govern the orientation of water dipoles, leading to a rotation-translation coupling mechanism that facilitates water transport through narrow carbon nanotubes [25,26]. According to Ben et al., the electrokinetic transport properties of nanofluidic devices under the influence of pressure, voltage, or salinity have been theoretically investigated under the action of an electric field [27]. Ritos et al. studied the flowing structure and average direction of water flowing in carbon nanotubes (CNTs) via molecular dynamics simulation. They found that the molecular ordering will be enhanced when applying the axial electric field, and the flow rate of water through the nanotube is affected [28]. Su and Guo also found that the electric field provides a means of regulating unidirectional water flow [29]. Panahi et al. studied the effect of the chirality of carbon nanotubes on the hydrodynamic transport of carbon nanotubes embedded in silicon nanochannels using molecular dynamics simulation [30]. Zhou et al. simulated the effect of electric charge on water molecular transport in single-walled carbon nanotubes [31]. Wang et al. proposed a design of the linear gradient electric field inducing unidirectional water flow into a single-walled CNT and determined the maximum velocity achievable by this single-file transport [32]. Kong et al. harnessed the vast specific surface area of nanoporous materials to engineer a high-performance shape memory system predicated on the electrocapillary effect. The system’s infiltration pressure can be reversibly controlled through voltage changes, resulting in significantly higher output energy density and displacement compared to piezoelectric and magnetostrictive materials [33].
It can be seen that the physical process and energy absorption/release characteristics of fluid penetrating into nanoporous materials can be regulated and optimized by applying an external force field. However, investigations of fluid penetration into nanoporous materials under the action of an electric field are mostly conducted by molecular dynamics simulation, which lacks experimental verification and practical data support. The porous material for the effective study of an electric field is primarily simplified as carbon nanotubes, which are different from the actual application of hydrophobic zeolite material. Therefore, this paper takes hydrophobic zeolite as the nanoporous material and studies the physical mechanism and energy absorption/transformation characteristics experimentally. Different functional liquids are used to test the infiltration and defiltration characteristics influenced by the strength of the electric field. This work can provide a reference for clarifying the mechanism of an electric field’s influence on the microscopic flow and energy conversion process of fluid permeation through the nanocore and provide data support for the optimization of nanofluidic systems through external electrical field regulation.
2. Experimental Setup
2.1. Construction of the Experimental System
The experimental setup primarily consists of the following parts shown in Figure 1: The pressure chamber, the electrode, the piston, and measuring transducers. The pressure chamber is the main body holding the mixture of nanoporous material and functional liquid. It is made of 1Cr13 stainless steel. The cavity of the chamber is designed as a cube. On the left and right walls of the chamber, a pair of plate electrodes is assembled to apply the electric field. On the front and back walls, a pressure transducer and a type-E thermal couple are screwed in to obtain the real-time signals of pressure and temperature during the experiment. On the top of the chamber, a steel piston is assembled. An O-ring is utilized to tightly seal the gap between the pressure chamber and the piston. During the experiment, a servo motor is used to compress the piston into the chamber at a speed of 0.02 mm/s. The pressure in the chamber is controlled to be changed in the range of 0 to 60 MPa.
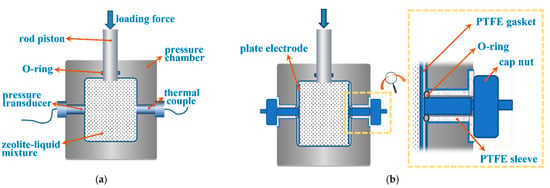
Figure 1.
Diagram of the experimental system construction. (a) Front view; (b) side view.
2.2. Sealing Method
The assembling and sealing method of the plate electrode is depicted in Figure 1b. The plate electrode and extension rod in the center constitute an entity that was formed from a block of stainless-steel material. The center of the extension rod is located at the intersection of the plate diagonal. The extension rod and the plate electrode are vertical to each other to serve the sealing. A section of the external thread is carved on the end of the extension rod, which will be used with a nut to fix and provide a pre-tight sealing force. The seal between the electrode and the pressure chamber is accomplished by an O-ring and a special tailor-made polytetrafluoroethylene (PTTE) gasket. By tightening the nut and thread on the rod, the O-ring is squeezed, and the gaps are populated. When applying the extrusion experiment, although the pressure is high, it primarily acts in the axes direction, which is vertical on the electrode’s plate and parallel to the extension rod. The pressure inside the chamber will push the electrode tightly against the chamber wall. Therefore, the higher the pressure inside the chamber is, the more reliable the sealing is.
2.3. Insulation Method
To apply a parallel electric field on the system, every single part of the experimental system should be isolated from the electrode plate, thus a 50 μm-thick layer of Teflon was coated on the whole body of the pair of electrodes and the whole body of the pressure chamber. To further avoid contact between the extension rod and the cavity wall of the chamber, the extension rod of the plate electrode is equipped with a polytetrafluoroethylene (PTFE) sleeve for insulation.
2.4. Experimental Sample Preparation
Zeolite ZSM-5 was used as the nanoporous material in the experiment. The silica-to-alumina ratio was 172.82. The Na2O concentration was 0.046%. According to a gas absorption experiment using Micromeritics ASAP 2020, the specific surface area was 630.93 m2/g. The specific nanopore volume was 510 mm3/g. Both micro and meso pores were discovered in the sample. The pore size of mesopores was 21.14 Å and the pore size of micropores was 5.24 Å. Three different kinds of functional liquid were used to obtain three different NEAS, which were deionized water, a 25% KCl solution (1.06 mol∙L−1), and a saturation KCl solution (4.24 mol∙L−1) [34]. Furthermore, 1.0 g of zeolite was suspended in 10 mL of functional liquid, forming the liquid–nanoporous material mixture. Before infiltration tests were carried out, the mixture was subjected to high-vacuum conditions (<0.005 MPa) in order to eliminate easily dissolved air bubbles.
2.5. Test Conditions and Procedures
The applied voltage of the test system was 0 V, 20 V, 40 V, and 60 V, respectively. The applied electric field was considered a parallel electric field, which was realized by a pair of parallel plate electrodes on the opposite side of the pressure chamber walls. The distance between the two plate electrodes was 25 mm. The electric field intensity corresponding to the four voltages in the experiment are 0 V∙m−1, 800 V∙m−1, 1600 V∙m−1, and 2400 V∙m−1. During the infiltration test, a constant downward velocity of 0.02 mm∙s−1 was applied to the piston in order to exert pressure on the mixture within the chamber. When the pressure exceeded 50 MPa, the piston retracted out of the chamber at the same velocity. Thus, the piston loading and unloading form a complete cycle. Each experiment was loaded/unloaded for 3 circles. In this study, the basic properties of the energy absorption/conversion system composed of ZSM-5 zeolite and different liquids are investigated under the electric field formed by different loading voltages.
3. Physical Process and Analysis Method
In an airtight pressure chamber, liquid can infiltrate into the channel of nanoporous material only when the loading pressure reaches a critical value. Figure 2 shows the pressure–distance characteristic curve of four selected working conditions under three loading/unloading cycles. Figure 2a,b show pressure–distance characteristic curves of the water/zeolite system and Figure 2c,d show pressure–distance characteristic curves of the saturated KCl solution/zeolite system. The working condition of Figure 2a,c is 0 V and the working condition of Figure 2b,d is 60 V.
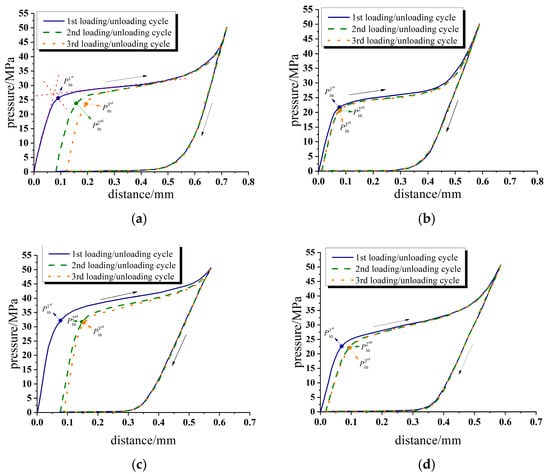
Figure 2.
Pressure–distance characteristic curve in the typical loading/unloading cycle. (a) Water/zeolite system, 0 V; (b) water/zeolite system, 60 V; (c) saturated KCl solution/zeolite, 0 V; (d) saturated KCl solution/zeolite, 60 V.
As can be seen from the figures, when the system pressure is relatively low at the initial loading stage, the relationship between distance and pressure is nearly linear. The slope of the pressure–distance curve approximately reflects the compressibility of the porous material and the experimental system. When the pressure reaches the infiltration pressure Pin, the liquid begins to intrude into the nano channels of the porous material. When the loading pressure is greater than Pin, as the loading pressure increases, more liquid molecules overcome the resistance of the nanopore and penetrate into the zeolite nanochannel. When the nanochannel is filled, the system enters the linear compression stage again. In this stage, the slope of the curve is theoretically equal to the bulk elastic modulus of the porous material filling with the liquid phase. Note that not all nano channels of the tested nanoporous material could be intruded upon under certain experimental loading pressure.
When unloading, liquid molecules do not flow out of the porous material at the beginning of the unloading process. Due to the frictional resistance of the inner wall of the porous material to the flow of liquid molecules and the limiting effect of the solid wall, the fluid begins to flow out only when the external loading pressure is below the critical defiltration pressure Pout. When the desorption process begins, the liquid molecules are gradually expelled from the nanochannel under the actuation of pressure difference and system interfacial energy. When the pressure in the chamber is reduced to 0.1 MPa, the pressure–distance characteristic curve does not completely return to origin point A. It indicates that there is an irreversible change in the system, which may be caused by part of the fluid permanently trapped in the zeolite pores or defects produced upon the previous intrusion−extrusion cycles [35].
According to Young’s equation [36]:
where Pin is the infiltration pressure of NEAS; is the equivalent surface tension, and d is the effective characteristic diameter of porous material. In this study, is considered as follows:
where γla is the surface tension between liquid and air, which is considered independent of the applied electrical field and remains constant. α is the equivalent contact angle.
where is the average pore size of porous material, which can be obtained by instrument measurement, h = 0.14 nm [37]. Thus,
In the current study, Pin is defined as the pressure value of the intersection point between the pressure–distance curve and the angle bisector between the linear stage before entering the hole and the linear stage of the platform after entering the nanopores, as shown in Figure 1a. From the pressure–distance characteristic curve, the value of Pin can be obtained. The equivalent surface tension can be calculated from Equation (4). The equivalent contact angle can be calculated from Equation (5).
To study the effect of electrical field impact on the surface tension and contact angle, Lippmann’s equation [38] is also used to describe the relationship between the voltage and surface tension under an applied electric field as follows:
where is the equivalent surface tension without the electric field applied; c is the capacitance per unit area between the two plate electrodes; V is the applied voltage; is the equivalent surface tension corresponding to the applied voltage V.
The relationship between the contact angle and surface tension is shown as follows:
where γla is the liquid–air interfacial tension, γsa is the solid–air interfacial tension, γsl is the solid–liquid interfacial tension, and α is the equivalent contact angle. Usually, γsl is denoted as for brevity [38]. γla and γsa are considered independent of the applied electrical field and remain constant [38]. The Young–Lippmann equation can be obtained from Equations (6) and (7) as follows:
where α0 is the contact angle when the electric field across the interface layer is zero. γla is the liquid–air interfacial tension depending on the type of solution, which can be obtained from previous literature findings [39]. α is the contact angle corresponding to the condition of applying voltage V.
Taking the two plate electrodes as parallel electric fields, the capacitance c between the two plate electrodes can be calculated by the following formula.
where is the dielectric constant of the insulating layer; is the relative dielectric constant. is the dielectric constant of the vacuum. d is the thickness of the insulation layer.
In terms of 25 °C, the relative dielectric constant of deionized water [40]. The dielectric constant of the Teflon coating = 2.1 F/m. . For the pressure chamber used in this experiment, the two plate electrodes are simplified as being composed of three parts: The Teflon coating, ultra-low conductivity liquid, and Teflon coating. The thickness of the insulation layer dteflon is 2 μm. The distance between the two plate electrodes df is 25 mm.
By applying the Young–Lippmann equation to this study, the effect of the applied electric field intensity on the equivalent surface tension and contact angle of the liquid in a large space can be calculated using experimental data with an applied voltage of 0 V as a reference.
By comparing the example working conditions with and without the applied electric field in Figure 2, the critical infiltration pressure, accessible pore volume, and outflow rate of both water and electrolyte solution systems have changed under applied electric fields. According to the pressure–displacement characteristic curve obtained from the experiment, the key parameters of the system are extracted and analyzed in detail.
4. Results and Discussion
4.1. Effect of Applied Electric Field on Water/Zeolite System
Firstly, deionized water is chosen as the ultra-low conductivity liquid, and the properties of the water/zeolite system under the influence of an applied electric field are discussed.
4.1.1. Influence on Infiltration Parameters
According to the pressure–displacement characteristic curves of the water/zeolite system under different electric field intensities, the infiltration pressure of deionized water that intrudes into nanopores under different electric field intensities is extracted and plotted in Figure 3a. With an increase in electric field intensity, the infiltration pressure of the system decreases. The hydrogen bond of the water molecule is very strong [41], and the electric field intensity applied in the experiment cannot ensure the liquid molecules are completely and orderly arranged in one direction or change the structure of the molecules. However, the constraint effect of the hydrogen bond on dipole steering in the confined nano environment is much weaker than that in the large volume environment [42]. Therefore, the electric field intensity in this range can still change the dipole steering of water molecules to some extent and affect their arrangement. The introduction of an applied electric field will weaken the effect of intermolecular hydrogen bonds [43], thus reducing the contact angle, changing the infiltrability of the whole system, and lowering the infiltration pressure.
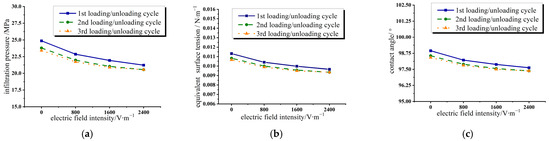
Figure 3.
Variation of infiltration parameters in three loading/unloading cycles under different electric field intensities in water/zeolite system. (a) Infiltration pressure; (b) equivalent surface tension; (c) contact angle.
The changes in the equivalent surface tension and contact angle of the water/zeolite system are calculated according to Equations (4) and (5) and shown in Figure 3b,c, respectively. It can be seen that the equivalent surface tension and contact angle change very little under the electric field intensity applied in the experiment. According to the Young–Lippmann equation stated in Equation (6), the equivalent surface tension of deionized water can be calculated. The calculated value of the equivalent surface tension decreases from 0.01131 N∙m−1 to 0.01128 N∙m−1 when the applied voltage increases from 0 V to 60 V. According to the experiment, the equivalent surface tension of deionized water obtained from the experimental value and Young’s equation is reduced from 0.01131 N∙m−1 to 0.00966 N∙m−1. Although the variation trend of the calculated value and the experimental value is the same, the variation amplitude is very different. The electric field intensity calculated from the experimental value has a greater influence on the wettability than that from the Young–Lippmann equation. The reasons are as follows: First, in the confined nano environment, the interaction and configuration of liquid molecules are very different from the state in the large space, and they are more sensitive to the influence of the external force field. Second, there is a strong coulomb field inside the pores of zeolite crystal particles, and the force field is very complex. The influence of the surface tension and contact angle on the applied electric field was estimated only in a simple case by using the Young–Lippmann equation.
4.1.2. Effect on Accessible Pore Volume and Relative Outflow Rate
We define the accessible pore volume Vacce as the pore volume of porous material into which liquid molecules can infiltrate during the loading process. It equals the volume occupied by piston A × Δd, where A is the cross-sectional area of the rod piston and Δd is the displacement of the rod piston. We define the relative outflow rate as the outflow volume of liquid after the loading/unloading cycle divides the inflow volume of liquid during the intrusion process of the first loading/unloading cycle.
In Figure 4a,b, the accessible pore volume and relative outflow rate of the water/zeolite system were extracted. It can be seen from Figure 4a that during the first loading process, the accessible pore volume gradually decreases with the increase in applied electric field intensity. This is due to the increasing repulsion between the zeolite crystal lattice and the liquid molecules.
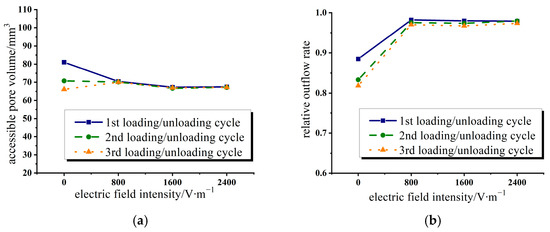
Figure 4.
Variation of accessible pore volume and relative outflow rate with electric field intensity in water/zeolite system. (a) Accessible pore volume; (b) relative outflow rate.
The most basic structural units constituting zeolite skeleton are silico-oxygen tetrahedron (SiO4) and aluminon-oxygen tetrahedron (AlO4). Silicon and aluminum atoms are at the center of the tetrahedron, and there are four oxygen atoms around each silicon/aluminum atom. In these tetrahedrons, both silicon and aluminum appear as high-priced oxidation states and take sp3 hybrid orbitals to bond with oxygen atoms. Silico-oxygen tetrahedrons and aluminon-oxygen tetrahedrons can be connected to each other through vertices to form different skeleton structures. Since aluminum is positively trivalent, the aluminum oxygen tetrahedron has a negative charge. Although there are positively charged cations (usually alkali metal or alkaline earth metal ions) to neutralize these negative charges, making zeolite finally electrically neutral [44], the pores and cavities inside zeolite crystals have strong polarity and coulomb fields. Under the action of an applied electric field, stronger forces will be generated among the liquid molecules entering the pores. It can be seen from the experimental results that the internal structure of zeolite molecules produces a mutual repulsive force on the liquid molecules under the action of an applied electric field. This enhanced interaction decreases the accessible pore volume of the liquid. Moreover, the enhanced mutual repulsion will facilitate the liquid expulsion process. Although the wettability of the system decreases with the increase in the electric field intensity, the coulomb force causes the infiltrated liquid molecules to flow out of the nanochannels.
For the second and third loading processes, after the electric field is applied, the accessible pore volume increases compared with the condition without an electric field. This is due to the increase in the relative outflow rate of the liquid after the application of the electric field, thus expanding the accessible space of the subsequent entry process. As shown in Figure 4b, the relative outflow rate of the system increases with the increase in the electric field intensity. Compared with the condition without an applied electric field, the relative outflow rate of the system is significantly increased after applying the electric field, reaching more than 95%. However, the improvement effect of further increasing the applied voltage and field strength on the outflow rate is not as obvious. In the design and application, the most economical and effective adjustment method can be adopted according to the actual situation.
4.2. Effect of Applied Electric Field on Electrolyte Solution/Zeolite System
When the electrolyte solution/zeolite system is subjected to an applied electric field, the performance parameters of the system change slightly differently from that of the non-electrolyte solution because, in this system, in addition to the water molecules being diverted under the action of the electric field, the ions in the solution will also swim to the two plate electrodes under the action of the electric field. Hereinafter, the variation trend and mechanism of the system parameters corresponding to two solutions with different electrolyte concentrations are discussed.
4.2.1. Influence on Infiltration Parameters
Figure 5 extracts the infiltration parameters of the 25% KCl solution/zeolite and saturated KCl solution/zeolite systems in three loading/unloading cycles under different electric field intensities. As can be seen in Figure 5a, with the increase in the electric field intensity, the infiltration pressure of the system decreases, and the decrease is much larger than that of the water/zeolite system in the previous section. It is believed that under the action of an applied electric field, the anion and cation in the solution move towards the plate electrodes under the action of an electric field force, resulting in the uneven distribution of the ion concentration in the solution. The ion concentration is extremely high near the plate electrodes, while the ion concentration is very low in the middle area, which is close to the deionized water. Therefore, after the change from no electric field to an applied electric field, there is a sharp decrease in the infiltration pressure. With the increase in the applied electric field intensity, the concentration degree of ions driven by the electric field force to the plate electrodes is greater, and the hydrogen bond between water molecules will also weaken with the increase in the electric field force, resulting in a further decrease in infiltration pressure.
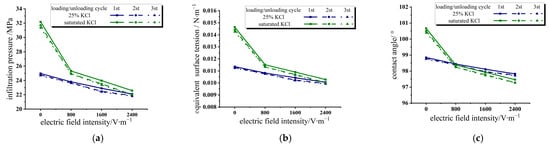
Figure 5.
Variation of infiltration parameters in three loading/unloading cycles under different electric field intensities in KCl solution/zeolite system. (a) Infiltration pressure; (b) equivalent surface tension; (c) contact angle.
According to Equations (4) and (5), we calculated the equivalent surface tension and contact angle variation of the two systems under different electric field intensities in the three loading/unloading cycles and plotted them in Figure 5b and Figure 5c, respectively. Both the equivalent surface tension and the contact angle decrease with the increase in applied electric field intensity. After the electric field is applied to the system, the performance of the electrolyte solution/zeolite system is close to that of the water/zeolite system. The greater the electric field intensity, the higher the degree of ions gathering near the two plate electrodes, and the more similar the equivalent surface tension and contact angle of the system are to the water/zeolite system.
Since the equivalent surface tension and contact angle between the water/zeolite system and the saturated KCl solution system are quite different, the applied electric field can be used to adjust the wettability energy of the saturated KCl solution system in real time, so as to realize the conversion and storage between electric energy and interfacial energy. When the system is decompressed, this part of the interfacial energy can also be partially converted into mechanical energy or even electrical energy through special system settings. It will open up greater application prospects for this energy absorption/conversion system.
4.2.2. Effect on the Accessible Pore Volume and Relative Outflow Rate
In Figure 6, the accessible pore volume and relative outflow rate of the 25% KCl solution and saturated KCl solution system were extracted as a function of the electric field intensity. In Figure 6a, the values of accessible pore volumes of two different solutions both decrease with the increase in applied voltage. The values of accessible pore volumes of two electrolyte solution/zeolite systems with different concentrations are close to each other because the performance of the electrolyte solution is close to that of the water/zeolite system after the electric field is applied.
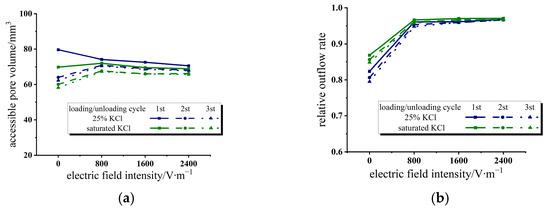
Figure 6.
Variation of accessible pore volume and relative outflow rate with electric field intensity in KCl solution/zeolite system. (a) Accessible pore volume; (b) relative outflow rate.
Under the influence of an applied electric field, the electrolyte solution/zeolite system is heterogeneous, and the components and behaviors of each part of the system are different. Near the two plate electrodes, due to the high concentration of ions gathering under the action of electric field force, the fluid penetration rate will be much lower than the area near the center layer of the two plate electrodes under the action of ion agglomeration. However, the high-concentration ion aggregation layer is relatively thin, and the overall performance of the system is still controlled by the behavior of the deionized water-like region near the central zone of the solution.
It can be seen from Figure 6b that the applied electric field also significantly improves the relative outflow rate of the electrolyte solution/zeolite system. The pores and cavities within zeolite crystals exhibit a strong polarity and Coulombic field. Cation exchange takes place within the nanochannel as cations diffuse into the zeolite framework. The nanopore surface may exhibit reduced polarization due to pre-existing negatively charged surface sites, such as hydroxyl groups or other defects, which can be counterbalanced by cations. The effective number density of surface defects decreases, resulting in a more lyophobic nanopore surface that exhibits reduced attraction to water molecules [45]. This leads to an improvement in the relative outflow rate.
However, in the present experimental range, further increasing the applied electric field intensity does not lift the improvement effect. Due to the limited number of defects within the zeolite framework, the relative outflow rate easily reaches its maximum as ions are introduced.
4.3. Microscopic Model of Liquid Phase Distribution under Electric Field
Under the action of an applied electric field, the microscopic changes of a low-conductivity liquid and a strong electrolyte solution are different. Figure 7a,b show the comparison of the microscopic changes in fluid molecule/ion distribution after applying an external parallel electric field in the pressure chamber when a non-conductive liquid and a strong electrolyte solution were used in the experiment.
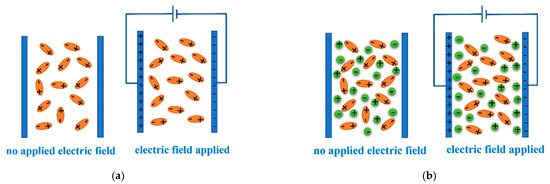
Figure 7.
A microscopic description of the distribution of the liquid molecule/ions under an applied electric field. (a) Water/zeolite system; (b) electrolyte solution/zeolite system.
As shown in Figure 7a, the non-conductive liquid in the current study is deionized water, which constitutes polar molecules with dipole moments. When there is no electric field, the natural dipole moment vectors of these polar molecules are randomly distributed in all directions, their vector sum is zero, and the whole system remains electrically neutral. However, under the action of an electric field, each polar molecule rotates due to the action of rotational torque under the electric field and tends to be arranged along the direction of the electric field. The attitude adjustment makes the infiltration process of liquid molecules into the pore more inclined to be in an ordered state, and the macroscopic performance shows that the infiltration pressure Pin decreases. Although the attitude adjustment is limited under the experimental electric field intensity, it is sufficient to change the performance of the system in the confined nano environment.
As shown in Figure 7b, when the solution contains ions, instead of the steering adjustment of solvent water molecules, the previously disordered positive and negative ions have a convergent motion, resulting in more negative charges gathering near the positive plate, while more positive charges gather near the negative plate. The initially homogeneous mixture in the pressure chamber resulted in a concentration gradient, with a high ion concentration near the two plate electrodes and a low ion concentration near the center layer of the pressure chamber. The performance of a strong electrolyte solution/zeolite system under an applied electric field is closer to that of the water/zeolite system without an applied electric field.
5. Conclusions
In this paper, the infiltration and defiltration of hydrophobic zeolite mixing with deionized aqueous water and two electrolyte solutions with different concentrations were studied under an electric field intensity of 0~2400 V∙m−1. Theoretical analysis and experimental results show that the introduction of an applied electric field can weaken the hydrogen bond between molecules, thus reducing the equivalent surface tension and contact angle, changing the infiltrability of liquid molecules into the nanopores and reducing the infiltration pressure of the system. The variation values of surface tension and contact angle calculated by the Young–Lippmann equation with the electric field are much smaller than those obtained by the experimental results, which indicates that the introduction of an external electric field has a more obvious effect on the system infiltration in the confined nano environment.
Under the action of an external electric field, the anions and cations in the electrolyte solution move close to the two plate electrodes, respectively, and the fluid properties in the central zone of the pressure chamber are close to the deionized water. Therefore, the system’s overall performance is close to the water/zeolite system. For both ultra-low conductivity liquid/zeolite and electrolyte solution/zeolite systems, applying an electric field can effectively improve the relative outflow rate of the liquid, thus improving the reusability of the system.
Author Contributions
Conceptualization, Y.Z.; methodology, Y.Z. and R.L.; validation, J.Z. and R.L.; formal analysis, Y.D.; investigation, Y.Z.; resources, Y.D. and Y.Z.; data curation, R.L.; writing—original draft preparation, J.Z.; writing—review and editing, Y.Z.; supervision, Y.D.; project administration, Y.D.; funding acquisition, Y.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research study was funded by National Natural Science Foundation of China (grant No. 51974246 and 51806173) and the Innovative Talent Promotion Program “Young Science and Technology Star Project” of Shaanxi Province in China (grant No. 2021KJXX-40).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Borman, V.; Belogorlov, A.; Tronin, I. Fast spontaneous transport of a non-wetting fluid in a disordered nanoporous medium. Transp. Porous. Media 2021, 139, 21–44. [Google Scholar] [CrossRef]
- Giacomello, A.; Casciola, C.; Grosu, Y.; Meloni, S. Liquid intrusion in and extru-sion from non-wettable nanopores for technological applications. Eur. Phys. J. B 2021, 94, 163. [Google Scholar] [CrossRef]
- Ashok, D.; Bahubalendruni, M.; Mertens, A.J. A novel nature inspired 3D open lattice structure for specific energy absorption. Proc. Inst. Mech. Eng. E. J. Process. Mech. Eng. 2022, 263, 2434–2440. [Google Scholar] [CrossRef]
- Lynch, C.; Rao, S.; Sansom, M. Water in nanopores and biological channels: A amolecular simulation perspective. Chem. Rev. 2020, 120, 10298–10335. [Google Scholar] [CrossRef] [PubMed]
- Faucher, S.; Aluru, N.; Bazant, M.; Blankschtein, D.; Brozena, A.; Cumings, J.; Pedro, D.; Elimelech, M.; Epsztein, R.; Fourkas, J.; et al. Critical knowledge gaps in mass transport through single-digit nanopores: A review and perspective. J. Phys. Chem. C 2019, 123, 21309–21326. [Google Scholar] [CrossRef]
- Gusev, V.Y. On thermodynamics of permanent hysteresis in capillary lyophobic systems and interface characterization. Langmuir 1994, 10, 235–240. [Google Scholar] [CrossRef]
- Eroshenko, V.A.; Fadeev, A.Y. Intrusion and extrusion of water in hydrophobized porous silica. Colloid J. 1995, 57, 446–449. [Google Scholar]
- Deng, X.; Wang, X.; Liu, X.; Zhao, W.; Li, X.; Liu, Y.; Chen, X. Correlation between the infiltration behaviors and nanoporous structures of silica gel/liquid energy absorption system. J. Appl. Phys. 2019, 125, 065106. [Google Scholar] [CrossRef]
- Chen, H.; Xu, Y.; Tong, Y.; Hu, J. The investigation of nanofluidic energy absorption system based on high porosity aerogel nano-materials. Microporous Mesoporous Mater. 2019, 277, 217–228. [Google Scholar] [CrossRef]
- Humplik, T.; Raj, R.; Maroo, S.; Laoui, T.; Wang, E. Effect of hydrophilic defects on water transport in MFI zeolites. Langmuir 2014, 30, 6446–6453. [Google Scholar] [CrossRef]
- Zhang, Y.; Liang, J.; Luo, R.; Min, S.; Dou, Y. Application characteristics of zeolite-based stuffing for the nanofluidic packer rubber. Energies 2022, 15, 7962. [Google Scholar] [CrossRef]
- Sun, Y.; Rogge, S.; Lamaire, A.; Vandenbrande, S.; Wieme, J.; Siviour, C.; Van, S.; Tan, J. High-rate nanofluidic energy absorption in porous zeolitic frameworks. Nat. Mater. 2021, 20, 1015–1023. [Google Scholar] [CrossRef] [PubMed]
- Ortiz, G.; Nouali, H.; Marichal, C.; Chaplais, G.; Patarin, J. Energetic performances of “ZIF-71–aqueous solution” systems: A perfect shock-absorber with water. J. Phys. Chem. C 2014, 118, 21316–21322. [Google Scholar] [CrossRef]
- Han, A.; Lu, W.; Kim, T.; Chen, X.; Qiao, Y. Influence of anions on liquid infiltration and defiltration in a zeolite Y. Phys. Rev. E 2008, 78, 031408. [Google Scholar] [CrossRef]
- Martin, T.; Lefevre, B.; Brunel, D.; Galarneau, A.; Di, R.; Fajula, F.; Gobin, P.; Quinson, J.; Vigier, G. Dissipative water intrusion in hydrophobic MCM-41 type materials. Chem. Commun. 2002, 24–25. [Google Scholar] [CrossRef] [PubMed]
- Han, A.; Lu, W.; Punyamutula, V.; Kim, T.; Qiao, Y. Temperature variation in liquid infiltration and defiltration in a MCM41. J. Appl. Phys. 2009, 105, 024309. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, N.; Luo, R.; Zhang, Y.; Zhou, Q.; Chen, X. Experimental study on thermal effect on infiltration mechanisms of glycerol into ZSM-5 zeolite under cyclic loadings. J. Phys. D Appl. Phys. 2015, 49, 025303. [Google Scholar] [CrossRef]
- Kong, X.; Qiao, Y. Thermal effects on pressure-induced infltration of a nanoporous system. Philos. Mag. Lett. 2005, 85, 331–337. [Google Scholar] [CrossRef]
- Salman, S.; Zhao, Y.; Zhang, X.; Su, J. Effect of temperature on the coupling transport of water and ions through a carbon nanotube in an electric field. J. Chem. Phys. 2020, 153, 184503. [Google Scholar] [CrossRef]
- Xu, B.; Wang, B.; Park, T.; Qiao, Y.; Zhou, Q.; Chen, X. Temperature dependence of fluid transport in nanopores. J. Chem. Phys. 2012, 136, 184701. [Google Scholar] [CrossRef]
- Liu, H.; Cao, G. Reusable Energy Absorption Performance Based on Nanofluidic Systems. J. Phys. Chem. C 2016, 120, 5213–5220. [Google Scholar] [CrossRef]
- Cao, G. Working Mechanism of Nanoporous Energy Absorption System under High Speed Loading. J. Phys. Chem. C 2012, 116, 8278–8286. [Google Scholar] [CrossRef]
- Zhang, S.; Zhu, Z.; Li, S.; Yu, F.; Tian, C.; Yao, L. A Simulation Methodology for Analyzing the Energy-Absorption Capabilities of Nanofluidic-System-Filled Tube under Split Hopkinson Pressure Bar Experiment. Materials 2022, 15, 7030. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Barbat, S.; Baccouche, R.; Belwafa, J.; Lu, W. Enhanced energy mitigation of thin-walled tube filled with liquid nanofoam under dynamic impact. Compos. B Eng. 2020, 193, 108047. [Google Scholar] [CrossRef]
- Zhang, X.; Su, J. Effect of nanotube diameter on the transport of water molecules in electric fields. J. Mol. Liq. 2021, 328, 115382. [Google Scholar] [CrossRef]
- Debora, N.; Bruno, H.; Mateus, H.; Marcia, C.; Matheus, J.; Ronaldo, J.; Alan, B. Water diffusion in carbon nanotubes under directional electric fields: Coupling between mobility and hydrogen bonding. Chem. Phys. 2020, 537, 110849. [Google Scholar]
- Werkhoven, B.; Van, R. Coupled water, charge and salt transport in heterogeneous nano-fluidic systems. Soft. Matter. 2020, 16, 1527–1537. [Google Scholar] [CrossRef]
- Ritos, K.; Borg, M.; Mottram, N.; Reese, J. Electric fields can control the transport of water in carbon nanotubes. Philos. Trans. A Math. Phys. Eng. Sci. 2016, 374, 20150025. [Google Scholar] [CrossRef]
- Su, J.; Guo, H. Control of unidirectional transport of single-file water molecules through carbon nanotubes in an electric field. ACS Nano 2011, 5, 351–359. [Google Scholar] [CrossRef]
- Panahi, A.; Sadeghi, P.; Akhlaghi, A.; Sabour, M. Investigating the effect of single-walled carbon nanotubes chirality on the electrokinetics transport of water and ions: A molecular dynamics study. Diam. Relat. Mater. 2020, 110, 108105. [Google Scholar] [CrossRef]
- Zhou, Y.; Dong, S. Molecular dynamics simulation of water conduction within carbon nanotube. Chin. Sci. Bull. 2013, 58, 59–62. (In Chinese) [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, Y.; Huang, J. Giant pumping of single-file water molecules in a carbon nanotube. J. Phys. Chem. B 2011, 115, 13275–13279. [Google Scholar] [CrossRef] [PubMed]
- Kong, X.; Qiao, Y. An electrically controllable nanoporous smart system. J. Appl. Phys. 2006, 99, 064313. [Google Scholar] [CrossRef]
- Liu, F.; Zhan, X.; Huang, Y. Determination of KCl solubility with hygrometer. J. Pharm. Sci. 2017, 32, 195–196. (In Chinese) [Google Scholar]
- Zhang, Y.; Luo, R.; Zhou, Q.; Chen, X.; Dou, Y. Effect of Degassing on the Stability and Reversibility of Glycerol/ZSM-5 Zeolite System. Appl. Sci. 2018, 8, 1065. [Google Scholar] [CrossRef]
- Rowlinson, J.; Widom, B. Molecular Theory of Capillarity; Dover Publications: New York, NY, USA, 2002. [Google Scholar]
- Mattia, D.; Gogotsi, Y. Review: Static and dynamic behavior of liquids inside carbon nanotubes. Microfluid. Nanofluidics 2008, 5, 289–305. [Google Scholar] [CrossRef]
- Lee, J.; Moon, H.; Fowler, J.; Schoellhammer, T.; Kim, C. Electrowetting and electrowetting-on-dielectric for microscale liquid handling. Sens. Actuators A Phys. 2002, 95, 259–268. [Google Scholar] [CrossRef]
- Glycerine Producers’ Association (Ed.) Physical Properties of Glycerine and Its Solutions; Glycerine Producers’ Association: New York, NY, USA, 1963. [Google Scholar]
- Winarto Takaiwa, D.; Yamamoto, E.; Yasuoka, K. Structures of water molecules in carbon nanotubes under electric fields. J. Chem. Phys. 2015, 142, 124701. [Google Scholar] [CrossRef]
- He, Y.; Sun, G.; Koga, K.; Xu, L. Electrostatic field-exposed water in nanotube at constant axial pressure. Sci. Rep. 2014, 4, 6596. [Google Scholar] [CrossRef]
- Rai, D.; Kulkarni, A.D.; Gejji, S.P.; Bartolotti, L.; Pathak, R. Exploring electric field induced structural evolution of water clusters, (H2O)(n) n=9-20: Density functional approach. J. Chem. Phys. 2013, 138, 9. [Google Scholar] [CrossRef]
- Li, J.; Qiu, J.; Sun, Y.; Long, Y. Studies on natural STI zeolite: Modification, structure, adsorption and catalysis. Microporous Mesoporous Mater. 2000, 37, 365–378. [Google Scholar] [CrossRef]
- Dong, F. Natural zeolite and its application prospects in the field of environmental protection. China Non-Met. Min. Ind. 2002, 4, 30–32. (In Chinese) [Google Scholar]
- Han, A.; Qiao, Y. Thermal effects on infiltration of a solubility-sensitive volume-memory liquid. Philos. Mag. Lett. 2007, 87, 25–31. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).