A Comprehensive Small-Signal Model Formulation and Analysis for the Quasi-Y Impedance-Source Inverter
Abstract
1. Introduction
- 1.
- The proposition of a comprehensive small-signal model for the QSY inverter—Besides the work developed by [30], in which the authors derive a small-signal model for the QSY converter using the averaged-switch model, only the transfer function is obtained, which usually is insufficient during the controller design stage. In this work, however, a small-signal model based on the state-space averaging technique is presented, in which not only the transfer function is derived but also all state variables to control () transfer functions, such as , , , , and , and all state variables to input () transfer functions: , , , , and . All of these transfer functions are obtained with the same methodology, using the modeling approach presented in the paper, and can be easily applied with the aid of mathematical processing software, avoiding complicated algebraic manipulations, which makes possible the proposition of further control strategies, using both single or multi-loop schemes.
- 2.
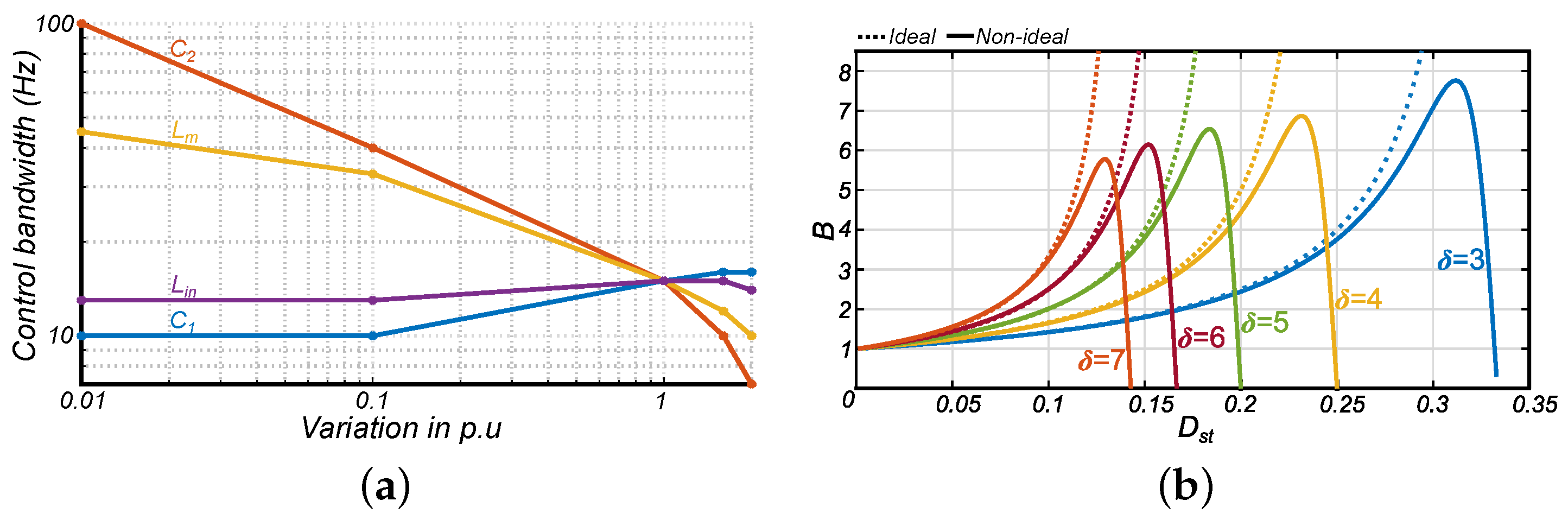
- Evaluation of the QSY inverter dynamic performance through the component’s parametric variation—Besides the work developed by [31], in which the Y-Source, T-source, and -Source converters are analyzed using the component’s parametric variation analysis, it seems that there is no other reference that presents this kind of dynamic performance evaluation for the QSY converter. Since the QSY network, when compared to the Y-Source, T-source, and -Source networks, has an additional capacitor () and inductor (), the methodology presented by [31] cannot be directly applied for the QSY converter. Hence, this paper contributes an evaluation of the dynamic performance of the QSY converter, through a parametric variation analysis using pole-zero maps. Therefore, it is possible to better understand the converter dynamics, the design of the QSY network components, and the design of different types of controllers.
- 3.
- Components’ design equations, considering the converter control and performance compromise—In the works developed by [32,33], the components of the QSY network are derived only in terms of design factors, based on current and voltage ripples. However, there is no clear indication of how to define these factors nor of how the different elements selection can impact the dynamic performance of the converter and modify the complexity of the voltage controller. Nonetheless, in the present paper, it is demonstrated how the different converter elements’ variation can affect (a) the converter dynamics and closed-loop stability, through pole-zero maps analysis; (b) the control bandwidth, and (c) the non-ideal voltage gain B. Based on the conclusions drawn concerning these issues, design equations are provided with proper guidelines, taking into account the compromise between converter performance and DC-link voltage control requirements. Furthermore, the RMS, peak, and average equations for different converter components currents and voltages are presented, which help the designer with the QSY converter project.
- 4.
- Implementation of a voltage controller for a QSY inverter—Considering control strategies for the QSY inverter, the only published works found are [34,35], in which different non-linear control techniques are used, based on model predictive control and MPPT approaches. However, the mentioned works only present simulation results to verify their control approach, without practical implementation. Instead, in this paper, a linear controller methodology is used for a DC-AC QSY converter, making use of the derived small-signal model with an indirect control scheme of DC-link voltage [36].
2. Steady-State Analysis and Components Design
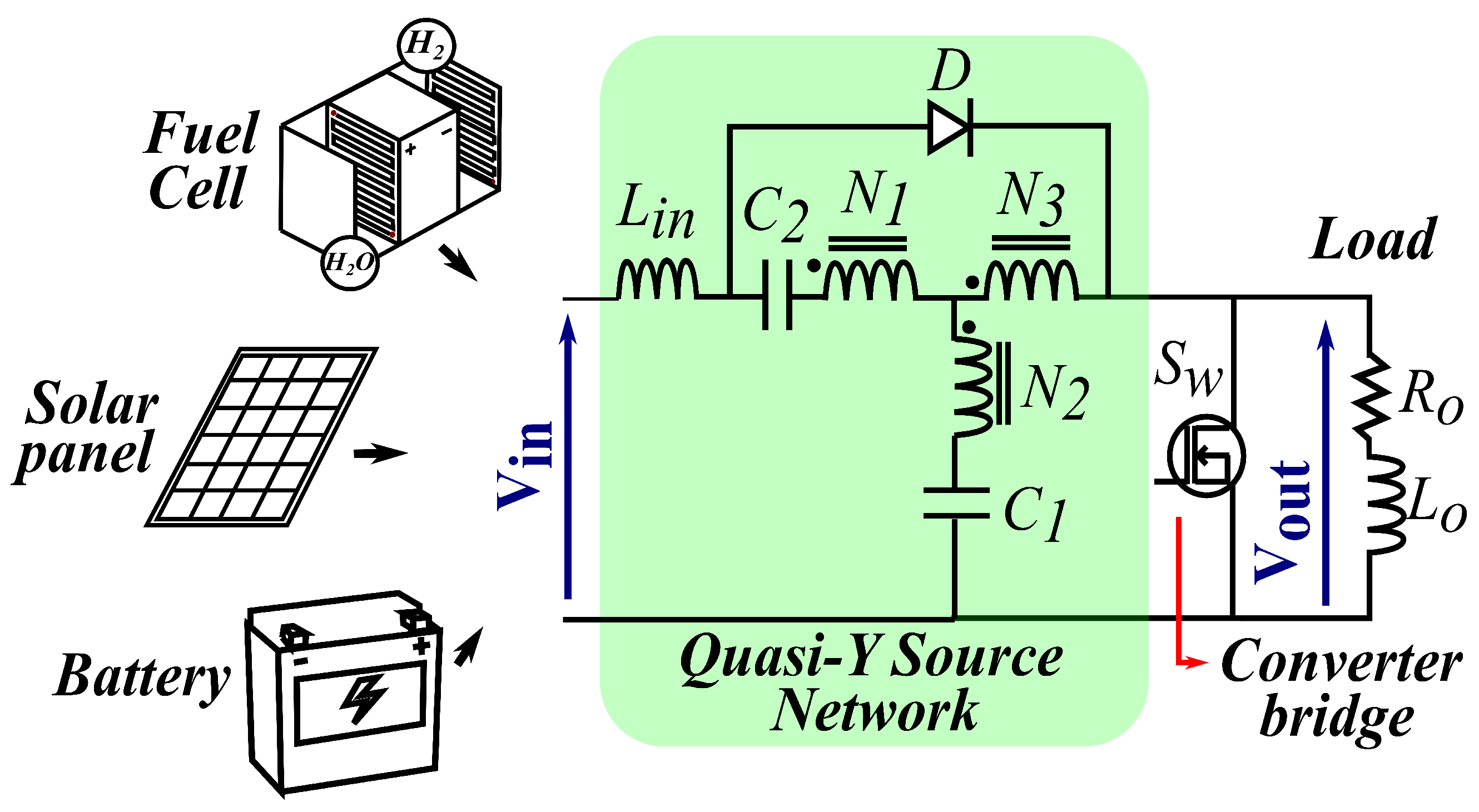
2.1. QSY Converter Configuration and Operation
2.2. Impedance Network Elements Design
2.2.1. Derivation of and
2.2.2. Derivation of
2.2.3. Derivation of
2.2.4. Derivation of
2.2.5. Derivation of
2.2.6. Determination of and
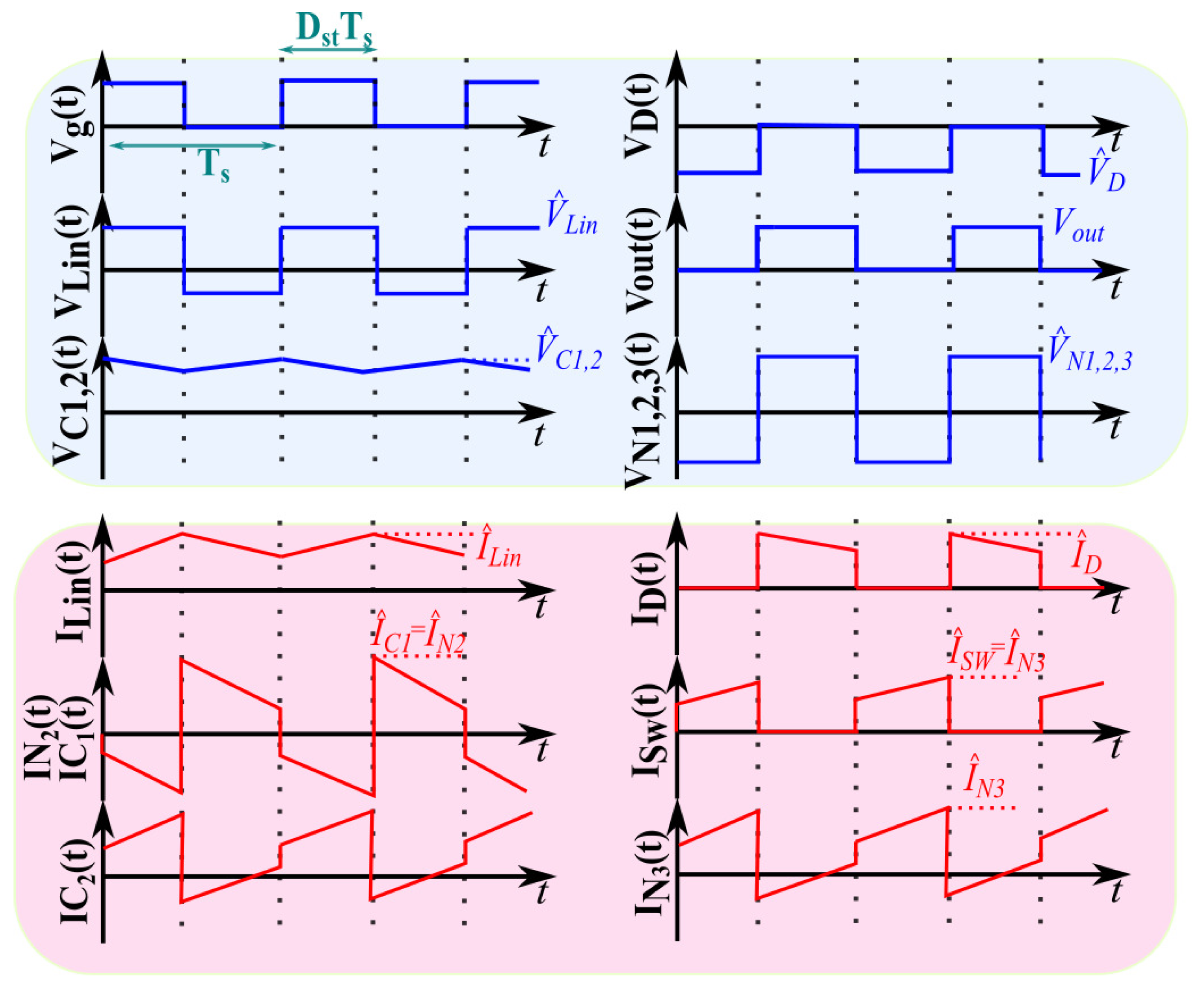
2.3. Electrical Quantities Expressions for the QSY Converter
3. Small-Signal Model Derivation and Analysis
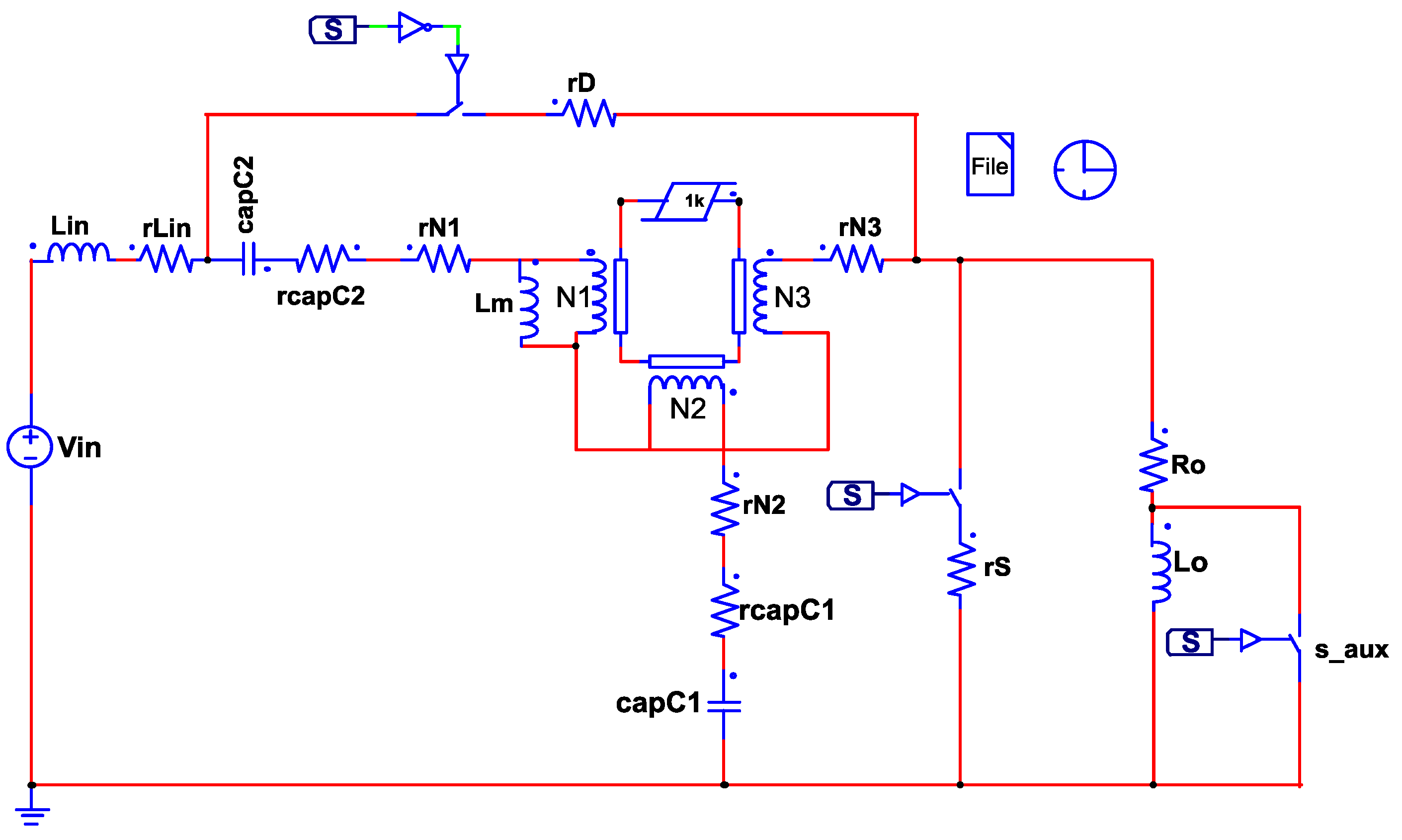
3.1. State-Space Model
3.2. Small-Signal Model Validation
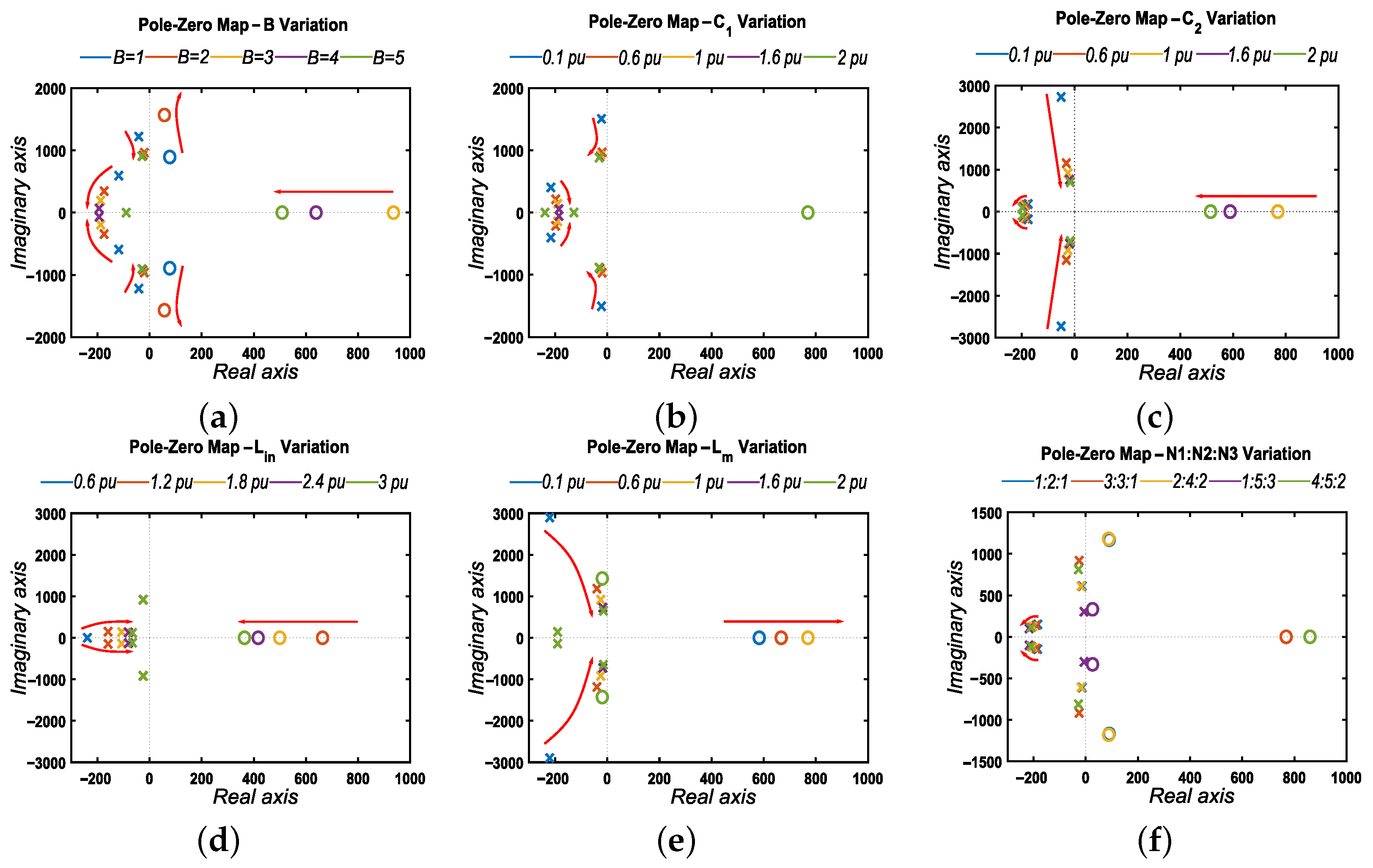
3.3. Parametric Variation Analysis
3.3.1.
3.3.2.
3.3.3.
3.3.4.
3.3.5. B,,
3.3.6. Coupled Inductor Winding Turns Ratio (::)
4. Closed-Loop Voltage Controller Design
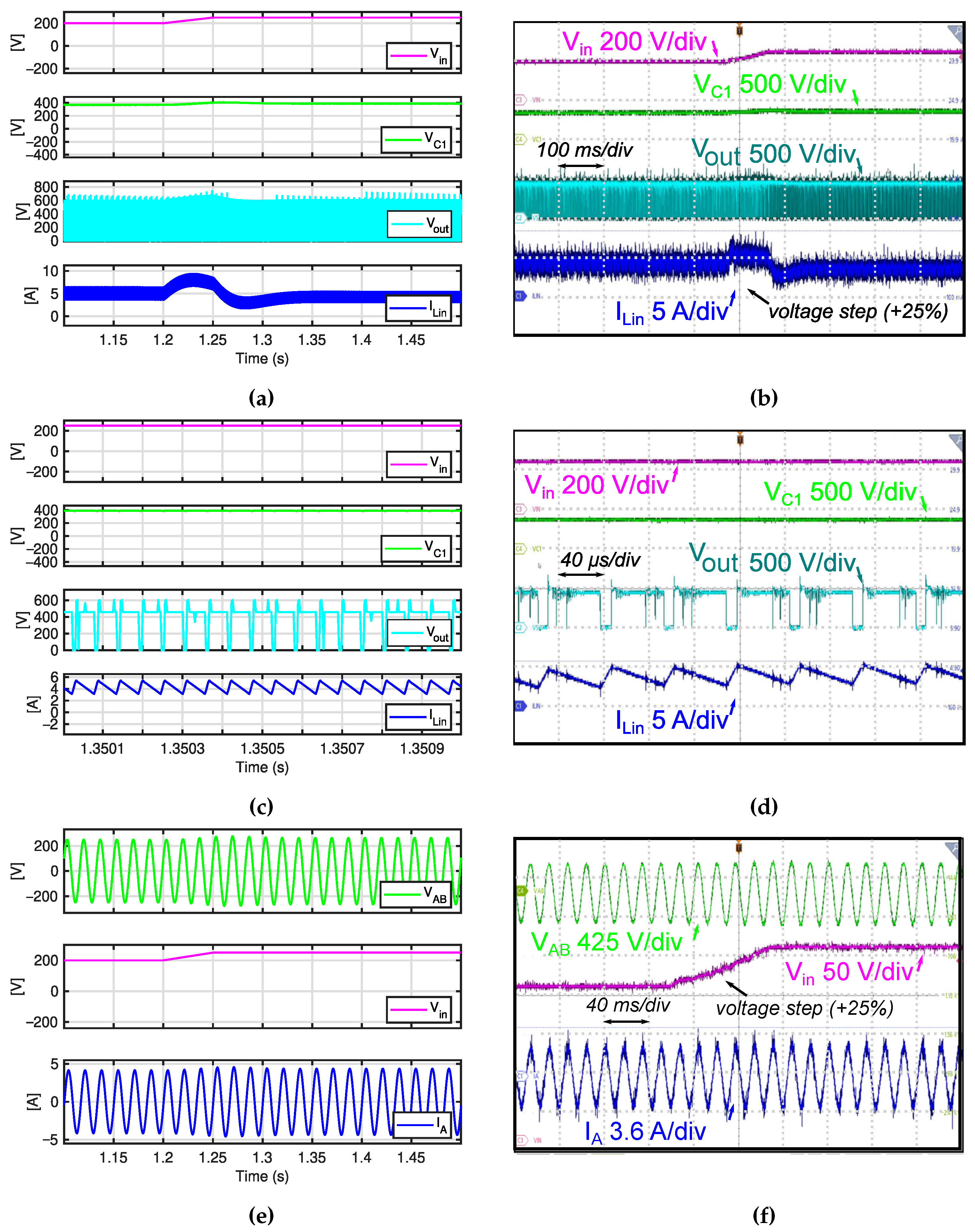
5. Experimental and Simulation Results
5.1. Simulation Considerations and Prototype Specifications
5.2. Experimental and Simulation Results Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Quasi-Y-Source(QSY) peak DC-link voltage | |
| QSY input voltage | |
| D | QSY network diode |
| D equivalent series resistance | |
| QSY network input inductor | |
| equivalent series resistance | |
| QSY input current | |
| QSY magnetizing inductance | |
| QSY magnetizing current | |
| QSY network capacitors | |
| equivalent series resistances | |
| and voltages | |
| :: | Coupled inductor winding turns ratio |
| QSY network winding factor | |
| Defined as | |
| QSY network output power transistor | |
| Three-phase bridge power transistors | |
| equivalent series resistance | |
| DC-AC modulation index for phases A,B,C | |
| DC-AC output line voltage | |
| Output load resistance | |
| Output load inductance | |
| Output inductor of DC-AC passive filter | |
| Output capacitor of DC-AC passive filter | |
| Phase currents of DC-AC converter | |
| Output load power | |
| Output load current | |
| Shoot-through duty-cycle | |
| Defined as | |
| Switching frequency | |
| Shoot-through switching frequency | |
| Switching period | |
| Gate signal for | |
| B | QSY converter voltage gain |
| Ripple factor for | |
| Ripple factor for | |
| Vacuum magnetic permeability | |
| Relative magnetic permeability | |
| A | Coupled inductor core cross-section area |
| l | Coupled inductor mean magnetic length |
| Auxiliary design factor | |
| Converter efficiency | |
| ,,, | Shoot-through state matrices |
| ,,, | Active state matrices |
| Factors for and matrices | |
| State-space model average matrices | |
| State-space model auxiliary matrices | |
| State-space model DC terms matrix | |
| State-space model output DC term | |
| Voltage to control transfer function | |
| Voltage controller transfer functions | |
| Open-loop uncompensated transfer function | |
| Open-loop compensated transfer function |
Appendix A
Appendix A.1. A1 and A2 Matrices λ Factors
References
- Ibrahim, I.A.; Ötvös, T.; Gilmanova, A.; Rocca, E.; Ghanem, C.; Wanat, M. International Energy Agency; Kluwer Law International BV: Alphen aan den Rijn, The Netherlands, 2021. [Google Scholar]
- Andersen, G.K.; Klumpner, C.; Kjær, S.B.; Blaabjerg, F. A new power converter for fuel cells with high system efficiency. Int. J. Electron. 2003, 90, 737–750. [Google Scholar] [CrossRef]
- Baddipadiga, B.P.; Ferdowsi, M. A high-voltage-gain dc-dc converter based on modified dickson charge pump voltage multiplier. IEEE Trans. Power Electron. 2016, 32, 7707–7715. [Google Scholar] [CrossRef]
- Siwakoti, Y.P.; Loh, P.C.; Blaabjerg, F.; Town, G. Y-source impedance network. Trans. Power Electron. 2014, 29, 3250–3254. [Google Scholar] [CrossRef]
- Zeng, Z.; Yang, H.; Zhao, R.; Cheng, C. Topologies and control strategies of multi-functional grid-connected inverters for power quality enhancement: A comprehensive review. Renew. Sustain. Energy Rev. 2013, 24, 223–270. [Google Scholar] [CrossRef]
- Grgić, I.; Vukadinović, D.; Bašić, M.; Bubalo, M. Photovoltaic System with a Battery-Assisted Quasi-Z-Source Inverter: Improved Control System Design Based on a Novel Small-Signal Model. Energies 2022, 15, 850. [Google Scholar] [CrossRef]
- Monjo, L.; Sainz, L.; Mesas, J.J.; Pedra, J. Quasi-Z-source inverter-based photovoltaic power system modeling for grid stability studies. Energies 2021, 14, 508. [Google Scholar] [CrossRef]
- Peng, F.Z. Z-source inverter. IEEE Trans. Ind. Appl. 2003, 39, 504–510. [Google Scholar] [CrossRef]
- Siwakoti, Y.P.; Peng, F.Z.; Blaabjerg, F.; Loh, P.C.; Town, G.E. Impedance-source networks for electric power conversion part I: A topological review. IEEE Trans. Power Electron. 2014, 30, 699–716. [Google Scholar] [CrossRef]
- Zhu, M.; Yu, K.; Luo, F.L. Switched inductor Z-source inverter. IEEE Trans. Power Electron. 2010, 25, 2150–2158. [Google Scholar]
- Zhu, M.; Li, D.; Loh, P.C.; Blaabjerg, F. Tapped-inductor Z-source inverters with enhanced voltage boost inversion abilities. In Proceedings of the 2010 IEEE International Conference on Sustainable Energy Technologies (ICSET), Kandy, Sri Lanka, 6–9 December 2010; pp. 1–6. [Google Scholar]
- Li, D.; Gao, F.; Loh, P.C.; Zhu, M.; Blaabjerg, F. Hybrid-source impedance networks: Layouts and generalized cascading concepts. IEEE Trans. Power Electron. 2010, 26, 2028–2040. [Google Scholar] [CrossRef]
- Loh, P.C.; Blaabjerg, F. Magnetically coupled impedance-source inverters. IEEE Trans. Ind. Appl. 2013, 49, 2177–2187. [Google Scholar] [CrossRef]
- Rezazadeh, H.; Monfared, M.; Nikbahar, A.; Sharifi, S. A family of high voltage gain quasi-Δ-source impedance networks. IET Power Electron. 2021, 14, 807–820. [Google Scholar] [CrossRef]
- Reddivari, R.; Jena, D.; Gautham, T. Analysis, design, and performance evaluation of differential-mode Y-source converters for voltage spikes mitigation. IEEE Trans. Ind. Appl. 2020, 56, 6701–6710. [Google Scholar] [CrossRef]
- Zhou, M.; Liu, C.; Zhang, M.; Mao, X.; Zhang, Y. High Step-up Soft Switching DC-DC Converter Integrated with Y-Source Network. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 3348–3358. [Google Scholar] [CrossRef]
- Siwakoti, Y.P.; Loh, P.C.; Blaabjerg, F.; Andreasen, S.J.; Town, G.E. Y-source boost DC/DC converter for distributed generation. IEEE Trans. Ind. Electron. 2014, 62, 1059–1069. [Google Scholar] [CrossRef]
- Wang, W.; Wang, Y.; Guan, Y.; Yao, T.; Wang, Y.; Xu, D. A Family of Impedance Source DC-DC Converters With Zero Input Current Ripple. IEEE Trans. Ind. Electron. 2022, 70, 8883–8894. [Google Scholar] [CrossRef]
- Guan, Y.; Cheng, Y.; Yao, T.; Wang, Y.; Wang, W.; Xu, D. A High-Performance DC–DC Converter With Soft Switching Characteristic and High Voltage Gain. IEEE Trans. Power Electron. 2022, 37, 12279–12288. [Google Scholar] [CrossRef]
- Yao, T.; Guan, Y.; Cheng, Q.; Wang, Y.; Dalla Costa, M.A.; Alonso, M.; Xu, D.; Wang, W. High Performance Y-source Converters Based on Switched Inductor. In Proceedings of the 2022 IEEE Industry Applications Society Annual Meeting (IAS), Detroit, MI, USA, 9–14 October 2022; pp. 1–5. [Google Scholar]
- Nikbahar, A.; Monfared, M. Smooth DC-Link Y-source inverters: Suppression of Shoot-through current and avoiding DC magnetism. IEEE Trans. Power Electron. 2022, 37, 12357–12369. [Google Scholar] [CrossRef]
- Siwakoti, Y.P.; Loh, P.C.; Blaabjerg, F.; Town, G.E. Effects of leakage inductances on magnetically coupled Y-source network. IEEE Trans. Power Electron. 2014, 29, 5662–5666. [Google Scholar] [CrossRef]
- Yadav, A.; Chandra, S.; Bajaj, M.; Sharma, N.K.; Ahmed, E.M.; Kamel, S. A topological advancement review of magnetically coupled impedance source network configurations. Sustainability 2022, 14, 3123. [Google Scholar] [CrossRef]
- Reddivari, R.; Jena, D. A correlative investigation of impedance source networks: A comprehensive review. IETE Tech. Rev. 2022, 39, 506–539. [Google Scholar] [CrossRef]
- Rajaei, A.; Yazdani, S.; Ebadi, E. PMSG-Based Stand-alone Wind Energy Conversion System Using Quasi Y-Source Inverter and Battery Storage. In Proceedings of the 2022 13th Power Electronics, Drive Systems, and Technologies Conference (PEDSTC), Tehran, Iran, 1–3 February 2022; pp. 81–85. [Google Scholar]
- Reddivari, R.; Jena, D. Improved Gamma type Y-source inverter for rooftop PV based VG applications. Int. J. Electr. Power Energy Syst. 2022, 142, 108261. [Google Scholar] [CrossRef]
- Ismeil, M.A.; Orabi, M.; Abdelaal, O. High Robust Control Model of High Step Up Three Phase Y Source Inverters based on Model Predictive Control. SVU-Int. J. Eng. Sci. Appl. 2023, 4, 76–83. [Google Scholar] [CrossRef]
- Siwakoti, Y.P.; Blaabjerg, F.; Loh, P.C. Quasi-Y-Sourceboost DC–DC converter. IEEE Trans. Power Electron. 2015, 30, 6514–6519. [Google Scholar] [CrossRef]
- Siwakoti, Y.P.; Blaabjerg, F.; Loh, P.C. Quasi-Y-Sourceinverter. In Proceedings of the 2015 Australasian Universities Power Engineering Conference (AUPEC), Wollongong, Australia, 27–30 September 2015; pp. 1–5. [Google Scholar]
- Shafiei, S.; Mehdizadeh, A.; Khorsandi, A. AC Equivalent Circuit of Quasi Y-Source Converter Using by Averaged-Switch Model. In Proceedings of the 2022 13th Power Electronics, Drive Systems, and Technologies Conference (PEDSTC), Tehran, Iran, 1–3 February 2022; pp. 603–608. [Google Scholar]
- Forouzesh, M.; Siwakoti, Y.P.; Blaabjerg, F.; Hasanpour, S. Small-signal modeling and comprehensive analysis of magnetically coupled impedance-source converters. IEEE Trans. Power Electron. 2016, 31, 7621–7641. [Google Scholar] [CrossRef]
- Shehata, E.; Thomas, J.; Brisha, A.; Wageh, M. Design and analysis of a quasi y-source impedance network dc-dc converter. In Proceedings of the 2017 Nineteenth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 19–21 December 2017; pp. 235–241. [Google Scholar]
- Ananth, D.; Chinna, D.S.; Sairam, G.; Naveen, M.; BhaskarRao, A.; Rao, B.J. Design and Analysis of High Gain Quasi Y-Source Impedance Network. Int. J. Sci. Res. Sci. Eng. Technol. 2020, 7, 1–7. [Google Scholar] [CrossRef]
- Abdelaal, O.; Ismeil, M.A.; Orabi, M. Model predicitve control of quasi y-source inverter. In Proceedings of the 2019 21st International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 17–19 December 2019; pp. 478–483. [Google Scholar]
- Fathima, K.; Vishnupriya, R.; Pavithra, M.; Devi, V.P. Improved DC bus voltage regulation for a DC distribution system using quasi Y source converter. In Proceedings of the 2017 International Conference on Power and Embedded Drive Control (ICPEDC), Chennai, India, 16–18 March 2017; pp. 446–452. [Google Scholar]
- Ding, X.; Qian, Z.; Yang, S.; Cui, B.; Peng, F. A PID control strategy for DC-link boost voltage in Z-source inverter. In Proceedings of the APEC 07-Twenty-Second Annual IEEE Applied Power Electronics Conference and Exposition, Anaheim, CA, USA, 25 February–1 March 2007; pp. 1145–1148. [Google Scholar]
- Witulski, A.F. Introduction to modeling of transformers and coupled inductors. IEEE Trans. Power Electron. 1995, 10, 349–357. [Google Scholar] [CrossRef]
- Middlebrook, R.D.; Cuk, S. A general unified approach to modelling switching-converter power stages. In Proceedings of the 1976 IEEE Power Electronics Specialists Conference, Cleveland, OH, USA, 8–10 June 1976; pp. 18–34. [Google Scholar]
- Siwakoti, Y.P.; Peng, F.Z.; Blaabjerg, F.; Loh, P.C.; Town, G.E.; Yang, S. Impedance-source networks for electric power conversion part II: Review of control and modulation techniques. IEEE Trans. Power Electron. 2014, 30, 1887–1906. [Google Scholar] [CrossRef]
- Venable, H.D. The K factor: A new mathematical tool for stability analysis and synthesis. In Proceedings of the Powercon, San Diego, CA, USA, 22–24 March 1983; Volume 10, pp. 1–12. [Google Scholar]
- Forouzesh, M.; Abdelhakim, A.; Siwakoti, Y.; Blaabjerg, F. Analysis and design of an energy regenerative snubber for magnetically coupled impedance source converters. In Proceedings of the 2018 IEEE Applied Power Electronics Conference and Exposition (APEC), San Antonio, TX, USA, 4–8 March 2018; pp. 2555–2561. [Google Scholar]
- Ridley, R. Flyback converter snubber design. Switch. Power Mag. 2005, 12, 1–7. [Google Scholar]






| Component | Expression |
|---|---|
| Variable | Expression | Variable | Expression |
|---|---|---|---|
| 0 | |||
| , |
| Component | Value | Component | Value |
|---|---|---|---|
| 4.24 mH | 0.85 | ||
| 15 F | 29.33 m | ||
| 2040 F | 142.68 m | ||
| 25 m | 25 m | ||
| 0.222 mH | :: | 37:186:112 | |
| 149.27 | 10 mH | ||
| 250 V | 18 kHz | ||
| 3.0135 | 155.328689 × |
| Coefficient | Value | Coefficient | Value |
|---|---|---|---|
| 1 | 1.03971074368126 | ||
| −1.99557051716865 | 2.84981554283603 | ||
| 9.95570517168651 | −1.03686092813842 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santos, R.; Rodrigues, M.V.M.; Arenas, L.D.O.; Gonçalves, F.A.S. A Comprehensive Small-Signal Model Formulation and Analysis for the Quasi-Y Impedance-Source Inverter. Energies 2023, 16, 4877. https://doi.org/10.3390/en16134877
Santos R, Rodrigues MVM, Arenas LDO, Gonçalves FAS. A Comprehensive Small-Signal Model Formulation and Analysis for the Quasi-Y Impedance-Source Inverter. Energies. 2023; 16(13):4877. https://doi.org/10.3390/en16134877
Chicago/Turabian StyleSantos, Rafael, Marcus V. M. Rodrigues, Luis De Oro Arenas, and Flávio A. S. Gonçalves. 2023. "A Comprehensive Small-Signal Model Formulation and Analysis for the Quasi-Y Impedance-Source Inverter" Energies 16, no. 13: 4877. https://doi.org/10.3390/en16134877
APA StyleSantos, R., Rodrigues, M. V. M., Arenas, L. D. O., & Gonçalves, F. A. S. (2023). A Comprehensive Small-Signal Model Formulation and Analysis for the Quasi-Y Impedance-Source Inverter. Energies, 16(13), 4877. https://doi.org/10.3390/en16134877






