Transport Phenomena in a Banded Solid Oxide Fuel Cell Stack—Part 2: Numerical Analysis
Abstract
1. Introduction
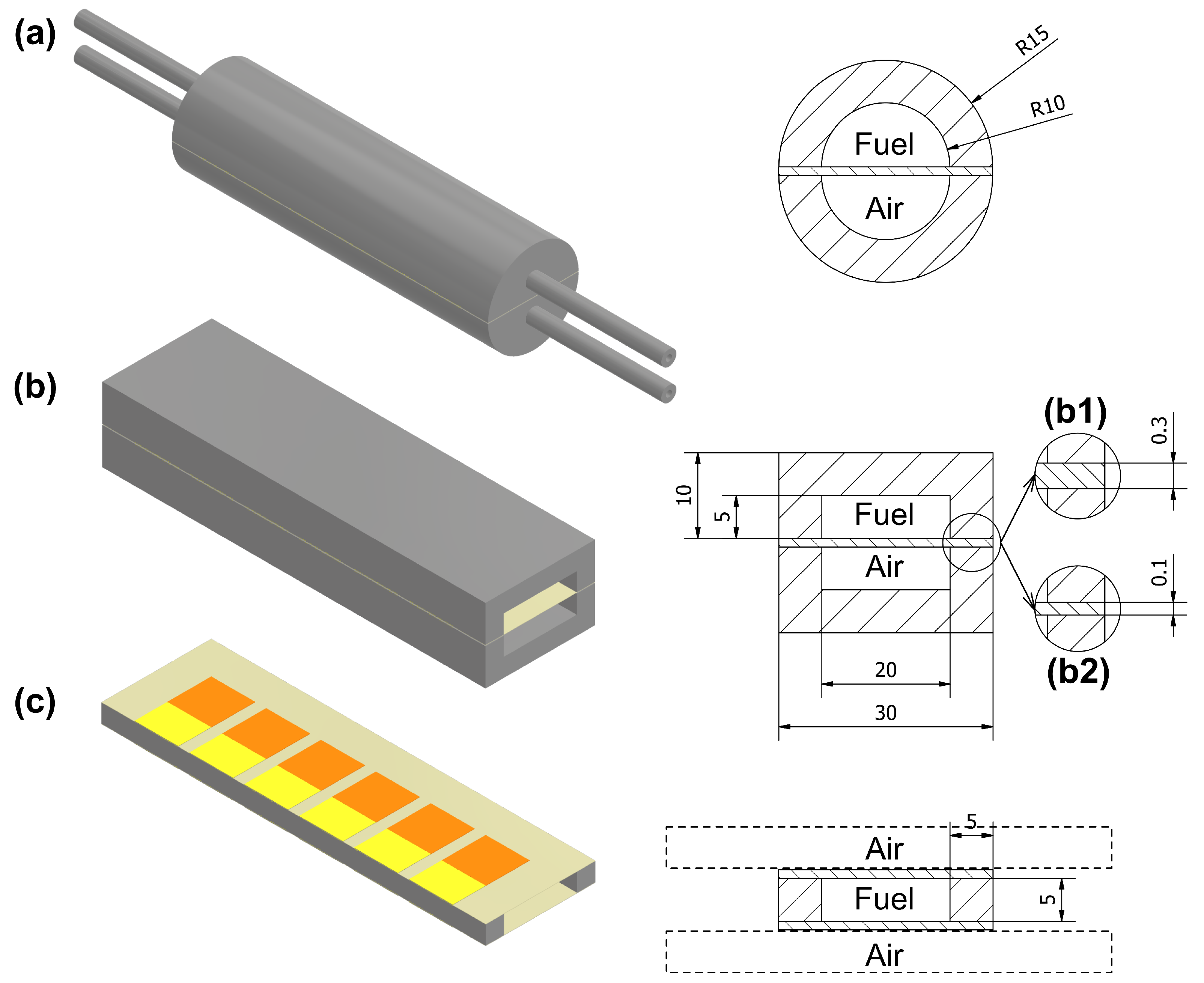
2. Geometry Description
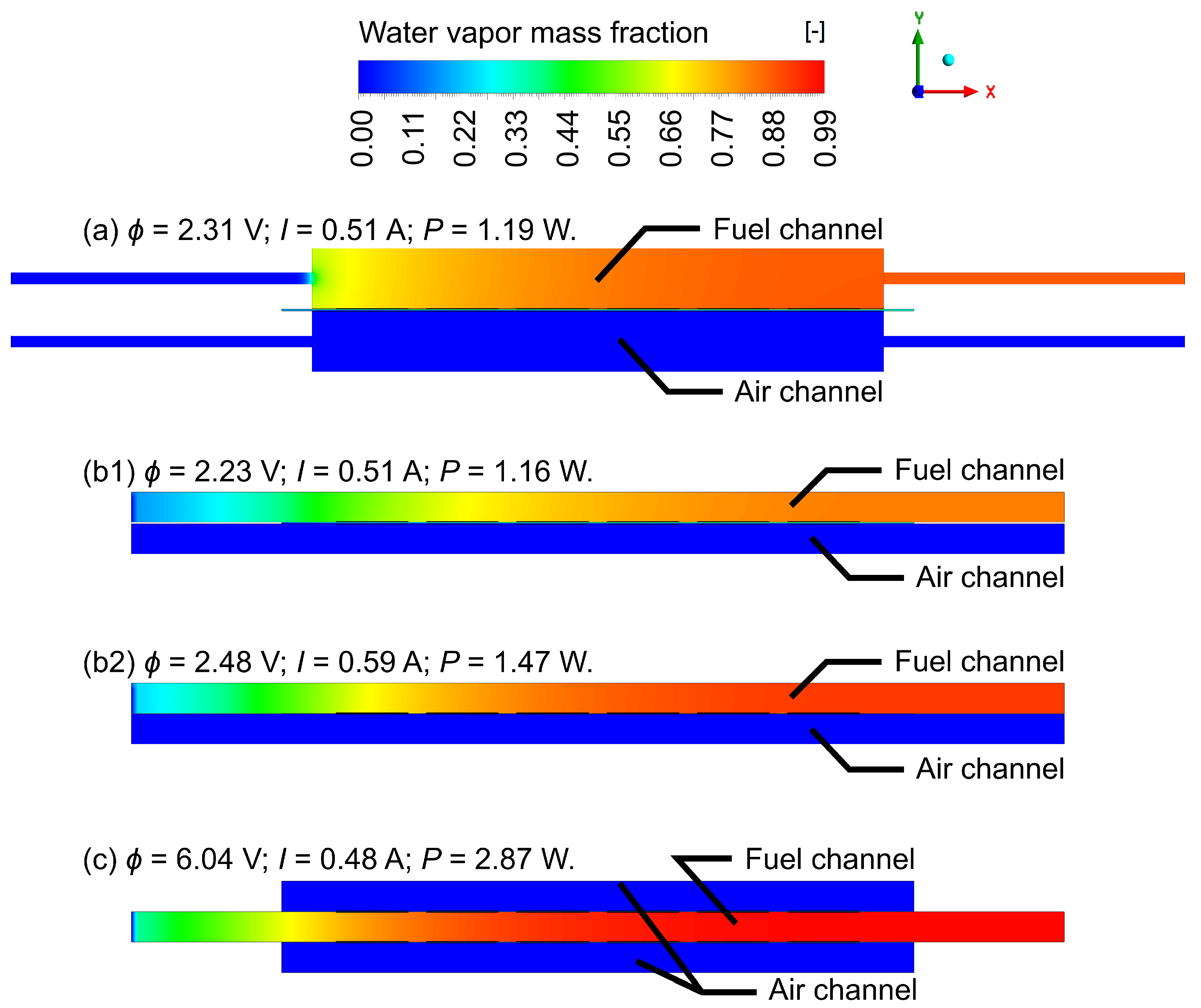
- (a)
- The electrolyte-supported design with 0.3 mm of electrolyte thickness. The stack is enclosed by two half-tubular covers, which make the fuel and air channels (initial prototype).
- (b)
- Electrolyte-supported stack is enclosed by rectangular covers. This solution reduces the stack volume and simultaneously increases the volumetric power density; this proposal has two subdesigns:
- (b1)
- supported on 0.3 mm electrolyte;
- (b2)
- supported on 0.1 mm electrolyte.
- (c)
- Extension of the system to multiple stacks. By combining two stacks, in which anodes are targeted face-to-face, a fuel channel is created, while cathodes facing the outer sides could be supplied with air without a separate channel, using, for example, a fan or placing the stack in a moving vehicle. This case consists of two stacks supported on a 0.1 mm electrolyte. This design allows reduction of the volume of the stack even more and, theoretically, double the power (because of the doubled number of cells).
3. Mathematical Model
4. Numerical Analysis
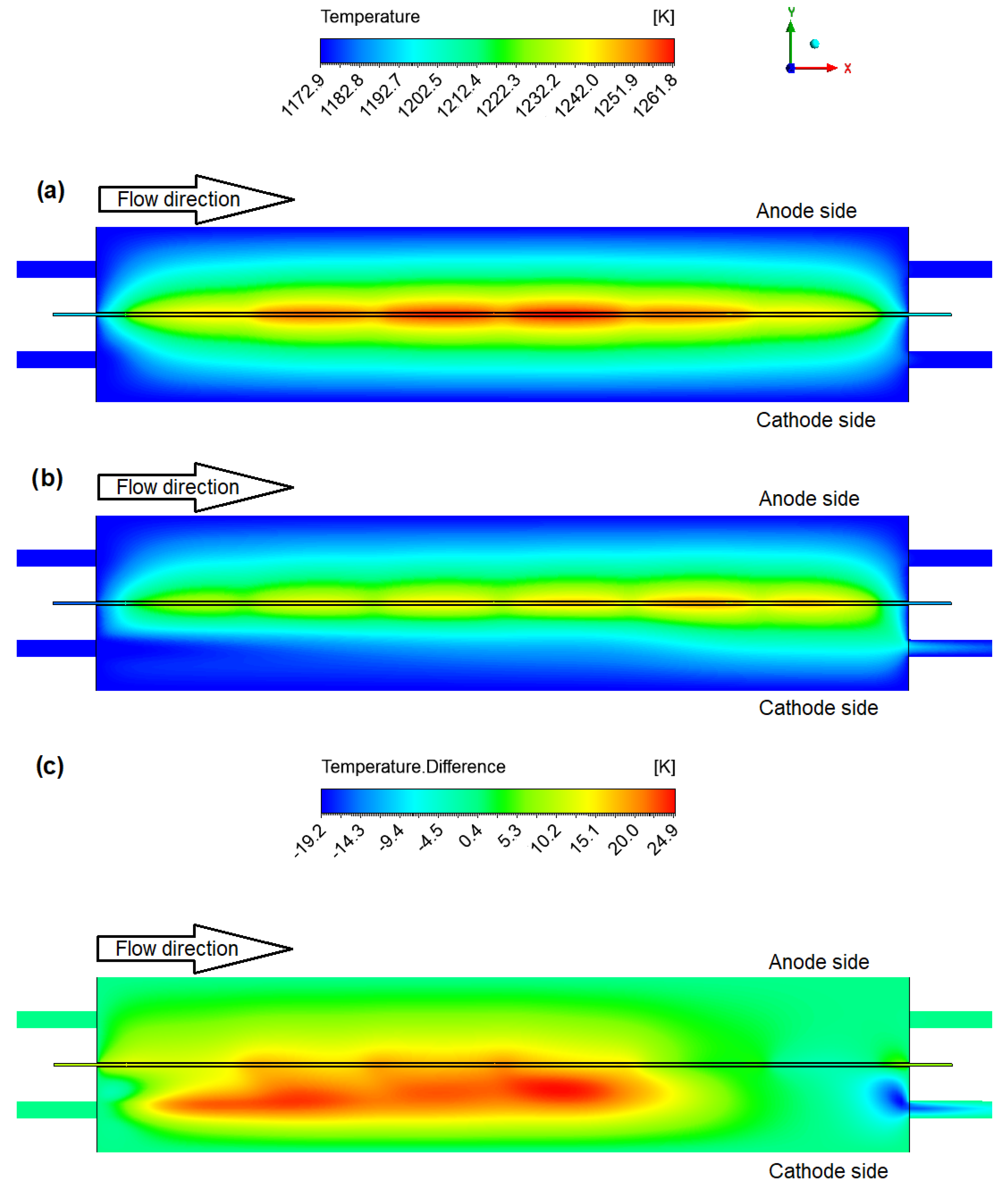
4.1. Gas Flow Rates Influence Study
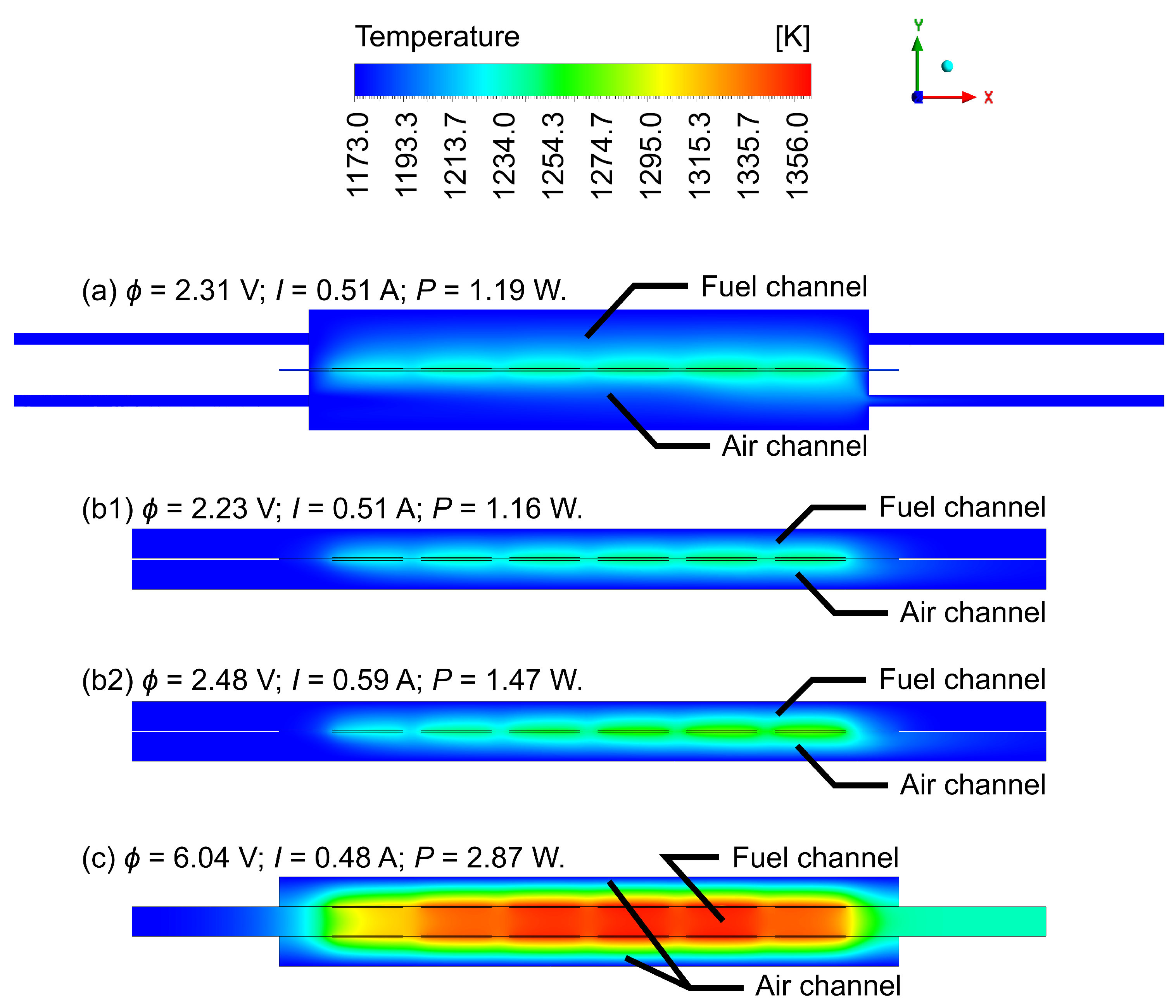
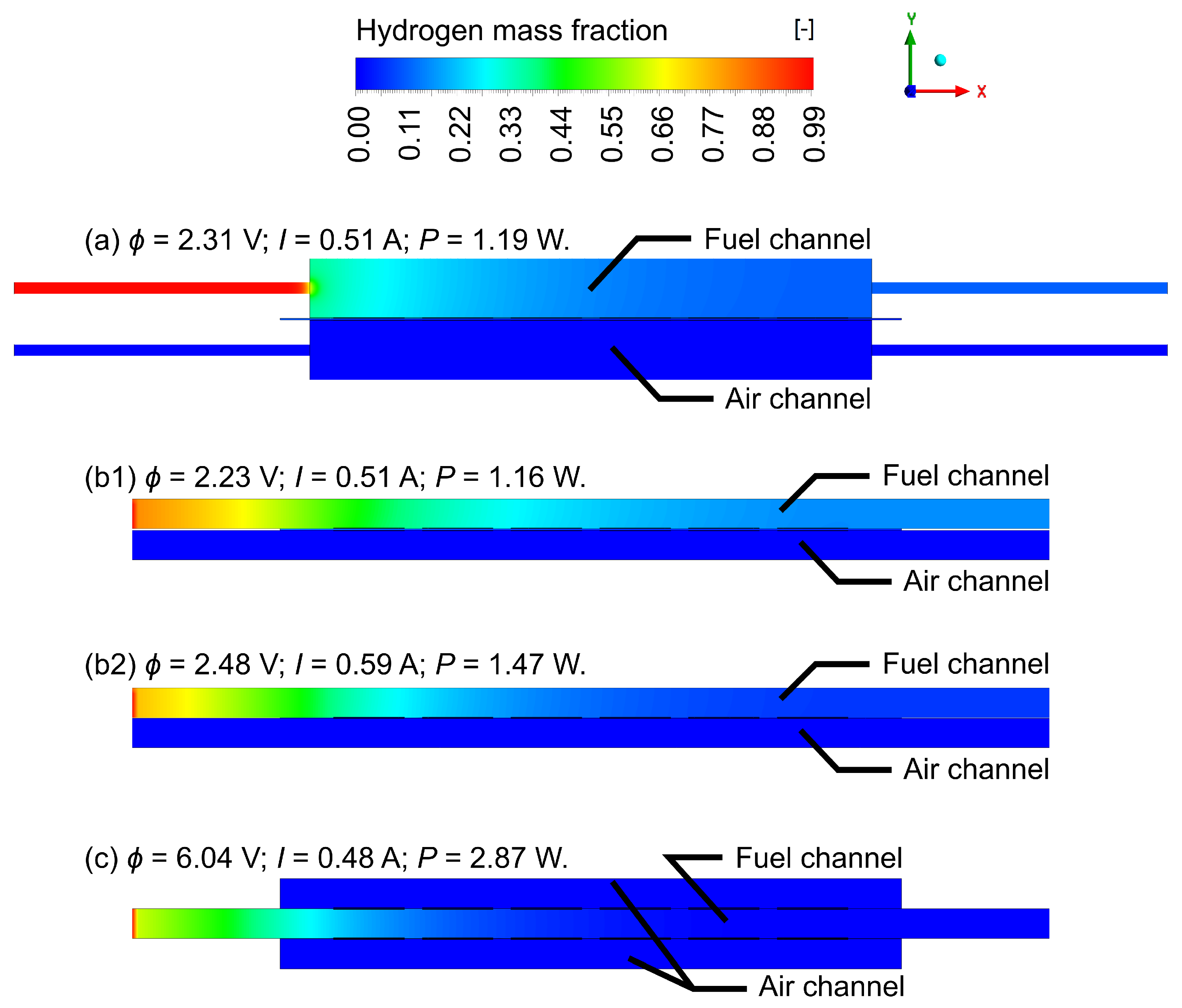
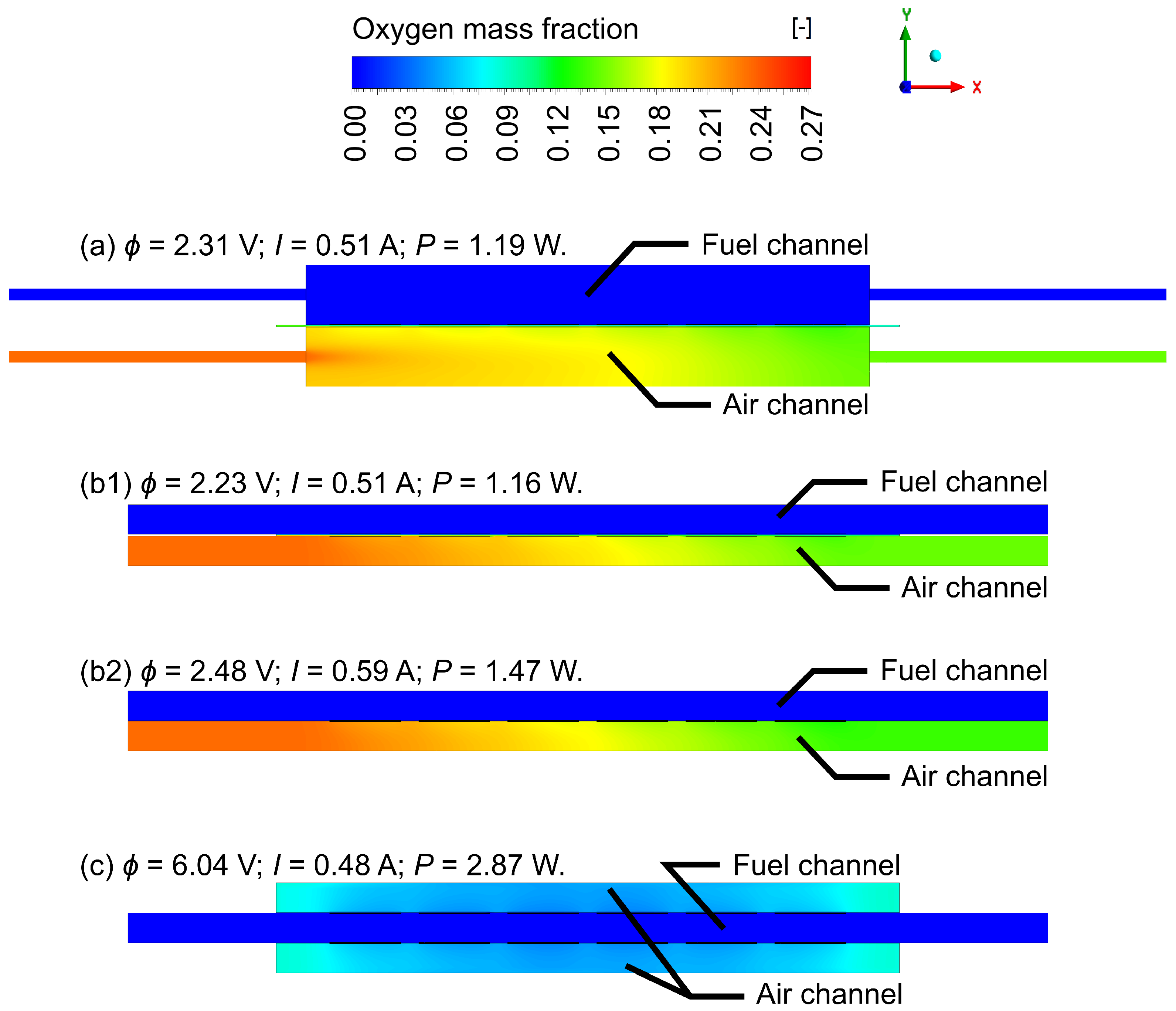
4.2. Geometric Improvements Study
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Faraday constant | (9.65 × 104 ) | |
| h | specific enthalpy | () |
| enthalpy change | () | |
| I | current | () |
| anode equilibrium exchange current | () | |
| cathode equilibrium exchange current | () | |
| i | current density flux | () |
| j | volumetric transfer current density | () |
| diffusion flux | () | |
| k | thermal conductivity | () |
| M | molar mass | () |
| p | static pressure | () |
| P | power | () |
| power density | () | |
| volumetric flux of species | () | |
| universal gas constant | ( ) | |
| source/sink term of momentum | () | |
| source/sink term of heat | () | |
| source/sink term of species rates | () | |
| source/sink term of mass | () | |
| T | temperature | () |
| velocity vector | () | |
| local species concentration | (kmol ) | |
| species mass fraction | (-) | |
| Greek letters | ||
| transfer coefficient | (-) | |
| concentration dependence | (-) | |
| porosity rate | (-) | |
| triple phase boundary length density | () | |
| double phase boundary length density | () | |
| local surface overpotential | () | |
| density | () | |
| conductivity | () | |
| stress tensor | () | |
| electric potential | () | |
| Sub- and superscripts | ||
| anodic | ||
| anode | ||
| cathodic | ||
| cathode | ||
| density | ||
| double phase boundary | ||
| effective value | ||
| electronic | ||
| equilibrium | ||
| i | reaction component | |
| ionic | ||
| reaction | ||
| reference value | ||
| solid | ||
| triple phase boundary | ||
| Abbreviations | ||
| 3D | three-dimensional | |
| CAD | computer-aided design | |
| CFD | computational fluid dynamics | |
| OCV | open circuit voltage | |
| SOFC | solid oxide fuel cell | |
References
- Buchaniec, S.; Sciazko, A.; Mozdzierz, M.; Brus, G. A Novel Approach to the Optimization of a Solid Oxide Fuel Cell Anode Using Evolutionary Alghorithms. IEEE Access 2019, 7, 34361–34372. [Google Scholar] [CrossRef]
- Ghorbani, B.; Vijayaraghavan, K. A review study on software-based modeling of hydrogen-fueled solid oxide fuel cells. Int. J. Hydrogen Energy 2019, 44, 13700–13727. [Google Scholar] [CrossRef]
- Pianko-Oprych, P.; Zinko, T. Simulation of the steady-state behaviour of a new design of a single planar Solid Oxide Fuel Cell. Pol. J. Chem. Technol. 2016, 1, 64–71. [Google Scholar] [CrossRef]
- Pianko-Oprych, P.; Zinko, T. Computational fluid dynamics calculation of a planar solid oxide fuel cell design running on syngas. Chem. Process Eng. 2017, 38, 513–521. [Google Scholar] [CrossRef]
- Mozdzierz, M.; Berent, K.; Kimijima, S.; Szmyd, J.S.; Brus, G. A Multiscale Approach to the Numerical Simulation of the Solid Oxide Fuel Cell. Catalysts 2019, 9, 253. [Google Scholar] [CrossRef]
- Chalusiak, M.; Wrobel, M.; Mozdzierz, M.; Berent, K.; Szmyd, J.S.; Kimijima, S.; Brus, G. A numerical analysis of unsteady transport phenomena in a Direct Internal Reforming Solid Oxide Fuel Cell. Int. J. Heat Mass Transf. 2019, 131, 1032–1051. [Google Scholar] [CrossRef]
- Wei, S.S.; Wang, T.H.; Wu, J.S. Numerical modeling of interconnect flow channel design and thermal stress analysis of a planar anode-supported solid oxide fuel cell stack. Energy 2014, 69, 553–561. [Google Scholar] [CrossRef]
- Dong, S.-K.; Jung, W.-N.; Rashid, K.; Kashimoto, A. Design and numerical analysis of a planar anode-supported SOFC stack. Renew. Energy 2016, 94, 637–650. [Google Scholar] [CrossRef]
- Pirasaci, T. Non-uniform, multi-stack solid oxide fuel cell (SOFC) system design for small system size and high efficiency. J. Power Sources 2019, 426, 135–142. [Google Scholar] [CrossRef]
- Babaie Rizvandi, O.; Miao, X.-Y.; Frandsen, H.L. Multiscale modeling of degradation of full solid oxide fuel cell stacks. Int. J. Hydrogen Energy 2021, 46, 27709–27730. [Google Scholar] [CrossRef]
- Fu, Q.; Li, Z.; Wei, W.; Liu, F.; Xu, X.; Liu, Z. Performance enhancement of a beam and slot interconnector for anode-supported SOFC stack. Energy Convers. Manag. 2021, 241, 114277. [Google Scholar] [CrossRef]
- Zheng, J.; Xiao, L.; Wu, M.; Lang, S.; Zhang, Z.; Chen, M.; Yuan, J. Numerical Analysis of Thermal Stress for a Stack of Planar Solid Oxide Fuel Cells. Energies 2022, 15, 343. [Google Scholar] [CrossRef]
- Miao, X.-Y.; Pirou, S.; Frandsen, H.L. Mitigating distortions during debinding of a monolithic solid oxide fuel cell stack using a multiscale, multiphysics model. J. Eur. Ceram. Soc. 2023, 43, 1992–2001. [Google Scholar] [CrossRef]
- Fan, J.; Shi, J.; Zhang, R.; Wang, Y.; Shi, Y. Numerical study of a 20-cell tubular segmented-in-series solid oxide fuel cell. J. Power Sources 2023, 556, 232449. [Google Scholar] [CrossRef]
- Prokop, T.A.; Berent, K.; Iwai, H.; Szmyd, J.S. A Three-Dimensional Numerical Assessment of Heterogeneity Impact on a Solid Oxide Fuel Cell’s Anode Performance. Catalysts 2018, 8, 503. [Google Scholar] [CrossRef]
- Brus, G. High-Temperature Solid Oxide Fuel Cell Stack. Polish Patent PL 234427, 28 February 2020. [Google Scholar]
- Mukerjee, S.; Leah, R.; Selby, M.; Stevenson, G.; Brandon, N.P. Chapter 9—Life and Reliability of Solid Oxide Fuel Cell-Based Products: A Review. In Solid Oxide Fuel Cell Lifetime and Reliability; Brandon, N.P., Ruiz-Trejo, E., Boldrin, P., Eds.; Academic Press: Cambridge, MA, USA, 2017; pp. 173–191. [Google Scholar] [CrossRef]


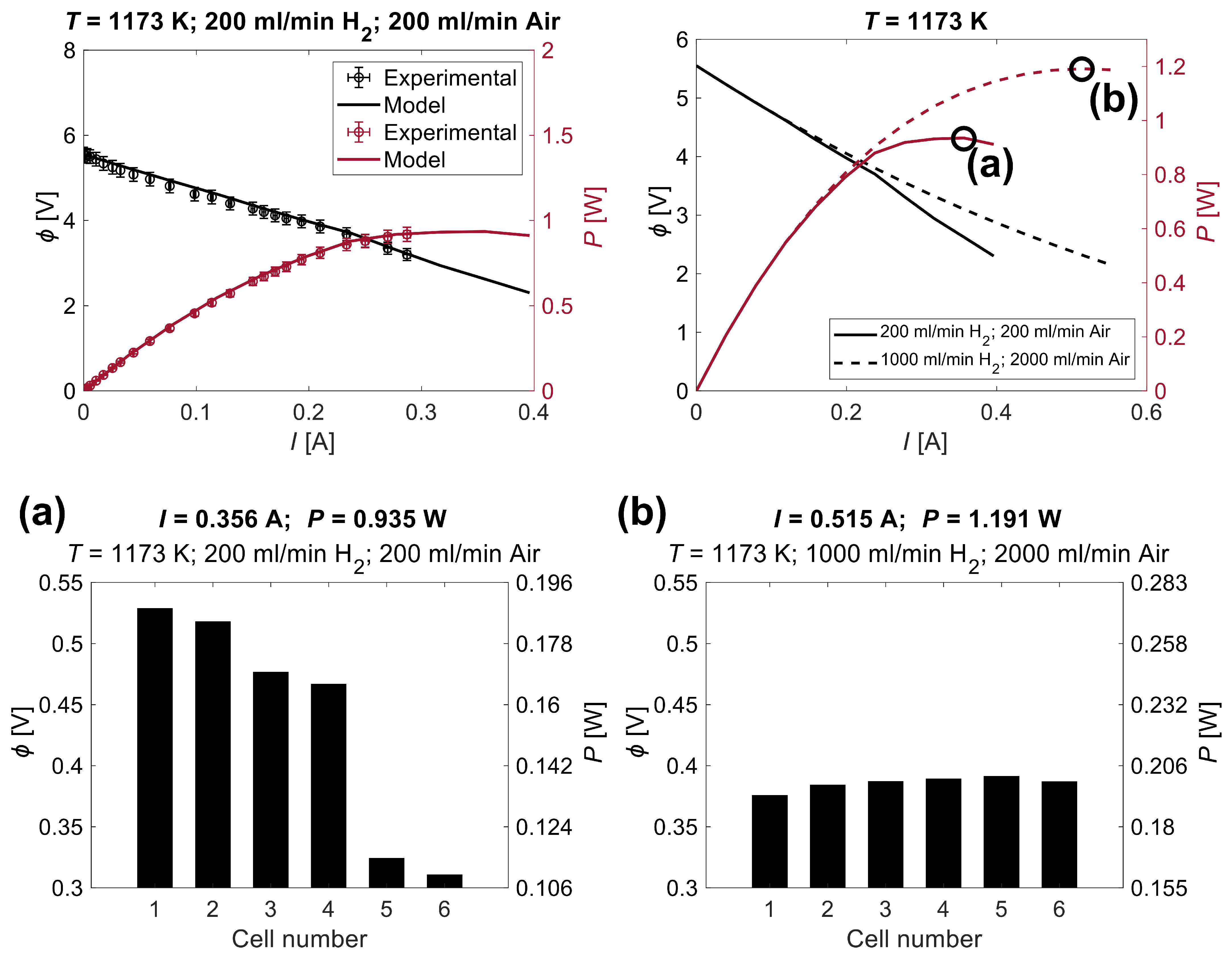
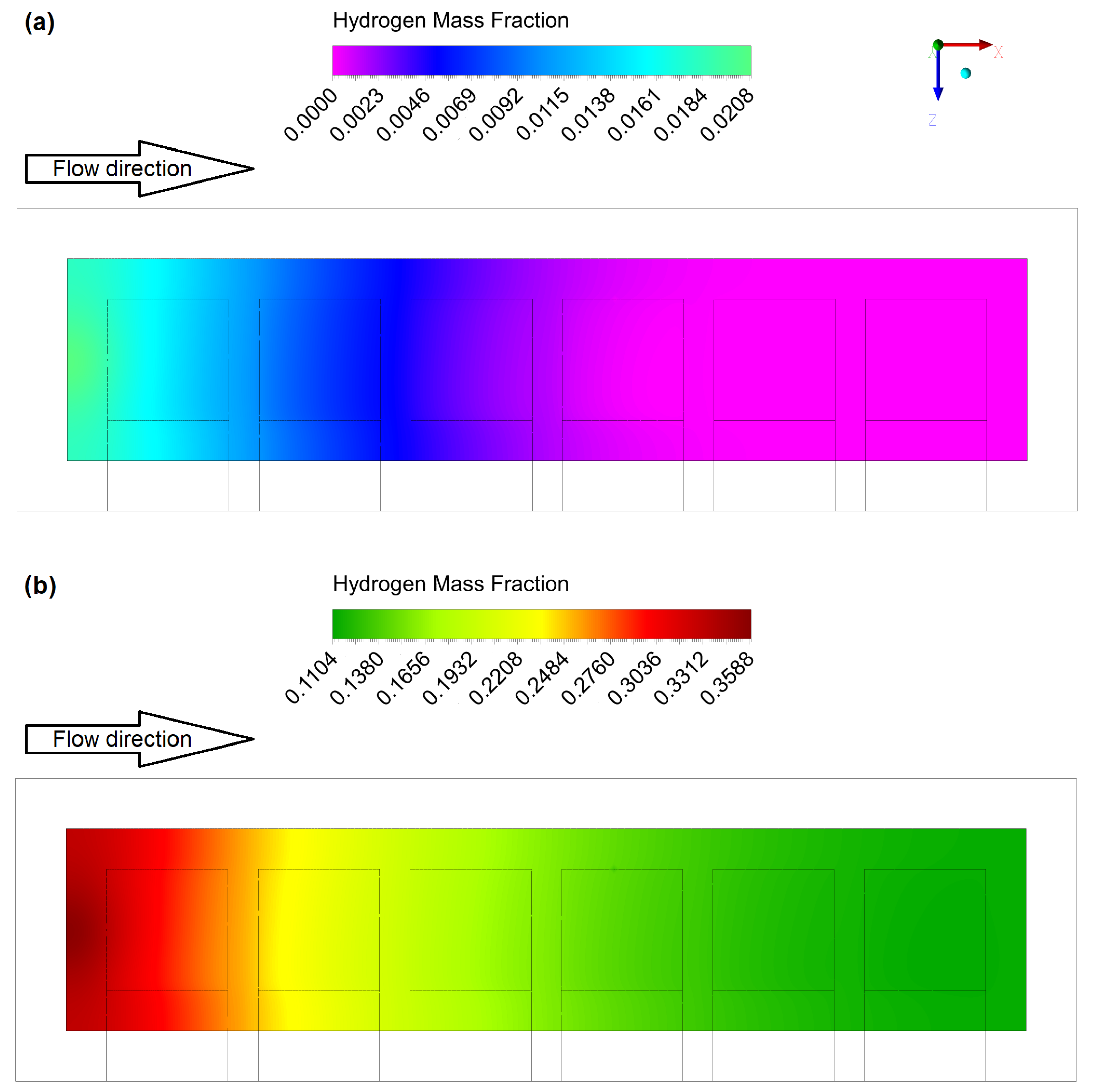
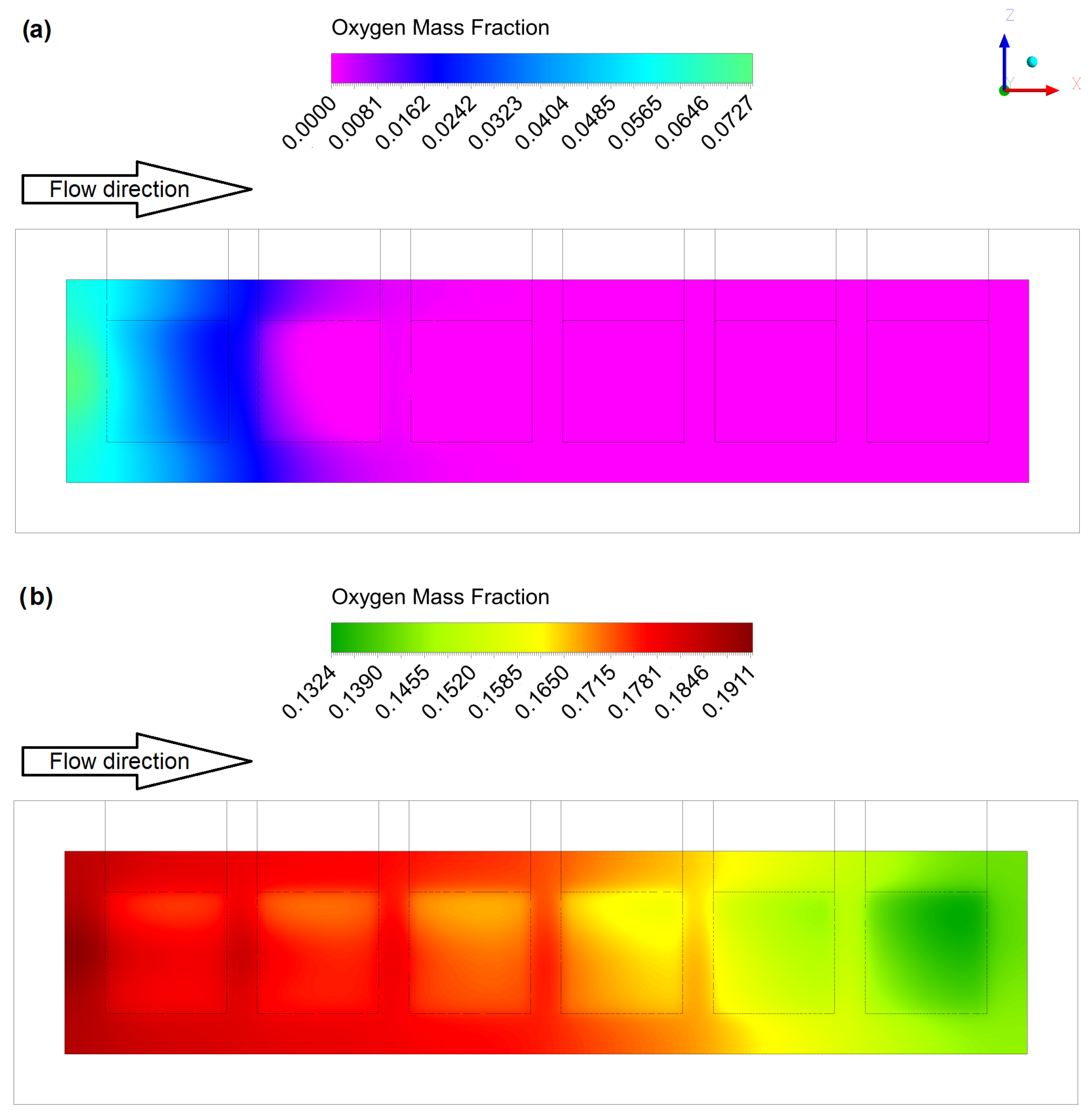



| Parameter | Description | Value |
|---|---|---|
| Applied: Section 4.1 for case “(a)” | ||
| Air inlet flow rate | constant value | 0.2 |
| Fuel (hydrogen) inlet flow rate | constant value | 0.2 |
| Applied: Section 4.1 for case “(b)” and all cases in Section 4.2 | ||
| Air inlet flow rate | constant value | 2 |
| Fuel (hydrogen) inlet flow rate | constant value | 1 |
| Applied: all cases | ||
| Inlets temperature | constant value | 1173 |
| Outer walls temperature | constant value | 1173 |
| Outer walls gas leakage | constant value | 0 |
| Air outlet temperature | constant value | 1173 |
| Fuel outlet temperature | constant value | 1173 |
| Air outlet pressure | constant value | 1 atm |
| Fuel outlet pressure | constant value | 1 atm |
| Anode current collectors external contact | constant potential value | 0 |
| Cathode current collectors external contact | constant current value | range 0–0.63 (case dependent) |
| Solid bodies outer walls current leakage | constant value | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Śreniawski, K.K.; Moździerz, M.; Brus, G.; Szmyd, J.S. Transport Phenomena in a Banded Solid Oxide Fuel Cell Stack—Part 2: Numerical Analysis. Energies 2023, 16, 4512. https://doi.org/10.3390/en16114512
Śreniawski KK, Moździerz M, Brus G, Szmyd JS. Transport Phenomena in a Banded Solid Oxide Fuel Cell Stack—Part 2: Numerical Analysis. Energies. 2023; 16(11):4512. https://doi.org/10.3390/en16114512
Chicago/Turabian StyleŚreniawski, Karol K., Marcin Moździerz, Grzegorz Brus, and Janusz S. Szmyd. 2023. "Transport Phenomena in a Banded Solid Oxide Fuel Cell Stack—Part 2: Numerical Analysis" Energies 16, no. 11: 4512. https://doi.org/10.3390/en16114512
APA StyleŚreniawski, K. K., Moździerz, M., Brus, G., & Szmyd, J. S. (2023). Transport Phenomena in a Banded Solid Oxide Fuel Cell Stack—Part 2: Numerical Analysis. Energies, 16(11), 4512. https://doi.org/10.3390/en16114512







